Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation

Abstract

Unsteady magneto-hydrodynamic heat and mass transfer analysis of hybrid nanofluid flow over stretching surface with chemical reaction, suction, slip effects and thermal radiation is analyzed in this problem. Combination of carbon nanotubes and silver nanoparticles are taken as hybrid nanoparticles and water is considered as base fluid. Using similarity transformation method, the governing equations are changed into system of ordinary differential equations. These equations together with boundary conditions are numerically evaluated by using finite-element method. The influence of various pertinent parameters on the profiles of fluids concentration, temperature, and velocity is calculated and the outcomes are plotted through graphs. The values of non-dimensional rates of heat transfer, mass transfer and velocity are also analyzed, and the results are depicted in tables. Temperature sketches of hybrid nanofluid intensified in both steady and unsteady cases as volume fraction of both nanoparticles rises.

1 Introduction

In modern days, the concept of nanofluids has turned into more extensive area for the research people owing to its enormous range of significances in biomedicine, heat exchangers, cooling of electronic devises, double windowpane, food, transportation, etc. To amplify the general fluids thermal conductivity such as ethylene glycol, water, kerosene, engine oils, we have to add different types of nanoparticles, like, graphene, silica, silver, gold, copper, alumina, carbon nanotubes, etc. to the base fluids. Good numbers of research articles are identified in survey of literature which deals the enhancement of the base fluids thermal conductivity by adding various types of nanoparticles [1,2,3,4,5,6]. Carbon-based nanomaterials can greatly contribute to environment sector and agriculture because of their enormous absorption potential due to their high surface area. Carbon-based nanomaterials are categorized into three kinds based on the shape of the nanoparticles, such as spheres or ellipsoidal shape, horn shape, and tube shape. CNTs are further categorized as single-wall carbon nanotubes (SWCNTs) and multi-wall carbon nanotubes (MWCNTs) depending on the number of concentric layers of rolled graphene sheets. Abbasi et al. [7] presented theoretical and experimental results on thermal conductivity of MWCNTs and TiO₂ nanoparticles and revealed that experimental values of thermal conductivity are higher than the theoretical values. Imtiaz et al. [8] detected higher temperature enhancement in MWCNTs than the SWCNTs in their work on heat transfer analysis of carbon nanotubes between rotating stretchable disks. Hayat et al. [9] deliberated flow and heat transfer analysis of carbon nanotubes–water-based nanofluid flow over a thin moving needle and noticed amplification in the sketches of velocity as volume fraction parameter rises. Estelle et al. [10] measured rheological and thermal conductivity properties of carbon nanotubes–water nanofluid in their experimental study and also measured the impact of volume fraction and type of base fluid on these properties. Hussain et al. [11] studied the influence of Darcy Forhheimer parameter on mass and heat transfer characteristics of carbon nanotubes-water-based nanofluid flow over flat plate/stretching cylinder by taking heterogeneous–homogeneous reactions. Sreedevi et al. [12] presented single and multi-walled carbon nanotubes heat transfer characteristics over a vertical cone with convective boundary conditions. Sudarsana Reddy et al. [13] deliberated Maxwell fluid flow between two stretchable rotating disks filled with carbon nanotubes-water nanofluid and detected reduction in the temperature of the both nanofluids with rising values of nanoparticle volume fraction parameter. Ahmadi et al. [14] presented flow and heat transfer characteristics of Bungiorno’s model nanofluid flow over a heated stretching sheet and identified augmentation in the values of Nusselt number with up surging values of Brownian motion parameter. Qasim et al. [15] perceived heat and mass transfer analysis of Bungiorno’s model nanofluid thin film flow over a stretching sheet and noticed reduction in the values of heat transfer rates as Brownian motion parameter values rises. Biglarian et al. [16] studied the influence of various types of nanoparticles and volume fraction of nanoparticles on heat transport and flow of unsteady nanofluid between parallel plates. Mahdy et al. [17] noticed elevation in the values of skin friction coefficient with rising values of Weissenberg number in their analysis on time-dependent hyperbolic tangential nanofluid flow over stretching wedge. Sheremet et al. [18] presented heat transfer analysis of Al₂O₃–water-based nanofluid flow in square inclined cavity with the left vertical wall is maintained sinusoidal temperature distribution. Hashim et al. [19] perceived the impact of thermophoresis and Brownian motion on mass and heat transport characteristics of Williamson nanofluid flow over a wedge.

“Hybrid nanofluids” are special kind of fluids having better thermal conductivity compared to the nanofluids and base fluids. Hybrid nanofluids have similar kind of applications as compared with the nanofluids. The superior thermal efficiency is predicted in hybrid nanofluids because of its better performance. Hybrid nanofluids are generated by dispersing two different types of nanoparticles in the base fluid. Megatif et al. [20] detected 38% intensification in the coefficient of heat transfer of CNT/TiO₂–water-based hybrid nanofluid with volume fraction of nanoparticles is 0.2 wt% in their experimental study. Sidik et al. [21] noticed that the hybrid nanofluids have higher thermal properties compared to the nanofluids with single nanoparticle and base fluids. Further, they observed that volume fraction and temperature are highly influencing the thermal properties of hybrid nanofluids. Ahammed et al. [22] experimentally investigated heat transport capabilities of alumina/graphene–water hybrid nanofluid flow in a minichannel. Rahman et al. [23] deliberated heat transfer capabilities of Al₂O₃/Cu–water hybrid nanofluid flow through an axisymmetric tube and perceived augmentation in rates of heat transfer as the values of volume fraction of hybrid nanofluid rises. Yarmand et al. [24] presented intensification in the heat transfer of hybrid nanofluid made up of platinum/graphene nanoplatelet–water at a four-sided microchannel whose boundaries are maintained with constant heat flux. Hussien et al. [25] experimentally examined the heat transport characteristics of GNPs/MWCNTs–water hybrid nanofluid flow through a minitube and detected 43.4% augmentation in the rate of heat transfer of hybrid nanofluid. Izadi et al. [26] presented lattice Boltzmann method (LBM) to analyze natural convection of hybrid nanofluid generated by Fe₂O₄–water over ┴-shaped cavity. Asadi et al. [27] studied MWCNT/Al₂O₃–water hybrid nanofluid heat transfer efficiency as a cooling fluid in energy management and thermal applications. Kumar et al. [28] theoretically and experimentally investigated heat transport enhancement of MWCNT/Al₂O₃–water nanofluid flow over minichannel heat sink and noticed intensification in the coefficient of heat transfer in the range of 30–35% as the hydraulic diameter of the decreases. Bhattad et al. [29] studied pressure drop and heat transfer characteristics of hybrid nanofluid made up of MWCNT/Al₂O₃–water on heat exchanger plate and detected 39.16% enhancement in heat transfer coefficient. Maddah et al. [30] perceived analysis of TiO₂/Al₂O₃–water-based hybrid nanofluid flow in turbulent flow regime. Akilu et al. [31] detected 6.9% augmentation in coefficient of heat transfer in their study taking carbon/ceramic copper oxide as hybrid nanoparticles and glycerol/ethylene glycol as base fluids. Waini et al. [32] deliberated analysis of Cu/Al₂O₃–water-based hybrid nanofluid over shrinking/stretching sheet and identified deterioration in the sketches of temperature with higher values of suction parameter. Recently, several authors [33,34,35,36,37,38,39,40,41] discussed about intensification in the values of heat transfer coefficient by taking different types of nanoparticles and hybrid nanoparticles over various geometries.

Careful observation on available literature reveals that no studies have reported to analyze the impact of slip effects and chemical reaction on mass and heat transport characteristics of magneto-hydrodynamic hybrid nanofluids prepared by considering MWCNTs/Silver as nanoparticles and water as base fluid over stretching sheet. The resultant equations are solved using finite-element method with Mathematica 10.0. The problem addressed in this analysis has immediate applications in generator cooling, transformer cooling, electronic cooling, etc.

2 Mathematical analysis of the problem

Consider unsteady, laminar, two-dimensional, MHD boundary layer heat and mass transfer of MWCNT/Ag–water-based hybrid nanofluid flow through a stretching sheet with slip effects as depicted in Fig. 1. Along the stretching surface and in the direction of flow the x-axis considered and y-axis is measured normal to it. U_w (x, t) is the velocity of the stretching sheet. A constant magnetic field of strength B₀ is applied normal to the plate. T_w and C_w are considered as sheet surface uniform temperature and concentration, and furthermore, T_∞ and C_∞ are taken as ambient fluid temperature and concentration, correspondingly. Under the above assumptions, the governing equations describing the momentum, energy and concentration in the presence of chemical reaction, slip effects and thermal radiation are given by Asadi et al. [27].

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial p}{\partial x} + \nu_{\text{hnf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\sigma B^{2} \left( t \right)}}{{\rho_{\text{hnf}} }}u$$

(2)

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{\text{hnf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\frac{{\partial q_{\text{r}} }}{\partial y}$$

(3)

$$\frac{\partial C}{\partial t} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} - C_{1} \left( {C - C_{\infty } } \right)$$

(4)

The following physical boundary conditions are

$$ \begin{aligned}& u = U_{\text{w}} + L\frac{\partial u}{\partial y},\,\quad v = v_{\text{w}} ,\quad T = T_{\text{w}} + k_{1} \frac{\partial T}{\partial y} , \quad \\ &C = C_{\text{w}} + k_{2} \frac{\partial C}{\partial y} ,\,\,{\text{at}}\,\,y = 0\end{aligned} $$

(5)

$$u \to 0,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \quad {\text{at}}\,\,y \to \infty$$

(6)

The subsequent similarity transformations are presented to streamline the mathematical study of the problem

$$ \begin{aligned}&\eta = y\sqrt {\frac{a}{{\nu_{\text{f}} \left( {1 - ct} \right)}}} ,\quad \psi = x\sqrt {\frac{{a\nu_{\text{f}} }}{1 - ct}f(\eta )} ,\quad \\ &\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\quad S\left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}\end{aligned} $$

(7)

Additionally,

$$\begin{aligned} U_{w} \left( {x, t} \right) & = \frac{b x}{1 - ct},\quad T_{\text{w}} \left( {x, t} \right) = T_{\infty } + \frac{{T_{0} U_{\text{w}} x}}{{\nu \left( {1 - ct} \right)^{{\frac{1}{2}}} }} \\ C_{\text{w}} \left( {x, t} \right) & = C_{\infty } + \frac{{C_{0} U_{\text{w}} x}}{{\nu \left( {1 - ct} \right)^{{\frac{1}{2}}} }},\quad B\left( t \right) = \frac{{B_{0} }}{{ \left( {1 - ct} \right)^{{\frac{1}{2}}} }} \\ \end{aligned}$$

(8)

By utilizing Rosseland estimation for radiation, the radiative heat flux q_r is demarcated as

$$q_{\text{r}} = - \frac{{4\sigma^{*} }}{{3K^{*} }}\frac{{\partial T^{4} }}{\partial y} = - \frac{{16\sigma^{*} T^{3} }}{{3K^{*} }}\frac{\partial T}{\partial y}$$

(9)

The transformed equations are

$$f^{\prime \prime \prime } + \frac{{A_{2} }}{{A_{1} }} f f^{{\prime \prime }} - \frac{{A_{2} }}{{A_{1} }}\left( {f^{{\prime }} } \right)^{2} - \frac{{A_{2} }}{{A_{1} }} \gamma \left\{ {f^{{\prime }} + \frac{\eta }{2}f^{{\prime \prime }} } \right\} - A_{1} M f^{{\prime }} = 0$$

(10)

$$\left( {1 + A_{4} R} \right)\theta^{{\prime \prime }} - \Pr \frac{{A_{3} }}{{A_{4} }} \frac{\gamma }{2} \left( {\eta \theta^{{\prime }} + 2\theta } \right) = 0$$

(11)

$$S^{\prime \prime } - {\text{Sc}} \frac{\gamma }{2} \left( { S^{{\prime }} + 2S} \right) - C_{\text{r}} \,{\text{Sc}} \,S = 0$$

(12)

The associated converted boundary conditions are

$$f\left( 0 \right) = V_{0} ,\,\quad f^{{\prime }} \left( 0 \right) = 1 + \lambda f^{\prime \prime } , \,\quad \theta \left( 0 \right) = 1 + \xi \theta^{{\prime }} , \quad S\left( 0 \right) = 1 + \beta S^{{\prime }}$$

(13)

$$f^{{\prime }} \left( \infty \right) \to 1, \quad \theta \left( \infty \right) \to 0,\quad S\left( \infty \right) \to 0$$

(14)

The associated non-dimensional parameters are defined as

$$\Pr = \frac{{v_{\text{f}} }}{{\alpha_{\text{f}} }},\quad \gamma = \frac{c}{a},\quad \lambda = L\left( {\frac{a }{2\nu }} \right),\quad M = \frac{{\sigma B_{0}^{2} }}{\rho a},\quad \xi = k_{1} \left( {\frac{a }{2\nu }} \right),$$

$$\beta = k_{2} \left( {\frac{a }{2\nu }} \right),\quad {\text{Sc}} = \frac{v}{{D_{\text{B}} }},\quad C_{\text{r}} = \frac{{C_{1} }}{a},\quad R = \frac{{16T_{\infty }^{3} \sigma^{*} }}{{3k^{*} k_{\text{f}} }},$$

$$ \begin{aligned}&A_{1} = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }},\quad \\ &A_{2} = \left( {1 - \phi_{2} } \right)\left[ {\left( {1 - \phi_{1} } \right) + \phi_{1} \left( {\frac{{\rho_{s1} }}{{\rho_{\text{f}} }}} \right) + \phi_{2} \left( {\frac{{\rho_{s2} }}{{\rho_{\text{f}} }}} \right)} \right],\end{aligned} $$

$$ \begin{aligned}& A_{3} = \left( {1 - \phi_{2} } \right)\left[ {\left( {1 - \phi_{1} } \right) + \phi_{1} \left( {\frac{{\left( {\rho c_{\text{p}} } \right)_{s1} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}} \right) + \phi_{2} \left( {\frac{{\left( {\rho c_{\text{p}} } \right)_{s2} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}} \right)} \right], \quad \\ &A_{4} = \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }},\end{aligned} $$

Fig. 1

Physical model and coordinate system

The density $\rho_{\text{hnf}}$, thermal conductivity $k_{\text{hnf}}$, dynamic viscosity $\mu_{\text{hnf}}$, and heat capacitance $\left( {\rho c_{\text{p}} } \right)_{\text{hnf}}$ of the hybrid nanofluid are specified by:

$$ \begin{aligned}&\mu_{\text{hnf}} = \frac{{\mu_{\text{f}} }}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }},\quad \\ &\rho_{\text{hnf}} = \left( {1 - \varphi_{2} } \right)\left[ {\left( {1 - \varphi_{1} } \right)\rho_{f} + \varphi_{1} \rho_{s1} } \right] + \varphi_{2} \rho_{s2} ,\end{aligned} $$

$$(\rho c_{\text{p}} )_{\text{hnf}} = \left( {1 - \varphi_{2} } \right)\left[ {\left( {1 - \varphi_{1} } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi_{1} \left( {\rho c_{\text{p}} } \right)_{s1} } \right] + \varphi_{2} \left( {\rho c_{\text{p}} } \right)_{s2} ,$$

$$k_{\text{hnf}} = k_{\text{nf}} *\left( {\frac{{k_{s2} + 2k_{\text{nf}} - 2\varphi_{2} \left( {k_{\text{nf}} - k_{s2} } \right)}}{{k_{s2} + 2k_{\text{nf}} + 2\varphi_{2} \left( {k_{\text{nf}} - k_{s2} } \right)}}} \right),$$

where

$$k_{\text{nf}} = k_{\text{f}} *\left( {\frac{{k_{s1} + 2k_{\text{f}} - 2\varphi_{1} \left( {k_{\text{f}} - k_{s1} } \right)}}{{k_{s1} + 2k_{\text{f}} + 2\varphi_{1} \left( {k_{\text{f}} - k_{s1} } \right)}}} \right)$$

The another object of this problem is to calculate skin-friction coefficient $(C_{\text{f}} )$, Nusselt number $( {\text{Nu}}_{x} )$, and Sherwood number $\left( {{\text{Sh}}_{x} } \right)$ and are given as

$$C_{{{\text{f}}x}} = \frac{{\tau_{\text{w}} }}{{\rho U_{\text{w}}^{2} }},\,\,{\text{Nu}}_{x} = \frac{{xq_{\text{w}} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)}}, \,\,{\text{Sh}}_{x} = \frac{{xq_{m} }}{{D_{\text{B}} \left( {C_{\text{w}} - C_{\infty } } \right)}}$$

(15)

where

$$\tau_{\text{w}} = \mu_{\text{hnf}} \left( {\frac{\partial u}{\partial y}} \right)_{y = 0} ,\quad q_{\text{w}} = \left. { - k_{\text{hnf}} \frac{\partial T}{\partial y}} \right|_{y = 0} ,\quad q_{m} = \left. { - D_{\text{B}} \frac{\partial C}{\partial y}} \right|_{y = 0} ,$$

(16)

Using the similarity variables, the above equations take the form

$$\text{Re}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} C_{{{\text{f}}x}} = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}f^{{\prime \prime }} \left( 0 \right),$$

$$\text{Re}^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{Nu}}_{x} = - \left( {1 + R} \right)A_{4} \theta^{{\prime }} \left( 0 \right) ,\quad \text{Re}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\text{Sh}}_{x} = - S^{{\prime }} \left( 0 \right)$$

(17)

where

$$\left( {\text{Re} = \frac{{xU_{\text{w}} }}{{v_{\text{f}} }}} \right)$$

represents the local Reynolds number.

3 Numerical solution of the problem

3.1 The finite-element method

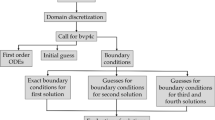
The variational finite-element process [42,43,44,45] is implemented to evaluate numerically above Eqs. (10)–(12) with boundary conditions (13)–(14). Compared with other numerical methods, finite element method is the better method to solve both ordinary and partial differential equations numerically. The steps involved in the finite element method are as follows.

3.1.1 Finite-element discretization

The whole domain is divided into a finite number of subdomains, which is called the discretization of the domain. Each subdomain is called an element. The collection of elements is called the finite-element mesh.

3.1.2 Generation of the element equations

• 1 From the mesh, a typical element is isolated and the variational formulation of the given problem over the typical element is constructed.

• 2 An approximate solution of the variational problem is assumed, and the element equations are made by substituting this solution in the above system.

• 3 The element matrix, which is called stiffness matrix, is constructed by using the element interpolation functions.

3.1.3 Assembly of element equations

The algebraic equations so obtained are assembled by imposing the inter-element continuity conditions. This yields a large number of algebraic equations known as the global finite-element model, which governs the whole domain.

3.1.4 Imposition of boundary conditions

The essential and natural boundary conditions are imposed on the assembled equations.

3.1.5 Solution of assembled equations

The assembled equations so obtained can be solved by any of the numerical techniques, namely the Gauss elimination method, LU decomposition method, etc. An important consideration is that of the shape functions which are employed to approximate actual functions.

For the solution of system of non-linear ordinary differential equation (10)–(12) together with boundary conditions (13)–(14), first we assume that

$$\frac{{{\text{d}}f}}{{{\text{d}}\eta }} = h$$

(18)

Equations (11)–(13) then reduce to

$$h^{{\prime \prime }} + \frac{{A_{2} }}{{A_{1} }}f h^{{\prime }} - \frac{{A_{2} }}{{A_{1} }}\left( h \right)^{2} - \frac{{A_{2} }}{{A_{1} }} \gamma \left\{ {h + \frac{{}}{2} h^{{\prime }} } \right\} - A_{1} M h = 0$$

(19)

$$\left( {1 + A_{4} R} \right)\theta^{\prime\prime} - \Pr \frac{{A_{3} }}{{A_{4} }}\frac{\gamma }{2}\left( {\theta^{{\prime }} + 2\theta } \right) = 0$$

(20)

$$S^{{\prime \prime }} - {\text{Sc}} \frac{\gamma }{2}\left( {S^{{\prime }} + 2S} \right) - C_{\text{r}} \,{\text{Sc}} \,S = 0$$

(21)

The boundary conditions take the form

$$\eta = 0, \quad f = V_{0} , \quad h = 1 + \lambda h^{{\prime }} , \,\quad \theta = 1 + \xi \theta^{{\prime }} , \quad S = 1 + \beta S^{{\prime }}$$

(22)

$$\eta \to \infty ,\quad h = 1,\quad \theta = 0,\quad S = 0$$

(23)

3.2 Variational formulation

The variational form associated with Eqs. (18)–(21) over a typical linear element $\left( {\eta_{e} , \eta_{e + 1} } \right)$ is given by

$$\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{1} \left( {\frac{{{\text{d}}f}}{{{\text{d}}\eta }} - h} \right){\text{d}}\eta = 0$$

(24)

$$\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{2} \left( {h^{{\prime \prime }} + \frac{{A_{2} }}{{A_{1} }}f h^{{\prime }} - \frac{{A_{2} }}{{A_{1} }}\left( h \right)^{2} - \frac{{A_{2} }}{{A_{1} }} \gamma \left\{ {h + \frac{{}}{2} h^{{\prime }} } \right\} - A_{1} M h} \right){\text{d}}\eta = 0$$

(25)

$$\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{3} \left( {\left( {1 + A_{4} R} \right)\theta^{{\prime \prime }} - \Pr \frac{{A_{3} }}{{A_{4} }}\frac{\gamma }{2}\left( {\theta^{{\prime }} + 2\theta } \right)} \right){\text{d}}\eta = 0$$

(26)

$$\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} w_{4} \left( {S^{{\prime \prime }} - {\text{Sc}} \frac{\gamma }{2}\left( {S^{{\prime }} + 2S} \right) - C_{\text{r}} \,{\text{Sc}}\,S} \right){\text{d}}\eta = 0$$

(27)

where $w_{1} ,\,w_{2} ,\, w_{3}$, and $w_{4}$ are arbitrary test functions and may be viewed as the variations in f, h, θ, and S, respectively.

3.3 Finite-element formulation

The finite-element model may be obtained from above equations by substituting finite-element approximations of the form

$$f = \mathop \sum \limits_{j = 1}^{2} f_{j} \psi_{j} ,\,\,\,\,h = \mathop \sum \limits_{j = 1}^{2} h_{j} \psi_{j} ,\,\,\,\,\theta = \mathop \sum \limits_{j = 1}^{2} \theta_{j} \psi_{j} ,\,\,\,\,S = \mathop \sum \limits_{j = 1}^{2} S_{j} \psi_{j} .$$

(28)

With, $w_{1} = w_{2} = w_{3} = w_{4} = \psi_{i} \left( {i = 1,2,3,4} \right).$

Here ψ_i are the shape functions for a typical element $\left( {\eta_{e} , \eta_{e + 1} } \right)$ and are defined as

$$\psi_{1}^{e} = \frac{{\left( {\eta_{e + 1} + \eta_{e} - 2 \eta } \right) \left( {\eta_{e + 1} - \eta } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }},\,\,\,\,\psi_{2}^{e} = \frac{{4\left( {\eta - \eta_{e} } \right)\left( {\eta_{e + 1} - \eta } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }},$$

$$\psi_{3}^{e} = \frac{{\left( {\eta_{e + 1} + \eta_{e} - 2 \eta } \right) \left( {\eta - \eta_{e} } \right)}}{{(\eta_{e + 1} - \eta_{e} )^{2} }},\,\,\,\,\eta_{e} \le \eta \le \eta_{e + 1} .$$

(29)

The finite element model of the equations thus formed is given by

$$\left[ {\begin{array}{*{20}l} {\left[ {K^{11} } \right]} \hfill & {\left[ {K^{12} } \right]} \hfill & {\left[ {K^{13} } \right]} \hfill & {\left[ {K^{14} } \right]} \hfill \\ {\left[ {K^{21} } \right]} \hfill & {\left[ {K^{22} } \right]} \hfill & {\left[ {K^{23} } \right]} \hfill & {\left[ {K^{24} } \right]} \hfill \\ {\left[ {K^{31} } \right]} \hfill & {\left[ {K^{32} } \right]} \hfill & {\left[ {K^{33} } \right]} \hfill & {\left[ {K^{34} } \right]} \hfill \\ {\left[ {K^{41} } \right]} \hfill & {\left[ {K^{42} } \right]} \hfill & {\left[ {K^{43} } \right]} \hfill & {\left[ {K^{44} } \right]} \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} f \hfill \\ h \hfill \\ \theta \hfill \\ S \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\left\{ {r^{1} } \right\}} \hfill \\ {\left\{ {r^{2} } \right\}} \hfill \\ {\left\{ {r^{3} } \right\}} \hfill \\ {\left\{ {r^{4} } \right\}} \hfill \\ \end{array} } \right]$$

where $[K^{mn} ]$ and $[r^{m} ]$ (m, n = 1, 2, 3, 4) are defined as

$$K_{ij}^{11} = \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta ,\,\,\,\,K_{ij}^{12} = - \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta ,\,\,\,\,K_{ij}^{13} = K_{ij}^{14} = 0, \,\,\,\,K_{ij}^{21} = 0.$$

$$\begin{aligned} K_{ij}^{22} & = \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - \frac{{A_{2} }}{{A_{1} }}\bar{f}_{1} \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - \frac{{A_{2} }}{{A_{1} }}\bar{f}_{2} \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{2} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ & \quad - \frac{1 }{2}\frac{{A_{2} }}{{A_{1} }} \bar{h}_{1} \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{1} \psi_{j} {\text{d}}\eta - \frac{1 }{2}\frac{{A_{2} }}{{A_{1} }}\bar{h}_{2} \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{2} \psi_{j} {\text{d}}\eta - \frac{{A_{2} }}{{A_{1} }} \gamma \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta \\ & \quad - \frac{{A_{2} }}{{A_{1} }}\frac{\eta }{2}\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - A_{1 } M\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta \\ \end{aligned}$$

$$K_{ij}^{23} = 0,\quad K_{ij}^{24} = 0,\quad K_{ij}^{31} = 0,\quad K_{ij}^{32} = 0$$

$$ \begin{aligned}K_{ij}^{33} &= \left( {1 + A_{4} R} \right)\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - \Pr \frac{{A_{3} }}{{A_{4} }}\frac{\gamma }{2}\eta \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ &\quad- \Pr \frac{{A_{3} }}{{A_{4} }} \gamma \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta ,\end{aligned} $$

$$K_{ij}^{34} = 0,\quad K_{ij}^{41} = 0, \quad K_{ij}^{42} = 0,\quad K_{ij}^{43} = 0$$

$$ \begin{aligned}K_{ij}^{44} &= \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \frac{{\partial \psi_{i} }}{\partial \eta }\frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta - {\text{Sc}} \frac{\gamma }{2}\mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \frac{{\partial \psi_{j} }}{\partial \eta }{\text{d}}\eta \\ &\quad- {\text{Sc}} \gamma \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta - Cr\, {\text{Sc}} \mathop \int \limits_{{\eta_{e} }}^{{\eta_{e + 1} }} \psi_{i} \psi_{j} {\text{d}}\eta\end{aligned} $$

$$ \begin{aligned}&r_{i}^{2} = 0,\quad r_{i}^{2} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,\quad\\ & r_{i}^{3} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} ,\quad r_{i}^{4} = - \left( {\psi_{i} \frac{{{\text{d}}\psi_{i} }}{{{\text{d}}\eta }}} \right)_{{\eta_{e} }}^{{\eta_{e + 1} }} .\end{aligned} $$

4 Results and discussion

The impact of slip effects on heat transport coefficient of MWCNT/Ag–water hybrid nanofluid flow over stretching sheet is analyzed in this analysis. Variations in the sketches of concentration, temperature, and velocity with respect to influenced parameters are calculated and plotted through graphs from Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 and 21. The thermophysical properties of nanoparticles and water are depicted in Table 1. Comparison of present numerical code with existing values is made and depicted in Table 2.

Fig. 2

The effect of (ϕ₁) on f′

Fig. 3

The effect of (ϕ₁) on θ

Fig. 4

The effect of (ϕ₁) on S

Fig. 5

The effect of (ϕ₂) on f′

Fig. 6

The effect of (ϕ₂) on θ

Fig. 7

The effect of (ϕ₂) on S

Fig. 8

The effect of (M) on f′

Fig. 9

The effect of (M) on θ

Fig. 10

The effect of (M) on S

Fig. 11

The effect of (R) on θ

Fig. 12

The effect of (Pr) on θ

Fig. 13

The effect of (Sc) on S

Fig. 14

The effect of (Cr) on S

Fig. 15

The effect of (V₀) on f′

Fig. 16

The effect of (V₀) on θ

Fig. 17

The effect of (V₀) on S

Fig. 18

The effect of (λ) on f′

Fig. 19

The effect of (λ) on θ

Fig. 20

The effect of (λ) on S

Fig. 21

The effect of (ξ) on θ

Table 1 Thermo-physical properties of water and nanoparticles

Table 2 Comparison of $\left( { - \theta^{{\prime }} \left( 0 \right)} \right)$ with the results of Waini et al. [32] for various values of (Pr) and $\phi_{1} = 0,\,\phi_{2} = 0$

Figures 2, 3, 4, 5, 6 and 7 reflect the sway of nanoparticle volume fraction parameters ϕ₁ and ϕ₂ on the sketches of concentration, temperature and velocity for both unsteady and steady cases of MWCNT/Ag–water hybrid nanofluid. The velocity scatterings depreciate with escalating values of both ϕ₁ and ϕ₂. Furthermore, this phenomenon is significantly higher in unsteady case than steady case of MWCNT/Ag–water hybrid nanofliud as shown in Figs. 2 and 5. With rising ϕ₁ and ϕ₂ values, the sketches of both concentration and temperature intensifies in both unsteady and state cases of hybrid nanofluid. Furthermore, this intensification is slightly higher in unsteady case than steady case of MWCNT/Ag–water hybrid nanofluid as shown in Figs. 3, 4, 6 and 7. This is due to the fact that with growing values of nanoparticle volume fraction parameters the thermal boundary layer thickness intensifies. This means the rate of heat transfer augments in the fluid area as the volume fraction of nanoparticle deteriorates.

We professed from Fig. 8 that the sketches of velocity declines in both unsteady and state case MWCNT/Ag–water-based hybrid nanofluid with escalating values of magnetic parameter (M) and this escalating tendency is slightly more in unsteady case than steady case MWCNT/Ag–water hybrid nanofluid. The scatterings of both temperature and concentration of unsteady and steady case MWCNT/Ag–water hybrid nanofluid with rising values of (M) is depicted in Figs. 9 and 10. The concentration and temperature scattering optimize with amplifying values of (M), and this amplifying nature is less in steady case MWCNT/Ag–water hybrid nanofluid than unsteady case. This is due to the fact that the presence of magnetic field in the flow creates a force known as the Lorentz force which acts as a retarding force, and consequently, the momentum boundary layer thickness decelerates throughout the flow region. To overcome from this Lorentz force fluid has to perform extra work, which intensifies the temperature of the fluid.

Thickness of thermal boundary layer with altered values of Radiation parameter (R) in both unsteady and steady case of MWCNT/Ag–water hybrid nanofluid is portrayed in Fig. 11 and detected that thermal boundary layer thickness upsurges with cumulating values of (R) in both cases. The intention for this nature is that, as the values of (R) rises, the Rosseland radiative absorptive k* diminutions. Consequently, the radiative heat flux $\frac{{\partial q_{\text{r}} }}{\partial y}$ values and the radiative rates of heat transfer into the liquid upsurges. This higher radiative heat transfer results the intensification in the thickness of thermal boundary layer. Moreover, this cumulating nature is slightly higher in unsteady case than steady case MWCNT/Ag–water hybrid nanofluid. Figure 12 shows the disparities in temperature scatterings with altered values of Prandtl number (Pr) for both unsteady and state case of MWCNT/Ag–water hybrid nanofluid. The temperature sketches worsen with up surging values of (Pr), and this phenomenon is marginally higher in steady case than unsteady case MWCNT/Ag–water-based hybrid nanofluid. Form the characterization of Prandtl number, values raises means thermal diffusivity of the liquid worsens which causes lesser heat dispersion. Subsequently, the distributions of thermal boundary layer thickness as well as temperature of nanoliquid are both deteriorate in the fluid region.

MWCNT/Ag–water-based hybrid nanofluid concentration scatterings shrinks in both unsteady and steady cases with rising values of Schmidt number (Sc), and this shrinking nature in concentration sketches is more in steady case than unsteady case of MWCNT/Ag–water-based hybrid nanofluid (Fig. 13). Figure 14 exhibits the significance of chemical reaction parameter (Cr) on concentration sketches in both steady and unsteady cases of MWCNT/Ag–water-based hybrid nanofluid and noticed deterioration in the profiles with cumulated values of (Cr). It is cleared that the deterioration is consequently higher in steady case than unsteady case hybrid nanofluid.

Figures 15, 16 and 17 show the disparities in the thickness of hydrodynamic, thermal and solutal boundary layers with altered values of suction parameter (V₀) in both unsteady and steady case MWCNT/Ag–water-based hybrid nanofluid. The thickness of hydrodynamic boundary layer escalates with amplifying values of (V₀) in both cases, whereas, the thickness of thermal and solutal boundary layers diminishes with higher values of (V₀). Furthermore, the escalating nature in the thickness of hydrodynamic boundary layer and diminishing nature in the thickness of both thermal boundary layer and solutal boundary layers is slightly more steady case than unsteady case of MWCNT/Ag–water-based hybrid nanofluid. The authenticity for this behavior is that sucking the warm liquid from liquid area definitely deteriorates the thickness of the concentration, thermal and hydrodynamic boundary layers, and consequently, all profiles of the liquid worsen.

The impact of velocity slip parameter $(\lambda )$ on scatterings of concentration, temperature and velocity is depicted in Figs. 18, 19 and 20. It is perceived from Fig. 18 that fluids velocity amplifies with improving values of $(\lambda )$ in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid. This is true because as the values of $(\lambda )$ rises the thickness of thermal boundary layer denigrates, consequently, velocity of the liquid grows. Nevertheless, the temperature and concentration sketches depreciate with intensifying values of $(\lambda )$ in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid. Furthermore, amplifying tendency in velocity sketches and depreciation in temperature, concentration scatterings is marginally more in steady case than unsteady case.

Figure 21 describes the sway of temperature slip parameter $(\xi )$ on thermal boundary layer thickness in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid. With up-surging values of $(\xi )$, the temperature sketches degenerates in both cases and this degenerating phenomenon is slightly more in steady case than unsteady case.

Tables 3 and 4 reveal the sway of pertinent parameters on non-dimensional rates of mass transfer, heat transfer, and velocity in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid. It is perceived that values of Sherwood number, Nusselt number, and skin friction coefficient decrease in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid as the values of $\phi_{1} ,\phi_{2} \,{\text{and }}\,M$ rises. With rise in the values of (Pr), the dimensionless values of (C_f) and (Nu_x) are intensifies in both steady and unsteady cases, while, the opposite trend is noticed in (Sh_x) values. As the values of (R) improves, the values of non-dimensional rates of mass transfer, heat transfer and rates of velocity values deteriorate in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid.

Table 3 Values of skin-friction coefficient $\left({f^{{\prime \prime}} \left(0 \right)} \right)$, Nusselt number $\left({- \theta^{{\prime}} \left(0 \right)} \right)$ and Sherwood number $\left({- S^{{\prime}} \left(0 \right)} \right)$

Table 4 Values of skin-friction coefficient $\left( {f^{{\prime \prime }} \left( 0 \right)} \right)$, Nusselt number $\left( { - \theta^{{\prime }} \left( 0 \right)} \right)$ and Sherwood number $\left( { - S^{{\prime }} \left( 0 \right)} \right)$

The values of (C_f), (Nu_x) and (Sh_x) upsurges in both steady and unsteady state hybrid nanofluid as the values of (Cr) intensifies. The non-dimensional rates of velocity, temperature, and concentration values are optimized as the values of (V₀) upsurges in unsteady state hybrid nanofluid as well as this behavior is similar in steady state hybrid nanofluid. The values of $\left( {f^{{\prime \prime }} \left( 0 \right)} \right)$ and $\left( { - \theta^{{\prime }} \left( 0 \right)} \right)$ diminish; however, the values of $\left( { - S^{{\prime }} \left( 0 \right)} \right)$ intensify with rising values of (Sc) in steady state case. The rates of velocity and Sherwood number values rise, whereas Nusselt number values diminish with (Sc) in unsteady case. As the values of $\left( \lambda \right)$ rise the values $\left( {f^{{\prime \prime }} \left( 0 \right)} \right)$ decelerate, whereas the values $\left( { - \theta^{{\prime }} \left( 0 \right)} \right)$ and $\left( { - S^{{\prime }} \left( 0 \right)} \right)$ intensify in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid. The non-dimensional rates of velocity and temperature values worsen with improved values of (ξ) in both unsteady and steady state cases. However, with the higher values of (ξ), the values of (Sh_x) rise in both cases.

5 Conclusion

The present study addressed MWCNT/Ag–water-based hybrid nanofluid heat and mass transfer analysis over a stretching sheet. The impact of velocity slip, temperature slip, chemical reaction, and thermal radiation on MWCNT/Ag–water-based hybrid nanofluid flow is also analyzed. We have investigated the sway of different crucial parameters through plots and tables. The most noteworthy findings are as follows:

• 1 We have noticed up to 22.4% enhancement in the rate of heat transfer from viscous fluid (water) to Ag–water-based nanofluid as the values of ϕ₁ rises from 0.01 to 0.1 and with fixed values of $M = 0.3, R = 1.0, V_{0} = 0.5, \Pr = 6.2, {\text{Cr}} = 0.1, \lambda = 0.5, \xi = 0.5, {\text{Sc}} = 1.0.$ However, 26.7% augmentation is perceived in the rate of heat transfer from Ag–water-based nanofluid to MWCNT/Ag–water-based hybrid nanofluid as the values of ϕ₁ and ϕ₂ increases from 0.01 to 0.1 and with fixed values of $M = 0.3, R = 1.0, V_{0} = 0.5, \Pr = 6.2, {\text{Cr}} = 0.1, \lambda = 0.5, \xi = 0.5, {\text{Sc}} = 1.0.$

• 2 As the volume fraction parameters of both nanofluids ϕ₁ and ϕ₂ intensifies the thickness of thermal boundary layer upsurges in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid.

• 3 Temperature and concentration of MWCNT/Ag–water-based hybrid nanofluid deteriorate as the values of (V₀) rise in both unsteady and steady cases.

• 4 Both temperature and concentration sketches worsen with rising values of velocity slip parameter $\left( \lambda \right)$ in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid.

• 5 Rising values of (M) lead to depreciation in the values of Sherwood number, Nusselt number, and skin friction coefficient.

• 6 The dimensionless rates of heat transfer shrinks with rising values of $\left( \xi \right)$ in both unsteady and steady cases of MWCNT/Ag–water-based hybrid nanofluid.