1 Introduction

With the shortage of traditional fossil energy supply, wind power, photovoltaic and other renewable energy have been developed and applied on a large scale. Renewable energy power generation has been achieved significant economic and environmental benefits in addressing energy shortages and climate change. However, due to the nature of intermittency and fluctuation of renewable power output, grid-connected renewable energy has impacted the power system's optimal operation, especially on preparing the reasonable power generation schedules by the dispatching decision-makers [1]. The main methods to cope with the random fluctuation of wind power and improve wind power's absorption capacity are improving wind power's prediction accuracy and configuring extensive capacity energy storage system along with the wind farms [2, 3].

The energy storage system has a fast-bidirectional regulation capability. When a wind farm equips with energy storage systems with a specific capacity, the wind farm has some regulation capacity to assist the peak shaving, frequency modulation, smooth output power, and control of the power's slope ramping rate grid. The wind power can actively participate in the power grid dispatch, improving the wind power absorption capacity and system operation economy [4, 5]. In [6], researchers examined transmission and energy storage interaction in high penetration of wind power. They proved that the location and capacity of energy storage configuration were essential to reduce generation cost. A two-stage stochastic optimization framework was proposed to determine the optimal size of energy storage in a hybrid wind-diesel system, and an efficient scenario reduction method was also proposed to reduce the computational burden [7]. By comparing the power generation performance of an independent wind or solar power plant with that of integrated wind, solar, and storage (IWSE) power plant, the researchers demonstrated that IWSE could provide lower generation costs, especially for systems with higher wind or solar power generation [8]. In [9], with the aid of energy storage technology, a general method for calculating the hybrid wind-solar power generation system's optimal capacity was proposed.

The above research used energy storage technology to solve the uncertainties well. Still, the risk tolerance of the system needs to be considered. At present, the standard risk measurement methods are utility functions, mean–variance, Value at Risk (\(VaR\)), and Conditional Value-at-Risk (\(CVaR\)) [10]. Because the monotonicity, sub-additivity, translation invariance, and positive homogeneity of \(CVaR\) meet the requirements of uniform risk measurement, it has attracted many scholars [11]. In [12], the researchers introduced the theory of \(CVaR\) and confidence method to describe the virtual power plant (VPP) operating uncertainty. A VPP routine scheduling optimization model was built to maximizing income. A novel approach was presented in [13] for look-ahead dispatch (LAD) considering large-scale wind power integration. An index designated the Conditional Value-at-Risk of wind power (\(CVaR-WP\)) was introduced to evaluate the risk of wind power adjustments. According to this model, the base points, participation factors, and flexible capacity of automatic generation control units were co-optimized. Based on the theory of \(CVaR\), an optimal bidding formula for risk aversion of demand-side resource aggregator was proposed for various flexible demand-side resources [14].

In this paper, based on the operation cost of the wind-storage combined system, \(CVaR\) method is used to deal with the possible risks caused by uncertainty. Based on \(CVaR\), we establish a dynamic economic dispatch model of the wind-storage combined system, which has considered AC optimal power flow. The scheduling strategy and risk assessment of the wind-storage combined dispatching system are studied using a revised IEEE 30-bus system and a revised IEEE 118-bus system.

In the remaining part of this paper, we describe the wind-storage combined system's operation cost in Section 2 In Section 3\(CVaR\) theory is introduced, then a dynamic economic dispatch model of the wind-storage combined system based on \(CVaR\) is proposed. Meanwhile, the model is transformed into a trackable MISOCP model. Case studies and numerical results are shown in Section 4, and finally, in Section 5, we conclude our research.

2 Operation cost of wind-storage combined system considering wind power uncertainty

2.1 Uncertainty of wind power output

When large-scale wind power connecting to the grid, the power system needs a new dispatching mode to deal with the uncertainty caused by wind power prediction errors. For medium and long-term planning and operation scheduling problems, Weibull distribution is often used to describe the average distribution of wind speed. However, this method does not consider the coupling between adjacent periods. In the view of the short-term day-ahead dynamic economic dispatch problem studied in this paper, to approach the actual situation as close as possible, the short-term forecast value of wind speed is used to predict wind farms' output. Therefore, it is necessary to study the error distribution of wind speed prediction.

The relationship between wind power and wind speed can be expressed by:

$${P}_{Wt}=\left\{\begin{array}{l}0\\ {k}_{1}v+{k}_{2}v\\ {P}_{r}\end{array}\begin{array}{ll}& \begin{array}{c}v\le {v}_{ci},v>{v}_{co}\\ {v}_{ci}<v<{v}_{r}\\ {v}_{r}\le v\le {v}_{co}\end{array}\end{array}\right.$$
(1)

Generally, the difference between the predicted \(\stackrel{-}{v}\) and actual \(v\) values of wind speed is defined as the prediction error \(\Delta v\) of wind speed, satisfied \(v=\stackrel{-}{v}+\Delta v\). The result shows that the prediction error of wind speed can be regarded as a random variable which obeys the normal distribution with the mean value of 0 and the standard deviation of \({\sigma }_{v}\) [15]. Then the probability of the actual wind speed can be expressed as

$${f}_{v}\left(v\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{v}}\mathrm{exp}\left[-\frac{{\left(v-\stackrel{-}{v}\right)}^{2}}{2{\sigma }_{v}^{2}}\right]$$
(2)

And its distribution function is:

$${D}_{Wt}\left(v\right)=\phi \left(\frac{v-\stackrel{-}{v}}{{\sigma }_{v}}\right)$$
(3)

Therefore, the distribution form of wind farm output can be obtained when the wind speed forecast value for the next \(T\) hours is obtained, and the standard deviation can be obtained using statistical methods.

2.2 Mathematical description of system operation cost

The influence of wind power's uncertainty on the economic dispatch problem is mainly about the balance of electric power. A wind-storage combined system helps deal with the impact of wind power uncertainty in power balance by charging in or discharging from the energy storage system according to the wind power error.

Since the capacity cost of the energy storage equipment is usually very high, it is impossible to configure the excessive capacity of energy storage to avoid all the wind power prediction errors. When the prediction error is too large for the energy storage system to meet the active power shortage, the power generation of thermal power units also need to be adjusted. Thus, thermal power units incur additional adjustment costs.

The total operating cost of the whole dispatching period \(T\) can be expressed as

$${\pi }_{G}=\sum_{t=1}^{T}\left\{\sum_{i=1}^{{S}_{G}}\left[{C}_{i,t}\left({P}_{Gi,t}\right)+{c}_{T}\times \left|\Delta {P}_{Gi,t}\right|\right]+\left.\sum_{i=1}^{{S}_{E}}{\lambda }_{ES}\left({u}_{ch,t,i}{P}_{ch,t,i}+{u}_{dis,t,i}{P}_{dis,t,i}\right)\right\}\right.$$
(4)

where the first item of (4) on the right side is the operation cost of the thermal power unit, including the operation cost under scheduling output and power adjustment cost; the second item is the charging and discharging cost of the energy storage system.

3 Dynamic economic dispatching optimization model for wind-storage combined system based on \(CVaR\)

Because of the uncertainty of wind power output and energy storage capacity limitation, operators face certain risks when deciding the dispatch schedules for power systems. The \(CVaR\) theory is applied to establish a dynamic economic dispatching optimization model to describe dispatching risk costs.

3.1 Mathematical description of \({\varvec{C}}{\varvec{V}}{\varvec{a}}{\varvec{R}}\)

\(CVaR\) is an improved risk analysis method proposed by Rockafeller and Uryasev extended from \(VaR\) [16, 17], which effectively overcomes the deficiency of \(VaR\) method in describing the degree of loss and its sub-additivity when adverse situations occur. \(CVaR\) is defined as the average loss value of a portfolio in a given period when the risk loss of the portfolio is higher than that of \(VaR\) at a given confidence level. It can be expressed by a mathematical formula as follows:

$$CVa{R}_{\beta }\left(X\right)=E\left[f\left(X,\xi \right)|f\left(X,\xi \right)>Va{R}_{\beta }\right]$$
(5)

where \(f\left(X,\xi \right)\) is the loss function of the portfolio \(X\), and \(\xi\) is a continuous random variable which may affect the loss function; \(E\left[f\left(X,\xi \right)|f\left(X,\xi \right)>Va{R}_{\beta }\right]\) denotes the expectation of \(f\left(X,\xi \right)\) under the condition of \(f\left(X,\xi \right)>Va{R}_{\beta }\).

Let the probability density of the random variable \(\xi\) be \(p\left(\xi \right)\), then the distribution function of the loss function \(f\left(X,\xi \right)\) is:

$$\phi \left(X,\alpha \right)={\int }_{f\left(X,\xi \right)\le \alpha }p\left(\xi \right)d\xi$$
(6)

For a given confidence level \(\beta\), the \(VaR\) of the portfolio \(X\) is:

$$Va{R}_{\beta }=\mathrm{min}\left\{\alpha \in R|\phi \left(X,\alpha \right)\ge \beta \right\}$$
(7)

The corresponding \(CVaR\) is expressed as:

$$CVa{R}_{\beta }=E\left[f\left(X,\xi \right)|f\left(X,\xi \right)>Va{R}_{\beta }\right]=\alpha +\frac{1}{1-\beta }{\int }_{\xi }\mathrm{max}\left\{f\left(X,\xi \right)-\alpha ,0\right\}p\left(\xi \right)d\xi$$
(8)

According to the above formulas, if the probability density function \(p\left(\xi \right)\) is known, \(Va{R}_{\beta }\) can be obtained, and then \(CVa{R}_{\beta }\) can be obtained as well.

The continuous \(CVaR\) can be calculated using (8). However, the calculation of \(CVaR\) cannot be satisfied with the condition of continuity in many cases. Therefore, it is necessary to deduce the calculation method of discrete \(CVaR\).

The discrete points in each probability scenario are used to replace the integral in (8). The calculation formula of discrete \(CVaR\) is as follows:

$$CVa{R}_{\beta }=E\left[f\left(X,\xi \right)|f\left(X,\xi \right)>Va{R}_{\beta }\right]=\alpha +\frac{1}{1-\beta }\sum_{n=1}^{N}{P}_{rn}{\left[f\left(X,\xi \right)-\alpha \right]}^{+}$$
(9)
$${\left[f\left(X,\xi \right)-\alpha \right]}^{+}=\mathrm{max}\left\{f\left(X,\xi \right)-\alpha ,0\right\}$$
(10)

where \(N\) denotes the total number of discrete segments and \({P}_{rn}\) is the probability of occurrence of paragraph \(n\).

According to [16], the following optimization problem is constructed to obtain the values of \(CVa{R}_{\beta }\) and \(Va{R}_{\beta }\):

$$\mathrm{min}f\left(X,z\right)=z+\frac{1}{1-\beta }\sum_{n=1}^{N}{P}_{rn}{\left[f\left(X,\xi \right)-z\right]}^{+}$$
(11)

The minimum value of the objective function \(f\left(X,z\right)\) is \(CVa{R}_{\beta }\), and the corresponding value of \(z\) is \(Va{R}_{\beta }\).

3.2 Dynamic economic dispatch model based on \({\varvec{C}}{\varvec{V}}{\varvec{a}}{\varvec{R}}\)

Wind power prediction error \(\Delta {P}_{Wt}\) is defined as\(\Delta {P}_{Wt}={\stackrel{\sim }{P}}_{Wt}-{P}_{Wt}\). Assuming that there are \(m\) possible scenarios for wind power prediction errors\(\Delta {P}_{Wt}\),\(\Delta {P}_{Wt}\in \left\{\Delta {P}_{Wt,1},\Delta {P}_{Wt,2},\cdots ,\Delta {P}_{Wt,m}\right\}\). The probability of occurrence of the scenario \(\Delta {P}_{Wt,i}\) is\(\mathrm{Pr}\left\{\Delta {P}_{Wt}=\Delta {P}_{Wt,i}\right\}={p}_{i}\),\({p}_{i}\ge 0\),\(\sum_{i=1}^{m}{p}_{i}=1\). Let \(p={\left({p}_{1},{p}_{2},\cdots ,{p}_{m}\right)}^{T}\) denote the probability vector of wind power prediction error.

\(CVaR\) is adopted as its measurement standard considering the aversion of system operation cost to wind power prediction error. Under \(CVaR\), the decision maker's goal is to find the optimal scheduled power generation to minimize \(CVa{R}_{\beta }\left({P}_{Gi,t}\right)\). Therefore, the equivalent description of the optimization problem can be as follows:

$$\begin{array}{cc}Minimize& CVa{R}_{\beta }\left({P}_{Gi,t}\right)=\alpha +\frac{1}{1-\beta }\sum_{i=1}^{m}{p}_{i}{\left[{\pi }_{G,i}-\alpha \right]}^{+}\end{array}$$
(12)

Subject to the following constraints (Eqs. 13–32):

  1. (1)

    AC Power flow equation constraints.

    The system needs to meet the active and reactive power balance at any instant.

    $${P}_{Gi,t}+{P}_{Wi,t}-\sum_{j\in {S}_{b}}\left[{e}_{i,t}\left({e}_{j,t}{G}_{ij}-{f}_{j,t}{B}_{ij}\right)+\left.{f}_{i,t}\left({f}_{j,t}{G}_{ij}+{e}_{j,t}{B}_{ij}\right)\right]={P}_{Di,t},i\in {S}_{b}\right.$$
    (13)
    $${Q}_{Ri,t}-\sum_{j\in {S}_{b}}\left[{f}_{i,t}\left({e}_{j,t}{G}_{ij}-{f}_{j,t}{B}_{ij}\right)-\left.{e}_{i,t}\left({f}_{j,t}{G}_{ij}+{e}_{j,t}{B}_{ij}\right)\right]={Q}_{Di,t},i\in {S}_{b}\right.$$
    (14)
    $$\begin{array}{c}{P}_{Gi,t}+\Delta {P}_{Gi,t}+{P}_{Wi,t}+\Delta {P}_{Wi,t}-{u}_{ch,t,i}{P}_{ch,t,i}+{u}_{dis,t,i}{P}_{dis,t,i}\\ -\sum_{j\in {S}_{b}}\left[{\stackrel{\sim }{e}}_{i,t}\left({\stackrel{\sim }{e}}_{j,t}{G}_{ij}-{\stackrel{\sim }{f}}_{j,t}{B}_{ij}\right)+{\stackrel{\sim }{f}}_{i,t}\left({\stackrel{\sim }{f}}_{j,t}{G}_{ij}+{\stackrel{\sim }{e}}_{j,t}{B}_{ij}\right)\right]={P}_{Di,t},i\in {S}_{b}\end{array}$$
    (15)
    $${Q}_{Ri,t}+\Delta {Q}_{Ri,t}-\sum_{j\in {S}_{b}}\left[{\stackrel{\sim }{f}}_{i,t}\left({\stackrel{\sim }{e}}_{j,t}{G}_{ij}-{\stackrel{\sim }{f}}_{j,t}{B}_{ij}\right)-\left.{\stackrel{\sim }{e}}_{i,t}\left({\stackrel{\sim }{f}}_{j,t}{G}_{ij}+{\stackrel{\sim }{e}}_{j,t}{B}_{ij}\right)\right]={Q}_{Di,t},i\in {S}_{b}\right.$$
    (16)
  2. (2)

    Constrain of the limitation of the generations and node voltage

    $${P}_{Gi}^{\mathrm{min}}\le {P}_{Gi,t}\le {P}_{Gi}^{\mathrm{max}},i\in {S}_{G}$$
    (17)
    $${Q}_{Ri}^{\mathrm{min}}\le {Q}_{Ri,t}\le {Q}_{Ri}^{\mathrm{max}},i\in {S}_{R}$$
    (18)
    $${P}_{Gi}^{\mathrm{min}}\le {P}_{Gi,t}+\Delta {P}_{Gi,t}\le {P}_{Gi}^{\mathrm{max}},i\in {S}_{G}$$
    (19)
    $${Q}_{Ri}^{\mathrm{min}}\le {Q}_{Ri,t}+\Delta {Q}_{Ri,t}\le {Q}_{Ri}^{\mathrm{max}},i\in {S}_{R}$$
    (20)
    $${\left({V}_{i}^{\mathrm{min}}\right)}^{2}\le {e}_{i,t}^{2}+{f}_{i,t}^{2}\le {\left({V}_{i}^{\mathrm{max}}\right)}^{2},i\in {S}_{b}$$
    (21)
    $${\left({V}_{i}^{\mathrm{min}}\right)}^{2}\le {\stackrel{\sim }{e}}_{i,t}^{2}+{\stackrel{\sim }{f}}_{i,t}^{2}\le {\left({V}_{i}^{\mathrm{max}}\right)}^{2},i\in {S}_{b}$$
    (22)
  3. (3)

    Ramping constraints of thermal power units

    $${P}_{Gi,d}\Delta t\le {P}_{Gi,t}-{P}_{Gi,t-1},i\in {S}_{G}$$
    (23)
    $${P}_{Gi,t}-{P}_{Gi,t-1}\le {P}_{Gi,u}\Delta t,i\in {S}_{G}$$
    (24)
    $${P}_{Gi,d}\Delta t\le {P}_{Gi,t}+\Delta {P}_{Gi,t}-{P}_{Gi,t-1}-\Delta {P}_{Gi,t-1},i\in {S}_{G}$$
    (25)
    $${P}_{Gi,t}+\Delta {P}_{Gi,t}-{P}_{Gi,t-1}-\Delta {P}_{Gi,t-1}\le {P}_{Gi,u}\Delta t,i\in {S}_{G}$$
    (26)
  4. (4)

    Energy storage constraints

    $${\alpha }_{\mathrm{min}}{P}_{ES,i}\le {P}_{ES,t,i}\le {\alpha }_{\mathrm{max}}{P}_{ES,i},i\in {S}_{E}$$
    (27)
    $${P}_{ES,t,i}={P}_{ES,t-1,i}+{u}_{ch,t,i}{P}_{ch,t,i}-{u}_{dis,t,i}{P}_{dis,t,i},i\in {S}_{E}$$
    (28)
    $${\beta }_{\mathrm{min}}{P}_{ES,i}\left(1/{\eta }_{ch,i}\right){u}_{ch,t,i}\le {P}_{ch,t,i}\le {\beta }_{\mathrm{max}}{P}_{ES,i}\left(1/{\eta }_{ch,i}\right){u}_{ch,t,i},i\in {S}_{E}$$
    (29)
    $${\beta }_{\mathrm{min}}{P}_{ES,i}{\eta }_{dis,i}{u}_{dis,t,i}\le {P}_{dis,t,i}\le {\beta }_{\mathrm{max}}{P}_{ES,i}{\eta }_{dis,i}{u}_{dis,t,i},i\in {S}_{E}$$
    (30)
    $${u}_{ch,t,i}+{u}_{dis,t,i}=1,i\in {S}_{E}$$
    (31)
    $${P}_{ES,1,i}={P}_{ES,T,i},i\in {S}_{E}$$
    (32)

3.3 Conversion of discrete variables

Because (4), (15), and (28) contain the production of 0–1 decision variables and continuous decision variables, it is difficult to solve the model directly. This model is transformed into mix-integer nonlinear programming (MINLP) problem using the big-M method [18] with adding auxiliary variables.

Introduce \({X}_{ch,t,i}\) and \({X}_{dis,t,i}\) to satisfy:

$${X}_{ch,t,i}={u}_{ch,t,i}{P}_{ch,t,i}$$
(33)
$${X}_{dis,t,i}={u}_{dis,t,i}{P}_{dis,t,i}$$
(34)

Then (4) can be transformed into

$${\pi }_{G}=\sum_{t=1}^{T}\left\{\sum_{i=1}^{{S}_{G}}\left[{C}_{i,t}\left({P}_{Gi,t}\right)+{c}_{T}\times \left|\Delta {P}_{Gi,t}\right|\right]+\left.\sum_{i=1}^{{S}_{E}}{\lambda }_{ES}\left({X}_{ch,t,i}+{X}_{dis,t,i}\right)\right\}\right.$$
(35)
$$s.t.\left\{\begin{array}{c}-M\left(1-{u}_{ch,t,i}\right)+{P}_{ch,t,i}\le {X}_{ch,t,i}\le \left(1-{u}_{ch,t,i}\right)+{P}_{ch,t,i}\\ -M{u}_{ch,t,i}\le {X}_{ch,t,i}\le M{u}_{ch,t,i}\\ -M\left(1-{u}_{dis,t,i}\right)+{P}_{dis,t,i}\le {X}_{dis,t,i}\le \left(1-{u}_{dis,t,i}\right)+{P}_{dis,t,i}\\ -M{u}_{dis,t,i}\le {X}_{dis,t,i}\le M{u}_{dis,t,i}\end{array}\right.$$
(36)

and (15), (28) can be transformed into

$$\begin{array}{c}{P}_{Gi,t}+\Delta {P}_{Gi,t}+{P}_{Wi,t}+\Delta {P}_{Wi,t}-{X}_{ch,t,i}+{X}_{dis,t,i}-{P}_{Di,t}\\ =\sum_{j\in {S}_{b}}\left[{\stackrel{\sim }{e}}_{i,t}\left({\stackrel{\sim }{e}}_{j,t}{G}_{ij}-{\stackrel{\sim }{f}}_{j,t}{B}_{ij}\right)+{\stackrel{\sim }{f}}_{i,t}\left({\stackrel{\sim }{f}}_{j,t}{G}_{ij}+{\stackrel{\sim }{e}}_{j,t}{B}_{ij}\right)\right],i\in {S}_{b}\end{array}$$
(37)
$${P}_{ES,t,i}={P}_{ES,t-1,i}+{X}_{ch,t,i}-{X}_{dis,t,i},i\in {S}_{E}$$
(38)

So far, the dynamic economic dispatch model based on \(CVaR\) is MINLP as:

$$\left\{\begin{array}{c}(12)\\ s.t.(13)-(14),(16)-(27),(29)-(38)\end{array}\right.$$
(39)

The nonlinearity of AC power flow constraints in (39) makes the MINLP is still challenging to solve.

3.4 Second-order cone description of optimization model

By using the second-order cone description technique [19], the MINLP (39) can be transformed into a second-order cone programming (SOCP) model, which can be solved efficiently.

System (39) is a nonconvex quadratic optimization problem. However, quite significantly, all the nonlinearity and non-convexity comes from one of the following three forms involved in AC power flow constraints:

  1. 1)

    \({e}_{i}^{2}+{f}_{i}^{2}={\left|{V}_{i}\right|}^{2}\),

  2. 2)

    \({e}_{i}{e}_{j}+{f}_{i}{f}_{j}=\left|{V}_{i}\right|\left|{V}_{j}\right|\mathrm{cos}\left({\theta }_{i}-{\theta }_{j}\right)\),

  3. 3)

    \({e}_{i}{f}_{j}-{f}_{i}{e}_{j}=-\left|{V}_{i}\right|\left|{V}_{j}\right|\mathrm{sin}\left({\theta }_{i}-{\theta }_{j}\right)\).

To capture this nonlinearity, variables \({c}_{ii}\), \({c}_{ij}\) and \({s}_{ij}\) for each bus \(i\) and each transmission line \((i,j)\) as \({c}_{ii}={e}_{i}^{2}+{f}_{i}^{2}\), \({c}_{ij}={e}_{i}{e}_{j}+{f}_{i}{f}_{j}\), and \({s}_{ij}={e}_{i}{f}_{j}-{f}_{i}{e}_{j}\). These variables satisfy the relation \({c}_{ij}^{2}+{s}_{ij}^{2}={c}_{ii}{c}_{jj}\). By replacing the variables, (13)–(14) and (21) can be transformed as follows:

$${P}_{Gi,t}+{P}_{Wi,t}-{P}_{Di,t}={G}_{ii}{c}_{ii}+\sum_{j\in {S}_{b}}\left({G}_{ij}{c}_{ij}-{B}_{ij}{s}_{ij}\right),i\in {S}_{b}$$
(40)
$${Q}_{Ri,t}-{Q}_{Di,t}=-{B}_{ii}{c}_{ii}+\sum_{j\in {S}_{b}}\left(-{B}_{ij}{c}_{ij}-{G}_{ij}{s}_{ij}\right),i\in {S}_{b}$$
(41)
$${\left({V}_{i}^{\mathrm{min}}\right)}^{2}\le {c}_{ii}\le {\left({V}_{i}^{\mathrm{max}}\right)}^{2},i\in {S}_{b}$$
(42)
$${c}_{ij}={c}_{ji},{s}_{ij}=-{s}_{ji}$$
(43)
$${c}_{ij}^{2}+{s}_{ij}^{2}={c}_{ii}{c}_{jj}$$
(44)

Similarly, (15), (37), and (22) can be transformed as follows:

$${P}_{Gi,t}+\Delta {P}_{Gi,t}+{P}_{Wi,t}+\Delta {P}_{Wi,t}-{X}_{ch,t,i}+{X}_{dis,t,i}-{P}_{Di,t}={G}_{ii}{\stackrel{\sim }{c}}_{ii}+\sum_{j\in {S}_{b}}\left({G}_{ij}{\stackrel{\sim }{c}}_{ij}-{B}_{ij}{\stackrel{\sim }{s}}_{ij}\right),i\in {S}_{b}$$
(45)
$${Q}_{Ri,t}+\Delta {Q}_{Ri,t}-{Q}_{Di,t}=-{B}_{ii}{\stackrel{\sim }{c}}_{ii}+\sum_{j\in {S}_{b}}\left(-{B}_{ij}{\stackrel{\sim }{c}}_{ij}-{G}_{ij}{\stackrel{\sim }{s}}_{ij}\right),i\in {S}_{b}$$
(46)
$${\left({V}_{i}^{\mathrm{min}}\right)}^{2}\le {\stackrel{\sim }{c}}_{ii}\le {\left({V}_{i}^{\mathrm{max}}\right)}^{2},i\in {S}_{b}$$
(47)
$${\stackrel{\sim }{c}}_{ij}={\stackrel{\sim }{c}}_{ji},{\stackrel{\sim }{s}}_{ij}=-{\stackrel{\sim }{s}}_{ji}$$
(48)
$${\stackrel{\sim }{c}}_{ij}^{2}+{\stackrel{\sim }{s}}_{ij}^{2}={\stackrel{\sim }{c}}_{ii}{\stackrel{\sim }{c}}_{jj}$$
(49)

To sum up, (39) is transformed into a mixed-integer second-order conic programming (MISOCP) model as follows:

$$\left\{\begin{array}{l}(12)\\ s.t.(17)-(21),(23)-(27),\\ (29)-(36),(38),(40)-(49)\end{array}\right.$$
(50)

This MISOCP model can be solved by GUROBI [20] efficiently.

4 Numerical results

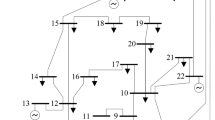
The numerical results on a revised IEEE 30-bus system and a revised IEEE 118-bus system are present. The revised IEEE 30-bus system has 5 units, 41 lines, and 2 wind farms with each capacity of 100 MW at node #10 and #15, respectively. The revised IEEE 118-bus system has 54 units and 186 lines, and 4 wind farms with each capacity of 160 MW at node #21, #64, #87, and #105, respectively. For each wind farm, one energy storage equipment is installed as a wind-storage combined system, and the capacity of each energy storage is set to 30% of the wind farm's capacity. The network data of the test system is extracted from MATPOWER 5.1. The revised IEEE 30-bus system's unit data is from [21], and the revised IEEE 118-bus system is from [1]. The maximum ramping rate per minute of each thermal power unit is set at 1% of the maximum output of the unit and \({c}_{T}\) is 74.3 $/MW. Detailed parameters of the wind farm and energy storage system list in Table 1

Table 1 Parameters of The Wind Farm and Energy Storage System
Full size table

Figures 1 and 2 show the load values and the wind speed prediction values of each farm of the IEEE 30- bus system and IEEE 118-bus system, respectively. Assume that the power prediction errors of wind farms obey the normal distribution of \(\sigma \text{=}10\text{\%}\mu\). The dispatching period is \(T=24\), and the time interval is \(\Delta t=1h\). The number of initial uncertain scenes obtained by the Monte Carlo simulation is 1000. For reducing the computational burden and improve the computational speed, the simultaneous backward reduction method described in [22] is used to reduce the number of scenarios to 10.

Fig. 1
figure 1

Load and wind speed prediction data for the revised IEEE 30-bus system

Full size image
Fig. 2
figure 2

Load and wind speed prediction data for the revised IEEE 118-bus system

Full size image

All simulations are done with a personal computer with 3.4-GHz CPU and 8 GB of RAM. The proposed method is implemented in MATLAB R2017a by using YALMIP R20181012 [23] package as s modeling software and GUROBI 7.0 [20] as a solver.

The formulation analysis in this section is divided into three parts. Section 4.1 shows that \(CVaR\) method is useful in estimating the risk of dispatch cost by analyzing the influence of confidence level on scheduling results, and decision-makers can make different dispatch schedules according to their risk tolerance. Section 4.2 determines the optimal energy storage capacity for operation by analyzing the impact of energy storage capacity on scheduling results. Moreover, the optimal initial energy storage state is given in section 4.3 by analyzing the relationship between the initial energy storage state and scheduling results.

4.1 Confidence level's impact on scheduling results and analysis

The confidence level \(\beta\) can reflect the level of risk aversion of decision-makers. Note that the system (50) is a standard dynamic economic dispatch model when the objective function (12) is replaced with minimizing (4). To study the influence of \(\beta\) on the total dispatch cost risk value, \(\beta =\mathrm{0.1,0.2},\cdots ,0.9\) of the system (50) and the standard dynamic economic dispatch model are selected to be solved on the IEEE 30-bus system and IEEE 118-bus system, respectively. The \(VaR\) and \(CVaR\) values of the total dispatch cost at \(\beta =\mathrm{0.1,0.2},\cdots ,0.9\) with increasing step 0.1 are shown in Figs. 3 and 5. The entire dispatch cost of the standard dynamic economic dispatch model is $92,567.52 and $1,232,000, respectively, which are higher than that under \(\beta =\mathrm{0.1,0.2},\cdots ,0.9\). Therefore, to a certain extent, it shows that the \(CVaR\) method can effectively reduce the economic loss of operation and reduce the waste of resources when errors occur in the predicted output value.

Fig. 3
figure 3

The relation curve between confidence level and total dispatch cost risk value for the revised IEEE 30-bus system

Full size image

Figure 3 shows the relationship between the confidence level and total dispatch cost risk value in the IEEE 30-bus system. In detail, Table 2 shows the actual cost values and the energy storage cost under different \(\beta\). Moreover, Fig. 4 illustrates the units' schedule under \(\beta =0.2\) for the IEEE 30-bus system as an instant. With \(\beta\) increasing, the total dispatch cost is increasing too. The reason is that the degree of confidence level represents the degree of risk aversion of the decision-makers. In other words, the bigger the value of \(\beta\), the more conservative the decision-makers make since they are willing to avoid possible higher losses.

Table 2 Units power cost and energy storage equipment cost under different confident levels of the revised IEEE 30-bus system
Full size table
Fig. 4
figure 4

Economic dispatch schedule under \(\beta =0.2\) for the revised IEEE 30-bus system

Full size image

At any confidence level, \(CVaR\) value of the total dispatch cost is higher than the \(VaR\) value, because \(CVaR\) represents the potential average loss beyond the \(VaR\) value. Therefore, it is more appropriate to use \(CVaR\) method to describe the magnitude of risk. When \(\beta\) increases with the same step, both \(VaR\) and \(CVaR\) increase, but the rate of increase and their difference decrease gradually. The reason is due to the normal distribution of uncertainty prediction errors of wind speed. With the rise of \(\beta\), the system's potential risk gradually moves to the tail of the normal distribution, which leads to the increase of the expected dispatch cost, while their growth rates slow down.

Besides, the confidence level can also be used as a safety index for the system's operation. The higher confidence level indicates that the system requires higher security than that of a lower confidence level. The total dispatch cost of the system increases higher, while the system's economy is getting worse.

Therefore, the decision-maker can determine the system's scheduling scheme according to his risk tolerance using the proposed dynamic economic dispatch model based on \(CVaR\).

Figure 5 shows the relationship between the confidence level and total dispatch cost risk value in the IEEE 118-bus system. The higher the confidence level \(\beta\) is, the bigger the dispatch cost risk value is. It is consistent with the results in the case of the IEEE 30-bus system mentioned above.

Fig. 5
figure 5

The relation curve between confidence level and total dispatch cost risk value for the revised IEEE 118-bus system

Full size image

4.2 Impact of operational energy storage capacity on scheduling results and analysis

The energy storage system sometimes cannot operate at full capacity because of overhaul or other operating conditions. Therefore, we need to consider the impact of different operational energy storage capacity on the scheduling results.

Under the condition of \(\beta =0.3\) and \(\beta =0.7\), the operational energy storage capacity is set to 20%, 40%, 60%, and 80% of the total energy storage capacity, respectively. The simulation results show that the \(CVaR\) of total dispatch cost varies with the operational energy storage capacity involved in the operation at the IEEE 30-bus system and the IEEE 118-bus system, respectively, in Figs. 6 and 7.

Fig. 6
figure 6

The relation curve between operational energy storage capacity and \(CVaR\) of total dispatch cost for the revised IEEE 30-bus system

Full size image
Fig. 7
figure 7

The relation curve between operational energy storage capacity and \(CVaR\) of total dispatch cost for the revised IEEE 118-bus system

Full size image

Figure 6 shows how \(CVaR\) of total dispatch cost changes with the operational energy storage capacity, named as ration of total energy storage capacity, in the IEEE 30-bus system. As the operating energy storage capacity increases, the \(CVaR\) of total dispatch cost decreases gradually at first and then tends to be stable. That is because the operational capacity is too small to meet wind power's prediction error at first. As a result, the thermal power units must adjust their output to meet the unbalanced load caused by wind power's prediction error. The power adjustment cost of the thermal power units are much higher than the charging and discharging cost of energy storage (\({c}_{T}>{\lambda }_{ES}\)). Therefore, the lower the capacity of energy storage in operation is, the higher \(CVaR\) of total dispatch cost is.

Figure 7 shows how \(CVaR\) of total dispatch cost changes with the ratio of total energy storage capacity in the revised IEEE 118-bus system. The changing trend of energy storage capacity with \(CVaR\) of total dispatch cost is the same as that of the revised IEEE 30-bus system.

As shown in Figs. 6 and 7, when the energy storage system's operational capacity is more than 80% of the total energy storage capacity, \(CVaR\) of total dispatch cost reaches the minimum values. Therefore, it is most appropriate to configure the energy storage capacity in operation no less than 80% of the total energy storage capacity.

Comparing \(CVaR\) of total dispatch cost in \(\beta =0.3\) and \(\beta =0.7\), \(CVaR\) of total dispatch cost in \(\beta =0.3\) is always lower than that in \(\beta =0.7\). It is consistent with the conclusion in section 4.1

4.3 Impact of initial/final energy storage state on scheduling results and analysis

The operation of energy storage equipment often requires the same initial and final state. To study the impact of initial and final energy storage state on scheduling results, under the condition of \(\beta =0.3\) and \(\beta =0.7\), the initial/final energy storage state is set to 40%, 50%, 60%, 70%, 80%, and 90% of the energy storage capacity, respectively. The simulation results show that the \(CVaR\) of total dispatch cost varies with the initial/final energy storage state at the revised IEEE 30-bus system and revised IEEE 118-bus system, respectively, as shown in Figs. 8, 9.

Fig. 8
figure 8

The relation curve between the initial/final energy storage state and \(CVaR\) of total dispatch cost for the revised IEEE 30-bus system

Full size image
Fig. 9
figure 9

The relation curve between the initial/final state of energy storage and \(CVaR\) of total dispatch cost for the revised IEEE 118-bus system

Full size image

Figure 8 shows that \(CVaR\) s of total dispatch costs are almost flat when the initial/final energy storage states are between 40 and 60% of the total capacity. However, when the initial/final state of energy storage exceeds 60% of the total energy storage capacity, the \(CVaR\) of total dispatch cost increases sharply.

Figure 9 shows the relationship between the initial capacity of total capacity and \(CVaR\) of total dispatch cost in the 118-bus system. The general trend of change is consistent with that of the 30-bus system. Therefore, it is better to set the initial/final state of an energy storage system between 40 and 60% of the total energy storage capacity.

Similarly, comparing \(CVaR\) of total dispatch cost in \(\beta =0.3\) and \(\beta =0.7\), the \(CVaR\) of total dispatch cost in \(\beta =0.3\) is always lower than that in \(\beta =0.7\). It is consistent with the conclusion in section 4.1 too.

5 Conclusions

In this paper, we propose a dynamic economic dispatch model of the wind-storage combined system based on \(CVaR\), which is hard to solve. We use the big-M method and second-order cone description technique to transform the original model into MISOCP. By comparing the dispatch costs of the IEEE 30-bus system and the IEEE 118-bus system at different confidence levels under different cases, it is shown that \(CVaR\) method can adequately estimate the dispatching risk and help decision-makers to make reasonable dispatch schedules according to their risk tolerance. Also, through the analysis of dispatch cost risk under different operational storage capacities and initial/final states, the lowest risk can be obtained when the storage capacity involved in the operation is not less than 80% of the total energy storage capacity, and the initial/final state is between 40 and 60% of the total energy storage capacity.