1 Introduction

Bingham material is a viscoplastic fluid retaining a yield strength. Toothpaste is a well-known example that won’t be fed until a certain pressure is employed in the tube. Enormous samples of Bingham fluid is observed in many geological and industrial materials such as handling of slurries, concrete paste, mudflow, lava, ceramic paste, painting oil, chocolate, etc. On the other hand, the MHD (magnetohydrodynamic) flow nature has applications in multiple flow-governing devices like- electrostatic precipitation, MHD power generators, accelerators, aerodynamic heating, etc., in the polymer connected technology and the petroleum industry.

The Bingham fluid was first introduced by Bingham [1], which shows a non-Newtonian behavior with a bi-viscous rheological model presented in [2]. Several theoretical studies were found in the literature discussing the Bingham fluid flow in different process conditions that address the channel flow. In this regard, the axisymmetric flow feature of Bingham fluid with the consideration of suddenly imposing an unchangeable pressure gradient was analyzed here [3]. On the basis of Couette-Poiseuille flow under slip conditions, a study on Bingham fluid was carried out by Chen and Zhu [4]. It was found that with the coexistence of double shear flow and plug flow, the increment in the slip parameter reveals an opposite nature for the shear rate and plug flow criteria. Analysis of the simultaneous approach of normal-mode of classical type and the approach of a non-modal kind on Bingham–Poiseuille flow was presented in [5]. Analytically, Eight different forms of velocity profiles were gained [6] by observing axially-orienting Couette-Poiseuille flow of Bingham fluid. By developing a single equation in pressure gradient explicitly for the flow of Bingham plastic through an annulus, an analytical solution was discussed, see [7]. A step was taken to inquire about a non-modal approach to Bingham plastic flow [8]. It was reported that the disturbance of non-axisymmetric phenomena has the critical energy Reynolds number in the lowest specification. The flow of dissipative fluid with the properties under temperature dependency was investigated [9]. As expected, this study observed that the thermal buoyancy parameter causes a hike in velocity as well as temperature. In [10], the start-up flow of Bingham plastic was presented by performing verification with small yield stress values. The analysis of the channel flow of Bingham rheological fluid by introducing a relaxation parameter with the aid of Lattice Boltzmann Method has performed by Ortega [11]. A semi-analytical solution based study of Bingham rheology with linearly varying yield stress along with plastic viscosity was presented in [12]. The use of a concentric annulus was conducted, see [13], to investigate velocity profiles of the analytical type of the pressure-driven flow of Bingham fluid. Some studies are recently performed where Bingham fluid was considered in different cases of the flow systems [14,15,16].

In order to manipulate the fluid flow in some real-life problems, the MHD effect is required to introduce. Relating to the MHD effect on Bingham fluid flow, the impact by raising the Hall and Ion-slip currents were theoretically discussed in several recent studies based on different process conditions of channel flow [17,18,19]. The Hall impact on MHD Couette flow of Bingham fluid along with the cases of suction, injection, Joule heating, viscous dissipation was analyzed in [20]. It was concluded that the velocity components fall when the yielding stress develops quantitatively, and viscosity influences the steady-state significantly. The MHD dissipative flow of Bingham fluid by concerning steady feature over a rotating porous disk with Ion-slip and Hall currents in a rotating system was considered in [21], along with that, the shear stress coefficient and the heat transfer coefficient were calculated. The Numerical simulation for Bingham fluids was pointed out in [22] while the Taylor Couette flows through two concentric cylinders are considered. Squeezed vortices were noticed by the influence of yield stress in the direction of the inner cylinder. The numerical determination of MHD flow through parallel plates for Bingham material with Hall current, viscous dissipation, and without suction was performed [23]. MHD Ciliary propulsion flow of microscopic organisms with Hall and Ion-slip effects was studied in [24]. It was mentioned that the development of the magnetic parameter tends down the bolus shaped by the flow.

The suction, injection, Joule heating, Hall current, Ion-slip current, surface heat flux are the possible effects that could be considered in Bingham material flow in channels with different wall boundary conditions as well as different types of plates like the stationary plate, moving plate, porous plate, Riga plate, rotating, and oscillatory plate, etc. [25,26,27]. All the presented studies concerned one or more of the above effects with one of the mentioned channel conditions for Bingham material flow. However, the MHD effect on the Bingham fluid in channels is yet to understand in different process conditions.

The present research focuses on the MHD effect personalized by Hall and Ion-slip currents. Thus, considering all the above base studies, our specific purpose is to investigate the flow characteristics numerically for time-dependent MHD Bingham material flow between two horizontal parallel plates where the upper plate is assumed to have a constant velocity. The generalized Ohm’s law [28] appears in the momentum balance, including both Hall and Ion-slip currents. Also, the Couette flow is considered when a pressure gradient drives the flow. Furthermore, Energy dissipation and uniform magnetic field are involved. The explicit FDM (Finite Difference Method) framework was utilized to solve the non-isothermal problem equations. The obtained results are plotted and shown graphically. Section 2 describes the physical model and its mathematical illustration. Section 3 describes the representation of shear stress and Nusselt number based on the present problem. The numerical technique is concisely presented in Sect. 4. Section 5 presents the outcome of the stability analysis for this problem. The results are discussed in Sect. 6 in five subsections-Mesh Sensitivity Test, Code Validation Test, Time Sensitivity Test (Steady-State Solutions), Validity Test (Comparison), and Effect of Magnetohydrodynamic Parameters.

2 Mathematical formulation of the problem

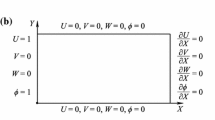
The transient MHD Bingham fluid is considered to be streaming between two infinitely elongated horizontal parallel plates planned at \(y = \pm h\,\) planes also ranging from \(x = 0\,\,{\text{to}}\,\,\infty \,\) and from \(\,{\text{z = 0}}\,\,{\text{to}}\,\,\infty\). The upper plate is set to be occupied a fixed velocity \(U_{0}\) and lower one is planned at motionless condition, while two individual unchanged temperatures \(T_{2} \,{\text{and}}\,\,T_{1} \,\) respectively are specified for both the upper and lower plates under the conditioning of \(T_{2} > T_{1}\). Such Couette-Poiseuille flow was studied in Ref. [20, 21]. Along the X-axis, a fixed pressure gradient \(\frac{{{\text{d}}p}}{{{\text{d}}x}}\) is employed on the fluid, also an external magnetic field \(B_{0}\) of uniform nature is acted vertical to the X-axis. The generation of secondary velocity at the Z-axis direction is expectedly happening due to the Hall and Ion-slip currents. The velocity vector for the governing fluid is given as, \({\mathbf{q}} = u{\mathbf{i}} + v{\mathbf{j}} + w{\mathbf{k}}\). Figure 1 presents the schematic flow configuration together with the boundary conditions of the problem.

Fig. 1
figure 1

The schematic flow configuration

Full size image

The generalized Ohm’s law describes the current density \({\mathbf{J}}\), with the electric field \({\mathbf{E}}\), whose representation follows:

$${\mathbf{J}} = \sigma \left[ {{\mathbf{E}} + {\mathbf{q}} \wedge {\mathbf{B}} - \beta \left( {{\mathbf{J}} \wedge {\mathbf{B}}} \right) + \frac{{\beta_{e} \beta_{i} }}{{B_{0} }}\left( {{\mathbf{J}} \wedge {\mathbf{B}}} \right) \wedge {\mathbf{B}}} \right]$$

where \(\sigma\) is the fluid’s electric conductivity, \(\beta_{e}\) is the Hall parameter and \(\beta_{i}\) is the Ion-slip parameter. The simultaneous expressions of the Hall and Ion-slip currents were studied from Ref. [21]. The simplified form of the above equation is:

$$\left( {{\mathbf{J}} \wedge {\mathbf{B}}} \right) = \frac{{\sigma_{{\text{e}}} B_{0} }}{{\alpha_{{\text{e}}}^{2} + \beta_{{\text{e}}}^{2} }}\left[ {\left( {\beta_{e} u - \alpha_{e} w} \right){\mathbf{i}} + \left( {\alpha_{e} u + \beta_{e} w} \right){\mathbf{k}}} \right];\,\,{\text{where}}\,\,\alpha_{e} = 1 + \beta_{i} \beta_{e} .$$

Thus the momentum equation, for this study, takes the following vector form:

$$\frac{{\partial {\mathbf{q}}}}{\partial t} + ({\mathbf{q}}.{\mathbf{\nabla }}){\mathbf{q}} = - \frac{1}{\rho }{\mathbf{\nabla }}p + \frac{1}{\rho }\nabla .\left( {\mu \nabla {\mathbf{q}}} \right) + \frac{1}{\rho }\left( {{\mathbf{J}} \wedge {\mathbf{B}}} \right)$$

Here, for Bingham fluid, the viscosity \(\mu\) is not a constant, as it is a non-Newtonian fluid. The initial approach for this fluid was described in [1]. Many of the other scholars are investigated later. The apparent viscosity is given by: \(\mu = K + \left( {\frac{{\tau_{0} }}{\left|{\dot{\gamma }}\right|}} \right)\), where K is the plastic viscosity of Bingham materials that gives resistance to the flow, and \(\tau_{0}\) is the yield stress below which Bingham materials behave like a solid, the rheological equation for the yield stress was described in [2]. This \(\mu\) is represented by, (see [20] and [23]):

$$\mu = K + \frac{{\tau_{0} }}{{\sqrt {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } }}$$

With the considerations described above, the study, for the unsteady two-dimensional (2D) non-newtonian Couette- Poiseuille flow of Bingham fluid considering Hall and Ion-slip currents, is governed by the mass conservation, momentum and energy balances [20, 23]. Finally, the governing equations take the following form:

Continuity equation:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(1)

Momentum equations:

$$\begin{aligned} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = & - \frac{1}{\rho }\frac{{dp}}{{dx}} + \frac{1}{\rho }\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) \\ & - \frac{1}{\rho }\frac{{\sigma _{{\text{e}}} B_{{_{0} }}^{2} }}{{\alpha _{{\text{e}}}^{2} + \beta _{{\text{e}}}^{2} }}\left[ {\alpha _{e} u + \beta _{e} w} \right] \\ \end{aligned}$$
(2)
$$\frac{\partial w}{{\partial t}} + u\frac{\partial w}{{\partial x}} + v\frac{\partial w}{{\partial y}} = \frac{1}{\rho }\frac{\partial }{\partial y}\left( {\mu \frac{\partial w}{{\partial y}}} \right) - \frac{1}{\rho }\frac{{\sigma_{{\text{e}}} B_{{_{0} }}^{2} }}{{\alpha_{{\text{e}}}^{2} + \beta_{{\text{e}}}^{2} }}\left[ {\alpha_{e} w - \beta_{e} u} \right]$$
(3)

Energy equation:

$$\begin{aligned} \frac{{\partial T}}{{\partial t}} + u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}} = & \frac{\kappa }{{c_{p} \rho }}\left( {\frac{{\partial ^{2} T}}{{\partial y^{2} }}} \right) + \frac{\mu }{{\rho c_{p} }}\left[ {\left( {\frac{{\partial u}}{{\partial y}}} \right)^{2} + \left( {\frac{{\partial w}}{{\partial y}}} \right)^{2} } \right] \\ & + \frac{1}{{\rho c_{p} }}\frac{{\sigma _{{\text{e}}}^{{\text{2}}} B_{{_{0} }}^{2} }}{{\alpha _{{\text{e}}}^{2} + \beta _{{\text{e}}}^{2} }}\left( {u^{2} + w^{2} } \right) \\ \end{aligned}$$
(4)

where \(x,y\) are the Cartesian coordinates; \(u,v\) are the \(x,y\) components of flow velocity respectively; \(p\) is pressure; \(\rho\) is the density of the fluid; \(\kappa\) is thermal conductivity and \(c_{p}\) is specific heat at the constant pressure and the viscosity

$$\mu = K + \frac{{\tau_{0} }}{{\sqrt {\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \left( {\frac{\partial w}{{\partial y}}} \right)^{2} } }}$$
(5)

The schematic flow characteristics are subjected to the following initial and boundary estimations:

$$t \le 0,\,\,\,u = 0,\,w = 0,\,T = T_{1} \,\,\,\,\,{\text{everywhere}}$$
(6)
$$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,u = 0,\,w = 0,\,T = T_{1} \,\,\,\,{\text{at}}\,\,{\text{x = 0}} \hfill \\ t > 0, \, u = 0,\,w = 0,\,T = T_{1} \,\,\,\,{\text{at}}\,\,y = - h \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,u = U_{0} ,\,w = 0,\,T = T_{2} \,\,\,\,{\text{at}}\,\,\,y = h \hfill \\ \end{gathered}$$
(7)

where \(y = - h\) represents the location of motionless lower plate and \(y = h\) means the position of moving upper plate. Both the plates are placed at a distance of \(2h\).

The following dimensionless variables (8) are used to assure dimensional covenant among the Eqs. (1–7)

$$\begin{gathered} X = \frac{x}{h},Y = \frac{y}{h},U = \frac{u}{{U_{0} }},V = \frac{v}{{U_{0} }},W = \frac{w}{{U_{0} }},P = \frac{p}{{\rho U_{0}^{2} }}, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau = \frac{{tU_{0} }}{h},\theta = \frac{{T - T_{1} }}{{T_{2} - T_{1} }}\,\,{\text{and}}\,\,\overline{\mu } = \frac{\mu }{K} \hfill \\ \end{gathered}$$
(8)

The retrieved dimensionless coupled nonlinear PDEs are given below:

$$\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0$$
(9)
$$\begin{aligned} \frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial X}} + V\frac{{\partial U}}{{\partial Y}} = & - \frac{{dP}}{{dX}} + \frac{1}{{R_{e} }}\frac{\partial }{{\partial Y}}\left( {\bar{\mu }\frac{{\partial U}}{{\partial Y}}} \right) \\ & - \frac{1}{{R_{e} }}\frac{{H_{a}^{2} }}{{\alpha _{{\text{e}}}^{2} + \beta _{{\text{e}}}^{2} }}\left( {\alpha _{e} U + \beta _{e} W} \right) \\ \end{aligned}$$
(10)
$$\begin{aligned} \frac{{\partial W}}{{\partial \tau }} + U\frac{{\partial W}}{{\partial X}} + V\frac{{\partial W}}{{\partial Y}} = & \frac{1}{{R_{e} }}\frac{\partial }{{\partial Y}}\left( {\bar{\mu }\frac{{\partial W}}{{\partial Y}}} \right) \\ & - \frac{1}{{R_{e} }}\frac{{H_{a}^{2} }}{{\alpha _{{\text{e}}}^{2} + \beta _{{\text{e}}}^{2} }}\left( {\alpha _{e} W - \beta _{e} U} \right) \\ \end{aligned}$$
(11)
$$\begin{aligned} \frac{{\partial \theta }}{{\partial \tau }} + U\frac{{\partial \theta }}{{\partial X}} + V\frac{{\partial \theta }}{{\partial Y}} = & \frac{1}{{P_{r} }}\frac{{\partial ^{2} \theta }}{{\partial Y^{2} }} + E_{c} \bar{\mu }\left[ {\left( {\frac{{\partial U}}{{\partial Y}}} \right)^{2} + \left( {\frac{{\partial W}}{{\partial Y}}} \right)^{2} } \right] \\ & + \frac{{E_{c} H_{a}^{2} }}{{\alpha _{{\text{e}}}^{2} + \beta _{{\text{e}}}^{2} }}\left[ {U^{2} + W^{2} } \right] \\ \end{aligned}$$
(12)
$$\overline{\mu } = 1 + \frac{{\tau_{D} }}{{\sqrt {\left( {\frac{\partial U}{{\partial Y}}} \right)^{2} + \left( {\frac{\partial W}{{\partial Y}}} \right)^{2} } }}$$
(13)

and the corresponding dimensionless boundary conditions are shown below:

$$\tau \le 0,\,\,\,U = 0,\,W = 0,\,\theta = 0\,\,\,\,\,\,\,{\text{everywhere}}$$
(14)
$$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,\,U = 0,\,W = 0,\,\theta = 0\,\,\,\,{\text{at}}\,\,X{ = 0} \hfill \\ \tau > 0, \, U = 0,\,W = 0,\,\theta = 0\,\,\,\,{\text{at}}\,\,Y = - 1 \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,U = 1,\,W = 0,\,\theta = 1\,\,\,\,{\text{at}}\,\,\,Y = 1 \hfill \\ \end{gathered}$$
(15)

The parameters used in non-dimensional operations of Eqs. (10–13) are given below:

\(\tau_{D} \,=\, \frac{{\tau_{0} h}}{{KU_{0} }}\)(Bingham number), \(R_{e} = \frac{{\rho U_{0} h}}{K}\) (Reynolds number), \(P_{r} \,= \,\frac{{\rho c_{p} U_{0} h}}{k}\) (Prandtl number), \(E_{C} = \frac{{U_{0} K}}{{\rho c_{p} h(T_{2} - T_{1} )}}\) (Eckert number) and \(Ha = \sqrt {\frac{{\sigma B_{0}^{2} h^{2} }}{K}}\) (Hartmann number).

3 Shear stress and Nusselt number

Some impressive physical quantities which are relevant to this study are presented here. The shear stress along with the Nusselt number, are investigated as a function of different parameters where both are calculated at the plates, upper and lower (moving and stationary). The mathematical explanations of shear stress and Nusselt number are taken from Ref. [19 and 25]. The shear stress along X- direction is represented by \(\tau_{L} \equiv \left[ {\mu \sqrt {\left( {\frac{\partial U}{{\partial Y}}} \right)^{2} + \left( {\frac{\partial W}{{\partial Y}}} \right)^{2} } } \right]_{{\text{ at the wall}}}\).

The Nusselt number along X-direction for stationary plate is represented by \(Nu_{L1} \equiv \frac{{\left( {\frac{\partial T}{{\partial Y}}} \right)_{Y = - 1} }}{{ - T_{m} }}\) and for moving plate it is represented by \(Nu_{L2} \equiv \frac{{\left( {\frac{\partial T}{{\partial Y}}} \right)_{Y = 1} }}{{ - \left( {T_{m} - 1} \right)}}\); where, \(T_{m}\) is the non-dimensional mean fluid temperature which is defined by \(T_{m} = \frac{{\int\nolimits_{ - 1}^{1} {U\theta dY} }}{{\int\nolimits_{ - 1}^{1} {UdY} }}\) and is calculated by the Simpson’s 1/3 rule with the numeric values of \(U\) and \(\theta\) obtained by FDM.

4 Numerical technique

Under the boundary settings of Eqs. (14 and 15), the explicit FDM was chosen to solve the obtained dimensionless nonlinear coupled PDEs in Eqs. (9–13). For which, the boundary layer regime was essential to divide into tiny mesh spaces. For this division, several lines, parallel to both the axes, were taken. A particular test (mesh sensitivity) was performed to choose these number of lines, see Sect. 6.1. In this study, the direction of X-axis is maintained along the plate while Y-axis is maintained perpendicular to the plate-direction, shown in Fig. 1. Along the X-axis, parallel to Y-axis, the appropriate number of lines were chosen \(m = 40\). Along the Y-axis, parallel to X-axis, the appropriate number of lines were chosen \(n = 40\). Thus it was arbitrarily decided that the size of each of the plates was, \(X_{\max } = 40\) i.e. X varied from 0 to 40 and the distance between the plates was, \(Y_{\max } = 2\) i.e. Y varying values from 0 to 2. Figure 2 represents the mesh spacing for the current study.

Fig. 2
figure 2

Finite difference grid space

Full size image

The uniform cell edges are \(\Delta X\) and \(\Delta Y\) along X and Y paths respectively which are taken as \(\Delta X \,= \,\frac{{X_{\max } }}{m} \,=\, 1.0,\,\,\left( {0 \le X \le 40} \right)\), \(\Delta Y \,=\, \frac{{Y_{\max } }}{n}\, =\, 0.05,\,\,\left( {0 \le Y \le 2} \right)\) with the smaller (in magnitude) time-step, \(\Delta \tau \,= \,0.0001\).

5 Stability and convergence analysis

The criteria of stability and convergence were analyzed along with the FDM due to demonstrate the expected order of convergence and the stable numeric computations. In the convergence test, Fourier exponential expansions for \(U\), \(W\) and \(\theta\) are used. With the use of created uniform mesh sizes, the stability and convergence criteria are simplified as follows:

$$\frac{U\Delta \tau }{{\Delta X}} - \frac{\left| V \right|\Delta \tau }{{\Delta Y}} + \frac{\Delta \tau }{{2R_{e} }}\frac{{H_{a}^{2} }}{{\alpha_{{\text{e}}}^{2} + \beta_{{\text{e}}}^{2} }}\alpha_{e} \le 1\,\,\,and$$
$$\frac{U\Delta \tau }{{\Delta X}} - \frac{\left| V \right|\Delta \tau }{{\Delta Y}} + \frac{2\Delta \tau }{{P_{r} \left( {\Delta Y} \right)^{2} }} \le 1$$

Therefore, the converged solutions will be found after the adoption of the above two inequalities being perfect. Using \(\Delta Y = 0.05,\,\,\Delta \tau = 0.0001\) and the initial conditions (\(U = 0\) and \(V = 0\)), the above inequalities give the restrictions for the dimensionless parameters. Finally, the constraints for the dimensionless parameters are obtained as: \(P_{r} \ge 0.08,\) \(\beta_{i} \ge 2,\) \(H_{a} \le 20\) and \(R_{e} \ge 0.0166\) with the constant value \(\,\beta_{e} = 0.10\) and \(E_{c} = 0.10\).

6 Results and discussion

Due to exploring the inner physical situation of the flow model, the numerical values in steady-state situations are reckoned for the non-dimensional primary velocity \(U\), secondary velocity \(W\), and temperature \(\theta\) within each plate's boundary layer region. First, establishing a compatible mesh zone is ascertained inside the boundary layer regime through the sensitivity test of meshes for the numerical computations, see Sect. 6.1. Secondly, a code validation test is performed by two different tools, MATLAB R2015a and COMPAQ VISUAL FORTRAN 6.6a (CVF 6.6a), to verify the accuracy of the coding, see Sect. 6.2. Thirdly, the sensitivity test of time is ascertained to assure the steady-state solutions for all profiles, see Sect. 6.3. Fourthly, to test the qualitative track of the present study, a comparison between the current result and the published result is described, see Sect. 6.4. Finally, the effect of magnetohydrodynamic parameters, Ion-slip parameter \(\beta_{i}\) and Hartmann number \(H_{a}\) on velocity profiles-\(U\) and \(W\), temperature field \(\theta\) also on shear stress \({\tau }_{L}\) and Nusselt number \({Nu}_{L}\) are discussed at both the stationary plate (lower plate) and moving plate (upper plate), see Sect. 6.5.

6.1 Mesh sensitivity test

To find out the precise grid space lines (i.e. values of \(m\) and \(n\)), several trial values of mesh spaces are experimented, out of these trial values three separate grid spacing as \(m = 40,\,n = 40;\,\,\) \(m = 100,\,n = 100\) and \(m{ = 150,}\,n{ = 150}\) are shown in Fig. 3 for the primary velocity field. The obtained curves are smooth and have a minor change. It is also checked for a quoted point of Fig. 3 by enlarging that part. The sub-figure (enlargement) of Fig. 3 shows that the doted, dash-dot and dashes lines are closed to each other that clarify the mesh independency of the model. Thus, \(m{ = 40}\) and \(n{ = 40}\) can be chosen as the appropriate mesh space lines. Therefore, further computations is continued for the mesh space lines, \(m{ = 40}\,\,{\text{and}}\,\,n{ = 40}\).

Fig. 3
figure 3

Influence of grid space lines on velocity field; where \(\beta_{i} = \,3.00,\)\(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\)

Full size image

6.2 Code validation test

The exactitude of numerical codes is simulated for propriety, by MATLAB R2015a and COMPAQ VISUAL FORTRAN (CVF) 6.6a tools, with explicit FDM technique. Using MATLAB code, the obtained primary velocity field and shear stress are shown in Fig. 4-a and c respectively for several values of Ion-slip parameter \(\left( {\beta_{i} } \right)\). Again, by using FORTRAN code, the obtained results of the same profiles, described above, are shown in Fig. 4-b and d respectively for the same values of Ion-slip parameter \(\left( {\beta_{i} } \right)\). The rigorously identical results are discerned for both the calculating tools MATLAB and CVF (see by relating Fig. 4(a) with 4(c), as well as Fig. 4(b) with 4(d)). Thus, the sensitivity of coding achieved accuracy. However, in all the following sections, it is decided to proceed with the results from MATLAB as a simulation tool.

Fig. 4
figure 4

Code validation test calculated for different Ion-slip parameter \(\left( {\beta_{i} } \right)\) at moving plate; where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\)

Full size image

6.3 Time sensitivity test (steady-state solutions)

To meet the steady-state solutions of the configured mathematical flow scheme developed here, the numeric computations for both the velocities (primary, secondary) and temperature profiles are sustained for multifarious sequential dimensionless times, such as \(\tau =\) 0.20, 0.70, 1.20, 2.00, 2.50 and 3.00. Figure 5-a, b and c are the representative graphs for the computed results of dimensionless primary velocity \(U,\) dimensionless secondary velocity \(W\) and dimensionless temperature \(\theta\) show a little change after \(\uptau =\) 2.00 and also show a negligible change between \(\uptau\) = 2.50 and \(\uptau\) = 3.00. Depending on this numerical experimentation, the time value \(\uptau =\) 3.00 is specified as the ultimate steady-state for all variables in this study.

Fig. 5
figure 5

Effect of time sensitivity test; where \(\beta_{e} = \,0.10,\) \(\beta_{i} = \,3.00,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at \(m{ = 40}\,\,{\text{and}}\,\,n{ = 40}\)

Full size image

Figure 5-a, b and c show that both velocity distributions and temperature distributions attain steady-state monotonically. Note that the temperature distribution is reached steady-state position faster than the velocity distributions.

6.4 Validity test (comparison)

The quantitative and qualitative measurement of the upshots of current study is analyzed with the published results of [23] through Figs. 6 and 7. It is shown from the Figs. 6 and 7, the reported results are not in quantitative similarity rather they are in an excellent qualitative similarity with the published results of [23]. Since the present results is verified by both CVF 6.6a and MATLAB R2015a tools, thus it can be claimed that the reported model is less blemished with the concern of published results.

Fig. 6
figure 6

Profile for Shear stress for different values of Hartman number \(\left( {H_{a} } \right)\) in nonappearance of Ion-slip at stationary plate (present study)

Full size image
Fig. 7
figure 7

Profile for Shear stress for different values of Hartman number \(\left( {H_{a} } \right)\) in nonappearance of Ion-slip at stationary plate (published study of [23])

Full size image

6.5 Effect of magnetohydrodynamic parameters

To quest and clarify the physical modulation of the flow structure, the influences of magnetohydrodynamic parameters- Ion-slip parameter \(\left( {\beta_{i} } \right)\) and Hartmann number \(\left( {H_{a} } \right)\) on velocity fields and temperature fields, shear stress and Nusselt number at the moving as well as stationary plates are illustrated via graphs in Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17. With a general use of Hall parameter \(\left( {\beta_{e} = 0.10} \right)\), Reynolds number \(\left( {R_{e} = 3.0} \right)\), Bingham number \(\left( {\tau_{D} = \,0.1} \right)\), Prandtl number \(\left( {P_{r} = 0.08} \right)\), and Eckert number \(\left( {E_{c} = 0.10} \right)\) that satisfies the stability condition of the present model discussed in Sect. 5. The magnitude of the dimensionless parameters that have been used, in this study, are chosen as investigated in some recent studies by Jha et al. [29] and Ibrahim and Anbessa [30]. For ensuring a concise discussion, the impacts of rest of the parameters namely, Hall parameter \(\beta_{e}\), Prandtl number \(P_{r}\), Eckert number \(E_{c}\), Reynolds number \(R_{e}\) and Bingham number \(\tau_{D}\) are not discussed.

Fig. 8
figure 8

Impacts of \(H_{a}\); where \(\beta_{i} = \,3.00\), \(\beta_{e} = \,0.10,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10\) , \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 9
figure 9

Impacts of \(\beta_{i}\); where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 10
figure 10

Impacts of \(H_{a}\); where \(\beta_{i} = \,3.00,\,\) \(\beta_{e} = \,0.10,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 11
figure 11

Impacts of \(\beta_{i}\); where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 12
figure 12

Impacts of \(H_{a}\); where \(\beta_{i} = \,3.00,\) \(\beta_{e} = \,0.10,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 13
figure 13

Impacts of \(\beta_{i}\); where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 14
figure 14

Impacts of \(H_{a}\); where \(\beta_{i} = \,3.00,\) \(\beta_{e} = \,0.10,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 15
figure 15

Impacts of \(\beta_{i}\); where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 16
figure 16

Impacts of \(H_{a}\); where \(\beta_{i} = \,3.00,\) \(\beta_{e} = \,0.10,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image
Fig. 17
figure 17

Impacts of \(\beta_{i}\); where \(\beta_{e} = \,0.10,\) \(H_{a} = \,3.00,\) \(R_{e} = \,3.00,\) \(E_{c} = 0.10,\) \(P_{r} = \,0.08\) and \(\tau_{D} = \,0.1\) at time \(\tau = 3.00\) (Steady State)

Full size image

The Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 could be represented with respect to \(y\) direction similar to Fig. 5, where the flow completely satisfies the boundary conditions and shows greater motion in the upper-middle of the channel which holds the Couette-Poiseuille flow phenomena. To observe the Couette-Poiseuille flow phenomena more clearly and to observe the flow properties adjacent to the plates, the Figs. 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 are presented in a different way, where the flow is chosen to discuss at both the upper and lower plates, in \(X\) direction. Thus, for both the plates, i.e. the lower stationary plate and the upper moving plate, the varying feature of the velocity distributions and temperature distributions are considered in the \(X\) direction.

6.5.1 Effects on primary velocity

The impacts of Hartmann number \(\left( {H_{a} } \right)\) and Ion-slip parameter \(\left( {\beta_{i} } \right)\) on the profiles primary velocity are shown in Figs. 8 and 9. Figure 8(a, b), reveals that, \(H_{a}\) opposes the primary velocity subject to the growth of \(H_{a}\) at both plates. It is happened quantitatively as expectations because the orthogonally applied magnetic field to the flow direction generates a force of resistance naming Lorentz force. It is found from Fig. 9(a, b) that \(\beta_{i}\) influences the primary velocity at both the plates. The inclusion of the Ion-slip parameter enhances the operative conductivity for which the primary velocity grows up. Viewing the primary velocities for both the plates, it is noted that the primary velocity characterized at moving plate is speedier than the stationary one.

6.5.2 Effects on secondary velocity

The varying estimations of secondary velocity with Hartmann number \(\left( {H_{a} } \right)\) and Ion-slip parameter \(\left( {\beta_{i} } \right)\) are shown in Figs. 10 and 11. From Figs. 10(a, b) and 11(a, b), it is clear that \(H_{a}\) and \(\beta_{i}\) both oppose the secondary velocity subject to their growth at both plates. By comparing the secondary velocity profiles among both plates, it is noted that the secondary velocity characterized at moving plate is speedier than the secondary velocity at stationary one.

6.5.3 Effects on temperature

The impacts of Hartmann number \(\left( {H_{a} } \right)\) and Ion-slip parameter \(\left( {\beta_{i} } \right)\) on temperature are graphed in Figs. 12 and 13. Figure 12(a, b), focused that, the temperature profile falls when the values of \(H_{a}\) develops at both the plates. It is marked from Fig. 13(a, b) that the temperature influences by \(\beta_{i}\) at stationary plate while \(\beta_{i}\) occurs diminution on temperature by the rising values of \(\beta_{i}\) at moving plate. By comparing temperatures among both plates, it is found that the moving plate’s temperature is greater than the stationary plate’s temperature. It is also verified by the close-up view of the quoted point of the curves of Figs. 12 and 13. The enlargement sub-figures of Figs. 12(a, b) and 13(a, b) show that the effects are clear.

6.5.4 Effects on shear stress

The impacts of Hartmann number \(\left( {H_{a} } \right)\) and Ion-slip parameter \(\left( {\beta_{i} } \right)\) on shear stress are shown in Figs. 14 and 15. From Fig. 14(a, b), it is found that \(H_{a}\) opposes the shear stress subject to the growth of \(H_{a}\) at both the plates. Figure 15(a, b) marks that, \(\beta_{i}\) influences the shear stress estimations at stationary plate as well as moving plate. By comparing shear stresses among both plates, it is noted that the shear stress characterized at the plate of motion is larger than the shear stress at the plate of stationary position.

6.5.5 Effects on Nusselt number

The impacts of Hartmann number \(\left( {H_{a} } \right)\) and Ion-slip parameter \(\left( {\beta_{i} } \right)\) on Nusselt number are shown in Figs. 16 and 17. Figure 16(a, b) marks that, the Nusselt number influences with the growth of \(H_{a}\) at both the plates. By observing, Fig. 17(a, b), it is noted that, \(\beta_{i}\) opposes the Nusselt number (heat transfer rate) at both the plates. By comparing Nusselt numbers among both plates, it is checked that the Nusselt number characterized at the plate of motion (upper plate) is greater than the Nusselt number at the plate of stationary position. Also, it is verified by enlarging the quoted point of the curves of Fig. 17(a, b). The enlargement sub-figures of Fig. 17(a, b) show that the effects are clear.

7 Conclusion

In this work, the unsteady viscous incompressible flow through the inner zone between two horizontally placed parallel plates incorporating the magnetohydrodynamic impact by both the Hall and Ion-slip currents was investigated numerically by using explicit FDM technique. The flow is involving the industrial-viscoplastic/Bingham fluids between two infinitely extended horizontal plates. For the exactitude of the estimations of numerical performance, the criteria for stabilisation and convergence were analyzed. The obtained converging ranges for respective materials are \(P_{r} \ge 0.08,\)\(H_{a} \le 20\), \(\beta_{i} \ge 2,\) and \(R_{e} \ge 0.0166\,\) with the constant value \(\beta_{e} = 0.10\) and \(E_{c} = 0.10\). The simulated outcomes are delineated graphically for several values of major parameters as Ion-slip parameter \(\left( {\beta_{i} } \right)\) and Hartmann number \(\left( {H_{a} } \right)\). For conciseness, the impacts of rest of the parameters, namely, the effects of Hall parameter \(\left( {\beta_{e} } \right)\), Reynolds number \(\left( {R_{e} } \right)\), Prandtl number \(\left( {P_{r} } \right)\), Eckert number \(\left( {E_{c} } \right)\) and Bingham number \(\left( {\tau_{D} } \right)\) are not discussed. Some significant outcomes of the study are given to the following section:

  1. 1.

    \(\beta_{i}\) influences the primary velocity along with shear stress while \(H_{a}\) opposes at both plates (stationary and moving).

  2. 2.

    \(H_{a}\) and \(\beta_{i}\) both oppose the secondary velocity at both plates.

  3. 3.

    The temperature grows when the rise of \(\beta_{i}\) happens, on contrary it opposes when the developement of \(H_{a}\) occurs at the plate of stationary position. At the plate of motion, it opposes with the enhancement of \(H_{a}\) and \(\beta_{i}\) both.

  4. 4.

    \(H_{a}\) influences the characteristics of Nusselt number at both the stationary-plate and the moving-plate while \(\beta_{i}\) opposes it for both plates.

  5. 5.

    The temperature profile reaches the steady-state earlier than both velocity profiles.

In future work, the presented numerical model of the Bingham material could be used to predict the magnetohydrodynamic flow phenomena in different process conditions, for example, a rotating channel is of great interest to the authors.