1 Introduction

Contact mechanics of solids have been an attractive topic of research for many years since it concerns the maintenance of mechanical and structural elements. Hence, researchers have focused on contact mechanics of mechanical components in order to enhance the reliability and durability of such contacts. Determination of surface contact stress indicates critical locations of contacts where stresses reach higher levels. Therefore, it shed light onto understand the deformation mechanism emerged on the contact surface. Early research on contact mechanics date back in 1882 by monographs of Hertz [1]. Cerruti [2] and Boussinesq [3] used the potential theory to find the stress and displacement in an elastic half-space due to surface tractions. Love [4] presented the potential theory approach. Muskhelishvili [5] developed analytical solutions for frictionless plane contact problems. Spence [6, 7] conducted a research on frictional contact problems involving flat indenters. Galin [8] examined the contact mechanics of isotropic solids. Comninou [9] studied stress singularities at a sharp edge of the indenter in frictional contact problem. Johnson [10] presented some benchmark analytical solutions to different kind of contact problems. Contact problems can be referred to as rigid-deformable contacts, deformable-deformable contacts, contacts of advanced materials. Guler and Erdogan [11] analyzed contact mechanics of two deformable elastic solids possessing graded coatings. The interaction between two non-linear deformable bodies that collide each other was investigated by the use of continuum mechanics formulation [12]. The major aim of the researchers is reducing surface contact stresses on machine components so that avoiding the surface damage and prolonging the machine life. Hence, they have focused on the utilization of new kinds of advanced materials or surface coatings as contacting components. It was reported that properly controlled material gradients in functionally graded materials (FGMs) provides a significant improvement in the resistance to contact deformation and damage in tribological applications [13,14,15]. Guler and Erdogan [16, 17] examined contact mechanics of FGM coatings bonded to homogenous half-planes. Dag et al. [18] studied the contact mechanics of laterally graded materials by means of analytical and computational approaches. Ke and Wang [19] carried out an analytical study to investigate the sliding contact mechanics of functionally graded materials with arbitrary spatial variations of material properties. Choi [20] determined the contact stress distributions on the graded elastic layer subjected to sliding frictional contact by a flat punch. Balci and Dag [21, 22] examined dynamic contact mechanics of FGM coating/homogenous substrate system under the effect of moving frictional punch.

In all the studies in the foregoing paragraph, Coulomb’s friction or so-called Amontons-Coulomb friction model was adopted. In Coulomb’s friction model, friction force is the function of applied load and direction of the velocity. This model was not able to express the pre-sliding and hysteresis characteristics of dynamic friction. Literature survey showed that there is no previous work related to the contact mechanics of solids under the effect of Dahl’s dynamic friction. Friction phenomenon is essential in motion control, wear, tribology and surface science. Relative sliding of the contacting surfaces was accompanied not only by friction but also by wear, as is the case in gross sliding fretting regime [23, 24]. Argatov and Chai [25] developed analytical method for the frictional contact problem of an elastic layer considering sliding wear process to find the steady state contact geometry for optimal properties. Páczelt et al. [26] conducted a study based on finite element method (FEM) to find the steady state optimal profiles of monotonically or reciprocally sliding punches under the effect of friction and wear. Hence, modelling of friction force and the wear are crucial in many application fields such as robotics, mechatronics, machine tool design, automotive and aerospace. An experimental comparison study was carried out for different friction models on the same micro stick–slip motion system [27]. Many of dynamic friction models have been proposed by Adams [28], Canudas De Wit et al. [29], Bliman and Sorine [30], Oden and Martins [31] and Dankowicz [32]. According to these studies, while friction force in static laws depends on macroscopically observed state variables, that in dynamic laws not only depends on macroscopically observed state variables but also depends on internal state variables consists of hidden quantities. Dahl [33] modeled friction as a function of relative displacement of two contact surfaces. In Dahl’s model, friction force depends on micro motions and these micro motions are later called as pre-sliding behavior. The main idea behind the Dahl’s friction model is that when the applied load is not adequate to exceed static friction, the asperities at the contact surface will deform which results in a pre-sliding motion. When applied load is larger enough, a relative sliding begins between contacting bodies. A text explaining the relationship between the Dahl’s model and Coulomb’s dry friction model is found in [34]. Dahl’s friction model is capable of modelling both pre-sliding and sliding regimes and the hysteresis in a continuous manner and this model is a basis for more advanced friction models. Dahl’s friction model was utilized in many studies concerning motion control in mechanisms, vibration response and friction compensation in robotic or control systems. Ganseman et al. [35] described a new dynamic friction model based on Canudas de Wit [29] and Dahl’s friction model [33] for the control system of an industrial robot. Augustynek and Urbas [36] considered Dahl, LuGre and elastoplastic friction models while solving the mathematical equations of a one-DOF spatial linkage including friction. Bastien et al. [37] described the modified Dahl and Masing models utilized for the prediction of the hysteresis behavior of components. The numerical and experimental investigations conducted on a belt tensioner for automotive engines showed that the reliability of the modified Dahl model. Urbas [38] utilized Dahl’s friction model in dynamic analysis of grab cranes. Lampaert et al. [39] discussed the compensation of friction in pre-sliding regime, and Dahl’s friction model was used as one of the most effective feed-forward friction compensation techniques. Yoon and Trumper [40] studied the influence of friction on control systems both in the pre-sliding and sliding regimes, and Dahl’s resonance identification method provided reasonable values for the parameters of the friction model. Dahl’s friction model was utilized to model friction-reducing performance of an axial oscillation tool (AOT) [41]. Gutowski and Leus [42] analyzed the influence of transverse tangential vibrations on friction and driving forces in a sliding motion and Dahl’s dynamic friction model was used. Jadav et al. [43] developed an analytical friction model based on Dahl’s friction to calculate the drive force required to slide a body over a surface that is subjected to coupled longitudinal and transverse vibrations.

There are many articles in the literature which consider static laws of friction while modelling contacts and they did not give idea about contact stresses on elastic solids especially in the pre-sliding regime. However, Dahl’s friction model utilized in several fields as mentioned in the previous paragraph. Thorough examination of the available literature showed that there is no similar work pertaining to the contact mechanics analysis of elastic bodies under the effect of Dahl’s dynamic friction model. Implementation of the Dahl’s friction model to contact mechanics enables to figure out contact stresses in both pre-sliding and sliding regimes. Friction force depends not only on a direction of the motion but also on a pre-sliding displacement, asperity stiffness, applied normal load and hysteresis loop’s shape factor. The formulation is derived considering two-dimensional elastodynamics, which provides acceptable solutions for both slow and high speed sliding conditions. Contact stresses are determined by solving the singular integral equation (SIE) of the contact problem with expansion-collocation method. Contact stresses obtained by analytical method are compared with those generated by means of finite element method in slow speed sliding case and a very good agreement is achieved. After verification of the analytical method, influences of the direction of the motion, pre-sliding displacement, coefficient of friction, asperity stiffness and hysteresis loop’s shape factor on contact stresses are examined. The analytical formulations for contact mechanics of elastic solids based on using Dahl’s dynamic friction model are provided in Sect. 2. In Sect. 3, derivation of the singular integral equation (SIE), numerical calculation of friction force and solution method of the SIE are explained. In Sect. 4, detailed information about the finite element model is provided. Section 5 presents some parametric results involving comparisons between analytical results and those of finite element analysis. Finally, Sect. 6 provides the major conclusions of this study.

2 Dahl’s dynamic friction model and formulation

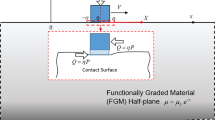
Contact mechanics problem is depicted in Fig. 1 where one of the contacting bodies is modeled as a rigid flat punch and other one is considered as an isotropic elastic half-plane. The rigid punch is pressed against elastic half-plane by a normal force N. Friction force is developed in tangential direction and this friction force is calculated through the use of Dahl’s dynamic friction model instead of Coulomb’s dry friction law.

Fig. 1
figure 1

Schematics for the contact problem considering Dahl’s dynamic friction model

Full size image

The rigid punch moves over the surface at a constant subsonic speed \(V\). Contact region extends from \(- a\) to \(a\) and close up view around the contact region is shown in rectangular region enclosed by dashed red line. \(\left( {x,y} \right)\) shows the axes of the stationary coordinate system while \(\left( {X,Y} \right)\) indicates those of the moving coordinate system which is attached to the center of the moving punch. \(\mu\) and \(\kappa\) are designated for the shear modulus and the Kolosov’s constant of the half-plane material, respectively. Kolosov’s constant for the isotropic material can be calculated by,

$$\kappa = \left\{ {\begin{array}{*{20}l} {\frac{3 - \nu }{{1 + \nu }},} & {{\text{plane}}\;{\text{stress,}}} \\ {3 - 4\nu ,} & {{\text{plane}}\;{\text{strain}}{.}} \\ \end{array} } \right.$$
(1)

The friction force developed is calculated by Dahl’s friction model [44] which belongs to the earliest dynamic friction models; it was designated to simulate a symmetrical hysteresis loops observed in bearings subjected to sinusoidal excitations with small amplitudes. This model was applied in standard models in aerospace industry [39]. According to this model, friction force depends on displacement rather than velocity and it does not capture Striebeck effect and stiction behavior [45]. Figure 2 shows these hysteresis loops of friction force as depicted in Ref. [46]. Dankowicz [32] conducted a research on the modelling of dynamic friction phenomena based on microscopic interactions between nominally flat surfaces. In Dankowicz’s study a coupling was introduced between the tangential motion and the separation of the surface due to the asperity contact between surfaces. However, the separation of the surface is not considered in the present work. Argatov and Butcher [47] presented the generalization of the Dankowicz’s model and authors considered the initial interfacial stiffness as the slope of the load deflection curve at the origin.

Fig. 2
figure 2

Hysteresis loop of friction force as a function of displacement for Dahl’s model

Full size image

The friction force proposed by Dahl is obtained by the following formula which reads [44]:

$$\frac{dF}{{dx}} = \sigma_{0} \,{\text{sign}}\left( {1 - {\text{sign}}\left( V \right)\,\frac{F}{{F_{C} }}} \right)\,\left| {1 - {\text{sign}}\,\left( V \right)\,\frac{F}{{F_{C} }}} \right|^{{\delta_{D} }} .$$
(2)

which can be converted into following equations for the easier numerical implementation:

$$F = \sigma_{0} \,z,$$
(3)
$$\frac{dz}{{dx}} = {\text{sign}}\left( {1 - {\text{sign}}\left( V \right)\,\frac{{\sigma_{0} \,z}}{{F_{C} }}} \right)\,\left| {1 - {\text{sign}}\left( V \right)\,\frac{{\sigma_{0} \,z}}{{F_{C} }}} \right|^{{\delta_{D} }} ,$$
(4)
$$F_{C} = \mu_{C} \,N.$$
(5)

where \(F\) is the friction force [N], \(z\) is the internal state variable interpreted as elastic deformation of surface asperities of adjacent bodies [m], \(V = {{dx} \mathord{\left/ {\vphantom {{dx} {dt}}} \right. \kern-\nulldelimiterspace} {dt}}\) is the punch speed [m/s], \(x\) is the body displacement [m], \(\sigma_{0}\) is the asperity stiffness [N/m], \(\delta_{D}\) is the shape factor for the hysteresis loop [-] and \(F_{C}\) is the friction force due to Coulomb’s dry friction [N]. Shorter asperities will begin to slide prior to their longer counterparts. Consequently, energy losses are inevitable even in the absence of macroscopic displacement. This is primarily manifested in the hysteresis loop observed experimentally in the friction force’s dependence on displacements on the order of few microns [32, 48]. Dahl’s friction model is described by dynamic equation system that simultaneously model pre-sliding and sliding friction regimes in a continuous manner. Dynamic friction models, as opposed to the static models, allow for recreating processes occurring in standstill friction conditions and at very small as well as high sliding velocities [44]. In case of modelling precisely positioned mechanical systems with friction, it is necessary to use dynamic friction models which consider both friction regimes [49,50,51]. Stress-displacement relations for isotropic medium reads:

$$\sigma_{xx} (x,y) = \frac{\mu }{\kappa - 1}\,\left[ {\left( {\kappa + 1} \right)\,\frac{\partial u}{{\partial x}} + \left( {3 - \kappa } \right)\frac{\partial v}{{\partial y}}\,} \right],$$
(6)
$$\sigma_{yy} (x,y) = \frac{\mu }{\kappa - 1}\,\left[ {\left( {3 - \kappa } \right)\,\frac{\partial u}{{\partial x}} + \left( {\kappa + 1} \right)\frac{\partial v}{{\partial y}}\,} \right],$$
(7)
$$\sigma_{xy} \left( {x,y} \right) = \mu \left[ {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right].$$
(8)

Equations of motion in planar theory of elastodynamics reads:

$$\frac{{\partial \sigma_{xx} \left( {x,y} \right)}}{\partial x} + \frac{{\partial \sigma_{xy} \left( {x,y} \right)}}{\partial y} = \rho_{M} \;\frac{{\partial^{2} u}}{{\partial t^{2} }},$$
(9)
$$\frac{{\partial \sigma_{xy} \left( {x,y} \right)}}{\partial x} + \frac{{\partial \sigma_{yy} \left( {x,y} \right)}}{\partial y} = \rho_{M} \;\frac{{\partial^{2} v}}{{\partial t^{2} }}.$$
(10)

where \(\rho_{M}\) is the mass density of the isotropic elastic material. Galilean transformation is introduced. \(\dot{x} > 0\) or \(\dot{X} > 0\) indicate the motion of punch is towards right direction, named as Forward Motion (FM) and \(\dot{x} < 0\) or \(\dot{X} < 0\) show the motion is towards left direction, called as Backward Motion (BM). Hence, following equations can be written between the stationary and moving coordinates as follows:

$$x = X \pm Vt,$$
(11)
$$y = Y.$$
(12)

when the sign becomes positive ( +) in Eq. (11), the motion of the punch becomes to the right direction whereas if the sign turns to be negative (-), motion of the punch is towards left direction. Punch speed is normalized utilizing the shear wave propagation speed of the elastic solid. The shear wave propagation speed in elastic solid is computed by,

$$c_{s} = \sqrt {\frac{\mu }{{\rho_{M} }}} .$$
(13)

Then, the normalized punch speed is determined as follows:

$$c = \frac{V}{{c_{s} }}.$$
(14)

Stress-displacement relations given by Eqs. (6)-(8) are substituted into Eqs. (9)-(10). The time dependency of the right hand sides of Eqs. (9)-(10) is eliminated through the utilization of Galilean Transformation and Eqs. (13)-(14). After some mathematical manipulations, the following partial differential equation system is obtained.

$$\left[ {\frac{\kappa + 1}{{\kappa - 1}} - c^{2} } \right]\frac{{\partial^{2} u}}{{\partial X^{2} }} + \frac{2}{\kappa - 1}\,\frac{{\partial^{2} v}}{\partial X\partial Y} + \frac{{\partial^{2} u}}{{\partial Y^{2} }} = 0,$$
(15)
$$\left( {1 - c^{2} } \right)\frac{{\partial^{2} v}}{{\partial X^{2} }} + \frac{2}{\kappa - 1}\,\frac{{\partial^{2} u}}{\partial X\partial Y} + \left[ {\frac{\kappa + 1}{{\kappa - 1}}} \right]\,\frac{{\partial^{2} v}}{{\partial Y^{2} }} = 0.$$
(16)

Equations (15)–(16) are solved analytically by Fourier transformation technique. Applying Fourier transform in X- direction, the following solutions are obtained for the displacement components in the homogenous elastic medium.

$$u\left( {X,Y} \right) = \frac{1}{2\pi }\,\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{4} {M_{j} \left( \rho \right)\,N_{j} \left( \rho \right)\,e^{{\left( {n_{j} Y + i\rho X} \right)}} } } \,d\rho ,\, - \infty < Y < 0,\, - \infty < X < \infty ,$$
(17)
$$v\left( {X,Y} \right) = \frac{1}{2\pi }\,\int\limits_{ - \infty }^{\infty } {\sum\limits_{j = 1}^{4} {M_{j} \left( \rho \right)\,\,e^{{\left( {n_{j} Y + i\rho X} \right)}} } } \,d\rho ,\, - \infty < Y < 0,\, - \infty < X < \infty ,$$
(18)

where

$$n_{1,2} = \pm \sqrt {1 - c^{2} } \,\left| \rho \right|,\,\,\Re \left( {n_{1} } \right) > 0,\Re \left( {n_{2} } \right) < 0,$$
(19)
$$n_{3,4} = \pm \sqrt {1 - \left( {\frac{\kappa - 1}{{\kappa + 1}}} \right)\,c^{2} } \,\left| \rho \right|,\,\,\,\Re \left( {n_{3} } \right) > 0,\,\Re \left( {n_{4} } \right) < 0.$$
(20)

and \(\rho\) is the Fourier transform variable. The following function is useful to join the vertical and horizontal displacement fields in the isotropic elastic medium:

$$N_{j} = i\frac{{\left( {\kappa + 1} \right)\,n_{j}^{2} + \rho^{2} \,\left( {1 - \kappa } \right)\,\left( {1 - c^{2} } \right)}}{{2\rho \,n_{j} }},\,\,j = 1, \ldots ,4.$$
(21)

Displacements given by Eqs. (17)-(18) involve four unknowns as \(M_{1} , \ldots ,M_{4} .\) These unknowns are determined by the use of following boundary conditions:

$$\sigma_{YY} \left( {X,0} \right) = \sigma_{XY} \left( {X,0} \right) = 0,\,\, - \infty < X < - a,\,a < X < \infty ,$$
(22)
$$\sigma_{YY} \left( {X,0} \right) = \sigma \left( X \right),\, - a < X < a,$$
(23)
$$\sigma_{XY} \left( {X,0} \right) = \tau \left( X \right),\, - a < X < a,$$
(24)

where \(\tau \left( X \right)\) is the shear stress beneath the flat punch. The regularity boundary condition requires that displacement components u and v should vanish at very further points in the medium. Since we adopted Dahl’s dynamic friction model, shear stress becomes:

$$\tau \left( X \right) = f\,\sigma \left( X \right),\,\, - a < X < a.$$
(25)

The friction force applied to the rigid punch \(F\) is derived based on Dahl’s dynamic friction model and it can be expressed as functions of Coulomb’s coefficient of friction \(\mu_{C} ,\) displacement \(X,\) asperity stiffness \(\left( {\sigma_{0} } \right)\) to applied load per depth ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) and shape factor of the hysteresis loop \(\delta_{D}\) as:

$$F = f\left( {\mu_{C} ,X,{{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N},\delta_{D} } \right) \times N,$$
(26)

where \(f\left( {\mu_{C} ,X,{{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N},\delta_{D} } \right)\) is the normalized friction force which can be obtained by dividing friction force by applied normal load. Parameters \(\mu_{C} ,\)\({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\), \(\delta_{D}\) describe the shape of Dahl’s dynamic friction force curve illustrated in Fig. 2, \(F\) or normalized friction force \(f = F/N\) is calculated at some pre-sliding displacement \(X\) values. Therefore, instead of assigning constant coefficient of friction and the friction force for all the motion of the punch, friction force applied to punch is calculated as function of \(\mu_{C} ,\)\(X,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\),\(\delta_{D}\). Dag [52] studied the spatial variation of the coefficient of friction due to the utilization of graded material in horizontal direction. However, the spatial variation of the friction force beneath the flat punch is ignored in the present study. Equilibrium equation requires that the integral of the normal stress on the contact surface should be equal to the applied normal load \(N.\)

$$\int\limits_{ - a}^{a} {\sigma \left( X \right)dX = - N.}$$
(27)

Unknowns \(M_{j} \;\left( {{\text{j = 1,}}...{,4}} \right)\) in displacement components provided by Eqs. (17)-(18) are not provided explicitly for brevity.

3 Solution technique

Analytical solution of the contact problem is performed based on the singular integral equation technique (SIE). The singular integral equation of the contact problem is obtained by the use of displacement derivative condition beneath the flat punch which necessitates:

$$v\left( {X,0} \right) = - v_{0} ,\,\, - a < X < a,$$
(28)
$$\frac{{\partial v\left( {X,0} \right)}}{\partial X} = 0,\,\, - a < X < a,$$
(29)

Asymptotic analyses are conducted to extract the singularity of the integral equation. At the end of mathematical manipulations, the singular integral equation of the problem can be written as follows:

$$- \omega_{2} \,f\,\sigma \left( X \right) - \frac{1}{\pi }\int\limits_{ - a}^{a} {\frac{{\pi \,\omega_{1} }}{t - X}} \,\sigma \left( t \right)\,dt = r\left( X \right),$$
(30)

where \(r\left( X \right) = {{4\mu } \mathord{\left/ {\vphantom {{4\mu } {\left( {\kappa + 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\kappa + 1} \right)}}\,{{\partial v\left( {X,0} \right)} \mathord{\left/ {\vphantom {{\partial v\left( {X,0} \right)} {\partial X}}} \right. \kern-\nulldelimiterspace} {\partial X}},\) and \(r\left( X \right) = 0\) for the rigid flat punch since derivative of the displacement equals to zero beneath the flat punch. The constants \(\omega_{1}\) and \(\omega_{2}\) depend on the first terms of asymptotic expansions.

$$\omega_{1} = \frac{{4\,\left( {e_{10} + e_{20} } \right)}}{{\pi \,\left( {\kappa + 1} \right)}},\,\,\omega_{2} = \frac{{4\,\left( {f_{10} + f_{20} } \right)}}{{\,\left( {\kappa + 1} \right)}},$$
(31)

In-plane stress on the contact surface is another significant stress component to be calculated since this stress component may play an important role in the occurrence of possible surface related failures such as surface cracking and propagating of the previously existing surface cracks. In-plane stress component is calculated considering Hooke’s law, constitutive relations and displacement gradients on the contact surface \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial X}}} \right. \kern-\nulldelimiterspace} {\partial X}}\) and \({{\partial v} \mathord{\left/ {\vphantom {{\partial v} {\partial Y}}} \right. \kern-\nulldelimiterspace} {\partial Y}}.\) After performing asymptotic analysis and mathematical manipulations, in-plane stress on the contact surface can be written as:

$$\sigma_{XX} \left( {X,0} \right) = \left( {2\omega_{4} + \frac{3 - \kappa }{{\kappa + 1}}} \right)\,\sigma \left( X \right) + \frac{2}{\pi }\int\limits_{ - a}^{a} {\frac{{f\pi \omega_{3} }}{t - X}} \,\sigma \left( t \right)\,dt$$
(32)

In Eqs. (30)–(32), \(f\) denotes normalized friction force which can be expressed as a function \(f = f\left( {\mu_{C} ,X,{{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} {N,\delta_{D} }}} \right. \kern-\nulldelimiterspace} {N,\delta_{D} }}} \right).\) The constants \(\omega_{3}\) and \(\omega_{4}\) depend on the first terms of asymptotic expansions.

$$\omega_{3} = \frac{{4\,\left( {g_{10} + g_{20} } \right)}}{{\pi \,\left( {\kappa + 1} \right)}},\,\,\omega_{4} = \frac{{4\,\left( {h_{10} + h_{20} } \right)}}{{\,\left( {\kappa + 1} \right)}},$$
(33)

First terms of asymptotic expansions \(\left( {e_{10} + e_{20} } \right),\) \(\left( {f_{10} + f_{20} } \right),\) \(\left( {g_{10} + g_{20} } \right),\) \(\left( {h_{10} + h_{20} } \right)\) are functions of material properties and dimensionless punch speed. Singular integral equation of the contact problem can be solved by either theoretical or numerical methods. In the present study, we adopted a numerical method called as expansion-collocation method [53]. Before applying this technique, singular integral equation has to be normalized such as:

$$X = a\,r,\,\, - a < X < a,\, - 1 < r < 1,$$
(34)
$$t = a\,s,\,\, - a < X < a,\,\, - 1 < s < 1,$$
(35)
$$\rho = \left( {{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-\nulldelimiterspace} a}} \right)\,\zeta ,$$
(36)
$$\sigma \left( X \right) = \sigma \left( {ar} \right) = - \left( {{N \mathord{\left/ {\vphantom {N a}} \right. \kern-\nulldelimiterspace} a}} \right)\,\phi \left( r \right),\,\sigma \left( t \right) = \sigma \left( {as} \right) = - \left( {{N \mathord{\left/ {\vphantom {N a}} \right. \kern-\nulldelimiterspace} a}} \right)\,\phi \left( s \right),$$
(37)

The normalized singular integral equation has the following form:

$$\omega_{2} \,f\,\phi \left( r \right) + \frac{1}{\pi }\int\limits_{ - 1}^{1} {\frac{{ - \pi \,\omega_{1} }}{s - r}} \,\phi \left( s \right)\,ds = 0,\, - 1 < r < 1,$$
(38)

The equilibrium equation in the normalized form becomes:

$$\int\limits_{ - 1}^{1} {\phi \left( s \right)ds = 1.}$$
(39)

The solution of the singular integral equation can be done by the use of series expansion such that [16]:

$$\phi \left( r \right) = W\left( r \right)\,\sum\limits_{j = 0}^{\infty } {A_{j} \,P_{j}^{{\left( {\alpha ,\beta } \right)}} \left( r \right)} ,\, - 1 < r < 1.$$
(40)

where \(c_{j} \,\left( {j \ge 0} \right)\) are the unknown coefficients to be determined. \(P_{j}^{{\left( {\alpha ,\beta } \right)}} \left( s \right)\) is the Jacobi polynomial of order \(j\) and \(W\left( s \right)\) is the corresponding weight function defined by,

$$W\left( r \right) = \left( {1 - r} \right)^{\alpha } \,\left( {1 + r} \right)^{\beta } ,\, - 1 < r < 1.$$
(41)

\(\alpha\) and \(\beta\) are the powers of the stress singularities. Due to the physics of the flat punch problem, both \(\alpha\) and \(\beta\) should be negative. Powers of the stress singularities are expressed as [54]:

$$\begin{gathered} f > 0:\quad \alpha = - 1 + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \pi }} \right. \kern-\nulldelimiterspace} \pi }\,,\;\beta = - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \pi }} \right. \kern-\nulldelimiterspace} \pi }\,, \hfill \\ f = 0:\quad \alpha = - 0.5,\quad \beta = - 0.5, \hfill \\ f < 0:\quad \alpha = - {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \pi }} \right. \kern-\nulldelimiterspace} \pi },\;\beta - 1 + {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \pi }} \right. \kern-\nulldelimiterspace} \pi }. \hfill \\ \end{gathered}$$
(42)
$$\varepsilon = \tan^{ - 1} \left( {\left| {{{\pi \omega_{1} } \mathord{\left/ {\vphantom {{\pi \omega_{1} } {\left( {f\,\omega_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {f\,\omega_{2} } \right)}}} \right|} \right).$$
(43)

The normalized friction force \(f\) is calculated numerically by solving Eqs. (3), (4) through the implementation of 4th order Runge–Kutta formulation [55]. Firstly, the pre-displacement interval of the hysteresis loop is specified as \(L = \left( {x_{f} - x_{i} } \right) = 0.1mm\) [44]. Then, other parameters such as punch speed \(V,\) Coulomb’s coefficient of friction \(\mu_{C} ,\) asperity stiffness \(\sigma_{0} ,\) and shape factor \(\delta_{D}\) are determined. For the first forward motion (1st FM), \(x_{f} = 0.0001\,{\text{m}}\) and \(x_{i} = 0.\) Increment amount is specified as:

$$h = {{\left( {x_{f} - x_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {x_{f} - x_{i} } \right)} {20}}} \right. \kern-\nulldelimiterspace} {20}}$$
(44)

Initial conditions are:

$$x\left( 0 \right) = 0,\,z\left( 0 \right) = 0,$$
(45)

Coefficients for the 4th order Runge–Kutta method at each displacement step is found by,

$$k_{1i} = d\left( {x_{i} ,z_{i} ,V,\mu_{C} ,\sigma_{0} ,N,\delta_{D} } \right),$$
(46)
$$k_{2i} = d\left( {x_{i} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2},z_{i} + \left( {k_{1i} /2} \right)h,V,\mu_{C} ,N,\sigma_{0} ,\delta_{D} } \right),$$
(47)
$$k_{3i} = d\left( {x_{i} + {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2},z_{i} + \left( {k_{2i} /2} \right)h,V,\mu_{C} ,N,\sigma_{0} ,\delta_{D} } \right),$$
(48)
$$k_{4i} = d\left( {x_{i} + h,z_{i} + z_{i} + \left( {k_{3i} \,h} \right),V,\mu_{C} ,N,\sigma_{0} ,\delta_{D} } \right),$$
(49)
$$z_{i + 1} = z_{i} + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-\nulldelimiterspace} 6} \times \left( {k_{1i} + 2k_{2i} + 2k_{3i} + k_{4i} } \right) \times h,$$
(50)

where \(d = \frac{dz}{{dx}} = {\text{sign}}\left( {1 - {\text{sign}}\left( V \right)\,\frac{{\sigma_{0} \,z}}{{F_{C} }}} \right)\,\left| {1 - {\text{sign}}\left( V \right)\,\frac{{\sigma_{0} \,z}}{{F_{C} }}} \right|^{{\delta_{D} }} .\) The non-dimensional friction force at each displacement step is then calculated as follows:

$$f_{i} = {{\sigma_{0} \,z_{i} } \mathord{\left/ {\vphantom {{\sigma_{0} \,z_{i} } N}} \right. \kern-\nulldelimiterspace} N}.$$
(51)

Table 1 shows non-dimensional friction force values \(f_{i}\) and coefficients of 4th order Runge–Kutta method \(k_{ji} \,\left( {{\text{j = 1,}}...{,4}} \right)\) with respect to some pre-sliding displacements.

Table 1 Some values of non-dimensional friction force and coefficients of 4th order Runge–Kutta method \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\,,\), \(\mu_{C} = 0.5.\)
Full size table

Applying the orthogonality property of the Jacobi polynomials [16, 56, 57], one can obtain the following functional equation:

$$\sum\limits_{j = 0}^{\infty } {c_{j} } \;\left[ {\frac{{\pi \,\omega_{1} }}{{2\sin \left( {\pi \alpha } \right)}}\,P_{j - 1}^{{\left( { - \alpha , - \beta } \right)}} \left( r \right)} \right] = 0,\, - 1 < r < 1.$$
(52)

Equation (52) is truncated at \(j = N\) and it yields \(N \times N\) linear algebraic equation system. Collocation points are selected as the roots of the Jacobi polynomials [16].

$$P_{N - 1}^{{\left( {\alpha + 1,\beta + 1} \right)}} \left( {r_{k} } \right) = 0,\,k = 1,...,N.$$
(53)

Comparing both sides of Eq. (52), the only non-zero coefficient is found as \(A_{0}\) which is expressed by,

$$A_{0} = - {{\sin \left( {\pi \alpha } \right)} \mathord{\left/ {\vphantom {{\sin \left( {\pi \alpha } \right)} \pi }} \right. \kern-\nulldelimiterspace} \pi }.$$
(54)

The normal stress on the contact surface can be expressed as follows:

$$\frac{{\sigma_{YY} \left( {X,0} \right)}}{{\left( {{N \mathord{\left/ {\vphantom {N {2a}}} \right. \kern-\nulldelimiterspace} {2a}}} \right)}} = - \frac{{2\sin \left( {\pi \alpha } \right)}}{\pi }\,\left( {1 - \frac{X}{a}} \right)^{\alpha } \,\left( {1 + \frac{X}{a}} \right)^{\beta } ,\,\, - a < X < a,$$
(55)

Once the normal contact surface on the contact surface is determined, in-plane contact stress can be calculated by substituting normal stress into Eq. (32). The mode-I stress intensity factors at the edges of the flat punch can be calculated as follows [16]:

$$k_{I} \left( { - a} \right) = \mathop {\lim }\limits_{X \to - a} \; - \frac{{\sigma_{YY} \left( {X,0} \right)}}{{2^{\alpha } \,\left( {a + X} \right)^{\beta } }} = \frac{{{N \mathord{\left/ {\vphantom {N a}} \right. \kern-\nulldelimiterspace} a}}}{{a^{\beta } }}\,A_{0} ,$$
(56)
$$k_{I} \left( a \right) = \mathop {\lim }\limits_{X \to a} \; - \frac{{\sigma_{YY} \left( {X,0} \right)}}{{2^{\beta } \,\left( {a - X} \right)^{\alpha } }} = \frac{{{N \mathord{\left/ {\vphantom {N a}} \right. \kern-\nulldelimiterspace} a}}}{{a^{\alpha } }}\,A_{0} ,$$
(57)

In normalized form, punch stress intensity factors (SIFs) are determined by,

$$K_{I} \left( { - a} \right) = K_{I} \left( a \right) = - \frac{{\sin \left( {\pi \alpha } \right)}}{\pi }.$$
(58)

4 Finite element method

Finite element method (FEM) has been frequently used in the solution of complex engineering problems [58]. The procedure shown by Fig. 3 shows the implementation of Dahl’s friction force to FE procedure and getting the contact stresses. For the verification of the present analytical study, a computational model involving a rigid flat punch and a homogenous elastic half-plane is constructed and it is illustrated in Fig. 4. The dimensions of the homogenous elastic half-plane is kept large to avoid any dimensional effects. Hence, dimensional ratios are \({{l_{p} } \mathord{\left/ {\vphantom {{l_{p} } W}} \right. \kern-\nulldelimiterspace} W} = 0.01,\) and \({{l_{p} } \mathord{\left/ {\vphantom {{l_{p} } H}} \right. \kern-\nulldelimiterspace} H} = 0.02.\) Normal load applied to the rigid punch is denoted by \(N\) and friction force is indicated by \(F\) whose direction may change depending on the motion cycle. For instance, the direction of \(F\) is towards right direction for the 1st Forward Motion (1st FM, \(\dot{X} > 0\)) while its direction is towards left for the 1st Backward Motion (1st BM, \(\dot{X} < 0\)). The magnitude of friction force \(F\) is calculated by multiplying non-dimensional friction force \(f\) by applied normal load \(N\).

Fig.3
figure 3

Scheme showing the implementation of Dahl’s friction model to FE procedure

Full size image
Fig. 4
figure 4

Finite element model established for the contact problem

Full size image

Dahl’s friction force is calculated by Runge–Kutta method for various values of parameters \(\mu_{C} ,\) \(\sigma_{0} l/N,\) \(X/L\), \(\delta_{D}\). Hence, the influence of these parameters on contact stresses are observed. The finite element mesh consists of 145,106 PLANE183 quadrilateral elements in total and contact surface is discretized by CONTA172 and TARGE169 elements available in ANSYS [59].

The motion of the rigid punch is controlled by a pilot node which is created at the center of the punch. Homogenous elastic half-plane is divided into two regions called as Zone 1 and Zone 2. Zone 1 consists of PLANE 183 quadrilateral elements with their triangular shape option. Triangular shape of PLANE183 is generated by merging three nodes of element at one single point. Hence, each element in Zone 1 covers smaller area than those elements used in Zone 2, which leads to utilization of greater number of elements. Moreover, density of the finite element mesh in Zone 1 is increased around the contact region in order to capture the sharp variations in the stress components. There are various methods for the solution of contact problems computationally such as Penalty, Lagrange, Lagrangian Multiplier and Augmented Lagrangian. In the present study, the Augmented Lagrangian method is adopted since this method provides better results in a faster way when compared to other methods [60]. Stainless Steel (T302) is selected as a homogenous isotropic material utilized in analyses. The properties of Stainless Steel (T302) are provided in Table 2.

Table 2 Material properties used in the simulations [63]
Full size table

Figure 5 shows the contact stress results obtained by present analytical study and those generated through the finite element analysis together in the same figure. Black and red solid lines respectively show the contact stress distributions found by analytical approach for dimensionless pre-sliding displacements \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\) and \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) While the former pre-sliding displacement indicates the early stages of the pre-sliding of the hysteresis loop, the latter one shows the closer site to the end of the pre-sliding. Figure 5(a),(b) show the normal and in-plane contact stresses for the first forward motion (1st FM), Fig. 5(c), (d) illustrate the normal and in-plane contact stresses for the first backward motion (1st BM), and Fig. 5(e),(f) indicate those stress components for the second forward motion (2nd FM). In this analysis, the speed of the punch is so slow \(V = 1.5 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\) hence performing elastostatic contact simulation is applicable in this kind of contact problem. For the 1st BM, tensile in-plane stress occurs around \({X \mathord{\left/ {\vphantom {X a}} \right. \kern-\nulldelimiterspace} a} = 1\) due to the change of the direction of motion. It can be inferred from Fig. 4 that contact stresses obtained by analytical approach and those of finite element analysis agree very well. Thus, verification of present analytical study is accomplished.

Fig. 5
figure 5

a, b Normal and in-plane contact stresses for the 1st Forward Motion (1st FM), c, d Normal and in-plane contact stresses for the 1st Backward Motion (1st BM), e, f Normal and in-plane contact stresses for the 2nd Forward Motion (2nd FM); \(V = 1.5 \times 10^{ - 3} \,{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},\) \(\mu_{C} = 0.7,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\;,\) \(\delta_{D} = 1.0\)

Full size image

5 Results

In this section, hysteresis loops, contact stresses and punch stress intensity factors are presented. Firstly, hysteresis loop of normalized friction force as a function of displacement is provided. In Piatkowski’s study [44], asperity stiffness and applied normal load are given as \(\sigma_{0} = 1.5922\;{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\mu m}}}} \right. \kern-\nulldelimiterspace} {{\mu m}}}\) and \(N = 55.3\;{\text{N}},\) hence dimensionless parameter can be written as \(\sigma_{0} l/N = 28792\) per depth of the contact model. Driving velocity for the Dahl’s dynamic friction model is generally assumed in the interval \(V = 0.5 - 1.5\;{{ \times {10}^{ - 3} {\text{m}}} \mathord{\left/ {\vphantom {{ \times {10}^{ - 3} {\text{m}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\) [44, 61, 62] which can be regarded as slow speed sliding. In the present study, however, two different velocity values are used. Sliding speeds \(V = 1.5\;{{ \times {10}^{ - 3} {\text{m}}} \mathord{\left/ {\vphantom {{ \times {10}^{ - 3} {\text{m}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\) and \(V = 1.884\;{{ \times {10}^{3} {\text{m}}} \mathord{\left/ {\vphantom {{ \times {10}^{3} {\text{m}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}}\) are designated to simulate both slow and high speed sliding cases, respectively. Hence, dimensionless punch speeds for each case are determined as \(c = 4.786 \times 10^{ - 7}\) and \(c = 0.6,\) respectively. The former dimensionless speed is very close to zero hence, dynamic effects due to the speed of the punch will be minimal. However, the latter speed is very high and punch dynamics will be influential in this case. These two sliding cases are named as slow speed and high speed sliding cases and they are denoted by the abbreviations ‘SS’ and ‘HS’ as shown in Table 3. The pre-sliding displacement of the hysteresis loop of friction force is determined as L = 0.1 mm [44]. If friction force reaches its steady saturated level within this interval, the actual pre-sliding displacement can be \(L_{a} < L{.}\) On the other hand, if friction force is not able to reach steady saturated level within \(L,\) the actual pre-sliding displacement is greater than \(L_{a} > L{.}\)

Table 3 Speeds of the punch for slow speed (SS) and high speed (HS) sliding cases
Full size table

Figure 6(a) shows hysteresis loop of normalized friction force \(f\) for different dimensionless punch speed \(c\). It can be observed that friction force does not depend on punch speed as concluded in Ref. [46]. Figure 6(b) indicates hysteresis loop of normalized friction force for various values of Coulomb’s friction in the pre-sliding interval. In the beginning of the 1st Forward Motion (1st FM), there is no friction force applied to the rigid punch in all cases. However, normalized friction force \(f\) gradually develops as the rigid punch displacement \(X\) increases. Although friction force reaches its steady value at early stages of displacement for \(\mu_{C} = 0.1\) such as \(x = 0 - 0.01{\text{mm}}\), a greater displacement value is required to obtain steady value of friction for larger \(\mu_{C}\) such as \(\mu_{C} = 0.5,\) \(\mu_{C} = 0.7.\) The difference between friction force acquired by 1st Forward Motion (1st FM) and 2nd Forward Motion (2nd FM) seems greater for larger values of coefficient of friction. Figure 5(c) depicts the hysteresis loop of normalized friction force as functions of \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}.\) Instead of increasing the asperity stiffness \(\sigma_{0}\) solely, the dimensionless ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is altered parametrically since change in the asperity stiffness and applied normal load per depth at the same proportion does not lead to any change in the hysteresis loop of friction force. Hence, asperity stiffness \(\sigma_{0}\) is changed relatively to the applied normal load per depth \(N/l\). Coulomb’s coefficient of friction is taken as \(\mu_{C} = 0.5.\) As the ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased, the required displacement is decreased to get steady saturated friction force. It is noteworthy to say that for surfaces with higher asperity stiffness, friction force develops more quickly and reaches steady level which indicates that pre-sliding displacement is smaller and gross sliding begins earlier. The difference between friction forces obtained at 1st Forward Motion (1st FM) and 2nd Forward Motion (2nd FM) becomes larger for surfaces with lower asperity stiffness. Figure 6(d) demonstrates hysteresis loop of friction force as functions of loop shape factor \(\delta_{D} .\). The loop shape factor depends on material properties. \(\delta_{D}\) is always greater than zero.

Fig. 6
figure 6

Hysteresis loop of normalized friction force as a function of displacement for various values of a Dimensionless punch speed \(c,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\,,\) \(\mu_{C} = 0.7,\) \(\delta_{D} = 1.0,\) b Coulomb’s coefficient of friction \(\mu_{C} ,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\,,\)\(\delta_{D} = 1.0,\) c Asperity stiffness to normal load per depth ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N},\) \(\mu_{C} = 0.5,\) \(\delta_{D} = 1.0,\) d shape factor \(\delta_{D} ,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\,,\) \(\mu_{C} = 0.5.\)

Full size image

Bliman [64] stated that the loop shape factor is in the interval of \(0 \le \delta_{D} < 1,\) for brittle materials and \(\delta_{D} \ge 1,\) for more ductile like materials. Hence, \(\delta_{D}\) is changed parametrically between 0.8 and 1.5. As \(\delta_{D}\) is decreased, frictional force reaches to steady value at early stages of pre-sliding displacement. However, increase in \(\delta_{D}\) leads to decrease in the friction force at whole range of displacement. Hence, friction force slowly develops on the surface of more ductile like materials. Figure 7 shows normalized normal and in-plane contact stresses for 1st Forward Motion (1st FM), 1st Backward Motion (1st BM) and 2nd Forward Motion (2nd FM). Solid lines display the contact stress results at small speed sliding case (SS) in which \(V = 1.5\;{{{\text{mm}}} \mathord{\left/ {\vphantom {{{\text{mm}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},\) or \(c = 4.786 \times 10^{ - 7} ,\) dot points indicates those obtained at high speed sliding case (HS) where \(V = 1880.4\;{{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}},\) or \(c = 0.6.\) Figures 7(a)-(b) are obtained for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) which can be considered as the beginning stage of the pre-sliding displacement of the hysteresis loop. Figure 7c, d show stress results for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.5\) and Figs 7e, f depict stress results for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0.\)

Fig. 7
figure 7

a, b Normal and in-plane contact stress at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) c, d Normal and in-plane contact stress at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.5,\) e, f Normal and in-plane contact stress at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0;\) \(\mu_{C} = 0.7,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000,\) \(\delta_{D} = 1.0\)

Full size image

Although there is a slight difference between normal stress curves obtained for 1st FM, 1st BM at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) this difference becomes notable at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.5\) and \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0\). However, normal contact stress obtained at 2nd FM becomes almost the same as that obtained for the 1st FM at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.5\) and \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0\). Normal contact stresses calculated for small speed sliding case (SS) and high speed sliding case (HS) are very close to each other in all cases. Due to the direction of motion, in-plane contact stress varies. In all cases, there is a stress singularity at contact ends. The tensile in-plane stress peak is observed at trailing end for 1st FM, it is seen at the leading end for 1st BM and it is seen at the trailing end for 2nd FM, again. At the beginning stage of the pre-sliding interval \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) in-plane stress for 2nd FM seems decreased relatively to that obtained for the 1st FM over the contact surface. For larger values of \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L},\) difference between in-plane contact stress obtained for 1st FM and 2nd FM is gradually decreased and it is almost negligible for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0.\) Moreover, in-plane contact stresses calculated at high speed sliding (HS) and slow speed sliding (SS) cases seem different. In HS case, in-plane contact stresses are greater along the contact. The difference between in-plane contact stresses calculated at HS and SS cases gradually increases as illustrated in Fig. 7e, f.

Figure 8 shows the normal and in-plane contact stresses for various values of Coulomb’s coefficient of friction for 1st Forward Motion (1st FM). Figure 8a, b provide contact stresses for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\)and Fig. 8c, d present those for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) It can be inferred from these figures that friction force does not develop so much at the beginning of the hysteresis loop i.e. \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2.\) However, friction force develops and becomes close to its saturated level towards the end of the hysteresis loop, i.e. \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) The change in contact stress with respect to different \(\mu_{C}\) seems larger at Fig. 8c, d than that observed at Fig. 8a, b since friction force developed and it almost reaches the steady saturated level at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) On the contrary, contact stress curves are close to each other in the case of \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\) due to early stage of pre-sliding and lower values of friction force. Normal contact stresses obtained for slow speed and high speed sliding cases are close to each other as shown in Fig. 8a–c. When in-plane contact stresses are examined, it can be seen that there is a remarkable difference between stresses in the contact zone. In-plane stresses at HS case is more compressive than stresses generated at SS case. Outside the contact region, the magnitude of in-plane stresses for HS case is greater than those obtained for SS case. At \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) although difference between HS and SS in-plane stresses seems slight outside the contact region, a notable difference occurs between HS and SS stresses for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) Moreover, change in the in-plane contact stress due to alteration of \(\mu_{C}\) is observed greater for the \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8\) case when compared to \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2.\)

Fig. 8
figure 8

a, b Normal and in-plane contact stress at 1st Forward motion (FM)\({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) c, d Normal and in-plane contact stress at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000,\) \(\delta_{D} = 1.0\)

Full size image

Figure 9 illustrates the influence of \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) ratio on contact stresses. \(\sigma_{0}\) shows the asperity stiffness in \(\left[ {{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{mm}}}}} \right. \kern-\nulldelimiterspace} {{\text{mm}}}}} \right]\) and \(N\) indicates the applied normal load to the flat punch in \(\left[ {\text{N}} \right].\) Hence, \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is the dimensionless parameter where \(N/l\) shows applied load per depth for the two-dimensional model. Figure 9a, b display contact stress distributions for the 1st Forward motion (1st FM). When the ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased, normal contact stress slightly slants towards the leading end. Moreover, normal stresses for HS and SS cases are quite close to each other. While increase in the ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) results in a formation of larger tensile in-plane stresses behind the trailing end of the contact, it leads to occurrence of larger compressive stresses ahead of the contact. In-plane stresses obtained for HS case in the contact region is greater than those obtained for SS case. The difference between in-plane stresses acquired at HS and SS cases becomes larger as the ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased. Figure 9c, d depict contact stress results for the 2nd Forward Motion (2nd FM). As the ratio \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased, normal contact stress slightly leans towards the leading end as found in Fig. 9a. However, in this case, the direction of friction force is in the opposite direction when \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 12500\) and it turns out to be same direction for larger values of \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}.\) This conclusion is also true for both SS and HS sliding cases. As \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased, in-plane contact stress increases in the contact region and greater tensile in-plane stress occurs behind the trailing end. Stresses ahead of the contact region becomes much compressive. When Fig. 9b–d are examined, difference between stress curves obtained for SS and HS cases is larger at 2nd FM when compared to that occurs at 1st FM in Fig. 9b.

Fig. 9
figure 9

a, b Normal and in-plane contact stress at 1st Forward motion (1st FM) c, d Normal and in-plane contact stress at 2nd Forward Motion (2nd FM); \(\mu_{C} = 0.5,\)\({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2,\) \(\delta_{D} = 1.0\)

Full size image

Figure 10 shows the influence of the shape factor \(\delta_{D}\) of the hysteresis loop on contact stresses at 1st Forward Motion (1st FM). As \(\delta_{D}\) is increased, normal contact stress slightly decreases around the trailing end while it slightly increases around the leading end. Stresses obtained at slow speed and high speed sliding conditions are close to each other as depicted in Fig. 10a. When \(\delta_{D}\) is increased, in-plane stress in the contact region slightly decreases. Moreover, increase in the shape factor \(\delta_{D}\) results in a formation of tensile in-plane stresses with lower in magnitude behind trailing end. In-plane contact stress ahead of the contact region slightly decreases as well. This conclusion is also true for not only in-plane stresses obtained in SS case but also true for those generated in HS case. The main difference between in-plane stresses obtained at SS and HS cases is observed in the contact region. In high speed sliding case (HS), in-plane stresses are much compressive due to boosted impact of punch dynamics.

Fig. 10
figure 10

a, b Normal and in-plane contact stress at 1st Forward motion (FM)\({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.4,\) \(\mu_{C} = 0.5,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\)

Full size image

Table 4 tabulates the stress intensity factors (SIFs) at sharp ends of the flat punch for slow speed sliding case (SS) where dimensionless punch speed is set to \(c = 4.786 \times 10^{ - 7} .\) In this case, dynamic impact of the punch is almost negligible since speed of the punch is very low. Non-dimensional stress intensity factor at the trailing end of the punch is shown by \(K_{I} \left( { - a} \right)\) while that at the leading end of the punch is indicated by \(K_{I} \left( a \right).\) Three consecutive motions, i.e. 1st FM, 1st BM and 2nd FM, and two different non-dimensional pre-sliding locations are selected. For all three motions, SIFs at leading and trailing ends are equal to each other and they vary with respect to non-dimensional pre-sliding location. For the 1st FM and 2nd FM, SIFs obtained at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8\) are less than those obtained at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\) whereas for the 1st BM, SIFs generated for \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\) are less than those generated at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\)

Table 4 Punch stress intensity factors at different locations in the hysteresis loop of friction force for SS case \(c = 4.786 \times 10^{ - 7} ,\) \(\mu_{C} = 0.7,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\)
Full size table

Table 5 lists the SIFs at punch ends for high speed sliding case (HS) where \(c = 0.6\). For the 1st FM and 2nd FM, punch stress intensity factors obtained at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8\) are less than those obtained at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2.\) However the reverse trend is observed for SIFs for 1st BM as seen in Table 4. Percent difference values are calculated between SIFs obtained at \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\) and \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.8.\) Results indicate that percent difference (Diff%) between SIFs obtained for high speed sliding case (HS) are greater than those acquired for slow speed sliding case (SS).

Table 5 Punch stress intensity factors at different locations in the hysteresis loop of friction force for HS case \(c = 0.6,\) \(\mu_{C} = 0.7,\) \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N} = 25000\).
Full size table

6 Conclusions

In this study, the implementation of Dahl’s dynamic friction model to contact mechanics of elastic isotropic solids is presented. Dynamic contact problem between a rigid flat punch and an isotropic elastic medium is treated and governing partial differential equations are derived based on theory of elasticity and equations of motion. According to Dahl’s friction model, it is observed that friction force applied to the punch depends on the Coulomb’s coefficient of friction, pre-sliding displacement, asperity stiffness/normal load per depth and hysteresis loop shape factor. Friction force is calculated for various values of pre-sliding displacement utilizing 4th order Runge–Kutta method. Analytical solutions are presented by the use of singular integral equation (SIE) technique. In addition, computational results are obtained by means of finite element method. Direct comparisons indicate that results of these two methods display a high degree of accuracy. Then, influences of Coulomb’s coefficient of friction, pre-sliding displacement, asperity stiffness/normal load per depth ratio and hysteresis loop shape factor on contact stresses are investigated for not only for small speed sliding (SS) case but also in high speed sliding (HS) case. The following conclusions can be drawn from the present study:

  • Normalized friction force in the hysteresis loop does not change even if punch speed reaches 0.6 times of shear wave propagation speed of the elastic body. This conclusion is also drawn by Dahl’s friction model. However, as punch speed is increased to greater levels, punch dynamics becomes influential on contact problem. Although there is a slight difference between normal contact stresses in SS and HS cases, a remarkable change is observed in the in-plane stress component. In-plane stress calculated in the HS case is much compressive in the contact zone.

  • Normal and in-plane contact stresses are calculated for different pre-sliding displacements. In early stages of pre-sliding (i.e. \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.2\)), contact stresses calculated at 1st FM, 1st BM and 2nd FM seem quite different from each other, however, at the end of pre-sliding interval (i.e. \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0\)) contact stresses calculated at 1st FM and 2nd FM starts to coincide with each other. It should also be remarked that difference between contact stresses obtained for high speed sliding case (HS) and slow speed sliding case (SS) tend to increase at further sites of pre-sliding displacement such as \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 0.5,\) \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L} = 1.0.\)

  • Coulomb’s coefficient of friction has a crucial impact on contact stresses. As coefficient of friction is increased, normal stress slants towards the leading end, and in-plane stress may reach considerable tensile level around the trailing end. Increase in coefficient of friction leads to greater change in contact stress at further sites of pre-sliding displacement when compared to that occurred at early stage of pre-sliding. Difference between contact stresses obtained for HS and SS cases becomes notable for greater values of coefficient of friction \(\mu_{C}\) and pre-sliding displacement \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L}.\) Contacting body may expose to surface cracking type failure due to the high tensile in-plane stress around trailing end especially for greater values of \(\mu_{C}\) and \({X \mathord{\left/ {\vphantom {X L}} \right. \kern-\nulldelimiterspace} L}.\)

  • Asperity stiffness to normal load per depth ratio \(\left( {{{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}} \right)\) affects contact stresses. As \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) is increased, normal stress leans towards the leading end and greater compressive in-plane stress is formed in the contact region. Increase in the \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}\) ratio results in a formation of greater tensile in-plane stress around the trailing end. At early stages of pre-sliding, the direction of friction force can remain in the opposite direction for the 2nd forward motion (2nd FM) especially for lower values of \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N},\) which makes in-plane stress tensile at the leading end. Difference observed between contact stresses obtained for HS and SS cases becomes remarkable at 2nd FM for larger values of \({{\sigma_{0} l} \mathord{\left/ {\vphantom {{\sigma_{0} l} N}} \right. \kern-\nulldelimiterspace} N}.\)

  • Shape factor of the hysteresis loop has a slight impact on contact stresses for both SS and HS sliding cases. As \(\delta_{D}\) is increased, normal contact stress slightly increases around the leading end. Increase in \(\delta_{D}\) leads to formation of in-plane contact stress with lower magnitude along the contact. In-plane contact stresses generated for HS sliding case is observed greater than those obtained for SS sliding case.

  • Friction force beneath the flat punch is assumed constant, and it can be regarded as a limitation of the present study. The spatial variation of the coefficient of friction affects the contact stress distributions [52]. This study presents contact mechanics analysis based on Dahl’s friction model which is used to simulate pre-displacement and hysteresis. Nevertheless, there are some advanced dynamic friction models in the literature which consider the rate dependency due to the viscous effect, and able to capture Stribeck effect and stiction behavior.

  • Application of different dynamic friction models to contact stress analysis of solids will be an interesting work. Thus, an assessment of friction models based on contact stress will be made.

  • Implementation of different dynamic friction models to contact mechanics of composite/anisotropic materials will be a future work since composite/anisotropic materials have been widely utilized in aerospace and robotic/control systems.

It is believed that contact stress results obtained in the present study may be useful for understanding the wear and fatigue behavior of elastic solids which are especially utilized as a mechanical component in mechanisms and robotic/control systems.