Abstract
Blast-induced ground vibration is still an adverse impact of blasting in civil and mining engineering projects that need much consideration and attention. This study proposes the use of Self-Adaptive Differential Evolutionary Extreme Learning Machine (SaDE-ELM) for the prediction of ground vibration due to blasting using 210 blasting data points from an open pit mine in Ghana. To ascertain the predictive performance of the proposed SaDE-ELM approach, several artificial intelligence and empirical approaches were developed for comparative purposes. The performances of various developed models were assessed using model performance indicators of mean squared error (MSE), Nash–Sutcliffe Efficiency Index (NSEI) and correlation coefficient (R). Furthermore, the Bayesian Information Criterion (BIC) was applied to select the best performing approach. The obtained prediction results based on the performance indicators showed that the SaDE-ELM outperformed all the competing models as it had the lowest MSE value of 0.01942, respectively. The SaDE-ELM also achieved the highest R and NSEI values of 0.8711 and 0.7537, respectively. The other artificial intelligent approaches had MSE, R and NSEI in the ranges of (0.02166–0.03006), (0.8012–0.8537) and (0.6188–0.7254), respectively. The empirical approaches performed poorly relative to the artificial intelligence approaches by having had MSE, R and NSEI in the ranges of (0.03419–0.06587), (0.7466–0.7833) and (0.1649–0.5665), respectively. The prediction superiority of SaDE-ELM was confirmed when it is achieved the lowest BIC value of − 293.40. Therefore, the proposed SaDE-ELM has demonstrated great potential to be used for on-site prediction, control and management of blast-induced ground vibration to prevent unwanted effects on the environment.
Similar content being viewed by others
1 Introduction
Blast-induced ground vibrations are a major environmental impact of blasting that results from seismic waves moving through the ground. It is noteworthy that the resulting ground vibration after a blast is unavoidable. However, the magnitude of occurrence is of utmost concern as higher magnitude can cause damage to mining pit wall, cracks on buildings of the neighbouring community, disturbance to humans and can even result in conflict between the mining company and the neighbouring community. Hence, there is a need to predetermine their level of occurrence before each blast is carried out through modelling and prediction.
In modelling and prediction of blast-induced ground vibration, several approaches ranging from conventional empirical approaches [1,2,3,4,5] to the use of computational intelligence ([6,7,8] and references therein) have been developed with the latter being superior to the former [9, 10]. It is worth mentioning that several computational intelligence approaches have been developed over the years for predicting blast-induced ground vibration. Authors such as Faradonbeh et al. [11] developed and applied gene expression programming (GEP) model to predict blast-induced ground vibration using blast data from a quarry in Malaysia. Hasanipanah et al. [12] developed and applied a classification and regression tree (CART) model to predict blast-induced ground vibration at Miduk copper mine, Iran. Shahnazar et al. [13] proposed a hybrid model of adaptive neuro-fuzzy inference system (ANFIS) optimised by particle swarm optimisation (PSO) to predict blast-induced ground vibration in Pengerang granite quarry, Malaysia. Taheri et al. [7] proposed a combination of artificial bee colony (ABC) and artificial neural network (ANN) for the prediction of blast-induced ground vibration at Miduk copper mine, Iran. Fouladgar et al. [14] proposed a novel swarm intelligence algorithm based on cuckoo search (NSICS) to create a precise equation for predicting the blast-induced ground vibration in Miduk copper mine, Iran. In Faradonbeh and Monjezi [15], an optimised gene expression programming (GEP) model using cuckoo optimisation algorithm (COA) was developed to predict blast-induced ground vibration with blast data from Gol-E-Gohar iron mine, Iran. Hasanipanah et al. [16], proposed a new hybrid model of fuzzy system (FS) designed by imperialistic competitive algorithm (ICA) for the prediction of blast-induced ground vibration resulting from blasting at Miduk copper mine, Iran. Sheykhi et al. [17] proposed a novel hybrid model of support vector regression (SVR) and fuzzy C-means clustering (FCM) for the estimation of blast-induced ground vibration. Mokfi et al. [18] applied group method of data handling (GMDH) as a novel approach to predict blast-induced ground vibration from a quarry in Penang, Malaysia. Nguyen et al. [19] proposed a hybrid hierarchical k-means clustering algorithm (HKM) and artificial neural network (ANN) for the prediction of blast-induced ground vibration. Arthur et al. [20] developed and applied Gaussian Process Regression (GPR) for predicting blast-induced ground vibration from an open pit mine in Ghana. Bui et al. [21] developed and applied the hybrid fuzzy C-means clustering (FCM) algorithm and quantile regression neural network (QRNN) for the prediction of blast-induced ground vibration. Nguyen et al. [22] developed a support vector regression model optimised by particle swarm optimisation (PSO) algorithm, genetic algorithm (GA), imperialist competitive algorithm (ICA) and artificial bee colony (ABC) for the prediction of blast-induced ground vibration. Yu et al. [23] applied random forest model optimised by Harris Hawks Optimisation Algorithm to predict blast-induced ground vibration. Among the numerous computational intelligent approaches developed over the years, the artificial neural network (ANN) with the backpropagation algorithm has been the most widely and successfully used approach in predicting blast-induced ground vibration [8]. The universality of the ANN approach can be attributed to their ability to map the input parameter(s) to the output parameter(s) without any prior assumptions about their corresponding statistical properties. This makes it easy for ANN to learn from the training data and generalise well on the test data [24]. Nevertheless, the ANN approach requires the fine-tuning of several user-defined parameters such as selecting suitable activation functions, number of neurons in the hidden layer(s), number of hidden layers, maximum number of iterations, weight initialisation, momentum coefficient and learning rate, to achieve optimal performance. This makes it time-consuming and computationally expensive. Additionally, the ANN approach has the possibility of falling into local minima because it uses variety of gradient descent algorithms, hence selecting the less optimal solution [24].
In addressing the fine-tuning problem of the ANN approach, Huang et al. [25] developed the Extreme Learning Machine (ELM) approach for solving both classification and regression problems. The ELM approach is a single-hidden layer feedforward neural network (SLFN) that assigns input weight and bias randomly. Unlike the ANN which requires iterative adjustment of the network parameters, the ELM arbitrarily selects the hidden layer nodes and input weights. The ELM thereafter determines analytically the SLFNs’ output weights using the Moore–Penrose generalised pseudo-inverse [26]. It then uses the smallest norm least square to arrive at the global solution. Within the recent years, the ELM approach has been extensively applied in several fields of sciences and engineering [27,28,29] including a few notable studies in blast-induced ground vibration prediction [30, 31]. Prediction results from these studies have shown how well the ELM approach is able to generalise across the entire testing data. Nevertheless, according to Zhai et al. [32] the ELM algorithm tends to be unstable as the hidden neurons and input weights are selected arbitrarily. Furthermore, the hidden layer feature mapping is something unknown to users. In that regard, Huang et al. [33] proposed the kernel-based ELM (KELM) which adds a positive regularisation coefficient in the computation of the output weight to enhance stability and a kernel matrix when the hidden layer feature mapping is unknown. Additionally, other researchers tend to rely on the search abilities of metaheuristic optimisation algorithms notably particle swarm optimisation (PSO) and genetic algorithm (GA) to select the optimal input weights and hidden neurons of the ELM approach [34,35,36,37]. With regard to blasting studies, authors such as Armaghani et al. [38] developed a novel hybrid ELM model optimised by autonomous groups particle swarm optimisation (AGPSO) algorithm for blast-induced ground vibration prediction. Murlidhar et al. [39] also developed a novel hybrid model of ELM optimised by biogeography-based optimisation (BBO) as well as a PSO-ELM model for flyrock prediction. The developed BBO-ELM and PSO-ELM models were compared to basic ELM model. Prediction results revealed the superiority of the optimised ELM models over the basic ELM model. Wei et al. [40] developed a Nested-ELM approach for the prediction of blast-induced ground vibration.
Review of relevant literature has shown that hybrid approaches based on ELM and optimisation algorithms are very rare. It is in this light that in the current study, the ELM approach is optimised by the Self-Adaptive Differential Evolution (SaDE) algorithm to form a hybrid model (SaDE-ELM) for blast-induced ground vibration prediction. This is aimed to serve as an advancement on the studies on the ELM approach. Here, the SaDE-ELM has been applied for the first time to predict blast-induced ground vibration. The SaDE is a powerful and efficient population-based stochastic search algorithm that is capable of determining the optimum control parameters and generation strategy of a differential evolution (DE) algorithm [41] in solving optimisation problems [42]. Here the ELM learning parameters (hidden node and input weights) are optimised by using the SaDE algorithm. In order to ascertain the predictive capabilities of the SaDE-ELM approach, a basic ELM, a kernel-based ELM, ANN approaches (generalised regression neural network (GRNN), radial basis function neural network (RBFNN) and backpropagation neural network (BPNN)) and five widely used empirical approaches (USBM [3 Bureau of Indian Standard [5], Ambrasey–Hendron [1], Langefors–Kihlstrom [2] and CMRI [4] were applied for comparison purposes. In this study, the proposed SaDE-ELM model could be used as an accurate and effective tool for the prediction of blast-induced ground vibration by the blast engineer in civil and mining operations.
The rest of the paper is as follows: The case study is presented in Sect. 2. Section 3 presents the methodology. Here a concise description of the mathematical framework of the ELM, KELM, SaDE-ELM, BPNN, GRNN and RBFNN is provided. Furthermore, the model development procedures as well as the model selection and performance indicators are outlined. The results obtained and their subsequent discussions are presented in Sect. 4. Section 5 presents sensitivity analysis on data parameters, and Sect. 6 finally concludes the paper.
2 Study area
In this study, the blasting datasets upon which the models were developed were obtained from an open pit mine in Ghana. The mine is sited in the western region of Ghana, precisely in the Tarkwa Nsuaem Municipal Assembly between longitude 1°59′ West and latitude 5°16′ North as shown in Fig. 1.
The mine employs the use of drilling, blasting, loading and hauling as its main mining cycle. For drilling, long vertical holes with an average depth of 9 m and 0.115 m diameter are adopted using drill rigs. In fragmenting its in situ rock formation, the mine employs the controlled blasting method to ensure control in blast-induced effects such as ground vibrations, fractures within remaining rock walls, over-break and noise. Here, the mine uses emulsion RIOMEX 7000 of composition: 70% emulsion and 30% ammonium nitrate as the main explosive substance. It has a density of 1.20 g/cc and a target density in the range 1.15–1.17 g/cc. It also has a measured VOD of 5039 m/s. Furthermore, a primer of 250 g booster and a detonator with 500 ms delay are used to prime the drilled holes. The charged holes are stemmed using crushed gravels. An average stemming height 3 m is maintained by the mine. Inter-hole surface connectors with 67 ms, 42 ms and 17 ms delays are used to connect all charged holes to the initiation point. The mine employs the use of the non-electronic initiation system to initiate the blast. It is worth mentioning that the mine employs the use of staggered explosive pattern for its blasting operation. After the charged holes are blasted, the rock fragments are loaded by excavators into Komatsu HD 465, Volvo AD35 and CAT 777F rear dump trucks which are hauled to the crushing for processing or to the waste dump.
3 Methodology
In this section, the theories of various ELM models as well as benchmark models of BPNN, GRNN, RBFNN would be presented. The description of the empirical models will not be presented here as they have extensively been treated in literature. Detailed explanations of their concepts are available in [1,2,3,4,5]
3.1 Extreme learning machine algorithms
3.1.1 Basic extreme learning machine
The ELM developed by Huang et al. [25] is a new learning algorithm for single-hidden layer feedforward neural networks (SLFNs). Unlike the traditional back-propagation learning algorithm which is iteratively used to tune the control parameters of the SLFNs, the ELM randomly chooses hidden neurons based on Gaussian Probability Distribution and analytically determines the output weights of the SLFNs using the Moore–Penrose generalised pseudo-inverse [25].
Given S arbitrary training samples \(\left( {x_{k} ,y_{k} } \right)\) where input vector \(x_{k} = \left[ {x_{k1} ,x_{k2} ,...,x_{kn} } \right]^{\rm T} \in R^{n}\), target vector \(y_{k} = \left[ {y_{k1} ,y_{k2} ,...,y_{kn} } \right] \in R^{m}\), a SLFN with activation function \(g\left( x \right)\) and M number of hidden neurons for the training samples is mathematically modelled using Eq. (1).
where \(w_{i} = \left( {w_{k1} ,w_{k2} ,...,w_{kn} } \right)\) is the connecting weight vector between the input nodes and the ith hidden node, \(b_{i}\) is the threshold of the ith hidden node and \(\beta_{i} = \left( {\beta_{k1} ,\beta_{k2} ,...,\beta_{kn} } \right)\) is the connecting output weight vector between the output nodes and the ith hidden node. It is noteworthy that the weight vector \(w_{i}\) is randomly chosen. The ELM’s output function can be expressed in Eq. (2) as:
where \(t\left( x \right)\) is the hidden layer’s output vector with respect to the input x.
Equation (1) can be compactly expressed in [Eq. (3)] as:
where H [Eq. (4)] is the output matrix of the hidden layer.
To train an SLFN with fixed input weights \(w_{i}\) and the hidden layer biases \(b_{i}\) is to find a least square solution \(\hat{\beta }\) of the linear system [Eq. (3)]. Applying the smallest norm least squares solution of Eq. (3), the resulting \(\hat{\beta }\) becomes Eq. (5).
where \(H^{\dag } = \left( {H^{T} H} \right)^{ - 1} H^{T} \, or \, H^{T} \left( {{\text{HH}}^{T} } \right)^{ - 1}\), depending on the singularity of \(H^{T} H\) or \({\text{HH}}^{T}\) is the Moore–Penrose generalised inverse of matrix H [25, 43].
3.1.2 Kernel-based extreme learning machine
In order to obtain an ELM that has a more stable and better generalisation solutions than that obtained by the least squares approach, Huang et al. [33] proposed the addition of a positive regularisation coefficient, \({\raise0.7ex\hbox{${1}$} \!\mathord{\left/ {\vphantom {{1} \lambda }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\lambda $}}\) in computing for the output weights β. This is expressed in Eq. (6) with its corresponding regularised ELM function expressed in Eq. (7).
According to Huang et al. [33], a kernel matrix \(\Omega\) [Eq. (8)] can be defined for the ELM if the \(t\left( x \right)\) is unknown.
where \(K\left( {x_{i} ,x_{j} } \right)\) is the kernel function. The radial basis function (RBF) kernel as expressed in Eq. (9) was selected for this study.
where \(\varphi\) is the kernel parameter. The KELM’s output function is then expressed in Eq. (10) as:
3.1.3 Self-adaptive differential evolution
Differential evolution (DE) developed by Storn and Price [41] is a powerful and efficient population-based stochastic search technique for solving optimisation problem. However, according to Qin et al. [42], the DE will be successful in its application provided it chooses the right trial vector generation strategies and their associated critical parameters. This can be done through a trial-and-error procedure which is computationally expensive. In addressing this limitation, Qin et al. [42] proposed the self-adaptive differential evolution (SaDE) algorithm. Here, both the trial vector generation strategies and their associated critical parameters are determined by a gradual self-adaptation by learning from previous experiences. These critical parameters include mutation scaling factor, F, crossover rate, CR and number of populations, NP. The SaDE algorithm is made up of three steps, namely: mutation, crossover and selection.
3.1.3.1 Mutation
Considering an optimisation problem as given in Eq. (11).
where \(x_{k} = \left[ {x_{k1} ,x_{k2} ,...,x_{kP} } \right]^{T}\), k = 1, 2,…, NP is a target vector of P decision variables. In the mutation step, mutant vector Vk [Eq. (12)] is generated in the current population by mutation strategy.
where t1, t2 and t3 are mutually exclusive integers randomly selected in the range [1, NP] and \(t1 \ne t2 \ne t3\).
3.1.3.2 Crossover
After the mutation, the crossover step takes place. Here, trial vector, Uk is produced between Vk and xk where the binomial crossover is undertaken as illustrated in Eq. (13).
where randreal (0,1) is a real number generated randomly in the range [0, 1] and lrand is an integer chosen randomly in the range [1, P].
3.1.3.3 Selection
The selection step is applied finally to keep the population size constant during the entire evolution process. The selection step is also used to determine whether the trial or the target vector survives to the subsequent generation in accordance to the one-to-one selection as expressed in Eq. (14).
where f(x) is the optimised objective function. It is worth noting that during, the evolution process, F and CR are tuned adaptively to improve DE for each individual as expressed in Eqs. (15) and (16), respectively.
where \(F_{{k,\left( {Q + 1} \right)}}\) and \({\text{CR}}_{{k,\left( {Q + 1} \right)}}\) are the mutation scaling factor and crossover rate for k individual with Q generation, respectively, rand1, rand2, rand3 and rand4 are selected randomly from the range [0,1], \(\upsilon_{1}\) and \(\upsilon_{2}\) are values used to control the generation of F and CR. They are both set to the value of 0.1. Fl and Fu are set to 0.1 and 0.9, respectively, with the F and CR values initialised to 0.5 in the first generation.
3.1.4 Self-adaptive differential evolutionary extreme learning machine
The SaDE-ELM is a hybrid algorithm developed by the integration of the self-adaptive differential evolution (SaDE) algorithm proposed by Qin et al. [42] and the ELM for SLFNs. This was developed due to the possibility of the basic ELM not reaching optimal solution for SLNs, when used to randomly generate the network hidden node biases and input weights when computing the output weights β. Hence, for the SaDE-ELM algorithm, the SaDE optimises the SLFNs hidden node biases and input weights while the ELM derives the SLFNs output weights.
With training data samples, an activation function \(g\left( \cdot \right)\) and M hidden nodes, the SaDE-ELM algorithm can be summarised as follows [44, 45].
3.1.4.1 Step 1 Initialisation
A group of population (NP) vectors \(\theta_{p,Q}\) are initialised as the first-generation population using Eq. (17). Here each NP vector includes all the network hidden node parameters.
where \(w_{i}\) and \(b_{i} \left( {i = 1,2,...,M} \right)\) are generated randomly, \(p = 1,2,3, \ldots ,{\text{NP}}\) and Q denotes the generation.
3.1.4.2 Step 2 Computations for RMSE and output weights
The root mean squared error (RMSE) and the network output weight matrix with respect to each population vector are computed using Eqs. (18) and (19), respectively.
where is \(H_{q,G}^{\dag }\) the Moore–Penrose generalised inverse of \(H_{q,G}\) [Eq. (20)].
New the best population vector, \(\theta_{q,G + 1}\) as expressed in Eq. (21), is computed using the value of the RMSE.
Here, \(\varvec{{\nu}}\) is the small positive pre-set tolerance rate. According to Ku and Xing [45], the NP vector having the best RMSE is stored as \(\theta_{{{\text{best}},1}}\) and \({\text{RMSE}}_{{\theta_{best,1} }}\), respectively, in the first generation. Moreover, every trial vectors \(u_{p,Q + 1}\) created at the (Q + 1)th generation are evaluated according to Eq. (17).
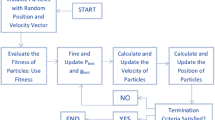
The framework of the SaDE-ELM model is given in Fig. 2.
The pseudocode of the SaDE-ELM algorithm is presented in Fig. 3.
3.1.5 Backpropagation neural network
The backpropagation neural network is an ANN technique that has been used extensively for both regression and classification problems. It consists of three layers interconnected in a feedforward manner. These layers are the input, hidden and output layers. The input layer receives inputs X1, X2,…, Xm from the surrounding environment and transmits them into the hidden layer via connecting weights, wij. The hidden layer contains neurons which are associated with a bias and a transfer function. Values known as bias bj are introduced in the transfer function to differentiate between different processing units. The bias is much like a weight, except that it has a constant input of 1. It is termed as the temperature of the neuron. The bias term is added to the weighted inputs, to result a net input, Netp [Eq. (22)], which are then transformed and processed by transfer function, fH in the hidden layer [Eq. (23)]. The processed inputs, Zj, are then sent to the output layer. In the output layer, Zj is weighted and a bias term, bk added to result in net input, Netk [Eq. (24)]. Netk is finally through the output layer transfer function, fO to produce the final predicted output \(\hat{y}\) as shown in Eq. (25) to be displayed as final predicted output result. A typical BPNN structure is shown in Fig. 4.
In the training process, during each iteration, the predicted output value is actual output value, ty. The error (Eq. (26)) between is backpropagated through the network by updating various connecting weights and bias of each neuron. This process is repeated for all input and output data pairs in the training datasets, until the network error converged to a minimum threshold defined by a corresponding cost function, usually the mean squared error.
3.1.6 Radial basis function neural network
The RBFNN is another feed forward network made up of three layers namely: the input, a single hidden and output layer fully interconnected as shown in Fig. 5. Unlike the BPNN, the RBFNN can have only a single hidden layer. The input layer transmits inputs \(X_{j} = \left( {X_{1} ,X_{2} ,X_{3} ,...,X_{m} } \right)\) from the external environment which are sent into the hidden layer without any weights being connected to them. The hidden layer contains neurons consisting of a radial basis function which serves as the transfer function. In the hidden layer, a Euclidean norm, \(\| {} \|\), is computed by each neuron. The Euclidean norm is the distance between the input to the network and the position of that neuron called centre, ci. The output, neti, from the hidden layer is obtained when the computed centre is inserted into the radial basis function as shown in Eq. (27). This study made use of the Gaussian radial basis activation function with a width parameter, \(\sigma_{i}\).
The output, neti from the hidden layer, is weighted using weights, \(w_{ik}\) and summed. This is then inserted into the linear transfer function in the output layer where a bias term, \(b_{0}\), is added to result in the final output, \(\hat{y}_{k}\) as shown in Eq. (28).
3.1.7 Generalised regression neural network
The GRNN is a single-pass learning algorithm which unlike the BPNN does not require iterative training. It consists of the four layers, namely the input, pattern, summation and output layers which are interconnected in a feed forward manner as shown in Fig. 6. The information from the external environment is received by the input layer and sent to the pattern layer, where the Euclidean distances between stored pattern units and each input are computed. The computed Euclidean distances are then sent into a radial basis activation function. The resulting output is sent to the summation layer which consists of the D-summation neuron and S-summation neuron. The D-summation neuron and S-summation neuron compute the sum of the unweighted and weighted outputs from the pattern neurons, respectively. In the output layer, the output of the S-summation neuron is divided by the output of the D-summation neuron, to produce the final output, \(\hat{Y}\left( x \right)\) as shown in Eq. (29).
Here k(x, xi) is the kernel of the radial basis function and wi is the activation weight for the pattern layer neurons.
For the study, a Gaussian activation function with a kernel, k(x, xi) and width parameter, σ defined in Eq. (30) was used.
3.2 Model development procedures
3.2.1 Input parameter selection and data partitioning
In this study, a total of 210 blasting datasets were collected from the study mine and prepared for the modelling of various approaches. In the modelling stage, the entire 210 blasting data points were partitioned into two sets using the holdout cross-validation partitioning technique [46]. In this technique, the whole datasets were partitioned into two distinct sets: training and testing. Here, the training set was used in constructing the models, whereas the testing set was used as a measure to independently assess the predictive performance of the developed models. In that regard, 130 data points out of the entire 210 were used as the training sets and the remaining 80 served as the test set. The training and test sets represent 62 and 38%, respectively. The reason for selection being, to produce good predictions results, artificial intelligent techniques requires enough training data. However, if the training data are more than enough, it will cause overfitting whereby the model cannot generalise well with unseen data. It is very important to know that there is no universally accepted ratio for splitting the data. Thus, this partitioning was done randomly with no underlining data splitting formula. Furthermore, to avoid overfitting and underfitting, the training set was purposely selected to represent the entire characteristic of the whole data in the study area. Likewise, the testing set chosen is evenly distributed across the area of study. The input parameters used in the modelling were distance from the monitoring station to the blasting point (m), powder factor (kg/m3), hole depth (m), maximum instantaneous charge (kg) and number of blast holes. For the empirical approaches, distance from the monitoring station to the blasting point (m) and maximum instantaneous charge (kg) were considered as the input parameters. These input parameters were selected because they have been found in the literature to be the controllable parameters that influence the intensity of blast-induced ground vibration [12, 20]. The peak particle velocity (PPV) values were used as the output parameter for all the approaches evaluated in this study. The obvious blast parameters of burden, spacing and stemming height were not included in the modelling process because they had constant numeric values throughout the datasets. Moreover, the essence was to avoid the inclusion of redundant input parameters. The powder factor, hole depth, maximum instantaneous charge and number of blast holes data points were obtained from the daily blast design plan. The distance from the monitoring station to the blasting point was obtained using Global Positioning System (GPS) coordinates between the two points. Finally, the PPV values were monitored and recorded using a 3000 EZ Plus Portable seismograph which was securely positioned near the closest house in the community near the mine pit. This closest community from the pit can vary between 573 and 1500 m depending on the location of the blast. It is worth mentioning that PPV values were able to be recorded for wide distances of 1500 m. However, these collected PPVs can be felt, but they have lower intensity as compared to those collected from a shorter distance as presented in Table 1. The geophone of the seismograph was firmly spiked on a flat terrain with the arrow on the geophone pointing to direction of the blast. However, the direction of the arrow changes depending on the location of the blast. It is worth mentioning that prior to blasting all operations in and around the pit are halted. Equipment working in the pit is packed at a safe distance from the blasting area. This ensures that the PPV values recorded are due to only the blasting. Furthermore, any form of vibration caused by movement around the seismograph is avoided during the monitoring of the blast-induced ground vibration. This was done to ensure accurate PPV readings. It is worth mentioning that, before recordings are done, the seismograph is calibrated. In the calibration process, the seismograph is first set to a continuous recording mode. Thereafter, the seismograph is set to record the ambient vibrations levels, i.e. vibrations from the surroundings. These recorded ambient vibrations levels are then set as below detection levels to avoid the reading of the surrounding vibrations during the monitoring and recording a blast. The statistical description of the data for the output and input parameters used in this study is presented in Table 2. Furthermore, the correlation coefficient matrix between various input and output parameters is presented in Table 3.
3.2.2 Data normalisation
In order to avoid input data with high range of values from influencing the prediction results so as to avoid overfitting, the respective input parameter (Table 1) data sets were scaled into the range [− 1, 1] using Eq. (31) [47] as pre-processing step before the development of various computational intelligent models.
where \(B_{i}\) is the normalised data, \(A_{i}\) represents the observed blast data, \(A_{\min }\) and \(A_{\max }\) denote the minimum values and maximum of the actual blast data with \(B_{\max }\) and \(B_{\min }\) values set at 1 and − 1, respectively.
3.2.3 Model building
In this study, the proposed SaDE-ELM approach is compared with two variations in the ELM approach (basic ELM and KELM), three standard computational intelligent approaches (BPNN, RBFNN, GRNN) and five empirical models (USBM, Indian Standard, Ambraseys–Hendron, Langefors–Kihlstrom and CMRI). Due to the use of SaDE algorithm, the development of the optimum SaDE-ELM hybrid model is dependent on the population size (NP), the crossover rate (CR), mutation scaling factor (F) as well as the number of hidden neurons of the ELM. Therefore, in this study NP was selected from the range of [10, 130] with a step size of 10. Mean squared error (MSE) was used as a fitness function to be minimised. The optimisation process was repeated 1000 times to find the optimal MSE value. According to Qin et al. [42], the proper selection of CR can result in a successful optimisation performance while a wrong choice can worsen the performance of the SaDE-ELM. Hence, the CR and F parameters were selected according to their universally accepted ranges of \(0 \le {\text{CR}} \le 1\) and \(0 \le F \le 2\), respectively [44]. The number of hidden neurons for the SaDE-ELM was determined through an experimental process. Moreover, since the SaDE is a stochastic algorithm, it produces a different performance results for each run. This makes the results very unstable and not dependable, which is a limitation of most computational intelligent approaches [48]. Hence, in the development of the SaDE_ELM as well as the other computational intelligent models, a random seed value was introduced to keep the results constant and stable irrespective of the number of runs. In the development of the basic ELM model, the adjustable parameters were the number of hidden layer neurons and the activation function in the hidden layer [49]. For the activation function, the sigmoid and sine were experimented on the data to select the one that produced the best prediction results. The optimal number of hidden layer neurons was also determined by a sequential experimental process. The development of the KELM model depends on the regularisation coefficient, the type of kernel function used and its kernel parameter. The popularly used RBF kernel [Eq. (9)] was used while the regularisation coefficient [Eq. (6)] and the kernel parameter [Eq. (9)] of the RBF kernel were determined through a sequential experimental process. In the case of BPNN, critical parameters considered include: the type of training algorithm, the number of hidden layers with their respective neuron numbers and the activation functions for both the hidden layer(s) and the output layer. This study applied three training algorithms, namely Scaled Conjugate Gradient [50], Bayesian Regularisation [51] and Levenberg–Marquardt [52]. Furthermore, one hidden layer BPNN was used because it has been found to universally approximate any given function [53]. Moreover, a BPNN with two and three hidden layers was also developed to ascertain the role of the hidden layer, in BPNN development. The hyperbolic tangent transfer function [54] was used for the hidden layer while the linear transfer function [55] was used for the output layer. For the RBFNN, the critical parameters (maximum number of neurons and smooth parameter of the RBF) that require adjustments in the model building phase were determined through a systematic experimental process. With regard to GRNN, the only critical parameter to be fine-tuned which is the smoothing parameter of RBF was determined through a sequential experimental process. For each computational intelligent approach, their corresponding optimal models were selected based on the mean squared error (MSE) and correlation coefficient (R) criteria. Here, the model that generalises on the test data to produce the lowest MSE and highest R is categorised as the optimum model. For the empirical models, their respective site-specific constants (k, β, n) were determined through regression analysis.
3.3 Model selection and performance indicators
The models’ performance assessment was carried out based on the testing data prediction results. To do that, mean squared errors (MSE), Nash–Sutcliffe Efficiency Index (NSEI) [56] and correlation coefficient (R) were applied. These are expressed mathematically in Eqs. (32) to (34). Afterward, the Bayesian Information Criterion (BIC) [57] (Eq. (35)) which is a model selection technique was used to choose the best performing model.
where n is the test data size, \(\overline{p}\) is the mean of the predicted values, \(p_{k}\) are the predicted values, \(\overline{a}\) is the mean of the actual values, \(a_{k}\) are the actual values and α is the number of parameters estimated by each model. Here, the parameters represent the number of input parameters used in the development of each model.
4 Results and discussion
4.1 Developed models
4.1.1 Computational intelligent approaches
Based on the experimental results, the best SaDE-ELM model had CF, F, NP and hidden neuron values of 1, 0.5, 70 and 7, respectively. The performance of the optimisation process is illustrated in Fig. 7. Table 4 shows the performance of the SaDE-ELM model with different values for the control parameters. The best KELM model was found to have a regularisation coefficient and kernel parameter values of 496 and 363, respectively. The best performing ELM model had a structure of [5–11–1] corresponding to five input parameters, one hidden layer of eleven neurons and one output with a sigmoid activation function. The best performing BPNN model was based on the Levenberg–Marquardt training algorithm with structure of [5–1–1] meaning five input parameters, one hidden layer (Table 5) of 1 neuron with the hyperbolic tangent transfer function for its hidden layer and the linear transfer function for its output layer. From Table 5, BPNN models with 2 and 3 hidden layers were not better than that with only one hidden layer as iterated by Hornik et al. [53]. The best RBFNN model had a structure of [5–9–1] also corresponding to five input parameters, one hidden layer of nine neurons and one output with the RBF having a smooth parameter value of 1.7. The best GRNN model was found to have a RBF smooth parameter of 0.40. The optimal training and testing results and control parameters for various computational intelligent approaches are shown in Table 6.
4.1.2 Empirical approaches
The developed empirical models are presented in Table 7. The training and testing results as well as the site-specific constants (k and β) for various empirical models are presented in Table 8.
4.2 Assessment of model performance
Using various performance indicators as outlined in Eqs. (32) to (34) on the test datasets, the predictive abilities of various developed models were assessed. The obtained assessment test results are presented in Table 9.
It is known that an excellent performing model must have MSE value closest to 0 as well as R and NSEI values closest to 1. Therefore, on the basis of the testing results, Table 9 and Fig. 8 show that the proposed SaDE-ELM model had the least MSE. This means that the proposed SaDE-ELM has better generalisation ability than the other investigated models as confirmed by Huang et al. [43]. This outstanding performance of the SaDE-ELM model can be attributed to the self-adaptive differential evolution property of the model which was used to optimise the hidden node biases and input weights of the basic ELM [42]. Comparatively, it can also be observed that the basic ELM, BPNN and KELM models were able to predict blast-induced ground vibration accurately than the RBFNN, GRNN and the conventional methods (Table 9). The overall analysis (Table 9) shows that all the computational intelligent models presented in this study outperformed the empirical approaches. This can also be confirmed by visual observation of Fig. 8.
With reference to Table 9, it can be gathered that the proposed SaDE-ELM model had the highest R value of 0.8711 signifying the presence of a very strong correlation between SaDE-ELM predicted PPV values and the actual values. The interpretation is that the SaDE-ELM could predict to an approximate accuracy of 87%. On the contrary, the ELM, KELM, BPNN and RBFNN models produced a prediction accuracy of approximately 85%. The rest of the methods performed poorly in that regard (Table 9). This is established in Fig. 9 where a diagrammatic representation of the R values is presented.
Using the NSEI indicator (Table 9), among the methods applied, it is observed that the proposed SaDE-ELM model had the highest NSEI value of 0.7537 which was the closest to 1. The NSEI quantitative results are graphically illustrated in Fig. 10. From the results, it can be stated that the SaDE-ELM could serve as a better fit in modelling blast-induced ground vibration than the other models presented in this study.
Figures 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 show the predicted and measured PPV on 1:1 slope line with respect to their various coefficient of determination (R2). It can be seen from these figures that the SaDE-ELM as compared to the other approaches had the highest correlation between the predicted and measured PPV.
4.3 Selection of best model
The computed BIC (Eq. (35)) values for each model developed are presented in Table 10. The BIC selects the best performing model by considering the model with the lowest BIC value. Therefore, referring from Table 10, the proposed SaDE-ELM model had the lowest BIC value of − 293.40. This further confirms the computational superiority of SaDE-ELM over the candidate models investigated. This is additionally viewed in Fig. 22. Therefore, this study selected the SaDE-ELM model for on-site prediction and control management of blast-induced ground vibration.
5 Sensitivity analysis
In order to ascertain the sensitivity of input parameters considered in this study on blast-induced ground vibration (PPV), the cosine amplitude method [58] was used. Using this method, each input parameter and the output parameter were expressed in a common X-region as shown in Eq. (36).
where each element \(x_{i}\) is a single column matrix of length p which is equivalent to the total number of datasets as shown in Eq. (37).
The sensitivity of each input parameter \(x_{i}\) on the PPV \(x_{j}\) was then computed using Eq. (38).
The computed sensitivity index for each of the input parameters is presented in Table 11 and is graphically illustrated in Fig. 23. With reference to Table 11 and Fig. 23, it can be noticed that the most influential parameter on the PPV was the powder factor and thus had the highest sensitivity index of 0.9452. This was closely followed by the maximum instantaneous charge, hole depth, number of blast holes, and the distance from the monitoring point and the blast face in decreasing order of influence. It is well established in the literature that distance from the monitoring point to the blast face is a very sensitive parameter to PPV estimation. However, in this study, it can be observed that it was the least sensitive to PPV estimation among various input parameters considered. This is due to the wide range of distance values (573 to 1500 m) recorded for the study.
6 Conclusions
In this study, the self-adaptive differential evolutionary extreme learning machine (SaDE-ELM) has been proposed as a novel approach for the prediction of blast-induced ground vibration. To comprehensively assess the performance of the SaDE-ELM, the basic ELM, KELM, three benchmark computational intelligent approaches (BPNN, RBFNN and GRNN) and five empirical approaches (Langefors–Kihlstrom, CMRI, Ambrasey–Hendron, Indian Standard and USBM) were applied. The obtained comparison results based on various performance indicators showed that the proposed SaDE-ELM approach was superior and more accurate in predicting blast-induced ground vibration than the other competing models. This was evident in the SaDE-ELM achieving the lowest MSE value 0.01942 and the highest NSEI and R values of 0.7537 and 0.8711, respectively. The other artificial intelligent approaches of ELM, KELM, BPNN, RBFNN and GRNN had MSE, R and NSEI in the ranges of (0.02166–0.03006), (0.8012–0.8537) and (0.6188–0.7254), respectively. The empirical approaches performed poorly relative to the artificial intelligence approaches by having had MSE, R and NSEI in the ranges of (0.03419–0.06587), (0.7466–0.7833) and (0.1649–0.5665), respectively. Furthermore, the computed BIC values for various methods showed that the SaDE-ELM approach had the lowest value of − 293.40 and thus was selected for the prediction of blast-induced ground vibration in this study. With the method demonstrating good prediction accuracy, it was concluded that the proposed SaDE-ELM model has high potential to be used by the mining and civil engineering industry for accurate and effective on-site prediction of blast-induced ground vibration. The empirical models performed poorly relative to the computational intelligent approaches. Sensitivity analysis conducted on the input parameters showed that powder factor and maximum instantaneous charge were the most influential parameters on the levels of blast-induced ground vibration. For future studies, the BPNN, GRNN and RBFNN can be optimised by the SaDE algorithm to ascertain the superiority of the resulting hybrid model.
References
Ambraseys NR, Hendron AJ (1968) Dynamic behavior of rock masses. In: Stagg K, Wiley J (eds) Rock mechanics in engineering practices. Wiley, London, pp 203–207
Langefors U, Kilhstrom B (1963) The modern technique of rock blasting. John Wiley and Sons, New York
Duvall WI, Petkof B (1959) Spherical propagation of explosion generated strain pulses in rock. U.S Dept. of the Interior, Washington DC
Roy PP (1991) vibration control in an opencast mine based on improved blast vibration predictors. Min Sci Technol 12:157–165
Indian Standard Institute (1973) Criteria for safety and design of structures subject to underground blasts. Bureau of Indian Standards, India
Monjezi M, Baghestani M, Faradonbeh RS, Saghand MP, Armaghani DJ (2016) Modification and prediction of blast-induced ground vibrations based on both empirical and computational techniques. Eng Comput 32(4):717–728
Taheri K, Hasanipanah M, Golzar SB, Majid MZA (2017) A hybrid artificial bee colony algorithm-artificial neural network for forecasting the blast-produced ground vibration. Eng Comput 33(3):689–700
Arthur CK, Temeng VA, Ziggah YY (2020) Multivariate adaptive regression splines (MARS) approach to blast-induced ground vibration prediction. Int J Min Reclam Env 34(3):198–222
Ghasemi E, Ataei M, Hashemolhosseini H (2013) Development of a fuzzy model for predicting ground vibration caused by rock blasting in surface mining. J Vib Control 19(5):755–770
Dehghani H, Ataee-Pour M (2011) Development of a model to predict peak particle velocity in a blasting operation. Int J Rock Mech Min 48(1):51–58
Faradonbeh RS, Armaghani DJ, Majid MZA, Tahir MM, Murlidhar BR, Monjezi M, Wong HM (2016) Prediction of ground vibration due to quarry blasting based on gene expression programming: a new model for peak particle velocity prediction. Int J Environ Sci Technol 13(6):1453–1464
Hasanipanah M, Faradonbeh RS, Amnieh HB, Armaghani DJ, Monjezi M (2017) Forecasting blast-induced ground vibration developing a CART model. Eng Comput 33(2):307–316
Shahnazar A, Rad HN, Hasanipanah M, Tahir MM, Armaghani DJ, Ghoroqi M (2017) A new developed approach for the prediction of ground vibration using a hybrid PSO-optimized ANFIS-based Model. Environ Earth Sci 76(15):527
Fouladgar N, Hasanipanah M, Amnieh HB (2017) Application of cuckoo search algorithm to estimate peak particle velocity in mine blasting. Eng Comput 33(2):181–189
Faradonbeh RS, Monjezi M (2017) Prediction and minimization of blast-induced ground vibration using two robust meta-heuristic algorithms. Eng Comput 33(4):835–851
Hasanipanah M, Amnieh HB, Khamesi H, Armaghani DJ, Golzar SB, Shahnazar A (2018) Prediction of an environmental issue of mine blasting: an imperialistic competitive algorithm-based fuzzy system. Int J Environ Sci Technol 15(3):551–560
Sheykhi H, Bagherpour R, Ghasemi E, Kalhori H (2018) Forecasting ground vibration due to rock blasting: a hybrid intelligent approach using support vector regression and fuzzy c-means clustering. Eng Comput 34(2):357–365
Mokfi T, Shahnazar A, Bakhshayeshi I, Derakhsh AM, Tabrizi O (2018) Proposing of a new soft computing-based model to predict peak particle velocity induced by blasting. Eng Comput 34(4):881–888
Nguyen H, Drebenstedt C, Bui XN, Bui DT (2020) Prediction of blast-induced ground vibration in an open-pit mine by a novel hybrid model based on clustering and artificial neural network. Nat Resour Res 29(2):691–709
Arthur CK, Temeng VA, Ziggah YY (2020) Novel approach to predicting blast-induced ground vibration using Gaussian process regression. Eng Comput 36(1):29–42
Bui XN, Choi Y, Atrushkevich V, Nguyen H, Tran QH, Long NQ, Hoang HT (2020) Prediction of blast-induced ground vibration intensity in open-pit mines using unmanned aerial vehicle and a novel intelligence system. Nat Resour Res 29(2):771–790
Nguyen H, Choi Y, Bui XN, Nguyen-Thoi T (2020) Predicting blast-induced ground vibration in open-pit mines using vibration sensors and support vector regression-based optimization algorithms. Sensors 20(1):132
Yu Z, Shi X, Zhou J, Chen X, Qiu X (2020) Effective assessment of blast-induced ground vibration using an optimized random forest model based on a Harris hawks optimization algorithm. Appl Sci 10(4):1403
Pal M, Maxwell AE, Warner TA (2013) Kernel-based extreme learning machine for remote-sensing image classification. Remote Sens Lett 4(9):853–862
Huang GB, Zhu QY, Siew CK (2006) Extreme learning machine: theory and applications. Neurocomputing 70(1–3):489–501
Ding S, Xu X, Nie R (2014) Extreme learning machine and its applications. Neural Comput Appl 25(3–4):549–556
Cao J, Yang J, Wang Y, Wang D, Shi Y (2015) Extreme learning machine for reservoir parameter estimation in heterogeneous sandstone reservoir. Math Probl Eng. https://doi.org/10.1155/2015/287816
Huang G, Huang GB, Song S, You K (2015) Trends in extreme learning machines: a review. Neural Netw 61:32–48
Ebtehaj I, Bonakdari H, Shamshirband S (2016) Extreme learning machine assessment for estimating sediment transport in open channels. Eng Comput 32(4):691–704
Zhongya Z, Xiaoguang J (2018) Prediction of peak velocity of blasting vibration based on artificial neural network optimized by dimensionality reduction of FAMIV. Math Probl Eng. https://doi.org/10.1155/2018/8473547
Li G, Kumar D, Samui P, Nikafshan Rad H, Roy B, Hasanipanah M (2020) Developing a new computational intelligence approach for approximating the blast-induced ground vibration. Appl Sci 10(2):434–454
Zhai J, Hu W, Zhang S (2014) A two-phase RBF-ELM learning algorithm. In: Proceedings of international conference on machine learning and cybernetics. Lanzhou, China, July 13–16, 2014. Springer, Berlin, Heidelberg, pp 319–328
Huang GB, Zhou H, Ding X, Zhang R (2011) Extreme learning machine for regression and multiclass classification. IEEE T Syst Man Cybern B 42(2):513–529
Song S, Wang Y, Lin X, Huang Q (2015) Study on GA-based training algorithm for extreme learning machine. In: Proceedings of 7th international conference on intelligent human-machine systems and cybernetics (IHMSC 2015). Hangzhou, Zhejiang, China, 26–27 August 2015. IEEE Computer Society, pp 132–135
Chen S, Shang Y, Wu M (2016) Application of PSO-ELM in electronic system fault diagnosis. In: Proceedings of 2016 IEEE international conference on prognostics and health management (ICPHM 2016). Ottawa, ON, Canada, June 20–22, 2016. IEEE Reliability Society, pp 1–5
Ali MH, Zolkipli MF, Mohammed MA, Jaber MM (2017) Enhance of extreme learning machine-genetic algorithm hybrid based on intrusion detection system. J Eng Appl Sci 12(16):4180–4185
Wei Y, Huang H, Chen B, Zheng B, Wang Y (2019) Application of extreme learning machine for predicting chlorophyll-a concentration inartificial upwelling processes. Math Probl Eng. https://doi.org/10.1155/2019/8719387
Armaghani DJ, Kumar D, Samui P, Hasanipanah M, Roy B (2020) A novel approach for forecasting of ground vibrations resulting from blasting: modified particle swarm optimization coupled extreme learning machine. Eng Comput. https://doi.org/10.1007/s00366-020-00997-x
Murlidhar BR, Kumar D, Armaghani JD, Mohamad ET, Roy B, Pham BT (2020) A Novel intelligent ELM-BBO technique for predicting distance of mine blasting-induced flyrock. Nat Resour Res. https://doi.org/10.1007/s11053-020-09676-6
Wei H, Chen J, Zhu J, Yang X, Chu H (2020) A novel algorithm of Nested-ELM for predicting blasting vibration. Eng with Comput. https://doi.org/10.1007/s00366-020-01082-z
Storn R, Price K (1997) Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359
Qin AK, Huang VL, Suganthan PN (2008) Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE T Evolut Comput 13(2):398–417
Huang W, Li N, Lin Z, Huang GB, Zong W, Zhou J, Duan Y (2013) Liver tumor detection and segmentation using kernel-based extreme learning machine. In: Proceedings of 2013 35th annual international conference of the IEEE engineering in medicine and biology society (EMBC 2013). Osaka, Japan, 3–7 July 2013. IEEE Engineering in Medicine and Biology Society, pp 3662–3665
Cao J, Lin Z, Huang GB (2012) Self-adaptive evolutionary extreme learning machine. Neural Process Lett 36(3):285–305
Ku J, Xing K (2017) Self-adaptive differential evolutionary extreme learning machine and its application in facial age estimation. In: Proceedings of 2017 international conference on computer network, electronic and automation (ICCNEA 2017). Xi'an, China, 23–25 September 2017. IEEE Computer Society, pp 112–117
Kohavi R (1995) A study of cross-validation and bootstrap for accuracy estimation and model selection. In: Proceeding of 4th International Joint conference on artificial intelligence. Montréal, Québec, Canada, August 20–25, 1995. pp 1137–1145
Mueller AV, Hemond HF (2013) Extended artificial neural networks: incorporation of a priori chemical knowledge enables use of ion selective electrodes for in-situ measurement of ions at environmentally relevant levels. Talanta 117:112–118
Byrne MD (2013) How many times should a stochastic model be run? An approach based on confidence intervals. In: Proceedings of the 12th international conference on cognitive modelling, Ottawa, Canada, 11–14 July 2013.
Jayaweera CD, Aziz N (2018) Development and comparison of Extreme Learning machine and multi-layer perceptron neural network models for predicting optimum coagulant dosage for water treatment. J Phys Conf Ser 1123(1):1–8
Møller MF (1993) A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw 6(4):525–533
Foresee FD, Hagan MT (1997) Gauss–Newton approximation to Bayesian learning. In: Proceedings of international conference on neural networks (ICNN'97). Houston, TX, USA, 12–12 June 1997. IEEE, pp 1930–1935
Hagan MT, Demuth HB, Beale MH, De Jesús O (1996) Neural network design. PWS Publishing Company, Boston
Hornik K, Stinchcombe M, White H (1989) Multilayer feed forward networks are universal approximators. Neural Netw 2:359–366
Harrington PDB (1993) Sigmoid transfer functions in backpropagation neural networks. Anal Chem 65(15):2167–2168
Beale MH, Hagan MT, Demuth HB (2017) Neural network toolbox™ user's guide. The MathWorks Inc, Natick
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models part I—a discussion of principles. J Hydrol 10:282–290
Schwarz G (1978) Estimating the dimension of a model. Ann Stat 6(2):461–464
Ji X, Liang SY (2017) Model-based sensitivity analysis of machining-induced residual stress under minimum quantity lubrication. Proc Inst Mech Eng B J Eng Manuf 231(9):1528–1541
Acknowledgement
The authors would like to thank the Ghana National Petroleum Corporation (GNPC) for providing funding to support this work through the GNPC Professorial Chair in Mining Engineering at the University of Mines and Technology (UMaT), Ghana.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author(s) declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Arthur, C.K., Temeng, V.A. & Ziggah, Y.Y. A Self-adaptive differential evolutionary extreme learning machine (SaDE-ELM): a novel approach to blast-induced ground vibration prediction. SN Appl. Sci. 2, 1845 (2020). https://doi.org/10.1007/s42452-020-03611-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-03611-3