Buoyancy-surface tension driven forces on electro-thermal-convection in a rotating dielectric fluid-saturated porous layer: effect of cubic temperature gradients

Abstract

This paper analyses the onset of buoyancy-surface tension driven forces on rotating electro-thermal-convection in a dielectric fluid-saturated porous layer under the influence of different basic temperature gradients. The lower surface is rigid-isothermal, and the upper surface is stress-free and flat at which the Robin-type of thermal boundary condition is invoked. The principle of exchange of stability is valid and the stability eigenvalue problem is solved numerically using the Galerkin method. The parameters influencing the stability characteristics of the system are the thermal Rayleigh number ($R_{t}$), electric Rayleigh number ($R_{e}$), Marangoni number ($Ma$), Taylor number ($Ta$), Darcy number ($Da$), Biot number ($Bi$) and the viscosity ratio ($\varLambda$). The onset of convection is delayed for a nonlinear temperature profile when compared to the linear temperature profile. It is observed that the strength of surface tension force and an AC electric field is to hasten the onset. The system is found to be more stable with increasing $Bi$, $Ta$ and $\varLambda$ as well as decrease in $Da$. The surface tension and electric forces complement each other and always observed to be $Ma_{c} < \text{R}_{ec}$.

1 Introduction

Electrohydrodynamics (EHD) is a phenomenon which occurs in several areas of engineering ranging from aircraft and space vehicles to micro-fluidic devices [1]. One practical application of using an electric field is to pump liquids in micro-channels since it will not persuade mechanical noises. When an external electric field is applied across a fluid layer, the Maxwell stress could instigate flow instability in the liquid layer with spatial changes in electrical properties. In earlier studies, the instability of flow in the design of engineering devices is basically considered to be triggered by an electric field due to abrupt changes [2, 3]. Of late, two intangible designs have been found with applications in the laptops cooling systems [4] and tools on a flight in space [5].

Thermal convective instability problems are studied in the presence of a uniform vertical electric field, called electro-thermal-convection (ETC). This mode of ETC has been studied by Taylor [6]. Turnbull and Melcher [7] described moderately simple laboratory-type experiments which can be expected to model the essential features of ETC to validate the theoretical prediction. Roberts [8] treated this problem in the presence of temperature gradients and electric potential differences across the fluid layer. Turnbull [9] carried out theoretical investigations on dielectrophoretic force effect on ETC, and subsequently many researchers [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] reviewed some related experimental and theoretical studies. Shivakumara et al. [32] studied ETC in a rotating dielectric fluid layer under a uniform vertical AC electric field. Of late, Ashwini et al. [33] investigated theoretically the effect of boundary conditions on penetrative ETC due to internal heating in a dielectric fluid-saturated porous layer. The abundant literature on this topic is available in the book by Nield and Bejan [34].

If the upper surface of the fluid layer is open to the atmosphere then the instability may also arise due to surface tension driven force, known as Marangoni convection. The convective instability may also be due to both buoyancy and surface tension forces called Bénard–Marangoni convection and studied extensively in an incompressible fluid layer (see [35, 36] and references therein). Char and Chiang [37] treated Bénard-Marangoni problem in AC electric field regime. Douiebe et al. [38] carried out theoretical investigations on Bénard-Marangoni ETC in the presence of rotation. Hennenberg et al. [39] was the first to discuss theoretically in detail the buoyancy-surface tension driven convection in a wetting liquid saturated porous medium, while Rudraiah [40] studied on the effect of Brinkman boundary layer on the onset of electroconvection in a porous medium giving an insight to the manufactures of smart materials.

The effect of Joule heating caused by passing AC electric field through electrolyte may cause non-uniform temperature distribution. The present paper deals with theoretical aspects of the problem of Bénard-Marangoni ETC in a rotating dielectric fluid-saturated porous layer. Moreover, the study of non-uniform basic temperature gradients on the onset is interesting as it paves the way to understand control of convective instability. The following different types of non-dimensional basic temperature gradients, $f(z)$ namely,

• 1. Linear temperature profile (model 1): $f(z) = \,1$

• 2. Cubic 1 temperature profile (model 2): $f(z) = 3(z - 1)^{2}$

• 3. Cubic 2 temperature profile (model 3): $f(z) = 0.66 + 1.02\,(z - 1)^{2}$

are considered in the discussion. The eigenvalue problem is solved numerically using the Galerkin method over a large range of governing physical parameters. The model 2 offers more stabilizing effect on the system and the system is found to be least stable for model 1.

2 Governing equations

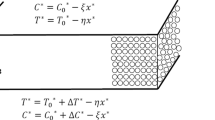
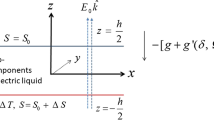
A dielectric fluid-saturated horizontal porous layer of depth $d$ in the presence of gravity acting vertically downward in the presence of a uniform vertical AC electric field is considered as presented in Fig. 1. The porous layer is rotating about the vertical axis with a constant angular velocity $\vec{\varOmega } = (0,0,\varOmega )$. The rigid lower boundary $z = 0$ and the upper stress-free non-deformable boundary $z = d$ are maintained at constant temperatures $T = T_{0}$ and $T = T_{1}$, respectively. At the upper free surface, surface tension force acts which varies linearly with temperature in the form $\sigma_{m} = \sigma_{0} - \sigma_{T} (T - T_{0} )$, where $\sigma_{T} = - \partial \sigma_{m} /\partial T$.

Fig. 1

Physical configuration

The basic equations under the Oberbeck-Boussinesq approximation are (see [8, 17, 19, 37])

$$ \nabla \cdot \vec{q} = 0 $$

(1)

$$ \rho_{0} \left[ {\frac{1}{\varphi }\frac{{\partial \vec{q}}}{\partial t} + \frac{1}{{\varphi^{2} }}\left( {\vec{q} \cdot \nabla } \right)\vec{q}} \right] = - \nabla P + \rho \vec{g} + \tilde{\mu }_{f} \,\nabla^{2} \vec{q} - \frac{{\mu_{f} }}{{k_{1} }}\vec{q} - \frac{2}{\varphi }(\varOmega \hat{k} \times \vec{q}) - \frac{1}{2}(\vec{E}.\vec{E})\;\nabla \varepsilon $$

(2)

$$ A\frac{\partial T}{\partial t} + (\vec{q} \cdot \nabla )T = \kappa \nabla^{2} T $$

(3)

$$ \nabla \cdot \left( {\varepsilon \vec{E}} \right) = 0,\,\nabla \times \vec{E} = 0\,{\text{or}}\,\vec{E} = - \nabla \phi $$

(4a, b)

$$ \rho = \rho_{0} \left[ {1 - \alpha \left( {T - T_{0} } \right)} \right] $$

(5)

$$ \varepsilon = \varepsilon_{0} \left[ {1 - \eta \left( {T - T_{0} } \right)} \right]\,(\alpha ,\,\eta > 0) $$

(6)

where $\vec{q} = (u,v,w)$ is the velocity, $T$ is the temperature, $\vec{E} = (E_{x} ,E_{y} ,E_{z\,} )$ is the electric field, $\varphi$ is the porosity of the porous medium, $\phi$ is the electric potential, $\alpha$ is the thermal expansion coefficient, $\vec{g}$ is the gravitational acceleration, $k_{1}$ is the permeability of the porous medium, $\varepsilon$ is the dielectric constant, $\kappa$ is the thermal diffusivity, $\alpha$ is the thermal expansion coefficient, $\eta$ is the dielectric constant expansion coefficient, $\mu_{f}$ is the fluid viscosity, $\tilde{\mu }_{f}$ is the effective viscosity, $A$ is the ratio of heat capacities, $\rho_{0}$ and $\varepsilon_{0}$ are the reference density and dielectric constant, respectively at $T = T_{0} .$

The basic state is quiescent and taken as

$$ \left[ {\vec{q},\,T,\,p,\,\rho ,\,\vec{E},\,\varepsilon } \right] = \left[ {0,\,T_{b} (z,t),\,p_{b} (z),\,\rho_{b} (z),\,\vec{E}_{b} (z),\,\varepsilon_{b} (z)} \right] $$

(7)

In the basic state, we have

$$ \frac{1}{{\rho_{0} }}\frac{{dp_{b} }}{dz} - \frac{{\rho_{b} }}{{\rho_{0} }}g + \frac{{E_{b}^{2} }}{2}\frac{{d\varepsilon_{b} }}{dz} = 0 $$

(8)

$$ A\frac{{\partial T_{b} }}{\partial t} = \kappa \frac{{\partial^{2} T_{b} }}{{\partial z^{2} }} $$

(9)

$$ \nabla \cdot \left( {\varepsilon_{b} \vec{E}_{b} } \right) = 0. $$

(10)

As propounded by Nield [41], it is also not our intention to treat here the full problem of temperature profiles depending explicitly on time. Instead, we introduce a simplification in the form of a quasi-static approximation which consists of freezing the basic temperature distribution $T_{b} (z,t)$ at a given instant of time. This simplification is justified so long as the disturbances are growing faster than the basic profile is evolving (Nield and Bejan [34]). Under the circumstances, the basic state temperature distribution admits a solution of the form

$$ - \frac{{dT_{b} }}{dz} = f(z) $$

(11)

where $f(z)$ is the basic temperature gradient such that

$$ \int\limits_{0}^{d} {f(z)\,dz} = \Delta T/d . $$

(12)

On solving Eq. (10), we get

$$ \varepsilon_{b} E_{bz} = \varepsilon_{0} E_{0} = \text{constant} \,({\text{say}}), $$

(13)

where

$$ E_{bz} = \frac{{E_{0} }}{1 + \eta \Delta T\,z/d}. $$

(14)

In the basic state Eq. 4(b) yields

$$ \phi_{b} = \frac{{ - E_{0} d}}{\eta \Delta T\,}\log (1 + \eta \Delta T\,z/d) $$

where $E_{0} = \frac{{ - \phi_{1} \eta \Delta T/d}}{\log (1 + \eta \Delta T)\,}$ is the externally imposed AC electric field at $z = d.$

3 Linear instability analysis

To study the instability of the system, the dependent variables are perturbed over their equilibrium counterparts in the form

$$ \left[ {\vec{q},\,\,\,p,\,\,\,\vec{E},\,\,\,T,\,\,\,\rho ,\,\,\varepsilon } \right] = \left[ {\vec{q^{\prime}},\,\,p_{b} + p^{\prime},\,\,E_{b} + \vec{E^{\prime}},\,\,T_{b} + T^{\prime},\,\,\rho_{b} + \rho^{\prime},\,\,\varepsilon_{b} + \varepsilon^{\prime}} \right] $$

(15)

where the primed quantities are the perturbed ones and considered to be very small in comparison with the basic state quantities. Substituting Eq. (15) into Eqs. (2)–(4), using the basic state solution, linearizing the equations, eliminating the pressure from the momentum equation by operating curl twice and retaining the vertical component lead finally to arrive at the following governing stability equations

$$ \left[ {\frac{1}{\varphi }\frac{\partial }{\partial t} - \frac{{\tilde{\mu }_{f} }}{{\rho_{0} }}\nabla^{2} + \frac{{\mu_{f} }}{{\kappa \rho_{0} }}} \right]\nabla^{2} w = \alpha g\nabla_{h}^{2} T - \frac{2\varOmega }{\varphi }\frac{\partial \xi }{\partial z} + \,\varepsilon_{0} E_{0} \eta f(z)\left[ {\nabla_{h}^{2} \left( {\frac{\partial \phi }{\partial z}} \right) + E_{0} \eta \nabla_{h}^{2} T} \right] $$

(16)

$$ \left[ {A\frac{\partial }{\partial t} - \kappa \,\nabla^{2} } \right]T = \,f(z)w $$

(17)

$$ \nabla^{2} \chi = - \eta E_{0} \frac{\partial T}{\partial z} $$

(18)

$$ \frac{1}{\varphi }\frac{\partial \xi }{\partial t} - \frac{{\tilde{\mu }_{f} }}{{\rho_{0} }}\nabla^{2} \xi = \frac{2\varOmega }{\varphi }\frac{\partial w}{\partial z} - \frac{{\mu_{f} }}{{\kappa \rho_{0} }}\xi $$

(19)

where $\xi = \partial v/\partial x - \partial u/\partial y$ is the z-component of vorticity vector and $\nabla_{h}^{2} = \partial^{2} /\partial x^{2} + \partial^{2} /\partial y^{2}$.

The lower boundary is rigid-isothermal, while the upper boundary is stress-free at which the surface tension force acts is non-deformable and a Robin-type of thermal boundary condition is invoked. Hence, the relevant boundary conditions on velocity and temperature are [39, 40, 42, 43]:

$$ w = \,\frac{\partial w}{\partial z} = \,0,\,\,\,T = 0,\,\,\xi = 0,\quad {\text{at}}\quad z = 0 $$

(20a)

$$ w = \mu_{f} \frac{{\partial^{2} w}}{{\partial z^{2} }} + \sigma_{T} \nabla_{h}^{2} T = 0,k_{t} \frac{\partial T}{\partial z} = h_{t} T,\frac{\partial \xi }{\partial z} = 0\quad {\text{at}}\quad z = d $$

(20b)

where $h_{t}$ is the heat transfer coefficient and $k_{t}$ is the effective thermal conductivity. In the case of finite electric susceptibility of the boundaries, the scalar electric potential satisfies the following boundary conditions

$$ \begin{aligned} \frac{\partial \phi }{\partial z} - \frac{a}{{1 + \chi_{e} }}\phi - T & = 0\quad \quad {\text{at}}\quad z = 0 \\ \frac{\partial \phi }{\partial z} + \frac{a}{{1 + \chi_{e} }}\phi - T & = 0\quad \quad {\text{at}}\quad z = d. \\ \end{aligned} $$

(20c)

At the lower rigid boundary $\,(z = 0)$, $\,T = 0$ and the limit $a \to \infty \,$ gives the condition $\phi = 0\,$, while at the upper free surface (z = d), $\,T \ne 0$ and in the limit when $\chi_{e} \to \infty$ it is noted that $D\phi - T = 0$ which is used as a boundary condition. Thus, we have used the following boundary conditions on electric potential

$$ \begin{aligned} &\phi = 0\quad \quad {\text{at}}\quad z = 0 \\ &\frac{\partial \phi }{\partial z} - T = 0\quad \quad {\text{at}}\quad z = d. \\ \end{aligned} $$

(20d)

The normal mode solution is assumed in the form

$$ \left[ {w,\,\,T,\,\,\phi ,\,\,\xi } \right] = \left[ {W(z),\,\,\varTheta (z),\,\,\varPhi (z),\,\,\varUpsilon (z)} \right]\,exp\left[ {i(a_{x} x + a_{y} y) + \omega t} \right], $$

(21)

where, $a_{x}$ and $a_{y}$ are the wave numbers in the x and y directions, respectively, $\omega$ (real or complex) is the growth term, while $W$, $\varTheta$, $\varPhi$ and $\xi$ are the perturbed velocity field, temperature, electric potential and vorticity respectively. By substituting Eq. (21) into Eqs. (16)–(19) yields

$$ \left[ {\frac{\omega }{\varphi } - \frac{{\tilde{\mu }_{f} }}{{\rho_{0} }}(D^{2} - a^{2} )\, + \frac{{\mu_{f} }}{{\kappa \rho_{0} }}} \right](D^{2} - a^{2} )W = - \alpha ga^{2} \varTheta - \frac{2\varOmega }{\varphi }\frac{\partial \varUpsilon }{\partial z} + \,\varepsilon_{0} E_{0} \eta f(z)\left[ {a^{2} \left( {D\varPhi } \right) + E_{0} \eta a^{2} \varTheta } \right] $$

(22)

$$ \left[ {A\,\omega - \kappa (D^{2} - a^{2} )} \right]\varTheta = f(z)W $$

(23)

$$ \left( {D^{2} - a^{2} } \right)\varPhi = - \eta E_{0} \,D\varTheta $$

(24)

$$ \left[ {\frac{\omega }{\varphi } - \frac{{\tilde{\mu }}}{{\rho_{0} }}(D^{2} - a^{2} ) + \frac{\mu }{{\kappa \rho_{0} }}} \right]\varUpsilon = \frac{2\varOmega }{\varphi }\,DW. $$

(25)

Here, $D$ stands for $d/dz$ and $a = \sqrt {a_{x}^{2} + a_{y}^{2} }$ is the overall horizontal wave number. In order to carry out the analysis, it is expedient to non-dimensionalize the equations as follows (an asterisk ‘$*$‘ denotes a dimensionless quantity):

$$ \begin{aligned}& \left( {x,\,\,y,\,\,z} \right) = d\left( {x*,y*,z*} \right),\quad W = (\kappa /d)\,W*,\quad \varTheta = \,(\Delta T)\varTheta *,\quad \varPhi = (\eta \,E_{0} \,\Delta T\,d)\,\varPhi *, \hfill \\ &\omega = (\kappa /d^{2} )\,\omega *,\quad f(z) = (\Delta T/d)\,f(z)*,\quad \varUpsilon = (\kappa /d^{2} )\,\varUpsilon *. \hfill \\ \end{aligned} $$

(26)

Substituting Eq. (26) into Eqs. (22)–(25) and dropping the asterisks for simplicity, we obtain

$$ \left[ {\varLambda (D^{2} - a^{2} ) - 1/Da - \omega \,\Pr } \right](D^{2} - a^{2} )W - a^{2} R_{t} \varTheta - \sqrt {Ta} \,D\varUpsilon - a^{2} R_{e} f(z)\,(\varTheta \, + D\varPhi ) = 0 $$

(27)

$$ \left[ {D^{2} - a^{2} - \omega } \right]\varTheta + f(z)W = 0 $$

(28)

$$ (D^{2} - a^{2} )\varPhi + D\varTheta = 0 $$

(29)

$$ \left[ {\varLambda (D^{2} - a^{2} ) - 1/Da - \omega \,\Pr } \right]\varUpsilon + \sqrt {Ta} \,DW = 0. $$

(30)

Here, $R_{t} = \alpha \,g\,\Delta T\,d^{3} /\nu \,\kappa$ is the thermal Rayleigh number, $R_{e} = \eta^{2} \varepsilon_{0} E_{0}^{2} (\Delta T)^{2} d^{2} /\mu \kappa$ the electric Rayleigh number, $\varLambda = \tilde{\mu }_{f} /\mu_{f}$ the viscosity ratio, $Da = k_{1} /d^{2}$ the Darcy number, $\Pr = \nu /\varphi \kappa$ the Prandtl number and $Ta = 4\,\varOmega^{2} d^{4} /\nu^{2}$ the Taylor number. The non-dimensional temperature gradient is taken as

$$ f(z) = a_{1} + 2a_{2} \left( {z - 1} \right) + 3a_{3} \left( {z - 1} \right)^{2} . $$

where $a_{1} ,a_{2}$ and $a_{3}$ are constants chosen as in Table 1 such that $\int\nolimits_{0}^{1} {f(z)\,dz} = 1$. For the case of $a_{1} = 1,\;\,a_{2} = 0$ and $a_{3} = 0$, we recover the classical linear basic state temperature distribution (see Table 1).

Table 1 Reference steady-state temperature gradients

The boundary conditions now become

$$ W = \,DW = \,0,\,\varTheta = \,\,0,\,\varPhi = 0,\,\varUpsilon = 0\,\,{\text{at}}\,\,z = 0 $$

(31a)

$$ W = \,\varLambda \,D^{2} W + a^{2} Ma\varTheta = \,0,\,D\varTheta + Bi\varTheta = \,0,\,D\varPhi - \varTheta = \,0,\,D\varUpsilon = 0\,\,{\text{at}}\,\,z = 1 $$

(31b)

where $Bi = h_{t} \,d/k_{t}$ is the Biot number and $Ma = \sigma_{T} \Delta Td/\mu_{f} \kappa$ is the Marangoni number. The condition $Bi = 0$ corresponds to the case of constant heat flux or adiabatic boundary condition, while $Bi \to \infty$ corresponds to the case of isothermal boundary condition.

4 Method of solution

Equations (27)–(30) constitute an eigenvalue problem and solved using the Galerkin method (Finlayson [44]). Accordingly, the unknown variables are expanded as follows:

$$ W = \sum\limits_{m = 1}^{N} {A_{m} W_{m} (z)} ,\,\varTheta = \sum\limits_{m = 1}^{N} {B_{m} \varTheta_{m} (z)} ,\,\varPhi \sum\limits_{m = 1}^{N} {C_{m} \varPhi_{m} } ,\,\varUpsilon = \sum\limits_{m = 1}^{N} {D_{m} \varUpsilon_{m} (z)} , $$

(32)

where $A_{m} ,\,\,B_{m}$, $C_{m}$, $D_{m}$ are constants, and $W_{m} ,$$\varTheta_{m}$, $\varPhi_{m}$, $\xi_{m}$ are trial (basis) functions and they are assumed in the following form

$$ W_{m} = \left( {z^{m + 1} - \,z^{m + 2} } \right)T_{m}^{*} ,\,\varTheta_{m} = \left( {2z^{m} - \,z^{m + 1} } \right)T_{m}^{*} ,\,\varPhi_{m} = \varUpsilon_{m} = (3\,z^{m + 1} - 2z^{m + 2} )T_{m}^{*} , $$

(33)

where $\,T_{1}^{*} ,\,\,T_{2}^{*} , \ldots \ldots T_{m}^{*}$ are modified Chebyshev polynomials of second kind. The trial functions are chosen satisfying the respective boundary conditions except $\varLambda D^{2} W + a^{2} Ma\varTheta = 0$, $D\varTheta + Bi\,\varTheta = 0$ and $D\varPhi - \,\varTheta = 0$ at $z = 1$ but the residual from these conditions are included as a residual from Eqs. (27)–(30). Substituting Eq. (32) into Eqs. (27)–(30), multiplying resulting Eqs. (27), (28), (29) and (30), respectively by $W_{n} (z)$, $\varTheta_{n} (z)$, $\varPhi_{n} (z)$ and $\varUpsilon_{n} (z)$, and integrating from $z = 0$ to $z = 1$ and thereby with the help of Eqs. (31a, b), the following equations are obtained:

$$ \left[ {\begin{array}{*{20}l} {E_{nm} } \hfill & {F_{nm} } \hfill & {G_{nm} } \hfill & {H_{nm} } \hfill \\ {I_{nm} } \hfill & {J_{nm} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{nm} } \hfill & {L_{nm} } \hfill & 0 \hfill \\ {P_{nm} } \hfill & 0 \hfill & 0 \hfill & {Q_{nm} } \hfill \\ \end{array} } \right]\,\,\left[ \begin{aligned} A_{n} \hfill \\ B_{n} \hfill \\ C_{n} \hfill \\ D_{n} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{aligned} \right] $$

(34)

where

$$ \begin{aligned} E_{nm} & = \int\limits_{0}^{1} {\left\{ {\varLambda \,[D^{2} W_{n} D^{2} W_{m} + 2a^{2} DW_{n} DW_{m} + a^{4} W_{n} W_{m} ]\, + \,(Da^{ - 1} + \omega \,\Pr^{ - 1} )[DW_{n} DW_{m} \, + a^{2} W_{n} W_{m} ]\,} \right\}dz} , \\ F_{nm} & = - a^{2} \int\limits_{0}^{1} {[R_{t} + R_{e} \,f(z)]W_{n} \varTheta_{m} } \,dz + a^{2} MaDW_{n} (1)\varTheta_{m} (1), \\ G_{nm} & = - a^{2} R_{e} \int\limits_{0}^{1} {f(z)W_{n} D\varPhi_{m} } dz, \\ H_{nm} & = - \sqrt {Ta} \int\limits_{0}^{1} {W_{n} D\varUpsilon_{m} } \,dz, \\ I_{nm} & = - \int\limits_{0}^{1} {f(z)\,\varTheta_{n} W_{m} } \,dz, \\ J_{nm} & = \int\limits_{0}^{1} {\left\{ {D\varTheta_{n} D\varTheta_{m} + (a^{2} + \omega )\,\varTheta_{n} \varTheta_{m} } \right\}} \,dz + Bi\,\varTheta_{n} (1)\varTheta_{m} (1), \\ K_{nm} & = - \int\limits_{0}^{1} {D\varTheta_{m} \varPhi_{n} } \,dz, \\ L_{nm} & = - \frac{1}{4} + \int\limits_{0}^{1} {\left\{ {D\varPhi_{n} D\varPhi {}_{m} + a^{2} \varPhi_{n} \varPhi_{m} } \right\}} \,dz, \\ P_{nm} & = - \sqrt {Ta} \int\limits_{0}^{1} {\varUpsilon_{n} DW_{m} } \,dz, \\ Q_{nm} & = \varLambda \int\limits_{0}^{1} {\left\{ {D\varUpsilon_{n} D\varUpsilon_{m} + a^{2} \varUpsilon_{n} \varUpsilon_{m} } \right\}} + \int\limits_{0}^{1} {\left( {Da^{ - 1} + \omega \,\Pr^{ - 1} \,} \right)\varUpsilon_{n} \varUpsilon_{m} dz.} \\ \end{aligned} $$

Equation (34) has the determinant of coefficient matrix, vanishes resulting in a non-trivial solution. That is,

$$ \left| {\begin{array}{*{20}l} {E_{nm} } \hfill & {F_{nm} } \hfill & {G_{nm} } \hfill & {H_{nm} } \hfill \\ {I_{nm} } \hfill & {J_{nm} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {K_{nm} } \hfill & {L_{nm} } \hfill & 0 \hfill \\ {P_{nm} } \hfill & 0 \hfill & 0 \hfill & {Q_{nm} } \hfill \\ \end{array} } \right| = 0. $$

(35)

The eigenvalues are extracted from Eq. (35) for $m = n = 1$ which gives the characteristic equation:

$$ \begin{aligned} Ma & = \frac{{4(15\eta_{3} + 2\omega )}}{{a^{2} 15\left\langle {\varTheta f(z)W} \right\rangle }}\left[ {(\eta_{1} + \omega \Pr^{ - 1} \eta_{2} ) + \frac{7Ta}{{20(315\eta_{5} + 13\omega \Pr^{ - 1} )}}} \right] - \frac{{a^{2} R_{t} }}{30} \\ & \quad - a^{2} R_{ea} \left[ {\left\langle {\varTheta f(z)W} \right\rangle + \frac{{\left\langle {Wf(z)D\varPhi } \right\rangle }}{{20\eta_{4} }}} \right] \\ \end{aligned} $$

(36)

where

$$ \begin{aligned} \eta_{1} & = \varLambda \left( {4 + \frac{{a^{4} }}{105} + \frac{{4a^{2} }}{15}} \right) + Da^{ - 1} \left( {\frac{2}{15} + \frac{{a^{2} }}{105}} \right), \\ \eta_{2} & = \frac{2}{15} + \frac{{a^{2} }}{105}, \\ \eta_{3} & = \frac{{2a^{2} }}{15} + \frac{1}{3} + \frac{Bi}{4}, \\ \eta_{4} & = - \frac{1}{4} + \frac{2}{15} + \frac{{13\,a^{2} }}{315}, \\ \eta_{5} & = \varLambda \left( {\frac{{13a^{2} }}{315} + \frac{2}{15}} \right) + Da^{ - 1} \frac{13}{315}, \\ \left\langle \cdots \right\rangle & = \int\limits_{0}^{1} {( \cdots )} \,dz. \\ \end{aligned} $$

To study the stability of the system, we take $\omega = i\omega_{i}$ in Eq. (36) and clear the complex quantities from the denominator which yields

$$ \begin{aligned} Ma & = \frac{4}{{a^{2} 15\left\langle {\varTheta f(z)W} \right\rangle }}\left[ {\frac{{\left( {15\eta_{1} \eta_{3} \Pr - 2\omega_{i}^{2} \eta_{2} } \right)}}{\Pr } + \frac{{7Ta\Pr \left( {4725\eta_{3} \eta_{5} \Pr + 26\omega_{i}^{2} } \right)}}{{20\left\{ {99225\,\eta_{5\,}^{2} \Pr^{2} + 169\omega_{i}^{2} } \right\}}}} \right] - \frac{{4R_{t} }}{30} \\ & \quad - 4R_{ea} \left\langle {\varTheta f(z)W} \right\rangle - \frac{{R_{ea} \left\langle {Wf(z)D\varPhi } \right\rangle }}{{5\eta_{4} }} + i\omega_{i} \Delta \\ \end{aligned} $$

(37)

where

$$ \Delta = \frac{4}{{a^{2} 15\left\langle {\varTheta f(z)W} \right\rangle }}\left[ {\frac{{\left( {15\eta_{2} \eta_{3} + 2\eta_{1} \Pr } \right)}}{\Pr } + \frac{{7Ta\Pr (630\Pr \eta_{5} - 195\eta_{3} )}}{{20\left\{ {99225\,\eta_{5\,}^{2} \Pr^{2} + 169\omega_{i}^{2} } \right\}}}} \right]. $$

(38)

Since $Ma$ being the physical quantity it must be real. Hence, from Eq. (37) it implies $\omega_{i} = 0$ or $\Delta = 0$ ($\omega_{i} \ne 0$) and ‘accordingly the condition for the steady onset ($\omega_{i} = 0$) is obtained. The steady onset occurs at $Ma = Ma^{s}$, where

$$ Ma^{s} \, = \frac{4}{{a^{2} 15\left\langle {\varTheta f(z)W} \right\rangle }}\left[ {15\eta_{1} \eta_{3} + \frac{{Ta \, (4725\eta_{3} \eta_{5} )}}{{283500\,\eta_{5}^{2} }}} \right] - \frac{{4R_{t} }}{30} - 4R_{ea} \left[ {\left\langle {\varTheta f(z)W} \right\rangle + \frac{{\left\langle {Wf(z)D\varPhi } \right\rangle }}{{20\eta_{4} }}} \right]. $$

(39)

The condition $\Delta = 0$ gives an expression for $\omega_{i}^{2}$ in the form

$$ \omega_{i}^{2} \, = - \frac{{(99225\eta_{2}^{2} \Pr )^{2} }}{169} + \frac{{7Ta\Pr^{2} }}{{260\eta_{2} }}\left[ {\frac{{1 - 2\beta_{1} \Pr }}{{1 + 2\beta_{2} \Pr }}} \right] $$

(40)

where $\beta_{1} = \frac{{21\eta_{5} }}{{13\eta_{3} }}$ and $\beta_{2} = \frac{{\eta_{1} }}{{15\eta_{2} \eta_{3} }}$.

Substituting the value of $\omega_{i}^{2}$ from Eq. (40) into Eq. (38) by noting $\Delta = 0$ yields the condition for the onset of oscillatory convection to occur at $Ma\, = Ma^{0}$, where

$$ Ma^{0} \, = \frac{{4(\alpha_{2} \alpha_{4} + \alpha_{3} \alpha_{4}^{2} + \alpha_{1} )}}{{a^{2} 15\alpha_{4} \left\langle {\varTheta f(z)W} \right\rangle }} - \frac{{4R_{t} }}{30} - 4R_{ea} \left\langle {\varTheta f(z)W} \right\rangle - \frac{{R_{ea} \left\langle {Wf(z)D\varPhi } \right\rangle }}{{5\eta_{4} }} $$

(41)

with

$$ \begin{aligned} \alpha_{1} & = 4725\eta_{3} \eta_{5} - \frac{2579850\Pr }{169}, \\ \alpha_{2} & = \left[ {15\eta_{1} \eta_{3} + \frac{{198450\eta_{2} \Pr }}{169}} \right] + \frac{7Ta\Pr }{130}, \\ \alpha_{3} & = - \frac{{7Ta\eta_{2} \Pr }}{(1690)}\,{\text{and}} \\ \alpha_{4} & = \frac{{195\eta_{3} - 630\eta_{5} \Pr }}{{15\eta_{2} \eta_{3} + 2\eta_{1} \Pr }}. \\ \end{aligned} $$

Imposing the condition $\omega_{i}^{2} > 0$, we note that

$$ \Pr < \frac{13}{2}\left[ {\frac{{2a^{2} + 5 + 3.75Bi}}{{13a^{2} + 42 + 13\sigma^{2} }}} \right]\,\,{\text{and}}\,\,Ta > \frac{{283500\eta_{2} \eta_{5}^{2} }}{13}\left[ {\frac{{1 + 2\beta_{2} \Pr }}{{1 - 2\beta_{1} \Pr }}} \right]. $$

Thus it is clear that oscillatory convection is possible provided $\Pr < 1$ and the Taylor number $Ta$ exceeds a threshold value as observed in the classical viscous liquids. For dielectric fluids, the value of Prandtl number is greater than unity (for example, Pr = 100 for silicone oil [45], 10,000 for caster oil [46] and 480 for corn oil [47]. Under the circumstance, we restrict ourselves to the case of steady onset.

5 Results and discussion

The solution of the eigenvalue problem can be expressed symbolically as

$$ f\left( {R_{t} ,\,\,\,R_{e} ,\,\,\,Bi,\,\,Ta,\,\,Da^{ - 1} ,\,\,\varLambda ,\,\,Ma,\,\,a,\,\,a_{1} ,\,\,a_{2} ,\,\,a_{3} \,} \right) = 0 $$

(42)

where in the minimum of $R_{t}$ or $R_{e}$ or $Ma$ is found with respect to the wave number ‘a’ for any chosen set of parametric values. The critical values $(Ma_{c} ,\,\,a_{c} )$ for $R_{t} = 0$ (absence of buoyancy force) and $(R_{tc} ,\,\,a_{c} )$ for $Ma = 0$ (absence of surface tension force) computed numerically are in line with those published previously. Our values of $Ma_{c}$ and the corresponding $a_{c}$ obtained for different $Ta$ when $R_{e} = Da^{ - 1} = 0$, $\varLambda = f(z) = 1$ and $Bi = 10^{3}$ compare very well with those of Pradhan [48] (see Table 2). The obtained $R_{tc}$ and $a_{c}$ values for different $Da$ when $R_{e} = Ma = Ta = 0$, $\varLambda = 1$ and $f(z) = 1$ for isothermal-lower rigid and insulated-upper surface are compared in Table 3 with those of Lebon and Cloot [49] and an excellent agreement is found. The results of Char and Chiang [37] are exhibited along with our obtained results in Fig. 2 for lower rigid-isothermal and upper free-insulated to temperature perturbations when $Ta = Da^{ - 1} = 0$, $\varLambda = 1$ and $Ma = 0$ for $f(z) = 1$. It is seen that the results complement each other showing the accuracy of the numerical computation.

Table 2 Comparison of $Ma_{c}$, $R_{tc}$ and $a_{c}$ for different values of $Ta$ when $Da^{ - 1} = \text{R}_{e} = 0$, $\varLambda = 1$ and $Bi = 1000$

Table 3 Comparison of R_tc and a_c for different values of $Da$ when $R_{e} = Bi = Ma = Ta = 0$ and $\varLambda = 1$

Fig. 2

Comparison of $R_{tc}$ as a function of $Bi$ for different values of $R_{e}$ for $Da^{ - 1} = Ta = 0$ and $\varLambda = 1$

Figure 3a, b give the variation of $Ma_{c}$ and $R_{tc}$ with $Bi$ for the case of cubic 1, cubic 2 and linear temperature profiles when $\varLambda = 1$, $Ta = 10$ and $Da^{ - 1} = 0$. For the case of $Bi = 0$, an insulated surface retains more energy within the porous layer and thus the system is less stable. However, increase in $Bi$ is to increase $R_{tc}$ and $Ma_{c}$ indicating their effect is to delay electro-thermal convection (ETC). This may be credited that an increase in $Bi$ leads thermal disturbances to dissipate easily into the ambient surroundings due to a better convective heat transfer co-efficient at the top surface and thus higher heating is required to make the system unstable. It is also apparent that the dielectric fluid-saturated porous layer under an AC vertical electric field becomes more stable with an increase in $Bi$.

Fig. 3

Variation of (a) $M_{ac}$ and (b) $R_{tc}$ verses $Bi$ for different values of $R_{e}$ and for $\varLambda = 1$, $Ta = 10$ and $Da^{ - 1} = 0$

Figure 4 shows the values of $R_{tc}$ ($Ma = 0$) and $Ma_{c}$ ($R_{t} = 0$) as a function of Taylor number $Ta$ for different values of $R_{e}$ when $\varLambda = 1$, $Bi = 2$, $Da^{ - 1} = 0$ and different forms of $f(z)$. It is found that $R_{tc}$ and $Ma_{c}$ increase with increasing $Ta$. Thus the Coriolis force has a stabilizing effect on the system for different forms of basic temperature gradients. The system is found to be more stable for cubic1 temperature gradient when compared to cubic2 and least stable for a linear temperature profile.

Fig. 4

Variation of $R_{tc}$ and $M_{ac}$ verses $Ta$ for different values of $R_{e}$ and for $\varLambda = 1$, $Bi = 2$ and $Da^{ - 1} = 0$

Figure 5 shows $R_{tc}$ and $Ma_{c}$ against $Da^{ - 1}$ when $Bi = 2$, $\varLambda = 1$ and $Ta = 10$. Increase in $Da^{ - 1}$ results in the decrease of permeability of the porous medium which in turn hinders the fluid flow in porous media and hence higher values of $R_{tc}$ are required for the onset of ETC. Figure 6 shows $R_{tc}$ and $Ma_{c}$ versus $\varLambda$ for $Bi = 2$, $Da^{ - 1} = 0$ and $Ta = 10$. Increase in the value of $\varLambda$ amounts to increase in the viscous diffusion which retards the fluid flow resulting in higher heating requirement for the onset of ETC. Moreover, from Figs. 3, 4, 5 and 6 it is evident that increase in $R_{e}$ leads to decrease in $Ma_{c}$ and $R_{tc}$, in general. That is, higher the strength of the electric field is to hasten the onset due to an increase in the destabilizing electrostatic energy to the system. In other words, the presence of electric field facilitates the transfer of heat more effectively and hence accelerates’ ETC at a lower value of $Ma_{c}$ or $R_{tc}$. This result is true for all the types of temperature profiles considered. That is, for different values of $R_{e}$, it is found that

$$ \left( {Ma_{c} } \right)_{linear\, < \,cubic2 < cubic1\,\,} < \left( {R_{tc} } \right)_{linear\, < \,cubic2 < cubic1} . $$

Fig. 5

Variation of $R_{tc}$ and $M_{ac}$ verses $Da^{ - 1}$ for different values of $R_{e}$ and for $\varLambda = 1,$$Bi = 2$ and $Ta = 10$

Fig. 6

Variation of $R_{tc}$ and $M_{ac}$ verses $\varLambda$ for different values of $R_{e}$ and for $Da^{ - 1} = 0$, $Bi = 2$ and $Ta = 10$

The locus of $R_{ec}$ and $M_{a\,c}$ for different $Ta$ when $\varLambda = 1$, $Da^{ - 1} = 25$, $R_{t} = 25$ and $Bi = 2$ is shown in Fig. 7. For all types of temperature gradients considered, it is found that $R_{ec}$ and $Ma_{c}$ increase as $Ta$ increases and hence rotation has a stabilizing effect on the system. Thus, when the electric force is predominant then the gravitational force becomes negligible. This is true for all the temperature gradients. The presence of electric field is to facilitate the heat transfer more effectively and hence hastens the onset of Bénard–Marangoni ETC. The system is found to be more stable for cubic 1 temperature gradient when compared to cubic 2 type of temperature gradient, and the least stable for the linear temperature gradient. That is,

$$ (Ma_{c} \,\,{\text{or}}\,\,R_{ec} )_{\text{linear}} < (Ma_{c} \,\,{\text{or}}\,\,R_{ec} )_{{{\text{cubic}}\,2}} < (Ma_{c} \,\,{\text{or}}\,\,R_{ec} )_{{{\text{cubic}}\,1}} $$

Fig. 7

Locus of $M_{{a}_{c}}$ verses $R_{ec}$ for different values of $Ta$ and for $\varLambda = 1$, $Da^{ - 1} = 25$, $\text{R}_{t} = 25$ and $Bi = 2$

6 Conclusions

The aforesaid findings give an outline to the entire exploration for the effect of coupling of buoyancy, surface tension, electric, viscous, Coriolis forces and the effect of permeability on the onset of ETC in a liquid-saturated layer of porous medium. The principle of exchange of stability is found to be valid and the problem of eigenvalue is solved using the Galerkin method for different basic temperature gradients. The results may be summarized as follows:

• Increase in the Darcy number is to speed up the onset of Bénard- Marangoni ETC while the adverse trend is observed with increasing ratio of viscosities.

• The system is more stable with increasing Biot number $Bi$.

• As Taylor number increases the critical stability parameters increase indicating the Coriolis force has a stabilizing effect on the system.

• The system is more stable for temperature gradient of cubic 1 while the linear temperature gradient is the least stable. That is,

  $$ (R_{ec} \,{\text{or}}\,Ma_{c} )_{\text{linear}} < (R_{ec} \,{\text{or}}\,Ma_{c} )_{\text{cubic2}} < (R_{ec} \,{\text{or}}\,Ma_{c} )_{\text{cubic1}} . $$

• The critical electric Rayleigh number $R_{ec}$ decreases with an increase in the Marangoni number $Ma$.