MEMS capacitive accelerometer: dynamic sensitivity analysis based on analytical squeeze film damping and mechanical thermoelasticity approaches

Abstract

In this work, we adopt a semi-analytical model to study a capacitive MEMS accelerometer based in silicon (Si). Such model takes into account the thermoelastic stiffness and linear expansion coefficients of anisotropic bulk Si. In addition, an analytical damping model, derived from the Reynolds equation, is incorporated in the model, in order to study dynamical characteristics of a MEMS capacitive accelerometer. Such approach takes into account the inertial effects on squeeze film damping in air, argon and helium gases, assumed as being ideal gases. The simulation model was compared with experimental measurements. The main figure of merit adopted is the electromechanical sensitivity (S_EM), assuming frequency response and considering the effect of gas pressure, as well as temperature, on the damping loss mechanisms in such devices. The resulted model implementation shows a good agreement with the experimental data. For all gases, the sensitivity at 20 Pa presents less variation than at 200 Pa. At 20 Pa, the linear response of the device reaches up to 300 Hz, approximately, for air and helium, assuming variation of ≈ 0.5 dB, no matter which temperature. For 200 Pa, the linear response drops down to about 150 Hz. Also, for the three gases, the variation of S_EM as a function of temperature is below 0.17 dB in the entire operational range, for both evaluated pressures, depending only on the silicon mechanical properties at low frequencies.

1 Introduction

The impact of microelectromechanical systems (MEMS) technology in the modern society is well known [1, 2]. This technology has been allowing the development of small, low-cost and robust devices and systems, such as microsensors and microactuators. Nowadays, microsensors are widely used in many commercial products, such as automotive airbag systems, smartphones, tablets and video games. Furthermore, high-performance MEMS sensors are used in key areas, such as defense and aerospace industries, to integrate inertial measurement units (IMUs) of navigation systems applied in micro- and nanosatellites [3,4,5].

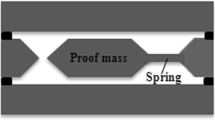
MEMS capacitive accelerometers detect accelerations by exploiting the movement of a seismic mass, resulting in a capacitance change between parallel plates mechanically suspended by clamped beams. A three-dimensional sketch of a MEMS capacitive acceleration transducer is shown, in exploded view, in Fig. 1. In this case, the microsensor is fabricated using a bulk-micromachined process in a silicon monocrystalline substrate (Si). Such process involves a selective anisotropic wet etching, usually deploying potassium hydroxide (KOH) as the etching agent [1].

Fig. 1

Exploded view of a MEMS capacitive acceleration transducer

There are several parameters used to completely characterize this kind of device, although the main requirements are defined according to their applications. The most common figures of merit are sensitivity, dynamic bandwidth, nonlinearity, resolution, etc. [6]. Sensitivity and dynamic bandwidth are the parameters explored in this work. The sensitivity, evaluated in a static point of view, depends on material physical properties and on geometrical parameters. The dynamic bandwidth is related to a relatively flat amplitude and linear phase bandwidth responses up to some maximum specified frequency, related to the device’s natural frequency. The evaluation of these combined parameters is assumed as a dynamic sensitivity. The performance of MEMS devices is associated with losses due to several damping effects, such as: damping of acoustic vibrations, damping due to cantilevers linking the seismic mass to the inertial frame, damping due to thermoelastic effects and squeeze film damping (SFD) [7, 8]. The last one is the predominant loss effect in planar MEMS structures [8]. One of the strategies used to improve the device dynamic performance is the adjustment of the atmosphere surrounding the seismic mass, in order to control the SFD effect, since it is possible to set the internal atmosphere in the capacitive MEMS during the packaging process.

Numerical methods, such as the finite element method (FEM), the finite volume method (FVM) and the finite difference method (FDM), are frequently used to evaluate the multi-physical behavior of these kinds of devices. Such methods demand considerably computational resources. The required computational resources increase as the complexity of the geometrical and physical models increases. When possible, simplified analytical approaches are the best way to validate first concept designs and to take the first insights on the nature of the system. Also, it is a tremendous value to establish and predict the behavior of such kind of system in real and operational conditions, for example, in aeronautical and aerospace situations, where the overall system may be exposed to the natural elements, as high temperature and pressure gradients, among others.

Also, it is worth to remark here that, most practical case to get the first insights, the developers estimate the dynamic sensitivity range as approximately 1/5 of the first natural frequency of general mechanical transducer devices (i.e., resonators, beams, cantilevers, etc.). This first “guess” seems very practical, but in some cases, the real dynamic sensitivity range can be underestimated, or it can show up completely misinterpreted if the developers are not be careful. Also, this supposed start point may not capture the surrounding atmospheric pressure dynamics in small enclosed systems, for instance. In such cases, the NIE-SFD model and similar approaches should be sufficient to provide the first insights about the system dynamics, for a variety of systems. However, for high-performance device applications, as the aforementioned aeronautical and aerospace purposes, for example, the IE-SFD model seems more appropriate on account of revealing more accurately dynamic behavior of this kind of devices in hard task scenarios; hence, it is allowing more realistic insights about the dynamic of such systems.

Based on analytical approximations, several squeeze film damping (SFD) models have been applied in the study of MEMS structures, such as the molecular models developed and tested by Christian [9], Newell [10], Kádár et al. [11], Li et al. [12], Bao et al. [13] and others. An analytical SFD model was used by Bourgeois et al. [14, 15] to study a capacitive MEMS accelerometer in nitrogen atmosphere, for different pressure. Their results show good agreement with experimental data. Recently, a new viscous damping model was proposed by Aoust et al. [16] to study MEMS resonators, for which additional damping sources have become important. Although analytical SFD models for MEMS structures have received distinct contributions [12, 17], and the same attention is true also in studies associated with thermoelastic features in silicon MEMS [14], the concomitant, squeeze film damping and thermoelastic mechanical effects experienced on dynamic sensitivity of MEMS accelerometers, based on analytical approach, were not tackled before according to the best of our understanding.

In this paper, we adopt a semi-analytical model to study a capacitive MEMS accelerometer. Such model takes into account the thermoelastic stiffness and linear expansion (α_L) coefficients of anisotropic bulk silicon. In addition, an analytical damping model, derived from the Reynolds equations [17, 18], is incorporated in the model in order to study dynamical characteristics of a MEMS capacitive accelerometer. Such approach takes into account the inertial effects on squeeze film damping (IE-SFD) in air, argon and helium gases, assumed as being ideal gases. The simulation model was compared with experimental measurements. The main figure of merit adopted is the electromechanical sensitivity (SEM), assuming frequency response (dynamic sensitivity) and considering the effect of gas pressure, as well as temperature, on the damping loss mechanisms in such devices.

2 Capacitive accelerometer model

The capacitive acceleration transducer illustrated in Fig. 1 allows the detection of an external force by means of the difference of capacitance between the fixed conductor plates and the seismic mass, displaced from the equilibrium by an inertial force. This difference is converted into an electrical voltage signal [19]. The electromechanical transducer can be modeled as a mass–spring–damper system, as illustrated in Fig. 2.

Fig. 2

Schematic illustration of the geometric structure of the MEMS capacitive acceleration transducer. a Front view of the seismic mass (mobile plate). b Side view showing the internal parts of the transducer. The variables are presented in Tables 4 and 5

Although the complete damping system is expressed by a nonlinear differential equation with time-dependent coefficients [4], for small displacements of the seismic mass, the equation can be linearized, for instance, by using a Taylor series around the operating point z = 0 [20, 21]. Making use of linear systems analysis techniques, we can write the transfer function of the system as the ratio between the z-axis displacement of the seismic mass and the applied acceleration a_z, taking into account the inertial effects of squeeze film damping gas, as follows [5]:

$$H_{\text{EM}} = \frac{z}{{a_{z} }} = \frac{{k_{\text{em}} }}{{s^{2} + K_{1} s + K_{0} }},$$

(1)

where k_em is the electromechanical constant and s = jω is the frequency term due to the Laplace transformation. The K₁ and K₀ coefficients are expressed, respectively, as

$$K_{1} = 2c_{\text{d}} M_{\text{eff}}^{ - 1} \left( {k_{\text{eq}} M_{\text{eff}} } \right)^{{\frac{ - 1}{2}}} \left( {k_{\text{eff}} + 2k_{\text{de}} } \right)^{{\frac{1}{2}}}$$

(2)

and

$$K_{0} = k_{\text{eff}} + 2k_{\text{de}} M_{\text{eff}}^{ - 1} ,$$

(3)

where c_d is the viscous gas damping coefficient which represents the total damping contributions coming from fluid and mechanics domains, k_de is the elastic gas damping coefficient related to the gas inertial mechanisms [17], $M_{\text{eff}}$ is the effective mass, and $k_{\text{eff}}$ is the effective electrostatic and mechanical elastic coefficient present in the system. Equations (2) and (3) carry a considerable amount of information in account of different physical aspects of the system dynamics. In other words, these equations capture the intrinsic nature of mechanical, electrical and fluidic phenomena involved in the dynamical process under study.

In the next sections, we shed light on how some of these main dynamical processes were modeled as well as present our primary considerations to make the system feasible to be solved according to the adopted approach. Meanwhile, we highlight that the geometrical details aspects of the capacitive accelerometer model used in this work can be found, in a deep view point, in these referenced works [4, 5].

2.1 Basic equations approach

In order to take into account the damping force due to the gas film located between the faces of the seismic mass and the fixed plates, a gas film lubrication approach derived from the modified Reynolds equation [18, 22] and based on the continuous theory of matter is employed [17]:

$$\frac{\partial }{\partial x}\left( {\frac{{\rho_{\text{f}} h_{0}^{3} }}{{12\eta_{\text{f}} }}Q_{\text{fr}} \frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\frac{{\rho_{\text{f}} h_{0}^{3} }}{{12\eta_{\text{f}} }}Q_{\text{fr}} \frac{\partial p}{\partial y}} \right) = p_{\text{f}} \frac{{\partial h_{0} \rho_{\text{f}} }}{\partial t},$$

(4)

where $\rho_{\text{f}}$ is the fluid density, $p_{\text{f}}$ is the fluid pressure, and $\eta_{\text{f}}$ is the fluid viscosity. Such approaches are named squeeze film damping models (SFD models). Also, SFD models allow improvements in the representation of the dynamic behavior of the actuator by including gas film inertial effects.

The inertial effects alter the natural frequency and the peak amplitude of the dynamic response of the system, as a function of the applied gas pressure [19]. Further, these effects are deeply related to system damping phenomena and both are introduced in virtue of the fluidic damping mechanisms, which can be quantified by both special coefficients, namely the elastic gas damping and the viscous gas damping. The effect of the elastic gas damping coefficient is neglected for squeeze number smaller than 0.2 and, under this condition, the predominant damping loss mechanism is the viscous damping [8, 13]. Assuming that the resultant force oscillates harmonically and moves the seismic mass, the relation between the damping coefficients is expressed by the damping force, F_d, on the plates due to the squeeze effect and it is given by the following equation:

$$F_{\text{d}} = \Re \left[ \varPhi \right]Zs - \omega \text{Im} \left[ \varPhi \right]Z = c_{\text{d}} Zs + k_{\text{de}} Z ,$$

(5)

where ω is the angular frequency, $\Re \left[ . \right]$ and $\text{Im} \left[ \cdot \right]$ denote, respectively, the real and imaginary parts of the complex number, and Z is the transformed z coordinate representation. At this point, it is interesting to highlight the origin of the viscous gas damping coefficient ($c_{\text{d}}$) as well as the elastic gas damping coefficient (k_de) terms. They are derived from the force of fluid per unit of speed parameter, $\varPhi$, which can be expressed in terms of the infinite series summation over odd indices m and n containing the terms given by [17, 23]:

$$\varPhi = \mathop \sum \limits_{\text{m,odd}}^{M} \mathop \sum \limits_{\text{n,odd}}^{N} \frac{1}{{Q_{\text{fr}} G_{\text{mn}} + j\omega D_{\text{mn}} }},$$

(6)

where G_mn and D_mn are the geometrical terms of the accelerometer seismic mass structure and Q_fr is the relative flow rate term. Considering that the fixed and mobile plates (seismic mass) are rectangular, the geometric terms G_mn and D_mn are calculated, respectively, as:

$$G_{\text{mn}} = \frac{{\left( {mn} \right)^{2} \pi^{6} h_{0}^{3} }}{{768\eta_{\text{f}} ab}}\left( {\frac{{m^{2} }}{{a^{2} }} + \frac{{n^{2} }}{{b^{2} }}} \right),$$

(7)

and

$$D_{\text{mn}} = \frac{{\left( {mn} \right)^{2} \pi^{4} h_{0} }}{{64\eta_{\text{f}} abpn_{\gamma } }},$$

(8)

where a and b are the widths of the seismic mass geometry, and n_γ is the isothermal process coefficient, which depends on the heat conduction and the temperature assumed as boundary conditions during the linearization of the modified Reynolds equation in frequency domain [17]. The relative flow rate coefficient model (Q_fr), which takes into account high squeeze effect number assuming inertial gas effects, can be defined as follows [17]:

$$Q_{{{\text{fr}}K}} = \mathop \sum \limits_{{k,{\text{odd}}}}^{K} \frac{{1 + 6K_{\text{s}} }}{{\frac{{k^{4} \pi^{4} }}{96} + \frac{{j\omega k^{2} \pi^{2} \rho_{\text{f}} h_{0}^{2} \left( {1 + 10K_{\text{s}} + 30K_{\text{s}}^{2} } \right)}}{{96\eta_{\text{f}} \left( {1 + 6K_{\text{s}} } \right)}}}},$$

(9)

where k ∊ {1, 3, …, K} and K_s is the rarefaction coefficient, which can be expressed as a contribution of the Knudsen number ($K_{\text{n}}$) and the slip-flow term ($\sigma_{\text{p}}$) as

$$K_{\text{s}} = \sigma_{\text{p}} K_{\text{n}} .$$

(10)

In addition, the slip-flow coefficient (σ_p), includes the effect of kinetics velocity variation of gas molecules due to thermal energy near the surface and is given by [24]:

$$\sigma_{\text{p}} = \frac{{2 - \alpha_{\text{v}} }}{{\alpha_{\text{v}} }}\left[ {1.016 - 0.1211\left( {1 - \alpha_{\text{v}} } \right)} \right],$$

(11)

where α_v is the coefficient that expresses the diffusion reflected fraction of gas molecules, also known as tangential momentum accommodation coefficient (TMAC) [24]. Moreover, the Knudsen number

$$K_{\text{n}} = \frac{{\lambda_{\text{lc}} }}{{h_{\text{o}} }}$$

(12)

carries the information of the mean free path of gas (λ_lc), assuming elastic collisions [17] which can be given as

$$\lambda_{\text{lc}} = \frac{{K_{\text{B}} T}}{{\sqrt[2]{2}\sigma_{\text{ch}} p}},$$

(13)

where K_B is the Boltzmann constant, T is the temperature, and σ_ch is the effective collision area of gas. We highlight that the main free path is a temperature-dependent coefficient. This is the first of our considerations related to fluidic temperature dependence coefficients. The second one concerns to the fluid viscosity of the gas, which circumvents the seismic mass, in the MEMS’s sensing plate (Fig. 1). Based on ideal gases law, one interesting approach to describe the dynamic viscosity and temperature relationship was introduced by Sutherland [25], where such quantity is very well described thanks to the well-known Sutherland formula expressed as [25]

$$\eta_{\text{f}} = \eta_{0} \left( {\frac{T}{{T_{0} }}} \right)^{{\frac{3}{2}}} \left( {\frac{{T_{0} + R}}{T + R}} \right),$$

(14)

where R is the Sutherland constant of the gases, which is related to the potential energy of molecular gas due to the mutual attraction interaction [25], and η₀ is the dynamic viscosity at reference temperature (T₀) [26]. Table 1 introduces some important parameters related to the Sutherland coefficients for argon, helium and air gases media, as well as presents the main free path and dynamic coefficients just as other important fundamental parameters [27].

Table 1 Gases’ coefficients

The set of equations from (4) to (14) presents the main model assumptions related to the fluidic dynamic nature of the MEMS transducer accelerometer system. Also, these equations enable us to infer about $c_{\text{d}}$ and k_de coefficients quantitatively [Eqs. (2) and (3)]. Further, equations $\lambda_{\text{lc}} = \frac{{K_{\text{B}} T}}{{\sqrt[2]{2}\sigma_{\text{ch}} p}}$ (13) and (14) allow us to capture some of the temperature effects arising from fluid dynamics in the MEMS transducer device.

Next, turning now to the electrical and mechanical aspects of the elastic coefficient ($k_{\text{eff}}$), which was introduced according to the equation of the linearized effective electromechanical stiffness coefficient given as [21, 28]

$$k_{\text{eff}} = \frac{48EI}{{l_{\text{b}}^{3} }} - \frac{{2\varepsilon_{\text{r}} \varepsilon_{\text{o}} W_{\text{m}}^{2} V_{\text{s}}^{2} }}{{h_{0}^{3} }},$$

(15)

where E is the Young’s modulus, I is the transversal moment of inertia of beams, ε_o is the electrical permitivity in vaccum, ε_r is the relative electrical permitivity, V_s is the excitation voltage signal, W_m is the seismic mass width, and l_b is the length of the beams. The first term in Eq. (15) is the equivalent clamped–clamped beams spring constant (k_eq), whereas the second term captures the equivalent spring softening effect in virtue of the electrostatic behavior, which is coming from the intrinsic capacitive nature of the system [28].

Further, it is profitable to introduce two main assumptions for temperature effects in our transducer MEMS modeling design approach, owing to mechanical domain features. The first one has direct impact on the Young’s modulus (E), as shown in Eq. (15), with implications on changes in the material elasticity property. The crystal silicon (Si) used has (100) orientation and [110] flat direction. The stiffness C_ijkl and compliance S_ijkl, both anisotropic mechanical properties and both based on the Hooke’s law, are usually expressed by a fourth-rank tensor [29]. Through the unit cell symmetry of Si crystal representation, it is common to show S and C in the orthotropic context and consequently present the properties according to the specific axis of interest using a reduced rank tensor notation. The Si crystal coefficient values to [100] orientation are shown in Table 2 [30, 31]. Therefore, the elastic properties are expressed by Young’s modulus (E) and the Poisson’s ratio (ν) and can be easily found using parallel and orthonormal angular projections by the x-, y- and z-axis directions of the silicon crystal [31]. In addition, the stiffness tensor can then be simply rotated in the orientation of interest [32].

Table 2 Stiffness (C 10⁹ Pa) and compliance (S 10⁻¹² Pa) coefficients of silicon at 293 K

For a crystalline Si material, the linear thermal expansion coefficient has the same behavior for all crystallographic directions [29, 33]. The contribution of the thermal effect on the Si stiffness coefficients can be expressed by [14, 34]:

$$C_{{T_{ij} }} = C_{{T0_{ij} }} \left[ {1 + \mathop \sum \limits_{h \ge 1} \left( {{\text{TCE}}_{{C_{ij} }} } \right)_{h} \left( {T - T_{0} } \right)^{h} } \right],$$

(16)

where T₀ is the reference temperature, C_T0ij is the stiffness coefficient at reference temperature, and TCE_cij is the thermal coefficient of elasticity of the considered elastic constant. The first-order temperature coefficients of the elastic constants are presented in Table 3 [14, 33].

Table 3 Temperature coefficients of the elastic constants for p-type (B) and n-type (P) substrates

The second temperature implication in our model approach in mechanical domain was taking into account the general deformation of the MEMS design, owing to the thermal expansion variations acting on the transducer geometrical parameters design. We estimated the thermal expansion variations for all geometrical parameters based on the Si linear thermal expansion coefficient α_L (10⁻⁶ K⁻¹) for temperatures ranging from 120 to 1500 K that is expressed according to [35]:

$$\alpha_{\text{L}} = 3725\left( {1 - {\text{e}}^{{ - 588 \times 10^{{ - 3\left( {T - 124} \right)}} }} } \right) + 5548 \times 10^{ - 4} T.$$

(17)

The last parameter which plays a role in Eqs. (3) and (4) is the effective mass ($M_{\text{eff}}$) expressed as

$$M_{\text{eff}} = M_{\text{s}} + u\frac{13}{35}m_{\text{b}} ,$$

(18)

and it is obtained using the seismic mass parameter design ($M_{\text{s}}$) plus the effective mass of the beams, that is obtained according to the Rayleigh principle by means of the deflection of the beam curvature and the kinetic energy of the beams relation [36]. The parameter m_b is the mass of the beam, and u is the number of beams; in this case, u = 2, i.e., there are two clamped–clamped beams. Further, the accelerometer’s seismic mass with the geometric shape previously described can be obtained as a function of the mask designed by [21].

$$M_{\text{s}} = \rho_{\text{si}} \left( {W_{\text{m}}^{2} t_{\text{m}} + \frac{{\sqrt[2]{2}}}{2}W_{\text{m}} t_{\text{m}}^{2} + \frac{{t_{\text{m}}^{3} }}{6}} \right),$$

(19)

where ρ_Si is the silicon density, $t_{\text{m}}$ is the thickness of the beams, and $W_{\text{m}}$ is the seismic mass width.

Introducing Eqs. (2) and (3) in Eq. (1) and making some manipulations, it is possible to evaluate the amplitude (A₀) and phase (θ_d) of the dynamic response of the MEMS capacitive transducer according to [8]:

$$A_{0} = \frac{{f_{0} }}{{M_{\text{eff}} }}\sqrt {\frac{1}{{\left( {\omega_{\text{a}}^{2} - \omega^{2} } \right)^{2} + c_{\text{d}}^{2} \omega^{2} /M_{\text{eff}}^{2} }}}$$

(20)

and

$$\theta_{\text{d}} = - \arctan \left( {\frac{{c_{\text{d}} \omega }}{{M_{\text{eff}} \left( {\omega_{\text{a}}^{2} - \omega^{2} } \right)}}} \right),$$

(21)

where f_o is the amplitude of external force; ω_a is the modified frequency, which is a function of the angular frequency with damping effects, and is given by

$$\omega_{\text{a}} = \sqrt {\frac{{k_{\text{eff}} + k_{\text{de}} }}{{M_{\text{eff}} }}} .$$

(22)

The well-known damping factor ξ_m and the angular natural frequency ω_rm equations are, respectively:

$$\xi_{\text{m}} = \frac{{c_{\text{d}} }}{{2\left( {k_{\text{eq}} M_{\text{eff}} } \right)^{{\frac{1}{2}}} }}$$

(23)

and

$$\omega_{\text{rm}} = \left( {\frac{{k_{\text{eff}} }}{{M_{\text{eff}} }}} \right)^{{\frac{1}{2}}} .$$

(24)

Finally, after introducing the main transducer coefficients taking into account both the SFD and the thermal fluidics and thermal mechanics approaches, it is pertinent to reveal an alternative form to Eq. (1), expressed as the electromechanical sensitivity

$$S_{\text{EM}} = S_{\text{E}} S_{\text{M}} = H_{\text{EM}} ,$$

(25)

where the mechanical static sensitivity of transducer can be expressed as [19],

$$S_{\text{M}} = \left. {\frac{{\partial \delta_{z} }}{{\partial a_{z} }}} \right|_{\omega = 0} \to S_{\text{M}} = \frac{1}{{\omega_{\text{rm}}^{2} }},$$

(26)

while the electrical sensitivity S_E has the form

$$S_{\text{E}} = \frac{{2\varepsilon_{\text{r}} \varepsilon_{\text{o}} W_{\text{m}}^{2} }}{{h_{\text{o}}^{3} }}.$$

(27)

Thus, according to Eq. (25) the electromechanical dynamic sensitivity of the MEMS system is captured by the transfer function of the system. In the next section, the general assumptions and the input parameters used in the study are presented.

2.2 The general assumptions and input parameters

The calculations were carried out assuming three main hypotheses to the thermal domain features:

• the system is closed and in thermodynamic equilibrium,

• the electric permittivity of all gases considered in this study is assumed independent of temperature and pressure, and

• the thermal expansion coefficient of the oxide layers is constant for entire temperature range.

The first hypothesis implies that the isothermal process coefficient (n_γ) in Eq. (8) is assumed to be constant. The second hypothesis is found on the fact that all the gases considered in this study present very slightly variations, at low pressures and low temperature variations [37, 38]. Finally, the third one is related to the doped silicon plates’ material definition that composes the capacitive transducer. It is based on silicon dioxide layers, which provide electrical isolation as shown in Fig. 1. The thermal expansion coefficient of the oxide layers was assumed to be constant and equal to $0.24 \times 10^{ - 6}$ K⁻¹ for the entire range of temperature [39].

The study was divided into four topics as presented below:

SFD Model validation—the inertial effect squeeze film damping (IE-SFD) and the non-inertial squeeze film damping (NIE-SFD) models [4, 17, 19, 40] were compared with the experimental data for the four pressure values, with three damping gases presented in Table 1, allowing us to check the validity of our model approach. An experimental setup allowed us the measurement of the frequency response of the sample in a vacuum chamber, as shown in Fig. 3 [41]. An external pick-off electronic circuit was developed to interrogate the MEMS accelerometer. The theoretical model (1) was adjusted in amplitude, offsetting the gain of the external electronic circuit [38]. The experimental data were obtained from tests conducted on an accelerometer sample at four different pressures, $p \in \left\{ {1000, 500, 100, 50 } \right\}$ Pa [38]. The general test procedures were based on IEEE Std 1293-1998 [41].

Fig. 3

Illustration of the experimental setup for the frequency response test

Dynamic of damping gas coefficients with IE-SFD model—the focus was to present the behavior of the viscous gas damping coefficient ($c_{\text{d}}$) and the elastic gas damping coefficient ($k_{\text{de}}$), both presented in Eq. (5), also the damping factor ($\xi_{\text{m}}$), Eq. (23), the magnitude displacement response (A₀), Eq. (20), and the phase frequency response ($\theta_{\text{d}}$), Eq. (21). All simulation results were obtained using the following conditions: air gas atmosphere packaging, from − 1 g acceleration step input and pressure sweep range from 20 to 1000 Pa. The temperature was kept constant at 293 K.

Temperature effects in design parameters and gases—in this topic, inferences on the effects of the thermoelasticity and thermal expansion on the main geometrical parameters were made. Also, the considerations about the air and helium gases behavior in the dynamics of the system were made by us. In all cases, the pressure was fixed (p = 50 Pa) and the temperature variations were defined as $T \in \left\{ {228, 293, 398} \right\}$ K, assuming a step input of − 1 m/s².

Electromechanical sensitivity—the electromechanical sensitivity (S_EM) as a function of the temperature and frequency was evaluated, where we assume two different pressures defined as 20 and 200 Pa and $T \in \left\{ {228, 293, 398} \right\}$ K.

The complementary parameters used in the study are presented in Table 4. In the section below are presented the obtained results.

Table 4 Complementary input parameters of the study (T = 293 K)

3 Results and discussion

This section was arranged according to the topics detailed in Sect. 2.2.

3.1 SFD model validation

The gas squeeze film damping model, taking into account inertial effects (IE-SFD), was evaluated by comparing the calculated frequency response with experimental data. Figure 4 illustrates the obtained results for air. Also, for comparison purposes the non-inertial effect SFD model (NIE-SFD), for the same conditions, was shown. The frequency behavior was evidenced from Fig. 4a–d for different pressure conditions. The spectral compatibility of the frequency responses curves between the IE-SFD model and experimental data is notable, whereas the NIE-SFD model presents losses in the dynamic information, when the pressure increases mainly (Fig. 5).

Fig. 4

Effect of the inertial effects on SFD model for air at a p = 1000 Pa, b p = 500 Pa, c p = 100 Pa and d p = 50 Pa

Fig. 5

Effect of the inertial effects on SFD model for a helium and b argon, both at p = 500 Pa

In fact, the IE-SFD model allows us an improvement to capture the dynamic features for all studied pressures compared with the NIE-SFD approach. Although the simulated peak frequency response using the IE-SFD model approach did not perfectly match the frequency peak response of experimental data, the IE-SFD model frequency response allows us to make the first insights about the real dynamic of the system, without applying numerical methods, as finite element method (FEM) and others.

The differences in the position of the frequency peak responses between the IE-SFD model and experimental data have origins mainly due to the MEMS transducer model simplifications, which were introduced at the pertinent section of this work as well as in virtue of the sources of imprecisions in the experimental data and characterization procedures.

Further, the fabrication process provides intrinsic sources of imprecisions on the geometrical design parameters of the chosen MEMS transducer sample used during the tests even though the latest possibility had been already evaluated by means of simulations of the variations of each design parameter independently [5]. The author assumed that a maximum fabrication process deviation by dry etching had a value equal to 5%, related to the nominal values presented at Table 4, for all geometrical design parameters. He concluded that varying each parameter in an independent way has not evidenced any expressive deviation in the frequency peak spectrum response [5]. He also suggested that combined deviations need to be checked, but this quantitative analysis was not evaluated.

The similar dynamic behavior was obtained for the other two gases. Figure 10 shows the comparison of the IE-SFD model with the experimental data for helium and argon at 500 Pa. Such results enlighten the important role of the inertial effects in the model [17].

Notwithstanding the differences in the peak frequencies observed between the IE-SFD model and experimental spectrum data responses, the aforementioned model is able to capture the main dynamic features of the accelerometer MEMS transducer. In the next section, the results for the main damping gas coefficients are presented via IE-SFD model.

3.2 Dynamic of damping gas coefficients with IE-SFD model

The behavior of the damping factor coefficient associated with Eq. (23), as a function of the pressure and frequency, is shown in Fig. 6, evidencing its importance at low frequencies and high values of pressure. As the pressure inside the packaging decreases, the damping factor effect becomes less significant; the same is observed when the frequency increases. The viscous gas damping coefficient (Fig. 7) presents the same behavior of the damping factor. In practice, the viscous gas damping forces dominate the damping mechanism at low frequencies, because the gas has enough time to escape through the sides of the borders of the seismic mass structure [8].

Fig. 6

Damping factor coefficient of the capacitive MEMS accelerometer transducer for air gas packaging atmosphere with pressures varying from 20 to 1000 Pa

Fig. 7

Viscous gas damping coefficient simulation of the capacitive MEMS accelerometer transducer for air gas packaging atmosphere with pressures varying from 20 to 1000 Pa

The computed elastic gas damping coefficient is exhibited in Fig. 8. As the frequency increases, the elastic gas damping factor increases and becomes the dominant damping loss element in SFD effect. In this condition, the fluid film has not enough time to escape and it is trapped between the plates. The squeeze effect is associated with the compression effects on the trapped gas [8].

Fig. 8

Elastic gas damping coefficient simulation of the capacitive MEMS accelerometer transducer for air packaging atmosphere with pressures varying from 20 to 1000 Pa

The elastic gas damping mechanism affects directly the linearity loss in dynamic systems involving gas pressure packaging in planar MEMS devices [19]. Clearly, this damping mechanism can be mitigated by using low-pressure packaging conditions. When the SFD effect is minimized, the linearity of the system response is improved. In this context, the dominant damping mechanism is the mechanical one, which is limited by the loss energy due to the mechanical resonance. It is evident that the suitable control of the packaging atmosphere pressure promotes the reduction in undesirable effects of SFD in the capacitive MEMS acceleration transducer.

The improvement in the linear dynamic characteristic of the device is well captured by the magnitude and phase responses, as shown in Figs. 9 and 10, respectively. In addition, when the pressure is reduced, the amplitude peak increases and moves from a region of higher to lower frequencies, approaching the natural mechanical resonance of the seismic mass structure. Taking into account frequency regimes below the amplitude resonance peak, for low pressure an almost constant behavior in frequency range is observed in Fig. 9. Also, as the pressure rises, the linear behavior in frequency is lost. The similar constant behavior in the phase frequency response is verified for low pressures, as shown in Fig. 10.

Fig. 9

Magnitude displacement step response for − 1 g input in the capacitive MEMS accelerometer transducer for air gas packaging atmosphere with pressures varying from 20 to 1000 Pa

Fig. 10

Phase step response for − 1 g input in the capacitive MEMS accelerometer transducer for air packaging atmosphere with pressures varying from 20 to 1000 Pa

3.3 Temperature effects in design parameters and gases

Table 5 summarizes the effect of thermoelasticity and thermal expansion on the main geometrical parameters (which of them were repeated from Table 3 for better presentation of the results), and some of the main physical variables associated with the mechanical structure of the MEMS transducer. The results show the variation of the parameters and variables at the limits of the operational range in terms of the nominal values at 293 K.

Table 5 MEMS device parameter results at the limits of operational temperature range

The gas volume, Vg, is virtually constant in the entire range of temperatures. Additionally, the ideal gases law leads us to consider the molar mass of all gases as being constant and, thereby, for simplification purposes, we assume Vg as constant and adopt the values of gases densities presented in Table 1.

The effective stiffness constant, k_eff, presented in Eq. (15), is related to electrical and mechanical stiffness coefficients of the MEMS transducer [4]. At a temperature of 228 K, the mechanical stiffness increases and k_eff increases 0.41% with respect to 293 K. On the other hand, at 398 K the mechanical stiffness is nearly 0.61% below the reference value at 293 K. This implies in a structural behavior with slightly higher mechanical elasticity. The k_eff is the parameter that presents the higher variation as a function of temperature.

Basically, the effect on the geometric parameters variation is negligible for the entire proposed operational range, but these effects were taken into account in the following analysis.

However, the viscous gas damping coefficient (c_d) presents a considerable variation for all three gases, as shown in Table 6. Argon gas exhibits the greater value of c_d for all temperatures, and also, it is the gas most affected by temperature.

Table 6 Viscous gas damping coefficient (c_d), for static condition at 1 atm pressure in air

The magnitude of the seismic mass displacement as a function of frequency for air, argon and helium gases is shown in Fig. 11, assuming a step input of − 1 m/s². Air and helium gases reveal similar behavior when the frequency raises. Complementarily, the dynamic behavior of the MEMS transducer with a gas film of argon is more sensitive to temperature variations near the frequency of 500 Hz, as compared with air and helium gases near the same frequency.

Fig. 11

Magnitude of the seismic mass displacement as a function of frequency for a air, b argon and c helium gases at p = 50 Pa, for T ϵ {228, 293 and 398} K

3.4 Electromechanical sensitivity

The effect of the gas trapped inside the MEMS device on the electromechanical sensitivity (S_EM) as a function of the temperature and frequency is presented in Figs. 12, 13, 14, 15, 16 and 17, calculated for two different pressures, namely 20 and 200 Pa. The pressure values were selected according to our convenience, allowing us to make inferences in our study at lower pressures, which are supported by comparative results shown in Sect. 3.1. In the case of temperature, the lower and upper temperature limits adopted by us are very close to the common temperature range limits used by many electronic device manufacturers.

Fig. 12

Dynamic electromechanical sensitivity for air at 200 Pa packaging atmosphere

Fig. 13

Dynamic electromechanical sensitivity for air at 20 Pa packaging atmosphere

Fig. 14

Dynamic electromechanical sensitivity for argon at 200 Pa packaging atmosphere

Fig. 15

Dynamic electromechanical sensitivity for argon at 20 Pa packaging atmosphere

Fig. 16

Dynamic electromechanical sensitivity for helium at 200 Pa packaging atmosphere

Fig. 17

Dynamic electromechanical sensitivity for helium gas at 20 Pa packaging atmosphere

The results obtained from the adopted model with inertial effects illustrate the importance of both gas and pressure as design parameters. Such influence is better observed in Fig. 18.

Fig. 18

Electromechanical sensitivity of the capacitive microaccelerometer as a function of frequency for a helium, b air and c argon at three temperatures and two different pressures, and d a comparison of the effect of the three gases at 20 Pa and ambient temperature

As expected, the dynamic sensitivity at 20 Pa presents less variation than at 200 Pa for all studied gases. In other words, at 20 Pa the dynamic sensitivity presents less abrupt dynamic behavior than at 200 Pa, independently of the chosen gas. In consequence, at 20 Pa, the linear response of the device reaches up to 300 Hz, approximately, for air and helium, assuming variation of ≈ 0.5 dB related to constant sensitivity (i.e., 1 Hz in coordinating axis at Fig. 18a–c), no matter which temperature. For 200 Pa, the linear response drops down to about 150 Hz. Also in Fig. 18a–c, we are enabled to observe that the overall sensitivity plateau level increases when the temperature increases to 228–398 K, independently of the pressure. This fact corroborates with the reduction in stiffness coefficients [Eq. (16)] as a consequence of reduction in the Young modulus of Si. As a result for the three gases, the variation of S_EM as a function of temperature is below 0.17 dB in the entire operational range, for both evaluated pressures, depending only on the silicon mechanical properties at low frequencies. Finally, Fig. 18d shows the dynamic of electromechanical sensitivity (S_EM) of three gases. It is possible to verify a close behavior between helium and air gases. The situation is not the same for argon where we verify a considerable loss in the S_EM level when the frequency increases compared to the other ones. This fact suggests that the dynamic of the MEMS accelerometer in such conditions, this is, at 20 Pa and 298 K of pressure and temperature, respectively, from argon gas was most affected by its gaseous coefficients, as the density and the Sutherland coefficients as well.

4 Conclusion

The theoretical dynamic behavior of capacitive MEMS acceleration transducer based on silicon bulk-micromachined design was presented and evaluated. The adopted analytical model is based on basic structural mechanics and electric circuits and includes the squeeze film damping effects for the molecular regime and the mechanical thermoelasticity, in order to represent the electromechanical sensitivity in the frequency domain.

The main damping loss mechanism related to the SFD effects was presented. The internal atmosphere, composed either by air, argon, or by helium, was simulated, using the proposed model approaches. Linear responses in low-frequency regimes are obtained only assuming low pressure inside the MEMS transducer, no matter the chosen gas. The bandwidth depends on the gas trapped inside the silicon structure.

The IE-SFD model presented is able to capture the main features of accelerometer MEMS transducer, and it shows a valuable tool to make the first inferences about the transducer dynamics by the sensor designers.