Introduction

The discovery of carbon nanostructures in 1991 [1], which sped both theoretical and experimental research in this area, marked the beginning of nanotechnology. Carbon nanotubes are among the most effective examples of nanoscale materials in terms of their structural and mechanical properties. In recent years, researchers' interest in comprehending the dynamic behavior of carbon nanotubes has increased significantly. The properties of carbon nanotubes are researched under two categories. Atomic/molecular dynamics modeling is one of them. The other group comprises strain gradient theory [2], micropolar theory [3], nonlocal elasticity theory [4], modified couple stress theory [5], and other theories based on several ideas of size-based continuity.

Unlike the conventional theory, the nonlocal elasticity theory considers size effects. To explain the size effect, Eringen [6] assumed that the stress at one location indicates distortions at all points in the continuum. Atomic interactions play a significant role in size dependency, especially at the nanoscale. The static and dynamic behavior of carbon nanotubes has been extensively studied in the literature by employing Eringen's nonlocal elasticity theory. Studies involving static evaluations have focused primarily on bending and torsion, while studies including dynamic analyses have considered wave propagation and vibration. Recent research has shown that evaluations of wave propagation and vibration for CNTs in different media (elastic, viscoelastic, etc.) yield accurate findings.

Murmu and Pradhan [7] researched the impacts of scale effect in an elastic medium on the vibration of single-walled carbon nanotubes. By applying nonlocal elasticity theory, Aydogdu [8] and Yaylı et al. [9] examined the axial vibration of a nanorod in an elastic medium. Lee and Chang [10] studied the vibrational behavior of single-walled carbon nanotubes filled with a viscous fluid in 2009. In 2010, Soltani et al. [11] researched the thermo-mechanical vibration of single-walled carbon nanotubes in a Pasternak medium. Khosravi et al. [12] studied the axial vibration of single-walled carbon nanotubes under various live loads in an elastic medium. Arda and Aydogdu [13] investigated the free rotational vibration of single-walled carbon nanotubes in a viscoelastic medium and studied how the nonlocal and ambient parameters affected vibrational frequencies. Additionally, Arda and Aydogdu [14] examined torsional vibration by considering the impacts of the nonlocal parameter in double-walled carbon nanotubes in viscoelastic media, stiffness and damping parameters of viscoelastic media, and the van der Waals contact between two nanotubes.

The most successful technique for describing nanostructures is wave propagation. It is also the basis for nanosensor converters. Natsuki et al. [15] investigated several analytical models to solve wave propagation in single- and double-walled carbon nanotubes in an elastic medium. Wang et al. [16] researched the size impact on wave propagation in double-walled carbon nanotubes. In their work, Lim and Yang [17] used an analytical nonlocal stress model in carbon nanotubes and size effects to investigate wave propagation. Ponnusamy and Amuthalakshmi [18] examined the impact of heat on wave propagation in an acoustic cavity of double-walled carbon nanotubes.

In 2013, Srivastava [19] studied acoustic wave propagation in carbon nanotubes. Tang et al. [20] covered the issue of viscoelastic wave propagation in viscoelastic single-walled carbon nanotubes by employing the nonlocal strain gradient theory. Zhen [21] investigated the influence of surface and nonlocal factors on wave propagation in fluid-filled single-walled viscoelastic nanotubes. Using the theory of the nonlocal second-order strain gradient elasticity, Guo et al. [22] examined the issue of transverse wave propagation in single-walled viscoelastic nanotubes. Using strain gradient theory, Boyina and Piska [23] have recently analyzed wave propagation in viscoelastic Timoshenko nanobeams under surface and magnetic field impacts. This study shows how the diameter of a carbon nanotube affects the phase velocities of shear and flexural waves.

The problem of wave propagation is extremely important in many technical and scientific fields. The research listed above has considered the deformation of CNTs. However, CNT deformation is nonlinear in nature [24]. For example, water waves, plasma physics, and nonlinear optics are significantly affected by nonlinear effects in various branches of physics and engineering. Nonlinear effects in nanotubes have been considered in some nonlinear vibration and nonlinear wave propagation problems. Many of these studies have considered Von Kármán geometric nonlinearity. Yang et al. [25] examined nonlinear free vibration in single-walled carbon nanotubes by utilizing nonlocal Timoshenko beam theory. In 2012, Ke et al. [26] used nonlocal theory to analyze the nonlinear vibration of piezoelectric nanobeams. Sellitto and Di Domenico [27] also studied nonlocal and nonlinear effects on thermal and elastic high-frequency wave propagation in nanosystems. Sobamowo et al. [28] researched the nonlinear vibration of single-walled simply supported and clamped carbon nanobeams with boundary conditions embedded in a multilayer elastic medium. Wang et al. [29] performed one of the rare studies on nonlinear wave propagation using the theory of nonlocal elasticity to evaluate wave propagation in single-walled nonlinearly curved carbon nanotubes. Norouzzadeh et al. [30] investigated nonlocal and strain gradient effects in Timoshenko nanobeams by nonlinear wave propagation analysis.

Gaygusuzolu and Akdal [31] used the theory of nonlocal elasticity in an elastic medium to understand weak nonlinear wave propagation (solitary waves) in nanorods. Consequently, they obtained the Korteweg–de Vries equation, which serves as the governing equation of long waves. The researchers examined the impacts of the nonlocal and stiffness parameters on the wave profile in an elastic medium. By means of the nonlocal elasticity theory, Gaygusuzoglu et al. [32] investigated nonlinear wave modulation in nanorods and reached the nonlinear Schrödinger equation as the governing equation of waves in a nonlocal elastic medium. The researchers investigated linear local and nonlocal, as well as nonlinear local and nonlocal situations, and discovered amplitude-dependent phase and group velocities and wave frequencies.

This work studies the nonlocal theory-based nonlinear interactions of two acoustic waves traveling through a nanorod in a viscoelastic medium by employing a multiple-scale expansion approach. First, a nonlinear field equation in one dimension is discovered. We also give the linear dispersion relation of waves so that you can examine the medium’s dispersive nature. We demonstrate that the coupled nonlinear Schrödinger equations control the nonlinear interaction of two waves in a nonlocal viscoelastic medium. The present study shows the nonlinear plane wave solutions for the obtained equations for a few particular circumstances.

The structure of the current study is displayed below. "Fundamental Equations and Theoretical Initiations" discusses the system's governing equation and provides information on nonlocal elasticity theory. "Investigation of Nonlinear Wave Interaction in Nanorods Using the Multiple-Scale Expansion Method" covers the fundamentals of the multiple-scale expansion approach and nonlinear wave interaction. This section presents the nonlinear plane wave solutions for some special cases of the coupled nonlinear Schrödinger equations. "Numerical Results and Discussion" includes the numerical analysis and discussion. Finally, "Conclusion" gives general results from the study.

Fundamental Equations and Theoretical Initiations

Model for a Nonlinear Local Viscoelastic Nanorod

The fundamental formulas for nanorod motion in local viscoelastic media are obtained in this section. The gradient tensor of deformation, established by Malvern [33], can be presented to derive the equation for nonlinear vibration in a nanotube.

$${\mathbf{F}} = {\mathbf{\nabla U}} + {\mathbf{I}}$$
(1)

Here, I is the unit matrix, and U represents the motion's displacement component. When no body forces are acting on the element in a medium subject to finite extension, the equation of motion can be expressed as follows in terms of material coordinates:

$${\mathbf{\nabla }}{\rm{[}}{\mathbf{SF}}^{\text{T}} ] + {\mathbf{f}} = \rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 }$$
(2)

Here, ρ0 is the medium's undeformed density, f denotes the distributed axial force that acts on the rod, and S refers to the second Piola-Kirchoff stress tensor, the energy-based conjugate of the Green stress tensor.

This study makes the following assumption regarding the axial force caused by the viscoelastic medium:

$${\mathbf{f}} = - k_e {\mathbf{U}} - d\frac{{\partial {\mathbf{U}}}}{\partial t}$$
(3)

where d refers to the damping coefficient, and ke is the elastic medium stiffness.

Accordingly, Hooke's law can be used as the governing equation. Thus, the equation is expressed as shown below:

$${\mathbf{S}} = {\mathbf{cE}}$$
(4)

Here, E denotes the Green strain tensor expressed as follows, and c represents the fourth-order tensor depicting the material's elastic behavior:

$${\mathbf{E}} = \frac{1}{2}{\rm{[}}{\mathbf{F}}^{\rm{T}} {\mathbf{F - 1}}{\rm{]}}$$
(5)

By restricting the rod’s boundary conditions and assuming that only radial deformation U(x,t) occurs in the medium, the gradient deformation tensor is transformed into a diagonal matrix in Cartesian coordinates:

$${\text{F}}_{xx} = 1 + \frac{\partial U}{{\partial x}}$$
(6)
$${\text{F}}_{yy} = 1$$
(7)
$${\text{F}}_{zz} = 1$$
(8)

The following equation may be obtained by concentrating only on the non-zero component of the Green strain tensor:

$$E_{xx} = \left( {1 + \frac{1}{2}\frac{\partial U}{{\partial x}}} \right)\frac{\partial U}{{\partial x}}$$
(9)

The following equation describes the stress–strain relationships for isotropic materials with Poisson’s ratio ν and elastic modulus EE:

$${\text{S}}_{ij} = \frac{E_E }{{(1 + \nu )}}\left[ {{\text{E}}_{ij} + \frac{\nu }{1 - 2\nu }{\text{E}}_{kk} \delta_{ij} } \right]$$
(10)

δinj refers to Kronecker’s delta. If shear stresses are eliminated when Eq. (9) is inserted into Eq. (10), the normal stress components are presented below:

$${\text{S}}_{xx} = \frac{E_E (1 - \nu )}{{(1 + \nu )(1 - 2\nu )}}\left( {1 + \frac{1}{2}\frac{\partial U}{{\partial x}}} \right)\frac{\partial U}{{\partial x}}$$
(11)
$${\text{S}}_{yy} = {\text{S}}_{zz} = \frac{\nu E_E }{{(1 + \nu )(1 - 2\nu )}}\left( {1 + \frac{1}{2}\frac{\partial U}{{\partial x}}} \right)\frac{\partial U}{{\partial x}}$$
(12)

Equation (13) can be obtained by rearranging Eqs. (11) and (12) using Eqs. (6), (7), and (8):

$$\begin{gathered} \left[ {\frac{3}{2}\left( {\frac{\partial U}{{\partial x}}} \right)^2 + 3\frac{\partial U}{{\partial x}} + 1} \right]\frac{\partial^2 U}{{\partial x^2 }} - \frac{k_e (1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}U - \frac{d(1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}\frac{\partial U}{{\partial t}} \hfill \\ = \frac{\rho_0 (1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}\frac{\partial^2 U}{{\partial t^2 }} \hfill \\ \end{gathered}$$
(13)

The nonlinear terms in Eq. (13) lose their significance for the infinite deformation of the viscoelastic medium, and Eq. (13) is reduced to the equation below:

$$\frac{\partial^2 U}{{\partial x^2 }} - \frac{k_e (1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}U - \frac{d(1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}\frac{\partial U}{{\partial t}} = \frac{\rho_0 (1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}\frac{\partial^2 U}{{\partial t^2 }}$$
(14)

The following non-dimensional variables will be introduced to make the equation non-dimensional:

$$\psi = U/r_0$$
(15)
$$\zeta = x/r_0$$
(16)

The radius of the nanorod is defined here by r0. Equations (15) and (16) can be used to rearrange Eqs. (13) and (14) to derive the subsequent non-dimensional equation:

$$\left[ {\frac{3}{2}\left( {\frac{\partial \psi }{{\partial \zeta }}} \right)^2 + 3\frac{\partial \psi }{{\partial \zeta }} + 1} \right]\frac{\partial^2 \psi }{{\partial \zeta^2 }} - K_e \psi - D\frac{\partial \psi }{{\partial t}} = \delta \frac{\partial^2 \psi }{{\partial t^2 }}$$
(17)

where the coefficients Ke, D, and δ are expressed as shown below:

$$K_e = \frac{k_e r_0^2 (1 + \nu )(1 - 2\nu )}{{(1 - \nu )}},\,\,D = \frac{dr_0^2 (1 + \nu )(1 - 2\nu )}{{(1 - \nu )}},\,\,\delta = \frac{\rho_0 r_0^2 (1 + \nu )(1 - 2\nu )}{{E_E (1 - \nu )}}$$
(18)

Mousavi and Fariborz [34] obtained Eq. (17) for the local nonlinear nanorod model in the following manner:

$$\left[ {\frac{3}{2}\left( {\frac{\partial \psi }{{\partial \zeta }}} \right)^2 + 3\frac{\partial \psi }{{\partial \zeta }} + 1} \right]\frac{\partial^2 \psi }{{\partial \zeta^2 }} = \delta \frac{\partial^2 \psi }{{\partial t^2 }}$$
(19)

The linear equation of motion is given below:

$$\frac{\partial^2 \psi }{{\partial \zeta^2 }} = \delta \frac{\partial^2 \psi }{{\partial t^2 }}.$$
(20)

Model for a Nonlinear Nonlocal Viscoelastic Nanorod

This section will cover nonlocal viscoelasticity and construct the equations of motion for nanorods in nonlocal viscoelastic media. Eringen [3] and Aydogdu [35] developed the constitutive equation for a nanorod by utilizing nonlocal elasticity theory, which is expressed as follows:

$$[1 - (e_0 a)^2 {{\nabla }}^2 {{][}}{\mathbf{SF}}^{\text{T}} ] = \lambda_L {\text{E}}_{rr} \delta_{kl} { + 2}\mu_L {\text{E}}_{kl}$$
(21)

where e0 refers to a constant, a represents the internal characteristic length, SFT denotes the nonlocal stress tensor, Ekl is the strain tensor, and λL and μL denote Lamé constants. To guarantee the correctness of nonlocal models, it is crucial to choose the nonlocal parameter carefully. Eringen [3] proposed e0 = 0.39 by comparing the lattice dynamic longitudinal wave frequency data at the end of the first Broullin zone (k = π/a), where k refers to the wavelength and the parameter a is selected as a characteristic length stretch throughout micro-, meso-, and macroscales. Eringen recommended the value e0 = 0.31 for Rayleigh surface waves [6]. According to Aydogdu [35], the nonlocal parameter e0 of CNTs depends on their geometrical and material properties.

It is essential to create the nonlocal viscoelastic constitutive relation of a nanorod to analyze the axial modulation of this structure. Hence it is possible to obtain the equation of motion for the nanorod embedded in a viscoelastic medium in the following way:

$${\mathbf{\nabla }}{\rm{[}}{\mathbf{SF}}^{\text{T}} ] + {\mathbf{f}} = \rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 }$$
(22)

The current work assumes axial force due to a viscoelastic medium in the following form:

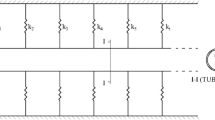
$${\mathbf{f}} = - k_e {\mathbf{U}} - d\frac{{\partial {\mathbf{U}}}}{\partial t}$$
(23)

where d is the damping coefficient, and ke refers to the elastic medium stiffness. Figure 1 displays a schematic diagram of the nanorod model in a viscoelastic medium.

Fig. 1
figure 1

An illustration of the nanorod model in a viscoelastic medium

Full size image

It is possible to solve Eq. (21) for SFT by taking the gradient of both sides to obtain the following equation:

$${\mathbf{\nabla }}{\rm{[}}{\mathbf{SF}}^{\text{T}} ] = (e_0 a)^2 \nabla^2 {\mathbf{\nabla }}{\rm{[}}{\mathbf{SF}}^{\text{T}} ] + {\mathbf{\nabla }}(\lambda_L {\text{E}}_{rr} \delta_{kl} { + 2}\mu_L {\text{E}}_{kl} )$$
(24)

The equation below can be derived by expressing the gradient of Eq. (22) and multiplying it by a nonlocal parameter:

$$(e_0 a)^2 \nabla^2 {\rm{[}}{\mathbf{SF}}^{\text{T}} ] = (e_0 a)^2 {\mathbf{\nabla }}\left[ {\rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 } - {\mathbf{f}}} \right]$$
(25)

Equation (25) takes the following form when Eq. (24) is inserted into it:

$${\mathbf{\nabla }}{\rm{[}}{\mathbf{SF}}^{\text{T}} ] = (e_0 a)^2 \nabla^2 \rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 } - (e_0 a)^2 \nabla^2 {\mathbf{f}} + {\mathbf{\nabla }}(\lambda_L {\text{E}}_{rr} \delta_{kl} { + 2}\mu_L {\text{E}}_{kl} )$$
(26)

When combined, Eqs. (22) and (26) yield the following differential equation:

$$\rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 } = (e_0 a)^2 \nabla^2 \rho_0 \frac{{\partial^2 {\mathbf{U}}}}{\partial t^2 } - (e_0 a)^2 \nabla^2 {\mathbf{f}} + {\mathbf{\nabla }}(\lambda_L {\text{E}}_{rr} \delta_{kl} { + 2}\mu_L {\text{E}}_{kl} ) + {\mathbf{f}}$$
(27)

In the context of nonlocal viscoelasticity, the following nonlinear non-dimensional equation of motion is obtained by applying non-zero displacement U to a one-dimensional case:

$$\begin{aligned} \left[ {\frac{3}{2}\left( {\frac{\partial \psi }{{\partial \zeta }}} \right)^2 + 3\frac{\partial \psi }{{\partial \zeta }} + 1} \right]\frac{\partial^2 \psi }{{\partial \zeta^2 }} & = \delta \left( {\frac{\partial^2 \psi }{{\partial t^2 }} - \mu \frac{\partial^4 \psi }{{\partial \zeta^2 \partial t^2 }}} \right) + K_e \left( {\psi - \mu \frac{\partial^2 \psi }{{\partial \zeta^2 }}} \right) \\ & \quad + D\left( {\frac{\partial \psi }{{\partial t}} - \mu \frac{\partial^3 \psi }{{\partial \zeta^2 \partial t}}} \right) \\ \end{aligned}$$
(28)

where μ, also known as the dimensionless nonlocal parameter, is \(\mu = (e_0 a/r_0 )^2\). The nonlinear equation of motion of the classical viscoelasticity theory can be obtained by setting μ = 0.

Investigation of Nonlinear Wave Interaction in Nanorods Using the Multiple-Scale Expansion Method

It might be challenging to find exact answers to nonlinear situations. This is particularly true for nonlinear dynamics under the nonlocal elasticity theory because the governing equations are complicated. However, dealing with nonlinear issues is usually not too difficult when nonlinearity is suitably weak. In this case, the dispersive properties of the medium may be used to derive evolution equations from the nonlinearity and dispersion equilibrium. Due to the aforementioned property, when nonlinearity and dispersion are in equilibrium, it is reasonable to apply the far-field theory of nonlinear waves, which has been completely developed in several fields of engineering and physics, to nonlocal elasticity theory.

This section studies the interaction of two acoustic waves in nonlocal viscoelastic media. To this end, we employ the multiple-scale expansion technique [36] and present the resulting coordinate stretching:

$$\zeta_n = \varepsilon^n \zeta ,\quad t_n = \varepsilon^n t,\quad n = 0,1,2,...$$
(29)

Here, the weakness of nonlinearity is measured by the small parameter ε.

The field quantities will be assumed to be functions of both slow \((\zeta_0 ,\zeta_1 ,\zeta_2 ,...;t_0 ,t_1 ,t_2 ,...)\) and fast variables (ζ, t). Therefore, the derivative expansions listed below are permissible:

$$\frac{\partial }{\partial \zeta } = \sum_{n = 0}^N {\varepsilon^n \frac{\partial }{\partial \zeta_n }} ,\quad \frac{\partial }{\partial t} = \sum_{n = 0}^N {\varepsilon^n \frac{\partial }{\partial t_n }}$$
(30)

The field quantities are expanded into an asymptotic series of ε as shown below:

$$\psi = \sum_{n = 1}^\infty {\varepsilon^n \psi_n (\zeta_0 ,\zeta_1 ,\zeta_2 ,...;t_0 ,t_1 ,t_2 ,...) = \,} \,\varepsilon \psi_1 + \varepsilon^2 \psi_2 + \varepsilon^3 \psi_3 + \cdots$$
(31)

The following differential equation is derived using the expansion to obtain Eq. (28):

$$\begin{gathered} \left[ {\frac{3}{2}\left( {\varepsilon \frac{{\partial \psi _1 }}{{\partial \zeta _0 }}} \right)^2 + 3\varepsilon ^3 \frac{{\partial \psi _1 }}{{\partial \zeta _0 }}\frac{{\partial \psi _1 }}{{\partial \zeta _1 }} + 3\varepsilon \frac{{\partial \psi _1 }}{{\partial \zeta _0 }} + 3\varepsilon ^2 \frac{{\partial \psi _2 }}{{\partial \zeta _0 }} + 3\varepsilon ^2 \frac{{\partial \psi _1 }}{{\partial \zeta _1 }} + ... + 1} \right] \times \left[ {\varepsilon \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^2 }}} \right. \hfill \\ + \left. {\varepsilon ^2 \frac{{\partial ^2 \psi _2 }}{{\partial \zeta _0^2 }} + \varepsilon ^3 \frac{{\partial ^2 \psi _3 }}{{\partial \zeta _0^2 }} + 2\varepsilon ^2 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^{\,} \partial \zeta _1 }} + 2\varepsilon ^3 \frac{{\partial ^2 \psi _2 }}{{\partial \zeta _0^{\,} \partial \zeta _1 }} + 2\varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^{\,} \partial \zeta _2 }} + \varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _1^2 }} + ...} \right] \hfill \\ = \delta \left[ {\varepsilon \frac{{\partial ^2 \psi _1 }}{{\partial t_0^2 }} + \varepsilon ^2 \frac{{\partial ^2 \psi _2 }}{{\partial t_0^2 }} + \varepsilon ^3 \frac{{\partial ^2 \psi _3 }}{{\partial t_0^2 }} + 2\varepsilon ^2 \frac{{\partial ^2 \psi _1 }}{{\partial t_0^{\,} \partial t_1^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^2 \psi _2 }}{{\partial t_0^{\,} \partial t_1^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial t_0^{\,} \partial t_2^{\,} }}} \right. \hfill \\ + \left. {\varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial t_1^2 }} + ...} \right] - \delta \mu \left[ {\varepsilon \frac{{\partial ^4 \psi _1 }}{{\partial t_0^2 \partial \zeta _0^2 }} + } \right.\varepsilon ^2 \frac{{\partial ^4 \psi _2 }}{{\partial t_0^2 \partial \zeta _0^2 }} + \varepsilon ^3 \frac{{\partial ^4 \psi _3 }}{{\partial t_0^2 \partial \zeta _0^2 }} + 2\varepsilon ^2 \frac{{\partial ^4 \psi _1 }}{{\partial t_0^2 \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} \hfill \\ + 2\varepsilon ^3 \frac{{\partial ^4 \psi _2 }}{{\partial t_0^2 \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^4 \psi _1 }}{{\partial t_0^2 \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + \varepsilon ^3 \frac{{\partial ^4 \psi _1 }}{{\partial t_0^2 \partial \zeta _1^2 }} + 2\varepsilon ^2 \frac{{\partial ^4 \psi _1 }}{{\partial \zeta _0^2 \partial t_0^{\,} \partial t_1^{\,} }} + \varepsilon ^3 \frac{{\partial ^4 \psi _1 }}{{\partial t_1^2 \partial \zeta _0^2 }} \hfill \\ + \left. {2\varepsilon ^3 \frac{{\partial ^4 \psi _2 }}{{\partial \zeta _0^2 \partial t_0^{\,} \partial t_1^{\,} }} + 4\varepsilon ^3 \frac{{\partial ^4 \psi _1 }}{{\partial t_0^{\,} \partial t_1^{\,} \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^4 \psi _1 }}{{\partial \zeta _0^2 \partial t_0^{\,} \partial t_2^{\,} }} + ...} \right] + K_e \left[ {\varepsilon \psi _1 + \varepsilon ^2 \psi _2 } \right. \hfill \\ \left. { + \varepsilon ^3 \psi _3 + ...} \right] - K_e \mu \left[ {\varepsilon \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^2 }}} \right. + \varepsilon ^2 \frac{{\partial ^2 \psi _2 }}{{\partial \zeta _0^2 }} + \varepsilon ^3 \frac{{\partial ^2 \psi _3 }}{{\partial \zeta _0^2 }} + 2\varepsilon ^2 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^{\,} \partial \zeta _1 }} + 2\varepsilon ^3 \frac{{\partial ^2 \psi _2 }}{{\partial \zeta _0^{\,} \partial \zeta _1 }} \hfill \\ + 2\varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _0^{\,} \partial \zeta _2 }}\left. { + \varepsilon ^3 \frac{{\partial ^2 \psi _1 }}{{\partial \zeta _1^2 }} + ...} \right] + D\left[ {\varepsilon \frac{{\partial \psi _1 }}{{\partial t_0^{\,} }} + \varepsilon ^2 \frac{{\partial \psi _2 }}{{\partial t_0^{\,} }} + \varepsilon ^3 \frac{{\partial \psi _3 }}{{\partial t_0^{\,} }} + \varepsilon ^2 \frac{{\partial \psi _1 }}{{\partial t_1^{\,} }}} \right. \hfill \\ \left. { + \varepsilon ^3 \frac{{\partial \psi _2 }}{{\partial t_1^{\,} }} + \varepsilon ^3 \frac{{\partial \psi _1 }}{{\partial t_2^{\,} }} + ...} \right] - D\mu \left[ {\varepsilon \frac{{\partial ^3 \psi _1 }}{{\partial t_0^{\,} \partial \zeta _0^2 }} + } \right.\varepsilon ^2 \frac{{\partial ^3 \psi _2 }}{{\partial t_0^{\,} \partial \zeta _0^2 }} + \varepsilon ^3 \frac{{\partial ^3 \psi _3 }}{{\partial t_0^{\,} \partial \zeta _0^2 }} \hfill \\ + 3\varepsilon ^2 \frac{{\partial ^3 \psi _1 }}{{\partial t_0^{\,} \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + 3\varepsilon ^3 \frac{{\partial ^3 \psi _2 }}{{\partial t_0^{\,} \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^3 \psi _1 }}{{\partial t_0^{\,} \partial \zeta _0^{\,} \partial \zeta _2^{\,} }} + 2\varepsilon ^3 \frac{{\partial ^3 \psi _1 }}{{\partial t_0^{\,} \partial \zeta _0^{\,} \partial \zeta _3^{\,} }} \hfill \\ \left. { + \varepsilon ^3 \frac{{\partial ^3 \psi _1 }}{{\partial t_0^{\,} \partial \zeta _1^2 }} + \varepsilon ^2 \frac{{\partial ^3 \psi _1 }}{{\partial t_1^{\,} \partial \zeta _0^2 }} + \varepsilon ^3 \frac{{\partial ^3 \psi _2 }}{{\partial t_1^{\,} \partial \zeta _0^2 }} + 3\varepsilon ^3 \frac{{\partial ^3 \psi _1 }}{{\partial t_1^{\,} \partial \zeta _0^{\,} \partial \zeta _1^{\,} }} + \varepsilon ^3 \frac{{\partial ^3 \psi _1 }}{{\partial t_2^{\,} \partial \zeta _0^2 }} + ...} \right] \hfill \\ \end{gathered}$$
(32)

The following set of differential equations is obtained as a result of putting all like powers of coefficients ε at zero:

The first-order, O(ε), equation:

$$\frac{\partial^2 \psi_1 }{{\partial \zeta_0^2 }} = \delta \frac{\partial^2 \psi_1 }{{\partial t_0^2 }} - \delta \mu \frac{\partial^4 \psi_1 }{{\partial t_0^2 \partial \zeta_0^2 }} + K_e \psi_1 - K_e \mu \frac{\partial^2 \psi_1 }{{\partial \zeta_0^2 }} + D\frac{\partial \psi_1 }{{\partial t_0^{\,} }} - D\mu \frac{\partial^3 \psi_1 }{{\partial t_0^{\,} \partial \zeta_0^2 }}$$
(33)

The second-order, O(ε2), equation:

$$\begin{gathered} 3\frac{\partial \psi_1 }{{\partial \zeta_0 }}\frac{\partial^2 \psi_1 }{{\partial \zeta_0^2 }} + \frac{\partial^2 \psi_2 }{{\partial \zeta_0^2 }} + 2\frac{\partial^2 \psi_1 }{{\partial \zeta_0^{\,} \partial \zeta_1 }} = \delta \left( {\frac{\partial^2 \psi_2 }{{\partial t_0^2 }} + 2\frac{\partial^2 \psi_1 }{{\partial t_0^{\,} \partial t_1^{\,} }}} \right) - \delta \mu \left( {\frac{\partial^4 \psi_2 }{{\partial t_0^2 \partial \zeta_0^2 }}} \right. + \hfill \\ \left. {2\frac{\partial^4 \psi_1 }{{\partial t_0^2 \partial \zeta_0^{\,} \partial \zeta_1^{\,} }} + 2\frac{\partial^4 \psi_1 }{{\partial \zeta_0^2 \partial t_0^{\,} \partial t_1^{\,} }}} \right) + K_e \left( {\psi_2 - \mu \frac{\partial^2 \psi_2 }{{\partial \zeta_0^2 }} - 2\mu \frac{\partial^2 \psi_1 }{{\partial \zeta_0^{\,} \partial \zeta_1 }}} \right) + \hfill \\ D\left( {\frac{\partial \psi_2 }{{\partial t_0^{\,} }} + \frac{\partial \psi_1 }{{\partial t_1^{\,} }} - \mu \frac{\partial^3 \psi_2 }{{\partial t_0^{\,} \partial \zeta_0^2 }} - 3\mu \frac{\partial^3 \psi_1 }{{\partial t_0^{\,} \partial \zeta_0^{\,} \partial \zeta_1^{\,} }}} \right) \hfill \\ \end{gathered}$$
(34)

The third-order, O(ε3), equation:

$$\begin{gathered} \frac{3}{2}\left( {\frac{\partial \psi_1 }{{\partial \zeta_0 }}} \right)^2 \frac{\partial^2 \psi_1 }{{\partial \zeta_0^2 }} + 3\frac{\partial \psi_1 }{{\partial \zeta_0 }}\frac{\partial^2 \psi_2 }{{\partial \zeta_0^2 }} + 3\frac{\partial \psi_2 }{{\partial \zeta_0 }}\frac{\partial^2 \psi_1 }{{\partial \zeta_0^2 }} + 2\frac{\partial^2 \psi_1 }{{\partial \zeta_0^{\,} \partial \zeta_2 }} + \frac{\partial^2 \psi_3 }{{\partial \zeta_0^2 }} + 2\frac{\partial^2 \psi_2 }{{\partial \zeta_0^{\,} \partial \zeta_1 }} \hfill \\ + \frac{\partial^2 \psi_1 }{{\partial \zeta_1^2 }} + 6\frac{\partial \psi_1 }{{\partial \zeta_0 }}\frac{\partial^2 \psi_1 }{{\partial \zeta_0^{\,} \partial \zeta_1 }} = \delta \left( {\frac{\partial^2 \psi_3 }{{\partial t_0^2 }} + 2\frac{\partial^2 \psi_2 }{{\partial t_0^{\,} \partial t_1^{\,} }} + 2\frac{\partial^2 \psi_1 }{{\partial t_0^{\,} \partial t_2^{\,} }} + \frac{\partial^2 \psi_1 }{{\partial t_1^2 }}} \right) - \delta \mu \left( {\frac{\partial^4 \psi_3 }{{\partial t_0^2 \partial \zeta_0^2 }}} \right. \hfill \\ + 2\frac{\partial^4 \psi_2 }{{\partial t_0^2 \partial \zeta_0^{\,} \partial \zeta_1^{\,} }} + 2\frac{\partial^4 \psi_1 }{{\partial t_0^2 \partial \zeta_0^{\,} \partial \zeta_2^{\,} }} + 2\frac{\partial^4 \psi_2 }{{\partial \zeta_0^2 \partial t_0^{\,} \partial t_1^{\,} }} + 4\frac{\partial^4 \psi_1 }{{\partial t_0^{\,} \partial t_1^{\,} \partial \zeta_0^{\,} \partial \zeta_1^{\,} }} + 2\frac{\partial^4 \psi_1 }{{\partial \zeta_0^2 \partial t_0^{\,} \partial t_2^{\,} }} \hfill \\ + \left. {\frac{\partial^4 \psi_1 }{{\partial t_0^2 \partial \zeta_1^2 }} + \frac{\partial^4 \psi_1 }{{\partial t_1^2 \partial \zeta_0^2 }}} \right) + K_e \psi_3 - K_e \mu \left( {\frac{\partial^2 \psi_3 }{{\partial \zeta_0^2 }} + 2\frac{\partial^2 \psi_2 }{{\partial \zeta_0^{\,} \partial \zeta_1 }} + 2\frac{\partial^2 \psi_1 }{{\partial \zeta_0^{\,} \partial \zeta_2 }} + \frac{\partial^2 \psi_1 }{{\partial \zeta_1^2 }}} \right) \hfill \\ + D\left( {\frac{\partial \psi_3 }{{\partial t_0^{\,} }} + \frac{\partial \psi_2 }{{\partial t_1^{\,} }} + \frac{\partial \psi_1 }{{\partial t_2^{\,} }}} \right) - D\mu \left( {\frac{\partial^3 \psi_3 }{{\partial t_0^{\,} \partial \zeta_0^2 }} + 3\frac{\partial^3 \psi_2 }{{\partial t_0^{\,} \partial \zeta_0^{\,} \partial \zeta_1^{\,} }} + 2\frac{\partial^3 \psi_1 }{{\partial t_0^{\,} \partial \zeta_0^{\,} \partial \zeta_2^{\,} }}} \right. \hfill \\ + \left. {2\frac{\partial^3 \psi_1 }{{\partial t_0^{\,} \partial \zeta_0^{\,} \partial \zeta_3^{\,} }} + \frac{\partial^3 \psi_1 }{{\partial t_0^{\,} \partial \zeta_1^2 }} + \frac{\partial^3 \psi_2 }{{\partial t_1^{\,} \partial \zeta_0^2 }} + 3\frac{\partial^3 \psi_1 }{{\partial t_1^{\,} \partial \zeta_0^{\,} \partial \zeta_1^{\,} }} + \frac{\partial^3 \psi_1 }{{\partial t_2^{\,} \partial \zeta_0^2 }}} \right) \hfill \\ \end{gathered}$$
(35)

where ψ1 is a function of both fast and slow variables.

The Solution of Field Equations

In the current section, we will solve the field equations governing distinct terms in the perturbation expansion of different order.

The Solution of the O(ε)-Order Equation

The differential equation in Eq. (33) has a linear form, and its solution can be presented as follows:

$$\psi_1 = \varphi e^{i\theta } + \varphi^{\prime}e^{i\theta^{\prime}} + c.c.$$
(36)

where the field equations' solution will yield the unknown complex amplitudes φ and φ', and the phasors θ and θ' are defined by θ = ωt0 − kζ0, θ' = ω't0 − k'ζ0. Here, the wave number and the angular frequency that satisfy the same dispersion relation are represented by the pairs (ω, k) and (ω', k'):

$${\rm{D}}(\omega ,k) = k^2 - \delta \omega^2 (1 + \mu k^2 ) + K_e (1 + \mu k^2 ) + i\omega D(1 + \mu k^2 ) = 0,\ \;{\rm{D}}(\omega^{\prime},k^{\prime}) = 0$$
(37)

Here, \(\varphi (\zeta_1 ,\zeta_2 ,...;t_1 ,t_2 ,...)\) and \(\varphi^{\prime}(\zeta_1 ,\zeta_2 ,...;t_1 ,t_2 ,...)\) are unknown functions whose governing equations will be discovered later.

The Solution of the O(ε2)-Order Equation

The O(ε2)-order Eq. (34) can be solved by first introducing Eq. (36) into Eq. (34) and obtaining

$$\begin{gathered} \frac{\partial^2 \psi_2 }{{\partial \zeta_0^2 }} - \delta \frac{\partial^2 \psi_2 }{{\partial t_0^2 }} - \delta \mu \frac{\partial^4 \psi_2 }{{\partial t_0^2 \partial \zeta_0^2 }} = \left\{ {2ik\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]\frac{\partial \varphi }{{\partial \zeta_1 }}} \right. \hfill \\ \left. { + i\left[ {2\delta \omega (1 + \mu k^2 ) - iD} \right]\frac{\partial \varphi }{{\partial t_1 }}} \right\}e^{i\theta } + \left\{ {2ik^{\prime}\left[ {1 - \delta \mu \omega^{{\prime} 2} + \mu (K_e + i\omega^{\prime}D)} \right]\frac{{\partial \varphi^{\prime}}}{\partial \zeta_1 }} \right. \hfill \\ + \left. {i\left[ {2\delta \omega^{\prime}(1 + \mu k^{{\prime} 2} ) - iD} \right]\frac{{\partial \varphi^{\prime}}}{\partial t_1 }} \right\}e^{i\theta^{\prime}} - 2ik^3 \varphi^2 e^{2i\theta } - 2ik^{{\prime} 3} \varphi^{{\prime} 2} e^{2i\theta^{\prime}} \hfill \\ - 2ikk^{\prime}(k + k^{\prime})\varphi \varphi^{\prime}e^{i(\theta + \theta^{\prime})} + 2ikk^{\prime}(k - k^{\prime})\varphi + c.c. \hfill \\ \end{gathered}$$
(38)

In this case, φ* is φ's complex conjugate, and |φ|2 is given by |φ|2 = φφ*. The form of Eq. (38) causes us to seek the following type of solution for ψ2:

$$\psi_2 = \psi_2^{(1)} e^{i\theta } + \psi_2^{{\prime} (1)} e^{i\theta^{\prime} } + \psi_2^{(2)} e^{2i\theta } + \psi_2^{{\prime} (2)} e^{2i\theta^{\prime} } + \psi_2^{( + )} e^{i(\theta + \theta^{\prime} )} + \psi_2^{{\prime} ( - )} e^{i(\theta - \theta^{\prime} )} + c.c.$$
(39)

where \(\psi_2^{(1)} ,\psi_2^{{\prime} (1)} , \ldots ,\psi_2^{{\prime} ( - )}\) denote some functions of slow variables. After putting the said solutions into Eq. (38), we obtain the equations below:

$$\begin{gathered} \left[ {k^2 - \delta \omega^2 (1 + \mu k^2 ) + K_e (1 + \mu k^2 ) + i\omega D(1 + \mu k^2 )} \right]\psi_2^{(1)} + \hfill \\ 2ik\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]\frac{\partial \varphi }{{\partial \zeta_1 }} + i\left[ {2\delta \omega (1 + \mu k^2 ) - iD} \right]\frac{\partial \varphi }{{\partial t_1 }} = 0 \hfill \\ \end{gathered}$$
(40)
$$\begin{gathered} \left[ {k^{{\prime} 2} - \delta \omega^2 (1 + \mu k^{{\prime} 2} ) + K_e (1 + \mu k^{{\prime} 2} ) + i\omega^{\prime}D(1 + \mu k^{{\prime} 2} )} \right]\psi_2^{{\prime} (1)} \hfill \\ + 2ik^{\prime}\left[ {1 - \delta \mu \omega^{{\prime} 2} + \mu (K_e + i\omega^{\prime}D)} \right]\frac{{\partial \varphi^{\prime}}}{\partial \zeta_1 } + i\left[ {2\delta \omega^{\prime}(1 + \mu k^{{\prime} 2} ) - iD} \right]\frac{{\partial \varphi^{\prime}}}{\partial t_1 } = 0 \hfill \\ \end{gathered}$$
(41)
$$\frac{2}{3}\left[ {4k^2 - 4\delta \omega^2 (1 + 4\mu k^2 ) + K_e (1 + 4\mu k^2 ) + i\omega D(1 + 4\mu k^2 )} \right]\psi_2^{(2)} - 2ik^3 \varphi^2 = 0$$
(42)
$$\frac{2}{3}\left[ {4k^{{\prime} 2} - 4\delta \omega^{{\prime} 2} (1 + 4\mu k^{{\prime} 2} ) + K_e (1 + 4\mu k^{{\prime} 2} ) + i\omega^{\prime}D(1 + 4\mu k^{{\prime} 2} )} \right]\psi_2^{{\prime} (2)} - 2ik^{{\prime} 3} \varphi^{{\prime} 2} = 0$$
(43)
$$\begin{gathered} \frac{2}{3}\left\{ {(k + k^{\prime})^2 - \delta (\omega + \omega^{\prime})^2 \left[ {1 + \mu (k + k^{\prime})^2 } \right] + K_e \left[ {1 + \mu (k + k^{\prime})^2 } \right]} \right. \hfill \\ \left. { + iD(\omega + \omega^{\prime})\left[ {1 + \mu (k + k^{\prime})^2 } \right]} \right\}\psi_2^{( + )} - 2ikk^{\prime}(k + k^{\prime})\varphi \varphi^{\prime} = 0 \hfill \\ \end{gathered}$$
(44)
$$\begin{gathered} \frac{2}{3}\left\{ {(k - k^{\prime})^2 - \delta (\omega - \omega^{\prime})^2 \left[ {1 + \mu (k - k^{\prime})^2 } \right] + K_e \left[ {1 + \mu (k - k^{\prime})^2 } \right]} \right. \hfill \\ + \left. {iD(\omega - \omega^{\prime})\left[ {1 + \mu (k - k^{\prime})^2 } \right]} \right\}\psi_2^{( - )} - 2ikk^{\prime}(k - k^{\prime})\varphi \varphi^{{\prime} *} = 0 \hfill \\ \end{gathered}$$
(45)

Here, the dispersion relation is represented by the coefficient ψ2(1) in Eq. (40) and must be zero. By applying the dispersion relation that we have found,

$$2k\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]\frac{\partial \varphi }{{\partial \zeta_1 }} + \left[ {2\delta \omega (1 + \mu k^2 ) - iD(1 + \mu k^2 )} \right]\frac{\partial \varphi }{{\partial t_1 }} = 0$$
(46)

For φ to satisfy Eq. (40) and have a non-zero solution, it should take the following form:

$$\varphi = \varphi (\xi ,\zeta_2 ,...;t_2 ,...),\quad \xi = \zeta_1 - \lambda t_1$$
(47)

Here, λ, the first wave's group velocity, is defined by

$$\lambda = \frac{{2k\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]}}{{(1 + \mu k^2 )\left[ {2\delta \omega - iD} \right]}}$$
(48)

Likewise, by solving Eq. (41), we obtain

$$2k^{\prime}\left[ {1 - \delta \mu \omega^{{\prime} 2} + \mu (K_e + i\omega^{\prime}D)} \right]\frac{{\partial \varphi^{\prime}}}{\partial \zeta_1 } + \left[ {2\delta \omega^{\prime}(1 + \mu k^{{\prime} 2} ) - iD(1 + \mu k^{{\prime} 2} )} \right]\frac{{\partial \varphi^{\prime}}}{\partial t_1 } = 0$$
(49)

For φ' to have a non-zero solution satisfying Eq. (41), it should take the following form:

$$\varphi^{\prime} = \varphi^{\prime}(\xi^{\prime},\zeta_2 ,...;t_2 ,...),\quad \xi^{\prime} = \zeta_1 - \lambda^{\prime}t_1$$
(50)

Here, λ', the second wave's group velocity, is defined by

$$\lambda^{\prime} = \frac{{2k^{\prime}\left[ {1 - \delta \mu \omega^{{\prime} 2} + \mu (K_e + i\omega^{\prime}D)} \right]}}{{(1 + \mu k^{{\prime} 2} )\left[ {2\delta \omega^{\prime} - iD} \right]}}$$
(51)

The governing equation of the function ψ2(1) is derived from the field quantities' higher-order expansion. When we solve Eq. (42) for the α = 2 mode, we obtain

$$\psi_2^{(2)} = \frac{3ik^3 }{{4k^2 + (1 + 4\mu k^2 )\left[ { - 4\delta \omega^2 + K_e + 2i\omega D} \right]}}\varphi^2 = \frac{3ik^3 }{{{\rm{D}}(2k,2\omega )}}\varphi^2$$
(52)

where \({\rm{D}}(lk,l\omega ) \ne 0\) for l = 2,3,…

Likewise, from the solution of Eq. (43), we obtain

$$\psi_2^{{\prime} (2)} = \frac{{3ik^{{\prime} 3} }}{{4k^{{\prime} 2} + (1 + 4\mu k^{{\prime} 2} )\left[ { - 4\delta \omega^{{\prime} 2} + K_e + 2i\omega^{\prime}D} \right]}}\varphi^{{\prime} 2} = \frac{{3ik^{{\prime} 3} }}{{{\rm{D}}(2k^{\prime},2\omega^{\prime})}}\varphi^{{\prime} 2}$$
(53)

where \({\rm{D}}(lk^{\prime},l\omega^{\prime}) \ne 0\) for l = 2,3,…

We can achieve the following results by solving Eqs. (44) and (45):

$$\psi_2^{( + )} = \frac{{3ikk^{\prime}(k + k^{\prime})}}{\Delta^+ }\varphi \varphi^{\prime}{\text{ and }}\psi_2^{( - )} = \frac{{3ikk^{\prime}(k - k^{\prime})}}{\Delta^- }\varphi \varphi^{{\prime} *}$$
(54)

where ∆± is defined by

$$\begin{gathered} \Delta^\pm = \left\{ {(k \pm k^{\prime})^2 - \delta (\omega \pm \omega^{\prime})^2 \left[ {1 + \mu (k \pm k^{\prime})^2 } \right] + K_e \left[ {1 + \mu (k \pm k^{\prime})^2 } \right]} \right. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\left. { + iD(\omega \pm \omega^{\prime})\left[ {1 + \mu (k \pm k^{\prime})^2 } \right]} \right\} \hfill \\ \end{gathered}$$
(55)

The Solution of the O(ε3)-Order Equation

We need the equations governing ψ3(1) and ψ3′(1) to finish the solution. The phasor can be used to express the solution for this order as shown below:

$$\psi_3 = \sum_{\alpha = 1}^3 {(\psi_3^{(\alpha )} e^{i\alpha \theta } + \psi_3^{{\prime} (\alpha )} e^{i\alpha \theta^{\prime} } )} + c.c.$$
(56)

By introducing Eqs. (39) and (56) into Eq. (35), we have

$$\begin{gathered} \left[ {k^2 + (1 + \mu k^2 )\left( { - \delta \omega^2 + K_e + i\omega D} \right)} \right]\psi_3^{(1)} = 2ik\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]\frac{{\partial \psi_2^{(1)} }}{\partial \zeta_1 } \hfill \\ + i\left[ {(1 + \mu k^2 )(2\delta \omega - iD)} \right]\frac{{\partial \psi_2^{(1)} }}{\partial t_1 } + i\left[ {(1 + \mu k^2 )(2\delta \omega - iD)} \right]\frac{\partial \varphi }{{\partial t_2 }} + 2ik\left[ {1 - \delta \mu \omega^2 } \right. \hfill \\ + \left. {\mu (K_e + i\omega D)} \right]\frac{\partial \varphi }{{\partial \zeta_2 }} - \left[ {(1 - \delta \mu \omega^2 ) + \mu (K_e + i\omega D)} \right]\frac{\partial^2 \varphi }{{\partial \zeta_1^2 }} + \mu k(3iD - 4\delta \omega )\frac{\partial \varphi }{{\partial \zeta_1 \partial t_1 }} \hfill \\ + \left[ {(1 + \mu k^2 )\left( {\delta + \frac{iD}{{2\omega }}} \right)} \right]\frac{\partial^2 \varphi }{{\partial t_1^2 }} + k^4 \left| \varphi \right|^2 \varphi + 2k^{{\prime} 2} \left| {\varphi^{\prime}} \right|^2 \varphi + 4ik^3 \psi_2^{(2)} \varphi^* \hfill \\ + 2ikk^{\prime}(k + k^{\prime})\psi_2^{( + )} \varphi^{{\prime} *} - 2ikk^{\prime}(k - k^{\prime})\psi_2^{( - )} \varphi^{\prime} \hfill \\ \end{gathered}$$
(57)

Here, the coefficient ψ3(1) is the dispersion relation and should equal zero. By rearranging Eq. (57),we obtain the following:

$$\begin{gathered} \left[ {(1 + \mu k^2 )(2\delta \omega - iD)} \right] \times \left[ {\left( {\frac{{\partial \psi_2^{(1)} }}{\partial t_1 } + \lambda \frac{{\partial \psi_2^{(1)} }}{\partial \zeta_1 }} \right) + i\left( {\frac{\partial \varphi }{{\partial t_2 }} + \lambda \frac{\partial \varphi }{{\partial \zeta_2 }}} \right)} \right] - \left[ {1 - \delta \mu \omega^2 } \right. \hfill \\ + \left. {\mu (K_e + i\omega D)} \right]\frac{\partial^2 \varphi }{{\partial \zeta_1^2 }} + \mu k(3iD - 4\delta \omega )\frac{\partial \varphi }{{\partial \zeta_1 \partial t_1 }} + (1 + \mu k^2 )\left( {\delta + \frac{iD}{{2\omega }}} \right)\frac{\partial^2 \varphi }{{\partial t_1^2 }} + k^4 \left| \varphi \right|^2 \varphi \hfill \\ + 2k^{{\prime} 2} \left| {\varphi^{\prime}} \right|^2 \varphi + 4ik^3 \psi_2^{(2)} \varphi^* + 2ikk^{\prime}(k + k^{\prime})\psi_2^{( + )} \varphi^{{\prime} *} - 2ikk^{\prime}(k - k^{\prime})\psi_2^{( - )} \varphi^{\prime} = 0 \hfill \\ \end{gathered}$$
(58)

The dependence of φ on ξ has already been used in this case. Furthermore, if we assume that ψ2(1) depends on t1 and ζ1 via ξ, the first terms in Eq. (58) disappear. Equation (58)'s second term can be rewritten as follows by adding a new variable, τ: t2 = τ ζ2 = εξ + λτ.

$$\frac{\partial \varphi }{{\partial t_2 }} + \lambda \frac{\partial \varphi }{{\partial \zeta_2 }} = \frac{1}{\varepsilon }\frac{\partial \varphi }{{\partial \xi }} - \frac{1}{\varepsilon }\frac{\partial \varphi }{{\partial \xi }} + \frac{\partial \varphi }{{\partial \tau }} = \frac{\partial \varphi }{{\partial \tau }}$$
(59)

By introducing the expressions of ψ2(2), ψ2(+), and ψ2(−) into Eq. (56), we derive the nonlinear Schrödinger equation:

$$i\frac{\partial \varphi }{{\partial \tau }} + \nu_1 \frac{\partial^2 \varphi }{{\partial \xi^2 }} + \nu_2 \left| \varphi \right|^2 \varphi + \nu_3 \left| {\varphi^{\prime}} \right|^2 \varphi = 0$$
(60)

where the coefficients ν1, ν2, and ν3 are defined by

$$\nu_1 = \frac{1}{2}\frac{\partial \lambda }{{\partial k}} = \frac{1}{2}\left\{ {\frac{\lambda }{k} - \frac{2k\mu \lambda }{{1 + \mu k^2 }} - \frac{{\lambda \left[ {2k\mu (2\delta \omega - iD) - 2k\delta \lambda (1 + \mu k^2 )} \right]}}{(2\delta \omega - iD)(1 + \mu k^2 )}} \right\}$$
(61)
$$\nu_2 = \frac{3}{4}\lambda k^3 (1 + \mu k^2 )\left\{ {1 - \frac{3k^2 }{{\left[ {4k^2 + (1 + 4\mu k^2 )} \right]( - 4\delta \omega^2 + K_e + 2i\omega D)}}} \right\}$$
(62)
$$\nu_3 = \frac{{3k^{{\prime} 2} k^2 }}{(1 + \mu k^2 )(2\delta \omega - iD)}\left\{ {1 - \frac{{3(k + k^{\prime})^2 }}{\Delta^+ } + \frac{{3(k - k^{\prime})^2 }}{\Delta^- }} \right\}$$
(63)

The equation governing ψ3′(1) can be obtained if comparable procedures are carried out on Eq. (35). For the governing equation of the prime quantities, it is possible to derive the coupled nonlinear Schrödinger equation in the following way:

$$i\frac{{\partial \varphi^{\prime}}}{\partial \tau } + \nu^{\prime}_1 \frac{{\partial^2 \varphi^{\prime}}}{{\partial \xi^{{\prime} 2} }} + \nu^{\prime}_2 \left| \varphi \right|^{{\prime} 2} \varphi^{\prime} + \nu^{\prime}_3 \left| \varphi \right|^2 \varphi^{\prime} = 0$$
(64)

where (ω, k) can be replaced with (ω', k') in these expressions to obtain the coefficients ν1′, ν2′, and ν3′ from Eqs. (61)–(63).

The coupled nonlinear Schrödinger equations are more difficult to solve than the single nonlinear Schrödinger equations. Currently, the coupled NLS equation can be solved only when the group velocities of waves are equal and the coefficient in the said equations has a special relation.

The Case of Equal Group Velocities

As a special case, it is useful to examine the probability that the group velocities corresponding to two different wave numbers are equal. If the variation of the group velocity with wave number k given by Eq. (48) has an extremum point, two values of k can be found to the right or left of this point such that the group velocities are equal.

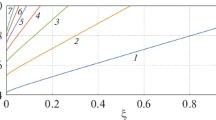
Figure 2 illustrates the variation of dλ/dk with wave number k for various nonlocal parameter values. Numerical calculations show that the dλ/dk value becomes zero at k = 2.83809 × 108 for μ = 1 × 10−18 m2, k = 2.4608 × 108 for μ = 2 × 10−18 m2, and k = 2.28951 × 108 for μ = 3 × 10−18 m2. Therefore, there may be two values of k around these values such that the group velocities are equal at these values. Thus, Fig. 3 shows the variation of the group velocity λ with the wave number k for various nonlocal parameter values. Therefore, in the problem under investigation, equal group velocities correspond to a special solution.

Fig. 2
figure 2

Variation of the coupled nonlinear Schrödinger equation’s expression dλ/dk [variation of Re(λ) with k] at different nonlocal parameter values with the wave number k

Full size image
Fig. 3
figure 3

Variation of the coupled nonlinear Schrödinger equation’s group velocity at different nonlocal parameter values with the wave number k

Full size image

In this case, ξ' = ξ, and Eqs. (60) and (64) take the following form:

$$i\frac{\partial \varphi }{{\partial \tau }} + \sigma_1 \frac{\partial^2 \varphi }{{\partial \xi^2 }} + \sigma_2 \left| \varphi \right|^2 \varphi + \sigma_3 \left| {\varphi^{\prime}} \right|^2 \varphi = 0$$
(65)
$$i\frac{{\partial \varphi^{\prime}}}{\partial \tau } + \sigma^{\prime}_1 \frac{{\partial^2 \varphi^{\prime}}}{{\partial \xi^{{\prime} 2} }} + \sigma^{\prime}_2 \left| {\varphi^{\prime}} \right|^2 \varphi^{\prime} + \sigma^{\prime}_3 \left| \varphi \right|^2 \varphi^{\prime} = 0$$
(66)

where the coefficients σi and σ′i (i = 1, 2, 3) can be obtained by writing λ' = λ in expressions (61)–(63).

The Solution for the Case of k' =  − k, ω' = ω

The above-mentioned specific case concerns the nonlinear interactions between two waves moving against each other. With the group velocity of the second wave being λ' = λ, the coupled nonlinear Schrödinger equations take the form presented below:

$$i\frac{\partial \varphi }{{\partial \tau }} + \gamma_1 \frac{\partial^2 \varphi }{{\partial \xi^2 }} + \gamma_2 \left| \varphi \right|^2 \varphi + \gamma_3 \left| {\varphi^{\prime}} \right|^2 \varphi = 0$$
(67)
$$i\frac{{\partial \varphi^{\prime}}}{\partial \tau } + \gamma_1 \frac{{\partial^2 \varphi^{\prime}}}{{\partial \xi^{{\prime} 2} }} + \gamma_2 \left| {\varphi^{\prime}} \right|^2 \varphi^{\prime} + \gamma_3 \left| \varphi \right|^2 \varphi^{\prime} = 0$$
(68)

where the coefficients γ1 = ν1, γ2 = ν2, and γ3 are defined by

$$\gamma_3 = \frac{3k^4 }{{(1 + \mu k^2 )\left[ {2\delta \omega - iD} \right]}}$$
(69)

It is possible to solve a single nonlinear Schrödinger equation under specific initial and compatibility conditions by utilizing inverse scattering techniques. However, no comparable advancement has been documented for coupled NLS equations. We will suggest a straightforward method for the field equation's progressive wave solution for the current issue in accordance with the study by Jeffrey [37]. To achieve this, we present

$$\xi^{\prime} = \zeta_1 - \lambda^{\prime}t_1 = \xi + (\lambda^{\prime} - \lambda )t_1$$
(70)

Next, we can rewrite Eqs. (60) and (64) in terms of ξ and τ as shown below:

$$i\frac{\partial \varphi }{{\partial \tau }} + \gamma_1 \frac{\partial^2 \varphi }{{\partial \xi^2 }} + \gamma_2 \left| \varphi \right|^2 \varphi + \gamma_3 \left| {\varphi^{\prime}} \right|^2 \varphi = 0$$
(71)
$$i\frac{{\partial \varphi^{\prime}}}{\partial \tau } + i\frac{{(\lambda^{\prime} - \lambda )}}{\varepsilon }\frac{{\partial \varphi^{\prime}}}{\partial \xi } + \gamma^{\prime}_1 \frac{{\partial^2 \varphi^{\prime}}}{\partial \xi^2 } + \gamma^{\prime}_2 \left| {\varphi^{\prime}} \right|^2 \varphi^{\prime} + \gamma^{\prime}_3 \left| \varphi \right|^2 \varphi^{\prime} = 0$$
(72)

We will now assume the following type of solution to these equations:

$$\varphi = \varphi_0 \exp \left[ {i\left( {\Omega_1 \tau - K_1 \xi } \right)} \right],\quad \varphi^{\prime} = \phi_0 \exp \left[ {i\left( {\Omega_2 \tau - K_2 \xi } \right)} \right]$$
(73)

where the constants Kα and Ωα (α = 1, 2) describe the corresponding waves' frequency and wave number, and the constants φ and φ', which represent the two constants, must meet the requirement that ξ → ∞, φ → φ0, and φ' → ϕ0. By inserting Eq. (73) into Eqs. (71) and (72) and requiring a non-zero solution for both φ0 and ϕ0, we obtain

$$\Omega_1 = - \gamma_1 K_1^2 + \gamma_2 \varphi_0^2 + \gamma_3 \phi_0^2$$
(74)
$$\Omega_2 = \frac{{(\lambda^{\prime} - \lambda )}}{\varepsilon }K_2^{\,} - \gamma^{\prime}_1 K_2^2 + \gamma^{\prime}_2 \varphi_0^2 + \gamma_3 \phi_0^2$$
(75)

These equations demonstrate how the wave amplitude affects the frequencies of nonlinear plane waves. Specifically, if we assume K1 = K2 = 0, the solution for ψ has the following form:

$$\psi \sim \in \left[ {\varphi_0 \cos \left( {{\mathop{\omega }\limits^{\frown}} t - k\zeta } \right) + \phi_0 \cos \left( {\overline{\omega }t - k^{\prime}\zeta } \right)} \right]$$
(76)

where the definitions of the frequencies \({\mathop{\omega }\limits^{\frown}}\) and \(\overline{\omega }\) are

$${\mathop{\omega }\limits^{\frown}} = \omega + \in^2 \left[ {\gamma_2 \varphi_0^2 + \gamma_3 \phi_0^2 } \right],\quad \overline{\omega } = \omega^{\prime} + \in^2 \left[ {\gamma^{\prime}_2 \phi_0^2 + \gamma^{\prime}_3 \varphi_0^2 } \right]$$
(77)

The frequency shift between the waves (φ, k, ω) and (φ', k', ω') can be seen in Eq. (77).

Numerical Results and Discussion

The current work investigates the nonlinear wave interaction of nanorods embedded in a viscoelastic medium by utilizing the nonlocal elasticity theory. This research uses single-walled carbon nanotubes’ (SWCNTs) material and mechanical properties to present numerical results. There is no agreement in the literature on Poisson's ratio of nanotubes. The recommended values range significantly from 0.19 to 0.34. Hence, ν is set to 0.3 in line with this study’s purpose. It is agreed upon that the nonlocal parameter μ is 0 ~ 4 × 10−18 m2. Certain material properties are set as follows: the density of material ρ0 = 2300 kg/m3, nanotube radius r0 = 10−9 m, and Young’s modulus \(E_E\) = 1 TPa.

Before proceeding with the analysis, let us write the dispersion relation obtained in Eq. (37) in the following form:

$$X\omega^2 + Y\omega + Z = 0,$$
(78)

where X, Y and Z are defined by

$$X = \delta (1 + \mu k^2 ),\quad Y = - iD(1 + \mu k^2 ),\quad Z = - K_e (1 + \mu k^2 ) - k^2$$
(79)

For a constant wave number, the natural frequency of a carbon nanotube and its decay rate (comparable to viscous damping) are represented by the real part Re(ω) and the imaginary part Im(ω), respectively. These values can be obtained as follows:

$$\begin{gathered} {\text{Re}} (\omega ) = \pm \frac{{\sqrt {{ - D^2 (1 + \mu k^2 ) + 4\delta (1 + \mu k^2 )\left[ {k^2 + K_e (1 + \mu k^2 )} \right]}} }}{2\delta (1 + \mu k^2 )} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, = \pm \sqrt {{\frac{K_e }{\delta } - \frac{D^2 }{{4\delta^2 }} + \frac{k^2 }{{\delta (1 + \mu k^2 )}}}} \hfill \\ \end{gathered}$$
(80)
$${\text{Im}} (\omega ) = D/2\delta$$
(81)

The equation above illustrates the linear relationship between the nanorod damping coefficient D and the imaginary part of frequency. Figures 4, 5, and 6 show the impacts of the nonlocal parameter, the damping coefficient, and the medium’s elastic coefficient on the real part that represents the system's natural frequency.

Fig. 4
figure 4

Variation in the natural frequency by wave number and damping coefficient for different values of μ (ke = 1 × 109 Nm−2)

Full size image
Fig. 5
figure 5

Variation in the natural frequency by wave number and nonlocal parameter for different values of the damping parameter (ke = 1 × 109 Nm−2)

Full size image
Fig. 6
figure 6

Variation in the natural frequency by wave number and stiffness parameter for different values of the damping parameter (μ = 1 × 10−18 m2)

Full size image

Figure 4 depicts the relationship between the wave number and damping coefficient of the medium and the wave frequency (natural frequency) for various values of the nonlocal parameter μ. As seen in the figure, the natural frequency values decrease with the increasing nonlocal parameter μ, and the natural frequency decreases with the increasing damping parameter.

Figure 5 illustrates how the system's natural frequency varies with wave number and nonlocal parameter for a range of damping parameter values. As seen in the figure, lower wave frequency values are obtained at larger damping coefficient values. It is also clearly seen that increases in the nonlocal parameter significantly reduce the system’s natural frequency. The study shows that if the damping coefficient value is less than d < 10−6, it is equivalent to d ≅ 0, i.e., it does not affect the system’s natural frequency.

Figure 6 shows the relationship between the natural frequency, wave number, and the medium's elastic parameter for a range of damping coefficient values. The figure illustrates that while the natural frequency increases with increasing wave number values, it does not change considerably with increasing elastic medium parameter (stiffness parameter) values. Additionally, a decrease in the natural frequency is observed with the increasing damping coefficient.

To see how the group velocity varies with the nonlocal parameter, the damping parameter, and the elastic parameter of the medium, let us first decompose the group velocity found in Eq. (48) into its real and imaginary parts as follows:

$$\lambda = \frac{{2k\left[ {1 - \delta \mu \omega^2 + \mu (K_e + i\omega D)} \right]}}{{(1 + \mu k^2 )\left[ {2\delta \omega - iD} \right]}} = a + ib$$
(82)

where the coefficients a and b are defined by

$$a = {\text{Re}} (\lambda ) = \frac{{2k\omega \left[ {2\delta - \mu D^2 + 2\mu \delta K_e - 2\mu \delta^2 \omega^2 } \right]}}{(1 + \mu k^2 )(D^2 + 4\delta^2 \omega^2 )}$$
(83)
$$b = {\text{Im}} (\lambda ) = \frac{{2kD\left[ {1 + \mu K_e - \mu \delta \omega^2 } \right]}}{(1 + \mu k^2 )(D^2 + 4\delta^2 \omega^2 )}$$
(84)

Figure 7 illustrates the relationship between Re(λ) and the viscoelastic medium's wave number and damping parameter for various nonlocal parameter values. As seen in the figure, for values of the nonlocal parameter μ = 1 × 10−18 m2 and μ = 2 × 10−18 m2, Re(λ) reaches a maximum at a certain wave number and then starts to decrease with the increasing wave number. In other words, increasing the nonlocal parameter value significantly reduces the real part of the group velocity. For μ = 0, it is seen that Re(λ) does not decrease after peaking at a certain wave number k and continues to increase with increasing wave number values. However, the impact of the damping coefficient d of the viscoelastic medium on the real part of the group velocity is negligibly small.

Fig. 7
figure 7

Variation in the real part of the group velocity with wave number and damping parameter for different values of the nonlocal parameter (ke = 1 × 109 Nm−2)

Full size image

Figure 8 clearly illustrates the similar effects of the damping parameter and the nonlocal parameter of the viscoelastic medium on the real part of the group velocity. The viscoelastic medium's damping parameter has a greater impact at low wave numbers. Nevertheless, the impact of the damping parameter decreases with increasing wave numbers. Figure 8 also shows that the impact of the nonlocal parameter on the real part of the group velocity is very large. As the nonlocal parameter values increase, the group velocity decreases rapidly. It can also be concluded that the effect of the viscoelastic medium's damping coefficient d decreases with the increased nonlocal parameter μ.

Fig. 8
figure 8

Variation in the real part of the group velocity with wave number and nonlocal parameter for different values of the damping parameter (ke = 1 × 109 Nm−2)

Full size image

Figure 9 illustrates the relationship between the wave number and the stiffness parameter of the medium and the real part of the group velocity for a range of nonlocal parameter values. The real part of the group velocity peaks at a certain wave number k and then decreases rapidly with increasing values of the wave number k and the nonlocal parameter μ. It is found that the medium stiffness parameter ke does not impact the real part of the group velocity.

Fig. 9
figure 9

Variation in the real part of the group velocity with wave number and stiffness parameter of the medium for different values of the nonlocal parameter (d = 1 × 10−6 Nsm−3)

Full size image

Let us examine the impacts of the system's nonlocal, damping, and stiffness parameters on the imaginary part of the group velocity. Figure 10 displays the linear relationship between the damping coefficient d of the viscoelastic medium and the imaginary part of the group velocity Im(λ). However, it has been previously observed that the damping coefficient has a negligible effect on the real part of the group velocity. This is an expected result since the imaginary part represents the system's damping and the real part refers to the system's natural group velocity. If the value of the damping parameter increases, the effect of the nonlocal parameter μ on the imaginary part of the group velocity weakens.

Fig. 10
figure 10

Variation in the imaginary part of the group velocity with damping parameter and nonlocal parameter for different values of the wave number (ke = 1 × 109 Nm−2)

Full size image

Figure 11 clearly shows the impact of the viscoelastic medium’s damping parameter on the imaginary part of the group velocity. The impact of the damping parameter on the imaginary part of the group velocity is larger for small frequency values, whereas the impact of the damping parameter on the imaginary part of the group velocity decreases rapidly for large frequency values.

Fig. 11
figure 11

Variation in the imaginary part of the group velocity with wave number and wave frequency for different values of the damping parameter (ke = 1 × 109 Nm−2, μ = 1 × 10−18 m2)

Full size image

Conclusion

By investigating potential interactions between two localized monochromatic acoustic waves, the coupled nonlinear Schrödinger equations are derived using the nonlinear field equations of a nanorod embedded in a viscoelastic medium. The analytical solution of these coupled nonlinear Schrödinger equations is usually challenging. Here, the resulting evolution equations are solved using nonlinear plane waves. The plane wave solutions show how the wave amplitude affects the frequencies of the nonlinear plane waves. As a special case, the possibility of equal group velocities corresponding to two different wave numbers is also analyzed. The following results are obtained from the numerical study:

  • The natural frequency increases with the increasing wave number. However, the natural frequency has lower values with increasing values of the nonlocal parameter and damping parameter of the viscoelastic medium.

  • The system’s natural frequency is not affected by increases in the stiffness parameter.

  • The viscoelastic medium's damping coefficient d has a negligibly small effect on the real part of the group velocity.

  • The effect of the nonlocal parameter on the real part of the group velocity is very large. It is seen that the effect of the damping parameter disappears in the presence of a nonlocal parameter in the medium.

  • It is found that the medium’s stiffness parameter ke does not affect the real part of the group velocity.

  • Conversely, the effect of the viscoelastic medium’s damping parameter on the imaginary part of the group velocity is greater than the effect of the nonlocal parameter, which is also an expected result.