Equivalence of a Beam on Elastic Foundation and a Beam on Elastic Supports with Transfer Matrix Method

Abstract

Purpose

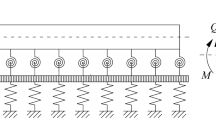
In this work, the mechanical equivalence and equivalent accuracy between a beam on elastic foundation (BOEF) and a beam on elastic supports (BOES) are analyzed considering static and dynamic characteristics using the transfer matrix method. The purpose of this paper is to investigate and obtain the critical equivalence condition between the two beam models, so as to facilitate the calculation of two kinds of structures in engineering and research.

Methods

The mathematical models for free vibration, deformation under static concentrated load, and dynamic response under moving load for both the BOEF and the BOES are established separately. The displacement of the two beam models under static load and the natural frequencies of the BOES are determined utilizing the transfer matrix method. Additionally, the partial differential equations of motion for the two beam models under moving load are established. Upon obtaining the ordinary differential equations utilizing Galerkin discretization, the first and second-order dynamic responses are obtained through numerical solutions and are superimposed. The equivalence coefficient for the two beam models is subsequently determined.

Results and Conclusions

The study further analyses the natural frequencies, deformation under static concentrated load, and dynamic response displacement under moving load for various equivalence coefficients across different key physical parameters. After validating the obtained equivalence coefficient with existing literature, the equivalent accuracy for the two beam models is further quantified. When the equivalence coefficient is K_eq = 1.2, the natural frequency difference is only one thousandth. Furthermore, this paper establishes the critical equivalence condition that K_eq = 10 for the BOEF and the BOES, wherein the natural frequency differential is around 1%. Research has shown that there is no significant difference in deformation under static load and dynamic response under moving load after equivalence.

Appendix

Corresponding field matrix U and left endpoint matrix U₀ of static deformation of the BOEF for the modal function Eq. (33)

$${\mathbf{U}}_{{\text{st}}} = \left[ {\begin{array}{*{20}c} {\sin \alpha x\sinh \alpha x} & {\sin \alpha x\cosh \alpha x} & {\cos \alpha x\sinh \alpha x} & {\cos \alpha x\cosh \alpha x} \\ {\alpha \left( {\cos \alpha x\sinh \alpha x + \sin \alpha x\cosh \alpha x} \right)} & {\alpha \left( {\cos \alpha x\cosh \alpha x + \sin \alpha x\sinh \alpha x} \right)} & {\alpha \left( { - \sin \alpha x\sinh \alpha x + \cos \alpha x\cosh \alpha x} \right)} & {\alpha \left( { - \sin \alpha x\cosh \alpha x + \cos \alpha x\sinh \alpha x} \right)} \\ { - 2EI\alpha^{2} \cos \alpha x\cosh \alpha x} & { - 2EI\alpha^{2} \cos \alpha x\sinh \alpha x} & {2EI\alpha^{2} \sin \alpha x\cosh \alpha x} & {2EI\alpha^{2} \sin \alpha x\sinh \alpha x} \\ { - 2EI\alpha^{3} \left( { - \sin \alpha x\cosh \alpha x + \cos \alpha x\sinh \alpha x} \right)} & { - 2EI\alpha^{3} \left( { - \sin \alpha x\sinh \alpha x + \cos \alpha x\cosh \alpha x} \right)} & {2EI\alpha^{3} \left( {\cos \alpha x\cosh \alpha x + \sin \alpha x\sinh \alpha x} \right)} & {2EI\alpha^{3} \left( {\cos \alpha x\sinh \alpha x + \sin \alpha x\cosh \alpha x} \right)} \\ \end{array} } \right]$$

(60)

$${\mathbf{U}} = \left[ {\begin{array}{*{20}c} {{\mathbf{U}}_{{\text{st}}} } & {\mathbf{O}} \\ {\mathbf{O}} & 1 \\ \end{array} } \right]$$

(61)

$${\mathbf{U}}_{0} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 1 & 0 \\ 0 & \alpha & \alpha & 0 & 0 \\ { - 2EI\alpha^{2} } & 0 & 0 & 0 & 0 \\ 0 & { - 2EI\alpha^{3} } & {2EI\alpha^{3} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

(62)