Generalized foundation Timoshenko beam and its calculating methods

Abstract

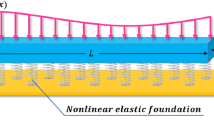
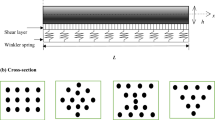
Due to the discrepancy between slope of deflection curve and rotation due to bending defined in Timoshenko beam theory, the distributed moment proportional to the rotation was extended into the two-parameter foundation, which in essence incorporated the horizontal interface friction produced by the foundation adhesion between the foundation and the beam. Thus, the present foundation can be interpreted by the mutually independent spring to idealize the Winkler foundation, the shear layer to incorporate the foundation cohesion, and the rotation spring to simulate the horizontal interface friction. This foundation was very comprehensive and can be termed as a generalized foundation. Neglecting one of those foundation parameters, the foundation can be degenerated into the classical generalized foundation, two-parameter foundation and Winkler foundation, respectively. Also this foundation provided a mechanical interpretation for understanding the horizontal interface friction produced by the foundation adhesion. Conducting the variational operation, a differential equation of Timoshenko beam on generalized foundation was achieved. To solve the differential equation, an initial parameter solution was deduced to formulate the transfer matrix method. A classical finite element formulation with cubic interpolating functions and a transcendental finite element formulation with the analytical solutions as the shape functions were presented. Four applications were investigated to verify the generalized foundation Timoshenko beam and the related calculating methods. Analytical and numerical results have good agreements with those published in the literature, which demonstrate the accuracy of the present foundation and the related methods. The convergence of the transcendental finite element does not depend on the mesh density of the discrete structures, while the classical finite element fails to achieve such performance. Transfer matrix method and transcendental finite element method provide an efficient and alternative tool for the analysis of elastic foundation beam. Transverse deflections of generalized foundation Timoshenko beam are more sensitive to the compressive stiffness of Winkler foundation than to the stiffness of shear layer and rotation spring of the foundation. Horizontal interface friction due to the foundation adhesion has the coequal influence as the foundation cohesion. It is reasonable to incorporate the horizontal interface friction into the elastic foundation.

Appendices

Appendix A: Coefficient functions for the case of Δ < 0

The spatial wave numbers $\alpha$ and $\beta$ are defined as Eq. (7). Coefficient functions are derived as:

$$\begin{aligned} a_{1} \left( x \right) & = ch\left( {\alpha x} \right)\cos \left( {\beta x} \right) \\ & \quad + \frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ b_{1} \left( x \right) & = \frac{C}{C + T}\left[ {\frac{{ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\beta } + \frac{{sh\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha }} \right] \\ c_{1} \left( x \right) & = \frac{{\beta \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]sh\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \alpha \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{{2\alpha \beta \left( {\alpha^{2} + \beta^{2} } \right)D\frac{C + T}{{C + R}}}} \, \\ d_{1} \left( x \right) & = - \frac{{sh\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{{2\alpha \beta D\frac{{\left( {C + T} \right)}}{C}}} \\ a_{2} \left( x \right) & = \frac{C + T}{C}\left\{ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right\} \\ & \quad \cdot \frac{{\beta sh\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \alpha ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\alpha \beta } \\ b_{2} \left( x \right) & = ch\left( {\alpha x} \right)\cos \left( {\beta x} \right) \\ & \quad + \frac{{\alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ c_{2} \left( x \right) & = - \frac{C + R}{C}\frac{{\alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} }}{{2\alpha \beta \left( {\alpha^{2} + \beta^{2} } \right)D}} \\ & \quad \cdot sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ d_{2} \left( x \right) & = - \frac{{\alpha \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]ch\left( {\alpha x} \right)\sin \left( {\beta x} \right) + \beta \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]sh\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha \beta D} \\ a_{3} \left( x \right) & = \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{{2\alpha \left( {C + R} \right)}}\left\{ {\alpha^{2} \left[ {3 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\} \\ & \quad sh\left( {\alpha x} \right)\cos \left( {\beta x} \right) + \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{{2\beta \left( {C + R} \right)}} \\ & \quad \left\{ {\beta^{2} \left[ {3 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\}ch\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ b_{3} \left( x \right) & = \frac{{DC\left( {\alpha^{2} + \beta^{2} } \right)^{2} }}{{2\alpha \beta \left( {C + R} \right)}} \cdot sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ c_{3} \left( x \right) & = ch\left( {\alpha x} \right)\cos \left( {\beta x} \right) \\ & \quad + \left[ {\frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta }} \right]sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ d_{3} \left( x \right) & = \frac{{C\left( {\alpha^{2} + \beta^{2} } \right)}}{{\left( {C + R} \right)}}\left[ {\frac{{sh\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha } - \frac{{ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\beta }} \right] \\ a_{4} \left( x \right) & = \frac{{D\left( {C + T} \right)\left( {\alpha^{2} + \beta^{2} } \right)}}{2\alpha \beta C}\left\{ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right\} \\ & \quad \cdot sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ b_{4} \left( x \right) & = \left\{ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {3 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\} \cdot \frac{{sh\left( {\alpha x} \right)\cos \left( {\beta x} \right)D}}{2\alpha } \\ & \quad + \left\{ {\beta^{2} \left[ {3 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]} \right\}\frac{{ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)D}}{2\beta } \\ c_{4} \left( x \right) & = \frac{C + R}{{C\left( {\alpha^{2} + \beta^{2} } \right)}}\left[ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]^{2} } \right] \\ & \quad \left[ {\frac{{sh\left( {\alpha x} \right)\cos \left( {\beta x} \right)}}{2\alpha } + \frac{{ch\left( {\alpha x} \right)\sin \left( {\beta x} \right)}}{2\beta }} \right] \\ d_{4} \left( x \right) & = ch\left( {\alpha x} \right)\cos \left( {\beta x} \right) - \frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} + \beta^{2} } \right)} \right]}}{2\alpha \beta } \\ & \quad sh\left( {\alpha x} \right)\sin \left( {\beta x} \right) \\ \end{aligned}$$

(38)

Appendix B: Coefficient functions for the case of Δ > 0

The spatial wave numbers $\alpha$ and $\beta$ are defined as Eq. (14). Coefficient functions are derived as:

$$\begin{aligned} a_{1} \left( x \right) & = ch\left( {\alpha x} \right)ch\left( {\beta x} \right) - \frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]}}{2\alpha \beta } \\ & \quad sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ b_{1} \left( x \right) & = \frac{C}{C + T}\left[ {\frac{{ch\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{2\beta } + \frac{{sh\left( {\alpha x} \right)ch\left( {\beta x} \right)}}{2\alpha }} \right] \\ c_{1} \left( x \right) & = \frac{{\beta \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]sh\left( {\alpha x} \right)ch\left( {\beta x} \right) - \alpha \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]ch\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{{2\alpha \beta \left( {\alpha^{2} - \beta^{2} } \right)D\frac{C + T}{{C + R}}}} \, \\ d_{1} \left( x \right) & = - \frac{{sh\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{{2\alpha \beta D\frac{{\left( {C + T} \right)}}{C}}} \\ a_{2} \left( x \right) & = \frac{C + T}{C}\left\{ { - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} } \right\} \\ & \quad \cdot \frac{{\beta sh\left( {\alpha x} \right)ch\left( {\beta x} \right) - \alpha ch\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{2\alpha \beta } \\ b_{2} \left( x \right) & = ch\left( {\alpha x} \right)ch\left( {\beta x} \right) + \frac{{\alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]}}{2\alpha \beta } \\ & \quad sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ c_{2} \left( x \right) & = - \frac{C + R}{C}\frac{{\alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} }}{{2\alpha \beta \left( {\alpha^{2} - \beta^{2} } \right)D}} \\ & \quad \cdot sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ d_{2} \left( x \right) & = - \frac{{\alpha \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]ch\left( {\alpha x} \right)sh\left( {\beta x} \right) + \beta \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]sh\left( {\alpha x} \right)ch\left( {\beta x} \right)}}{2\alpha \beta D} \\ a_{3} \left( x \right) & = \frac{{D\left( {C + T} \right)\left( {\alpha^{2} - \beta^{2} } \right)}}{{2\alpha \left( {C + R} \right)}}\left\{ {\alpha^{2} \left[ {3 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]} \right\} \\ & \quad sh\left( {\alpha x} \right)ch\left( {\beta x} \right) + \frac{{D\left( {C + T} \right)\left( {\alpha^{2} - \beta^{2} } \right)}}{{2\beta \left( {C + R} \right)}} \\ & \quad \left\{ { - \beta^{2} \left[ {3 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] - \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]} \right\}ch\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ b_{3} \left( x \right) & = \frac{{DC\left( {\alpha^{2} - \beta^{2} } \right)^{2} }}{{2\alpha \beta \left( {C + R} \right)}} \cdot sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ c_{3} \left( x \right) & = ch\left( {\alpha x} \right)ch\left( {\beta x} \right) - \left[ {\frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]}}{2\alpha \beta }} \right] \\ & \quad sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ d_{3} \left( x \right) & = \frac{{C\left( {\alpha^{2} - \beta^{2} } \right)}}{{\left( {C + R} \right)}}\left[ {\frac{{sh\left( {\alpha x} \right)ch\left( {\beta x} \right)}}{2\alpha } - \frac{{ch\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{2\beta }} \right] \\ a_{4} \left( x \right) & = \frac{{D\left( {C + T} \right)\left( {\alpha^{2} - \beta^{2} } \right)}}{2\alpha \beta C}\left\{ { - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} } \right\} \\ & \quad \cdot sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ b_{4} \left( x \right) & = - \left\{ {\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \alpha^{2} \left[ {3 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]} \right\} \\ & \quad \cdot \frac{{sh\left( {\alpha x} \right)ch\left( {\beta x} \right)D}}{2\alpha } - \left\{ {\beta^{2} \left[ {3 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]} \right\} \\ & \quad \frac{{ch\left( {\alpha x} \right)sh\left( {\beta x} \right)D}}{2\beta } \\ c_{4} \left( x \right) & = \frac{C + R}{{C\left( {\alpha^{2} - \beta^{2} } \right)}}\left[ { - \beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]^{2} } \right] \\ & \quad \left[ {\frac{{sh\left( {\alpha x} \right)ch\left( {\beta x} \right)}}{2\alpha } + \frac{{ch\left( {\alpha x} \right)sh\left( {\beta x} \right)}}{2\beta }} \right] \\ d_{4} \left( x \right) & = ch\left( {\alpha x} \right)ch\left( {\beta x} \right) + \frac{{\beta^{2} \left[ {1 + \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right] + \alpha^{2} \left[ {1 - \frac{D}{C + R}\left( {\alpha^{2} - \beta^{2} } \right)} \right]}}{2\alpha \beta } \\ & \quad sh\left( {\alpha x} \right)sh\left( {\beta x} \right) \\ \end{aligned}$$

(39)

Appendix C: Coefficient functions for the case of Δ = 0

The spatial wave numbers $\alpha$ and $\beta$ are defined as Eq. (16). Coefficient functions are derived as:

$$\begin{aligned} a_{1} \left( x \right) & = ch\left( {\alpha x} \right) - \frac{\alpha }{2}\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right)x \\ b_{1} \left( x \right) & = \frac{C}{C + T}\left[ {\frac{{ch\left( {\alpha x} \right)x}}{2} + \frac{{sh\left( {\alpha x} \right)}}{2\alpha }} \right] \\ c_{1} \left( x \right) & = \frac{C + R}{{D\left( {C + T} \right)}}\frac{{\left( {1 + \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right) - \alpha \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)ch\left( {\alpha x} \right)x}}{{2\alpha^{3} }} \\ d_{1} \left( x \right) & = - \frac{{Csh\left( {\alpha x} \right)x}}{{2\alpha D\left( {C + T} \right)}} \\ a_{2} \left( x \right) & = \frac{C + T}{C}\alpha^{2} \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)^{2} \frac{{sh\left( {\alpha x} \right) - \alpha ch\left( {\alpha x} \right)x}}{2\alpha } \\ b_{2} \left( x \right) & = ch\left( {\alpha x} \right) + \frac{\alpha }{2}\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right)x \\ c_{2} \left( x \right) & = - \frac{C + R}{C}\frac{{\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)^{2} }}{2\alpha D} \cdot sh\left( {\alpha x} \right)x \\ d_{2} \left( x \right) & = - \frac{{\alpha \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)ch\left( {\alpha x} \right)x + \left( {1 + \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right)}}{2\alpha D} \\ a_{3} \left( x \right) & = \frac{{\alpha^{2} D\left( {C + T} \right)}}{{2\left( {C + R} \right)}}\left[ {\alpha \left( {3 - \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right) - \alpha^{2} \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)ch\left( {\alpha x} \right)x} \right] \\ b_{3} \left( x \right) & = \frac{{\alpha^{3} DC}}{{2\left( {C + R} \right)}} \cdot sh\left( {\alpha x} \right)x \\ c_{3} \left( x \right) & = ch\left( {\alpha x} \right) - \frac{\alpha }{2}\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right)x \\ d_{3} \left( x \right) & = \frac{{\alpha^{2} C}}{{\left( {C + R} \right)}}\left[ {\frac{{sh\left( {\alpha x} \right)}}{2\alpha } - \frac{{ch\left( {\alpha x} \right)x}}{2}} \right] \\ a_{4} \left( x \right) & = \frac{{\alpha^{3} D\left( {C + T} \right)}}{2C}\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)^{2} sh\left( {\alpha x} \right)x \\ b_{4} \left( x \right) & = - \frac{D}{2}\left[ {\alpha \left( {3 - \frac{{\alpha^{2} D}}{C + R}} \right)sh\left( {\alpha x} \right) + \alpha^{2} \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)ch\left( {\alpha x} \right)x} \right] \\ c_{4} \left( x \right) & = \frac{C + R}{C}\left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)^{2} \left[ {\frac{{sh\left( {\alpha x} \right)}}{2\alpha } + \frac{{ch\left( {\alpha x} \right)x}}{2}} \right] \\ d_{4} \left( x \right) & = ch\left( {\alpha x} \right) + \frac{{\alpha \left( {1 - \frac{{\alpha^{2} D}}{C + R}} \right)}}{2}sh\left( {\alpha x} \right)x \\ \end{aligned}$$

(40)