Eigenfrequencies of a Three-Dimensional Arbitrarily-Curved Beam

Abstract

Research Problem

The eigenvalue problem for the vibrations of an arbitrarily-curved three-dimensional beam with circular cross-section is solved by a series expansion method under various boundary conditions.

Methodology

The governing differential equations of motion are derived based on Euler-Bernoulli beam theory using the Hamilton’s principle. The general equations are given for any space curved beam with variable curvature and torsion, and solved for a specific example using the method of power series.

Results and Conclusions

The eigenfrequencies of a specific 3D beam were computed and compared with the eigenfrequencies of straight, circular, and helical beams, all having the same length. It was found that the eigenfrequencies of the 3D beam tend to increase slower compared to the other cases as the mode number increases. The main contribution of this study is the computation of the eigenfrequencies of a truly three-dimensional beam: torsion and curvature change continously along the beam length. In constrast, the most studied 3D case, helical beam, has constant curvature and torsion.

Introduction

While many of the curved elements used in engineering structures are very common shapes like circular arcs and helixes, arbitrarily shaped elements also find usage, which may be expected to expand with the ever increasing complexity of mechanisms, aerospace and civil structures. The general equations for the small vibrations of an arbitrarily-shaped space beam were derived long ago; the definitive reference for this (and many other problems) is [1].

Most studies about curved beams consider in plane and out of plane vibrations of plane structures with sometimes variable curvature and cross sections. An older paper [2] demonstrated the natural frequencies of circular arcs by using the Rayleigh Ritz method.

Finite elements with classical beam element shapes were used in [3] to find the natural frequencies of out-of-plane motion of any plane structure composed of slender elastic curved members.

An approximate method for the analysis of both in-plane and out-of-plane free vibrations of horizontally curved beams with arbitrary shape and variable cross-section is presented in [4]. To obtain natural frequencies and mode shapes, [5] performed experimental and numerical studies. Timoshenko beam theory is used to investigate the out-of-plane free vibrations of curved beams with variable curvature on a Pasternak foundation in [6]. Solutions were found by using a Runge–Kutta solver combined with the Regula-Falsi method.

The performance of two curved beam finite element models based on coupled polynomial displacement fields is investigated for out-of-plane vibration of arches in [7]. The analysis of homogenous curved beams of arbitrary cross section taking into account the coupling of extension, flexure and torsion, nonuniform warping as well as shear deformation effects were studied in [8].

More complex systems also have attracted attention. The nonlinear behavior of naturally curved and twisted beams was investigated in [9]. Green–Lagrange strains and Saint–Venant’s torsion of a cylindrical shaft were taken into account.

Geometrically exact beam theory and the weak formulation of the differential equations of equilibrium for the nonlinear elastic analysis of members curved in space with warping and Wagner effects taken into account were considered in [10]; the application of nonlinear differential equations of equilibrium to various problems were also illustrated. A non-linear formulation for curved, extensible, shear flexible, elastic planar beams is presented in [11]. They formulated the problem using a variational principle and compared numerical results with test results. The arbitrarily large in-plane deflections of planar curved beams made of Functionally Graded Materials (FGM) were examined in [12]. A Series solution for the vibration analysis of composite laminated deep curved beams with general boundary conditions was given in [13].

The studies on general 3D beams seem to be scarce. Theoretical development of dynamic equations for undamped gyroelastic beams which are dynamic systems with continuous inertia, elasticity, and gyricity was worked out in [14]. In this case, the motion of the beam is three-dimensional. The deformed configuration space of 3D rods can be carried out in an objective manner by means of a semi configuration dependent approach; this was done in [15].

Experimental studies utilizing acoustic emissions on the deformation of rolling element bearings whose main load carrying portion is a curved beam were carried out in [16, 17]. Curved finite elements for the deformation analysis of 3D beams, including results for circular and helical beams were given in [18]. An interesting study utilizing artificial neural networks (ANN) for optimization of functionally graded microplates in terms of vibration and buckling can be found in [19].

Hilbert and wavelet transforms in model parameter identification, including a footbridge which can be considered as a curved beam, were considered in [20]. Another study employing ANN in metamodel-assisted optimization of mechanical structures is [21]. Bending and vibration of a sandwich nanoplate whose properties vary as a sigmoid function were examined in [22].

In this paper, we consider an arbitrary space curved (3D) beam in the Euler–Bernoulli approximation [23]; our focus is on the beam being an arbitrarily curved one. A twelfth order partial differential equation system consisting of three equations with variable coefficients is derived and the natural frequencies are computed under different boundary conditions. Boundary conditions are taken as fixed–fixed, simply supported-simply supported, fixed-simply supported, fixed-free and simply supported-free. The fact that curvature and torsion of the beam changes quite arbitararily along the beam length is the main thrust of this study. In contrast a helical beam, for example, has constant curvature and torsion, which simplifies its equations of motion compared to the truly three dimensional beam considered here.

Curvature and torsion of the beam are taken in a certain form so that an analytical solution by the method of power series can be obtained; it should be noted that the given form of the curvature and torsion are still quite general in that they change along the beam. More general, variable-curvature-torsion beam shapes would likely involve numerical solutions. The solution given here is valuable in that it is obtained by analytical means due to the specific form of the curvature and torsion functions.

Materials and Methods

Considering a space-curved beam of arbitrary shape, the curve formed by the centroids of the cross sections at any station along its length will be called the beam axis. z-axis is along the tangent of the beam axis, y-axis is in the direction of the principal normal, and x-axis is in the direction of the bi-normal to the beam axis. The cross-section remains unchanged along the beam axis, and it is assumed to be a circle of radius r; but the formulation can easily generalized to more general cross-section shapes.

The material of the beam is assumed to be elastic and any other losses such as friction are ignored; the governing differential equations of motion can be derived through the Hamilton’s principle,

$$\delta \int_{t_{1}}^{t_{2}}L=0$$

(1)

where

$$L=T-V$$

(2)

is the Lagrangian; T and V are the kinetic and potential energies, respectively. They can be expressed as

$$T=\frac{1}{2}\int_{0}^{s}m ({\dot{u}}^{2}+{\dot{w}}^{2}+{\dot{v}}^{2}+\frac{1}{2}{r}^{2}{\dot{\beta }}^{2}) ds$$

(3)

$$V=\frac{1}{2}\int_{0}^{s}\left({M}_{x}\left({\kappa }_{x}-{\kappa }_{{\text{x}}0}\right)+{M}_{y}\left({\kappa }_{y}-{\kappa }_{{\text{y}}0}\right)+{M}_{z}\left(\tau -{\tau }_{0}\right)\right) ds$$

(4)

In Eq. (3), the first three terms show the kinetic energy due to translational motion and the last term is the kinetic energy due to rotary motion around the z-axis. The rotary inertia terms around the x and y axes are ignored. u, v, w are the displacement components along the x, y, z axes. $\beta$ is the rotation of the cross-section around the z-axis. s is the arclength along the beam axis, m is the mass per unit length of the beam material. ${M}_{x} , {M}_{y} , {M}_{z}$ are stress resultants (bending and torsional moments) at the cross-section, ${\kappa }_{x}$ and ${\kappa }_{y}$ show the curvatures around x and y axes. The subscript zero refer to the values before the deformation. The relations between the bending moments and curvatures are

$${M}_{x}=A ({\kappa }_{x}-{\kappa }_{{\text{x}}0})$$

(5)

$${M}_{y}=B ({\kappa }_{y}-{\kappa }_{{\text{y}}0})$$

(6)

where

$$A=E{I}_{x}$$

(7)

$$B=E{I}_{y}$$

(8)

are the bending rigidities, with E showing the elastic modulus of the beam material and ${I}_{x}$, ${I}_{y}$ the second moment of areas of the cross section around x and y-axes. For a circular cross section of radius r they are equal. The relation between the torsional moment and twist is

$${M}_{z}=C (\tau -{\tau }_{0})$$

(9)

where

$$C = G\,J$$

(10)

denotes the torsional rigidity. With GJ unspecified, the equations are still valid for a general cross-sectional shape with the condition that the twist axis coincides with the centroid and the factor in front of the $\beta$ term in Eq. (3) changed accordingly.

The curvatures and twist before and after the deformation are given by [1] and is rederived by using the modern vector approach in the “Appendix 1” as

$${\kappa }_{x}={\kappa }_{{\text{x}}0}+\beta {\kappa }_{{\text{y}}0}-\frac{\partial }{\partial s}\left({v}^{\prime}-w {\kappa }_{{\text{x}}0}+u {\tau }_{0}\right)-{\tau }_{0} ({u}^{\prime}-v {\tau }_{0}+w {\kappa }_{{\text{y}}0})$$

(11)

$${\kappa }_{y}={\kappa }_{{\text{y}}0}-\beta {\kappa }_{{\text{x}}0}+\frac{\partial }{\partial s}({u}^{\prime}-v {\tau }_{0}+w {\kappa }_{{\text{y}}0})-{\tau }_{0} ({v}^{\prime}-w {\kappa }_{{\text{x}}0}+u {\tau }_{0})$$

(12)

$$\tau ={\tau }_{0}+{\beta }^{\prime}+{\kappa }_{{\text{x}}0}\left({u}^{\prime}-v {\tau }_{0}+w {\kappa }_{{\text{y}}0}\right)+{\kappa }_{{\text{y}}0} ({v}^{\prime}-w {\kappa }_{{\text{x}}0}+u {\tau }_{0})$$

(13)

The condition that the beam axis does not extend should also be added:

$$u=\frac{v {\kappa }_{{\text{x}}0}}{{\kappa }_{{\text{y}}0}}+\frac{{w}^{\prime}}{{\kappa }_{{\text{y}}0}}$$

(14)

These equations are for a circular cross-section beam with completely general variable curvature and torsion radii. In the following, a specific example will be considered for which the curvatures and the torsion are given as

$${\kappa }_{{\text{x}}0}=\frac{1}{s}$$

(15)

$${\kappa }_{{\text{y}}0}=\frac{1}{s}$$

(16)

$${\tau }_{0}=\frac{1}{s}$$

(17)

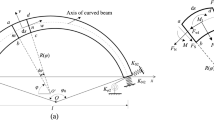
The actual shape of the curve is shown in Fig. 1, and its derivation is explained in “Appendix 3”.

Fig. 1

The shape of the space curve considered

The displacements v and w are non-dimensionalized by L, the length of the beam [u will be eliminated by using Eq. (14)] and the time by $\sqrt{\mu {L}^{4}/b}$. Thus, in Fig. 1, the nondimensional length of the curve becomes 1. The range of the curve is taken as $1\le s\le 2$ to avoid the singular behavior at $s=0$ in Eqs. (26–28).

The following combinations of boundary conditions are considered at both ends of the beam:

$s=1$ and $s=2$: fixed–fixed

$$w=0,\quad \beta =0,\quad u=\frac{\partial u}{\partial s}=0,\quad v=\frac{\partial v}{\partial s}=0$$

(18)

simply supported-simply supported

$$w=0,\quad \beta =0,\quad u=\frac{{\partial }^{2}u}{\partial {s}^{2}}=0,\quad v=\frac{{\partial }^{2}v}{\partial {s}^{2}}=0$$

(19)

fixed-simply supported

$$w=0,\quad \beta =0,\quad u=\frac{\partial u}{\partial s}=0,\quad u=\frac{{\partial }^{2}u}{\partial {s}^{2}}=0,\quad v=\frac{\partial v}{\partial s}=0,\quad v=\frac{{\partial }^{2}v}{\partial {s}^{2}}=0$$

(20)

fixed-free

$$w=\frac{\partial {w}_{s}}{\partial s}=0,\quad \beta =\frac{\partial \beta }{\partial s}=0,\quad u=\frac{\partial u}{\partial s}=0,\quad \frac{{\partial }^{2}u}{\partial {s}^{2}}=\frac{{\partial }^{3}u}{\partial {s}^{3}}=0,\quad v=\frac{\partial v}{\partial s}=0,\quad \frac{{\partial }^{2}v}{\partial {s}^{2}}=\frac{{\partial }^{3}v}{\partial {s}^{3}}=0$$

(21)

simply supported-free

$${w}_{0}=\frac{\partial {w}_{s}}{\partial s}=0,\quad {\beta }_{0}=\frac{\partial {\beta }_{s}}{\partial s}=0,\quad{u}_{0}=\frac{{\partial }^{2}{u}_{s}}{\partial {s}^{2}}=0,\quad \frac{{\partial }^{2}{u}_{s}}{\partial {s}^{2}}=\frac{{\partial }^{3}{u}_{s}}{\partial {s}^{3}}=0,\quad{v}_{0}=\frac{{\partial }^{2}{v}_{s}}{\partial {s}^{2}}=0,\quad \frac{{\partial }^{2}{v}_{s}}{\partial {s}^{2}}=\frac{{\partial }^{3}{v}_{s}}{\partial {s}^{3}}=0$$

(22)

Substituting Eqs. (3–17) into the Hamilton’s principle, Eq. (1), and performing the variations, a system of partial differential equations for $w(s,t)$, $v(s,t)$ and $\beta (s,t)$ is obtained. To find the mode shapes, harmonic variation is assumed

$$w\left(s,t\right)=W\left(s\right){e}^{i\lambda t}$$

(23)

$$v\left(s,t\right)=V\left(s\right){e}^{i\lambda t}$$

(24)

$$\beta \left(s,t\right)={\mathcal{B}}\left(s\right){e}^{i\lambda t}$$

(25)

Result is the following linear system of ordinary differential equations with variable coefficients

$${s}^{6}{W}^{(6)}+6 {s}^{5}{ W}^{(5)}-{s}^{4} \upsilon {W}^{\left(4\right)}+\left(-8 {s}^{2}-{s}^{6}{\lambda }^{2}+6 {s}^{2} \upsilon \right){W}^{\prime\prime}+\left(16 s-2 {s}^{5}{\lambda }^{2}- 12 s \upsilon \right){W}^{\prime}-\left(28-{s}^{4}{\lambda }^{2}\right) W+{s}^{5}{V}^{\left(5\right)}-3 {s}^{4}{V}^{\left(4\right)}-2 {s}^{3} \upsilon {V}^{\left(3\right)}+2 {s}^{2}\left(1+4 \upsilon \right){V}^{\prime\prime}+ \left(-20 s-{s}^{5}{\lambda }^{2}-12 s \upsilon \right){V}^{\prime}+\left(28-{s}^{4}{ \lambda }^{2}\right) V-{s}^{4}\left(1+\upsilon \right){\mathcal{B}}^{\left(3\right)}+2 {s}^{3}\left(2+\upsilon \right){\mathcal{B}}^{\prime\prime}- 2 {s}^{2}\left(4+\upsilon \right){\mathcal{B}}^{\prime}+10 s \mathcal{B}=0$$

(26)

$${s}^{5}{W}^{(5)}+8 {s}^{4}{W}^{(4)}-2 {s}^{3} \upsilon {W}^{\left(3\right)}-2 {s}^{2}\left(1+\upsilon \right){W}^{\prime\prime}+\left(-12 s-{s}^{5}{\lambda }^{2}+8 s \upsilon \right){W}^{\prime}+20 W+2 {s}^{4}{V}^{\left(4\right)}-4 {s}^{2}\left(3+\upsilon \right){V}^{\prime\prime}+8 s \left(3+\upsilon \right){V}^{\prime}+2 \left(-10-{s}^{4}{\lambda }^{2}\right) V- 2 {s}^{3}\left(1+\upsilon \right){\mathcal{B}}^{\prime\prime}+2 {s}^{2}\left(2+\upsilon \right){\mathcal{B}}^{\prime}-2 s \mathcal{B}=0$$

(27)

$${s}^{3}\left(1+\upsilon \right){W}^{(3)}+2 {s}^{2}\left(2+\upsilon \right){W}^{\prime\prime}-2 s \upsilon {W}^{\prime}+2 W+2 {s}^{2}\left(1+\upsilon \right){V}^{\prime\prime}-2 s \upsilon {V}^{\prime}- 2 V+{s}^{3} \upsilon {\mathcal{B}}^{\prime\prime}-\left(2 s-{s}^{3}{\lambda }^{2}\right) \mathcal{B}=0$$

(28)

To solve the eigenvalue problem consisting of Eqs. (26, 27, 28) and boundary conditions, Eqs. (18, 19, 20, 21, 22), assume an analytic power series solution around the middle of the range of $s$, i.e., around $s=3/2$,

$$w\left(s\right)=\sum_{n=0}^{\infty }{a}_{n}{(s-3/2)}^{n}$$

(29)

$$v\left(s\right)=\sum_{n=0}^{\infty }{b}_{n}{(s-3/2)}^{n}$$

(30)

$$\beta \left(s\right)=\sum_{n=0}^{\infty }{c}_{n}{(s-3/2)}^{n}$$

(31)

Substituting in Eqs. (26, 27, 28) results in recurrence relations for ${a}_{n}$, ${b}_{n}$ and ${c}_{n}$. The first six coefficients of ${a}_{n}$, the first four coefficients of ${b}_{n}$ and the first two coefficients of ${c}_{n}$ can not be evaluated (in agreement with the number of boundary conditions).

An interesting feature of the solution procedure should be mentioned here: Normally, in solving differential equations by power series, the coefficients can be found in a naturally occurring order. For the set of equations solved here, at each step we needed to solve unknown coefficients between two levels of recurrence relations; otherwise we would have 14 coefficients instead of the 12 that is needed.

In the next section, results of the computation of eigenvalues of the problem consisting of Eqs. (26–28) with boundary conditions Eqs. (18–22) will be presented for the first 10 eigenfrequencies,

$${\lambda }_{n} , n=\mathrm{1,2},3,\dots , 10$$

(32)

In actual computations 50 terms were used for each of Eqs. (29–31), since it was found that, after 20–30 terms the significant figures do not change; so 50 terms should be a safe choise.

Results

In order to make comparisons, the eigenfrequencies are listed together with the eigenfrequencies of a straight beam, a circular beam, and a helicoidal beam all having the same length as the space-curved beam (i.e., all have length 1). The equations for the other three types of beam are listed in “Appendix 2”.

The following tables show the eigenfrequencies of all four beams for various boundary conditions (Tables 1, 2, 3, 4, 5).

Table 1 Eigenfrequencies for fixed–fixed boundary conditions

Table 2 Eigenfrequencies for simply supported-simply supported boundary conditions

Table 3 Eigenfrequencies for fixed-simply supported boundary conditions

Table 4 Eigenfrequencies for fixed-free boundary conditions

Table 5 Eigenfrequencies for simply supported-free boundary conditions

The following figures show the eigenfrequencies as a function of mode number (Figs. 2, 3, 4, 5, 6).

Fig. 2

Eigenfrequencies for fixed–fixed boundary conditions

Fig. 3

Eigenfrequencies for simply supported-simply supported boundary conditions

Fig. 4

Eigenfrequencies for fixed-simply supported boundary conditions

Fig. 5

Eigenfrequencies for fixed-free boundary conditions

Fig. 6

Eigenfrequencies for simply supported-free boundary conditions

It seems that for all boundary conditions considered, the eigenfrequencies of the 3D beam seem to increase slower than the other beams with the same mode number. The 3D beam also has the lowest eigenfrequency at any mode number. While the eigenfrequencies of straight and circular beams increase monotonically with mode number, the rate of increase of helicoidal and 3D beam, both being space beams, changes drastically with mode number. For example, for the fixed-simply supported case (in Fig. 4), the increase in helicoidal beam from 8 to 9th modes, and the increase in the 3D beam from 5 to 6th mode are quite small compared to others. In the fixed–fixed case (in Fig. 2), the eigenfrequencies of the helicoidal and 3D beams are close to each other for all mode numbers considered. For the other boundary conditions (in Figs. 3, 5, 6), the two dimensional beams (straight and circular) generally have eigenfrequencies between the helicoidal and 3D beams. The most interesting outcome of this study seems to be the fact that the eigenfrequencies of the 3D beam increase very slowly with the mode number.

Finally, it should be noted that most of the results obtained in this study and the ones used in comparisons were obtained by analytical methods, although some of the works on helical beams use finite element methods. The equations derived for the general 3D beam in the present study are a system of variable coefficient linear ordinary differential equations. Although some forms of these types of equations can be solved by specific methods that might give simpler analytical expressions, it is not the case here. Therefore, the equations were solved by the series expansion method, and the convergence of the results were verified. The operations were complictaed enough to render hand computations impossible and the symbolic manipulation capabilities of Mathematica were the method of choice. In terms of computational load, these coputations require much less resources than finite element methods, for example.

Appendices

Appendix 1

The following is the derivation of the relations between the curvatures and torsion of an arbitrarily curved space-beam before and after the deformation [24]. Following Love [1], we denote the axis along the arc length of the spatial curve formed by the centroids of the cross-sections (which will be called the wire axis) as z. x and y axes are chosen to be the principal axes of the cross-section (Fig. 7).

Fig. 7

Frenet vectors and coordinate system attached to beam axis

The xyz system is therefore attached to the wire axis with z denoting the tangent direction while x and y representing the orientation of the cross-section with respect to z. The principal normal (N) and the binormal (B) at any point on the wire axis are within the cross-section, however, they do not coincide with x and y axes, in general. We denote the angle between N and y as γ. The change in γ as one moves along the main helix axis, $d\gamma /ds$ is termed the torsional twist, where s is the arclength along z. The unit tangent along z is denoted T. These are related by the Frenet equations:

$$\frac{d{\varvec{T}}}{ds}=\kappa {\varvec{N}}$$

(33a)

$$\frac{d{\varvec{N}}}{ds}=-\kappa {\varvec{T}}+\tau {\varvec{B}}$$

(33b)

$$\frac{d{\varvec{B}}}{ds}=-\tau {\varvec{N}}$$

(33c)

where $\kappa$ is the principal curvature and τ is the torsion of the wire axis. Frenet equations can also be expressed as

$$\frac{d{\varvec{T}}}{ds}=\boldsymbol{\Delta }\times {\varvec{T}}$$

(34a)

$$\frac{d{\varvec{N}}}{ds}=\boldsymbol{\Delta }\times {\varvec{N}}$$

(34b)

$$\frac{d{\varvec{B}}}{ds}=\boldsymbol{\Delta }\times {\varvec{B}}$$

(34c)

where

$$\boldsymbol{\Delta }=\tau {\varvec{T}}+\kappa {\varvec{B}}$$

(35)

is the Frenet vector. It is the angular velocity of the TNB system as its origin moves with unit velocity along the wire axis. The xyz system differs from the TNB system by a rotation around T ( z axis) through the angle γ between N and y; therefore

$${\text{i}} = \sin \gamma \;{\text{N}} - \cos \gamma \;{\text{B}}$$

(36a)

$${\text{j}} = \cos \gamma \,{\text{N}} + \sin \gamma \;{\text{B}}$$

(36b)

$${\text{k}} = {\text{T}}$$

(36c)

where ${\text{i}}$, ${\text{j}}$, ${\text{k}}$ are the unit vectors along xyz. The changes in these can be expressed as

$$\frac{d{\varvec{i}}}{ds}={\varvec{\omega}}\times {\varvec{i}}=\lambda {\varvec{j}}-{\kappa }_{y}{\varvec{k}}$$

(37a)

$$\frac{d{\varvec{j}}}{ds}={\varvec{\omega}}\times {\varvec{j}}=-\lambda {\varvec{i}}-{\kappa }_{x}{\varvec{k}}$$

(37b)

$$\frac{d{\varvec{k}}}{ds}={\varvec{\omega}}\times {\varvec{k}}={\kappa }_{y}{\varvec{i}}-{\kappa }_{x}{\varvec{j}}$$

(37c)

where

$${\varvec{\omega}}=\boldsymbol{\Delta }+\frac{d\gamma }{ds}{\varvec{k}}$$

(38)

is the angular velocity of the xyz system as its origin moves with unit velocity along the wire axis; it differs from the Frenet vector by torsional twist. In the xyz system

$${\upomega } = \kappa_x {\text{i}} + \kappa_y {\text{j}} + \lambda \;{\text{k}}$$

(39)

where

$${\kappa }_{x}=-\kappa {\text{cos}}\gamma$$

(40a)

$${\kappa }_{y}=\kappa {\text{sin}}\gamma$$

(40b)

are the curvatures around x and y directions, and

$$\lambda =\frac{d\gamma }{ds}+\tau$$

(41)

is the total twist with first term showing the torsional and the second the geometric twist. Also, we note the following, obtained from Eq. (37), to be used in the sequel

$${\kappa }_{x}={\varvec{k}}\cdot \frac{d{\varvec{j}}}{ds}$$

(42a)

$${\kappa }_{y}={\varvec{i}}\cdot \frac{d{\varvec{k}}}{ds}$$

(42b)

$$\lambda ={\varvec{j}}\cdot \frac{d{\varvec{i}}}{ds}$$

(42c)

The derivative of any vector

$${\text{A}} = A_x \;{\text{i}} + A_y \;{\text{j}} + A_z \;{\text{k}}$$

(43)

can be expressed as

$$\frac{d{\varvec{A}}}{ds}=\frac{\delta {\varvec{A}}}{\delta s}+{\varvec{\omega}}\times {\varvec{A}}$$

where

$$\frac{\delta {\varvec{A}}}{\delta s}=\frac{d{A}_{x}}{ds} {\varvec{i}}+\frac{d{A}_{y}}{ds} {\varvec{j}}+\frac{d{A}_{z}}{ds} {\varvec{k}}$$

Let ${\text{i}}_{0}$, ${\text{j}}_{0}$, ${\text{k}}_{0}$ denote the base vectors attached to a point on the wire axis before the deformation as explained before. After the deformation, the point moves to a new location and base vectors change to ${\text{i}}$, ${\text{j}}$, ${\text{k}}$. The deformation vector is denoted as

$$\mathbf{u}=u{{\varvec{i}}}_{0}+v{{\varvec{j}}}_{0}+w{{\varvec{k}}}_{0}$$

(44)

The point, initially located at ${\text{R}}$, moves to

$${{\varvec{r}}} = {{\varvec{R}}} + u$$

(45)

Differentiating this expression with respect to the arclength

$$k={k}_{0}+\frac{d{\varvec{u}}}{ds}$$

(46)

where ${\text{k}} = d{\text{r}}/ds$, ${\text{k}}_{0} = d{\text{R}}/ds$. Since the bar is assumed to be unextended, it does not matter what arclength is meant by s. The relation between the base vectors of undeformed and deformed coordinate systems is written as

$${\text{i}} = L_1 \,{\text{i}}_{0} + M_1 \,{\text{j}}_{0} + N_1 \,{\text{k}}_{0}$$

(47a)

$${\text{j}} = L_2 \,{\text{i}}_{0} + M_2 \,{\text{j}}_{0} + N_2 \,{\text{k}}_{0}$$

(47b)

$${\text{k}} = L_3 \,{\text{i}}_{0} + M_3 \,{\text{j}}_{0} + N_3 \,{\text{k}}_{0}$$

(47c)

Using Eq. (43), in Eq. (46) we find, from Eq. (47c),

$${L}_{3}=\frac{dU}{ds}-{\tau }_{0} V+{\kappa }_{y0} W$$

(48a)

$${M}_{3}=\frac{dV}{ds}-{\kappa }_{x0} W+{\tau }_{0} U$$

(48b)

$${N}_{3}=1+\frac{dW}{ds}-{\kappa }_{y0} U+{\kappa }_{x0} V$$

(48c)

$L_3$ and $M_3$ are $O(\left\| {{\varvec{U}}} \right\|)$ (assuming deformation and deformation gradient are of the same small order) while $N_3$ is $O(1)$. Since $\left\| {\text{k}} \right\|^2 = L_3^2 + M_3^2 + N_3^2 = 1$, substituting from Eq. (48) and ignoring $O(\left\| {{\varvec{U}}} \right\|)$ terms,

$$N_3 = 1$$

(49)

and to $O(\left\| {\text{u}} \right\|)$,

$$\frac{dW}{ds}-{\kappa }_{y0} U+{\kappa }_{x0} V=0$$

(50)

which expresses that the wire axis is not extended. Thus, we have found how the tangent to the wire axis changes (${\text{k}}_0 \to {\text{k}}$) expressed in Eqs. (48a), (48b) and (49). To complete the transformation, we need another parameter. Love [1] takes the angle between x axes before and after the deformation and denotes the sine of this angle as $\beta$, i.e.,

$${M}_{1}=\beta$$

(51)

The other entries in the transformation matrix Eq. (47) are found by requiring that the matrix is orthonormal; ignoring nonlinear terms,

$$L_1 = 1$$

(52a)

$$N_1 = - L_3$$

(52b)

$${L}_{2}=-\beta$$

(52c)

$$M_2 = 1$$

(52d)

$$N_2 = - M_3$$

(52e)

Therefore, the complete transformation of base vectors during deformation is given in terms of u, v, w, $\beta$ as

$${\varvec{i}}={{\varvec{i}}}_{0}+\beta {{\varvec{j}}}_{0}-{L}_{3}{{\varvec{k}}}_{0}$$

(53a)

$${\varvec{j}}=\beta {{\varvec{i}}}_{0}+{{\varvec{j}}}_{0}-{M}_{3}{{\varvec{k}}}_{0}$$

(53b)

$${\varvec{k}}={L}_{3}{{\varvec{i}}}_{0}+{M}_{3}{{\varvec{j}}}_{0}- {{\varvec{k}}}_{0}$$

(53c)

where L₃ and M₃ are given by Eqs. (48a)–(48b). Using these in Eq. (42) we find the relations between curvatures and twist before and after the deformation:

$${\kappa }_{x}={\kappa }_{x0}+{\kappa }_{y0}\beta -\frac{d {M}_{3}}{ds}-{\tau }_{0}{L}_{3}$$

(54a)

$${\kappa }_{y}={\kappa }_{y0}-{\kappa }_{x0}\beta -\frac{d {L}_{3}}{ds}-{\tau }_{0}{M}_{3}$$

(54b)

$$\tau ={\tau }_{0}+\frac{d \mathcal{B}}{ds}-{\kappa }_{x0}{L}_{3}-{\kappa }_{y0}{M}_{3}$$

(54c)

For the case considered in this paper ${\kappa }_{x}={\kappa }_{y}=1/s$, $\gamma$ is constant ($\pi /4$) and

$${\kappa }^{2}={\kappa }_{x}^{2}+{\kappa }_{y}^{2}=2/{s}^{2}$$

Appendix 2

The following are the eigenfrequency equations for straight, circular and helicoidal beams.

For a straight beam;

$${u}^{\prime\prime\prime\prime}-{\lambda }^{2}u=0$$

(55)

For a circular beam [1],

$${u}^{(6)}+2{u}^{\prime\prime\prime\prime}+\left(1-{\lambda }^{2}\right){u}^{\prime\prime}+{\lambda }^{2}u=0$$

(56)

For a helicoidal beam,

$$\left(\frac{\left(1+\upsilon \right)}{{\kappa }_{{\text{y}}0}^{2}}\right){w}^{\left(6\right)}+\left(\frac{2\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{2}-2\left(2\left(1+\upsilon \right)+\left(1+\upsilon \right)\right){\tau }_{0}^{2}}{{\kappa }_{{\text{y}}0}^{2}}\right){w}^{\prime\prime\prime\prime}+\left(\frac{\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{4}+\left(-4\left(1+\upsilon \right)-2\left(1+\upsilon \right)+1\right){\kappa }_{{\text{y}}0}^{2}{\tau }_{0}^{2}+\left(1+\upsilon \right){\tau }_{0}^{4}}{{\kappa }_{{\text{y}}0}^{2}}-{\lambda }^{2}\right){w}^{\prime\prime}+\left(-\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{2}{\tau }_{0}^{2}+{\lambda }^{2}\right)w+\left(-\frac{2\left(\left(1+\upsilon \right)+\left(1+\upsilon \right)\right){\tau }_{0}}{{\kappa }_{{\text{y}}0}}\right){v}^{\prime\prime\prime\prime}+\left(\frac{{\tau }_{0}\left(\left(-\left(1+\upsilon \right)-2\left(1+\upsilon \right)+1\right){\kappa }_{{\text{y}}0}^{2}+2\left(\left(1+\upsilon \right)+\left(1+\upsilon \right)\right){\tau }_{0}^{2}\right)}{{\kappa }_{{\text{y}}0}}\right){v}^{\prime\prime}+\left(\left(1+\upsilon \right){\kappa }_{{\text{y}}0}{\tau }_{0}^{3}\right)v+\left(\left(2\left(1+\upsilon \right)+1\right){\tau }_{0}\right){\beta }^{\prime\prime}+\left(\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{2}{\tau }_{0}\right)\beta =0$$

(57)

$$\left(-\frac{2\left(\left(1+\upsilon \right)+\left(1+\upsilon \right)\right){\tau }_{0}}{{\kappa }_{{\text{y}}0}}\right){w}^{\prime\prime\prime\prime}+\left(\frac{{\tau }_{0}\left(\left(-\left(1+\upsilon \right)-2\left(1+\upsilon \right)+1\right){\kappa }_{{\text{y}}0}^{2}+2\left(\left(1+\upsilon \right)+\left(1+\upsilon \right)\right){\tau }_{0}^{2}\right)}{{\kappa }_{{\text{y}}0}}\right){w}^{\prime\prime}+\left(\left(1+\upsilon \right){\kappa }_{{\text{y}}0}{\tau }_{0}^{3}\right)w+\left(-1-\upsilon \right){v}^{\prime\prime\prime\prime}+\left({\kappa }_{{\text{y}}0}^{2}+2\left(\left(1+\upsilon \right)+2\left(1+\upsilon \right)\right){\tau }_{0}^{2}\right){v}^{\prime\prime}+\left(\left(-1-\upsilon \right){\tau }_{0}^{4}+{\lambda }^{2}\right)v+\left(\left(\left(1+\upsilon \right)+1\right){\kappa }_{{\text{y}}0}\right){\beta }^{\prime\prime}+\left(\left(-1-\upsilon \right){\kappa }_{{\text{y}}0}{\tau }_{0}^{2}\right)\beta =0$$

(58)

$$\left(\left(2\left(1+\upsilon \right)+1\right){\tau }_{0}\right){w}^{\prime\prime}+\left(\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{2}{\tau }_{0}\right)w+\left(\left(\left(1+\upsilon \right)+1\right){\kappa }_{{\text{y}}0}\right){v}^{\prime\prime}+\left(\left(-1-\upsilon \right){\kappa }_{{\text{y}}0}{\tau }_{0}^{2}\right)v+{\beta }^{\prime\prime}-\left(\left(1+\upsilon \right){\kappa }_{{\text{y}}0}^{2}\right)\beta =0$$

(59)

Equations (57–59) can be derived by using the general formulation given in [1].

Appendix 3

The shape of a space curve with given curvature and torsion can be found by using the canonical representation of curves in differential geometry [25]. If the equation of the curve is, in natural coordinates, $\mathbf{r}=\mathbf{r}(s)$, with r position vector and s showing the arclength, writing the Taylor series around s = 1,

$$\mathbf{r}=\mathbf{r}\left(1\right)+\frac{d\mathbf{r}(1)}{ds}\left(s-1\right)+\frac{1}{2!}\frac{{d}^{2}\mathbf{r}(1)}{d{s}^{2}}{\left(s-1\right)}^{2}+\frac{1}{3!}\frac{{d}^{3}\mathbf{r}(1)}{d{s}^{3}}{\left(s-1\right)}^{3}+\frac{1}{4!}\frac{{d}^{4}\mathbf{r}(1)}{d{s}^{4}}{\left(s-1\right)}^{4}+\frac{1}{5!}\frac{{d}^{5}\mathbf{r}(1)}{d{s}^{5}}{\left(s-1\right)}^{5}+O({(s-1)}^{6})$$

(60)

By placing the one end (s = 1) of the curve at the origin, the first term r (1) becomes zero. Since the whole curve can be rotated like a rigid body, its orientation can be chosen so that the Frenet vectors at the origin are in the directions of the base vectors, i.e.,

$${\varvec{T}}\left(0\right)={{\varvec{e}}}_{1}$$

(61)

$${\varvec{N}}\left(0\right)={{\varvec{e}}}_{2}$$

(62)

$${\varvec{B}}\left(0\right)={{\varvec{e}}}_{3}$$

(63)

The first derivative above is the tangent vector

$$\frac{d{\varvec{x}}}{ds}= {\varvec{T}}$$

(64)

The higher derivatives can be evaluated by using the Frenet equations

$$\frac{d{\varvec{T}}}{ds}={\varvec{\kappa}}{\varvec{N}}$$

(65a)

$$\frac{d{\varvec{N}}}{ds}=-{\varvec{\kappa}}{\varvec{T}}+\tau {\varvec{B}}$$

(65b)

$$\frac{d{\varvec{B}}}{ds}=-\tau {\varvec{N}}$$

(65c)

and still higher derivatives can be found by differentiating the Frenet equations. For the curve considered in this paper,${\kappa }^{2}={\kappa }_{x}^{2}+{\kappa }_{y}^{2}=2/{s}^{2}$, and $\tau =1/s$. The result, up to order five is

$${\varvec{x}}=\left(-1-\frac{1}{3}{\left(-1+s\right)}^{3}+\frac{1}{4}{\left(-1+s\right)}^{4}-\frac{2}{15}{\left(-1+s\right)}^{5}+s\right){{\varvec{e}}}_{1}+\left(\frac{{\left(-1+s\right)}^{2}}{\sqrt{2}}-\frac{{\left(-1+s\right)}^{3}}{3\sqrt{2}}-\frac{{\left(-1+s\right)}^{4}}{12\sqrt{2}}+\frac{{\left(-1+s\right)}^{5}}{5\sqrt{2}}\right){{\varvec{e}}}_{2}+\left(\frac{{\left(-1+s\right)}^{3}}{3\sqrt{2}}-\frac{{\left(-1+s\right)}^{4}}{4\sqrt{2}}+\frac{1}{15}\sqrt{2}{\left(-1+s\right)}^{5}\right){{\varvec{e}}}_{3}$$

(66)

This is plotted in Fig. 1 for $1\le s\le 2$.