Vibration Suppression of Optical Payload Based on Parallel Manipulator

Abstract

Purpose

Currently, the observational resolution of Earth observation satellites and space telescopes is progressively advancing. Nevertheless, the detrimental effects of vibrations induced by solar panel oscillation, control torque gyroscopic reaction force, and internal noise within satellites seriously affect the observational precision of satellite-mounted precision optical payloads. This paper introduces the application of electromagnetic damping to mitigate optical payload vibrations.

Methods

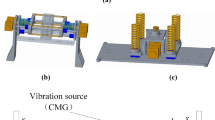
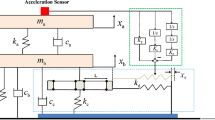
The electromagnetic damping mechanism is investigated through electromagnetic laws, and the magnetic field characteristics of the damper are validated using ANSOFT Maxwell. An optical payload isolation system with Gough–Stewart parallel configuration is constructed with flexible hinges. The Newton–Euler method is employed to formulate the dynamic equation governing the system. Through analyze the external disturbance frequency band, the isolation bandwidth and natural frequency of the system are determined, subsequently guiding the determination of the structural parameters. On this basis, a prototype of optical payload vibration isolation system is designed, and a ground vibration isolation experiment system is established to validate its performance under various excitations.

Results

The electromagnetic damper employed in this article features viscous damping characteristics. The parallel manipulator prototype can effectively attenuate the vibrations over the entire frequency range starting from approximately 1 Hz.

Conclusions

The electromagnetic damper is beneficial to the damping control of the vibration isolation system. The simulation and experimental results both demonstrate the effective vibration isolation capabilities of the system, affirming the feasibility of utilizing the platform for isolating vibrations in space optical payloads. Furthermore, these findings offer valuable theoretical and experimental insights for future space applications.

Appendices

Appendix A

Expressions of the matrices in Eq. 28 are presented as follows:

$$\begin{aligned} \mathbf{{P}} = \left[ {\begin{array}{*{20}{c}} { - {\theta _c}{\phi _c}}&{}{{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}0&{}{ - {\theta _s}{\phi _c}a}&{}{{\phi _s}a}\\ { - {\theta _c}{\phi _c}}&{}{ - {\phi _s}}&{}{{\theta _s}{\phi _c}}&{}0&{}{ - {\theta _s}{\phi _c}a}&{}{ - {\phi _s}a}\\ {\frac{1}{2}{\theta _c}{\phi _c} - \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} - \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{\frac{{\sqrt{3} }}{2}{\theta _s}{\phi _c}a}&{}{\frac{1}{2}{\theta _s}{\phi _c}a}&{}{{\phi _s}a}\\ {\frac{1}{2}{\theta _c}{\phi _c} + \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} + \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{\frac{{\sqrt{3} }}{2}{\theta _s}{\phi _c}a}&{}{\frac{1}{2}{\theta _s}{\phi _c}a}&{}{ - {\phi _s}a}\\ {\frac{1}{2}{\theta _c}{\phi _c} + \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{\frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} - \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _s}{\phi _c}a}&{}{\frac{1}{2}{\theta _s}{\phi _c}a}&{}{{\phi _s}a}\\ {\frac{1}{2}{\theta _c}{\phi _c} - \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{\frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} + \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _s}{\phi _c}a}&{}{\frac{1}{2}{\theta _s}{\phi _c}a}&{}{ - {\phi _s}a} \end{array}} \right] , \end{aligned}$$

(40)

$$\begin{aligned} \mathbf{{Q}} = \left[ {\begin{array}{*{20}{c}} { - {\theta _c}{\phi _c}}&{}{{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{ - {\phi _s}{h_a} - {\varphi _s}{\theta _s}{\phi _c}b}&{}{ - {\theta _c}{\phi _c}{h_a} - {\varphi _c}{\theta _s}{\phi _c}b}&{}{\left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b}\\ { - {\theta _c}{\phi _c}}&{}{ - {\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{{\phi _s}{h_a} + {\varphi _s}{\theta _s}{\phi _c}b}&{}{ - {\theta _c}{\phi _c}{h_a} - {\varphi _c}{\theta _s}{\phi _c}b}&{}{ - \left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b}\\ {\frac{1}{2}{\theta _c}{\phi _c} - \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} - \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{{Q_{34}}}&{}{{Q_{35}}}&{}{\left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b}\\ {\frac{1}{2}{\theta _c}{\phi _c} + \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{ - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} + \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{{Q_{44}}}&{}{{Q_{45}}}&{}{ - \left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b}\\ {\frac{1}{2}{\theta _c}{\phi _c} + \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{\frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} - \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{{Q_{54}}}&{}{{Q_{55}}}&{}{\left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b}\\ {\frac{1}{2}{\theta _c}{\phi _c} - \frac{{\sqrt{3} }}{2}{\phi _s}}&{}{\frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c} + \frac{1}{2}{\phi _s}}&{}{{\theta _s}{\phi _c}}&{}{{Q_{64}}}&{}{{Q_{65}}}&{}{ - \left( {{\varphi _c}{\phi _s} - {\varphi _s}{\theta _c}{\phi _c}} \right) b} \end{array}} \right] , \end{aligned}$$

(41)

where ${\theta _c}$ means $\cos \theta$, ${\theta _s}$ means $\sin \theta$, ${\phi _c},{\phi _s}, {\phi _c}, {\varphi _s}$ have a similar meaning, and

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{Q_{34}} = \left( {\frac{1}{2}{\phi _s} + \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _s} + \frac{{\sqrt{3} }}{2}{\varphi _c}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{35}} = \left( { - \frac{{\sqrt{3} }}{2}{\phi _s} + \frac{1}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _c} - \frac{{\sqrt{3} }}{2}{\varphi _s}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{44}} = \left( { - \frac{1}{2}{\phi _s} + \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( { - \frac{1}{2}{\varphi _s} + \frac{{\sqrt{3} }}{2}{\varphi _c}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{45}} = \left( {\frac{{\sqrt{3} }}{2}{\phi _s} + \frac{1}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _c} + \frac{{\sqrt{3} }}{2}{\varphi _s}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{54}} = \left( {\frac{1}{2}{\phi _s} - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _s} - \frac{{\sqrt{3} }}{2}{\varphi _c}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{55}} = \left( {\frac{{\sqrt{3} }}{2}{\phi _s} + \frac{1}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _c} + \frac{{\sqrt{3} }}{2}{\varphi _s}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{64}} = \left( { - \frac{1}{2}{\phi _s} - \frac{{\sqrt{3} }}{2}{\theta _c}{\phi _c}} \right) {h_a} - \left( {\frac{1}{2}{\varphi _s} + \frac{{\sqrt{3} }}{2}{\varphi _c}} \right) {\theta _s}{\phi _c}b}\\ {{Q_{65}} = \left( { - \frac{{\sqrt{3} }}{2}{\phi _s} + \frac{1}{2}{\theta _c}{\phi _c}} \right) {h_a} + \left( {\frac{1}{2}{\varphi _c} - \frac{{\sqrt{3} }}{2}{\varphi _s}} \right) {\theta _s}{\phi _c}b} \end{array}} \right. . \end{aligned}$$

(42)

Appendix B

Expressions of the matrices in Eq. 35 are presented as follows:

$$\begin{aligned} \mathbf{{C}} = 3c\left[ {\begin{array}{*{20}{c}} {\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}0&{}0&{}{{\theta _c}{\theta _s}\phi _c^2a}&{}0\\ 0&{}{\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0\\ 0&{}0&{}{2\theta _s^2\phi _c^2}&{}0&{}0&{}0\\ 0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}{\theta _s^2\phi _c^2{a^2}}&{}0&{}0\\ {{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}{\theta _s^2\phi _c^2{a^2}}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\phi _s^2{a^2}} \end{array}} \right] . \end{aligned}$$

(43)

$$\begin{aligned} {\mathbf{{K}}_a} = 3k\left[ {\begin{array}{*{20}{c}} {\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}0&{}0&{}{{\theta _c}{\theta _s}\phi _c^2a}&{}0\\ 0&{}{\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0\\ 0&{}0&{}{2\theta _s^2\phi _c^2}&{}0&{}0&{}0\\ 0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}{\theta _s^2\phi _c^2{a^2}}&{}0&{}0\\ {{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}{\theta _s^2\phi _c^2{a^2}}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\phi _s^2{a^2}} \end{array}} \right] . \end{aligned}$$

(44)

$$\begin{aligned} {\mathbf{{K}}_f} = \frac{{6{k_f}}}{{{L^2}}}\left[ {\begin{array}{*{20}{c}} {1 + \theta _s^2\phi _c^2}&{}0&{}0&{}0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0\\ 0&{}{1 + \theta _s^2\phi _c^2}&{}0&{}{{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0\\ 0&{}0&{}{2\left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) }&{}0&{}0&{}0\\ 0&{}{{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}{\left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {a^2}}&{}0&{}0\\ { - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}{\left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {a^2}}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\phi _c^2{a^2}} \end{array}} \right] . \end{aligned}$$

(45)

$$\begin{aligned} {\mathbf{{N}}_c} = 3c\left[ {\begin{array}{*{20}{l}} {\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}0&{}0&{}\begin{array}{l} \left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {h_a} + \\ \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b \end{array}&{}0\\ 0&{}{\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}\begin{array}{l} - \left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {h_a} - \\ \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b \end{array}&{}0&{}0\\ 0&{}0&{}{2\theta _s^2\phi _c^2}&{}0&{}0&{}0\\ 0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}{\left( {{\varphi _c}{\theta _s}b + {\theta _c}{h_a}} \right) {\theta _s}\phi _c^2a}&{}0&{}0\\ {{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}{\left( {{\varphi _c}{\theta _s}b + {\theta _c}{h_a}} \right) {\theta _s}\phi _c^2a}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\left( {{\varphi _c}{\phi _s} + {\varphi _s}{\theta _c}{\phi _c}} \right) {\phi _s}ab} \end{array}} \right] . \end{aligned}$$

(46)

$$\begin{aligned} {\mathbf{{N}}_{ka}} = 3k\left[ {\begin{array}{*{20}{l}} {\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}0&{}0&{}\begin{array}{l} \left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {h_a} + \\ \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b \end{array}&{}0\\ 0&{}{\theta _c^2\phi _c^2 + \phi _s^2}&{}0&{}\begin{array}{l} - \left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) {h_a} - \\ \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b \end{array}&{}0&{}0\\ 0&{}0&{}{2\theta _s^2\phi _c^2}&{}0&{}0&{}0\\ 0&{}{ - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}{\left( {{\varphi _c}{\theta _s}b + {\theta _c}{h_a}} \right) {\theta _s}\phi _c^2a}&{}0&{}0\\ {{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}{\left( {{\varphi _c}{\theta _s}b + {\theta _c}{h_a}} \right) {\theta _s}\phi _c^2a}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\left( {{\varphi _c}{\phi _s} + {\varphi _s}{\theta _c}{\phi _c}} \right) {\phi _s}ab} \end{array}} \right] . \end{aligned}$$

(47)

$$\begin{aligned} {\mathbf{{N}}_{kf}} = \frac{{6{k_f}}}{{{L^2}}}\left[ {\begin{array}{*{20}{l}} {1 + \theta _s^2\phi _c^2}&{}0&{}0&{}0&{}\begin{array}{l} \left( {1 + \theta _s^2\phi _c^2} \right) {h_a} - \\ \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b \end{array}&{}0\\ 0&{}{1 + \theta _s^2\phi _c^2}&{}0&{}\begin{array}{l} \left( {{\varphi _c}{\theta _c}{\phi _c} + {\varphi _s}{\phi _s}} \right) {\theta _s}{\phi _c}b - \\ \left( {1 + \theta _s^2\phi _c^2} \right) {h_a} \end{array}&{}0&{}0\\ 0&{}0&{}{2\left( {\theta _c^2\phi _c^2 + \phi _s^2} \right) }&{}0&{}0&{}0\\ 0&{}{{\theta _c}{\theta _s}\phi _c^2a}&{}0&{}\begin{array}{l} \left( {{\varphi _c}{\theta _c}b - {\theta _s}{h_a}} \right) {\theta _c}\phi _c^2a + \\ {\varphi _c}\phi _s^2ab \end{array}&{}0&{}0\\ { - {\theta _c}{\theta _s}\phi _c^2a}&{}0&{}0&{}0&{}\begin{array}{l} \left( {{\varphi _c}{\theta _c}b - {\theta _s}{h_a}} \right) {\theta _c}\phi _c^2a + \\ {\varphi _c}\phi _s^2ab \end{array}&{}0\\ 0&{}0&{}0&{}0&{}0&{}{2\left( {{\varphi _c}{\phi _c} + {\varphi _s}{\theta _c}{\phi _s}} \right) {\phi _c}ab} \end{array}} \right] . \end{aligned}$$

(48)