1 Introduction

In the field of aerospace engineering, harsh vibration environment has become a principal factor restricting the development of spacecraft and space exploration activities [1]. The extreme dynamic environment of heavy launch vehicles is one of the main reasons for the launch failure of the entire satellite system [2]. Therefore, reducing the effects of the satellite vibration environment is critical to improving the safety and reliability of satellite launches [3].

The whole-spacecraft vibration isolation usually requires a redesign of the adaptor with vibration isolation performance, but without changing the original structure of the satellite, or introduction of vibration isolation devices between the carrier rocket and the satellite [4]. A vibration isolator installed between the adapter and the payload to isolate the vibration load has been widely studied [5]. In general, the commonly used vibration isolation systems are mainly divided into passive [6,7,8,9], active [10,11,12,13], and semi-active [14, 15] ways. Simple equipment, high reliability, and requiring no external energy are usually considered as advantages of the passive vibration isolator. However, the application of passive vibration isolator is limited to low-frequency vibration isolation because it cannot be adjusted adaptively according to the changing environment [16]. It is difficult to solve the dense frequency and multi-mode problems using the existing adaptive and semi-active control methods. In this study, an active adaptive bionic vibration isolation mechanism is proposed to solve the key problem of low frequency, dense frequency, and multi-mode vibration in the launch process of heavy launch vehicle, so as to meet the requirements of the heavy launch vehicle development.

The biomimetic vibration isolation mechanism has become a hotspot in the research field of vibration control [17]. For example, Yoon et al. proposed an impact isolator activated by woodpecker to control unnecessary high-frequency mechanical excitation [18]. Many researchers began to study the mechanism of bionic vibration isolation and made some significant improvement [19,20,21]. Jing et al. proposed a variety of different types of bio-inspired vibration isolators and successfully applied them in engineering practice to achieve good vibration isolation effect [21,22,23,24,25,26,27]. However, most of the biomimetic vibration isolators are passive, and it is necessary to develop an active adaptive bionic isolator to achieve the vibration control effect with automatic adjustment.

In this study, the generalized vibration transmissibility developed based on the NOFRFs is used to analyze the isolation performance of the whole-spacecraft system with the AVS-VI. The concept of NOFRFs was proposed by Lang and Billings [28] and has been applied to solve many engineering problems by researchers [29,30,31,32]. For example, the NOFRFs have been applied to structural damage diagnosis and nonlinear system engineering [33,34,35]. Each order of NOFRFs is a one-dimensional frequency function and can be easily displayed and analyzed. Because the solution of NOFRFs is numerical, the stability analysis cannot be performed.

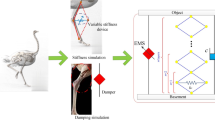
In this paper, we propose the AVS-VI for adaptive vibration reduction. Through a positive stiffness and negative stiffness structure (a parallel quadrilateral linkage implementation), we achieve the high-static–low -dynamic stiffness (HSLDS) system. Combining viscous elastic elements with the PID active controller and piezoelectric actuator acting on the nonlinear negative stiffness structure, we develop a new type of efficient adaptive variable stiffness vibration isolator.

2 The Whole-Spacecraft System with Active Variable Stiffness Vibration Isolator

Figure 1 shows the equivalent model with active variable stiffness vibration isolator (AVS-VI), where \(m_{\mathrm{a}} \) and \(m_{\mathrm{b}} \) are the masses of the satellite and adapter system, respectively; \(k_{i} \) and \(c_{i} \) (\(i \quad =\) a, b) are the coefficients of linear stiffness and damping of the whole-spacecraft system, respectively. The whole-spacecraft system can be simplified into a model with two degrees of freedom, which has been verified in our previous experiments [36]. A horizontal stiffness (HS) spring \(k_{\mathrm{d}} \) acting on the positive stiffness (PS) spring \(k_{\mathrm{c}} \) through the parallelogram linkage mechanism realizes a high-static–low-dynamic stiffness (HSLDS) system. The high-speed piezoelectric actuator is added to the negative stiffness (NS) mechanism to \(k_{\mathrm{d}} \) spring preload, \(X_{\mathrm {0}}\). The part of linkage mechanism of the negative stiffness was introduced in [37], and the PID active controller is added to the piezoelectric actuator, where the acceleration sensor is attached to the whole-spacecraft system to achieve the vibration control effect of automatic adjustment. Combined with high viscoelastic damping, a new high efficiency semi-active controller is developed. It is worth noting that the effect of gravity is ignored in this study.

Fig. 1
figure 1

Equivalent model of the whole-spacecraft system with AVS-VI

Full size image

Based on Newton’s second law, the corresponding kinetic equations of the equivalent model of whole-spacecraft system can be established as follows:

$$\begin{aligned} \begin{array}{l} m_{\mathrm{a}} \ddot{{x}}_{\mathrm{a}} +k_{\mathrm{a}} \left( {x_{\mathrm{a}} -x_{\mathrm{b}} } \right) +c_{\mathrm{a}} \left( {\dot{{x}}_{\mathrm{a}} -\dot{{x}}_{\mathrm{b}} } \right) +m_{\mathrm{a}} \ddot{{x}}_{\mathrm{d}} =0 \\ m_{\mathrm{b}} \ddot{{x}}_{\mathrm{b}} +k_{\mathrm{a}} \left( {x_{\mathrm{b}} -x_{\mathrm{a}} } \right) +c_{\mathrm{a}} \left( {\dot{{x}}_{\mathrm{b}} -\dot{{x}}_{\mathrm{a}} } \right) +k_{\mathrm{b}} x_{\mathrm{b}} +c_{\mathrm{b}} \dot{{x}}_{\mathrm{b}} +c_{\mathrm{c}} \dot{{x}}_{\mathrm{b}} +\left( {k_{\mathrm{c}} -\frac{2k_{\mathrm{d}} }{L}X_{0} } \right) x_{\mathrm{b}} +m_{\mathrm{b}} \ddot{{x}}_{\mathrm{d}} =0 \\ \end{array} \end{aligned}$$
(1)

where \(x_{i} \) (\(i \quad =\) a, b) express the displacement of the whole-spacecraft system. \(c_{\mathrm{c}} \) is the coefficient of viscoelastic damping, and L is the length of the NS parallelogram linkage mechanism.

$$\begin{aligned} X_{0} =-\left( {K_{0} x_{\mathrm{a}} +K_{1} \dot{{x}}_{\mathrm{a}} +K_{2} \ddot{{x}}_{\mathrm{a}} } \right) \end{aligned}$$
(2)

where \(K_{i} \quad (i \quad =\) 0, 1, 2) represent the coefficients of PID active controller, and \(x_{\mathrm{d}} \) is the acceleration excitation [38].

$$\begin{aligned} \begin{array}{l} x_{\mathrm{d}} =\frac{A_{\mathrm{d}} }{\left( {2\pi f} \right) ^{2}}\sin \left( {2\pi ft} \right) \\ \dot{{x}}_{\mathrm{d}} =\frac{A_{\mathrm{d}} }{2\pi f}\cos \left( {2\pi ft} \right) \\ \ddot{{x}}_{\mathrm{d}} =-A_{\mathrm{d}} \sin \left( {2\pi ft} \right) \\ \end{array} \end{aligned}$$
(3)

3 Analysis Method on Account of the Transmissibility of NOFRFs

In the frequency domain, the output spectra of a nonlinear system \(X\left( {j\omega } \right) _{\mathrm{AVS-VI}} \) can be expressed as the sum of the n-th order output frequency response [39].

$$\begin{aligned} X\left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} =\sum \limits _{n=1}^N {X_{n} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} } \end{aligned}$$
(4)

where N is the maximum order of the nonlinear system

$$\begin{aligned} X_{n} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} =\frac{1}{2^{n}}\sum \limits _{\omega _{k_{1} } +\cdots +\omega _{k_{n} } =\omega } {H_{n} \left( {\hbox {j}\omega _{k_{1} } ,\ldots ,\hbox {j}\omega _{k_{n} } } \right) _{\mathrm{AVS-VI}} } A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{1} } } \right) \cdots A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{n} } } \right) \end{aligned}$$
(5)

and

$$\begin{aligned} A_{\mathrm{d}} \left( {\hbox {j}\omega } \right) =\left\{ {\begin{array}{ll} \left| {A_{\mathrm{d}} } \right| \hbox {e}^{\hbox {jsign}\left( k \right) } &{} \hbox {if }\omega \in \left\{ {k\omega _{f} ,k=\pm 1} \right\} \\ 0 &{} \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$
(6)

where \(X\left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} \) and \(A_{\mathrm{d}} \left( {\hbox {j}\omega } \right) \) describe the output and input spectra of the nonlinear system, respectively, and \(H_{n} \left( {\hbox {j}\omega _{k_{1} } ,\ldots ,\hbox {j}\omega _{k_{n} } } \right) _{\mathrm{AVS-VI}} \) represents the n-th order generalized frequency response functions (GFRFs) of the nonlinear system [39].

A new concept known as the NOFRFs, which over the GFRFs lies in their single dimension order functions, was presented by Lang and Billings [28]. Based on the acceleration excitation, this concept can be mathematically described as

$$\begin{aligned} G_{n}^{H} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} =\frac{\frac{1}{2^{n}}\sum \limits _{\omega _{k_{1} } +\cdots +\omega _{k_{n} } =\omega } {H_{n} \left( {\hbox {j}\omega _{k_{1} } ,\ldots ,\hbox {j}\omega _{k_{n} } } \right) _{\mathrm{AVS-VI}} } A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{1} } } \right) \cdots A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{n} } } \right) }{\frac{1}{2^{n}}\sum \limits _{\omega _{k_{1} } +\cdots +\omega _{k_{n} } =\omega } {A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{1} } } \right) \cdots A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{n} } } \right) } } (n=1,\ldots ,N) \end{aligned}$$
(7)

with

$$\begin{aligned} A_{\mathrm{d}_{{n}}} \left( {\hbox {j}\omega } \right) =\frac{1}{2^{n}}\sum \limits _{\omega _{k_{1} } +\cdots +\omega _{k_{n} } =\omega } {A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{1} } } \right) \cdots A_{\mathrm{d}} \left( {\hbox {j}\omega _{k_{n} } } \right) } \ne 0 \end{aligned}$$
(8)

and rewrite the n-th order output spectra of nonlinear system as:

$$\begin{aligned} X\left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} =\sum \limits _{n=1}^N {X_{n} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} } =\sum \limits _{n=1}^N {G_{n}^{H} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} A_{\mathrm{d}_{n} } \left( {\hbox {j}\omega } \right) } \end{aligned}$$
(9)

In Eq. (9), \(G_{n}^{H} \left( {\hbox {j}\omega } \right) _{\mathrm{AVS-VI}} \) express the n-th order NOFRFs of the nonlinear system, and \(A_{\mathrm{d}_{n} } \left( {\hbox {j}\omega } \right) \) can be described as the Fourier transform of \(x_{\mathrm{d}}^{n}\left( t \right) \) [32].

$$\begin{aligned} A_{\mathrm{d}_{n}} \left( {\hbox {j}\omega } \right) =\hbox {FFT}\left[ {x_{\mathrm{d}}^{n}\left( t \right) } \right] \end{aligned}$$
(10)

The NOFRFs of the nonlinear system is equal to the GFRFs of the system [40].

$$\begin{aligned} \begin{array}{l} G_{n}^{H} \left( {\hbox {j}\left( {-n+2k} \right) \omega _{f} } \right) _{\mathrm{AVS-VI}} =\frac{\frac{1}{2^{n}}H_{n} (\overbrace{\hbox {j}\omega _{f} ,\ldots ,\hbox {j}\omega _{f} }^k,\overbrace{-\hbox {j}\omega _{f} ,\ldots ,-\hbox {j}\omega _{f} }^{n-k})_{\mathrm{AVS-VI}} C_{n}^{k} \left| {A_{\mathrm{d}} } \right| ^{n}\hbox {e}^{{\mathrm{j}}\left( {-n+2k} \right) }}{\frac{1}{2^{n}}C_{n}^{k} \left| {A_{\mathrm{d}} } \right| ^{n}\hbox {e}^{{\mathrm{j}}\left( {-n+2k} \right) }} \\ =H_{n} (\overbrace{\hbox {j}\omega _{f} ,\ldots ,\hbox {j}\omega _{f} }^k,\overbrace{-\hbox {j}\omega _{f} ,\ldots ,-\hbox {j}\omega _{f} }^{n-k})_{\mathrm{AVS-VI}} \\ \end{array} \end{aligned}$$
(11)

and the input spectrum can be simplified as

$$\begin{aligned} A_{\mathrm{d}_{n} } \left( {\hbox {j}\left( {-n+2k} \right) \omega _{f} } \right) =\frac{1}{2^{n}}C_{n}^{k} \left| {A_{\mathrm{d}} } \right| ^{n}\hbox {e}^{\text{ j }\left( {-n+2k} \right) } \end{aligned}$$
(12)

Based on the output frequency response, the first-order harmonic of NOFRFs can be expressed as [41]:

$$\begin{aligned} \begin{aligned} X\left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}}&=X_{1} \left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}} +X_{3} \left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}} +\cdots \\&=G_{1} \left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}} A_{\mathrm{d}_{1} } \left( {\hbox {j}\omega _{f} } \right) +G_{3} \left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}} A_{\mathrm{d}_{3} } \left( {\hbox {j}\omega _{f} } \right) +\cdots \\ \end{aligned} \end{aligned}$$
(13)

In most cases, when the system reaches the fourth-order nonlinearity, the analysis based on NOFRFs can meet the accuracy requirements. The fourth-order output frequency response of the nonlinear system can be expressed as [42]:

$$\begin{aligned} X\left( {\hbox {j}\omega _{f} } \right) _{\mathrm{AVS-VI}}= & {} G_{1}^{H} \left( {\hbox {j}\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{1} } \left( {\hbox {j}\omega _{f} } \right) +G_{3}^{H} \left( {\hbox {j}\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{3} } \left( {\hbox {j}\omega _{f} } \right) \end{aligned}$$
(14)
$$\begin{aligned} X\left( {\hbox {j}2\omega _{f} } \right) _{\mathrm{AVS-VI}}= & {} G_{2}^{H} \left( {\hbox {j}2\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{2} } \left( {\hbox {j}2\omega _{f} } \right) +G_{4}^{H} \left( {\hbox {j}2\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{4}} \left( {\hbox {j}2\omega _{f} } \right) \end{aligned}$$
(15)
$$\begin{aligned} X\left( {\hbox {j}3\omega _{f} } \right) _{\mathrm{AVS-VI}}= & {} G_{3}^{H} \left( {\hbox {j}3\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{3} } \left( {\hbox {j}3\omega _{f} } \right) \end{aligned}$$
(16)
$$\begin{aligned} X\left( {\hbox {j}4\omega _{f} } \right) _{\mathrm{AVS-VI}}= & {} G_{4}^{H} \left( {\hbox {j}4\omega _{f} } \right) _{{\mathrm{AVS-VI}} } A_{\mathrm{d}_{4} } \left( {\hbox {j}4\omega _{f} } \right) \end{aligned}$$
(17)

The generalized vibration transmissibility is obtained by the root-mean-square processing of the fourth-order harmonics of the nonlinear system [43]:

$$\begin{aligned} \hbox {Tran}_{x} =\frac{\sqrt{\left\| {X(\hbox {j}\omega _{f} )} \right\| _{^{\hbox {AVS-VI}}}^{2} +\left\| {X(\hbox {j}2\omega _{f} )} \right\| _{^{\hbox {AVS-VI}}}^{2} +\left\| {X(\hbox {j}3\omega _{f} )} \right\| _{^{\hbox {AVS-VI}}}^{2} +\left\| {X(\hbox {j}4\omega _{f} )} \right\| _{^{\hbox {AVS-VI}}}^{2} } }{2A_{\mathrm{d}} } \end{aligned}$$
(18)

4 Effects of AVS-VI on Account of the Transmissibility of NOFRFs

In this section, in order to analyze the effect of vibration reduction in the whole-spacecraft system, the generalized vibration transmissibility of NOFRFs is used for calculating the whole-spacecraft system with AVS-VI. The parameters and values of an equivalent model of the whole-spacecraft system with AVS-VI are presented in Table 1, which are calculated from [36, 37].

Table 1 Parameters of the whole-spacecraft system and the AVS-VI
Full size table

The influence of higher harmonics should not be neglected due to the nonlinearity of system in practical engineering. Therefore, this paper adopts the generalized vibration transmissibility of NOFRFs to analyze the whole-spacecraft system. The generalized vibration transmissibility of NOFRFs considers the higher harmonics to evaluate the isolation effect of AVS-VI. Figure. 2 compares the transmissibility of NOFRFs of the whole-spacecraft system with AVS-VI with different acceleration excitations. It can be seen that the transmissibility amplitude of the first-order formant decreases with the increase in acceleration excitation \(A_{\mathrm {d}}\) because of the adaptive vibration control of AVS-VI. The whole-spacecraft system presents soft nonlinear characteristics, which can be seen from Fig. 2b.

Fig. 2
figure 2

Transmissibility of system and enlargement under different acceleration excitations \(A_{\mathrm {d}}\)

Full size image

Figure 3a,b compares the vibration reduction effects of isolator without and with only damping \(c_{\mathrm {c}}\), and with AVS-VI based on the transmissibility of NOFRFs under the acceleration excitation of \(A_{\mathrm {d}}= 0.3\,\hbox {g}\). It can be seen that the vibration suppression effect of the whole-spacecraft system with AVS-VI is obviously better than the whole-spacecraft system with only damping \(c_{\mathrm {c}}\). The vibration reduction effects of PS-NS and AVS-VI are examined by Fig. 3c,d under the acceleration excitation of \(A_{\mathrm {d}}=\)0.4 g. It can be seen that the vibration suppression effect of the whole-spacecraft system with AVS-VI is obviously better than the whole-spacecraft system with PS-NS in terms of the first-order formant, while the transmissibility amplitudes of the second-order formant are almost unchanged.

Fig. 3
figure 3

Transmissibility response curves of \(x_{\mathrm {a}}\): without and with only damping \(c_{\mathrm {c}}\), and with AVS-VI (a, b), with PS-NS and with AVS-VI (c, d)

Full size image

In order to prove that AVS-VI can generate fast and large adaptive dynamic stiffness control. Figure 4 shows the transmissibility amplitudes curves of \(x_{\mathrm {a}}\) with different acceleration excitations of \(A_{\mathrm {d}}=0.1\) g, 0.2 g, 0.3 g, 0.4 g, and 0.5 g, respectively. It can be seen that with different acceleration excitation, the transmissibility amplitudes of the first-order formant of the whole-spacecraft system also change, while the transmissibility amplitudes of the second-order formant are almost unchanged. Table 2 details the decreases of transmissibility amplitudes at the first-order formant without and with AVS-VI under different acceleration excitations. It can be concluded that under different acceleration excitations, the decrease in vibration isolation of AVS-VI is up to above 65%, and the natural frequency of the whole-spacecraft system also changes.

Fig. 4
figure 4

Transmissibility amplitude curves of \(x_{\mathrm {a}}\) with different acceleration excitations \(A_{\mathrm {d}}\)

Full size image
Table 2 Transmissibility amplitudes at the first-order formant with different acceleration excitations
Full size table

5 Parameter Analysis Based on the Transmissibility

Parameter changes are crucial in the structure design of vibration suppression. In order to study the effects of AVS-VI parameters on the generalized transmissibility of the whole-spacecraft system, the influence of each parameter on the vibration reduction performance is investigated by changing one parameter with other parameters unchanged. Figure 5 shows the transmissibility amplitudes curves of the whole-spacecraft system with different parameters, i.e., damping \(c_{\mathrm {c}}\), positive stiffness \(k_{\mathrm {c}}\), and negative stiffness \(k_{\mathrm {d}}\), of AVS-VI under \(A_{\mathrm {d}} = 0.2\) g, respectively. It can be seen that the transmissibility amplitudes of the first-/second-order formant clearly decrease with the increase in damping \(c_{\mathrm {c}}\), and positive stiffness \(k_{\mathrm {c}}\), respectively. As the negative stiffness \(k_{\mathrm {d}}\) increases, the transmissibility amplitudes of the first-order formant clearly decrease, but those of the second-order formant are almost un-changed.

Fig. 5
figure 5

Transmissibility amplitude curves of \(x_{\mathrm {a}}\) with different parameters changing: damping \(c_{\mathrm {c}}\), positive stiffness \(k_{\mathrm {c}}\), negative stiffness \(k_{\mathrm {d}}\)

Full size image

Figure 6 shows the transmissibility amplitudes curves of the whole-spacecraft system with different active controller parameters P, I, and D. It can be seen that as the active controller P and I increase, the transmissibility amplitudes of the first-order formant clearly decrease, those of the second-order formant have no clear change, and the natural frequency of the whole-spacecraft system obviously decreases.

Fig. 6
figure 6

Transmissibility amplitude curves of the first-/second-order formant of \(x_{\mathrm {a}}\) with different active controller parameters, P, I, and D

Full size image
Fig. 7
figure 7

Percentage of energy absorption of AVS-VI under different parameters: \(k_{\mathrm {d}}\) (a), \(k_{\mathrm {c}}\) (b), \(c_{\mathrm {c}}\) (c), P (d), I (e), and D (f)

Full size image

6 Energy Absorption Analysis

In order to examine the effectiveness of AVS-VI in reducing the excessive vibration from the whole-spacecraft system, the percentage of energy absorption \(\eta _{\mathrm{AVS-VI}} \left( t \right) \) is proposed, which can be expressed as

$$\begin{aligned} \eta _{\mathrm{AVS-VI}} \left( t \right)= & {} \frac{E_{\mathrm{Unprotected}} \left( t \right) -E_{\mathrm{AVS-VI}} \left( t \right) }{E_{\mathrm{Unprotected}} \left( t \right) }\times 100\% \end{aligned}$$
(19)
$$\begin{aligned} E_{\mathrm{a}} \left( t \right)= & {} \frac{1}{2}m_{\mathrm{a}} \dot{{x}}_{\mathrm{a}}^{2} +\frac{1}{2}k_{\mathrm{a}} \left( {x_{\mathrm{a}} -x_{\mathrm{b}} } \right) ^{2}+c_{\mathrm{a}} \int _0^t {\left[ {\left( {\dot{{x}}_{\mathrm{a}} -\dot{{x}}_{\mathrm{b}} } \right) } \right] } \hbox {d}t \end{aligned}$$
(20)
$$\begin{aligned} E_{\mathrm{b}} \left( t \right)= & {} \frac{1}{2}m_{\mathrm{b}} \dot{{x}}_{\mathrm{b}}^{2} +\frac{1}{2}k_{\mathrm{b}} \left( {x_{\mathrm{b}} -x_{\mathrm{d}} } \right) ^{2}+c_{\mathrm{b}} \int _0^t {\left[ {\left( {\dot{{x}}_{\mathrm{b}} -\dot{{x}}_{\mathrm{d}} } \right) } \right] } \hbox {d}t \end{aligned}$$
(21)
$$\begin{aligned} E_{\mathrm{total}} \left( t \right)= & {} E_{\mathrm{a}} \left( t \right) \hbox {+}E_{\mathrm{b}} \left( t \right) \end{aligned}$$
(22)

where \(E_{i} \left( t \right) \) (\(i \quad =\) a, b) represent the energy absorbed by the satellite and adapter system, respectively, while \(\frac{1}{2}m_{\mathrm{a}} \dot{{x}}_{\mathrm{a}}^{2} \), \(\frac{1}{2}k_{\mathrm{a}} \left( {x_{\mathrm{a}} -x_{\mathrm{b}} } \right) ^{2}\), and \(c_{\mathrm{a}} \int _0^t {\left( {\dot{{x}}_{\mathrm{a}} -\dot{{x}}_{\mathrm{b}} } \right) } \hbox {d}t\) represent the kinetic, potential, and dissipated energies of damping of the satellite system, respectively.

The effects of different parameters of the AVS-VI, i.e., horizontal stiffness \(k_{\mathrm {d}}\), positive stiffness \(k_{\mathrm {c}}\), viscoelastic damping \(c_{\mathrm {c}}\), active controller parameters P, I, and D on the percentage of energy absorption are examined by Fig. 7. It can be seen that the percentage of energy absorption of the first-order formant clearly decreases as the horizontal stiffness \(k_{\mathrm {d}}\), positive stiffness \(k_{\mathrm {c}}\), viscoelastic damping \(c_{\mathrm {c}}\), active controller parameters P, I, and D increase, and the influences of horizontal stiffness \(k_{\mathrm {d}}\) and stiffness \(k_{\mathrm {c}}\) are more distinct than that of viscoelastic damping \(c_{\mathrm {c}}\). Therefore, from the energy perspective, the AVS-VI also has a good vibration suppression effect and fast adaptive dynamic stiffness control.

7 Conclusions

In this study, a novel AVS-VI is proposed to reduce excessive vibration of the whole-spacecraft isolation system. The whole-spacecraft system is described as two-degree-of-freedom system, and the vibration isolation device composed of a horizontal stiffness spring, positive stiffness spring, parallelogram linkage mechanism, piezoelectric actuator, acceleration sensor, viscoelastic damping, and PID active controller is considered. The generalized vibration transmissibility of NOFRFs and the energy absorption rate are used to analyze and design the whole-spacecraft system with AVS-VI. The following conclusions are drawn from the investigation:

  1. (1)

    The design and optimization of AVS-VI are completed in the design stage, which can realize a fast and large dynamic stiffness control of vibration isolator according to the changing external excitations.

  2. (2)

    The AVS-VI is effective in reducing the extravagant vibration of the whole-spacecraft system. The decrease in vibration isolation of the AVS-VI is up to above 65% under different acceleration excitations.

  3. (3)

    The isolation performance of the whole-spacecraft system is assessed by the transmissibility of NOFRFs. Compared with the vibration reduction in simple viscoelastic damping and PS-NS, the AVS-VI shows a flexible and better isolation performance in the vibration isolation of the whole-spacecraft system.

  4. (4)

    With suitably adjusted parameters such as positive stiffness, damping, active controller PID coefficient, and negative stiffness, the vibration reduction effects of AVS-VI can be improved.