Skip to main content
SpringerLink
Log in

Estimation of Torque Variation due to Torsional Vibration in a Rotating System Using a Kalman Filter-Based Approach

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

It is observed that the motor-running machines that the fluctuation in power supply causes torsional vibration in the rotating systems. Estimation of torque helps in efficient operation of machines with limited sensors. Measurement noise and the effect of exogenous inputs in torque estimation are main problems.

Methods

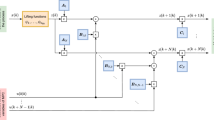
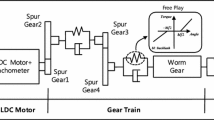
Here, authors have used a Kalman filter-based input estimation technique for indirect estimation of torque variation in a rotating system. Two mathematical models of the rotating system are used in the present work. The estimation becomes unstable when degrees of freedom is more than the number of parameters to be estimated. For such scenario a modified approach, that consists of using a penalty is proposed. Experimental measurements are performed on a drivetrain to verify the proposed technique.

Results

Results are presented for different braking torques. It is found that the estimated torque is close to the measured torque. The effect of the penalty on estimation is studied. A stability analysis is performed with different values of penalty values. Finally, a sensitivity analysis is performed to check for the robustness of the algorithm.

Conclusions

It is found that the estimated torque converges to the measured torque with a higher penalty value. The estimator is found robust as the estimated torque matches well with the measured torque for different test cases. Sensitivity analysis shows that for more accurate estimation, accuracy of model stiffness is of the essence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Licari J, Ugalde-Loo CE, Ekanayake JB, Jenkins N (2012) Damping of torsional vibrations in a variable-speed wind turbine. IEEE Trans Energy Convers 28(1):172–180. https://doi.org/10.1109/tec.2012.2224868

    Article  Google Scholar 

  2. Mohanty AR (2014) Machinery condition monitoring: Principles and practices. CRC Press, Boca Raton

    Book  Google Scholar 

  3. Murakami T, Yu F, Ohnishi K (1993) Torque sensorless control in multidegree-of-freedom manipulator. IEEE Trans Industr Electron 40(2):259–265. https://doi.org/10.1109/41.222648

    Article  Google Scholar 

  4. Liu Y, Zhu ZQ, Howe D (2006) Instantaneous torque estimation in sensorless direct-torque-controlled brushless DC motors. IEEE Trans Ind Appl 42(5):1275–1283. https://doi.org/10.1109/IAS.2005.1518743

    Article  Google Scholar 

  5. Kalman RE (1960) A new approach to linear filtering and prediction problems. Trans ASME J Basic Eng 82:35–45. https://doi.org/10.1115/1.3662552

    Article  MathSciNet  Google Scholar 

  6. Chui CK, Chen G (2017) Kalman filtering. Springer International Publishing. https://doi.org/10.1007/978-3-540-87849-0

    Book  MATH  Google Scholar 

  7. Khanam S, Dutt JK, Tandon N (2014) Extracting rolling element bearing faults from noisy vibration signal using Kalman filter. J Vib Acoust 10(1115/1):4026946

    Google Scholar 

  8. Shrivastava A, Mohanty AR (2018) Estimation of single plane unbalance parameters of a rotor-bearing system using Kalman filtering based force estimation technique. J Sound Vib 418:184–199. https://doi.org/10.1016/j.jsv.2017.11.020

    Article  Google Scholar 

  9. Shrivastava A, Mohanty AR (2019) Identification of unbalance in a rotor-bearing system using Kalman filter–based input estimation technique. J Vib Control 26(11–12):1081–1091. https://doi.org/10.1177/1077546319891642

    Article  MathSciNet  Google Scholar 

  10. Shrivastava A, Mohanty AR (2019) Identification of unbalance in a rotor system using a joint input-state estimation technique. J Sound Vib 442:414–427. https://doi.org/10.1016/j.jsv.2018.11.019

    Article  Google Scholar 

  11. Song X, Zhai H, Liang D (2019) Dynamic load identification and displacement prediction based on FBG for a cantilever beam. J Vib Eng Technol 7:131–137. https://doi.org/10.1007/s42417-019-00091-7

    Article  Google Scholar 

  12. Lee SC , Ahn HS (2010) Sensorless torque estimation using adaptive Kalman filter and disturbance estimator. In: Proceedings of 2010 IEEE/ASME International Conference on mechatronic and embedded systems and applications, Qingdao, July, 2010, pp 87–92. IEEE. https://doi.org/10.1109/MESA.2010.5552094

  13. Shrivastava A, Mohanty AR (2019) Kalman filter-based force estimation in a clamped plate using reduced order model and noisy measurements. Inverse Probl Sci Eng 27(8):1170–1193. https://doi.org/10.1080/17415977.2018.1503657

    Article  MathSciNet  MATH  Google Scholar 

  14. Chan YT, Hu AGC, Plant JB (1979) A Kalman filter based tracking scheme with input estimation. IEEE Trans Aerosp Electron Syst 2:237–244. https://doi.org/10.1109/TAES.1979.308710

    Article  Google Scholar 

  15. Tuan PC, Ji CC, Fong LW, Huang WT (1996) An input estimation approach to on-line two-dimensional inverse heat conduction problems. Numer Heat Transfer 29(3):345–363. https://doi.org/10.1080/10407799608914986

    Article  Google Scholar 

  16. Ma CK, Tuan PC, Lin DC, Liu CS (1998) A study of an inverse method for the estimation of impulsive loads. Int J Syst Sci 29(6):663–672. https://doi.org/10.1080/00207729808929559

    Article  Google Scholar 

  17. Xie C, Hua L, Han X et al (2018) Analytical formulas for gear body-induced tooth deflections of spur gears considering structure coupling effect. Int J Mech Sci 148(05):174–190. https://doi.org/10.1016/j.ijmecsci.2018.08.022

    Article  Google Scholar 

  18. Mohammad KS, Worden K, Tomlinson GR (1992) Direct parameter estimation for linear and non-linear structures. J Sound Vib 152(3):471–499. https://doi.org/10.1016/0022-460X(92)90482-D

    Article  MATH  Google Scholar 

Download references

Funding

No funding was received to assist with the preparation of this manuscript.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur, 721302, India

    Satyajit Mahapatra, Akash Shrivastava, Biswajit Sahoo & Amiya Ranjan Mohanty

Authors
  1. Satyajit Mahapatra
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Akash Shrivastava
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Biswajit Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Amiya Ranjan Mohanty
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Satyajit Mahapatra.

Ethics declarations

Conflict of interests

The authors have no relevant financial or non-financial interests to disclose. The authors have no competing interests to declare that are relevant to the content of this article. All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript. The authors have no financial or proprietary interests in any material discussed in this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mahapatra, S., Shrivastava, A., Sahoo, B. et al. Estimation of Torque Variation due to Torsional Vibration in a Rotating System Using a Kalman Filter-Based Approach. J. Vib. Eng. Technol. 11, 1939–1950 (2023). https://doi.org/10.1007/s42417-022-00681-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00681-y

Keywords

Search

Navigation