Skip to main content
SpringerLink
Log in

Vibration Reduction for an Asymmetric Elastically Supported Beam Coupled to an Inertial Nonlinear Energy Sink

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose

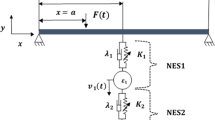
The present paper addresses the vibration reduction for an elastic beam with an asymmetric boundary condition that is clamped at one end and elastically supported at the other end. An inertial nonlinear energy sink (NES) is installed on the elastic support end to suppress the beam's vibration.

Methods

The nonlinear terms introduced by the NES are transferred as the external excitations acting on the beam. The motion equations of the beam with an NES are derived according to Hamilton's principle and the Galerkin truncation method. The beam's natural frequencies and corresponding mode shapes are analytically obtained and verified with the results of the finite element method. The responses of the beam are numerically and analytically solved by the fourth order Runge–Kutta method and the harmonic balance method (HBM), respectively.

Results

The good agreement among the results validates the present derivation of the theoretical model and numerical solutions. The steady-state responses of the beam with and without the NES are compared and analyzed in the time domain.

Conclusions

The results demonstrate that adding the inertial enhanced NES can effectively reduce the resonance amplitude of the beam. Furthermore, a parametric optimization is conducted for NES to improve its performance. The results of this paper contribute to the application of NESs on the boundaries of elastic structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Tigli OF (2012) Optimum vibration absorber (tuned mass damper) design for linear damped systems subjected to random loads. J Sound Vib 331:3035–3049

    Article  Google Scholar 

  2. Davis CL, Lesieutre GA (2000) An actively tuned solid-state vibration absorber using capacitive shunting of piezoelectric stiffness. J Sound Vib 232:601–617

    Article  Google Scholar 

  3. Roberson RE (1952) Synthesis of a nonlinear dynamic vibration absorber. J Franklin Inst 254:205–220

    Article  MathSciNet  Google Scholar 

  4. Vakakis AF (2001) Inducing passive nonlinear energy sinks in vibrating systems. J Vib Acoust 123:324–332

    Article  Google Scholar 

  5. Gourdon E, Lamarque CH (2006) Nonlinear energy sink with uncertain parameters. J Comput Nonlinear Dyn 1:187–195

    Article  Google Scholar 

  6. Xue JR, Zhang YW, Ding H, Chen LQ (2019) Vibration reduction evaluation of a linear system with a nonlinear energy sink under a harmonic and random excitation. Appl Math Mech 41:1–14

    Article  MathSciNet  MATH  Google Scholar 

  7. H. Y. Chen, X. Y. Mao, H. Ding and L. Q. Chen, Elimination of multimode resonances of composite plate by inertial nonlinear energy sinks, Mechanical Systems and Signal Processing 135, 2020.

  8. Vakakis AF, Manevitch LI, Gendelman O, Bergman L (2003) Dynamics of linear discrete systems connected to local, essentially nonlinear attachments. J Sound Vib 264:559–577

    Article  Google Scholar 

  9. Ding H, Chen LQ (2020) Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dyn 100:3061–3107

    Article  Google Scholar 

  10. X. Li, K. Liu, L. Xiong and L. Tang, Development and validation of a piecewise linear nonlinear energy sink for vibration suppression and energy harvesting, Journal of Sound and Vibration 503, 2021.

  11. Wei Y, Wei S, Zhang Q, Dong X, Peng Z, Zhang W (2019) Targeted energy transfer of a parallel nonlinear energy sink. Appl Math Mech 40:621–630

    Article  MathSciNet  Google Scholar 

  12. Blanchard A, Bergman LA, Vakakis AF (2019) Vortex-induced vibration of a linearly sprung cylinder with an internal rotational nonlinear energy sink in turbulent flow. Nonlinear Dyn 99:593–609

    Article  MATH  Google Scholar 

  13. Zang J, Chen LQ (2017) Complex dynamics of a harmonically excited structure coupled with a nonlinear energy sink. Acta Mech Sin 33:801–822

    Article  MathSciNet  MATH  Google Scholar 

  14. Grinberg I, Lanton V, Gendelman OV (2012) Response regimes in linear oscillator with 2DOF nonlinear energy sink under periodic forcing. Nonlinear Dyn 69:1889–1902

    Article  MathSciNet  Google Scholar 

  15. Tsakirtzis S, Panagopoulos PN, Kerschen G, Gendelman O, Vakakis AF, Bergman LA (2006) Complex dynamics and targeted energy transfer in linear oscillators coupled to multi-degree-of-freedom essentially nonlinear attachments. Nonlinear Dyn 48:285–318

    Article  MathSciNet  MATH  Google Scholar 

  16. Ture Savadkoohi A, Vaurigaud B, Lamarque CH, Pernot S (2011) Targeted energy transfer with parallel nonlinear energy sinks, part II: theory and experiments, Nonlinear Dynamics 67: 37-46

  17. Nguyen TA, Pernot S (2011) Design criteria for optimally tuned nonlinear energy sinks—part 1: transient regime. Nonlinear Dyn 69:1–19

    Article  Google Scholar 

  18. Sun M, Chen JE (2018) Dynamics of nonlinear primary oscillator with nonlinear energy sink under harmonic excitation: effects of nonlinear stiffness. Math Probl Eng 1–13:2018

    MathSciNet  MATH  Google Scholar 

  19. Georgiades F, Vakakis AF (2007) Dynamics of a linear beam with an attached local nonlinear energy sink. Commun Nonlinear Sci Numer Simul 12:643–651

    Article  MATH  Google Scholar 

  20. Samani FS, Pellicano F (2009) Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers. J Sound Vib 325:742–754

    Article  Google Scholar 

  21. Zhang YW, Yuan B, Fang B, Chen LQ (2016) Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink. Nonlinear Dyn 87:1159–1167

    Article  Google Scholar 

  22. Mamaghani AE, Khadem SE, Bab S (2016) Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dyn 86:1761–1795

    Article  MATH  Google Scholar 

  23. Ahmadabadi ZN, Khadem SE (2012) Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech Mach Theory 50:134–149

    Article  Google Scholar 

  24. Parseh M, Dardel M, Ghasemi MH (2015) Investigating the robustness of nonlinear energy sink in steady state dynamics of linear beams with different boundary conditions. Commun Nonlinear Sci Numer Simul 29:50–71

    Article  MathSciNet  MATH  Google Scholar 

  25. Kani M, Khadem SE, Pashaei MH, Dardel M (2015) Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn 83:1–22

    Article  MathSciNet  Google Scholar 

  26. Zhang YW, Hou S, Zhang Z, Zang J, Ni ZY, Teng YY, Chen LQ (2020) Nonlinear vibration absorption of laminated composite beams in complex environment. Nonlinear Dyn 99:2605–2622

    Article  Google Scholar 

  27. Zhang WX, Chen JE (2020) Influence of geometric nonlinearity of rectangular plate on vibration reduction performance of nonlinear energy sink. J Mech Sci Technol 34:3127–3135

    Article  Google Scholar 

  28. Smith MC (2002) Synthesis of mechanical networks: the inerter. IEEE Trans Autom Control 47:1648–1662

    Article  MathSciNet  MATH  Google Scholar 

  29. Li Y, Jiang JZ, Neild S (2017) Inerter-based configurations for main-landing-gear shimmy suppression. J Aircr 54:684–693

    Article  Google Scholar 

  30. D. Xin, Y. Liu and Z. Michael, Application of inerter to aircraft landing gear suspension, in: Control Conference, 2015.

  31. Shen YJ, Chen L, Yang XF, Shi DH, Yang J (2016) Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. J Sound Vib 361:148–158

    Article  Google Scholar 

  32. Giaralis A, Petrini F (2017) Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter, J Struct Eng 143.

  33. Zhang Z, Lu ZQ, Ding H, Chen LQ (2019) An inertial nonlinear energy sink. J Sound Vib 450:199–213

    Article  Google Scholar 

  34. Zhang Z, Ding H, Zhang YW, Chen LQ (2021) Vibration suppression of an elastic beam with boundary inerter-enhanced nonlinear energy sinks. Acta Mech Sin 37:387–401

    Article  MathSciNet  Google Scholar 

  35. Ding H, Zhu MH, Chen LQ (2018) Nonlinear vibration isolation of a viscoelastic beam. Nonlinear Dyn 92:325–349

    Article  Google Scholar 

  36. Ding H, Dowell EH, Chen LQ (2018) Transmissibility of bending vibration of an elastic beam, J Vib Acoustics 140.

  37. Mao XY, Ding H, Chen LQ (2017) Vibration of flexible structures under nonlinear boundary conditions, J Appl Mech 84.

  38. Ye SQ, Mao XY, Ding H, Ji JC, Chen LQ (2020) Nonlinear vibrations of a slightly curved beam with nonlinear boundary conditions, International Journal of Mechanical Sciences 168.

  39. Dill EH (2006) Continuum mechanics: elasticity, plasticity, viscoelasticity, CRC press.

  40. Ding H, Lu ZQ, Chen LQ (2019) Nonlinear isolation of transverse vibration of pre-pressure beams. J Sound Vib 442:738–751

    Article  Google Scholar 

  41. Ding H, Ji J, Chen LQ (2019) Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mech Syst Signal Process 121:675–688

    Article  Google Scholar 

  42. Chen M, Papageorgiou C, Scheibe F, Wang FC, Smith M (2009) The missing mechanical circuit element. IEEE Circuits Syst Mag 9:10–26

    Article  Google Scholar 

Download references

Acknowledgements

The work described in this paper was fully supported by the National Natural Science Foundation of China (Grant No. 12102015), the General Program of Science and Technology Development Project of Beijing Municipal Education Commission (Project No. KM202110005030), and grants from the Fundamental Research Program of Shenzhen Municipality (Project No: JCYJ20170818094653701).

Author information

Authors and Affiliations

  1. Faculty of Materials and Manufacturing, Beijing University of Technology, Beijing, 100124, People’s Republic of China

    Wei Zhang, Zhi-Yong Chang & Jie Chen

  2. Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures, Beijing, 100124, People’s Republic of China

    Wei Zhang, Zhi-Yong Chang & Jie Chen

  3. Architecture and Civil Engineering Research Center, City University of Hong Kong Shenzhen Research Institute, Shenzhen, 518057, People’s Republic of China

    Jie Chen

Authors
  1. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhi-Yong Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jie Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jie Chen.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, W., Chang, ZY. & Chen, J. Vibration Reduction for an Asymmetric Elastically Supported Beam Coupled to an Inertial Nonlinear Energy Sink. J. Vib. Eng. Technol. 11, 1711–1723 (2023). https://doi.org/10.1007/s42417-022-00666-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00666-x

Keywords

Search

Navigation