Skip to main content
SpringerLink
Log in

Vibration suppression and stability analysis of a beam at large amplitude excitation using a two-degree-of-freedom nonlinear energy sink

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

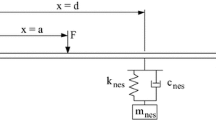
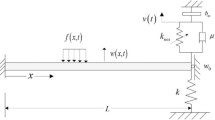
A two-degree-of-freedom (TDOF) nonlinear energy sink (NES) is proposed to suppress the vibration of a simply supported beam subjected to a large amplitude excitation corresponding to its fundamental frequency. The Euler–Bernoulli beam theory along with the Euler–Lagrange equation is utilized for the dynamical modeling of the beam-NES system. The numerical solutions are compared with an approximate analytical solution based on the complexification-averaging method. As the beam response significantly depends on the values of the NES parameters, the optimal values are obtained by employing the particle swarm optimization. After comparison with a single-degree-of-freedom (SDOF) NES, it is found that at lower excitation amplitude SDOF NES is more effective than TDOF NES, however, as the excitation amplitude increases, the TDOF NES gets more effective in terms of resonant peak suppression and energy dissipation. The TDOF NES reduces the first peak amplitude of about 95% as well as dissipates the vibration energy of about 90–98.98%. The chaotic response of the beam is examined using the largest Lyapunov exponents with different parameters. The higher values of the NES stiffness, mass and the excitation amplitude make the system chaotic. Moreover, the analysis of steady-state response shows that a higher value of NES damping reduces the unstable band and thus provides stable response.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Yang, F., Sedaghati, R., Esmailzadeh, E.: Vibration suppression of structures using tuned mass damper technology: A state-of-the-art review. J. Vib. Control 28(7–8), 812–836 (2022)

    Article  MathSciNet  Google Scholar 

  2. Xiao, Y., Wen, J., Yu, D., Wen, X.: Flexural wave propagation in beams with periodically attached vibration absorbers : Band-gap behavior and band formation mechanisms. J. Sound Vib. 332, 867–893 (2013). https://doi.org/10.1016/j.jsv.2012.09.035

    Article  ADS  Google Scholar 

  3. Iqbal, M., Kumar, A., Jaya, M.M., Bursi, O.S.: Flexural band gaps and vibration control of a periodic railway track. Sci. Rep. (2021). https://doi.org/10.1038/s41598-021-97384-3

    Article  PubMed  PubMed Central  Google Scholar 

  4. Iqbal, M., Kumar, A., Bursi, O.S.: Vibration control of a periodic piping system employing metamaterial concept. Fifteenth Int Congr Artif Mater Nov Wave Phenom 2021, 167–169 (2021). https://doi.org/10.1109/Metamaterials52332.2021.9577113

    Article  Google Scholar 

  5. Iqbal, M., Jaya, M.M., Bursi, O.S., Kumar, A.: Flexural band gaps and response attenuation of periodic piping systems enhanced with localized and distributed resonators. Sci. Rep. (2020). https://doi.org/10.1038/s41598-019-56724-0

    Article  PubMed  PubMed Central  Google Scholar 

  6. Iqbal, M., Kumar, A.: Lateral flexural vibration reduction in a periodic piping system enhanced with two-degrees-of-freedom resonators. Proc IMechE Part L J Mater Des Appl (2021). https://doi.org/10.1177/14644207211027603

    Article  Google Scholar 

  7. Gendelman, O.V., Lamarque, C.H.: Dynamics of linear oscillator coupled to strongly nonlinear attachment with multiple states of equilibrium. Chaos Solitons Fractals 24, 501–509 (2005). https://doi.org/10.1016/j.chaos.2004.09.088

    Article  ADS  MathSciNet  Google Scholar 

  8. Gendelman, O.V., Gorlov, D.V., Manevitch, L.I., Musienko, A.I.: Dynamics of coupled linear and essentially nonlinear oscillators with substantially different masses. J. Sound Vib. 286, 1–19 (2005). https://doi.org/10.1016/j.jsv.2004.09.021

    Article  ADS  Google Scholar 

  9. Starosvetsky, Y., Gendelman, O.V.: Vibration absorption in systems with a nonlinear energy sink: Nonlinear damping. J. Sound Vib. 324, 916–939 (2009). https://doi.org/10.1016/j.jsv.2009.02.052

    Article  ADS  Google Scholar 

  10. Sigalov, G., Gendelman, O.V., Al-Shudeifat, M.A., et al.: Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink. Nonlinear Dyn. 69, 1693–1704 (2012). https://doi.org/10.1007/s11071-012-0379-1

    Article  MathSciNet  Google Scholar 

  11. Gourdon, E., Lamarque, C.H., Pernot, S.: Contribution to efficiency of irreversible passive energy pumping with a strong nonlinear attachment. Nonlinear Dyn. 50, 793–808 (2007). https://doi.org/10.1007/s11071-007-9229-y

    Article  Google Scholar 

  12. Gourdon, E., Lamarque, C.H.: Energy pumping with various nonlinear structures: numerical evidences. Nonlinear Dyn. 40, 281–307 (2005)

    Article  MathSciNet  Google Scholar 

  13. Al-shudeifat, M.A.: Piecewise Nonlinear Energy Sink. Proc ASME Int Des Eng Tech Conf Comput Inf Eng Conf 8, 1–7 (2018). https://doi.org/10.1115/detc2015-47301

    Article  Google Scholar 

  14. Benarous, N.I.R., Gendelman, O.V.: Nonlinear energy sink with combined nonlinearities: enhanced mitigation of vibrations and amplitude locking phenomenon. Proc Inst Mech Eng Part C J Mech Eng Sci 230, 21–33 (2016). https://doi.org/10.1177/0954406215579930

    Article  Google Scholar 

  15. Al-Shudeifat, M.A.: Highly efficient nonlinear energy sink. Nonlinear Dyn. 76, 1905–1920 (2014)

    Article  MathSciNet  Google Scholar 

  16. Qiu, D., Seguy, S., Paredes, M.: A novel design of cubic stiffness for a nonlinear energy sink (NES) based on conical spring. Lect Notes Mech Eng (2017). https://doi.org/10.1007/978-3-319-45781-9_57

    Article  Google Scholar 

  17. Qiu, D., Paredes, M., Seguy, S.: Variable pitch spring for nonlinear energy sink: Application to passive vibration control. Proc Inst Mech Eng Part C J Mech Eng Sci 233, 611–622 (2019). https://doi.org/10.1177/0954406218761485

    Article  Google Scholar 

  18. Nucera, F., Vakakis, A.F., McFarland, D.M., Bergman, L.A., Kerschen, G.: Targeted energy transfers in vibro-impact oscillators for seismic mitigation. Nonlinear Dyn. 50, 651–677 (2007)

    Article  Google Scholar 

  19. Tung, T., Stéphane, P., Lamarque, C.H.: Competitive energy transfer between a two degree-of-freedom dynamic system and an absorber with essential nonlinearity. Nonlinear Dyn. 62, 573–592 (2010). https://doi.org/10.1007/s11071-010-9745-z

    Article  MathSciNet  Google Scholar 

  20. Nucera, F., Iacono, F.L., McFarland, D.M., Bergman, L.A., Vakakis, A.F.: Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: experimental results. J. Sound Vib. 313(1–2), 57–76 (2008)

    Article  ADS  Google Scholar 

  21. Georgiades, F., Vakakis, A.F.: Dynamics of a linear beam with an attached local nonlinear energy sink. Commun. Nonlinear Sci. Numer. Simul. 12(12), 643–651 (2007). https://doi.org/10.1016/j.cnsns.2005.07.003

    Article  ADS  Google Scholar 

  22. Tsakirtzis, S., Vakakis, A.F., Panagopoulos, P.: Broadband energy exchanges between a dissipative elastic rod and a multi-degree-of-freedom dissipative essentially non-linear attachment. Int J Non Linear Mech 42, 36–57 (2007). https://doi.org/10.1016/j.ijnonlinmec.2006.11.013

    Article  Google Scholar 

  23. Kumar, R.K., Kumar, A.: NES - Based Multi - mode Vibration Absorber for a Sandwich Plate in Thermal Environment. J Vib Eng Technol (2023). https://doi.org/10.1007/s42417-023-01079-0

    Article  Google Scholar 

  24. Samani, F.S., Pellicano, F.: Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers. J. Sound Vib. 325, 742–754 (2009). https://doi.org/10.1016/j.jsv.2009.04.011

    Article  ADS  Google Scholar 

  25. Ahmadabadi, Z.N., Khadem, S.E.: Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech. Mach. Theory 50, 134–149 (2012). https://doi.org/10.1016/j.mechmachtheory.2011.11.007

    Article  Google Scholar 

  26. Chen, Y., Qian, Z., Chen, K., et al.: Seismic performance of a nonlinear energy sink with negative stiffness and sliding friction. Struct Control Heal Monit (2019). https://doi.org/10.1002/stc.2437

    Article  Google Scholar 

  27. Sc, P., Prasad, C.K., Thampan, V.: A Study on Vibration Control of Structures due to Seismic Excitation using Tuned Mass Damper. Int. J. Sci. Eng. Res. 8, 105–112 (2017)

    Google Scholar 

  28. Wierschem, N.E., Luo, J., Al-Shudeifat, M., Hubbard, S., Ott, R., Fahnestock, L.A., Bergman, L.A.: Experimental Testing and Numerical Simulation of a Six-Story Structure Incorporating Two-Degree-of-Freedom Nonlinear Energy Sink. J. Struct. Eng. 140(6), 04014027 (2014)

    Article  Google Scholar 

  29. Kumar, R.K., Kumar, A.: Vibration attenuation of a beam supporting an unbalanced rotor using nonlinear energy sink. J Brazilian Soc Mech Sci Eng 6, 1–14 (2023). https://doi.org/10.1007/s40430-023-04064-6

    Article  Google Scholar 

  30. Bab, S., Khadem, S.E., Shahgholi, M.: Vibration attenuation of a rotor supported by journal bearings with nonlinear suspensions under mass eccentricity force using nonlinear energy sink. Meccanica 50, 2441–2460 (2015). https://doi.org/10.1007/s11012-015-0156-6

    Article  MathSciNet  Google Scholar 

  31. Khazaee, M., Khadem, S.E., Moslemi, A., Abdollahi, A.: A comparative study on optimization of multiple essentially nonlinear isolators attached to a pipe conveying fluid. Mech. Syst. Signal Process. (2019). https://doi.org/10.1016/j.ymssp.2019.106442

    Article  Google Scholar 

  32. Chen, J.E., He, W., Zhang, W., et al.: Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks. Nonlinear Dyn. 91, 885–904 (2018). https://doi.org/10.1007/s11071-017-3917-z

    Article  Google Scholar 

  33. Lee, Y.S., Vakakis, A.F., McFarland, D.M., Bergman, L.A.: Non-linear system identification of the dynamics of aeroelastic instability suppression based on targeted energy transfers. Aeronaut. J. 114, 61–62 (2010). https://doi.org/10.1017/s0001924000003547

    Article  Google Scholar 

  34. Yang, K., Zhang, Y.W., Ding, H., et al.: Nonlinear energy sink for whole-spacecraft vibration reduction. J Vib Acoust Trans ASME. Doi (2017). https://doi.org/10.1115/1.4035377

    Article  Google Scholar 

  35. Yao, G., Qiao, Y.: Vibration suppression and energy absorption of plates in subsonic air fl ow using an energy harvester enhanced nonlinear energy sink. J. Vib. Control (2022). https://doi.org/10.1177/10775463221077779

    Article  Google Scholar 

  36. Hou, S., Teng, Y., Zhang, Y., Zang, J.: Enhanced energy harvesting of a nonlinear energy sink by internal resonanc. Int. J. Appl. Mech. 11, 1–19 (2020). https://doi.org/10.1142/S175882511950100X

    Article  Google Scholar 

  37. Tsakirtzis, S., Panagopoulos, P.N., Kerschen, G., Gendelman, O., Vakakis, A.F., Bergman, L.A.: Complex dynamics and targeted energy transfer in linear oscillators coupled to multi-degree-of-freedom essentially nonlinear attachments. Nonlinear Dyn. 48, 285–318 (2007)

    Article  MathSciNet  Google Scholar 

  38. Raze, G., Kerschen, G.: Multimodal vibration damping of nonlinear structures using multiple nonlinear absorbers. Int J Non Linear Mech 119, 103308 (2019). https://doi.org/10.1016/j.ijnonlinmec.2019.103308

    Article  Google Scholar 

  39. Wierschem, N.E., Quinn, D.D., Hubbard, S.A., et al.: Passive damping enhancement of a two-degree-of-freedom system through a strongly nonlinear two-degree-of-freedom attachment. J. Sound Vib. 331, 5393–5407 (2012). https://doi.org/10.1016/j.jsv.2012.06.023

    Article  ADS  Google Scholar 

  40. Georgiades, F., Vakakis, A.F.: Passive targeted energy transfers and strong modal interactions in the dynamics of a thin plate with strongly nonlinear attachments. Int. J. Solids Struct. 46, 2330–2353 (2009). https://doi.org/10.1016/j.ijsolstr.2009.01.020

    Article  Google Scholar 

  41. Chen, H.Y., Mao, X.Y., Ding, H., Chen, L.Q.: Elimination of multimode resonances of composite plate by inertial nonlinear energy sinks. Mech. Syst. Signal Process. 135, 106383 (2020). https://doi.org/10.1016/j.ymssp.2019.106383

    Article  Google Scholar 

  42. Parseh, M., Dardel, M., Ghasemi, M.H., Pashaei, M.H.: Steady state dynamics of a non-linear beam coupled to a non-linear energy sink. Int J Non Linear Mech 79, 48–65 (2016). https://doi.org/10.1016/j.ijnonlinmec.2015.11.005

    Article  Google Scholar 

  43. Manevitch, L.I.: The description of localized normal modes in a chain of nonlinear coupled oscillators using complex variables. Nonlinear Dyn. 25, 95–109 (2001). https://doi.org/10.1023/A:1012994430793

    Article  MathSciNet  Google Scholar 

  44. Parseh, M., Dardel, M., Ghasemi, M.H.: Investigating the robustness of nonlinear energy sink in steady state dynamics of linear beams with different boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 29, 50–71 (2015). https://doi.org/10.1016/j.cnsns.2015.04.020

    Article  MathSciNet  Google Scholar 

  45. Taleshi, M., Dardel, M., Pashaie, M.H.: Passive targeted energy transfer in the steady state dynamics of a nonlinear plate with nonlinear absorber. Chaos Solitons Fractals 92, 56–72 (2016). https://doi.org/10.1016/j.chaos.2016.09.017

    Article  ADS  MathSciNet  Google Scholar 

  46. Zhang, Y.W., Hou, S., Zhang, Z., et al.: Nonlinear vibration absorption of laminated composite beams in complex environment. Nonlinear Dyn. 99, 2605–2622 (2020). https://doi.org/10.1007/s11071-019-05442-3

    Article  Google Scholar 

  47. Rao, S.S.: Mechanical vibrations, 5th edn. Pearson Education Inc, Publishing as Prentice Hall, Upper Saddle River (1995)

    Google Scholar 

  48. Dhooge A, Govaerts W, University G, Kuznetsov YA (2003) MATCONT: A MATLAB Package for Numerical Bifurcation Analysis of ODEs

  49. Kani, M., Khadem, S.E., Pashaei, M.H., Dardel, M.: Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn. 83, 1–22 (2016). https://doi.org/10.1007/s11071-015-2304-x

    Article  MathSciNet  Google Scholar 

  50. Browser, M.H.: Stephen Wolfram, The Mathematica Book, 5th edn. Wolfram Media, Champaign (2003)

    Google Scholar 

  51. Wang, D., Tan, D., Liu, L.: Particle swarm optimization algorithm : an overview. Soft. Comput. (2017). https://doi.org/10.1007/s00500-016-2474-6

    Article  Google Scholar 

  52. Thomsen, J.: Vibrations and stability advanced theory, analysis, and tools. Springer (2021)

    Book  Google Scholar 

  53. Mendes, E.M.A.M., Nepomuceno, E.G.: A very simple method to calculate the (Positive) largest lyapunov exponent using interval extensions. Int J Bifurc Chaos 26, 1–7 (2016). https://doi.org/10.1142/S0218127416502266

    Article  MathSciNet  Google Scholar 

  54. Guegan D, Leroux J, Guegan D, et al (2010) Local Lyapunov Exponents : A new way to predict chaotic systems To cite this version : HAL Id : halshs-00511996 Local Lyapunov Exponents : A new way to predict chaotic systems

Download references

Acknowledgements

This work was supported by Science and Engineering Research Board, Govt. of India, core research grant CRG/2018/002539 (SER-1332-MID).

Author information

Authors and Affiliations

  1. Department of Mechanical and Industrial Engineering, Indian Institute of Technology Roorkee, Roorkee, 247667, India

    Rajni Kant Kumar & Anil Kumar

Authors
  1. Rajni Kant Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Anil Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anil Kumar.

Ethics declarations

Conflict of interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

For two-mode expansion of beam, the set of real first-order differential equations are as follows:

$$\begin{aligned}\dot{\alpha}_{1} &=-\frac{1}{8{w}^{3}{M}_{11}}\Big\{4{w}^{3}\overline{\gamma }{\alpha }_{1}-4{w}^{4}{M}_{11}{\alpha }_{2}+4{w}^{2}{M}_{12}{\alpha }_{2} -3\overline{{K}_{1}}{\alpha }_{5}^{2}{\alpha }_{6}{\varphi }_{1}\left(\overline{d}\right)-3\overline{{K}_{1}}{\alpha }_{6}^{3}{\varphi }_{1}\left(\overline{d}\right)-4{w}^{3}{\alpha }_{5}\overline{{\lambda }_{1}}{\varphi }_{1}\left(\overline{d}\right)\\ &\quad +3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}^{2}{\varphi }_{1}^{2}\left(\overline{d}\right)+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}^{2}\left(\overline{d}\right)+9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{6}^{2}{\varphi }_{1}^{2}\left(\overline{d}\right)+4{w}^{3}{\alpha }_{1}\overline{{\lambda }_{1}}{\varphi }_{1}^{2}\left(\overline{d}\right)-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{5}{\varphi }_{1}^{3}\left(\overline{d}\right)\\ &\quad -3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{6}{\varphi }_{1}^{3}\left(\overline{d}\right)-9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{6}{\varphi }_{1}^{3}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{2}{\varphi }_{1}^{4}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{2}^{3}{\varphi }_{1}^{4}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}^{2}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)\\&\quad +6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)+9\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{6}^{2}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)+4{w}^{3}{\alpha }_{3}\overline{{\lambda }_{1}}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)-6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)\\&\quad -6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)- 6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)-18\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)\\ &\quad +6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{3}{\varphi }_{1}^{3}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{4}{\varphi }_{1}^{3}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)+9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{4}{\varphi }_{1}^{3}\left(\overline{d}\right){\varphi }_{2}\left(\overline{d}\right)\\ &\quad -6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)-3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{6}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)-9\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{6}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}^{2}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)\\ &\quad+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)+9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}^{2}{\varphi }_{1}^{2}\left(\overline{d}\right){\varphi }_{2}^{2}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{4}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}^{3}\left(\overline{d}\right)+3\overline{{K}_{1}}{\alpha }_{4}^{3}{\varphi }_{1}\left(\overline{d}\right){\varphi }_{2}^{3}\left(\overline{d}\right)\Big\}\end{aligned}$$

(A1)

$$\begin{aligned}\dot{\alpha}_{2}&=-\frac{1}{8{w}^{3}{M}_{11}}\{4 {\varphi }_{1}\left(\hat{a} \right)\overline{F}{w}^{3}+4{w}^{4}{M}_{11}{\alpha }_{1}-4{w}^{2}{M}_{12}{\alpha }_{1}+4{w}^{3}\overline{\gamma }{\alpha }_{2}+3\overline{{K}_{1}}{\alpha }_{5}^{3}{\varphi }_{1}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{5}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d})\\ &\quad -4{w}^{3}{\alpha }_{6}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}^{2}{\varphi }_{1}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{6}^{2}{\varphi }_{1}^{2}(\overline{d})+4{w}^{3}{\alpha }_{2}\overline{{\lambda }_{1}}{\varphi }_{1}^{2}(\overline{d})\\ &\quad +9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{5}{\varphi }_{1}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{5}{\varphi }_{1}^{3}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{6}{\varphi }_{1}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}^{3}{\varphi }_{1}^{4}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}^{2}{\varphi }_{1}^{4}(\overline{d})\\ &\quad -9\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+4{w}^{3}{\alpha }_{4}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +18\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{3}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{3}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{4}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +9\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}^{2}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad - 6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}^{2}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}^{3}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})\} \end{aligned}$$
$$\begin{aligned}\dot{\alpha}_{3} &=-\frac{1}{8{w}^{3}{M}_{11}}\{4{w}^{3}\overline{\gamma }{\alpha }_{3}-4{w}^{4}{M}_{11}{\alpha }_{4}+4{w}^{2}{M}_{12}{\alpha }_{4}-3\overline{{K}_{1}}{\alpha }_{5}^{2}{\alpha }_{6}{\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{6}^{3}{\varphi }_{2}(\overline{d})-4{w}^{3}{\alpha }_{5}\overline{{\lambda }_{1}}{\varphi }_{2}(\overline{d})\\ &\quad + 3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+4{w}^{3}{\alpha }_{1}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad -6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{2}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +3\overline{{K}_{1}}{\alpha }_{2}^{3}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}^{2}{\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}{\alpha }_{6}{\varphi }_{2}^{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{6}^{2}{\varphi }_{2}^{2}(\overline{d})+4{w}^{3}{\alpha }_{3}\overline{{\lambda }_{1}}{\varphi }_{2}^{2}(\overline{d})\\ &\quad -6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad -18\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad -6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{5}{\varphi }_{2}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{6}{\varphi }_{2}^{3}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{6}{\varphi }_{2}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})\\ &\quad +6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{4}{\varphi }_{2}^{4}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{4}^{3}{\varphi }_{2}^{4}(\overline{d})\}\end{aligned}$$
$$\begin{aligned}\dot{\alpha}_{4} &=-\frac{1}{8{w}^{3}{M}_{11}}\{4{\varphi }_{2}\left(\hat{a} \right)\overline{F}{w}^{3}+4{w}^{4}{M}_{11}{\alpha }_{3}-4{w}^{2}{M}_{12}{\alpha }_{3}+4{w}^{3}\overline{\gamma }{\alpha }_{4}+3\overline{{K}_{1}}{\alpha }_{5}^{3}{\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{5}{\alpha }_{6}^{2}{\varphi }_{2}(\overline{d}) \\ &\quad -4{w}^{3}{\alpha }_{6}\overline{{\lambda }_{1}}{\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +4{w}^{3}{\alpha }_{2}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{6}{\varphi }_{1}^{2}{\varphi }_{2}(\overline{d})\\ &\quad -3\overline{{K}_{1}}{\alpha }_{1}^{3}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}^{2}{\varphi }_{1}^{3}(\overline{d}){\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}^{2}{\varphi }_{2}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}{\alpha }_{6}{\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{6}^{2}{\varphi }_{2}^{2}(\overline{d})\\ &\quad +4{w}^{3}{\alpha }_{4}\overline{{\lambda }_{1}}{\varphi }_{2}^{2}(\overline{d})+18\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad +6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad +9\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{5}{\varphi }_{2}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{5}{\varphi }_{2}^{3}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{6}{\varphi }_{2}^{3}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})\\ &\quad -6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}^{3}{\varphi }_{2}^{4}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}^{2}{\varphi }_{2}^{4}(\overline{d})\}\end{aligned}$$
$$\begin{aligned}\dot{\alpha}_{5}&=-\frac{1}{8{w}^{3}{\varepsilon }_{1}}\{3\overline{{K}_{1}}{\alpha }_{5}^{2}{\alpha }_{6}+3\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{6}+3\overline{{K}_{1}}{\alpha }_{6}^{3}+3\overline{{K}_{2}}{\alpha }_{6}^{3}-6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}{\alpha }_{7}+3\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{7}^{2}-3\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{8}-9\overline{{K}_{2}}{\alpha }_{6}^{2}{\alpha }_{8}\\ &\quad +6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{7}{\alpha }_{8}-3\overline{{K}_{2}}{\alpha }_{7}^{2}{\alpha }_{8}+9\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{8}^{2}-3\overline{{K}_{2}}{\alpha }_{8}^{3}-4{w}^{4}{\alpha }_{6}{\varepsilon }_{1}+4{w}^{3}{\alpha }_{5}\overline{{\lambda }_{1}}+4{w}^{3}{\alpha }_{5}\overline{{\lambda }_{2}}\\ &\quad -4{w}^{3}{\alpha }_{7}\overline{{\lambda }_{2}}-3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}^{2}{\varphi }_{1}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}(\overline{d})\\ &\quad -9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d})-4{w}^{3}{\alpha }_{1}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d})\\ &\quad -3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{2}{\varphi }_{1}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{2}^{3}{\varphi }_{1}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}^{2}{\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}{\alpha }_{6}{\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{6}^{2}{\varphi }_{2}(\overline{d})-4{w}^{3}{\alpha }_{3}\overline{{\lambda }_{1}}{\varphi }_{2}(\overline{d})\\ &\quad +6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +18\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})\\ &\quad +6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{5}{\varphi }_{2}^{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{6}{\varphi }_{2}^{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{6}{\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\ &\quad -6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{4}{\varphi }_{2}^{3}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{4}^{3}{\varphi }_{2}^{3}(\overline{d})\}\end{aligned}$$
$$\begin{aligned}\dot{\alpha}_{6}&=-\frac{1}{8{w}^{3}{\varepsilon }_{1}}\{-3\overline{{K}_{1}}{\alpha }_{5}^{3}-3\overline{{K}_{2}}{\alpha }_{5}^{3}-3\overline{{K}_{1}}{\alpha }_{5}{\alpha }_{6}^{2}-3\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}^{2}+9\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{7}+3\overline{{K}_{2}}{\alpha }_{6}^{2}{\alpha }_{7}-9\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{7}^{2}+3\overline{{K}_{2}}{\alpha }_{7}^{3}\\&\quad+6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}{\alpha }_{8}-6\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{7}{\alpha }_{8}-3\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{8}^{2}\\&\quad+3\overline{{K}_{2}}{\alpha }_{7}{\alpha }_{8}^{2}+4{w}^{4}{\alpha }_{5}{\varepsilon }_{1}+4{w}^{3}{\alpha }_{6}\overline{{\lambda }_{1}}+4{w}^{3}{\alpha }_{6}\overline{{\lambda }_{2}}-4{w}^{3}{\alpha }_{8}\overline{{\lambda }_{2}}+9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{5}^{2}{\varphi }_{1}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{5}{\alpha }_{6}{\varphi }_{1}(\overline{d})\\&\quad+3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{6}^{2}{\varphi }_{1}(\overline{d})-4{w}^{3}{\alpha }_{2}\overline{{\lambda }_{1}}{\varphi }_{1}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d})-3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{5}{\varphi }_{1}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{6}{\varphi }_{1}^{2}(\overline{d})\\&\quad+3\overline{{K}_{1}}{\alpha }_{1}^{3}{\varphi }_{1}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}^{2}{\varphi }_{1}^{3}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{5}^{2}{\varphi }_{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{4}{\alpha }_{5}{\alpha }_{6}{\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{6}^{2}{\varphi }_{2}(\overline{d})\\ &\quad -4{w}^{3}{\alpha }_{4}\overline{{\lambda }_{1}}{\varphi }_{2}(\overline{d})-18\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{4}{\alpha }_{5}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})\\&\quad-6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}{\alpha }_{6}{\varphi }_{1}(\overline{d}){\varphi }_{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{1}^{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{2}^{2}{\alpha }_{3}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})\\&\quad+6\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{2}{\alpha }_{4}{\varphi }_{1}^{2}(\overline{d}){\varphi }_{2}(\overline{d})-9\overline{{K}_{1}}{\alpha }_{3}^{2}{\alpha }_{5}{\varphi }_{2}^{2}(\overline{d})\\&\quad-3\overline{{K}_{1}}{\alpha }_{4}^{2}{\alpha }_{5}{\varphi }_{2}^{2}(\overline{d})-6\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}{\alpha }_{6}{\varphi }_{2}^{2}(\overline{d})+9\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{3}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+6\overline{{K}_{1}}{\alpha }_{2}{\alpha }_{3}{\alpha }_{4}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})\\&\quad+3\overline{{K}_{1}}{\alpha }_{1}{\alpha }_{4}^{2}{\varphi }_{1}(\overline{d}){\varphi }_{2}^{2}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{3}^{3}{\varphi }_{2}^{3}(\overline{d})+3\overline{{K}_{1}}{\alpha }_{3}{\alpha }_{4}^{2}{\varphi }_{2}^{3}(\overline{d})\}\end{aligned}$$
$$\begin{aligned}\dot{\alpha}_{7}&=-\frac{1}{8{w}^{3}{\varepsilon }_{2}}\{-3\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{6}-3\overline{{K}_{2}}{\alpha }_{6}^{3}+6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}{\alpha }_{7}-3\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{7}^{2}\\&\quad+3\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{8}+9\overline{{K}_{2}}{\alpha }_{6}^{2}{\alpha }_{8}-6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{7}{\alpha }_{8}+3\overline{{K}_{2}}{\alpha }_{7}^{2}{\alpha }_{8}-9\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{8}^{2}\\&\quad+3\overline{{K}_{2}}{\alpha }_{8}^{3}-4{w}^{4}{\alpha }_{8}{\varepsilon }_{2}-4{w}^{3}{\alpha }_{5}\overline{{\lambda }_{2}}+4{w}^{3}{\alpha }_{7}\overline{{\lambda }_{2}}\}\end{aligned}$$

\(\begin{aligned}\dot{\alpha}_{8}&=-\frac{1}{8{w}^{3}{\varepsilon }_{2}}\{3\overline{{K}_{2}}{\alpha }_{5}^{3}+3\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}^{2}-9\overline{{K}_{2}}{\alpha }_{5}^{2}{\alpha }_{7}-3\overline{{K}_{2}}{\alpha }_{6}^{2}{\alpha }_{7}+9\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{7}^{2}-3\overline{{K}_{2}}{\alpha }_{7}^{3}-6\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{6}{\alpha }_{8}+6\overline{{K}_{2}}{\alpha }_{6}{\alpha }_{7}{\alpha }_{8}+3\overline{{K}_{2}}{\alpha }_{5}{\alpha }_{8}^{2}-3\overline{{K}_{2}}{\alpha }_{7}{\alpha }_{8}^{2}+4{w}^{4}{\alpha }_{7}{\varepsilon}_{2}-4{w}^{3}{\alpha }_{6}\overline{{\lambda }_{2}}+4{w}^{3}{\alpha }_{8}\overline{{\lambda}_{2}}\}.\end{aligned}\)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, R.K., Kumar, A. Vibration suppression and stability analysis of a beam at large amplitude excitation using a two-degree-of-freedom nonlinear energy sink. Acta Mech 235, 971–990 (2024). https://doi.org/10.1007/s00707-023-03765-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03765-2

Search

Navigation