Transient, Steady-State and Total Dynamic Responses of Mindlin Viscoelastic Plates Subjected to Harmonic Transversal Load and In-Plane Compression

Abstract

Purpose

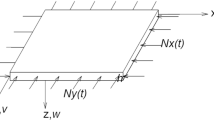
This research proves a novel closed-form solution for the forced vibration analysis of a Mindlin viscoelastic plate subjected to harmonic transversal load and constant in-plane compression, simultaneously.

Method

The excitation frequency of the harmonic transversal load is considered as equal to the natural frequency of the viscoelastic plate. The viscoelastic properties obey the Boltzmann integral law with constant bulk modulus. The displacement field is approximated by the product of a known geometrical function and an unknown time function. The simple hp cloud method is employed for discretization. Calculating the natural and viscous damping frequencies, geometry, mass and stiffness matrices in the Laplace–Carson domain, and introducing the best values to replace the Laplace parameter, the dynamic responses of Mindlin viscoelastic plates are determined.

Results and Conclusion

The transient, steady-state and total dynamic responses of moderately thick viscoelastic plates are explicitly formulated in the time domain based on the elastic bending analysis at time zero, for the first time. In the numerical results, the effects of material properties and loading on the total dynamic responses are investigated.

Appendices

Appendix 1

Forced Vibration Analysis of Simply Supported Bernoulli Viscoelastic Beams Subjected to Harmonic Transversal Load and Axial Compression

The equation of a Bernoulli viscoelastic beam subjected to a harmonic transversal load and axial compression, (as illustrated in Fig. 

Fig. 7

A simply supported viscoelastic beam subjected to harmonic transversal load and axial compression

7) can be written as follows [28]:

$$\frac{{\partial }^{2}M}{\partial {x}^{2}}-p\frac{{\partial }^{2}w}{\partial {x}^{2}}=\rho \frac{{\partial }^{2}w}{\partial {t}^{2}}-q\left(t\right),$$

(65)

in which $M$ is the bending moment, $w$ is the transversal deflection, $t$ is the time and $\rho$ is the mass per unit length.

The bending moment can be expressed as:

$$M={\int }_{A}\sigma \left(x,t\right)zdA.$$

(66)

The stress–strain relation of a linear viscoelasticity based on the Boltzmann integral can be defined as [26]:

$$\sigma \left(x,t\right)=E\left(t\right)\varepsilon \left(0\right)+\underset{0}{\overset{t}{\int }}E\left(t-\tau \right)\dot{\varepsilon }\left(\tau \right)d\tau , \dot{\varepsilon }\left(t\right)=\partial \varepsilon /\partial t,$$

(67)

where $E\left(t\right)$ is the modulus of elasticity.

For Bernoulli beams, the strain–deflection relation can be written as:

$$\varepsilon \left(x,t\right)=-z\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}.$$

(68)

Investigating simply supported boundary conditions, the deflection may be approximated using the separation of variables method as follows:

$$w\left(x,t\right)=F\left(t\right)\mathit{sin}\frac{\pi x}{l}.$$

(69)

It is noted that only one term of the series of $\mathrm{sin}\frac{n\pi x}{l}$ has been considered, since the goal of this step is to concentrate on the time domain solution.

The time-dependent elasticity modulus can be expressed as:

$$E\left(t\right)={E}_{0}\eta \left(t\right), {E}_{0}=E\left(t=0\right),$$

(70)

in which $\eta \left(t\right)$ is the relaxation function of viscoelastic material which is defined in Eq. (9).

Substituting Eqs. (66–70) into Eq. (65), Eq. (71) is obtained:

$${E}_{0}\eta \left(t\right)\frac{I{\pi }^{4}}{{l}^{4}}F\left(0\right)+{E}_{0}\frac{I{\pi }^{4}}{{l}^{4}}\underset{0}{\overset{t}{\int }}\eta \left(t-\tau \right)\dot{F}\left(\tau \right)d\tau -\frac{{\pi }^{2}}{{l}^{2}}pF\left(t\right)+m\ddot{F}\left(t\right)=q\left(t\right),$$

(71)

where $I={\int }_{A}{z}^{2}dA$ is the moment of inertia.

The compressive load may be given as:

$$p={\alpha }_{1}{P}_{e}, { P}_{e}=\frac{{\pi }^{2}{E}_{0}I }{{l}^{2}}, 0\le {\alpha }_{1}<1,$$

(72)

in which ${\alpha }_{1}$ is constant.

For Bernoulli viscoelastic plates, $\Omega$ is defined as the fundamental natural frequency calculated by the free vibration analysis of Bernoulli viscoelastic beams at time zero, ${\Omega }^{2}=\frac{{E}_{0}I{\pi }^{4}}{m{l}^{4}}$. If the beam is subjected to axial compression too, the natural frequency is decreased ${\omega }_{0}=\Omega \sqrt{1-{\alpha }_{1}}$, [24]. In this paper, the beam is subjected to harmonic transversal load $q\left(t\right)=q\mathrm{sin}{\omega }_{0}t$ and axial compression, simultaneously. In other word, the excitation frequency is equal to the natural frequency and the time-dependent behavior of the viscoelastic beam is studied.

Replacing Eq. (72) in Eq. (71), Eq. (73) is obtained:

$$\eta \left(t\right)F\left(0\right)+\underset{0}{\overset{t}{\int }}\eta \left(t-\tau \right)\dot{F}\left(\tau \right)d\tau -{\alpha }_{1}F\left(t\right)+\frac{\ddot{F}\left(t\right)}{{\Omega }^{2}}={q}_{0}\mathrm{sin}{\omega }_{0}t,$$

$${\Omega }^{2}=\frac{{E}_{0}I{\pi }^{4}}{m{l}^{4}}, {q}_{0}=\frac{q{l}^{4}}{{\pi }^{4}{E}_{0}I}.$$

(73)

Equation (73) can be simplified as follows:

$$s{F}^{*}{\eta }^{*}-{\alpha }_{1}{F}^{*}+\frac{{\ddot{F}}^{*}}{{\Omega }^{2}}={q}_{0}{\left(\mathrm{sin}{\omega }_{0}t\right)}^{*}, {\eta }^{*}=\frac{{c}_{1}}{s}+\frac{{c}_{2}}{s+\lambda },$$

(74)

in which ${\eta }^{*}$, ${F}^{*}$, ${\ddot{F}}^{*}$ and ${\left(\mathrm{sin}{\omega }_{0}t\right)}^{*}$ are the Laplace transformation of $\eta \left(t\right)$, $F\left(t\right)$, $\ddot{F}(t)$ and $\mathrm{sin}{\omega }_{0}t$, respectively.

For the steady-state response, the time function is approximated as follows:

$$F\left(t\right)=A\mathrm{sin}{\omega }_{0}t+B\mathrm{cos}{\omega }_{0}t.$$

(75)

Hence, Eqs. (76–77) are derived:

$$\ddot{F}\left(t\right)=-A{{\omega }_{0}}^{2}\mathit{sin}{\omega }_{0}t-B{{\omega }_{0}}^{2}\mathit{cos}{\omega }_{0}t=-{{\omega }_{0}}^{2}F\left(t\right),$$

(76)

$${\ddot{F}}^{*}=-{{\omega }_{0}}^{2}{F}^{*}.$$

(77)

Inserting Eq. (77) into Eq. (74), Eq. (78) is obtained:

$$s{F}^{*}{\eta }^{*}-{\alpha }_{1}{F}^{*}-\frac{{{\omega }_{0}}^{2}{F}^{*}}{{\Omega }^{2}}={q}_{0}{\left(\mathrm{sin}{\omega }_{0}t\right)}^{*}, {{\omega }_{0}}^{2}={\Omega }^{2}\left(1-{\alpha }_{1}\right).$$

(78)

Equation (78) can be simplified as follows:

$${F}^{*}\left(\overline{\eta }-1\right)={q}_{0}{\left(\mathrm{sin}{\omega }_{0}t\right)}^{*}, \overline{\eta }=s{\eta }^{*}.$$

(79)

On the other hand:

$${F}^{*}=\frac{A{\omega }_{0}+Bs}{{s}^{2}+{{\omega }_{0}}^{2}}, {\left(\mathrm{sin}{\omega }_{0}t\right)}^{*}=\frac{{\omega }_{0}}{{s}^{2}+{{\omega }_{0}}^{2}}.$$

(80)

Supposing ${c}_{1}+{c}_{2}=1$ and by substituting Eqs. (80) into Eq. (79), Eq. (81) is derived:

$$\left(A{\omega }_{0}+Bs\right)\left(-\frac{{c}_{2}\lambda }{s+\lambda }\right)={q}_{0}{\omega }_{0}$$

(81)

or

$$-{c}_{2}\lambda \left(A{\omega }_{0}+Bs\right)={q}_{0}{\omega }_{0} \left(s+\lambda \right).$$

(82)

If Eq. (82) is solved by unifying the sentences:

$$A=-\frac{{q}_{0}}{{c}_{2}},$$

(83)

$$B=-\frac{{q}_{0}}{{c}_{2}} \frac{{\omega }_{0}}{\lambda }.$$

(84)

Therefore, the steady-state response of a Bernoulli viscoelastic beam can be expressed as follows

$$w\left(x,t\right)=-\frac{{q}_{0}}{{c}_{2}}\left(\mathrm{sin}{\omega }_{0}t+ \frac{{\omega }_{0}}{\lambda }\mathrm{cos}{\omega }_{0}t\right)\mathit{sin}\frac{\pi x}{l}.$$

(85)

But, if Eq. (82) is solved numerically:

$$s=0\Rightarrow A=-\frac{{q}_{0}}{{c}_{2}},$$

(86)

$$B={\omega }_{0}\left(\frac{{q}_{0} \left(s+\lambda \right)}{-{c}_{2}\lambda }-A\right)/s, \forall s>0.$$

(87)

Although Eq. (87) is hold $\forall s>0$, the numerical solution showed that selecting the large value for $s$, decreases the accuracy. And selecting $s\approx \lambda$ is the proper selection.

On the other hand, the transient response of a Bernoulli viscoelastic beam can be expressed as follows [24]:

$$w\left(x\text{,}t\right)=\mathit{sin}\frac{\pi x}{l}J\left(t\right), J\left(t\right)={e}^{-{\alpha }_{0}t}\left(C\mathrm{sin}{\omega }_{0}t+D\mathrm{cos}{\omega }_{0}t\right),$$

$${\omega }_{0}=\Omega \sqrt{1-{\alpha }_{1}}, {\alpha }_{0}=\frac{{c}_{2}\lambda }{2\left(1-{\alpha }_{1}\right)}.$$

(88)

Thus, the total dynamic response can be written as:

$$w\left(x\text{,}t\right)=\mathit{sin}\frac{\pi x}{l}\left(F\left(t\right)+ J\left(t\right)\right)=w\left(x\text{,}t=0\right)\left[-\frac{{q}_{0}}{{c}_{2}}\mathit{sin}{\omega }_{0}t-\frac{{q}_{0}}{{c}_{2}} \frac{{\omega }_{0}}{\lambda }\mathit{cos}{\omega }_{0}t+{e}^{-{\alpha }_{0}t}\left(C\mathit{sin}{\omega }_{0}t+D\mathit{cos}{\omega }_{0}t\right)\right].$$

(89)

$C$ and $D$ can be calculated using the initial conditions at time zero:

$$w\left(x\text{,} t=0\right)=0\Rightarrow D=\frac{{q}_{0}}{{c}_{2}} \frac{{\omega }_{0}}{\lambda },$$

(90)

$$\dot{w}\left(x\text{,} t=0\right)=0\Rightarrow C=-B\frac{{\alpha }_{0}}{{\omega }_{0}}-A\cong \frac{{q}_{0}}{{c}_{2}}, \frac{{\alpha }_{0}}{{\omega }_{0}}\ll 1.$$

(91)

In other words, the transient response can be written as:

$$w\left(x\text{,}t\right)=w\left(x\text{,} t=0\right){e}^{-{\alpha }_{0}t}\left(\frac{{q}_{0}}{{c}_{2}}\mathrm{sin}{\omega }_{0}t+\frac{{q}_{0}}{{c}_{2}} \frac{{\omega }_{0}}{\lambda }\mathrm{cos}{\omega }_{0}t\right).$$

(92)

Finally, the total dynamic response of Bernoulli viscoelastic plates subjected to harmonic transversal load $q\left(t\right)=q\mathrm{sin}{\omega }_{0}t$ and axial compression $p={\alpha }_{1}{P}_{e}$ can be expressed as:

$$w\left(x\text{,}t\right)=w\left(x\text{,} t=0\right)H\left(t\right), H\left(t\right)=\left(1-{e}^{-{\alpha }_{0}t}\right)\left(-\frac{{q}_{0}}{{c}_{2}}\mathrm{sin}{\omega }_{0}t-\frac{{q}_{0}}{{c}_{2}} \frac{{\omega }_{0}}{\lambda }\mathrm{cos}{\omega }_{0}t\right).$$

(93)

Appendix 2

Constructing the Simple hp Cloud Approximation Functions

Considering a selected set of scattered nodes as illustrated in Fig. 

Fig. 8

Distribution of 25 nodes on the domain of a rectangular plate

8:

$${\mathbf{Q}}_{N}=\left\{{\mathbf{x}}_{1}\text{,}{\mathbf{x}}_{2}\text{,}\dots \text{,}{\mathbf{x}}_{N}\right\}.$$

(94)

Each node is centered at ${\mathbf{x}}_{i}$, related to the elliptical cloud ${\varphi }_{i}$ and has the effective radius ${h}_{ix}$ and ${h}_{iy}.$

The basis functions, the simple hp cloud meshless approximation functions, are defined as:

$${\mathbf{N}}^{i}\left(\mathbf{x}\right)={\psi }_{i}\left(\mathbf{x}\right){\mathbf{L}}_{{\varvec{i}}}\left(\mathbf{x}\right),$$

(95)

where ${\psi }_{i}$ are the Shepard functions and ${\mathbf{L}}_{{\varvec{i}}}$ are the complete polynomial of order 2 as follows:

$${\mathbf{L}}_{i}=[1 x-{x}_{i} y-{y}_{i}{ \left(x-{x}_{i}\right)}^{2 } \left(x-{x}_{i}\right)\left(y-{y}_{i}\right) {\left(y-{y}_{i}\right)}^{2}.$$

(96)

By defining the weight functions as:

$${W}_{i}\left(\mathbf{x}\right)=1-6{{r}_{i}}^{2}+8{{r}_{i}}^{3}+3{{r}_{i}}^{4} , {r}_{i}\left(\mathbf{x}\right)=\sqrt[2]{{\left(\frac{x-{x}_{i}}{{h}_{ix}}\right)}^{2}+{\left(\frac{y-{y}_{i}}{{h}_{iy}}\right)}^{2}} \text{,} {r}_{i}\le 1.$$

(97)

Shepard functions are calculated in the following form:

$${\psi }_{i}\left(\mathbf{x}\right)=\frac{{W}_{i}\left(\mathbf{x}\right)}{\sum_{\beta }{W}_{\beta }\left(\mathbf{x}\right)}.$$

(98)