Introduction

In the practical engineering, the vibration is always regarded as a negative factor. The unnecessary vibration can cause structural fatigue damage, reduce equipment life, and generate unpleasant noises. To reduce the natural frequency without affecting the system's carrying capacity [1], a new idea is proposed that the system can reach the state of QZS by introducing negative stiffness elements.

There are many negative stiffness components as QZS vibration isolators. Carrella et al. [2] proposed the classical three-spring vibration isolation system, which can improve the traditional linear vibration isolator limited by the support load. This paper explored the influence of spring inclined Angle on dynamic stiffness, and obtained the optimal inclined Angle. Peng et al. [3] have proposed a kind of QZS vibration isolator with spring connecting rod structure as negative stiffness mechanism, the effectiveness of the system was verified by analyzing the system's transmissibility, damping ratio and response, which was the prototype of the design of QZS vibration isolator in China. Based on the simple three-spring structure, Kovacic et al. [4] have optimized its structural design, the system was geometrically and physically nonlinear using two springs with nonlinear prestress instead of inclined springs. The frequency of the first period-doubling bifurcation was found and the effect of damping on the frequency was determined. Zhu et al. [5] have proposed a 2-DOF seismic system model based on smooth discontinuous oscillators. This model consists of two vibration isolation units in the horizontal orthogonal direction, each of which has stable QZS and can reduce the initial vibration isolation frequency to less than 0.5 Hz. Platus et al. [6] have proposed the idea that negative stiffness offsets positive stiffness through parallel connection of axial spring and two mutually articulated rods, and designed vibration isolation mechanism. Kang et al. [7] have designed a spring with QZS characteristics with CAM, pulley and Euler beam, which reduces the initial natural frequency by changing the included angle to adapt to the impact of load changes on the vibration isolation performance of QZS vibration isolator, and has solved the problem that the system’s vibration isolation performance was affected by load changes. Thanh et al. [8] have proposed a pneumatic active vibration isolation system at low excitation frequency, and has adopted the radial basis function neural network model to calculate the optimal gain of the auxiliary controller, thus reducing chattering phenomenon in the control process. Zhou et al. [9] have proposed a low stiffness annular Halbach air-gap structure scheme of passive magnetic suspension vibration isolation units, the use of electromagnetic force balance gravity of object, on the principle of the non-contact structure can make the unit will get very low or even zero stiffness properties, which has excellent low-frequency vibration isolation performance. Yang et al. [10] have applied quasi-zero-stiffness vibration isolator in the field of vibration isolation of rehabilitation robot. By installing vibration isolator at the bottom of rehabilitation robot, the impact of ground vibration on its working performance was reduced, thus reducing the harm to human body. Sun et al. [11] have realized the design of QZS vibration isolator of large line through parallel connection of spring and multi-link mechanism, and has solved the isolation problem of low-frequency and large amplitude vibration. Wang et al. [12] have proposed a structural model of a new QZS vibration isolator using double connecting rods, springs and curved surfaces as negative stiffness mechanisms, which can effectively reduce the resonance frequency and maximum transmissibility amplitude of the model, it had not only good low-frequency vibration isolation performance, with high-frequency vibration isolation performance comparable to that of a linear system. Yao et al. [13] have designed an X-type structure and applied it to the QZS vibration isolation system, and optimized the stiffness value parameters to make the transmissibility jump disappear and make the system more stable. Zou [14] has proposed a single degree of freedom vibration isolation system using scissor-like structures to achieve the nonlinear stiffness and damping. It was verified that the structure can not only meet the need of low-frequency vibration isolation, but also suppress the high amplitude vibration in the resonance region. Shiri et al. [15] have based on the special structure of current carrying planar spiral coils, a fast algorithm for calculating magnetic force was proposed. Awrejcewicz et al. [16] have proposed non-linear dynamic asymptotic method for solving QZS nonlinear characteristics of vibration isolation system.

As a negative stiffness component, the electromagnetic spring has the following advantages in designing QZS vibration isolation system: Low stiffness, fast response, high static bearing capacity density, low loss height and strong environmental adaptability. Because of a series of advantages above, it has a broad application prospect in precision instrument processing, vibration isolation and other fields. Therefore, this paper uses electromagnetic spring as a negative stiffness element to design a new electromagnetic QZS vibration isolator.

The Model of Electromagnetic QZS Vibration Isolator Model

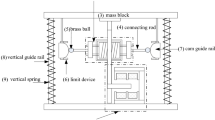
The electromagnetic QZS vibration isolator is composed of four linear springs and two electromagnetic springs, which, provides positive and negative stiffness, respectively. The electromagnetic springs are symmetrically distributed along the axis, and the electromagnetic force generated is transmitted to the vertical direction through the CAM mechanism. The structure of electromagnetic QZS vibration isolator is shown in Fig. 1. The CAM center and the sphere center is located in the same horizontal plane. The load and the ball synchronously changes along the CAM guide.

Fig. 1
figure 1

The structure diagram of electromagnetic QZS vibration isolator

Full size image

The main components of electromagnetic QZS vibration isolator are: (1) E-magnet, using 0.5 mm thick silicon steel overlay synthesis. (2) electromagnetic coil, made of enameled copper wire winding, the number of turns is 2000, the working current range is 0–5 A. (3) armature, parameters are consistent with E-silicon steel sheet, which can move left and right with excitation. To reduce the influence of magnetic field coupling effect, magnetic isolation layer is installed behind. (4) Support mechanism side plate, made of non-magnetic aluminum alloy, used to fix E-magnets. (5) Supporting mechanism bottom plate, there are sliders that guide and limit the keeper's movement. (6) Bearing platform. (7) The vertical guide rail, outside the spring, used to support the bearing platform. (8) Connecting rod. (9) Brass ball. (10) CAM guide. (11) Guide rail connecting rod.

The electromagnetic spring is composed of an armature and an E-magnet and a coil winding. Electromagnetic fields are generated near the e-magnet as the current flows into the coil, thus generating negative stiffness. As positive stiffness mechanism of the vibration isolation system, the four centrosymmetric linear springs are installed on the guide rail to ensure that the vibration isolator does not appear the instability phenomenon. When the isolated object is loaded on the bearing platform, the original length of the spring is compressed to make the vibration isolation system produce vertical upward support force. The guideway connecting rod is fastened on the bearing platform to ensure that the all springs have the same movement. The worm gear and worm mechanism can achieve adjustable positive stiffness via adjusting the preload degree.

Statics Analysis of Vibration Isolation System

Electromagnetic Force Calculation

Calculation of the Relationship Between Air Gap Variation and Vertical Displacement

As shown in Fig. 2, \(z\) is defined as the displacement of the CAM in the vertical direction, the displacement downward is positive. Then, the relationship between air gap and vertical displacement is

Fig. 2
figure 2

CAM air-gap displacement relation diagram

Full size image
$$\Delta \delta ={(r}_{1}+{r}_{2})-\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2}}.$$
(1)

Then

$$\delta ={\delta }_{0}-\Delta \delta ={\delta }_{0}-{(r}_{1}+{r}_{2})+\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2}},$$
(2)

where \({r}_{1}\) is the radius of CAM rail, \({r}_{2}\) is the radius of CAM, \(\theta\) is the angle generated between the CAM and the center line after the CAM movement \(z\), \({\delta }_{0}\) is the initial air gap value.

The Theoretical Calculation

Maxwell Method for Calculating Electromagnetic Force

Maxwell’s formula is derived from the concept of magnetic field lines proposed by Faraday and Maxwell [17]

$$F=\frac{1}{{\mu }_{0}}\oint \left[\left(B-{n}^{0}\right)B-\frac{1}{2}{B}^{2}{n}^{0}\right]\mathrm{d}S.$$
(3)

Equation (3) is simplified and can be obtained

$$F=\frac{{\varphi }^{2}}{2{\mu }_{0}S} .$$
(4)

It can be obtained by substituting \(\varphi =B \cdot S\) into Eq. (4)

$$F=\frac{{\varphi }^{2}}{2{\mu }_{0}S}=\frac{{B}^{2}S}{2{\mu }_{0}}.$$
(5)

The air gap is the armature stroke, without considering the influence of magnetic leakage or air gap, and the magnetic induction intensity of the air gap is

$$B=\frac{N \cdot U}{2 \cdot R\delta } \cdot {\mu }_{0}=\frac{N \cdot I}{2 \cdot \delta }{ \cdot \mu }_{0}.$$
(6)

The expression of electromagnetic force can be obtained by substituting (6) into (5)

$$F=\frac{(NI{)}^{2}{\mu }_{0}}{4{\delta }^{2}} \cdot S,$$
(7)

where S is the cross-sectional area of magnetic circuit, m2; δ is the length of air gap, m; N is the number of turns of coil; \(I\) is the strength of current flowing through the coil, A; \({\mu }_{0}\) is the vacuum permeability(value: \(4\pi \times {10}^{-7}\) Wb/A m).

Electromagnetic force is calculated by magnetic circuit analysis

In this section, the armature and E magnets with silicon steel materials were researched, and three assumptions need to be made for the system before the calculated of magnetic flux and reluctance of the magnetic circuit [18]: ① It is assumed that the thickness of the silicon steel sheet is infinitesimal, the silicon steel sheet resulting on the magnetic circuit is not included. ② The silicon steel sheet is always in an unsaturated state. ③ The left and the right side of the magnetic circuit can be obtained similarly as the electromagnetic spring is a symmetrical structure.

From Kirchhoff first magnetic circuit law [19], the total magnetic flux \(\varphi\) flowing through a point in the magnet is the sum of the magnetic flux \({\Phi }_{g}\) through the air gap and the leakage flux \({\Phi }_{l}\) in the case of magnetic flux leakage, as:

$$\Phi ={\Phi }_{g}+{\Phi }_{l}.$$
(8)

The calculation formula of magnetoresistance can be obtained by referring to the information [20]:

$$R=\frac{L}{{\mu }_{D}{\mu }_{0}S},$$
(9)

where \(L\) is the average length of magnetic circuit; \(S\) is the cross-sectional area of magnetic circuit; \({\mu }_{\mathrm{D}}\) is the relative permeability of the material; \({\mu }_{0}\) is the vacuum permeability.

According to Eq. (9), the reluctance of each part can be calculated.

\({R}_{1}\) R_1 is the magneto resistance of armature.

$${R}_{1}={\int }_{0}^{\mathrm{h}}\frac{{l}_{3}}{{\mu }_{D}{\mu }_{0}{r}_{1}}\mathrm{d}h.$$
(10)

\({R}_{2}\) is the magneto resistance of work air gaps. Because of the edge effect of magnetic circuit, the acting area of work air gaps is 5%, which is larger than the actual area.

$${R}_{2}=1.05{\int }_{0}^{h}\frac{2{l}_{2}}{{\mu }_{0}{l}_{4}}\mathrm{d}h.$$
(11)

\({R}_{3}\) is the magneto resistance of E-type magnet.

$${R}_{3}={\int }_{0}^{h}\frac{2{l}_{1}-2{l}_{7}+{l}_{6}+\frac{{l}_{4}+{l}_{5}+{l}_{7}+{l}_{6}}{2}}{{\mu }_{D}{\mu }_{0}{l}_{4}}\mathrm{d}h,$$
(12)

where \({l}_{4}={l}_{5}={l}_{6}={l}_{7}\) is shown in Fig. 3. According to the empirical formula, the average magnetic circuit length at the corner of E-type magnet can be calculated by \(\frac{{l}_{4}+{l}_{7}}{2}\). Then, it is simplified and can be obtained:

Fig. 3
figure 3

Magnetic circuit diagram and Equivalent magnetic circuit

Full size image
$${R}_{3}={\int }_{0}^{h}\frac{{2l}_{1}+{l}_{4}}{{\mu }_{D}{\mu }_{0}{l}_{4}}\mathrm{d}h.$$
(13)

According to the magnetic circuit series theorem, the total reluctance \({\mathrm{R}}_{\mathrm{s}}\) of the left magnetic circuit can be calculated as

$${R}_{\mathrm{s}}=\left({\int }_{0}^{h}\frac{{l}_{3}}{{\mu }_{\mathrm{D}}{\mu }_{0}{r}_{1}}+{\int }_{0}^{h}\frac{2{l}_{1}-2{l}_{7}+{l}_{6}+\frac{{l}_{4}+{l}_{5}+{l}_{7}+{l}_{6}}{2}}{{\mu }_{\mathrm{D}}{\mu }_{0}{l}_{4}}+1.05{\int }_{0}^{h}\frac{2{l}_{2}}{{\mu }_{0}{l}_{4}}\right)\mathrm{d}h.$$
(14)

From Kirchhoff second law of magnetic circuit [21]:

$$\sum IN=\sum Hl=\sum \Phi R.$$
(15)

It can also be expressed as:

$${F}_{\mathrm{m}}={\varphi }_{2}{R}_{2}+{\varphi }_{4}{R}_{4},$$
(16)

where \({F}_{\mathrm{m}}=IN\) is the magnetomotive force generated by the coil; \({\varphi }_{4}\) is the magnetic flux passing through \({R}_{1}\) and \({R}_{3}\); \({R}_{4}\) is the sum of the reluctance of the armature and the E-type magnet, \({R}_{4}\) value of \({R}_{1}+{R}_{3}\).

$${\varphi }_{4}=\frac{{F}_{\mathrm{m}}{R}_{4}}{{R}_{4}^{2}+{R}_{2}{R}_{4}} .$$
(17)

Combining the above equations, the electromagnetic force produced by the electromagnetic institutions can be obtained:

$$F={\left(\frac{{F}_{\mathrm{m}}{R}_{4}}{{S}^{2}{R}_{4}^{2}+{R}_{2}{R}_{4}}\right)}^{2} \cdot \frac{S}{2{\mu }_{0}}=\frac{(NI{)}^{2}}{2{\mu }_{0}S}{\left(\frac{{R}_{4}}{{R}_{4}^{2}+{R}_{2}{R}_{4}}\right)}^{2} .$$
(18)

The EI-type electromagnet can be calculated with the above two methods under the condition of the working air gap smaller by electromagnetic force. While, Maxwell formula is generally considered as better candidate for calculating the electromagnetic force, as the size of the air gap is far smaller than the design size of the structure, it is assumed that there is no magnetic flux leakage in the system by default.

Substituting the structural dimensions in Fig. 1 into Eq. (7) can be obtained

$${ f}_{\mathrm{m}}=2F \cdot \mathrm{tan}\theta =\frac{{\left(NI\right)}^{2}{\mu }_{0}S}{{\delta }^{2}} \cdot \mathrm{tan}\theta .$$
(19)

The relationship between the electromagnetic force and ampere-turns of the mechanism can be obtained by combining formulas (2) and (19)

$${f}_{\mathrm{m}}=\frac{{\left(NI\right)}^{2}{\mu }_{0}S}{{{(\delta }_{0}-{(r}_{1}+{r}_{2})+\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2})}}^{2}} \cdot \frac{z}{\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2}}}.$$
(20)

According to formula (20), the electromagnetic suction is mainly related to the number of ampere-turns \(NI\), the cross-sectional area of the magnetic circuit \(S\) and the gap according to formula (20), the electromagnetic suction is mainly related to the number of ampere-turns \(NI\), the cross-sectional area of the magnetic circuit \(S\) and the gap \(\delta\). The number of turns \(N\) and the cross-sectional area \(S\) of the magnetic circuit can be determined by structural parameters. Therefore, the structure can control the electromagnetic force by adjusting the current \(I\) and changing the size of air gap \(\delta\).

The Simulation Calculation

The finite element simulation model of electromagnetic negative stiffness mechanism is established by Maxwell module in ANSYS. Compared with the theoretical electromagnetic force, the simulated electromagnetic force is obtained. The model of the device includes symmetrical E-silicon steel sheet, energized coil and movable armature. The E-magnet is fixed on the bracket, and the electromagnetic force is adjusted by the current passing through the energized coil.

The relationship between electromagnetic force and armature displacement and current is shown in Fig. 4. As can be seen from the Fig. 3, the less electromagnetic force is generated along with the less current. With the increase of the current, the electromagnetic force increases. In conclusion, the electromagnetic force is proportional to the current and inversely proportional to the air gap. The specific design parameters of the negative stiffness mechanism (Table 1) and the theoretical value and simulation value are shown in Table 2.

Fig. 4
figure 4

Relationship between electromagnetic force and armature displacement and coil current

Full size image
Table 1 Design parameters of electromagnetic negative stiffness mechanism
Full size table
Table 2 Comparison of electromagnetic force theoretical value and finite element simulation value
Full size table

As shown in Table 2, the maximum error of given electromagnetic force is 17%, while, the minimum error is 6%. Ferromagnetic material is saturated. Furthermore, the limitations of meshing and solving domain setting in finite element analysis, which inevitably leads to certain errors in calculation results. Therefore, this paper uses theoretical formula to calculate the electromagnetic force generated by the energized coil at the armature.

Figures 5, 6, 7 and 8 show the cloud distribution of magnetic flux density and vector distribution of magnetic field intensity of different air gaps, respectively.

Fig. 5
figure 5

Magnetic dense cloud diagram when I = 1.5 A

Full size image
Fig. 6
figure 6

Magnetic dense cloud diagram when I = 2.3 A

Full size image
Fig. 7
figure 7

Magnetic vector diagram when I = 1.5 A

Full size image
Fig. 8
figure 8

Magnetic vector diagram when I = 2.3 A

Full size image

Calculation of Recovery Force and Stiffness of vibration Isolation System

A QZS vibration isolator includes paralleling the electromagnetic negative stiffness mechanism and four springs positive stiffness mechanism. The vertical downward direction is defined as the positive direction as the mass is M. When the load-bearing platform moves upward, the recovery force \(f\left(z\right)\) of the vibration isolation system can be expressed as

$$f\left(z\right)=mg-4k\left({z}_{0}-z\right)+{f}_{\mathrm{m}}.$$
(21)

Substitute Eqs. (20) into (21), the recovery force can be written as

$$f\left(z\right)=mg-4k\left({z}_{0}-z\right)+\frac{{\left(NI\right)}^{2}{\mu }_{0}S \cdot z}{{{(\delta }_{0}-{(r}_{1}+{r}_{2})+\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2})}}^{2}\sqrt{{(r}_{1}+{r}_{2}{)}^{2}-{z}^{2}}},$$
(22)

where \({z}_{0}\) is the vertical displacement of the load-bearing platform with the system reaches the static equilibrium position, and \({\delta }_{0}\) is the initial air gap length.

By differentiating Eq. (22), the system stiffness can be expressed as

$$\begin{aligned} K\left( z \right) & = 4k + \frac{{\left( {NI} \right)^{2} \mu_{0} S}}{{\sqrt {(\left( {r_{1} + r_{2} } \right)^{2} - z^{2} )(m - \left( {r_{1} + r_{2} } \right) + \sqrt {\left( {r_{1} + r_{2} } \right)^{2} - z^{2} } )^{2} } }} \\ & \quad + \frac{{2\left( {NI} \right)^{2} \mu_{0} S \cdot z^{2} }}{{(\left( {r_{1} + r_{2} } \right)^{2} - z^{2} )(m - \left( {r_{1} + r_{2} } \right) + \sqrt {\left( {r_{1} + r_{2} } \right)^{2} - z^{2} } )^{3} }} \\ & \quad + \frac{{\left( {NI} \right)^{2} \mu_{0} S \cdot z^{2} }}{{\sqrt {(\left( {r_{1} + r_{2} } \right)^{2} - z^{2} )^{3} (m - \left( {r_{1} + r_{2} } \right) + \sqrt {\left( {r_{1} + r_{2} } \right)^{2} - z^{2} } )^{2} } }}{ }.{ } \\ \end{aligned}$$
(23)

When \(I=0\) and the system parameters satisfy Eq. (23), \(mg=4k{z}_{0}\). Then, the ball of the electromagnetic negative stiffness device and the CAM are located on the same axis. That is, the vibration isolator can be regarded as a passive QZS vibration isolator as the system reaches static equilibrium (\(\theta =0\)). Limiting to the load changes, the worm wheel and worm mechanism on the base can be adjusted to change the pre-compression amount of the spring, resulting the static equilibrium state. The force–displacement and rigidity–displacement curves of QZS isolators under different currents are shown in Figs. 9 and 10 below.

Fig. 9
figure 9

Recovery force–current–displacement relationship curve

Full size image
Fig. 10
figure 10

Stiffness–current–displacement relationship curve

Full size image

The design parameters includes the stiffness of the spring \(k=500\) N/m, bearing capacity \(m=10\) kg. The recovery force curve of the system is greatly affected by current. The system recovery force changes more rapidly along with increase of current, when the current \(I=2.3\) A, the system restoring force tends to a constant value while the system near the static equilibrium position, as shown in Fig. 9. The stiffness of the system is affected by the current. The system always presents negative stiffness as the current is small. On the other hand, the system stiffness tends to zero at the static equilibrium position and reaches the quasi-zero state. While, the system presents positive stiffness in other range.

The Force–Displacement Relation of Vibration Isolation System Fitted Curve

Owning to the less displacement near the static equilibrium position. To simplify the calculation, the third-order Taylor series expansion can be performed on Eq. (23) at \(z\) = 0.

Taylor’s formula

$$f\left(z\right)=\frac{f\left({z}_{0}\right)}{0!}+\frac{{f}^{\mathrm{^{\prime}}}({z}_{0})}{1!}+\frac{{f}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}({z}_{0})}{2!}+\cdots +\frac{{f}^{\left(n\right)}\left({z}_{0}\right)}{n!}.$$
(24)

Then

$$f\left(z\right)\approx 2.1\times {10}^{-2}{z}^{3}$$
(25)
$$K\left(z\right)\approx 6.3{\times {10}^{-2}z}^{2}$$
(26)

It can be concluded from Figs. 11 and 12, in the range of 10 mm near the static equilibrium position, the error between the approximate force and the exact value is small, so the fitting expression can be used to analyze the dynamic characteristics.

Fig. 11
figure 11

Force–displacement and fitting curve of vibration isolation system

Full size image
Fig. 12
figure 12

Stiffness–displacement and fitting curve of vibration isolation system

Full size image

As shown in system restoring force (Fig. 11) and stiffness (Fig. 12). When the displacement is small at the static equilibrium position, the theoretical expression can be approximated by Taylor's expansion, while with the increase of displacement, the error gradually increases.

The Dynamic Characteristics of Electromagnetic QZS Vibration Isolation System

The Dynamic Model

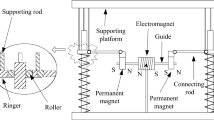
The electromagnetic spring is connected in parallel with linear spring and damper to construct a single degree of freedom electromagnetic QZS vibration isolation system. The structure principle is shown in Fig. 13.

Fig. 13
figure 13

Structural schematic diagram of electromagnetic QZS vibration isolation system

Full size image

Assume that the initial motion position for the ball with the guide rail center is located at the same horizontal plane. Where, the mass of the isolated object is \(\mathrm{m}\), the centroid was located in the center of the structure, the linear spring stiffness is \(\mathrm{k}\), the system damping is \(\mathrm{c}\), the external excitation is \(F\mathrm{cos}(\Omega T)\), the force transmitted to the base is \({F}_{t}\), and the displacement of the object to be isolated from the initial position under the action of the excitation force is \(Z\).

According to Newton’s second law, the system dynamics equation under harmonic excitation is obtained in formula 27.

$$m\ddot{Z}+c\dot{Z}+{F}_{z}={F}_{\mathrm{h}}\mathrm{cos}\left(\Omega T\right),$$
(27)

where \(\omega =\Omega \cdot {\omega }_{n}\), \({\omega }_{n}=\sqrt{k/m}\), ξ \(=c/m \cdot {\omega }_{n}\), \(z=Z/{z}_{0}\), \({\widehat{F}}_{z}={F}_{z}/k{z}_{0}\), \({\widehat{F}}_{\mathrm{h}}={F}_{\mathrm{h}}/k{z}_{0}\), \(T={\omega }_{n} \cdot t\), where \({\omega }_{n}\) indicates the natural frequency of the vibration isolation system, ξ indicates the damping ratio of the vibration isolation system, and the dimensionless recovery force and excitation force of \({\widehat{F}}_{z}\) and \({\widehat{F}}_{\mathrm{h}}\), respectively. The dimensionless system dynamics equation can be obtained by substituting the above parameters into Eq. (27)

$$\ddot{\widehat{z}}+\xi \dot{\widehat{z}}+{\widehat{F}}_{z}={\widehat{F}}_{h}\mathrm{cos}\left(\omega t\right).$$
(28)

Analysis of Amplitude–Frequency Characteristics

According to Eq. (28), the dynamics equation of QZS vibration isolation system contains a cubic term, which is a typical nonlinear system. Harmonic balance method [22] is used to solve the amplitude-frequency response of the system. The system response solution is

$$\widehat{z}=A\mathrm{cos}\left(\omega t+\varphi \right).$$
(29)

Then, Substitute Eqs. (29) into (28), and make the harmonic coefficients on both sides of the equation equal, ignoring the high-order harmonic term. Finally, the amplitude–frequency characteristic equation of the vibration isolation system under harmonic excitation is obtained.

$$(-{\omega }^{2} \cdot z+{\widehat{F}}_{z}{)}^{2}+(-\xi \cdot \omega \cdot z{)}^{2}={\widehat{F}}_{\mathrm{h}}^{2},$$
(30)

where \({\widehat{F}}_{z}=2.1\times {10}^{-2}{z}^{3}\)

Influence of System Parameters on Amplitude–Frequency Characteristics

As shown in formula 30, the amplitude frequency characteristics of QZS vibration isolation system and excitation amplitude F and system damping ratio is deduced, the influences of system parameters on the amplitude–frequency characteristics of the system are analyzed below.

Influence of Different Excitation Amplitude F on Amplitude–Frequency Characteristics

Figure 14 shows the amplitude–frequency characteristic curves, the system damping ratio is set to ξ \(=0.1\) and the excitation amplitude F is set to 0.2, 0.6, 1.0 and 1.5, respectively. When F = 0.2, the amplitude value is 3.8, and the corresponding resonance frequency is 0.55 (black line); When F = 0.6, the amplitude–frequency curve is shown in the red line in the figure. At this time, the amplitude value is 6.5, and the corresponding resonance frequency is 0.9 (red line); when F = 1.0, the amplitude value is 8.5, and the corresponding resonance frequency is 1.22 (blue line); when F = 1.5, the amplitude value is 10.4, and the corresponding resonance frequency is 1.47 (green line). In summary, both the resonance peak value and resonance frequency of the system increase with improved excitation amplitude F, enhancing the nonlinear characteristics of the system. While, the system presents linear characteristics as the excitation amplitude F decreases to a certain extent, the phenomenon of jump and resonance peak may disappear.

Fig. 14
figure 14

Influence of different excitation amplitude F on amplitude-frequency characteristics

Full size image

Influence of System Damping Ratio ξ on Amplitude–Frequency Characteristics

Figure 15 shows the simulated amplitude–frequency characteristic curve the excitation amplitude F assign as 0.6 and the system damping ratio ξ is set to 0.05, 0.1, 0.2 and 0.4, respectively. When ξ = 0.05, the total amplitude is 9.2, and the corresponding resonance frequency is 1.3 (black line); When ξ = 0.1, the total amplitude is 4.6, and the corresponding resonance frequency is 0.65 (red line); When ξ = 0.2, the jumping phenomenon basically disappears and the nonlinear characteristic weakens (blue line); when ξ = 0.4, the system presents linear characteristics (green line). Therefore, it can be concluded that the influence of the system damping ratio on the amplitude–frequency characteristics is as follows: with the increase of the system damping ratio, both the resonance peak value and resonance frequency of the system decrease, weakening the nonlinear characteristics of the system. To a certain extent, the system presents a linear characteristic, the jumping phenomenon disappears as the system damping ratio increases.

Fig. 15
figure 15

Influence of different damping ratios on amplitude-frequency characteristics

Full size image

Influence of System Parameters on Force Transmissibility

It is assumed that the dimensionless force \({\widehat{F}}_{t}\) transmits to the base

$${\widehat{F}}_{t}=\xi \cdot \dot{z}+{\widehat{F}}_{z}.$$
(31)

\(\widehat{z}=Acos\left(\omega t+\varphi \right)\) into Eq. (31)

$${\widehat{F}}_{t}=-\upxi \cdot \upomega \cdot \mathrm{z} \cdot \mathrm{sin}\left(\mathrm{\omega t}+\mathrm{\varphi }\right)+{\widehat{F}}_{z}\mathrm{cos}\left(\omega t+\varphi \right).$$
(32)

Therefore, the magnitude \(\left|{\widehat{F}}_{t}\right|\) of the force transfers to the base is:

$$\left|{\widehat{F}}_{t}\right|=\sqrt{(\xi \omega z{)}^{2}+{\widehat{F}}_{z}^{2}}.$$
(33)

The force transmissibility T of the vibration isolation system is defined as the ratio of the amplitude of the force transmitted to the base to the excitation amplitude, expressed in the form of decibels. Then, the force transmissibility of the system is

$$T=\frac{\left|{\widehat{F}}_{t}\right|}{F}=\frac{\sqrt{(\xi \omega z{)}^{2}+{\widehat{F}}_{z}^{2}}}{F} . (34)$$
(34)

According to Eq. (34), the force transmissibility electromagnetic QZS vibration isolator is related to excitation amplitude F and damping ratio ξ of system parameters. The influences of these parameters on the force transmissibility is analyzed below.

Influence of system damping ratio ξ variation on force transmissibility

The relationship between force transmissibility and damping ratio of QZS vibration isolation system is studied without changing the structural parameters of electromagnetic QZS vibration isolator. Excitation amplitude F is assigned to 0.6, system damping ratio is set to ξ = 0.05, ξ = 0.2, ξ = 0.4, ξ = 0.8, respectively, and the influence curve of damping ratio on force transmissibility is shown in Fig. 16.

Fig. 16
figure 16

Influence of system damping ratio ξ variation on force transmissibility

Full size image

In low-frequency region, the resonance frequency as well as transmission peak value reduce with the increase of system damping ratio, enhancing the vibration isolation performance, and weakening the nonlinear characteristics. The jumping phenomenon disappears as the damping ratio increases to 0.8. In high-frequency region, the force transmissibility increases with the increase of damping, decreasing isolation effect. Therefore, an appropriate damping ratio should be selected to achieve the best low-frequency isolation performance of the QZS vibration isolator.

Influence of excitation amplitude F on force transmissibility

The damping ratio is fixed to \(\delta \hspace{0.17em}\)= 0.1, and the excitation amplitude F = 0.2, F = 0.6, F = 1.0, F = 1.5 were respectively taken, and the influence curve of the excitation force on the force transmissibility is obtained as shown in Fig. 17. In low-frequency region, the resonance frequency and transmissibility peak of the vibration isolation system increase with the enhanced excitation amplitude F, and the low-frequency isolation region and initial vibration isolation frequency of the system decrease, and the vibration isolation performance decreases. In high-frequency region, the transmissibility is not affected by the excitation amplitude F. Therefore, in engineering practice, when the structural parameters are constant, the low-frequency vibration isolation performance of the vibration isolation system should be improved by reducing the excitation amplitude F.

Fig. 17
figure 17

Influence of excitation amplitude F on force transmissibility

Full size image

Comparison of Force Transmissibility Between Linear System and QZS System

Figure 18 shows the comparison between electromagnetic QZS vibration isolation system and equivalent linear vibration isolation system. The dimensionless resonance frequency is reduced from 1 to 0.53, and the dimensionless resonance amplitude is reduced from 16.33 to 7.39 (Fig. 18). Electromagnetic QZS vibration isolation system has better vibration isolation performance, it is reflected that the QZS vibration isolation system has lower peak value of force transmissibility and wider vibration isolation frequency band.

Fig. 18
figure 18

Performance comparison of two vibration isolation systems

Full size image

Conclusion and Prospect

To solve the contradiction between low natural frequency and high carrying capacity of traditional linear vibration isolators. This paper presented a new type of electromagnetic QZS vibration isolator. The calculation model of electromagnetic force and recovery force of vibration isolation system was obtained by analyzing the static characteristics. The dynamic model of system was established. The effects of damping ratio and excitation amplitude on the amplitude–frequency characteristics and the transmissibility of system was obtained by harmonic balance method. By decreasing excitation amplitude and increasing damping ratio, the initial vibration isolation frequency of the system is reduced with the broadening frequency band of vibration isolation. Which meets the requirements of low-frequency vibration signal isolation in engineering application. However, it is necessary to further explore the possibility of maintaining QZS state of vibration isolation system under different loads, so as to expand the application range of vibration isolator. Second, the application of QZS vibration isolation system in engineering practice should be explored, the design and development of compact adjustable QZS vibration isolation system with large load and high performance is carried out to meet the vibration isolation requirements under different vibration working environments.