1 Introduction

It can be known from the classical linear vibration isolation theory that the system has vibration isolation effect only when the external excitation frequency is greater than \(\sqrt 2\) times the natural frequency of the vibration isolation system. In order to expand the vibration isolation frequency bandwidth, the natural frequency of the system should be reduced. It means that the stiffness of the system is decreased, and the load-carrying capacity of the vibration system is reduced, which may cause the vibration-isolating device to be unstable during operation. Therefore, the vibration isolators with high static stiffness and low dynamic stiffness are expected in practical engineering. In recent years, a large number of studies have shown that (Ma et al. 2015; Anvar et al. 2017) high static and low dynamic stiffness isolator can effectively solve the contradiction between low-frequency vibration frequency bandwidth and vibration reduction effect and have excellent low-frequency vibration isolation performance.

In general, the high static and low dynamic stiffness isolator is a parallel connection between the positive stiffness and the negative stiffness mechanism. The positive stiffness mechanism determines the bearing capacity of the isolator, and the negative stiffness mechanism is used to reduce the dynamic stiffness of the system. Therefore, the isolator with high static and low dynamic stiffness can withstand the load quality of a large equipment, and the device has a low dynamic stiffness when vibrating at the static equilibrium position. According to the vibration isolation principle of high static and low dynamic stiffness isolator, many scholars have designed various types of vibration isolator. Alabuzhev first combined the negative stiffness device with the linear spring, studied the dynamic response of the structure, and comprehensively expounded the concept of quasi-zero-stiffness vibration isolation system (Alabuzhev et al. 1989).Carrella et al. (2007, 2008, 2009) designed a classic "three-spring" structure by connecting two tilting springs in parallel with a vertical linear spring. Meng et al. (2015) and Niu et al. (2014) proposed a design of a quasi-zero-stiffness isolator with a coned disk spring of equal thickness and variable thickness. Huang et al. (2014) proposed a method for designing a quasi-zero-stiffness system in parallel with a linear spring and a Euler flexure beam with negative stiffness. Zhou et al. (2015a, 2015b) designed a quasi-zero-stiffness vibration isolation system with a cam roller device. Wu and Sun (Wu et al. 2016; Sun and Jing 2015, 2016; Sun et al. 2014) designed the high static and low dynamic stiffness isolator of scissors structure. Lee et al. (2007) designed the negative stiffness mechanism of buckling steel sheet and studied the negative stiffness characteristics of steel sheet by using the theory of continuous thin shell. Carrella et al. (2008) proposed a three-permanent stiffness mechanism. Xu et al. (2013) designed a low-frequency isolator with quasi-zero-stiffness characteristics using a magnetic spring. Wang et al. (2021) presented a new quasi-zero-stiffness vibration isolator using double connecting rods, springs and curved surfaces as negative stiffness spring. Yao et al. (2020) designed an X-type structure quasi-zero-stiffness vibration isolation isolator. Su et al. (2020) designed a new high-static-low-dynamic stiffness vibration isolator in which the electromagnetic spring acted as a negative stiffness. Han et al. (2021) used the bi-stable Miura-origami tube as negative stiffness spring and designed a nonlinear vibration isolator with quasi-zero-stiffness. Liu et al. (2021a) proposed a quasi-zero-stiffness device by four piezoelectric buckled beams and a vertical spring, and the dynamic analysis was studied by harmonic balance method. The result shown that compared with a linear isolator, the proposed device can achieve lower isolation frequency and lower peak transmissibility. Liu et al. (2021b) designed a new quasi-zero-stiffness vibration isolation systems by inspiring the origami metamaterial.

The design parameters of the existing high-static and low-dynamic stiffness isolators are fixed, and the negative stiffness mechanism does not have the ability to adjust on-line. The aging of traditional negative stiffness elements will cause the vibration isolation system to deviate from the equilibrium position, which will lead to a decrease in vibration isolation performance. In actual engineering, it is very easy to have a mismatch between positive stiffness and load, which will cause the system dynamic response to have a rigid offset. Based on the above reasons, a new adjustable high static–low dynamic stiffness vibration isolator is presented. Compared with the existing high-static and low-dynamic vibration isolators, the vibration isolator proposed in this paper realizes on-line adjustment of negative and positive stiffness in structure. It can solve the problem of reduced vibration isolation performance due to load changes in practical projects.

The organization of this paper is as follows. In Sect. 2, a new design of adjustable high static–low dynamic stiffness vibration isolator is presented. In Sect. 3, the finite element simulation of electromagnetic positive and electromagnetic negative stiffness device is carried out. In Sect. 4, the stiffness characteristic of vibration isolator is analyzed. The dynamical equation of vibration system is established, and the influence of system parameters on the force transmission rate is discussed. A prototype is manufactured, and experimental tests are conducted. Finally, conclusions are presented in Sect. 5.

2 Structure Design of Vibration Isolator

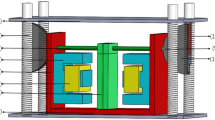
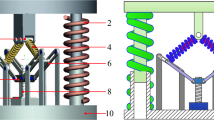
The vibration isolator with adjustable high static and low dynamic stiffness designed in this paper is shown in Fig. 1, and three dimensional is shown in Fig. 2. It can be seen that the main components of the vibration isolator are (1) electromagnetic positive stiffness device, (2) electromagnetic negative stiffness device, (3) mass block, (4) connecting rod, (5) brass ball, (6) limit device, (7) cam guide rail, (8) vertical guide rail and (9) vertical spring.

Fig. 1
figure 1

Schematic of the adjustable high static–low dynamic stiffness vibration isolator

Full size image
Fig. 2
figure 2

3-D model of the adjustable high static–low dynamic stiffness vibration isolator

Full size image

When the center of the cam is at the same level as the center of the ball, the system is in an equilibrium position. When the mass block is excited by the outside, the ball slides along the cam guide. In order to ensure the stability of the isolator with high static and low dynamic stiffness, limit devices are installed at both ends of the cam guide. When the vertical spring is aging or the load-bearing mass changes, the coil current of the positive and negative electromagnetic stiffness devices can be adjusted to restore the system to meet the conditions of low-frequency vibration isolation characteristics.

3 Mathematical Model of Electromagnetic Positive/Negative Stiffness Device

3.1 Structure of Electromagnetic Positive Stiffness Device

The structure of the electromagnetic positive stiffness device is shown in Fig. 3. The armature connector is used to fix the supporting armature. The E-type magnet is synthesized by superposition of silicon steel sheet. The parameters of silicon steel sheet are consistent with armature. The armature is composed of silicon steel sheets with thickness of 0.5 mm. In order to reduce the effect of magnetic field coupling, the upper and lower magnetic isolation layers are installed. The differential coil is made of enameled wire winding with 600 turns, and its working current range is 0–5A. The magnetic suspension bracket is made of aluminum alloy without magnetic conductivity, which can fix E-type magnet. In order to achieve the purpose of adjustable positive stiffness, the positive electromagnetic stiffness device can change the electromagnetic force produced by the electromagnet by adjusting the coil current.

Fig. 3
figure 3

Chart of electromagnetic positive stiffness mechanism

Full size image

3.2 Model of Electromagnetic Positive Stiffness Device

Electromagnetic force is the basic index reflecting the performance of electromagnetic positive stiffness device. It can provide a reliable theoretical basis for the following dynamic analysis of high static and low dynamic stiffness system. The electromagnetic force of the electromagnetic positive stiffness device is a function related to the coil current and air gap. The positive direction is set downward. The expression of the electromagnetic force can be obtained by using the simplified magnetic circuit method (Takeshi et al. 2007)

$$F_{p} = \frac{{\mu_{0} AN}}{4}^{2} \left[ {\frac{{i_{1}^{2} }}{{\left( {h - x} \right)^{2} }} - \frac{{i_{2}^{2} }}{{\left( {h + x} \right)^{2} }}} \right] .$$
(1)

3.3 Structure of Electromagnetic Negative Stiffness Device

The structural design of the electromagnetic negative stiffness device is shown in Fig. 4. The electromagnet consists of a permanent magnet and a spiral coil. The material of the electromagnet support is aluminum alloy without magnetic conductivity, which is used to fix the electromagnet. The material of the guide rail is non-magnetic aluminum alloy. The working principle of the electromagnetic negative stiffness device is to achieve the purpose of adjusting the equivalent stiffness by changing the current of the electromagnet coil. The permanent magnets on both sides and the intermediate electromagnet generate a repulsive force. When the coil current changes, the repulsive force changes to cause the two permanent magnets to slide on the smooth rail. The three-dimensional model is drawn by Solidwoks software, as shown in Fig. 5.

Fig. 4
figure 4

Chart of electromagnetic negative stiffness mechanism

Full size image
Fig. 5
figure 5

3-D solid model of electromagnetic negative stiffness mechanism

Full size image

3.3.1 Finite Element Simulation of Electromagnetic Negative Stiffness Device

The finite element simulation model of the electromagnetic negative stiffness mechanism is established by the finite element software Ansoft Maxwell, and the magnitude of the electromagnetic force is calculated. The finite element simulation model is shown in Fig. 6a. According to the simulation model Fig. 6b, the upper and lower black permanent magnets correspond to the structure (1) and (4) in Fig. 4, the aluminum alloy guide rails correspond to the structure (5) in Fig. 4, and the middle part is the electromagnetic structure composed of permanent magnet and solenoid coil. The specific structural parameters are shown in Table 1.

Fig. 6
figure 6

Finite element model of electromagnetic negative stiffness mechanism

Full size image
Table 1 Structural parameters of the electromagnetic negative stiffness mechanism
Full size table

By changing the coil current and the gap between the movable permanent magnet and the outside of the coil, the electromagnetic force under different conditions is obtained, as shown in Fig. 7. It can be seen that the electromagnetic force is proportional to the current and inversely proportional to the gap. Figures 8 and 9 show the flux distribution and magnetic field strength vector distribution of several different currents and gaps.

Fig. 7
figure 7

Graph of electromagnetic force–current–gap

Full size image
Fig. 8
figure 8

Distribution diagram of magnetic flux density

Full size image
Fig. 9
figure 9

Distribution diagram of magnetic intensity vector

Full size image

In order to facilitate the mechanical analysis of the system, the finite element simulation data are used to simulate a mathematical expression that is simple in structure and can be used to describe the model of the electromagnetic negative stiffness device. According to the data obtained by finite element simulation, the curves are fitted by software, and the approximate formula is:

$$f_{m} = w_{1} e^{{\frac{I}{{w_{2} }} - \frac{d}{{w_{3} }}}}$$
(2)

where w1 = 123.6, w2 = 12.8, w3 = 20.5, d is the distance between the movable permanent magnet and the end face of the spiral coil, and I is the current in the coil. The finite element simulation values and fitting curves are shown in Figs. 10 and 11. It can be seen that the error between the approximate formula and the finite element simulation data is small, and it can be used to describe the variation law of electromagnetic force of the electromagnetic negative stiffness device.

Fig. 10
figure 10

Comparison between fitted curve and finite element value when I is 0A,1A and 2A

Full size image
Fig. 11
figure 11

Comparison between fitted curve and finite element value when I is 3A, 4A and 5A

Full size image

4 Characteristic Analysis and Experimental Research of the System

4.1 Static Analysis

When the isolator starts to work, the sphere slides along the cam guide, as shown in Fig. 12. The vertical spring stiffness is k, the radius of the cam is \(r_{1}\), and the radius of the spherical head is \(r_{2}\). The defined coordinate z is the displacement in the vertical direction from the static equilibrium position, and the downward direction is positive.

Fig. 12
figure 12

Schematic diagram of position of roller and cam when system activated

Full size image

The restoring force of the vibration isolation system is expressed as:

$$f(z) = mg - 4k(z_{0} - z) - \frac{{\mu_{0} AN^{2} I_{1}^{2} }}{4}\left( {\frac{1}{{(h - z)^{2} }} - \frac{1}{{(h + z)^{2} }}} \right) - 2f_{m} \tan \alpha$$
(3)

where z0 is the deflection of the vertical spring at the equilibrium position, \(I_{1}\) is the coil current of electromagnetic positive stiffness structure,\(I_{2}\) is the coil current of electromagnetic negative stiffness structure, and \(\alpha\) is the angle between the center line and the horizontal direction.

Noting that \(\tan \alpha = {z \mathord{\left/ {\vphantom {z {\sqrt {(r_{2} + r_{2} )^{2} - z^{2} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {(r_{2} + r_{2} )^{2} - z^{2} } }}\), Eq. (3) can be written as

$$f(z) = mg - 4k(z_{0} - z) - \frac{{\mu_{0} AN^{2} I_{1}^{2} }}{4}\left( {\frac{1}{{(h - z)^{2} }} - \frac{1}{{(h + z)^{2} }}} \right) - \frac{{2zw_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} }}{{\sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}$$
(4)

where d0 is the distance between the permanent magnets on both sides of the electromagnetic negative stiffness device and the spiral coil when the system is at the static equilibrium position.

Differentiating Eq. (4), the stiffness K can be obtained:

$$\begin{aligned} K(z) & = 4k - \frac{{\mu_{0} AN^{2} I_{1}^{2} }}{4}\left( {\frac{2}{{(h - z)^{3} }} + \frac{2}{{(h + z)^{3} }}} \right) - \frac{{2z^{2} w_{1} }}{{[(r_{1} + r_{2} )^{2} - z^{2} ]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }}e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} \\ & \quad - \frac{{2w_{1} }}{{\sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} + \frac{{2z^{2} w_{1} }}{{[(r_{1} + r_{2} )^{2} - z^{2} ]w_{3} }}e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} \\ \end{aligned}$$
(5)

By setting \(x = 0\) and \(K = 0\), we can obtain the condition that should be satisfied when the system achieves quasi-zero-stiffness.

$$4k - \frac{{2w_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}}} }}{{r_{1} + r_{2} }} - \frac{{A\mu_{0} N^{2} I_{1}^{2} }}{{h^{3} }} = 0$$
(6)

If \(I_{1} = I_{2} = 0\) and the parameters satisfy Eq. (6), the isolator can be regarded as a passive quasi-zero-stiffness isolator. Assume that when the rated load of the system is m, the center line between the ball and the cam is just in the horizontal state, that is \(mg = 4kz_{0}\), the armature of the electromagnetic positive stiffness device is at the initial position, and the system reaches the static balance. At this time, the current of the electromagnetic positive stiffness device is zero. If the load changes, the operating point of the system can be restored to the original equilibrium position by adjusting the current of the electromagnetic positive stiffness device. The force and stiffness of the system under the rated load are as follows:

$$f(z) = 4kz - \frac{{2zw_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} }}{{\sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}$$
(7)
$$K(z) = 4k - \frac{{2z^{2} w_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} }}{{[(r_{1} + r_{2} )^{2} - z^{2} ]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} }} - \frac{{2w_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} }}{{\sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }} + \frac{{2z^{2} w_{1} e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} + (r_{1} + r_{2} ) - \sqrt {(r_{1} + r_{2} )^{2} - z^{2} } }}{{w_{3} }}}} }}{{[(r_{1} + r_{2} )^{2} - z^{2} ]w_{3} }}$$
(8)

The system parameters are k = 1500 N/m, d0 = 0.005 m, r1 = 0.045 m, r2 = 0.006 m, respectively. Using Eq. (6), it can be calculated that the current in the electromagnetic negative stiffness device is \(I_{{2{\text{QZS}}}}\) = 3.56 A when the system achieves the quasi-zero-stiffness.

The relationship between force, current and displacement of vibration isolator is shown in Fig. 13. It can be seen that the nonlinearity of the system becomes stronger with the increase of the current. The relationship between stiffness, current and displacement of vibration isolator is shown in Fig. 14. It can be seen from the figure, when the current is small, the system always exhibits positive stiffness. When the current increases to \(I_{{2{\text{QZS}}}}\), the stiffness of system at the static equilibrium position is zero, and the stiffness is always positive in other intervals. When the current is too large, the electromagnetic negative stiffness device plays a leading role in the system, which will cause the system to have a negative stiffness within a certain interval.

Fig. 13
figure 13

Curve of force–current–displacement

Full size image
Fig. 14
figure 14

Curve of stiffness-current-displacement

Full size image

When the displacement of the system is small near the static equilibrium position, Eq. (8) can be expanded by the Taylor series,

$$f(z) \approx az + bz^{3}$$
(9)
$$K \approx a + 3bz^{2}$$
(10)

where \(a = 4k - \frac{{2w_{1} }}{{r_{1} + r_{2} }}e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}}}\), \(b = \left[ {\frac{{w_{1} }}{{w_{3} (r_{1} + r_{2} )^{2} }} - \frac{{w_{1} }}{{(r_{1} + r_{2} )^{3} }}} \right]e^{{\frac{{I_{2} }}{{w_{2} }} - \frac{{d_{0} }}{{w_{3} }}}}\).

The comparison curves between the exact expressions and the approximate expressions are shown in Fig. 15. It can be seen that the error between the exact and approximate expressions of force and stiffness increases with the increase in displacement. When the displacement of the system is small at the static equilibrium position, the error is neglected, so the Taylor series expansion can simulate the exact expression.

Fig. 15
figure 15

Comparison between approximate and exact expressions (\(I_{2} = 3.56{\text{A}}\))

Full size image

4.2 The Force Transmissibility Analysis

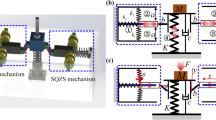
The dynamic model of the vibration isolation system under the external excitation force is shown in Fig. 16. The initial movement position is that the ball is located at the apex of the cam guide. The mass block is M, the damping is c, the external excitation is Fh, and the force transmitted to the base is Ft. The displacement of the mass block from the initial position to the downward direction is Z.

Fig. 16
figure 16

Dynamical model of single-degree-of-freedom system

Full size image

The dynamic equation of the system is

$$M\ddot{Z} + c\dot{Z} + aZ + bZ^{3} = F_{h} \cos \left( {\Omega T} \right)$$
(11)

Introducing the non-dimensional parameters, \(\Omega_{0} = \sqrt {{k \mathord{\left/ {\vphantom {k M}} \right. \kern-\nulldelimiterspace} M}}\), \(\Omega = \Omega_{0} \omega\), \(\xi = {c \mathord{\left/ {\vphantom {c {\sqrt {Mk} }}} \right. \kern-\nulldelimiterspace} {\sqrt {Mk} }}\), \(t = \Omega_{0} T\), \(F = {{F_{h} } \mathord{\left/ {\vphantom {{F_{h} } {(kz_{0} )}}} \right. \kern-\nulldelimiterspace} {(kz_{0} )}}\), \(\phi = {a \mathord{\left/ {\vphantom {a k}} \right. \kern-\nulldelimiterspace} k}\), \(\gamma = {{(bz_{0}^{2} )} \mathord{\left/ {\vphantom {{(bz_{0}^{2} )} k}} \right. \kern-\nulldelimiterspace} k}\), \(z = {Z \mathord{\left/ {\vphantom {Z {z_{0} }}} \right. \kern-\nulldelimiterspace} {z_{0} }}\), Eq. (11) becomes

$$\ddot{z} + \xi \dot{z} + \phi z + \gamma z^{3} = F\cos \left( {\omega t} \right)$$
(12)

The transmitted force as shown in Fig. 16 is given as

$$F_{t} = \xi \dot{z} + \phi z + \gamma z^{3}$$
(13)

Suppose the response of the system has the form \(z(t) = r\cos (\omega t + \psi )\), substitute it to Eq. (13) and omit the higher harmonic terms. The magnitude of the transmitted force is obtained:

$$\hat{F}_{t} = \sqrt {\left( {\xi \omega r} \right)^{2} + \left( {\phi r + \frac{3}{4}\gamma r^{3} } \right)^{2} }$$
(14)

Thus, the force transmissibility of system is given:

$$T = \frac{{\sqrt {\left( {\xi \omega r} \right)^{2} + \left( {\phi r + \frac{3}{4}\gamma r^{3} } \right)^{2} } }}{F}$$
(15)

According to Eq. (15), the force transmission rate of the single-degree-of-freedom high-static and low-dynamic-stiffness vibration isolation system is related to the excitation amplitude F, damping ratio \(\xi\), and system parameters that vary with current. The influence of each parameter on the force transmission rate is analyzed in detail as follows:

(1) The excitation amplitude F is varied. When the system parameters \(\xi_{{}} = 0.2\), \(I_{2} = 3.56\), the force transmissibility for several values of the excitation amplitude parameter is plotted in Fig. 17. With the increase of the excitation amplitude, the transmission rate peak and the resonance frequency are increased, and the low frequency isolation range of the system decreases. When the excitation frequency is large, the curve is close to coincident, and the force transfer rate effect tends to be consistent. It can also be seen from Fig. 17 that compared with the equivalent linear system, the peak value of the transmission rate of the high static and low dynamic stiffness vibration isolation system is smaller, the starting vibration isolation frequency is lower, the vibration isolation range is larger, and the vibration isolation performance is better.

Fig. 17
figure 17

Force transmissibility curve of the system when parameter F is varied

Full size image

(2) The damping ratio \(\xi\) is varied. When the system parameters F = 2, I2 = 3.56, the force transmissibility for several values of the damping ratio is plotted in Fig. 18. When the damping is relatively small, the jump phenomenon is obvious. As the damping ratio increases, both the peak transmission rate and the resonant frequency decrease, and the system's vibration isolation effect gradually increases in the low-frequency band and gradually decreases in the high-frequency band. When the damping ratio increases to a certain level, the system exhibits a linear characteristic and the jump phenomenon disappears. Compared with the equivalent linear system, the peak value of the transmission rate of the high static and low dynamic stiffness vibration isolation system is smaller, the starting vibration isolation frequency is lower, and the vibration isolation range is enlarged.

Fig. 18
figure 18

Force transmissibility curve of the system when parameter \(\xi\) is varied

Full size image

(3)The current I2 is varied. When the system parameters \(F = 1\), \(\xi = 0.2\), the force transmissibility given for several values of the current is plotted in Fig. 19. When the current is small, the system exhibits a linear characteristic. As the current increases, the peak value of the system's force transmission rate decreases, while the resonance frequency increases, and the effective vibration isolation range becomes smaller. Therefore, for this type of high static low dynamic stiffness isolators, the variation of current parameters will affect system stability and vibration isolation performance.

Fig. 19
figure 19

Force transmissibility curve of the system when parameter I2 is varied

Full size image

4.3 Experimental Research

According to the design scheme of the high static–low dynamic stiffness vibration isolator, a prototype is manufactured as shown in Fig. 20a. The electromagnetic negative stiffness device is set at the equilibrium position. According to the design idea, the electromagnetic positive stiffness device does not work under rated load. At this time, the current of the electromagnetic negative stiffness device is adjusted to obtain a better low frequency vibration isolation performance. In order to verify the vibration isolation performance of the adjustable high-static-low-dynamic stiffness isolator, a test platform is built as Fig. 20b.

Fig. 20
figure 20

Prototype and test platform

Full size image

The force transmission rate curves of the adjustable high static–low dynamic stiffness vibration system and equivalent linear system are shown in Fig. 21. It can be seen that the resonance frequency of the equivalent linear system is 7.8 Hz, and the peak value of the force transmission rate is 54.32 dB. When the input current is 4 A, the resonance frequency of the high static and low dynamic stiffness vibration isolation system is 3.6 Hz, and the peak force transmission rate is 33.57 dB. When the input current is 5A, the resonance frequency is 2.8 Hz, and the peak value of the force transmission rate is 26.43 dB. It shows that the principle of the designed electromagnetic negative stiffness device is correct, which can effectively reduce the natural frequency of the system and widen the vibration isolation frequency range of the system. Compared with the equivalent linear system, the vibration isolation effect is relatively better.

Fig. 21
figure 21

Comparison of transmissibility curves under different currents

Full size image

5 Conclusions

In this paper, a new structure of high static–low dynamic stiffness vibration isolator is designed. Through finite element simulation, the force expressions of electromagnetic positive stiffness device and electromagnetic negative stiffness device are obtained. The static analysis shows that the current is the key parameter for the system to achieve quasi-zero-stiffness at the static equilibrium position. The dynamical equation of the high static–low dynamic stiffness vibration isolation system has been solved by using the harmonic balance method. The effects of system parameters on the force transmissibility are investigated. The prototype of the high static–low dynamic stiffness isolator is tested, and the experimental results of the force transmissibility are obtained. The results indicate that the new isolator outperforms the linear system and has the advantages of widening the vibration isolation range and improving the low-frequency vibration isolation effect.