Introduction

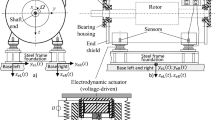
Large rotating machines are often directly mounted on elastic steel frame foundations, which sometimes lead to vibration problems, where e.g. critical speeds are lying in the operation speed range [1,2,3,4,5]. Implementing active vibration control [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] is an appropriate method to reduce vibrations, which is used in different technical applications. Here, the active vibration system consists of active machine foot mounts—actuators, which are positioned under the machine feet and only acting in vertical direction—and vibration sensors, which are mounted at each machine foot and detect the vertical vibrations leading this information to separate controllers (Fig. 1). This concept was basically described and investigated in [25], but only for induction motors and it was only based on a plane 2D-model. In this paper, a general model for rotating machines mounted on actuators is derived, based on a 3D model. Additionally, the gyroscopic effect of the rotor is considered here in the paper. The 3D model is kept very simple here, because the main task is here not to derive a detailed model, but to present the concept of active vibration control, using a method called here “vibration mode coupling by asymmetry”, which will explained in this paper.

Fig. 1
figure 1

Rotating machine (here induction motor) mounted on actuators

Full size image

Vibration Model

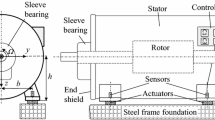
The vibration model is a simplified 3D model (Fig. 2), where the machine mass \({m}_{\rm{sr}}\) and the moments of inertia \({\theta }_{\rm{sry}}\), \({\theta }_{\rm{srz}}\), \({\theta }_{\rm{sx}}\) and \({\theta }_{\rm{rx}}\) of the machine are concentrated at the center of gravity \(S\). The rotational angular frequency of the machine is described by Ω.

Fig. 2
figure 2

Simplified 3D model of a rotating machine, mounted on actuators

Full size image

In this simplified model, the rotor stiffness and the stiffness of the bearings, as well as the bearing support stiffness and the stator stiffness is assumed infinitely high. The foundation stiffness is here assumed to be so much higher as the actuator stiffness, so that the foundation stiffness is here also defined infinitely high in that model.

Therefore, following considerations are made:

  • The machine mass \({m}_{\rm{sr}}\) consists of the stator mass \({m}_{\rm{s}}\) and of the rotor mass \({m}_{\rm{r}}\) (index s for stator and index r for rotor) and is considered as a single mass in the mass matrix.

    $${m}_{\rm{sr}}={m}_{\rm{s}}+{m}_{\rm{r}}.$$
    (1)

  • The same is valid for the moments of inertia \({\theta }_{\rm{sry}}\) and \({\theta }_{\rm{srz}}\), which consist of the moments of inertia of the stator \({\theta }_{\rm{sy}}\) and \({\theta }_{\rm{sz}}\) and of the rotor \({\theta }_{\rm{ry}}\) and \({\theta }_{\rm{rz}}\), and are also considered in the mass matrix.

    $${\theta }_{\rm{sry}} ={\theta }_{\rm{sy}} +{\theta }_{\rm{ry}};\, {\theta }_{\rm{srz}} ={\theta }_{\rm{sz}} +{\theta }_{\rm{rz}}.$$
    (2)

  • The moment of inertia \({\theta }_{\rm{sx}}\) of the stator and of the rotor \({\theta }_{\rm{rx}}\) at the x-axis have to be considered separately, because of the necessity that the rotation at the x-axis of the rotor has to be free. Therefore, \({\theta }_{\rm{sx}}\) has to be considered in the mass matrix; however, \({\theta }_{\rm{rx}}\) in the gyroscopic matrix.

  • The centers of gravity of the stator and of the rotor are here at identical positions, lying in point S.

The bearing point on the drive side is described by \({B}_{\rm{D}}\) and on the non-drives side by \({B}_{\rm{N}}\). The machine feet are described by the points \({A}_{\rm{DL}}\), \({A}_{\rm{DR}}\), \({A}_{\rm{NL}}\) and \({A}_{\rm{NR}}\). Index \(D\) is used for drive side, index \(N\) for non-drive side and index \(L\) for left side and \(R\) for right side, with the definition:

$$i=D,N;j=L,R.$$
(3)

The mass of each amateur of the actuators is described by \({m}_{\rm{aDL}}\), \({m}_{\rm{aDR}}\), \({m}_{\rm{aNL}}\) and \({m}_{\rm{aNR}}\). The stiffness matrix and the damping matrix of each actuator—only considering translation stiffness and damping—are described by

$${\mathbf{C}}_{\mathbf{a}\mathbf{i}\mathbf{j}}=\left[\begin{array}{ccc}{c}_{\rm{azij}}& 0& 0\\ 0& {c}_{\rm{ayij}}& 0\\ 0& 0& {c}_{\rm{axij}}\end{array}\right];\,{\mathbf{D}}_{\mathbf{a}\mathbf{i}\mathbf{j}}=\left[\begin{array}{ccc}{d}_{\rm{azij}}& 0& 0\\ 0& {d}_{\rm{ayij}}& 0\\ 0& 0& {d}_{\rm{axij}}\end{array}\right].$$
(4)

For the universal case, each actuator may have different mass and different stiffness and damping matrices. Five global coordinate systems are used here, one at the center of gravity \(S\) and one for each machine foot.

Using a vibration sensor for each machine foot, each vertical (z-direction) machine foot displacement or velocity or acceleration can be lead back to a separate controller \({C}_{\rm{rDL}}\), \({C}_{\rm{rDR}}\), \({C}_{\rm{rNL}}\) and \({C}_{\rm{rNR}}\), creating adequate signals to produce the vertical actuator forces \({f}_{\rm{azDL}}\), \({f}_{\rm{azDR}}\), \({f}_{\rm{azNL}}\) and \({f}_{\rm{azNR}}\). Each controller may have a different arbitrary controller structure, described in the Laplace domain, with the Laplace variable \(s\) by following transfer function:

$${\text{Controller }}{C}_{{rij}}:{G}_{\text{cij},\gamma }\left(s\right)=\frac{{\sum }_{{{\mu}{ {ij}}}=0}^{mij}{b}_{\upmu {\text{ij}},\gamma }\cdot {S}^{\mu {ij}}}{{\sum }_{{vij}=0}^{nij}{a}_{\text{vij},\gamma }\cdot {S}^{{vij}}},$$
(5)

where \({b}_{{\upmu {\text{ij}}},\upgamma }\) and \({a}_{{\upnu {\text{ij}}},\upgamma }\) are the constants of the polynomial functions. The index \(\gamma \) depends on the chosen feedback strategy:

$$ \gamma = \left\{ \begin{gathered} 0\,\,\,\,\,\,\,\,\,{:}\,{\text{No}}\,{\text{feedback (open}}\,{\text{control}}\,{\text{loops)}} \hfill \\ z\,\,\,\,\,\,\,\,\,{:}\,{\text{Feedback}}\,{\text{of}}\,{\text{the}}\,{\text{vertical}}\,{\text{motor}}\,{\text{feet}}\,{\text{displacements }}z_{{{\text{aDL}}}} ,z_{{{\text{aDR}}}} ,z_{{{\text{aNL}}}} ,z_{{{\text{aNR}}}} \hfill \\ v\,\,\,\,\,\,\,\,\,{:}\,{\text{Feedback}}\,{\text{of}}\,{\text{the}}\,{\text{vertical}}\,{\text{motor}}\,{\text{feet}}\,{\text{velocities}}\,\,v_{{\text{z,aDL}}} ,v_{{\text{z,aDR}}} ,v_{{\text{z,aNL}}} ,v_{{\text{z,aNR}}} \hfill \\ a\,\,\,\,\,\,\,\,\,{:}\,{\text{Feedback}}\,{\text{of}}\,{\text{the}}\,{\text{vertical}}\,{\text{motor}}\,{\text{feet}}\,{\text{accelerations }}\,a_{{\text{z,aDL}}} ,a_{{\text{z,aDR}}} ,a_{{\text{z,aNL}}} ,a_{{\text{z,aNR}}} \hfill \\ \end{gathered} \right.. $$
(6)

At the center of gravity \(S\) an excitation vector \(\mathbf{e}\) is positioned, described by

$$\mathbf{e}\left(t\right)={\left[{\mathbf{e}}_{\mathbf{f}};\,{\mathbf{e}}_{\mathbf{m}}\right]}^{T}={\left[{e}_{\rm{fz}}; {e}_{\rm{fy}};\,{e}_{\rm{fx}};\,{e}_{\rm{mz}};\,{e}_{\rm{my}};\,{e}_{\rm{mx}}\right]}^{T},$$
(7)

where \({\mathbf{e}}_{\mathbf{f}}\) is a dynamic force vector including the dynamic forces \({e}_{\rm{fz}}, {e}_{\rm{fy}}\rm{ and }{e}_{\rm{fx}}\) in z-, y- and x-directions and \({\mathbf{e}}_{\mathbf{m}}\) is a dynamic moment vector including the dynamic moments \({e}_{\rm{mz}}, {e}_{\rm{my}}\rm{ and }{e}_{\rm{mx}}\) at the x-, y- and x-axes.

Mathematical Model

Formulation in the Time Domain

Due to small displacements caused by the excitation vector \(\mathbf{e}\), a linearization of the machine feet displacements is possible, leading to the following kinematic constraints.

  • For vertical direction:

    $$\begin{array}{c}{z}_{\rm{aDL}}={z}_{\rm{s}}-{b}_{\rm{L}}\cdot {\varphi }_{\rm{sx}}+{a}_{\rm{D}}\cdot {\varphi }_{\rm{sy}}; {z}_{\rm{aNL}}={z}_{\rm{s}}-{b}_{\rm{L}}\cdot {\varphi }_{\rm{sx}}-{a}_{\rm{N}}\cdot {\varphi }_{\rm{sy},}\\ {z}_{\rm{aDR}}={z}_{\rm{s}}+{b}_{\rm{R}}\cdot {\varphi }_{\rm{sx}}+{a}_{\rm{D}}\cdot {\varphi }_{\rm{sy}}; {z}_{\rm{aNR}}={z}_{\rm{s}}+{b}_{\rm{R}}\cdot {\varphi }_{\rm{sx}}-{a}_{\rm{N}}\cdot {\varphi }_{\rm{sy}}.\end{array}$$
    (8)

  • For horizontal direction:

    $$\begin{array}{c}{y}_{\rm{aDL}}={y}_{\rm{s}}-h\cdot {\varphi }_{\rm{sx}}-{a}_{\rm{D}}\cdot {\varphi }_{\rm{sz}}; {y}_{\rm{aNL}}={y}_{\rm{s}}-h\cdot {\varphi }_{\rm{sx}}+{a}_{\rm{N}}\cdot {\varphi }_{\rm{sz},}\\ {y}_{\rm{aDR}}={y}_{\rm{s}}-h\cdot {{\varphi }}_{\rm{sx}}-{a}_{\rm{D}}\cdot {\varphi }_{\rm{sz}}; {y}_{\rm{aNR}}={y}_{\rm{s}}-h\cdot {\varphi }_{\rm{sx}}+{a}_{\rm{N}}\cdot {\varphi }_{\rm{sz}}.\end{array}$$
    (9)

  • For axial direction:

    $$\begin{array}{c}{x}_{\rm{aDL}}={x}_{\rm{s}}+{b}_{\rm{L}}\cdot {\varphi }_{\rm{sz}}+h\cdot {\varphi }_{\rm{sy}}; {x}_{\rm{aNL}}={x}_{\rm{s}}+{b}_{\rm{L}}\cdot {\varphi }_{\rm{sz}}+h\cdot {{\varphi }}_{\rm{sy}},\\ {x}_{\rm{aDR}}={x}_{\rm{s}}-{b}_{\rm{R}}\cdot {\varphi }_{\rm{sz}}+h\cdot {\varphi }_{\rm{sy}}; {x}_{\rm{aNR}}={x}_{\rm{s}}-{b}_{\rm{R}}\cdot {\varphi }_{\rm{sz}}+h\cdot {\varphi }_{\rm{sy}}.\end{array}$$
    (10)

Therefore, all machine feet displacements can be described by the movement of the machine center point \(S,\) where \({x}_{\rm{s}}\), \({y}_{\rm{s}}\) and \({z}_{\rm{s}}\) are the translational movements of point \(S\) and \({\varphi }_{\rm{sx}}\), \({\varphi }_{\rm{sy}}\) and \({\varphi }_{\rm{sz}}\) are the rotational movements of point \(S\).

Also the displacements of the bearing, center points \({B}_{\rm{D}}\) and \({B}_{\rm{N}}\) can be described by the movement of point \(S\):

  • For vertical direction:

    $${z}_{\rm{bD}}={z}_{\rm{s}}+{l}_{\rm{D}}\cdot {\varphi }_{\rm{sy}}; {z}_{\rm{bN}}={z}_{\rm{s}}-{l}_{\rm{N}}\cdot {\varphi }_{\rm{sy}}.$$
    (11)

  • For horizontal direction:

    $${y}_{\rm{bD}}={y}_{\rm{s}}-{l}_{\rm{D}}\cdot {\varphi }_{\rm{sz}}; {y}_{\rm{bN}}={y}_{\rm{s}}+{l}_{\rm{N}}\cdot {\varphi }_{\rm{sz}}.$$
    (12)

  • For axial direction:

    $${x}_{\rm{bD}}={x}_{\rm{s}}; {x}_{\rm{bN}}={x}_{\rm{s}}.$$
    (13)

Following differential equation can now be derived, where \(\mathbf{e}\) is the excitation vector, and \({\mathbf{f}}_{\mathbf{a}}\) the vector of the actuator forces:

$$\mathbf{M}\cdot \ddot{\mathbf{q}}+\left(\mathbf{D}+\mathbf{G}\right)\cdot \dot{\mathbf{q}}+\mathbf{C}\cdot \mathbf{q}=\mathbf{e}+{\mathbf{f}}_{\mathbf{a}}$$
(14)

with the homogeneous differential equation, if all control loops are open:

$$\mathbf{M}\cdot \ddot{\mathbf{q}}+\left(\mathbf{D}+\mathbf{G}\right)\cdot \dot{\mathbf{q}}+\mathbf{C}\cdot \mathbf{q}= {\bf 0}$$
(15)

The vector \(\mathbf{q}\left(t\right)\) contains the coordinates for displacements and the rotations of the machine center point \(S\):

$$\mathbf{q}\left(t\right)={\left[{z}_{\rm{s}};\,{y}_{\rm{s}};\,{x}_{\rm{s}};\,{\varphi }_{\rm{sz}};\,{\varphi }_{\rm{sy}};\,{\varphi }_{\rm{sx}}\right]}^{T}.$$
(16)

The excitation vector \(\mathbf{e}\left(t\right)\) can be described according to (7). The actuator force vector \({\mathbf{f}}_{\mathbf{a}}\) can be split into the actuator force vector for each machine foot:

$$ \begin{aligned} {\mathbf{f}}_{{\mathbf{a}}} \left( t \right) & = {\mathbf{f}}_{{{\mathbf{aDL}}}} \left( t \right) + {\mathbf{f}}_{{{\mathbf{aDR}}}} \left( t \right) + {\mathbf{f}}_{{{\mathbf{aNL}}}} \left( t \right) + {\mathbf{f}}_{{{\mathbf{aNR}}}} \left( t \right) \\ & = f_{{{\text{azDL}}}} \left( t \right) \cdot \underbrace {{\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ {a_{{\text{D}}} } \\ { - b_{{\text{L}}} } \\ \end{array} } \right]}}_{{{\mathbf{P}}_{{{\mathbf{aDL}}}} }} + f_{{{\text{azDR}}}} \left( t \right) \cdot \underbrace {{\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ {a_{{\text{D}}} } \\ {b_{{\text{R}}} } \\ \end{array} } \right]}}_{{{\mathbf{P}}_{{{\mathbf{aDR}}}} }} + f_{{{\text{azNL}}}} \left( t \right) \cdot \underbrace {{\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ { - a_{{\text{N}}} } \\ { - b_{{\text{L}}} } \\ \end{array} } \right]}}_{{{\mathbf{P}}_{{{\mathbf{aNL}}}} }} + f_{{{\text{azNR}}}} \left( t \right) \cdot \underbrace {{\left[ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ { - a_{{\text{N}}} } \\ {b_{{\text{R}}} } \\ \end{array} } \right]}}_{{{\mathbf{P}}_{{{\mathbf{aNR}}}} }}. \\ \end{aligned} $$
(17)

The vectors \({\mathbf{P}}_{\mathbf{a}\mathbf{D}\mathbf{L}}\), \({\mathbf{P}}_{\mathbf{a}\mathbf{D}\mathbf{R}}\), \({\mathbf{P}}_{\mathbf{a}\mathbf{N}\mathbf{L}}\) and \({\mathbf{P}}_{\mathbf{a}\mathbf{N}\mathbf{R}}\) are the actuator force transmission vectors.

The mass matrix \(\mathbf{M}\), the damping matrix \(\mathbf{D}\) and the stiffness matrix \(\mathbf{C}\) are described by

$$\mathbf{M}=\left[\begin{array}{ccc}{m}_{\rm{1,1}}& \cdots & {m}_{\rm{1,6}}\\ \vdots & \ddots & \vdots \\ {m}_{\rm{6,1}}& \dots & {m}_{\rm{6,6}}\end{array}\right]; \mathbf{D}=\left[\begin{array}{ccc}{d}_{\rm{1,1}}& \cdots & {d}_{\rm{1,6}}\\ \vdots & \ddots & \vdots \\ {d}_{\rm{6,1}}& \dots & {d}_{\rm{6,6}}\end{array}\right]; \mathbf{C}=\left[\begin{array}{ccc}{c}_{\rm{1,1}}& \cdots & {c}_{\rm{1,6}}\\ \vdots & \ddots & \vdots \\ {c}_{\rm{6,1}}& \dots & {c}_{\rm{6,6}}\end{array}\right].$$
(18)

The coefficients of the matrices are shown in “Appendix A”. The gyroscopic matrix \(\mathbf{G}\) is described by

$$\mathbf{G}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \Omega \cdot {\theta }_{\rm{rx}}& 0\\ 0& 0& 0& -\Omega \cdot {\theta }_{\rm{rx}}& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right].$$
(19)

Further, a state space formulation, based on [15,16,17,18], is used.

Index “st” is used for the matrices of the state space to avoid mix-up with the stiffness matrix \(\mathbf{C}\) and damping matrix \(\mathbf{D}\). According to Fig. 3 the state space vector \(\mathbf{x}(t)\) and the output vector \(\mathbf{y}(t)\) can be described as follows:

Fig. 3
figure 3

State space model for vibration control of the vibration system with negative feedback of the output vector

Full size image
$$\mathbf{x}\left(t\right)=\left[\begin{array}{c}\mathbf{q}\left(t\right)\\ \dot{\mathbf{q}}\left(t\right)\end{array}\right];\mathbf{y}\left(t\right)=\left[\begin{array}{c}\mathbf{q}\left(t\right)\\ \dot{\mathbf{q}}\left(t\right)\\ \ddot{\mathbf{q}}\left(t\right)\end{array}\right].$$
(20)

The system matrix \({\mathbf{A}}_{\mathbf{s}\mathbf{t}}\), the input matrix \({\mathbf{B}}_{\mathbf{s}\mathbf{t}}\), the output matrix \({\mathbf{C}}_{\mathbf{s}\mathbf{t}}\), and the straight-way matrix \({\mathbf{D}}_{\mathbf{s}\mathbf{t}}\) can be written as

$$\begin{array}{c}{\mathbf{A}}_{\mathbf{s}\mathbf{t}}=\left[\begin{array}{cc}{\boldsymbol 0}_{6}& {\mathbf{I}}_{6}\\ -{\mathbf{M}}^{-1}\cdot \mathbf{C}& -{\mathbf{M}}^{-1}\cdot \left(\mathbf{D}+\mathbf{G}\right)\end{array}\right]{;\;\mathbf{B}}_{\mathbf{s}\mathbf{t}}=\left[\begin{array}{c}{\boldsymbol 0}_{6}\\ {\mathbf{M}}^{-1}\end{array}\right]\\ {} \\ {\mathbf{C}}_{\mathbf{s}\mathbf{t}}=\left[\begin{array}{cc}{\mathbf{I}}_{6}& {\boldsymbol 0}_{6}\\ {\boldsymbol 0}_{6}& {\mathbf{I}}_{6}\\ -{\mathbf{M}}^{-1}\cdot \mathbf{C}& -{\mathbf{M}}^{-1}\cdot \left(\mathbf{D}+\mathbf{G}\right)\end{array}\right];\;{\mathbf{D}}_{\mathbf{s}\mathbf{t}}=\left[\begin{array}{c}{\boldsymbol 0}_{6}\\ {\boldsymbol 0}_{6}\\ {\mathbf{M}}^{-1}\end{array}\right]\end{array}$$
(21)

with the zero-matrix \({0}_{6}\in \boldsymbol{ }{\mathbb{R}}^{6\times 6}\) and the unit-matrix \({\mathbf{I}}_{6}\in \boldsymbol{ }{\mathbb{R}}^{6\times 6}\). Therefore, the state space equations can be described by:

$$\dot{\mathbf{x}}\left(t\right)={\mathbf{A}}_{\mathbf{s}\mathbf{t}}\cdot \mathbf{x}\left(t\right)+{\mathbf{B}}_{\mathbf{s}\mathbf{t}}\cdot \left[\mathbf{e}\left(t\right)+{\mathbf{f}}_{\mathbf{a}}\left(t\right)\right],$$
(22)
$$\mathbf{y}\left(t\right)={\mathbf{C}}_{\mathbf{s}\mathbf{t}}\cdot \mathbf{x}\left(t\right)+{\mathbf{D}}_{\mathbf{s}\mathbf{t}}\cdot \left[\mathbf{e}\left(t\right)+{\mathbf{f}}_{\mathbf{a}}\left(t\right)\right].$$
(23)

The actuator force vector \({\mathbf{f}}_{\mathbf{a}}\left(t\right)\) can be written using the controller matrix \({\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\), which will be defined later, as

$${\mathbf{f}}_{\mathbf{a}}\left(t\right)=-{\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot \mathbf{y}\left(t\right).$$
(24)

Formulation in the Laplace Domain

Derivation of the Transfer Matrix of the System

To derive the transfer matrix of the system, Eqs. (22), (23) and (24) are transferred into the Laplace domain, with setting the initial conditions to zero:

$$\mathbf{X}\left(s\right)\cdot s={\mathbf{A}}_{\mathbf{s}\mathbf{t}}\cdot \mathbf{X}\left(s\right)+{\mathbf{B}}_{\mathbf{s}\mathbf{t}}\cdot \left[\mathbf{E}\left(s\right)+{\mathbf{F}}_{\mathbf{a}}\left(s\right)\right],$$
(25)
$$\mathbf{Y}\left(s\right)={\mathbf{C}}_{\mathbf{s}\mathbf{t}}\cdot \mathbf{X}\left(s\right)+{\mathbf{D}}_{\mathbf{s}\mathbf{t}}\cdot \left[\mathbf{E}\left(s\right)+{\mathbf{F}}_{\mathbf{a}}\left(s\right)\right],$$
(26)
$${\mathbf{F}}_{\mathbf{a}}\left(s\right)=-{\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot \mathbf{Y}\left(s\right).$$
(27)

After changing Eq. (25) to \(\mathbf{X}\left(s\right)\) and inserting (27) follows:

$$\mathbf{X}\left(s\right)={\left({\mathbf{I}}_{12}\cdot s-{\mathbf{A}}_{\mathbf{s}\mathbf{t}}\right)}^{-1}{\cdot \mathbf{B}}_{\mathbf{s}\mathbf{t}}\cdot \left(\mathbf{E}\left(s\right)-{\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot \mathbf{Y}(s)\right)$$
(28)

with the unit-matrix \({\mathbf{I}}_{12}\in \boldsymbol{ }{\mathbb{R}}^{12\times 12}\). When inserting (28) and (27) into (26) and putting \(\mathbf{Y}(s)\) on the left side, following equation results:

$$\mathbf{Y}\left(s\right)+{\mathbf{C}}_{\mathbf{s}\mathbf{t}}\cdot {\left({\mathbf{I}}_{12}\cdot s-{\mathbf{A}}_{\mathbf{s}\mathbf{t}}\right)}^{-1}{\cdot \mathbf{B}}_{\mathbf{s}\mathbf{t}}\cdot {\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot \mathbf{Y}\left(s\right)+{\mathbf{D}}_{\mathbf{s}\mathbf{t}}\cdot {\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot \mathbf{Y}\left(s\right)=\left[{\mathbf{C}}_{\mathbf{s}\mathbf{t}}\cdot {\left({\mathbf{I}}_{12}\cdot s-{\mathbf{A}}_{\mathbf{s}\mathbf{t}}\right)}^{-1}{\cdot \mathbf{B}}_{\mathbf{s}\mathbf{t}}+{\mathbf{D}}_{\mathbf{s}\mathbf{t}}\right]\cdot \mathbf{E}\left(s\right).$$
(29)

Finally, the equation can be written by

$$ \begin{aligned} {\mathbf{Y}}\left( s \right) = & \left[ {{\mathbf{I}}_{18} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} } \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right] \cdot {\mathbf{E}}\left( s \right) \\ \end{aligned} $$
(30)

with the unit-matrix \({\mathbf{I}}_{18}\in \boldsymbol{ }{\mathbb{R}}^{18\times 18}\). Therefore, the output vector \(\mathbf{Y}(s)\) gets dependent on the different feedback strategies (6), with \(\mathbf{Y}(s)\to {\mathbf{Y}}_{{\varvec{\upgamma}}}(s)\):

$$ \begin{aligned} {\mathbf{Y}}_{{{\varvec{\upgamma}}}} \left( s \right) = & \left[ {{\mathbf{I}}_{18} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} } \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right] \cdot {\mathbf{E}}\left( s \right). \\ \end{aligned} $$
(31)

Now the controller matrix \({\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\) has to be derived, which is described in “Appendix B”. Finally, the output vector \({\mathbf{Y}}_{{\varvec{\upgamma}}}(s)\) can be calculated by

$${\mathbf{Y}}_{{\varvec{\upgamma}}}\left(s\right)={\mathbf{G}}_{{\varvec{\upgamma}}}\left(s\right)\cdot \mathbf{E}\left(s\right),$$
(32)

and the transfer matrix \({\mathbf{G}}_{{\varvec{\upgamma}}}\left(s\right)\) can be written by

$$ \begin{aligned} {\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( s \right) = & \left[ {{\mathbf{I}}_{18} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} } \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right]. \\ \end{aligned} $$
(33)

The transfer vector for each single excitation can now be derived, with the Laplace-transformed excitation vector \(\mathbf{E}\left(s\right)\):

$$\mathbf{E}\left(s\right)={\left[{E}_{\rm{fz}}\left(s\right); {E}_{\rm{fy}}\left(s\right);\,{E}_{\rm{fx}}\left(s\right);\,{E}_{\rm{mz}}\left(s\right);\,{E}_{\rm{my}}\left(s\right);\,{E}_{\rm{mx}}\left(s\right)\right]}^{T}.$$
(34)

Further, the index \(\kappa \) is used for each single excitation:

$$\kappa =\rm{fz},\rm{fy},\rm{fx},\rm{mz},\rm{my},\rm{mx}.$$
(35)

The output vector \({\mathbf{Y}}_{{\varvec{\upgamma}},{\varvec{\upkappa}}}(s)\) for a single excitation \({\mathbf{E}}_{{\varvec{\upkappa}}}\left(s\right)\) can be calculated by

$$ {\mathbf{Y}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( s \right) = {\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( s \right) \cdot {\mathbf{E}}_{{{\varvec{\upkappa}}}} \left( s \right) = \underbrace {{{\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( s \right) \cdot {\mathbf{P}}_{{{\mathbf{e}},{{\varvec{\upkappa}}}}} }}_{{{\mathbf{G}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( s \right)}}\user2{ } \cdot E_{{\upkappa }} \left( s \right) $$
(36)

with the excitation transmission vectors:

$${\mathbf{P}}_{\mathbf{e},\mathbf{f}\mathbf{z}}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]; {\mathbf{P}}_{\mathbf{e},\mathbf{f}\mathbf{y}}=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right] ;\,{\mathbf{P}}_{\mathbf{e},\mathbf{f}\mathbf{x}}=\left[\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right];\,{\mathbf{P}}_{\mathbf{e},\mathbf{m}\mathbf{z}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\right];\,{\mathbf{P}}_{\mathbf{e},\mathbf{m}\mathbf{y}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1\\ 0\end{array}\right]; {\mathbf{P}}_{\mathbf{e},\mathbf{m}\mathbf{x}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right].$$
(37)

Therefore, the transfer vector for a single excitation can be written by

$$ \begin{aligned} {\mathbf{G}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( s \right) & = \frac{{{\mathbf{Y}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( s \right)}}{{E_{{\upkappa }} \left( s \right)}} = {\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( s \right) \cdot {\mathbf{P}}_{{{\mathbf{e}},{{\varvec{\upkappa}}}}} \\ & = \left[ {{\mathbf{I}}_{18} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} } \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{18} \cdot s - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right] \cdot {\mathbf{P}}_{{{\mathbf{e}},{{\varvec{\upkappa}}}}} . \\ \end{aligned} $$
(38)

Calculation of the Poles of the System

To analyze the stability of the system, it is necessary to calculate the poles. Therefore, the excitation vector \(\mathbf{E}\left(s\right)\) has to set to the zero vector \(\mathbf{E}\left(s\right)= {\boldsymbol 0}\). Finally, the poles can be calculated by solving the determinant equation:

$$\rm{det}\left[{\mathbf{I}}_{12}\cdot s-{\mathbf{A}}_{\mathbf{s}\mathbf{t}}+{\mathbf{B}}_{\mathbf{s}\mathbf{t}}\cdot {\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\cdot {\left[{\mathbf{I}}_{18}+{\mathbf{D}}_{\mathbf{s}\mathbf{t}}\cdot {\mathbf{T}}_{\mathbf{s}\mathbf{t},{\varvec{\upgamma}}}\right]}^{-1}\cdot {\mathbf{C}}_{\mathbf{s}\mathbf{t}}\right]=0.$$
(39)

The derivation of this equation is shown in “Appendix C”.

Formulation in the Fourier Domain

For analyzing the frequency responses for harmonic excitations, the formulations have to be transferred into the Fourier domain. The frequency response matrix can be determined with using the transformation \(s\to j\omega \) for (33):

$$ \begin{aligned} {\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( {j\omega } \right) & = \left[ {{\mathbf{I}}_{18} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot j\omega - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} \left( {j\omega } \right)} \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{12} \cdot j\omega - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right]. \\ \end{aligned} $$
(40)

Therefore, the frequency response vector for a single excitation can be written by

$$ \begin{aligned} {\mathbf{G}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( {j\omega } \right) & = \frac{{{\mathbf{Y}}_{{{{\varvec{\upgamma}}},{{\varvec{\upkappa}}}}} \left( {j\omega } \right)}}{{E_{{\upkappa }} \left( {j\omega } \right)}} = {\mathbf{G}}_{{{\varvec{\upgamma}}}} \left( {j\omega } \right) \cdot {\mathbf{P}}_{{{\mathbf{e}},{{\varvec{\upkappa}}}}} = \\ & = \left[ {{\mathbf{I}}_{\boldsymbol {18}} + \left( {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{\boldsymbol {12}} \cdot j\omega - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right) \cdot {\mathbf{T}}_{{{\mathbf{st}},{{\varvec{\upgamma}}}}} \left( {j\omega } \right)} \right]^{ - 1} \\ & \quad \left[ {{\mathbf{C}}_{{{\mathbf{st}}}} \cdot \left( {{\mathbf{I}}_{\boldsymbol {12}} \cdot j\omega - {\mathbf{A}}_{{{\mathbf{st}}}} } \right)^{ - 1} \cdot {\mathbf{B}}_{{{\mathbf{st}}}} + {\mathbf{D}}_{{{\mathbf{st}}}} } \right] \cdot {\mathbf{P}}_{{{\mathbf{e}},{{\varvec{\upkappa}}}}} \\ \end{aligned}. $$
(41)

Vibration Velocities of the Bearing Housings Related to Each Kind of Excitation

The frequency response functions for the bearing housing vibration velocities in vertical, horizontal and axial direction related to each kind of excitation, can be described by

  • For vertical direction:

    $${\rm{Drive side}: G}_{\upgamma ,\widehat{\rm{v}}\rm{bDz},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{7}+{l}_{\rm{D}}\cdot {{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{11},$$
    (42)
    $${\rm{Non}-\rm{drive side}: G}_{\upgamma ,\widehat{\rm{v}}\rm{bNz},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{7}-{l}_{N}\cdot {{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{11}.$$
    (43)

  • For horizontal direction:

    $${\rm{Drive side}: G}_{\upgamma ,\widehat{\rm{v}}\rm{bDy},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{8}-{l}_{\rm{D}}\cdot {{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{10},$$
    (44)
    $$\rm{Non}-\rm{drive side}: {G}_{\upgamma ,\widehat{\rm{v}}\rm{bNy},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{8}+{l}_{N}\cdot {{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{10}.$$
    (45)

  • For axial direction:

    $${\rm{Drive side}: G}_{\upgamma ,\widehat{\rm{v}}\rm{bDx},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{9},$$
    (46)
    $$\rm{Non}-\rm{drive side}: {G}_{\upgamma ,\widehat{\rm{v}}\rm{bNx},\upkappa }\left(j\Omega \right)={{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{9},$$
    (47)

    where \({{G}_{\upgamma ,\upkappa }\left(j\Omega \right)}_{n}\) is the nth element of the frequency response vector \({\mathbf{G}}_{{\varvec{\upgamma}},{\varvec{\upkappa}}}\left(j\Omega \right)\).

Actuator Forces Related to Each Kind of Excitation

The frequency response functions for the actuator forces related to each kind of excitation can be analyzed by

$${\rm{Drive side},\rm{ left}: G}_{\upgamma ,\widehat{\rm{f}}\rm{azDL},\upkappa }\left(j\Omega \right),$$
(48)
$${\rm{Drive side},\rm{ right}: G}_{\upgamma ,\widehat{\rm{f}}\rm{azDR},\upkappa }\left(j\Omega \right),$$
(49)
$${\rm{Non}-\rm{drive side},\rm{ left}: G}_{\upgamma ,\widehat{\rm{f}}\rm{azNL},\upkappa }\left(j\Omega \right),$$
(50)
$$\rm{Non}-\rm{drive side},\rm{ right}: {G}_{\upgamma ,\widehat{\rm{f}}\rm{azNR},\upkappa }\left(j\Omega \right).$$
(51)

The formulas are shown in “Appendix D”.

Mathematical Formulation for Special Controller Structures

Up to now, arbitrarily controller structures have been considered. In this section, special controller structures are analyzed, so that the control parameter can be directly implemented into the mass matrix and/or the damping matrix and/or the stiffness matrix, using standard controllers (P-, I-, PI-, PD-(ideal), PID-(ideal) controllers), which can be seen in Table 1. Therefore, the differential equation can be described now by

$${\tilde{\mathbf{M}}}\cdot \ddot{\mathbf{q}}+\left(\tilde{\mathbf{D}}+\mathbf{G}\right)\cdot \dot{\mathbf{q}}+\tilde{\mathbf{C}}\cdot \mathbf{q}=\mathbf{e}.$$
(52)
Table 1 Matrices, depending on standard controller structures and different feedback strategies
Full size table

When the control parameters are implemented into the mass matrix, \(\tilde{\mathbf{M}}\) becomes \({\mathbf{M}}_{\mathbf{c}\mathbf{o}\mathbf{n}}\). When they are implemented into the damping matrix, \(\tilde{\mathbf{D}}\) becomes \({\mathbf{D}}_{\mathbf{c}\mathbf{o}\mathbf{n}}\), and if they are implemented into the stiffness matrix, \(\tilde{\mathbf{C}}\) becomes \({\mathbf{C}}_{\mathbf{c}\mathbf{o}\mathbf{n}}\). The structure of these matrices is shown in (60). The inhomogeneous differential Eq. (52) can be solved, based on the common approach. When analyzing the natural vibrations of the system, the eigenvalues and the eigenvectors have to be derived, by solving the homogeneous differential equation:

$${\tilde{\mathbf {M}} }\cdot \ddot{\mathbf{q}}+\left({\tilde{\mathbf {D}} }+\mathbf{G}\right)\cdot \dot{\mathbf{q}}+{\tilde {\mathbf {C}} }\cdot \mathbf{q}= {\boldsymbol 0}$$
(53)

With the common ansatz

$$\mathbf{q}\left(t\right)=\widehat{\mathbf{q}}\cdot {e}^{\lambda t},$$
(54)

the eigenvalue equation can be derived:

$$\left[{\tilde {\mathbf {M}} }\cdot {\lambda }^{2}+\left({\tilde {\mathbf {D}} }+\mathbf{G}\right)\cdot \lambda +{\tilde {\mathbf {C}} }\right]\cdot \widehat{\mathbf{q}}= {\boldsymbol 0}$$
(55)

Solving the determinant equation

$$\rm{det}\left[\tilde{\mathbf{M}}\cdot {\lambda }^{2}+\left(\tilde{\mathbf{D}}+\mathbf{G}\right)\cdot \lambda +\tilde{\mathbf{C}}\right]=0$$
(56)

leads to the eigenvalues \(\lambda \). With these eigenvalues, the eigenvectors \(\widehat{\mathbf{q}}\) can be calculated, based on (55), by common approach. The eigenvalues correspond to the poles, calculated by (39).

Following relations are used now:

$$\rm{For the mass matrix }{\mathbf{M}}_{\mathbf{c}\mathbf{o}\mathbf{n}}:\ {\mathbf{M}}_{\mathbf{c}\mathbf{o}\mathbf{n}}={{\varvec{\Psi}}}_{\mathbf{c}\mathbf{o}\mathbf{n}} {\text{ and }}\psi =m,$$
(57)
$${\rm{For the damping matrix }\mathbf{D}}_{\mathbf{c}\mathbf{o}\mathbf{n}}:\boldsymbol{ }{\mathbf{D}}_{\mathbf{c}\mathbf{o}\mathbf{n}}={{\varvec{\Psi}}}_{\mathbf{c}\mathbf{o}\mathbf{n}}{\text{ and }}\psi =d,$$
(58)
$$\rm{For the stiffness matrix }{\mathbf{C}}_{\mathbf{c}\mathbf{o}\mathbf{n}}:\boldsymbol{ }{\mathbf{C}}_{\mathbf{c}\mathbf{o}\mathbf{n}}={{\varvec{\Psi}}}_{\mathbf{c}\mathbf{o}\mathbf{n}}{\text{ and }} \psi =c.$$
(59)

Therefore, the matrices with the integrated controller parameters can be described by

$${{\varvec{\Psi}}}_{\mathbf{c}\mathbf{o}\mathbf{n}}=\left[\begin{array}{cccc}{\psi }_{\rm{1,1}}+{K}_{\psi \rm{DL}}+{K}_{\psi \rm{DR}}+{K}_{\psi \rm{NL}}+{K}_{\psi \rm{NR}}& {\psi }_{\rm{1,2}}& {\psi }_{\rm{1,3}}&{\psi }_{\rm{1,4}}\\ {\psi }_{\rm{2,1}}& {\psi }_{\rm{2,2}}& {\psi }_{\rm{2,3}}& {\psi }_{\rm{2,4}}\\ {\psi }_{\rm{3,1}}& {\psi }_{\rm{3,2}}& {\psi }_{\rm{3,3}}& {\psi }_{\rm{3,4}}\\ {\psi }_{\rm{4,1}}& {\psi }_{\rm{4,2}}& {\psi }_{\rm{4,3}}& {\psi }_{\rm{4,4}}\\ {{\psi }_{\rm{5,1}}+\rm{a}}_{\rm{D}}\cdot \left[{K}_{\psi \rm{DL}}+{K}_{\psi \rm{DR}}\right]-{\rm{a}}_{\rm{N}}\cdot \left[{K}_{\psi \rm{NL}}+{K}_{\psi \rm{NR}}\right]& {\psi }_{\rm{5,2}}& {\psi }_{\rm{5,3}}& {\psi }_{\rm{5,4}}\\ {\psi }_{\rm{6,1}}+{b}_{\rm{R}}\cdot \left[{K}_{\psi \rm{DR}}+{K}_{\psi \rm{NR}}\right]-{b}_{\rm{L}}\cdot \left[{K}_{\psi \rm{DL}}+{K}_{\psi \rm{NL}}\right]& {\psi }_{\rm{6,2}}& {\psi }_{\rm{6,3}}& {\psi }_{\rm{6,4}}\end{array}\right.\cdots $$
$$ \begin{aligned} & \cdots \begin{array}{*{20}l} {\psi _{{1,5}} + {\text{a}}_{{\text{D}}} \cdot \left[ {K_{{\psi {\text{DL}}}} + K_{{\psi {\text{DR}}}} } \right] - {\text{a}}_{{\text{N}}} \cdot \left[ {K_{{\psi {\text{NL}}}} + K_{{\psi {\text{NR}}}} } \right]} \\ {\psi _{{2,5}} } \\ {\psi _{{3,5}} } \\ {\psi _{{4,5}} } \\ {\psi _{{5,5}} + a_{{\text{D}}}^{2} \cdot \left[ {K_{{\psi {\text{DL}}}} + K_{{\psi {\text{DR}}}} } \right] + a_{{\text{N}}}^{2} \cdot \left[ {K_{{\psi {\text{NL}}}} + K_{{\psi {\text{NR}}}} } \right]} \\ {\psi _{{6,5}} + a_{{\text{D}}} \cdot \left[ {b_{{\text{R}}} \cdot K_{{\psi {\text{DR}}}} - b_{{\text{L}}} \cdot K_{{\psi {\text{DL}}}} } \right] + a_{{\text{N}}} \cdot \left[ {b_{{\text{L}}} \cdot K_{{\psi {\text{NL}}}} - b_{{\text{R}}} \cdot K_{{\psi {\text{NR}}}} } \right]} \\ \end{array} \cdots \\ & \left. { \cdots \begin{array}{*{20}l} {\psi _{{1,6}} + b_{{\text{R}}} \cdot \left[ {K_{{\psi {\text{DR}}}} + K_{{\psi {\text{NR}}}} } \right] - b_{{\text{L}}} \cdot \left[ {K_{{\psi {\text{DL}}}} + K_{{\psi {\text{NL}}}} } \right]} \hfill \\ {\psi _{{2,6}} } \hfill \\ {\psi _{{3,6}} } \hfill \\ {\psi _{{4,6}} } \hfill \\ {\psi _{{5,6}} + a_{{\text{D}}} \cdot \left[ {b_{{\text{R}}} \cdot K_{{\psi {\text{DR}}}} - b_{{\text{L}}} \cdot K_{{\psi {\text{DL}}}} } \right] + a_{{\text{N}}} \cdot \left[ {b_{{\text{L}}} \cdot K_{{\psi {\text{NL}}}} - b_{{\text{R}}} \cdot K_{{\psi {\text{NR}}}} } \right]} \hfill \\ {\psi _{{6,6}} + b_{{\text{L}}}^{2} \cdot \left[ {K_{{\psi {\text{DL}}}} + K_{{\psi {\text{NL}}}} } \right] + b_{{\text{R}}}^{2} \cdot \left[ {K_{{\psi {\text{DR}}}} + K_{{\psi {\text{NR}}}} } \right]} \hfill \\ \end{array} } \right]. \\ \end{aligned} $$
(60)

The parameters \({K}_{\psi \rm{ij}}\) are the control parameters of the standard controllers depending on the controller structure and the chosen feedback strategy. The cells in Table 1 marked with “—” cannot be performed, if the differential equation system (52) is used. The colored cells with the identical color lead to the same differential equation, if the control parameters are identical. When comparing Eq. (60) with Eq. (18) and with the matrix coefficients described in “Appendix A”, it can be stated that here the coefficients of the stiffness and the damping matrix—with the integrated control parameters—can be calculated by

$${\rm{c}}_{\rm{azij},\rm{con}}={c}_{\rm{azij}}+{K}_{\rm{cij}}; {d}_{\rm{azij},\rm{con}}={d}_{\rm{azij}}+{K}_{\rm{dij}}.$$
(61)

Therefore, the stiffness and damping of each actuator can be influenced here directly. However, such a mathematical coherences is not possible for the coefficients of the mass matrix, because when “adding” an “additional mass” to the actuator mass by the controller parameters, this additional mass would also be effective in y- and x-directions, but in this direction, the actuators do not work. This is also obvious when comparing Eq. (60) with Eq. (18), regarding the coefficients of the mass matrix.

Simulation Model

Besides the mathematically solutions in the sections before, it is also possible to use an adequate simulation program, e.g. SIMULINK in combination with MATLAB. The block diagram is shown in Fig. 4.

Fig. 4
figure 4

Block diagram for simulation in SIMULINK

Full size image

The blocks \(f\_ez\) … \(m\_ex\)—marked with blue—are the sources of excitation and the blocks \(v\_zbD\),\(v\_zbN\),\(v\_ybD\), \(v\_ybN\) and \(v\_xbD=v\_xbN\)—marked with magenta—present the bearing housing vibrations on the drive side and non-drive side in the different directions (x, y, z). Also, a state space block—marked with orange—is used for the simulation as well as different subsystems (Fig. 5).

Fig. 5
figure 5

Subsystem 1 and subsystem 2 in SIMULINK model

Full size image

Subsystem 1 is used for implementing the kinematic constraints (11)–(13) and subsystems 2, 3 and 4 for implementing the kinematic constraints (8)–(10). Subsystems 2, 3 and 4 have the same structure; therefore, only subsystem 2 is shown in Fig. 5. The “demux” in the feedback loop in combination with the “switches” is used to decide which kind of feedback should be analyzed (“open control loops”, “displacement feedback”, “velocity feedback” or “acceleration feedback”) in Fig. 4. Each controller is considered by a separate block—marked with cyan—by a different transfer function. The gains—marked with yellow—are the transmission vectors of the forces and moments, described in Eqs. (17) and (37).

Symmetrical Machine Design

If analyzing the natural vibrations of the system with open control loops, six different natural mode shapes will occur here for the used model, in which the movements are more or less coupled, leading to more or less vertical machine feet movements, depending on the used parameters. However, the fourth row of the homogenous differential Eq. (15) with open control loops—with the coefficient of the matrices, which are shown in “Appendix A”—has to be analyzed here in detail:

$$ \begin{aligned} & \ddot{\varphi }_{{{\text{sz}}}} \cdot (\theta_{{{\text{sz}}}} + m_{{{\text{aDL}}}} \cdot b_{{\text{L}}}^{2} + m_{{{\text{aDR}}}} \cdot b_{{\text{R}}}^{2} + m_{{{\text{aNL}}}} \cdot b_{{\text{L}}}^{2} + m_{{{\text{aNR}}}} \cdot b_{{\text{R}}}^{2} + m_{{{\text{aDL}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + m_{{{\text{aDR}}}} \cdot a_{{\text{D}}}^{2} + m_{{{\text{aNL}}}} \cdot a_{{\text{N}}}^{2} + m_{{{\text{aNR}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \ddot{x}_{{\text{s}}} \cdot \left( {m_{{{\text{aDL}}}} \cdot b_{{\text{L}}} - m_{{{\text{aDR}}}} \cdot b_{{\text{R}}} + m_{{{\text{aNL}}}} \cdot b_{{\text{L}}} - m_{{{\text{aNR}}}} \cdot b_{{\text{R}}} } \right) \\ & \quad + \ddot{\varphi }_{{{\text{sy}}}} \cdot \left( {m_{{{\text{aDL}}}} \cdot b_{{\text{L}}} \cdot h - m_{{{\text{aDR}}}} \cdot b_{{\text{R}}} \cdot h + m_{{{\text{aNL}}}} \cdot b_{{\text{L}}} \cdot h - m_{{{\text{aNR}}}} \cdot b_{{\text{R}}} \cdot h} \right) \\ & \quad + \ddot{y}_{{\text{s}}} \cdot \left( { - m_{{{\text{aDL}}}} \cdot a_{{\text{D}}} - m_{{{\text{aDR}}}} \cdot a_{{\text{D}}} + m_{{{\text{aNL}}}} \cdot a_{{\text{N}}} + m_{{{\text{aNR}}}} \cdot a_{{\text{N}}} } \right) \\ & \quad + \ddot{\varphi }_{{{\text{sx}}}} \cdot \left( {m_{{{\text{aDL}}}} \cdot a_{{\text{D}}} \cdot h + m_{{{\text{aDR}}}} \cdot a_{{\text{D}}} \cdot h - m_{{{\text{aNL}}}} \cdot a_{{\text{N}}} \cdot h - m_{{{\text{aNR}}}} \cdot a_{{\text{N}}} \cdot h} \right) \\ & \quad + \dot{x}_{{\text{s}}} \cdot \left( {d_{{{\text{axLD}}}} \cdot b_{{\text{L}}} - d_{{{\text{axRD}}}} \cdot b_{{\text{R}}} + d_{{{\text{axLN}}}} \cdot b_{{\text{L}}} - d_{{{\text{axRN}}}} \cdot b_{R} } \right) \\ & \quad + \dot{\varphi }_{{{\text{sz}}}} \cdot (d_{{{\text{axLD}}}} \cdot b_{{\text{L}}}^{2} + d_{{{\text{axRD}}}} \cdot b_{{\text{R}}}^{2} + d_{{{\text{axLN}}}} \cdot b_{{\text{L}}}^{2} + d_{{{\text{axRN}}}} \cdot b_{{\text{R}}}^{2} + d_{{{\text{ayLD}}}} \cdot a_{{\text{D}}}^{2} + d_{{{\text{ayRD}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + d_{{{\text{ayLN}}}} \cdot a_{{\text{N}}}^{2} + d_{{{\text{ayRN}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \dot{\varphi }_{{{\text{sy}}}} \cdot \left( {d_{{{\text{axLD}}}} \cdot h \cdot b_{{\text{L}}} - d_{{{\text{axRD}}}} \cdot h \cdot b_{{\text{R}}} + d_{{{\text{axLN}}}} \cdot h \cdot b_{{\text{L}}} - d_{{{\text{axRN}}}} \cdot h \cdot b_{{\text{R}}} + \Omega \cdot \theta_{{{\text{rx}}}} } \right) \\ & \quad + \dot{y}_{{\text{s}}} \cdot \left( { - d_{{{\text{ayLD}}}} \cdot a_{{\text{D}}} - d_{{{\text{ayRD}}}} \cdot a_{{\text{D}}} + d_{{{\text{ayLN}}}} \cdot a_{n} + d_{{{\text{ayRN}}}} \cdot a_{{\text{N}}} } \right) \\ & \quad + \dot{\varphi }_{{{\text{sx}}}} \cdot \left( {d_{{{\text{ayLD}}}} \cdot h \cdot a_{{\text{D}}} + d_{{{\text{ayRD}}}} \cdot h \cdot a_{{\text{D}}} - d_{{{\text{ayLN}}}} \cdot h \cdot a_{{\text{N}}} - d_{{{\text{ayRN}}}} \cdot h \cdot a_{{\text{N}}} } \right) \\ & \quad + x_{{\text{s}}} \cdot \left( {c_{{{\text{axLD}}}} \cdot b_{{\text{L}}} - c_{{{\text{axRD}}}} \cdot b_{{\text{R}}} + c_{{{\text{axLN}}}} \cdot b_{{\text{L}}} - c_{{{\text{axRN}}}} \cdot b_{R} } \right) \\ & \quad + \varphi_{{{\text{sz}}}} \cdot (c_{{{\text{axLD}}}} \cdot b_{{\text{L}}}^{2} + c_{{{\text{axRD}}}} \cdot b_{{\text{R}}}^{2} + c_{{{\text{axLN}}}} \cdot b_{{\text{L}}}^{2} + c_{{{\text{axRN}}}} \cdot b_{{\text{R}}}^{2} + c_{{{\text{ayLD}}}} \cdot a_{{\text{D}}}^{2} + c_{{{\text{ayRD}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + c_{{{\text{ayLN}}}} \cdot a_{{\text{N}}}^{2} + c_{{{\text{ayRN}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \varphi_{{{\text{sy}}}} \cdot \left( {c_{{{\text{axLD}}}} \cdot h \cdot b_{{\text{L}}} - c_{{{\text{axRD}}}} \cdot h \cdot b_{{\text{R}}} + c_{{{\text{axLN}}}} \cdot h \cdot b_{{\text{L}}} - c_{{{\text{axRN}}}} \cdot h \cdot b_{{\text{R}}} } \right) \\ & \quad + y_{{\text{s}}} \cdot \left( { - c_{{{\text{ayLD}}}} \cdot a_{{\text{D}}} - c_{{{\text{ayRD}}}} \cdot a_{{\text{D}}} + c_{{{\text{ayLN}}}} \cdot a_{n} + c_{{{\text{ayRN}}}} \cdot a_{{\text{N}}} } \right) \\ & \quad + \varphi_{{{\text{sx}}}} \cdot \left( {c_{{{\text{ayLD}}}} \cdot h \cdot a_{{\text{D}}} + c_{{{\text{ayRD}}}} \cdot h \cdot a_{{\text{D}}} - c_{{{\text{ayLN}}}} \cdot h \cdot a_{{\text{N}}} - c_{{{\text{ayRN}}}} \cdot h \cdot a_{{\text{N}}} } \right) \\ & \quad = 0. \\ \end{aligned} $$
(62)

For a symmetrical design of the rotating machine—so that the center of gravity \(S\) lies symmetrically between the machine feet with a vertical distance \(h\), following coherences occur:

$$b={b}_{\rm{L}}={b}_{\rm{R}}; a={a}_{\rm{D}}={a}_{\rm{N}}.$$
(63)

If now actuators with identical mass and with identical horizontal and axial stiffness and damping for each actuator are used:

$${m}_{\rm{a}}={m}_{\rm{aDL}}={m}_{\rm{aDR}}={m}_{\rm{aNL}}={m}_{\rm{aNR}},$$
(64)
$${c}_{\rm{ay}}={c}_{\rm{ayDL}}={c}_{\rm{ayDR}}={c}_{\rm{ayNL}}={c}_{\rm{ayNR}},$$
(65)
$${c}_{\rm{ax}}={c}_{\rm{axDL}}={c}_{\rm{axDR}}={c}_{\rm{axNL}}={c}_{\rm{axNR}},$$
(66)
$${d}_{\rm{ay}}={d}_{\rm{ayDL}}={d}_{\rm{ayDR}}={d}_{\rm{ayNL}}={d}_{\rm{ayNR}},$$
(67)
$${d}_{\rm{ax}}={d}_{\rm{axDL}}={d}_{\rm{axDR}}={d}_{\rm{axNL}}={d}_{\rm{axNR}},$$
(68)

the whole system (machine and actuators) becomes a symmetrical system and Eq. (62) will change to

$$ \begin{aligned} \ddot{\varphi }_{{{\text{sz}}}} \cdot & (\theta_{{{\text{sz}}}} + m_{{{\text{aDL}}}} \cdot b_{{\text{L}}}^{2} + m_{{{\text{aDR}}}} \cdot b_{{\text{R}}}^{2} + m_{{{\text{aNL}}}} \cdot b_{{\text{L}}}^{2} + m_{{{\text{aNR}}}} \cdot b_{{\text{R}}}^{2} + m_{{{\text{aDL}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + m_{{{\text{aDR}}}} \cdot a_{{\text{D}}}^{2} + m_{{{\text{aNL}}}} \cdot a_{{\text{N}}}^{2} + m_{{{\text{aNR}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \dot{\varphi }_{{{\text{sz}}}} \cdot (d_{{{\text{axLD}}}} \cdot b_{{\text{L}}}^{2} + d_{{{\text{axRD}}}} \cdot b_{{\text{R}}}^{2} + d_{{{\text{axLN}}}} \cdot b_{{\text{L}}}^{2} + d_{{{\text{axRN}}}} \cdot b_{{\text{R}}}^{2} + d_{{{\text{ayLD}}}} \cdot a_{{\text{D}}}^{2} + d_{{{\text{ayRD}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + d_{{{\text{ayLN}}}} \cdot a_{{\text{N}}}^{2} + d_{{{\text{ayRN}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \varphi_{{{\text{sz}}}} \cdot (c_{{{\text{axLD}}}} \cdot b_{{\text{L}}}^{2} + c_{{{\text{axRD}}}} \cdot b_{{\text{R}}}^{2} + c_{{{\text{axLN}}}} \cdot b_{{\text{L}}}^{2} + c_{{{\text{axRN}}}} \cdot b_{{\text{R}}}^{2} + c_{{{\text{ayLD}}}} \cdot a_{{\text{D}}}^{2} + c_{{{\text{ayRD}}}} \cdot a_{{\text{D}}}^{2} \\ & \quad + c_{{{\text{ayLN}}}} \cdot a_{{\text{N}}}^{2} + c_{{{\text{ayRN}}}} \cdot a_{{\text{N}}}^{2} ) \\ & \quad + \dot{\varphi }_{{{\text{sy}}}} \cdot \Omega \cdot \theta_{{{\text{rx}}}} \\ & = 0. \\ \end{aligned} $$
(69)

When analyzing this equation of motion, it is obvious that the system gets decoupled now regarding this mode, when the gyroscopic term \({\dot{\varphi }}_{\rm{sy}}\cdot \Omega \cdot {\theta }_{\rm{rx}}\) is neglected. In this case, only a pure rotation at the z-axis occurs here for this mode. However, the vertical machine feet movements (8) are independent to a pure rotation at the z-axis. Therefore, no vertical machine feet movements will occur in this mode shape and the vertical stiffness \({c}_{\rm{azij}}\) and the vertical damping \({d}_{\rm{azij}}\) of each actuator is irrelevant in this case. Therefore, the actuator forces, which only operate in vertical direction, will also not influence this mode shape. However, all other mode shapes have vertical machine feet movements and will be influenced by the vertical actuator forces. Therefore, a symmetrical machine design in combination with identical actuators—presenting a symmetrical system—causes natural mode shapes, where all mode shapes have vertical machine feet displacements except the decoupled mode shape, where only rotation at the z-axis occurs, if the influence of the gyroscopic term \({\dot{\varphi }}_{\rm{sy}}\cdot \Omega \cdot {\theta }_{\rm{rx}}\) is so small, that it can be neglected. However, if only one actuator will be changed, so that it has a different stiffness in y-direction or/and in x-direction or/and a different damping in y-direction or/and in x-direction compared to the other actuators—becoming an asymmetrical system—the mode shapes will get more coupled and they all will have vertical machine feet displacements. Therefore, this method is called here “vibration mode coupling by asymmetry”.

Numerical Example

Now, a numerical example is shown, where the natural vibrations, as well as the forced vibrations of a rotating machine are analyzed.

Boundary Conditions

The data of the rotating machine are shown in Table 2. As it can be seen in Table 2, the rotating machine has a symmetrical machine design (\({b}_{\rm{L}}={b}_{\rm{R}};\,{a}_{D}={a}_{N}\)).

Table 2 Data of the rotating machine
Full size table

Two different cases regarding the actuator stiffness are considered:

  • Case 1 (symmetrical system): all actuators have the same stiffness.

  • Case 2 (asymmetrical system): one actuator (non-drive side, right) has a different stiffness in y-direction and in x-direction, compared to the other actuators.

The data of the actuators are described in Table 3.

Table 3 Data of the actuators
Full size table

As a simplification—based on [3] and [25]—the damping coefficients of the actuators can be derived by

$$ d_{{{\text{aqij}}}} = \frac{{2D_{{\text{a}}} \cdot c_{{{\text{aqij}}}} }}{{\sqrt {\frac{{\sum\nolimits_{i = D,N;j = L,R} {c_{{{\text{aqij}}}} } }}{{m_{s} + \sum\nolimits_{i = D,N;j = L,R} {m_{{{\text{aij}}}} } }}} }};\,{\text{with}}\,q = x,y,z. $$
(70)

For the control system, I-controllers with feedbacks of the vertical machine feet accelerations are chosen with identical controller parameters for all four controllers, so that following controller transfer function for all four controller can be used:

$${G}_{\rm{cij},\rm{a}}\left(s\right)=\frac{{b}_{0,\rm{a}}}{s} \rm{with}:{b}_{0,\rm{a}}=4.0 \cdot {10}^{5}\frac{\rm{kg}}{\rm{s}}.$$
(71)

This corresponds to the control parameters \({K}_{\psi \rm{ij}}={K}_{\rm{dij}}=4.0 \cdot {10}^{5}\frac{\rm{kg}}{\rm{s}}\) in “Mathematical Formulation for Special Controller Structures”, with the matrices of Table 1, fourth row and fourth column (marked with green).

Natural Vibration Analysis

Solving Eq. (39) or (56), the pols \({s}_{n}\) (eigenvalues \({\lambda }_{n}\))—with the real part \({\alpha }_{n}\) and the imaginary part \({\omega }_{n}\)—as well as the modal damping value \({D}_{n}\) can be derived. The modal damping value \({D}_{n}\) is calculated by

$${D}_{n}=\frac{{-\alpha }_{n}}{\sqrt{{\alpha }_{n}^{2}+{\omega }_{n}^{2}}}.$$
(72)

Natural Vibrations During Stillstand

First, the natural frequencies \({f}_{n}={\omega }_{n}/2\pi \) and the modal damping values \({D}_{n}\) during stillstand (\(n=0 \rm{rpm}\)) are calculated (Table 4).

Table 4 Natural frequency \({f}_{n}\) and modal damping value \({D}_{n}\) of each eigenmode, depending on the different cases and depending on open or closed control loops, during stillstand (\(n=0 \rm{rpm}\))
Full size table

Table 4 shows the calculated natural frequencies and modal damping values for both cases, with open control loops and with closed control loops, during stillstand (\(n=0 \rm{rpm}\)). It is obvious that for case 1, the modal damping values of five modes can be increased by the controllers. However, mode 5 cannot be influenced for case 1. The reason is that this mode shape is only a rotation of the machine at the z-axis (Fig. 6). Therefore, no vertical movements of the machine feet occur, which is mathematical shown in “Symmetrical Machine Design”. If only one actuator is changed (case 2)—here the stiffness in x- and y-directions—this mode shape is changed, so that also vertical machine feet displacements will occur (Fig. 7).

Fig. 6
figure 6

Mode 5 for case 1 (symmetrical system) with open control loops, during stillstand (n = 0 rpm)

Full size image
Fig. 7
figure 7

Mode 4 for case 2 (asymmetrical system) with open control loop, during stillstand (n = 0 rpm)

Full size image

For the case 2, all mode shapes have vertical machine feet displacements and, therefore, can be influenced by the controllers, which can be seen in Table 4, by analyzing the natural frequencies and modal damping values.

Natural Vibrations During Rotation

Now, the natural frequencies and the modal damping values are calculated, when the rotor is rotating. When analyzing Figs. 8 and 9, it is obvious, that up to a rotor speed of about 4000 rpm the natural frequencies and the modal damping values are nearly independent of the rotor speed. For the symmetrical system, modes 1, 3 and 6 are completely independent of the rotor speed and for the asymmetrical system, only mode 3 is independent of the rotor speed.

Fig. 8
figure 8

Natural frequencies and modal damping values at different rotor speeds for a open control loops and b closed control loops, for case 1 (symmetrical system)

Full size image
Fig. 9
figure 9

Natural frequencies and modal damping values at different rotor speeds for a open control loops and b closed control loops, for case 2 (asymmetrical system)

Full size image

Frequency Response Functions

According to “Formulation in the Fourier Domain”, the amplitudes of the frequency response functions between the bearing housing vibration velocities and the excitations and between the actuator forces and the excitations are computed. The amplitudes of the frequency response functions are calculated in \(\left[\rm{dB}\right]\) with the reference gauge in Si-Unit, in a frequency range from \(10\) to \(100 \rm{Hz}.\)

Regarding the bearing housing vibration velocities:

$${\left|{G}_{\upgamma ,\widehat{\rm{v}}\rm{biq},\upkappa }\left(j\Omega \right)\right|}_{\rm{dB}}=20\cdot \rm{log}\boldsymbol{ }\left(\frac{\left|{G}_{\upgamma ,\widehat{\rm{v}}\rm{biq},\upkappa }\left(j\Omega \right)\right|}{{\left|{G}_{\upgamma ,\widehat{\rm{v}}\rm{biq},\upkappa }\left(j\Omega \right)\right|}_{\rm{ref}}}\right)$$
(73)

with \(\upgamma =0,z,v,a ; i=D,N; q=x,y,z; \kappa =fz,fy,fx,mz,my,mx\)

and \({ \left|{G}_{\upgamma ,\widehat{\rm{v}}\rm{biq},\upkappa }\left(j\Omega \right)\right|}_{\rm{ref}}=\left\{\begin{array}{c}1\frac{\rm{m}/\rm{s}}{\rm{N}} for \kappa =fz,fy,fx\\ 1\frac{\rm{m}/\rm{s}}{\rm{Nm}} for \kappa =mz,my,mx\end{array}.\right.\)

Regarding the actuator forces:

$${\left|{G}_{\upgamma ,\widehat{\rm{f}}\rm{azij},\upkappa }\left(j\Omega \right)\right|}_{\rm{dB}}=20\cdot \rm{log}\boldsymbol{ }\left(\frac{\left|{G}_{\upgamma ,\widehat{\rm{f}}\rm{azij},\upkappa }\left(j\Omega \right)\right|}{{\left|{G}_{\upgamma ,\widehat{\rm{f}}\rm{azij},\upkappa }\left(j\Omega \right)\right|}_{\rm{ref}}}\right)$$
(74)

with \(\upgamma =0,z,v,a ; i=D,N; j=L,R; \kappa =fz,fy,fx,mz,my,mx\)

and \({ \left|{G}_{\upgamma ,\widehat{\rm{f}}\rm{azij},\upkappa }\left(j\Omega \right)\right|}_{\rm{ref}}=\left\{\begin{array}{c}1\frac{\rm{N}}{\rm{N}} for \kappa =fz,fy,fx\\ 1\frac{\rm{N}}{\rm{Nm}} for \kappa =mz,my,mx\end{array}\right..\)

Additionally, the phase response functions are calculated for the actuator forces.

Frequency Response Functions During Stillstand

First, the frequency response functions during stillstand \(\left(n=0 \rm{rpm}\right)\) are analyzed. To reduce the scope, only the amplitude responses regarding the bearing housing vibration velocities on the drive side are pictured. The amplitudes of the frequency response functions for the non-drive side are here identical to the amplitudes of the frequency response functions for the drive side for case 1, and for case 2 very similar, and give no additional information. All diagrams have the same structure. On the left side, the analyses for case 1 (symmetrical system) are pictured and on the right side, the analyses for case 2 (asymmetrical system). The analyses for the bearing housing vibrations show in the first row, the amplitude response functions for z-direction, in the second row for y-direction, and in the third row, for x-direction. The analyses for the actuator forces show in the first row the amplitude response functions and in the second row the phase response functions.

Excitation by a Vertical Force \({f}_{\rm{z}}\)

Figure 10 shows that there is no difference regarding the amplitude response functions for case 1 and case 2 for excitation with a vertical force \({f}_{\rm{z}}\), and that only bearing housing vibrations in vertical direction occur. The reason is that the axial and horizontal stiffness of the actuators will not influence here this vibration mode. With open control loops, a clear resonance frequency occurs for z-direction. When closing the control loops, this resonance is be damped clearly. The corresponding frequency response functions of the actuators are shown in Fig. 11.

Fig. 10
figure 10

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation force fz (z-direction) for open and closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Fig. 11
figure 11

Frequency response functions for the actuator forces related to the excitation force fz (z-direction) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Excitation by a Horizontal Force \({f}_{\rm{y}}\)

Figure 12 shows that for an excitation with a horizontal force, the amplitude response functions differ clearly for case 1 and case 2. For case 1, only bearing housing vibrations in y-direction occur, but for case 2, additionally bearing housing vibrations in z- and x-directions exist.

Fig. 12
figure 12

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation force fy (y-direction) for open and closed control loops, for case 1 and case 2, n = 0 rpm

Full size image

The reason is the asymmetry caused by the actuators, which lead to coupled vibration shapes. Figure 12 shows that for both cases all resonances are clearly damped by the control system.

The frequency response functions of the actuators are shown in Fig. 13.

Fig. 13
figure 13

Frequency response functions for the actuator forces related to the excitation force fy (y-direction) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Excitation by an Axial Force \({f}_{\rm{x}}\)

Figure 14 shows that for an excitation with an axial force \({f}_{\rm{x}}\), only vertical and axial bearing housing vibrations occur for case 1. Again, for case 2, bearing housing vibrations in all three directions exist. When closing the control loops, all resonances are again clearly damped for case 1 and case 2. The frequency response functions of the actuators are shown in Fig. 15.

Fig. 14
figure 14

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation force fx (x-direction) for open and closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Fig. 15
figure 15

Frequency response functions for the actuator forces related to the excitation force fx (x-direction) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Excitation by a Moment \({m}_{\rm{z}}\)

Figure 16 shows that for an excitation by a moment at the z-axis \({m}_{\rm{z}}\) only horizontal bearing housing vibrations occur for case 1. However, for case 2, bearing housing vibrations in all three directions exist again. The frequency response functions of the actuators are shown in Fig. 17.

Fig. 16
figure 16

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation moment mz (at the z-axis) for open and closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Fig. 17
figure 17

Frequency response functions for the actuator forces related to the excitation moment mz (at the z-axis) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image

It can be clearly seen in Fig. 16 that the controllers do not influence the horizontal bearing housing vibrations in case 1, because this vibration mode has no vertical machine feet displacements. This is obvious when the natural vibration mode in Fig. 6 is analyzed. Therefore, no actuator forces occur (Fig. 17). However, in case 2, all vibrations can be clearly influenced by the controllers, also the horizontal bearing housing vibrations, because here also vertical machine feet displacements exists (see natural vibration mode in Fig. 7) and, therefore, actuator forces occur (Fig. 17).

Excitation by a Moment \({m}_{\rm{y}}\)

Figure 18 shows that for an excitation with an moment at the y-axis \({m}_{\rm{y}}\), vertical and axial bearing housing vibrations occur for case 1. However, for case 2, bearing housing vibrations in all three directions exist. When closing the control loops, all resonances are damped clearly again for case 1 and case 2. The corresponding frequency response functions of the actuators are shown in Fig. 19.

Fig. 18
figure 18

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation moment my (at the y-axis) for open and for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Fig. 19
figure 19

Frequency response functions for the actuator forces related to the excitation moment my (at the y-axis) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Excitation by a Moment \({m}_{\rm{x}}\)

Figure 20 shows that for an excitation with an moment at the x-axis \({m}_{\rm{x}}\), only horizontal bearing housing vibrations occur for case 1. However, for case 2, bearing housing vibrations in all three directions exist. When closing the control loops, all resonances are again damped clearly for case 1 and case 2. The frequency response functions of the actuators are shown in Fig. 21.

Fig. 20
figure 20

Amplitude response functions for the bearing housing vibration velocities on the drive side related to the excitation moment mx (at the x-axis) for open and for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image
Fig. 21
figure 21

Frequency response functions for the actuator forces related to the excitation moment mx (at the x-axis) for closed control loops, for case 1 and case 2, n = 0 rpm

Full size image

Frequency Response Functions During Rotation

For the analysis of the frequency response function during rotation, only excitation by the moment \({m}_{\rm{z}}\) and the bearing housing vibration velocity in y-direction \({\widehat{v}}_{\rm{bDy}}\) are here considered, because this is the critical case, where for a symmetrical system, the active vibration control is not working, which is shown for standstill in “Excitation by a Moment mz”. Therefore, 3D diagrams are used now, where the amplitude response functions are pictured depending on excitation frequency \(f\) and rotational speed \(n\) (Figs. 22, 23).

Fig. 22
figure 22

Amplitude response functions for the bearing housing vibration velocity in horizontal direction on the drive side related to the excitation moment mz (at the z-axis), depending on rotor speed n, for a open control loops and for b closed control loops for case 1 (symmetrical system)

Full size image
Fig. 23
figure 23

Amplitude response functions for the bearing housing vibration velocity in horizontal direction on the drive side related to the excitation moment mz (at the z-axis), depending on rotor speed n, for a open control loops and for b closed control loops for case 2 (asymmetrical system)

Full size image

Figure 22 shows that for the symmetrical system there is nearly no difference in the amplitude response functions—bearing housing vibration velocity in horizontal direction on the drive side related to the excitation moment mz—between operation with open control loops (a) and with closed control loops (b) for rotor speeds up to 4 × 104 rpm. Above a rotor speed of 104 rpm, a splitting of the dominant resonance frequency at 63.5 Hz into two resonance frequencies begins and above 4 × 104 rpm the control system is able to reduce the amplitudes significantly, but below this rotor speed the control system is ineffective. However, these rotor speeds are fare away from the maximum rotor speed in this example, which lies at 3600 rpm. If the asymmetrical system is used, the amplitude response functions—bearing housing vibration velocity in horizontal direction on the drive side related to the excitation moment mz—change significantly (Fig. 23). The control system is very sufficient for all rotor speeds now. The maximum amplitude can be reduced by about 10 dB, when operating with closed control loops instead of operating with open control loops, and by about 14.3 dB when compared to the symmetrical system.

Discussion of the Results

The example shows that when analyzing the natural vibrations (“Natural Vibration Analysis”) of the two systems—case 1 (symmetrical system) and case 2 (asymmetrical system)—it is obvious that for case 1 all natural modes but one—mode 5 (Fig. 6)—can be influenced by the controllers in the speed range of the machine (\(n=0\dots 3600 \rm{rpm})\). However, for case 2 all natural modes can be influenced, because of the chosen asymmetry, caused by the actuators. This is also demonstrated by analyzing the frequency response functions (“Frequency Response Functions”), where all forced vibrations can be clearly reduced by the controllers for case 2. However, for case 1, the forced vibrations, which are caused by the moment \({m}_{\rm{z}}\) at the vertical axis, will not be influenced by the controllers, in the operating speed range. The amplitude response functions for the bearing housing vibration velocity in horizontal direction related to the excitation moment mz at the z-axis can be clearly reduced in case 2 by a factor of about 5.2—which corresponds to a reduction of 14.3 dB—using the active control, compared to case 1.

Conclusion

In the paper, a simplified 3D model for active vibration control of rotating machines mounted on active machine foot mounts—actuators, which are controlled by separate controllers, operating only in vertical direction—is derived and the mathematical coherences are described. The mathematical model is derived in the time domain and then transferred into the Laplace domain, where the transmission behavior and the calculation of the pols are derived, and afterwards transferred into the Fourier domain, where the frequency response functions regarding bearing housing vibrations and actuator forces are expressed. Additionally, a calculation method for special controller structures in combination with certain feedback strategies is demonstrated, where the controller parameters can be directly implemented into the system matrices—stiffness matrix, damping matrix and mass matrix. Last, but not least, the mathematical formulations have been implemented into a block diagram, using the simulation program Simulink. All different mathematical methods have been validated with each other and with an external finite element model.

The focus of the paper was—beside the mathematical description of the simplified 3D model—to show mathematically that a symmetrical machine design, where the center of gravity lies symmetrically between the machine feet with a vertical distance, in combination with identical actuators, leads to a symmetrical system, where all vibration shapes but one can be influenced by the controllers, when the gyroscopic effect is so low that it can be neglected. The vibration shape, where the machine is only rotating at its vertical axis, cannot be influenced by the controllers, because vertical machine feet displacements do not exist in this pure (decoupled) vibration shape. The main task of the paper is to show, that when changing the axial and/or horizontal stiffness and/or damping of only one actuator—which will lead to an asymmetrical system—the vibration modes get more coupled, so that a pure rotation at the vertical axis will no longer occur. Now, the vibration shapes will become more coupled and all vibration shapes can be influenced by the controllers, which is here called “vibration mode coupling by asymmetry”.