1 Introduction

In theories of liquid crystals [1,2,3,4] and of granular media [5,6,7,8], a directive field is often needed to describe the various liquid crystalline ordered phases. From this standpoint it often seems mandatory to have an additional directive (i.e. vectorial or tensorial) order parameter in order to describe the thermodynamics of complicated ordering phenomena and responses to directed external fields of soft matter systems. Contrarily, for diblock copolymers [9] (Grain boundaries of diblock copolymers have been analyzed experimentally [10, 11]) and microemulsions [12,13,14], a wide range of phenomena can be explained on the basis of a single order parameter describing the local concentration of one species versus the other, i.e. monomer A vs. B or water vs. oil. This is a result of a high degree of symmetry. It is still possible to describe a huge variety of ordered phases and responses to directed external fields. So the number of model parameters is kept at a minimum, while the richness of phenomena is still strikingly high. For instance bicontinuous microemulsions develop lamellar order adjacent to planar hydrophilic (hydrophobic) surfaces (in experiment and theory) [15,16,17]. Thus, the question arises how many order parameters are needed to describe the structure of microemulsions adjacent to a planar hydrophilic solid surface. Simple extensions to two order parameters have been undertaken [18]. However, local ordering of domains even in the bulk is surprising because it is hidden in many cases due to orientational averaging but it seems to govern the system on a local scale [19, 20]. For instance, aqueous lipid systems form oriented cubic structures at the planar solid interface [21]

Bicontinuous microemulsions appear to be isotropic on the macroscopic scale mostly inspected visually and on the nano-scale mostly observed by small angle scattering experiments. Microemulsions consist of well-separated water and oil domains with the interface being covered by a surfactant that mediates between them and gives them thermodynamic stability. The well-known Teubner-Strey [12] formula describes a pronounced isotropic Debye–Scherrer ring that is connected to altering water and oil domains of the well-known sponge structure. The underlying theory only needs a single order parameter. A high degree of symmetry is assumed, and so only three parameters remain essential, namely the domain size d, the correlation length ξ, and an amplitude of the fluctuations connected to the osmotic compressibility B. The typical ratio ξ/d of approx. 0.5 indicates that typically a single water or oil domain correlates only well with the next surface, but already much less well with the second next surface. Within such a correlation volume of 2 × 2 × 2 domains, the rare case of more detailed structure might appear. Here, two domains are involved to shape a correlated structure. The main questions are: (a) which special structure is found inside the volume of correlation, (b) how can the structure be made visible, and (c) does one need more order parameters to describe the inner structure of the correlation volume? The last question relates everything, because possibly a special local structure is preferred for some reason and neighboring correlation volumes might be related to each other in terms of orientation. Here, the close vicinity of the transition between lamellar and gyroid phases is highly interesting [22], while especially the gyroid phase attracts much attention in theory and biological systems [6]. It is shown that lipid membranes act as templates for chiral chitin networks in butterfly wings.

We tried to observe phenomena of aligned domains experimentally by preparing different microemulsions with nonionic surfactants of varying efficiency exposed to a planar hydrophilic surface. The observations base on grazing incidence small angle neutron scattering that resolve the near surface structure with varying depth resolution. Rheology experiments also aim at the internal structure of the complex fluid. The different nano-structures and findings are discussed in context of the present literature.

2 Materials and Methods

2.1 Materials

N-decane was obtained from Sigma Aldrich. The surfactants C8E3, C10E4 and C12E5 (with increasing emulsification efficiency [23, 24]) were obtained from Bachem, Weil am Rhein, Germany. The critical micelle concentrations (CMCs) of the three surfactants are reported to be 7.5, 0.68 and 0.064 mmol/l [25]. Deuterated n-decane and heavy water were obtained from Armar chemicals, Döttingen, Switzerland. All these chemicals were used without further purification. Deionized water was obtained from the Purelab Ultra filter from ELGA at 18.2 MΩcm. The microemulsion with C10E4 had a surfactant concentration of 17% vol and followed the procedure of Ref. [15, 16]. The new microemulsions with C8E3 and C12E5 had the following concentrations of 27.0/0.0/36.5/32.3/4.2 and 8.0/3.6/42.4/46.0/0.0 volume percent of surfactant/H2O/D2O/n-decane/d-decane. The mixtures are thermodynamically stable and form after short shaking of the vials. The approximate phase inversion temperatures of 20 °C and 36 °C were selected for the scattering experiments. All samples were visually inspected with crossed polarizers to confirm that the bulk structures are isotropic. At these high symmetric concentrations of oil and water, no spherical micelles (co)exist.

2.2 Experiments

Grazing incidence small angle neutron scattering (GISANS) measurements were performed on the instrument KWS1 at the MLZ in Garching with the reactor FRM-2 [26, 27]. Introductions about GISANS can be found in Refs. [28, 29]. The measurements of the C10E4 microemulsion have been described elsewhere [15] and initiated the usual procedure for all our GISANS measurements. The wavelength λ for the C8E3 and C12E5 microemulsions was λ = 10.5 Å. The silicon slab had a dimension of 15 × 5 × 2 cm3. The microemulsion was kept in our cell with a thickness of 0.5 mm. The temperature was set accordingly to the phase inversion temperature. For the two different microemulsions we set the apparent detector distances to 4 and 8 m with a symmetric slit collimation of 40 × 4 mm2. Due to a sample stage offset, the real detector distances were 3.7 and 7.7 m. The measured scattering patterns were corrected for detector efficiency to obtain intensities at the same scale.

The selected scattering length of the overall microemulsion of 2.46 × 10−6 Å−2 lead to a critical angle αc of 0.21° and a scattering depth Λ0 of 450 Å at zero incidence angle. Historically, in our interpretations, we defined the scattering depth Λ at small, finite incidence angles αi below the critical angle αc according to Λ = Λ0 × (1 −αi2/αc2)−1/2. When coming close to and going beyond the critical angle, the absorption becomes important, and the correct scattering depth z1/e is defined [30]:

$$z_{1/e} = \frac{\lambda }{{\sqrt 2 \pi \left( {l_{i} + l_{f} } \right)}},$$
(1)

with the characteristic functions:

$$l_{i,f} = \left[ {\alpha_{c}^{2} - \alpha_{i,f}^{2} + \sqrt {\left( {\alpha_{c}^{2} - \alpha_{i,f}^{2} } \right)^{2} + 4\beta^{2} } } \right]^{1/2} ,$$
(2)

where β describes all (from the primary intensity) outgoing radiation (due to absorption, incoherent and coherent scattering) according to

$$\beta = \frac{\lambda }{4\pi }\left( {N\alpha_{{{\text{abs}}}} + N\alpha_{{{\text{inc}}}} + {\Sigma }_{{{\text{coh}}}} } \right),$$
(3)

with N being the number density of scatterers, αabs the absorption cross section, αinc the incoherent cross section, and Σcoh the coherent (small angle) cross section. We estimated the small angle cross section from the known bulk scattering according to \({\Sigma }_{{{\text{coh}}}} = \frac{1}{2}\left( {\frac{\lambda }{2\pi }} \right)^{2} P_{2/3} \mathop \sum \nolimits_{i \ne j} \phi_{i} \phi_{i} \left( {\varrho_{i} - \varrho_{j} } \right)^{2}\) with the domain volume fractions ϕi and the domain scattering length densities ρi. As domains we counted oil, water and surfactant. The scattering invariant ratio P2/3 is defined as \(P_{2/3} = \smallint I\left( Q \right)QdQ/\smallint I\left( Q \right)Q^{2} dQ\). For the known shape of the bulk scattering we took the Teubner-Strey formula [12] \(I\left( Q \right) = 1/\left( {\left( {k_{0}^{2} + \xi^{ - 2} } \right)^{2} - 2\left( {k_{0}^{2} - \xi^{ - 2} } \right)Q^{2} + Q^{4} } \right)\) without the need for absolute calibration. The bulk scattering parameters d (k0 = 2π/d) and ξ were taken from tables [31, 32].

Safely below the critical angle of total reflection αc, the two scattering depths are dominated by the tunneling phenomenon and so Λ ≈ 2z1/e (for simplicity the incident and exit angle are assumed to be identical αi = αf [33]). In considerations about the near surface scattering [16] we showed that the virtual zero of characteristic scattering signals is connected to Λ for moderate scattering depts, while in the limit of large scattering depts the extrapolated virtual zero becomes z1/e.

3 Results and Discussion

The experimental grazing incidence scattering patterns are shown in Fig. 1 as a function of the surfactant (with growing emulsification efficiency) and of the scattering depth. The scattering depths of µm correspond to incidence angles being larger than the critical angle of total reflection. For the most efficient surfactant the single correlation peak stays for all scattering depths, even for infinity (We state in Ref. [16] that second next domains are not well correlated anymore. This means a constantly low correlation length even for the ordered structures while their characteristic expansion can be considerably larger. So different correlation compartments scatter independently, and the classical Bragg scattering that scales with the squared grain volume is not obatained.). This indicates capillary condensation on macroscopic length scales. Close to the Qz ≈ 0.005 Å−1 line, there are 2 weak peaks (Qy =  ± 0.01 Å−1) that we believe to indicate lateral correlations of protrusions or stalks of neighboring membranes. Those perforations must be quite well ordered laterally in order express visibly peaks. The medium efficient surfactant displays a rather narrow correlation peak that stays for scattering depths Λ ≤ 630 Å and then is replaced by the isotropic Debye–Scherrer scattering [15, 16]. So, there is a lamellar order next to the interface that vanishes surely at 850 Å. In a previous more detailed analysis, we analyzed the superposition of lamellar order and isotropic scattering that is clearly present at Λ = 630 Å, and found the more exact boundary at 400 Å (or ~ 600 Å in a second experiment) [15, 16]. The detailed value might depend on the hydrophilicity of the surface being dependent on the cleaning procedure. The least efficient surfactant displays a rather broad scattering maximum between Qy =  ± 0.02 Å−1 and Qz = 0.02–0.04 Å−1 that stays for scattering depths of up to 1020 Å. Only for infinite scattering depth a broad Debye–Scherrer ring indicates the isotropic state at large depths. The loss of intensity towards the horizon is due to refraction effects (even seen for the middle efficiency sample). So there must be a rather persistently oriented domain structure adjacent to the hydrophilic surface that only loses orientational correlation deeply in the bulk. The meaning of the broad scattering maximum will be resolved in the discussion below.

Fig. 1
figure 1

The experimental grazing incidence scattering patterns as a function of the different surfactants (C8E3, C10E4, C12E5) (increasing emulsification efficiency from left to right) and the scattering depth Λ (indicated in the images). The errors of the scattering depths are 10, 26, 150 Å, and 10 µm according to resolution effects [34]. The “divergence” [35] of the scattering depth at the critical angle increases this error. All color scales are linear and scale to the “maximum” intensity

Full size image

For this, we plotted the intensities of a region of interest (QY ≈ 0, QZ at maximum) as a function of the scattering depth Λ in (Fig. 2). For the most efficient surfactant, the trend has virtual zero intensity at around 370 Å indicating that a structure evolves from a depth of 370 Å on towards the bulk. The medium efficient surfactant was calculated from dividing the bicontinuous signal by the lamellar signal [15]. It displays a similar trend where it is known that from a depth of ~ 400–600 Å on perforations of the lamellar structure and the bicontinuous structure are found [16]. Such structures can be described by a Laplace transformation of a near surface structure with depth d, a transition region with a depth ζ, and the scattering depth Λ. The fraction f2 of the bulk scattering would read then [16]:

Fig. 2
figure 2

The scattering of a region of interest for the microemulsions with differently efficient surfactants. For C10E4, the rescaled intensity ratio of the bicontinuous versus the lamellar signal is depicted. Lines are guides for the eye

Full size image
$$f_{2} \left( {\Lambda } \right) = {\exp}\left( { - 2\frac{d}{{\Lambda }}} \right) \cdot \frac{{\Lambda }}{2}{\exp}\left( {\frac{{\zeta^{2} }}{{{\Lambda }^{2} }}} \right)\left( {1 - {\text{erf}}\left( {\frac{\zeta }{{\Lambda }}} \right)} \right),$$
(4)

which can be linearized by a Taylor expansion around d = 300 Å and ζ = 300 Å to:

$$f_{2} \left( {\Lambda } \right) = - 140.70 + 0.33786{\Lambda }{.}$$
(5)

This function nearly reproduces the observed trend (on a different scale). A much different trend is observed for the lowest efficient surfactant where no virtual zero is found in the positive range of Λ. When describing the near surface scattering fraction f1 one obtains:

$$f_{1} \left( {\Lambda } \right) = \frac{{\Lambda }}{2} - f_{2} \left( {\Lambda } \right),$$
(6)

with a linearization of

$$f_{1} \left( {\Lambda } \right) = 140.70 + 0.16214{\Lambda }{.}$$
(7)

This function nearly reproduces the observed trend (on a different scale). Thus, we would conclude that the scattering signal of the weakest efficient surfactant arises mainly from the near surface structure.

4 Discussion

Epitaxy near a planar surface is leading to very diverse structures [36,37,38,39] ranging from lamellar over hexagonal to cubic structures. Unfavorable suppression of Bragg peaks in the lateral dimension can be very weak due to orientational averaging or random orientation although the lateral correlation lengths may be very large. Thus the Bragg pattern in a GISANS experiment may look like from a lamellar ordering even though the underlying structure is hexagonal or cubic. However, the considered microemulsion systems are at the phase inversion temperature where the mean curvature is zero. The preferred minimal surfaces [40] are of the type bicontinuous, lamellar or cubic. Hexagonal cylinders or cubic arrangements of spherical domains can safely be excluded in our case. The near-surface lamellar ordering for the medium efficiency was computer simulated [15]. And the known trend of growing non-ionic surfactant molecules [31, 32] with rather high symmetry is that the one-phase bicontinous region of the phase diagram becomes more and more governed by a lamellar phase region. This means that from C8E3 to C12E5 the mean Gaussian curvature changes from larger to smaller values. This also means that the bending rigidity [24] and the negative saddle splay modulus are increasing on absolute scale. Thus, this supports directly the capillary condensation with a lamellar phase in the case of the most efficient surfactant. The medium and low efficient systems on the other hand prefer bicontinuous structures in the bulk. The highly interesting question arises what happens for the lowest efficiency at the solid interface.

For the lowest efficiency, the measurements display a broad maximum that is limited by an angle of approx. ± 38°. Knowing that the cubic gyroid structure [40] is a bicontinuous phase with a minimal surface, the to be considered Bragg peaks possess the indices (111) for non-symmetric protonation due to the surfactant, (1½½) and (110) for the ideal symmetric gyroid structure. The narrow placement of those Bragg peaks with instrumental smearing and possibly low correlation lengths would explain a continuous maximum to an angle of around ± 35°. A possible structure of the near-surface structure is depicted in (Fig. 3). The normal direction was assumed to be the (111) direction, because the distortion of the first domain is presumably minimal. Using this alignment of the domains presumably minimizes also the surface energy to the solid due to very low distortions. Thus, we assume that the lowest efficient system displays a gyroid structure that is induced by the hydrophilic surface boundary.

Fig. 3
figure 3

A scheme of a gyroid phase adjacent to a planar hydrophilic surface (blue transparent window). The surface indicates the surfactant film with blue facing the aqueous phase while orange indicates the oil domain. The finishing of the water domain was artificially forced by the last addend of the expression cos(x0)sin(y0) + sin(x0)cos(z0) + cos(y0)sin(z0) + 0.1 × (z-|z|)2 that describes the surfactant surface at its zero with the turned coordinates x0 = 2y/√6 + z/√3, y0 = −x/√2−y/√6 + z/√3, z0 = x/√2−y/√6 + z/√3. The orientation of the gyroid phase points with the (111)-axis to the normal z-direction

Full size image

Two different structures are identified near the interface: a presumably cubic gyroid and a lamellar interphase for the C8E3 and C10E4 surfactants. Especially the gyroid phase is interesting, because it is a minimal surface structure that is slightly more regularly ordered than the bicontinuous sponge phase. In orientationally averaged bulk samples, these two structures would be indistinguishable. Only the near surface structure reveals a higher degree of order. The surprising result is that the intrinsic correlation length ξ of 83 Å [31, 32] would limit the correlation volume to dimensions of two domains in all directions with a volume of (2ξ)3. Only the connectivity of the membranes might effectively lead to strings and arrays of relatively well-aligned sub-volumes that reach deeper into the volume than the bare correlation length would motivate. In the experiments, the maximum scattering depth where the gyroid phase is found is much larger than the correlation volume. This means, that a possible directive order parameter is weakly present in the experiments describing the aligning interaction between neighboring intrinsic correlation sub-volumes. For magnetic particles, strings and arrays are found with much stronger directive interactions [19, 20]. In the case of lamellar order at medium efficiency, we found four to six perfect domains of ~ 100 Å [15, 16] each before the isotropic structure evolves, while the correlations length is also ~ 100 Å. Also this finding is an indication of a weak directive order parameter, and a local order of (2ξ)3 sub volumes is discussed [16].

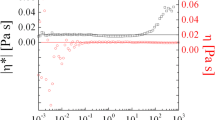
When comparing viscosities of microemulsions (in the range of 2–5cP [41]) and diffusion constants (in the range of 5 × 10−8cm2/s [42]) an effective particle radius of about 10–20 nm = 100–200 Å is reasonable indicating the diffusion of correlation volumes as described above. Interestingly [16], the diffusion effects can govern the viscosity measurements (Fig. 4) for shear rates lower than approx. 0.5 s−1 when the Deborah number [43, 44] is big enough. The characteristic shear rate is a macroscopic number when the diffusion reaches macroscopic length scales of µm. This effect indicates a formation of macroscopic traces of correlation volumes, i.e. the system is able to memorize diffusion paths. The Carreau model [45] describes the viscosity of networks with a much higher zero shear limit (limit not observed in Fig. 4) and a crossover to the bulk viscosity. Contrarily, liquid water [46, 47] does not memorize diffusion paths in terms of hydrogen bonds along such a long path of macroscopic scales. And so, no Deborah number is observed in classical rheology experiments on water.

Fig. 4
figure 4

The viscosity of the C10E4 microemulsion as a function of shear rate (solid symbols) compared to the same microemulsion with a PEP5–PEO15 diblock copolymer (open symbols, indices give polymer molar masses in kg/mol) of Ref. [16] where erroneously the polymer influence was neglected. The steep increase at \(\dot{\gamma }{ < 0}{\text{.03}}\;{\text{s}}^{{ - {1}}}\) is a clear indication of sample surface tension, while the weak shoulder with a dip at \(\dot{\gamma } = 0.3\;{\text{s}}^{{ - {1}}}\) indicates the presence of large structures that is also seen in the sample with polymer

Full size image

The near-surface ordering of the gyroid structure opens an experimental view on the local ordering that usually is hidden in the bulk phase where no preferential ordering is achieved. For biological lipid systems, the mechanism of alignment and choice of chirality is highly important when the amphiphilic system acts as template for chitin networks [6]. So far, all known studies of domain alignment took place at planar surfaces with single philicity [15,16,17, 21] including the current one. However, for diblock copolymers relative orientations of ordered domains are studied at grain boundaries [10, 11]. The next step of textured surfaces is left for future works. Also computer simulations would provide a very good view on such locally ordered domains that are lost on larger distances and that lead to an isotropic appearance even for scattering experiments on the bulk phase. The detailed analysis of the domain structures (experimental and simulated) would benefit from the Minkowski tensorial analysis [5,6,7,8].

The aspect of the vicinity to the phase transition between lamellar and gyroid mesophases [22] usually leads to a strong development of fluctuations where the system can be aligned better by external fields [48, 49]. We observed that with increasing surfactant efficiency the near surface order changed between gyroid to lamellar, and finally resulted in a capillary condensation [50]. So in our experiments the vicinity to the phase transition is given which presumably facilitates the domain alignment. The directive order parameter stays rather weak in the case of the near surface ordering, because the bulk phase is randomly oriented. For the case of capillary condensation, the effect might be stronger because the extension is macroscopic.

The large extension of the near-surface ordered interphase is a sign of a directive order parameter. So the concepts of a vectorial [1,2,3,4] or tensorial [5,6,7,8] order parameters need to be included in the theoretical description. The term bicontinuous microemulsion now includes different tendencies of local lamellar or cubic ordering that so far has not been distinguished—neither experimentally nor theoretically.

The capillary condensation of lamellar order for the C12E5 system is an indication of a stronger directive order parameter, and astonishingly displays order only from a depth of 400 Å on while the repeat distance is 800 Å. This indicates that the first membrane is found at a depth of 400 Å, which shorter than the repeat distance. Similarly, in spectroscopic experiments [51] a shorter distance of the first membrane was found. This is a confinement effect by the conservation of volume between the first membrane and the solid surface that reduces the amplitude of all undulations and therefore the Helfrich interaction is reduced.

5 Conclusions

We have clear indications that the C8E3 system displays an aligned cubic gyroid structure at the interface that also maintains locally in the bulk phase. This local order in the bulk is usually hidden for scattering experiments, because of the orientational averaging. The local bulk order extends with in a correlation volume of (2ξ)3 ≈ (200 Å)3 of approx. 2 × 2 × 2 domains, which is connected to a second order parameter. Furthermore, at the interface those sub-volumes are aligned and string along each other to reach deeper into the bulk volume than the bare correlation length ξ would describe, which is also connected to high viscosities at very low shear rates. For the C10E4 system, we already [15] described the near-surface lamellar order that also reaches deeper into the bulk volume than the bare correlation length. This deeper near-surface order is a clear sign of a second (directive) order parameter. Finally, the C12E5 system is dominated by the capillary condensation over a macroscopic volume, which again would support the existence of a directive order parameter. Interestingly, the bulk bicontinuous microemulsions possess a differently preferred local structure. Thus a new hidden property of bicontinuous microemulsions is observed. The unexpected, strongly elevated viscosities at very low shear rates explain very high forces when machines start up from the viewpoint of lubricants. We would call the observed network structure of directional order parameters the “dark matter” of complex fluids.