1 Introduction

Vortex-antivortex pairs can spontaneously form and move within a superconducting material when it is in a mixed state. In this state, first proposed by Andronov et al. and experimentally conducted by Sivakov et al., [1, 2], vortices and anti-vortices self-organize into a lattice-like structure, commonly referred to as the Abrikosov lattice. The presence of these pairs enables the material to maintain its superconducting properties even in the presence of an external magnetic field. The behavior and interactions of vortex-antivortex pairs in superconductors constitute a subject of extensive research within the field of condensed matter physics. Understanding their dynamics is of paramount importance for various applications, including the design of superconducting devices such as superconducting wires, detectors, and superconducting quantum bits (qubits) for quantum computing [3]. Also, as it is well-known, when an external current is applied to mesoscopic superconducting sample, it can induce resistive states caused by the appearance of phase-slips (topological fluctuations of the order parameter and occur as the barrier separating two competing order parameter configurations vanishes) or by the motion of kinematic vortices, also a phase slip occurs when the superconducting state vanishes somewhere in the sample, enabling discontinuities in the phase by some multiple of \(2\pi\) [4,5,6].

In the realm of superconductivity research and development, B. D. Josephson made significant contributions by analyzing the junctions of superconducting materials. He demonstrated the appearance of an supercurrent via tunneling between a insultor region, a hallmark of quantum mechanics, (this study led to the development a Superconducting Quantum Interference Devices). There were two main models, DC and AC, which differed in the number of Josephson junctions. In its original design, lead Pb and niobium Nb were used, both being among the first known superconducting elements with low critical temperatures of \(7.2\) \(K\) and \(9.2\) \(K\), respectively. The junctions were formed due to an oxide layer on the material’s surface, with the primary focus being on the quest for evidence of magnetic flux quantization [7, 8].

The manipulation and control of vortex-antivortex pairs’ motion can be crucial for optimizing the performance of superconducting materials in practical applications. This includes the minimization of energy losses and the maintenance of the superconducting state under various conditions. Researchers employ various techniques, such as pinning sites and external currents, to control and investigate the behavior of these pairs. It is worth noting that recent efforts have been directed toward the practical application of these findings. For instance, Elfeky et al. explored the analysis of the impact of quasiparticles, including vortex-antivortex pairs, on the fidelity of quantum circuit development [9]. Takahara et al., studied the magnetic transport properties in thin films of doped EGTO (\(Eu_{1-x}La_xTiO_3\)) to observe the evolution of ferromagnetic properties [10]. Additionally, it is interesting to mention how Hijano et al., utilized the Mattis-Bardeen theory to observe the response of superconductors in Hall response devices, as a result of research that has expanded the Usadel equation, allowing the analysis of the disordered Hall effect in superconductors, including its dependence on frequency [11].

Furthermore, it is noteworthy that V. M. Bevz et al., determined the maximum velocity of magnetic flux quanta through the energy relaxation of unpaired electrons. They introduced an approach for the quantitative determination of the number and velocity of vortices based on Aslamazov and Larkin’s prediction of kinks in current-voltage curves when the number of fluxons crossing the constriction is increased by one. They found a vortex velocity of \(v = 12 km/s\). These experimental observations are complemented by results from time-dependent Ginzburg-Landau modeling [12].

Fig. 1
figure 1

Layout of the studied sample: a thin film with \(L=12\xi\), \(W=8\xi\), \(a=2\xi\), \(r_i=0.6\xi\), and \(r_0=2.6\xi\), with \(d\ll \xi\), J is the external applied current. For our analysis, we choose \(x_1=3\xi\), \(x_2=6\xi\) and \(x_3=9\xi\)

Full size image

2 Theoretical formalism

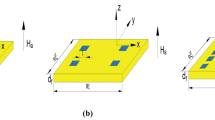
In the present work, we will study the superconducting matter in a single-codensate thin sample of size \(12\xi \times 8\xi\); with a roundabout-like defect of external (internal) circular radius \(r_o=2.6\xi\) \((r_i=0.6\xi\)), positioned at coordinates \(x_1=3\xi\), \(x_2=6\xi\) and \(x_3=9\xi\), in the x-axis (see Fig. 1). The width of the electrodes is \(a=2\xi\), through which a uniform DC current density J is injected, the same size was used for the thickness of the rectangular section of the weak link region. To conclude the description of the analyzed system, it is worth noting that the thickness of the film, denoted as \(d\ll \xi\), therefore, we will extrapolate to the two-dimensional problem [13,14,15,16,17,18,19]. The general form of the time-dependent Ginzburg Landau (TDGL) equation in dimensionless units in the (x, y)-plane is given by [20,21,22]:

$$\begin{aligned} \frac{u}{\sqrt{1+\Gamma ^2|\psi (x,y)|^2}}\left[ \frac{\partial }{\partial t}+i\varphi (x,y)+\frac{\Gamma ^2}{2}\frac{\partial |\psi (x,y)|^2}{\partial t}\right] \psi =\nonumber \\ (\nabla -i\textbf{A}(x,y))^2 \psi +(f(x,y)-|\psi (x,y)|^2)\psi (x,y) \; \end{aligned}$$
(1)

which is coupled to the equation for the electrostatic potential:

$$\begin{aligned} \Delta \varphi =\textrm{div}\left\{ \text {Im}[\bar{\psi }(\nabla -\textrm{i}{} \textbf{A}(x,y))\psi ] \right\} \end{aligned}$$
(2)

In the Eq. 1, the weak link (roundabout-like defect) is characterized by the anisotropy coefficient \(f(x,y)=1.0\), outside the weak link and \(f(x,y)=-0.5\) in the weak link region [23]. The distances are scaled by the coherence length \(\xi\), time is in units of the Ginzburg Landau time \(t_{GL}=\pi \hbar \big /8k_BTcu\), the electrostatic potential \(\varphi\) is given in units of \(\varphi _0=\hbar \big /2et_{GL}\), and the vector potential \(\textbf{A}\) is scaled by \(H_{c2}\xi\), where \(H_{c2}\) is the bulk upper critical field. We use the parameters \(u=5.79\) and \(\Gamma =t_E\psi _0/\hbar =10\), \(t_E\) is the inelastic scattering time [24]. Neumann boundary conditions are taken at all sample boundaries, except at the electrodes, where we used \(\psi =0\) and \(\nabla \varphi \mid _{n}=-J\), where J is the external applied current density in units of \(J_0=c\sigma \hbar /2et_{GL}\), \(\sigma\) is normal electrical conductivity, and the mesh grid of resolution \(\delta =0.1\). Although we consider \(T=0\) in our simulations, the generalizd time dependent-Ginzburg-landau equations can be applied to superconductors at \(T \ge 0.5Tc\), or equivalently, the sizes can be adjusted according to \(\xi (T)=\xi (0)/\sqrt{1-T/T_c}\).Footnote 1 For instance, for \(T=0.96T_c\), and \(\xi (0)=10\) nm, we have \(\xi =50\) nm. This gives \(L=600\) nm and \(W=400\) nm [25].

3 Results and discussion

We have considered three scenarios for to study the role of the defect on the vortex-state of the sample: Case 1, the defect is localized at position \(x_1=3\xi\); case 2, the defect localized at the central position of the sample, \(x_2=6\xi\); and finally considered a case 3, where we localized the defect in \(x_3=9\xi\). We do not consider external applied magnetic field and a DC current density J is uniformly applied through the electrodes. It is important to emphasize that the two-dimensional plate being simulated represents a superconductor with a specific critical temperature.

Fig. 2
figure 2

(a) Time average voltage V and b) Curve of the resistivity (\(\partial V/\partial J)\), both as a function of the applied current density J for the three cases of positions of the defect. The subindices are left (L) (case 1); center (C), (case 2); and right (R), (case 3) denoting the position of the defect

Full size image

3.1 \(V-I\) and \(R-I\) characteristic curves

The first thing we are interested to study is the response of the superconductor system to an external DC current density J, for this, we plot the voltage-current I-V and resistivity-voltage curves I-R for the three studied cases. In the Fig. 2 (a), is plotted the time average voltage V and in the Fig. 2(b), is plotted the resistivity (\(\partial V/\partial J)\), both as a function of the applied current density J for the three aforementioned positions of the defect. The arrows indicate the critical currents densities (current in which the first and subsequent vortex-antivortex pairs appears in the sample). So, we can see that \(J_{1L}\approx 0.243\), \(J_{2L}\approx 0.813\), \(J_{3L}\approx 0.906\); \(J_{1C}\approx 0.366\), \(J_{2C}\approx 0.317\), and finally \(J_{1R}\approx 1.99\), \(J_{2R}\approx 2.67\), and \(J_{3R}\approx 3.167\). As it is known, the appearance of phase slip-lines is due to the non-homogeneity of the superconducting currents in the sample. We considered cases where the position of the defect highly affects the configuration and symmetry of the supercurrents, leading to a high dependence of the position of the defect on the critical currents. We can appreciate a significant enhancement of the first critical current density for a case 3, so, the defect is in a position more distant from the left metallic contacts, therefore, the current distribution in the defect is symmetrical and homogeneous, leading to the appearance of the vortex-anti-vortex pairs at higher currents. For the case 1, the supercurrent is highly inhomogeneus bear to defect, leading to a lower critical current. The IR resistive curve exhibits typical behavior: within the range, \(J_1\le J \le J_2\), curves have a local maximum that is related to the dynamics of the phase-slip-lines. In the interval \(J_2 \le J\le J_3\), the system is in a partially normal state, where the superconductivity is nearly destroyed in the film. Above \(J_3\), the normal state sets in (except for the case 2 where the sample reach the normal state in \(J_{2C}\)).

Fig. 3
figure 3

Average velocity of the Vortex-anti-vortex pairs, Vm, for (a) case 1 and 3 and (b) Case 2

Full size image
Fig. 4
figure 4

Average voltage V as a function of the time t for the three studied cases. (Inset)(a) three studied cases

Full size image

3.2 Kinematic-vortex velocity \(V_m\)

In the Fig. 3 (a, b), is plotted the average velocity \(V_m\) of the Vortex-anti-vortex pairs for (a) case 1 and 3 and (b) Case 2. It is very interesting to note that for the asymmetrical case 1 and case 3 (Fig. 3 (a)), for applied currents \(J\ge 3.2\) for the case 3, and \(J\ge 3.5\), \(V_m\rightarrow 0\), this means that the kinematic-vortex is no longer formed, and then, this pairs experiences a decreasing of its velocity, we can explain this phenomenon by the surface-barrier-effect role, the surface barrier energy (in the external surface and in the internal surface of the defect) decreases due to the increase of the Lorentz force for higher J. As a consequence, the vortex pairs increasing its kinetic energy to leave the sample [25]. Otherwise, for the symmetrical case 2 (Fig. 3 (b)), we see that the velocity \(V_m\) increases with J, for \(J\ge 1.5\), \(V_m\) increases. The velocity of annihilation of vortex-anti vortex pairs is \(V_m(1,3)\approx 10(V_m(2))\), is very interesting to note that the pinning center position could be related by the velocities of gap-like samples, given that \(V_m\) in gap-like samples can be ten times larger than those of gapless systems, and it is related to its larger superconducting-normal transition current [25]. The difference in the velocities is also case-dependent, due that the defect leading to a depreciation of the superconductivity and allowing a faster motion of the vortices. In the Fig. 4, is plotted the time average voltage V as a function of the time t for the three studied cases. As is well-known, the temporal behavior of the voltage curve produced by the vortex anti-vortex dynamics is highly affected by the configuration, dimensionality, or nature of the system. If we appreciate the Fig. 3(a), the average velocity at \(J\ge 2.2\) presents a non-conventional behavior for the case 1 and for the case 3. This leads us to not find a determined pattern in the oscillation frequency of the kinematics-vortex in the voltage-time curve. We considered that the presence of the defect and its asymmetric position play a fundamental role in the value of the surface energy barriers and super currents.

Fig. 5
figure 5

Logarithm of the modulus of the order parameter \(ln(\mid \psi \mid )\). (left) Case 1 at a) \(J=0.28\), b) \(J=0.50\), (right) Case 2 at a) \(J=0.38\); b) \(J=1.00\). Red (blue) regions represents a superconducting (normal) state \(\psi =1(0)\)

Full size image

3.3 Kinematic-vortex state

In this subsection, we plot the logarithm of the modulus of the order parameter \(\mid \ln (\psi )\mid\) for the studied cases, each of them at specific, J with the aim of observing the processes of creation and annihilation of vortex-antivortex pairs. Within of the Fig. 5, we have plotted the logarithm of the modulus of the order parameter \(ln(\mid \psi \mid )\). In the left panel, denoted as Case 1, at \(J=0.28\), we can observe the ingress of vortex-antivortex pairs taking place at the upper ends of the system. Over time, these pairs travel through the neck of the defect, converging at the left end of the inner circle. It’s noteworthy to mention that this inner circle is also a superconductor, with equal critical temperature of the sample. Notably, the red (blue) regions represent a superconducting (normal) state, denoted as \(\psi =1(0)\). Additionally, it’s interesting to note that the entire process occurs within the defect. As the pairs approach each other, a higher normal state is achieved, resulting in a significant increase in resistivity. Eventually, the pairs meet and annihilate, returning to a superconducting state, but with higher resistance than initially. For the right panel (Case 2), in (a) at \(J=0.38\), the vortex anti-vortex pairs are created in the center of the defect, Subsequently, these pairs travel through the neck of the defect until they annihilate at the upper ends. It’s worth noting that when the pair creation process occurs in the center and annihilation takes place at the ends, a lower resistive state is observed over time, as opposed to previous cases. In (b), for Case 2 at \(J=1.00\), pairs are once again created at the ends and annihilated in the center, resulting in a high resistive state during both the creation and annihilation processes.

Fig. 6
figure 6

Logarithm of the modulus of the order parameter \(ln(\mid \psi \mid )\), for the case 3. At (a) \(J=0.50\), (b) \(J=1.00\), and c) \(J=2.00\). Red (blue) regions represents a superconducting (normal) state \(\psi =1(0)\)

Full size image

In the Fig. 6, we plot the results for the case 3, where the defect is positioned on the right-hand side of the sample. We present the temporal evolution of the kinematics vortex at a) \(J=0.5\), b) \(J=1.0\), and c) \(J=2.0\). For \(J=0.5\), b) \(J=1.0\), we can appreciate that the formation of vortex-antivortex pairs occurs in the external border of the sample at a vertical line across \(x_r=x_3+r_i=9.6\xi\), with a subsequent annihilation in the inner circle, specifically in a point localized in the internal defect, \(x_r=x_3+r_i=9\xi +0.6\xi =9.6\xi\) and \(y_r=W/2=4\xi\). In the scenario for \(J=0.5\) occurs a resistive state during the early stages of pair creation, followed by a reduction until annihilation, where the resistive state once again becomes prominent. This initial stage is not observed when \(J=1.00\), in which the resistive state progressively strengthens as annihilation approaches. Finally, for \(J=2.00\) (and for \(J=1.0\)), the vortex anti-vortex creation is observed at a vertical line across \(x_3-r_i=9\xi -0.6\xi 8.4\xi\), and annihilation occurs in a left point on the equator of the defect, \(x_l=x_3-r_i=8.4\xi\) and \(y_l=W/2=4\xi\), maintaining a consistently high resistive state throughout the process.

Fig. 7
figure 7

Logarithm of the modulus of the order parameter \(ln(\mid \psi \mid )\) for (a) case 1, at \(J=1.00\), and \(J=2.00\), b) for the third case, at \(J=2.50\), \(J=2.76\). Red (blue) regions represents a superconducting (normal) state \(\psi =1(0)\)

Full size image

In Fig. 7, it is evident that achieving analogous resistive effects between the case 1 and case 3 requires a higher value of J. For \(J=1.0\) we observe that kinematic-vortex enter on the right side of the defect on a line passing outside the inner circle but inside the outer circle (Fig. 7(up) (a)). As the J increases, the point where the next vortex anti-vortex pairs enter the film moves away from the defect and are located in a point tangent to the outer circle \(x_r=x_1+r_o=3\xi +2.6\xi =5.6\xi\). A similar scenario can be observed in the Fig. 7 down)(b) at \(J=2.76\) for the case 3. With a similar way of the case 1, the kinematic-vortex enter on the left side of the defect on a line passing outside the inner circle but inside the outer circle, then is J increases, the point where the next vortex anti-vortex pairs enter the film moves away from the defect and are located in a point tangent to the outer circle \(x_l=x_3-r_o=9\xi -2.6\xi =6.4\xi\). It is interesting to note that for the cases where the defect is located asymmetrically on the sample, at high J, the phase-slip lines occur in points equidistant from the center \(\Delta x=0.4\xi\).

4 Conclusions

In this contribution, we solve the generalized Ginzburg-Landau equations to study the superconducting state of a thin-film with an internal shape pinning-center made of a material at low critical temperature. We analyze current-voltage \(I-V\), resistivity-voltage \(I-R\) and voltage-time \(V-t\) curves, velocity of vortex anti-vortex pairs annihilation, and superconducting electronic density considering three positions of the defect in the sample. We found a high dependence of the defect position on the critical currents, points where the vortex anti-vortex pairs enters to sample and its velocity, it is due to asymmetry on the currents caused by the position of the defect. Finally, we found an interesting and novel behavior of the phase slip line, a distinctive deformation in the current flow is observed, resulting in a counterflow effect. When pairs are created from the center towards the ends, this counterflow assumes an ovular shape. Conversely, when pairs are generated at the ends and move towards the center, this counterflow develops with a focus on the vortices, eventually forming a pattern resembling a figure in shape of X at their convergence, with the counterflow concentrated within the vortex cores. Also, we found that for higher J, the point where the vortex anti-vortex pairs enter the film moves away from the defect and are located in a point tangent to the outer circle (case 1 and case 3) of the defect. Our results show a way to control the dynamics of the vortices, critical currents, and points of annihilation or creation of the cinematic vortices by including defects in the sample, important in the design and development of devices applied in industry and engineering. Understanding the mechanisms of dissipation in mesoscopic superconductors is not only of fundamental value but also crucial for further technological advancements, particularly in the development of superconducting devices such as single-photon and single-electron detectors.