1 Introduction

Humans and animals exhibit remarkable skills in manipulating tools and their bodies, such as striking whips or tails to accurately hit targets less than 1.5 s. These rapid and precise movements with complex dynamics are not fully understood. Deciphering these dynamics can not only advance robotic arm control, but also offer new insights into the mechanisms behind fast, accurate movement control.

Biologically, the manipulation of elongated structures like arms, tails, or objects is common. These systems typically consist of many flexibly connected segments, often powered by muscles, as seen in snake bodies [1], reptile and mammal tails [2, 3], and the legs of harvestmen [4]. Research such as that whip and hand movements had been investigated and analyzed in arm targeting [5], yet the intricacies of motion planning and muscle-mimicking control are still largely unexplored.

In robotics, manipulating flexible objects represents a significant challenge due to computational and dynamic complexities introduced by their high flexibility. While most research has concentrated on slower, general manipulations, like folding laundry [6], setting tablecloths [7], and performing surgical operations [8, 9], few studies have addressed fast, goal-directed control with flexible objects [10,11,12]. Furthermore, these studies have largely overlooked the potential of reinforcement learning and optimization algorithms.

Our work contributes to the State-Of-The-Art (SOTA) by merging data-driven and physics-based algorithms to facilitate fast and accurate movement control. It reviews and compares existing works on targeted robotic manipulation of flexible objects (see below), with a particular focus on the control of a 2-jointed arm manipulating a flexible whip. While this research specifically addresses whip manipulation, the proposed control framework is versatile enough to be applied to end-effector space control of robots with a high degree of freedom, broadening our understanding and capabilities in both biological and robotic domains of fast, accurate manipulation.

The research in robotic manipulation of deformable objects focuses mainly on slow control tasks such as folding cloth and surgery operations [8, 9]. In this paper, we focus on fast and accurate whip targeting. “Accurate" means that a human arm is controlled for striking a whip tip to hit a target in space, rather than other parts of a whip. The related SOTA works of manipulating flexible objects (e.g., cables) to hit targets are introduced as follows and compared to our proposed framework (see Table 1). A self-supervised learning framework was proposed for a robot arm to manipulate cables to knock cups [10]. Their method is based on the use of iteration learning with a convolutional neural network. Moreover, the movement is not accurate and fast (< 1.5 s) targeting, since the manipulated cable tip was fixed to a wall. To achieve whip targeting, a simple (non-learning) control framework based on dynamic primitives was presented, in which a DIRECT global method was applied to optimize joint motion parameters (e.g., duration) with constant impedance control [13]. The framework was validated only in a simulated robot arm. Besides, there is no investigation into motion learning and adaptation. A batch Newton method and differential dynamic programming were compared in robotic trajectory optimization of manipulating a soft rod to hit wooden blocks [14]. The rod flexibility is not comparable to a whip used for accurate and fast targeting. In addition, their trajectory optimization methods are based on predefined wooden block positions, rather than visual feedback. They were not compared with learning approaches, e.g., reinforcement learning [15]. Their optimization methods only fit to the fixed targets and one of them can not reach convergence. The iterative residual policy, a general learning framework was proposed for controlling two joints (of a UR5 robot) to manipulate ropes to hit targets [11]. However, the framework was validated with prior constraint knowledge in physical robot whipping, since learning converges only after three iterations in some experimental scenarios. Moreover, the framework is not data-efficient in simulated whipping control, since it heavily depends on big training datasets, i.e., 54 million trajectories. Furthermore, the learned motion trajectories may fall into local optimality, because a simple (greedy) motion update rule was adopted. In addition to control, how to bridge the gap between simulated and real robot whip targeting remains an open issue in deformable object manipulation [16]. This is because training learning-based controllers is effortfully costly in real, and distorted in simulated modeling of flexible objects. Sim2real of robotic whip targeting control will be presented and analyzed in this paper. Other related works and their sim2real have been introduced in comprehensive reviews [17,18,19]. Most of them focus mainly on slow manipulation of deformable objects (e.g., cloth), rather than fast (< 1.5 s) and targeted movement control guided by visual feedback in this paper.

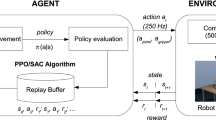
Table 1 Comparison between our proposed and SOTA methods
Full size table

The main motivation of this work is to reverse-engineer motion learning and muscle control in a fast targeting behavior by a flexible tool, which has not yet been well investigated. It will push not only scenario boundary from slow and non-targeted to fast and targeted manipulation control of flexible tools, but also methodology from a data-driven or physics-based algorithm to their integration. These progresses advance the understanding of motion learning and muscle-like control on sophisticated manipulation of bionic systems. Its significance depends on a novel learning-based framework for achieving fast and accurate manipulation by combining data-driven and physics-based algorithms. It consists of a motion planner learned or optimized by an algorithm, an online impedance adaptation controller, a sim2real mechanism, and a visual feedback mechanism (see Fig. 1). Its specific novelties lie in,

  1. 1.

    Integration of data-driven and physics-based methods guided by visual feedback. Six data-driven methods are applied, consisting of four SOTA DRLs [20,21,22,23], a deterministic optimization [24], and a genetic algorithm [25]. Each of them is integrated into a physics-based control method, i.e., OIAC. The integration imitates human arm motion planning and (online) adaptation in whip targeting;

  2. 2.

    Sim2real for accurate and fast movement learning and control. Our proposed framework is validated from simulated and real whip targeting control. The trajectories of the whip tips are 89.09\(\%\) similar in the simulated and real environment, therefore, validating a feasible transfer from simulated to real whip targeting control.

The rest of this article is organized as follows. The proposed methods are described in Sect.  2. The experimental results of the simulated and real whip targeting are introduced in Sect. 3. Sections 4 and 5 contain a comprehensive discussion and conclude the article, respectively.

2 Methods

Simulated and physical two-jointed arms were controlled to strike a whip to hit targets, respectively. In the controller (see Fig. 1), arm joint movements and duration are learned or optimized by an algorithm, while the joint impedance (control) is online modulated. The learning or optimization process was performed in simulation and later validated in the physical whip targeting.

Fig. 1
figure 1

The LEarning-based MOvement coNtrol (LEMON) framework for a whip-targeting task. The motion planner provides the desired joint positions \(\varvec{q_\text {d}}\in \mathbb {R}^{1\times 2}([q_\text {s}, q_\text {e}])\) and velocities \(\varvec{\dot{q_\text {d}}}\in \mathbb {R}^{1\times 2}([\dot{q}_\text {s}, \dot{q}_\text {e}])\) that are sent to an online adaptive impedance controller to generate the joint torque commands \([\tau _\text {s}, \tau _\text {e}]\). The learning/optimization objective is to minimize the distance L between a whip tip and a target, guided by the visual feedback (state)

Full size image

2.1 Simulation

A whip targeting control environment was built into the advanced physics simulator MuJoCo, which outperforms its counterparts in more accurate and faster modeling [26]. Moreover, it is more efficient to perform Sim2real in DRL, i.e., to train DRL algorithms in simulations and then to transfer knowledge into real robots [27, 28]. A ‘lumped-parameter’ model (Fig. 2) was built to simulate complex whip continuum dynamics, which consists of a series of N rotational springy and damped nodes. Each sub-model is comprised of a rotational joint and an ideal point-mass m [kg], which connects a massless cylinder with length l [m]. A rotational spring with k \([N \cdot m/rad]\) and a rotational damper with b \([N \cdot m \cdot s/rad]\) consists of a rotational joint, and N of these discrete sub-models are connected serially to comprise the experimentally-fitted whip [13]. The whip parameters [N, l, m, k, b] can be seen in Table 2. The parameters are adopted from [29], which have been numerically validated in real whip (targeting) kinematics [5]. The N-node whip model is connected to the upper-limb model with a freely-rotating hinge. Note that complex whip dynamics are unknown for the following motion planner and control system.

Fig. 2
figure 2

The combined planar upper-limb and whip model (see its dimension in Table 2)

Full size image
Table 2 Experimentally-fitted whip model dimension [5, 13]
Full size table

2.2 Motion Planner and Control

2.2.1 Zero-Torque Trajectory

The desired upper-limb joint angles follow a minimum-jerk trajectory given by,

$$\begin{aligned} \varvec{q}_{\text {d}}(t)=\varvec{q}_{\text {i}}+\left( \varvec{q}_{\text {f}}-\varvec{q}_{\text {i}}\right) \left\{ 10\left( \frac{t}{D}\right) ^{3}-15\left( \frac{t}{D}\right) ^{4}+6\left( \frac{t}{D}\right) ^{5}\right\} , \end{aligned}$$
(1)

where \(\varvec{q_\text {d} (t)} \in {R}^{2}\) is the joint position; \(\varvec{q_\text {i}}\) and \(\varvec{q_\text {f}}\) denote the initial and final zero-torque joint positions, respectively; t is the time; D means the trajectory duration time; If the current time t is longer than D, the zero-torque trajectory of joints would remain at the final positions \(\varvec{q_\text {f}}\). The planned motion parameters \(\varvec{q_\text {i}}\), \(\varvec{q_\text {f}}\), and D were learned or optimized by one of six applied algorithms (see them in Sect. 2.3).

2.2.2 OIAC[30]

A first-order impedance controller with gravity compensation is used in the upper-limb model,

$$\begin{aligned} \varvec{\tau }&= \varvec{K}\left( \varvec{q}_{\text {d}}-\varvec{q}\right) +\varvec{B}\left( \dot{\varvec{q}}_{\text {d}}-\dot{\varvec{q}}\right) +\varvec{\tau }_{\text {G}}, \end{aligned}$$
(2)
$$\begin{aligned} \varvec{\tau }_{\text {G}}&= \varvec{J}_{\text {s}}^{T} \varvec{f}_{\text {s}}+\varvec{J}_{\text {e}}^{T} \varvec{f}_{\text {e}}+\varvec{J}_{\text {w}}^{T} \varvec{f}_{\text {w}}, \end{aligned}$$
(3)

where \(\varvec{q}\in {R}^{2}\) is two joints displacement vector; \(\varvec{{\tau }_{\text {G}}}\) denotes gravity compensation for the upper-limb and whip model; \(\varvec{{J}}\) and \(\varvec{{f}}\) denote the jacobian matrices and the gravitational forces on each part; The subscripts s, e, and w correspond to the shoulder joint, elbow joint, and whip, respectively; \(\varvec{K}\in {R}^{2\times 2}\), \(\varvec{B}\in {R}^{2\times 2}\), which represent both the shoulder joint and elbow joint neuromuscular mechanical impedance; The proposed OIAC aims at online adapting \(\varvec{K}\) and \(\varvec{B}\) impedance matrices to the joint tracking error reduction,

$$\begin{aligned} \varvec{K}(t)&= \left[ \begin{array}{ll} k_{\text {ss}}(t) &{} k_{\text {se}}(t) \\ k_{\text {es}}(t) &{} k_{\text {ee}}(t) \end{array}\right]&\varvec{B}(t)&= \left[ \begin{array}{ll} b_{\text {ss}}(t) &{} b_{\text {se}}(t) \\ b_{\text {es}}(t) &{} b_{\text {ee}}(t) \end{array}\right] \end{aligned}$$
(4)

where the diagonal and off-diagonal terms correspond to the impedance generated by the monoarticular and biarticular muscles of the upper limb, respectively.

$$\begin{aligned} J&=J_{\text {c}} +J_{\text {p}}, \end{aligned}$$
(5)
$$\begin{aligned} J_{\text {c}}&= \frac{1}{2} \int _{0}^{D}\left( \Vert {\text {vec}}(\tilde{\varvec{K}})\Vert _{\varvec{Q}_{\varvec{K}}}^{2}+\Vert {\text {vec}}(\tilde{\varvec{B}})\Vert _{\varvec{Q}_{\varvec{B}}}^{2}\right) d t , \end{aligned}$$
(6)
$$\begin{aligned} J_{\text {p}}&= \int _{0}^{D} \dot{V}(t) d t \quad V(t) = \frac{1}{2} \varepsilon ^{T}(t) \varvec{I}(\varvec{q}) \varvec{\varepsilon }(t), \end{aligned}$$
(7)

where the cost function of OIAC is J; \(J_\text {c}\) is the weighted norms of matrices \(\varvec{K}\) and \(\varvec{B}\) from the zero-torque trajectory; \(\varvec{Q}_{\varvec{K}}\) and \(\varvec{Q}_{\varvec{B}} \in {R}^{4 \times 4}\) are positive symmetric weighting matrices, which affect optimization speed through dimension [31]; D denotes the duration time; \(J_\text {p}\) is the task error function; \(\varvec{I}(\varvec{q})\) is the upper-limb model inertial matrix; \(\varepsilon (t)\) is the time-varying tracking error given by,

$$\begin{aligned} \varvec{\varepsilon }(t)&= \varvec{e}(t)+\beta \dot{\varvec{e}}(t),\, \varvec{e}(t) = \varvec{q}_{\text {d}}(t)-\varvec{q}(t) \end{aligned}$$
(8)
$$\begin{aligned} \varvec{K}(t)&= \varvec{F}(t) \varvec{e}^{T}(t),\, \varvec{B}(t) = \varvec{F}(t) \dot{\varvec{e}}^{T}(t), \,\varvec{F}(t) = \frac{\varvec{\varepsilon }(t)}{\gamma (t)}, \end{aligned}$$
(9)
$$\begin{aligned} \gamma (t)&= \frac{\text {a}}{1+\text {C}\Vert \varepsilon (t)\Vert ^{2}}, \end{aligned}$$
(10)

where \(\varvec{e}(t)\) and its derivative calculate the joints position and velocity error separately comparing with the desired ones; \(\beta\) is 0.6; (Equation (9)) is used for the real \(\varvec{K}\), \(\varvec{B}\); (Equation (10)) shows the adaptation scale factor; a is 0.2, and C is 5; The mathematical derivation and other details can be seen in [31].

2.3 Learning/Optimization

Four RL algorithms and OIAC are integrated into the proposed LEMON control framework, respectively. To learn a policy for the whip targeting task, the pseudocode of LEMON is listed in Algorithm. 1.

Algorithm 1
figure a

LEMON algorithm for whip targeting

Full size image

2.3.1 Proximal Policy Optimization (PPO) [20]

PPO is an algorithm for learning optimal control policies in environments with discrete and continuous action spaces. A trust region optimization algorithm is used to improve the stability and reliability of policy gradient methods in the actor-critic method. The current state \(s_t\) is fed into two same structure networks, actor and critic. Both feedforward networks have hidden layers of size 64 and 64. The learning rate is set to 1e-4. The actor produces the decision Gaussian distribution \(\pi (s_t|\theta )\), which the action a is sampled. The critic assesses the output V(s) corresponding to the \(s_t\). The objective function of PPO is the expected return of the policy, with a term that encourages the new policy to be close to the old policy (Eq.(11)):

$$\begin{aligned} J_{\text {PPO}}(\theta )=\sum _{t=1}^{T}\left( \frac{\pi _{\theta }\left( a_{t} \mid s_{t}\right) }{\pi _{o l d}\left( a_{t} \mid s_{t}\right) } \hat{A}_{t}-\beta \textrm{KL}\left[ \pi _{\text{ old }} \mid \pi _{\theta }\right] \right) , \end{aligned}$$
(11)

where \(\hat{A}_{t}\) is the advantage function; \(\textrm{KL}\left[ \pi _{\text{ old }} \mid \pi _{\theta }\right]\) is the KL-divergence constraint; \(\beta\) dynamically changes with the adaptive KL penalty.

2.3.2 Deep Deterministic Policy Gradient (DDPG) [21]

To some extent, it could be seen as an extension of the Deep Q Network (DQN), since it follows similar strategies of Q-learning. There are two kinds of neural networks, i.e., an actor that maps the states to actions and a critic that estimates the value of taking a specific action in a specific state. The Q-network is used to compute the gradient of the policy expected return with respect to the policy parameters, and the actor and critic networks are both updated by using the transitions stored in the replay buffer. Each network is a two-layer feedforward neural network with 256 hidden nodes. Rectified Linear Units (ReLU) [32] activation functions are employed between each layer for both the actor and critic networks. Additionally, a final tanh unit is applied following the actor network output. The critic network takes both the state and action as input for its first layer. The learning rate for these networks is set to 3e-4. The objective function of DDPG is given by,

$$\begin{aligned} J_{\text {DDPG}}(\theta )=\sum _{t=1}^{T} \left( Q_{\phi }\left( s_{t}, a_{t}\right) -\ln {\pi _{\theta }\left( a_{t} \mid s_{t}\right) }\right) \end{aligned}$$
(12)

2.3.3 Twin Delayed Deep Deterministic Policy Gradients (TD3) [22]

TD3 is an extension of DDPG that applies clipped double Q-learning, delayed policy updates, and target policy smoothing, and the target Q-value for the Q-network update is the minimum of the two Q-network predictions.

There are two sets of critic networks and an actor network adopted in TD3. The state \(\varvec{s_{ts}}\) is the input to the actor network, which is formed by three-layer feedforward neural network with (9, 256, 256) hidden nodes and ReLU activation functions. The input of critic network is a state-action pair to compute a target value Q and through two Q-network and reduce the risk of deviation, shown in (Eq. (13)). A soft updating factor \(\tau\) is imported TD3 to update network parameters, thus the delayed method brings a low variance action updates (Eq. (14)). Moreover, a Gaussian noise \(\epsilon\) is added to the target policy to improve TD3 capacity of exploration (see Eq. (15)). Therefore, the stability of the DDPG is facilitated by this network structure, and TD3 becomes more robust and more reliable in learning than DDPG in some tasks [33]. It also uses fixed target networks for the actor and the critic, which helps reduce the correlation between the target and the prediction, making the training more stable and consistent. TD3 also introduces a delay between the update of the actor and the critic networks to further improve the stability and robustness of the algorithm.

$$\begin{aligned}&Q_{\text {target}}=r+\gamma \underset{i=1,2}{\text {min}}Q_{\phi _{i}}(s_t,a_t) , \end{aligned}$$
(13)
$$\begin{aligned}&\phi _{i^{\prime }}\leftarrow \tau \phi _{i}+(1-\tau )\phi _{i^{\prime }}, \end{aligned}$$
(14)
$$\begin{aligned}&\epsilon \sim {\text {clip}}(\mathcal {N}(0, \sigma ),-c, c) \end{aligned}$$
(15)

2.3.4 Soft Actor-Critic (SAC) [23]

SAC is an off-policy algorithm, which is used to optimize the expected cumulative reward of a stochastic policy. The hidden layers neuros and learning rate are set the same as DDPG and TD3. Different from these two off-policies, it includes an entropy regularization term in the objective function. The term will balance exploration and exploitation, making it suitable for tasks with unknown dynamics, so it encourages exploration and stability in the learning process. The objective function of SAC is given by,

$$\begin{aligned} J_{\text {SAC}}(\theta )=\sum _{t=1}^{T} \left( r\left( s_{t}, a_{t}\right) +\alpha H\left( \pi \left( \cdot \mid \theta _{t}\right) \right) \right) , \end{aligned}$$
(16)

where \(H\left( \pi \left( \cdot \mid s_{t}\right) \right)\) reflects how random the policy in state s; \(\alpha\) is regularization coefficient to control the entropy, it is 0.2 in the whip task;

2.3.5 Reward Design

The reward function decides how to evaluate the action value, it affects the policy formulation and entire training results. Here the distance is utilized in the reward function given by,

$$\begin{aligned} r(s_t,a_t)&= {\left\{ \begin{array}{ll} r = -10*d &{}\text { if } 0.1< d\\ r = -5*d &{} \text { if } 0.06< d\le 0.1 \\ r = 50 &{} \text { if } d\le 0.06, \end{array}\right. } \end{aligned}$$
(17)

where if the distance is smaller than 0.06m, it would be considered as the tip hits the target successfully in the simulated and real environment;

2.3.6 Locally-based Divide Rectangle (DIRECT-L)

A DIRECT-L algorithm was applied to control simulated whip targeting control [13]. It weights more toward the local search than the global and samples the objective function points at \(\Omega\) (Eq. (18)) to start its search. To simplify the analysis and reduce the algorithm running time, it is usually normalized as \(\left[ 0,1\right]\), and also considered as a bound-constrained optimization problem. It is used for sampling the new centers of the new hypercube. The DIRECT-L selects potential hypercube in S. Normally, the optimal potential hypercube exists either in the local search low function values at the centers or in the large enough to be good targets for global search. Thus, not all such hypercube is divided, selecting the smallest and biggest value of f to subdivide the hypercube into subgroups.

$$\begin{aligned}&\Omega = \left\{ x \in \mathbb {R}^{N}: lb \le x \le hb\right\} \sim \Omega = \left\{ x \in \mathbb {R}^{N}: 0 \le x \le 1\right\} , \end{aligned}$$
(18)
$$\begin{aligned}&\min _{x \in \Omega } f(x), \quad f: \mathbb {R}^{N} \rightarrow \mathbb {R}, \end{aligned}$$
(19)

where f is Lipschitz continuous on \(\Omega\); N is the number of dimension; lb is the low boundary of the action; hb is the high boundary of the action.

2.3.7 Genetic Algorithm (GA)[34]

Since the objective function is hard to express with the action space elements, another powerful optimization method GA is raised to solve the black box problem. A complete GA includes three main operators such as selection, crossover, and mutation. Each solution is represented as a chromosome and every parameter corresponds to a gene. Fitness (f) is the GA evaluation standard. Generally, the value of f is higher, the individual is fitter for the environment, so the objective minimum distance is transferred as,

$$\begin{aligned} f&= \frac{D_{\text {max}}-d_{\text {real}}}{D_{\text {max}}} , \end{aligned}$$
(20)

where \(D_\text {max}\) means the maximum distance value from the tip to the target; \(d_{\text {real}}\) means the real distance value from the tip to the target.

2.4 Visual Tracking

The Intel camera D435Footnote 1 was used for the vision tracking mission, located 3.5 meters in front of the robot arm and targets. It provides the distance between the whip tip and a target as feedback to learning/optimization algorithms. Mean-shift is a popular method for object tracking in computer vision because it does not require any prior information about the object’s shape or motion [35]. Therefore, the method was selected for real-time tracking deformable and fast whip movements. After the pre-processing of the Gaussian filtering, the target and whip tip were segmented by the different Hue, Saturation, and Value (HSV) thresholds in frames, respectively. Figure 3 shows how to track the real-time distance between the tip and the target.

Fig. 3
figure 3

Vision tracking of the whip tip and targets over time t

Full size image

3 Results

The length of the real robot arm is the same as the simulated one (see Fig. 4). Each joint of the upper limb model is driven by a Dynamixel motorFootnote 2 [36]. This simple actuation design has no external spring, damper, and gear. It follows an actuation trend in robotic movement control, i.e., lightweight and reduced inertia. Its resulting control challenges (e.g., adaptivity) will be addressed by our proposed LEMON framework (see Fig. 1). The experiments were run on Ubuntu 20.04 laptop with graphic card RTX3060, and each RL learning or optimization algorithm took seven training hours on average. The experimental video can be seen at the footnote.Footnote 3

Fig. 4
figure 4

The real two-joint robot arm consisting of the joints \(J_{0,1}\) for 2D movement control. Detailed parameters of its weight and length refer to a real human arm model [37], which can be checked in Table 3

Full size image
Table 3 Arm model dimension
Full size table

3.1 Comparisons between Learning/optimization Methods

3.1.1 Task Definition

The task is to learn or optimize the planned movement parameters (see Eq. (1)) of the proposed LEMON control framework by one of the six algorithms. They aim at minimizing the distance L between a whip tip and a target. 300 random targets were generated to compare the generalization performance of the six algorithms in simulated whip targeting. The targets were situated in a circle with a radius of 0.1 m (see green dots in Fig. 5). Note that the hit threshold value \(L^{*}\) is set to 0.06 m, i.e., the target is considered to be hit if \(L \le L^{*}\).

Fig. 5
figure 5

Targets distribution zone

Full size image

3.1.2 Performance

The generalization performance of a learning or optimization algorithm is quantified by its average required trials of successfully hitting 300 targets,

$$\begin{aligned} \overline{N_{\text {hit}}} =\frac{1}{300} \sum _{i=1}^{300} n_{\text {hit}}, \end{aligned}$$
(21)

where \(\overline{N_{\text {hit}}}\) means the average required trials; \(n_{\text {hit}}\) denotes the required trials of successfully hitting a target. A fewer \(\overline{N_{\text {hit}}}\) refers to a better learning generalization.

DRL algorithms excluding the PPO, perform better than the nonlinear optimization DIRECT-L and a genetic algorithm, since the on-policy strategy adopted in the PPO is low-efficient in exploration and exploitation. Besides, we can see that the SAC outperforms the other five counterparts in learning generalization (see Fig. 6). This is because entropy regularization is introduced to boost its exploring capacity in the SAC, therefore leading to better learning generalization with fewer average hits.

Fig. 6
figure 6

Trial averages for hitting 300 random targets (see Eq. 21) by six learning or optimization algorithms

Full size image

Figure 7 shows the average rewards of four DRL algorithms over 500 episodes. An episode reward was the average of 100 (trial) accumulated rewards. The first 50 episodes were used for allocating random data into the replay buffer. We can see that the SAC outperforms the three counterparts owing to its better exploration ability.

Fig. 7
figure 7

Average rewards of four DRL algorithms over 500 episode training

Full size image

3.2 Comparison between the OIAC and Constant Impedance Controller

The comparison indicates the benefits of replacing constant impedance control with the OIAC. The stiffness matrix \(\varvec{K}\) and damping matrix \(\varvec{B}\) used for the constant impedance controller are given by [13]:

$$\begin{aligned} \varvec{K}&= \left[ \begin{array}{ll} 29.5 &{} 14.3 \\ 14.3 &{} 39.3 \end{array}\right] ,&\varvec{B}&= \left[ \begin{array}{ll} 2.95 &{} 1.43 \\ 1.43 &{} 3.93 \end{array}\right] . \end{aligned}$$
(22)

We can see that the position tracking error governed by the OIAC is reduced to \(22.36\%\) of constant impedance control (see Fig. 8 and Table 4). Besides, the velocity tracking error guided by the OIAC is decreased to \(13.29\%\) of constant impedance control. Therefore, the integration of the SAC and OIAC outputs others in better learning generalization and higher tracking control accuracy.

Table 4 Performance of different impedance controllers with SAC
Full size table
Fig. 8
figure 8

Errors of the position and velocity in the shoulder and elbow joint; (a) left: shoulder joint position errors; right: elbow joint position errors; (b) left: shoulder joint velocity errors; right: elbow joint velocity errors; (c) compares the absolute maximum errors in two joints; pos_s, vel_s, pos_e, and vel_e are the abbreviations of position and velocity for shoulder, and elbow, respectively

Full size image

3.3 Sim2real

We can see that the whip trajectories in the simulated and real environments are \(89.09\%\) similar (see Fig. 9), which is quantified by the average similarity parameter \(\rho _{\text {similar}}\),

$$\begin{aligned} \rho _{\text {similar}}=\frac{1}{\text {n}}\sum _{k=1}^{n}\sum _{i=1}^{m}\left( 1-\sqrt{\frac{( P_{k}^{i}- S_{k}^{i} )^2}{( P_{k}^{i} )^2} } \right) , \end{aligned}$$
(23)

where n denotes the number of simulated and physical whip tip trajectories, i,e, n=18 (trials), each of which has m data points; \(\sqrt{( P_{k}^{i}- S_{k}^{i} )^2}\) is the Euclidean distance between \(P_{k}^{i}\) of a physical whip tip trajectory and \(S_{k}^{i}\) of the related simulated one. Learned trajectories of hitting three different targets in simulated and physical whip targeting are \(89.09\%\) similar over iterations (see Fig. 9), respectively. The high similarity indicates that it is practicable to achieve sim2real in this task though some slight gaps between the simulated and real environments.

Fig. 9
figure 9

Simulated and physical whip tip trajectories over learning iterations; (a–c) refer to targets 1–3 (green dots)

Full size image

Thus, it is feasible to achieve sim2real because the whip movements are very similar in both environments. Figure 10 (b-d) shows the distance L between a whip tip and a target, stiffness, and damping values in a whip targeting task. The amplitudes of the shoulder joint stiffness and damping values are higher than those of the elbow joint, as the shoulder joint is a leading joint in the control task.

Fig. 10
figure 10

Sim2real: (a) 12 snapshots of a simulated whip targeting and a physical whip targeting; (b) distance L between a whip tip and a target; (c, d) stiffness \(\varvec{K}(t)\) and damping \(\varvec{B}(t)\), respectively (parameters of the OIAC)

Full size image

4 Discussion

4.1 Algorithmic Comparison

GA and DIRECT-L optimization methods are worse than most DRL methods in learning generalization of whip targeting control. Required iterations by the GA depend heavily on the quality of initial population formulations. The new population is composed of operations such as replication, crossover, and mutation of the previous generation of individuals. There is no clear direction for optimization in the whip task, so the recursive iterations are more than other algorithms. For the DIRECT-L, the optimization process presents regularity, as the optimal solution is either a smallest or largest hypercube. Thus, it has a specific optimization direction for the fixed target and will change to the opposite one when the result is always divergent. However, the dividing hypercube method is usually better at the low-dimension discrete space. As the spatial dimension increases, the optimization becomes hard. Therefore, its performance is worse than off-policy DRL in continuous control tasks, e.g., whip targeting control. The PPO, as an on-policy DRL, is the same as an updated policy. Therefore, the data used in a previous policy will be replaced. It is a good algorithm to solve the continuous action problem, but not fit for the whipping task in this project. If a target is not hit in one single trial, a robot will try a new policy to generate new datasets. The historical data from previous policies is not kept, thus its optimization effect is worse than off-policy DRL. Off-policy DRL algorithms refer to the previous data experience saved by a replay buffer. The performance of DDPG and TD3 is similar in whip targeting control, since both of them are based on a determined policy. Besides, the TD3 is an extension of the DDPG. Different from the DDPG and TD3, a central feature of the SAC is entropy regularization that prevents the policy from converging to a local optimum. Therefore, the exploration of the SAC is more efficient than the DDPG and TD3. A Q-function and policy are used to estimate the action-value and determine the best actions, which allow for learning a policy and a value function in the SAC. Its output action is within the range of the tanh formula, while the TD3 output action refers to the tanh formula with noise. The actor-critic network will be more robust with the noisy formula, but its generated actions will be close to the boundary. The TD3 is a good strategy for other tasks, but not for the presented whip targeting. This is because the actions which can hit targets are usually not around the boundary. Based on the above reasons, SAC is more suitable to learn whip targeting control tasks.

4.2 Limitations

The proposed learning-based control framework is a prototype with several limitations that illustrate directions for future work. First, it was validated on joint space control of a two-DoF robot. Further work is required for end-effector space of a UR5 robot arm with the combination of reinforcement learning and online adaptive admittance/impedance control [15, 31, 38]. This will reduce control dimension to three, compared to six of UR5 joint space. Second, it assumes that the targets are fixed. An advanced vision algorithm can be developed to predict moving target trajectories, which is integrated into the presented control framework. Third, its application is limited to flexible tool targeting control, which can be extended to industrial scenarios, e.g., pick and throw objects into boxes. Finally, its motivation is to explore the benefits of integrating data-driven and physics-based algorithms into fast and accurate robot manipulation with flexible tools. In future, experimental data of human whip targeting will be recorded to analyze and compare differences between human and machine intelligence. This may lead to next-generation robot arm manipulation and novel understandings on fast and accurate human motor control.

5 Conclusion

The upper limb model is used to reverse-engineer the fast movement control of a deformable object, e.g., whip targeting. The whole process includes an impedance controller to ensure the stability of the movement. When the coordinates of targets are fixed, the tracking error of OIAC is better than that of the constant impedance controller. At the same time, a variety of optimization methods were tested to compare learning strategies for hitting different targets, where the model has to provide quickly adjustments. Finally, SAC and OIAC showed better effects and is a more suitable optimization method for this paper. Human muscle properties will be analyzed and understood by reproducing whip targeting in a 7-DoF robot with a muscle-like controller in future [38].