Performance Analysis of 5 G Wireless Hybrid Precoding Using Evolutionary Algorithms

Abstract

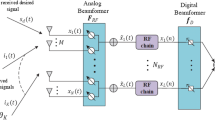
Emerging 5G communication solutions utilize the millimeter wave (mmWave) band to alleviate the spectrum deficit. In the mmWave range, Multiple Input Multiple Output (MIMO) technologies support a large number of simultaneous users. In mmWave MIMO wireless systems, hybrid analog/digital precoding topologies provide a reduced complexity substitute for digital precoding. Bit Error Rate (BER) and Spectral efficiency performances can be improved by hybrid Minimum Mean Square Error (MMSE) precoding, but the computation involves matrix inversion process. The number of antennas at the broadcasting and receiving ends is quite large for mm-wave MIMO systems, thus computing the inverse of a matrix of such high dimension may not be practically feasible. Due to the need for matrix inversion and known candidate matrices, the classic Orthogonal Matching Pursuit (OMP) approach will be more complicated. The novelty of research presented in this manuscript is to create a hybrid precoder for mmWave communication systems using metaheuristic algorithms that do not require matrix inversion processing. The metaheuristic approach has not employed much in the formulation of a precoder in wireless systems. Five distinct evolutionary algorithms, such as Harris–Hawks Optimization (HHO), Runge–Kutta Optimization (RUN), Slime Mould Algorithm (SMA), Hunger Game Search (HGS) Algorithm and Aquila Optimizer (AO) are considered to design optimal hybrid precoder for downlink transmission and their performances are tested under similar practical conditions. According to simulation studies, the RUN-based precoder performs better than the conventional algorithms and other nature-inspired algorithms based precoding in terms of spectral efficiency and BER.

Appendices

Appendix A for HHO

$$\begin{aligned}{} & {} E _{\textrm{initial}}=2rand-1 \end{aligned}$$

(13)

$$\begin{aligned}{} & {} E _{\textrm{r} } =2 E_{\text{ initial } }\left( 1-\frac{t }{\textrm{T}}\right) \end{aligned}$$

(14)

$$\begin{aligned}{} & {} {\varvec{F}}_{\mathrm { {\textbf {B}}}}(t +1)=\left\{ \begin{array}{c} {\varvec{F}}_{\mathrm { {\textbf {Brand}}}}(t )-a _1\vert {\varvec{F}}_{\mathrm { {\textbf {Brand}}}}(t )-2a _2 {\varvec{F}}_{\mathrm { {\textbf {B}}}}(t )\vert , \quad q \ge 0.5 \\ \left( {\textbf {F }}_{\mathrm { {\textbf {Brabbit}}}}(t )-{\varvec{F}}_{\mathrm { {\textbf {Bm}}}}(t )\right) -a _3\left( \textrm{LB}+a _4(\textrm{UB}-\textrm{LB})\right) , q <0.5 \end{array}\right. \end{aligned}$$

(15)

where $a _1, a _2, a _3, a _4$, and $q$ are iteratively adjusted arbitrary numbers in between 0 and 1. The variables’ upper and lower limits are displayed as $\textrm{LB}$ and $\textrm{UB}$. ${\textbf {F }}_{\mathrm { {\textbf {Brand}}}}$ is a randomly picks hawk from the present population[14].

$$\begin{aligned} {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}=\frac{1}{\mathrm N} \sum _{i=1}^\mathrm N {\textbf {F }}_{\mathrm { {\textbf {Bi}}}}(t ) \end{aligned}$$

(16)

For soft besiege:

$$\begin{aligned} {\textbf {F }}_{\mathrm { {\textbf {B}}}}(t +1)=\Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )-E _{\mathrm r} \vert \textrm{J}{\textbf {F }}_{\mathrm { {\textbf {Brabbit}}}}(t )-{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )\vert \end{aligned}$$

(17)

where $\textrm{J}=2(1-$ rand $), \Delta {\varvec{ {F}}}_{\mathrm { {\textbf {B}}}}(t )={\varvec{ F}}_{\mathrm { {\textbf {Brabbit}}}}(t )-{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )$.

For hard besiege:

$$\begin{aligned} {\textbf {F }}_{\mathrm { {\textbf {B}}}}(t +1)={\textbf {F }}_{\mathrm { {\textbf {Brabbit}}}}(t )-E _{\mathrm r}\vert \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )\vert \end{aligned}$$

(18)

For soft besiege with progressive rapid dives:

$$\begin{aligned}{} & {} {\textbf {F }}_{ { {\textbf {B}}}}(t +1)=\left\{ \begin{array}{l} {\textbf {Y }}, \text{ if } f_{o b j}({\textbf {Y }})<f_{o b j}\left( {\textbf {F }}_{{ {\textbf {B}}}}(t )\right) \\ {\textbf {Z }}, \text{ if } f_{o b j}({\textbf {Z }})<f_{o b j}\left( {\textbf {F }}_{ { {\textbf {B}}}}(t ))\right) \end{array}\right. \end{aligned}$$

(19)

$$\begin{aligned}{} & {} {\textbf {Y }}={\textbf {F }}_{\mathrm { {\textbf {Brabbit}}}}(t )-E _{\mathrm r}\vert \textrm{J} {\textbf {F }}_{\mathrm { {\textbf {Brabbit}}}}(t )-{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )\vert \end{aligned}$$

(20)

$$\begin{aligned}{} & {} {\textbf {Z }}={\textbf {Y }}+{\textbf {S }} \times {\text {Levy}}({{\textrm{dim}}}) \end{aligned}$$

(21)

The dimensionality of task is $\textrm{dim}$ and ${\textbf {S }}$ is a random vector by size $1 \times \textrm{dim}$ and Levy is the levy flight function.

$$\begin{aligned} {\text {Levy}}(x )=0.01 \times \frac{m \tau }{|n |^{0.5}}, \tau =\left( \frac{\gamma (1+\beta ) \times \sin \left( \frac{\pi \beta }{2}\right) }{\gamma \left( \frac{1+\beta }{2}\right) \times \beta \times 2\left( \frac{\beta -1}{2}\right) }\right) ^{1 / \beta } \end{aligned}$$

(22)

$m ,n$ are arbitrary values inside of (0,1), $\mathrm {\beta }$ has a default value of 1.5.

For hard besiege with progressive rapid dives:

$$\begin{aligned}{} & {} {\textbf {F }}_{{ {\textbf {B}}}}(t +1)=\left\{ \begin{array}{l} {\textbf {Y }}, \text{ if } f_{o b j}({\textbf {Y }})<f_{o b j}\left( {\textbf {F }}_{{ {\textbf {B}}}}(t )\right) \\ {\textbf {Z }}, \text{ if } f_{o b j}({\textbf {Z }})<f_{o b j}\left( {\textbf {F }}_{{ {\textbf {B}}}}(t )\right) \end{array}\right. \end{aligned}$$

(23)

$$\begin{aligned}{} & {} {\varvec{ Y}}= {\varvec{F}}_{{ {\textbf {Brabbit}}}}(t )-E _{\mathrm r}\vert \mathrm J {\textbf {F }}_{{ {\textbf {Brabbit}}}}(t )-{\varvec{ F}}_{{ {\textbf {Bm}}}}(t )\vert \end{aligned}$$

(24)

Appendix B for SMA

$$\begin{aligned}{} & {} \overrightarrow{{\textbf {M }}( \text{ SmellIndex } (i ))}=\left\{ \begin{array}{c} 1+\varphi \cdot \log \left( \frac{BF -{\textbf {P }}(i )}{BF -WF }+1\right) \text{, } \text{ condition } \\ 1-\varphi \cdot \log \left( \frac{BF -{\textbf {P }}(i )}{BF -WF }+1\right) , \text{ others } \end{array}\right. \end{aligned}$$

(25)

$$\begin{aligned}{} & {} \text{ Smell \, index } ={\text {sort}} ({\textbf {P }}) \end{aligned}$$

(26)

where ${\textbf {P }}(i )$ belongs to the top half of the population and the value of $\varphi$ lies in range 0 to 1. $BF$ and $WF$ are the best and worst fitness values currently attained, SmellIndex is the order of fitness values sorted in ascending manner [18].

$$\begin{aligned} {\textbf {p }}=\tanh \vert {\textbf {P }}(i )-DF \vert \end{aligned}$$

(27)

${\textbf {P }}(i )$ indicates the fitness of $\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}}$, $DF$ represents the best fitness measured across all iterations.

$$\begin{aligned}{} & {} \overrightarrow{{\textbf {u b}}}=[-\delta , \delta ] \text{ and } \delta ={\text {arctanh}}\left( -\left( \frac{t }{\mathrm {~T}}\right) +1\right) \end{aligned}$$

(28)

$$\begin{aligned}{} & {} \overrightarrow{{\textbf {u c}} }=[-\alpha , \alpha ] \text{ and } \alpha =1-\left( \frac{t }{\mathrm {~T}}\right) \end{aligned}$$

(29)

$$\begin{aligned}{} & {} \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}{ }^*}=\left\{ \begin{array}{c} \text{ rand } \cdot (\textrm{UB}-\textrm{LB})+\textrm{LB}, \text{ rand }<\rho \\ \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}(t )}+\overrightarrow{u b} \cdot \left( M \cdot \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Ba}}}}(t )}-\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bb}}}}(t )}\right) , \varphi <{\textbf {p }} \\ \overrightarrow{u c} \cdot \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )}, \varphi \ge {\textbf {p }} \end{array}\right. \end{aligned}$$

(30)

where $\textrm{LB}$ and $\textrm{UB}$ stand for the search range’s lower and upper limits, respectively.${\varvec{ F}}_{\mathrm { {\textbf {Ba}}}},{\varvec{ F}}_{\mathrm { {\textbf {Bb}}}}$ represents two individuals selected from the swarm.

Appendix C for HGS

$\textrm{l}$ is the parameter set as per the experiment, $\textrm{dim}$ is the dimension of the task and ${\textbf {Hungry }}$ represents the hunger of each entity, ${\textbf {sum }}_{\textrm{Hungry}}$ is the sum of hungry feelings of all entities [21].

If $f_{o b j}(i )$ is the fitness value of each entity then $BF$ and $WF$ are the best and worst fitness attained.

$$\begin{aligned} {\text {{\textbf {Hungry }}}}(i )=\left\{ \begin{array}{lr} 0, &{} {\textbf {All Fitness }}(i )==BF \\ {\text {{\textbf {Hungry }}}}(i )+{Q }, &{} {\textbf {All Fitness }}(i) !=BF \end{array}\right. \end{aligned}$$

(31)

where ${\textbf {AllFitness }}(i )$ maintains the fitness of individual entity in the current iteration [21].

$$\begin{aligned} {Q }=\left\{ \begin{array}{cc} LQ \times (1+r ), &\quad TQ <LQ \\ TQ , &\quad TQ \ge LQ \end{array}\right. \end{aligned}$$

(32)

The hunger sensation $Q$ is limited to a lower bound $LQ$.

$$\begin{aligned}{} & {} TQ =\frac{f_{o b j}(i )-BF }{WF -BF } \times r _6 \times 2 \times (\textrm{UB}-\textrm{LB}) \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \overrightarrow{P _{\textrm{1}}(\textrm{l})}=\left\{ \begin{array}{cc} {\text {{\textbf {Hungry }}}}(i ) \cdot \frac{\textrm{N}}{{\textbf {sum }}_{\textrm{Hungry}}} &{} \times r _4,r _3<\textrm{l}\\ &{}1,r _3>\textrm{l} \end{array}\right. \end{aligned}$$

(34)

$$\begin{aligned}{} & {} \overrightarrow{P _{\textrm{2}}(\textrm{l})}=\left( 1-\exp \left( -\mid {\textbf {Hungry }}(i )-{\textbf {sum }}_{\textrm{Hungry}} \mid \right) \right) \times r _5 \times 2 \end{aligned}$$

(35)

$r _3$, $r _4$ and $r _5$ are random numbers lies in between 0 and 1.

$$\begin{aligned} E _{\textrm{F}}= & {} {\text {sech}}\left( \vert f_{o b j}(i) -BF \vert \right) \end{aligned}$$

(36)

$$\begin{aligned} {\text {sech}}(x )= & {} \frac{2}{e^x +e^-x } \end{aligned}$$

(37)

$$\begin{aligned} \mathbf {R _{\textrm{F}}}= & {} 2 \alpha \times \text{ rand } - \alpha \end{aligned}$$

(38)

$$\begin{aligned} \alpha= & {} 2 \times \left( 1-\frac{t }{\textrm{T}}\right) \end{aligned}$$

(39)

$$\begin{aligned} \begin{aligned}&\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t +1)}= \\&{\left\{ \begin{array}{ll}\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )} \cdot (1+{\text {randn}}(1)), \quad r _1<\textrm{l}\\ \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}}+\mathbf {R _{\textrm{F}}} \cdot \overrightarrow{P _{\textrm{2}}} \cdot \vert \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}}-\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )}\vert , \quad r _1>\textrm{l}, r _2>E _{\textrm{F}}\\ \overrightarrow{P _{\textrm{1}}} \cdot \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}}-\mathbf {R _{\textrm{F}}} \cdot \overrightarrow{P _{\textrm{2}}} \cdot \vert \overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}}-\overrightarrow{{\textbf {F }}_{\mathrm { {\textbf {B}}}}(t )}\vert , \quad r _1>\textrm{l}, r _2<E _{\textrm{F}}\end{array}\right. } \end{aligned} \end{aligned}$$

(40)

Appendix D for RUN

when cost function is viewed as a minimization problem

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}={\textbf {F }}_{\mathrm { {\textbf {Bn}}}}-\Delta {\textbf {F }}_{\mathrm { {\textbf {Bn}}}}, {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}={\textbf {F }}_{\mathrm { {\textbf {Bn}}}}+\Delta {\textbf {F }}_{\mathrm { {\textbf {Bn}}}} \end{aligned}$$

(41)

$$\begin{aligned}{} & {} \text{ if } \text{ rand } <0.5 \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {B}}}}(n +1)=\left( {\textbf {F }}_{\mathrm { {\textbf {Bc}}}}+r \cdot SF \cdot g \cdot {\textbf {F }}_{\mathrm { {\textbf {Bc}}}}\right) \nonumber \\{} & {} +SF \cdot SM +\mu \cdot {\text {randn}} \cdot \left( {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}-{\textbf {F }}_{\mathrm { {\textbf {Bc}}}}\right) \nonumber \\{} & {} \text{ else } \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {B}}}}(n +1)=\left( {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}+r \cdot SF \cdot g \cdot {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}\right) \nonumber \\{} & {} +SF \cdot SM +\mu \cdot {\text {randn}} \cdot \left( {\textbf {F }}_{\mathrm { {\textbf {Br1}}}}-{\textbf {F }}_{\mathrm { {\textbf {Br2}}}}\right) \nonumber \\{} & {} \text{ end } \end{aligned}$$

(42)

Where $r$ is an integer, so it can be either 1 or – 1. The value of $g$ lies in range 0 to 2. $SF$ is an adaptive factor, where $\mu$ is a random number[23].

$$\begin{aligned}{} & {} SF =2.(0.5- \text{ rand } ) \times f \end{aligned}$$

(43)

$$\begin{aligned}{} & {} f =\textrm{a} \times \exp \left( -\textrm{b} \times \text{ rand } \times \left( \frac{i }{\textrm{T}}\right) \right) \end{aligned}$$

(44)

$\textrm{a}$ and $\textrm{b}$ are constants chosen between 0 and 1.

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bc}}}}=\varphi \times {\textbf {F }}_{\mathrm { {\textbf {Bn}}}}+(1-\varphi ) \times {\textbf {F }}_{\mathrm { {\textbf {Br1}}}} \end{aligned}$$

(45)

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}=\varphi \times {\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}+(1-\varphi ) \times {\textbf {F }}_{\mathrm { {\textbf {Blbest}}}} \end{aligned}$$

(46)

where $\varphi$ is randomly picked from range 0 to 1. The most effective answer is ${\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}$. The best position at each cycle is represented by ${\textbf {F }}_{\mathrm { {\textbf {Blbest}}}}$.

$$\begin{aligned}{} & {} {\textbf {k }}_1=\frac{1}{2 \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}}\left( \text{ rand } \times {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}-u \times {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}\right) \end{aligned}$$

(47)

$$\begin{aligned}{} & {} u ={\text {round}}(1+ \text{ rand } ) \times (1- \text{ rand } ) \end{aligned}$$

(48)

$$\begin{aligned}{} & {} {\textbf {k }}_2=\frac{1}{2 \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}}\left( {\text {rand}} \cdot \left( {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}+{\text {rand}}_1 \cdot {\textbf {k }}_1 \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right. \nonumber \\{} & {} \left. -\left( u \cdot {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}+{\text {rand}}_2 \cdot {\textbf {k }}_1 \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right) \end{aligned}$$

(49)

$$\begin{aligned}{} & {} {\textbf {k }}_3= \frac{1}{2 \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}}\left( \text{ rand } \cdot \left( {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}+{\text {rand}}_1 \cdot \left( \frac{1}{2} {\textbf {k }}_2\right) \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right. \nonumber \\{} & {} \left. -\left( u \cdot {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}+{\text {rand}}_2 \cdot \left( \frac{1}{2} {\textbf {k }}_2\right) \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right) \end{aligned}$$

(50)

$$\begin{aligned}{} & {} {\textbf {k }}_4=\frac{1}{2 \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}}\left( {\text {rand}} \cdot \left( {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}+{\text {rand}}_1 \cdot {\textbf {k }}_3 \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right. \nonumber \\{} & {} \left. -\left( u \cdot {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}+{\text {rand}}_2 \cdot {\textbf {k }}_3 \cdot \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}\right) \right) \end{aligned}$$

(51)

$$\begin{aligned}{} & {} SM =\frac{1}{6}\left( {\textbf {x }}_{\textrm{RK}}\right) \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}} \end{aligned}$$

(52)

$$\begin{aligned}{} & {} {\textbf {x }}_{\textrm{RK}}={\textbf {k }}_1+2 \times {\textbf {k }}_2+2 \times {\textbf {k }}_3+{\textbf {k }}_4 \end{aligned}$$

(53)

$$\begin{aligned}{} & {} \Delta {\textbf {F }}_{\mathrm { {\textbf {B}}}}=2 \times \text{ rand } \times \mid {\textbf {Stp }}\mid \end{aligned}$$

(54)

$$\begin{aligned} {\textbf {Stp }}= & {} {\text {rand}} \times \left( \left( {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}- \text{ rand } \times {\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}\right) +\gamma \right) \end{aligned}$$

(55)

$$\begin{aligned}{} & {} \gamma ={\text {rand}} \times \left( {\textbf {F }}_{\mathrm { {\textbf {Bn}}}}-{\text {rand}} \times (u -\textrm{l})\right) \times \exp \left( -4 \times \frac{i }{\textrm{T}}\right) \end{aligned}$$

(56)

${\textbf {F }}_{\mathrm { {\textbf {Bw}}}}$ and ${\textbf {F }}_{\mathrm { {\textbf {Bb}}}}$ are determined by the following:

$$\begin{aligned}{} & {} \text{ if } f_{o b j}\left( {\textbf {F }}_{\mathrm { {\textbf {Bn}}}}\right) <f_{\text{ obj } }\left( {\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}\right) \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}={\textbf {F }}_{\mathrm { {\textbf {Bn}}}}\nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}={\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}\nonumber \\{} & {} \text{ else } \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}={\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}\nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bw}}}}={\textbf {F }}_{\mathrm { {\textbf {Bn}}}}\nonumber \\{} & {} \text{ end } \end{aligned}$$

(57)

$$\begin{aligned}{} & {} \text{ if } \text{ rand }<0.5 \nonumber \\{} & {} \text{ if } w <\textrm{l} \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bnew2}}}}={\textbf {F }}_{\mathrm { {\textbf {Bnew1}}}}+r \cdot w . \mid \left( {\textbf {F }}_{\mathrm { {\textbf {Bnew1}}}}-{\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}\right) + \text{ randn } \mid \nonumber \\{} & {} \quad \text{ else } \nonumber \\{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bnew2}}}}=\left( {\textbf {F }}_{\mathrm { {\textbf {Bnew1}}}}-{\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}\right) +r .w \mid \left( u {\textbf {F }}_{\mathrm { {\textbf {Bnew1}}}}-{\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}\right) + \text{ randn } \mid \nonumber \\{} & {} \text {end }\nonumber \\{} & {} \text {end } \end{aligned}$$

(58)

$$\begin{aligned}{} & {} w ={\text {rand}}(0,2) \cdot \exp \left( -c \left( \frac{i }{\textrm{T}}\right) \right) \end{aligned}$$

(59)

$c$ is a random number which equals to $5\times \text {rand}$.

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}=\frac{{\textbf {F }}_{\mathrm { {\textbf {Br1}}}}+{\textbf {F }}_{\mathrm { {\textbf {Br2}}}}+{\textbf {F }}_{\mathrm { {\textbf {Br3}}}}}{3} \end{aligned}$$

(60)

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bnew1}}}}=\beta \times {\textbf {F }}_{\mathrm { {\textbf {Bavg}}}}+(1-\beta ) \times {\textbf {F }}_{\mathrm { {\textbf {Bbest}}}} \end{aligned}$$

(61)

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {Bnew3}}}}=\left( {\textbf {F }}_{\mathrm { {\textbf {Bnew2}}}}- \text{ rand } . {\textbf {F }}_{\mathrm { {\textbf {Bnew2}}}}\right) +SF .\left( \text{ rand. } {\textbf {x }}_{\textrm{RK}}\right. \nonumber \\{} & {} \left. +\left( v \cdot {\textbf {F }}_{\mathrm { {\textbf {Bb}}}}-{\textbf {F }}_{\mathrm { {\textbf {Bnew2}}}}\right) \right) \end{aligned}$$

(62)

where $v =2\times \text{ rand }$

Appendix E for AO

The spiral shape is displayed in the search using $x ,y$.

$$\begin{aligned}{} & {} x =r \cos (\theta ), y =r \sin (\theta ) \end{aligned}$$

(63)

$$\begin{aligned}{} & {} r =r _1+0.00565 \textrm{A} \end{aligned}$$

(64)

$$\begin{aligned}{} & {} \theta =-0.005 \textrm{A}+\frac{3 \pi }{2} \end{aligned}$$

(65)

For a given number of search cycles, $r _1$ accepts a value between 1 and 20. $\textrm{A}$ is an integer between 1 and $\textrm{dim}$ [25].

$$\begin{aligned}{} & {} E _1=2rand-1 \end{aligned}$$

(66)

$$\begin{aligned}{} & {} E _2=2\left( 1-\frac{t }{\textrm{T}}\right) \end{aligned}$$

(67)

$E _1$ stands for a number of AO motions that are utilized to follow the prey as it elopes. The flight slope of the AO utilized to track the prey during the escape from the first position (1) to the last position (t) is represented by $E _2$, which has decreasing values from 2 to 0 [25].

$$\begin{aligned}{} & {} {\textbf {F }}_{\mathrm { {\textbf {B1}}}}(t +1)={\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}(t )+\left( 1-\frac{t }{\textrm{T}}\right) \left( {\textbf {F }}_{\mathrm { {\textbf {Bm}}}}(t )-{\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}(t ) \times \text{ rand } \right) \end{aligned}$$

(68)

$$\begin{aligned}{} & {} {\textbf {F }}_{ { {\textbf {B2}}}}(t +1)={\textbf {F }}_{ { {\textbf {Bbest}}}}(t )\times {\text {Levy}}({\text {{dim}}})+{\textbf {F }}_{ { {\textbf {BR}}}}(t )+(y -x ) \times \text{ rand } \end{aligned}$$

(69)

At the ${i }^{t h}$ iteration, ${\textbf {F }}_{\mathrm { {\textbf {BR}}}}(t )$ is a random solution selected from the interval $[1-\textrm{N}]$.$Levy(x )$ is explained in eq.(22)

$$\begin{aligned}{} & {} \left( {\textbf {F }}_{\mathrm { {\textbf {B3}}}}(t +1)=\left( {\textbf {F }}_{\mathrm { {\textbf {Bbest}}}}(t )-{\textbf {F }}_{\mathrm { {\textbf {Bm}}}}(t )\right) \times \alpha - \text{ rand } \right. \nonumber \\{} & {} \left. +((\textrm{UB}-\textrm{LB}) \times \text{ rand } +\textrm{LB})\right) \times \delta \end{aligned}$$

(70)

The exploitation adjustment parameters $\alpha$ and $\delta$, are set to 0.1. The following problem’s $\textrm{LB}$ and $\textrm{UB}$ abbreviations refers lower and upper bounds, respectively [25].

$$\begin{aligned}{} & {} {\textbf {F }}_{ { {\textbf {B4}}}}(t +1)=QF \times {\textbf {F }}_{{ {\textbf {Bbest}}}}(t )-\left( E _1 \times {\textbf {F }}_{{ {\textbf {B}}}}(t ) \times \text{ rand } \right) \nonumber \\{} & {} -E _2 \times {\text {Levy}}({{\textrm{dim}}})+{\text {rand}} \times E _1 \end{aligned}$$

(71)

$$\begin{aligned}{} & {} QF (t )=t ^{\frac{2 \text{ rand-1 } }{(1-\textrm{T})^2}} \end{aligned}$$

(72)

$QF$ is the quality function employed to balance search tactics.