Bayesian fused lasso modeling via horseshoe prior

Abstract

Bayesian fused lasso is one of the sparse Bayesian methods, which shrinks both regression coefficients and their successive differences simultaneously. In this paper, we propose a Bayesian fused lasso modeling via horseshoe prior. By assuming a horseshoe prior on the difference of successive regression coefficients, the proposed method enables us to prevent over-shrinkage of those differences. We also propose a Bayesian nearly hexagonal operator for regression with shrinkage and equality selection with horseshoe prior, which imposes priors on all combinations of differences of regression coefficients. Simulation studies and an application to real data show that the proposed method gives better performance than existing methods.

1 Introduction

Recently, a wide variety of data have come to be used in statistical analysis. Especially, the analysis of high-dimensional data, such as image data and financial data is taking on added significance. To handle these data, it is important to perform variable selection and variable fusion, which correspond to extracting relevant variables and capturing the group structure of data, respectively. To this end, sparse regularization methods such as lasso (Tibshirani, 1996), fused lasso (Tibshirani et al., 2005), and a hexagonal operator for regression with shrinkage and equality selection (HORSES) (Jang et al., 2015) have been proposed. These methods allow us to execute variable selection and variable fusion by the estimation of regression coefficients.

Meanwhile, many Bayesian approaches to these regularization methods, in which priors on regression coefficients correspond to regularization terms, have also been proposed. For example, Park and Casella (2008) proposed Bayesian lasso, which shrinks regression coefficients by assuming that they follow a Laplace distribution. Furthermore, Park and Casella (2008) developed a Gibbs sampling using a hierarchical expression of the Laplace distribution. Castillo et al. (2015) proposed Bayesian lasso with a quantification of uncertainty. Kyung et al. (2010) expanded Bayesian lasso by assuming Laplace distributions not only on regression coefficients but also on their successive differences, which is called Bayesian fused lasso.

A Laplace prior tends to shrink its targets, such as regression coefficients and their successive differences, too much. To overcome this problem, the Student-t prior and the normal-exponential-gamma (NEG) distribution (Griffin and Brown, 2005), which have heavier tails than a Laplace prior, have also been used. Song and Cheng (2020) proposed using a Student-t prior to construct Bayesian fusion models. Shimamura et al. (2019) proposed Bayesian fused lasso based on the hierarchical expression of an NEG prior. In addition, a horseshoe prior (Carvalho et al., 2010) is also often used instead of a Laplace prior. A horseshoe prior has an infinite spike at zero and a Cauchy-like tail, which leads to simultaneous weak shrinkage on non-zero elements and strong shrinkage on exactly zero ones. Makalic and Schmidt (2015) introduced a linear regression model in which a horseshoe prior is assumed on the regression coefficients and developed a simple Gibbs sampler for it. There are also many studies for regression models with horseshoe prior (Bhattacharya et al. (2016); Johndrow et al. (2020); Lee et al. (2021)). However, the existing methods assume a horseshoe prior on only the regression coefficients.

In this paper, we propose Bayesian fused lasso modeling with horseshoe prior under the framework of linear regression models. To formulate the Bayesian model, we assume a Laplace prior on the regression coefficients and a horseshoe prior on their successive differences. We also propose Bayesian nearly HORSES (nHORSES) with horseshoe prior, where the horseshoe prior is assumed on every pair of differences of regression coefficients. We develop a Gibbs sampler for the parameters by using the hierarchical expression of the half-Cauchy prior (Wand et al., 2011) shown by Makalic and Schmidt (2015). Through the proposal, we focus on grouping variables which have the similar role in the prediction more flexibly than the existing methods.

We note that Banerjee (2022) proposed imposing a horseshoe prior on differences of coefficients. However, Banerjee (2022) used the model assumed in the one-dimensional fused lasso signal approximation in Friedman et al. (2007), which is a special case of a linear regression model. In addition, Banerjee (2022) did not perform variable selection, unlike our proposed method.

The remainder of the paper is organized as follows. Section 2 describes the Bayesian models and introduces sparse Bayesian modelings with horseshoe prior. In Sect. 3, we propose Bayesian fused lasso and Bayesian nHORSES with horseshoe prior, and then develop Gibbs samplings for them. Section 4 presents Monte Carlo simulations and an application to real data to compare our proposed method with existing methods. We conclude our paper in Sect. 5.

2 Sparse Bayesian linear regression modeling

In this section, we review Bayesian linear regression, Bayesian lasso, and Bayesian fused lasso. We also describe Bayesian linear regression via horseshoe prior.

2.1 Preliminaries

Let $\varvec{y}=(y_1,y_2,\ldots ,y_n)^{T}$ be an n-dimensional vector of the response variable and $\varvec{X}=(\varvec{x}_{1},\varvec{x}_{2},\ldots ,\varvec{x}_{n})^{T}$ be an $n\times p$ design matrix. A linear regression model is formulated as

$$\begin{aligned} \varvec{y}=\varvec{X\beta }+\varvec{\epsilon }, \end{aligned}$$

where $\varvec{\beta }=(\beta _{1},\beta _{2},\ldots ,\beta _{p})^{T}$ is a p-dimensional regression coefficient vector and $\varvec{\epsilon }=(\epsilon _{1},\epsilon _{2},\ldots ,\epsilon _{n})^{T}$ is an n-dimensional error vector that is distributed as $\textrm{N}_{n}(\varvec{0}_{n},\sigma ^{2}I_{n})$. Here $\varvec{0}_{n}$ is an n-dimensional vector of zeros, $\sigma ^{2}$ is an error variance, and $I_{n}$ is an $n\times n$ identity matrix. Without loss of generality, we suppose that the response variable is centered and the explanatory variable is standardized as follows:

$$\begin{aligned} \sum _{i=1}^{n}y_{i}=0,\quad \sum _{i=1}^{n}x_{ij}=0,\quad \sum _{i=1}^{n}x_{ij}^{2}=n, \quad (j=1,2,\ldots ,p). \end{aligned}$$

Then, the likelihood function is given by

$$\begin{aligned} f(\varvec{y}\mid \varvec{X};\varvec{\beta },\sigma ^{2})=\prod _{i=1}^{n}f(y_{i}\mid \varvec{x}_{i};\varvec{\beta },\sigma ^{2}), \end{aligned}$$

where

$$\begin{aligned} f(y_{i}\mid \varvec{x}_{i};\varvec{\beta },\sigma ^{2})=\frac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left\{ -\frac{(y_{i} -\varvec{x}_{i}^{T}\varvec{\beta })^{2}}{2\sigma ^{2}}\right\} . \end{aligned}$$

2.2 Bayesian lasso

Tibshirani (1996) proposed lasso, which performs parameter estimation and variable selection simultaneously in terms of frequentist. He also mentioned that the lasso solution is identical to a posterior mode obtained by imposing the Laplace distribution on the parameter vector $\varvec{\beta }$ as its prior.

Based on the perspective of Tibshirani (1996), Park and Casella (2008) established a Bayesian estimation for lasso. The estimation is called Bayesian lasso. Bayesian lasso considers a conditional Laplace prior in the form:

$$\begin{aligned} \begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2}){}&={(\sigma ^2)}^{-\frac{p}{2}}\prod _{j=1}^{p}\textrm{Laplace}\left( \frac{\beta _j}{\sqrt{\sigma ^2}} \;\bigg |\; 0,\lambda \right) \\&=\prod _{j=1}^{p}\frac{\lambda }{2\sqrt{\sigma ^{2}}}\exp \left( -\frac{\lambda }{\sqrt{\sigma ^{2}}}|\beta _{j}|\right) , \end{aligned} \end{aligned}$$

(1)

where $\lambda \ (>0)$ is a hyper-parameter. Conditioning $\varvec{\beta }$ on $\sigma ^2$ makes the posterior distribution unimodal (for example, see Appendix A in Park and Casella (2008)).

The prior distribution in (1) can be rewritten as

$$\begin{aligned} \frac{\lambda }{2\sqrt{\sigma ^{2}}}\exp \left( -\frac{\lambda }{\sqrt{\sigma ^{2}}}|\beta |\right) =\int _{0}^{\infty }\frac{1}{\sqrt{2\pi \sigma ^{2}\tau ^{2}}}\exp \left( -\frac{\beta ^{2}}{2\sigma ^{2}\tau ^{2}}\right) \frac{\lambda ^{2}}{2}\exp \left( -\frac{\lambda ^{2}}{2}\tau ^{2}\right) d\tau ^{2} \end{aligned}$$

by using a scale mixture of normals (Andrews and Mallows, 1974). This equation means that the Laplace distribution is represented as the convolution of the following two distributions:

$$\begin{aligned} \begin{aligned}&\pi (\varvec{\beta }\mid \sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2})=\prod _{j=1}^{p}\frac{1}{\sqrt{2\pi \sigma ^{2}\tau _{j}^{2}}}\exp \left( -\frac{\beta _{j}^{2}}{2\sigma ^{2}\tau _{j}^{2}}\right) ,\\&\pi (\tau _{1}^{2},\ldots ,\tau _{p}^{2})=\prod _{j=1}^{p}\frac{\lambda ^{2}}{2}\exp \left( -\frac{\lambda ^{2}}{2}\tau _{j}^{2}\right) . \end{aligned} \end{aligned}$$

For the parameter $\sigma ^2$, the improper prior distribution $\pi (\sigma ^2) \propto 1/\sigma ^2$ or any inverse gamma distribution for $\sigma ^2$ is assumed. Based on the likelihood and the prior distributions, a Gibbs sampling for Bayesian lasso is developed. We omit the Gibbs samplers. For details, we refer the reader to Park and Casella (2008).

2.3 Bayesian fused lasso

The fused lasso (Tibshirani et al., 2005) encourages sparsity in both the coefficients and their successive differences. Kyung et al. (2010) proposed Bayesian fused lasso as a Bayesian counterpart to fused lasso. Bayesian fused lasso assumes a prior distribution for $\varvec{\beta }$ of the following form:

$$\begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2})\propto (\sigma ^{2})^{-\frac{2p-1}{2}}\exp \left( -\frac{\lambda _{1}}{\sigma } \sum _{j=1}^{p}|\beta _{j}|-\frac{\lambda _{2}}{\sigma }\sum _{j=2}^{p}|\beta _{j}-\beta _{j-1}|\right) , \end{aligned}$$

(2)

where $\lambda _1$ and $\lambda _2$ are positive hyper-parameters. Similar to Bayesian lasso, a scale mixture of normals is applied. Then the prior distribution (2) is transformed into

$$\begin{aligned} \begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2}) \propto {}&(\sigma ^{2})^{-\frac{2p-1}{2}}\prod _{j=1}^{p}\int \frac{1}{\sqrt{2\pi \tau _{j}^{2}}} \exp \left( -\frac{\beta _{j}^{2}}{2\sigma ^{2}\tau _{j}^{2}}\right) \frac{\lambda _{1}^{2}}{2} \exp \left( -\frac{\lambda _{1}^{2}}{2}\tau _{j}^{2}\right) d\tau _{j}^{2} \\ {}&\times \prod _{j=2}^{p}\int \frac{1}{\sqrt{2\pi \tilde{\tau }_{j}^{2}}}\exp \left\{ -\frac{(\beta _{j} -\beta _{j-1})^2}{2\sigma ^{2}\tilde{\tau }_{j}^{2}}\right\} \frac{\lambda _{2}^{2}}{2}\exp \left( -\frac{\lambda _{2}^{2}}{2}\tilde{\tau }_{j}^{2}\right) d\tilde{\tau }_{j}^{2}. \end{aligned} \end{aligned}$$

Using this hierarchical relationship, Kyung et al. (2010) developed a Gibbs sampling for Bayesian fused lasso.

To perform the fully Bayesian estimation, Kyung et al. (2010) further assumed the gamma distribution for the hyper-parameters $\lambda _{1}$ and $\lambda _{2}$ as

$$\begin{aligned} \begin{aligned} {}&\lambda _{1}^2\sim \textrm{Ga}(r_{1},\delta _{1}),\\&\lambda _{2}^2\sim \textrm{Ga}(r_{2},\delta _{2}), \end{aligned} \end{aligned}$$

where $r_{1}, r_{2},\delta _{1}$, and $\delta _{2}$ are positive hyper-parameters. Here, the probability density function of the gamma distribution is given by

$$\begin{aligned} \textrm{Ga}(x\mid m,c)=\frac{c^{m}}{\mathrm {\Gamma }(m)}x^{m-1}\exp (-cx), \quad (x\ge 0), \end{aligned}$$

where m is a shape parameter, c is a rate parameter, both taking positive values, and ${\mathrm \Gamma }(\cdot )$ is the gamma function. In Kyung et al. (2010), $r_{1}=1$, $r_{2}=1, \delta _{1}=10$, and $\delta _{2}=10$ are used because the gamma distribution is relatively flat with these parameter values. We omit the full conditional posteriors and the Gibbs samplers. For details, we refer the reader to Kyung et al. (2010).

Next, we explain HORSES by Jang et al. (2015). HORSES was proposed as an extension of fused lasso; HORSES imposes an $L_1$ penalty on all combinations of differences of regression coefficients. In the Bayesian framework, this corresponds to assuming a Laplace prior of the form:

$$\begin{aligned} \begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2}) \propto {}&(\sigma ^{2})^{-\frac{p^{2}+p}{4}}\prod _{j=1}^{p}\textrm{Laplace}\left( \frac{\beta _{j}}{\sqrt{\sigma ^{2}}} \;\bigg |\; 0,\lambda _{1}\right) \\ {}&\times \prod _{j>k}^{p}\textrm{Laplace}\left( \frac{\beta _{j}-\beta _{k}}{\sqrt{\sigma ^{2}}} \;\bigg |\; 0,\lambda _{2}\right) \end{aligned} \end{aligned}$$

for regression coefficients $\varvec{\beta }$. Note that HORSES is also known as generalized fused lasso (She, 2010).

The Laplace distribution shrinks all of the regression coefficients to the same extent. Shimamura et al. (2019) proposed Bayesian fused lasso and Bayesian nHORSES with NEG prior. This method assumes a Laplace prior on the regression coefficients and an NEG prior on their differences. Because an NEG prior has two properties, a spike at zero and extreme flatness of its tail, the method with an NEG prior has the advantage that exactly identical regression coefficients tend to be estimated as identical, while different regression coefficients tend to be estimated as different.

2.4 Bayesian linear regression model with horseshoe prior

Makalic and Schmidt (2015) proposed the following Bayesian linear regression model:

$$\begin{aligned} \begin{aligned} \varvec{y}\mid \varvec{X},\varvec{\beta },\sigma ^{2}&\sim \textrm{N}_{n}(\varvec{X\beta },\sigma ^{2}\varvec{I}_{n}), \\ \beta _{j}\mid \lambda _{j}^{2},\tau ^{2},\sigma ^{2}&\sim \textrm{N}(0,\lambda _{j}^{2}\tau ^{2}\sigma ^{2}), \\ \sigma ^{2}&\sim \sigma ^{-2}d\sigma ^{2}, \\ \lambda _{j}&\sim \mathrm{C^{+}}(0,1), \\ \tau&\sim \mathrm{C^{+}}(0,1). \end{aligned} \end{aligned}$$

(3)

Here, $\mathrm{C^{+}}(0,a)\ (a>0)$ is a half-Cauchy distribution, which has the following density function:

$$\begin{aligned} p(x)=\frac{2a}{\pi \left( x^{2}+a^{2}\right) }, \quad (x > 0).\ \ \ \ \ \end{aligned}$$

The hierarchies of priors in (3) represent the horseshoe prior proposed in Carvalho et al. (2010). In the model with horseshoe prior, the half-Cauchy prior distribution is assumed on hyper-parameters $\lambda _{j}$ and $\tau$. Hyper-parameter $\lambda _{j}$ adjusts the level of local shrinkage for regression coefficient $\beta _{j}$, while hyper-parameter $\tau$ determines the degree of global shrinkage for all regression coefficients. Owing to having these two types of hyper-parameters, the horseshoe prior simultaneously enjoys a heavy tail and infinitely tall spike at zero. These properties induce exactly identical regression coefficients to tend to be estimated as identical, while different regression coefficients tend to be estimated as different.

To develop a Gibbs sampling for the parameters, Makalic and Schmidt (2015) used a hierarchical expression of the half-Cauchy distribution (Wand et al., 2011), which means that x follows $\textrm{C}^{+}(0,A)$ when $x^{2}$ and a have the following priors:

$$\begin{aligned} x^{2}\mid a\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{a}\right) ,\ \ \ a\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{A^{2}}\right) , \end{aligned}$$

(4)

where A is a positive constant. Here, $\textrm{IG}(x\mid \nu _{0},\eta _{0})$ is the inverse gamma distribution whose probability density function is given by

$$\begin{aligned} \textrm{IG}(x\mid \nu _{0},\eta _{0})=\frac{\eta _{0}^{\nu _{0}}}{\mathrm {\Gamma }(\nu _{0})}x^{-\nu _{0}-1}\exp \left( -\frac{\eta _{0}}{x}\right) ,\quad (x>0), \end{aligned}$$

where $\nu _{0}$, $\eta _{0}$ $(> 0)$ are hyper-parameters. Using (4), the priors of the model (3) can be expressed as follows:

$$\begin{aligned} \begin{aligned} \varvec{y}\mid \varvec{X},\varvec{\beta },\sigma ^{2}&\sim \textrm{N}_{n}(\varvec{X\beta },\sigma ^{2}\varvec{I}_{n}), \\\beta _{j}\mid \lambda _{j}^{2},\tau ^{2},\sigma ^{2}&\sim \textrm{N}(0,\lambda _{j}^{2}\tau ^{2}\sigma ^{2}), \\ \sigma ^{2}&\sim \sigma ^{-2}d\sigma ^{2}, \\ \lambda _{j}^{2}\mid \nu _{j}&\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{\nu _{j}}\right) , \\ \tau ^{2}\mid \xi&\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{\xi }\right) , \\ \nu _{1},\ldots ,\nu _{p},\xi&\sim \textrm{IG}\left( \frac{1}{2},1\right) . \end{aligned} \end{aligned}$$

We omit the full conditional posteriors and the Gibbs samplers. For details, we refer the reader to Makalic and Schmidt (2015) and Nalenz and Villani (2018).

3 Proposed method

In this section, we propose the Bayesian linear regression modeling, which assumes the horseshoe prior on successive differences of regression coefficients. We also extend this approach to HORSES.

3.1 Bayesian fused lasso with horseshoe prior

We propose assuming a Laplace prior on regression coefficients and a horseshoe prior on their successive differences as follows:

$$\begin{aligned}{} & {} \pi (\varvec{\beta }\mid \sigma ^{2}) \propto {}(\sigma ^{2})^{-\frac{p}{2}}\prod _{j=1}^{p}\textrm{Laplace}\left( \frac{\beta _{j}}{\sqrt{\sigma ^{2}}} \;\bigg |\; \tilde{\lambda }_{1}\right) \nonumber \\ {}{} & {} \quad \times \int \left[ \prod _{j=2}^{p} \int \frac{1}{\sqrt{2\pi \lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}}\exp \left\{ -\frac{(\beta _{j} -\beta _{j-1})^2}{2\lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}\right\} \frac{2}{\pi (1+\lambda _{j}^{2})}d\lambda _{j}^{2}\right] \frac{2}{\pi (1+\tilde{\tau }^{2})}d\tilde{\tau }^{2}. \nonumber \\ \end{aligned}$$

(5)

By assuming the prior (5), small differences between successive regression coefficients are largely shrunk, while large differences are not much shrunk. Note that we assumed not a horseshoe prior but a Laplace prior on regression coefficients. It is because the MCMC chain for a model only with horseshoe prior does not converge in almost all cases. This problem might be related to the geometric ergodicity of MCMC chain. Therefore, we adopt the combination of Laplace prior and horseshoe prior to obtain a stable estimation.

Using a scale mixture of normals (Andrews and Mallows, 1974), the prior (5) can be expressed as follows:

$$\begin{aligned}{} & {} \pi (\varvec{\beta }\mid \sigma ^{2})\propto {} \int \ldots \int (\sigma ^{2})^{-\frac{2p-1}{2}}(\tilde{\tau }^{2})^{-\frac{p-1}{2}}\pi (\tilde{\tau }^{2}\mid \xi ) \nonumber \\{} & {} \qquad \times \pi (\xi )\prod _{j=1}^{p}(\tau _{j}^{2})^{-\frac{1}{2}}\prod _{j=2}^{p}(\lambda _{j}^{2})^{-\frac{1}{2}} \exp \left( -\frac{1}{2\sigma ^{2}}\varvec{\beta }^{T}\varvec{B}^{-1}\varvec{\beta }\right) \nonumber \\{} & {} \qquad \times \prod _{j=1}^{p}\pi (\tau _{j}^{2})\prod _{j=2}^{p}\pi (\lambda _{j}^{2}\mid \nu _{j})\prod _{j=2}^{p} \pi (\nu _{j})d\tilde{\tau }^{2}d\xi \prod _{j=1}^{p}d\tau _{j}^{2}\prod _{j=2}^{p}d\lambda _{j}^{2}\prod _{j=2}^{p}d\nu _{j}. \end{aligned}$$

(6)

Here, the inverse of matrix $\varvec{B}$ is represented by

$$\begin{aligned} \varvec{B}^{-1}=\left( \begin{array}{cccccc} \frac{1}{\tau _{1}^{2}}+\frac{1}{\lambda _{2}^{2}\tilde{\tau }^{2}}&{}-\frac{1}{\lambda _{2}^{2} \tilde{\tau }^{2}}&{}0&{}\ldots &{}0&{}0\\ -\frac{1}{\lambda _{2}^{2}\tilde{\tau }^{2}}&{}\frac{1}{\tau _{2}^{2}}+\frac{1}{\lambda _{2}^{2} \tilde{\tau }^{2}}+\frac{1}{\lambda _{3}^{2}\tilde{\tau }^{2}}&{}-\frac{1}{\lambda _{3}^{2}\tilde{\tau }^{2}}&{}\ldots &{}0&{}0\\ 0&{}-\frac{1}{\lambda _{3}^{2}\tilde{\tau }^{2}}&{}\frac{1}{\tau _{3}^{2}}+\frac{1}{\lambda _{3}^{2} \tilde{\tau }^{2}}+\frac{1}{\lambda _{4}^{2}\tilde{\tau }^{2}}&{}\ldots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\ldots &{}\frac{1}{\tau _{p-1}^{2}}+\frac{1}{\lambda _{p-1}^{2}\tilde{\tau }^{2}} +\frac{1}{\lambda _{p}^{2}\tilde{\tau }^{2}}&{}-\frac{1}{\lambda _{p}^{2}\tilde{\tau }^{2}}\\ 0&{}0&{}0&{}\ldots &{}-\frac{1}{\lambda _{p}^{2}\tilde{\tau }^{2}}&{}\frac{1}{\tau _{p}^{2}} +\frac{1}{\lambda _{p}^{2}\tilde{\tau }^{2}} \end{array}\right) . \end{aligned}$$

The detailed calculation of (6) is given in Appendix A. Therefore, the priors on $\varvec{\beta },\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2},\lambda _{2}^{2},\ldots , \lambda _{p}^{2},\nu _{2},\ldots ,\nu _{p},\xi$ are given by

$$\begin{aligned} \begin{aligned} \varvec{\beta }\mid \sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2},\lambda _{2}^{2}, \ldots ,\lambda _{p}^{2}&\sim \textrm{N}_{p}({\varvec{0}}_{p},\sigma ^{2}\varvec{B}), \\ \tau _{j}^{2}&\sim \textrm{EXP}\left( \frac{\tilde{\lambda }_{1}^{2}}{2}\right) , \\ \tilde{\tau }^{2}\mid \xi&\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{\xi }\right) , \\ \lambda _{j}^{2}\mid \nu _{j}&\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{\nu _{j}}\right) ,\quad (j=2,\ldots ,p), \\ \xi ,\nu _{j}&\sim \textrm{IG}\left( \frac{1}{2},1\right) ,\quad (j=2,\ldots ,p), \end{aligned} \end{aligned}$$

where $\textrm{EXP}(x\mid d)$ is an exponential prior with density function

$$\begin{aligned} \textrm{EXP}(x\mid d)=d\exp (-dx),\quad (x\ge 0). \end{aligned}$$

Here d is positive. In addition, we assume the priors on $\sigma ^{2}$ and $\tilde{\lambda }_{1}^{2}$ as

$$\begin{aligned} \begin{aligned} \sigma ^{2}{}&\sim \textrm{IG} \left( \frac{\nu _{0}}{2},\frac{\eta _{0}}{2} \right) ,\\ \tilde{\lambda }_{1}^{2}&\sim \textrm{Ga}(r_{1},\delta _{1}). \end{aligned} \end{aligned}$$

(7)

By using the likelihood and the priors for the parameters, we can obtain the full conditional distributions as follows:

$$\begin{aligned} \varvec{\beta }\mid \varvec{y},\varvec{X},\sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2}, \lambda _{2}^{2},\ldots ,\lambda _{p}^{2}&\sim \textrm{N}_{p}(\varvec{A}^{-1}\varvec{X}^{T}\varvec{y},\sigma ^{2}\varvec{A}^{-1}), \\ \varvec{A}&=\varvec{X}^{T}\varvec{X}+\varvec{B}^{-1},&\\ \sigma ^{2}\mid \varvec{y},\varvec{X},\varvec{\beta },\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2}, \lambda _{2}^{2},\ldots ,\lambda _{p}^{2}&\sim \textrm{IG}\left( \frac{n_{1}}{2},\frac{s_{1}}{2}\right) , \\ n_{1}&=n+2p-1+\nu _{0},&\\ s_{1}&=(\varvec{y}-\varvec{X\beta })^{T}(\varvec{y}-\varvec{X\beta })+\varvec{\beta }^{T}\varvec{B}^{-1}\varvec{\beta }+\eta _{0},&\\ \frac{1}{\tau _{j}^{2}}\mid \beta _{j},\sigma ^{2},\tilde{\lambda }_{1}^{2}&\sim \textrm{IGauss} \left( \sqrt{\frac{\sigma ^{2}\tilde{\lambda }_{1}^{2}}{\beta _{j}^{2}}},\tilde{\lambda }_{1}^{2}\right) , \\ \tilde{\lambda }_{1}^{2}\mid \tau ^{2}_{1},\ldots ,\tau ^{2}_{p}&\sim \textrm{Ga}\left( p+r_{1}, \frac{1}{2}\sum _{j=1}^{p}\tau _{j}^{2}+\delta _{1}\right) , \\ \tilde{\tau }^{2}\mid \beta _{1},\ldots ,\beta _{p},\sigma ^{2},\lambda _{2}^{2},\ldots ,\lambda _{p}^{2},\xi&\sim \textrm{IG}\left( \frac{p}{2},\frac{1}{2\sigma ^{2}}\sum ^{p}_{j=2}\frac{(\beta _{j}-\beta _{j-1})^{2}}{\lambda _{j}^{2}}+\frac{1}{\xi }\right) , \\ \lambda _{j}^{2}\mid \beta _{j},\beta _{j-1},\sigma ^{2},\tilde{\tau }^{2},\nu _{j}&\sim \textrm{IG}\left( 1,\frac{(\beta _{j}-\beta _{j-1})^{2}}{2\sigma ^{2}\tilde{\tau }^{2}}+\frac{1}{\nu _{j}}\right) , \\ \nu _{j}\mid \lambda _{j}^{2}&\sim \textrm{IG}\left( 1,\frac{1}{\lambda _{j}^{2}}+1\right) , \\ \xi \mid \tilde{\tau }^{2}&\sim \textrm{IG}\left( 1,\frac{1}{\tilde{\tau }^{2}}+1\right) . \end{aligned}$$

By using the full conditional distributions, we can perform the Gibbs sampling.

3.2 Bayesian nHORSES with horseshoe prior

Next, we propose assuming a Laplace prior on the regression coefficients and a horseshoe prior on all combinations of their differences as follows:

$$\begin{aligned} \begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2},\tilde{\tau }^{2}) \propto {}&(\sigma ^{2})^{-\frac{p}{2}}\prod _{j=1}^{p}\textrm{Laplace}\left( \frac{\beta _{j}}{\sqrt{\sigma ^{2}}} \;\bigg |\; \tilde{\lambda }_{1}\right) \\ {}&\times \prod _{j>k} \int \frac{1}{\sqrt{2\pi \lambda _{j,k}^{2}\tilde{\tau }^{2}\sigma ^{2}}}\exp \left\{ -\frac{(\beta _{j} -\beta _{k})^2}{2\lambda _{j,k}^{2}\tilde{\tau }^{2}\sigma ^{2}}\right\} \frac{2}{\pi (1+\lambda _{j,k}^{2})}\frac{2}{\pi (1+\tilde{\tau }^{2})}d\lambda _{j,k}^{2}. \end{aligned} \end{aligned}$$

(8)

Therefore, the priors on $\varvec{\beta },\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2},\lambda _{1,2}^{2},\ldots , \lambda _{p-1,p}^{2},\nu _{1,2},\ldots ,\nu _{p-1,p}$, and $\xi$ are given by

$$\begin{aligned} \begin{aligned} \varvec{\beta }\mid \sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2},\lambda _{1,2}^{2}, \ldots ,\lambda _{p-1,p}^{2}&\sim \textrm{N}_{p}({\varvec{0}}_{p},\sigma ^{2}\varvec{B}), \\ \tau _{j}^{2}&\sim \textrm{EXP}\left( \frac{\tilde{\lambda }_{1}^{2}}{2}\right) , \\ \lambda _{j,k}^{2}\mid \nu _{j,k}&\sim \textrm{IG}\left( \frac{1}{2},\frac{1}{\nu _{j,k}}\right) , \\ \nu _{j,k}&\sim \textrm{IG}\left( \frac{1}{2},1\right) , \end{aligned} \end{aligned}$$

where $\lambda _{j,k}^{2}=\lambda _{k,j}^{2}$, $\nu _{j,k}^{2}=\nu _{k,j}^{2}$ and the (i, j)-element of $\varvec{B}^{-1}$ is represented as

$$\begin{aligned} {\varvec{B}^{-1}}_{(i,j)}=\left\{ \begin{aligned} {}&\frac{1}{\tau _{j}^{2}}+\frac{1}{\tilde{\tau }^{2}}\sum _{l\ne i}\frac{1}{\lambda _{i,l}^{2}},\quad (i=j),\\&-\frac{1}{\lambda _{i,j}^{2}},\quad (i\ne j). \end{aligned} \right. \end{aligned}$$

By assuming an inverse gamma prior on $\sigma ^2$ and a gamma prior on $\tilde{\lambda }_{1}^{2}$ in (7), the full conditional distributions are represented as

$$\begin{aligned} \varvec{\beta }\mid \varvec{y},\varvec{X},\sigma ^{2},\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2}, \lambda _{1,2}^{2},\ldots ,\lambda _{p-1,p}^{2}&\sim \textrm{N}_{p}(\varvec{A}^{-1}\varvec{X}^{T}\varvec{y},\sigma ^{2}\varvec{A}^{-1}), \\ \varvec{A}=&\varvec{X}^{T}\varvec{X}+\varvec{B}^{-1}, \\ \sigma ^{2}\mid \varvec{y},\varvec{X},\varvec{\beta },\tau _{1}^{2},\ldots ,\tau _{p}^{2},\tilde{\tau }^{2}, \lambda _{1,2}^{2},\ldots ,\lambda _{p-1,p}^{2}&\sim \textrm{IG}\left( \frac{n_{1}}{2},\frac{s_{1}}{2}\right) , \\ n_{1}&=n+p(p+1)/2+\nu _{0}, \\ s_{1}&=(\varvec{y}-\varvec{X\beta })^{T}(\varvec{y}-\varvec{X\beta })+\varvec{\beta }^{T}\varvec{B}^{-1}\varvec{\beta }+\eta _{0}, \\ \frac{1}{\tau _{j}^{2}}\mid \beta _{j},\sigma ^{2},\tilde{\lambda }_{1}^{2}&\sim \textrm{IGauss} \left( \sqrt{\frac{\sigma ^{2}\tilde{\lambda }_{1}^{2}}{\beta _{j}^{2}}},\tilde{\lambda }_{1}^{2}\right) , \\ \tilde{\lambda }_{1}^{2}\mid \tau ^{2}_{1},\ldots ,\tau ^{2}_{p}&\sim \textrm{Ga}\left( p+r_{1}, \frac{1}{2}\sum _{j=1}^{p}\tau _{j}^{2}+\delta _{1}\right) , \\ \lambda _{j,k}^{2}\mid \beta _{j},\beta _{k},\sigma ^{2},\tilde{\tau }^{2},\nu _{j,k}&\sim \textrm{IG} \left( 1,\frac{(\beta _{j}-\beta _{k})^{2}}{2\sigma ^{2}\tilde{\tau }^{2}}+\frac{1}{\nu _{j,k}}\right) , \\ \nu _{j,k}\mid \lambda _{j,k}^{2}&\sim \textrm{IG}\left( 1,\frac{1}{\lambda _{j,k}^{2}}+1\right) . \end{aligned}$$

By using the full conditional distributions, we can perform the Gibbs sampling for Bayesian nHORSES.

Note that the hyper-parameter $\tilde{\tau }^2$ in the prior (8) is treated as a tuning parameter. The value of the tuning parameter is selected by any model selection criterion such as the widely applicable information criterion (WAIC) (Watanabe, 2010).

4 Numerical studies

In this section, we compare the proposed method with existing methods through Monte Carlo simulations and show its effectiveness. In addition, we apply the proposed method to the Appalachian Mountains Soil Data (Bondell and Reich (2008); Jang et al. (2015)).

4.1 Monte carlo simulation

We conducted Monte Carlo simulations with artificial data generated from the true model:

$$\begin{aligned} \varvec{y}=\varvec{X\beta ^{*}}+\varvec{\epsilon }, \end{aligned}$$

where $\varvec{\beta }^{*}$ is the p-dimensional true coefficient vector and the error vector $\varvec{\epsilon }$ is distributed normally as $\textrm{N}_{n}(\varvec{0}_{n},\sigma ^2\varvec{I}_n)$. In addition, $\varvec{x}_{i}$ $(i=1,2,\ldots ,n)$ is distributed according to the multivariate normal distribution $\textrm{N}_{p}(\varvec{0}_p, \varSigma )$.

We considered the following settings:

Case 1: $\varvec{\beta }^{*}=\varvec{\beta }_{1}^{*}$ or $\varvec{\beta }_{2}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=\rho$,   $(i\ne j)$,

Case 2: $\varvec{\beta }^{*}=\varvec{\beta }_{1}^{*}$ or $\varvec{\beta }_{2}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=0.5^{|i-j|},\quad (i\ne j)$,

Case 3: $\varvec{\beta }^{*}=\varvec{\beta }_{3}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=0.5,\ \quad (i\ne j)$,

Case 4: $\varvec{\beta }^{*}=\varvec{\beta }_{3}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=0.5^{|i-j|},\quad (i\ne j)$,

Case 5: $\varvec{\beta }^{*}=\varvec{\beta }_{4}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=\rho$,   $(i\ne j)$,

Case 6: $\varvec{\beta }^{*}=\varvec{\beta }_{5}^{*}$, $\varSigma _{ii}=1$, $\varSigma _{ij}=\rho$,   $(i\ne j)$,

where $\varSigma _{ij}$ is the (i, j)-th element of $\varSigma$. For each case, we considered $\sigma =0.5,1.5$. We simulated data with $\varvec{\beta }_{1}^{*}=(\varvec{0.0}_{5}^{T}, \varvec{1.0}_{5}^{T}, \varvec{0.0}_{5}^{T}, \varvec{1.0}_{5}^{T})^{T}$ and $\varvec{\beta }_{2}^{*}=(\varvec{0.0}_{5}^{T}, \varvec{2.0}_{5}^{T}, \varvec{0.0}_{5}^{T}, \varvec{2.0}_{5}^{T})^{T}$ for Cases 1 and 2. In addition, we considered $\varvec{\beta }_{3}^{*}=(\varvec{3.0}_{5}^{T}, \varvec{-1.5}_{5}^{T}, \varvec{1.0}_{5}^{T}, \varvec{2.0}_{5}^{T},\varvec{0.0}_{30}^{T})^{T}$, $\varvec{\beta }_{4}^{*}=(\varvec{3.0}_{5}^{T}, \varvec{-1.5}_{5}^{T}, \varvec{1.0}_{5}^{T}, \varvec{2.0}_{5}^{T},\varvec{0.0}_{130}^{T})^{T}$ and $\varvec{\beta }_{5}^{*}=(\varvec{3.0}_{5}^{T}, \varvec{-1.5}_{5}^{T}, \varvec{1.0}_{5}^{T}, \varvec{2.0}_{5}^{T},\varvec{0.0}_{980}^{T})^{T}$ for Cases 3, 4, 5, and 6. In Case 1, we considered $\rho =0.5,0.9$. In Cases 5 and 6, we considered $\rho =0.5,0.5^{|i-j|}$. We considered $n=50$, $p=20$ for Cases 1 and 2, $n=30, 50$, $p=50$ for Cases 3 and 4, $n=50$, $p=150$ for Case 5, and $n=200$, $p=1000$ for Case 6. Therefore, Cases 1 and 2 correspond to $n>p$ cases, whereas Cases 3, 4, 5, and 6 correspond to $n \le p$ cases. For Cases 5 and 6, we used the fast sampling method from multivariate normal distribution based on Woodbury matrix identity (Hager (1989); Bhattacharya et al. (2016)). We simulated 100 datasets for each case. Cases 1 and 2 are according to example 1 in Shen and Huang (2010), whereas Cases 3, 4, 5, and 6 are, respectively, according to examples 2 and 3 in the same reference. For each Case 1 to Case 4, the Gibbs sampling was run with 5000 iterations, where we discarded the first 2000 iterations as burn-in. For Cases 5 and 6, the Gibbs sampling was run with 10,000 iterations with the first 7000 samples discarded as burn-in for BFL and BFNEG. For BFH, the Gibbs sampler was run in the same way except for the situation with $\rho =0.5^{|i-j|}$ and $\sigma =0.5$. In this situation, the Gibbs sampling was run with 13,000 iterations with the first 10,000 as burn-in.

We checked the convergence of MCMC chains by using Gelman–Rubin diagnostic. When the MCMC chain converges, the potential scale reduction factor $\hat{R}$ (Gelman and Rubin (1992); Brooks and Gelman (1998)) becomes close to 1.0. The factor $\hat{R}$ was computed by using its relationship with the effective sample size (Vats and Knudson, 2021). We used the package stableGR of the software R to compute $\hat{R}$. The package can be obtained from https://cran.r-project.org/web/packages/stableGR/index.html. As Vehtari et al. (2021) recommended, we checked whether $\hat{R}$ is below 1.01 or not. The maximum values of $\hat{R}$ in MCMC samples for 100 datasets for each regression coefficients were lower than 1.01 (see Table S.1 in the supplementary material, for example.). Thus, we considered the MCMC chains are converged.

We compared Bayesian fused lasso with horseshoe prior (BFH) to Bayesian fused lasso (BFL) and Bayesian fused lasso with NEG prior (BFNEG). For BFNEG, the shape parameter in the gamma distribution in the NEG prior was set to 0.5 according to the simulation study in Griffin and Brown (2011), while the rate parameter was selected by WAIC in Cases 1 to 5. For Case 6, the rate parameter was set to 1.0, because it was too time-consuming to finish. The values of WAIC for the selected model are summarized in Table S.3 in the supplementary material.

To evaluate the accuracy of the estimation of regression coefficients, we used mean squared error (MSE):

$$\begin{aligned} \textrm{MSE}=\frac{1}{100}\sum _{k=1}^{100}(\hat{\varvec{\beta }}^{(k)}-\varvec{\beta }^{*})^{T}(\hat{\varvec{\beta }}^{(k)} -\varvec{\beta }^{*}), \end{aligned}$$

where $\hat{\varvec{\beta }}^{(k)}=(\hat{\beta }_{1}^{(k)},\ldots ,\hat{\beta }_{p}^{(k)})^{T}$ is the regression coefficient vector estimated from the k-th dataset. We also computed $\mathrm{MSE_{diff}}$, expressed as

$$\begin{aligned} \mathrm{MSE_{diff}}=\frac{1}{100}\sum _{k=1}^{100}(\hat{\varvec{\beta }}_\textrm{diff}^{(k)}-\varvec{\beta }_\textrm{diff}^{*})^{T}(\hat{\varvec{\beta }}_\textrm{diff}^{(k)}-\varvec{\beta }_\textrm{diff}^{*}), \end{aligned}$$

where $\varvec{\beta }_\textrm{diff}^{*}$ is a vector of the non-zero differences of the true regression coefficients and $\hat{\varvec{\beta }}_\textrm{diff}^{(k)}$ is the estimated value of $\varvec{\beta }_\textrm{diff}^{*}$ from the k-th dataset. $\mathrm{MSE_{diff}}$ is an index to assess how close the differences of estimated regression coefficients which are not zero are to the true differences. For example, regression coefficients for Case 1 are given by $\varvec{\beta }^{*}=(\varvec{0.0}_{5}^{T},\varvec{2.0}_{5}^{T},\varvec{0.0}_{5}^{T},\varvec{2.0}_{5}^{T})^{T}$ and the non-zero successive differences are between the 5th and 6th, 10th and 11th, and 15th and 16th elements of $\varvec{\beta }^{*}$. Then, $\mathrm{MSE_{diff}}$ is calculated as follows:

$$\begin{aligned} \begin{aligned} \mathrm{MSE_{diff}}=&\frac{1}{100}\sum _{k=1}^{100}\left[ \left\{ (\hat{\beta }_{6}^{(k)}-\hat{\beta }_{5}^{(k)}) -(\beta _{6}^{*}-\beta _{5}^{*})\right\} ^{2}\right. \\&\left. +\left\{ (\hat{\beta }_{11}^{(k)}-\hat{\beta }_{10}^{(k)})-(\beta _{11}^{*}-\beta _{10}^{*})\right\} ^{2}+\left\{ (\hat{\beta }_{16}^{(k)}-\hat{\beta }_{15}^{(k)})-(\beta _{16}^{*} -\beta _{15}^{*})\right\} ^{2}\right] . \end{aligned} \end{aligned}$$

In addition, we computed prediction squared error

$$\begin{aligned} \textrm{PSE}=\frac{1}{100}\sum _{k=1}^{100}(\hat{\varvec{\beta }}^{(k)}-\varvec{\beta }^{*})^{T} \varSigma (\hat{\varvec{\beta }}^{(k)}-\varvec{\beta }^{*}) \end{aligned}$$

to evaluate the accuracy of prediction.

Table 1 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 1 and $\rho =0.5$

Table 2 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 1 and $\rho =0.9$

Table 3 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 2

Table 4 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 3

Table 5 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 4

Table 6 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 5

Table 7 MSE, $\mathrm{MSE_{diff}}$, and PSE for Case 6

The results are summarized in Tables 1, 2, 3, 4, 5,  6, and 7. For Cases 1 to 5, the proposed method BFH shows the smallest MSEs and PSEs in all situations. This indicates that BFH outperformed other methods when $n>p$ and but also when $n \le p$. In addition, BFH gives smaller $\mathrm{MSE_{diff}}$s than BFL in almost all situations. The reason is why BFH does not shrink non-zero differences of regression coefficients too much compared to BFL. Furthermore, BFH gives smaller values of $\mathrm{MSE_{diff}}$ in 21 situations, out of the 24 situations, in comparison to BFNEG. These results show that BFH gives a closer estimation to the true regression coefficients. For Case 6, BFNEG provides smaller MSEs and PSEs than BFH and is competitive with BFH in terms of $\mathrm {MSE_{diff}}$s. Similar to BFNEG, BFL gives smaller MSEs and PSEs than BFH. However, BFH outperforms BFL in terms of $\mathrm {MSE_{diff}}$s in all situations.

We next conducted simulations for Bayesian HORSES methods. The following settings were considered:

Case 7: $\varvec{\beta }^{*}=(3.0, -1.5, 1.0, 2.0, \varvec{0.0}_{4}^{T}, 3.0, -1.5, 1.0, 2.0, \varvec{0.0}_{4}^{T})^{T}$,

$\varSigma _{ii}=1$, $\varSigma _{ij}= {\left\{ \begin{array}{ll} 0.7&{}(\beta _i\ne 0 \text{ and } \beta _j\ne 0, \beta _i=0 \text{ and } \beta _j=0)\\ 0.2 &{}\text{ otherwise } \end{array}\right. }$ $\quad (i\ne j)$,

Case 8: $\varvec{\beta }^{*}=(3.0, \varvec{0.0}_{2}^{T}, -1.5, \varvec{0.0}_{2}^{T}, 3.0, \varvec{0.0}_{2}^{T}, -1.5)^{T}$,

$\varSigma _{ii}=1$, $\varSigma _{ij}= {\left\{ \begin{array}{ll} 0.7&{}(\beta _i\ne 0 \text{ and } \beta _j\ne 0)\\ 0&{}\text{ otherwise } \end{array}\right. }$ $\quad (i\ne j)$,

Case 7 means that variables with non-zero coefficients are highly correlated; this is true of those with zero coefficients, while Case 8 does that variables with non-zero coefficients are highly correlated. For each case, we considered $\sigma$ = 0.5, 1.5. The sample size and the number of parameters were, respectively, set by $n=40$, 80, $p=16$ for Case 7 and $n=30$, 50, $p=10$ for Case 8. We compared Bayesian nHORSES with horseshoe prior (BHH) to Bayesian HORSES (BH) and Bayesian nHORSES with NEG prior (BHNEG). We chose the hyper-parameters $\lambda _{2}^{2}$ for BH, $\tilde{\tau }^{2}$ for BHH and the rate parameter in the gamma distribution in the NEG prior for BHNEG by WAIC. The values of WAIC for the selected model are summarized in Table S.4 in the supplementary material. We set the shape parameter in the gamma distribution in the NEG prior for BHNEG as 0.5.

We measured the accuracy of the estimation of regression coefficients by MSE and performance for prediction by PSE. We only considered MSE and PSE for the Bayesian HORSES methods, because the structure of the coefficient vector $\varvec{\beta }^*$ is too complicated to assess the performance of capturing groups of variables by an index such as $\mathrm{MSE_{diff}}$.

The results in Cases 7 and 8 are summarized in Tables  8 and 9, respectively. Table  8 shows that BHH gives smaller MSEs and PSEs in many situations. BH achieves the smallest MSE and PSE in $n=40$ and $\sigma =1.5$ and PSE in $n=80$ and $\sigma =0.5$. Table  9 shows that BHH outperforms BH and BHNEG in all situations in terms of MSEs and PSEs. From these results, we believe that BHH might be a useful method for analyzing the complex structure treated by HORSES.

Table 8 MSE and PSE for Case 7

Table 9 MSE and PSE for Case 8

4.2 Application

We applied Bayesian nHORSES with horseshoe prior in Section 3.2 to the Appalachian Mountains Soil Data, which was analyzed in Bondell and Reich (2008) and Jang et al. (2015). This dataset is available from https://blogs.unimelb.edu.au/howard-bondell/#tab25 and was used for showing the relationship between soil characteristics and rich cove forest diversity. The dataset was collected at twenty 500 $\mathrm {m^{2}}$ plots in the Appalachian Mountains. Forest diversity, which is represented as the number of different plant species, is used for a response variable and 15 soil characteristics in 20 plots are used as explanatory variables. The data are the average of five equally spaced measurements in each plot. We standardized the dataset before the analysis.

We compared BHH to BH and BHNEG. For this application, we chose the hyper-parameters $\lambda _{2}^{2}$ for BH from five candidates between $10^{-4}$ and $10^{-2}$, $\tilde{\tau }^{2}$ for BHH from five candidates between $10^{4}$ and $10^{6}$, and the rate parameter in the gamma distribution in the NEG prior for BHNEG from five candidates between 0.1 and 1. The values of the hyper-parameters were selected by WAIC. The values of WAIC for the selected model are summarized in Table S.5 in the supplementary material. We set the shape parameter in the gamma distribution in the NEG prior for BHNEG as 0.5.

We executed a leave-one-out cross-validation to assess the performance of the models. In each estimation, the Gibbs sampling was run with 10,000 iterations and 5000 iterations were discarded as burn-in. We also computed the maximum $\hat{R}$ from MCMC samples for 20 datasets in the leave-one-out cross-validation. The maximum values of 20 $\hat{R}$s for each regression coefficients were lower than 1.01 (see Table S.2 in the supplementary material.). Thus, we considered the MCMC chains are converged.

The mean values of cross-validation, CV, are summarized in Table  10. From Table 10, the value of CV for BHH is smaller than that for BH. BHNEG gives the smallest value of CV, but gives the largest value of standard deviation. On the other hand, BHH gives the smallest value of standard deviation and the second largest value of CV.

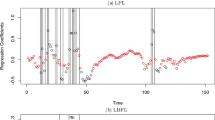
Table 11 shows the regression coefficients and its 95% credible intervals estimated by all 20 samples. The mean of estimated regression coefficients and 95% credible intervals are also described in Fig. 1. From Fig. 1, we observe that the range of the credible intervals of BH tends to be larger than ones of BHH and BHNEG. From Table 11 and Fig. 1, the regression coefficients of BHH and BHNEG for “base saturation”, “sum cations”, “CEC buffer”, “calcium”, and “potassium” are negative. Therefore, those regression coefficients seem to form a same group, which is supported by the results in Jang et al. (2015). BHH provides positive coefficients for “phosphorus”, “copper”, and “exchangeableacidity” and negative for “zinc”, while BHNEG negative for “exchangeableacidity” and positive for “zinc”. The results by BHH are same as Jang et al. (2015). From the viewpoint of the range of credible intervals, we observe that BHNEG is the most stable in three and BHH captures the difference between variables.

Table 10 Results for the Appalachian Mountains Soil Data

Table 11 Estimated regression coefficients for Appalachian Mountains Soil Data

Fig. 1

95% credible intervals of estimated regression coefficients

5 Conclusion and discussion

We proposed Bayesian fused lasso modeling with horseshoe prior, and then developed the Gibbs sampler for the parameters by using a scale mixture of normals and a hierarchical expression of a half-Cauchy prior. In addition, we extended the method to the Bayesian nHORSES. Through numerical studies, we showed our proposed method is better than the existing methods in terms of prediction and estimation accuracy.

There are several studies about fused lasso modeling with regression coefficients on a general graph, which includes the fusion of all possible pairs of coefficients (Wang et al. (2016); Lee et al. (2021); Banerjee (2022)). Our proposed method can be also expanded as the model whose parameters exist on a general graph. Let $G=(V,E)$ be an arbitrary undirected graph, where V is the node set whose elements consists of indexes of explanatory variables in the design matrix $\varvec{X}$ and E is the edge set that represents a relationship among the explanatory variables. Based on the graph, we consider the following prior on regression coefficients:

$$\begin{aligned} \begin{aligned} \pi (\varvec{\beta }\mid \sigma ^{2},\tilde{\tau }^{2}) \propto {}&(\sigma ^{2})^{-\frac{p}{2}}\prod _{j=1}^{p}\textrm{Laplace}\left( \frac{\beta _{j}}{\sqrt{\sigma ^{2}}} \;\bigg |\; \tilde{\lambda }_{1}\right) \\&\hspace{-15mm} \times \prod _{(j,k)\in E} \int \frac{1}{\sqrt{2\pi \lambda _{j,k}^{2}\tilde{\tau }^{2}\sigma ^{2}}}\exp \left\{ -\frac{(\beta _{j} -\beta _{k})^2}{2\lambda _{j,k}^{2}\tilde{\tau }^{2}\sigma ^{2}}\right\} \frac{2}{\pi (1+\lambda _{j,k}^{2})}\frac{2}{\pi (1+\tilde{\tau }^{2})}d\lambda _{j,k}^{2}. \end{aligned} \end{aligned}$$

By using this prior, we can construct a Bayesian nHORSES with horseshoe prior on a general graph. The sampling algorithm by MCMC may be built in a similar manner of the algorithm of Bayesian nHORSES with horseshoe prior.

In Bayesian nHORSES with horseshoe prior, we select the value of global shrinkage parameter $\tilde{\tau }^2$ by WAIC. It would be interesting to assume any proper prior on $\tilde{\tau }^2$. For high-dimensional data, our proposed method requires much computational burden. The reduction of computational time is thus necessary. For example, we might be able to make the sampling algorithm faster by using the approximation method of the horseshoe posterior (Johndrow et al., 2020). We leave these topics as future work.

A Detailed calculation of the formula (6)

The detailed calculation of rewriting (5) as (6) is as follows:

$$\begin{aligned}{} & {} \pi (\varvec{\beta }\mid \sigma ^{2}) \propto {}(\sigma ^{2})^{-\frac{p}{2}}\prod _{j=1}^{p}\int \frac{1}{\sqrt{2\pi \tau _{j}^{2}}}\exp \left( -\frac{\beta _{j}^{2}}{2\sigma ^{2}\tau _{j}^{2}}\right) \frac{\tilde{\lambda }_{1}^{2}}{2}\exp \left( -\frac{\tilde{\lambda }_{1}^{2}}{2}\tau _{j}^{2}\right) d\tau _{j}^{2} \\ {}{} & {} \quad \times \int \left[ \prod _{j=2}^{p} \int \frac{1}{\sqrt{2\pi \lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}} \exp \left\{ -\frac{(\beta _{j}-\beta _{j-1})^2}{2\lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}\right\} \right. \\ {}{} & {} \quad \times \int \left. \frac{\left( \frac{1}{\nu _{j}}\right) ^{\frac{1}{2}}}{\mathrm {\Gamma }\left( \frac{1}{2}\right) }(\lambda _{j}^{2}) ^{-\frac{3}{2}}\exp \left( -\frac{1}{\nu _{j}\lambda _{j}^{2}}\right) \frac{1}{\mathrm {\Gamma }\left( \frac{1}{2}\right) } (\nu _{j})^{-\frac{3}{2}}\exp \left( -\frac{1}{\nu _{j}}\right) d\nu _j d\lambda _j^{2}\right] \\ {}{} & {} \quad \times \int \frac{(\frac{1}{\xi })^{\frac{1}{2}}}{\mathrm {\Gamma }\left( \frac{1}{2}\right) }(\tilde{\tau }^{2})^ {-\frac{3}{2}}\exp \left( -\frac{1}{\xi \tilde{\tau }^{2}}\right) \frac{1}{\mathrm {\Gamma }(\frac{1}{2})}(\xi ) ^{-\frac{3}{2}}\exp \left( -\frac{1}{\xi }\right) d\xi d\tilde{\tau }^{2} \\ {}{} & {} \quad \propto {} \int \ldots \int \prod _{j=1}^{p}\frac{1}{\sqrt{2\pi \sigma ^{2}\tau _{j}^{2}}}\exp \left( -\frac{\beta _{j} ^{2}}{2\sigma ^{2}\tau _{j}^{2}}\right) \prod _{j=1}^{p}\frac{\tilde{\lambda }_{1}^{2}}{2}\exp \left( -\frac{\tilde{\lambda }_{1}^{2}}{2}\tau _{j}^{2}\right) \\ {}{} & {} \quad \times \prod _{j=2}^{p}\frac{1}{\sqrt{2\pi \lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}}\exp \left\{ -\frac{(\beta _{j}-\beta _{j-1})^2}{2\lambda _{j}^{2}\tilde{\tau }^{2}\sigma ^{2}}\right\} \prod _{j=2}^{p}\frac{(\frac{1}{\nu _{j}})^{\frac{1}{2}}}{\mathrm {\Gamma }(\frac{1}{2})}(\lambda _{j} ^{2})^{-\frac{3}{2}}\exp \left( -\frac{1}{\nu _{j}\lambda _{j}^{2}}\right) \\ {}{} & {} \quad \times \frac{(\frac{1}{\xi })^{\frac{1}{2}}}{\mathrm {\Gamma }(\frac{1}{2})}(\tilde{\tau }^{2}) ^{-\frac{3}{2}}\exp (-\frac{1}{\xi \tilde{\tau }^{2}})\frac{1}{\mathrm {\Gamma }(\frac{1}{2})}(\xi )^ {-\frac{3}{2}}\exp \left( -\frac{1}{\xi }\right) \prod _{j=2}^{p}\frac{1}{\mathrm {\Gamma }(\frac{1}{2})} (\nu _{j})^{-\frac{3}{2}}\exp \left( -\frac{1}{\nu _{j}}\right) \\ {}{} & {} \quad \times d\tilde{\tau }^{2}d\xi \prod _{j=1}^{p}d\tau _{j}^{2}\prod _{j=2}^{p}d\lambda _{j}^{2}\prod _ {j=2}^{p}d\nu _{j}\\{} & {} \quad \propto {} \int \ldots \int (\sigma ^{2})^{-\frac{2p-1}{2}}(\tilde{\tau }^{2})^{-\frac{p-1}{2}} \pi (\tilde{\tau }^{2}\mid \xi )\pi (\xi )\prod _{j=1}^{p}(\tau _{j}^{2})^{-\frac{1}{2}}\prod _{j=2}^{p} (\lambda _{j}^{2})^{-\frac{1}{2}}\exp \left( -\frac{1}{2\sigma ^{2}}\varvec{\beta }^{T}\varvec{B}^{-1}\varvec{\beta }\right) \\ {}{} & {} \quad \times \prod _{j=1}^{p}\pi (\tau _{j}^{2})\prod _{j=2}^{p}\pi (\lambda _{j}^{2}\mid \nu _{j}) \prod _{j=2}^{p}\pi (\nu _{j})d\tilde{\tau }^{2}d\xi \prod _{j=1}^{p}d\tau _{j}^{2}\prod _{j=2} ^{p}d\lambda _{j}^{2}\prod _{j=2}^{p}d\nu _{j}. \end{aligned}$$