Further Results on the [k]-Roman Domination in Graphs

Abstract

In 2016, Beeler et al. defined the double Roman domination as a variation of Roman domination. Sometime later, in 2021, Ahangar et al. introduced the concept of [k]-Roman domination in graphs and settled some results on the triple Roman domination case. In 2022, Amjadi et al. studied the quadruple version of this Roman-domination-type problem. Given any labeling of the vertices of a graph, AN(v) stands for the set of neighbors of a vertex v having a positive label. In this paper we continue the study of the [k]-Roman domination functions ([k]-RDF) in graphs which coincides with the previous versions when $2\le k \le 4$. Namely, f is a [k]-RDF if $f(N[v])\ge k+|AN(v)|$ for all v. We prove that the associate decision problem is NP-complete even when restricted to star convex and comb convex bipartite graphs and we also give sharp bounds and exact values for several classes of graphs.

1 Introduction

In this paper we deal with a variant of the well-known concept of Roman domination in graphs. Roman domination in graphs was initially introduced by Cockayne et al. [9] related to a historic defensive strategy to defend the Roman Empire decreed by the Emperor Constantine I The Great (see [17]). Namely, under a sudden attack, each undefended place in the Empire must have a strong neighbor in which 2 legions are deployed, in such a way that the stronger city could send a legion to defend the attacked one, without leaving undefended its own place.

Formally, a Roman dominating function (RDF) in a finite graph $G=(V,E)$ is a labelling f of the vertices of the graph with labels $\{0,1,2\}$ in such a way that every single vertex labelled with 0 must have an adjacent vertex labelled with 2. The Roman domination number of the graph, $\gamma _R(G)$, is the minimum weight (the sum of all vertex labels) of an RDF. An RDF f having minimum weight, $w(f)=\sum f(v)$, is called a $\gamma _R(G)$-function. More than two hundred papers have followed the original work by Cockayne et al. developing a wide study of Roman domination and several of its variations. Any labelling f of the vertices of a graph may be expressed as an ordered vertex partition $f=(V_0,V_1,\ldots ,V_p)$ where $V_j=\{v\in V:f(v)=j\}.$

Many of these variations consist of either increasing the effectivity of the defensive strategy under single attacks or simultaneous attacks [1, 7] or defending both edges and vertices [2] and so on.

The open neighborhood (resp. closed neigborhood) of a vertex u in a graph, N(u) (resp. N[u]), is the set of adjacent vertices to u (resp. the set of adjacent vertices to u,  including the vertex itself). That is to say, $N[u]=N(u)\cup \{u\}$. Given a labelling f of the vertices of a graph G,  we call the active neighborhood of u, and it is denoted by AN(u),  the set $\{ w\in N(u): f(w)>0 \}$. Similarly, $AN[u]=AN(u)\cup \{u\}.$

In 2016, Beeler et al. [7] introduced the double Roman domination that improves the defensive strategy by labelling the vertices with labels $\{0,1,2,3\}$ such that the weight of the closed neighborhood of any vertex u is at least $2+|AN(u)|$. This condition is equivalent to requiring that each city could be defended by at least two legions located in it, or in its neighboring cities so that the latter are not left unprotected.

In 2021, Ouldrabah and Volkmann [14] studied upper bounds of the double Roman domination number and approach the relation of this parameter with the matching number of a graph. Gao et al. [10] investigate the double Roman domination number of generalized Petersen graphs, given an answer to a question posed by Beeler in its germinal paper.

Besides, a wide range of variations of this problem have attracted a lot of attention of the researchers. In 2019, A. Ahangar et al. [3] published a paper regarding to the total version of Roman $\{2\}$-domination in trees. Later, in 2022, A. Ahangar et al. [5] studied further results on the $\{2\}$-Roman domination in graphs and the relation with other domination-type parameters like domination or total domination.

Since the work by Beeler, two more variations have been developed. The triple Roman domination, by Ahangar et al. [4] and the quadruple Roman domination in graphs, by Amjadi et al. [6, 13].

We started this work with the aim of proving a set of results for the general case in order to avoid an unfruitful spread of works dealing with a number of similar constructions. During the time that this paper was under revision, we became aware of the publication of a paper by N. Khalili et al. [12] in which, independently, they established a similar study for the [k]-Roman domination problem. We also thank the anonymous referee that pointed out this fact. Hence, to avoid any confusion, we will refer to that paper by Khalili et al. for the case of overlapping contents.

Broadly speaking, the [k]-Roman domination is a way of modeling a defensive system similar to that formalized by Roman domination, with a greater degree of robustness but whose cost does not increase as much in proportion to the protection it provides. That is why it is interesting to study the general case that allows choosing in each situation, according to need, the value of k that provides the best balance between reliability, robustness and network protection at the lowest possible cost.

So, in this paper we continue with the natural generalization of these variations of Roman domination. A function $f:V\rightarrow \{0,1,\ldots ,k+1\}$ such that $f(N[u])\ge k+|AN(u)|$ for all vertex u with $f(u)<k$ is called a [k]-Roman dominating function and it is denoted by [k]-RDF. We say that a vertex u is [k]-Roman dominated if $f(N[u])\ge k+|AN(u)|$ holds. The minimum weight of a [k]-RDF in the graph G is the [k]-Roman domination number ([k]-RDN) of G, denoted by $\gamma _{[kR]}(G)$. A [k]-RDF having minimum possible weight is called a $\gamma _{[kR]}(G)$-Roman dominating function, for short a $\gamma _{[kR]}(G)$-RDF.

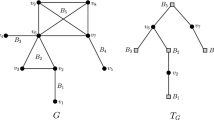
From now on, we only consider simple, undirected and finite graphs $G=(V,E)$ without loops or multiedges. The symbols $\delta (G), \Delta (G)$ stand for, respectively, the minimum and the maximum degree among all the vertices in V. A vertex with degree equal to 1 is called a leaf and a vertex which is adjacent to exactly one leaf (resp. several leaves) is called a weak support vertex (resp. strong support vertex). As usually, we denote by $P_{n}, C_{n}, K_n$ the path, the cycle and the complete graph with n vertices, respectively. We denote the diameter of the graph G by Diam(G), which is the maximum distance between a pair of vertices of G. A tree with exactly two non-leaf vertices is called a bi-star or a double star, $D_{s,t}$, where the non leaves vertices are adjacent to, respectively, $1\le s\le t$ leaves. An star (comb) convex bipartite graph $G=(A,B,E)$ with associated star tree (comb tree) $T=(A,F)$ is a bipartite graph with vertex classes A, B such that $N_G(y)\subseteq A$ induces a subtree in T. Given two graphs G, H we denote by $G \vee H$ the graph obtained from the disjoint union of G and H by adding the edges joining each vertex of G with every vertex of H.

A dominating set (resp. total dominating set) in a graph is a subset $D \subseteq V$ such that any vertex belonging to $V\backslash D$ (resp. V) has a neighbor in D. The domination (resp. total domination) number, $\gamma (G)$ (resp. $\gamma _t (G)$), of a graph is the size of a smallest dominating set (resp. total dominating set) in G.

It is possible to deduce a first upper bound from the fact that the function that labels each vertex of an isolated-vertex free graph G with a $\lceil \frac{k+1}{2} \rceil$ is a [k]-RDF. We sincerely thank the referee for pointing out that it is possible to characterize all graphs reaching this limit.

Proposition 1.1

If G is a connected graph of order $n\ge 2$, then $\gamma _{[kR]} (G) \le \lceil \frac{k+1}{2} \rceil n$ with equality if and only if $G=K_2$ and k is odd.

Proof

First of all, let f be the function that labels each vertex of G with a $\lceil \frac{k+1}{2} \rceil$. Since f is a [k]-RDF the inequality holds. If $G = K_2$ and k is odd, then clearly $\gamma _{[kR]}(K_2)=k+1=\lceil \frac{k+1}{2} \rceil n.$ Conversely, assume that $\gamma _{[kR]}(G)=\lceil \frac{k+1}{2} \rceil n.$ If $k = 1$, then it follows from the bound $\gamma _R(G) \le \frac{4n}{5}$ for $n \ge 3$ (see [8]) that $n = 2$ and so $G = K_2$. Therefore, in what follows we may suppose that $k\ge 2$. Assume first that $n\ge 3$. If G has a strong support vertex, say v, then the function that labels v with a $k + 1$, each leaf adjacent to v with a 0 and each other vertex of G with a $\lceil \frac{k+1}{2} \rceil$ is a [k]-RDF of G of weight less than $\lceil \frac{k+1}{2} \rceil n$, which is a contradiction. If G has a weak support vertex, say v, and u is the leaf adjacent to v, then the function that labels u with a k, v with a 0 and each other vertex of G with a $\lceil \frac{k+1}{2} \rceil$ is a [k]-RDF of G of weight less than $\lceil \frac{k+1}{2} \rceil n$, again a contradiction. Hence we can assume that $\delta (G) \ge 2$. Let v be a vertex with minimum degree $\delta (G).$ If k is even, then the function that labels v with a 0 and each other vertex of G with a $\lceil \frac{k+1}{2} \rceil$ is a [k]-RDF of G of weight less than $\lceil \frac{k+1}{2} \rceil n$ which is a contradiction. If k is odd, then the function that labels v with a 1 and each other vertex of G with a $\lceil \frac{k+1}{2} \rceil$ is a [k]-RDF of G of weight less than $\lceil \frac{k+1}{2} \rceil n$ which is a contradiction. It follows that $n = 2$ and $G = K_2$. Then we have $\gamma _{[kR]}(K_2)=k+1= \lceil \frac{k+1}{2} \rceil n$ and this implies that k is odd.

Next, we remember a fact already showed in [12]. $\square$

Observation 1.2

[12] If G is an ntc graph, there exists a [k]-RDF such that no vertex needs to have a 1 label.

2 Bounds

In general, it is not easy to calculate the exact value of the [k]-RDN, even for some particular families of graphs. So, in this section we are going to present several upper and lower bounds for the [k]-RDN that permit us to estimate it with as much precision as possible.

As we may study this parameter for individual connected components, we focus our attention only on non-trivial connected (ntc) graphs. Through the following results, we prove upper bounds on the [k]-RDN improving the one given by Proposition 1.1.

From now on, we consider a $\gamma _{[kR]}$-RDF $f=(V_0,\emptyset ,V_2,\ldots , V_{k+1})$ of V. The following bound was also proved by Khalili et al. [12] but we present a similar version of the result in which we add some information about the structure of the extremal graphs that achieve the bound.

Proposition 2.1

[12] Let G be an ntc-graph of order n and maximum degree $\Delta$. Then

$$\begin{aligned} \gamma _{[kR]} (G) \le kn-k\Delta +1. \end{aligned}$$

If the equality holds and v is a vertex with maximum degree of V,  then $Diam(G)\le 4, |N(h)\backslash N[v]| \le 1$ for all $h\in N(v)$ and the set of vertices $V\backslash N[v]$ induces an edgeless subgraph of G.

Proof

Let us consider a vertex $v \in V$ of maximum degree $\Delta$ and let us define the function $f:V \longrightarrow \left\{ 0,1,\ldots , k+1 \right\}$ as follows: $f(v) = k+1, f(w) = 0$ for all $w \in N(v)$ and $f(x) = k$ for the remaining vertices. It is straightforward to see that f is a [k]-RDF, and hence

$$\begin{aligned} \gamma _{[kR]}(G) \le f(V) = k+1+k(n-\Delta - 1) = kn-k\Delta +1. \end{aligned}$$

Let us consider an ntc-graph G such that $\gamma _{[kR]}(G) = kn-k\Delta +1$ and let v be a vertex of maximum degree. If $\Delta =n-1,$ we are done. Therefore, let us assume that $\Delta \le n-2$ and let us denote by $H=N[v]$ and $W=V \backslash H$, which implies that $W\ne \emptyset .$

We have to discuss two particular situations.

• (a) If there is an edge $w_1w_2$ joining two vertices of W,  then we define the following function.

  $$\begin{aligned} \begin{array}{rcl} g(z) &{} = &{} \left\{ \begin{array}{ll} k+1 &{} z\in \{v,w_1\}, \\ 0 &{} z\in N(v) \cup \{w_2\}, \\ k &{} \text {otherwise.} \end{array} \right. \end{array} \end{aligned}$$

• (b) If there is a vertex $h_j\in H$ with $|N(h_j)\cap W|\ge 2,$ then we define the following function.

  $$\begin{aligned} \begin{array}{rcl} g(z) &{} = &{} \left\{ \begin{array}{ll} k+1 &{} z\in \{v,h_j\}, \\ 0 &{} z\in N(v)-h_j, \\ 0 &{} z \in N(h_j)\cap W, \\ k &{} \text {otherwise.} \end{array} \right. \end{array} \end{aligned}$$

In both cases, it is straightforward to see that g is a [k]-RDF and

$$\begin{aligned} g(V) \le 2(k+1)+k(n-1-\Delta -2)=kn-k\Delta +2-k<\gamma _{[kR]}(G), \end{aligned}$$

which is a contradiction. So, the result holds. $\square$

It is worth noting that the latter upper bound is sharp. For example, the bound is matched when G is any graph with a universal vertex.

Proposition 2.2

Let G be an ntc-graph with $n \ge 4$ vertices, maximum degree $\Delta \le n-2$, minimum degree $\delta \ge 2$ and girth $g(G) \ge 4.$ Then

$$\begin{aligned} \gamma _{[kR]}(G) \le kn - k\Delta . \end{aligned}$$

Proof

Consider a vertex $v \in V$ of maximum degree $d(v)=\Delta$ and let us define the function $f:V \longrightarrow \{ 0, 1, 2, \ldots , k+1 \}$ as follows $f(v) = k, f(z)=0$, for all $z \in N(v)$ and $f(z) = k$, for all $z\not \in N[v].$

As $\delta \ge 2$, every neighbor of v must have at least one neighbor in G that does not belong to N(v) because the girth is at least four. Therefore, the function f that we have just defined is a [k]-RDF and hence,

$$\begin{aligned} \gamma _{\left[kR \right]} (G) \le f(V) = k + k(n-\Delta -1) = kn-k\Delta . \end{aligned}$$

$\square$

The upper bound given by Proposition 2.2 is attained, for example, if G is the cycle with 4 vertices and k is even. Let us go a step forward and improve this bound.

Proposition 2.3

Let G be an ntc-graph with $n \ge 4$ vertices, maximum degree $\Delta \le n-2$, minimun degree $\delta \ge 2$ and girth $g(G) \ge 5.$ Then,

Proof

Consider a vertex $u \in V\ (G)$ with maximum degree, $d(u)=\Delta$ and let us define the function $f:V \longrightarrow \{ 0, 1,\ldots , k+1\}$ such that $f(u)=k, f(z)=0,$ for all $z\in N(u)$ and , for every vertex $v\in V-N[u]$. Taking into account that $\delta \ge 2$, every neighbor of u must have at least another neighbor in G not belonging to N(u), because the girth is at least 5. Summing up, f is a [k]-RDF and therefore,

$\square$

It is straightforward to check that the latter bound matches the exact value for the $C_5$ cycle when k is an odd integer. Next, we try to improve these bounds for regular graphs.

Proposition 2.4

Let G be an r-regular ntc-graph with $r \ge 2$ and girth $g(G) \ge 7$. Then,

Proof

Let v be a vertex of the graph G. Let us denote by $N_{0}=\{v\}$, $N_1 = N(v)$ and $N_2 = N(N_1)\backslash N_0.$ Clearly, $|N_0|=1, |N_1|=r$ and $|N_2|=r(r-1).$

Consider the function $f:V \longrightarrow \left\{ 0, 1,\ldots , k+1\right\}$ defined in the following way $f(v)=0, f(z)=k,$ for all $z \in N_1,$ $f(z)=0,$ for all $z \in N_2$ and $f(z)=\left\lceil \llceil \frac{k+1}{2} \right\rceil \rrceil$ for the remaining vertices. Since $r,k\ge 2$ then v is [k]-Roman dominated by the vertices in N(v). Besides, since $r\ge 2$ and $g\ge 7$ then each vertex in $N_2$ is [k]-Roman dominated by $N_1$ and $V{\setminus } (N_0\cup N_1 \cup N_2).$ Clearly, f is a [k]-RDF and therefore

$\square$

In this case, if we consider $k=7$ and the graph $G=C_7,$ then the bounds given by Proposition 1.1 and by Propositions 2.1, 2.2, 2.3 and 2.4 are $\{28,36,35,23,22\},$ respectively. It is easy to check that the last bound is the exact value of $\gamma _{[7R]}(C_7)$.

We also show a similar result for non-regular graphs.

Proposition 2.5

Let G be an ntc-graph with minimun degree $\delta \ge 3$ and girth $g(G) \ge 7.$ Then

Proof Let us consider a vertex $v \in V$ with $d(v) = \Delta$ and let us denote by $N_0 = \{ v \}, N_1 = N(v),$ and $N_2 = N(N_1)\backslash N_0$. As $g(G) \ge 7$ and $\delta (G) \ge 3,$ then each vertex in $N_2$ has, at least, two neighbors in $V\backslash (N_0\cup N_1\cup N_2).$ Let f be the function $f:V \longrightarrow \{0, 1, \ldots , k+1 \}$ defined as follows $f(v) = k-1,\ f(z)=2,$ for all $z \in N_{1}, f(z)=0,$ for all $z\in N_2$ and for the remaining vertices. Taking into account that $g(G) \ge 7,$ each vertex in $V\backslash (N_0\cup N_1\cup N_2)$ has a neighbor in this set and, therefore, f is a [k]-RDF. Then,

because $|N_2|\ge 2\Delta .$ $\Box$

Proposition 2.6

Let G be an ntc-graph with order n, maximum degree $\Delta$ and minimun degree $\delta .$ Then

$$\begin{aligned} \gamma _{[kR]}(G) \le \left\lfloor \frac{n(k+1)}{\delta + 1} \left( 1+ \ln \frac{k (\delta + 1)}{k+1} \right) \right\rfloor . \end{aligned}$$

Proof

Let $0< p <1$ be a fixed positive real number. Given a fixed subset of vertices $M \subseteq V,$ let us consider the value of p as the probability that a vertex v belongs to M,  for any $v\in V$. Let us denote by $W= N[M]^c$.

Since $0< p < 1$ we have that,

$$\begin{aligned} \begin{array}{rcl} P[v\in W] &{} = &{} P[v\in M^c \cap N(M)^c] \\ &{} = &{} (1-p) (1-p)^{d(v)} \le (1-p)^{d(v) + 1} \le (1-p)^{\delta + 1}. \end{array} \end{aligned}$$

It is straightforward to see that the forecasted value for the size of M is $E[|M|] = np$ and, analogously, $E[|W|] \le n(1-p)^{\delta + 1}$.

Next, consider the labelling of the vertices of G given by the function defined as follows,

$$\begin{aligned} f(x)= \left\{ \begin{array}{crl} k+1, &{} &{} \text{ if } v\in M, \\ 0, &{} &{} \text{ if } v\in N(M)\backslash M, \\ k, &{} &{} \text{ if } v\not \in N[M]. \end{array} \right. \end{aligned}$$

which is a [k]-RDF.

We may estimate the awaited value of f(V) to be

$$\begin{aligned} E[f(V)] = (k+1)E[|M|]+kE[|W|] \le (k+1)np+kn (1-p)^{\delta +1}. \end{aligned}$$

It is worth noting that $1 - p < e^{-p}$ whenever $0< p < 1$ and hence

$$\begin{aligned} E[f(V)] \le (k+1) np + kne^{-p(\delta +1)}. \end{aligned}$$

Among all possible values of the integer p,  the one that lead us to the minimum value of E[f(V)] must satisfy

$$\begin{aligned} (k+1)\ n - kn (\delta +1) e^{-p(\delta +1)} = 0, \end{aligned}$$

which implies that

$$\begin{aligned} e^{-p(\delta +1)} = \frac{k+1}{k(\delta +1)}. \end{aligned}$$

We can easily deduce the optimum value of p from this expression,

$$\begin{aligned} p = \displaystyle \frac{1}{\delta +1} \ln \frac{k (\delta +1)}{k+1} \end{aligned}$$

and finally,

$$\begin{aligned} \begin{array}{rcl} \gamma _{[kR]}(G) &{} \le &{} \displaystyle (k+1)n\frac{1}{\delta +1}\ln \frac{k (\delta +1)}{k+1} + kn\frac{k+1}{k (\delta +1)} \\ &{} = &{}\displaystyle \frac{n(k+1)}{\delta + 1} \left( 1+ \ln \frac{k (\delta + 1)}{k+1} \right) \end{array} \end{aligned}$$

and the result holds. $\square$

Proposition 2.7

Let G be an ntc-graph of order $n\ge 2$ and maximum degree $\Delta \ge k$. Then,

Proof

We make use of a discharging procedure, similar to the one used in [16] for the double Roman domination, to prove this result. Let us consider any $\gamma _{[kR]}(G)$-function $f=(V_0,\emptyset , V_2, \ldots ,V_{k+1})$ and let $s(v)=f(v)$ be the initial charge of each vertex $v\in V.$ Next, we apply the discharging procedure defined by means of the following rule,

R.:

Every vertex v with $s(v)=j$ sends a charge of $\displaystyle \frac{(j-1)(k+1)}{k(\Delta +1)}$ to each vertex in $N(v)\cap V_0,$ for all $2\le j \le k+1.$

Let us denote by $s'(v)$ the final charge of vertex v after applying the procedure. Let j be a positive integer such that $2\le j\le k+1$. For every vertex $v_j$ with $f(v_j)=j$ we have that

$$\begin{aligned} \begin{array}{rcl} s'(v_j)\ge & {} \displaystyle s(v_j)-d(v_j)\frac{(j-1)(k+1)}{k(\Delta +1)}\ge j -\frac{\Delta (j-1)(k+1)}{k(\Delta +1)}. \end{array} \end{aligned}$$

Let us denote by $h(j)= \displaystyle j-\frac{\Delta (j-1)(k+1)}{k(\Delta +1)}$ which is a monotone function with respect to the variable j. Observe that

$$\begin{aligned} \begin{array}{rcl} h(k+1) &{} = &{} \displaystyle k+1-\frac{\Delta (k+1)}{\Delta +1} = \frac{k+1}{\Delta +1}, \\ h(2) &{} = &{} \displaystyle 2-\frac{\Delta (k+1)}{k(\Delta +1)} = \frac{k\Delta +2k-\Delta }{k(\Delta +1)}. \\ \end{array} \end{aligned}$$

As $\Delta \ge k,$ then $(k-1)(k-\Delta ) \le 0$ and therefore

$$\begin{aligned} \begin{array}{rcl} 0 &{} \ge &{} k^2-(\Delta +1)k+\Delta \\ &{} = &{} k^2+k-(k\Delta +2k-\Delta ), \end{array} \end{aligned}$$

yielding that $k\Delta +2k-\Delta \ge k(k+1)$, which lead us to $h(2)\ge \frac{k+1}{\Delta +1}.$

So, due to the monotony of the function h,  we can assure that $s'(v)\ge \frac{k+1}{\Delta +1}$ for all v with $f(v)>0.$

On the other hand, let $v_0\in V$ be a vertex with $f(v)=0.$ As f is a [k]-RDF, we have that

$$\begin{aligned} f(N[v]) =f(N(v))\ge |AN(v)|+k. \end{aligned}$$

(2.1)

Hence, each vertex $v_0\in V_0$ must have some active neighbor w with $f(w)\ge 2$. Let us denote these neighbors by $N(v_0)\cap (V\backslash V_0)=\{w_{j,1},\ldots ,w_{j,p_j}: f(w_{j,i})=j, 2 \le j\le k+1 \}.$ From expression (2.1) it is deduced that,

$$\begin{aligned} f(N[v]) =f(N(v))=\sum _{j=2}^{k+1} j\cdot p_j \ge \sum _{j=2}^{k+1} p_j+k. \end{aligned}$$

(2.2)

And so,

$$\begin{aligned} s'(v_0)= & {} \displaystyle \sum _{j=2}^{k+1} p_j \frac{j-1}{k} \frac{k+1}{\Delta +1} \\= & {} \displaystyle \frac{k+1}{k(\Delta +1)} \sum _{j=2}^{k+1} p_j (j-1) \\= & {} \displaystyle \frac{k+1}{k(\Delta +1)} \left( \sum _{j=2}^{k+1} j\cdot p_j - \sum _{j=2}^{k+1} p_j \right) \\\ge & {} \displaystyle \frac{k+1}{k(\Delta +1)} k = \frac{k+1}{\Delta +1}. \end{aligned}$$

Summing up,

$$\begin{aligned} \gamma _{[kR]}(G)=\sum _{v\in V} f(v)=\sum _{v\in V} s(v)=\sum _{v\in V} s'(v) \ge \sum _{v\in V} \frac{k+1}{\Delta +1} \ge \frac{(k+1)n}{\Delta +1}. \end{aligned}$$

As $\gamma _{[kR]}(G)$ is an integer, the result holds. $\square$

This lower bound is tight, for example, for every graph with an universal vertex or for the cycle graph $C_6$, for which $\gamma _{[kR]}=2k+2.$ Another proof of the special case $k=2$ can be found in [18].

3 Exact Values

In this section, we deal with the problem of obtaining the exact value of the parameter [k]-RDN.

We start noting the following fact.

Observation 3.1

$\gamma _{[kR]}(G)=k$ if and only if $G=K_1.$

Proposition 3.2

Let G be an ntc-graph of order $n\ge 2$. Then $\gamma _{[kR]}(G)=k+1$ if and only if $\Delta (G)=n-1.$

Proof

To begin with, let us assume that $v\in V$ is a vertex of maximum degree $d(v)=\Delta (G)=n-1\ge 1,$ which implies that $G\ne K_1$ and therefore, by Observation 3.1, $\gamma _{[kR]}(G)\ge k+1.$ Next, we may define the function $g(v)=k+1$ and $g(z)=0$ for all $z\ne v.$ Clearly, g is a [k]-RDF with weight $k+1$ and hence $\gamma _{[kR]}(G)\le k+1,$ as desired.

On the other hand, let us assume that $\gamma _{[kR]}(G)= k+1.$ Let f be a $\gamma _{[kR]}(G)$-function with $f=(V_0,\emptyset ,V_2,\ldots ,V_{k+1})$. For all vertex $u\in V$ we have that

$$\begin{aligned} k+1=\gamma _{[kR]}(G)\ge f(N[u]) \ge |AN(u)|+k, \end{aligned}$$

and we derive that $|AN(u)|\le 1$ for all $u\in V.$ So $f(w)=k+1$ for all $w\in AN(u)$ and for every $u\in V$. As $f(V)=k+1$ we may deduce that $|V_{k+1}|=1$ and $V_0=V\backslash V_{k+1}$, and so $\Delta =n-1.$ $\Box$

Proposition 3.3

There are no graphs G such that $\gamma _{[kR]}(G)=k+2,$ for all $k\ge 3.$

Proof

Let us assume that $\gamma _{[kR]}(G)=k+2$ and let $f=(V_0, \emptyset , \ldots ,V_{k+1})$ be a $\gamma _{[kR]}(G)$-function. As $V_1=\emptyset$ and $\gamma _{[kR]}(G)=k+2,$ then we have that $V_{k+1}=\emptyset .$ Let $v\in V_0.$ Because $V_{k+1}=\emptyset ,$ it follows that $|AN(v)|\ge 2$. By definition of a [k]-RDF we deduce that

$$\begin{aligned} k+2=\gamma _{[kR]}(G)\ge f(N[v]) \ge k+|AN(v)|=k+j\ge k+2. \end{aligned}$$

Therefore, $j=2$ for all $v\in V_0.$ Besides, $k\ge 3$ implies that $\gamma _{[kR]}(G)=k+2 < 2k$ and then $|V\backslash V_0|=2$. As a consequence, we may assume that $V\backslash V_0=\{w_1,w_2\}$ with $w_1\in N(w_2),$ $v\in N(w_2)$ for all $v\in V_0$. Hence $\Delta (G)=n-1$, which is a contradiction. $\Box$

Given a positive integer $n\ge 2,$ we denote by $M^k(n)$ the following value:

$$\begin{aligned} M^k(n) = \left\{ \begin{array}{ccl} (k+1)\left\lfloor \frac{n}{3}\right\rfloor &{} &{} \text{ if } n \equiv 0\ (\text {mod}\ 3), \\ (k+1)\left\lfloor \frac{n}{3}\right\rfloor +k &{} &{} \text{ if } n \equiv 1\ (\text {mod}\ 3), \\ (k+1)\left\lfloor \frac{n}{3}\right\rfloor + (k+1) &{} &{} \text{ if } n \equiv 2\ (\text {mod}\ 3). \end{array} \right. \end{aligned}$$

Proposition 3.4

Let $n\ge 2$ be a positive integer. Then $\gamma _{[kR]} (P_n)=M^k(n)$.

Proof

Let q be an integer such that $n=3m+q,$ with $0\le q\le 2.$ We consider the stars $K_{1,2}^j,$ with set of vertices $\{v_0^j,\ v_1^j,\, v_2^j\}$ and set of edges $\{v_0^jv_1^j,v_0^jv_2^j \},$ for $1\le j\le m.$ We denote by $R_q$ the set:

$$\begin{aligned} R_{q}= \left\{ \begin{array}{crl} \emptyset &{} &{} \text{ if } q=0, \\ \{v_{3m+1}\} &{} &{} \text{ if } q=1, \\ V(P_2)=\{v_{3m+1},v_{3m+2}\} &{} &{} \text{ if } q=2. \end{array} \right. \end{aligned}$$

Following these notations, we can express the path $P_n$ as the ordered set of vertices and edges

$$\begin{aligned} P_n=v_1^1v_0^1v_2^1v_1^2v_0^2v_2^2 \ldots v_1^mv_0^mv_2^m \end{aligned}$$

and, eventually, the vertices of $R_q$ and the necessary edges joining them.

It is straightforward to see that $\gamma _{[kR]}(P_2)=k+1 \ge M^k(2)$ and $\gamma _{[kR]}(\{v\})=k \ge M^k(1)$ for any isolated vertex. Moreover, for every $1 \le j \le m,$ we have that $\gamma _{[kR]}(K_{1,2}^j)=k+1\ge M^k(3)$ and the only $\gamma _{[kR]}$-function is defined as $f^j(v_0^j)=k+1$ and $f^j(v_1^j)=f^j(v_2^j)=0.$

Now, we define the following function on $V(P_n)$:

$$\begin{aligned} f(v)= \left\{ \begin{array}{crl} k+1 &{} &{} \text {if } v=v_0^j \ \ 1\le j \le m, \\ 0 &{} &{} \text {if } v=v_i^j \ \ \ 1\le j \le m, \ \ \ 1\le i \le 2 \\ h(v) &{} &{} \text {if}\, v\in R_q \,\text {and}\, h \,\text {is a}\, \gamma _{[kR]}\,\text {-function in}\, R_q \,\text {for}\, q\ge 1. \end{array} \right. \end{aligned}$$

Clearly, the function f is a [k]-RDF in $P_n$ and $f(V(P_n))=M^k(n).$ Then,

$$\begin{aligned} \gamma _{[kR]}(P_n)\le M^k(n). \end{aligned}$$

Now, we have to prove the inequality $\gamma _{[kR]}(P_n)\ge M^k(n)$.

Let g be a $\gamma _{[kR]}(P_n)$-function such that no vertex is labelled as 1 under g. We proceed by induction on the number of vertices n. Note that $\gamma _{[kR]}(P_2) = k+1\ge M^k(2)$, $\gamma _{[kR]}(P_3)=k+1\ge M^k(3)$ and, on the other hand, it is not difficult to check that $\gamma _{[kR]}(P_4)=2k+1\ge M^k(4)$ and $\gamma _{[kR]}(P_5)=2k+2 \ge M^k(5)$.

Now, let us consider $n\ge 6$ and suppose that $\gamma _{[kR]}(P_{n'})\ge M^k{(n')}$, for all $2\le n'<n$. Let $V(P_n)=\{w_1, w_2,\ldots , w_n\}$ be the set of (ordered) vertices of the path $P_n$. The following cases are considered,

Case a.- Assume that $\displaystyle g|_{P_{n-3}}$ is a [k]-RDF on $P_{n-3}$.

If $g(w_{n-1})+g(w_n)\ge k+1$ then we have that $g(V(P_n))\ge M^k(n-3) +(k+1)=M^k(n).$

If $g(w_{n-1})+g(w_n)=k$ then $g(w_{n-2})\ge 2$ and therefore, $g(w_{n-2})+g(w_{n-1})+g(w_n)\ge k+1.$ Hence $g(V(P_n))\ge M^k(n-3) +(k+1)=M^k(n).$

Case b.- On the contrary, suppose that $\displaystyle g|_{P_{n-3}}$ is not a [k]-RDF on $P_{n-3}.$

Since $\displaystyle g|_{P_{n-3}}$ is not a [k]-RDF on $P_{n-3}$ and g is a [k]-RDF on $P_{n},$ we have that $g(w_{n-3})< k$ and $g(w_{n-2})\ge 2.$

Subcase b.1.- Assume $\displaystyle g(w_{n-4})\ne 0.$

In this case, it is easy to check that $g(w_{n-4})+g(w_{n-3})+g(w_{n-2}) \ge k+2$ and, therefore $g(w_{n-4})+g(w_{n-3})+g(w_{n-2})+g(w_{n-1})+g(u_n)\ge k+2+k=2k+2$.

Let $g'$ be the function defined as follows

$$\begin{aligned} g'(w)= \left\{ \begin{array}{crl} 0 &{} &{} \text{ if } w\in \{w_{n-2},w_n\}, \\ k+1 &{} &{} \text{ if } w\in \{w_{n-3},w_{n-1}\}, \\ g(w) &{} &{} \text{ otherwise. } \end{array} \right. . \end{aligned}$$

So, $g'$ is a [k]-RDF on $P_n$ and $\displaystyle g'\left| _{P_{n-3}}\right.$ is [k]-RDF on $P_{n-3}$. Taking into account the Case a, we have that,

$$\begin{aligned} \gamma _{[kR]}(P_n)=g(V(P_n))\ge g'(V(P_n))\ge M^k(n). \end{aligned}$$

Subcase b.2.- Assume $\displaystyle g(w_{n-4})=0.$

It is clear that $g(w_{n-5})\ge 2, g(w_{n-4})+g(w_{n-3})+g(w_{n-2})\ge k+1$ and $g(w_{n-1})+g(w_n)\ge k$.

Again, we may define a function $g'$ in the following way,

$$\begin{aligned} g'(w)= \left\{ \begin{array}{crl} 0 &{} &{} \text{ if } w\in \{w_{n-2},w_n\}, \\ k+1 &{} &{} \text{ if } w=w_{n-1}, \\ k &{} &{} \text{ if } w=w_{n-3}, \\ g(w) &{} &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

Then, $g'$ is a [k]-RDF on $P_n$ and $\displaystyle g'\left| _{P_{n-3}}\right.$ is a [k]-RDF on $P_{n-3}$ and, therefore $g\left( V\left( P_n\right) \right) \ge \ g'\left( V\left( P_n\right) \right) \ge M^k(n).$ $\square$

4 Complexity Results

In [4], Ahangar et al. proved that the decision problem associated to the triple Roman domination problem is NP-complete for chordal and bipartite graphs. Later, Poureidi and Fathali [15] showed that this problem still remains NP-complete when restricted to star convex and comb convex bipartite graphs.

Recently, Khalili et al. [12] proved that the [k]-Roman domination decision problem is NP-complete for bipartite and chordal graphs.

The goal of this section is to generalize the result by Poureide and Fathali to prove that the [k]-Roman domination decision problem is NP-complete even when restricted to star convex and comb convex bipartite graphs.

To begin with, we state the decision problem associated to the [k]-Roman domination problem.

[k]-RDN PROBLEM Instance: Graph $G =(V,E)$ and a positive integer r.Question: Does G have a [k]-RDF f with $f(V)\le r$?

To see that [k]-RDN PROBLEM is NP-complete, we show the equivalence with an instance of the 3SAT problem, which is a well-known NP-complete problem.

3SAT PROBLEM Instance: A formula L in 3-conjuctive normal form.Question: Is L satisfiable?

Let us denote by $X=\{x_1, \ldots ,x_q\}$ a set of $q\ge 3$ variables and let $C=\{c_j:j=1,\ldots , p\}$ be a set of p clauses. $L=(C;X)$ is an instance of 3-SAT problem given that each clause $c_j$ contains exactly 3 (positive or negative) instances of variables $x_i$’s. That is to say, $c_j=(c_j^1,c_j^2,c_j^3)$ where each of $c_j^l$ is either a variable $x_i$ or the negation of a variable in X. We denote by $x_i^-$ the negation of a variable $x_i.$

Theorem 4.1

[k]-RDN PROBLEM is NP-complete even for star convex bipartite graphs.

Proof

Clearly, the [k]-RDN PROBLEM is a member of ${\mathcal {N}}{\mathcal {P}}$, since we can check in polynomial time whether a function $f:V\rightarrow \{0,1, \ldots ,k+1 \}$ is a [k]-RDF of weight at most r.

We prove that [k]-RDN PROBLEM is still a NP-complete decision problem even when restricted to star convex bipartite graphs by describing a polynomial transformation with the 3SAT PROBLEM.

Let $L=(X;C)$ be an arbitrary instance of 3SAT with $X=\{x_1,x_2,\ldots ,x_{q} \}$ and $C=\{c_1,c_2,\ldots , c_p\}$. We construct an star convex bipartite graph $\Gamma (L)=\Gamma = (A,B,E)$ with an associated tree $T=(A,F)$ and we give a positive integer r such that, L is satisfiable if and only if $\Gamma$ has a [k]-RDF f with $f(V_\Gamma ) \le r= 2q(k+1).$

Fig. 1

The auxiliary gadget associated to each corresponding variable $x_i$

First, let us think about a fixed variable $x_i$. We consider the following gadget associated to $x_i$ (see Fig. 1): a vertex $x_i$; $k+1$ vertices, namely $\{ y_1^i,\ldots ,y_{k+1}^i\},$ adjacent to the vertex $x_i$; two vertices $x_i^+, x_i^-$ adjacent to $x_i;$ and $k+1$ vertices, namely $\{ z_1^i,\ldots ,z_{k+1}^i\}$, that are adjacent to both vertices $x_i^+$ and $x_i^-$.

Once we have such a gadget for each vertex $x_i$ in $\Gamma$, we add an additional vertex t to the graph which is adjacent to each vertex in the set $\{x_i^+,x_i^-: i=1,\ldots ,p\}$ and which is the center of the associated star graph T.

Finally, we add to $\Gamma$ a set of vertices $\{c_1, \ldots , c_p\}$ corresponding to the clauses. Note that $c_j=(c_j^1,c_j^2,c_j^3)$ where each of $c_j^l$ is either $x_i^+$ or the negation $x_i^-$, for some $i\in \{1,...,q\}$. The edge $c_jx_i^+$ (respectively $c_jx_i^-$) belongs to E if and only if there exist $l\in \{1,2,3\}$ such that $x_i^+=c_j^l$ (respectively $x_i^-=c_j^l$).

Let us point out that $\Gamma$ is a bipartite graph with vertex classes given by $A=\{ t, x_i, z_j^i,c_l: 1 \le i \le q, 1 \le j \le k+1, 1\le l\le p \}$ and $B=\{ x_i^+,x_i^-, y_j^i: \ 1 \le i \le q, 1\le j \le k+1 \}$. Moreover, $\Gamma$ is an star convex bipartite graph with associated star graph $T=(A,F)$ where t is adjacent to every vertex in $A\!\smallsetminus \!\{t\}.$ (see Fig. 2)

Clearly, we can make the graph $\Gamma$ in polynomial time regarding to the size of the sets of variables and clauses.

Fig. 2

An example of the star convex bipartite graph $\Gamma$ with $q=p=3$

On the one hand, let us assume that L is satisfiable and let us assume that W is an assignment of state of the variables in X that makes L evaluate as true. Let f be the function defined as follows. Let $f(t)=f(c_l)=f(z_j^i)=f(y^i_j)=0; f(x_i)=k+1$ for all $1 \le i \le q, 1 \le j \le k+1, 1\le l\le p.$ Besides, if $x_i$ is false under W then $f(x_i^-)=k+1$ and $f(x_i^+)=0.$ Otherwise, $f(x_i^-)=0$ and $f(x_i^+)=k+1.$ It is straightforward to check that f is a [k]-Roman domination function of $\Gamma$ with weight $w(f)=2q(k+1).$

On the other hand, let us assume that there exists a [k]-RDF $f=(V_0,V_1,...,V_{k+1})$ of $\Gamma$ having weight $w(f)\le 2q(k+1).$

First of all, note that $\{y_i^j:i=1,\ldots ,q; j=1, \ldots ,k+1 \}$ are leaves having $x_i$ as an strong support vertex. Hence, $f(x_i)+f(y_1^i)+ \ldots + f(y_{k+1}^i) \ge k+1,$ for all $i=1,\ldots ,q.$ Moreover, $\{z_i^j:i=1,\ldots ,q; j=1, \ldots ,k+1 \}$ are vertices of degree 2 having $x_i^+$ and $x_i^-$ as the only common neighbors. Therefore $f(x_i^+)+f(x_i^-)+f(z_1^i)+ \ldots + f(z_{k+1}^i) \ge k+1,$ for all $i=1,\ldots ,q.$ Then, we have that

$$\begin{aligned} f(x_i^+)+f(x_i)+f(x_i^-)+\sum _{j=1}^{k+1}f(z_j^i)+ \sum _{j=1}^{k+1}f(y_j^i) \ge 2(k+1) \end{aligned}$$

for all $i=1,\ldots , q.$ Since $w(f)\le 2q(k+1)$ then it implies that $f(c_l)=f(t)=0$ for all $l=1,\ldots , p.$ Besides, it must be $f(x_i)+f(y_1^i)+ \ldots + f(y_{k+1}^i) = k+1$ and $f(x_i^+)+f(x_i^-)+f(z_1^i)+ \ldots + f(z_{k+1}^i) = k+1,$ which is only possible if

• 1. $f(x_i)=k+1$ for all $i=1,\ldots ,q.$

• 2. $f(y_j^i)=f(z_j^i)=0$ for all $i=1,\ldots ,q$ and $j=1,\ldots ,k+1.$

• 3. either $\left( f(x_i^+)=k+1 \right.$ and $\left. f(x_i^-)=0\right)$ or $\left( f(x_i^+)=0 \right.$ and $\left. f(x_i^-)=k+1\right)$.

Let us consider the truth assignment W that assigns the value true to the variable $x_i$ if and only if $f(x_i^+)=k+1$ and $f(x_i^-)=0,$ and that assigns the value false otherwise. To finish the proof we only have to show that W satisfies the instance L of the 3SAT problem.

Let $c_l$ be a clause of $L=(X;C)$ such that $c_j=(c_j^1,c_j^2,c_j^3),$ where each of $c_j^l$ is either a variable $x_i$ or the negation of a variable in X. As $f(c_l)=0$ and $N_\Gamma (c_l)\subseteq \{ x_i^+,x_i^-:i=1,\ldots ,q \}.$ Then it must exist $1\le i_0 \le q$ and $1\le l \le 3$ such that

• 1. $c_j^l=x_{i_0}^+, f(x_{i_0}^+)=k+1$ and $f(x_{i_o}^-)=0$ which implies that W assigns the value true to $x_{i_0}$ and $c_j$ is satisfied.

• 2. $c_j^l=x_{i_0}^-, f(x_{i_0}^-)=k+1$ and $f(x_{i_o}^+)=0$ which implies that W assigns the value false to $x_{i_0}$ and $c_j$ is satisfied.

In any case, the clause $c_j$ is satisfied and therefore the boolean formula L so is. That finishes the proof. $\square$

Let us note that we can construct a comb convex bipartite graph in a similar way to the star convex graph considered in the proof of the Theorem 4.1. This lead us to the following result.

Theorem 4.2

[k]-RDN PROBLEM is NP-complete even for comb convex bipartite graphs.

The key of the proof is to add an adequate set of vertices for each variable $x_i$ instead of a single vertex t as we did in the proof. As the reasoning of the proof is analogous, to avoid repetitions of arguments that are too similar, we leave the details to the reader.