Abstract
In 2009, Lipman published his polished book (Lipman in Foundations of Grothendieck duality for diagrams of schemes, Lecture Notes in Mathematics, vol. 1960, Springer, Berlin, pp 1–259, 2009), the product of a decade’s work, giving the definitive, state-of-the-art treatment of Grothendieck duality. In this article, we achieve a sharp improvement: we begin by giving a new proof of the base-change theorem, which can handle unbounded complexes and work in the generality of algebraic stacks (subject to mild technical restrictions). This means that our base-change theorem must be subtle and delicate, the unbounded version is right at the boundary of known counterexamples—counterexamples (in the world of schemes) that had led the experts to believe that major parts of the theory could only be developed in the bounded-below derived category. Having proved our new base-change theorem, we then use it to define the functor \(f^!\) on the unbounded derived category and establish its functoriality properties. In Sect. 1, we will use this to clarify the relation among all the various constructions of Grothendieck duality. One illustration of the power of the new methods is that we can improve Lipman (Lecture Notes in Mathematics, vol. 1960, Springer, Berlin, pp 1–259, 2009, Theorem 4.9.4) to handle complexes that are not necessarily bounded. There are also applications to the theory developed by Avramov, Iyengar, Lipman and Nayak on the connection between Grothendieck duality and Hochschild homology and cohomology but, to keep this paper from becoming even longer, these are being relegated to separate articles. See for example (Neeman in K-Theory—Proceedings of the International Colloquium, Mumbai, 2016, Hindustan Book Agency, New Delhi, pp 91–126, 2018).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Executive Summary
Let \(f:X\longrightarrow Y\) be a separated morphism of noetherian schemes, essentially of finite type. There is a pushforward map \(\textbf{R}f_*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\), which has a left adjoint \({\textbf{L}}f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) and a right adjoint \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). In duality theory, it is customary to consider yet another functor \(f^!\); in all treatments up to now it has been viewed as a functor \(f^!:{{\textbf{D}}^+_{\textrm{qc}}}(Y)\longrightarrow {{\textbf{D}}^+_{\textrm{qc}}}(X)\). Here \({{\textbf{D}}^+_{\textrm{qc}}}\) means the (cohomologically) bounded-below derived category. Duality theory studies the interplay among these functors.
Grothendieck duality is an old subject. There are basically two approaches to it: one can develop the theory via residual and Cousin complexes as in Hartshorne [18] and Conrad [10], or one can proceed more functorially, as outlined by Deligne [13] and Verdier [42] and developed very fully in Lipman [25]. The key to the second approach is the base-change theorem of Verdier, it is fundamental to developing the properties of the functor \(f^!\). There is also a proof of the base-change theorem due to Hartshorne, but it comes at the end, after the theory has been substantially set up.
The first result in this paper is a new proof of the base-change theorem, valid much more generally than the old proofs. Unlike the old proofs it is based on the compact generation of the triangulated categories involved, see Lemmas 5.19 and 5.20. Let us give a version of Lemma 5.20 here—this is not the most general statement we can prove but gives the flavor:
Lemma 0.1
Suppose we are given a 2-cartesian square of quasi-compact, quasi-separated algebraic stacks

where X and Z have quasi-finite, separated diagonals. Suppose v is flat, while the morphism g is concentrated as in [17, Definition 2.4] and quasi-proper.Footnote 1 Let E be an object \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\). Suppose further that one of the two hypotheses holds:
-
(i)
The map f is of finite Tor-dimension, and the map g is pseudo-coherent.Footnote 2
-
(ii)
The object E belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
Then, the base-change map \(\Phi :u^*g^\times E\longrightarrow f^\times v^* E\) is an isomorphism.
The old theorem of Hartshorne and Verdier is the special case of Lemma 0.1(ii) in the case where all the stacks are noetherian schemes, and the modern proof given here is not hard—see Sect. 5. The new Lemma 0.1(i) is more delicate; the proof involves an application of a generalized Thomason’s localization theorem whose original version, for schemes, allows us to extend perfect complexes from open subsets of a scheme. The reader might wish to compare our proof to the existing ones in the literature—the proof we give of Lemma 0.1(ii) is similar in spirit to the one in Lipman [25], but the twist required to prove the new Lemma 0.1(i) is a little subtle. And the new result is close to best possible, [31, Example 6.5] shows that unless we impose some condition the base-change map \(\Phi \) need not be an isomorphism in the unbounded derived category.
We have a new proof of a strengthening of an old theorem. We can say something for algebraic stacks, but for this executive summary let us focus on what the new result says for noetherian schemes. The treatments of Grothendieck duality to date have used the old base-change theorem, with the result that many theorems were known only for bounded-below complexes. Lemma 0.1(i) will allow us to fix this; we will circumvent the problems and define \(f^!\) unconditionally, on the unbounded derived category. The majority of the paper is devoted to developing the functor \(f^!\) and its functoriality properties. Given how much space it takes to set up the theory properly, in this article, we confined ourselves to only one application and the sketch of a second:
-
(i)
We extend Lipman [25, Theorem 4.9.4], one of the major results in the book. The theorem has several ramifications, which Lipman explores in his book but we do not have the space for here. Nevertheless, it is possible to reduce it to a simple statement we can include: suppose \(f:X\longrightarrow Y\) is a proper morphism of noetherian schemes. Suppose the complex \(E\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) is bounded above. Then, \(f^\times E\) does not have to be bounded above. Let \(u:U\longrightarrow X\) be a flat morphism so that fu is of finite Tor-dimension. Is \(u^*f^\times E\) bounded above? Although Lipman [25] considers the question and its implications, the techniques available at the time were able to prove this only when E is bounded. We will extend this to any bounded-above complex.
-
(ii)
The theory developed here immediately applies to the results of Avramov, Iyengar, Lipman and Nayak [3, 4], see also [21]; the relation they found, between Grothendieck duality and Hochschild homology and cohomology, extends to the unbounded derived category to give reduction isomorphisms valid unconditionally, for unbounded complexes. To keep this article from becoming even longer, the exposition is being postponed to the manuscript [33].
In this article, we do not study formal schemes at all although there is a version of the theory of [3, 4] valid for formal schemes, see Shaul [40].
2 Introduction
Let us begin by recalling an old theorem of Nagata. Suppose X and Y are noetherian schemes and \(f:X\longrightarrow Y\) is a separated morphism of finite type. Then, f may be factored as \(X{\mathop {\longrightarrow }\limits ^{u}}\overline{X}{\mathop {\longrightarrow }\limits ^{p}}Y\) with u an open immersion and p proper. Note that the open immersion u is certainly flat, and is a monomorphism in the category of schemes. And a proper map of noetherian schemes is most definitely of finite type and universally quasi-proper, see the footnotes to Lemma 0.1.
As above let \(f:X\longrightarrow Y\) be a separated morphism of finite type between noetherian schemes, and let \(X{\mathop {\longrightarrow }\limits ^{u}}\overline{X}{\mathop {\longrightarrow }\limits ^{p}}Y\) be a factorization as given by Nagata. The functor \(f^!:{{\textbf{D}}^+_{\textrm{qc}}}(Y)\longrightarrow {{\textbf{D}}^+_{\textrm{qc}}}(X)\) is traditionally defined to be the composite \({{\textbf{D}}^+_{\textrm{qc}}}(Y){\mathop {\longrightarrow }\limits ^{p^\times }}{{\textbf{D}}^+_{\textrm{qc}}}(\overline{X}){\mathop {\longrightarrow }\limits ^{u^*}}{{\textbf{D}}^+_{\textrm{qc}}}(X)\). It needs to be checked that \(f^!\) does not depend on the choice of Nagata compactification and is pseudofunctorial. This has been done in the bounded-below derived category but not in the unbounded derived category. The key lemma in proving that \(f^!\) has good properties is the base-change theorem in Hartshorne [18, Corollary 3.4(a) on p. 383, elaborated in (5) on p. 191] or Verdier [42, Theorem 2 on p. 394, proof pp. 400–407] which says that, if we have a cartesian square of noetherian schemes

with g proper and v flat, then the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is an isomorphism. The reader can see the way base-change is used in the proof of the pseudofunctoriality of \(f^!\) in Lipman [25, proof of Theorem 4.8.1]. Unfortunately the base-change theorem is true as stated only in the bounded-below derived category. An (unbounded) counterexample may be found in [31, Example 6.5].
In this paper, we fix the problem—we prove statements that hold in the unbounded derived category. In the Introduction, we will not state our results in maximal possible generality; instead we strive for clarity and reasonably useful generality. To formulate our results, it will be helpful to introduce
Notation 1.1
We will assume given a 2-subcategory \({\mathbb {S}_{{\textbf{e}}}}\) of the 2-category of noetherian algebraic stacks. The 2-morphisms are simple: any 2-morphism in the category of algebraic stacks, between 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\), belongs to \({\mathbb {S}_{{\textbf{e}}}}\). The objects \(X\in {\mathbb {S}_{{\textbf{e}}}}\) will be assumed to be noetherian stacks with quasi-affine diagonals, to admit finitely-presentable, representable, separated and étale covers \(\overline{X}\longrightarrow X\) with \(\overline{X}\) satisfying the resolution property, and to satisfy one of the two conditions below
-
(i)
either X is a \({{\mathbb {Q}}}\)-stack
-
(ii)
or the diagonal of X is quasi-finite.
All Noetherian Deligne–Mumford stacks satisfy the hypotheses—this includes all noetherian algebraic spaces, which includes noetherian schemes.
Now, for the 1-morphisms: we assume every \(f:X\longrightarrow Y\) in \({\mathbb {S}_{{\textbf{e}}}}\) to be separated, as well as concentrated as in [17, Definition 2.4]. All morphisms of noetherian algebraic spaces are concentrated. We furthermore suppose
-
(iii)
If X is an object of \({\mathbb {S}_{{\textbf{e}}}}\) and \(u:U\longrightarrow X\) is an open immersion, then u belongs to \({\mathbb {S}_{{\textbf{e}}}}\).
-
(iv)
Pullbacks in the 2-category of algebraic stacks, of diagrams
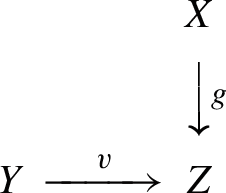
in \({\mathbb {S}_{{\textbf{e}}}}\), belong to \({\mathbb {S}_{{\textbf{e}}}}\).
-
(v)
Every morphism \(f:X\longrightarrow Y\) in \({\mathbb {S}_{{\textbf{e}}}}\) admits in \({\mathbb {S}_{{\textbf{e}}}}\) a Nagata compactification. For us a Nagata compactification is a 2-isomorphism \(pu\longrightarrow f\), where u, p are composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{u}}\overline{X}{\mathop {\longrightarrow }\limits ^{p}}Y\), where u is a dominant, flat monomorphism and p of finite type and universally quasi-proper (for noetherian algebraic spaces the condition on p means that it is proper).
Remark 1.2
For the non-expert on stacks: if your major focus is the case of schemes or algebraic spaces, then all noetherian algebraic spaces satisfy the hypotheses on the objects. The only hypothesis on the morphisms which might be tricky is the existence of Nagata compactifications: it is known for morphisms of finite type of algebraic spaces, and in the case of schemes one can even allow morphisms essentially of finite type.
In the case of more general stacks, most of the hypotheses are very mild. There is the question of the existence of Nagata compactifications, it is still open how generally they exist, see below for what is known. But an important restriction is that the 1-morphisms are assumed concentrated.
Let G be a finite group, for example \({{\mathbb {Z}}}/p\) where p is a prime number, and let k be a field of characteristic p. If BG is the classifying stack, then the morphism \(f:BG\longrightarrow {\textrm{Spec}(k)}\) provides an example of a non-concentrated morphism of Deligne–Mumford stacks. In this case, there are equivalences \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(k)}\big )={{\textbf{D}}}(k)\) and \({{\textbf{D}}_{\textbf{qc}}}(BG)={{\textbf{D}}}(kG)\), and under these equivalences the functor \(\textbf{R}f_*\) identifies with \({{\textrm{RHom}}}^{}_{kG}(k,-)\). It is known not to respect coproducts, hence there is no right adjoint \(f^\times \). This makes it a challenge to extend Grothendieck duality to such f’s. There are non-concentrated f’s out there and, as presented below, the theory cannot possibly work for them.
The class of concentrated morphisms was designed to exclude such pathologies. A morphism \(g:X\longrightarrow Y\) is concentrated if \(\textbf{R}f_*\) is uniformly bounded above for all pullbacks f of g. That is: there is an integer n so that, for all pullbacks f of g, we have \(\textbf{R}f_*{{\textbf{D}}_{\textbf{qc}}}^{\le 0}\subset {{\textbf{D}}_{\textbf{qc}}}^{\le n}\). This recent notion was defined by Hall and Rydh [17, Definition 2.4], and their article goes on to show (among other things) that for concentrated morphisms many nice properties hold. To the extent that we are able to state our results in the generality of algebraic stacks (rather than algebraic spaces), this article hinges on very recent work about algebraic stacks—we depend heavily on the machinery developed in [17].
Example 1.3
The following are examples of \({\mathbb {S}_{{\textbf{e}}}}\)’s as in Notation 1.1:
-
(i)
\({\mathbb {S}_{{\textbf{e}}}}\) could be the category whose objects are noetherian schemes, and whose morphisms are separated maps essentially of finite type. The fact that any morphism in this \({\mathbb {S}_{{\textbf{e}}}}\) has a Nagata compactification is due to Nayak [29, Theorem 3.6], although in the special case where f is of finite type this is the old theorem of Nagata discussed in the first paragraph of the Introduction. See Nagata [28] for the original proof or Conrad [10] for a more modern treatment, following Deligne.
-
(ii)
\({\mathbb {S}_{{\textbf{e}}}}\) could be the category whose objects are noetherian algebraic spaces, and whose morphisms are separated maps of finite type. The existence of Nagata compactifications for this \({\mathbb {S}_{{\textbf{e}}}}\) is the main theorem of Conrad, Lieblich and Olsson [11], although the special case of algebraic spaces of finite type over an excellent scheme may essentially be found in Raoult’s thesis (1974, unpublished), with sketches in his articles [34, 35].
-
(iii)
We may take for \({\mathbb {S}_{{\textbf{e}}}}\) the 2-category whose objects are noetherian Deligne–Mumford \({{\mathbb {Q}}}\)-stacks, and whose 1-morphisms are those maps which are separated and of finite type. The proof of the existence of Nagata compactifications for such maps may be found in Rydh’s unpublished paper [37], available on the author’s web page.
-
(iv)
\({\mathbb {S}_{{\textbf{e}}}}\) could be the 2-category whose objects are noetherian stacks with quasi-finite and separated diagonal, and whose 1-morphisms are the maps which are separated, of finite type and representable. The proof of the existence of Nagata compactifications is again in Rydh’s unpublished paper [37]. All representable maps are concentrated. The existence of an étale map \(\overline{X}\longrightarrow X\) with \(\overline{X}\) satisfying the resolution property follows from Rydh [38, Theorem 7.2(iii)].
Remark 1.4
There are other recent results giving Nagata compactifications for morphisms of stacks. The first such theorem was Kresch [23, Theorem 5.3], but Rydh [37, Theorem F] is more general, we have already met the \({\mathbb {S}_{{\textbf{e}}}}\) it produces in Example 1.3(iii). There is also a result of Edidin, but for us the problem is that in the factorization \(f=pu\) the p is not in general concentrated. Edidin’s result is unpublished, but the proof may be found in Rydh’s survey article [36], which is available on the author’s web page.
Rydh’s methods allow him to compactify certain maps even without the characteristic zero hypothesis. However, the current version of Rydh [37] is undergoing revision and the correct, precise statement will hopefully appear in a future manuscript.
Remark 1.5
We have already discussed the importance of the hypothesis that the morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) must be concentrated. Remember also that they are assumed separated: I’m not sure how inescapable this is, but if there is a theory that can handle non-separated morphisms, then it must somehow take care of pathologies like Example A.2.
Since morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) are assumed concentrated and separated the following proposition becomes relevant. The author thanks David Rydh for pointing this out and providing the proof.
Proposition 1.6
Any separated and concentrated morphism \(f:X\longrightarrow Y\), of noetherian algebraic stacks, has relatively tame stabilizers. In the terminology of Abramovich, Olsson and Vistoli [1], any such f is a relatively tame Artin stack.
Proof
The question is local in Y so we can assume that Y is affine. Separated implies that the stabilizers of X are proper. For X to be concentrated, it is necessary that BG is concentrated for every stabilizer G, see Hall and Rydh [16, Theorem C, 1\(\Longrightarrow \)2]. This rules out non-finite G, as BA is never concentrated if A is an abelian variety, see [16, Theorem B or Proposition 1.5]. For finite G, we have that BG is concentrated iff G is linearly reductive by [16, Theorem B or Theorem 1.2].
Conversely: if all stabilizer groups of X are finite and linearly reductive, then X is concentrated; see [16, Theorem 2.1(2)]. \(\square \)
In this article, we will define \(f^!\) on the unbounded derived category. For this, we prove a technical refinement of Lemma 0.1, which will be our replacement for the base-change theorem. Again we do not state the most general version.
Theorem 1.7
Suppose we are given a diagram, where the objects satisfy the restrictions of Notation 1.1

Assume that the square is 2-cartesian, the map g is concentrated, of finite type and universally quasi-proper, the map v is flat, and the image of \(u'\) is contained in the set on which f is of finite Tor-dimension. Let \({\textbf{L}}{u'}^*:{{\textbf{D}}_{\textbf{qc}}}(W)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(U)\), \(u^*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\), \(v^*:{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\), \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\) and \(g^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) be the usual pullback maps but in the unbounded derived category. If \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is the base-change map, then \({\textbf{L}}{u'}^*\Phi :{\textbf{L}}{u'}^* u^*g^\times \longrightarrow {\textbf{L}}{u'}^* f^\times v^*\) is an isomorphism. Furthermore, the isomorphic functors \({\textbf{L}}{u'}^* u^*g^\times \cong {\textbf{L}}{u'}^* f^\times v^*\) respect coproducts.
Once we have this theorem, we can make deductions. The next theorem will give a list of formal consequences. It follows that any \({\mathbb {S}_{{\textbf{e}}}}\), satisfying the conditions of Notation 1.1, also satisfies all the conclusions of Theorem 1.8. The short summary is that we will construct on \({\mathbb {S}_{{\textbf{e}}}}\) a structure, some 2-functors and natural transformations among them, see Theorem 1.8 (i)–(vii). To fix ideas, we make the blanket assumption that all our 2-functors and natural transformations strictly respect identities. After introducing the players, the 2-functors and natural transformations, comes a long list of compatibility properties which our structure satisfies. After stating the theorem, most of the remainder of the introduction will use the compatibility properties in Theorem 1.8 to show that the structure is unique up to canonical isomorphism. The end of the introduction will mention a couple of applications.
Theorem 1.8
Let the 2-category \({\mathbb {S}_{{\textbf{e}}}}\) be as above, and let \(\mathbb {T}\textrm{ri}\) be the 2-category of triangulated categories. There are three contravariant 2-functors \({\mathbb {S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\) which we will denote \((-)^*\), \((-)^\times \) and \((-)^!\). The formulas are
-
(i)
On objects: for any object \(X\in {\mathbb {S}_{{\textbf{e}}}}\) we have \(X^*=X^\times =X^!={{\textbf{D}}_{\textbf{qc}}}(X)\). We emphasize: on objects the three 2-functors are identical and unsurprising, all three send an object X to \({{\textbf{D}}_{\textbf{qc}}}(X)\). It is what they do to 1-morphisms and 2-morphisms that distinguishes them.
-
(ii)
On 1-morphisms: for a 1-morphism \(f:X\longrightarrow Y\) in \({\mathbb {S}_{{\textbf{e}}}}\) our \(f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is the usual derived pullback \({\textbf{L}}f^*\), our \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is the usual \(f^\times \) [i.e. the right adjoint of the right adjoint of \(f^*\)], and our \(f^!:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is a new functor (at least new in this generality).
The 2-functors \((-)^*\) and \((-)^\times \) are pseudofunctorial, meaning that for composable morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}\) we have isomorphisms \(\tau (f,g):(gf)^*\longrightarrow f^*g^*\) and \(\delta (f,g):(gf)^\times \longrightarrow f^\times g^\times \), but the 2-functor \((-)^!\) is only oplax, we just have a natural map \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\), it need not be an isomorphism in general.
These are the 2-functors in the theory, now for the natural transformations. We begin with the straightforward ones:
-
(iii)
There is an oplax natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\).
-
(iv)
The 2-functor \((-)^*\) is a premonoid, there is a pseudonatural transformation \(\mu :(-)^*\times (-)^*\longrightarrow (-)^*\) satisfying an obvious associativity property.
The formalism of 2-functors which are premonoids is treated extensively and in glorious generality in the category-theory literature. The reader might wish to look (for example) at Chikhladze, Lack and Street [9]; the modern terminology for our premonoids is monoidales. In this article, we give a minimal discussion in Sects. 12 and 13, with only the results we absolutely need. For the Introduction, suffice it to say that the natural transformation \(\mu \) takes the object \(X\in {\mathbb {S}_{{\textbf{e}}}}\) to the usual tensor product functor \(\mu _X^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). To say that this is part of a pseudonatural transformation is just a concise way of packaging the usual information that, for each 1-morphism \(f\in {\mathbb {S}_{{\textbf{e}}}}\), the functor \(f^*\) is strong monoidal and this strong monoidal structure is compatible with composition.
-
(v)
The functors \((-)^\times \) and \((-)^!\) are oplax modules over \((-)^*\). That is we have oplax natural transformations \(\chi :(-)^*\times (-)^\times \longrightarrow (-)^\times \) and \(\sigma :(-)^*\times (-)^!\longrightarrow (-)^!\) satisfying the obvious associativity property.
Once again, there is considerable category-theoretic literature on functors acted on by monoidales (our premonoids), see for example Day and Street [12] or Lack [24]. The usual setting is infinitely more general than ours, we will come back to this in Remark 12.10. In the literature, the current name for our modules is actegories. In this article, our treatment is minimal and very restrictive, narrowly tailored to the application we have in mind—see §12 for our formalism. Part of our definition, of a module over a 2-functor which is a premonoid, insists that on objects the natural transformations coincide. That is, if \(X\in {\mathbb {S}_{{\textbf{e}}}}\) is an object, then \(\chi (X):X^*\times X^\times \longrightarrow X^\times \) and \(\sigma (X):X^*\times X^!\longrightarrow X^!\) are also just the tensor-product functor \(\mu _X^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). More detail is provided in §12, for the Introduction, let this suffice.
Back to the Theorem: there are some more natural transformations, but to define them, we need to introduce the 2-categories \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) and \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). The 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) are the objects of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), and the flat 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) are the objects of \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). The 1-morphisms, in both \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) and \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), are the 2-cartesian squares in \({\mathbb {S}_{{\textbf{e}}}}\)

with flat horizontal maps. The difference is that in \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) we view \((\diamondsuit )\) as a morphism \(f\longrightarrow g\), while in \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), it is a morphism \(u\longrightarrow v\). On both \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) and \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), there are projection 2-functors \(p_1^{}\) and \(p_2^{}\) to \({\mathbb {S}_{{\textbf{e}}}}\), taking an object \(f:X\longrightarrow Y\) in either \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) or \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to \(p_1^{}(f)=X\) and \(p_2^{}(f)=Y\). Consider the 2-functors

and

Now, we are ready for the remaining natural transformations.
-
(vi)
On the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\): there are three lax natural transformations \(\tau ,\Phi ,\theta :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\). Of them \(\tau \) is pseudonatural.
-
(vii)
On the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\): there is a pseudonatural transformation \(\tau :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\), and oplax natural transformations \(\Phi :(-)^\times \circ p_2^{}\longrightarrow (-)^\times \circ p_1^{}\) and \(\theta :(-)^!\circ p_2^{}\longrightarrow (-)^!\circ p_1^{}\).
These are the 2-functors and natural transformations, now it is time for the relations among them. Perhaps we should begin with (vi) and (vii), to explain what might look like ambiguous notation: on the face of it \(\tau \), \(\theta \) and \(\Phi \) have different meanings, depending on whether the input category is \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) or \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\).
On objects: in the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), the natural transformations \(\tau \), \(\Phi \) and \(\theta \) all take an object \(u:W\longrightarrow X\) to \(\tau (u)=\Phi (u)=\theta (u)=u^*\). In the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the object \(f:W\longrightarrow Y\) maps under \(\tau \) to \(\tau (f)=f^*\), under \(\Phi \) to \(\Phi (f)=f^\times \), while \(\theta \) takes it to \(\theta (f)=f^!\).
The 1-morphisms, in both \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) and \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), are 2-cartesian squares \((\diamondsuit )\) as above. And the naturality requires us to provide 2-morphisms. If we view \((\diamondsuit )\) as a morphism \((\diamondsuit ):f\longrightarrow g\) in \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the natural transformation \(\Phi \) must provide a 2-morphism comparing \(\Phi (f)\big [p_2^{}(\diamondsuit )\big ]^*\) with \(\big [p_1^{}(\diamondsuit )\big ]^*\Phi (g)\) [in a 1-category they would just be equal]. The direction we choose is lax, the 2-morphism goes in the direction \(\Phi (\diamondsuit ):\big [p_1^{}(\diamondsuit )\big ]^*\Phi (g)\longrightarrow \Phi (f)\big [p_2^{}(\diamondsuit )\big ]^*\), and is nothing other than the usual base-change map \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\). Similarly, the natural transformation \(\tau \) must give us a map \(\tau (\diamondsuit ):\big [p_1^{}(\diamondsuit )\big ]^*\tau (g)\longrightarrow \tau (f)\big [p_2^{}(\diamondsuit )\big ]^*\); we choose the canonical isomorphism \(\tau (\diamondsuit )=(\diamondsuit )^*:u^*g^*\longrightarrow f^*v^*\). The fact that \(\tau (\diamondsuit )\) is an isomorphism qualifies \(\tau \) to be pseudonatural, in the case of \(\Phi \) there is a direction.
Of course \((\diamondsuit )\) can also be viewed as a 1-morphism \((\diamondsuit ):u\longrightarrow v\) in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). The natural transformation \(\Phi \) takes the objects \(u,v\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to \(\Phi (u)=u^*\) and \(\Phi (v)=v^*\), and the naturality requires us to provide a comparison 2-morphism between \(\Phi (u)\big [p_2^{}(\diamondsuit )\big ]^\times \) and \(\big [p_1^{}(\diamondsuit )\big ]^\times \Phi (v)\). This time the direction is oplax: the map we choose has the direction \(\Phi (\diamondsuit ):\Phi (u)\big [p_2^{}(\diamondsuit )\big ]^\times \longrightarrow \big [p_1^{}(\diamondsuit )\big ]^\times \Phi (v)\), and the reason for what seems confusing notation is that it is the identical map to the horizontal version, namely \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\). Similarly, \(\tau (\diamondsuit ):\tau (u)\big [p_2^{}(\diamondsuit )\big ]^*\longrightarrow \big [p_1^{}(\diamondsuit )\big ]^*\tau (v)\) is just the isomorphism \(\tau (\diamondsuit )=(\diamondsuit )^*:u^*g^*\longrightarrow f^*v^*\). The assertion that we have natural transformations really comes down to the standard fact that the base-change map is compatible with the concatenation of 2-cartesian squares, both horizontally and vertically, as is the map \((\diamondsuit )^*\).
What is really being asserted is that there is a parallel which works for \((-)^!\). We assert the existence of a 2-morphism \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\), which serves as a lax natural transformation in the case of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) and an oplax natural transformation for \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), that is respects the concatenation of 2-cartesian squares, both vertical and horizontal.
We have explained at length the natural transformations \(\tau \), \(\Phi \) and \(\theta \), and now we come to the other natural transformations and their interplay.
1.8.1
On objects, the oplax natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\) must provide, for every object \(X\in {\mathbb {S}_{{\textbf{e}}}}\), a 1-morphism \(\psi (X):X^\times \longrightarrow X^!\). This map is \(\psi (X)=\textrm{id}:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\).
1.8.2
The natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\) is a homomorphism of \((-)^*\)-modules. That is the square of natural transformations

strictly commutes.
1.8.3
On the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) the natural transformations \(\Phi \) and \(\theta \) are strictly compatible with \(\psi \). That is the following square of natural transformations strictly commutes:

1.8.4
On the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the compatibility of \(\Phi \), \(\theta \) is less strict. If we consider the diagram of 2-functors on \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\)

then the object \(f\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) maps under \(\Phi \) to \(f^\times \) and under \(\theta \) to \(f^!\). The natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\) provides us with a 2-morphism \(\psi (f):f^\times \longrightarrow f^!\) (see Remark 1.11 for details), and the assignment taking the object \(f\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) to the 2-morphism \(\psi (f):f^\times \longrightarrow f^!\) extends to a modification of natural transformations, that is a morphism \(\Phi \longrightarrow \theta \).
1.8.5
On the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), the squares

and

both 2-commute. More precisely: in both cases the composites of the shape \(\llcorner \) take the object \(u:W\longrightarrow X\) in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to \(\mu _W^{}(u^*\times u^*)\), while the composites of the shape \(\urcorner \) take u to \(u^*\mu _X^{}\). The pseudonatural transformation \(\mu :(-)^*\times (-)^*\longrightarrow (-)^*\) gives a 2-isomorphism \(\mu (W,X):\mu _W^{}(u^*\times u^*)\longrightarrow u^*\mu _X^{}\), and we assert that this extends to modifications making both squares 2-commute.
We leave to the reader the analogous statement about \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\).
We have had a string of results telling us that pairs of composites of our natural transformations agree, or maybe only agree up to modification. The remaining results are conditions under which these maps induce isomorphisms.
1.8.6
Let \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) be a pair of composable 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\). The map \(\rho (f,g):{(gf)}^!\longrightarrow f^!g^!\), which is part of the structure of the oplax 2-functor \((-)^!\), is an isomorphism if one of the conditions below holds:
-
(1)
f is of finite Tor-dimension.
-
(2)
g is of finite type and universally quasi-proper.
-
(3)
The composite gf is of finite type and universally quasi-proper.
-
(4)
We restrict to the subcategory \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
1.8.7
Let \(f:X\longrightarrow Y\) be a 1-morphism in \({\mathbb {S}_{{\textbf{e}}}}\). The map \(\psi (f):f^\times \longrightarrow f^!\) is an isomorphism if f is of finite type and universally quasi-proper.
1.8.8
Let \((\diamondsuit )\) be the 2-cartesian square pictured between (v) and (vi) above. The base-change map \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\) is an isomorphism if one of the following holds:
-
(1)
f is of finite Tor-dimension. More generally if \(u':U\longrightarrow W\) is a map whose image lies in the subset of \(\,W\) on which f is of finite Tor-dimension, then \({u'}^*\theta (\diamondsuit ):{u'}^*u^*g^!\longrightarrow {u'}^*f^!v^*\) is an isomorphism.
-
(2)
We restrict to the subcategory \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
1.8.9
Let \(f:X\longrightarrow Y\) be a 1-morphism in \({\mathbb {S}_{{\textbf{e}}}}\) and let E, F be objects in \({{\textbf{D}}_{\textbf{qc}}}(Y)\). Then, \(\chi (f):\mu _X^{}(f^*\times f^\times )\longrightarrow f^\times \mu _Y^{}\) and \(\sigma (f):\mu _X^{}(f^*\times f^!)\longrightarrow f^!\mu _Y^{}\) are both natural transformation of functors \({{\textbf{D}}_{\textbf{qc}}}(Y)\times {{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\), and we can evaluate them at the pair (E, F). Let us write \(\chi (f,E,F):f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\) and \(\sigma (f,E,F):f^*E\otimes f^! F\longrightarrow f^!(E\otimes F)\) for the resulting 1-morphisms in the category \({{\textbf{D}}_{\textbf{qc}}}(X)\). Then,
-
(1)
Both \(\chi (f,E,F)\) and \(\sigma (f,E,F)\) are isomorphisms if E is a perfect complex.
-
(2)
\(\sigma (f):\mu _X^{}(f^*\times f^!)\longrightarrow f^!\mu _Y^{}\) is an isomorphism as long as f is of finite Tor-dimension. That is: if f is of finite Tor-dimension, then \(\sigma (f)\) evaluates to an isomorphism on every pair of objects \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Y)\). More generally: if \(u:W\longrightarrow X\) is a flat morphism so that fu is of finite Tor-dimension, then \(u^*\sigma (f):u^*\mu _X^{}(f^*\times f^!)\longrightarrow u^*f^!\mu _Y^{}\) is an isomorphism.
1.8.10
Let the notation be as in 1.8.9. The morphism \(\chi (f,E,F):f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\) corresponds, under the adjunction \(\textbf{R}f_*\dashv f^\times \), to a morphism \(\xi (f,E,F):\textbf{R}f_*(f^*E\otimes f^\times F)\longrightarrow E\otimes F\). The map \(\xi (f,E,F)\) is just the composite

where the isomorphism is by the projection formula and the map \(\varepsilon :\textbf{R}f_*f^\times \longrightarrow \textrm{id}\) is the counit of adjunction.
It might help a little if we work out, explicitly, what some of the 2-categorical formalism says. We begin with
Remark 1.9
We made the blanket assumption that our 2-functors strictly respect identities. Hence, \(\textrm{id}^*=\textrm{id}^\times =\textrm{id}^!=\textrm{id}\) and the 2-morphisms

are all identities. We also made the blanket assumption that our natural transformations strictly respect identities. The 2-cartesian squares

can be viewed as identity morphisms \((\clubsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) and \((\diamondsuit )\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), and we learn that

are all identities. Similarly, for the natural transformation \(\psi \): the 2-morphism \(\psi (\textrm{id}):\textrm{id}^\times \longrightarrow \textrm{id}^!\) is the identity. The fact that the natural transformations \(\mu :(-)^*\times (-)^*\longrightarrow (-)^*\), \(\chi :(-)^*\times (-)^\times \longrightarrow (-)^\times \) and \(\sigma :(-)^*\times (-)^!\longrightarrow (-)^!\) respect identities comes down to saying that, for any object \(X\in {\mathbb {S}_{{\textbf{e}}}}\) and for the identity map \(\textrm{id}:X\longrightarrow X\), the 2-morphisms

are all identities.
Remark 1.10
In Theorem 1.8(iii), we learned about the existence of an oplax natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\), while in 1.8.1 we were told that, for X an object of \({\mathbb {S}_{{\textbf{e}}}}\), the map \(\psi (X):X^\times \longrightarrow X^!\) is the identity \(\textrm{id}:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). What this means is the following.
Let \(f:X\longrightarrow Y\) be a 1-morphism in \({\mathbb {S}_{{\textbf{e}}}}\). The under the 2-functors \((-)^\times \) and \((-)^!\) it is mapped (respectively) to \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(f^!:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). The natural transformation must provide us with a comparison map between \(f^\times =\psi (X)f^\times \) and \(f^!=f^!\psi (Y)\), and the direction is oplax, the map \(\psi (f)\) goes \(\psi (X)f^\times \longrightarrow f^!\psi (Y)\), or more simply we have a map \(\psi (f):f^\times \longrightarrow f^!\). The assertion that this is a natural transformation includes the statement that \(\psi (f)\) must be compatible with composition in the obvious way.
Since this particular natural transformation is such that \(\psi (X)=\textrm{id}_X^{}\) for every object X, we may also view it as a lax natural transformation \((-)^!\longrightarrow (-)^\times \). If we do this, then the map goes in the direction \(f^\times \psi (Y)\longrightarrow \psi (X)f^!\), that is the lax direction.
Remark 1.11
Let us evaluate the strictly commutative diagram of 1.8.3 at the 1-morphism \((\diamondsuit ):u\longrightarrow v\) in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). The 2-functors
take \((\diamondsuit )\), respectively, to \(g^\times \), \(f^\times \), \(g^!\) and \(f^!\). The natural transformation \(\Phi \) and \(\theta \) both take the object u to the 1-morphism \(u^*\) and the object v to the 1-morphism \(v^*\). And the natural transformation \(\psi \) is the identity on objects. In other words: on objects both composite natural transformations are simple, they take u to \(u^*\) and v to \(v^*\).
The evaluation of the diagram on \((\diamondsuit )\), therefore, becomes

and 1.8.3 asserts that this commutes. The reader can check the \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) version: if we evaluate the 2-commutative diagram of 1.8.4 at the 1-morphism \((\diamondsuit )\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) we end up with the commutative square above. In other words, 1.8.3 and 1.8.4, evaluated at the 1-morphism \((\diamondsuit )\) in either \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) or \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), give rise to identical commutative squares.
Remark 1.12
Let us evaluate the second 2-commutative diagram of 1.8.5 at \((\diamondsuit )\). It yields the commutative diagram

where the maps labeled \(\mu (W,X)\) and \(\mu (Y,Z)\) come from the modification, which we must apply both at the source and at the target. The vertices of the diagram are all functors \({{\textbf{D}}_{\textbf{qc}}}(Z)\times {{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\) and the arrows are all natural transformations. Hence, the top left and bottom right give two functors  and the two composites give natural transformations between them. If we evaluate at an object \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\times {{\textbf{D}}_{\textbf{qc}}}(Z)\) we obtain two morphisms in \({{\textbf{D}}_{\textbf{qc}}}(W)\) which the theorem asserts must be equal. Concretely, this comes down to the commutative diagram
and the two composites give natural transformations between them. If we evaluate at an object \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\times {{\textbf{D}}_{\textbf{qc}}}(Z)\) we obtain two morphisms in \({{\textbf{D}}_{\textbf{qc}}}(W)\) which the theorem asserts must be equal. Concretely, this comes down to the commutative diagram

in the category \({{\textbf{D}}_{\textbf{qc}}}(W)\).
In the next few remarks, we will show how to use the properties listed in Theorem 1.8 to conclude that the functor \(f^!\), the map \(\psi :f^\times \longrightarrow f^!\), the map \(\rho (f,g):{(gf)}^!\longrightarrow f^! g^!\), the base-change map \(\theta (\diamondsuit )\) for a 2-cartesian square \((\diamondsuit )\) and the map \(\sigma :f^*E\otimes f^!F\longrightarrow f^!(E\otimes F)\) are all determined up to unique isomorphism.
Remark 1.13
If \(f:X\longrightarrow Y\) is a flat monomorphism, we can consider the 2-cartesian square

Since \(\textrm{id}:X\longrightarrow X\) is definitely of finite Tor-dimension 1.8.8(1) applies and \(\theta (\diamondsuit ):\textrm{id}^*f^!\longrightarrow \textrm{id}^! f^*\) is an isomorphism. It gives us a canonical isomorphism \(\theta (\diamondsuit ):f^!\longrightarrow f^*\).
Still considering the simple 2-cartesian square \((\diamondsuit )\) above, the general commutative diagram of Remark 1.11 specializes to

From the previous paragraph, we know that \(\theta (\diamondsuit ):f^!\longrightarrow f^*\) is an isomorphism, and now we learn that the map \(\psi (f):f^\times \longrightarrow f^!\) can be computed as the composite

Remark 1.14
Suppose we are given two composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}\), with f a flat monomorphism and g of finite type and universally quasi-proper. Since \((-)^!\) is an oplax 2-functor, we have a map \(\rho (f,g):{(gf)}^!\longrightarrow f^!g^!\), which is an isomorphism by 1.8.6 (1) or (2). By Remark 1.13, the map \( \theta (\diamondsuit ):f^!\longrightarrow f^*\) is an isomorphism, while 1.8.7 tells is that \(\psi (g):g^\times \longrightarrow g^!\) is an isomorphism. Combining these, we obtain a canonical isomorphism

Moreover, because \(\psi :(-)^\times \longrightarrow (-)^!\) is a natural transformation, it respects composition, and we have a commutative square

If we identify \({(gf)}^\times \) with \(f^\times g^\times \) via the canonical isomorphism \(\delta (f,g)\), and identify \({(gf)}^!\) with \(f^*g^\times \) via the isomorphism (1.1) above, then the map \(\psi (gf):{(gf)}^\times \longrightarrow {(gf)}^!\) reduces to \(\Phi (\diamondsuit )g^\times : f^\times g^\times \longrightarrow f^* g^\times \).
Since every morphism in \({\mathbb {S}_{{\textbf{e}}}}\) is 2-isomorphic to a composite gf, with f a flat monomorphism (even dominant) and g of finite type and universally quasi-proper, these computations tell us that Theorem 1.8 gives us no choice on how to define \(h^!\) and \(\psi (h):h^\times \longrightarrow h^!\) for any 1-morphism \(h\in {\mathbb {S}_{{\textbf{e}}}}\).
Remark 1.15
Suppose we are given the 2-cartesian square \((\diamondsuit )\) below

Assume that u and v are flat, and that f and g are of finite type and universally quasi-proper. By Remark 1.11, the square

commutes, but by 1.8.7 the vertical maps are isomorphisms. Hence, for 2-cartesian squares \((\diamondsuit )\), with flat horizontal maps and vertical maps that are of finite type and universally quasi-proper, the base-change map \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\) can be canonically identified with the ordinary base-change map \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\).
Now, suppose we have a 2-cartesian square

where u, v are flat as usual, but where f and g are flat monomorphisms. We may consider the larger diagrams

The squares are still all 2-cartesian, and the diagrams concatenate to isomorphic squares

In other words: in the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) we have a 2-isomorphism \((\heartsuit )\circ (\spadesuit )\cong (\bullet )\cong (\#)\circ (\clubsuit )\). The natural transformation \(\theta \) respects composition, allowing us to compute \(\theta (\bullet )\) as two different composites. This yields a commutative diagram

Reading the perimeter of this diagram we see that, up to identifying via the isomorphisms \(\theta (\spadesuit ):f^!\longrightarrow f^*\) and \(\theta (\#):g^!\longrightarrow g^*\), the map \(\theta (\heartsuit )\) is just the canonical isomorphism \(u^*g^*\longrightarrow f^*v^*\).
We have computed the base-change map \(\theta (\diamondsuit )\) in the special cases where f, g are either flat monomorphisms or of finite type and universally quasi-proper. Now, let \((\diamondsuit )\) be arbitrary and factor \(g:X\longrightarrow Z\) up to 2-isomorphism as \(X{\mathop {\longrightarrow }\limits ^{t'}}S{\mathop {\longrightarrow }\limits ^{p'}}Z\), with \(t'\) a dominant, flat monomorphism and \(p'\) of finite type and universally quasi-proper. Pull back to form the 2-cartesian squares

We have just factored the 1-morphism \((\diamondsuit )\), in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), as \((\diamondsuit )\cong (\dagger \dagger )\circ (\dagger )\). Since \(\theta \) is a natural transformation of functors on \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) it respects composition, and we may compute \(\theta (\diamondsuit )\) in terms of \(\theta (\dagger \dagger )\) and \(\theta (\dagger )\). This allows us to compute \(\theta (\diamondsuit )\) for all \((\diamondsuit )\).
Remark 1.16
Suppose we have a 2-cartesian square in \({\mathbb {S}_{{\textbf{e}}}}\)

where u, v are flat monomorphisms. In the following diagrams, all the squares are 2-cartesian:

The concatenation of these two diagrams are 2-isomorphic, namely

and because \(\theta \) is a natural transformation on the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), we now compute \(\theta (\#)\) in two different ways. The reader can check that the following diagram commutes:

In this diagram, \(\rho (u,g)\) is an isomorphism because u is of finite Tor-dimension, and \(\theta (\diamondsuit )\) and \(\theta (\heartsuit )\) are the isomorphisms of Remark 1.13. Up to the isomorphisms in the diagram, we have that \(\rho (f,v)\) agrees with \(\theta (\spadesuit )\).
If f and g are proper, then Remark 1.15 informs us that, up to canonical isomorphism, \(\theta (\spadesuit )\) agrees with the usual base-change map \(\Phi (\spadesuit )\). In [31, Example 6.5], we see that \(\Phi (\spadesuit )\) does not have to be an isomorphism; in the example the stacks are all noetherian, affine schemes, the maps f and g are finite and u, v are dominant open immersions. Hence, \(\rho (f,v)\) need not be an isomorphism in general, and placing further restrictions on the stacks is unlikely to help.
Remark 1.17
If \(f:X\longrightarrow Y\) is a morphism in \({\mathbb {S}_{{\textbf{e}}}}\), then the subset of X on which f is of finite Tor-dimension is open. I am not aware of a place in the literature where this is stated explicitly, even for schemes—but the reader can find a proof in Corollary 5.15.
Remark 1.18
Suppose we are given two composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}\). Let \(u:U\longrightarrow X\) be the inclusion of the open subset on which f is of finite Tor-dimension. Then, u and fu are of finite Tor-dimension. Since \((-)^!\) is an oplax 2-functor, the square below commutes

In this square, \(\rho (fu,g)\), \(\rho (u,gf)\) and \(\rho (u,f)\) must be isomorphisms by 1.8.3, and hence \(u^!\rho (f,g)=u^*\rho (f,g)\) is an isomorphism.
More generally, if \(w:W\longrightarrow X\) is a map in \({\mathbb {S}_{{\textbf{e}}}}\) whose image is contained in the set on which f is of finite Tor-dimension, then w must factor through u, and \({\textbf{L}}w^*\rho (f,g)\) will also be an isomorphism.
Remark 1.19
Suppose \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) are composable 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\). Suppose further that we are given a 2-commutative diagram in \({\mathbb {S}_{{\textbf{e}}}}\)

where the horizontal maps are all dominant, flat monomorphisms, the vertical maps are all of finite type and universally quasi-proper, the square is 2-cartesian and \(p'u'\cong f\), \(qv\cong g\). Since \((-)^!\) is an oplax 2-functor, we obtain a commutative diagram

By 1.8.6 (1) and (2), the horizontal maps are isomorphisms and, up to these isomorphisms, the map \(\rho (f,g)=\rho (p'u',qv)\) is computed by \({u'}^!\rho (p',v)q^!\). But in the last paragraph of Remark 1.16 we noted that \(\rho (p',v)\) can be computed as the composite

where \(\Phi :u^*p^\times \longrightarrow {p'}^\times {u'}^*\) is the base-change map of the cartesian square in \((\dagger )\). This means that \(\rho (f,g)\) can be expressed as the composite

Thus, as long as we have enough diagrams \((\dagger )\) we can compute the map \(\rho (f,g)\) for every composable \(f,g\in {\mathbb {S}_{{\textbf{e}}}}\). In Lemma 8.13, we produce enough diagrams \((\dagger )\).
Remark 1.20
From 1.8.10, we know the map \(\chi \) explicitly for every f. If we evaluate the strictly commutative square of 1.8.2 at a 1-morphism \(f:X\longrightarrow Y\) in \({\mathbb {S}_{{\textbf{e}}}}\), we obtain the commutative square

If f is of finite type and universally quasi-proper the vertical maps are isomorphisms by 1.8.7, hence we know \(\sigma (f):\mu _X^{}(f^*\times f^!)\longrightarrow f^! \mu _Y^{}\) whenever f is of finite type and universally quasi-proper.
Now, suppose f is a flat monomorphism. We have the 2-cartesian square

which we may view as a 1-morphism \((\diamondsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), and we evaluate the second 2-commutative diagram of 1.8.5 at \((\diamondsuit )\); the reader might wish to refer to Remark 1.12, where this was made a little more explicit. Anyway: we obtain the commutative diagram

Recall that \(\theta (\diamondsuit ):f^!\longrightarrow f^*\) is the isomorphism of Remark 1.13, and we discover that, up to this isomorphism, the map \(\sigma (f):\mu _X^{}(f^*\times f^!)\longrightarrow f^!\mu _Y^{}\) agrees with \(\mu (f):\mu _X^{}(f^*\times f^*)\longrightarrow f^*\mu _Y^{}\).
This means that we know \(\sigma (f)\) if f is either a flat monomorphism or of finite type and universally quasi-proper. But every morphism in \({\mathbb {S}_{{\textbf{e}}}}\) is 2-isomorphic to a composite gf, with g of finite type and universally quasi-proper and f a (dominant) flat monomorphism. Since \(\sigma \) is a natural transformation of 2-functors it respects composition, and if we write out explicitly what this means we discover that we can compute \(\sigma (gf)\) in terms of \(\sigma (f)\) and \(\sigma (g)\). There is a formula for \(\sigma (gf)\) which we leave to the reader.
This concludes the series of remarks in which we showed that the compatibilities of 1.8.1 through 1.8.10 force upon us a canonically unique choice for each of the data specified in Theorem 1.8 (i)–(vii). The difficulty, which will occupy us for most of the paper, is to show that the recipe that is forced on us works. This means the following.
In Remark 1.14, we learned that if we choose a Nagata compactification for a 1-morphism \(f\in {\mathbb {S}_{{\textbf{e}}}}\), meaning we write the map f as \(f\cong pu\) with u a dominant, flat monomorphism and p of finite type and universally quasi-proper, then the composite 1.1 is an isomorphism which we will write \(\varphi (f,pu):f^!\longrightarrow u^*p^\times \). This means that, if \(f\cong pu\cong qv\) are two Nagata compactifications of f, then we have isomorphisms

where \(\varphi (pu,qv)\) is defined to be the composite. It is automatic from this definition that the \(\varphi (pu,qv)\) must compose correctly: given three factorizations \(f\cong pu\cong qv\cong rw\) we must have \(\varphi (qv,rw)\varphi (pu,qv)=\varphi (pu,rw)\).
What we will do in this paper is introduce a category of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\), whose objects are morphisms \(f:X\longrightarrow Y\) together with Nagata compactifications \(pu\longrightarrow f\). There is a functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\) which forgets the Nagata compactification, and the main point is that this functor is a groupoid completion. It has the property that any functor from \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) to a groupoid factors uniquely through F, and any natural transformation of functors that factor through F must factor through F. In order to define \((-)^!\) on the 1-category \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\), it suffices to produce a functor \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\longrightarrow \mathbb {T}\textrm{ri}\big [{{\textbf{D}}_{\textbf{qc}}}(Y),{{\textbf{D}}_{\textbf{qc}}}(X)\big ]\) which takes all morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) to isomorphisms in \(\mathbb {T}\textrm{ri}\). And thereafter all our constructions will be made on categories like \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\), and will be shown to factor through F by the universal property.
This article is foundational, and one of the points is that the results could be used as a starting point for developing the theory of the functor \((-)^!\). Therefore, the body of the article, as well as the entire Introduction up to this point, goes to some lengths to avoid using any results in the literature on Grothendieck duality. In what little remains of the Introduction this will change: we are about to mention an application and compare to other results in the literature, and for this there is no virtue in being self-contained.
Remark 1.21
We mention in passing one application. Suppose \(g:Y\longrightarrow Z\) is a 1-morphism in \({\mathbb {S}_{{\textbf{e}}}}\) of finite type and universally quasi-proper, \(f:X\longrightarrow Y\) is flat morphism of stacks, and \(gf:X\longrightarrow Z\) is of finite Tor-dimension. Then, \(f^*g^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is a bounded functor. This means there exist integers A and B so that

where  means the ith cohomology sheaf of the complex E. In Hartshorne’s old terminology of [18], bounded functors would be called “way out left” and “way out right”.
means the ith cohomology sheaf of the complex E. In Hartshorne’s old terminology of [18], bounded functors would be called “way out left” and “way out right”.
Now, \(f^*\) is bounded and \(g^\times \) is always bounded below, meaning the second implication is standard. We have to prove \(f^*g^\times \) bounded above. Note that the image of f must be contained in the open subset \(U\subset Y\) on which g is of finite Tor-dimension, and hence f factors through the open immersion \(U\hookrightarrow Y\). We may, therefore, confine ourselves to the case where f is an open immersion, in particular f is a morphism in \({\mathbb {S}_{{\textbf{e}}}}\). But then the map \(\rho (f,g):{(gf)}^!\longrightarrow f^!g^!\cong f^*g^\times \) is an isomorphism (for example by 1.8.6(2)), and we are reduced to proving that \(h^!\) is bounded above for \(h:X\longrightarrow Z\) a 1-morphism in \({\mathbb {S}_{{\textbf{e}}}}\) of finite type and of finite Tor-dimension. Choose an affine scheme Y, a faithfully flat map \(v:Y\longrightarrow Z\) and form the pullback

The map h is of finite Tor-dimension, hence so is its flat base-change \(i:W\longrightarrow Y\). By 1.8.8(1), the map \(\theta :u^*h^!\longrightarrow i^!v^*\) is an isomorphism. As u is faithfully flat it suffices to prove that \(u^*h^!\cong i^!v^*\) is bounded above, and since v is faithfully flat \(v^*\) is bounded, and it suffices to prove that \(i^!\) is bounded above. We are reduced to the case where Z is an affine scheme.
Now, choose an affine scheme W and a smooth, surjective map \(\ell :W\longrightarrow X\). Since \(\ell \) is flat 1.8.6(1) tells us that \(\rho (\ell ,h):(h\ell )^!\longrightarrow \ell ^!h^!\) is an isomorphism. We wish to show that \(h^!\) is bounded, but \(\ell ^!(-)=\omega \otimes \ell ^*(-)\) where \(\omega \) is some shift of the relative canonical bundle. Therefore, \(h^!\) will be bounded if and only if \(\ell ^!h^!\cong (h\ell )^!\) is—we are reduced to the case where \(h:X\longrightarrow Z\) is a morphism of affine schemes, still of finite Tor-dimension and of finite type.
The map h is quasiprojective, meaning it factors as \(X{\mathop {\longrightarrow }\limits ^{j}}{{\mathbb {P}}}_Z^n{\mathop {\longrightarrow }\limits ^{\pi }}Z\) with j a locally closed immersion. Factor j as \(X{\mathop {\longrightarrow }\limits ^{i}}V{\mathop {\longrightarrow }\limits ^{v}}{{\mathbb {P}}}_Z^n\) with v an open immersion and i a closed immersion. The maps v and \(\pi \) are both smooth, and as \(h=\pi vi\) is of finite Tor-dimension it follows that i is a proper map of finite Tor-dimension. Since all three maps are of finite Tor-dimension, we have that \(f^!=i^!v^!\pi ^!\), and \(i^!=i^\times \) and \(\pi ^!=\pi ^\times \) are bounded above by [26, Corollary 4.3.1] while \(v^!=v^*\) is obviously bounded. This completes the proof of our claim.
Thus, our techniques allow us to extend to unbounded derived categories of stacks the boundedness results of Lipman [25, Theorem 4.9.4]. The reader is also referred to Nayak [29, Theorem 5.9], who improved on Lipman’s results by relaxing Lipman’s hypothesis that the maps must be of finite type. Lipman’s book [25] studies the boundedness of the functor \(f^!\) extensively. The boundedness of \(f^!\) can be seen to be equivalent to 1.8.9(2), and the reader might wish to look at Lipman [25, Exercise 4.7.6(f)] for further equivalent statements. Also interesting is that the boundedness of \(f^!\), for f of finite Tor-dimension, can be used to prove Theorem 1.7. As it stands, this would be circular since we used Theorem 1.7 to prove the boundedness of \(f^!\); but it is possible to give a direct proof of the boundedness, and hence a second proof of Theorem 1.7. We hope to include this in a subsequent paper.
It should be noted that the direct proof I have of the boundedness of \(f^!\) still hinges on Lemma 5.19; somehow the key to everything is Thomason’s localization theorem.
Remark 1.22
If we restrict to the 2-subcategory \(\mathbb {S}_{{\textbf{f}}}\subset {\mathbb {S}_{{\textbf{e}}}}\) where the morphisms are the maps of finite Tor-dimension, then the theory simplifies, and \((-)^!\) becomes a pseudofunctor. On maps of finite Tor-dimension \(\rho (f,g)\) is an isomorphism.
If we restrict further to the 1-subcategory \(S_{{\textbf{f}}}\subset \mathbb {S}_{{\textbf{f}}} \) where the objects are schemes, one can also proceed as in Alonso, Jeremías and Lipman [2, Section 5.7]: they defined \(f^!E\) to be  , which they could do without the results of this article because
, which they could do without the results of this article because  belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Y)\) and the classical theory (for schemes) defined \(f^!\) on \({{\textbf{D}}^+_{\textrm{qc}}}(Y)\). By 1.8.9 the map
belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Y)\) and the classical theory (for schemes) defined \(f^!\) on \({{\textbf{D}}^+_{\textrm{qc}}}(Y)\). By 1.8.9 the map  is an isomorphism for \(f\in \mathbb {S}_{{\textbf{f}}} \), and hence their functor agrees on \(S_{{\textbf{f}}} \) with the one in this article. Their methods allowed them to produce an isomorphism \({(gf)}^!\longrightarrow f^!g^!\) when f, g are of finite Tor-dimension, and to prove associativity as well as a base-change theorem.
is an isomorphism for \(f\in \mathbb {S}_{{\textbf{f}}} \), and hence their functor agrees on \(S_{{\textbf{f}}} \) with the one in this article. Their methods allowed them to produce an isomorphism \({(gf)}^!\longrightarrow f^!g^!\) when f, g are of finite Tor-dimension, and to prove associativity as well as a base-change theorem.
The recent work of Avramov, Iyengar, Lipman and Nayak [3, 4] makes it especially interesting to understand base-change for morphisms of finite Tor-dimension. In the articles [3, 4], the authors find new formulas for \(f^!\), which do not involve compactifications, but are only valid for morphisms of finite Tor-dimension. It was in trying to understand this recent work that I came to the theorems in this article. Since this article is already very long, the discussion of the relation with the theory of [3, 4] is left to [33].
3 Notation
All our algebraic stacks will be assumed quasi-compact and quasi-separated, Furthermore: for most of the article, we will assume our stacks noetherian—the reason for this restriction will be discussed in Example A.1, as well as in Remarks 6.1 and 6.11.
In this entire article, we work only in derived categories of the form \({{\textbf{D}}_{\textbf{qc}}}(X)\) for algebraic stacks X. Therefore, all functors we consider will be assumed derived: if \(f:X\longrightarrow Y\) is a morphism of stacks we will always write \(f^*\) for \({\textbf{L}}f^*\), \(f_*\) will stand for \(\textbf{R}f_*\), the tensor \(\otimes \) will mean derived tensor \(\otimes ^{\textbf{L}}_{}\), and  will be the right adjoint of \(\otimes \), the internal derived Hom of \({{\textbf{D}}_{\textbf{qc}}}(X)\). We distinguish the internal
will be the right adjoint of \(\otimes \), the internal derived Hom of \({{\textbf{D}}_{\textbf{qc}}}(X)\). We distinguish the internal  from \({{\textrm{Hom}}}\), which takes its values in complexes of abelian groups. In more traditional notation, our
from \({{\textrm{Hom}}}\), which takes its values in complexes of abelian groups. In more traditional notation, our  would be written
would be written  Footnote 3 and our \({{\textrm{Hom}}}\) would be the usual \({{\textrm{RHom}}}\). The reader will note that our convention differs from much of the classical literature, we never leave the category \({{\textbf{D}}_{\textbf{qc}}}(X)\)—one facet is that our
Footnote 3 and our \({{\textrm{Hom}}}\) would be the usual \({{\textrm{RHom}}}\). The reader will note that our convention differs from much of the classical literature, we never leave the category \({{\textbf{D}}_{\textbf{qc}}}(X)\)—one facet is that our  is rarely local. On page 26, we present an argument showing that, if P is a perfect complex and R is arbitrary, then
is rarely local. On page 26, we present an argument showing that, if P is a perfect complex and R is arbitrary, then  is isomorphic to \(R\otimes P^\vee \) for some \(P^\vee \). From the nature of \(P^\vee \) it then follows that
is isomorphic to \(R\otimes P^\vee \) for some \(P^\vee \). From the nature of \(P^\vee \) it then follows that  has to be local. The only other useful theorem I know, providing a situation in which our
has to be local. The only other useful theorem I know, providing a situation in which our  can be proved local, is when P is pseudo-coherent and R is bounded below—this is an old result of Illusie [20, Proposition 3.7], we will meet it again in the proof of Lemma 5.2.
can be proved local, is when P is pseudo-coherent and R is bounded below—this is an old result of Illusie [20, Proposition 3.7], we will meet it again in the proof of Lemma 5.2.
Suppose \(f:X\longrightarrow Y\) is a concentrated morphism of stacks, as in [17, Definition 2.4]. Then, [17, Theorem 2.6(3)] tells us that \(f_*:{{\textbf{D}}_{\textbf{qc}}}(X) \longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\) respects coproducts, while from [15, Theorem A.3], we know that \({{\textbf{D}}_{\textbf{qc}}}(X)\) is a well generated triangulated category—hence \({{\textbf{D}}_{\textbf{qc}}}(X)\) satisfies Brown representability by [32, Proposition 8.4.2] and \(f_*\) has a right adjoint by [32, Theorem 8.4.4]. The right adjoint of \(f_*:{{\textbf{D}}_{\textbf{qc}}}(X) \longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\) will henceforth be denoted \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y) \longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\).
Still assuming that the map f is concentrated: from [17, Definition 2.4] it follows that there exists an integer \(\ell \) with \(f_*{{\textbf{D}}_{\textbf{qc}}}(X)^{\le n}\subset {{\textbf{D}}_{\textbf{qc}}}(Y)^{\le n+\ell }\). Hence, the adjoint \(f^\times \) takes \(\big ( {{\textbf{D}}_{\textbf{qc}}}(Y)^{\le n+\ell }\big )^\perp \) to \(\big ( {{\textbf{D}}_{\textbf{qc}}}(X)^{\le n}\big )^\perp \); in other words \(f^\times {{\textbf{D}}_{\textbf{qc}}}(Y)^{> n+\ell }\subset {{\textbf{D}}_{\textbf{qc}}}(X)^{> n}\). Consequently \(f^\times {{\textbf{D}}^+_{\textrm{qc}}}(Y)\subset {{\textbf{D}}^+_{\textrm{qc}}}(X)\).
Finally: the category-theoretic conventions are as in MacLane’s book [27]. If  ,
,  and
and  are functors, and \(\varphi :G\longrightarrow G'\) is a natural transformation, then \(H\varphi F\) is the obvious natural transformation \(HGF\longrightarrow HG'F\). That is, the natural transformation \(H\varphi F\) sends an object
are functors, and \(\varphi :G\longrightarrow G'\) is a natural transformation, then \(H\varphi F\) is the obvious natural transformation \(HGF\longrightarrow HG'F\). That is, the natural transformation \(H\varphi F\) sends an object  to the morphism \(H\varphi _{Fa}^{}:HGFa\longrightarrow HG'Fa\), where
to the morphism \(H\varphi _{Fa}^{}:HGFa\longrightarrow HG'Fa\), where  is the image of the object
is the image of the object  under
under  , the morphism \(\varphi _{Fa}^{}:GFa\longrightarrow G'Fa\) is where the object
, the morphism \(\varphi _{Fa}^{}:GFa\longrightarrow G'Fa\) is where the object  goes under the natural transformation \(\varphi :G\longrightarrow G'\), and \(H\varphi _{Fa}^{}\) is the image of this morphism under H.
goes under the natural transformation \(\varphi :G\longrightarrow G'\), and \(H\varphi _{Fa}^{}\) is the image of this morphism under H.
4 A Review of Thomason’s Localization Theorem
The idea that working in derived categories can be facilitated by looking at objects satisfying finiteness properties is old—it goes back to SGA6, where there are several articles by Illusie introducing perfect complexes and variants. Illusie works in great generality, dealing with derived categories of sheaves of  -modules on a ringed topos X, and its various subcategories. In this paper, we consider the special case of an algebraic stack X, and the derived category \({{\textbf{D}}_{\textbf{qc}}}(X)\) of sheaves of
-modules on a ringed topos X, and its various subcategories. In this paper, we consider the special case of an algebraic stack X, and the derived category \({{\textbf{D}}_{\textbf{qc}}}(X)\) of sheaves of  -modules with quasicoherent cohomology. The perfect complexes are those which, when you pull them back via a faithfully flat map \({\textrm{Spec}(R)}\longrightarrow X\), become isomorphic to bounded complexes of vector bundles on \({\textrm{Spec}(R)}\).
-modules with quasicoherent cohomology. The perfect complexes are those which, when you pull them back via a faithfully flat map \({\textrm{Spec}(R)}\longrightarrow X\), become isomorphic to bounded complexes of vector bundles on \({\textrm{Spec}(R)}\).
The modern approach to Illusie’s ideas is from the homotopy-theoretic perspective—we briefly remind the reader. Perfect complexes on quasi-compact, quasi-separated schemes have two key properties: they are both compact objects and strongly dualizable objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\). We recall
Definition 3.1
Let  be a triangulated category with coproducts. An object
be a triangulated category with coproducts. An object  is compact if \({{\textrm{Hom}}}(P,-)\) commutes with coproducts.
is compact if \({{\textrm{Hom}}}(P,-)\) commutes with coproducts.
Definition 3.2
Let  be a symmetric monoidal category—this means
be a symmetric monoidal category—this means  has a symmetric tensor product and this tensor product has a unit \(\mathbb {1}\). An object
has a symmetric tensor product and this tensor product has a unit \(\mathbb {1}\). An object  is strongly dualizable if there exists an object
is strongly dualizable if there exists an object  and morphisms \(\varepsilon :P^\vee \otimes P\longrightarrow \mathbb {1}\) and \(\eta :\mathbb {1}\longrightarrow P\otimes P^\vee \) so that the two composites
and morphisms \(\varepsilon :P^\vee \otimes P\longrightarrow \mathbb {1}\) and \(\eta :\mathbb {1}\longrightarrow P\otimes P^\vee \) so that the two composites

are identities.
Remark 3.3
We follow the conventions of homotopy theory, where the objects of Definition 3.2 are called strongly dualizable. There are parts of the literature which refer to the same objects as rigid.
If X is a quasi-compact, quasi-separated stack the perfect complexes in \({{\textbf{D}}_{\textbf{qc}}}(X)\) are precisely the strongly dualizable objects. From [17, Lemma 4.4(1)], we know that the compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\) are all perfect. For many stacks the inclusion is an equality: more precisely this happens exactly for concentrated stacks. A stack is X is concentrated if the map \(X\longrightarrow {\textrm{Spec}({{\mathbb {Z}}})}\) is concentrated. All tame Deligne–Mumford stacks are concentrated, hence for those stacks the compact objects and (strongly dualizable objects)= (perfect complexes) are the same. Note that our results do not assume that the stacks are concentrated, we do not want to assume tameness. The morphisms between them will be assumed concentrated, but not the objects. Hence, in our arguments, care will be taken to deal with the case when the compact objects are properly contained in the perfect complexes.
If  is a symmetric monoidal category and
is a symmetric monoidal category and  are objects, with P strongly dualizable, we have natural maps
are objects, with P strongly dualizable, we have natural maps
where \(\alpha \) takes \(\varphi :Q\otimes P\longrightarrow R\) to the composite \(Q{\mathop {\longrightarrow }\limits ^{\textrm{id}\otimes \eta }}Q\otimes P\otimes P^\vee {\mathop {\longrightarrow }\limits ^{\varphi \otimes \textrm{id}}}R\otimes P^\vee \), while \(\beta \) takes the map \(\rho :Q\longrightarrow R\otimes P^\vee \) to the composite \(Q\otimes P{\mathop {\longrightarrow }\limits ^{\rho \otimes \textrm{id}}}R\otimes P^\vee \otimes P{\mathop {\longrightarrow }\limits ^{\textrm{id}\otimes \varepsilon }}R\). The reader will easily check that \(\beta \alpha =\textrm{id}\) and \(\alpha \beta =\textrm{id}\), and since these inverse isomorphisms are natural in Q and R they give us a canonical isomorphism  , meaning that \(R\otimes P^\vee \) satisfies the universal property defining the internal Hom-object
, meaning that \(R\otimes P^\vee \) satisfies the universal property defining the internal Hom-object  . The special case \(R=\mathbb {1}\) tells us that \(P^\vee \) is unique up to canonical isomorphism. If \(f:X\longrightarrow Y\) is a morphism of stacks then \(f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is a strong monoidal functor, meaning it respects the tensor product. It easily follows that \(f^*\) takes strongly dualizable objects to strongly dualizable objects, more precisely \(f^*(P^\vee )\) is canonically isomorphic to \((f^*P)^\vee \). And the argument above shows that
. The special case \(R=\mathbb {1}\) tells us that \(P^\vee \) is unique up to canonical isomorphism. If \(f:X\longrightarrow Y\) is a morphism of stacks then \(f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is a strong monoidal functor, meaning it respects the tensor product. It easily follows that \(f^*\) takes strongly dualizable objects to strongly dualizable objects, more precisely \(f^*(P^\vee )\) is canonically isomorphic to \((f^*P)^\vee \). And the argument above shows that  is canonically isomorphic to
is canonically isomorphic to  . We will often use this.
. We will often use this.
We recall in this preliminary section some useful facts, well-known for the \(f^*\) that arise from morphisms of schemes. The argument below notes that the statements are formal.
Notation 3.4
Let  be an oplax monoidal functor of symmetric monoidal categories, which means that we are given the data of
be an oplax monoidal functor of symmetric monoidal categories, which means that we are given the data of
-
(i)
A natural map
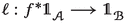 .
. -
(ii)
For every pair of objects
 , a natural map \(\mu =\mu (A,A'):f^*(A\otimes A')\longrightarrow f^*A\otimes f^*A'\).
, a natural map \(\mu =\mu (A,A'):f^*(A\otimes A')\longrightarrow f^*A\otimes f^*A'\).
Furthermore, these maps satisfy the obvious compatibilities with the symmetric monoidal structures of  and
and  . If \(\ell \) and \(\mu (A,A')\) are all isomorphisms then \(f^*\) is called strong monoidal. Next, we recall some natural transformations.
. If \(\ell \) and \(\mu (A,A')\) are all isomorphisms then \(f^*\) is called strong monoidal. Next, we recall some natural transformations.
-
(iii)
Assume \(f^*\) has a right adjoint \(f_*\). [If \(f:X\longrightarrow Y\) is a morphism of stacks then \(f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is an example.] The projection natural transformation p is a natural transformation between two functors
 . It takes a pair of objects
. It takes a pair of objects 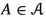 and
and 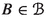 to a map \(p=p(f,A,B):A\otimes f_*B \longrightarrow f_*(f^*A\otimes B)\). The map p corresponds under the adjunction \(f^*\dashv f_*\) to the composite
to a map \(p=p(f,A,B):A\otimes f_*B \longrightarrow f_*(f^*A\otimes B)\). The map p corresponds under the adjunction \(f^*\dashv f_*\) to the composite 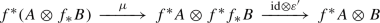
where \(\varepsilon ':f^*f_*\longrightarrow \textrm{id}\) is the counit of the adjunction \(f^*\dashv f_*\).
-
(iv)
Assume that \(f^*\) is such that the projection natural transformation p in (iii) is an isomorphism—in this case we say that the projection formula holds. Suppose further that \(f_*\) has a right adjoint \(f^\times \). [An \(f^*\) coming from a concentrated morphism of algebraic stacks \(f:X\longrightarrow Y\) is an example. We saw the existence on \(f^\times \) in Sect. 2, and the projection formula holds by [17, Corollary 4.12]].Footnote 4 Suppose we are given a pair of objects
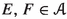 ; we define \(\xi (f,E,F)\) to be the composite
; we define \(\xi (f,E,F)\) to be the composite 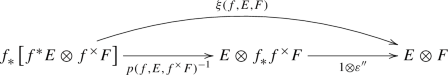
where the first map is the inverse of the projection formula map p of (iii), while \(\varepsilon '':f_*^{}f^\times \longrightarrow \textrm{id}\) is the counit of the adjunction \(f_*^{}\dashv f^\times \). By the adjunction \(f_*\dashv f^\times \), the map \(\xi (f,E,F)\) corresponds to a map
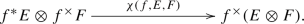
The maps \(\xi (f,E,F)\) and \(\chi (f,E,F)\) are natural in E and F, and there is a sense in which they are also natural in f. In Sect. 12, we will meet a fancy formulation of this naturality.
Proposition 3.5
Let the situation be as in Notation 3.4(iv), in particular the projection formula holds for \(f^*\). Assume further that \(f^*\) is strong monoidal (not only lax monoidal). If E is strongly dualizable then the map \(\chi :f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\) is an isomorphism.
Proof
Since E is strongly dualizable, there exists an object  with morphisms
with morphisms  and
and  as in Definition 3.2, and because \(f^*\) is strong monoidal the morphisms
as in Definition 3.2, and because \(f^*\) is strong monoidal the morphisms  and
and  also satisfy the hypotheses of Definition 3.2. Let
also satisfy the hypotheses of Definition 3.2. Let  be arbitrary, and observe the following isomorphisms:
be arbitrary, and observe the following isomorphisms:

The first and fourth isomorphisms come because E and \(f^*E\) are strongly dualizable, see the inverse isomorphisms \(\alpha \) and \(\beta \) of the paragraph before Notation 3.4. The second and fifth isomorphisms are by the adjunction \(f_*\dashv f^\times \), and the third isomorphism is by the projection formula.
Of course it remains to show that this composite of isomorphisms agrees with \({{\textrm{Hom}}}(B,-)\) applied to the morphism \(\chi :f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\). Since the maps are all explicitly described in Notation 3.4 this amounts to a straightforward diagram chase. Unfortunately I could not make this large diagram fit on the page, we leave it to the reader. \(\square \)
One of the natural questions is whether it is possible to extend a perfect complex from an open substack of a stack to the whole stack. An old theorem of Serre says that any coherent sheaf on an open subset of a noetherian scheme X extends to all of X, and perfect complexes can be thought of as an analog of coherent sheaves. The question might be natural enough, but the answer is No—there exist noetherian schemes X, open subsets \(U\subset X\), and perfect complexes on U that do not extend. There is a K-theoretic obstruction: a perfect complex P on X defines a class \([P]\in K_0(X)\), and the class in \(K_0(U)\) of the restriction of \(P|_U^{}\) is the image of \([P]\in K_0(X)\) under the restriction map \(K_0(X)\longrightarrow K_0(U)\). If X is singular it is possible for the map \(K_0(X)\longrightarrow K_0(U)\) not to be surjective, in which case there will exist perfect complexes on U that cannot possibly extend.
This much was known early on. Until Thomason and Trobaugh [41] no one realized that this is the only obstruction. In fact, [41] proved more: if X is a quasi-compact, semi-separated scheme, \(U\subset X\) is a quasi-compact open subset with \(j:U\longrightarrow X\) the immersion, \(P\in {{\textbf{D}}_{\textbf{qc}}}(U)\) is a perfect complex with \([P]\in K_0(U)\) lying in the image of the map \(K_0(X)\longrightarrow K_0(U)\), and if \(f:P\longrightarrow j^*G\) is any morphism in \({{\textbf{D}}_{\textbf{qc}}}(U)\), then there is a perfect complex \(P'\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and a morphism \(f':P'\longrightarrow G\) so that f is isomorphic to \(j^*f'\).
The proof in [41] is algebro-geometric, very much in the spirit of SGA6. In [30], there is a short, sweet proof of a much more general theorem, using homotopy-theoretic techniques. The general version of Thomason’s localization theorem, and its proofs, can be formalized as facts about compact objects in triangulated categories. To minimize the number of abstract definitions introduced, let us not state the most general version here—we mention only that this general theorem applies to many quasi-compact, quasi-separated stacks, and this underpins our argument.
Before we leave the realm of abstraction there is one more concept we will use.
Definition 3.6
Let  be a triangulated category. We say that
be a triangulated category. We say that  is compactly generated if it has coproducts, and there is a set
is compactly generated if it has coproducts, and there is a set  of compact objects in
of compact objects in  satisfying the following equivalent conditions:
satisfying the following equivalent conditions:
-
(i)
If \({{\textrm{Hom}}}(G,X)=0\) for all
 then \(X=0\).
then \(X=0\). -
(ii)
Any localizing subcategory of
 containing
containing 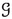 must be all of
must be all of 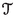 . [A full subcategory
. [A full subcategory 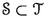 is localizing if it contains zero and is closed under coproducts and triangles].
is localizing if it contains zero and is closed under coproducts and triangles].
The equivalence of (i) and (ii) is not supposed to be obvious, but it is a special case of [32, Proposition 8.4.1]. A set  satisfying the equivalent conditions of Definition 3.6 is called a set of compact generators. The categories \({{\textbf{D}}_{\textbf{qc}}}(X)\) are known to be compactly generated for all quasi-compact, quasi-separated algebraic spaces, and also for a large class of stacks. As we will see in Sects. 5 and 6, what makes perfect complexes so useful is the fact that they contain a set of compact generators.
satisfying the equivalent conditions of Definition 3.6 is called a set of compact generators. The categories \({{\textbf{D}}_{\textbf{qc}}}(X)\) are known to be compactly generated for all quasi-compact, quasi-separated algebraic spaces, and also for a large class of stacks. As we will see in Sects. 5 and 6, what makes perfect complexes so useful is the fact that they contain a set of compact generators.
5 A Review of Formal Nonsense Concerning Base Change
Base-change maps will play a key role in this article, so we include here a little reminder of the formal theory. We give a fairly abstract treatment: let  be a 2-subcategory of the category of categories which contains all natural transformations between its 1-morphisms—for example
be a 2-subcategory of the category of categories which contains all natural transformations between its 1-morphisms—for example  could be the 2-category whose objects are triangulated categories, the 1-morphisms are triangulated functors, and the 2-morphisms are any natural transformations.
could be the 2-category whose objects are triangulated categories, the 1-morphisms are triangulated functors, and the 2-morphisms are any natural transformations.
Definition 4.1
Suppose we are given in  a 2-commutative square
a 2-commutative square

This means that we are given in  the 1-morphisms
the 1-morphisms  ,
,  ,
,  and
and  , as well as the natural transformation \(\tau :f^*v^*\longrightarrow u^*g^*\). Suppose also that \(f^*\) and \(g^*\) have in
, as well as the natural transformation \(\tau :f^*v^*\longrightarrow u^*g^*\). Suppose also that \(f^*\) and \(g^*\) have in  right adjoints \(f_*\) and \(g_*\), respectively. The induced base-change map is the 2-commutative square
right adjoints \(f_*\) and \(g_*\), respectively. The induced base-change map is the 2-commutative square

where \(\beta :v^*g_*\longrightarrow f_*u^*\) is defined to be the map corresponding under the adjunction \(f^*\dashv f_*\) to the composite

where \(\varepsilon :g^*g_*\longrightarrow \textrm{id}\) is the counit of the adjunction \(g^*\dashv g_*\).
Remark 4.2
Recall that the adjunction \(f^*\dashv f_*\) takes a map \(\beta :x\longrightarrow f_* y\) to the composite \(f^*x{\mathop {\longrightarrow }\limits ^{f^*\beta }}f^*f_* y{\mathop {\longrightarrow }\limits ^{\varepsilon '}}y\), with \(\varepsilon ':f^*f_*\longrightarrow \textrm{id}\) the counit of the adjunction. Applying this to the \(\beta \) of Definition 4.1, we deduce the commutativity of the square

Definition 4.3
Let the notation be as in Definition 4.1, but assume further:
-
(i)
The map \(\beta :v^*g_*\longrightarrow f_*u^*\) is an isomorphism.
-
(ii)
The functors \(f_*\) and \(g_*\) both have right adjoints, denoted \(f^\times \) and \(g^\times \), respectively.
Then, the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is obtained by applying Definition 4.1 to the 2-commutative square

Concretely: the map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) corresponds under the adjunction \(f_*\dashv f^\times \) to the composite

where \(\widetilde{\varepsilon }:g_*g^\times \longrightarrow \textrm{id}\) is the counit of the adjunction \(g_*\dashv g^\times \).
Remark 4.4
Applying Remark 4.2 to the base-change map of Definition 4.3, we obtain the commutativity of the square

where \(\widehat{\varepsilon }:f_*f^\times \longrightarrow \textrm{id}\) is the counit of the adjunction \(f_*\dashv f^\times \).
Example 4.5
Suppose we are given a 2-commutative square of quasi-compact, quasi-separated algebraic stacks

Applying \((-)^*\), we obtain a 2-commutative square

with \(\tau :f^*v^*\longrightarrow u^*g^*\) an isomorphism. The maps \(f^*\) and \(g^*\) have right adjoints \(f_*\) and \(g_*\), and Definition 4.1 gives the base-change square

This map \(\beta \) need not always be an isomorphism, but [17, Theorem 2.6(4)] tells us that, as long as
-
(i)
The square \(\diamondsuit \) is 2-cartesian,
-
(ii)
The morphism v is flat while g is concentrated,
then \(\beta \) is indeed an isomorphism. Since g is concentrated [17, Lemma 2.5(1)] guarantees that so is its pullback f, and in Sect. 2 we saw that when f, g are concentrated then \(f_*\), \(g_*\) have right adjoints \(f^\times \), \(g^\times \). We are in the situation of Definition 4.3, and have the base-change 2-commutative square

Back to gorgeous generality. In Notation 3.4, we learned that, if f is an oplax monoidal functor, then one can construct a projection natural transformation \(p:A\otimes f_*B\longrightarrow f_*(f^*A\otimes B)\). If p is an isomorphism one can go further and construct a morphism \(\chi :f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\). Next, we recall how these are compatible with the base-change maps above; the next Lemma is virtually the same as [25, Proposition 3.7.3].
Lemma 4.6
Suppose we are given in  a 2-commutative square
a 2-commutative square

Suppose the categories  ,
,  ,
,  and
and  are all symmetric monoidal, and the functors \(f^*\), \(g^*\), \(u^*\) and \(v^*\) are all oplax monoidal. Suppose further that the map \(\tau :f^*v^*\longrightarrow u^*g^*\) is compatible with the oplax monoidal structure maps \(\mu \), in the sense that the following hexagon commutes:
are all symmetric monoidal, and the functors \(f^*\), \(g^*\), \(u^*\) and \(v^*\) are all oplax monoidal. Suppose further that the map \(\tau :f^*v^*\longrightarrow u^*g^*\) is compatible with the oplax monoidal structure maps \(\mu \), in the sense that the following hexagon commutes:

Finally, assume also that \(f^*\) and \(g^*\) have right adjoints \(f_*\) and \(g_*\) in  .
.
Then, for any objects  and
and  , the following diagram commutes:
, the following diagram commutes:

Proof
We have to prove the equality of two composites of the form \(x\longrightarrow f_*y\), and the adjunction \(f^*\dashv f_*\) reduces us to proving the equality of the corresponding composites \(f^*x\longrightarrow y\). Concretely, we need to prove the commutativity of

where the commutative triangles are simply places where we have replaced the diagonal morphism \(x\longrightarrow f_*y\) by the corresponding \(f^*x\longrightarrow y\), as in the definitions. The naturality of \(\tau \) and \(\mu _f^{}\) gives the commutativity of the squares in the diagram

Hence, what remains is to prove the commutativity of the perimeter in the diagram

The square \((\clubsuit )\) is the tensor product of \(f^*v^*A\) with the commutative square of Remark 4.2, hence commutes. The square \((\spadesuit )\) commutes because it is \(u^*\) of the square spelling out the definition of the morphism \(g^*(A\otimes g_*B)\longrightarrow g^*A\otimes B\) corresponding to the map \(p_g^{}:A\otimes g_*B\longrightarrow g_*(g^*A\otimes B)\); see Notation 3.4(iii).
It remains to show the commutativity of the perimeter in the diagram

The square \((\diamondsuit )\) obviously commutes, the square \((\heartsuit )\) commutes by the naturality of \(\mu _u^{}\), and the heptagon commutes because \(\tau \) is compatible with the oplax monoidal structures of \(v^*f^*\) and \(u^*g^*\), see the hypotheses of the Lemma. \(\square \)
We follow with another relatively standard fact, see for example [25, Exercise 4.7.3.4(c)].
Lemma 4.7
Let the notation be as in Lemma 4.6, but assume in addition that
-
(i)
The map \(\tau :f^*v^*\longrightarrow u^*g^*\) is an isomorphism.
-
(ii)
The functors \(f_*\) and \(g_*\) have right adjoints \(f^\times \) and \(g^\times \).
-
(iii)
The base-change map \(\beta :v^*g_*\longrightarrow f_*u^*\) is invertible, and hence the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is given as in Definition 4.3.
-
(iv)
The projection formula holds for \(f^*\) and \(g^*\).
Then, for any pair of objects  , the following square commutes:
, the following square commutes:

Proof
We need to show the equality of two maps \(x\longrightarrow f^\times y\), and it suffices to prove the equality of the corresponding maps \(f_*x\longrightarrow y\). Concretely, this means we must show the commutativity of the perimeter of the diagram

In passing from the diagram of the Lemma to the perimeter of the diagram above the map \(\chi (f,v^*E,v^*F): f^*v^*E\otimes f^\times v^*F\longrightarrow f^\times v^*(E\otimes F)\) was replaced by the corresponding morphism \(\xi (f,v^*E,v^*F):f_*(f^*v^*E\otimes f^\times v^*F\longrightarrow v^*(E\otimes F)\), see Notation 3.4(iv), while the vertical map on the right \(\Phi :u^*g^\times (E\otimes F)\longrightarrow f^\times u^*(E\otimes F)\) was replaced by the composite \(f_*u^*g^\times (E\otimes F)\longrightarrow v^*(E\otimes F)\) as in Definition 4.3. Now, the square \((\heartsuit )\) commutes by the naturality of \(\beta \), and the triangle commutes just because \(\xi (g,E,F):g_*(g^*E\otimes g^\times F)\longrightarrow E\otimes F\) is the map corresponding to \(\chi (g,E,F):g^*E\otimes g^\times F\longrightarrow g^\times (E\otimes F)\) under the adjunction \(g_*\dashv g^\times \). It suffices, therefore, to prove the commutativity of the remaining hexagon. If we expand out the maps \(\xi (g,E,F)\) and \(\xi (f,v^*E,v^*F)\) as in Notation 3.4(iv) we are left with proving the commutativity of the perimeter of

The square \((\diamondsuit )\) commutes by the naturality of \(\mu _v^{}\), hence we are reduced to proving the commutativity of the perimeter of

The square \((\spadesuit )\) commutes by the naturality of p, while \((\clubsuit )\) is the tensor product of \(v^*E\) with the commutative square of Remark 4.4. Finally the remaining diagram is the commutative heptagon of Lemma 4.6, for the pair of objects  and
and  . \(\square \)
. \(\square \)
Remark 4.8
The example we care about is Example 4.5, where we start with a 2-commutative square of algebraic stacks

and apply \({{\textbf{D}}_{\textbf{qc}}}(-)\) to obtain a 2-commutative square

The hypotheses of Lemma 4.6 are always satisfied. The hypotheses of Lemma 4.7 hold as long as the square \((\diamondsuit )\) is 2-cartesian, g is concentrated and v is flat.
6 An Improved Flat Base-Change Theorem
This section is devoted to the proof of Theorem 1.7=Theorem 6.10 and proceeds by a series of lemmas. If \(\alpha :V\longrightarrow Z\) is an open immersion of noetherian schemes, the first lemma is easy and can be proved in many ways. We want the non-noetherian version, and to state it we begin with
Reminder 5.1
Let Z be an algebraic stack. An object \(D\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) is called pseudo-coherent if there exists a flat cover \(f:{\textrm{Spec}(R)}\longrightarrow Z\) so that \(f^*D\) is isomorphic in \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\cong {{\textbf{D}}}(R)\) to a bounded-above complex of finitely generated, projective R-modules.
One small historical comment: if the reader compares the above with Illusie’s definition, it is obvious that a pseudo-coherent complex in our sense is also pseudo-coherent in Illusie’s. For the converse we need to show that, if a complex in \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\) is pseudo-coherent in Illusie’s sense, then it is isomorphic in \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\) to a bounded-above complex of finitely generated, projective R-modules. For this, we need the equivalence \({{\textbf{D}}}(R)\cong {{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\) of [7, Theorem 5.1], which was not known at the time Illusie wrote his exposés in SGA6. The point is that finite generation of an R-module is local in the flat topology, and hence the top cohomology module of a complex in \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\), which is pseudo-coherent in Illusie’s sense, must be finitely generated. But now an easy induction produces a resolution for the complex as in our definition.
Lemma 5.2
Let Z be an algebraic stack and let \(\alpha :V\longrightarrow Z\) be a flat morphism. Suppose \(D\in {{\textbf{D}}^b_{\textrm{qc}}}(Z)\) is pseudo-coherent, and assume \(\alpha ^*D=0\). Then, for any \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), we have  .
.
Proof
The hypotheses tell us that D is pseudo-coherent and belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\); hence we may apply [20, Proposition 3.7] with \(F=G=D\) to deduce that the natural map  is an isomorphism. Since \(\alpha ^*D=0\) we conclude that
is an isomorphism. Since \(\alpha ^*D=0\) we conclude that  .
.
But now  is a monoid in the monoidal category \({{\textbf{D}}_{\textbf{qc}}}(Z)\) and
is a monoid in the monoidal category \({{\textbf{D}}_{\textbf{qc}}}(Z)\) and  is a module over it—there are canonical maps
is a module over it—there are canonical maps

which compose to an isomorphism. Applying \(\alpha ^*\) we have that the composite

is also an isomorphism. Hence,  is a direct summand of the middle term, which vanishes since
is a direct summand of the middle term, which vanishes since  . \(\square \)
. \(\square \)
The next easy Lemma (in the case of schemes) may be found in [21, 1.6.1]; we include the proof for the convenience of the reader.
Lemma 5.3
Let \(f:X\longrightarrow Y\) be a concentrated morphism of quasi-compact, quasi-separated algebraic stacks. Suppose \(f_*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\) is the derived pushforward map, and \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) its right adjoint. Then, the natural map is an isomorphism

Proof
Let \(C\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) be arbitrary. The lemma follows from the sequence of isomorphisms

The first isomorphism is by the adjunction \({} f^*\dashv f_*\), the second and fifth are by the adjunction of \(\otimes \) and  , the third is by the adjunction \(f_*\dashv f^\times \), and the fourth is by the projection formula (which holds for concentrated morphisms by [17, Corollary 4.12]). \(\square \)
, the third is by the adjunction \(f_*\dashv f^\times \), and the fourth is by the projection formula (which holds for concentrated morphisms by [17, Corollary 4.12]). \(\square \)
Remark 5.4
There exist algebraic stacks X for which the derived category \({{\textbf{D}}_{\textbf{qc}}}(X)\) is not compactly generated—see [15, Theorem 1.1] for examples. In this article, we view the phenomenon as pathological, our results will mostly focus on the good stacks X for which \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated. There are many interesting classes of such stacks and much work has gone into studying them, for the best theorems to date the reader is referred to Hall and Rydh [17, Introduction].
Since in this section we will make some effort to state our results in the maximal generality in which the proofs hold, it will help to make a convention.
Convention 5.5
We will say that a stack X satisfies Thomason’s condition if \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated, and moreover for any quasi-compact open set \(U\subset X\) the subcategory \({{\textbf{D}}}_{\textbf{qc},X-U}^{}(X)\) is generated by the compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\) that happen to lie in the subcategory. We remind the reader: a complex belongs to \({{\textbf{D}}}_{\textbf{qc},X-U}^{}(X)\subset {{\textbf{D}}_{\textbf{qc}}}(X)\) if its restriction to U is acyclic. Thomason [41] proved that every quasi-compact, semi-separated scheme satisfies Thomason’s condition. The current best theorems for algebraic stacks tell us that a stack X satisfies Thomason’s condition if either X is a \({{\mathbb {Q}}}\)-stack of s-global type in the notation of [39, Section 2], or X is quasi-compact and its diagonal is separated and quasi-finite—see Hall and Rydh [17, Theorems A, B and 4.10(2)]. The following observation will be useful.
Observation 5.6
If X and \(X'\) are quasi-compact, quasi-separated stacks, if X satisfies Thomason’s condition and if \(i:X'\longrightarrow X\) is a locally closed immersion, then \(X'\) satisfies Thomason’s condition.
Proof
The map i is a locally closed immersion of quasi-compact, quasi-separated stacks, hence it is quasi-affine. From [17, Lemma 8.2] we have that the objects \(i^*C\), with \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) compact, are compact generators of \({{\textbf{D}}_{\textbf{qc}}}(X')\).
If \(U'\subset X'\) is a quasi-compact open subset then there exists a quasi-compact open subset \(U\subset X\) with \(U'=U\cap X'\). As X satisfies Thomason’s condition the objects \(C\in {{\textbf{D}}}_{\textbf{qc},\,X-U}^{}(X)\), with compact image in \({{\textbf{D}}_{\textbf{qc}}}(X)\), generate \({{\textbf{D}}}_{\textbf{qc},\,X-U}^{}(X)\). But then the objects \(i^*C\) generate \({{\textbf{D}}}_{\textbf{qc},\,X'-U'}^{}(X')\) and are compact in \({{\textbf{D}}_{\textbf{qc}}}(X')\). \(\square \)
We will find useful the following little fact.
Lemma 5.7
Let \(g:X\longrightarrow Z\) be a morphism of stacks, and assume \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated. Then, the following
is a class of compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\). Moreover the thick subcategory generated by S—that is the smallest subcategory containing S and closed under triangles and direct summands—is the category \({{\textbf{D}}_{\textbf{qc}}}(X)^c\) of all compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\).
Proof
If \(\widetilde{C}\) is a compact object in \({{\textbf{D}}_{\textbf{qc}}}(Z)\) then [17, Lemma 4.4(1)] tells us that \(\widetilde{C}\) is a perfect complex, hence so is \(g^*\widetilde{C}\). If C is a compact object in \({{\textbf{D}}_{\textbf{qc}}}(X)\) we learn from [17, Lemma 4.4(2)] that \(C\otimes g^*\widetilde{C}\) is also a compact object in \({{\textbf{D}}_{\textbf{qc}}}(X)\).
Next, let  be the localizing subcategory generated by the class of compacts S. The objects of S lie in
be the localizing subcategory generated by the class of compacts S. The objects of S lie in  and are compact in the larger \({{\textbf{D}}_{\textbf{qc}}}(X)\), hence are certainly compact in
and are compact in the larger \({{\textbf{D}}_{\textbf{qc}}}(X)\), hence are certainly compact in  . Since S generates
. Since S generates  we may apply [32, Lemma 4.4.5] to conclude that
we may apply [32, Lemma 4.4.5] to conclude that  , where \(\text {Thick}(S)\) stands for the thick subcategory generated by S. Since \(S\subset {{\textbf{D}}_{\textbf{qc}}}(X)^c\) and \({{\textbf{D}}_{\textbf{qc}}}(X)^c\) is thick, we conclude that
, where \(\text {Thick}(S)\) stands for the thick subcategory generated by S. Since \(S\subset {{\textbf{D}}_{\textbf{qc}}}(X)^c\) and \({{\textbf{D}}_{\textbf{qc}}}(X)^c\) is thick, we conclude that  . We need to prove the inclusion
. We need to prove the inclusion  .
.
Choose, therefore, any compact \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\); the subcategory  defined by
defined by

is obviously a localizing subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) containing all the compact objects \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\). But \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated, hence  , and in particular
, and in particular  . Therefore,
. Therefore,  . Thus,
. Thus,  contains all the compact objects of \({{\textbf{D}}_{\textbf{qc}}}(X)\): in symbols
contains all the compact objects of \({{\textbf{D}}_{\textbf{qc}}}(X)\): in symbols  . But it is clear that for an object in
. But it is clear that for an object in  , being compact in the larger \({{\textbf{D}}_{\textbf{qc}}}(X)\) implies compactness in
, being compact in the larger \({{\textbf{D}}_{\textbf{qc}}}(X)\) implies compactness in  . Hence,
. Hence,  . \(\square \)
. \(\square \)
Notation 5.8
For most of this section, we will suppose we are given a 2-cartesian square of stacks

We always assume the stacks quasi-compact and quasi-separated, and the morphism g will be concentrated as in [17, Definition 2.4]. Note that any noetherian stack is automatically quasi-compact and quasi-separated, and any representable morphism is concentrated. As all morphisms of quasi-compact, quasi-separated algebraic spaces are representable they are concentrated.
Lemma 5.9
With the notation as in 5.8, assume the stack Z has quasi-affine diagonal and that \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated. Let S be a set of compact generators in \({{\textbf{D}}_{\textbf{qc}}}(X)\). Then,
-
(i)
A morphism \(\varphi :E\longrightarrow E'\) in \({{\textbf{D}}_{\textbf{qc}}}(W)\) is an isomorphism if and only if, for all compact objects \(C\in S\), the functor
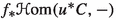 takes \(\varphi \) to an isomorphism.
takes \(\varphi \) to an isomorphism. -
(ii)
An object \(E\in {{\textbf{D}}_{\textbf{qc}}}(W)\) vanishes if and only if, for every compact object \(C\in S\), the functor
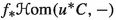 takes E to zero.
takes E to zero.
Proof
It suffices to prove (ii), as (i) follows by applying (ii) to the mapping cone of the morphism \(\varphi :E\longrightarrow E'\).
Suppose, therefore, that E is an object of \({{\textbf{D}}_{\textbf{qc}}}(W)\) and that  for all \(C\in S\). Let \(Y'\) be an affine scheme and \(v':Y'\longrightarrow Y\) a faithfully flat map; we may extend the diagram of 5.8 by pulling back along \(v'\), obtaining
for all \(C\in S\). Let \(Y'\) be an affine scheme and \(v':Y'\longrightarrow Y\) a faithfully flat map; we may extend the diagram of 5.8 by pulling back along \(v'\), obtaining

We are assuming that g is concentrated, and [17, Lemma 2.5(1)] tells us that so are its pullbacks \(f'\) and f. We are given that  for all \(C\in S\), hence also
for all \(C\in S\), hence also  for all \(C\in S\). By [17, Theorem 2.6(4)] the base-change map is an isomorphism \({v'}^*f_*\cong f'_*{u'}^*\), hence
for all \(C\in S\). By [17, Theorem 2.6(4)] the base-change map is an isomorphism \({v'}^*f_*\cong f'_*{u'}^*\), hence  . Now, [17, Lemma 4.4(1)] tells us that the compact object \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) is a perfect complex, therefore, so is \(u^*C\in {{\textbf{D}}_{\textbf{qc}}}(W)\), and the natural map
. Now, [17, Lemma 4.4(1)] tells us that the compact object \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) is a perfect complex, therefore, so is \(u^*C\in {{\textbf{D}}_{\textbf{qc}}}(W)\), and the natural map  is an isomorphism; we conclude that
is an isomorphism; we conclude that  . Taking global sections we have that \({{\textrm{Hom}}}_{W'}^{}({u'}^*u^*C,{u'}^*E) ={{\textrm{Hom}}}_X^{}(C,u_*u'_*{u'}^*E)=0\) for every \(C\in S\). But the objects of S generate, hence \(u_*u'_*{u'}^*E=0\).
. Taking global sections we have that \({{\textrm{Hom}}}_{W'}^{}({u'}^*u^*C,{u'}^*E) ={{\textrm{Hom}}}_X^{}(C,u_*u'_*{u'}^*E)=0\) for every \(C\in S\). But the objects of S generate, hence \(u_*u'_*{u'}^*E=0\).
But \(Y'\) is assumed affine and Z has quasi-affine diagonal, hence the map \(vv':Y'\longrightarrow Z\) is quasi-affine. Its pullback \(uu':W'\longrightarrow X\) is also quasi-affine, and by [17, Corollary 2.8] the functor \(u_*u'_*:{{\textbf{D}}_{\textbf{qc}}}(W')\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) is conservative. The vanishing of \(u_*u'_*{u'}^*E\) implies the vanishing of \({u'}^*E\). The map \(v'\) is faithfully flat and hence so is its pullback \(u'\), therefore, the vanishing of \({u'}^*E\) implies the vanishing of E. \(\square \)
Corollary 5.10
With the notation as in 5.8, assume the stack Z has quasi-affine diagonal, and the categories \({{\textbf{D}}_{\textbf{qc}}}(X)\) and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) are both compactly generated. Then, \({{\textbf{D}}_{\textbf{qc}}}(W)\) is generated by the compact objects \(u^*C\otimes f^*D\), where \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(D\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) are compact.
The case of the corollary where the diagram is of quasi-compact, quasi-separated schemes was proved in Bondal and Van den Bergh [8, Lemma 3.4.1], while the case where Z has affine diagonal may be found in Ben-Zvi, Francis and Nadler [6, Proposition 3.24].
Proof
In Notation 5.8, we assume that g is concentrated, hence so is its pullback f; by [17, Theorem 2.6(3)], we know that \(f_*\) preserves coproducts, while from the proof of [31, Theorem 5.1], it follows that \(f^*\) takes compacts to compacts. Hence, \(f^*D\) is compact for any compact \(D\in {{\textbf{D}}_{\textbf{qc}}}(Y)\). The object \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) is compact, hence perfect by [17, Lemma 4.4(1)]. Therefore, \(u^*C\) is perfect in \({{\textbf{D}}_{\textbf{qc}}}(W)\). Now, [17, Lemma 4.4(2)] allows us to conclude that \(u^*C\otimes f^*D\) is compact in \({{\textbf{D}}_{\textbf{qc}}}(W)\).
It remains to show that the objects \(u^*C\otimes f^*D\) generate. Suppose that E is an object of \({{\textbf{D}}_{\textbf{qc}}}(W)\) so that, for all compact \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(D\in {{\textbf{D}}_{\textbf{qc}}}(Y)\), we have \({{\textrm{Hom}}}_W^{}(u^*C\otimes f^*D,E)=0\); we need to show \(E=0\). To this end, consider the isomorphisms

The vanishing of this for all compact \(D\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) tells us that  for all compact \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\), and Lemma 5.9(ii) now gives that \(E=0\). \(\square \)
for all compact \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\), and Lemma 5.9(ii) now gives that \(E=0\). \(\square \)
Remark 5.11
As a curiosity we note that it is not clear whether W satisfies Thomason’s condition whenever X and Y do. Even the simplest cases are unclear, for example when the maps are all representable, étale and separated.
We are building up to Lemma 5.19; in the generality in which we will state it we need
Reminder 5.12
Let \(g:X\longrightarrow Z\) be a concentrated morphism of quasi-compact, quasi-separated stacks. The morphism g is called quasi-proper if \(g_*\) takes pseudo-coherent objects of \({{\textbf{D}}_{\textbf{qc}}}(X)\) to pseudo-coherent objects of \({{\textbf{D}}_{\textbf{qc}}}(Z)\); see Reminder 5.1 for the definition of pseudo-coherence of objects. The morphism g is universally quasi-proper if all pullbacks of g are quasi-proper. The morphism g is called pseudo-coherent if there exists a 2-commutative square

with \(u'\) smooth and surjective, with the map \({\textrm{Spec}(S)}\longrightarrow X\times _Z^{}{\textrm{Spec}(R)}\) also smooth and surjective, and where \(g'\) admits a factorization \({\textrm{Spec}(S)}{\mathop {\longrightarrow }\limits ^{i}}{{\mathbb {A}}}^n_R\longrightarrow {\textrm{Spec}(R)}\) with i a closed immersion and so that \(i_*\) takes the structure sheaf  to a pseudo-coherent object in \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_R)\cong {{\textbf{D}}}\big (R[x_1^{},x_2^{},\ldots , x_n^{}]\big )\).
to a pseudo-coherent object in \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_R)\cong {{\textbf{D}}}\big (R[x_1^{},x_2^{},\ldots , x_n^{}]\big )\).
Remark 5.13
In Reminder 5.12, we do not assume g to be representable. Pseudo-coherence of morphisms is preserved by flat base-change, with quasi-properness this is less clear. All finite-type morphisms of noetherian stacks are pseudo-coherent, and all proper maps of noetherian stacks are quasi-proper. For non-noetherian stacks, we learn from Kiehl [22, p. 315, Theorem 2.2] that every proper pseudo-coherent map is quasi-proper. But there are also non-representable examples of quasi-proper maps. Let X be a scheme of finite type over S and G a linearly reductive group over S acting on X. If the GIT quotient \(X/\!\!/G\) exists then the map \([X/G]\longrightarrow X/\!\!/G\), from the stack [X/G] to the GIT quotient, is always quasi-proper but rarely representable.
Lemma 5.14
Let X be a quasi-compact, quasi-separated stack and \(C\in {{\textbf{D}}^b_{\textrm{qc}}}(X)\) a pseudo-coherent object. Then, the locus where C is perfect is open. More precisely: let
Then, for \(n\gg 0\) the sets \(V_n\) are open. Therefore, so is \(V=\cup _{n\gg 0}^{} V_n\), which is the set of points at which C is perfect.
Proof
The question is local in the flat topology on X, hence we may assume X to be an affine scheme \(X={\textrm{Spec}(R)}\). Being pseudo-coherent, the object \(C \in {{\textbf{D}}_{\textbf{qc}}}(X)\cong {{\textbf{D}}}(R)\) is isomorphic to a bounded above complex of finitely generated projective R-modules—choose and fix such an isomorph C. As we are assuming that C has bounded cohomology we may (after shifting) suppose that \(H^i(C)=0\) for all \(i<0\). We assert that \(V_n\) is open for all \(n\ge 0\).
Let \(\mathfrak {p}\in {\textrm{Spec}(R)}\) be a prime ideal of R belonging to \(V_n\) with \(n\ge 0\). In the definition of \(V_n\), we may take f to be the map \({\textrm{Spec}(R_\mathfrak {p})}\longrightarrow {\textrm{Spec}(R)}\), where \(R_\mathfrak {p}\) is the localization of R at \(\mathfrak {p}\)—from the fact that \(\mathfrak {p}\in V_n\) it follows that \(f^*C=R_\mathfrak {p}\otimes _R^{}C\) has Tor-amplitude contained in \([-n,\infty )\). Hence, for any \(R_\mathfrak {p}\) module N, we have \(H^i(C\otimes N)=0\) for all \(i<-n\le 0\). Thus, the brutal truncation \(C_{\le -n}^{}\) of the complex C, given below

is acyclic except in degree \(-n\), as is the complex \(C_{\le -n}^{}\otimes N\). The complex \(C_{\le -n}^{}\) is a projective resolution over R of the finitely-presented module \(M=\textrm{Coker}(\partial )\), and the fact that, for every \(R_\mathfrak {p}\)-module N, the complex \(C_{\le -n}^{}\otimes N\) is acyclic in degrees \(\ne -n\) says that \(R_\mathfrak {p}\otimes M\) is flat as an \(R_\mathfrak {p}\) module, hence projective. But then M must be projective and finitely generated in a Zariski-open neighborhood of \(\mathfrak {p}\), and on this neighborhood the complex C is quasi-isomorphic to the perfect complex

\(\square \)
Corollary 5.15
Let \(g:X\longrightarrow Z\) be a pseudo-coherent morphism of quasi-compact, quasi-separated stacks. Then, the subset \(U\subset X\) of points where g is of finite Tor-dimension is open. More precisely: for any n let \(U_n\subset X\) be defined as the set of all points \(x\in X\) at which the Tor-amplitude of g is contained in \([-n,\infty )\). Then, \(U_n\) is open for \(n\gg 0\), and hence so is the union \(U=\cup _{n\gg 0}^{}U_n\).
Proof
The pseudo-coherence of g means that there exists a 2-commutative square

as in Reminder 5.12. Since \(u'\) and \(u''\) are both faithfully flat, it suffices to prove the assertion for \(g'\). Explicitly: we need to show the openness for large n of the set \(U_n\subset {\textrm{Spec}(S)}\), of all prime ideals \(\mathfrak {p}\subset S\) where the localization \(S_\mathfrak {p}\) has Tor-amplitude over R contained in the interval \([-n,\infty )\). But \(g'\) admits a factorization \({\textrm{Spec}(S)}{\mathop {\longrightarrow }\limits ^{i}}{{\mathbb {A}}}^n_R{\mathop {\longrightarrow }\limits ^{j}}{\textrm{Spec}(R)}\) with j flat, and it suffices to prove the assertion for i. We are given that i is a closed immersion and  is pseudo-coherent, and we may apply Lemma 5.14 to deduce that, for \(n\gg 0\), the set \(V_n\subset {{\mathbb {A}}}^n_R\) on which
is pseudo-coherent, and we may apply Lemma 5.14 to deduce that, for \(n\gg 0\), the set \(V_n\subset {{\mathbb {A}}}^n_R\) on which  has Tor-amplitude contained in \([-n,\infty )\) is open in \({{\mathbb {A}}}^n_R\). Hence, \(U_n=V_n\cap {\textrm{Spec}(S)}\) is open in \({\textrm{Spec}(S)}\). \(\square \)
has Tor-amplitude contained in \([-n,\infty )\) is open in \({{\mathbb {A}}}^n_R\). Hence, \(U_n=V_n\cap {\textrm{Spec}(S)}\) is open in \({\textrm{Spec}(S)}\). \(\square \)
Lemma 5.16
Let \(g:X\longrightarrow Z\) be a pseudo-coherent morphism of quasi-compact, quasi-separated stacks. Suppose \(z\in Z\) is a point so that the map g is of finite Tor-dimension at every \(x\in X\) with z in the closure of g(x). Then, there exist an integer \(\ell \) and a 2-cartesian square

with Y an affine scheme, with v flat, with \(z\in v(Y)\), and so that \(f^*{{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge n}\subset {{\textbf{D}}_{\textbf{qc}}}(W)^{\ge n-\ell }\).
Proof
We assume g pseudo-coherent, hence there exists a 2-commutative square

as in Reminder 5.12. The map \(u'\) is surjective (and smooth), hence we may choose a point \(\mathfrak {p}\in {\textrm{Spec}(R)}\) with \(u'(\mathfrak {p})=z\). Let \(R_\mathfrak {p}\) be the localization of R at the prime ideal \(\mathfrak {p}\), let \(v:Y\longrightarrow Z\) be the composite \({\textrm{Spec}(R_\mathfrak {p})}\longrightarrow {\textrm{Spec}(R)}{\mathop {\longrightarrow }\limits ^{u'}}Z\), and form the pullback square

We will prove that this square satisfies the requirements of the Lemma.
By construction z belong to the image of the flat map \(v:Y\longrightarrow Z\), and \(Y={\textrm{Spec}(R_\mathfrak {p})}\) is an affine scheme. It remains to show that, for some integer \(\ell \), we have \(f^*{{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge 0}\subset {{\textbf{D}}_{\textbf{qc}}}(W)^{\ge -\ell }\). We have a smooth and surjective map \(\rho :{\textrm{Spec}(S_\mathfrak {p})}\longrightarrow W\), which is the pullback along the map \({\textrm{Spec}(R_\mathfrak {p})}\longrightarrow {\textrm{Spec}(R)}\) of the smooth and surjective map \({\textrm{Spec}(S)}\longrightarrow X\times _Z^{}{\textrm{Spec}(R)}\), and it clearly suffices to show that \(\rho ^*f^*{{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge 0}\subset {{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(S_\mathfrak {p})}\big )^{\ge -\ell }\).
By hypothesis g is of finite Tor-dimension at every point \(x\in X\) such that the closure of g(x) contains z. Hence, f is of finite Tor-dimension at every point of W. The map \(\rho \) is flat by construction, and so \(f\rho \) is of finite Tor-dimension at every point of \({\textrm{Spec}(S_\mathfrak {p})}\). But the map \(f\rho \) factors as \({\textrm{Spec}(S_\mathfrak {p})}{\mathop {\longrightarrow }\limits ^{i}}{{\mathbb {A}}}^n_{R_\mathfrak {p}}{\mathop {\longrightarrow }\limits ^{j}}{\textrm{Spec}(R_\mathfrak {p})}\), and as j is flat \(j^*{{\textbf{D}}_{\textbf{qc}}}(Y)= j^*{{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R_\mathfrak {p})}\big )^{\ge 0}\subset {{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_{R_\mathfrak {p}})^{\ge 0}\). Thus, it suffices to prove that \(i^*{{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_{R_\mathfrak {p}})^{\ge 0}\subset {{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(S_\mathfrak {p})}\big )^{\ge -\ell }\) for some integer \(\ell \). The map i is a closed immersion hence affine, and it, therefore, suffices to prove that \(i_*i^*{{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_{R_\mathfrak {p}})^{\ge 0}\subset {{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^n_{R_\mathfrak {p}})^{\ge -\ell }\).
The projection formula tells us that  , and we know that
, and we know that  is pseudo-coherent. The fact that ji and, therefore, i are of finite Tor-dimension at every point \(s\in {\textrm{Spec}(S_\mathfrak {p})}\) tells us first that
is pseudo-coherent. The fact that ji and, therefore, i are of finite Tor-dimension at every point \(s\in {\textrm{Spec}(S_\mathfrak {p})}\) tells us first that  is perfect at every point of the closed subset \({\textrm{Spec}(S_\mathfrak {p})}\subset {{\mathbb {A}}}^n_{R_\mathfrak {p}}\), while on the complement of \({\textrm{Spec}(S_\mathfrak {p})}\subset {{\mathbb {A}}}^n_{R_\mathfrak {p}}\) the complex
is perfect at every point of the closed subset \({\textrm{Spec}(S_\mathfrak {p})}\subset {{\mathbb {A}}}^n_{R_\mathfrak {p}}\), while on the complement of \({\textrm{Spec}(S_\mathfrak {p})}\subset {{\mathbb {A}}}^n_{R_\mathfrak {p}}\) the complex  vanishes—thus, it is perfect at every point of \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\). Lemma 5.14, applied to the pseudo-coherent object
vanishes—thus, it is perfect at every point of \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\). Lemma 5.14, applied to the pseudo-coherent object  on the stack \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\), expresses \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\) as a union \({{\mathbb {A}}}^n_{R_\mathfrak {p}}=\cup _{\ell \gg 0}^{}V_\ell \) with \(V_\ell \) increasing and open for large \(\ell \). As \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\) is quasi-compact there exists an integer \(\ell \) with \(V_\ell ={{\mathbb {A}}}^n_{R_\mathfrak {p}}\), that is the Tor-amplitude of
on the stack \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\), expresses \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\) as a union \({{\mathbb {A}}}^n_{R_\mathfrak {p}}=\cup _{\ell \gg 0}^{}V_\ell \) with \(V_\ell \) increasing and open for large \(\ell \). As \({{\mathbb {A}}}^n_{R_\mathfrak {p}}\) is quasi-compact there exists an integer \(\ell \) with \(V_\ell ={{\mathbb {A}}}^n_{R_\mathfrak {p}}\), that is the Tor-amplitude of  is contained in the interval \([-\ell ,\infty )\). The result follows. \(\square \)
is contained in the interval \([-\ell ,\infty )\). The result follows. \(\square \)
Lemma 5.17
Let \(g:X\longrightarrow Z\) be a concentrated, pseudo-coherent morphism of quasi-separated, quasi-compact stacks, let \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) be a perfect complex, and assume \(g_*C\) is pseudo-coherent. [If \(g:X\longrightarrow Z\) is quasi-proper, the last assumption is a consequence of C being perfect.] Let \(V\subset Z\) be the open set obtained by applying Lemma 5.14 to the pseudo-coherent \(g_*C\in {{\textbf{D}}_{\textbf{qc}}}(Z)\)—that is, V is the set of points at which \(g_*C\) is perfect. Then, V contains the set of points \(z\in Z\) such that g is of finite Tor-dimension at every point \(x\in X\) with z in the closure of g(x).
Proof
Let \(z\in Z\) be a point such that g is of finite Tor-dimension at any \(x\in X\) with z in the closure of g(x). By Lemma 5.16, there exists an integer \(\ell \) and a 2-cartesian square

with \(Y={\textrm{Spec}(R)}\) an affine scheme, with v flat, with \(z\in v(Y)\), and so that \(f^*{{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge n}\subset {{\textbf{D}}_{\textbf{qc}}}(W)^{\ge n-\ell }\). As C is perfect the Tor-amplitude of C is in some bounded interval \([-m,m]\), and as u is flat the Tor-amplitude of \(u^*C\) is also in the interval \([-m,m]\). Therefore, \(u^*C\otimes f^*{{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge n} \subset {{\textbf{D}}_{\textbf{qc}}}(W)^{\ge n-\ell -m}\), and hence
Here the morphism f, being the fullback of the concentrated morphism g, is concentrated by [17, Lemma 2.5(1)], and the equality in the sequence of inclusions above is the projection formula for the concentrated morphism f, which holds by [17, Corollary 4.12]. The inclusion \(f_*u^*C\otimes {{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge n} \subset {{\textbf{D}}_{\textbf{qc}}}(Y)^{\ge n-\ell -m}\) tells us that \(f_*u^*C\) is an object of \({{\textbf{D}}_{\textbf{qc}}}(Y)={{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\cong {{\textbf{D}}}(R)\) with Tor-amplitude contained in the interval \([-\ell -m,\infty )\). On the other hand [17, Theorem 2.6(4)], applied to the cartesian square above in which the v is flat and g is concentrated, tells us that \(v^*g_*\cong f_*u^*\), and we deduce that \(v^*g_*C\cong f_*u^*C\). As \(g_*C\) is assumed pseudo-coherent so is \(v^*g_*C\), and being of Tor-amplitude contained in \([-\ell -m,\infty )\) it must be perfect. Hence, z is contained in the open set V of points at which \(g_*C\) is perfect. \(\square \)
Corollary 5.18
Let \(g:X\longrightarrow Z\) be a concentrated, pseudo-coherent morphism of quasi-separated, quasi-compact stacks, and suppose g is of finite Tor-dimension. We have
-
(i)
If \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) is perfect and \(g_*C\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) is pseudo-coherent, then \(g_*C\) is perfect.
-
(ii)
If g is quasi-proper then \(g_*\) takes perfect complexes to perfect complexes.
-
(iii)
Assume that g is quasi-proper and that \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated. Then,
-
(a)
\(g_*\) takes compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\) to compact objects in \({{\textbf{D}}_{\textbf{qc}}}(Z)\).
-
(b)
If \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated then \(g^\times \) respects coproducts, and the natural transformation \(\chi (E,F):g^*E\otimes g^\times F\longrightarrow g^\times (E\otimes F)\), which was defined in Notation 3.4(iv), is an isomorphism for every \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\).
-
(a)
Proof
In proving (i), apply Lemma 5.17 noting that, because g is of finite Tor-dimension, every \(z\in Z\) satisfies the technical condition of the Lemma. Hence, \(V=Z\), that is the complex \(g_*C\in {{\textbf{D}}^+_{\textrm{qc}}}(Z)\) is perfect at every point in Z. In the notation of Lemma 5.14, we have \(Z=V=\cup _{n\gg 0}^{}V_n\) with \(V_n\) open, and the quasi-compactness of Z gives that \(Z=V_n\) for some n. Thus, \(g_*C\) is a pseudo-coherent complex of Tor-amplitude contained in \([-n,\infty )\), hence \(g_*C\) is perfect.
Part (ii) is immediate from (i): if g is quasi-proper then \(g_*\) takes any perfect complex \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) to a pseudo-coherent \(g_*C\), which must be perfect by (i).
To prove (iii)(a), we use Lemma 5.7: the class \(S=\{C\otimes g^*\widetilde{C}\mid C\in {{\textbf{D}}_{\textbf{qc}}}(X)^c,\,\,\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)^c\}\) is a class of compact objects in \({{\textbf{D}}_{\textbf{qc}}}(X)\) and \({{\textbf{D}}_{\textbf{qc}}}(X)^c\) is its thick closure. If we let  be the full subcategory of objects \(L\in {{\textbf{D}}_{\textbf{qc}}}(X)\) with \(g_*L\) compact, then
be the full subcategory of objects \(L\in {{\textbf{D}}_{\textbf{qc}}}(X)\) with \(g_*L\) compact, then  is obviously a thick subcategory. We wish to show that
is obviously a thick subcategory. We wish to show that  , and it suffices to show that
, and it suffices to show that  .
.
But now we are in business: objects in S are of the form \(C\otimes g^*\widetilde{C}\), with \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) both compact. The projection formula holds for the concentrated morphism \(g:X\longrightarrow Z\) by [17, Corollary 4.12], hence \(g_*(C\otimes g^*\widetilde{C})\cong g_*C\otimes \widetilde{C}\). By [17, Lemma 4.4(1)] the compact object \(C\in {{\textbf{D}}_{\textbf{qc}}}(X)\) is perfect, and by (ii) above so is \(g_*C\in {{\textbf{D}}_{\textbf{qc}}}(Z)\). But now [17, Lemma 4.4(2)] tells us that \(g_*C\otimes \widetilde{C}\) is compact.
This proved (iii)(a). The first part (iii)(b) is a formal consequence: we know that \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated while (iii)(a) tells us that \(g_*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\) takes compacts to compacts, and [31, Theorem 5.1] allows us to conclude that \(g^\times \) respects coproducts.
Finally note that \(\chi \) is a natural transformation between functors both of which respect coproducts. Given an object \(F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), the full subcategory  of all objects E for which map \(\chi (E,F)\) is an isomorphism is localizing. On the other hand, Proposition 3.5 tells us that every compact object belongs to
of all objects E for which map \(\chi (E,F)\) is an isomorphism is localizing. On the other hand, Proposition 3.5 tells us that every compact object belongs to  , and as \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is assumed compactly generated we have
, and as \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is assumed compactly generated we have  . \(\square \)
. \(\square \)
Lemma 5.19
Let \(v:Y\longrightarrow Z\) be a flat morphism of quasi-compact, quasi-separated stacks, and let \(C',E\) be objects in \({{\textbf{D}}_{\textbf{qc}}}(Z)\). Assume \(C'=C''\otimes \widetilde{C}\), with \(C''\) pseudo-coherent and \(\widetilde{C}\) compact. Assume further that at least one of the two conditions below is satisfied:
-
(i)
Z satisfies Thomason’s condition, and the image of \(v:Y\longrightarrow Z\) is contained in the subset \(V=\cup _{n\gg 0}^{}V_n\subset Z\) given by Lemma 5.14 applied to the pseudo-coherent object \(C''\in {{\textbf{D}}_{\textbf{qc}}}(Z)\).
-
(ii)
E belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
Then, the map

is an isomorphism.
Proof
If E is bounded below then  is an isomorphism by [20, Proposition 3.7]. The difficulty is in case (i) of the Lemma.
is an isomorphism by [20, Proposition 3.7]. The difficulty is in case (i) of the Lemma.
Suppose, therefore, that we are in case (i) of the Lemma; the fact that the image of v is contained in V means that \(Y=\cup _{n\gg 0}^{}v^{-1}V_n\). Lemma 5.14 tells us that \(V_n\) is open for \(n\gg 0\), hence so is \(v^{-1}V_n\), and they obviously increase with n. As Y is quasi-compact, there exists an integer \(n\gg 0\) with \(Y=v^{-1}V_n\). Now, \(V_n\) is the union of its quasi-compact open subsets \(V_{n,\alpha }\), hence Y is the union of \(v^{-1}V_{n,\alpha }\), and being quasi-compact Y must be a finite union of \(v^{-1}V_{n,\alpha }\). Since the set of quasi-compact open substacks of \(V_n\) is closed under finite unions, we may choose a quasi-compact open subset \(U\subset V_n\) with \(v^{-1}U=Y\). The map \(v:Y\longrightarrow Z\) factors as \(Y{\mathop {\longrightarrow }\limits ^{\beta }}U{\mathop {\longrightarrow }\limits ^{\alpha }}Z\) with \(\alpha \) an open immersion and \(\alpha ^*C''\) perfect. We wish to show that the composite

is an isomorphism, and the second map is an isomorphism because \(\alpha ^*C' \cong \alpha ^*C''\otimes \alpha ^*\widetilde{C}\) is perfect. Hence, it suffices to prove that the map  is an isomorphism—we are reduced to the case where \(v:Y\longrightarrow Z\) is an open immersion with \(v^*C''\) perfect and Y quasi-compact. The quasi-compact open immersion \(v:Y\longrightarrow Z\) is representable, therefore, a concentrated morphism by [17, Lemma 2.5(3)], and [17, Theorem 2.6(3)] gives that \(v_*\) respects coproducts. From [31, Theorem 5.1] it follows that \(v^*\) takes compact objects to compact objects—we are given that \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) is compact, hence \(v^*\widetilde{C}\) is compact, and [17, Lemma 4.4(2)] allows us to conclude that \(v^*C'\cong v^*C''\otimes v^*\widetilde{C}\) is a compact object in \({{\textbf{D}}_{\textbf{qc}}}(Y)\).
is an isomorphism—we are reduced to the case where \(v:Y\longrightarrow Z\) is an open immersion with \(v^*C''\) perfect and Y quasi-compact. The quasi-compact open immersion \(v:Y\longrightarrow Z\) is representable, therefore, a concentrated morphism by [17, Lemma 2.5(3)], and [17, Theorem 2.6(3)] gives that \(v_*\) respects coproducts. From [31, Theorem 5.1] it follows that \(v^*\) takes compact objects to compact objects—we are given that \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) is compact, hence \(v^*\widetilde{C}\) is compact, and [17, Lemma 4.4(2)] allows us to conclude that \(v^*C'\cong v^*C''\otimes v^*\widetilde{C}\) is a compact object in \({{\textbf{D}}_{\textbf{qc}}}(Y)\).
The object \(C'\oplus \Sigma C'\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) restricts to a compact object in \({{\textbf{D}}_{\textbf{qc}}}(Y)\), whose image in \(K_0(Y)\) vanishes. We are assuming that Z satisfies Thomason’s condition. Thomason’s localization theorem, therefore, guarantees the existence of a compact object \(G\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) and a morphism \(\alpha :G\longrightarrow C'\oplus \Sigma C'\), so that the restriction to the quasi-compact open subset \(Y\subset Z\) is a quasi-isomorphism—for the case of semi-separated schemes see Thomason–Trobaugh [41], in the generality required here see [30], whose relevant results are summarized in [31, statements 2.1.4 and 2.1.5].
Now, complete \(\alpha \) to a triangle

The complex \(D\in {{\textbf{D}}^b_{\textrm{qc}}}(Z)\) is pseudo-coherent and \(v^*D=0\). Lemma 5.2 tells us that, for every object \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), we have  . Look at the morphism of triangles
. Look at the morphism of triangles

The object G is compact, hence perfect by [17, Lemma 4.4(1)]. This guarantees that \(\gamma \) is an isomorphism, and \(\beta \) is an isomorphism since the domain and codomain both vanish. From the morphism of triangles we learn that \(\delta \) is an isomorphism. \(\square \)
Lemma 5.20
As in Notation 5.8 suppose we are given a 2-cartesian square of quasi-compact, quasi-separated stacks

Assume that \({{\textbf{D}}_{\textbf{qc}}}(X)\) and \({{\textbf{D}}_{\textbf{qc}}}(Z)\) are compactly generated, that Z has quasi-affine diagonal, that v is flat and that g is quasi-proper and concentrated. Assume further that at least one of the two conditions below is satisfied:
-
(i)
The stack Z satisfies Thomason’s condition, the map g is pseudo-coherent, and the map f has finite Tor-dimension.
-
(ii)
E belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
Then, the base-change map \(\Phi :u^*g^\times E\longrightarrow f^\times v^* E\) is an isomorphism.
Proof
We wish to show that the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is an isomorphism in \({{\textbf{D}}_{\textbf{qc}}}(W)\), and by Lemmas 5.7 and 5.9 it suffices to prove that the functor  takes \(\Phi \) to an isomorphism for every object \(C=C''\otimes g^*\widetilde{C}\), with \(C''\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) both compact. Fix, therefore, a compact object \(C''\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and a compact object \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), and put \(C =C''\otimes g^*\widetilde{C}\). I assert:
takes \(\Phi \) to an isomorphism for every object \(C=C''\otimes g^*\widetilde{C}\), with \(C''\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) both compact. Fix, therefore, a compact object \(C''\in {{\textbf{D}}_{\textbf{qc}}}(X)\) and a compact object \(\widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), and put \(C =C''\otimes g^*\widetilde{C}\). I assert:
-
(iii)
The natural map
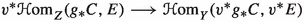 is an isomorphism.
is an isomorphism.
We will return to the proof of (iii) later, let us first see that our Lemma follows.
To prove the Lemma, consider the commutative diagram below (for a careful check of the commutativity see Lipman [25, Lemma 4.6.5])

In this diagram, \(\beta :v^*g_*\longrightarrow f_*v^*\) is the base-change map of Definition 4.1, the map \(\varepsilon :g_*g^\times \longrightarrow \textrm{id}\) is the counit of the adjunction \(g_*\dashv g^\times \), and \(\varepsilon ':f_*f^\times \longrightarrow \textrm{id}\) is the counit of the adjunction \(f_*\dashv f^\times \). The commutative triangle at the bottom is there merely to remind us of the definition of the isomorphism (4) of Lemma 5.3

The map (1) is an isomorphism because C is perfect, the map (2) is the isomorphism  of Lemma 5.3, and (3) is an isomorphism by (iii) above, to be proved later. The vertical arrows on the right of the diagram compute
of Lemma 5.3, and (3) is an isomorphism by (iii) above, to be proved later. The vertical arrows on the right of the diagram compute  applied to the composite defining \(\Phi :u^*g^\times E\longrightarrow f^\times v^*E\), essentially by the definition of \(\Phi \). And the commutative diagram shows how to factor this map through a series of isomorphisms.
applied to the composite defining \(\Phi :u^*g^\times E\longrightarrow f^\times v^*E\), essentially by the definition of \(\Phi \). And the commutative diagram shows how to factor this map through a series of isomorphisms.
It remains to prove assertion (iii) above. The object \(C''\) is assumed compact in \({{\textbf{D}}_{\textbf{qc}}}(X)\), and [17, Lemma 4.4(1)] tells us that \(C''\) is perfect. Since g is quasi-proper the object \(g_*C''\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) is pseudo-coherent. This makes \(g_*C=g_*(C''\otimes g^*\widetilde{C})\cong g_*C''\otimes \widetilde{C}\) the tensor product of a pseudo-coherent object and a compact object. We are in the situation of Lemma 5.19. If \(E\in {{\textbf{D}}^+_{\textrm{qc}}}(Z)\) then (iii) follows immediately from Lemma 5.19(ii). We have to prove that, under the hypotheses of case (i) of our current Lemma, we may apply Lemma 5.19(i) to the object \(C'=g_*C=g_*C''\otimes \widetilde{C}\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) and the map \(v:Y\longrightarrow Z\). We know that \(C''\) is compact in \({{\textbf{D}}_{\textbf{qc}}}(X)\), hence perfect. Therefore, \(u^*C''\in {{\textbf{D}}_{\textbf{qc}}}(W)\) is perfect. We also know that \(g_*C''\) is pseudo-coherent, thus so is \(v^*g_*C''\cong f_*u^*C''\). We apply Corollary 5.18(i) to the morphism \(f:W\longrightarrow Y\) and the perfect complex \(u^*C''\in {{\textbf{D}}_{\textbf{qc}}}(X)\)—by hypothesis f is of finite Tor-dimension and, being the pullback of g, it is concentrated and pseudo-coherent. The conclusion is that \(v^*g_*C''\cong f_*u^*C''\) is perfect, and hence v takes Y to the set of points \(V\subset Z\) where \(g_*C''\) is perfect. Lemma 5.19(i) applies. \(\square \)
Remark 5.21
For noetherian schemes case (ii) of Lemma 5.20 is classical and due to Hartshorne [18] and Verdier [42]. In fact, one of the two classical approaches to Grothendieck duality used Lemma 5.20(ii) as the cornerstone on which the theory is built—in the category \({{\textbf{D}}^+_{\textrm{qc}}}\), of course. In [31, Example 6.5], we observed that the base-change map need not be an isomorphism on unbounded objects. The main new tool of this article is Lemma 5.20(i), and the rest of the article shows how to deduce from this little lemma that everything works fine in the larger category \({{\textbf{D}}_{\textbf{qc}}}\), as long as one is just a little careful with composites.
There is a modern treatment of Lemma 5.20(ii) in Lipman [25, Section 4.6], quite similar to the one above. What is really new and different in this paper is that the crucial Lemma 5.19 has a version (i), leading to Lemma 5.20(i). The reader will note that the proof of Lemma 5.19(i) is rather subtler than that of the easy, classical Lemma 5.19(ii).
7 Geometric Manipulations to Obtain a Sharper Version of the Base-Change Lemma 5.20
In this section, we go through some geometric gymnastics to obtain a refinement of Lemma 5.20—we will still be appealing to the topological techniques involving compact generation, but in combination with the construction of auxiliary stacks and diagrams of morphisms among them. Before we start, let us note
Remark 6.1
In Example A.1, we will see a cartesian square of affine schemes, satisfying all the hypotheses of Lemma 5.20 except for the pseudo-coherence of g. But the map \(u^*g^\times \longrightarrow f^\times v^*\) is not an isomorphism, not even when restricted to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\). The pseudo-coherence seems essential.
When the stacks are noetherian all finite-type maps are pseudo-coherent and all proper maps are quasi-proper, making the hypotheses of Lemma 5.20 easy to fulfill. In the non-noetherian case quasi-proper, pseudo-coherent maps are hard to come by—there is a theorem of Kiehl [22, p. 315, Theorem 2.2] saying that every proper, pseudo-coherent map is quasi-proper but, while proper maps are plentiful, much of the geometric acrobatics we are about to witness will not preserve the pseudo-coherence of morphisms.
This means that very soon we will start assuming all our stacks noetherian. But to better pinpoint where the noetherian hypothesis seems essential, the next few lemmas remain in gorgeous generality.
Lemma 6.2
Suppose we are given a diagram of 2-cartesian squares of quasi-compact, quasi-separated stacks

Assume Y and Z have quasi-affine diagonals and satisfy Thomason’s condition, the category \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated, the morphisms f and g are quasi-proper, the morphism g is concentrated and pseudo-coherent, \(v'\) and v are flat and e is of finite Tor-dimension. If \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) is the base-change map of the square

then \({u'}^*\Phi : {u'}^*u^*g^\times \longrightarrow {u'}^*f^\times v^*\) is an isomorphism.
Proof
Since \({{\textbf{D}}_{\textbf{qc}}}(X)\) and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) are compactly generated and Z has quasi-affine diagonal, Corollary 5.10 tells us that \({{\textbf{D}}_{\textbf{qc}}}(W)\) is compactly generated. Pseudo-coherence and concentratedness are preserved by flat base-change and f, being the pullback of the concentrated and pseudo-coherent g by the flat map v, must also be concentrated and pseudo-coherent. Consider the two 2-cartesian squares

Since e is of finite Tor-dimension Lemma 5.20 applies to both squares, and tells us that the base-change maps for these two squares are isomorphisms. That is we have isomorphisms \(\Phi _1^{}:{u'}^*f^\times \longrightarrow e^\times {v'}^*\) and \(\Phi _2^{}:{u'}^*u^*g^\times \longrightarrow e^\times {v'}^*v^*\). But the isomorphism \(\Phi _2^{}\) can be written as the composite

where we know that \(\Phi _1^{}\) is an isomorphism. Hence, so is \({u'}^*\Phi ={\big [\Phi _1^{}v^*\big ]}^{-1}\Phi _2^{}\). \(\square \)
The next few lemmas are similar; it might help to set up common notation for all of them. We begin with a reminder of some standard notation.
Reminder 6.3
Recall that, if  is a finitely presented quasicoherent sheaf of Z, then
is a finitely presented quasicoherent sheaf of Z, then  stands for the stack
stands for the stack  where
where  is the symmetric algebra of
is the symmetric algebra of  over
over  . The stack Z is said to have the resolution property if every finitely presented sheaf
. The stack Z is said to have the resolution property if every finitely presented sheaf  over Z admits an epimorphism
over Z admits an epimorphism  , with
, with  a finite-rank vector bundle on Z. If \(g:X\longrightarrow Z\) has a factorization
a finite-rank vector bundle on Z. If \(g:X\longrightarrow Z\) has a factorization  , with j a closed immersion and
, with j a closed immersion and  a finitely-presented quasicoherent sheaf on Z, and if Z has the resolution property, then we can factor g as
a finitely-presented quasicoherent sheaf on Z, and if Z has the resolution property, then we can factor g as  with \(j'\) also a closed immersion.
with \(j'\) also a closed immersion.
Notation 6.4
For the next three results, the setup will be as follows. As in Notation 5.8, we will suppose given a 2-cartesian square of quasi-compact, quasi-separated stacks

We will assume that v is flat and g is concentrated and pseudo-coherent. We will also assume given a separated, finitely-presentable, representable, étale morphism \(\theta _Z^{}:\overline{Z}\longrightarrow Z\) (which may be the identity \(\textrm{id}:Z\longrightarrow Z\)). Assume that \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated and Y and Z have quasi-affine diagonals. Suppose further that, for all separated, finitely-presentable, representable étale maps \(\alpha :Y'\longrightarrow Y\) and \(\beta :Z'\longrightarrow Z\) and for every finitely presented quasicoherent sheaf  on either \(Y'\) or \(Z'\), the stack
on either \(Y'\) or \(Z'\), the stack  satisfies Thomason’s condition. Assume also that g factors as
satisfies Thomason’s condition. Assume also that g factors as  , where
, where  is a finitely presented quasicoherent sheaf on Z and j is a closed immersion. By Corollary 5.15 the set \(U\subset W\) on which f is of finite Tor-dimension is open—let \(u':U\longrightarrow W\) be the open immersion. Let \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) be the base-change map.
is a finitely presented quasicoherent sheaf on Z and j is a closed immersion. By Corollary 5.15 the set \(U\subset W\) on which f is of finite Tor-dimension is open—let \(u':U\longrightarrow W\) be the open immersion. Let \(\Phi :u^*g^\times \longrightarrow f^\times v^*\) be the base-change map.
The next three results all have the following shape: under some added hypotheses on the data above, which become less restrictive as we progress, some slight variants of some of (i), (ii) and possibly (iii) below hold.
-
(i)
The natural transformation \({u'}^*\Phi \theta _{Z*}^{}: {u'}^*u^*g^\times \theta _{Z*}^{}\longrightarrow {u'}^*f^\times v^*\theta _{Z*}^{}\) is an isomorphism.
-
(ii)
The isomorphic functors \({u'}^*u^*g^\times \theta _{Z*}^{}\cong {u'}^*f^\times v^*\theta _{Z*}^{}\) respect coproducts.
-
(iii)
If we further assume that all the stacks in the diagram are noetherian, then for any object \(z\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) we have that \({u'}^*u^*g^\times z=0\) if and only if \({u'}^*u^*g^*z=0\).
Lemma 6.5
With the conventions of Notation 6.4, assume further that \(\theta _Z^{}:\overline{Z}\longrightarrow Z\) is the identity map \(\textrm{id}:Z\longrightarrow Z\), and that the quasicoherent sheaf  is a finite-rank vector bundle on Z. Then, the conclusions of Notation 6.4 (i), (ii) and (iii) are true.
is a finite-rank vector bundle on Z. Then, the conclusions of Notation 6.4 (i), (ii) and (iii) are true.
Proof
The map g is assumed to factor as \(g=qj\), where  is a closed immersion and
is a closed immersion and  is the projection. Let
is the projection. Let  be the pullback of the vector bundle
be the pullback of the vector bundle  by the map \(v:Y\longrightarrow Z\), then our 2-cartesian square factors as a concatenation of two 2-cartesian squares
by the map \(v:Y\longrightarrow Z\), then our 2-cartesian square factors as a concatenation of two 2-cartesian squares

The vertical morphisms in this diagram are all concentrated. The stacks Z,  and
and  have quasi-affine diagonals and satisfy Thomason’s condition. The maps \(p_*\) and \(q_*\) obviously take pseudo-coherent complexes to pseudo-coherent complexes, that is p and q are quasi-proper. The map q is smooth while \(g=qj\) is pseudo-coherent by hypothesis, hence j is pseudo-coherent. Pseudo-coherence is stable by flat base change, hence i is also pseudo-coherent. Since i and j are proper and pseudo-coherent, Kiehl [22, p. 315, Theorem 2.2] tells us they are quasi-proper.
have quasi-affine diagonals and satisfy Thomason’s condition. The maps \(p_*\) and \(q_*\) obviously take pseudo-coherent complexes to pseudo-coherent complexes, that is p and q are quasi-proper. The map q is smooth while \(g=qj\) is pseudo-coherent by hypothesis, hence j is pseudo-coherent. Pseudo-coherence is stable by flat base change, hence i is also pseudo-coherent. Since i and j are proper and pseudo-coherent, Kiehl [22, p. 315, Theorem 2.2] tells us they are quasi-proper.
Since p is flat it is certainly of finite Tor-dimension, and Lemma 5.20 tells us that the base-change map \(\Phi _1^{}:w^*q^\times \longrightarrow p^\times v^*\) is an isomorphism.
Since p is smooth, the open subset \(U\subset W\) on which \(f=pi\) is of finite Tor-dimension is equal to the subset on which i is of finite Tor-dimension; see [19, page 246, 3.6]. Choose an open set  with \(U=V\cap W\). If \(u':U\longrightarrow W\) is the open immersion, we wish to show that \({u'}^*\Phi : {u'}^*u^*g^\times \longrightarrow {u'}^*f^\times v^*\) is an isomorphism. The question is local in U, and replacing V by a quasi-compact open subset we may assume V is quasi-compact and open in
with \(U=V\cap W\). If \(u':U\longrightarrow W\) is the open immersion, we wish to show that \({u'}^*\Phi : {u'}^*u^*g^\times \longrightarrow {u'}^*f^\times v^*\) is an isomorphism. The question is local in U, and replacing V by a quasi-compact open subset we may assume V is quasi-compact and open in  . Now, consider the diagram with 2-cartesian squares
. Now, consider the diagram with 2-cartesian squares

then the map \(i':U\longrightarrow V\) is of finite Tor-dimension. By Lemma 6.2 we have that, if \(\Phi _2^{}:u^*j^\times \longrightarrow i^\times w^*\) is the base-change map of the square

then \({u'}^*\Phi _2^{}:{u'}^*u^*j^\times \longrightarrow {u'}^*i^\times w^*\) is an isomorphism. Let us summarize what we have so far: we began with a diagram of 2-cartesian squares

We have studied the base-change maps of the squares

and proved that
-
(i)
\(\Phi _1^{}:w^*q^\times \longrightarrow p^\times v^*\) is an isomorphism.
-
(ii)
The functor \({u'}^*\) takes the base-change map \(\Phi _2^{}:u^*j^\times \longrightarrow i^\times w^*\) to an isomorphism.
If \(\Phi :u^*g^\times =u^*j^\times q^\times \longrightarrow i^\times p^\times v^*=f^\times v^*\) is the base-change map of the 2-cartesian square

then we can write it as the composite

where \(i^\times \Phi _1^{}\) is an isomorphism, while \(\Phi _2^{}q^\times \) becomes an isomorphism if we compose it with \({u'}^*\). Therefore, \({u'}^*\Phi \) is an isomorphism, and we have proved (i).
Next, we prove (ii), that is we show that the isomorphic functors \({u'}^*u^*g^\times \cong {u'}^*f^\times v^*\) respect coproducts. The question is still local in U, hence we may continue assuming that, in the diagrams above, U and V are quasi-compact. Write \({u'}^*f^\times v^*\) as \({u'}^*i^\times p^\times v^*\). The base-change map \({u'}^*i^\times \longrightarrow {i'}^\times {w'}^*\) is an isomorphism by Lemma 5.20(i), hence the functor \({u'}^*f^\times v^*\) is isomorphic to \({i'}^\times {w'}^*p^\times v^*\). The functors \({w'}^*\) and \(v^*\) preserve coproducts because they have right adjoints. It, therefore, suffices to show that \({i'}^\times \) and \(p^\times \) preserve coproducts, and we will prove this by applying Corollary 5.18(iii)(b). We know that \(i'\) and p are pseudo-coherent and proper—hence quasi-proper by Kiehl’s theorem. They are also concentrated and of finite Tor-dimension, hence to apply Corollary 5.18(iii)(b), we only need to check that the categories \({{\textbf{D}}_{\textbf{qc}}}(U)\), \({{\textbf{D}}_{\textbf{qc}}}(V)\),  and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) are compactly generated. For \({{\textbf{D}}_{\textbf{qc}}}(Y)\) and
and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) are compactly generated. For \({{\textbf{D}}_{\textbf{qc}}}(Y)\) and  , this is part of the hypotheses of Notation 6.4. Note also that by the hypotheses of Notation 6.4, we know that Z has quasi-affine diagonal and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) and \({{\textbf{D}}_{\textbf{qc}}}(X)\) are compactly generated, and Corollary 5.10 guarantees that \({{\textbf{D}}_{\textbf{qc}}}(W)\) is compactly generated. But the maps \(u':U\longrightarrow W\) and
, this is part of the hypotheses of Notation 6.4. Note also that by the hypotheses of Notation 6.4, we know that Z has quasi-affine diagonal and \({{\textbf{D}}_{\textbf{qc}}}(Y)\) and \({{\textbf{D}}_{\textbf{qc}}}(X)\) are compactly generated, and Corollary 5.10 guarantees that \({{\textbf{D}}_{\textbf{qc}}}(W)\) is compactly generated. But the maps \(u':U\longrightarrow W\) and  are open immersions and [17, Lemma 8.2] (see also Observation 5.6) tell us that the compact generation of \({{\textbf{D}}_{\textbf{qc}}}(W)\) and
are open immersions and [17, Lemma 8.2] (see also Observation 5.6) tell us that the compact generation of \({{\textbf{D}}_{\textbf{qc}}}(W)\) and  implies the compact generation of \({{\textbf{D}}_{\textbf{qc}}}(U)\) and \({{\textbf{D}}_{\textbf{qc}}}(V)\).
implies the compact generation of \({{\textbf{D}}_{\textbf{qc}}}(U)\) and \({{\textbf{D}}_{\textbf{qc}}}(V)\).
It remains to prove (iii), in which all the stacks are assumed noetherian. With the notation as above choose an affine scheme \(S'\) of finite type and faithfully flat over V, and form the diagram of 2-cartesian squares of finite-type maps of noetherian stacks

By construction the horizontal maps are flat, the vertical maps are closed immersions, and \(i'\) and, therefore, \(\gamma \) are of finite Tor-dimension. By the faithful flatness of \(\sigma \) we have that, for any object \({\mathfrak {u}}\in {{\textbf{D}}_{\textbf{qc}}}(U)\), the object \(\sigma ^*{\mathfrak {u}}\) vanishes if and only if \({\mathfrak {u}}\) does. Hence, given \(z\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), we have \({u'}^*f^\times v^*z=0\) if and only if \(\sigma ^*{u'}^*f^\times v^*z\cong \sigma ^*{u'}^*i^\times p^\times v^*z=0\). But Lemma 5.20, applied to the cartesian square

gives an isomorphism \(\sigma ^*{u'}^*i^\times \cong \gamma ^\times \theta ^*{w'}^*\), and it follows that \({u'}^*f^\times v^*z=0\) if and only if \(\gamma ^\times \theta ^*{w'}^*p^\times v^*z=0\).
But now \(\gamma \) is a closed immersion of affine noetherian schemes, and the functors \(\gamma ^*\) and \(\gamma ^\times \) are very concrete. Let \(S'={\textrm{Spec}(R')}\) and \(S={\textrm{Spec}(R)}\) and identify \({{\textbf{D}}_{\textbf{qc}}}(S)\cong D(R)\) and \({{\textbf{D}}_{\textbf{qc}}}(S')\cong {{\textbf{D}}}(R')\), then the functor \(\gamma ^*\) identifies with \(R\otimes _{R'}^{}(-)\) while \(\gamma ^\times \) is the functor \({{\textrm{Hom}}}_{R'}^{}(R,-)\). Support theory, more concretely [21, Proposition A.3(1)] applied to the object \(E=R\in {{\textbf{D}}}(R')\) with Zariski-closed support and to the object \(F=\theta ^*{w'}^*p^\times v^*z\) in \({{\textbf{D}}}(R')\), tells us that \(\gamma ^\times \theta ^*{w'}^*p^\times v^*z=0\) if and only if \(\gamma ^*\theta ^*{w'}^*p^\times v^*z= \sigma ^*{u'}^*i^*p^\times v^*z=0\), and the faithful flatness of \(\sigma \) tells us that this happens if and only if \({u'}^*i^*p^\times v^*z=0\). Summarizing what we have so far: \({u'}^*f^\times v^*z=0\) if and only if \({u'}^*i^*p^\times v^*z=0\).
It remains to show that \({u'}^*i^*p^\times v^*z=0\) if and only if \({u'}^*i^*p^* v^*z={u'}^*f^*v^*z=0\). But the map  is a locally closed immersion, hence \(i_*u'_*\) is conservative—it reflects vanishing. Hence, it remains to show that \(i_*u'_*{u'}^*i^*p^\times v^*z=0\) if and only if \(i_*u'_*{u'}^*i^*p^*v^*z=0\). But the projection formula—which holds for the concentrated morphism \(iu'\) by [17, Corollary 4.12]—gives an isomorphism
is a locally closed immersion, hence \(i_*u'_*\) is conservative—it reflects vanishing. Hence, it remains to show that \(i_*u'_*{u'}^*i^*p^\times v^*z=0\) if and only if \(i_*u'_*{u'}^*i^*p^*v^*z=0\). But the projection formula—which holds for the concentrated morphism \(iu'\) by [17, Corollary 4.12]—gives an isomorphism  . Hence, it will certainly suffice to show that, for any objects
. Hence, it will certainly suffice to show that, for any objects  and \(y\in {{\textbf{D}}_{\textbf{qc}}}(Y)\), we have \(F\otimes p^*y=0\) if and only if \(F\otimes p^\times y=0\). Since the map p is flat and proper Lemma 5.20 says that \(p^\times \) commutes with flat base change, and hence the assertion can be checked flat-locally. Replacing Y by an affine faithfully flat cover \({\textrm{Spec}(R)}\) on which the vector bundle
and \(y\in {{\textbf{D}}_{\textbf{qc}}}(Y)\), we have \(F\otimes p^*y=0\) if and only if \(F\otimes p^\times y=0\). Since the map p is flat and proper Lemma 5.20 says that \(p^\times \) commutes with flat base change, and hence the assertion can be checked flat-locally. Replacing Y by an affine faithfully flat cover \({\textrm{Spec}(R)}\) on which the vector bundle  trivializes, what remains to be proved is
trivializes, what remains to be proved is
-
(iii)
Let R be a noetherian ring. Let \(p:{{\mathbb {P}}}^n_R\longrightarrow {\textrm{Spec}(R)}\) be the natural projection, let y be an object in \({{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(R)}\big )\cong {{\textbf{D}}}(R)\), and let F be an object in \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {P}}}^n_R)\). Then, \(F\otimes p^*y=0\) if and only if \(F\otimes p^\times y=0\).
Of course, at this point, we could really stop—in the special case of \(p:{{\mathbb {P}}}^n_R\longrightarrow {\textrm{Spec}(R)}\) the functor \(p^\times \) is well understood and we can appeal to computations in the literature. But in this article, we are partly interested in how much of the theory can be developed on very formal, category-theoretic grounds, without any computation; in the manuscript, [33] we will explain how the formal theory can be used to render the traditional computations very easy. Let us, therefore, proceed to prove (iii) using zero concrete computations.
Our particular p is flat and proper, hence Corollary 5.18(iii) tells us that \(p_*\) respects compacts and \(p^\times \) respects coproducts. By Corollary 5.18(iii)(b), with  , it follows that there is a natural isomorphism \(p^\times (-)\cong p^*(-)\otimes p^\times R\). Therefore, proving (iii) is equivalent to proving that \(F\otimes p^*y\otimes p^\times R=0\) if and only if \(F\otimes p^*y=0\). Support theory, more precisely [21, Proposition A.3(1)], tells us that it suffices to prove that \(\text {supp}(p^\times R)={{\mathbb {P}}}_R^n\).
, it follows that there is a natural isomorphism \(p^\times (-)\cong p^*(-)\otimes p^\times R\). Therefore, proving (iii) is equivalent to proving that \(F\otimes p^*y\otimes p^\times R=0\) if and only if \(F\otimes p^*y=0\). Support theory, more precisely [21, Proposition A.3(1)], tells us that it suffices to prove that \(\text {supp}(p^\times R)={{\mathbb {P}}}_R^n\).
Given a point \(x\in {{\mathbb {P}}}^n_R\) with residue field k(x), we wish to show that \(k(x)\otimes p^\times R\ne 0\). Let \(\mathfrak {p}\in {\textrm{Spec}(R)}\) be p(x); it is a prime ideal \(\mathfrak {p}\subset R\). Let \(k=k(\mathfrak {p})\) be its residue field. Consider the cartesian square

The map p is flat, hence Tor-independent base-change gives an isomorphism \({\gamma '}^*p_*\longrightarrow {p'}_*\gamma ^*\). Taking right adjoints gives an isomorphism \(\gamma _*{p'}^\times \longrightarrow p^\times \gamma '_*\). Applying this to the object \(k\in {{\textbf{D}}}(k)\cong {{\textbf{D}}_{\textbf{qc}}}\big ({\textrm{Spec}(k)}\big )\) we have an isomorphism \(\gamma _*{p'}^\times k\longrightarrow p^\times k \cong p^*k\otimes _{{{\mathbb {P}}}_R^n}^{}p^\times R\). We wish to show that \(k(x)\otimes _{{{\mathbb {P}}}_R^n}^{}p^\times R\ne 0\), and because \(k(x) \otimes _{{{\mathbb {P}}}_R^n}^{}p^*k\) is a (nonzero) direct sum of suspensions of k(x), it suffices to prove the non-vanishing of
The projection formula tells us that \(k(x) \otimes _{{{\mathbb {P}}}_R^n}^{}[\gamma _*{p'}^\times k]\cong \gamma _*\big [\gamma ^*k(x)\otimes _{{{\mathbb {P}}}_k^n}^{} {p'}^\times k]\). The morphism \(\gamma \) is affine, hence \(\gamma _*\) is conservative—it suffices to prove the non-vanishing of \(\gamma ^*k(x)\otimes _{{{\mathbb {P}}}_k^n}^{} {p'}^\times k\). But \(\gamma ^*k(x)\) is a non-vanishing direct sum of suspensions of the residue field \(k(\gamma ^{-1}x)\), and it suffices to prove \(k(\gamma ^{-1}x)\otimes _{{{\mathbb {P}}}_k^n}^{} {p'}^\times k\) does not vanish. In other words, we are reduced to the case where \(R=k\) is a field.
Assume, therefore, that \(R=k\) is a field, therefore, \({{\mathbb {P}}}^n_k\) is smooth and projective over the field k. The subcategory of compact objects in \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {P}}}^n_k)\) is equal to \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\), and by [8, Theorem 1.1] every finite-type homological functor on \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\) is representable. In particular, there is an object \(E\in {{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\) and an isomorphism of functors \({{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}(-,E)\longrightarrow {{\textrm{Hom}}}_k^{}\big (p_*(-),k\big )\cong {{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}(-,p^\times k)\) on the category \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\). That is, even though we do not (yet) know whether \(p^\times k\) belongs to \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\), when we restrict the functor \({{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}(-,p^\times k)\) to the subcategory \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\), we obtain a representable functor, represented by E. The identity in \({{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}(E,E)\) maps to an element of \({{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}(E,p^\times k)\), that is a morphism \(\rho :E\longrightarrow p^\times k\), and Yoneda’s lemma tells us that \(\rho \) induces the isomorphism of functors on \({{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\). Hence, for every object \(F\in {{\textbf{D}}}_{\textbf{coh}}^b({{\mathbb {P}}}^n_k)\), the functor \({{\textrm{Hom}}}(F,-)\) takes \(\rho \) to an isomorphism. But now the category of all \(F'\in {{\textbf{D}}_{\textbf{qc}}}({{\mathbb {P}}}^n_k)\) such that \({{\textrm{Hom}}}(F',-)\) takes \(\rho \) to an isomorphism is a localizing subcategory of \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {P}}}^n_k)\) containing all the compacts, hence it is all of \({{\textbf{D}}_{\textbf{qc}}}({{\mathbb {P}}}^n_k)\). It follows that \(\rho \) is an isomorphism, and \(p^\times k\) is compact.
This means that \(\text {supp}(p^\times k)\) is a closed subset of \({{\mathbb {P}}}^n_k\), and Hilbert’s Nulstellensatz says the closed points are dense. It suffices to show that every closed point in \({{\mathbb {P}}}^n_k\) belongs to \(\text {supp}(p^\times k)\). But for a closed point x the support of k(x) is closed, and [21, Proposition A.3(1)] tells us that \(k(x)\otimes p^\times k=0\) if and only if \({{\textrm{Hom}}}\big (k(x),p^\times k\big )=0\). But \({{\textrm{Hom}}}_{{{\mathbb {P}}}_k^n}^{}\big (k(x),p^\times k\big )={{\textrm{Hom}}}_{k}^{}\big (p_*k(x),k\big )\ne 0\). \(\square \)
Remark 6.6
In the proof of Lemma 6.5, the noetherian hypothesis enters when we use support theory. Support theory is known to work beautifully for noetherian schemes, while the obvious generalizations fail miserably in the non-noetherian case. But the noetherian hypothesis will become even more crucial later.
Lemma 6.7
With the conventions of Notation 6.4, assume further that the stack \(\overline{Z}\) in the given étale map \(\theta _Z^{}:\overline{Z}\longrightarrow Z\) satisfies the resolution property. Then, the conclusions of Notation 6.4 (i) and (ii) are true.
Proof
Pull back along the map \({\theta _Z^{}}:\overline{Z}\longrightarrow Z\) to obtain the diagram

We are assuming that \({{\textbf{D}}_{\textbf{qc}}}(X)\) is compactly generated, that \(\overline{Z}\) satisfies Thomason’s condition (and in particular \({{\textbf{D}}_{\textbf{qc}}}(\overline{Z})\) is compactly generated), while Z is assumed to have quasi-affine diagonal. From Corollary 5.10 we deduce that \({{\textbf{D}}_{\textbf{qc}}}(\overline{X})\) is compactly generated. The map \({\theta _Z^{}}\) is assumed representable, hence so are its pullbacks \({\theta _U^{}}\), \({\theta _W^{}}\), \({\theta _X^{}}\) and \({\theta _Y^{}}\). Being representable these maps are also concentrated. The map \(\overline{g}\) is the pullback of the pseudo-coherent map g which factors as  , hence \(\overline{g}\) is pseudo-coherent and factors as
, hence \(\overline{g}\) is pseudo-coherent and factors as  . Since \(\overline{Z}\) has the resolution property Reminder 6.3 permits us to factor \(\overline{g}\) further as
. Since \(\overline{Z}\) has the resolution property Reminder 6.3 permits us to factor \(\overline{g}\) further as  , with
, with  a finite-rank vector bundle on \(\overline{Z}\). Lemma 6.5 now applies to the diagram
a finite-rank vector bundle on \(\overline{Z}\). Lemma 6.5 now applies to the diagram

and we deduce that
-
(i)
The map \({\overline{u}'}^*\overline{\Phi }:{\overline{u}'}^*\overline{u}^*\overline{g}^\times \longrightarrow {\overline{u}'}^*\overline{f}^\times \overline{v}^*\) is an isomorphism.
-
(ii)
The isomorphic functors \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \cong {\overline{u}'}^*\overline{f}^\times \overline{v}^*\) respect coproducts.
-
(iii)
In the case where the stacks are all noetherian, if \(z\in {{\textbf{D}}_{\textbf{qc}}}(\overline{Z})\) is an object then \({\overline{u}'}^*\overline{u}^*\overline{g}^\times z \cong {\overline{u}'}^*\overline{f}^\times \overline{v}^*z=0\) if and only if \({\overline{u}'}^*\overline{u}^*\overline{g}^*z \cong {\overline{u}'}^*\overline{f}^*\overline{v}^*z=0\).
We will not use (iii) in the proof of the current Lemma, but will refer back to it in the proof of the next Proposition. In fact, we will be referring back to the diagrams of this proof.
Back to the proof of the current Lemma: flat base-change for the concentrated maps \({\theta _W^{}}\), \({\theta _Y^{}}\) and \({\theta _Z^{}}\) gives isomorphisms
-
(iv)
\({u'}^*{\theta _{W*}^{}}\cong {\theta _{U*}^{}}{\overline{u}'}^*\), \(u^*{\theta _{X*}^{}}\cong {\theta _{W*}^{}}\overline{u}^*\), \(v^*{\theta _{Z*}^{}}\cong {\theta _{Y*}^{}}\overline{v}^*\).
while flat base-change for the concentrated morphisms g and f gives isomorphisms
-
(v)
\(\theta _Z^*g_*\cong \overline{g}_*\theta _X^*\), \(\theta _Y^*f_*\cong \overline{f}_*\theta _W^*\), and taking right adjoints \({\theta _{X*}^{}}\overline{g}^\times \cong g^\times {\theta _{Z*}^{}}\), \({\theta _{W*}^{}}\overline{f}^\times \cong f^\times {\theta _{Y*}^{}}\).
Combining (iv) and (v) and a diagram chase, we have that \({u'}^*\Phi {\theta _{Z*}^{}}:{u'}^*u^*g^\times {\theta _{Z*}^{}}\longrightarrow {u'}^*f^\times v^*{\theta _{Z*}^{}}\) is isomorphic to \({\theta _{U*}^{}}{\overline{u}'}^*\overline{\Phi }: {\theta _{U*}^{}}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \longrightarrow {\theta _{U*}^{}} {\overline{u}'}^*\overline{f}^\times \overline{v}^*\). By (i), we know that \({\overline{u}'}^*\overline{\Phi }\) is an isomorphism, hence so is \({\theta _{U*}^{}}{\overline{u}'}^*\overline{\Phi }\cong {u'}^*\Phi {\theta _{Z*}^{}}\). From (ii), we know that the isomorphic functors \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \cong {\overline{u}'}^*\overline{f}^\times \overline{v}^*\) respect coproducts, as does the functor \({\theta _{U*}^{}}\) for the concentrated morphism \(\theta _U\). Hence, the isomorphic functors \({\theta _{U*}^{}}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \cong {\theta _{U*}^{}} {\overline{u}'}^*\overline{f}^\times \overline{v}^*\) respect coproducts, but they are also isomorphic to \({u'}^*u^*g^\times {\theta _{Z*}^{}}\cong {u'}^*f^\times v^*{\theta _{Z*}^{}}\). \(\square \)
Proposition 6.8
Let the conventions be as in Notation 6.4, but now assume that \(\theta _Z^{}:\overline{Z}\longrightarrow Z\) is an étale cover with \(\overline{Z}\) satisfying the resolution property. Then, part (iii) of Notation 6.4 is true, as are the following strengthenings of (i) and (ii) of Notation 6.4:
-
(i)
The natural transformation \({u'}^*\Phi : {u'}^*u^*g^\times \longrightarrow {u'}^*f^\times v^*\) is an isomorphism.
-
(ii)
The isomorphic functors \({u'}^*u^*g^\times \cong {u'}^*f^\times v^*\) respect coproducts.
Proof
By Lemma 6.7, we have that \({u'}^*\Phi \theta _{Z*}^{}\) is an isomorphism and the isomorphic functors \({u'}^*u^*g^\times \theta _{Z*}^{}\longrightarrow {u'}^*f^\times v^*\theta _{Z*}^{}\) respect coproducts. If \(P\in {{\textbf{D}}_{\textbf{qc}}}(\overline{Z})\) is any object, then \(P\otimes \theta _{Z}^{*}(-)\) is a functor \({{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(\overline{Z})\) respecting coproducts, and hence
-
(iii)
The natural transformation \({u'}^*\Phi \theta _{Z*}^{}\big [P\otimes \theta _{Z}^{*}(-)\big ]\) is an isomorphism.
-
(iv)
The isomorphic functors \({u'}^*u^*g^\times \theta _{Z*}^{}\big [P\otimes \theta _{Z}^{*}(-)\big ]\,\,\cong \,\, {u'}^*f^\times v^*\theta _{Z*}^{}\big [P\otimes \theta _{Z}^{*}(-)\big ]\) respect coproducts.
The projection formula for the concentrated morphism \(\theta _Z^{}:\overline{Z}\longrightarrow Z\) gives an isomorphism \(\theta _{Z*}^{}\big [P\otimes \theta _{Z}^{*}(-)\big ]\,\,\cong \,\,(\theta _{Z*}^{}P)\otimes (-)\), and (iii) and (iv) rewrite as
-
(v)
The natural transformation \({u'}^*\Phi \big [(\theta _{Z*}^{}P)\otimes (-)\big ]\) is an isomorphism.
-
(vi)
The isomorphic functors \({u'}^*u^*g^\times \big [(\theta _{Z*}^{}P)\otimes (-)\big ]\,\,\cong \,\,{u'}^*f^\times v^*\big [(\theta _{Z*}^{}P)\otimes (-)\big ]\) respect coproducts.
Let  be the full subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) of all objects \(E \in {{\textbf{D}}_{\textbf{qc}}}(Z)\) so that
be the full subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) of all objects \(E \in {{\textbf{D}}_{\textbf{qc}}}(Z)\) so that
-
(vii)
The natural transformation \({u'}^*\Phi (E\otimes -)\) is an isomorphism.
-
(viii)
The isomorphic functors \({u'}^*u^*g^\times (E\otimes -)\,\,\cong \,\,{u'}^*f^\times v^*(E\otimes -)\) respect coproducts.
By (v) and (vi), we know that for any object \(P\in {{\textbf{D}}_{\textbf{qc}}}(\overline{Z})\), the object \(\theta _{Z*}^{}P\) belongs to  . Clearly
. Clearly  is a thick subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\). By [17, Lemma A.1], we have that every compact object in \({{\textbf{D}}_{\textbf{qc}}}(Z)\) lies in
is a thick subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\). By [17, Lemma A.1], we have that every compact object in \({{\textbf{D}}_{\textbf{qc}}}(Z)\) lies in  .
.
Let E be a compact object of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) and let \(F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) be arbitrary. By Lemma 4.7, we have a commutative diagram

The horizontal maps are isomorphisms; for \(\mu _u^{}\) and \(f^\times \mu _v^{}\) this is obvious, and for \(\chi (g,E,F)\) and \(\chi (f,v^*E,v^*F)\) we note that E is compact, hence perfect, hence \(v^*E\) is also perfect, and Proposition 3.5 applies. Applying the functor \({u'}^*\), we obtain the commutativity of the right-hand square in

and the left-hand square commutes by the naturality of the oplax structure map \(\mu _{{u'}^*}^{}:{u'}^*(A\otimes B)\longrightarrow {u'}^*A\otimes {u'}^*B\). The fact that  contains all the compact objects E says that the vertical map on the right is an isomorphism and the isomorphic functors respect coproducts. The commutativity says that the same is true on the left. Therefore, define the subcategory
contains all the compact objects E says that the vertical map on the right is an isomorphism and the isomorphic functors respect coproducts. The commutativity says that the same is true on the left. Therefore, define the subcategory  to contain all the objects \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) so that
to contain all the objects \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) so that
-
(ix)
The natural transformation \({u'}^*u^*g^*(E)\otimes {u'}^*\Phi (-)\) is an isomorphism.
-
(x)
The isomorphic functors \({u'}^*u^*g^*(E)\otimes {u'}^*u^*g^\times (-)\,\,\cong \,\,{u'}^*u^*g^*(E)\otimes {u'}^*f^\times v^*(-)\) respect coproducts.
The above argument showed that \({{\textbf{D}}_{\textbf{qc}}}(Z)^c\) is contained in  , while
, while  is obviously localizing. As \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated we conclude that
is obviously localizing. As \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated we conclude that  , in particular
, in particular  . Therefore, (i) and (ii) follow.
. Therefore, (i) and (ii) follow.
It remains to prove that, under the hypotheses of Proposition 6.8, part (iii) of Notation 6.4 is true. Let  be the full subcategories annihilated (respectively) by the functors \({u'}^*u^*g^\times \) and \({u'}^*u^*g^*\); we need to prove that
be the full subcategories annihilated (respectively) by the functors \({u'}^*u^*g^\times \) and \({u'}^*u^*g^*\); we need to prove that  . With the notation as in the proof of Lemma 6.7, part (iii) of the proof of Lemma 6.7 tells us that
. With the notation as in the proof of Lemma 6.7, part (iii) of the proof of Lemma 6.7 tells us that  , where
, where  is full subcategory annihilated by \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \) while
is full subcategory annihilated by \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \) while  is the full subcategory annihilated by \({\overline{u}'}^*\overline{u}^*\overline{g}^*\). The idea will be to relate
is the full subcategory annihilated by \({\overline{u}'}^*\overline{u}^*\overline{g}^*\). The idea will be to relate  to
to  and
and  to
to  .
.
Recall the diagrams in the proof of Lemma 6.7: because the map \(\theta _U^{}:\overline{U}\longrightarrow U\) is finite-type, representable, separated and étale it is quasi-affine, hence \(\theta _{U*}^{}\) is conservative. Thus, the kernel  (respectively,
(respectively,  of \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \) (respectively, \({\overline{u}'}^*\overline{u}^*\overline{g}^*\)) is equal to the kernel of \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \) (respectively, \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^*\)). In the proof of Lemma 6.7, we saw that \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \cong {u'}^*u^*g^\times \theta _{Z*}^{}\), while the isomorphism \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^* \cong {u'}^*u^*g^*\theta _{Z*}^{}\) is by Tor-independent base change (\(\theta _Z^{}\) is étale, in particular flat). This gives
of \({\overline{u}'}^*\overline{u}^*\overline{g}^\times \) (respectively, \({\overline{u}'}^*\overline{u}^*\overline{g}^*\)) is equal to the kernel of \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \) (respectively, \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^*\)). In the proof of Lemma 6.7, we saw that \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^\times \cong {u'}^*u^*g^\times \theta _{Z*}^{}\), while the isomorphism \(\theta _{U*}^{}{\overline{u}'}^*\overline{u}^*\overline{g}^* \cong {u'}^*u^*g^*\theta _{Z*}^{}\) is by Tor-independent base change (\(\theta _Z^{}\) is étale, in particular flat). This gives
-
(xi)
For \(i\in \{1,2\}\), we have
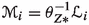 , and hence
, and hence 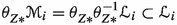 .
.
Notation 3.4(iv) gives us maps natural in \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) of the form \(\chi (g,E,F):g^*E\otimes g^\times F\longrightarrow g^\times (E\otimes F)\), and these induce maps \({u'}^*u^*\chi (g,E,F):{u'}^*u^*g^*E\otimes {u'}^*u^*g^\times F\longrightarrow {u'}^*u^*g^\times (E\otimes F)\). Let  be the full subcategory
be the full subcategory

Proposition 3.5 tells us that the map \(\chi (g,E,F)\) is an isomorphism whenever E is compact, hence \({u'}^*u^*\chi (g,E,F)\) is also an isomorphism when E is compact—in other words \({{\textbf{D}}_{\textbf{qc}}}(Z)^c\) is contained in  . On the other hand by Proposition 6.8(ii), we know that the functor \({u'}^* u^*g^\times \) respects coproducts, and this makes \({u'}^*u^*\chi (g,E,F)\) a natural transformation between functors both of which respect coproducts (in both the variable E and the variable F). It follows that
. On the other hand by Proposition 6.8(ii), we know that the functor \({u'}^* u^*g^\times \) respects coproducts, and this makes \({u'}^*u^*\chi (g,E,F)\) a natural transformation between functors both of which respect coproducts (in both the variable E and the variable F). It follows that  is a localizing subcategory, and since
is a localizing subcategory, and since  and \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated we have that
and \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated we have that  . That is \({u'}^*u^*\chi (g,E,F)\) is an isomorphism for all \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\). If
. That is \({u'}^*u^*\chi (g,E,F)\) is an isomorphism for all \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\). If  , that is if \({u'}^*u^*g^\times F=0\), the isomorphism \({u'}^*u^*g^\times (E\otimes F)\cong {u'}^*u^*g^*E\otimes {u'}^*u^*g^\times F\) tells us that \({u'}^*u^*g^\times (E\otimes F)=0\), that is
, that is if \({u'}^*u^*g^\times F=0\), the isomorphism \({u'}^*u^*g^\times (E\otimes F)\cong {u'}^*u^*g^*E\otimes {u'}^*u^*g^\times F\) tells us that \({u'}^*u^*g^\times (E\otimes F)=0\), that is  . Thus,
. Thus,  is not only localizing, it is also a tensor ideal. Since \({u'}^*u^*g^*\) is a strong monoidal functor its kernel
is not only localizing, it is also a tensor ideal. Since \({u'}^*u^*g^*\) is a strong monoidal functor its kernel  is also a localizing tensor ideal.
is also a localizing tensor ideal.
For \(i\in \{1,2\}\), we have the inclusions

where the equality is by the projection formula and the inclusion because  is a tensor ideal. From (xi), it follows that
is a tensor ideal. From (xi), it follows that  . But then
. But then
-
(xii)
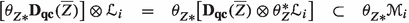 .
.
Combining (xi) and (xii), we have inclusions

and if we let \({\textrm{Loc}}(-)\) be the operation taking a subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) to the localizing subcategory it generates, then

By [17, Lemma A.1], we have that  , and so
, and so  . The equality
. The equality  now gives
now gives  . \(\square \)
. \(\square \)
In order to use Proposition 6.8, we need a result that produces for us maps \(g:X\longrightarrow Z\) which factor as  . The following little Lemma is what we will use.
. The following little Lemma is what we will use.
Lemma 6.9
Let \(\alpha :V\longrightarrow X\) be a finite-type morphism of quasi-compact, quasi-separated stacks. Assume V is a quasi-affine scheme and X has quasi-affine diagonal. Then, the map \(\alpha :V\longrightarrow X\) factors as  , with \(\beta \) a locally closed immersion and
, with \(\beta \) a locally closed immersion and  a finitely presented quasicoherent sheaf on X.
a finitely presented quasicoherent sheaf on X.
Proof
Since V is quasi-affine and X has quasi-affine diagonal, the map \(\alpha \) must be quasi-affine. The sheaf  is a quasicoherent sheaf on X, and can be expressed as a filtered direct limit of finitely presented quasicoherent sheaves: that is
is a quasicoherent sheaf on X, and can be expressed as a filtered direct limit of finitely presented quasicoherent sheaves: that is  with each
with each  finitely presented. For each \(\lambda \), the map \(\alpha :V\longrightarrow X\) factors as
finitely presented. For each \(\lambda \), the map \(\alpha :V\longrightarrow X\) factors as  , where
, where  is Spec of the symmetric algebra on the sheaf
is Spec of the symmetric algebra on the sheaf  . I assert
. I assert
-
(i)
We may choose \(\lambda \) so that \(i_\lambda ^{}\) is a locally closed immersion.
Assuming (i) we let  , where \(\mathbb {1}\) is the trivial line bundle on X. Then, the following factorization does the trick:
, where \(\mathbb {1}\) is the trivial line bundle on X. Then, the following factorization does the trick:  with
with  the standard open immersion.
the standard open immersion.
It remains to prove (i). Fortunately the question is local in the flat topology. Choose an affine scheme S of finite type over X and a faithfully flat map \(\sigma :S\longrightarrow X\), and form the pullback square

Since \(\alpha \) is quasi-affine and of finite type, so is the pullback \(\alpha '\). We have that the map \(\alpha '\) is a finite-type morphism from a quasi-compact open subset of an affine scheme to an affine scheme, and that  is the filtered colimit of sheaves
is the filtered colimit of sheaves  . It is an easy exercise to show that we may choose an
. It is an easy exercise to show that we may choose an  so that, in the factorization
so that, in the factorization  , the map \(i'_\lambda \) is a locally closed immersion. \(\square \)
, the map \(i'_\lambda \) is a locally closed immersion. \(\square \)
Until now, we have given almost all of our arguments in non-noetherian, general forms. The next theorem is the first point at which I have no idea how to proceed without the noetherian hypothesis.
Theorem 6.10
As in Notation 5.8, suppose we are given a 2-cartesian square of noetherian stacks

Assume that g is of finite type, separated, concentrated and universally quasi-proper, and that v is flat. Assume that W, X, Y and Z have quasi-affine diagonals. Furthermore, assume that there exist finite type, separated, representable étale covers \(\overline{W}\longrightarrow W\), \(\overline{X}\longrightarrow X\) and \(\overline{Z}\longrightarrow Z\), with \(\overline{W}\), \(\overline{X}\) and \(\overline{Z}\) having the resolution property. Suppose that  satisfies Thomason’s condition for any coherent sheaf
satisfies Thomason’s condition for any coherent sheaf  on any of the stacks \(\overline{W}\), \(\overline{X}\), \(\overline{Y}\) or \(\overline{Z}\) which admit morphisms to W, X, Y or Z which are finite-type, separated, representable and étale. Let \(\overline{U}\subset W\) be the open subset of all the points at which f is of finite Tor-dimension. Consider the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\); if \(\rho :U\longrightarrow W\) is a morphism whose image lies in the open subset \(\overline{U}\subset W\), then \(\rho ^*\Phi : \rho ^*u^*g^\times \longrightarrow \rho ^*f^\times v^*\) is an isomorphism, and the isomorphic functors \(\rho ^*u^*g^\times \cong \rho ^*f^\times v^*\) respect coproducts.
on any of the stacks \(\overline{W}\), \(\overline{X}\), \(\overline{Y}\) or \(\overline{Z}\) which admit morphisms to W, X, Y or Z which are finite-type, separated, representable and étale. Let \(\overline{U}\subset W\) be the open subset of all the points at which f is of finite Tor-dimension. Consider the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\); if \(\rho :U\longrightarrow W\) is a morphism whose image lies in the open subset \(\overline{U}\subset W\), then \(\rho ^*\Phi : \rho ^*u^*g^\times \longrightarrow \rho ^*f^\times v^*\) is an isomorphism, and the isomorphic functors \(\rho ^*u^*g^\times \cong \rho ^*f^\times v^*\) respect coproducts.
Proof
The openness of the subset \(\overline{U}\subset W\) is by Corollary 5.15, which applies because any finite-type morphism \(f:W\longrightarrow Y\) of noetherian stacks is pseudo-coherent. The assertion of the Theorem is local in the flat topology on W: it suffices to produce a single flat morphism \(\rho :U\longrightarrow W\), whose image is all of \(\overline{U}\), so that \(\rho ^*\Phi \) is an isomorphism and the isomorphic functors \(\rho ^*u^*g^\times \cong \rho ^*f^\times v^*\) respect coproducts. We will now do the construction.
Choose a smooth surjection \(\alpha :V\longrightarrow X\) with V an affine scheme, and apply Lemma 6.9 to the maps \(\alpha :V\longrightarrow X\) and \(g\alpha :V\longrightarrow Z\). We obtain commutative squares of finite-type maps

with  and
and  coherent sheaves on Z and X, respectively, and with \(\beta \) and \(\beta '\) locally closed immersions. The map g is concentrated by hypothesis, while \(\alpha \), \(\beta \), \(\beta '\), \(\gamma \) and \(\gamma '\) are representable, hence concentrated. Form the diagram with 2-cartesian squares
coherent sheaves on Z and X, respectively, and with \(\beta \) and \(\beta '\) locally closed immersions. The map g is concentrated by hypothesis, while \(\alpha \), \(\beta \), \(\beta '\), \(\gamma \) and \(\gamma '\) are representable, hence concentrated. Form the diagram with 2-cartesian squares

The two horizontal maps in the bottom row are separated and universally quasi-proper—the morphism g by hypothesis, the morphism  by construction. Hence, their pullbacks, the horizontal maps on the top row, are also separated and universally quasi-proper. We have an obvious map
by construction. Hence, their pullbacks, the horizontal maps on the top row, are also separated and universally quasi-proper. We have an obvious map  , and we know that the two composites
, and we know that the two composites

are locally closed immersions. On the other hand, the map \(\pi \) is separated and representable, hence the morphism  is also a locally closed immersion. Let \(X''\) be the stack-theoretic closure of V in
is also a locally closed immersion. Let \(X''\) be the stack-theoretic closure of V in  and let \(X'\) be the stack-theoretic closure of V in
and let \(X'\) be the stack-theoretic closure of V in  .
.
This gives a 2-commutative square of concentrated morphisms

Here \(X'\) and \(X''\) are two compactifications of V, while the map \(V\longrightarrow X\) is faithfully flat. The maps g and \(g'\) are separated and universally quasi-proper, while the morphisms q and \(q'\) have factorizations  and
and  , with
, with  and
and  closed immersions. If \(V'\) is the pullback in the square
closed immersions. If \(V'\) is the pullback in the square

then we obtain diagrams where all the squares are 2-cartesian

The horizontal maps are all flat, in fact the maps i and \(f'i\) are even open immersions. The vertical maps are all quasi-proper maps of noetherian stacks. All the vertical morphisms are concentrated by construction. The stacks W, X, Y and Z are assumed to have quasi-affine diagonals, and the stacks \(W'\) and \(X'\) are closed substacks of  and
and  , with
, with  a coherent sheaf on Y and
a coherent sheaf on Y and  a coherent sheaf on Z. Hence, \(W'\) and \(X'\) also have quasi-affine diagonals. For any coherent sheaf
a coherent sheaf on Z. Hence, \(W'\) and \(X'\) also have quasi-affine diagonals. For any coherent sheaf  on any \(\overline{V}\), admitting a map to W, X, Y or Z which is finite-type, representable, separated and étale, we assumed that
on any \(\overline{V}\), admitting a map to W, X, Y or Z which is finite-type, representable, separated and étale, we assumed that  satisfies Thomason’s condition. The stacks \(W'\) and \(X'\) were constructed as closed substacks of
satisfies Thomason’s condition. The stacks \(W'\) and \(X'\) were constructed as closed substacks of  and
and  , with
, with  a coherent sheaf on Y and
a coherent sheaf on Y and  a coherent sheaf on Z, and Observation 5.6 guarantees that \(W'\) and \(X'\) satisfy Thomason’s condition. Finally \(X''\) is a closed substack of some
a coherent sheaf on Z, and Observation 5.6 guarantees that \(W'\) and \(X'\) satisfy Thomason’s condition. Finally \(X''\) is a closed substack of some  , where
, where  is a coherent sheaf on X—hence \({{\textbf{D}}_{\textbf{qc}}}(X'')\) is compactly generated.
is a coherent sheaf on X—hence \({{\textbf{D}}_{\textbf{qc}}}(X'')\) is compactly generated.
Let \(\Phi _3^{}:{u''}^*{g'}^\times \longrightarrow {f'}^\times {u'}^*\) be the base-change map of the square labeled (3) in the diagram. From the diagram

and Lemma 6.2 we learn that \(i^*\Phi _3^{}:i^*{u''}^*{g'}^\times \longrightarrow i^*{f'}^\times {u'}^*\) is an isomorphism.
Since the map q has a factorization as  , and Z admits a finite-type, representable, separated and étale morphism \(\overline{Z}\longrightarrow Z\) with \(\overline{Z}\) satisfying the resolution property, we can apply Proposition 6.8 to the square labeled (4) in the diagram. Let \(\Phi _4:{u'}^*q^\times \longrightarrow p^\times v^*\) be its base-change map; we learn that any flat morphism \(\varepsilon :U\longrightarrow W'\), whose image is contained in the open set of points \(x\in W'\) on which p has finite Tor-dimension, yields an isomorphism \(\varepsilon ^*\Phi _4^{}:\varepsilon ^*{u'}^*q^\times \longrightarrow \varepsilon ^*p^\times v^*\), and the isomorphic functors \(\varepsilon ^*{u'}^*q^\times \cong \varepsilon ^*p^\times v^*\) respect coproducts. We are given a flat map \(f'i:V'\longrightarrow W'\), let \(U=(f'i)^{-1}F\) be the inverse image of the open substack \(F\subset W'\) on which the map p is of finite Tor-dimension, and let \(\sigma :U\longrightarrow V'\) be the open immersion. We may apply the above to \(\varepsilon =f'i\sigma :U\longrightarrow W'\), and deduce that \(\sigma ^*i^*{f'}^*\Phi _4\) is an ismorphism and \(\sigma ^*i^*{f'}^*p^\times v^*\) respects coproducts. Consider the square labeled (2); together with Lemma 5.20 this square tells us that the base-change map \(\Phi _2^{}:i^*{f'}^\times \longrightarrow \textrm{id}^\times {(f'i)}^*\) is an isomorphism, and thus \(i^*{f'}^*\) is isomorphic to \(i^*{f'}^\times \). Combining with the above we have that \(\sigma ^*i^*{f'}^\times \Phi _4^{}\cong \sigma ^*i^*{f'}^*\Phi _4\) is an isomorphism, and the functor \(\sigma ^*i^*{f'}^\times p^\times v^*\cong \sigma ^*i^*{f'}^*p^\times v^*\) respects coproducts. Hence, \(\sigma ^*i^*\) takes each of the two composable morphisms
, and Z admits a finite-type, representable, separated and étale morphism \(\overline{Z}\longrightarrow Z\) with \(\overline{Z}\) satisfying the resolution property, we can apply Proposition 6.8 to the square labeled (4) in the diagram. Let \(\Phi _4:{u'}^*q^\times \longrightarrow p^\times v^*\) be its base-change map; we learn that any flat morphism \(\varepsilon :U\longrightarrow W'\), whose image is contained in the open set of points \(x\in W'\) on which p has finite Tor-dimension, yields an isomorphism \(\varepsilon ^*\Phi _4^{}:\varepsilon ^*{u'}^*q^\times \longrightarrow \varepsilon ^*p^\times v^*\), and the isomorphic functors \(\varepsilon ^*{u'}^*q^\times \cong \varepsilon ^*p^\times v^*\) respect coproducts. We are given a flat map \(f'i:V'\longrightarrow W'\), let \(U=(f'i)^{-1}F\) be the inverse image of the open substack \(F\subset W'\) on which the map p is of finite Tor-dimension, and let \(\sigma :U\longrightarrow V'\) be the open immersion. We may apply the above to \(\varepsilon =f'i\sigma :U\longrightarrow W'\), and deduce that \(\sigma ^*i^*{f'}^*\Phi _4\) is an ismorphism and \(\sigma ^*i^*{f'}^*p^\times v^*\) respects coproducts. Consider the square labeled (2); together with Lemma 5.20 this square tells us that the base-change map \(\Phi _2^{}:i^*{f'}^\times \longrightarrow \textrm{id}^\times {(f'i)}^*\) is an isomorphism, and thus \(i^*{f'}^*\) is isomorphic to \(i^*{f'}^\times \). Combining with the above we have that \(\sigma ^*i^*{f'}^\times \Phi _4^{}\cong \sigma ^*i^*{f'}^*\Phi _4\) is an isomorphism, and the functor \(\sigma ^*i^*{f'}^\times p^\times v^*\cong \sigma ^*i^*{f'}^*p^\times v^*\) respects coproducts. Hence, \(\sigma ^*i^*\) takes each of the two composable morphisms

to an isomorphism. But the composite is equal to the composite

where \(\Phi \) is the base-change map of the square labeled (0) and \(\Phi _1\) is the base-change map of the square labeled (1). In the case of the square labeled (1), the map \(q':X''\longrightarrow X\) factors as  , where
, where  is a coherent sheaf on X, where the map
is a coherent sheaf on X, where the map  is a closed immersion, and where X admits a finite-type, separated, representable and étale cover \(\overline{X}\longrightarrow X\) with \(\overline{X}\) satisfying the resolution property. Hence, we may apply Proposition 6.8. We have an open immersion \(i:V'\longrightarrow W''\), and the composite \(V'{\mathop {\longrightarrow }\limits ^{i}}W''{\mathop {\longrightarrow }\limits ^{p'}}W\) is the pullback of the faithfully flat map \(V\longrightarrow X\). Therefore, i maps \(V'\) into a substack of \(W''\) where \(p'\) is even flat—certainly of finite Tor-dimension. Hence, \(i^*\Phi _1^{}\) is an isomorphism and the isomorphic functors \(i^*{p'}^\times u^*\cong i^*{u''}^*q^\times \) respect coproducts. Since \(i^*\Phi _1^{}\) is an isomorphism so is \(\sigma ^*i^*\Phi _1^{}g^\times \). Summarizing what we have so far:
is a closed immersion, and where X admits a finite-type, separated, representable and étale cover \(\overline{X}\longrightarrow X\) with \(\overline{X}\) satisfying the resolution property. Hence, we may apply Proposition 6.8. We have an open immersion \(i:V'\longrightarrow W''\), and the composite \(V'{\mathop {\longrightarrow }\limits ^{i}}W''{\mathop {\longrightarrow }\limits ^{p'}}W\) is the pullback of the faithfully flat map \(V\longrightarrow X\). Therefore, i maps \(V'\) into a substack of \(W''\) where \(p'\) is even flat—certainly of finite Tor-dimension. Hence, \(i^*\Phi _1^{}\) is an isomorphism and the isomorphic functors \(i^*{p'}^\times u^*\cong i^*{u''}^*q^\times \) respect coproducts. Since \(i^*\Phi _1^{}\) is an isomorphism so is \(\sigma ^*i^*\Phi _1^{}g^\times \). Summarizing what we have so far:
-
(i)
\(\sigma ^*i^*\) takes \({p'}^\times \Phi \) to an isomorphism, or more simply that \(\sigma ^*i^*{p'}^\times \) takes \(\Phi \) to an isomorphism.
-
(ii)
The functor \(\sigma ^*i^*{p'}^\times f^\times v^*\cong \sigma ^*i^*{p'}^\times u^* g^\times \) respects coproducts because it is isomorphic to the functor \(\sigma ^*i^*{f'}^\times p^\times v^*\) which was proved to respect coproducts above. Concretely: if
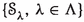 is a set of objects in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map
is a set of objects in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map 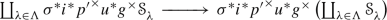
is an isomorphism
-
(iii)
The functor \(\sigma ^*i^*{p'}^\times u^*\) respects coproducts since \(\sigma ^*\) obviously does and \(i^*{p'}^\times u^*\) was proved to respect coproducts above. This certainly implies that if
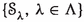 is a set of objects in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map
is a set of objects in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map 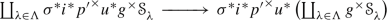
is an isomorphism.
Let \(\varphi \) be the natural map

and consider the composite

In (iii), we saw that \(\alpha \) is an isomorphism, while in (ii), we learned that so is the composite \((\sigma ^*i^*{p'}^\times \varphi )\circ \alpha \). Hence,
-
(iv)
The functor \(\sigma ^*i^*{p'}^\times \) takes the natural map
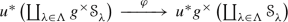
to an isomorphism.
Next, we apply Proposition 6.8(iii) to the (trivial) 2-cartesian square

and the map \(i\sigma :U\longrightarrow W''\). The map \(i\sigma \) is an open immersion (hence flat), the map \(p'\) is of finite Tor-dimension on the image of \(i\sigma \) and admits a factorization  with \(\alpha \) a closed immersion, and W has a finite-type, representable, separated and étale cover \(\overline{W}\longrightarrow W\) with \(\overline{W}\) satisfying the resolution property. The hypotheses of Proposition 6.8 hold and the stacks are noetherian. We have
with \(\alpha \) a closed immersion, and W has a finite-type, representable, separated and étale cover \(\overline{W}\longrightarrow W\) with \(\overline{W}\) satisfying the resolution property. The hypotheses of Proposition 6.8 hold and the stacks are noetherian. We have
-
(v)
If \(\phi :E\longrightarrow E'\) is a morphism in \({{\textbf{D}}_{\textbf{qc}}}(W)\), by applying assertion (iii) of Notation 6.4 to the mapping cone of \(\phi \) we deduce that \(\sigma ^*i^*{p'}^*\phi \) is an isomorphism if and only if \(\sigma ^*i^*{p'}^\times \phi \) is.
In (i), we saw that \(\sigma ^*i^*{p'}^\times \Phi \) is an isomorphism for the base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\), while in (iv), we saw that \(\sigma ^*i^*{p'}^\times \varphi \) is an isomorphism when \(\varphi \) is the natural map

By (v), we now conclude that \(\sigma ^*i^*{p'}^*\Phi \) and \(\sigma ^*i^*{p'}^*\varphi \) are also isomorphisms. Thus, we have that the map \(\rho =p'i\sigma :U\longrightarrow W\) satisfies
-
(vi)
The map \(\rho ^*\Phi \) is an isomorphism.
-
(vii)
\(\rho ^*\varphi \) is an isomorphism, and because \(\rho ^*\) and \(u^*\) respect coproducts it follows that, for any set of objects
 in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map
in the category \({{\textbf{D}}_{\textbf{qc}}}(Z)\), the natural map 
is an isomorphism. In other words, \(\rho ^*u^*g^\times \) respects coproducts.
It remains to show that the Theorem follows. By our construction, F was the open subset of \(W'\) where p is of finite Tor-dimension, the map \(f'i\) is an open immersion \(V'\longrightarrow W'\), and \(U=F\cap V'\) is just the open subset of \(V'\) at which the composite \(pf'i=fp'i\) is of finite Tor-dimension. Let \(\overline{U}\subset W\) be the open set at which \(f:W\longrightarrow Y\) is of finite Tor-dimension; by construction the map \(p'i:V'\longrightarrow W\) is faithfully flat, and hence \(U=(p'i)^{-1}\overline{U}\) and \(p'iU=\overline{U}\). The image of the flat map \(\rho :U\longrightarrow W\) is precisely \(\overline{U}\subset W\), and the Theorem now follows from (vi), (vii) and the first paragraph of the proof. \(\square \)
Remark 6.11
In the proof of Theorem 6.10, there are two points at which we appealed to the noetherian hypothesis: it entered when we cited Proposition 6.8(iii) in the proof of assertion (i) above, the proof of Proposition 6.8(iii) used support theory—in Remark 6.6 we already mentioned the failure of support theory in the non-noetherian situation. But we also relied on the noetherian hypothesis when we used compactifications. And it is the compactifications where the hypothesis seems crucial.
All our lemmas proving that base-change is an isomorphism assumed that the vertical maps are quasi-proper, and the geometric way to achieve this is with proper, pseudo-coherent maps. But when we start with a pseudo-coherent, proper map \(g:X\longrightarrow Z\), and then produce \(q:X'\longrightarrow Z\), \(q':X''\longrightarrow X\) and \(g':X''\longrightarrow X'\) by taking the closure of some V in a suitable  , then the maps constructed will be proper but there is no reason to expect them to be pseudo-coherent. Taking compactifications cannot, as far as I know, be done in a way that achieves pseudo-coherence. And this problem will plague the rest of the article.
, then the maps constructed will be proper but there is no reason to expect them to be pseudo-coherent. Taking compactifications cannot, as far as I know, be done in a way that achieves pseudo-coherence. And this problem will plague the rest of the article.
And as Example A.1 and Remark 6.1 show, base-change fails to be an isomorphism without something like quasi-properness.
8 Elementary Properties of Nagata Compactifications
In Notation 1.1, we defined Nagata compactifications in the 2-category of algebraic stacks: they are pairs of composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{u}}\overline{X}{\mathop {\longrightarrow }\limits ^{p}}Y\), with p of finite type and universally quasi-proper and u a dominant, flat monomorphism. It might be useful to assemble together in this section the elementary properties of the maps u and p in a Nagata compactification. We begin with
Lemma 7.1
Let \(f:X\longrightarrow Y\) be a 1-morphism of noetherian stacks, and assume f is concentrated, of finite type and quasi-proper. Then, f is closed.
Proof
Since f is of finite type and the stacks are noetherian, the image f(Z) of any closed subset \(Z\subset X\) is constructible. It suffices, therefore, to show that f(Z) is specialization-closed; in other words we need to show that, if \(z\in Z\) is a point, then f(Z) contains the closure of f(z). Choose, therefore, a field k and a morphism \(g:{\textrm{Spec}(k)}\longrightarrow X\) whose image is z, and in an abuse of notation we will write k for the structure sheaf of \({\textrm{Spec}(k)}\), and \(g_*k\) will be its (derived) pushforward to \({{\textbf{D}}_{\textbf{qc}}}(X)\).
Now, \(g_*k\) is supported on Z, hence it can be expressed as the homotopy colimit of complexes \(C_\lambda \in {{\textbf{D}}}_{\textbf{coh}}^b(Z)\). Since f is concentrated, it respects coproducts and hence homotopy colimits, and \(f_*g_*k\) can be expressed as the homotopy colimit of the \(f_*C_\lambda \). Since \(f_*g_*k\) is nonzero at the point \(f(z)\in Y\) there must be a \(C_\lambda \) with \(f_*C_\lambda \) nonzero at f(z). Now, because f is quasi-proper \(f_*C_\lambda \) belongs to \({{\textbf{D}}}_{\textbf{coh}}^b(Y)\) and its support is closed. Thus, the support of \(f_*C_\lambda \) is a closed set in Y containing f(z), and the proof will be finished if we show that the support of \(f_*C_\lambda \) is contained in the image of Z.
But this follows from the projection formula, which holds for the concentrated morphism f: if \(y\in Y\) is a point outside f(Z) and k(y) is any object of \({{\textbf{D}}_{\textbf{qc}}}(Y)\) supported at y, then \(f_*C_\lambda \otimes k(y)\cong f_*\big (C_\lambda \otimes f^*k(y)\big )=0\), where the vanishing is because \(C_\lambda \) is supported on Z and \(f^*k(y)\) is supported on the disjoint \(f^{-1}y\). \(\square \)
Lemma 7.2
Let \(X{\mathop {\longrightarrow }\limits ^{p}}Y{\mathop {\longrightarrow }\limits ^{q}}Z\) be two composable 1-morphisms of noetherian stacks with q of finite type and separated, and with qp of finite type and universally quasi-proper. Then, p is of finite type and universally quasi-proper. Furthermore: if qp is concentrated and/or separated then so is p.
Proof
We are assuming q separated so the diagonal map \(Y\longrightarrow Y\times _Z^{}Y\) is proper and representable, as is its pullback \(X\longrightarrow X\times _Z^{}Y\). Since Y is of finite type over Z the stack \(X\times _Z^{}Y\) is of finite type over the noetherian stack X. Thus, \(X\longrightarrow X\times _Z^{}Y\) is a proper, representable morphism of noetherian algebraic stacks, hence concentrated, separated, of finite type and universally quasi-proper.
But the map \(qp:X\longrightarrow Z\) is assumed of finite type and univerally quasi-proper, and we allow ourselves to consider the option that it might also be concentrated and/or separated. Hence, its pullback \(X\times _Z^{}Y\longrightarrow Y\) also has these properties. Therefore, the composite \(X\longrightarrow X\times _Z^{}Y\longrightarrow Y\) is of finite type and universally quasi-proper, and if qp is concentrated and/or separated then so is the composite. \(\square \)
To avoid possible confusion, we recall
Definition 7.3
Let  be a 2-category. A monomorphism \(f:Y\longrightarrow Z\) is a 1-morphism so that the (strictly) commutative square
be a 2-category. A monomorphism \(f:Y\longrightarrow Z\) is a 1-morphism so that the (strictly) commutative square

is 2-cartesian.
Lemma 7.4
A surjective flat monomorphism is an isomorphism.
Proof
Let \(f:Y\longrightarrow Z\) be a surjective, flat monomorphism. The surjectivity and flatness imply that f is faithfully flat, while the fact that f is a monomorphism tells us that the square

is 2-cartesian. But then the pullback of f by the faithfully flat map f is an isomorphism, and faithfully flat descent assures us that f must be an isomorphism. \(\square \)
Lemma 7.5
Let \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) be composable 1-morphisms in a 2-category  , with g a monomorphism. Then, the square
, with g a monomorphism. Then, the square

is 2-cartesian.
Proof
In the diagram,

the square on the right is 2-cartesian because g is a monomorphism, while the square on the left is trivially 2-cartesian. Hence, the concatenated square is 2-cartesian. \(\square \)
Remark 7.6
Let  be a 2-category. Suppose P and Q are properties of 1-morphisms in
be a 2-category. Suppose P and Q are properties of 1-morphisms in  so that
so that
-
(i)
The identity 1-morphisms have property P and property Q, any 1-morphism isomorphic to a morphism having property P (respectively, Q) has property P (respectively, Q), and composites of morphisms having property P (respectively, Q) have property P (respectively, Q).
-
(ii)
In any 2-cartesian square,
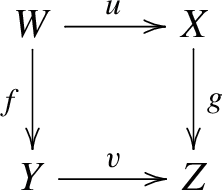
if v has property P and g has property Q then u has property P and f has property Q.
If \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) are composable morphisms such that
-
(iii)
g is a monomorphism,
-
(iv)
and gf has property P and g has property Q.
then f has property P, by (ii) applied to the 2-cartesian square of Lemma 7.5.
Example 7.7
We apply Remark 7.6 to the 2-category of algebraic stacks, with P the property of being a flat monomorphism and Q the class of all morphisms. If \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) are composable morphisms of algebraic stacks, with gf a flat monomorphism and g a monomorphism, then f is a flat monomorphism.
Example 7.8
Next, we apply Remark 7.6 but with P being the class of all dominant, flat monomorphisms and Q the class of all flat morphisms. Note that the pullback of a dominant map by a flat map is dominant, so the hypotheses of Remark 7.6 hold.
From Remark 7.6, we learn that if \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) is a pair of composable 1-morphisms with gf a dominant, flat monomorphism and g a flat monomorphism, then f must be a dominant, flat monomorphism. And of course g must also be dominant: the stack-theoretic closure of the image of g contains the stack-theoretic closure of the image of gf, but since gf is dominant this is all of Z.
We end the section with
Corollary 7.9
Suppose we are given a 2-commutative square of noetherian algebraic stacks

with g separated and of finite type, with f concentrated, universally quasi-proper and of finite type, with v a flat monomorphism and with \(u''\) a dominant, flat monomorphism. Then, the square \((\dagger )\) is 2-cartesian.
Proof
Form the pullback square

and let \(u':W\longrightarrow P\) be the map given by the morphism from the 2-commutative \((\dagger )\) to the 2-cartesian \((\bullet )\). We obtain a 2-commutative diagram

We are given that v is a flat monomorphism, and its pullback u must also be. But \(u''\cong uu'\) is a dominant, flat monomorphism by hypothesis, and Example 7.8, applied to the composable maps \(X{\mathop {\longrightarrow }\limits ^{u'}}X'{\mathop {\longrightarrow }\limits ^{u}}X''\), now informs us that both u and \(u'\) are dominant, flat monomorphisms.
On the other hand p, being the pullback of g, is separated and of finite type, and \(f\cong pu'\) is concentrated, of finite type and universally quasi-proper. Lemma 7.2 informs us that \(u'\) must be concentrated, of finite type and universally quasi-proper. From Lemma 7.1 we deduce that \(u'\) is closed: in particular \(u'(W)\subset P\) is a closed subset. Since it is dominant it must be all of P. This makes \(u'\) a surjective, flat monomorphism, and Lemma 7.4 guarantees that \(u'\) is an isomorphism. \(\square \)
9 The Categories \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\)
Let \({\mathbb {S}_{{\textbf{e}}}}\) be a 2-subcategory of the 2-category of noetherian algebraic stacks, satisfying the hypotheses of Notation 1.1. Part of the structure of 2-categories gives us, for every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), a category of 1-morphisms \(X\longrightarrow Z\). As is customary we denote this category \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\). For our purposes, it will be better to work with slightly different categories.
Definition 8.1
Let \({\mathbb {S}_{{\textbf{e}}}}\) be a 2-category as in Notation 1.1, and let X, Z be any two objects of \({\mathbb {S}_{{\textbf{e}}}}\). We define a category \({\mathbb {FNS}_{{\textbf{e}}}}(X,Z)\) as follows
-
(i)
The objects of \({\mathbb {FNS}_{{\textbf{e}}}}(X,Z)\) are 2-commutative triangles in \({\mathbb {S}_{{\textbf{e}}}}\)
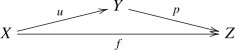
Note that the isomorphism \(pu\longrightarrow f\) giving the 2-commutativity is part of the data of an object in \({\mathbb {FNS}_{{\textbf{e}}}}(X,Z)\).
-
(ii)
A morphism in \({\mathbb {FNS}_{{\textbf{e}}}}(X,Z)\), from object

is an equivalence class of data in \({\mathbb {S}_{{\textbf{e}}}}\). First let us give the data, and then define the equivalence relation. The following information suffices to determine a morphism in \({\mathbb {FNS}_{{\textbf{e}}}}\):
-
(a)
A 2-morphism \(f\longrightarrow f'\) in \({\mathbb {S}_{{\textbf{e}}}}\);
-
(b)
A 2-commutative diagram
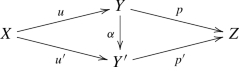
in \({\mathbb {S}_{{\textbf{e}}}}\), where again the 2-isomorphisms \(\alpha u\longrightarrow u'\) and \(p\longrightarrow p'\alpha \) are part of the data;
-
(c)
These should be compatible in that the square
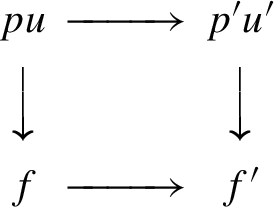
must commute in the category \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\).
But we want to identify these data up to equivalence: we allow ourselves to replace \(\alpha \) by an isomorph \(\alpha '\). More fully, what this means is that given a 2-commutative diagram
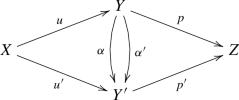
that is 2-isomorphisms \(\varphi :\alpha u\longrightarrow u'\), \(\psi :\alpha '\longrightarrow \alpha \) and \(\rho :p\longrightarrow p'\alpha '\), then we are allowed to replace
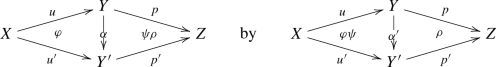
To avoid any possible confusion: we are free to replace \(\alpha \) by \(\alpha '\), as long as the natural isomorphisms are changed from the pair
$$\begin{aligned} \varphi :\alpha u\longrightarrow u',\,\, \psi \rho :p\longrightarrow p'\alpha \quad \text { to the pair}\quad \varphi \psi :\alpha ' u\longrightarrow u',\,\, \rho :p\longrightarrow p'\alpha '. \end{aligned}$$ -
(a)
-
(iii)
Composition is obvious, once we note that the equivalence relation is preserved by composition.
-
(iv)
We record the following full subcategories of \({\mathbb {FNS}_{{\textbf{e}}}}(X,Z)\): the objects of \({\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\), \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) and \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) are the 2-commutative diagrams
where:
-
(a)
In \({\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\), we assume that u is a flat morphism.
-
(b)
In \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\), we suppose that p is of finite type and universally quasi-proper.
-
(c)
\({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) is the full subcategory of \({\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\cap {\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) where u is assumed not only to be flat, but also to be a dominant monomorphism.
-
(a)
Remark 8.2
The variant we care about most is \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\). To recast the definition in simple words: an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) is a morphism \(f:X\longrightarrow Z\) in \({\mathbb {S}_{{\textbf{e}}}}\) together with a Nagata compactification, and the morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) are the obvious maps of the data. The one quirk is that we mod out by the possible 2-categorical structure, identifying morphisms up to equivalence. The lax versions \({\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\) and \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) will come up in proofs, hence we recorded them.
There is a forgetful functor \(F:{\mathbb {FNS}_{{\textbf{e}}}}(X,Y)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\) which remembers only \(f:X\longrightarrow Z\). This map is not an equivalence; after all the category \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\) is a groupoid while \({\mathbb {FNS}_{{\textbf{e}}}}(X,Y)\) is not, and neither is any of the three subcategories we introduced. What we will show in the next few lemmas is that the variant \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) admits a formal calculus of right fractions, allowing us to easily prove that the map from the groupoid completion of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\) is an equivalence.
Remark 8.3
Suppose we choose a representative of a morphism in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\); part of the data this specifies, according to Definition 8.1(ii), is the 2-commutative diagram

We assert that the morphism \(\alpha :Y\longrightarrow Y'\) must be of finite type and universally quasi-proper.
The proof is by Lemma 7.2: since the morphism lies in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) both \(p'\) and \(p\cong \alpha p'\) are of finite type and universally quasi-proper. All morphisms of \({\mathbb {S}_{{\textbf{e}}}}\) are assumed separated, hence Lemma 7.2 applies and tells us that \(\alpha \) is of finite type and universally quasi-proper.
Remark 8.4
If we assume that all our stacks are schemes then life becomes much simpler: given two objects in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), i.e. two diagrams

there is at most one commutative diagram

After all the map u is assumed dominant and \(p'\) is a separated morphism, hence the equality \(u'=\alpha u\) uniquely specifies \(\alpha \) (if it exists). If all the objects of \({\mathbb {S}_{{\textbf{e}}}}\) are schemes then \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) is a partially ordered set.
Lemma 8.5
Let \(F:{\mathbb {RNS}_{{\textbf{e}}}}(X,Y)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\) be as in Remark 8.2. Given two objects \(b,c\in {\mathbb {RNS}_{{\textbf{e}}}}(X,Y)\) and a morphism \(\varphi :F(b)\longrightarrow F(c)\) in \({\mathbb {S}_{{\textbf{e}}}}\), there is an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and a pair of morphisms \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Y)\) so that \(\varphi =F(\beta )F(\alpha )^{-1}\).
Proof
The objects b and c are a pair of factorizations \(pu\longrightarrow f\) and \(p'u'\longrightarrow f'\), and the morphism \(\varphi :F(b)\longrightarrow F(c)\) comes down to a map \(f\longrightarrow f'\) in \({\mathbb {S}_{{\textbf{e}}}}\). These assemble in \({\mathbb {S}_{{\textbf{e}}}}\) to a 2-commutative square

Now, form the 2-cartesian square

and consider the induced map \(X\longrightarrow Y\times _Z^{} Y'\). It is a morphism in \({\mathbb {S}_{{\textbf{e}}}}\), hence we may choose a Nagata compactification \(X{\mathop {\longrightarrow }\limits ^{u''}}\overline{Y} {\mathop {\longrightarrow }\limits ^{r}}Y\times _Z^{}Y'\).
Since p is of finite type and universally quasi-proper, so is its pullback q, and because \(p'\) and r are also of finite type and universally quasi-proper, so is the composite \(p'qr:\overline{Y}\longrightarrow Z\). The map \(u'':X\longrightarrow \overline{Y}\) is a dominant, flat monomorphism by construction. Hence, \(X{\mathop {\longrightarrow }\limits ^{u''}}\overline{Y}{\mathop {\longrightarrow }\limits ^{p'qr}}Z\) is a Nagata compactification of the composite; we let this be our object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\). The maps \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) are now obvious. \(\square \)
Lemma 8.6
Let \(\varphi ,\psi \) be two morphisms  in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) with \(F(\varphi )=F(\psi )\). Then, there exists an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and a morphism \(\rho :a\longrightarrow b\) with \(\varphi \rho =\psi \rho \).
in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\) with \(F(\varphi )=F(\psi )\). Then, there exists an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and a morphism \(\rho :a\longrightarrow b\) with \(\varphi \rho =\psi \rho \).
Proof
If we choose representatives in the equivalence classes giving \(\varphi \) and \(\psi \), we obtain two 2-commutative diagrams in \({\mathbb {S}_{{\textbf{e}}}}\)

The assertion that \(F(\varphi )=F(\psi )\) says that in \({\mathbb {S}_{{\textbf{e}}}}\) the two 2-morphisms \(pu\longrightarrow p'u'\) agree. Let \(\Delta \) be the diagonal map \(Y'\longrightarrow Y'\times _Z^{}Y'\), and let \(s:Y\longrightarrow Y'\times _Z^{}Y'\) be the map corresponding to the pair of 1-morphisms  , coupled with the two 2-morphisms \(p'\alpha \longrightarrow p\longleftarrow p'\alpha '\). Now, consider the 2-commutative square
, coupled with the two 2-morphisms \(p'\alpha \longrightarrow p\longleftarrow p'\alpha '\). Now, consider the 2-commutative square

Form the pullback

and choose a 1-morphism \(X\longrightarrow P\) giving a map from the 2-commutative to the 2-cartesian square. Choose a Nagata compactification \(X{\mathop {\longrightarrow }\limits ^{w}}Y''{\mathop {\longrightarrow }\limits ^{r}}P\). The map \(p':Y'\longrightarrow Z\) is separated and of finite type, hence
-
(i)
The pullback \(Y'\times _Z^{}Y'\longrightarrow Y'\) is of finite type, and since \(Y'\) is noetherian so is \(Y'\times _Z^{}Y'\).
-
(ii)
The diagonal map \(\Delta :Y'\longrightarrow Y'\times _Z^{}Y'\) is a proper map of noetherian stacks, hence of finite type and universally quasi-proper.
Therefore, the pullback \(q:P\longrightarrow Y\) is also of finite type and universally quasi-proper, as are \(r:Y''\longrightarrow P\) and \(p:Y\longrightarrow Z\). Therefore, the composite \(pqr:Y''\longrightarrow Z\) is of finite type and universally quasi-proper. This makes the 2-commutative diagram

a morphism \(\rho :a\longrightarrow b\) in \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\), and a belongs to the subcategory \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\). We leave it to the reader to check that \(\varphi \rho =\psi \rho \).
In this check, the reader should note that it is not true that \(\alpha qr= \alpha 'qr\). If \(\pi _1^{}\), \(\pi _2^{}\) are the two projections \(Y'\times _Z^{}Y'\longrightarrow Y'\), all we have are isomorphisms \(\alpha qr \cong \pi _1^{}sqr\cong \pi _1^{}\Delta q'r\cong q'r \cong \pi _2^{}\Delta q'r\cong \pi _2^{}sqr\cong \alpha ' qr\), and that these 2-ismorphisms are compatible with all the given 2-morphisms of the data. But 2-isomorphisms are not equalities: before passing to the equivalence relation it is not true that \(\varphi \rho =\psi \rho \). \(\square \)
We proved Lemmas 8.5 and 8.6 in the generality of \({\mathbb {RNS}_{{\textbf{e}}}}(X,Z)\), but it says something interesting even if we concentrate on the case where all the objects lie in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\). For future use we state this abstractly.
Remark 8.7
We suppose given a functor  satisfying
satisfying
-
(i)
The category
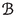 is a groupoid, meaning all the morphisms in
is a groupoid, meaning all the morphisms in  are invertible.
are invertible. -
(ii)
Given a morphism \(\varphi :F(b)\longrightarrow F(c)\) in
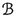 , there is a pair of morphisms \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) in the category
, there is a pair of morphisms \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) in the category 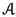 with \(\varphi =F(\beta )F(\alpha )^{-1}\).
with \(\varphi =F(\beta )F(\alpha )^{-1}\). -
(iii)
Let \(\varphi ,\psi \) be two morphisms in
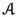 with \(F(\varphi )=F(\psi )\). Then, there exists a morphism
with \(F(\varphi )=F(\psi )\). Then, there exists a morphism 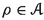 with \(\varphi \rho =\psi \rho \)
with \(\varphi \rho =\psi \rho \)
Note that the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) satisfies (i), (ii) and (iii); (i) is obvious since the 2-category of stacks is a groupoid, (ii) by Lemma 8.5, and (iii) by Lemma 8.6. The following is a formal consequence:
Lemma 8.8
Let  be a functor satisfying conditions (i), (ii) and (iii) of Remark 8.7. Let
be a functor satisfying conditions (i), (ii) and (iii) of Remark 8.7. Let  be the groupoid completion of
be the groupoid completion of  , that is the category where we formally invert all the morphisms. Then, the category
, that is the category where we formally invert all the morphisms. Then, the category  satisfies the right Ore condition, and in the canonical factorization of the functor F as
satisfies the right Ore condition, and in the canonical factorization of the functor F as  , the functor \(F'\) is fully faithful.
, the functor \(F'\) is fully faithful.
Proof
We should remind ourselves what it means for the category  to satisfy the right Ore condition. The following two conditions must be satisfied:
to satisfy the right Ore condition. The following two conditions must be satisfied:
-
(i)
Any pair of morphisms \(c\longrightarrow d\longleftarrow b\) in
 can be completed to a commutative square
can be completed to a commutative square 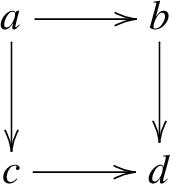
-
(ii)
Any pair of morphisms
 in
in  admitting a coequalizer also admits an equalizer. That is, if there exists a morphism \(c\longrightarrow d\) so that the composites
admitting a coequalizer also admits an equalizer. That is, if there exists a morphism \(c\longrightarrow d\) so that the composites  are equal, then there also exists a morphism \(a\longrightarrow b\) so that the composites
are equal, then there also exists a morphism \(a\longrightarrow b\) so that the composites 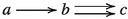 are equal.
are equal.
Let us begin by proving that these two conditions are satisfied.
We start with (ii): suppose we are given in  morphisms
morphisms  so that the two composites \(b\longrightarrow d\) are equal. Applying the functor F we have that the two composites
so that the two composites \(b\longrightarrow d\) are equal. Applying the functor F we have that the two composites  are also equal. But the category
are also equal. But the category  is a groupoid by Remark 8.7(i), hence the morphism \(F(c)\longrightarrow F(d)\) is an isomorphism, and the two morphisms
is a groupoid by Remark 8.7(i), hence the morphism \(F(c)\longrightarrow F(d)\) is an isomorphism, and the two morphisms  must be equal. Remark 8.7(iii) now informs us that there exists in
must be equal. Remark 8.7(iii) now informs us that there exists in  a morphism \(a\longrightarrow b\) so that the composites
a morphism \(a\longrightarrow b\) so that the composites  are equal.
are equal.
Next, we prove (i): suppose that we are given in  morphisms \(c\longrightarrow d\longleftarrow b\). Applying the functor F, we obtain morphisms \(F(c)\longrightarrow F(d)\longleftarrow F(b)\), but
morphisms \(c\longrightarrow d\longleftarrow b\). Applying the functor F, we obtain morphisms \(F(c)\longrightarrow F(d)\longleftarrow F(b)\), but  is a groupoid so the map \(F(d)\longleftarrow F(b)\) is invertible. The composite \(F(c)\longrightarrow F(d)\longrightarrow F(b)\) is a morphism \(\varphi :F(c)\longrightarrow F(b)\), and by Remark 8.7(ii) it may be written as \(\varphi =F(\beta )F(\alpha )^{-1}\) for some morphisms \(c{\mathop {\longleftarrow }\limits ^{\alpha }}\widetilde{a}{\mathop {\longrightarrow }\limits ^{\beta }}b\) in the category
is a groupoid so the map \(F(d)\longleftarrow F(b)\) is invertible. The composite \(F(c)\longrightarrow F(d)\longrightarrow F(b)\) is a morphism \(\varphi :F(c)\longrightarrow F(b)\), and by Remark 8.7(ii) it may be written as \(\varphi =F(\beta )F(\alpha )^{-1}\) for some morphisms \(c{\mathop {\longleftarrow }\limits ^{\alpha }}\widetilde{a}{\mathop {\longrightarrow }\limits ^{\beta }}b\) in the category  . We have produced in
. We have produced in  morphisms
morphisms

and what we know is that the functor F takes this to a commutative square. Consider the two composites  ; we do not know that they agree in
; we do not know that they agree in  , but the functor F takes them to equal maps. Applying Remark 8.7(iii) there exists a morphism \(a\longrightarrow \widetilde{a}\) so that the two composites
, but the functor F takes them to equal maps. Applying Remark 8.7(iii) there exists a morphism \(a\longrightarrow \widetilde{a}\) so that the two composites  are equal, and hence we obtain in
are equal, and hence we obtain in  a commutative square
a commutative square

This completes the proof of (i).
Let  be the groupoid completion of
be the groupoid completion of  . Since
. Since  satisfies the right Ore conditions, the calculus of right fractions is very simple: any morphism \(\varphi :b\longrightarrow c\) in
satisfies the right Ore conditions, the calculus of right fractions is very simple: any morphism \(\varphi :b\longrightarrow c\) in  can be represented as \(\beta \alpha ^{-1}\) for morphisms \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) in the category
can be represented as \(\beta \alpha ^{-1}\) for morphisms \(b{\mathop {\longleftarrow }\limits ^{\alpha }}a{\mathop {\longrightarrow }\limits ^{\beta }}c\) in the category  , any pair of morphisms
, any pair of morphisms  in
in  may be put on a “common denominator”, meaning there are morphisms
may be put on a “common denominator”, meaning there are morphisms  in
in  with \(\varphi =\beta \alpha ^{-1}\) and \(\varphi '=\beta '\alpha ^{-1}\). Furthermore, if we represent two morphisms
with \(\varphi =\beta \alpha ^{-1}\) and \(\varphi '=\beta '\alpha ^{-1}\). Furthermore, if we represent two morphisms  in
in  as \(\varphi =\beta \alpha ^{-1}\) and \(\varphi '=\beta '\alpha ^{-1}\), then \(\varphi =\varphi '\) if and only if there exists in
as \(\varphi =\beta \alpha ^{-1}\) and \(\varphi '=\beta '\alpha ^{-1}\), then \(\varphi =\varphi '\) if and only if there exists in  a morphism \(\gamma \) with \(\beta \gamma =\beta '\gamma \).
a morphism \(\gamma \) with \(\beta \gamma =\beta '\gamma \).
The functor F is a functor from  to the groupoid
to the groupoid  , hence factors uniquely as
, hence factors uniquely as  . Remark 8.7(ii) shows that the functor \(F'\) is full, while Remark 8.7(iii) proves it faithful. \(\square \)
. Remark 8.7(ii) shows that the functor \(F'\) is full, while Remark 8.7(iii) proves it faithful. \(\square \)
Proposition 8.9
In the special case where the functor  of Lemma 8.8 is the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) of Remark 8.2, the factorization \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z){\mathop {\longrightarrow }\limits ^{\pi }}{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z){\mathop {\longrightarrow }\limits ^{F'}}{\mathbb {S}_{{\textbf{e}}}}(X,Z)\) is such that \(F'\) is an equivalence.
of Lemma 8.8 is the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) of Remark 8.2, the factorization \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z){\mathop {\longrightarrow }\limits ^{\pi }}{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z){\mathop {\longrightarrow }\limits ^{F'}}{\mathbb {S}_{{\textbf{e}}}}(X,Z)\) is such that \(F'\) is an equivalence.
Proof
By Lemma 8.8, we know that \(F'\) is fully faithful. But in the category \({\mathbb {S}_{{\textbf{e}}}}\) we assume that any morphism \(f:X\longrightarrow Z\) has a Nagata compactification, and the functors F and \(F'\) are, therefore, essentially surjective. \(\square \)
For every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), we have found a category \({{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) equivalent to \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\). We now want to do a similar construction for triples of objects.
Definition 8.10
Let \({\mathbb {S}_{{\textbf{e}}}}\) be a 2-category as in Notation 1.1, and let X, Y, Z be three objects in \({\mathbb {S}_{{\textbf{e}}}}\). We define the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) as follows:
-
(i)
The objects in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) are 2-commutative diagrams in \({\mathbb {S}_{{\textbf{e}}}}\)
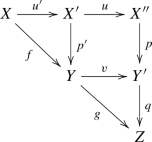
where the horizontal maps are all dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper. Corollary 7.9 tells us that the one square in the diagram is automatically 2-cartesian.
-
(ii)
The morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), from the object
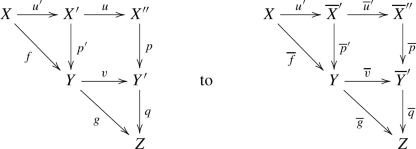
are equivalence classes of 2-commutative diagrams in \({\mathbb {S}_{{\textbf{e}}}}\)
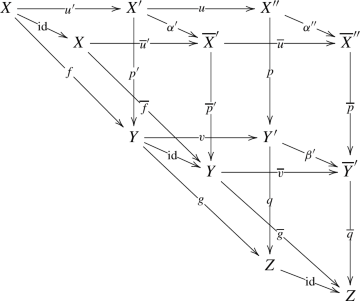
-
(iii)
Two such diagrams connecting a given pair of objects give, among other things, three pairs of 1-morphisms
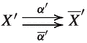 ,
, 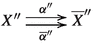 and
and 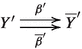 . These diagrams are declared to be equivalent if there are 2-isomorphisms \(\alpha '\cong \overline{\alpha }'\), \(\alpha ''\cong \overline{\alpha }''\) and \(\beta '\cong \overline{\beta }'\) compatible with all the other 2-morphisms in the diagrams.
. These diagrams are declared to be equivalent if there are 2-isomorphisms \(\alpha '\cong \overline{\alpha }'\), \(\alpha ''\cong \overline{\alpha }''\) and \(\beta '\cong \overline{\beta }'\) compatible with all the other 2-morphisms in the diagrams. -
(iv)
For future use we record the minor variant \({\mathbb {LNS}_{{\textbf{e}}}}(X,Y,Z)\): the objects are 2-commutative diagrams as in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), the square is 2-cartesian, but the vertical maps are unrestricted and the only restriction on the horizontal maps is that they are assumed flat.
Remark 8.11
There is a functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\); it takes an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) to the pair of composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\). An object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) should be thought of as the composable 1-morphisms together with a bunch of compatible Nagata compactifications, and the morphisms are equivalence classes of maps respecting the data.
The category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) also has three obvious functors
each of which forgets some of the data. For example \(\pi _{23}^{}\) takes the object

of the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) to the object

of the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(Y,Z)\).
Remark 8.12
In Definition 8.10(ii), we saw that a representative of a morphism \(\varphi :a\longrightarrow b\) in the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), where the objects a and b are the diagrams

is a 2-commutative diagram where the “new” 1-morphisms—the ones which do not form part of the data of the objects—are the triple \(\alpha ':X'\longrightarrow \overline{X}'\), \(\alpha '':X''\longrightarrow \overline{X}''\) and \(\beta ':Y'\longrightarrow \overline{Y}'\). We assert that the 1-morphisms \(\alpha '\), \(\alpha ''\) and \(\beta '\) are all of finite type and universally quasi-proper.
The proof is by Remark 8.3: if we apply the functors of Remark 8.11, we obtain three maps \(\pi _{}^{}(\varphi ):\pi _{}^{}(a) \longrightarrow \pi _{12}^{}(b)\), \(\pi _{12}^{}(\varphi ):\pi _{12}^{}(a) \longrightarrow \pi _{23}^{}(b)\) and \(\pi _{13}^{}(\varphi ):\pi _{13}^{}(a) \longrightarrow \pi _{13}^{}(b)\), and each of them is represented by a diagram where the “new” 1-morphism is (respectively) \(\alpha '\), \(\alpha ''\) and \(\beta '\). Remark 8.3 guarantees that these 1-morphisms are of finite type and universally quasi-proper.
Lemma 8.13
The functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) is essentially surjective.
Proof
Suppose we are given an object in \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\), that is a pair of composable morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\). Choose Nagata compactification for f and g. So far this constructs for us an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) and an object \(b\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(Y,Z)\), which we assemble together in the 2-commutative diagram

Now, the composite \(X'{\mathop {\longrightarrow }\limits ^{p'}}Y{\mathop {\longrightarrow }\limits ^{v}}Y'\) is a morphism in the category \({\mathbb {S}_{{\textbf{e}}}}\), and has a Nagata compactification \(X'{\mathop {\longrightarrow }\limits ^{u}}X''{\mathop {\longrightarrow }\limits ^{p}}Y'\). This means that the composites are 2-isomorphic, u is a dominant, flat monomorphism and p is of finite type and universally quasi-proper. This completes for us the diagram

which is an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) lifting \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\). \(\square \)
Lemma 8.14
Let \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) be the functor of Remark 8.11, and suppose we are given a morphism \(\varphi :F(b)\longrightarrow F(c)\) in \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\). There exists a pair of morphisms \(b{\mathop {\longleftarrow }\limits ^{\sigma }}a{\mathop {\longrightarrow }\limits ^{\theta }}c\) in the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), with \(\varphi =F(\theta )F(\sigma )^{-1}\).
Proof
We are given two objects \(b,c\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), that is diagrams in \({\mathbb {S}_{{\textbf{e}}}}\) satisfying all the requirements of Definition 8.10(i)

We are also given a morphism \(\varphi :F(b)\longrightarrow F(c)\), meaning a pair of 2-morphisms \(\varphi _f^{}:f\longrightarrow \overline{f}\) and \(\varphi _g^{}:g\longrightarrow \overline{g}\) in \({\mathbb {S}_{{\textbf{e}}}}\). Apply the functors \(\pi _{12}^{}\) and \(\pi _{23}^{}\) of Remark 8.11, and then Lemma 8.5, and we construct the diagram A below

together with maps
so that
-
(i)
The horizontal maps in A are dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper.
-
(ii)
\(\varphi _f^{}=F(\theta ')F(\sigma ')^{-1}\) and \(\varphi _{g}^{}=F(\theta '')F(\sigma '')^{-1}\).
What we are about to prove is a refinement of Lemma 8.14. Since we will need the refinement in the proof of Lemma 8.15 we state it formally here.
8.14.1
Suppose we have chosen an object A and maps \(\sigma '\), \(\sigma ''\), \(\theta '\) and \(\theta ''\) satisfying (i) and (ii) above. The object a in the statement of Lemma 8.14 can be chosen so that \(\pi _{12}^{}(a)=\pi _{12}^{}(A)\) and \(\pi _{23}^{}(a)=\pi _{23}^{}(A)\), and the morphisms \(b{\mathop {\longleftarrow }\limits ^{\sigma }}a{\mathop {\longrightarrow }\limits ^{\theta }}c\) in the statement of Lemma 8.14 can be chosen so that
It remains to prove 8.14.1 and hence also Lemma 8.14. Choose representatives of the maps \(\sigma '\), \(\sigma ''\), \(\theta '\) and \(\theta ''\). Concretely, this means we choose maps \(\alpha '_\sigma :\widehat{X}'\longrightarrow X'\), \(\alpha '_\theta :\widehat{X}'\longrightarrow \overline{X}'\), \(\beta '_\sigma :\widehat{Y}'\longrightarrow Y'\) and \(\beta '_\theta :\widehat{Y}'\longrightarrow \overline{Y}'\) rendering some triangles 2-commutative. By Remark 8.3 the 1-morphisms \(\alpha '_\sigma \), \(\alpha '_\theta \), \(\beta '_\sigma \) and \(\beta '_\theta \) are of finite type and universally quasi-proper.
Choose a Nagata compactification for the composite \(\widehat{X}'{\mathop {\longrightarrow }\limits ^{\widehat{p}'}}Y{\mathop {\longrightarrow }\limits ^{\widehat{v}}}\widehat{Y}'\), giving the 2-commutative triangle

which we view as an object \(D\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\widehat{Y}')\). We know that \(\beta '_\sigma \) and \(\beta '_\theta \) are of finite type and universally quasi-proper, hence

can be viewed as objects \(E\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',Y')\) and \(G\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\overline{Y}')\). But we also have the diagrams

which define objects \(E'\in {\mathbb {RNS}_{{\textbf{e}}}}(\widehat{X}',Y')\) and \(G'\in {\mathbb {RNS}_{{\textbf{e}}}}(\widehat{X}',\overline{Y}')\). Furthermore, we are given 2-morphisms \(\lambda :\beta '_\sigma \widehat{v}\widehat{p}'\longrightarrow vp'\alpha '_\sigma \) and \(\mu :\beta '_\theta \widehat{v}\widehat{p}'\longrightarrow \overline{v}\overline{p}'\alpha '_\theta \), in other words morphisms \(\lambda :F(E)\longrightarrow F(E')\) and \(\mu :F(G)\longrightarrow F(G')\). Lemma 8.5 applies, and we produce objects \(H\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',Y')\) and \(\overline{H}\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\overline{Y}')\), together with maps \(E{\mathop {\longleftarrow }\limits ^{\gamma }}H{\mathop {\longrightarrow }\limits ^{\delta }}E'\) and \(G{\mathop {\longleftarrow }\limits ^{\gamma '}}\overline{H}{\mathop {\longrightarrow }\limits ^{\delta '}}G'\) with \(\lambda =F(\delta )F(\gamma )^{-1}\) and \(\mu =F(\delta ')F(\gamma ')^{-1}\). Let H and \(\overline{H}\) be the diagrams

The morphisms \(\gamma :H\longrightarrow E\) and \(\gamma ':\overline{H}\longrightarrow G\) have representatives giving the 2-commutative triangles

Replacing H and \(\overline{H}\) by isomorphs we may assume that the 2-isomorphisms \(t\longrightarrow \beta '_\sigma r\zeta \) and \(\overline{t}\longrightarrow \beta '_\theta r\xi \) are identities. Remark 8.3 tells us that \(\zeta \) and \(\xi \) are of finite type and universally quasi-proper, therefore, the following are morphisms \(D'{\mathop {\longrightarrow }\limits ^{i}}D{\mathop {\longleftarrow }\limits ^{j}}\overline{D}'\) in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\widehat{Y}')\)

and the morphisms \(\gamma :H\longrightarrow E\) and \(\gamma ':\overline{H}\longrightarrow G\) satisfy \(\gamma =\beta '_\sigma i\) and \(\gamma '=\beta '_\theta j\).
But Lemmas 8.5, 8.6 and 8.8 combine to tell us that the morphisms of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\widehat{Y}')\) satisfy the right Ore condition, hence the morphisms \(D'{\mathop {\longrightarrow }\limits ^{i}}D{\mathop {\longleftarrow }\limits ^{j}}\overline{D}'\) can be completed in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(\widehat{X}',\widehat{Y}')\) to a commutative square

Let the morphisms \(k:\widehat{D}\longrightarrow D'\) and \(\ell :\widehat{D}\longrightarrow \overline{D}'\) be represented by the 2-commutative diagrams

and let the morphisms \(\delta :H\longrightarrow E'\) and \(\delta ':\overline{H}\longrightarrow G'\) be represented by the 2-commutative diagrams

This produces for us the 2-commutative diagram

which we view as an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), as well as 1-morphisms \(\alpha '_\sigma :\widehat{X}'\longrightarrow X'\), \(\alpha '_\theta :\widehat{X}'\longrightarrow \overline{X}'\), \(\beta '_\sigma :\widehat{Y}'\longrightarrow Y'\) and \(\beta '_\theta :\widehat{Y}'\longrightarrow \overline{Y}'\), \(\chi \tau :\widehat{X}''\longrightarrow X''\) and \(\overline{\chi }\overline{\tau }:\widehat{X}''\longrightarrow \overline{X}''\), together with a great deal of 2-commutativity that assembles to give the morphisms \(b{\mathop {\longleftarrow }\limits ^{\sigma }}a{\mathop {\longrightarrow }\limits ^{\theta }}c\) as in 8.14.1. We leave the details to the reader. \(\square \)
Lemma 8.15
Let \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) be the functor of Remark 8.11, and let \(\varphi ,\psi \) be two morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) with \(F(\varphi )=F(\psi )\). Then, there exists a morphism \(\rho \in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) with \(\varphi \rho =\psi \rho \).
Proof
We are given two morphisms  in the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), satisfying \(F(\varphi )=F(\psi )\). Applying the functors \(\pi _{12}^{}\) and \(\pi _{23}^{}\) of Remark 8.11, we obtain the pairs of morphisms
in the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), satisfying \(F(\varphi )=F(\psi )\). Applying the functors \(\pi _{12}^{}\) and \(\pi _{23}^{}\) of Remark 8.11, we obtain the pairs of morphisms

in the categories \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) and \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(Y,Z)\), with \(F\big (\pi _{12}^{}(\varphi )\big )=F\big (\pi _{12}^{}(\psi )\big )\) and \(F\big (\pi _{23}^{}(\varphi )\big )=F\big (\pi _{23}^{}(\psi )\big )\). By Lemma 8.6 there exist morphisms \(\rho ^{}_{12}\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) and \(\rho ^{}_{23}\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(Y,Z)\) so that the two composites

are equal. We assemble \(a_{12}^{}\) and \(a_{23}^{}\) together into the diagram A below

where \(a_{12}^{}=\pi _{12}^{}(A)\) and \(a_{23}^{}=\pi _{23}^{}(A)\), and the morphisms \(\rho _{12}^{}\) and \(\rho _{23}^{}\) can be rewritten as maps
Now, we apply 8.14.1 to the identity map \(\textrm{id}:F(b)\longrightarrow F(b)\), to the diagram A above, and with \(\sigma '=\theta '=\rho _{12}^{}\) and \(\sigma ''=\theta ''=\rho _{23}^{}\). From 8.14.1, we learn that there exists an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) with \(\pi _{12}^{}(a)=\pi _{12}^{}(A)\) and \(\pi _{23}^{}(a)=\pi _{23}^{}(A)\), and a morphism \(\rho :a\longrightarrow b\) with \(\pi _{12}^{}(\rho )=\rho _{12}^{}\) and \(\pi _{23}^{}(\rho )=\rho _{23}^{}\). Replacing the pair of morphisms

we are reduced to proving the Lemma in the special case where \(\pi _{12}^{}(\varphi )=\pi _{12}^{}(\psi )\) and \(\pi _{23}^{}(\varphi )=\pi _{23}^{}(\psi )\). To explain it all more concretely: the objects \(b,c\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) are given by 2-commutative diagrams in \({\mathbb {S}_{{\textbf{e}}}}\) satisfying all the requirements of Definition 8.10(i)

The morphisms  are represented by pairs
are represented by pairs  ,
,  and
and  , together with a bunch of 2-isomorphisms giving the 2-commutativity in Definition 8.10(ii). The reduction we have proved so far is that we may assume \(\pi _{12}^{}(\varphi )=\pi _{12}^{}(\psi )\) and \(\pi _{23}^{}(\varphi )=\pi _{23}^{}(\psi )\), meaning there are 2-commutative diagrams
, together with a bunch of 2-isomorphisms giving the 2-commutativity in Definition 8.10(ii). The reduction we have proved so far is that we may assume \(\pi _{12}^{}(\varphi )=\pi _{12}^{}(\psi )\) and \(\pi _{23}^{}(\varphi )=\pi _{23}^{}(\psi )\), meaning there are 2-commutative diagrams

where the curved arrows represent the part of the data of \(\varphi \) and \(\psi \) that pertains to this portion of the diagram. But the equivalence relation allows us to replace \(\alpha '_\varphi \) and \(\beta '_\varphi \) by the isomorphic \(\alpha '_\psi \) and \(\beta '_\psi \), as long as we are careful to perturb the rest of the data to match. Doing this, we may choose representatives of \(\varphi \) and \(\psi \) so that on the \(\pi _{12}^{}\) and \(\pi _{23}^{}\) portions they are identical: we may assume that our representatives for \(\varphi \) and \(\psi \) give the same data

and Remark 8.3 guarantees that \(\alpha '\) and \(\beta '\) are of finite type and universally quasi-proper.
The above gives a single 2-morphism \(\beta 'vp'\longrightarrow \overline{v}\overline{p}'\alpha '\), but the morphisms \(\varphi \) and \(\psi \) give two liftings of it

which are not necessarily equivalent, in other words what is pictured above is two 2-commutative diagrams, one with \(\alpha ''_\varphi \) and one with \(\alpha ''_\psi \), which might not compress into a single 2-commutative diagram. Anyway these define two morphisms in \({\mathbb {RNS}_{{\textbf{e}}}}(X',\overline{Y}')\) with the same image under F. Lemma 8.6 assures us that there exists an equalizer; concretely the above can be extended to a diagram

which becomes 2-commutative if we delete the middle row. Now, Lemma 8.6 allows us to choose \(X'{\mathop {\longrightarrow }\limits ^{\widehat{u}}}X''{\mathop {\longrightarrow }\limits ^{\widehat{s}}}\overline{Y}'\) to be in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X',\overline{Y}')\), meaning we may assume that \(\widehat{u}\) is a dominant, flat monomorphism and, by Remark 8.3, we may also assume \(\alpha ''_\rho \) of finite type and univerally quasi-proper. We construct the 2-commutative diagram a below

The horizontal maps are dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper, hence a is an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\). And the maps \(\textrm{id}:X'\longrightarrow X'\), \(\alpha ''_\rho :\widehat{X}''\longrightarrow X''\) and \(\textrm{id}:Y'\longrightarrow Y'\) assemble to give a morphism \(\rho :a\longrightarrow b\), and we remind the reader that a and b are the 2-commutative diagrams

We leave it to the reader to check that the composites  are equal in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), meaning the representatives we constructed are equivalent. \(\square \)
are equal in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), meaning the representatives we constructed are equivalent. \(\square \)
Proposition 8.16
In Definition 8.10 we constructed a category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) and in Remark 8.11 we noted that there is an obvious functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\). Since \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) is a groupoid the functor F factors canonically as \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z){\mathop {\longrightarrow }\limits ^{\pi }}{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z){\mathop {\longrightarrow }\limits ^{F'}}{\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\), where \({{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) is the groupoid completion of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\).
In this canonical factorization the functor \(F'\) is an equivalence.
Proof
Lemma 8.8, coupled with Lemmas 8.14 and 8.15, tell us that the functor \(F'\) is fully faithful, while Lemma 8.13 establishes the essential surjectivity. \(\square \)
Definition 8.17
We will also need to refer to the four-object version, but fortunately we do not care about its categorical structure, only the class of objects. We, therefore, define \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\subset {\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\) to be the classes whose elements are 2-commutative diagrams

In both \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\) and \({\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\), the squares are assumed 2-cartesian and the horizontal maps are assumed flat. For \({\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\), these are the only restrictions, while in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\), we further restrict the horizontal maps to be dominant monomorphisms, and the vertical maps to be of finite type and universally quasi-proper.
Remark 8.18
As in Remark 8.11, we will want to consider some forgetful maps out of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\). For example, the map \(\pi _{124}^{}\) forgets the column and row containing Y in the diagram of Definition 8.17. That is it leaves us with the diagram

Mercifully, the only fact we will need about \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\) is that it has plenty of objects.
Lemma 8.19
The obvious map \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(W,X)\times {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) is essentially surjective.
Proof
Suppose we are given an object \(W{\mathop {\longrightarrow }\limits ^{e}}X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}(W,X)\times {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\). Choose Nagata compactifications for e, f and g, that is construct a 2-commutative diagram

where the horizontal maps are dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper. Now, apply Lemma 8.13 to the composable morphisms \(W'{\mathop {\longrightarrow }\limits ^{u'o''}}X'{\mathop {\longrightarrow }\limits ^{vp'}}Y\) to complete to a 2-commutative diagram

where the horizontal maps are dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper. The fact that the squares are 2-cartesian is by Corollary 7.9. \(\square \)
10 The 2-Functor \((-)^!\)
In the last section, we met a great many auxiliary categories, and the reader might wonder what the point is. Now, we begin to explain, starting with the objects.
Remark 9.1
On the category of algebraic stacks, there is the assignment that takes a stack X to its derived category \({{\textbf{D}}_{\textbf{qc}}}(X)\). It can be made into a 2-functor in several ways, in this remark we recall the following two. Given a 1-morphism \(f:X\longrightarrow Z\) there are 1-morphisms \(f^*,f^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\), and given a 2-morphism \(f\longrightarrow g\) there are induced 2-isomorphisms \(f^*\longrightarrow g^*\) and \(f^\times \longrightarrow g^\times \). Since \((gf)^*\) is canonically isomorphic to \(f^*g^*\) and \((gf)^\times \) is canonically isomorphic to \(f^\times g^\times \), we have 2-functors \((-)^*\) and \((-)^\times \), defined on the entire 2-category of algebraic stacks. We will mostly be interested in the restriction to the 2-subcategory \({\mathbb {S}_{{\textbf{e}}}}\), that is in the 2-functors \((-)^*:{\mathbb {S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\) and \((-)^\times :{\mathbb {S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\). Here \(\mathbb {T}\textrm{ri}\) is the 2-category whose objects are triangulated categories, the 1-morphisms are triangulated functors, and the 2-morphisms are natural transformations. The 2-functors \((-)^*\) and \((-)^\times \) give, for every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), functors
In the last section, we saw the categories \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and \({{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and studied some functors between them. We obtain composites

where \(F'\) is an equivalence by Proposition 8.9. Concretely, these composites take an object in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), i.e. a 2-commutative triangle

to \(f^*\) (respectively, \(f^\times \)). But on the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\), there are equivalent functors: the definition of an object in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\) gives a 2-isomorphism \(pu\longrightarrow f\), hence 2-isomorphisms \(u^*p^*\longrightarrow f^*\) and \( u^\times p^\times \longrightarrow f^\times \). The reader can convince herself that the map taking an object in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \(u^*p^*\) (respectively, \(u^\times p^\times \)) extends to a functor in such a way that the comparison isomorphism \(u^*p^*\longrightarrow f^*\) (respectively, \(u^\times p^\times \longrightarrow f^\times \)) is a natural transformation.
Construction 9.2
So far all the categories \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) seem to have bought us are complicated functors equivalent to the simple \((-)^*\) and \((-)^\times \). Now, we begin to change this.
-
(i)
For any object \(a\in {\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\), that is for a 2-commutative triangle
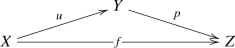
we define P(a) to be the object in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\) given by the composite \(P(a)=u^*p^\times \). That is P(a) is the composite 1-morphism \({{\textbf{D}}_{\textbf{qc}}}(Z){\mathop {\longrightarrow }\limits ^{p^\times }}{{\textbf{D}}_{\textbf{qc}}}(Y){\mathop {\longrightarrow }\limits ^{u^*}}{{\textbf{D}}_{\textbf{qc}}}(X)\) in \(\mathbb {T}\textrm{ri}\).
-
(ii)
For any object \(a\in {\mathbb {LNS}_{{\textbf{e}}}}(X,Y,Z)\), we define P(a) to be a 2-morphism in \(\mathbb {T}\textrm{ri}\), more specifically a morphism in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\). Even more specifically, it will be a 2-morphism \(P\big (\pi _{13}^{}(a)\big )\longrightarrow P\big (\pi _{12}^{}(a)\big )P\big (\pi _{23}^{}(a)\big )\). After all the preliminaries, it is time to give the definition. An object \(a\in {\mathbb {LNS}_{{\textbf{e}}}}(X,Y,Z)\) is a diagram
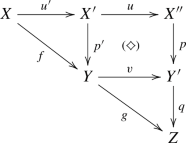
while \(\pi _{12}^{}(a)\), \(\pi _{13}^{}(a)\) and \(\pi _{22}^{}(a)\) are, respectively, the 2-commutative diagrams
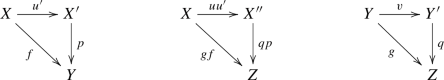
We have promised the reader a 2-morphism \(P\big (\pi _{13}^{}(a)\big )\longrightarrow P\big (\pi _{12}^{}(a)\big )P\big (\pi _{23}^{}(a)\big )\), meaning a map \((uu')^*(qp)^\times \longrightarrow ({u'}^*{p'}^\times )(v^*q^\times )\). And the formula is that P(a) is the composite
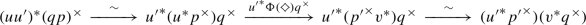
where the first map is by the canonical isomorphisms of Remark 9.1 coupled with associativity, the second map is induced by the base-change \(\Phi (\diamondsuit )\) for the 2-cartesian square \((\diamondsuit )\) in the diagram defining a, and the third is associativity of composition. Note that v is assumed flat so the base-change map is well defined.
-
(iii)
When a is an element of \({\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\), it turn out that P(a) is a relation. Since something has to be proved we state it as a lemma.
Lemma 9.3
With the notation as in Definition 8.17 and Remark 8.18, any object \(a\in {\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\) yields an equality in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(W)\big )\) of the morphisms
Proof
The object \(a\in {\mathbb {LNS}_{{\textbf{e}}}}(W,X,Y,Z)\) is a diagram

and the objects \(\pi _{123}^{}(a)\), \(\pi _{134}^{}(a)\), \(\pi _{234}^{}(a)\) and \(\pi _{124}^{}(a)\) are, respectively, the diagrams


The maps \(P\big (\pi _{234}^{}(a)\big )P\big (\pi _{124}^{}(a)\big )\) and \(P\big (\pi _{123}^{}(a)\big )P\big (\pi _{134}^{}(a)\big )\) are, respectively, the composites

and the equality of these composites comes from the commutativity of the square in

and the fact that base-change maps concatenate, that is \(\Phi (\diamondsuit \heartsuit )=\Phi (\diamondsuit )\Phi (\heartsuit )\) and \(\Phi \left( \!\!\begin{array}{c}\heartsuit \\ \spadesuit \end{array}\!\!\right) =\Phi (\spadesuit )\Phi (\heartsuit )\). \(\square \)
Construction 9.4
Now, it is time to construct \((-)^!\).
-
(i)
If \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) is an object we define \(a^!=P(a)\), with P(a) as in Construction 9.2(i). That is \(a^!=u^*p^\times \) with the notation of Construction 9.2(i).
This deals with the objects of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), next we worry about the morphisms. Suppose \(\varphi :a\longrightarrow b\) represents a morphism in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\). Recall: the morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) are equivalence classes of 2-commutative diagrams, and for the construction, we choose a representative. For us right now, the relevant part of the data given by the representative is the 2-commutative

Out of this, we construct the 2-commutative diagram C below

We are given that \(p'\) is separated, of finite type and universally quasi-proper, and Remark 8.3 tells us that so is \(\alpha \). Thus, the vertical maps are all of finite type and universally quasi-proper while the horizontal maps are dominant, flat monomorphisms. The diagram is an object \(C\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,Z)\).
By Construction 9.2(ii), we have a morphism \(P(C):P\big (\pi _{13}^{}(C)\big )\longrightarrow P\big (\pi _{12}^{}(C)\big )P\big (\pi _{23}^{}(C)\big )\), meaning a map \(P(C):{(u\circ \textrm{id})}^*{(p'\alpha )}^\times \longrightarrow \textrm{id}^*\textrm{id}^\times {u'}^* {p'}^\times \). Note that up to isomorphism the 2-morphism \(P(C)\in {\mathbb {S}_{{\textbf{e}}}}\) is given by the base-change map \(\Phi (\diamondsuit ):u^*\alpha ^\times \longrightarrow \textrm{id}^\times {u'}^*\), and Lemma 5.20(ii) applies to the square \((\diamondsuit )\) because \(\textrm{id}:X'\longrightarrow X'\) is of finite Tor-dimension. We deduce that P(C) is an isomorphism. And now we come to
-
(ii)
With the notation as above—that is with \(\varphi :a\longrightarrow b\) a representative of a morphism in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), and with everything else as constructed out of \(\varphi \) in the preceding paragraphs—we define \(\varphi ^!:a^!\longrightarrow b^!\) to be the composite
where the first isomorphism is the map induced by the 2-isomorphism \(p\longrightarrow p'\alpha \) that is part of the data of \(\varphi \), and P(C) is as above. Note that \(\varphi ^!\), being the composite of two isomorphisms, must be an isomorphism in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\).
There is nothing to stop us from defining \((-)^!\) on all objects of \({\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\) following the recipe above, but then \((-)^!\) will fail to take the morphisms to isomorphisms. As we will see, this is a key property.
Lemma 9.5
If \(\varphi ,\psi \) are two equivalent representatives of a morphism \(a\longrightarrow b\) in the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) then \(\varphi ^!=\psi ^!\), with the notation as in Construction 9.4(ii).
Proof
Two representatives \(\varphi ,\psi \) of a morphism in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and an equivalence between them gives, among other things, the 2-commutative diagram

of Definition 8.1(ii). By Remark 8.3, \(\alpha \) and \(\alpha '\) are of finite type and universally quasi-proper. Out of this, we cook up the 2-commutative diagram C below

All the horizontal maps are dominant, flat monomorphisms, all the vertical maps are of finite type and universally quasi-proper, and Corollary 7.9 tells us that the squares are all 2-cartesian. Therefore, C is an object in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,Z,Z)\). By Lemma 9.3, this gives the relation \(P\big (\pi _{123}^{}(C)\big )P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\). But \(P\big (\pi _{234}^{}(C)\big )=\textrm{id}\) and \(P\big (\pi _{134}^{}(C)\big )\) is the isomorphism \(u^*(p'\alpha ')^\times \longrightarrow u^*(p'\alpha )^\times \) induced by the isomorphism \(\alpha '\longrightarrow \alpha \), and we conclude that in the diagram below the triangle commutes

The two equal composites, from top left to bottom right, are by definition \(\varphi ^!\) and \(\psi ^!\). \(\square \)
Lemma 9.6
The assignment \((-)^!\) defines a functor \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\).
Proof
In Construction 9.4(i), we defined \(a^!\) for a an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), and in Construction 9.4(ii) we defined \(\varphi ^!:a^!\longrightarrow b^!\), whenever \(\varphi :a\longrightarrow b\) is the representative of a morphism. In Lemma 9.5, we showed that equivalent representatives map to equal morphisms in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\), hence we have an unambiguous construction that sends objects to objects and morphisms to morphisms. Identities obviously map to identities, and it remains to show that \((-)^!\) respects composition.
Let \(a{\mathop {\longrightarrow }\limits ^{\varphi }}b{\mathop {\longrightarrow }\limits ^{\psi }}c\) be composable morphisms in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\). Choose representatives; part of the data this gives is the 2-commutative diagram

Out of this, we construct the 2-commutative diagram

We are given that \(p''\) is of finite type and universally quasi-proper, and Remark 8.3 says that so are \(\alpha \) and \(\beta \). Hence, the vertical maps are all of finite type and universally quasi-proper. The horizontal maps are given to be dominant, flat monomorphisms, and Corollary 7.9 informs us that the squares are all 2-cartesian. Thus, the diagram defines an object \(C\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,X,Z)\). From Lemma 9.3 we learn that \(P\big (\pi _{123}^{}(C)\big )P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\); observing that \(P\big (\pi _{123}^{}(C)\big )=\textrm{id}\) this simplifies to \(P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\). Let \(C'\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,Z)\) be the object

which is isomorphic to \(\pi _{124}^{}(C)\) via the isomorphism \(p'\longrightarrow p''\beta \), and consider the diagram

The commutativity of the triangle in the bottom right is the identity \(P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\), and the commutativity of the square is by definition of the horizontal maps, both are induced by the base-change map \(\Phi (\heartsuit )\) (see Construction 9.2(ii)). The commutativity of the perimeter tells us that \(\psi ^!\varphi ^!=(\psi \varphi )^!\). \(\square \)
Remark 9.7
Our lemmas so far tell us that we have constructed a functor \((-)^!:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\). In Construction 9.4(ii) we noted that, for any morphism \(\varphi :a\longrightarrow b\) in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), the morphism \(\varphi ^!\in \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\) is an isomorphism. Therefore, \((-)^!\) factors canonically through the groupoid completion: there is a canonical factorization as

In Proposition 8.9, we showed that the forgetful map \(F':{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) is an equivalence. This means that, up to canonical equivalence, we have defined a functor \((-)^!:{\mathbb {S}_{{\textbf{e}}}}(X,Z)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\). More precisely: the functor \(F':{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) is not only an equivalence, \(F'\) is surjective on objects and has a right inverse—constructing one amounts to choosing a preimage for every object. For every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), choose a right inverse \(R(X,Z):{\mathbb {S}_{{\textbf{e}}}}(X,Z)\longrightarrow {{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) for \(F'\). Make the choice is such a way that, for every object \(X\in {\mathbb {S}_{{\textbf{e}}}}\), the object \(\textrm{id}:X\longrightarrow X\) of \({\mathbb {S}_{{\textbf{e}}}}(X,X)\) maps to the object

in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X)\). Now, define \((-)^!:{\mathbb {S}_{{\textbf{e}}}}(X,Z)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\) to be the composite

Since all right inverses of \(F'\) are canonically isomorphic, the functor \((-)^!\) is unique up to canonical isomorphism. And with our choice for what happens to identities we have guaranteed that \(\textrm{id}^!=\textrm{id}\).
Note that we are committing the notational crime of writing \((-)^!\) for all of these functors, not distinguishing whether the source category is \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), \({{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) or \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\).
Construction 9.8
We have three functors \(\pi _{12}^{}\), \(\pi _{13}^{}\) and \(\pi _{23}^{}\) out of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), to \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y)\), \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) and \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(Y,Z)\), respectively. We can now compose them with the functors \((-)^!\) of Remark 9.7, and wonder how these three composite functors might be related. To address this,
-
(i)
Let \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) be an object. We define the morphism \(\rho (a): \pi _{13}^{}(a)^!\longrightarrow \pi _{12}^{}(a)^!\pi _{23}^{}(a)^!\) to be \(P(a):P\big (\pi _{13}^{}(a)\big )\longrightarrow P\big (\pi _{12}^{}(a)\big )P\big (\pi _{23}^{}(a)\big )\) as in Construction 9.2(ii).
Lemma 9.9
The assignment \(\rho \) of Construction 9.8 is a natural transformation of functors on \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\).
Proof
Let \(\varphi :a\longrightarrow b\) be a representative of a morphism in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), that is a 2-commutative diagram

satisfying all the hypotheses. Out of this, we cook up the following 2-commutative diagrams, which we will refer to as B and C, respectively:

Of the vertical maps \(p'\), p, \(\overline{p}'\), \(\overline{p}\) and \(\overline{q}\) are given to be separated, of finite type and universally quasi-proper, and Remark 8.12 guarantees that so are \(\alpha '\), \(\alpha ''\) and \(\beta '\). Thus, all the vertical morphisms are of finite type and universally quasi-proper and the horizontal maps are dominant, flat monomorphisms. Corollary 7.9 tells us that the squares are 2-cartesian, hence the diagram B is an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,Y,Z)\) and the diagram C is an object in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Y,Z)\).
By Lemma 9.3, the objects \(B\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,X,Y,Z)\) and \(C\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Y,Z)\) give one relation each. We have the identities
Now, recall that B and C were constructed out of the representative \(\varphi \) of a morphism \(a\longrightarrow b\) in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), and I assert that the Lemma will be proved by untangling what each of the entries in the two relations is, in terms of a, b and \(\varphi \). Let us begin with the relation that comes from C.
We have that \(\textrm{id}=P\big (\pi _{123}^{}(C)\big )\), hence the relation given by C simplifies to \(P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\). Let \(\lambda :q\longrightarrow \overline{q}\beta '\) be the isomorphism, and consider the diagram

The square obviously commutes, and the composite along the bottom row is by definition the map induced by \(\pi _{23}^{}(\varphi )^!:v^*q^\times \longrightarrow {v'}^*\overline{q}^\times \). The commutativity, combined the relation given by C, tells us that \(\pi _{23}^{}(\varphi )^!\rho (a)=P\big (\pi _{134}^{}(C)\big )\lambda ^\times \).
Now, we study the relation coming from B. If \(\mu :qp\longrightarrow \overline{q}\overline{p}\alpha ''\) is the isomorphism in the data, then by definition \(\pi _{13}^{}(\varphi )^! =P\big (\pi _{124}^{}(B)\big )\mu ^\times \), while \(\rho (b)\) is by definition equal to \(P\big (\pi _{234}^{}(B)\big )\). The relation coming from B rewrites as \(\rho (b)\pi _{13}^{}(\varphi )^!= P\big (\pi _{123}^{}(B)\big )P\big (\pi _{134}^{}(B)\big )\mu ^\times \). Let \(\nu :p'\longrightarrow \overline{p}'\alpha '\) be the isomorphism, and we have identities
The second equality is because \(P\big (\pi _{134}^{}(B)\big )\mu ^\times =\nu ^\times P\big (\pi _{134}^{}(C)\big )\lambda ^\times \), which comes from the isomorphism of \(\pi _{134}^{}(B)\) with \(\pi _{134}^{}(C)\). The third equality is because \(\pi _{23}^{}(\varphi )^!\rho (a)= P\big (\pi _{134}^{}(C)\big )\lambda ^\times \) by the paragraph above studying the identity coming from C, and because \(\pi _{12}^{}(\varphi )^!=\pi _{123}^{}(B)\nu ^\times \) by definition. But the equality of the first and last terms means that the square

commutes, and hence \(\rho \) is a natural transformation. \(\square \)
Remark 9.10
The functors \(\pi _{12}^{}(-)^!\), \(\pi _{23}^{}(-)^!\) and \(\pi _{13}^{}(-)^!\) all factor through the map \(\pi :{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\), and hence so does the natural transformation \(\rho : \pi _{13}^{}(-)^!\longrightarrow \pi _{12}^{}(-)^!\pi _{23}^{}(-)^!\). But Proposition 8.16 tells us that the map \(F':{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) is an equivalence. In Remark 9.7, we chose, for every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), a functor \(R(X,Z):{\mathbb {S}_{{\textbf{e}}}}(X,Z)\longrightarrow {{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) right inverse to the projection, and defined the functor \((-)^!\) on \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\) using this right inverse. We leave it to the reader to check that we can now define an unambiguous natural transformation which takes the object \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) to the morphism \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\) in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\). The map \(\rho (f,g)\) does not depend on any new choices: it is determined by the R(X, Y), R(Y, Z) and R(X, Z) which were fixed in Remark 9.7.
Theorem 9.11
We have so far constructed the following map from the 2-category \({\mathbb {S}_{{\textbf{e}}}}\) to the 2-category \(\mathbb {T}\textrm{ri}\):
-
(i)
On objects: we take \(X\in {\mathbb {S}_{{\textbf{e}}}}\) to \({{\textbf{D}}_{\textbf{qc}}}(X)\in \mathbb {T}\textrm{ri}\).
-
(ii)
On 1-morphisms and 2-morphisms: For each pair of objects \(X,Y\in {\mathbb {S}_{{\textbf{e}}}}\) we have defined a functor \((-)^!:{\mathbb {S}_{{\textbf{e}}}}(X,Y)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Y),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\).
-
(iii)
Composition: for any triple of objects \(X,Y,Z\in {\mathbb {S}_{{\textbf{e}}}}\) we have defined a natural transformation \(\rho :[(-)\circ (?)]^!\longrightarrow (?)^!\circ (-)^!\).
These combine to make \((-)^!\) an oplax 2-functor of 2-categories.
Proof
What needs proof is the associativity property of \(\rho \). We need to show that, for any object \(W{\mathop {\longrightarrow }\limits ^{e}}X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in the category \({\mathbb {S}_{{\textbf{e}}}}(W,X)\times {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\), the following square commutes:

The square involves objects obtained by applying the functor \((-)^!\) to
and the definition of \((-)^!\) suggests that it might be convenient to first choose preimages for these under the equivalences of categories \(F':{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(-,?)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(-,?)\). And we might as well choose preimages in a way that facilitates the computation. Lemma 8.19 tells us that every object \(a\in {\mathbb {S}_{{\textbf{e}}}}(W,X)\times {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\) is in the essential image of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\). If we let a be the object \(W{\mathop {\longrightarrow }\limits ^{e}}X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) we may extend it to an object \(A\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(W,X,Y,Z)\), that is a 2-commutative diagram

Now, choose
to be (respectively) the liftings via \(F':{{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(-,?)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(-,?)\) of the objects
and then
and the relation \(P\big (\pi _{123}^{}(A)\big )P\big (\pi _{134}^{}(A)\big )= P\big (\pi _{234}^{}(A)\big )P\big (\pi _{124}^{}(A)\big )\) of Lemma 9.3 is exactly the identity \(\rho (e,f)\rho (fe,g)=\rho (f,g)\rho (e,gf)\). \(\square \)
The oplax 2-functor \((-)^!\) is not a pseudofunctor, meaning there are in general pairs of morphisms for which \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\) need not be an isomorphism. We end the section with
Proposition 9.12
Let \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) be composable 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\). The map \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\) is an isomorphism if any one of the following holds:
-
(i)
f is of finite Tor-dimension.
-
(ii)
g is of finite type and universally quasi-proper.
-
(iii)
gf is of finite type and universally quasi-proper.
-
(iv)
We restrict to the bounded-below derived category. More formally: if \(I:{{\textbf{D}}^+_{\textrm{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Z)\) is the inclusion, then for any composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in \({\mathbb {S}_{{\textbf{e}}}}\) the map \(\rho (f,g)I:(gf)^!I\longrightarrow f^!g^!I\) is an isomorphism.
Proof
We begin with (ii): assume g is of finite type and universally quasi-proper. Choose a Nagata compactification for f, that is write f as the composite \(X{\mathop {\longrightarrow }\limits ^{u'}}X'{\mathop {\longrightarrow }\limits ^{p'}}Y\), with \(u'\) a dominant, flat monomorphism and \(p'\) of finite type and universally quasi-proper. Then, the diagram C below

is 2-commutative, the horizontal maps are all dominant, flat monomorphisms and the vertical maps are of finite type and universally quasi-proper. Hence, C is an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\). But up to isomorphism \(\rho (f,g)=P(C)\) is given by the base-change map \(\Phi (\diamondsuit )=\textrm{id}\).
Now, for the proof of (i) and (iv). Choose a lifting via the equivalence
of the object \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\), more concretely choose a diagram \(A\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) of the form

In (i), the map \(f\cong p'u'\) is assumed of finite Tor-dimension while \(u'\) is given to be flat, hence the image of \(u'\) is contained in the open set on which the finite-type map \(p'\) is of finite Tor-dimension. Theorem 6.10 informs us that \({u'}^*\Phi (\heartsuit ):{u'}^*u^*p^\times \longrightarrow {u'}^*{p'}^\times v^*\) is an isomorphism. Composing on the right with \(q^\times \) we deduce that \({u'}^*\Phi (\heartsuit )q^\times :{u'}^*u^*p^\times q^\times \longrightarrow {u'}^*{p'}^\times v^*q^\times \) is also an isomorphism, but up to isomorphism this is the morphism \(\rho (f,g)=P(A):(gf)^!\longrightarrow f^! g^!\). This proves (i).
Now, for (iv): f and g are unrestricted, but let \(E\in {{\textbf{D}}^+_{\textrm{qc}}}(Z)\) be a bounded-below object. Then, \(q^\times E\) is an object of \({{\textbf{D}}^+_{\textrm{qc}}}(Y')\), and by Lemma 5.20(ii), the map \(\Phi (\heartsuit )(q^\times E):u^*p^\times q^\times E\longrightarrow {p'}^\times v^*q^\times E\) is an isomorphism. Applying \({u'}^*\), we deduce that \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\) evaluates at E to give an isomorphism.
Finally, we prove (iii): assume that gf is of finite type and universally quasi-proper. Choose a Nagata compactification for g, that is write g as the composite \(Y{\mathop {\longrightarrow }\limits ^{v}}Y'{\mathop {\longrightarrow }\limits ^{q}}Z\) with q of finite type and universally quasi-proper and v a dominant, flat monomorphism. We know that q and \(qvf\cong gf\) are of finite type and universally quasi-proper and Lemma 7.2 tells us that so is vf. By Theorem 9.11, we have the identity \(\rho (v,q)\rho (f,qv)=\rho (f,v) \rho (vf,q)\). We wish to show that \(\rho (f,g)\cong \rho (f,qv)\) is an isomorphism, and by (ii) we know that \(\rho (v,q)\) and \(\rho (vf,q)\) both are—from the identity it suffices to prove that \(\rho (f,v)\) is an isomorphism. Thus, we are reduced to proving (iii) in the case where g is a dominant, flat monomorphism.
Let us factor gf as \(gf\cong ip'\), where i is the (closed) immersion of the stack-theoretic closure of the image of gf. By Lemma 7.1 the image of the finite-type, universally quasi-proper map \(gf:X\longrightarrow Z\) is closed; as a set the closure of the image is just the image, and \(p'\) is surjective. We have a 2-commutative square \((\clubsuit )\) and form the 2-cartesian square \((\diamondsuit )\) below

The surjective map \(p':X\longrightarrow Q\) factors (up to isomorphism) through the map \(\beta \) which, being the pullback of the flat monomorphism g, must be a surjective, flat monomorphism. Lemma 7.4 tells us that \(\beta \) is an isomorphism. Therefore, f is isomorphic to \(j\beta ^{-1}p'\). Put \(p=\beta ^{-1}p'\) and we have \(f\cong jp\) where j, being the pullback of the closed immersion i, is a closed immersion.
Now, Theorem 9.11 gives the identity \(\rho (p,j)\rho (jp,g)=\rho (j,g)\rho (p,gj)\). Since j and \(gj\cong i\) are closed immersions (ii) tells us that \(\rho (p,gj)\) and \(\rho (p,j)\) are isomorphisms. We want to show that \(\rho (f,g)\cong \rho (jp,g)\) is an isomorphism, and the identity tells us it suffices to prove that \(\rho (j,g)\) is an isomorphism. That is: we are reduced to proving that \(\rho (f,g)\) is an isomorphism when g is a dominant, flat monomorphism and f and gf are both closed immersions. The 2-commutative diagram C below

has the property that the horizontal maps are all dominant, flat monomorphisms while the vertical maps are of finite type and universally quasi-proper, hence C is an object of \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) lifting \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\), and P(C) computes \(\rho (f,g)\). We are reduced to showing that P(C) is an isomorphism, meaning that the base-change map \(\Phi (\heartsuit ):(gf)^\times \longrightarrow f^\times g^*\) is an isomorphism. Since f is an affine morphism \(f_*\) is conservative, and it suffices to show that \(f_*\Phi (\heartsuit ):f_*(gf)^\times \longrightarrow f_*f^\times g^*\) is an isomorphism. The fact that g is a concentrated, flat monomorphism means that the natural map \(g^*g_*\longrightarrow \textrm{id}\) is an isomorphism, hence it suffices to show that the composite

is an isomorphism. But for the closed immersions gf and f the functors \(g_*f_*(gf)^\times \) and \(f_*f^\times g^*\) simplify (respectively) to  and
and  . We are reduced to showing that the natural map
. We are reduced to showing that the natural map

is an isomorphism. Since \(g^*g_*\cong \textrm{id}\) it certainly suffices to show that the composite

is an isomorphism.
Define  to be the full subcategory of all objects M for which the natural map \(M\longrightarrow g_*g^*M\) is an isomorphism. Clearly
to be the full subcategory of all objects M for which the natural map \(M\longrightarrow g_*g^*M\) is an isomorphism. Clearly  is a localizing subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\). In the 2-cartesian square \((\heartsuit )\) above, the vertical maps are concentrated and the horizontal maps are flat, hence the base-change map \(g^*(gf)_*\longrightarrow f_*\) is an isomorphism. Therefore, \(g_*g^*(gf)_*\cong g_*f_*\) and we deduce that every object in \((gf)_*{{\textbf{D}}_{\textbf{qc}}}(X)\) belongs to the category
is a localizing subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\). In the 2-cartesian square \((\heartsuit )\) above, the vertical maps are concentrated and the horizontal maps are flat, hence the base-change map \(g^*(gf)_*\longrightarrow f_*\) is an isomorphism. Therefore, \(g_*g^*(gf)_*\cong g_*f_*\) and we deduce that every object in \((gf)_*{{\textbf{D}}_{\textbf{qc}}}(X)\) belongs to the category  . Since
. Since  is localizing it follows that the localizing subcategory generated by \((gf)_*{{\textbf{D}}_{\textbf{qc}}}(X)\) is contained in
is localizing it follows that the localizing subcategory generated by \((gf)_*{{\textbf{D}}_{\textbf{qc}}}(X)\) is contained in  , that is
, that is  contains all of \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\), the subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) of objects supported on the closed subset X. The object
contains all of \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\), the subcategory of \({{\textbf{D}}_{\textbf{qc}}}(Z)\) of objects supported on the closed subset X. The object  is bounded below and pseudo-coherent—the pseudo-coherence is because gf is a closed immersion—and moreover
is bounded below and pseudo-coherent—the pseudo-coherence is because gf is a closed immersion—and moreover  belongs to \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\). Lemma 5.2 tells us that
belongs to \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\). Lemma 5.2 tells us that  belongs to \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) for every \((-)\). Since
belongs to \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) for every \((-)\). Since  , the horizontal map below is an isomorphism
, the horizontal map below is an isomorphism

and, to show that (9.1) is an isomorphism, it suffices to prove the composite (9.2) an isomorphism.
We are assuming that \({{\textbf{D}}_{\textbf{qc}}}(Z)\) satisfies Thomason’s condition, hence the category \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) is generated by the compact objects it contains, and  contains all of them. For every compact object \(C\in {{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) and any object \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) we have that the map \(C\otimes E\longrightarrow (g_*g^*C)\otimes E\cong C\otimes (g_*g^*E)\) is an isomorphism, where the first map is an isomorphism because
contains all of them. For every compact object \(C\in {{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) and any object \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) we have that the map \(C\otimes E\longrightarrow (g_*g^*C)\otimes E\cong C\otimes (g_*g^*E)\) is an isomorphism, where the first map is an isomorphism because  . Since C is strongly dualizable, we can rewrite this as saying that
. Since C is strongly dualizable, we can rewrite this as saying that  is an isomorphism. Let
is an isomorphism. Let  be the full subcategory of all objects \(L\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) such that the natural map
be the full subcategory of all objects \(L\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) such that the natural map  is an isomorphism. We have proved that every compact object in \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) belongs to
is an isomorphism. We have proved that every compact object in \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) belongs to  , but
, but  is localizing and the compact objects in \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) generate \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\). Hence, \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) is contained in
is localizing and the compact objects in \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) generate \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\). Hence, \({{\textbf{D}}}_{\textbf{qc},X}^{}(Z)\) is contained in  , in particular
, in particular  and the composite in (9.2) is an isomorphism. \(\square \)
and the composite in (9.2) is an isomorphism. \(\square \)
11 The Oplax Natural Transformation \(\psi :(-)^\times \longrightarrow (-)^!\)
We want to construct something on \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\) but (as usual) begin with \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\).
Construction 10.1
Let \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) be an object, that is a 2-commutative diagram

with u a dominant, flat monomorphism (and p of finite type and universally quasi-proper). We define \(\psi (a):u^\times p^\times \longrightarrow u^*p^\times \) to be the morphism \(\Phi (\heartsuit )p^\times \), where \(\heartsuit \) is the 2-cartesian square

Note that the square is 2-cartesian because u is a monomorphism, and the base-change map \(\Phi (\heartsuit ):\textrm{id}^*u^\times \longrightarrow \textrm{id}^\times u^*\) exists because the square is 2-cartesian and u is flat.
Lemma 10.2
On the category \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\cong {{\textbf{G}}\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\), the \(\psi (-)\) of Construction 10.1 gives a natural transformation of \(\psi :(-)^\times \longrightarrow (-)^!\).
Proof
We recall that the map \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) is a groupoid completion, hence has a universal property with respect to functors and natural transformations: any natural transformation between functors that factor through F must factor through F. It, therefore, suffices to show that Construction 10.1 yields a natural transformation between the composite functors  The composite \((-)^!\circ F\) is, by the construction of \((-)^!\), naturally isomorphic to the functor taking the object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \(P(a)=u^*p^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). By Remark 9.1, the composite \((-)^\times \circ F\) is naturally isomorphic to the functor taking the object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \(u^\times p^\times \cong (pu)^\times \) and the reader might find it convenient to think of this as \(P(a')\) where \(a'\in {\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\) is the 2-commutative diagram
The composite \((-)^!\circ F\) is, by the construction of \((-)^!\), naturally isomorphic to the functor taking the object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \(P(a)=u^*p^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). By Remark 9.1, the composite \((-)^\times \circ F\) is naturally isomorphic to the functor taking the object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to \(u^\times p^\times \cong (pu)^\times \) and the reader might find it convenient to think of this as \(P(a')\) where \(a'\in {\mathbb {LNS}_{{\textbf{e}}}}(X,Z)\) is the 2-commutative diagram

A representative of a morphism \(\varphi :a\longrightarrow b\) in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) gives, among other data, a 2-commutative diagram

Out of this, we cook up the diagram C below

In the diagram C, the horizontal maps are all given to be dominant, flat monomorphisms, and the map \(\alpha \) is of finite type and universally quasi-proper by Remark 8.3. The square \((\diamondsuit )\) is 2-cartesian because u is a monomorphism, and the square \((\heartsuit )\) is 2-cartesian by Corollary 7.9. The remaining square is trivially 2-cartesian, and the diagram belongs to \({\mathbb {LNS}_{{\textbf{e}}}}(X,X,X,Z)\).
Lemma 9.3 gives the relation \(P\big (\pi _{123}^{}(C)\big )P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\), and since \(P\big (\pi _{123}^{}(C) =\textrm{id}\) this simplifies to \(P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\). Let \(\mu :p\longrightarrow p'\alpha \) and \(\lambda :\alpha u\longrightarrow u'\) be the given isomorphisms determined by \(\varphi :a\longrightarrow b\). Then,
hence \(P\big (\pi _{124}^{}(C)\big )\mu ^\times =\mu ^\times \psi (a)\). Therefore,
where the first equality is by the definition of \(\varphi ^!:a^!\longrightarrow b^!\), and the second and third equalities are from the discussion above. Now, in \({\mathbb {LNS}_{{\textbf{e}}}}(X,X,Z)\) we have the isomorphic objects \(\pi _{134}^{}(C)\) and A below

where the isomorphism is induced by \(\lambda :\alpha u\longrightarrow u'\). By Construction 10.1 we have \(\psi (b)=P(A)\), and by the isomorphism of A with \(\pi _{134}^{}(C)\) we have \(P(A)\lambda ^\times =P\big (\pi _{134}^{}(C)\big )\). Hence,
in other words the square

commutes, that is \(\psi \) is a natural transformation. \(\square \)
Theorem 10.3
Define \(\psi :(-)^\times \longrightarrow (-)^!\) as follows:
-
(i)
For an object \(X\in {\mathbb {S}_{{\textbf{e}}}}\), we define \(\psi (X):{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\) to be the identity functor.
-
(ii)
For a morphism \(f:X\longrightarrow Z\) in \({\mathbb {S}_{{\textbf{e}}}}\), we define \(\psi (f):f^\times \longrightarrow f^!\) to be as in Lemma 10.2.
These data define an oplax natural transformation of 2-functors.
Remark 10.4
We should perhaps expand a little, reminding the reader of the definitions. We have a pair of oplax 2-functors \((-)^\times \) and \((-)^!\), where it so happens that \((-)^\times \) is actually a pseudofunctor. To say that the data given define a natural transformation asserts
-
(i)
For every pair of objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), the data in Theorem 10.3(ii) yield a natural transformation of functors \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\); this much we have already proved, see Lemma 10.2.
-
(ii)
The construction respects identities. This is easy.
-
(iii)
The construction is compatible with composition in \({\mathbb {S}_{{\textbf{e}}}}\). Concretely: for composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) let \(\delta \) be the canonical isomorphism \(\delta (f,g):(gf)^\times \longrightarrow f^\times g^\times \), let \(\rho (f,g):(gf)^!\longrightarrow f^!g^!\) be the natural map of Theorem 9.11 and let \(\psi :(-)^\times \longrightarrow (-)^!\) be the natural transformation of Lemma 10.2. These are compatible in the sense that the square below commutes
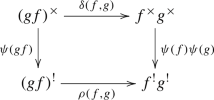
This last part still needs to be proved.
Proof
Our object \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) may be lifted to \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\); choose such a lifting, that is a 2-commutative diagram

satisfying a bunch of conditions. Out of this, we cook up the 2-commutative diagram B below

The horizontal maps are all given to be dominant, flat monomorphisms. The square \((\heartsuit )\) is given to be 2-cartesian, the square \((\clubsuit )\) is 2-cartesian by the definition of \(u'\) being a monomorphism, and the square \((\diamondsuit )\) is 2-cartesian by Lemma 7.5 applied to the composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{u'}}X'{\mathop {\longrightarrow }\limits ^{u}}X''\). Hence, B is an object in \({\mathbb {LNS}_{{\textbf{e}}}}(X,X,Y,Z)\) and Lemma 9.3 gives the relation \(P\big (\pi _{123}^{}(B)\big )P\big (\pi _{134}^{}(B)\big )= P\big (\pi _{234}^{}(B)\big )P\big (\pi _{124}^{}(B)\big )\). We have \(\psi (f)=P\big (\pi _{123}^{}(B)\big )\), \(\psi (gf)=P\big (\pi _{124}^{}(B)\big )\) and \(\rho (f,g)=P\big (\pi _{234}^{}(B)\big )\) and our relation becomes
It remains to identify \(P\big (\pi _{134}^{}(B)\big )\), and for this it is handy to consider the two diagrams

The diagram on the left is an extract from the object \(B\in {\mathbb {LNS}_{{\textbf{e}}}}(X,X,Y,Z)\), hence the squares \((\diamondsuit )\) and \((\heartsuit )\) are 2-cartesian. The square \((\spadesuit )\) is 2-cartesian because v is a monomorphism, while the remaining square is obviously 2-cartesian. And the concatenations are isomorphic by the isomorphism \(\lambda :pu\longrightarrow vp'\). Hence, \(\Phi \left( \!\!\begin{array}{c}\diamondsuit \\ \heartsuit \end{array}\!\!\right) = (p'u')^\times \Phi (\spadesuit )\lambda ^\times \). This shows that \( \psi (f)P\big (\pi _{134}^{}(B)\big )= \psi (f)\Phi \left( \!\!\begin{array}{c}\diamondsuit \\ \heartsuit \end{array}\!\!\right) q^\times \) is equal to the composite

and (10.1) yields the commutativity of the square

\(\square \)
Remark 10.5
In general, the natural transformation \(\psi \) is not an isomorphism. But in passing, we note that if \(f:X\longrightarrow Z\) is of finite type and universally quasi-proper, then \(\psi (f):f^\times \longrightarrow f^!\) is an isomorphism. The point is that, by Lemma 10.2, we may choose any preimage of f under the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\) for the purpose of computing \(\psi (f)\), and the preimage we choose is

The recipe of Construction 10.1 is to form the 2-cartesian square

and \(\psi (f)=\Phi (\heartsuit )f^\times \) is obviously an isomorphism.
12 Base Change
We begin by defining the building blocks for the constructions of this section.
Definition 11.1
The category \(\textbf{Sq}\) is defined as follows:
-
(i)
The objects are the 2-cartesian squares in \({\mathbb {S}_{{\textbf{e}}}}\)
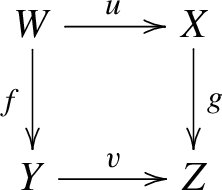
with v flat.
-
(ii)
The morphisms are the 2-isomorphisms of such squares. That is a morphism from the square

is the data of morphisms \(f\longrightarrow f'\), \(g\longrightarrow g'\), \(u\longrightarrow u'\) and \(v\longrightarrow v'\) compatible with the isomorphisms \(vf\longrightarrow gu\) and \(v'f'\longrightarrow g'u'\).
-
(iii)
We will also wish to consider two subcategories: the objects are the same, but the morphisms in \(\textbf{Sq}_H^{}\subset \textbf{Sq}\) are the maps where \(f\longrightarrow f'\) and \(g\longrightarrow g'\) are assumed to be identities, and the morphisms in \(\textbf{Sq}_V^{}\subset \textbf{Sq}\) are the ones where \(u\longrightarrow u'\) and \(v\longrightarrow v'\) are assumed to be identities.
Construction 11.2
The category \(\textbf{Sq}_H^{}\) is a disjoint union of subcategories \(\textbf{Sq}_H^{}(f,g)\), where the vertical maps are fixed to be some f and g. This leads us to the definition of a 2-category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\):
-
(i)
The objects of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) are the 1-morphisms \(f:W\longrightarrow Y\) in \({\mathbb {S}_{{\textbf{e}}}}\).
-
(ii)
Given two objects \(f,g\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}(f,g)\) is the category \(\textbf{Sq}_H^{}(f,g)\) above.
-
(iii)
The composition map \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}(f,g)\times {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}(g,h)\longrightarrow {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}(f,h)\) is the concatenation of 2-cartesian squares.
There is also an obvious vertical version, the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) is defined as follows
-
(iv)
The objects of \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) are the flat 1-morphisms \(u:W\longrightarrow X\) in \({\mathbb {S}_{{\textbf{e}}}}\).
-
(v)
Given objects \(u,v\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\) is the full subcategory \(\textbf{Sq}_V^{}\) containing the objects (i.e. the 2-cartesian squares) in which the horizontal maps are u and v.
-
(vi)
The composition map \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\times {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(v,w)\longrightarrow {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,w)\) is the concatenation of 2-cartesian squares.
There are two obvious functors \(p_1^{},p_2^{}:{\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\longrightarrow {\mathbb {S}_{{\textbf{e}}}}\) and two functors \(p_1^{},p_2^{}:{\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\longrightarrow {\mathbb {S}_{{\textbf{e}}}}\), where \(p_1^{}\) takes an object \(A\longrightarrow B\), of either \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) or \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), to the object \(A\in {\mathbb {S}_{{\textbf{e}}}}\), while \(p_2^{}\) takes \(A\longrightarrow B\) to B.
Remark 11.3
For any object in \(\textbf{Sq}\), that is for any 2-cartesian square

with v flat, there is a base-change map \(\Phi :u^*g^\times \longrightarrow f^\times v^*\). Furthermore, this base-change map is compatible with the concatenation of squares. In this Remark, we note how this could be rephrased in terms of 2-functors on the categories \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) and \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\).
Consider first the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). There are the two 2-functors \(p_1^{},p_2^{}:{\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\longrightarrow {\mathbb {S}_{{\textbf{e}}}}\), and we may compose them with the 2-functor \((-)^\times :{\mathbb {S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\) to obtain two 2-functors \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\). Concretely the functor \((-)^\times \circ p_1^{}\) takes the morphism \((\dagger )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\), while \((-)^\times \circ p_2^{}\) takes \((\dagger )\) to \(g^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). Now, we will define a natural transformation \(\Phi :(-)^\times \circ p_2^{}\longrightarrow (-)^\times \circ p_1^{}\). The definition is
-
(i)
On objects: the natural transformation \(\Phi \) takes an object \(Y{\mathop {\longrightarrow }\limits ^{v}}Z\) of \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to the functor \(v^*:{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\).
-
(ii)
On 1-morphisms: for the 1-morphism \((\dagger )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), we need to give a 2-morphism in \(\mathbb {T}\textrm{ri}\), and we need to choose a direction—our natural transformation will be oplax. This requires us to give 2-morphism \(u^*g^\times \longrightarrow f^\times v^*\). The map we choose is the base-change map \(\Phi (\dagger )\).
The assertion that \(\Phi \) is an oplax natural transformation says that the formula in (ii) is functorial and respects composition.
On the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the construction is similar. We consider the two composite functors \((-)^*\circ p_1^{}\) and \((-)^*\circ p_2^{}\); concretely \((-)^*\circ p_1^{}\) takes the 1-morphism \((\dagger )\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) to \(u^*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\) while \((-)^*\circ p_2^{}\) takes \((\dagger )\) to \(v^*:{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(Y)\). The natural transformation \(\Phi \) takes an object \(X{\mathop {\longrightarrow }\limits ^{g}}Z\) of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) to \(g^\times :{{\textbf{D}}_{\textbf{qc}}}(Z)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). And this time the natural transformation is lax, it takes a 1-morphism \((\dagger )\) to the base-change map \(\Phi (\dagger ):u^*g^\times \longrightarrow f^\times v^*\).
This section is about mimicking all of this for \((-)^!\) in place of \((-)^\times \). As usual, we begin by constructing a category equivalent to \(\textbf{Sq}\).
Construction 11.4
For objects W, X, Y, Z in \({\mathbb {S}_{{\textbf{e}}}}\), we give a category \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) as follows:
-
(i)
The objects are 2-commutative diagrams
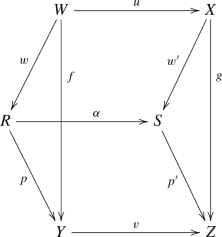
where the squares

are all 2-cartesian, where all the horizontal maps are flat, the maps p and \(p'\) are of finite type and universally quasi-proper and the maps w and \(w'\) are dominant, flat monomorphisms.
-
(ii)
A morphism in \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\), from object
is an equivalence class of data. The data are a pair of 1-morphisms \(R\longrightarrow \overline{R}\) and \(S\longrightarrow \overline{S}\), together with a bunch of 2-morphisms giving all the 2-commutativity one might expect. Two representatives are declared equivalent if they differ from each other by perturbing the maps \(R\longrightarrow \overline{R}\) and \(S\longrightarrow \overline{S}\) by an isomorphism.
An object of \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) can be thought of as an object in \(\textbf{Sq}\) where we give compatible Nagata compactifications for the vertical maps. We also fix the objects \(W,X,Y,Z\in {\mathbb {S}_{{\textbf{e}}}}\) for the construction. There is a natural forgetful functor from \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) to a category we will call \(\textbf{Sq}(W,X,Y,Z)\subset \textbf{Sq}\), the full subcategory of \(\textbf{Sq}\) whose objects are the 2-cartesian squares

with W, X, Y and Z fixed.
Lemma 11.5
The forgetful map \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\) is a groupoid completion: that is \(\textbf{Sq}(W,X,Y,Z)\) can be obtained from \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) by formally inverting all the morphisms.
Proof
First, we factor the functor F as the composite

where \(\rho :\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \mathbb {R}\textbf{Sq}(W,X,Y,Z)\) is the functor that remembers only the Nagata compactification on the right. Thus, an object of \(\mathbb {R}\textbf{Sq}(W,X,Y,Z)\) is a 2-commutative diagram

where the square is 2-cartesian, the horizontal maps are flat, \(w'\) is a dominant, flat monomorphism and \(p'\) is of finite type and universally quasi-proper. The functor \(\rho \) is an equivalence of categories, a quasi-inverse is given by forming the 2-cartesian square

and letting \(w:X\longrightarrow R\) be the map to the pullback. We leave the details to the reader.
Since \(\rho \) is an equivalence it suffices to prove that \(\sigma \) is a groupoid completion. This is by Proposition 8.9, since the category \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) is a disjoint union of subcategories equivalent to \({\mathbb {S}_{{\textbf{e}}}}(W,X)\times {\mathbb {S}_{{\textbf{e}}}}(W,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\times \mathbb {N}\textbf{Sq}(X,Z)\). \(\square \)
Construction 11.6
We consider two composites

where \(\pi _1^{},\pi _2^{}\) are the obvious projections. Let \({\mathfrak {R}},{\mathfrak {S}}\) be the composites, that is \({\mathfrak {R}},{\mathfrak {S}}\) are, respectively, the functors taking the object

of the category \(\textbf{Sq}(W,X,Y,Z)\) to the objects \({\mathfrak {R}}(\dagger )=u^*g^!\) and \({\mathfrak {S}}(\dagger )=f^!v^*\) in \(\mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(W)\big )\). We wish to define a natural transformation \(\theta :{\mathfrak {R}}\longrightarrow {\mathfrak {S}}\).
Since \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\) is a groupoid completion functor, it suffices to produce a natural transformation \({\mathfrak {R}}F\longrightarrow {\mathfrak {S}}F\), it will automatically factor as \(\theta F\). Suppose, therefore, that we are given an object in \(A\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\); the data are the 2-cartesian squares

and 2-isomorphisms \(pw\longrightarrow f\), \(p'w'\longrightarrow g\) rendering 2-commutative the entire picture. We define \(\Theta (A)\) to be the composite

where \((\diamondsuit )^*:u^*{w'}^* \longrightarrow {w}^*\alpha ^*\) is the isomorphism induced by the 2-commutative square \((\diamondsuit )\), and \(\Phi (\heartsuit ):\alpha ^*{p'}^\times \longrightarrow {p}^\times v^*\) is the base-change map of the square \((\heartsuit )\).
Proposition 11.7
With the notation as in Construction 11.6, the map sending an object \(A\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\) to \(\Theta (A)\) defines a natural transformation \(\Theta :{\mathfrak {R}}F\longrightarrow {\mathfrak {S}}F\) and, as mentioned in Construction 11.6, the natural transformation \(\Theta \) factors uniquely as \(\Theta =\theta F\) with \(\theta :{\mathfrak {R}}\longrightarrow {\mathfrak {S}}\) also a natural transformation.
Proof
What needs proof is the naturality of \(\Theta \). A morphism \(\varphi :A\longrightarrow B\) in the category \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) has a representative giving (among other things) the data of a 2-commutative diagram

and 2-morphisms \(u\longrightarrow \overline{u}\) and \(v\longrightarrow \overline{v}\). The naturality of \(\Theta \) with respect to the 2-morphisms \(u\longrightarrow \overline{u}\) and \(v\longrightarrow \overline{v}\) is easy and left to the reader, in the rest of the proof we will assume these maps to be identities. Out of the data, we cook up the diagram C below

The horizontal maps are all given to be flat. The map \(\zeta \) is of finite type and universally quasi-proper by Remark 8.3, and Corollary 7.9 applies to the square \((\spadesuit )\) and tells us that it must be 2-cartesian. The square \((\clubsuit )\) is given to be 2-cartesian, while the square

via the isomorphisms \(\lambda :p\longrightarrow \overline{p}\zeta \) and \(\mu :p'\longrightarrow \overline{p}'\zeta '\). Now, \((\diamondsuit )\) is given to be 2-cartesian, hence so is the isomorphic \(\left( \!\!\begin{array}{c}\heartsuit \\ \clubsuit \end{array}\!\!\right) \), and as \((\clubsuit )\) is also 2-cartesian so is \((\heartsuit )\). Therefore, C is an object of \({\mathbb {LNS}_{{\textbf{e}}}}(W,W,Y,Z)\) and Lemma 9.3 gives the relation \(P\big (\pi _{123}^{}(C)\big )P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\). Note that in the above we also learned that \(\Phi \left( \!\!\begin{array}{c}\heartsuit \\ \clubsuit \end{array}\!\!\right) \mu ^\times =\lambda ^\times \Phi (\diamondsuit )\), and hence \(P\big (\pi _{134}^{}(C)\big )\mu ^\times =w^*\lambda ^\times \Phi (\diamondsuit )\). Therefore,
where the first equality is the relation coming from C, the second equality is by the discussion above, and the third is by the definition of \({\mathfrak {S}}(\varphi )\).
Next, contemplate the diagrams

The diagram on the left is extracted from C, hence the squares are 2-cartesian. The morphisms \(w'\) and \(\overline{w}'\) are given to be dominant, flat monomorphisms, while \(\zeta '\) is of finite type and universally quasi-proper by Remark 8.3. Corollary 7.9 tells us the square \((\dagger )\) is 2-cartesian. The remaining square is trivially 2-cartesian, and the concatenations are isomorphic via the isomorphisms \(\gamma :w'u\longrightarrow \alpha w\) and \(\delta :\overline{w}'u\longrightarrow \overline{\alpha }\overline{w}\). Therefore, \(\Phi (\spadesuit \heartsuit )\gamma ^*=\delta ^*u^*\Phi (\dagger )\). Observing that \(P\big (\pi _{124}^{}(C)\big )=\Phi (\spadesuit \heartsuit ){\overline{p}'}^\times \), we deduce that
The first equality is because \(\Theta (A)=w^*\Phi (\diamondsuit )\gamma ^*\) by definition, the second equality comes from the previous paragraph, the third equality expands \(\Phi (\spadesuit \heartsuit )\gamma ^*\) as right before the string of equalities, and the last equality is because \( \Theta (B)= P\big (\pi _{234}^{}(C)\big )\delta ^*\) and \({\mathfrak {R}}(\varphi )=\Phi (\dagger ){\overline{p}'}^\times \mu ^\times \). Thus, the square

commutes, and \(\Theta \) is indeed a natural transformation. \(\square \)
Theorem 11.8
Let \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) be the 2-category of Construction 11.2 (i), (ii) and (iii). Consider the composite 2-functors

There is a lax natural transformation \(\theta :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\) given by the rules
-
(i)
Given an object \(f:W\longrightarrow Y\) of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), then \(\theta (f)=f^!:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\).
-
(ii)
Given a morphism in \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), that is a 2-cartesian square with flat horizontal morphisms
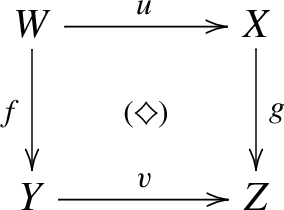
we need to define a 2-morphism \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\). The definition is as in Proposition 11.7.
Proof
For any pair of 1-morphisms \(f,g\in {\mathbb {S}_{{\textbf{e}}}}\), we have two functors \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}(f,g)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\), namely \(\big [p_1^{}(-)\big ]^*\circ g^!\) and \(f^!\circ \big [p_2^{}(-)\big ]^*\). In Proposition 11.7, we established that \(\theta \) defines a natural transformation \(\theta :\big [p_1^{}(-)\big ]^*\circ g^!\longrightarrow f^!\circ \big [p_2^{}(-)\big ]^*\). Identities are obviously respected, hence what remains to be proved is that \(\theta \) is compatible with composition. That is: we have to show that, if

are two composable morphisms in \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), then the diagram

commutes. To prove this, we choose compatible preimages of \((\clubsuit )\in \textbf{Sq}(\widetilde{W},W,\widetilde{Y},Y)\), \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\) and \((\clubsuit \diamondsuit )\in \textbf{Sq}(\widetilde{W},W,X,Z)\) via the map \(F:\mathbb {N}\textbf{Sq}(-,-,-,-)\longrightarrow \textbf{Sq}(-,-,-,-)\). More precisely: let \(X{\mathop {\longrightarrow }\limits ^{w'}}R'{\mathop {\longrightarrow }\limits ^{p'}}Z\) be a Nagata compactification of \(g:X\longrightarrow Z\). From the pullback diagram

and then let \(w:W\longrightarrow R\) and \(\widetilde{w}:\widetilde{W}\longrightarrow \widetilde{R}\) be the maps to the pullback. We obtain a 2-commutative diagram

By construction, \((\heartsuit )\) and \((\spadesuit )\) are 2-cartesian, and since \((\clubsuit )\cong \left( \!\!\begin{array}{c}\dagger \\ \heartsuit \end{array}\!\!\right) \) and \((\diamondsuit )\cong \left( \!\!\begin{array}{c}\bullet \\ \spadesuit \end{array}\!\!\right) \) are given to be 2-cartesian it follows that \((\dagger )\) and \((\bullet )\) must also be 2-cartesian. The 2-commutative diagrams

together with the 2-morphisms \(\widetilde{p}\widetilde{w}\longrightarrow \widetilde{f}\), \(pw\longrightarrow f\) and \(p'w'\longrightarrow g\), give a lifting of the objects

via the maps \(\mathbb {N}\textbf{Sq}(-,-,-,-)\longrightarrow \textbf{Sq}(-,-,-,-)\). By the definition of \(\theta \) it suffices to prove the commutativity of

which is immediate from the definitions. \(\square \)
Theorem 11.9
Let \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) be the 2-category of Construction 11.2 (iv), (v) and (vi). Consider the composite 2-functors

There is an oplax natural trasformation \(\theta :(-)^!\circ p_2^{}\longrightarrow (-)^!\circ p_1^{}\) given by the rules
-
(i)
Given an object \(u:W\longrightarrow X\) of \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), then \(\theta (u)=u^*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\).
-
(ii)
Given a morphism in \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), that is a 2-cartesian square with flat horizontal morphisms
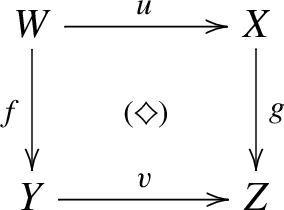
we need to define a 2-morphism \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\). The definition is as in Proposition 11.7.
Proof
For any pair of flat 1-morphisms \(u,v\in {\mathbb {S}_{{\textbf{e}}}}\), we have two functors \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\longrightarrow \mathbb {T}\textrm{ri}\big ({{\textbf{D}}_{\textbf{qc}}}(Z),{{\textbf{D}}_{\textbf{qc}}}(X)\big )\), namely \(u^*\circ \big [p_2^{}(-)\big ]^!\) and \(\big [p_1^{}(-)\big ]^!\circ v^*\). In Proposition 11.7 we established that \(\theta \) defines a natural transformation \(\theta :u^*\circ \big [p_2^{}(-)\big ]^!\longrightarrow \big [p_1^{}(-)\big ]^!\circ v^*\). Identities are obviously respected, hence what remains to be proved is that \(\theta \) is compatible with composition. That is: we have to show that, if

are two composable morphisms in \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), then the pentagon

commutes. For future reference, we name this pentagon Compent. We begin with the easy cases:
Case 1. The pentagon Compent commutes if either g is of finite type and universally quasi-proper, or \(\widetilde{g}\) is a dominant, flat monomorphism.
Proof of Case 1. Let us treat the case where g is assumed of finite type and universally quasi-proper, the case where \(\widetilde{g}\) is a dominant, flat monomorphism is similar and left to the reader. The point is that, under the assumption, the square \((\diamondsuit )\) has a particularly simple lifting to \(\mathbb {N}\textbf{Sq}(W,X,Y,Z)\) namely the diagram

Choose any lifting to \(\mathbb {N}\textbf{Sq}(\widetilde{W},\widetilde{X},W,X)\) of the square \((\clubsuit )\), and we have that our chosen

are compatible liftings to \(\mathbb {N}\textbf{Sq}(\widetilde{W},\widetilde{X},W,X)\) and \(\mathbb {N}\textbf{Sq}(\widetilde{W},\widetilde{X},Y,Z)\) of the objects \((\clubsuit )\) and \(\left( \!\!\begin{array}{c}\clubsuit \\ \diamondsuit \end{array}\!\!\right) \). With respect to this choice the reader will easily check the commutativity of

and this completes the proof of Case 1.
Case 2. The composition pentagon commutes if \(\widetilde{g}\) is of finite type and universally quasi-proper, and g is a dominant, flat monomorphism.
Proof of Case 2. We may choose Nagata compactifications for the composite \(g\widetilde{g}:\widetilde{X}\longrightarrow Z\), then pull back to extend to a diagram

This gives us the 2-commutative cube

and I assert that all the faces are 2-cartesian. We know this for four of the faces: for the faces \((\clubsuit )\) and \((\diamondsuit )\) this is given, and for \((\heartsuit )\) and \((\spadesuit )\) this is by construction. We have to prove something in the case of the 2-commutative squares

We are given that in these squares the horizontal maps are dominant, flat monomorphisms while the vertical maps are concentrated, of finite type and universally quasi-proper. Corollary 7.9, therefore, tells us that the squares are 2-cartesian.
To prove the commutativity of the pentagon Compent, we will consider the pair of diagrams B and C below

The squares are all 2-cartesian and the horizontal maps are all flat, hence B belongs to \({\mathbb {LNS}_{{\textbf{e}}}}(\widetilde{W},W,Y,Z)\) while C belongs to \({\mathbb {LNS}_{{\textbf{e}}}}(\widetilde{W},W,X,Z)\), and Lemma 9.3 gives one relation from each of B and C. We have the identities
Note that \(P\big (\pi _{234}^{}(B)\big )=\textrm{id}=P\big (\pi _{234}^{}(C)\big )\), while \((\heartsuit ):w'\widetilde{u}\longrightarrow \alpha w\) and \((\diamondsuit ):ug\longrightarrow vf\) give isomorphisms of the concatenations of

from which we deduce that \((\diamondsuit )^*P\big (\pi _{124}^{}(C)= P\big (\pi _{124}^{}(B)(\heartsuit )^*\). The relations from B and C combine to
and we deduce
where the first equality comes from the identities \(\rho (\widetilde{f},f)= P\big (\pi _{123}^{}(B)\big )\) and \(\theta \left( \!\!\begin{array}{c}\clubsuit \\ \diamondsuit \end{array}\!\!\right) = P\big (\pi _{134}^{}(B)\big )(\heartsuit )^*\), and the third equality is because, for our very simple morphisms \((\clubsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(\widetilde{u},u)\) and \((\diamondsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\), we have \(\theta (\diamondsuit )=(\diamondsuit )^*\), \(\theta (\clubsuit )= P\big (\pi _{123}^{}(C)\big )\) and \(\rho (\widetilde{g},g)=P\big (\pi _{134}^{}(C)\big )\). And this finishes the proof of Case 2.
Now, we move to the general case; the idea is to reduce to Case 1 and Case 2 using the fact, which we already know from Theorem 9.11, that the composition maps \(\rho (\alpha ,\beta ):(\beta \alpha )^!\longrightarrow \alpha ^!\beta ^!\) are associative. We may choose Nagata compactifications for the morphisms \(\widetilde{g}:\widetilde{X}\longrightarrow X\) and \(g:X\longrightarrow Z\), and then pull back to extend to diagrams

In other words: in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), we factor the 1-morphisms \((\clubsuit )\) and \((\diamondsuit )\), up to 2-isomorphisms, as composites \((\clubsuit )\cong \left( \!\!\begin{array}{c}\heartsuit \\ \spadesuit \end{array}\!\!\right) \) and \((\diamondsuit )\cong \left( \!\!\begin{array}{c}\bullet \\ \dagger \end{array}\!\!\right) \) where the vertical maps of \((\heartsuit )\) and \((\bullet )\) are dominant, flat monomorphisms while the vertical maps of \((\spadesuit )\) and \((\dagger )\) are of finite type and universally quasi-proper. By the naturality of \(\theta \) and \(\rho \), we may replace \((\clubsuit )\) and \((\diamondsuit )\) by the isomorphic \(\left( \!\!\begin{array}{c}\heartsuit \\ \spadesuit \end{array}\!\!\right) \) and \(\left( \!\!\begin{array}{c}\bullet \\ \dagger \end{array}\!\!\right) \), in other words we may assume the isomorphisms are equalities. We wish to prove the commutativity of the pentagon in

Now, \(f^!=(\overline{p}\overline{w})^!{\mathop {\longrightarrow }\limits ^{\rho (\overline{w},\overline{p})}}\overline{w}^!\overline{p}^!\) and \(\widetilde{f}^!=(pw)^!{\mathop {\longrightarrow }\limits ^{\rho (w,p)}}w^!p^!\) are isomorphisms by Proposition 9.12 (i) or (ii), and it suffices to prove that the two composites from top left to bottom right are equal. But Case 1 gives the commutativity of the pentagons (1) and (2) below

which reduces us to proving the commutativity of the perimeter; for future reference let us call this perimeter Perim. Now, consider the diagram Bigdia below

In Bigdia, the pentagons (1) and (2) commute by Case 1 while pentagon (3) commutes by Case 2. If we attach to the left and right bottom corners of Bigdia the obviously commutative diagrams

and

then the perimeter of the union of Bigdia, Rslant and Lslant agrees with Perim, up to the associativity proved for \(\rho \) in Theorem 9.11. The proof is, therefore, complete. \(\square \)
Remark 11.10
In Construction 11.6, we considered the two composites

which we called \({\mathfrak {R}}\) and \({\mathfrak {S}}\), and provided a procedure which was proved in Proposition 11.7 to provide a natural transformation \(\theta :{\mathfrak {R}}\longrightarrow {\mathfrak {S}}\). This was motivated by Remark 11.3 where it was observed that, if we replace \((-)^!\) by \((-)^\times \), then the natural transformation \(\theta \) is analogous to the usual base-change map \(\Phi \). More formally: we could study the composite functors

let us name them \({\mathfrak {R}}'\) and \({\mathfrak {S}}'\). To make it concrete: an object in the category \(\textbf{Sq}(W,X,Y,Z)\) is a 2-cartesian square \((\diamondsuit )\) with flat horizontal maps below

and the four functors we consider take \((\diamondsuit )\) to \({\mathfrak {R}}'(\diamondsuit )=u^*g^\times \), \({\mathfrak {R}}(\diamondsuit )=u^*g^!\), \({\mathfrak {S}}'(\diamondsuit )=f^\times v^*\) and \({\mathfrak {S}}(\diamondsuit )=f^!v^*\). The natural transformations \(\Phi :{\mathfrak {R}}'\longrightarrow {\mathfrak {S}}'\) and \(\theta :{\mathfrak {R}}\longrightarrow {\mathfrak {S}}\) take the object \((\diamondsuit )\) (respectively) to the base-change map \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\) and the (more complicated) base-change map \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\). Of course we also have the natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\) of Theorem 10.3 and we might wonder how the two are related. We prove
Proposition 11.11
Let the notation be as in Remark 11.10. Then, the following square of natural transformations commutes:

Proof
The commutativity may be checked object by object, and we are free to view our object \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\) as belonging to \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\). In the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), choose a factorization of \((\diamondsuit )\) as

where \(w'\) is a dominant, flat monomorphism and \(p'\) is of finite type and universally quasi-proper—in other words choose a Nagata compactification for the map \(g:X\longrightarrow Z\) and pull back. We wish to show the commutativity of the square

and concretely this is the square (1) in the diagram below

The map \(\rho (w,p)\) is an isomorphism by Proposition 9.12 (i) or (ii), and the square (2) commutes by Theorem 10.3. Hence, it suffices to prove the commutativity of the perimeter. Now, in Theorem 11.9, we proved the commutativity of the pentagon

and the commutativity of the pentagon

is formal, base-change maps concatenate. The perimeter we need to show commutative is, therefore, equal to the perimeter of

and the square (3) commutes by Theorem 10.3. We are reduced to proving that the squares (4) and (5) commute, in other words we are reduced to the special cases where the vertical maps are either dominant, flat monomorphisms or of finite type and universally quasi-proper. We prove these cases below.
Case 1. The Proposition is true for objects \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\) where the vertical maps are of finite type and universally quasi-proper.
Proof of Case 1. We are given an object \((\diamondsuit )\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\), that is a 2-cartesian square

and we assume the vertical maps f and g are of finite type and universally quasi-proper. To evaluate the various maps, we lift the object \((\diamondsuit )\) via the functor \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\), and the lifting we choose is the 2-commutative diagram

For this choice the square, we need to prove commutative reduces to

Case 2. The Proposition is true for objects \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\) where the vertical maps are dominant, flat monomorphisms.
Proof of Case 2. In this case, the lifting we choose for the object \((\diamondsuit )\), via the functor \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\), is the 2-commutative diagram

Out of this, we concoct the 2-commutative diagram C below

The square \((\diamondsuit )\) is given to be 2-cartesian, and the square \((\clubsuit )\) is 2-cartesian because f is a monomorphism. The remaining square is obviously 2-cartesian. All the horizontal maps are flat, hence C is an object in \({\mathbb {LNS}_{{\textbf{e}}}}(W,W,Y,Z)\) and Lemma 9.3 gives the relation \(P\big (\pi _{123}^{}(C)\big )P\big (\pi _{134}^{}(C)\big )= P\big (\pi _{234}^{}(C)\big )P\big (\pi _{124}^{}(C)\big )\).
In this relation, we have \(P\big (\pi _{123}^{}(C)\big )=\psi (f)\), \(P\big (\pi _{134}^{}(C)\big )=\Phi (\diamondsuit )\), and \(P\big (\pi _{234}^{}(C)\big )=\textrm{id}\). The relation becomes \(\psi (f)\Phi (\diamondsuit )= P\big (\pi _{124}^{}(C)\big )\), and our problem is to identify \(P\big (\pi _{124}^{}(C)\big )\). For this, it helps to consider the two 2-commutative diagrams

The diagram on the left is an extract from C and so the squares \((\clubsuit )\) and \((\diamondsuit )\) are 2-cartesian. The square \((\spadesuit )\) is 2-cartesian because g is a monomorphism, and the square \((\heartsuit )\) is trivially 2-cartesian. And the concatenations are isomorphic via the isomorphism \((\diamondsuit ):gu\longrightarrow vf\). It follows that \(P\big (\pi _{124}^{}(C)\big )=\Phi (\clubsuit \diamondsuit )= (\diamondsuit )^*\Phi (\spadesuit )=(\diamondsuit )^*\psi (g)\), meaning that the square below commutes

\(\square \)
Remark 11.12
In Theorem 11.8, we gave, on the category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), a natural transformation \(\theta :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\) analogous to the base-change map \(\Phi :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\). In Theorem 11.9, we gave, on the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), a natural transformation \(\theta :(-)^!\circ p_2^{}\longrightarrow (-)^!\circ p_1^{}\) analogous to the base-change map \(\Phi :(-)^\times \circ p_2^{}\longrightarrow (-)^\times \circ p_1^{}\). On a 1-morphism \((\diamondsuit )\), in either category, \(\theta \) comes down to the map \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^! v^*\) while \(\Phi \) is the map \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\).
We have produced lots of 2-functors and natural transformations: we can assemble some of them into the two squares below, where the square on the left has the 2-category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) for input while the square on the right begins with the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\)

If we combine Theorems 11.8 and 11.9 with Proposition 11.11 we learn that these squares can be filled in by modifications. Since we are in the world of 2-categories let us elaborate a tiny bit.
Given an object \(f:W\longrightarrow Y\) of the 2-category \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\), the 2-functor \(p_2^{}\) takes it to Y while the 2-functor \(p_1^{}\) takes it to W. The natural transformation \(\Phi \) takes the object f to the 1-morphism \(f^\times :{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\) while the natural transformation \(\theta \) takes f to \(f^!:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\). The natural transformation \(\textrm{id}\) is the identity on objects. What is being asserted is that the assignment taking the object \(f\in {\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) to the 2-morphism \(\psi (f):f^\times \longrightarrow f^!\) extends to a modification of the composites in the square on the left, i.e. is compatible with the rest of the structure. This follows from Proposition 11.11.
Given an object \(u:W\longrightarrow X\) in the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), the 2-functor \(p_2^{}\) takes it to X while the 2-functor \(p_1^{}\) takes it to W. The natural transformations \(\Phi \) and \(\theta \) both take the object u to the 1-morphism \(u^*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\), and the natural transformation \(\psi \) is the identity on objects. What is being asserted for the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) is that the square strictly commutes; no modification is necessary. Once again, the proof amounts to an application of Proposition 11.11.
We end this section with a result telling us that, under suitable conditions, the map \(\theta (\diamondsuit )\) is an isomorphism.
Proposition 11.13
Let \((\diamondsuit )\) be an object of \(\textbf{Sq}(W,X,Y,Z)\), given by the 2-cartesian square

The map \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\) is an isomorphism if either of the two conditions below is satisfied
-
(i)
f is of finite Tor-dimension. More generally: if \(u':U\longrightarrow W\) is a map whose image lies in the subset of \(\,W\) on which f is of finite Tor-dimension, then \({u'}^*\theta (\diamondsuit ):{u'}^*u^*g^!\longrightarrow {u'}^*f^!v^*\) is an isomorphism.
-
(ii)
We restrict to the subcategory \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\subset {{\textbf{D}}_{\textbf{qc}}}(Z)\).
Proof
We begin by choosing a preimage A for \((\diamondsuit )\) under the functor \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\), that is the data of A consists of the 2-cartesian squares

as well as 2-isomorphisms \(pw\longrightarrow f\) and \(p'w'\longrightarrow g\) which give an isomorphism of the concatenation with \((\diamondsuit )\). By Proposition 11.7 we are free to use any preimage. The map \(\theta (\diamondsuit )\) has the property that \(\theta (\diamondsuit )\cong \Theta (A)\), where \(\Theta (A)\) was defined to be the composite

The map \((\heartsuit )^*\) is an isomorphism unconditionally. Therefore, \({u'}^*\theta (\diamondsuit )\) is an isomorphism if and only if \({u'}^*{w}^*\Phi (\spadesuit )\) is an isomorphism.
The map w is flat, and the image of \(wu'\) lies in the subset on which p is of finite Tor-dimension if and only if the image of \(u'\) lies in the subset on which \(pw\cong f\) is of finite Tor-dimension. The assertions of the Proposition now follow from Theorem 6.10 (i) and (ii), which give conditions under which \((wu')^*\Phi (\spadesuit )\) is an isomorphism. \(\square \)
13 The 2-Functor \((-)^*\) is a Monoid and \((-)_*\) and \((-)^\times \) are Modules Over It
Consider the 2-categories \({\mathbb {S}_{{\textbf{e}}}}\) and \(\mathbb {T}\textrm{ri}\): we have met the 2-functors \((-)^*\), \((-)^\times \) and \((-)^!\), all of which are 2-functors \({\mathbb {S}_{{\textbf{e}}}}\longrightarrow \mathbb {T}\textrm{ri}\). On objects the three 2-functors agree—all three take the object \(X\in {\mathbb {S}_{{\textbf{e}}}}\) to \({{\textbf{D}}_{\textbf{qc}}}(X)\in \mathbb {T}\textrm{ri}\). The category \({{\textbf{D}}_{\textbf{qc}}}(X)\) is not only triangulated, it also has a tensor product, and it is natural to wonder how our three 2-functors behave with respect to the tensor product. Of them \((-)^*\) is best: it respects the tensor product. This section is devoted to formal nonsense about 2-functors like \((-)^*\) and their adjoints. We will formulate a language in which we can say that the 2-functor \((-)^*\) is a monoid and the 2-functor \((-)^\times \) is a module over it. This turns out to be a compact way of packing a great many naturality properties.
We begin with
Definition 12.1
A 2-category  is called premonoidal if there is a 2-functor
is called premonoidal if there is a 2-functor  satisfying the obvious associativity conditions. For this article we will assume that the associativity is strict.
satisfying the obvious associativity conditions. For this article we will assume that the associativity is strict.
Example 12.2
Let  be the 2-category whose objects are finite products of triangulated categories, and whose morphisms are finite products of functors \(F:\prod _{i=1}^nB_i\longrightarrow B'\), where \(B'\) and each \(B_i\) are triangulated, and where F is triangulated (separately) in each variable \(B_i\). We allow the empty product as an object of
be the 2-category whose objects are finite products of triangulated categories, and whose morphisms are finite products of functors \(F:\prod _{i=1}^nB_i\longrightarrow B'\), where \(B'\) and each \(B_i\) are triangulated, and where F is triangulated (separately) in each variable \(B_i\). We allow the empty product as an object of  . The premonoidal structure takes two objects of
. The premonoidal structure takes two objects of  , that is \(\prod _{i=1}^m B_i\) and \(\prod _{j=1}^n B'_j\), to the object \(\prod _{i=1}^m B_i\times \prod _{j=1}^n B'_j\). The empty product is the unit for this premonoidal structure. The 2-morphisms are unrestricted, they are just the natural transformations.
, that is \(\prod _{i=1}^m B_i\) and \(\prod _{j=1}^n B'_j\), to the object \(\prod _{i=1}^m B_i\times \prod _{j=1}^n B'_j\). The empty product is the unit for this premonoidal structure. The 2-morphisms are unrestricted, they are just the natural transformations.
For the next definition, it helps to introduce the following notation: if  is any 2-category then
is any 2-category then  is the n-fold diagonal, the 2-functor taking an object
is the n-fold diagonal, the 2-functor taking an object  to
to  . Given 2-functors
. Given 2-functors  , where
, where  is premonoidal, we will be considering composite 2-functors of the form
is premonoidal, we will be considering composite 2-functors of the form

and, in the notation, we will almost always omit the \({\mathfrak {M}}\) and sometimes even omit the \(\Delta _n\). Thus, \({\mathfrak {M}}\circ \big [F\times G\big ]\circ \Delta _2\) will usually be abbreviated to \(\big [F\times G\big ]\circ \Delta _2\) and sometimes even to \(F\times G\).
The next concept is not new, it has occurred in the category-theoretic literature many times (under different names). We will come to this again in Remark 12.10.
Definition 12.3
Let  be a 2-category and let
be a 2-category and let  be a premonoidal 2-category. A 2-functor
be a premonoidal 2-category. A 2-functor  is a premonoid if it comes equipped with an associative pseudonatural transformation \(\mu :[(-)^*\times (-)^*]\circ \Delta _2^{} \longrightarrow (-)^*\). The associativity means that we are also given a modification isomorphism between the composites below
is a premonoid if it comes equipped with an associative pseudonatural transformation \(\mu :[(-)^*\times (-)^*]\circ \Delta _2^{} \longrightarrow (-)^*\). The associativity means that we are also given a modification isomorphism between the composites below

such that the associativity pentagon for the five composites \([(-)^*\times (-)^*\times (-)^*\times (-)^*]\circ \Delta _4^{}\longrightarrow (-)^*\) commutes.
Example 12.4
With  as in Example 12.2, let
as in Example 12.2, let  be the 2-category of algebraic stacks. There is a 2-functor
be the 2-category of algebraic stacks. There is a 2-functor  , we have met it before:
, we have met it before:
-
(i)
On objects: the object
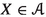 is mapped to
is mapped to 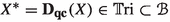 .
. -
(ii)
On 1-morphisms: the 1-morphism \(f:X\longrightarrow Y\) is mapped to the 1-morphism \(f^*:{{\textbf{D}}_{\textbf{qc}}}(Y)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\).
-
(iii)
On 2-morphisms: given
 , the 2-functor \((-)^*\) maps it to
, the 2-functor \((-)^*\) maps it to 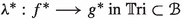 .
.
So far we have not mentioned the tensor product but, as we have already observed, for any object  the object \(X^*={{\textbf{D}}_{\textbf{qc}}}(X)\) is a symmetric premonoid in
the object \(X^*={{\textbf{D}}_{\textbf{qc}}}(X)\) is a symmetric premonoid in  , meaning there is a symmetric tensor product \({{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). It is the functor taking the pair of objects \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(X)\) to \(E\otimes F\in {{\textbf{D}}_{\textbf{qc}}}(X)\). And this does extend to a pseudonatural transformation \(\mu \).
, meaning there is a symmetric tensor product \({{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). It is the functor taking the pair of objects \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(X)\) to \(E\otimes F\in {{\textbf{D}}_{\textbf{qc}}}(X)\). And this does extend to a pseudonatural transformation \(\mu \).
-
(iv)
On objects: the object
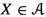 is sent to the tensor-product functor \(\mu _{X}^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\).
is sent to the tensor-product functor \(\mu _{X}^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). -
(v)
On morphisms: for any pair of objects
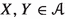 we have two functors
we have two functors 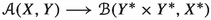 , namely \(\mu _{X}^{}\circ [(-)^*\times (-)^*]\) and \((-)^*\circ \mu _{Y}^{}\). We need to provide a natural transformation \(\mu \) between them and, as we are assuming \(\mu \) to be pseudonatural, this map must be an isomorphism—for once the direction does not matter. Concretely it means that for every morphism \(f:X\longrightarrow Y\) and any pair of objects \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) we give an isomorphism \(f^*(E\otimes F)\cong f^*E\otimes f^*F\), and these must be compatible with composition and be natural in everything in sight.
, namely \(\mu _{X}^{}\circ [(-)^*\times (-)^*]\) and \((-)^*\circ \mu _{Y}^{}\). We need to provide a natural transformation \(\mu \) between them and, as we are assuming \(\mu \) to be pseudonatural, this map must be an isomorphism—for once the direction does not matter. Concretely it means that for every morphism \(f:X\longrightarrow Y\) and any pair of objects \(E,F\in {{\textbf{D}}_{\textbf{qc}}}(Y)\) we give an isomorphism \(f^*(E\otimes F)\cong f^*E\otimes f^*F\), and these must be compatible with composition and be natural in everything in sight.
Until now, we have not worried much about the variance of our 2-functors, there was no need to, the 2-functors \((-)^*\), \((-)^\times \) and \((-)^!\) all have the same variance, and they form our main object of study. This section is the exception, in the next few results, variance plays a role.
The next definition is a 2-category generalization of an old notion, introduced in Dubuc and Street [14]. What we call natural transformations below goes by the name “dinatural transformations” in [14], where the “di” stands for diagonal.
Definition 12.5
Let  be a 2-category and let
be a 2-category and let  be a premonoidal 2-category. Suppose we are given functors
be a premonoidal 2-category. Suppose we are given functors  , with E, G contravariant and F, H covariant. A natural transformation \(\mu :E\times F\longrightarrow G\times H\) is the following data:
, with E, G contravariant and F, H covariant. A natural transformation \(\mu :E\times F\longrightarrow G\times H\) is the following data:
-
(i)
On objects: for every object
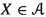 we are given a 1-morphism \(\mu _X^{}:E(X)\times F(X)\longrightarrow G(X)\times H(X)\) in the category
we are given a 1-morphism \(\mu _X^{}:E(X)\times F(X)\longrightarrow G(X)\times H(X)\) in the category 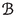 .
. -
(ii)
Let
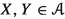 be objects. We have two functors
be objects. We have two functors 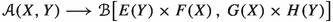 , namely $$\begin{aligned} H(-)\mu _X^{}E(-)\quad \text {and}\quad G(-)\mu _Y^{}F(-). \end{aligned}$$
, namely $$\begin{aligned} H(-)\mu _X^{}E(-)\quad \text {and}\quad G(-)\mu _Y^{}F(-). \end{aligned}$$We must be given, for every pair of objects
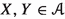 , a natural transformation \(\mu (X,Y)\) between these functors. The direction of this natural transformation determines whether \(\mu \) is lax or oplax: for us the lax direction will be \( G(-)\mu _Y^{}F(-)\longrightarrow H(-)\mu _X^{}E(-)\).
, a natural transformation \(\mu (X,Y)\) between these functors. The direction of this natural transformation determines whether \(\mu \) is lax or oplax: for us the lax direction will be \( G(-)\mu _Y^{}F(-)\longrightarrow H(-)\mu _X^{}E(-)\). -
(iii)
The \(\mu (X,Y)\) must be compatible with composition.
Elaboration 12.6
It might be worth elaborating a little. The hypothesis about the variance of the 2-functors E, F, G, H means that, for any 1-morphism \(f:X\longrightarrow Y\), we have induced 1-morphisms
and any 2-morphism \(\lambda :f\longrightarrow g\) induces 2-morphisms
Definition 12.5(ii) says that, for any 1-morphism f, we must be given a 2-morphism between the composites

The natural transformation is lax if this 2-morphism goes up, oplax if it goes down.
The meaning of Definition 12.5(iii) is that, if we are given composable 1-morphisms \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in the 2-category  , then the 2-morphism of the hexagon
, then the 2-morphism of the hexagon

is compatible with the composite of the 2-morphisms of the hexagons

once we attach the 2-commutative

and recall the 2-morphisms relating
where the direction of these 2-morphisms depends on which of E, F, G, H is lax and which is oplax (we left this vague).
Reminder 12.7
Let  be a contravariant pseudofunctor of 2-categories. Suppose that, for every 1-morphism \(f:X\longrightarrow Y\) in
be a contravariant pseudofunctor of 2-categories. Suppose that, for every 1-morphism \(f:X\longrightarrow Y\) in  , the 1-morphism \(L(f):L(Y)\longrightarrow L(X)\) has a right adjoint. Then, there is a canonical covariant pseudofunctor
, the 1-morphism \(L(f):L(Y)\longrightarrow L(X)\) has a right adjoint. Then, there is a canonical covariant pseudofunctor  so that, for every 1-morphism
so that, for every 1-morphism  , we have that L(f) is left adjoint to R(f). We should perhaps remind the reader how this works:
, we have that L(f) is left adjoint to R(f). We should perhaps remind the reader how this works:
-
(i)
On objects: for an object
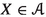 put \(R(X)=L(X)\).
put \(R(X)=L(X)\). -
(ii)
On 1-morphisms: for a 1-morphism \(f:X\longrightarrow Y\) let \(R(f):L(X)\longrightarrow L(Y)\) be some choice of a right adjoint to \(L(f):L(Y)\longrightarrow L(X)\). Recall that we assume our 2-functors L strictly respect identities, meaning \(L(\textrm{id})=\textrm{id}\), and we choose \(R(\textrm{id})=\textrm{id}\).
-
(iii)
On 2-morphisms: given a 2-morphism \(\lambda :f\longrightarrow g\) in
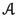 we have in
we have in  a 2-morphism \(L(\lambda ):L(f)\longrightarrow L(g)\), but the adjunctions \(L(f)\dashv R(f)\) and \(L(g)\dashv R(g)\) give rise to further 2-morphism, the unit and counit 2-morphisms \(\eta _f^{}:\textrm{id}\longrightarrow R(f)L(f)\), \(\varepsilon _f^{}:L(f)R(f)\longrightarrow \textrm{id}\), \(\eta _g^{}:\textrm{id}\longrightarrow R(g)L(g)\) and \(\varepsilon _g^{}:L(g)R(g)\longrightarrow \textrm{id}\). We define \(R(\lambda )\) to be the composite
a 2-morphism \(L(\lambda ):L(f)\longrightarrow L(g)\), but the adjunctions \(L(f)\dashv R(f)\) and \(L(g)\dashv R(g)\) give rise to further 2-morphism, the unit and counit 2-morphisms \(\eta _f^{}:\textrm{id}\longrightarrow R(f)L(f)\), \(\varepsilon _f^{}:L(f)R(f)\longrightarrow \textrm{id}\), \(\eta _g^{}:\textrm{id}\longrightarrow R(g)L(g)\) and \(\varepsilon _g^{}:L(g)R(g)\longrightarrow \textrm{id}\). We define \(R(\lambda )\) to be the composite 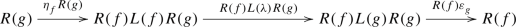
-
(iv)
Let \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) be composable 1-morphisms in
 . Since L is a pseudofunctor, we are given an isomorphism \(\tau :L(gf)\longrightarrow L(f)L(g)\). Now, R(g)R(f) is a right adjoint for L(f)L(g) and R(gf) is a right adjoint for L(gf), and the construction in (iii) produces out of \(\tau :L(gf)\longrightarrow L(f)L(g)\) an induced isomorphism \(\sigma :R(g)R(f)\longrightarrow R(gf)\).
. Since L is a pseudofunctor, we are given an isomorphism \(\tau :L(gf)\longrightarrow L(f)L(g)\). Now, R(g)R(f) is a right adjoint for L(f)L(g) and R(gf) is a right adjoint for L(gf), and the construction in (iii) produces out of \(\tau :L(gf)\longrightarrow L(f)L(g)\) an induced isomorphism \(\sigma :R(g)R(f)\longrightarrow R(gf)\).
Some checking is required to verify that this recipe delivers a pseudofunctor, but all of it is straightforward.
Dually with left adjoints: given a pseudofunctor  such that, for every 1-morphism
such that, for every 1-morphism  the morphism R(f) has a left adjoint, then there is a canonical pseudofunctor L with \(L(f)\dashv R(f)\) for all 1-morphisms
the morphism R(f) has a left adjoint, then there is a canonical pseudofunctor L with \(L(f)\dashv R(f)\) for all 1-morphisms  .
.
Lemma 12.8
As in Definition 12.5 let  be a 2-category and let
be a 2-category and let  be a premonoidal 2-category. Suppose we are given 2-functors
be a premonoidal 2-category. Suppose we are given 2-functors  , with E, G contravariant and F, H covariant. Assume that \(L,L',R, R'\) are pseudofunctors, and that the pairs L, R and \(L',R'\) are as in Reminder 12.7, in particular for every 1-morphism
, with E, G contravariant and F, H covariant. Assume that \(L,L',R, R'\) are pseudofunctors, and that the pairs L, R and \(L',R'\) are as in Reminder 12.7, in particular for every 1-morphism  we have \(L(f)\dashv R(f)\) and \(L'(f)\dashv R'(f)\). Then,
we have \(L(f)\dashv R(f)\) and \(L'(f)\dashv R'(f)\). Then,
-
(i)
If \(L,L'\) are contravariant, in which case \(R,R'\) must be covariant, then there is a canonical bijection between lax natural transformations \(\lambda :E\times L\times F\longrightarrow G\times L'\times H\) and lax natural transformations \(\mu :E\times R\times F\longrightarrow G\times R'\times H\) which agree on objects.
-
(ii)
If \(L,L'\) are covariant, in which case \(R,R'\) must be contravariant, then there is a canonical bijection between oplax natural transformations \(\lambda :E\times L\times F\longrightarrow G\times L'\times H\) and oplax natural transformations \(\mu :E\times R\times F\longrightarrow G\times R'\times H\) which agree on objects.
Proof
We will prove the case where \(L,L'\) are contravariant and leave the covariant case to the reader. A natural transformation \(\lambda :E\times L\times F\longrightarrow G\times L'\times H\) gives, for every 1-morphism \(f:X\longrightarrow Y\) in  , a hexagon as in Elaboration 12.6 with a 2-morphism filling it. If we focus on the part involving L and \(L'\) and compose the composable morphisms in the hexagon that do not involve L and \(L'\), then we reduce to a square
, a hexagon as in Elaboration 12.6 with a 2-morphism filling it. If we focus on the part involving L and \(L'\) and compose the composable morphisms in the hexagon that do not involve L and \(L'\), then we reduce to a square

with a 2-cell filling it. Since we are assuming that \(\lambda \) is lax and \(L,L'\) are contravariant, the 2-morphism goes in the direction \(\lambda :L'(f)p\longrightarrow q L(f)\). Base-change gives us a 2-morphism \(\mu :p R(f)\longrightarrow R'(f)q\), which delivers the required 2-morphism in the hexagon for \(\mu :E\times R\times F\longrightarrow G\times R'\times G\). Perhaps we should remind the reader: if \(\eta :\textrm{id}\longrightarrow R'(f)L'(f)\) is the unit of the adjunction \(L'(f)\dashv R'(f)\) and \(\varepsilon :L(f)R(f)\longrightarrow \textrm{id}\) is the counit of the adjunction \(L(f)\dashv R(f)\), then \(\mu \) is defined is as the composite

and, comparing with Reminder 12.7, we see that this is natural in f. This construction is bijective, we leave to the reader the formula for the inverse. In other words, we have produced a natural bijection between

The compatibility with composition is clearly respected by this bijection. \(\square \)
Definition 12.9
Let  be a 2-category,
be a 2-category,  a premonoidal 2-category, and
a premonoidal 2-category, and  a premonoid as in Definition 12.3. For the sake of definiteness assume the 2-functor \((-)^*\) is contravariant.
a premonoid as in Definition 12.3. For the sake of definiteness assume the 2-functor \((-)^*\) is contravariant.
A module over \((-)^*\), covariant or contravariant, lax or oplax, is a (possibly lax or oplax) 2-functor  so that:
so that:
-
(i)
For all objects
 we have \(F(X)=X^*\).
we have \(F(X)=X^*\). -
(ii)
We must be given a natural transformation \(a:\big [(-)^*\times F(-)\big ]\circ \Delta _2 \longrightarrow F(-)\), possibly lax or oplax, which on objects agrees with \(\mu :\big [(-)^*\times (-)^*\big ]\circ \Delta _2 \longrightarrow (-)^*\), and so that the square
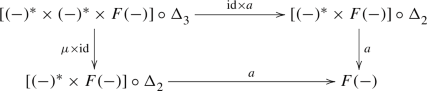
2-commutes. The modification isomorphism giving the 2-commutativity of the square above must agree on every object
 with the modification isomorphism of the 2-commutative square below
with the modification isomorphism of the 2-commutative square below 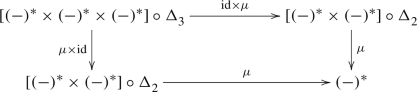
Perhaps we should elaborate a little on the last assertion. Let X be an object of  : then \(F(X)=X^*\) by assumption, and furthermore, we assume that \(\mu _X^{}:X^*\times X^*\longrightarrow X^*\) agrees with \(a_X^{}:X^*\times F(X)\longrightarrow F(X)\). The modifications in the two 2-commutative squares in Definition 12.9(ii) are both determined by 2-isomorphisms between the functors \(\mu _X^{}(\mu _X^{}\times \textrm{id})=a_X^{}(\mu _X^{}\times \textrm{id})\) and \(\mu _X^{}(\textrm{id}\times \mu _X^{})=a_X^{}(\textrm{id}\times a_X^{})\). The assumption is that these 2-isomorphisms are identical. Since we assumed that the associativity pentagon commutes for the five composites \([(-)^*\times (-)^*\times (-)^*\times (-)^*]\circ \Delta _4^{}\longrightarrow (-)^*\), it follows that so does the associativity pentagon for the five composites \([(-)^*\times (-)^*\times (-)^*\times F(-)]\circ \Delta _4^{}\longrightarrow F(-)\).
: then \(F(X)=X^*\) by assumption, and furthermore, we assume that \(\mu _X^{}:X^*\times X^*\longrightarrow X^*\) agrees with \(a_X^{}:X^*\times F(X)\longrightarrow F(X)\). The modifications in the two 2-commutative squares in Definition 12.9(ii) are both determined by 2-isomorphisms between the functors \(\mu _X^{}(\mu _X^{}\times \textrm{id})=a_X^{}(\mu _X^{}\times \textrm{id})\) and \(\mu _X^{}(\textrm{id}\times \mu _X^{})=a_X^{}(\textrm{id}\times a_X^{})\). The assumption is that these 2-isomorphisms are identical. Since we assumed that the associativity pentagon commutes for the five composites \([(-)^*\times (-)^*\times (-)^*\times (-)^*]\circ \Delta _4^{}\longrightarrow (-)^*\), it follows that so does the associativity pentagon for the five composites \([(-)^*\times (-)^*\times (-)^*\times F(-)]\circ \Delta _4^{}\longrightarrow F(-)\).
Remark 12.10
There is an immense literature about modules over what we call premonoids, we gave a tiny sample in the paragraphs immediately following Theorem 1.8 (iv) and (v). Given a premonoid in  , tensor product with it is a pseudomonad, and our modules are special cases of pseudo-algebras or lax algebras over it—most of the category-theoretic literature treats the more general situation. But what seems really unusual about our definition is the restriction that on objects of
, tensor product with it is a pseudomonad, and our modules are special cases of pseudo-algebras or lax algebras over it—most of the category-theoretic literature treats the more general situation. But what seems really unusual about our definition is the restriction that on objects of  the monoid and the algebra should be identical.
the monoid and the algebra should be identical.
This restriction does spare us from having to worry about what happens to units. As it happens in our main example \(X^*={{\textbf{D}}_{\textbf{qc}}}(X)\) is a monoidal category (with a unit), and each \(f^*\) respects the unit. As we assume that \(a_X^{}:X^*\times F(X)\longrightarrow F(X)\) agrees with \(\mu _X^{}\), the action must be unital.
Example 12.11
The trivial example of a module is \(F(-)=(-)^*\) with \(a=\mu \), that is the action map a agrees with the multiplication map \(\mu \). For non-trivial examples we will use
Proposition 12.12
Let  be a 2-category, let
be a 2-category, let  be a premonoidal 2-category, and let
be a premonoidal 2-category, and let  be a premonoid as in Definition 12.3. Suppose
be a premonoid as in Definition 12.3. Suppose  are 2-functors as in Reminder 12.7, in particular \(L(f)\dashv R(f)\) for all 1-morphisms
are 2-functors as in Reminder 12.7, in particular \(L(f)\dashv R(f)\) for all 1-morphisms  .
.
If \(L(-)\) is contravariant then \(L(-)\) is a lax module over \((-)^*\) if and only if \(R(-)\) is a lax module. If \(L(-)\) is covariant then \(L(-)\) is an oplax module over \((-)^*\) if and only if \(R(-)\) is.
Proof
Suppose \(L(-)\) is contravariant, and apply Lemma 12.8(i) with \(E=(-)^*\), with F, G and H the trivial 2-functors on the empty product, and with \(L=L'\) and \(R=R'\) as given. Then, lax natural transformations \(a:\big [(-)^*\times L(-) \big ]\circ \Delta _2\longrightarrow L(-)\) are in bijection with lax natural transformations \(b:\big [(-)^*\times R(-) \big ]\circ \Delta _2\longrightarrow R(-)\) which agree on objects. If we restrict to the case where \(L(X)=R(X)=X^*\) for every object  , and where the maps \(a_X^{}\) and \(b_X^{}\) agree with \(\mu _X^{}:X^*\times X^*\longrightarrow X^*\), then we have that a lax module structure on L induces a lax module structure on R and vice versa. Note that the 2-commutativity of the square in Definition 12.9(ii) is an assertion of the equality of certain pairs of natural transformations whose behavior on objects is determined, and the fact that the map of Lemma 12.8(i)is a bijection tells us that equality holds for L if and only if it holds for R.
, and where the maps \(a_X^{}\) and \(b_X^{}\) agree with \(\mu _X^{}:X^*\times X^*\longrightarrow X^*\), then we have that a lax module structure on L induces a lax module structure on R and vice versa. Note that the 2-commutativity of the square in Definition 12.9(ii) is an assertion of the equality of certain pairs of natural transformations whose behavior on objects is determined, and the fact that the map of Lemma 12.8(i)is a bijection tells us that equality holds for L if and only if it holds for R.
The case where L is covariant is similar, in the proof simply substitute Lemma 12.8(ii) for Lemma 12.8(i). \(\square \)
Example 12.13
As in Example 12.4 let  be the 2-category of algebraic stacks, let
be the 2-category of algebraic stacks, let  be the 2-category of finite products of triangulated categories, and let
be the 2-category of finite products of triangulated categories, and let  be the premonoid we are familiar with. The natural transformation \(\big [(-)^*\otimes (-)^*\big ]\circ \Delta _2\longrightarrow (-)^*\) is pseudonatural, meaning it is both lax and oplax. In Example 12.11, we noted that \((-)^*\) is always a (contravariant) module over \((-)^*\), and from Proposition 12.12, we learn that the 2-functor \((-)_*\), which always exists and is right adjoint to \((-)^*\), has a canonical structure of a lax module. If the left adjoint \((-)_!\) exists, it is an oplax module.
be the premonoid we are familiar with. The natural transformation \(\big [(-)^*\otimes (-)^*\big ]\circ \Delta _2\longrightarrow (-)^*\) is pseudonatural, meaning it is both lax and oplax. In Example 12.11, we noted that \((-)^*\) is always a (contravariant) module over \((-)^*\), and from Proposition 12.12, we learn that the 2-functor \((-)_*\), which always exists and is right adjoint to \((-)^*\), has a canonical structure of a lax module. If the left adjoint \((-)_!\) exists, it is an oplax module.
Concretely: for a pair of objects  the natural transformation \(a:\big [(-)^*\times (-)_*\big ]\circ \Delta _2\longrightarrow (-)_*\) gives a map
the natural transformation \(a:\big [(-)^*\times (-)_*\big ]\circ \Delta _2\longrightarrow (-)_*\) gives a map  . If \(f:X\longrightarrow Y\) is a 1-morphism in
. If \(f:X\longrightarrow Y\) is a 1-morphism in  , and \(E\in Y^*={{\textbf{D}}_{\textbf{qc}}}(Y)\) and \(F\in X_*={{\textbf{D}}_{\textbf{qc}}}(X)\) are objects, this comes down to a map in \({{\textbf{D}}_{\textbf{qc}}}(Y)\) of the form \(E\otimes f_*F\longrightarrow f_*(f^*E\otimes F)\), and this is nothing other than the projection natural transformation p(f, E, F) of Notation 3.4(iii). In general, it is not an isomorphism.
, and \(E\in Y^*={{\textbf{D}}_{\textbf{qc}}}(Y)\) and \(F\in X_*={{\textbf{D}}_{\textbf{qc}}}(X)\) are objects, this comes down to a map in \({{\textbf{D}}_{\textbf{qc}}}(Y)\) of the form \(E\otimes f_*F\longrightarrow f_*(f^*E\otimes F)\), and this is nothing other than the projection natural transformation p(f, E, F) of Notation 3.4(iii). In general, it is not an isomorphism.
However, we can shrink the category  : if instead of allowing all 1-morphisms, we assume that the 1-morphisms in
: if instead of allowing all 1-morphisms, we assume that the 1-morphisms in  are concentrated then the projection formula holds, meaning the lax natural transformation a becomes pseudonatural, and hence also oplax. Furthermore, for any 1-morphism \(f:X\longrightarrow Y\) in
are concentrated then the projection formula holds, meaning the lax natural transformation a becomes pseudonatural, and hence also oplax. Furthermore, for any 1-morphism \(f:X\longrightarrow Y\) in  the 1-morphism \(f_*\) has a right adjoint \(f^\times \), and Reminder 12.7 recalls how to extend this to a 2-functor \((-)^\times \). Proposition 12.12 applies and informs us that \((-)^\times \) is an oplax contravariant module over \((-)^*\). Concretely: let \(f:X\longrightarrow Y\) be a morphism in
the 1-morphism \(f_*\) has a right adjoint \(f^\times \), and Reminder 12.7 recalls how to extend this to a 2-functor \((-)^\times \). Proposition 12.12 applies and informs us that \((-)^\times \) is an oplax contravariant module over \((-)^*\). Concretely: let \(f:X\longrightarrow Y\) be a morphism in  and let \(E,F\in Y^*=Y^\times ={{\textbf{D}}_{\textbf{qc}}}(Y)\) be objects. In Notation 3.4(iv), we saw a morphism \(\chi (f,E,F):f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\), and what we have now learned is that this is the evaluation of a natural transformation of 2-functors \(\chi :\big [(-)^*\times (-)^\times \big ]\circ \Delta _2\longrightarrow (-)^\times \) at the 1-morphism f and the pair of objects E, F.
and let \(E,F\in Y^*=Y^\times ={{\textbf{D}}_{\textbf{qc}}}(Y)\) be objects. In Notation 3.4(iv), we saw a morphism \(\chi (f,E,F):f^*E\otimes f^\times F\longrightarrow f^\times (E\otimes F)\), and what we have now learned is that this is the evaluation of a natural transformation of 2-functors \(\chi :\big [(-)^*\times (-)^\times \big ]\circ \Delta _2\longrightarrow (-)^\times \) at the 1-morphism f and the pair of objects E, F.
In this section, we developed the theory in some generality, but the situation we care about is where  is as in Example 12.2, that is its objects are finite products of triangulated categories, and
is as in Example 12.2, that is its objects are finite products of triangulated categories, and  is a 2-subcategory of the 2-category of algebraic stacks as in Notation 1.1. Since the morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) are all concentrated, we are in the situation where \((-)^\times \) is an oplax module over \((-)^*\).
is a 2-subcategory of the 2-category of algebraic stacks as in Notation 1.1. Since the morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) are all concentrated, we are in the situation where \((-)^\times \) is an oplax module over \((-)^*\).
Reminder 12.14
Before we end this section, we study the compatibility of the module structure on \((-)^\times \) with base-change, and although the result generalizes, we confine our treatment to the case we care about, where \({\mathbb {S}_{{\textbf{e}}}}\) is as in Notation 1.1. We begin by reminding the reader of Remark 11.10: the category \(\textbf{Sq}(W,X,Y,Z)\) has for its objects the 2-cartesian squares \((\diamondsuit )\) below

with v flat. There are four natural projections, the obvious functors

If A is any of top, bot (for bottom), left or right let \(\pi _A^*\) be the composite functor \((-)^*\circ \pi _A^{}\) and let \(\pi _A^\times \) be the composite functor \((-)^\times \circ \pi _A^{}\). In Remark 11.10, we observed that base-change gives a natural transformation \(\Phi :\pi _{\text {top}}^*\pi _{\text {right}}^\times \longrightarrow \pi _{\text {left}}^\times \pi _{\text {bot}}^*\) of functors on the category \(\textbf{Sq}(W,X,Y,Z)\). Even more obviously the 2-commutativity gives a natural isomorphism \(\tau :\pi _{\text {top}}^*\pi _{\text {right}}^*\longrightarrow \pi _{\text {left}}^*\pi _{\text {bot}}^*\). On the other hand, we are given that \((-)^\times \) is an oplax module over the premonoid \((-)^*\), which means that we have natural transformations

With all these natural transformations, we could wonder how they might be related. We prove
Proposition 12.15
Consider the diagram below, of natural transformations of functors of the form  ,
,

where the top arrow is an abbreviation for \(\mu _W^{}\) applied to the composite

This diagram commutes.
Proof
The assertion is that the two composites agree, and these are ordinary natural transformations of 1-functors on 1-categories. Hence, it can be checked object by object: if \((\diamondsuit )\) below

is an object of the category \(\textbf{Sq}(W,X,Y,Z)\) we assert the equality of the evaluation at \((\diamondsuit )\) of two maps, each of which produces out of \((\diamondsuit )\) a natural transformation between functors  Each of the natural transformations sends an object \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\times {{\textbf{D}}_{\textbf{qc}}}(Z)\) to a morphism in \({{\textbf{D}}_{\textbf{qc}}}(W)\), and it suffices to show that, for each pair of objects \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), we obtain the same morphism \(u^*g^* E\otimes u^*g^\times F\longrightarrow f^\times v^*(E\otimes F)\) in the category \({{\textbf{D}}_{\textbf{qc}}}(W)\). But this has already been proved, way back in Lemma 4.7. \(\square \)
Each of the natural transformations sends an object \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\times {{\textbf{D}}_{\textbf{qc}}}(Z)\) to a morphism in \({{\textbf{D}}_{\textbf{qc}}}(W)\), and it suffices to show that, for each pair of objects \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), we obtain the same morphism \(u^*g^* E\otimes u^*g^\times F\longrightarrow f^\times v^*(E\otimes F)\) in the category \({{\textbf{D}}_{\textbf{qc}}}(W)\). But this has already been proved, way back in Lemma 4.7. \(\square \)
14 The Module Structure of \((-)^!\) over \((-)^*\)
In Sect. 12, we proved that \((-)^*\) is a premonoid and \((-)^\times \) is a module over it; this turned out to be formal nonsense. Now, we want to generalize to the 2-functor \((-)^!\). We begin with
Construction 13.1
Let X, Y, Z be three objects in \({\mathbb {S}_{{\textbf{e}}}}\). The fact that \((-)^*\) is a premonoid and \((-)^\times \) is a module over it gives, among other things, natural transformations

where \((-)^*_1\) is the restriction of the 2-functor \((-)^*\) to \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\), while \((-)^*_2\) and \((-)^\times _2\) are the restrictions of \((-)^*\) and \((-)^\times \) to \({\mathbb {S}_{{\textbf{e}}}}(Y,Z)\). We can combine these to form the composite

Now, fix the objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\) and let \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) be the object

that is the 2-commutative diagram with u a dominant, flat monomorphism and p of finite type and universally quasi-proper. Applying the above composite to the object \(u\in {\mathbb {S}_{{\textbf{e}}}}(X,Y)\) and \(p\in {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\), we deduce a 2-morphism in  of the form
of the form

Define \(\sigma _a\) to be the above, that is \(\chi (Y,Z)\mu (X,Y)\) evaluated at the pair (u, p). We have a recipe that takes an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) to a morphism \(\sigma _a^{}:\mu _X^{}(a^*\times a^!)\longrightarrow a^!\mu _Z^{}\). We assert:
Lemma 13.2
The recipe of Construction 13.1 defines a natural transformation of functors of the form  , more specifically a natural transformation
, more specifically a natural transformation

Proof
We have to prove naturality. Let \(\varphi :a\longrightarrow b\) be the representative of a morphism in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\); the data include the 2-commutative diagram

Let \(\lambda :p\longrightarrow p'\alpha \) be the 2-isomorphism giving the 2-commutativity of the triangle on the right. Out of the data, we construct the 2-commutative diagram C below

and the morphism \(\varphi ^!\) is defined to be \(\varphi ^!=P(C)\lambda ^\times \), see Construction 9.4(ii). We wish to prove the commutativity of the square

Let us begin with the case where \(p'=\textrm{id}\), \(p=\alpha \) and \(\lambda :p\longrightarrow \textrm{id}\circ \alpha \) is the identity. Then, the square (1) reduces to

and it commutes by Proposition 12.15 applied to the cartesian square \((\diamondsuit )\). The idea of the rest of the proof is that the general case follows from the commutativity of (2) by applying very minor adjustments. To spell it out: if we precompose everything in (2) with \([{p'}^*\times {p'}^\times ]\) it gives the commutative square

and if we compose the horizontal maps, on the right, with the map \(\chi (Y',Z):\mu _{Y'}^{}[{p'}^*\times {p'}^\times ]\longrightarrow {p'}^\times \mu _Z^{}\), then we obtain the commutative square

But because \(\chi :\big [(-)^*\times (-)^\times \big ]\circ \Delta _2\longrightarrow (-)^\times \) is an oplax natural transformation of 2-functors it respects composition, and the square below commutes

Applying the functor \(u^*\) gives the commutative square

Composing the horizontal maps, on the left, with the map \(\mu (X,Y):\mu _X^{}[u^*\times u^*]\longrightarrow u^*\mu _Y^{}\) gives the commutative square

And the commutative squares (3) and (5) concatenate to (1). \(\square \)
Remark 13.3
Since the functors \((-)^*\) and \((-)^!\) both factor through the groupoid completion functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\), the natural transformation \(\sigma (X,Z)\) factors uniquely through F. We have defined on \({\mathbb {S}_{{\textbf{e}}}}(X,Z)\) a natural transformation \(\sigma (X,Z):\mu _X^{}\circ \big [(-)^*\times (-)^!\big ]\longrightarrow (-)^!\circ \mu _Z^{}\). We assert:
Theorem 13.4
The following defines an oplax natural transformation \(\sigma :\big [(-)^*\times (-)^!\big ]\circ \Delta _2\longrightarrow (-)^!\) of 2-functors on \({\mathbb {S}_{{\textbf{e}}}}\):
-
(i)
On objects: for an object \(X\in {\mathbb {S}_{{\textbf{e}}}}\), we define \(\sigma _X^{}:X^*\times X^!\longrightarrow X\) to be \(\mu _X^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\).
-
(ii)
On morphisms: for two objects \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\), we define the natural transformation \(\sigma (X,Z):\mu _X^{}\circ \big [(-)^*\times (-)^!\big ]\longrightarrow (-)^!\circ \mu _Z^{}\) as in Lemma 13.2 and Remark 13.3.
The natural transformation \(\sigma \) makes \((-)^!\) into an oplax module over \((-)^*\).
Proof
Let us begin by showing that \(\sigma \) is a natural transformation of 2-functors: for this, we need to show that it respects composition. If \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) are composable morphisms in \({\mathbb {S}_{{\textbf{e}}}}\) we need to show the commutativity of the pentagon

and we begin with easy cases.
Case 1. The pentagon Pent commutes if f is a dominant, flat monomorphism or if g is of finite type and universally quasi-proper.
Proof of Case 1. We prove the case where g is of finite type and universally quasi-proper, and leave the other case to the reader. To compute the maps involved, it helps to choose a preimage in \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) of the object \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) in the category \({\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\), and our choice of preimage is the 2-commutative diagram C below

The map \(\rho (f,g)\) was defined to be \(P(C):\pi _{13}^{}(C)^!\longrightarrow \pi _{12}^{}(C)^!\pi _{23}^{}(C)^!\), which for our choice of C comes down to the canonical isomorphism \(u^*\delta (p,g):u^*(gp)^\times \longrightarrow u^*p^\times g^\times \). Thus, Pent is the concatenation of the square

and the pentagon

The square (1) commutes trivially, while (2) is what we get by applying \(u^*\) to the commutative pentagon which spells out the fact that the oplax natural transformation \(\chi :\big [(-)^*\times (-)^\times \big ]\circ \Delta _2\longrightarrow (-)^\times \) respects composition.
Case 2. The pentagon Pent commutes if g is a dominant, flat monomorphism and f is of finite type and universally quasi-proper.
Proof of Case 2. We are given the composable maps \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\), and choose a Nagata compactification for the composite \(gf:X\longrightarrow Z\). This produces for us the 2-commutative diagram C below

The map f is assumed of finite type and universally quasi-proper, as is the map p by construction. The map g is assumed to be a dominant, flat monomorphism, as is u (by construction). Hence, C is an object of the category \({\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\) lifting the object \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) via the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Y,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Y)\times {\mathbb {S}_{{\textbf{e}}}}(Y,Z)\). The map \(\rho (f,g)\) was defined to be \(P(C):\pi _{13}^{}(C)^!\longrightarrow \pi _{12}^{}(C)^!\pi _{23}^{}(C)^!\), and for our C this comes down to \(\Phi (\diamondsuit ):u^*p^\times \longrightarrow f^\times g^*\). The commutativity of Pent now follows by evaluating the commutative diagram of Proposition 12.15 at the object \((\diamondsuit )\in \textbf{Sq}(X,R,Y,Z)\).
Proof of the commutativity of Pent in the general case. Suppose f and g are general, and choose Nagata compactifications for each of them. That is factor f and g as \(f=pu\) and \(g=qv\), with \(u:X\longrightarrow R\), \(v:Y\longrightarrow S\) dominant, flat monomorphisms and \(p:R\longrightarrow Y\), \(q:S\longrightarrow Z\) of finite type and universally quasi-proper. Now, consider the diagram

We wish to prove the commutativity of the pentagon (1). Case 1 gives the commutativity of (2) and (3), and the maps \(\rho (u,p):f^!\longrightarrow u^!p^!\) and \(\rho (v,q):g^!\longrightarrow v^!q^!\) are both isomorphisms by Proposition 9.12 (i) or (ii). Thus, the map labeled \(\rho \rho \mu _Z^{}\) at the bottom of the diagram is an isomorphism, and it suffices to prove the commutativity of the perimeter; for future reference we call it Perim.
To this end, consider the diagram

The perimeter agrees with Perim, the pentagons (4) and (5) commute by Case 1, the pentagon (6) commutes by Case 2, and the regions (7) and (8) commute trivially. We have finished the proof that Pent commutes, that is we now know that \(\sigma :\big [(-)^*\times (-)^!\big ]\circ \Delta _2\longrightarrow (-)^!\) is an oplax natural transformation.
To finish the proof of the theorem, we need to establish the associativity in Definition 12.9(ii). We should perhaps remind the reader.
The fact that \((-)^*\) is a premonoid gives a pseudonatural transformation \(\mu :\big [(-)^*\times (-)^*\big ]\circ \Delta _2\longrightarrow (-)^*\), and a modification isomorphism \(m:\mu (\mu \times \textrm{id})\longrightarrow \mu (\textrm{id}\times \mu )\). For every object X this gives a functor \(\mu _X^{}:X^*\times X^*\longrightarrow X^*\), and a natural isomorphism \(m_X^{}:\mu _X^{}(\mu _X^{}\times \textrm{id})\longrightarrow \mu _X^{}(\textrm{id}\times \mu _X^{})\). The 2-functor \((-)^!\) is such that for all objects X we have \(X^!=X^*\), the natural transformation \(\sigma :\big [(-)^*\times (-)^!\big ]\circ \Delta _2\longrightarrow (-)^!\) is such that for every object X the map \(\sigma _X^{}:X^*\times X^!\longrightarrow X^!\) satisfies \(\sigma _X^{}=\mu _X^{}\), and the definition tells us that, in order for \((-)^!\) to be a module over \((-)^*\), if we view \(m_X^{}:\mu _X^{}(\mu _X^{}\times \textrm{id})\longrightarrow \mu _X^{}(\textrm{id}\times \mu _X^{})\) as a natural transformation \(m_X^{}:\sigma _X^{}(\mu _X^{}\times \textrm{id})\longrightarrow \sigma _X^{}(\textrm{id}\times \sigma _X^{})\), then it extends to a modification. We have no choice in what the modification does on objects, what needs checking is that this is compatible with rest of the structure. Concretely: if \(X,Z\in {\mathbb {S}_{{\textbf{e}}}}\) are objects and \(f:X\longrightarrow Z\) is a 1-morphism, then we have the following square:

and we need to prove it commutative for every 1-morphism f. To do this, recall the definition of \(\sigma (X,Z)\). First choose a lifting a of f via the functor \(F:{\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\longrightarrow {\mathbb {S}_{{\textbf{e}}}}(X,Z)\), that is choose an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) with \(F(a)=f\). Concretely a is a Nagata compactification for f; it is a 2-isomorphism \(pu\longrightarrow f\), where \(X{\mathop {\longrightarrow }\limits ^{u}}Y{\mathop {\longrightarrow }\limits ^{p}}Z\) are composable 1-morphisms with u a dominant, flat monomorphism and p of finite type and universally quasi-proper. The definition in Construction 13.1 is that \(\sigma _a^{}\) is the composite

The Theorem now follows from the commutativity of

which is a consequence of the associativity of the multiplication \(\mu :\big [(-)^*\times (-)^*\big ]\circ \Delta _2\longrightarrow (-)^*\), coupled with the commutativity of

which comes because the action \(\chi :\big [(-)^*\times (-)^\times \big ]\circ \Delta _2\longrightarrow (-)^\times \) is also associative. \(\square \)
Proposition 13.5
The oplax natural transformation \(\psi :(-)^\times \longrightarrow (-)^!\) respects the action of \((-)^*\). In other words, \(\psi \) is a homomorphism of \((-)^*\)-modules. Even more precisely: we have a square of oplax natural transformation of oplax 2-functors

On objects, both \(\chi \) and \(\sigma \) send the object \(X\in {\mathbb {S}_{{\textbf{e}}}}\) to the functor \(\mu _X^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\), and \(\psi \) takes the object X to \(\textrm{id}:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). The composite natural transformations agree on objects, both composites take \(X\in {\mathbb {S}_{{\textbf{e}}}}\) to the functor \(\mu _X^{}:{{\textbf{D}}_{\textbf{qc}}}(X)\times {{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(X)\). The assertion is that the assignment taking X to the identity 2-morphism \(\textrm{id}:\mu _X^{}\longrightarrow \mu _X^{}\) extends to a modification isomorphism of the composites. More concretely: the two composites are actually equal, not just 2-isomorphic.
Proof
We have studied what happens on objects and it remains to verify the assertion on 1-morphisms. Any 1-morphism \(f:X\longrightarrow Z\) in \({\mathbb {S}_{{\textbf{e}}}}\) can be factored as \(f\cong pu\) with u a dominant, flat monomorphism and p of finite type and universally quasi-proper, and the map \(\rho (u,p):f^!\longrightarrow u^!p^!\) is an isomorphism by Proposition 9.12 (i) or (ii). Evaluating the square (1) at \(f\in {\mathbb {S}_{{\textbf{e}}}}\) produces two 2-morphisms  which we wish to show equal, and it suffices to prove that the composites
which we wish to show equal, and it suffices to prove that the composites  are equal. But natural transformations respect composition, allowing us to rewrite this composite, and we are reduced to proving the commutativity of (1) when evaluated at u and at p. Thus, it suffices to consider two special cases.
are equal. But natural transformations respect composition, allowing us to rewrite this composite, and we are reduced to proving the commutativity of (1) when evaluated at u and at p. Thus, it suffices to consider two special cases.
Case 1. The two composites in the square of the Proposition agree on 1-morphisms f which are of finite type and universally quasi-proper.
Proof of Case 1. We begin by choosing the following object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) with \(F(a)=f\)

For this object \(\psi (a):f^\times \longrightarrow f^!\) is the identity map, and \(\sigma (X,Z):\mu _X^{}\big [f^*\times f^!\big ]\longrightarrow f^!\mu _Z^{}\) agrees with \(\chi (X,Z):\mu _X^{}\big [f^*\times f^\times \big ]\longrightarrow f^\times \mu _Z^{}\). Therefore, the agreement of the two composites at f is trivial.
Case 2. The two composites in the square of the Proposition agree on 1-morphisms f which are dominant, flat monomorphisms.
Proof of Case 2. Once again we begin by choosing an object \(a\in {\mathbb{N}\mathbb{S}_{{\textbf{e}}}}(X,Z)\) with \(F(a)=f\), our choice is

This time \(f^!=f^*\), the map \(\sigma (X,Z):\mu _X^{}\big [f^*\times f^!\big ]\longrightarrow f^!\mu _Z^{}\) agrees with \(\mu (X,Z):\mu _X^{}\big [f^*\times f^*\big ]\longrightarrow f^*\mu _Z^{}\), and the map \(\psi (f):f^\times \longrightarrow f^*\) identifies, by Construction 10.1, with the base-change map \(\Phi (\diamondsuit ):f^\times \longrightarrow f^*\), where \((\diamondsuit )\) is the 2-cartesian square

We wish to prove the commutativity of

and the proof is by evaluating the commutative diagram of Proposition 12.15 on the object \((\diamondsuit )\in \textbf{Sq}(X,X,X,Z)\). \(\square \)
Remark 13.6
We remind the reader of the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\): the objects are flat morphisms \(u:W\longrightarrow X\) in \({\mathbb {S}_{{\textbf{e}}}}\), the 1-morphisms \(u\longrightarrow v\) are 2-cartesian squares

and the 2-morphisms are isomorphisms of 2-cartesian squares which are identities on u and v. The functors \(p_1^{},p_2^{}:{\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\longrightarrow {\mathbb {S}_{{\textbf{e}}}}\) take an object \(u:W\longrightarrow X\) to \(p_1^{}(u)=W\) and \(p_2^{}(u)=X\). In Theorem 11.9, we produced an oplax natural transformation \(\theta :(-)^!\circ p_2^{}\longrightarrow (-)^!\circ p_1^{}\), and in Remark 11.12 we noted the(easier) oplax natural transformation \(\Phi :(-)^\times \circ p_2^{}\longrightarrow (-)^\times \circ p_1^{}\). Although we have not mentioned it yet, there is also the trivial pseudonatural transformation \(\tau :(-)^*\circ p_2^{}\longrightarrow (-)^*\circ p_1^{}\). We should remind the reader.
The three 2-functors \((-)^*\circ p_1^{}\), \((-)^\times \circ p_1^{}\) and \((-)^!\circ p_1^{}\) all take the object \(u:W\longrightarrow X\) of the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to the object \({{\textbf{D}}_{\textbf{qc}}}(W)\in \mathbb {T}\textrm{ri}\). The three 2-functors \((-)^*\circ p_2^{}\), \((-)^\times \circ p_2^{}\) and \((-)^!\circ p_2^{}\) all take the object \(u:W\longrightarrow X\) to \({{\textbf{D}}_{\textbf{qc}}}(X)\in \mathbb {T}\textrm{ri}\). When we evaluate at the 1-morphism \((\diamondsuit )\) above the functors \((-)^*\circ p_1^{}\), \((-)^\times \circ p_1^{}\) and \((-)^!\circ p_1^{}\) take \((\diamondsuit )\) (respectively) to \(f^*\), \(f^\times \) and \(f^!\), while the functors \((-)^*\circ p_2^{}\), \((-)^\times \circ p_2^{}\) and \((-)^!\circ p_2^{}\) take \((\diamondsuit )\) (respectively) to \(g^*\), \(g^\times \) and \(g^!\).
So much for the functors. The three natural transformations \(\tau \), \(\Phi \) and \(\theta \) all take the object \(u:W\longrightarrow X\) to the 1-morphism \(u^*:{{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}_{\textbf{qc}}}(W)\) in \(\mathbb {T}\textrm{ri}\). Each 1-morphism \((\diamondsuit )\) in \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) must map to a 2-morphism, and the rule is \(\tau (\diamondsuit ):u^*g^*\longrightarrow f^*v^*\) is the canonical isomorphism, \(\Phi (\diamondsuit ):u^*g^\times \longrightarrow f^\times v^*\) is the base-change map, and \(\theta (\diamondsuit ):u^*g^!\longrightarrow f^!v^*\) is the 2-morphism of Construction 11.6 and Proposition 11.7. Of these \(\Phi \) and \(\theta \) have a direction, both are oplax, while \(\tau (\diamondsuit )\) is an isomorphism, making \(\tau \) a pseudonatural transformation.
These are 2-functors and natural transformations we knew about back in Sect. 11, but now that we have the premonoid structure on \((-)^*\) and the fact that \((-)^\times \) and \((-)^!\) are both \((-)^*\)-modules we have many more natural transformations to play with. We can wonder whether some composites might be equal, or at least have modifications mapping one to the other. The next Proposition proves such an assertion, but to state it we introduce a tiny bit of notation. Until now, the map \(\Delta _2\) was a strict 2-functor \(\Delta _2:{\mathbb {S}_{{\textbf{e}}}}\longrightarrow {\mathbb {S}_{{\textbf{e}}}}\times {\mathbb {S}_{{\textbf{e}}}}\), the doubling map. To state the next Proposition, we commit the notational crime of allowing \(\Delta _2:{\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\longrightarrow {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\times {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\) to also be the doubling map. With this criminal notation, we observe that the following squares are strictly commutative

With this notation, we prove
Proposition 13.7
The following diagrams 2-commute

and

More explicitly: we have four natural transformations, two composites in each diagram. If we trace what happens to an object \(u:W\longrightarrow X\) in the category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), the two composites shaped like \(\urcorner \) take u to \(\mu _W^{}(u^*\times u^*)\), while the two composites of the shape \(\llcorner \) take u to \(u^*\mu _X^{}\). The fact that \((-)^*\) is a premonoid gives us a 2-isomorphism \(\mu (W,X):\mu _W^{}(u^*\times u^*)\longrightarrow u^*\mu _X^{}\), and we assert that this extends to a modification that works in both diagrams.
Proof
We have analyzed what happens to an object \(u\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), it remains to check something on 1-morphisms \((\diamondsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). For the diagram (1) the proof is by evaluating the commutative diagram of Proposition 12.15 at the object \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\).
For the diagram (2) we actually need to prove something. Let \((\diamondsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\) be a 1-morphism, we need to show that the diagram commutes when evaluated at \((\diamondsuit )\). If \((\diamondsuit )\) is the 2-cartesian square

we may choose a Nagata compactification \(X{\mathop {\longrightarrow }\limits ^{t'}}S{\mathop {\longrightarrow }\limits ^{p'}}Z\) for the map \(g:X\longrightarrow Z\), and pull back to form the diagram where the squares are 2-cartesian

In other words: \((\diamondsuit )\) is 2-isomorphic in \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}(u,v)\) to the composite \((\spadesuit )\circ (\heartsuit )\). Replacing \((\diamondsuit )\) by the 2-isomorphic \((\spadesuit )\circ (\heartsuit )\) we may assume the isomorphism is an equality.
When we evaluate the diagram (2) at \((\diamondsuit )=(\spadesuit )\circ (\heartsuit )\) we arrive at two 2-morphisms  which we wish to show equal. By Proposition 9.12 (i) or (ii) the map \(\rho (t,p):f^!\longrightarrow t^!p^!\) is an isomorphism, hence it suffices to prove that the composites
which we wish to show equal. By Proposition 9.12 (i) or (ii) the map \(\rho (t,p):f^!\longrightarrow t^!p^!\) is an isomorphism, hence it suffices to prove that the composites  are equal. But natural transformations respect composition and these composites can be rewritten; it suffices to prove the commutativity of (2) when evaluated at \((\spadesuit )\) and at \((\heartsuit )\). In other words, we are reduced to the two special cases below.
are equal. But natural transformations respect composition and these composites can be rewritten; it suffices to prove the commutativity of (2) when evaluated at \((\spadesuit )\) and at \((\heartsuit )\). In other words, we are reduced to the two special cases below.
Case 1.The two composites in the diagram (2) agree on 1-morphisms \((\diamondsuit )\) where the vertical maps are of finite type and universally quasi-proper.
Proof of Case 1. We begin by choosing a preimage for \((\diamondsuit )\) under the functor \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\), that is an object \(a\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\) with \(F(a)=(\diamondsuit )\). The preimage we choose is the diagram

With this choice, the definitions make the computation explicit, and diagram (2) evaluated at \(a\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\) reduces to diagram (1) evaluated at \((\diamondsuit )\). We already know diagram (1) to be commutative.
Case 2.The two composites in the diagram (2) agree on 1-morphisms \((\diamondsuit )\) where the vertical maps are dominant, flat monomorphisms.
Proof of Case 2. We begin by choosing a preimage for \((\diamondsuit )\) under the functor \(F:\mathbb {N}\textbf{Sq}(W,X,Y,Z)\longrightarrow \textbf{Sq}(W,X,Y,Z)\), that is an object \(a\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\) with \(F(a)=(\diamondsuit )\). The preimage we choose is the diagram

With this choice, the definitions make the computation explicit, and diagram (2) evaluates at \(a\in \mathbb {N}\textbf{Sq}(W,X,Y,Z)\) to give the following composites:

and the equality is because of the premonoid structure on \((-)^*\). \(\square \)
Reminder 13.8
We would like to restate the second part of Proposition 13.7 slightly, making it more clearly parallel to Proposition 12.15. We briefly remind the reader of the notation introduced in Reminder 12.14: the category \(\textbf{Sq}(W,X,Y,Z)\) has for its objects the 2-cartesian squares \((\diamondsuit )\) below

with v flat. There are four natural projections, the obvious functors

If A is any of top, bot (for bottom), left or right let \(\pi _A^*\) be the composite functor \((-)^*\circ \pi _A^{}\) and let \(\pi _A^!\) be the composite functor \((-)^!\circ \pi _A^{}\). In Construction 11.6 and Proposition 11.7, we produced the base-change natural transformation \(\theta :\pi _{\text {top}}^*\pi _{\text {right}}^!\longrightarrow \pi _{\text {left}}^!\pi _{\text {bot}}^*\). With \(\tau :\pi _{\text {top}}^*\pi _{\text {right}}^*\longrightarrow \pi _{\text {left}}^*\pi _{\text {bot}}^*\) the canonical isomorphism, we have
Proposition 13.9
Consider the diagram below, of natural transformations of functors of the form  ,
,

where the top arrow is an abbreviation for \(\mu _W^{}\) applied to the composite

This diagram commutes.
Proof
Let \((\diamondsuit )\in \textbf{Sq}(W,X,Y,Z)\) be an object, we need to show that the diagram commutes when evaluated at \((\diamondsuit )\). But this is just by evaluating the commutative diagram (2) of Proposition 13.7 at the 1-morphism \((\diamondsuit )\in {\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). \(\square \)
Remark 13.10
The advantage of Proposition 13.9 over Proposition 13.7 is that the naturality in u and v is explicit. One way to explain this is the following: for the purpose of the proof it was convenient to work with natural transformations on the 2-category \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\), it allowed us to factor \((\diamondsuit )\) as the composite \((\diamondsuit )=(\spadesuit )\circ (\heartsuit )\) and reduce our computations to the special cases of \((\spadesuit )\) and \((\heartsuit )\). The cost was that we fixed u and v. But the arrows in the diagram of Proposition 13.9 are all natural, even in u and v, and to prove commutativity one only needs to check the statement on objects—and the result of Proposition 13.7 allows us to evaluate the diagram at a general object.
As in Remark 11.12, the reader can amuse herself by working out the \({\mathbb{H}\mathbb{S}_{{\textbf{e}}}}\) analog of what Proposition 13.7 proved for \({\mathbb{V}\mathbb{S}_{{\textbf{e}}}}\). Now, that we have proved Proposition 13.9, which is symmetric and natural in all arrows, the proofs are straightforward.
We end the paper with a result saying that, under certain hypotheses on \(f:X\longrightarrow Y\), the map \(\sigma \) is an isomorphism.
Proposition 13.11
Let \(X{\mathop {\longrightarrow }\limits ^{f}}Y{\mathop {\longrightarrow }\limits ^{g}}Z\) be composable 1-morphisms in \({\mathbb {S}_{{\textbf{e}}}}\), and assume f is flat and gf is of finite Tor-dimension. Then, \(f^*\sigma (g):f^*\mu _Y^{}(g^*\times g^!)\longrightarrow f^*g^!\mu _Z^{}\) is an isomorphism.
Also: the 2-morphism \(\sigma (g): \mu _Y^{}(g^*\times g^!)\longrightarrow g^!\mu _Z^{}\) yields an isomorphism whenever we evaluate it at a pair of objects \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) with E a perfect complex.
Proof
In Proposition 3.5, we saw that, for any morphism \(p:\overline{Y}\longrightarrow Z\) in \({\mathbb {S}_{{\textbf{e}}}}\), any perfect complex \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) and any object \(F\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), the map \(\chi (p,E,F):p^*E\otimes p^\times F\longrightarrow p^\times (E\otimes F)\) is an isomorphism. Now, take our map \(g:Y\longrightarrow Z\) and choose a Nagata compactification \(Y{\mathop {\longrightarrow }\limits ^{u}}\overline{Y}{\mathop {\longrightarrow }\limits ^{p}}Z\). The map \(\sigma (g)\), evaluated at the pair of objects \((E,F)\in {{\textbf{D}}_{\textbf{qc}}}(Z)\), is defined to be the composite

In this composite, the map \(\mu (Y,\overline{Y})\) is an isomorphism, while the second map is an isomorphism as long as E is perfect. This proves the second part of the Proposition.
Now, for the first part: we assume gf of finite Tor-dimension. With the Nagata compactification \(Y{\mathop {\longrightarrow }\limits ^{u}}\overline{Y}{\mathop {\longrightarrow }\limits ^{p}}Z\) for the map \(g:Y\longrightarrow Z\) as above, consider the diagram

The morphism uf is the composite of the flat maps u and f and is, therefore, flat. As \(gf=puf\) is of finite Tor-dimension, it follows that p is of finite Tor-dimension on the image of uf. Theorem 6.10 applies and we deduce, among other things, that the composite \((uf)^*p^\times \textrm{id}^*=f^*g^!\) respects coproducts. Therefore, the map \(f^*\sigma (g):f^*g^*E\otimes f^*g^!F\longrightarrow f^*g^!(E\otimes F)\) is a natural transformation between functors of E which are triangulated and respect coproducts. The full subcategory  , of all objects \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) such that the map \(f^*\sigma (g)\) is an isomorphism for every F, is a localizing subcategory and contains all the perfect complexes. Hence,
, of all objects \(E\in {{\textbf{D}}_{\textbf{qc}}}(Z)\) such that the map \(f^*\sigma (g)\) is an isomorphism for every F, is a localizing subcategory and contains all the perfect complexes. Hence,  is localizing and contains all the compacts—since \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated, we deduce
is localizing and contains all the compacts—since \({{\textbf{D}}_{\textbf{qc}}}(Z)\) is compactly generated, we deduce  . \(\square \)
. \(\square \)
Notes
If we assume the stacks X and Z noetherian, then \(g:X\longrightarrow Z\) is quasi-proper as long as \(\textbf{R}g_*\) takes bounded-above complexes with coherent cohomology to bounded-above complexes with coherent cohomology. This happens if g is proper and representable, but there are also non-representable examples.
If the stacks X and Z are noetherian and g is of finite type, then g is pseudo-coherent.
The \({\textbf{q}}\) stands for the derived quasi-coherator, the right adjoint to the inclusion \({{\textbf{D}}_{\textbf{qc}}}(X)\longrightarrow {{\textbf{D}}}\big (\text {Mod(X)}\big )\). As we have already said: the classical construction, using the quasi-coherator, is irrelevant to us. We only want the formal properties of
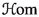 , and can construct it without ever leaving \({{\textbf{D}}_{\textbf{qc}}}(X)\), using Brown representability to give the existence of a right adjoint to the tensor product.
, and can construct it without ever leaving \({{\textbf{D}}_{\textbf{qc}}}(X)\), using Brown representability to give the existence of a right adjoint to the tensor product.Another large class of \(f^*\) for which the projection formula holds may be found in [5, Proposition 2.15]. There is overlap with [17, Corollary 4.12], but to apply [5, Proposition 2.15] to morphisms of stacks \(f:X\longrightarrow Y\) it is not enough to assume f concentrated, we must also suppose \({{\textbf{D}}_{\textbf{qc}}}(Y)\) compactly generated.
References
Abramovich, D., Olsson, M., Vistoli, A.: Tame stacks in positive characteristic. Ann. Inst. Fourier (Grenoble) 58(4), 1057–1091 (2008)
Alonso Tarrío, L., López, A.J., Lipman, J.: Bivariance, Grothendieck duality and Hochschild homology I: construction of a bivariant theory. Asian J. Math. 15(3), 451–497 (2011)
Avramov, L.L., Iyengar, S.B.: Gorenstein algebras and Hochschild cohomology. Mich. Math. J. 57, 17–35 (2008). Special volume in honor of Melvin Hochster
Avramov, L.L., Iyengar, S.B., Lipman, J., Nayak, S.: Reduction of derived Hochschild functors over commutative algebras and schemes. Adv. Math. 223(2), 735–772 (2010)
Balmer, P., Dell’Ambrogio, I., Sanders, B.: Grothendieck–Neeman duality and the Wirthmüller isomorphism. Compos. Math. 152(8), 1740–1776 (2016)
Ben-Zvi, D., Francis, J., Nadler, D.: Integral transforms and Drinfeld centers in derived algebraic geometry. J. Am. Math. Soc. 23(4), 909–966 (2010)
Bökstedt, M., Neeman, A.: Homotopy limits in triangulated categories. Compos. Math. 86, 209–234 (1993)
Bondal, A.I., Van den Bergh, M.: Generators and representability of functors in commutative and noncommutative geometry. Mosc. Math. J. 3(1), 1–36, 258 (2003)
Chikhladze, D., Lack, S., Street, R.: Hopf monoidal comonads. Theory Appl. Categ. 24(19), 554–563 (2010)
Conrad, B.: Deligne’s notes on Nagata compactifications. J. Ramanujan Math. Soc. 22(3), 205–257 (2007)
Conrad, B., Lieblich, M., Olsson, M.: Nagata compactification for algebraic spaces. J. Inst. Math. Jussieu 11(4), 747–814 (2012)
Day, B., Street, R.: Monoidal bicategories and Hopf algebroids. Adv. Math. 129(1), 99–157 (1997)
Deligne, P.: Cohomology à support propre en construction du foncteur \(f^!\), Residues and Duality, Lecture Notes in Mathematics, vol. 20. Springer, pp. 404–421 (1966)
Dubuc, E., Street, R.: Dinatural Transformations, Reports of the Midwest Category Seminar, IV. Lecture Notes in Mathematics, vol. 137. Springer, Berlin (1970)
Hall, J., Neeman, A., Rydh, D.: One positive and two negative results for derived categories of algebraid stacks. J. Inst. Math. Jussieu 18(5), 1087–1111 (2019)
Hall, J., Rydh, D.: Algebraic groups and compact generation of their derived categories of representations. Indiana Univ. Math. J. 64(6), 1903–1923 (2015)
Hall, J., Rydh, D.: Perfect complexes on algebraic stacks. Compos. Math. 153(11), 2318–2367 (2017)
Hartshorne, R.: Residues and duality, Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne. Lecture Notes in Mathematics, No. 20. Springer, Berlin (1966)
Illusie, L.: Conditions de finitude, Théorie des intersections et théorème de Riemann-Roch. Springer, Berlin (1971). Séminaire de Géométrie Algébrique du Bois-Marie 1966–1967 (SGA 6, Exposé III), pp. 222–273. Lecture Notes in Mathematics, vol. 225
Illusie, L.: Généralités sur les conditions de finitude dans les catégories dérivées, Théorie des intersections et théorème de Riemann-Roch. Springer, Berlin (1971). Séminaire de Géométrie Algébrique du Bois-Marie 1966–1967 (SGA 6, Exposé I), pp. 78–159. Lecture Notes in Mathematics, vol. 225
Iyengar, S.B., Lipman, J., Neeman, A.: Relation between two twisted inverse image pseudofunctors in duality theory. Compos. Math. 151(4), 735–764 (2015)
Kiehl, R.: Ein “Descente’’-Lemma und Grothendiecks Projektionssatz für nichtnoethersche Schemata. Math. Ann. 198, 287–316 (1972)
Kresch, A.: On the geometry of Deligne–Mumford stacks, Algebraic geometry—Seattle, 2005, Part 1. Proc. Sympos. Pure Math., vol. 80. Amer. Math. Soc., Providence, pp. 259–271 (2009)
Lack, S.: A coherent approach to pseudomonads. Adv. Math. 152(2), 179–202 (2000)
Lipman, J.: Notes on derived functors and Grothendieck duality, Foundations of Grothendieck duality for diagrams of schemes, Lecture Notes in Mathematics, vol. 1960. Springer, Berlin, pp. 1–259 (2009)
Lipman, J., Neeman, A.: Quasi-perfect scheme maps and boundedness of the twisted inverse image functor. Ill. J. Math. 51, 209–236 (2007)
Mac Lane, S.: Categories for the Working Mathematician. Lecture Notes in Mathematics, vol. 5. Springer, New York (1971)
Nagata, M.: Imbedding of an abstract variety in a complete variety. J. Math. Kyoto Univ. 2, 1–10 (1962)
Nayak, S.: Compactification for essentially finite-type maps. Adv. Math. 222(2), 527–546 (2009)
Neeman, A.: The connection between the K-theory localisation theorem of Thomason, Trobaugh and Yao, and the smashing subcategories of Bousfield and Ravenel. Ann. Sci. École Normale Supérieure 25, 547–566 (1992)
Neeman, A.: The Grothendieck duality theorem via Bousfield’s techniques and Brown representability. J. Am. Math. Soc. 9, 205–236 (1996)
Neeman, A.: Triangulated Categories, Annals of Mathematics Studies, vol. 148. Princeton University Press, Princeton (2001)
Neeman, A.: The relation between Grothendieck duality and Hochschild homology, \(K\)-Theory—Proceedings of the International Colloquium, Mumbai, 2016. Hindustan Book Agency, New Delhi, pp. 91–126 (2018)
Raoult, J.-C.: Compactification des espaces algébriques normaux. C. R. Acad. Sci. Paris Sér. A-B 273, A766–A767 (1971)
Raoult, J.-C.: Compactification des espaces algébriques. C. R. Acad. Sci. Paris Sér. A 278, 867–869 (1974)
Rydh, D.: Compactification of stacks and extending stackiness across the boundary (2009) (Unpublished; available of author’s web page)
Rydh, D.: Compactification of tame Deligne–Mumford stacks (2009) (Unpublished; available of author’s web page)
Rydh, D.: Étale dévissage, descent and pushouts of stacks. J. Algebra 331, 194–223 (2011)
Rydh, D.: Noetherian approximation of algebraic spaces and stacks. J. Algebra 422, 105–147 (2015)
Shaul, L.: Derived Hochschild functors over commutative adic algebras. arXiv:1307.5658
Thomason, R.W., Trobaugh, T.F.: Higher algebraic K-theory of schemes and of derived categories, The Grothendieck Festschrift (a collection of papers to honor Grothendieck’s 60’th birthday), vol. 3. Birkhäuser, Basel, pp. 247–435 (1990)
Verdier, J.-L.: Base change for twisted inverse images of coherent sheaves, vol. Collection: Algebraic Geometry. Tata Inst. Fund. Res., pp. 393–408 (1968)
Acknowledgements
The author would like to thank Jack Hall, Joe Lipman and David Rydh, for extensive comments and helpful suggestions that led to major improvements on earlier versions of this manuscript.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
There is no conflict of interest to report.
Additional information
Communicated by Majid Gazor.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The research was partly supported by the Australian Research Council (No. DP200102537). Part of the work was carried out at the Max Planck Institute for Mathematics in Bonn, during the 2016 Program on Higher Structures in Geometry and Physics.
Appendix A. Some Counterexamples
Appendix A. Some Counterexamples
Example A.1
Let us illustrate the fact that the hypothesis of Lemma 5.20, requiring the morphism g to be quasi-proper, cannot easily be weakened—it does not suffice for g to be proper and finitely-presentable. Let \(R=k[x,y]\) be the polynomial ring in two variables, let M be the R/(y)-module \(M=k(\!(x)\!)/k[[x]]\), and let S be the Nagata extension \(R\oplus M\), with M a square-zero ideal. Let \(g':S\longrightarrow S'\) be the surjective ring homomorphism with kernel the ideal yS. We have a pushout square of ring homomorphisms

Applying the functor \({\textrm{Spec}(-)}\), we obtain a cartesian square of affine schemes

with g a finitely-presented closed immersion, f of finite Tor-dimension, and v an open immersion, hence flat. With the exception that g is not a quasi-proper map, the hypotheses of Lemma 5.20 are all satisfied. We want to show that the conclusion fails, more precisely we will show that \(u^*g^\times M\) and \(f^\times v^*M\) are not isomorphic. Note that M belongs to \({{\textbf{D}}^+_{\textrm{qc}}}(Z)\), hence we will have a counterexample to the non-pseudo-coherent versions of both Lemma 5.20 (i) and (ii).
Tensoring with the map \(v':S\longrightarrow S[1/x]\) takes the S-module \(M= k(\!(x)\!)/k[[x]]\) to zero—in other words \(v^* M=0\). Hence, \(f^\times v^*M=0\). Next, we will show that \(u^*g^\times M\ne 0\); thus the natural map \(u^*g^\times \longrightarrow f^\times v^*\) cannot possibly be an isomorphism.
To this end, recall that the ring \(S'\), viewed as an S-module, fits in an exact sequence

where the map \(y:S\longrightarrow S\) is multiplication by y. There is a triangle in \({{\textbf{D}}_{\textbf{qc}}}(W)\cong {{\textbf{D}}}(S)\) of the form \(\Sigma M\longrightarrow P\longrightarrow S'\longrightarrow \) where P is a perfect complex, more specifically it is the mapping cone on \(y:S\longrightarrow S\). Now, note that in \({{\textbf{D}}}\big (S[1/x]\big )\), we have the computation

which allows us to compute \(f_*u^*g^\times M\) by applying the functor  to our triangle \(\Sigma M\longrightarrow P\longrightarrow S'\longrightarrow \) in \({{\textbf{D}}}(S)\). As P is perfect, we have that
to our triangle \(\Sigma M\longrightarrow P\longrightarrow S'\longrightarrow \) in \({{\textbf{D}}}(S)\). As P is perfect, we have that

and from the triangle we learn that  . But then
. But then  is not annihilated by the functor \(S[1/x]\otimes (-)\), hence \(H^2(f_*u^*g^\times M)\ne 0\).
is not annihilated by the functor \(S[1/x]\otimes (-)\), hence \(H^2(f_*u^*g^\times M)\ne 0\).
Example A.2
Let k be a field, let \(R=k[x,y]\) be the polynomial ring, and let the multiplicative group \({{{\mathbb {G}}}_m}\) act by the rule \(t\cdot (x,y)=(t^{-1}x,ty)\). Let \(X={\textrm{Spec}(R)}\); then the map \(f:[X/{{{\mathbb {G}}}_m}]\longrightarrow X/\!\!/{{{\mathbb {G}}}_m}\), from the stack \([X/{{{\mathbb {G}}}_m}]\) to the GIT quotient \(X/\!\!/{{{\mathbb {G}}}_m}\), is a quasi-proper map. In this case, the invariant subring \(R^{{{\mathbb {G}}}_m}\) is the polynomial ring in one variable \(k[xy]\subset k[x,y]\), that is \(X/\!\!/{{{\mathbb {G}}}_m}={\textrm{Spec}(R^{{{\mathbb {G}}}_m})}\) is just the affine line \({{\mathbb {A}}}^1_k\). The open subset \(U={\textrm{Spec}(R[1/x])}\subset {\textrm{Spec}(R)}=X\) is acted on freely by \({{{\mathbb {G}}}_m}\) and the quotients \(U/\!\!/{{{\mathbb {G}}}_m}\) and \(X/\!\!/{{{\mathbb {G}}}_m}\) are the same—more precisely, we have an open immersion \(u:[U/{{{\mathbb {G}}}_m}]\longrightarrow [X/{{{\mathbb {G}}}_m}]\), and the composite \(fu:[U/{{{\mathbb {G}}}_m}]\longrightarrow X/\!\!/{{{\mathbb {G}}}_m}\) is an isomorphism. In this example, we will show that \(u^*f^\times \ne \textrm{id}\); thus, even though for the quasi-proper map f we would expect \(f^!\cong f^\times \) and for the open immersion u we would expect \(u^!\cong u^*\), the fact that \(fu=\textrm{id}\) does not imply that \(\textrm{id}^!=(fu)^!=u^!f^!=u^*f^\times \).
Of course f is not separated, hence this is no contradiction to the theorems of the article. But it does show that something delicate happens with non-separated morphisms. Note that \({{\mathbb {A}}}^1_k\) is a finite-dimensional regular scheme, so any morphism to it is of finite Tor-dimension—in particular f is of finite Tor-dimension, while the open immersion u is flat. If we believed that Theorem 1.8 should hold for non-separated morphisms we might expect 1.8.6 to be true—but for our composite fu we have that u is flat and \(fu=\textrm{id}\) is proper, meaning that both 1.8.6 (1) and (3) would predict that \(\rho (u,f):(fu)^!\longrightarrow u^!f^!\) should be an isomorphism.
If we grade the ring \(R=k[x,y]\) by the weight of the representations of \({{{\mathbb {G}}}_m}\), then x has degree -1 and y has degree 1. An object in \({{\textbf{D}}_{\textbf{qc}}}\big ([X/{{{\mathbb {G}}}_m}]\big )\) is equivalent to a complex of graded R-modules, and the functor \(f_*\) takes such a complex to its subcomplex of \({{{\mathbb {G}}}_m}\)-invariants. The functor \(f^\times \) takes a complex C of \(R^{{{\mathbb {G}}}_m}\)-modules to the (derived) graded Hom-complex \({{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R,C)\). We wish to show that \(u^*f^\times \ne \textrm{id}\), and it suffices to produce an object \(C\in {{\textbf{D}}_{\textbf{qc}}}({{\mathbb {A}}}^1_k)\) with \(u^*f^\times C=0\). Our C will be \(C=k\), where \(k=k[xy]/(xy)\) is the skyscraper sheaf on \( X/\!\!/{{{\mathbb {G}}}_m}\), which we view as a complex concentrated in degree 0. We wish to compute \(u^*f^\times k\). By the above \(f^\times k\) is given by \({{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R,k)\).
If we write \(R=\oplus _{n=-\infty }^\infty R_n\), where n is the degree, then \(R_n\) is a free module of rank 1 over the ring \(R^{{{\mathbb {G}}}_m}\), generated by \(y^n\) if \(n\ge 0\), and \(x^n\) if \(n\le 0\). Therefore, \({{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R_n,k)=k\) for every n. Thus, \(f^\times k={{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R,k)\) has cohomology concentrated in degree 0, and \(H^0(f^\times k)\) is a graded R-module, where in each degree it is k. We need to compute the R-module structure on \(f^\times k =H^0(f^\times k)\), meaning we must figure out how multiplication by x and y acts on \(f^\times k\). That is we have maps \(x:(f^\times k)_n\longrightarrow (f^\times k)_{n-1}\) and \(y:(f^\times k)_n\longrightarrow (f^\times k)_{n+1}\) which we need to compute.
If \(n\ge 0\) then \(R_{-n}\) is the free \(R^{{{\mathbb {G}}}_m}\)-module generated by \(x^n\), so multiplication by x is an isomorphism \(R_{-n}\longrightarrow R_{-n-1}\) and hence induces an isomorphism
which rewrites as \(x:(f^\times k)_{n+1}\longrightarrow (f^\times k)_{n}\). If \(n>0\) multiplication by y takes the generator \(x^n\in R_{-n}\) to \(yx^n=[xy]x^{n-1}\), that is to an element of the submodule \((xy)R_{-n+1}\subset R_{-n+1}\). Therefore, multiplication by y acts as the zero map \(0:{{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R_{-n+1},k)\longrightarrow {{\textrm{Hom}}}_{R^{{{\mathbb {G}}}_m}}^{}(R_{-n},k)\), which rewrites as \(0:(f^\times k)_{n-1}\longrightarrow (f^\times k)_{n}\). Similar computations, which we leave to the reader, show that for \(n\le 0\) multiplication by y is an isomorphism \((f^\times k)_{n-1}\longrightarrow (f^\times k)_{n}\), whereas for \(n<0\) multiplication by x is the zero map \(0:(f^\times k)_{n+1}\longrightarrow (f^\times k)_{n}\). This computation shows that \(u^*f^\times k=R[1/x]\otimes f^\times k=0\), since multiplication by sufficiently high powers of x annihilates every cohomology class in \(H^0(f^\times k)\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Neeman, A. An Improvement on the Base-Change Theorem and the Functor \(f^!\). Bull. Iran. Math. Soc. 49, 25 (2023). https://doi.org/10.1007/s41980-023-00768-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41980-023-00768-6



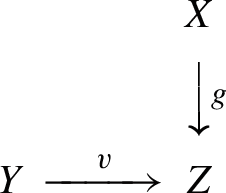
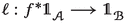 .
. , a natural map
, a natural map  . It takes a pair of objects
. It takes a pair of objects 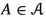 and
and 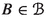 to a map
to a map 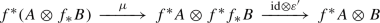
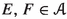 ; we define
; we define 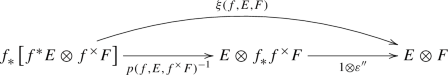
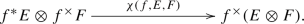
 then
then  containing
containing  must be all of
must be all of  . [A full subcategory
. [A full subcategory 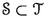 is localizing if it contains zero and is closed under coproducts and triangles].
is localizing if it contains zero and is closed under coproducts and triangles].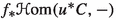 takes
takes 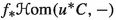 takes E to zero.
takes E to zero.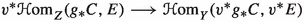 is an isomorphism.
is an isomorphism.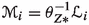 , and hence
, and hence 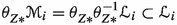 .
.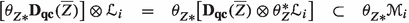 .
.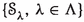 is a set of objects in the category
is a set of objects in the category 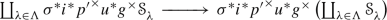
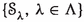 is a set of objects in the category
is a set of objects in the category 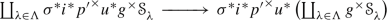
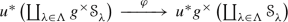
 in the category
in the category 
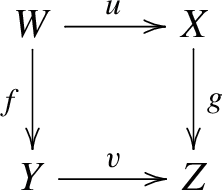





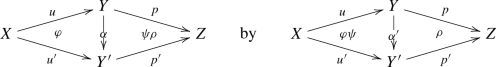

 is a groupoid, meaning all the morphisms in
is a groupoid, meaning all the morphisms in  are invertible.
are invertible. , there is a pair of morphisms
, there is a pair of morphisms  with
with  with
with  with
with  can be completed to a commutative square
can be completed to a commutative square 
 in
in  admitting a coequalizer also admits an equalizer. That is, if there exists a morphism
admitting a coequalizer also admits an equalizer. That is, if there exists a morphism  are equal, then there also exists a morphism
are equal, then there also exists a morphism  are equal.
are equal.

 ,
,  and
and  . These diagrams are declared to be equivalent if there are 2-isomorphisms
. These diagrams are declared to be equivalent if there are 2-isomorphisms 

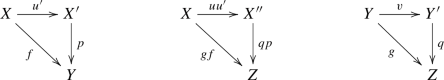
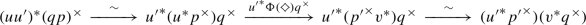
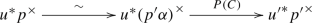
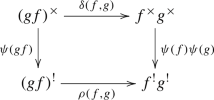
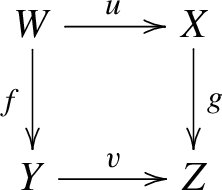






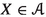 is mapped to
is mapped to 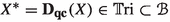 .
. , the 2-functor
, the 2-functor 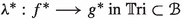 .
.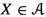 is sent to the tensor-product functor
is sent to the tensor-product functor 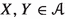 we have two functors
we have two functors 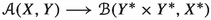 , namely
, namely 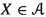 we are given a 1-morphism
we are given a 1-morphism 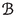 .
.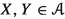 be objects. We have two functors
be objects. We have two functors 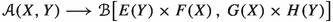 , namely
, namely 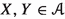 , a natural transformation
, a natural transformation 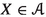 put
put  we have in
we have in  a 2-morphism
a 2-morphism 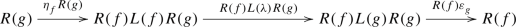
 . Since L is a pseudofunctor, we are given an isomorphism
. Since L is a pseudofunctor, we are given an isomorphism 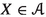 we have
we have 
 with the modification isomorphism of the 2-commutative square below
with the modification isomorphism of the 2-commutative square below 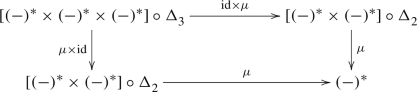
 , and can construct it without ever leaving
, and can construct it without ever leaving