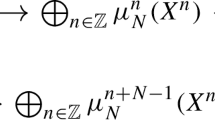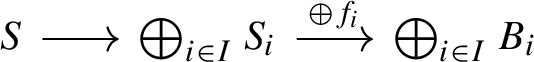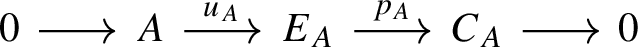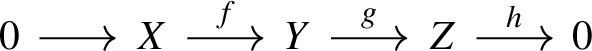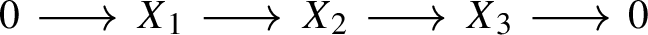Well Generatedness and Adjoints for Homotopy Categories of N-complexes

Abstract

Let R be a ring and $N \ge 2$. First, we prove that any deconstructible class of modules ${\mathcal {F}}$ over R induces two coreflective subcategories of the homotopy category $\textbf{K}_N(\mathrm {Mod-}{R})$ of (unbounded) N-complexes of right R-modules: the one whose objects are all N-complexes with components in ${\mathcal {F}}$, $\textbf{K}_N({\mathcal {F}})$, and the one whose objects are the N-acyclic complexes with components in ${\mathcal {F}}$, $\textbf{A}_N({\mathcal {F}})$. Second, we prove that for any decomposable class of modules $\mathcal G$, the homotopy category of N-complexes, $\textbf{K}_N(\mathcal G)$, is well generated. In particular, the homotopy category of N-complexes of projective modules is $\aleph _1$-generated, which extends the well known result of Neeman for $N=2$.

1 Introduction

One reason for looking for right adjoint functors of certain inclusions between homotopy categories of complexes of modules (over a not necessarily commutative ring R) comes from the new perspective given in [24] and [29] for the study of Grothendieck duality. In these papers, Grothendieck duality is studied in terms of the existence of a triangulated equivalence q between the homotopy categories of projective, $\textbf{K}(\textrm{Proj})$, and of injective, $\textbf{K}(\textrm{Inj})$, right R-modules. The importance of this condition is that it can be extended to non-affine schemes [27].

Suppose that R is commutative and noetherian and has a dualizing complex Y. Then the triangulated equivalence q is the composition

where j is the inclusion, $k=Y \otimes -$ and $\textrm{Flat}$ is the class of all flat R-modules. In [24] it is proved that both j and k have right adjoints $j'$ and $k'$ respectively, and that the composition $j'k'$ is the quasi-inverse of q. Thus, the key in the proof that q is an equivalence is the construction of the right adjoint of the inclusion j.

One of the main results in [29] is that the inclusion functor j has a right adjoint for any (not necessarily commutative) ring R. What Neeman actually proves is that $\textbf{K}(\textrm{Proj})$ is a well generated triangulated category. Then, the existence of the aforementioned adjoint comes from Brown representability.

On the other hand, the notion of N-complex was first used in Algebraic Topology by Mayer [26]. From an algebraic point of view, the N-complexes (and the equivalent N-differential objects) were studied by Kapranov [25] and Dubois-Violette [11, 12], where the homological algebra related to them were developed. This theory is fundamental in the homological study of N-homogeneous algebras, [4] and [5], and has applications in Physics, see, for instance, [13] and [14]. Moreover, N-complexes appear naturally in N-Koszul algebras, an extension of Koszul algebras, see [3]. Recently, homotopy and derived categories of N-complexes have been studied by Gillespie [19], Bahiraei, Hafezi and Nematbakhsh [1], Yang and Ding [34], Iyama, Kato and Miyachi [23] and Brightbill and Miemietz [6].

The main objective in this paper is to study the existence of adjoints of inclusions and the well-generatedness of certain homotopy categories of N-complexes of modules over the ring R, for a natural number N greater than or equal to 2.

Our first main result is about adjunctions. We prove that deconstructible classes of modules (see Definition 2.3) induce coreflective subcategories in the homotopy category of N-complexes of modules, $\textbf{K}_N(\mathrm {Mod-}{R})$, see Corollary 3.7. As a consequence of this result, we obtain that many of the subcategories known to be coreflective in the classical homotopy categories, are coreflective for $N \ge 2$ as well. For instance, we obtain [30, Theorem 3.2] (which has been extended to N-complexes in [2, Lemma 4.3]) and [18, Theorem 3.8] in the setting of N-complexes (notice that [18, Theorem 3.9] is proved for noetherian rings and we do not use this hypothesis).

The second main result is about well generatedness. In Sect. 4, we prove that the homotopy category of N-complexes of projective modules, $\textbf{K}_N(\textrm{Proj})$, is $\aleph _1$-compactly generated, extending Neeman’s [29, Theorem 1.1] to this setting. Notice that Bahiraei, Hafeze and Nematbakshsh [1] have recently proven that $\textbf{K}_N(\textrm{Proj})$ is $\aleph _0$-compactly generated when R is left coherent.

We follow the approach of Saorín and Stovicek [31], where the key notions are that of deconstructible and decomposable classes of modules (see Definition 2.3).

2 Preliminaries

Given a set A, we denote by |A| its cardinality. The cofinality of a cardinal $\kappa$ is the smallest cardinal, denoted ${{\,\textrm{cf}\,}}(\kappa )$, such that there exists a family of ordinals smaller than $\kappa$, $\{\alpha _\nu \mid \nu < {{\,\textrm{cf}\,}}(\kappa )\}$, with $\bigcup _{\nu < {{\,\textrm{cf}\,}}(\kappa )}\alpha _\nu =\kappa$. The cardinal $\kappa$ is called regular if ${{\,\textrm{cf}\,}}(\kappa )=\kappa$; otherwise, it is called singular.

Let $\mathcal B$ be an additive category and $\mathcal C$, a full subcategory of $\mathcal {B}$. We say that $\mathcal {C}$ is precovering if every object B of $\mathcal B$ has a $\mathcal C$-precover, i. e., a morphism $f:X \rightarrow B$ with $X \in \mathcal C$, such that ${\text {Hom}}_{\mathcal B}(X',f)$ is an epimorphism for each $X'\in \mathcal C$. We say that $\mathcal C$ is coreflective in $\mathcal B$ if the inclusion functor $\mathcal C \rightarrow \mathcal B$ has a right adjoint. This is equivalent to every object B of $\mathcal B$ having a coreflection, that is, a $\mathcal C$-precover $f:X \rightarrow B$ with ${\text {Hom}}(X',f)$ bijective for every $X'\in \mathcal C$.

Given an ordinal $\lambda$, a $\lambda$-sequence is a direct system $(X_\alpha ,u_{\alpha \beta }\mid \alpha< \beta < \lambda )$ such that, for each $\beta < \lambda$ limit, the direct limit of $(X_\alpha ,u_{\alpha \gamma }\mid \alpha< \gamma < \beta )$ exists and the induced morphism $\varinjlim _{\alpha < \beta }X_\alpha \rightarrow X_\beta$ is an isomorphism. If the $\lambda$-sequence has a direct limit, then the canonical morphism$u_0:X_0 \rightarrow \varinjlim _{\alpha < \lambda } X_\alpha$ is called the transfinite composition of the $\lambda$-sequence.

The definition of well generation commonly used for triangulated categories is based on the notion of small object. Suppose that $\mathcal B$ has arbitrary direct sums and let $\kappa$ be an infinite cardinal. An object B of $\mathcal B$ is $\kappa$-small if for any family of objects, $\{B_i \mid i \in I\}$, and any morphism $f:B \rightarrow \bigoplus _{i \in I}B_i$, there exists a subset $I' \subseteq I$ of cardinality less than $\kappa$ such that f factors through $\bigoplus _{i \in I'}B_i$. The definition of well generated category that we use here is [31, Definition 4.6], which is equivalent in triangulated categories to Neeman’s original definition [28] (see the comment before [31, Definition 4.6]).

Definition 2.1

Let $\mathcal B$ be an additive category with arbitrary direct sums and $\kappa$ an infinite regular cardinal. We say that $\mathcal B$ is $\kappa$-well generated if there exists a set of objects ${\mathcal {S}}$ of $\mathcal B$ such that:

• (1) For each non-zero object B of $\mathcal B$ there exists an object $S \in {\mathcal {S}}$ and a non-zero morphism $f:S \rightarrow B$.

• (2) Each object in ${\mathcal {S}}$ is $\kappa$-small.

• (3) For any morphism in $\mathcal B$ of the form $f:S \rightarrow \bigoplus _{i \in I}B_i$ with $S \in {\mathcal {S}}$ and $\{B_i\mid i \in I\}\subseteq \mathcal B$, there exists a morphism $f_i:S_i \rightarrow B_i$ with $S_i \in {\mathcal {S}}$ for each $i \in I$, such that f factorizes as

  

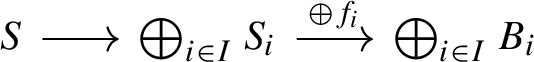
Remark 2.2

Notice that in (2) of [31, Definition 4.6] it is claimed that every object S in ${\mathcal {S}}$ is $\kappa$-small relative to the class of all split monomorphisms, i. e., ${\text {Hom}}(S,-)$ preserves direct limits of $\kappa$-sequences of split monomorphisms. This condition is equivalent to the notion of $\kappa$-smallness used in this paper, since the direct limit of a $\kappa$-sequence of split monomorphisms is the direct sum of the objects in the direct system.

An exact category is a pair $(\mathcal A;\mathcal E)$, where $\mathcal A$ is an additive category and $\mathcal E$ is a class of kernel-cokernel pairs, called conflations, satisfying the axioms [E0], [E1] and [E2], and their duals $[E0^{op}]$, $[E1^{op}]$ and $[E2^{op}]$, of [7]. If for any conflation

we call f an inflation and g a deflation, the axioms essentially say that the identity morphism of every object is an inflation and a deflation, that inflations and deflations are closed under compositions, that the pushout of any inflation along any morphism is an inflation, and that the pullback of any deflation along any morphism is a deflation. Through this paper we assume that all exact categories satisfy:

Assumption 1

Transfinite compositions of inflations exist and are inflations.

This assumption guarantees that there exist direct sums in $\mathcal A$ and that direct sums of conflations are conflations [31, Lemma 1.4].

We introduce two types of classes of objects which will play a fundamental role in our results: decomposable and deconstructible classes. Deconstructible classes in exact categories were introduced in [31].

Definition 2.3

Let $(\mathcal A;\mathcal E)$ be an exact category, ${\mathcal {F}}$ and $\mathcal G$ classes of objects of $\mathcal A$ closed under isomorphisms and A an object of $\mathcal A$.

• (1) We say that A is $\mathcal {G}$-decomposable if there exists a family of objects of $\mathcal G$, $\{G_i\mid i \in I\}$, such that $A \cong \bigoplus _{i \in I}G_i$. We denote by ${{\,\textrm{Sum}\,}}(\mathcal G)$ the class consisting of all $\mathcal G$-decomposable objects and, if $\kappa$ is a cardinal, by ${{\,\textrm{Sum}\,}}_\kappa (\mathcal G)$ the class consisting of all $\mathcal G$-decomposable objects which are isomorphic to a direct sum of less than $\kappa$ objects belonging to $\mathcal G$.

• (2) We say that ${\mathcal {F}}$ is decomposable if there exists a set of objects ${\mathcal {S}} \subseteq {\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Sum}\,}}({\mathcal {S}})$.

• (3) We say that A is $\mathcal {G}$-filtered if A is the direct limit of a $\lambda$-sequence in $\mathcal A$, $(G_\alpha ,u_{\alpha \beta }\mid \alpha< \beta < \mu )$ satisfying that $u_{\alpha \beta }$ is an inflation and ${\text {Coker}}u_{\alpha \beta } \in \mathcal G$ for each $\alpha < \beta$. We denote by ${{\,\textrm{Filt}\,}}_{\mathcal E}(\mathcal G)$ or simply ${{\,\textrm{Filt}\,}}({\mathcal {S}})$ (if the exact structure is understood) the class consisting of all $\mathcal G$-filtered objects. When $u_{\alpha \beta }$ are inclusions between modules or complexes, we simply denote the filtration by $(G_\alpha \mid \alpha < \kappa )$.

• (4) We say that ${\mathcal {F}}$ is deconstructible if there exists a set ${\mathcal {S}} \subseteq {\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Filt}\,}}({\mathcal {S}})$.

We will use the following immediate characterization of decomposable and deconstructible classes. The second follows from the fact that ${{\,\textrm{Filt}\,}}({\mathcal {S}})$ is closed under filtrations for any class of objects ${\mathcal {S}}$ [31, Corollary 2.11] (a class of objects ${\mathcal {F}}$ is closed under filtrations if every ${\mathcal {F}}$-filtered object belongs to ${\mathcal {F}}$).

Lemma 2.4

Let $(\mathcal A;\mathcal E)$ be an exact category and ${\mathcal {F}}$ a class of objects of $\mathcal A$.

• (1) ${\mathcal {F}}$ is decomposable if and only if ${\mathcal {F}}$ is closed under direct sums and there exists a set ${\mathcal {S}} \subseteq {\mathcal {F}}$ such that ${\mathcal {F}} \subseteq {{\,\textrm{Sum}\,}}(\mathcal {S})$.

• (2) ${\mathcal {F}}$ is deconstructible if and only if ${\mathcal {F}}$ is closed under filtrations and there exists a set ${\mathcal {S}} \subseteq {\mathcal {F}}$ such that ${\mathcal {F}} \subseteq {{\,\textrm{Filt}\,}}(\mathcal {S})$.

Let $(\mathcal A;\mathcal E)$ be a Frobenius exact category, that is, an exact category with enough injectives and projectives and such that the classes of all projective and of all injective objects coincide. The stable category associated to $(\mathcal A;\mathcal E)$ is the category $\underline{\mathcal A}$ whose class of objects is $\mathcal A$ and whose set of morphisms ${\text {Hom}}_{\underline{\mathcal A}}(A,B)$, for each pair of objects $A,B \in \mathcal A$, is the quotient group ${\text {Hom}}_{\mathcal A}(A,B)/I(A,B)$, where I(A, B) is the subgroup of all morphisms that factors through an injective object. If A and f is an object and a morphism, respectively, in $\mathcal A$, we denote by $\underline{A}$ and $\underline{f}$ the corresponding object and morphism in the stable category. The same notation is used for subcategories of $\mathcal A$.

The stable category can be turned into a triangulated category in the following way:

• For any object $A \in \mathcal A$, fix a conflation

  

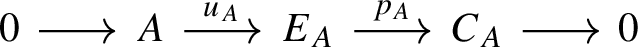
  with $E_A$ injective, and define the suspension functor as $\Sigma \underline{A} = \underline{C_A}$.

• For any morphism $f:A \rightarrow B$ in $\mathcal A$, we can construct the following commutative diagram

  

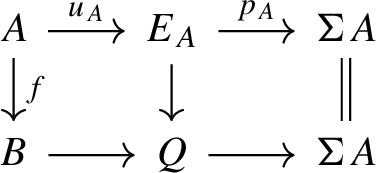
  in which the left-hand square is the pullback of $u_A$ and f. The sequence in $\underline{{\mathcal {S}}}$,

  

  is called a standard triangle. The exact triangles in $\underline{\mathcal A}$ are those sequences isomorphic in $\underline{\mathcal A}$ to a standard triangle.

Recall that a full subcategory ${\mathcal {X}}$ of a triangulated category $\mathcal T$ is closed under cones if every triangle in $\mathcal T$

with $X,Y\in {\mathcal {X}}$, satisfies that $Z \in {\mathcal {X}}$.

Now we consider N-complexes over the additive category $\mathcal B$ for N a natural number greater than or equal to 2. An N-complex is a sequence of morphisms in $\mathcal B$

such that

$$\begin{aligned} d_X^{i+N-1}\cdots d_X^{i+1}d_X^i=0 \end{aligned}$$

Given a natural number $0 \le r \le N$ and an integer n, we denote by $d^{\{n,r\}}_X$, if $r>0$, the composition

$$\begin{aligned} d_X^{n+r-1}\cdots d_X^{n+1}d_X^n, \end{aligned}$$

and by $d_X^{\{n,0\}}$ the identity of $X^n$. Sometimes, we omit the superscript n and we simply write $d_X^{\{r\}}$. Note that $d_X^{\{N\}} = 0$. We denote by $\textbf{C}_N(\mathcal B)$ (resp. $\textbf{C}^+_N(\mathcal B)$, $\textbf{C}^-_N(\mathcal B)$, $\textbf{C}^b_N(\mathcal B)$) the category whose objects are all unbounded N-complexes (resp. bounded below, bounded above, bounded) with components in $\mathcal B$ and whose morphisms are all cochain maps.

Given a complex X in $\textbf{C}_N(\mathcal B)$ and an integer n, we denote by $\tau _{\ge n}X$ the hard truncation of X, i. e., the complex of $\textbf{C}^+_N(\mathcal B)$ given by $(\tau _{\ge n} X)^i = X^i$ and $d^i_{\tau _{\ge n} X} = d^i_X$, if $i \ge n$, $(\tau _{\ge n} X)^i = 0$ and $d^i_{\tau _{\ge n} X} = 0$ if $i < n$.

We consider the class $\mathcal {S}_N(\mathcal {B})$ consisting of all semi-split conflations in $\textbf{C}_N(\mathcal B)$, that is, those kernel-cokernel pairs in $\textbf{C}_N(\mathcal B)$ which are degreewise split exact. We call the inflations (resp. deflations) associated to this exact structure semi-split monomorphisms (resp. semi-split epimorphisms). It is well known that $(\textbf{C}_N(\mathcal B),{\mathcal {S}}_N(\mathcal B))$ is an exact category [23, Lemma 1.1], which actually is Frobenius [23, Proposition 1.5] and [19, Theorem 4.3]. If for every object $M \in \mathcal {B}$, $r \in {\mathbb {Z}}$ and $r \in \{1, \ldots , N\}$, we consider the corresponding disk on B, $\mu _r^s(M)$, which is the N-complex with M in degrees $s-r+1,s-r+2,\ldots , s$, with $d^{s-r+1}= \cdots = d^s=1_M$, with 0 in degree n and with $d^n=0$ for $n \notin \{s-r+1,\ldots , s\}$, we obtain a projective-injective complex in $(\textbf{C}_N(\mathcal B),{\mathcal {S}}_N(\mathcal B))$ [23, Lemma 2.2]. If ${\mathcal {B}}$ is the category of right modules over a ring, then every projective and injective complex in $(\textbf{C}_N(\mathcal B),{\mathcal {S}}_N(\mathcal B))$ is a direct sum of disks [19, Proposition 4.1 and Theorem 3.3].

A cochain map f between N-complexes X and Y is called null-homotopic if there exists, for each $i \in {\mathbb {Z}}$, a morphism $s^i:X^i \rightarrow Y^{i-N+1}$ such that

$$\begin{aligned} f^n = \sum _{j=0}^{N-1} d_Y^{\{j\}}s^{i+N-j-1}d_X^{\{N-j-1\}} \end{aligned}$$

Two chain maps between N-complexes, f, g, are homotopic, written $f \sim g$, if $f-g$ is null-homotopic.

The homotopy category of unbounded cochain N-complexes is the category $\textbf{K}_N(\mathcal B)$ whose objects are all N-complexes and such that, for each N-complexes X and Y, ${\text {Hom}}_{\textbf{K}_N(\mathcal B)}(X,Y)$ is the quotient group ${\text {Hom}}_{\textbf{C}_N(\mathcal B)}(X,Y)/ \sim$. As it is proved in [23, Theorem 1.7], $\textbf{K}_N(\mathcal B)$ coincides with the stable category of the Frobenius exact category $(\textbf{C}_N(\mathcal B),{\mathcal {S}}_N(\mathcal B))$. Following the notation fixed for stable categories, we denote by $\underline{A}$, $\underline{f}$ and $\underline{{\mathcal {X}}}$ the corresponding object, morphisms and subcategory in $\textbf{K}_{N}(\mathcal B)$ of an object A, morphism f and subcategory ${\mathcal {X}}$ of $\mathcal B$.

All rings in this paper are associative with unit and not necessarily commutative, and all modules are right modules. Given a cardinal number $\kappa$, every $<\kappa$-generated module trivially is $\kappa$-small in the sense of Definition 2.1. A module M is $\kappa$-presented if there is an exact sequence $R^{(I)} \rightarrow R^{(J)} \rightarrow M \rightarrow 0$ with $|I|=|J|=\kappa$. A deconstructible (resp. decomposable) class of modules ${\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Filt}\,}}({\mathcal {S}})$ (resp. ${\mathcal {F}}={{\,\textrm{Sum}\,}}({\mathcal {S}})$) for a set ${\mathcal {S}}$ of $<\kappa$-presented modules will be called $\kappa$-deconstructible (resp. $\kappa$-decomposable). We denote by $\textrm{Proj}$, $\textrm{Inj}$, $\textrm{Flat}$, ${{\,\textrm{GProj}\,}}$, ${{\,\textrm{GInj}\,}}$ and ${{\,\textrm{GFlat}\,}}$ the classes of projective, injective, flat, Gorenstein-projective, Gorenstein-injective and Gorenstein-flat modules, respectively.

One of the main technical tools we will use is the deconstruction of a class of complexes. This procedure is based on the Hill Lemma, which we state now for module categories [20, Theorem 4.2.6]. We will not need the more general version for Grothendieck categories [32, Theorem 2.1].

Theorem 2.5

Let $\kappa$ be an infinite regular cardinal and ${\mathcal {S}}$ a set of $< \kappa$-presented modules. Let M be a module with an ${\mathcal {S}}$-filtration $(M_\alpha \mid \alpha < \lambda )$. Then there exists a family of submodules ${\mathcal {H}}$ of M (which we call the family associated to the filtration $(M_\alpha \mid \alpha < \lambda )$) such that:

• (H1) $M_\alpha \in {\mathcal {H}}$ for each $\alpha < \lambda$.

• (H2) ${\mathcal {H}}$ is closed under arbitrary sums and intersections.

• (H3) For any $N,P \in {\mathcal {H}}$ with $N \le P$, $\frac{P}{N}$ is ${\mathcal {S}}$-filtered.

• (H4) For any $N \in {\mathcal {H}}$ and $X \subseteq M$ with cardinality smaller than $\kappa$, there exists $P \in {\mathcal {H}}$ such that $N \cup X \subseteq P$ and $\frac{P}{N}$ is $<\kappa$-presented.

Now assume that $\mathcal B=\mathrm {Mod-}{R}$ for some ring R. In this case, since $\textbf{C}_N(\mathrm {Mod-}{R})$ is an abelian category, we have the abelian exact structure which consists of all kernel-cokernel pairs which are degreewise exact. Let $X \in \textbf{C}_N(\mathrm {Mod-}{R})$ be an N-complex. We denote:

• $Z_{(r)}^n(X) = {\text {Ker}}d_X^{\{n,r\}}$;

• $B_{(r)}^n(X)={\text {Im}}d_X^{\{n-r,r\}}$,

• and $H_{(r)}^n(X) = \frac{Z_{(r)}^n(X)}{B^n_{(N-r)}(X)}$,

for each $r \in \{1, \ldots , N-1\}$. We say that X is N-acyclic if $H_{(r)}^n(X)=0$ for each $n \in {\mathbb {Z}}$ and $r \in \{1, \ldots , N-1\}$.

Given a class of modules ${\mathcal {F}}$, we denote by $\textbf{C}_N({\mathcal {F}})$ the class of all N-complexes X with $X^n \in {\mathcal {F}}$ and by $\textbf{A}_N({\mathcal {F}})$ the class of all N-acyclic complexes in $\textbf{C}_N({\mathcal {F}})$. Let us state some properties of N-acyclic complexes.

Lemma 2.6

Let R be a ring.

• (1) [25, Proposition 1.5] An N-complex X is N-acyclic if and only if there exists $r \in \{1, \ldots , N-1\}$ such that $Z_{(r)}^n(X)=B^n_{(N-r)}(X)$ for each $n \in {\mathbb {Z}}$.

• (2) Let X be an N-complex and Y an N-acyclic subcomplex of X. Then $X=Y$ if and only if there exists $r \in \{1, \ldots , N-1\}$ with $r \ge \frac{N}{2}$ such that $Z_{(r)}^n(X)=Z_{(r)}^n(Y)$ for each $n \in {\mathbb {Z}}$.

• (3) The class $\textbf{A}_N(\mathrm {Mod-}{R})$ is closed under unions of complexes and has the 2-out-of-3 property, that is, given a conflation in $\textbf{C}_N(\mathrm {Mod-}{R})$ (in the abelian exact structure),

  

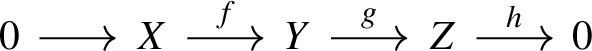
  if two of X, Y, Z are N-acyclic, then so is the third.

Proof

(1) [25, Proposition 1.5].

(2) First, notice that for every $s \in \{1, \ldots , N-1\}$ with $s \le r$ and $n \in {\mathbb {Z}}$, the equality $Z^n_{(r)}(X)=Z^n_{(r)}(Y)$ implies that $Z^n_{(s)}(X)=Z^n_{(s)}(Y)$. In particular, the hypotheses of (2) imply that this is true for $s=N-r$.

Now, take $x \in X^n$ and notice that $d^{\{n,r\}}(x) \in Z_{(N-r)}^{n+r}(X)=Z_{(N-r)}^{n+r}(Y)$. Since Y is acyclic, $d^{\{n,r\}}(x) \in B_{(r)}^{n+r}(Y)$, so that there exists $y \in Y^n$ with $d^{\{n,r\}}(y)=d^{\{n,r\}}(x)$. In particular, $x-y \in Z_{(r)}^n(X)=Z_{(r)}^n(Y)$, which implies that $x \in Y^n$.

(3) The class $\textbf{A}_N(\mathrm {Mod-}{R})$ is trivially closed under unions. The 2-out-of-3 property is proved by diagram chasing and using (1) of this lemma. $\square$

As in module categories, we can define $\kappa$-presented complexes in $\textbf{C}_N(\mathrm {Mod-}{R})$ for every infinite regular cardinal $\kappa$. These complexes are $\kappa$-small as the following result shows, which essentially is the extension of [29, Lemma 4.5] to any cardinal $\kappa$ and $N > 2$.

Lemma 2.7

Let R be a ring, $\kappa$ a cardinal with uncountable cofinality and $X \in \textbf{C}_N(\mathrm {Mod-}{R})$

• (1) If $X^n$ is $<\kappa$-generated for each integer n, then X is $\kappa$-small in $\textbf{C}_N(\mathrm {Mod-}{R})$.

• (2) If $\kappa$ is regular, then X is $< \kappa$-presented (resp. $< \kappa$-generated) if and only if $X^n$ is $< \kappa$-presented (resp. $< \kappa$-generated) for each integer n.

Proof

(1) Take a family of N-complexes $\{X_i:i \in I\}$ and a cochain map $f:X \rightarrow \bigoplus _{i \in I}X_i$. For each integer n, since $X^n$ is $<\kappa$-generated, there exists a subset $I_n$ of I with cardinality less than $\kappa$ such that $f^n$ factors through $\bigoplus _{i \in I_n}X_i^n$ in $\mathrm {Mod-}{R}$. Setting $J = \bigcup _{n \in {\mathbb {Z}}}I_n$, we obtain a subset of I with cardinality less than $\kappa$ (because $\kappa$ has uncountable cofinality) such that that f factors through $\bigoplus _{j \in J}X_j$.

(2) The same proof of [10, Lemma 2.3] applies to this setting. $\square$

As in the case of modules, if ${\mathcal {X}}$ is a deconstructible class of complexes such that ${\mathcal {X}}={{\,\textrm{Filt}\,}}({\mathcal {S}})$ for a set consisting of $<\kappa$-presented complexes for some regular cardinal $\kappa$, we say that ${\mathcal {X}}$ is $\kappa$-deconstructible.

3 Coreflective Subcategories of Homotopy Categories of N-complexes

In this section, we prove that certain subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$ are coreflective. Since the homotopy category of N-complexes is the stable category of some Frobenius exact category, we first establish a characterization of coreflective subcategories of stable categories using ideas from [9, Section 5], where a similar result is obtained for stable categories of abelian categories.

Let $(\mathcal A;\mathcal E)$ be a Frobenius exact category. We assume that $\mathcal A$ has split idempotents, which means that for every object A of $\mathcal A$ and idempotent endomorphism e of A, there exists an object B and morphisms $p:A \rightarrow B$ and $i:B \rightarrow A$ with $pi=1_B$ and $ip=e$. This condition implies that retracts and direct summands are the same thing (in general, every direct summand is a retract and the converse is true when the category has split idempotents). In general, $\underline{\mathcal A}$ need not have split idempotents, even if $\mathcal A$ has. However, in some common cases, $\underline{\mathcal A}$ does have split idempotents [9, Proposition 5.9].

Let ${\mathcal {X}}$ be an additive subcategory of $\mathcal A$ (i. e., a full subcategory containing the zero object and closed under finite direct sums). If A and B are objects in $\mathcal A$ which are isomorphic in $\underline{\mathcal A}$, then A is isomorphic in $\mathcal A$ to a direct summand of $B \oplus P$ for some projective object P. In particular, if ${\mathcal {X}}$ contains all projective modules and is closed under direct summands, then $A \in {\mathcal {X}}$ provided that $B \in {\mathcal {X}}$.

We now consider some closure properties of additive subcategories, which will allow us to characterize certain coreflective subcategories of the stable category.

Proposition 3.1

Let $(\mathcal A; \mathcal E)$ be a Frobenius exact category with split idempotents and ${\mathcal {X}}$ an additive subcategory of $\mathcal A$ containing all projective objects.

• (1) ${\mathcal {X}}$ is precovering in $\mathcal A$ if and only if $\underline{{\mathcal {X}}}$ is precovering in $\underline{\mathcal A}$.

• (2) If ${\mathcal {X}}$ is closed under direct summands, then $\underline{{\mathcal {X}}}$ is closed under cones if and only if ${\mathcal {X}}$ is closed under cokernels of inflations (i. e., every inflation $X \rightarrow Y$ with $X,Y \in {\mathcal {X}}$ has its cokernel in ${\mathcal {X}}$ as well).

Proof

(1) Clearly, if ${\mathcal {X}}$ is precovering in $\mathcal A$, then $\underline{{\mathcal {X}}}$ is precovering in $\underline{\mathcal A}$. Conversely, let A be an object in $\mathcal A$ and take an $\underline{{\mathcal {X}}}$-precover of $\underline{A}$, $\underline{u}:\underline{X} \rightarrow \underline{A}$. Since there are enough projective objects, there exists a deflation $v:P \rightarrow A$ in $\mathcal A$ with P projective. Then, it is easy to see that $u \oplus v:X \oplus P \rightarrow A$ is an ${\mathcal {X}}$-precover of A.

(2) Suppose that $\underline{{\mathcal {X}}}$ is closed under cones and take a conflation

with $X,Y \in {\mathcal {X}}$. By [22, 2.7], this conflation induces a triangle in $\underline{\mathcal A}$,

which, by hypothesis, satisfies that $Z \in {\mathcal {X}}$.

Conversely, take a standard triangle

with $X,Y \in {\mathcal {X}}$, which is induced by the diagram in $\mathcal A$,

Since the left-hand square is a pushout, there exists, by [7, Proposition 2.12], a conflation

Using that $E_X \oplus Y \in {\mathcal {X}}$ and that ${\mathcal {X}}$ is closed under cokernels of conflations, we conclude that $Z \in {\mathcal {X}}$ as required.

Finally, from this and the fact that ${\mathcal {X}}$ is closed under direct summands, it is easy to see that any exact triangle with its first two terms in ${\mathcal {X}}$ satisfies that the cone is in ${\mathcal {X}}$ as well. $\square$

Using this result and [9, Corollary 4.5] we immediately get:

Theorem 3.2

Let $(\mathcal A;\mathcal E)$ be a Frobenius exact category with split idempotents such that the stable category $\underline{\mathcal A}$ has split idempotents as well. Let ${\mathcal {X}}$ be an additive subcategory of $\mathcal A$ closed under direct summands and containing all projective objects. The following assertions are equivalent:

• (1) $\underline{{\mathcal {X}}}$ is a coreflective subcategory of $\underline{\mathcal A}$ and $\Sigma \underline{{\mathcal {X}}} \subseteq \underline{{\mathcal {X}}}$.

• (2) ${\mathcal {X}}$ is precovering in $\mathcal A$ and closed under under cokernels of inflations, i. e., if

  

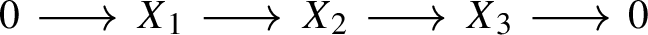
  is a conflation with $X_1$ and $X_2$ belonging to ${\mathcal {X}}$, then $X_3$ belongs to ${\mathcal {X}}$ as well.

Applied to the homotopy category of N-complexes, this result gives our criterion for coreflectivity:

Corollary 3.3

Let R be a ring and ${\mathcal {X}}$, a full subcategory of $\textbf{C}_N(\mathrm {Mod-}{R})$ which is precovering, closed under cokernels of semi-split monomorphisms and that contains all disks. Then $\underline{{\mathcal {X}}}$ is a coreflective subcategory of $\textbf{K}_N(\mathrm {Mod-}{R})$ that satisfies $\Sigma \underline{{\mathcal {X}}} \subseteq \underline{{\mathcal {X}}}$.

Proof

First, notice that $\textbf{C}_N(\mathrm {Mod-}{R})$ is Grothendieck and, consequently, has split idempotents. Moreover, $\textbf{K}_N(\mathrm {Mod-}{R})$ has split idempotents as a consequence of [9, Proposition 5.9]. Now, since ${\mathcal {X}}$ is precovering it is closed under direct sums and, as it contains all disks, it contains all contractible complexes by [19, Proposition 4.1 and Theorem 3.3]. Then, the result follows from the previous one. $\square$

Maybe, the more difficult condition of the preceding corollary to check is the precovering one. At this point is where the notion of deconstructibility and the Hill Lemma 2.5 are important, since deconstructible classes are precovering (see [31, Corollary 2.15], and [16, Theorem 5.5] and [8, Theorem 3.3] for different proofs in the category of modules). So, we are going to prove that certain classes of N-complexes are deconstructible. The deconstruction of 2-complexes has been treated in [32] and in [10].

First, we prove that $\textbf{C}_N({\mathcal {F}})$ is deconstructible when ${\mathcal {F}}$ is, extending [32, Proposition 4.3] to N-complexes.

Theorem 3.4

Let R be a ring, $\kappa$, an infinite regular cardinal and ${\mathcal {F}}$, a $\kappa$-deconstructible class of modules. Then $\textbf{C}_N({\mathcal {F}})$ is $\kappa$-deconstructible.

Proof

First, notice that every $\textbf{C}_N({\mathcal {F}})$-filtered module belongs to $\textbf{C}_N({\mathcal {F}})$, since ${\mathcal {F}}$ is closed under filtrations. In view of Lemma 2.4, we only have to prove that every complex in $\textbf{C}_N({\mathcal {F}})$ is filtered by $<\kappa$-presented complexes belonging to $\textbf{C}_N({\mathcal {F}})$. The idea of the proof is essentially the one used in [32, Proposition 4.3].

Let $X \in \textbf{C}_N({\mathcal {F}})$ and fix, using the Hill Lemma 2.5, a family of submodules of $X^n$, ${\mathcal {H}}^n$, associated to some ${\mathcal {F}}$-filtration of $X^n$ by $<\kappa$-presented modules. We construct the ${\mathcal {F}}$-filtration $(X_\alpha \mid \alpha < \mu )$ of X recursively on $\alpha$ with the additional properties that $X_\alpha ^n\in {\mathcal {H}}^n$ and $\frac{X_{\alpha +1}^{n}}{X_\alpha ^n}$ being $<\kappa$-presented for each $n \in {\mathbb {Z}}$ and $\alpha < \mu$. This implies that $X_\alpha \in \textbf{C}_N(\mathrm {Mod-}{R})$ by (H3) of 2.5, since ${\mathcal {F}}$ is closed under filtrations, and that $\frac{X_{\alpha +1}}{X_\alpha }$ is $<\kappa$-presented by Lemma 2.7.

If $\alpha =0$, set $X_\alpha =0$.

If $\alpha$ is limit, set $X_\alpha = \bigcup _{\gamma < \alpha }X_\gamma$. Notice that $X_\alpha ^n \in {\mathcal {H}}^n$ by (H2) of Hill Lemma 2.5.

If $\alpha$ is successor, say $\alpha = \gamma +1$, fix $n \in {\mathbb {Z}}$ such that $X_\gamma ^n \ne X^n$ and take $x \in X^n-X_\gamma ^n$. Set $X^m_\alpha =X^m_\gamma$ if $m < n$. For $m=n$, use (H4) of Hill Lemma 2.5 to find $X_\alpha ^n \in {\mathcal {H}}^n$ such that $X_\gamma ^n+xR \le X^n_\alpha$ and $\frac{X_\alpha ^n}{X_\gamma ^n}$ is $<\kappa$-presented. By (H3) of Hill Lemma and the induction hypothesis, this quotient belongs to ${\mathcal {F}}$ as well. For $m \ge n$, if $X_\alpha ^m$ has been already constructed, write $X_\alpha ^m = X_\gamma ^m+W^m$ for some $<\kappa$-generated module $W^m$, and apply again (H4) of Hill Lemma to find $X_\alpha ^{m+1} \in {\mathcal {H}}^{m+1}$ with $X_\gamma ^{m+1}+d_X^m(W^m)\le X_\alpha ^{m+1}$ and $\frac{X_\alpha ^{m+1}}{X_\gamma ^{m+1}}$ being $<\kappa$-presented. This quotient belongs to ${\mathcal {F}}$ by (H3) of Hill Lemma 2.5, which concludes the construction. $\square$

Now, we see that $\textbf{A}_N({\mathcal {F}})$ is deconstructible when ${\mathcal {F}}$ is. We need the following extension of [10, Lemma 4.2] to N-complexes, whose proof is essentially the same but with the obvious modifications. Recall that if $\kappa$ is an infinite regular cardinal greater than the cardinality of R, a right R-module M is $<\kappa$-presented if and only if it is $<\kappa$-generated if and only if $|M|<\kappa$. We will use this fact freely in the proof of the following result.

Lemma 3.5

Let R be a ring, $\kappa$, an uncountable regular cardinal with $|R|<\kappa$ and ${\mathcal {S}}$, a set of $< \kappa$-presented modules. Let X be an N-complex in $\textbf{A}_N({{\,\textrm{Filt}\,}}({\mathcal {S}}))$ and let, for each $m \in {\mathbb {Z}}$, ${\mathcal {H}}^m$ be the family of submodules associated to some ${\mathcal {S}}$-filtration of $X^m$ (given by the Hill Lemma 2.5). Let $Z_1$ and $Z_2$ be subcomplexes of X satisfying:

• (1) $Z_1$ is N-acyclic with $Z_1^m \in {\mathcal {H}}^m$ for each $m \in {\mathbb {Z}}$.

• (2) $Z_2$ is $<\kappa$-generated.

Then there exists an N-acyclic subcomplex Y of X such that $Z_1+Z_2 \le Y$, $\frac{Y}{Z_1}$ is $< \kappa$-presented and $Y^m \in {\mathcal {H}}^m$ for each $m \in {\mathbb {Z}}$.

Proof

We denote $d_X^m$ simply by $d^m$. We are going to construct a family of modules, $\{H_n^m \mid n \in {\mathbb {N}}, m \in {\mathbb {Z}}\}$, such that $H_n^m \le X^m$ for each $n \in {\mathbb {N}}$ and $m \in {\mathbb {Z}}$, and satisfying:

• (A) $H_0^m=0$ for each $m < 0$;

• (B) $H_0^m \in {\mathcal {H}}^m$, $Z_1^m+Z^m_2 \le H_0^m$ and $\frac{H_0^m}{Z_1^m}$ is $< \kappa$-presented for each $m \ge 0$;

and, for each $n > 0$:

• (C) $H^m_n = 0$ for each $m < -n$.

• (D) $H_n^{-n} \in {\mathcal {H}}^{-n}$, $Z_1^{-n}+Z_2^{-n} \le H_n^{-n}$, and $\frac{H_n^{-n}}{Z_1^{-n}}$ is $< \kappa$-presented.

• (E) $H_n^m \in {\mathcal {H}}^m$, $H_{n-1}^m \le H_n^m$ and $\frac{H_n^m}{H_{n-1}^{m}}$ is $< \kappa$-presented for each $m > -n$. In addition:

  • If n is odd: $H_{n-1}^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}} \le d^{m}(H^m_n)$.

  • If n is even: $d^{m-1}(H_{n-1}^{m-1}) \le H_n^{m}$.

We make the construction recursively on n.

$\underline{Case\,\,n=0}$. Set $H_0^m=0$ for each $m<0$. For $m\ge 0$, apply (H4) of Hill Lemma 2.5 to get $H^m_0 \in {\mathcal {H}}^m$ containing $Z_1^m+ Z_2^m$ and such that $\frac{H_0^m}{Z_1^m}$ is $<\kappa$-presented.

$\underline{Case\,\,n=1}$. Set $H_1^m =0$ if $m < -1$. Fix $m\ge -1$ and notice that, since $Z_1$ is N-acyclic, $\frac{H^{m+1}_0 \cap {\text {Ker}}d^{\{m+1,N-1\}}}{d^{m}(Z^{m}_1)} = \frac{H^{m+1}_0 \cap {\text {Ker}}d^{\{m+1,N-1\}}}{Z_1^{m+1}\cap {\text {Ker}}d^{\{m+1,N-1\}}}$ is isomorphic to a submodule of $\frac{H_0^{m+1}}{Z_1^{m+1}}$ and, consequently, is $<\kappa$-generated by (B). In particular, $H_0^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}}=d^{m}(Z_1^{m})+T$ for some $<\kappa$-generated submodule T of $H_0^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}}$. Using that X is N-acyclic, we can find $U \le X^{m}$ a $<\kappa$-generated submodule such that $T \le d^{m}(U)$. Now take, using (H4) of Hill Lemma 2.5, there exists $H_1^{m}\in {\mathcal {H}}^{m}$ such that $Z_1^{m}+Z_2^{m}+U \le H_1^{m}$ and $\frac{H_1^{m}}{Z_1^{m}}$ is $<\kappa$-presented (if $m=-1)$, and $H_0^m+U\le H_1^m$ and $\frac{H_1^m}{H_0^m}$ is $<\kappa$-presented (if $m>-1$). Notice that, in any case, $H_0^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}} = d^m(Z_1^m)+T \le d^m(Z_1^{m})+d^m(U) \le d^m(H^m_1)$.

Suppose that $n>1$ and that we have already constructed $H^m_{n-1}$ for each $m \in {\mathbb {Z}}$. Set $H_n^m = 0$ for each $m < -n$. For $m = -n$, apply again (H4) of Hill Lemma 2.5 to find $H_{n}^{-n} \in {\mathcal {H}}^{-n}$ such that $Z_1^{-n}+Z_2^{-n} \le H_n^{-n}$ and $\frac{H_n^{-1}}{Z_1^{-n}}$ is $< \kappa$-presented.

If $m > -n$, we distinguish between n being odd or even.

$\underline{n\,\,is\,\,even}$. Since $\frac{H^{m-1}_{n-1}}{Z^{m-1}_{1}}$ is $<\kappa$-presented (notice that it has a finite filtration by $<\kappa$-generated modules), there exists $T \le H^{m-1}_{n-1}$ with $|T| < \kappa$ such that $H^{m-1}_{n-1}=Z^{m-1}_{1}+T$. Using (H4) of Hill Lemma 2.5, we can find $H^m_n \in {\mathcal {H}}^m$ such that $H^m_{n-1}+d^{m-1}(T) \le H^m_{n}$ and $\frac{H^m_n}{H^m_{n-1}}$ is $< \kappa$-presented. Now, since $d^{m-1}(Z^{m-1}_{1})\le H^m_{n-1}$ by induction hypothesis, we obtain that $d^{m-1}(H^{m-1}_{n-1}) \le H^m_n$ as well.

$\underline{n\,\,is\,\,odd}$. First notice that, since $Z_1$ is N-acyclic, $\frac{H_{n-1}^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}}}{d^m(Z_1^m)}$ is isomorphic to a submodule of $\frac{H_{n-1}^{m+1}}{Z_1^{m+1}}$ and, consequently, it is $<\kappa$-generated (notice that $\frac{H_{n-1}^{m+1}}{Z_1^{m+1}}$ has a finite filtration by $<\kappa$-generated modules and is $<\kappa$-generated as well). In particular, $H_{n-1}^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}}=d^{m}(Z_1^{m})+T$ for some $<\kappa$-generated submodule T of $H_{n-1}^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}}$. Using that X is N-acyclic, we can find $U \le X^{m}$ a $<\kappa$-generated submodule such that $T \le d^{m}(U)$. Now take, using (H4) of Hill Lemma 2.5, $H_n^{m}\in {\mathcal {H}}^{m}$ such that $H^m_{n-1}+U \le H_n^{m}$ and $\frac{H_n^{m}}{H_{n-1}^m}$ is $<\kappa$-presented. Notice that $H_{n-1}^{m+1} \cap {\text {Ker}}d^{\{m+1,N-1\}} \le d^m(Z_1^m)+d^m(U) \le d^m(H_n^m)$. This concludes the construction.

Finally, denote $Y^m=\bigcup _{n \in {\mathbb {N}}}H^m_n$ for each $m \in {\mathbb {Z}}$. These modules define an N-acyclic subcomplex Y of X by (E) and Lemma 2.6. Moreover, it contains $Z_1+Z_2$ by (B) and (D), and by (H2) of Hill Lemma 2.5, $Y^m \in {\mathcal {H}}^m$, since $H_n^m \in {\mathcal {H}}^m$ for each $m \in {\mathbb {Z}}$ and $n \in {\mathbb {N}}$. Now, $\frac{Y^m}{Z^m_1}$ has a countable filtration by $<\kappa$-presented modules as a consequence of (B) and (E). Using that $\kappa$ is regular and uncountable, $\frac{Y^m}{Z_1^m}$ is $<\kappa$-presented, and so is $\frac{Y}{Z_1}$ by Lemma 2.7. $\square$

As a consequence of this result we get:

Theorem 3.6

Let R be a ring, $\kappa$, an uncountable regular cardinal with $|R|< \kappa$ and ${\mathcal {F}}$ a $\kappa$-deconstructible class of modules. Then $\textbf{A}_N({\mathcal {F}})$ is $\kappa$-deconstructible.

Proof

First notice that $\textbf{A}_N({\mathcal {F}})$ is closed under filtrations as a direct consequence of Lemma 2.6. Now, in order to find a set ${\mathcal {S}} \subseteq \textbf{A}_N({\mathcal {F}})$ of $<\kappa$-presented complexes such that every complex in $\textbf{C}_N({\mathcal {F}})$ is ${\mathcal {S}}$-filtered, the argument of the proof of [10, Theorem 4.3] works in this setting using Lemmas 2.6 and 3.5. $\square$

Combining Theorems 3.4 and 3.6 with Corollary 3.3 we obtain:

Corollary 3.7

Let R be a ring and ${\mathcal {F}}$ be a deconstructible class of modules. Then $\textbf{K}_N({\mathcal {F}})$ and $\underline{\textbf{A}_N({\mathcal {F}})}$ are coreflective subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$.

Now we apply this result to the classes of projective, injective, flat, Gorenstein-projective, Gorenstein-injective and Gorenstein-flat modules, respectively, which are known to be deconstructible for some types of rings. In particular, we obtain [18, Theorem 3.8] for non-Noetherian rings, and [2, Lemma 4.3], which extends [30, Theorem 3.2] to N-complexes.

Recall that a ring R is right Gorenstein regular if it has finite right global Gorenstein dimension, and is right $\Sigma$-pure injective if $R^{(I)}$ is pure-injective for every set I, that is, it is injective with respect to every pure monomorphism.

Corollary 3.8

Let R be a ring.

• (1) $\textbf{K}_N(\textrm{Proj})$, $\textbf{K}_N(\textrm{Flat})$, $\textbf{K}_N({{\,\textrm{GFlat}\,}})$, $\underline{\textbf{A}_N(\textrm{Proj})}$, $\underline{\textbf{A}_N(\textrm{Flat})}$ and $\underline{\textbf{A}_N({{\,\textrm{GFlat}\,}})}$ are coreflective subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$.

• (2) If R is right noetherian, then $\textbf{K}_N(\textrm{Inj})$ and $\underline{\textbf{A}_N(\textrm{Inj})}$ are coreflective subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$.

• (3) If R is right noetherian and ${{\,\textrm{GInj}\,}}$ is closed under filtrations, then $\textbf{K}_N({{\,\textrm{GInj}\,}})$ and $\underline{\textbf{A}_N({{\,\textrm{GInj}\,}})}$ are coreflective subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$.

• (4) If R is right Gorenstein regular or right $\Sigma$-pure-injective, then $\textbf{K}({{\,\textrm{GProj}\,}})$ and $\underline{\textbf{A}_N({{\,\textrm{GProj}\,}})}$ are coreflective subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$.

Proof

All results follow from Corollary 3.7 noting that:

• (1) the classes of projective, flat and Gorenstein flat modules are deconstructible for any ring (the case of projective modules is by Kaplansky theorem; for the other two cases, see [17, Proposition 7.4.3] and [33, Corollary 3.12]).

• (2) If R is right noetherian, the class of injective modules is deconstructible.

• (3) If R is right noetherian and ${{\,\textrm{GInj}\,}}$ is closed under filtrations, then ${{\,\textrm{GInj}\,}}$ is deconstructible [15, Proposition 1].

• (4) If R is right regular Gorenstein or right $\Sigma$-pure-injective, the class of Gorenstein projective modules is deconstructible [10, Corollary 5.9].

4 Well Generated N-homotopy Categories

In this section we study when certain subcategories of $\textbf{K}_N(\mathrm {Mod-}{R})$ are well generated. One useful result to study the well generatedness of a stable category is [31, Theorem 4.2(4)]. We give here a more direct proof of this fact:

Theorem 4.1

Let $(\mathcal A;\mathcal E)$ be a Frobenius exact category with direct sums and ${\mathcal {S}}$, a set of $\kappa$-small objects satisfying (3) of Definition 2.1. Then $\underline{{{\,\textrm{Filt}\,}}({\mathcal {S}})}$ is $\kappa$-well generated by the set $\underline{{\mathcal {S}}}$.

Proof

We prove that $\underline{{\mathcal {S}}}$ is the set of generators of $\underline{{{\,\textrm{Filt}\,}}({\mathcal {S}})}$. Since direct sums in $\underline{\mathcal A}$ are computed in $\mathcal A$ and then reflected into $\underline{\mathcal A}$, the hypotheses of the theorem imply that $\underline{{\mathcal {S}}}$ satisfies (2) and (3) of Definition 2.1.

Let us prove that $\underline{{\mathcal {S}}}$ satisfies (1) of Definition 2.1. Take $\underline{X} \in \underline{{{\,\textrm{Filt}\,}}({\mathcal {S}})}$ an object such that the only morphism $\underline{f}:\underline{S}\rightarrow \underline{X}$ with $\underline{S}\in \underline{{\mathcal {S}}}$ is the zero morphism. We prove that $\underline{X}=0$.

Take an ${\mathcal {S}}$-filtration of X, $(X_\alpha ,u_{\alpha \beta }\mid \alpha< \beta < \mu )$, and denote by $u_\alpha :X_\alpha \rightarrow X$ the canonical morphism for each $\alpha < \mu$. We prove, recursively on $\alpha$, that $\underline{u}_\alpha =0$ for each $\alpha < \mu$.

If $\alpha =0$, then $X_0=0$, so that $\underline{u}_0=0$.

Suppose that we have just proved that $\underline{u}_\alpha =0$ for some $\alpha < \mu$, and let us see that $\underline{u}_{\alpha +1}=0$. Since $\underline{u}_\alpha =0$, there exists an injective object E and morphisms $v:X_\alpha \rightarrow E$ and $w:E \rightarrow X$ such that $wv=u_\alpha$. Since $u_{\alpha \alpha +1}$ is an inflation, we can extend $u_{\alpha \alpha +1}$ to a $v':X_{\alpha +1} \rightarrow E$. Now notice that $(u_{\alpha +1}-wv')u_{\alpha \alpha +1}=0$ which implies that, if $p:X_{\alpha +1} \rightarrow C$ is the cokernel of $u_{\alpha \alpha +1}$, there exists $h:C \rightarrow X$ with $hp=u_{\alpha +1}-wv'$. Using the hypothesis and the fact that $C \in {\mathcal {S}}$, we conclude that $\underline{hp}=0$ and, consequently, that $\underline{u}_{\alpha +1}=0$. $\square$

Going back to our setting of N-complexes, in order to find well generated subcategories of the homotopy category, we need to find deconstructible classes of N-complexes in the exact structure defined by the semi-split short exact sequences. While, as we have seen in the preceding section, deconstructible classes of modules give deconstructible classes of N-complexes in the abelian exact structure, we will see that decomposable classes of modules give deconstructible classes of complexes in $(\textbf{C}_N(\mathrm {Mod-}{R}), {\mathcal {S}}_N(\mathrm {Mod-}{R}))$.

If ${\mathcal {F}}$ is a decomposable class of modules then, in general, $\textbf{C}_N({\mathcal {F}})$ is not a decomposable class of complexes. As a consequence of Theorem 3.4, $\textbf{C}_N({\mathcal {F}})$ is deconstructible. What we prove now is that it is deconstructible in the exact category $(\textbf{C}_N(\mathrm {Mod-}{R}),{\mathcal {S}}_N(\mathrm {Mod-}{R}))$.

Theorem 4.2

Let R be a ring, $\kappa$, an infinite regular cardinal and ${\mathcal {F}}$, a $\kappa$-decomposable class of modules. Then $\textbf{C}_N({\mathcal {F}})$ is $\kappa$-deconstructible in the exact category $(\textbf{C}_N(\mathrm {Mod-}{R}),{\mathcal {S}}_N(\mathrm {Mod-}{R}))$. More precisely, if ${\mathcal {S}}$ is a set of $<\kappa$-presented modules in ${\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Sum}\,}}({\mathcal {S}})$, then $\textbf{C}_N({\mathcal {F}})$ coincides with the class of all N-complexes filtered by $C_N^+({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$ in the semi-split exact structure.

Proof

First, let us see that $\textbf{C}_N({\mathcal {F}})$ is closed under filtrations in the exact category $(\textbf{C}_N(\mathrm {Mod-}{R}),{\mathcal {S}}_N(\mathrm {Mod-}{R}))$. Given an N-complex X and a $\textbf{C}_N({\mathcal {F}})$-filtration $(X_\alpha \mid \alpha < \lambda )$ of X with the inclusion $X_\alpha \rightarrow X_\beta$ a semi-split monomorphism for each $\alpha < \beta$, we obtain, for each $n \in {\mathbb {Z}}$, an ${\mathcal {F}}$-filtration $(X_\alpha ^n\mid \alpha < \lambda )$ of $X^n$ such that $X_\alpha ^n$ is a direct summand of $X_\beta ^n$ for each $\alpha < \beta$. If we take a submodule $Y_\alpha ^n$ of $X^n_{\alpha +1}$ such that $X^n_{\alpha +1}=X_\alpha ^n\oplus Y_\alpha ^n$, then, reasoning as in [21, Lemma 3.3], $X^n \cong \bigoplus _{\alpha < \lambda }Y_\alpha ^n$, so that $X^n \in {\mathcal {F}}$ and $X \in \textbf{C}_N({\mathcal {F}})$.

The hypotheses of the theorem imply that we can find an infinite regular cardinal $\kappa$ and a set of $<\kappa$-generated modules ${\mathcal {S}} \subseteq {\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Sum}\,}}({\mathcal {S}})$. By Lemma 2.4, the proof will be done if we see that every complex in $\textbf{C}_N({\mathcal {F}})$ is filtered by complexes belonging to $\textbf{C}_N^+({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$ in the exact structure defined by ${\mathcal {S}}_N(\mathrm {Mod-}{R})$. Take a family $\{F^n_i:i \in I^n\}\subseteq {\mathcal {S}}$ such that $X^n = \bigoplus _{i \in I^n}F^n_i$ for each $n \in {\mathbb {Z}}$. We are going to prove that X has a filtration, $(X_\alpha \mid \alpha < \lambda )$, such that, for each $n \in {\mathbb {Z}}$, there exists an ascending chain of subsets of $I^n$, $\{I^n_\alpha :\alpha < \lambda \}$, satisfying:

• (1) For each $n \in {\mathbb {Z}}$: $I^n = \bigcup _{\alpha < \lambda }I^n_\alpha$.

• (2) For each $n \in {\mathbb {Z}}$ and $\alpha < \lambda$:

  • (a) $X_\alpha ^n = \bigoplus _{i \in I^n_\alpha }F^n_i$.

  • (b) $|I^n_{\alpha +1}-I_\alpha ^n| < \kappa$.

  • (c) There exists $m_{\alpha +1} \in {\mathbb {Z}}$ such that $I^m_\alpha = I_{\alpha +1}^{m}$ for each $m < m_{\alpha +1}$.

Then, $(X_\alpha \mid \alpha < \lambda )$ will be a $\textbf{C}_N^+({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$-filtration of X in the exact structure defined by ${\mathcal {S}}_N(\mathrm {Mod-}{R})$.

We construct the $X_\alpha$ and $I_\alpha$ recursively on $\alpha$.

If $\alpha =0$, take $X_0=0$ and $I_0^n = \emptyset$ for each $n \in {\mathbb {Z}}$.

If $\alpha$ is limit, set $X_\alpha =\bigcup _{\gamma < \alpha }X_\gamma$ and $I_\alpha ^n = \bigcup _{\gamma < \alpha }I_\gamma ^n$ for each $n \in {\mathbb {Z}}$. Notice that $X_\alpha ^n=\bigoplus _{i \in I_\alpha ^n} F^n_i$.

Suppose that we have constructed the complex $X_\alpha$ and the sets $I^n_\alpha$ for some ordinal $\alpha$, and let us construct $X_{\alpha +1}$ and $I_{\alpha +1}^n$ for each $n \in {\mathbb {Z}}$. If $X_\alpha = X$ there is nothing to construct. Otherwise, there exists $n \in {\mathbb {Z}}$ such that $X_\alpha ^n \ne X^n$. Then set $I_{\alpha +1}^m=I_\alpha ^m$ and $X_{\alpha +1}^m = X_\alpha ^m$ for each $m < n$. In order to construct $X^n_{\alpha +1}$ take a non-zero element $x \in X^n-X_\alpha ^n$. We can find a finite set $J_\alpha ^n$ such that $X_\alpha ^n + xR \le \bigoplus _{i \in I^n_\alpha \cup J_\alpha ^n}F_\alpha ^i$, so that we can take $I_{\alpha +1}^n=I_\alpha ^n \cup J_\alpha ^n$ and $X_{\alpha +1}^n = \bigoplus _{i \in I^n_\alpha \cup J_\alpha ^n}F_\alpha ^i$.

Now we can construct $X_{\alpha +1}^m$ and $I_{\alpha +1}^m$ recursively on m for $m > n$. Assume that we have constructed $X_{\alpha +1}^m$ and $I_{\alpha +1}^m$ for some $m \ge n$. Since $I^m_{\alpha +1}-I^m_\alpha$ has cardinality smaller than $\kappa$, $F^m_i$ is $< \kappa$-generated for each $i \in I^m$ and $\kappa$ is regular, there exists a $< \kappa$-generated submodule W of $X^{m+1}$ such that $d^m_X(X_{\alpha +1}^m) = X_{\alpha }^{m+1}+W$. Then, we can find a set $J_\alpha ^{m+1}$ of cardinality less than $\kappa$ such that $W \le \bigoplus _{i \in J_\alpha ^{m+1}}F^{m+1}_i$. The construction is finished taking $I_{\alpha +1}^{m+1} = I_{\alpha }^{m+1} \cup J_{\alpha }^{m+1}$ and $X_{\alpha +1}^{m+1} = \bigoplus _{i \in I_{\alpha +1}^m}F^{m+1}_i$. $\square$

Corollary 4.3

Let R be a ring, $\kappa$, an uncountable regular cardinal and ${\mathcal {F}}$, a $\kappa$-decomposable class of modules. Then $\textbf{K}_N({\mathcal {F}})$ is $\kappa$-well generated by the set $\underline{\textbf{C}_N^+({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))}$, where ${\mathcal {S}}$ is a set of $< \kappa$-presented modules satisfying ${{\,\textrm{Sum}\,}}({\mathcal {S}})={\mathcal {F}}$.

Proof

Let ${\mathcal {S}}$ be a set of $<\kappa$-presented modules in ${\mathcal {F}}$ such that ${\mathcal {F}}={{\,\textrm{Sum}\,}}({\mathcal {S}})$. By Theorem 4.2, $\textbf{C}_N({\mathcal {F}})={{\,\textrm{Filt}\,}}_{{\mathcal {S}}_N(\mathrm {Mod-}{R})}(\textbf{C}^+_N({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}})))$. By Lemma 2.7, every module in $\textbf{C}^+_N({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$ is $<\kappa$-small. Then, the result will follow from Theorem 4.1 once we prove that $\underline{\textbf{C}^+_N({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))}$ satisfies (3) of Definition 2.1.

Take a morphism $f:X \rightarrow \bigoplus _{i \in I}F_i$ with $X \in \textbf{C}^+_N({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$ and $F_i \in \textbf{C}_N({\mathcal {F}})$ for each $i \in I$. Using Theorem 4.2, we can find a regular cardinal $\mu$ and a filtration $(F_{i\alpha }\mid \alpha < \mu )$ of $F_i$ by complexes in $\textbf{C}_N^+({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$ in the exact structure ${\mathcal {S}}_N(\mathrm {Mod-}{R})$. Denote by $p_j:\bigoplus _{i \in I}F_i \rightarrow F_j$ the canonical projection for each $j \in I$. Since ${\text {Im}}p_jf$ is $<\kappa$-generated, we can find $\alpha _j \le \mu$ with $\alpha _j < \kappa$ such that ${\text {Im}}p_jf \le F_{j\alpha _j}$ for each $j \in J$. Since $\alpha _j < \kappa$, $F_{j\alpha _j} \in \textbf{C}_N({{\,\textrm{Sum}\,}}_\kappa ({\mathcal {S}}))$. Now, the family of morphisms $\{p_jf\mid j \in I\}$ induces a morphism $g:X \rightarrow \bigoplus _{j \in J}F_{j \alpha _j}$ and, clearly, the morphism f factors as

where m is the integer satisfying that $X^n=0$ for each $n < m$. This concludes the proof. $\square$

As a consequence of this result, we can extend [30, Theorem 1.1] to the homotopy category of N-complexes of projective modules.

Corollary 4.4

Let R be a ring. Then, the homotopy category $\textbf{K}_N(\textrm{Proj})$ is $\aleph _1$-well generated by the set $\textbf{C}_N^+(\mathcal P)$, where $\mathcal P$ is the set of all countable presented projective modules.

Proof

Follows immediately from the preceding corollary by noting that the class of all projective modules is $\aleph _1$-decomposable by Kaplansky’s theorem. $\square$