1 Introduction

The United Nations (UN) has declared various forms of poverty, including energy poverty. The UN proposes three lines of action to reduce energy poverty: (a) better access to electrical services and energy for poor households, (b) efficiency in the use of electricity, and (c) greater use of renewable energy sources (Banerjee et al. 2021). Furthermore, The combined effects of the current influence of fossil fuels, volatile energy prices, the impacts of climate change, and the lack of energy education have an unfavorable impact on the global energy system and negatively influence energy sustainability criteria (Fakhri et al. 2015; Gao et al. 2020). However, it has been documented that energy services are essential to satisfy the demands for electrical energy, public lighting services, transportation, communication, and thermal comfort (Perea et al. 2020).

Furthermore, it has been documented that individuals living in cities spend up to 90% of their time inside buildings, including their homes and workplaces (Wong & Huang 2004). As a result, cities consume more than 70% of the total final energy globally (Zhang et al. 2021) and the rapid increase in demand for cooling and heating in buildings, to provide thermal comfort to occupants, makes them one of the largest end users of energy (De Dear et al. 2020; Parkinson et al. 2020; Sakhri et al. 2022).

Thermal comfort as a purpose of multiple investigations, has allowed the exploration of various ways to achieve (Ramírez-Dolores et al. 2020) this from: (a) the use of conventional Heating, Ventilation, and Air Conditioning (HVAC) systems. Conventional HVAC systems require a high economic investment for their acquisition, operation, and maintenance. Therefore, they are not accessible to a large part of the world's population. Additionally, it has been estimated that approximately 50% of the energy consumption of residential and office buildings is due to the excessive energy demand of HVAC systems (Kistelegdi et al. 2022), and (b) the use of low or zero energy consumption systems such as those described below and that can be grouped into three categories. The use of these systems can be used individually or in combination to achieve the desired thermal comfort:

I) Solar Passive Cooling System (SPCS): This alternative has been extensively evaluated and tested in regions with a hot and humid climate, it has been demonstrated that the thermal load of buildings can be reduced through SPCS by using reflective inclined roofs or implementing openings in the roof surface (Rincon et al. 2001; Roslan et al. 2016).

II) Natural Ventilation (NV): The architectural forms of built spaces have a significant impact on improving thermal sensation. Bayoumi (2017) suggests providing fresh air by exposing the space to the outside environment through doors, windows, or movable partitions. However, the control of door systems, windows, and openings in building facades can be operated manually or automated with home automation applications integrated into efficient building management to support air circulation (Moret et al. 2019). Haase and Amato (2009) have established that for a tropical climate, the improvement in the comfort index due to natural ventilation ranges between 9 and 41% (Kuala Lumpur conditions in April). For a subtropical climate, the improvements vary between 3 and 14%. These results showed that NV has significant potential in tropical climates.

III) Geothermal Heat Exchangers (Horizontal and verticals): The principle of operation consists of placing a pipe in the subsoil and the air is induced into the pipe system as a working cooling fluid, which transfers heat during its journey, while the soil functions as a source or sink, thus taking advantage of its heat capacity (Zajch & Gough 2021; Durmaz and Yalcinkaya 2019). However, although it is a system that has low maintenance costs, these devices must be designed under specific climatic and geological conditions as well as adapted to the building to provide comfort temperatures inside the spaces dedicated to human activity (Yang et al. 2017; Sakhri et al. 2020). According to the position of the pipe where the air or working fluid circulates, these systems can be vertical or horizontal. Vertical systems require drilling equipment capable of constructing wells over 10 m deep, which implies high costs (Molina-Rodea et al. 2024). On the other hand, horizontal heat exchangers require shallower wells (usually less than 2 m) and can be built at lower costs, which is why in this work we focus on horizontal heat exchangers.

The development of the horizontal ground heat exchanger technique has evolved through at least four well-differentiated stages. In each of these stages, strategies are sought to increase the effectiveness of heat exchange between the air and the subsoil:

  • a) Earth to Air Heat Exchanger (EAHE) linear horizontal configuration

The principle of operation consists of placing a pipe horizontal lineal at a certain depth in which the internal temperature of the subsoil can be maintained with a maximum variation of 1 °C throughout the year, air is induced into the pipe system as a working cooling fluid, which transfers heat during its journey, while the soil functions as a source or sink, thus taking advantage of its heat capacity (Ozgener 2011; Rosti et al. 2019).

It is important to note that EAHE systems have commonly been developed to take advantage of the thermal inertia of the soil in the first meters of depth (1.5–2.0 m) because temperature variations at the surface are attenuated at greater depth (Pfafferott 2003; Florides and Kalogirou 2007; Ahmad and Prakash 2023), It has also been proven that soil properties such as density, humidity, and specific heat directly influence the performance of EAHE (Soni et al. 2015). Due to the low heat transfer between the pipe and the ground, the horizontal pipe length is required to be of considerable length, with documented cases of up to 30 m (Misra et al. 2018). This achieves acceptable efficiency, but the high cost of installing the long pipe has prompted the search for alternative pipe configurations (Ozgener 2011).

  • b) EAHE horizontal configuration (with pipes in series, parallel or spiral)

The next stage in the development of heat exchangers involved implementing other pipe configurations that, when placed horizontally, could shorten their length or at least the space required to install them (Peretti et al. 2013; Benrachi et al. 2020). The selected and tested configurations are parallel, series, and spiral. The drawback of these configurations is that they require a welding or coupling process between pipes and accessories, which can cause the structure to be damaged by corrosion in the welding or by loss of adhesion between glued elements (PVC case). Additionally, spiral configurations can deform when buried by soil layers.

  • c) Water Air Heat Exchanger (WAHE) linear horizontal configuration (immersed in water with velocity V = 0)

However, in nature, in certain regions, we can find underground water a few meters deep, which is relevant not only as a source of supply of vital liquid but also as a natural cooling or heating system for buried pipes, which gives rise to Water Air Heat Exchangers (WAHE). It is known that groundwater can be moving or static and this influences the performance of geothermal heat exchangers.

Recent studies have reflected its importance and generated new expectations in this line of research (Jakhar et al. 2016; Li et al. 2020; Díaz-Hernández et al. 2020; Zhao et al. 2022). Some field observations in horizontal pipe with configuration linear indicate that groundwater (in static state) influences thermal performance by significantly increasing heat transport (Lim et al. 2007; Li et al. 2020).

  • d) WAHE linear horizontal configuration (immersed in water with velocity V > 0)

Other researchers have been able to identify that the effectiveness of EAHE could increase up to 55% if they are placed within aquifers with moving water (Luo et al. 2015). In this case, it becomes relevant to know the velocity distribution of the water since this could significantly increase the thermal performance based on the increase in flow velocity and the decrease in temperatures (Choi et al. 2013; Li et al. 2020).

There are multiple studies on heat exchangers between parallel or countercurrent flows and between perpendicular flows. These studies have reported correlations to calculate parameters related to heat transfer, such as the Nusselt number (Hilpert 1933; Martinelli 1947; Petukhov and Kirillov 1958; Petukhov and Popov 1963; Fand and Keswani 1972; Morgan 1975; Churchill and Bernstein 1977; Dittus and Boelter 1985; Gnielinski 2009). However, there is no reported work directly related to the angle that the horizontal pipe through which the air circulates must have with respect to the direction of the water flow (oblique flow) to achieve maximum effectiveness.

Manohar and Ramroop (2010) pointed out that there was little experimental work on oblique tubes and that studies needed to be carried out to consider the impact of the angle between the tubes exchanging heat. Zhang et al. (2015) proposed a preliminary correlation for an average Nusselt number. This correlation can be applied in angles (α) that meet the condition: 0° < α ≤ 90°. It is important to note that, despite being a relevant correlation, it presents sensitivity at angles close to 0°, in addition to the lack of precision in the ranges of the Reynolds and Prandtl numbers.

The present investigation focuses on determining the optimal position between the horizontal air-carrying pipe of the heat exchanger and the direction of the groundwater flow. The placement of heat exchangers in the subsurface with different angular orientations with respect to the direction of groundwater flow prompted the need for experimentation at scale in an open-channel flume with controlled water velocity. This allowed for testing different configurations or values of oblique angles between the two flows.

Five angles between the flows were tested in this research. Further detailing could be achieved in subsequent studies by reducing the aperture between each experimental configuration. Based on the foregoing, it can be considered that the main objective of this research is to determine the configuration and position of an EAHE exchanger concerning the water flow around the system geometry that provides the best thermal effectiveness.

2 Methodology

This study was carried out during August 2022 evaluating a scale heat exchanger prototype. The experimental tests were implemented in the southern region of Veracruz, Mexico (Fig. 1), under hot humid climate with rain in summer conditions (Am, Köppen-Geiger climate classification), and using the water flow of a natural open-air channel (stream).

Fig. 1
figure 1

Location of the study site (Coatzacoalcos City, Mexico). (Revuelta-Acosta et al. 2022)

Full size image

The following sections establish the methodological sequence used, starting with the equations for Thermo-hydraulic and heat transfer analysis; afterwards, the site where the experimentation was carried out, the prototype built, and the assembly of the temperature sensors are described; the experimental description is presented, which describes the positions of the prototype in which the experimentation was carried out, the time in which the temperature data were recorded and the instrumentation elements that make up the entire system; the theoretical analysis of the hydraulic behavior is carried out focused on the pressure drops and air flow regime taking into account the design and operating conditions of the heat exchanger, as well as the theoretical outlet temperatures of the heat exchanger. Finally, the thermal effectiveness of the exchanger is evaluated where the main variable is the geometry (position of the WAHE) between the airflow inside the exchanger and the direction of water flow in the external part.

2.1 Thermo-hydraulic analysis

The Air Water Heat Exchanger (WAHE) system used in this research is modeled in three heat transfer processes, firstly, the convective heat transfer between the inner surface of the pipe and the air flowing through the pipe, second, heat transfer by conduction due to the thickness of the pipe (Misra et al. 2018) and the third is the heat transfer by convection between the external surface of the pipe and the water flowing in the open channel (Incropera et al. 2007). The WAHE is then modeled as a heat exchanger between the fluid that it carries inside with the fluid that moves around its surface.

For this analysis, the system needed to reach stable temperature conditions, therefore, the following assumptions were considered:

  • Heat transfer is considered in a steady state.

  • The thermophysical properties of water (thermal conductivity and specific heat) do not change over time, nor due to position.

  • The speed and temperature of the water circulating through the outside of the heat exchanger are constant during each experiment.

  • The speed of the air entering the WAHE is considered constant (Relative standard deviation < 0.023%).

  • The WAHE pipe is in a uniform circular cross-section area.

2.1.1 Heat transfer by convection between the inner surface of the pipe and the air

The inner diameter of the pipe is given as (Eq. 1):

$${D}_{in}= {D}_{out}-2 (x)$$
(1)

where:

\({D}_{in}\): Inner diameter of WAHE pipe (m).

\({D}_{out}\): Outer diameter of WAHE pipe (m).

\(x\): Thickness of pipe (m).

The Reynolds number (Re) for the air flow circulating inside the pipe is calculated by Eq. 2:

$$Re= \frac{{\rho }_{air}{V}_{air}{D}_{in}}{{\mu }_{air}}$$
(2)

where:

\({\rho }_{air}\): Air density (\(\frac{Kg}{{m}^{3}}\)).

\({V}_{air}\): Air speed (\(\frac{m}{s}\)).

\({\mu }_{air}\): Dynamic air viscosity (\(\frac{Kg}{m\bullet s}\)).

The relative roughness \({(\varepsilon }_{R})\) of the pipe can be determined by means of the Moody diagram or calculated by Eq. (3):

$${\varepsilon }_{R}= \frac{{\varepsilon }_{A}}{{D}_{in}}$$
(3)

where:

\({\varepsilon }_{A}\): Absolute material roughness (mm).

The friction factor \(f\) (Eq. 4) for pipes is determined by the Petukhov relation (Agrawal et al. 2018; Misra et al. 2018):

$$f=(0.79{\text{ln}}Re-1.64{)}^{-2}$$
(4)

Due to the convection process between the inner surface of the pipe and the air flowing through the pipe, it is necessary to determine the Prandtl number (Eq. 5):

$$Pr=\frac{{{\mu }_{air}Cp}_{air}}{{k}_{air}}$$
(5)

where:

\(Pr:\) Prandtl number.

\({Cp}_{air}\): Specific heat of air (\(\frac{J}{Kg\cdot K}\)).

\({K}_{air}\): Thermal conductivity of air (\(\frac{W}{m\cdot K}\)).

The Nusselt number (Nu) for the fluid inside the pipe (Eqs. 6 and 7) is obtained in the following way (De Paepe & Janssens 2003) if the conditions of the Petukhov relationship are met.

$$if \,2300\le Re<{5 x 10}^{6} and \,0.5<Pr<{10}^{6}$$
$$\mathrm{if }\,Re<2300 \,Nu=3.66$$
(6)
$${\text{if}} \,Re>2300 \,Nu= \frac{f/8\left(Re-1000\right)Pr}{1+12.7 \sqrt{\frac{f}{8}} \left({Pr}^\frac{2}{3}-1\right)}$$
(7)

The convection heat transfer coefficient (\(h\)) is obtained from the following Eq. (8):

$$h= \frac{Nu{ K}_{air}}{{D}_{out}}$$
(8)

where:

\(h\): Convection heat transfer coefficient \((\frac{W}{{m}^{2}\bullet K})\).

For the subsequent calculation of the effectiveness, it is required to estimate the heat transfer area and the mass flow (\({\dot{m}}_{air}\)) as indicated in Eqs. (9), and (10).

$$A= \pi D{\Sigma }_{L}$$
(9)

where:

\({\Sigma }_{L}:\) Sum of straight sections (\(m)\).

$${\dot{m}}_{air}= {\rho }_{air}\frac{{\pi D}_{in}^{2}}{4}{V}_{air}$$
(10)

2.1.2 Convective heat transfer between the external surface of the pipe and the water flowing in the open channel

The Reynolds number for the flow \({Re}_{w}\)) that affects the pipe immersed in water is calculated with (Eq. 11):

$${Re}_{w}= \frac{{\rho }_{w}{V}_{w}{D}_{out}}{{\mu }_{w}}$$
(11)

where:

\({\rho }_{w}\): Density of water (\(\frac{Kg}{{m}^{3}}\)).

\({V}_{w}\): Water speed (\(\frac{m}{s}\)) measured in situ.

\({\mu }_{w}\): Dynamic viscosity of water (\(\frac{Kg}{m\cdot s}\)).

\({\rho }_{w}{, V}_{w}, {\mu }_{w}\): are properties of water as a function of temperature.

The Prandtl number for the water flow (\({Pr}_{w})\) is obtained from the following expression (Eq. 12):

$${Pr}_{w}=\frac{{{\mu }_{w}Cp}_{w}}{{k}_{w}}$$
(12)

where:

\({Cp}_{w}\): Specific heat of water (\(\frac{J}{Kg\cdot K}\)).

\({K}_{w}\): Thermal conductivity of water (\(\frac{W}{m\cdot K}\)).

The Nusselt number for the fluid outside the pipe (\({Nu}_{w}\)) could be approximated from the correlations proposed by Hilpert, Zukauskas or Churchill and Bernstein (Zukauskas 1972; Manohar and Ramroop 2010), however, due to the different experimental configurations, the Nusselt number is obtained through Eq. (13) as suggested by Gallo et al. (2012).

$${Nu}_{w}=\frac{{h}_{w} {D}_{out}}{{K}_{w}}$$
(13)

where:

\({h}_{w}\): Convection heat transfer coefficient (underwater flow considerations).

heat transfer coefficient, \({h}_{w}\), was calculated from the convection heat transfer component of Eq. (14).

$${Q}_{total}={Q}_{conv}+{Q}_{cond}={h}_{w}A\left({T}_{s}-{T}_{\infty }\right)+UA({T}_{air-in}-{T}_{air-out})$$
(14)

where:

\({Q}_{total}\): Total heat loss component (W).

\({Q}_{conv}\): Convective heat loss component (W).

\({Q}_{cond}\): Conduction heat loss component (W).

\({T}_{s}\): Surface temperature (°C).

\({T}_{\infty }\): Water temperature (°C).

\(U\): Overall heat transfer coefficient.

\({T}_{air-in}\): Air temperature at the WAHE inlet (°C).

\({T}_{air-out}\): Air temperature at the outlet of the WAHE (°C).

2.1.3 Heat transfer by conduction in the pipe

However, to determine \({Q}_{total}\), it is necessary to know the global heat transfer coefficient (\(U\)), which is determined by Eq. (15):

$$U=\frac{1}{{R}_{Total}}$$
(15)

where:

\({R}_{total}\): Overall thermal resistance.

The total thermal resistance between the airflow and the groundwater flow where the heat exchanger operates is given by Eq. (16):

$${R}_{Total}={R}_{C}+{R}_{pipe}+{R}_{W}$$
(16)

where:

\({R}_{C}\): Thermal resistance due to heat transfer by convection.

\({R}_{pipe}\): Thermal resistance due to the thickness of the pipe.

\({R}_{W}\): Thermal resistance due to contact of the pipe and the flow of water.

Thermal resistance due to convective heat transfer (\({R}_{C})\) between the airflow and the internal surface of the pipe is determined by the Eq. (17):

$${R}_{C}=\frac{1}{2\pi {r}_{in}{\Sigma }_{L}h}$$
(17)

where:

\(h\): Convection heat transfer coefficient obtained in Eq. (8).

Thermal resistance due to pipe thickness (\({R}_{pipe}\)) is determined below (Misra et al. 2018):

$${R}_{pipe}=\frac{{\text{ln}}\left(\frac{{r}_{out}}{{r}_{in}}\right)}{2\pi {\Sigma }_{L}{K}_{pipe}}$$
(18)

where:

\({K}_{pipe}\): Thermal conductivity of pipe material (\(\frac{W}{m\cdot K}\)).

\({r}_{out}\): Outer radius of WAHE pipe (m).

The thermal resistance due to the contact of the pipe and the groundwater flow (\({R}_{W})\) is determined by Eq. (19):

$${R}_{W}=\frac{1}{2\pi {r}_{out}{\Sigma }_{L}{h}_{w}}$$
(19)

where:

\({h}_{w}\): Pipe convection coefficient underwater flow conditions.

2.1.4 Calculation of the thermal effectiveness of the exchanger and the \({{\varvec{T}}}_{{\varvec{a}}{\varvec{i}}{\varvec{r}}-{\varvec{o}}{\varvec{u}}{\varvec{t}}}\)

The thermal effectiveness of the WAHE can be calculated from Eq. (20):

$$\varepsilon =\frac{{T}_{air-in}-{T}_{air-out}}{{T}_{air-in}-{T}_{\infty }}$$
(20)

Solving the term \({T}_{air-out}\) of the Eq. (20), the outlet air temperature can be determined (Al-Ajmi et al. 2006; Misra et al. 2018) of the WAHE as a function of the stream water temperature (\({T}_{\infty }\)) and the inlet air temperature (\({T}_{air-in}\)) as expressed below (Eq. 21):

$${T}_{air-out}={T}_{air-in}-({T}_{air-in}-{T}_{\infty })\varepsilon$$
(21)

where:

\(\varepsilon\): WAHE thermal Effectiveness.

The number of transfer units (NTU) is determined by Eq. (22):

$$NTU=\frac{UA}{{\dot{m}}_{air}{Cp}_{air}}$$
(22)

The cooling potential of the WAHE (\(\dot{Q})\) is calculated through Eq. (23):

$$\dot{Q}= {\dot{m}}_{air}{Cp}_{air}({T}_{air-out}-{T}_{air-in})$$
(23)

Due to convection between the wall and the air, the heat transferred (\({\dot{Q}}_{conv})\) It can also be defined by the Eq. 24:

$${\dot{Q}}_{conv}=hA{\Delta T}_{lm}$$
(24)

where:

\({\Delta T}_{lm}\): Logarithmic mean temperature difference (°C).

\({\Delta T}_{lm}\) It is defined by Eq. (25).

$${\Delta T}_{lm}=\frac{{(T}_{in}-{T}_{air-out})}{{\text{ln}}\left[{(T}_{in}-{T}_{wall}\right)/({T}_{air-out}-{T}_{wall})]}$$
(25)

2.2 Site description

The site where the experimental phase was developed is in Coatzacoalcos, Veracruz (18°08' north latitude y 94°27' west longitude). The measurements were carried out specifically in the summer season, this city is located on the coastal strip of southeastern Mexico. The climate of Coatzacoalcos is Am (Köppen-Geiger climate classification) and is characterized by having a clear sky with high temperature, solar radiation, and relative humidity most days of the year (Revuelta-Acosta et al. 2022).

The heat exchanger was placed in a stream with flow through a natural channel of clean water, which has a width of 1 m and depth of 0.45 m (Fig. 2); The speed of the water is 0.043 ± 0.005 m/s.

Fig. 2
figure 2

Natural water channel where the experimentation took place

Full size image

2.3 Design, construction, and instrumentation of the prototype

The heat exchanger prototype consists of three main sections: I) 0.457 m long horizontal pipe, II) 0.330 m vertical inlet pipe, and III) 0.330 m vertical outlet pipe. The heat exchanger was made entirely of commercial copper, with a diameter of 19.050 mm. (3/4″). The horizontal section was submerged in water, and the entry and exit section has 0.165 m of its length submerged and the remaining 0.165 m is out of water (Fig. 3).

Fig. 3
figure 3

Schematic diagram of the experimental WAHE (S1 to S4 represent the temperature sensors in the straight horizontal section, Sin the inlet temperature sensor (Tair-in) y Sout the outlet temperature sensor (Tair-out))

Full size image

The air–water heat exchanger (WAHE) has a total of 1.120 m of straight sections of which 0.787 m are immersed in water, dimensions are presented in Fig. 3. The placement of the exchanger is considered to avoid contact between the lower surface of the equipment and the bottom of the body of water.

Water temperature was recorded at depth by a sensor, measured, and recorded every 6 s for 30 min for each of the five configurations that were tested. Once the corresponding section of the WAHE was submerged and secured, the air blower was started, which remained active throughout the measurement interval without interruption in its operation and variation in airspeed.

The straight sections of the heat exchanger were connected by 90-degree elbows of the same material and welded to obtain leak-proof joints and prevent water infiltration. Drilling holes were made in the pipe and temperature sensors were inserted into the center of the pipe, the free space between the sensor cable and the pipe surface was filled with expanded polystyrene and cyanoacrylate. 6 sensors were mounted on the WAHE along the pipe, immediately at the air inlet, passing through the pipe immersed in water where 4 sensors were placed which were secured to prevent possible leaks, and finally the air outlet sensor. air located before air discharge.

The arrangement of the sensors is shown in Fig. 3, which were connected to the data acquisition system. For the proper functioning of the WAHE, it was essential to ensure the installation of the sensors in the WAHE to avoid disconnections or interruption of data records when varying the positioning angle of the prototype. In addition, hydrostatic tests were carried out to verify the non-existence of infiltrations.

2.4 Description of experimental set-up

During the measurement period, inlet temperatures were monitored (Tin); temperatures of the sensors located in the horizontal section S1 which is located at the far left of the base of the Water Air Heat Exchanger (WAHE), S2 and S3 located in the central position of the tube, and S4 which is located at the right end of the tube, The sensors were placed in the submerged horizontal pipe, the air outlet temperatures (Tout) and the stream water temperature (\({T}_{\infty }\)) were also monitored. Measurements were recorded every 6 s, for 30 min, per configuration (each position tested). The experiments were carried out continuously and repeated under the same conditions.

Five heat exchanger positioning configurations were tested depending on the direction of water flow and the direction in which the flow of air entering the WAHE is induced. Figure 4 represents the directions tested in this study and the positions are indicated with different colors. Figure 5 (a) shows the parallel flow heat exchanger; (b) quasi-parallel oblique; (c) Counterflow; (d) oblique quasi-counterflow, and (e) crossflow.

Fig. 4
figure 4

WAHE positions tested

Full size image
Fig. 5
figure 5

(a) WAHE in flow parallel; (b) Quasi-parallel oblique; (c) Counterflow. (d) Quasi-counterflow oblique; and (e) Crossflow

Full size image

The elements attached to the prototype correspond to an air blower, seven thermocouples, and a data acquisition system. This experiment has been designed to guarantee measurements of the outlet temperature, effectiveness, and thermal response that this system can provide when the position varies concerning the water and airflow.

The experimentation allowed the characterization of the WAHE in operating conditions under water flowing through a natural channel, it also allows the monitoring of the temperature conditions to which the equipment is subjected during the tests under and above the water level.

In the experimental configurations, the water speed was assumed constant for all tests at 0.043 m/s, while the water temperature (\({T}_{\infty }\)) is from 27.45 to 30.12 °C according to each of the five experimental configurations.

2.5 Instruments used in experimentation

Ambient air was passed through the WAHE using a centrifugal blower (Coleman brand, speed: 2000 rpm, power: 110–120 V), the airspeed mean in the pipe is 4.30 m/s with standard deviation of ± 0.06 m/s.

Seven sensors (Pt-100 sensors, IST brand) were used to record air temperature variations in different sections along the pipe and the water (measurement uncertainty of ± 0.05 °C). To record the data for each experiment, it was necessary to connect the sensors to an acquisition system. (make-Keysight, Model-34972A). After the acquisition, the data were analyzed in RStudio. The speed of the water in the stream bed and the speed of the air entering the heat exchanger were determined with a flowmeter of the brand Flowatch – JDC Electronics. This instrument operates in a range of 0.1 to 18 m/s and an accuracy of ± 2% and is powered by a 3V direct current.

2.6 Selection of operating variables

Based on the specialized literature on EAHE and WAHE, it is inferred that the variables that have the greatest impact on the calculation of thermal effectiveness are the internal diameter of the pipe and the velocity of the air circulating through the pipe. The blower available can provide air speeds of a maximum 4.30 m/s, in a pipe 0.0171 m in diameter. These values give us Reynolds numbers of 4420, therefore, the fluid regime is turbulent. With the speed, there are friction factor values of 0.0401.

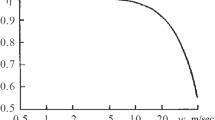
Figure 6 shows the behavior of the Reynolds number and the airspeed; their relationship is linear and direct for an air speed of 4.30 m/s. The relationship between the friction factor and the airspeed is inverse (Fig. 7) and for the operating speed of the air blower (4.30 m/s), we are in the linear region.

Fig. 6
figure 6

Reynolds number versus air speed

Full size image
Fig. 7
figure 7

Friction factor versus air speed

Full size image

Finally, the friction factor is a significant parameter for estimating the pressure drop, its relationship is direct and for the blower speed, the pressure drop is of the order 20.99 Pa (Fig. 8).

Fig. 8
figure 8

Pressure drops as a function of airspeed

Full size image

3 Results

In the experimental phase, the WAHE system immersed in water was operated maintaining the same airflow speed (4.30 m/s) inside the pipe. Recorded data measurements included the following parameters:

  • Inlet air temperature.

  • Air temperature in the WAHE pipe immersed in water for which the four sensors were placed 10 cm apart.

  • Outlet air temperature.

  • Water temperature.

The results obtained from this research are presented in two sections:

  1. a)

    In the first, the average temperatures recorded by the sensors located in the submerged pipe section and the sensor that recorded the water temperature are reported. The data analyzed correspond to the regions where the temperature stabilized in each data record.

  2. b)

    The second section has been dedicated to the criteria to determine the best position of the WAHE: the behavior of the air temperature along the heat exchanger in each tested position is presented.

The temperature data used for the evaluation of the heat exchanger correspond to when the system is in a stable state, a state that is obtained as time passes during the test. To determine whether the stable state has been achieved, statistical tests related to the slope of the graph of the temperature data vs. Time. The slope is calculated by intervals and their uncertainty, and with them, the confidence interval is determined. If we have the case that the interval contains values of zero slope, it will be assumed that we are in a steady-state region.

To determine the regions where the temperature stabilized, it was necessary to apply the statistical uncertainty test (explained at the beginning of this section) and the F-test (Fisher test) significance tests were also applied to contrast variances. The F-test was applied at a 5% significance level and the Student's t-test was applied to contrast the temperature means, which was applied at a 10% significance level. Statistical tests were used to determine the time intervals in which the temperature variable no longer presented significant changes in the means, which also allows for inferring a temperature stability criterion.

Figure 9 shows the behavior of the temperature recorded by sensors 1 to 4, when the prototype operated in Quasi-parallel oblique flow, from the beginning of the experimental test considering the start of the blower until the moment it was stopped out of operation. The region shaded in gray represents the interval in which the recorded temperature does not show significant differences in its means, while the regions that are not shaded are considered unstable in temperature, due to the significant differences in their means.

Fig. 9
figure 9

Stabilized WAHE temperatures in Quasi-parallel oblique

Full size image

The gray color presented in Figs. 9, 10, 11, 12, and 13 indicates the stable temperature region in each case, respectively.

Fig. 10
figure 10

Stabilized WAHE temperatures in Quasi-counterflow oblique

Full size image
Fig. 11
figure 11

Stabilized WAHE temperatures in counterflow

Full size image
Fig. 12
figure 12

Stabilized WAHE temperatures in cross flow

Full size image
Fig. 13
figure 13

Stabilized WAHE temperatures in parallel flow

Full size image

Figure 10 presents the stable temperature records for the Quasi-counterflow oblique position. Sensor 1 shows 74 stable records, in sensor 2 124 records were obtained, while in sensor 3 and sensor 4, 74 records were obtained, respectively. Each recording was made with a difference of 6 s in the five experimental cases.

Figure 11 shows the records for the counterflow position; in this case, there are 74 stable values for sensor 1 and 74 for sensor 2. While in sensors 3 and 4 the tests indicate stability in 99 records, respectively.

Figure 12 shows the temperatures recorded by the sensors when the WAHE was operated in cross-flow. 99 continuous stability values were recorded for the temperature of sensor 1, for sensor 2 there were 74 values, and for sensor 3, 99 were obtained. stable records and for sensor 4, 24 stable temperature records were identified.

Finally, the stable temperatures for the case of parallel flow are presented in Fig. 13. Continuing with the same pattern as in the other cases, since the start-up period, approximately 50 temperature records were identified that did not achieve stability.

Table 1 shows the mean temperatures recorded by the sensors at each tested position and the mean stream water temperature at the intervals where a steady state has been achieved.

Table 1 Air and water temperatures for each experimental case when a steady state has been achieved in all five sensors
Full size table

Figure 14 shows the variation of the air temperature along the pipe immersed in water for all experimental positions, it is observed that, under significantly similar operating conditions, the air temperature at the outlet of the WAHE is lower when the system is positioned in Quasi-parallel oblique, However, the Quasi-counterflow oblique and counterflow positions manifested exit temperatures close to that of Quasi-parallel oblique. It is also observed that the air temperature at the outlet of the system is higher for the crossflow position.

Fig. 14
figure 14

Air temperature along the pipe immersed in water

Full size image

From Eq. 20, the total thermal effectiveness of the five experimental cases was obtained. Figure 15 shows the results of ε considering the temperature parameters recorded in the stable state.

Fig. 15
figure 15

Total thermal effectiveness of each experimental setup for steady-state temperature measurements

Full size image

Figure 15 shows that in the Quasi-counterflow oblique (black line) and Quasi-parallel oblique (blue line) configurations, the thermal effectiveness is greater than 95%. The counterflow WAHE configuration reported effectiveness between a minimum of 92% and a maximum of 98%. While the crossflow configuration reported effectiveness between 86% (minimum) and 91% (maximum). Finally, the red line represents the thermal effectiveness of the parallel configuration, in this case, the minimum value was obtained at 83% and the maximum effectiveness was 88%. The total thermal effectiveness values range from 83 to 99% for the five WAHE configurations, these values have been achieved because the temperature of the water flow acts as a sink that constantly removes heat due to the convection process.

Figure 16 shows the average thermal effectiveness, which was obtained at each measurement point (location of the horizontal sensors in the submerged pipe).

Fig. 16
figure 16

Average thermal effectiveness in each sensor per experimental setup

Full size image

When evaluating the thermal aspects of Earth to Air Heat Exchangers, it is commonly found that the relationship between thermal effectiveness and the number of transfer units (NTU) fits a logarithmic form. Figure 17 plots the obtained NTU intervals for each configuration or position of the heat exchanger concerning the stream flow. The configurations with the lowest NTU value are Parallel and crossflow. Those with intermediate values are counterflow and Quasi-parallel oblique and the one in which the highest values of NTU are obtained is Quasi-counterflow oblique.

Fig. 17
figure 17

NTU ranges for each heat exchanger configuration

Full size image

The statistical parameters (maximum, mean, minimum, and standard deviation) of the thermal effectiveness and NTU of the five experimental cases are presented in Table 2.

Table 2 Statistical parameters of ε (%) and NTU for each experimental configuration
Full size table

4 Discussion

The device used in this work allowed us to determine the configuration and position of an WAHE exchanger concerning the water flow around the system geometry by significantly increasing the convective heat transfer coefficient on the heat exchange surface (Gallo et al. 2012) which provides the best thermal effectiveness.

Due to the small amount of published data on the influence of angle on the thermal effectiveness of oblique flows, it is not possible to compare our experimental results with similar published works. However, the thermal effectiveness could be calculated for the five configurations, considering that it is for the recorded data when the system has stabilized and, in this case, it corresponds to the readings of sensor 4. The thermal effectiveness obtained from the experimental data is ordered from smallest to largest:

  • Parallel/axial

  • Cross/transverse

  • Counterflow/axial

  • Quasi-parallel oblique

  • Quasi-counterflow oblique

The results obtained agree with those reported by Antonopoulos (1985), where it is established that the heat transfer in the oblique flow was greater than for axial and transverse flows. Furthermore, this same work considers that the transverse heat transfer is greater than the axial one.

From Fig. 16, the thermal effectiveness values change depending on the length (L) of the WAHE. For a short heat exchanger (< 7.8 cm) the best thermal effectiveness is given for the cases: (a) Quasi-counterflow oblique, (b) Quasi-parallel oblique, and (c) parallel; while the lowest effectiveness is given for: (d) crossflow, and (d) counterflow. If the heat exchanger has a length between 7.8 and 27.8 cm, an increasing effectiveness is observed in the case of Quasi-parallel oblique and a lower effectiveness for counterflow. Finally, for a length > 27.8 cm, the thermal effectiveness corresponds to what is described in the previous paragraph.

5 Conclusions

The experimental study has been carried out to investigate the thermal behavior and the effects of operating a scale prototype of an air–water heat exchanger in the presence of water impinging on the outside of the pipe. The analysis yielded the following conclusions:

  • The flow of water when it hits the horizontal section of the heat exchanger has proven to be a positive factor that increases the effectiveness of the system and reduces the temperature of the air at the outlet.

  • The thermal resistance method allows us to analyze heat transfer and link the Thermo-hydraulic behavior of the fluid (air) that circulates inside the system and the flow of water that affects the outside.

  • The results of this study have shown that the configurations tested in, Quasi-counterflow oblique and quasi-parallel oblique, are the options where lower air temperatures occur, concerning the parallel and Crossflow positions. Parallel is the alternative that could be determined as the last option since there are higher air temperatures at the exit of the heat exchanger.

  • The positions where the highest thermal effectiveness was obtained are Quasi-counterflow oblique, Quasi-parallel oblique, and counterflow.

  • In the parallel flow and Quasi-parallel oblique positions, the stable state was reached faster, compared to the other cases. Furthermore, when the WAHE is placed in a Quasi-parallel oblique, lower outlet air temperatures are obtained in less time. This position is the option that the authors consider as the best alternative for the operation of an WAHE in the presence of water flow.

  • If the WAHE analysis is carried out under conditions like those of this work, it would be expected to obtain outlet air temperatures closer to the thermal comfort temperature and consequently increase the thermal effectiveness of the system.

It is important that in future research measurements of temperature and water, velocity be made, these two parameters are of vital importance for the determination of thermal parameters such as the temperature of the air at the outlet, thermal effectiveness, the logarithmic average of temperature, temperature of surface of the tube immersed in water and the Reynolds number of the water flow, which directly influences the calculation of the Nusselt number and which in turn is required for the determination of the convection heat transfer coefficient. Furthermore, it is relevant that future works will analyze the effects of the variation in the speed of the air when it circulates through the heat exchanger because it can cause pressure drops and changes in the flow regime.