1 Introduction

The increase in the gas entry temperature improves the thermodynamic efficiency of the modern gas turbine engines with consequent reduction in their specific fuel consumption and, at the same time, performance increase. To achieve this goal, it is important to enhance the cooling of the turbine blades, in particular those of the first stages. Actually, turbine blades are cooled both externally, by means of film cooling on their outer surfaces, and internally, by means of forced convection. To accomplish this cooling, a small quantity of air, leaked out of the compressor, passes through straight channels inside the blade before being discharged outside so to provide film cooling as well. Some of these channels are connected by “U” (180°) turns which, acting in concert with blade rotation, are accountable for very complex turbulent flows, unavoidably coupled to unevenness in the convective heat transfer coefficient distribution. The knowledge of the connections existing between flow field and convective heat transfer coefficient could be a useful tool for the designers to find out technical solutions oriented to improve the internal blade cooling.

A variety of visualization and measurement techniques have been used to study both the flow field and the convective heat transfer that occur in static (not rotating) smooth channels with sharp “U” turns. Arts et al. (1992) and Iacovides et al. (1999) studied the thermo-fluid-dynamics of a two-pass channel by using laser Doppler anemometry (LDA) for the flow field and liquid crystals for the heat transfer. To investigate the heat transfer, liquid crystals have been also used by Lau et al. (1994) to analyze a four-pass channel and by Liou et al. (1998) to study the effects of the wall thickness of the divider between channels. Liou and Chen (1999) measured the convective heat transfer by means of thermocouples, and in order to associate it with the flow field, they investigated this latter one both qualitatively by “smoke visualization” and quantitatively by means of LDA. In a subsequent work, Liou et al. (2000) compared some fluid dynamic parameters, such as turbulent kinetic energy (TKE), mean kinetic energy (MKE) and normal-to-wall velocity component (w), to the Nusselt number profiles in the turn region and in the outlet duct with the aim to identify possible correlations. The heated thin foil technique coupled with infrared thermography (IRT) has been used by Astarita and Cardone (2000) to study the influence of the Reynolds number (Re) and of the channel aspect ratio (AR) on the convective heat transfer coefficient distributions. Son et al. (2002) carried out particle image velocimetry (PIV) tests to investigate the flow field at high Reynolds numbers in order to detect the physical correlations with the main features of the convective heat transfer coefficient maps. A numerical analysis has been performed by Su et al. (2004) to study the effects caused by Re, AR and buoyancy on both the heat transfer and flow field.

The effects of rotation on flow field and convective heat transfer in channels with a sharp “U” turn have been experimentally investigated in a large number of works. Cheah et al. (1996) performed LDA velocity field measurements, in a rotating U-duct of strong curvature, the axis of rotation being parallel to that of curvature. With the same technique, Iacovides et al. (1999) measured the turbulent flow field in a square-ended U-bend with the axis of rotation orthogonal to that of curvature and performed measurements of the local heat transfer coefficient with the aim to identify possible correlations. The naphthalene sublimation technique was used to perform high spatial resolution measurements of the convective heat transfer coefficient distributions in a two-pass channel with rectangular (Kukreja et al. 1998; Kim et al. 2007) and trapezoidal section (Lee et al. 2007; Schüler et al. 2009). IRT has been used by Cardone et al. (1998) to perform wall heat transfer measurements in a rotating two-pass square channel with a sharp “U” turn. A large number of thermocouples were used to study the influence of Reynolds and Rotation numbers (Liou and Chen 1999) and of the channel orientation with respect to the rotation axis (Al-Hadhrami and Han 2003) on the surface convective heat transfer.

A number of numerical analyses of the flow field evolution and of the convective heat transfer coefficient distribution in rotating channels with a sharp “U” turn have been also performed. The effects of channel rotation (Coriolis and centrifugal forces), turn and channel orientation with respect to axis of rotation on the flow field and convective heat transfer coefficient distributions were investigated by Al-Qahtani et al. (2002), while the influence of AR, Re and buoyancy was studied by Su et al. (2004). Murata and Mochizuki (2004) studied how the secondary flow field, modified by rotation, influences the convective heat transfer. Iacovides et al. (1996) and Iacovides and Raisee (1999) studied the mean and turbulent flow in rotating U-ducts of strong curvature, with the axis of rotation parallel to that of curvature. Kim et al. (2007) performed a numerical simulation by using the commercial software FLUENT 6.1 to get detailed information about the main and secondary flow fields.

In this paper, the convective heat transfer coefficient distributions and the main and secondary flow fields in a two-pass square channel, both in the static and in the rotating case, are experimentally studied through detailed measurements performed by using the infrared thermography and the PIV techniques, respectively. A description of the experimental apparatus and the experimental procedure used to perform the two kinds of measurements is provided in Sects. 2 and 3.

A first objective of the present experimental study is to provide a deeper knowledge of the rotational effects on the internal flow field responsible for the convective heat transfer coefficient distribution. To this aim, in Sect. 4, a detailed comparison between the distributions of the turbulent kinetic energy (TKE), mean kinetic energy (MKE) and normal-to-wall velocity component w (all measured close to the channel wall) and of the normalized Nusselt number (Nu/Nu*) maps has been accomplished, for both the static and the rotating case.

A further attempt of the present work is to try to identify the direct influence of the quantities TKE, MKE and w on the convective heat transfer coefficient distributions. Therefore, in Sect. 5, a parametric study is developed to find an empirical correlation whose parameters provide the relative importance of the effects produced by these quantities on the normalized Nusselt number Nu/Nu* distributions. In the parametric study, MKE has been ignored because, as it will be seen in Sect. 4, its distributions are scarcely correlated with those of Nu/Nu*. In Sect. 6, the main results are summarized.

The authors wish to conclude this introductory section by advising the reader that the experimental data relative to the convective heat transfer coefficient measurements have been already differently presented in a previous work (Gallo et al. 2007) that had the objective of providing a detailed description of the convective heat transfer coefficient distributions for both the static and rotating cases. In the present work, these experimental data are used to realize the maps of Nu/Nu* able to better describe the correlations between the convective heat transfer coefficient distributions and the flow field.

2 Experimental apparatus

The experimental apparatus is shown in Fig. 1. A Plexiglas two-pass channel with a sharp “U” turn is mounted on a revolving platform that is connected to an electric motor by a transmission belt. The electric motor is fed by an inverter, so that the platform rotational speed can be varied in a continuous way in the range 0–60 rpm.

Fig. 1
figure 1

Sketch of the experimental apparatus

Full size image

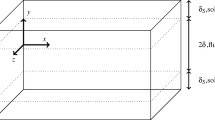
The channel, sketched in Fig. 2, has a square cross-section of 60 mm on a side (D) and the central partition wall, which divides the two adjacent ducts, is 12 mm thick. In Fig. 2, it is also highlighted the test region (in green) that is formed by the “U” turn and by the portions of the inlet and outlet ducts, both having a length of 120 mm (2D). Since the length of the inlet duct ahead of the measurement zone is 1,080 mm (18D), the flow can be considered as almost hydro-dynamically fully developed at the entry section of the test region.

Fig. 2
figure 2

Test channel and coordinate system

Full size image

Water, which is used as a working fluid, is extracted from a tank by a pump (Fig. 1) and then passes through an orifice meter that monitors the flow rate, a rotating hydraulic coupling and finally, after flowing in the test channel, is discharged back in the tank. The water mass flow rate can be regulated in a continuous way with a by-pass circuit, and the water temperature in the tank is kept constant by means of a heat exchanger.

The necessity of scaling-up the test geometry derives not only from the need to have a higher data spatial resolution but also to neglect tangential conduction effects in the IR measurements. Besides, the authors have decided to increase significantly the convective heat transfer coefficient h at the heat exchanging surface by using water as working fluid as well as to use a much larger channel in order to get a rotational speed reduction and, therefore, negligible heat losses toward the ambient. In this way, they were able to obtain a quite good spatial resolution and minor tangential conduction in the acquired measurements.

In order to synchronize the rotating channel with the PIV acquisition system and the thermographic system, a digital magnetic pickup sensor is used and the signal provided by this detector is also used to continuously monitor the value of the angular speed.

To perform measurements of the convective heat transfer coefficient by using the heated thin foil technique (described in detail in the next section), one of the channel walls of the test region is made of a printed circuit board. The printed circuit is designed so as to achieve a constant heat flux over the viewed surface (except beneath the partition wall) by Joule effect. The circuit tracks, arranged in a Greek fret mode, are 5 μm thick and 2.9 mm wide and placed at a 3-mm pitch. Very close tolerances in the construction of the tracks allow having a very uniform heat flux over the heated surface. The overall thickness of the board is 0.5 mm. The length of the printed circuit board (600 mm) ensures in the inlet duct before the turn an almost thermally fully developed flow.

The circuit is connected to a stabilized DC power supply, via a mercury rotating contact situated on the rotational axis, and the power input is monitored by precisely measuring voltage drop and current across it. The external surface of the printed circuit board, which is viewed by the infrared camera and where the heating tracks are located, is coated with a thin layer of thermally black paint, which has a directional emissivity coefficient equal to 0.95 in the wavelength of interest.

3 Experimental procedures and techniques

The most relevant dimensionless numbers are the Reynolds number Re and the Rotation number Ro (which is the inverse of the Rossby number), defined as:

$$ Re = \frac{\rho UD}{\mu } $$
(1)
$$ Ro = \frac{\omega D}{U} $$
(2)

where D is the channel hydraulic diameter, U is the fluid mean velocity, ω is the channel rotational speed, and ρ and μ are the fluid mass density and dynamic viscosity coefficient, respectively. The Reynolds number governs the static behavior of the flow field in the channel, while Ro is a dimensionless measure of the Coriolis effects. The maximum error in the evaluation of the Reynolds and Rotation numbers is smaller than ±2% (Kline and McClintok 1953). Experimental tests have been performed, for the static case at Re = 20,000, while for the rotating case at Re = 20,000 and Ro = 0.3.

3.1 Heat transfer measurements

In order to evaluate the convective heat transfer coefficient h, the heated thin foil heat flux sensor (Astarita et al. 2006) coupled with the scanning of the surface temperature by an infrared camera has been used. In particular, for each pixel of the digitized thermal image, h is calculated by means of

$$ h = \frac{{q_{\text{w}} - q_{\text{r}} }}{{T_{\text{w}} - T_{\text{b}} }} $$
(3)

where q w is the Joule heat flux, q r is the radiative flux to ambient and channel, T w and T b are the inside wall and local bulk temperature, respectively. The local bulk temperature T b is evaluated by measuring the stagnation temperature of the flow at the channel entrance and by making a one-dimensional energy balance along the channel, that is, along the channel main axis. The radiative thermal losses q r are computed from the measured temperature of the external wall T e and losses due to tangential conduction and to convection toward the ambient are not considered, because they are evaluated to be negligible.

Since the pertinent Biot number (see Eq. 4) is not significantly smaller than 1, the heated (from the ambient side) wall may not be considered isothermal across its thickness (see Fig. 3).

Fig. 3
figure 3

Temperature profile nearby the heated wall

Full size image
$$ Bi = h \cdot t/\lambda $$
(4)

In order to evaluate the value of T w, a steady-state energy balance is performed by means of

$$ h \cdot \left( {T_{\text{w}} - T_{\text{b}} } \right) = \frac{\lambda }{t} \cdot \left( {T_{\text{e}} - T_{\text{w}} } \right) $$
(5)

where λ and t are the thermal conductivity and the thickness of the printed circuit support, respectively, and the copper tracks are considered isothermal across their thickness. From Eqs. 3 and 5, it is possible to evaluate h and T w.

Experimental results are expressed in terms of the local surface distributions of the Nusselt number:

$$ Nu = \frac{h \cdot D}{k} $$
(6)

which is normalized by means of the Dittus and Bölter correlation (Dittus and Bölter 1930):

$$ Nu^{*} = 0.023 \cdot \text{Re}^{0.8} \cdot { \Pr }^{0.4} $$
(7)

where k and Pr are the fluid thermal conductivity coefficient and Prandtl number, respectively.

From an uncertainty analysis, based on the method of Kline and McClintok (1953), it has been evaluated that, for the static case, the error in the evaluation of the normalized Nusselt number in the outlet duct is smaller than ±10%, while in the inlet duct the error results to be less than ±3.5%. For the rotating case, the maximum error, at the leading and trailing sides of the outlet duct, results to be smaller than ±15%, while in the inlet duct, for both surfaces (leading and trailing, see later), the maximum error results to be less than ±5%.

3.2 PIV measurements

In order to identify the connections between the convective heat transfer coefficient distributions and the flow field, in the turn region and in the outlet duct for both the static and rotating case, PIV measurements have been performed to investigate both the main (in planes parallel to the coordinate plane xy) and the secondary (in planes parallel to the coordinate planes xz and yz) flow fields.

The light sheet, which is generated by a double-cavity Nd:YAG LASER, has a pulse duration of 6 ns, a wavelength of 532 nm and a maximum energy per pulse of about 200 mJ. Seeding is made up of fluorescent polymer particles with a diameter ranging from 1 to 20 μm and a density of 1.19 g/cm3. The relaxation time (Raffel et al. 2007) for the used working fluid, that is water at about 20°C, has a maximum value of 6.7 μs. Moreover, the particles scatter light at different wavelengths, so that it is possible to drastically reduce the spurious reflections with the use of an optical filter. To display, acquire and record digital images, the following items are used: a video camera with a CCD sensor (1,008 × 1,018 pixels, 256 gray levels); a computer equipped with an acquisition board; and a laser-acquisition system synchronizer.

The acquired images are processed by a high-accuracy PIV iterative algorithm based on an image deformation method; the detailed description of the steps of the used PIV algorithm is reported in the work by Astarita and Cardone (2005). It has been verified through a statistical investigation that a sample of 1,000 images assures the statistical convergence of the three mean velocity components and of their fluctuations.

For the rotating case, the distributions of the mean velocity components have been obtained adopting two different procedures for the yz- and xz-planes, whose detailed description is provided in a previous work of the same authors (Gallo and Astarita 2010).

In the turn region, the three groups of mean velocity components distributions, associated with the three coordinate planes (xy, yz and zx) and previously filtered by means of a Wiener filter, have been interpolated on a common 3D grid. The goal is to perform a 3D reconstruction of mean flow and vortical fields, whose visualization should clarify the role exerted by some flow structures on the convective heat transfer coefficients. The vortical structures are visualized by using the iso-Ω surfaces, Ω representing the mean vorticity module defined by

$$ \Upomega = \frac{{\left( {\sqrt {\left( {\Upomega_{x}^{2} + \Upomega_{y}^{2} + \Upomega_{z}^{2} } \right)} } \right) \cdot D}}{U} $$
(8)

The vorticity components Ω x , Ω y and Ω z are evaluated with the formulae based on Stokes’ theorem (Son and Kihm 2001; Foucaut and Stanislas 2002).

3.3 Comparison procedure

In order to compare the results obtained by the heat transfer measurements with those relative to the flow field ones, it is necessary to choose the fluid dynamic quantities whose behavior, close to the wall, can influence the convective heat transfer coefficient. In agreement with the works of Liou et al. (2000) and Son et al. (2002), it has been decided to associate the convective heat transfer coefficient distributions with the following three characteristic flow quantities, measured as close as possible to the wall, namely mean kinetic energy (MKE), normal-to-wall velocity component w and turbulent kinetic energy TKE.

$$ {\text{MKE}} = \frac{{u^{2} + v^{2} }}{{2U^{2} }} $$
(9)
$$ {\text{TKE}} = \frac{{\left( {\overline{{u^{\prime}u^{\prime}}} + \overline{{v^{\prime}v^{\prime}}} + \overline{{w^{\prime}w^{\prime}}} } \right)}}{{2U^{2} }} \times 100 $$
(10)

where u and v are the mean velocity components parallel to the heated wall and u′, v′ and w′ are the fluctuations of the Cartesian velocity components.

The MKE magnitude may indicate the effect of the near-wall mean planar kinetic energy on the Nusselt number distribution, while the normal-to-wall velocity component may give a measure of the effects of the secondary flows. Indeed, the velocity component w directed toward the wall points out the presence of an impinging flow. This could cause boundary layer thinning, or break-up, with consequent development of stronger temperature gradients near the wall, responsible for convective heat transfer enhancement. Finally, high TKE values correspond to an increase in the turbulent diffusion and, therefore, in the heat transfer.

For the static case, the MKE distributions have been evaluated with Eq. 9 by using the velocity components distributions (u, v) measured at z/D = 0.03, that is the investigated plane closest to the heated side wall. For the rotating case, the investigated planes, closest to the leading and trailing walls, are placed at z/D = 0.08 and z/D = 0.92, respectively.

Figure 4 reports the yz- and xz-planes investigated in the turn region and in the outlet duct for the static and the rotating cases. Since the evaluation of the TKE, defined by Eq. 10, requires the knowledge of the three velocity components fluctuations, it is needed to reconstruct their distribution in the second half of the turn and in the outlet duct, for the static case, and in the whole turn region and in the outlet duct, for the rotating case. Having the PIV images (acquired in the different investigated planes of the turn region and of the outlet duct) a different spatial resolution, it has been necessary to perform a preliminary interpolation in order to match up the grids of the main (xy-planes) and secondary (yz- and xz-planes) flow fields. For the static case, the fluctuation values, measured in the main and secondary flow fields at z/D = 0.03, have been interpolated on a square common grid in the second half of the turn and on a rectangular common grid in the outlet duct. For the rotating case, at z/D = 0.08 and z/D = 0.92, they have been interpolated on two square common grids in the two halves of the turn and on a rectangular common grid in the outlet duct. On these grids, the TKE distributions have been obtained by averaging the fluctuations of the velocity components common to two of the three coordinate planes (xy, yz and zx).

Fig. 4
figure 4

yz- and zx-planes used to reconstruct the flow fields and the TKE distributions close to the heated wall: a static case, b rotating case

Full size image

At last, the influence of normal-to-wall velocity component on the surface heat transfer is described by showing how the secondary flow fields, measured in the turn region and in the outlet duct, behave close to the heated side wall (Ro = 0) and to the leading and trailing sides (Ro = 0.3).

4 Results

4.1 Static case

The normalized Nusselt number Nu/Nu* and the mean kinetic energy distributions for the static case (Re = 20,000) are reported in Figs. 5 and 6, respectively. The surface map of Nu/Nu* exhibits a weak gradient at the inlet of the turn (G-1, Fig. 5) which could be associated with the MKE (Fig. 6) gradient present in the same zone. This last gradient is due to the low pressure zone located at the tip of the partition wall generated by the main flow curvature.

Fig. 5
figure 5

Normalized Nusselt number distribution for the static case (Re = 20,000)

Full size image
Fig. 6
figure 6

Mean kinetic energy distribution with superimposed streamlines, static case: z/D = 0.03, Re = 20,000

Full size image

The flow from the inlet duct in the first half of the turn impinges on the front wall generating two counter-rotating vortices close to the two external corners (y/D = 0.5, Fig. 7), also highlighted by the counter-current flow present in the first half of the turn (see streamlines, Fig. 6). These vortices generate an impinging flow on the two side walls accountable for the high convective heat transfer zone positioned near the front wall of the first half of the turn (H-1, Fig. 5). In the second half of the turn, along the front wall it is possible to see a decrease in the convective heat transfer coefficient (L-2, Fig. 5) that was already observed by Astarita et al. (2006). Indeed, the two counter-rotating vortices, visualized in the first half of the turn, tend to promote the birth of another couple of counter-rotating vortices, known in literature as Dean vortices (y/D = 1.2 and 1.37, Fig. 7), which develop owing to the pressure gradient associated with the centrifugal forces present in the turn. These vortices, detected by two iso-vorticity surfaces positioned close to the side walls (e.g., see surfaces (II) in Fig. 5b of Gallo and Astarita 2010), are characterized by a strong curvature. Indeed, they move away from the front wall toward the external wall of the outlet duct.

Fig. 7
figure 7

Secondary flow fields measured in the turn (static case, Re = 20,000): a distributions of the mean velocity component w/U with the streamlines superimposed, b sketch of the test region with the investigated xz-planes

Full size image

The flow coming from the first half of the turn bumps against the external wall of the second half generating a couple of counter-rotating vortices positioned in the corners between the two side walls and the external one (Fig. 8). The impinging flows associated with these two vortices are responsible for the high heat transfer zone present along the external wall of the second part of the turn (H-2, Fig. 5). The Dean vortices persist in the outlet duct (Fig. 9) and, in the first hydraulic diameter by the two external corners, generate two intense normal flows directed toward the two side walls, which determine the local increase in Nu/Nu* along the external wall of the outlet duct (H-3, Fig. 5). It ought to be observed that the region with high values of MKE measured in the outlet duct (Fig. 6) is not well correlated with Nu/Nu* because high values of MKE correspond to either high or low values of heat transfer (H-3 and L-3, Fig. 5).

Fig. 8
figure 8

Secondary flow fields measured in the second half of the turn (static case, Re = 20,000): a distributions of the mean velocity component w/U with the streamlines superimposed, b sketch of the test region with the investigated yz-planes

Full size image
Fig. 9
figure 9

Secondary flow fields measured in the outlet duct (static case, Re = 20,000): a distributions of the mean velocity component w/U with the streamlines superimposed (1 ≤ x/D ≤ 2), b sketch of the test region with the investigated yz-planes

Full size image

By observing the TKE distribution reconstructed in the outlet duct (Fig. 10), it is possible to notice that its high values, measured both on the external boundary of the large recirculation bubble (present in the outlet duct close to the partition wall, see streamlines of Fig. 6) and on downstream of the reattachment zone, can be correlated with the high values of the normalized Nusselt number measured in the same regions (H-4, Fig. 5).

Fig. 10
figure 10

Turbulent kinetic energy distribution in the outlet duct, static case: z/D = 0.03, Re = 20,000

Full size image

Low convective heat transfer should be identified in proximity of the flow recirculation zones that are present near the turn two external angles and downstream of the second-turn internal angle close to the partition wall. Accordingly, the map of Nu/Nu* (Fig. 5) shows two low heat transfer zones: one near the recirculation zone located in the first-turn external angle (L-1, Fig. 5) and the other in the outlet duct near the partition wall (L-4, Fig. 5). The comparatively small dimensions and the not very low values of Nu/Nu* of the latter region can be ascribed to the characteristics of the large recirculation bubble that is present in the outlet duct at the partition wall. In fact, as it can be observed in Fig. 9, this bubble is formed by two vortical flows that, going upstream with helicoidal trajectories, limit the effects of the flow entrapment (Animation 1 of Gallo and Astarita 2010). The absence of a well-defined low heat transfer zone close to the second external angle could be explained by the small dimensions of this recirculation bubble. Finally, it is important to stress the presence, in the outlet duct central part, of an elongated zone with local relatively low values of Nu/Nu* (L-3, Fig. 5) which can be associated with the flow separation from the heated wall. Indeed, near the central part of the two side walls (Fig. 9), the normal-to-wall velocity component is directed inwards.

4.2 Rotating case

4.2.1 Leading wall

The normalized Nusselt number Nu/Nu* and the mean kinetic energy distributions for the leading wall (Re = 20,000 and Ro = 0.3) are reported in Figs. 11 and 12, respectively. In the turn region, from the map of Nu/Nu* (Fig. 11), it is possible to notice two very high heat transfer zones located at the inlet of the turn and along the front wall (respectively, H-1 and H-2, Fig. 11).

Fig. 11
figure 11

Normalized Nusselt number distribution for the rotating case: leading wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image
Fig. 12
figure 12

Mean kinetic energy distribution with the streamlines superimposed, rotating case: leading wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image

To explain the origin of these two high heat transfer zones, it is necessary to understand how the rotation modifies the flow in the inlet duct and in the turn region. In the inlet duct, the Coriolis force promotes the formation of secondary flows constituted by two counter-rotating cells (Fig. 13). With respect to the non-rotating case, their presence reduces the convective heat transfer at the leading wall and, as it will be seen in Sect. 4.2.2, enhances it at the trailing wall. The convection, associated with these secondary flows, shifts the axial velocity peak location toward the trailing wall (Fig. 13), which is also known in literature as unstable wall or pressure side (Qin and Pletcher 2006). Therefore in the first half of the turn, the flow from the inlet duct bumps against the front wall near the trailing wall, then moves, along the front wall, toward the leading wall and finally comes back toward the turn inlet by forming a strong vortex that extends in the whole turn region (Fig. 14).

Fig. 13
figure 13

Flow field in the inlet duct, rotating case: sketch of the secondary flow field and of the axial velocity profile

Full size image
Fig. 14
figure 14

3D reconstruction of the vorticity distribution in the turn region (rotating case, Re = 20,000 and Ro = 0.3): a iso-Ω surfaces (Ω = 4.7) and streamlines, b sketch of the test region

Full size image

The high convective heat transfer zone at the inlet of the turn (H-1, Fig. 11) is located in a place characterized by the collision between the flow from the inlet duct and the counter-current flow, which is present in the first half of the turn (see streamlines, Fig. 12), and promotes an increase in the TKE (Fig. 15).

Fig. 15
figure 15

Turbulent kinetic energy distribution in the first half of the turn, rotating case: leading wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image

The high Nu/Nu* zone, located along the front wall of the turn region (H-2, Fig. 11), is due to the strong vortex revealed in the turn region which produces a strong impinging flow in the corner between the front and leading walls (Fig. 14). This high heat transfer zone has an extension larger than the one already found for the static case (H-1, Fig. 5) because the centrifugal force, pushing this strong vortex against the front wall, causes a delay of its curvature toward the turn region exit section. As in the turn region the Coriolis force becomes equal to zero, the large vortex (positioned in the turn first half nearby the leading wall) bends toward the trailing wall in the second half (Fig. 14) and the vortex separation from the leading wall produces a heat transfer reduction there (L-1, Fig. 11).

From the second external angle of the turn region, another high heat transfer zone extends along the external wall for about three hydraulic diameters (H-3 and H-4, Fig. 11). In the interval 0 < x/D < 1 (H-3, Fig. 11), the lower part of this high heat transfer zone can be associated with the high level of TKE (Fig. 16), while the higher one with the presence of an impinging flow. In fact, similar to the same region of the static case, the flow coming from the first half of the turn bumps against the external wall. In this case, on account of the channel rotation, the bifurcation zone is shifted toward the trailing wall and this produces two asymmetric counter-rotating vortices positioned nearby the corners formed by the external wall with the leading and trailing walls (Fig. 17). The remaining part of this high heat transfer zone (H-4, Fig. 11) may be ascribed to the presence of impinging flows as shown by the secondary flow fields measured in several sections of the outlet duct (Fig. 18).

Fig. 16
figure 16

Turbulent kinetic energy distribution in the second half of the turn, rotating case: leading wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image
Fig. 17
figure 17

Secondary flow fields measured in the second half of the turn (rotating case, Re = 20,000 and Ro = 0.3): a distributions of the mean velocity component w/U with the streamlines superimposed, b sketch of the test region with the investigated yz-planes

Full size image
Fig. 18
figure 18

Secondary flow fields measured in the outlet duct (rotating case, Re = 20,000 and Ro = 0.3): a distributions of the mean velocity component w/U with the streamlines superimposed (1 ≤ x/D ≤ 1.67), c distributions of the mean velocity component w/U with the streamlines superimposed (1.83 ≤ x/D ≤ 2.5), b and d sketch of the test region with the investigated yz-planes

Full size image

In the outlet duct, the streamlines of Fig. 12 point out the presence of a recirculation bubble, smaller than the one relative to the static case, which is not surrounded by high values of Nu/Nu* (L-2, Fig. 11). This different behavior can be related to the asymmetric configuration of the recirculation bubble induced by the rotation. Indeed, in the static case, the large recirculation bubble downstream of the turn region is characterized by a reverse flow formed by two counter-rotating vortices positioned near the two inner corners (Fig. 9a). The rotation of the channel induces a strong increase in the size of the vortex positioned near the corner between the trailing and the partition walls at expense of the other one (Fig. 18).Footnote 1 The extinction of this last vortex is responsible for the reduction in the TKE values (Fig. 19) and then for the heat transfer decrease in the region surrounding the small recirculation bubble. The heat transfer increase, measured near the partition wall downstream of the recirculation bubble (H-5, Fig. 11), can be only associated with the flow reattachment (see streamlines of Fig. 12). This is also highlighted by the secondary flow fields measured in the outlet duct (1.5 < x/D < 2.5, Fig. 18), which, most probably, generates a bifurcation flow on the partition wall and the consequent formation of a small vortex in the low corner of the leading wall. Owing to its small size, this vortex has not been detected by the secondary flow fields measured in this zone. At x/D = 2 (Fig. 18c), it is possible to notice a zone with high positive values of the normal-to-wall velocity component located close to the partition wall. Along the main flow direction, this region increases its intensity and extends toward the leading wall by sucking the fluid which flows there. This phenomenon could promote a flow separation related to the local low heat transfer zone already noticed in the outlet duct (L-3, Fig. 11).

Fig. 19
figure 19

Turbulent kinetic energy distribution in the outlet duct, rotating case: leading wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image

4.2.2 Trailing wall

The normalized Nusselt number Nu/Nu* and the mean kinetic energy distributions for the trailing wall (Re = 20,000 and Ro = 0.3) are reported in Figs. 20 and 21, respectively. Similar to the cases discussed before, the comparison between the two distributions shows that MKE and Nu/Nu* exhibit a quite poor spatial correlation.

Fig. 20
figure 20

Normalized Nusselt number distribution for the rotating case: trailing wall (z/D = 0.08), Re = 20,000 and Ro = 0.3

Full size image
Fig. 21
figure 21

Mean kinetic energy distribution with the streamlines superimposed, rotating case: trailing wall (z/D = 0.92), Re = 20,000 and Ro = 0.3

Full size image

In the inlet duct (Fig. 20), the measured values of the convective heat transfer coefficient are higher than those for the static case. As already said in Sect. 4.2.1, this is a consequence of the secondary flow field (Fig. 13) generated by the Coriolis force.

In the turn region, it is possible to see that the iso-Nusselt curves tend to advance into the first half of the turn and to insinuate themselves in the second half (L-1, Fig. 18). This can be related to the features of the main flow field exhibited in this region. In fact, as can be seen in Fig. 21, the streamlines also tend to advance in the turn first half, bending only nearby the front wall.

In the second half of the turn, a high convective heat transfer zone is noticed close to the second external angle (H-1, Fig. 20). This zone may be associated with the presence of the impinging flow caused by the vortex located in the corner formed by the trailing and external walls (Fig. 17).

As mentioned in the previous Sect. 4.2.1, in the turn region the secondary flow field is substantially affected by a strong vortex (Fig. 14). Since the Coriolis force becomes equal to zero there, the vortex bends toward the trailing wall generating, immediately after the exit of the turn, a strong impinging flow. As shown by the secondary flow fields measured in the outlet duct (1 < x/D < 2, Fig. 18a, c), the impinging flow on the trailing wall has an extension of about one hydraulic diameter in the main flow direction. This can be considered as the most important cause of the very high heat transfer zone observed in the same region of the outlet duct (H-2, Fig. 20). At last, the high heat transfer zone, placed near to the partition wall of the outlet duct at about x/D = 3 (H-3, Fig. 20), seems to be in agreement with the secondary flow field measured in this region which, being characterized by only one vortical structure, promotes an impinging flow nearby the corner between the partition and trailing walls (Fig. 18c).

5 Parametric analysis

From the previous discussion, it appears that there is not a strong correlation between the Nu/Nu* and the MKE distributions. This behavior can be accounted for the relatively large distance between the wall and the MKE measurement plane. This does not permit to consider MKE as a parameter strictly associated with the real wall velocity gradient which may be related to the convective heat transfer coefficient. On the other hand, the impinging flows and the TKE distributions often show a good correlation with the Nu/Nu* maps, and some high heat transfer regions seem to be generated by the combination of their effects. Therefore, the Nu/Nu* maps and the distributions of TKE and w (reconstructed close to the channel walls) are parametrically studied. The aim is to devise an empirical correlation between the TKE as well as the normal-to-wall velocity component and the local distributions of Nu/Nu*. It ought to be observed that the effects of the normal-to-wall velocity directed toward the wall (w +) and those of the one directed toward the core flow (w −) have been split. Indeed, the normal-to-wall velocity directed toward the wall w +, promoting a thinning and/or break-up of the boundary layer, should enhance heat transfer, while the normal-to-wall velocity component directed toward the core flow w −, being sign of a flow separation, should cause a Nu/Nu* reduction.

On the grids, relative to both the static and the rotating case and defined in Sect. 4 (Fig. 4), it is possible to evaluate TKE and w (by averaging the fluctuations u′, v′ and w′ that are in common to two of the three coordinate planes and the mean velocity component w, respectively) as well as to have the Nu/Nu* values experimentally measured at the wall. For both the static and rotating case, the quantities TKE, w + and w −, evaluated in each zone, have been normalized with the corresponding maximum value present in the same region which, in the following, will be indicated with the subscript n.

The existence of a linear relation that binds Nu/Nu*, TKEn, w − n and w + n is assumed, which is characterized by the following equation:

$$ \frac{Nu}{{Nu^{*} }} = K + a \cdot {\text{TKE}}_{\text{n}} + b \cdot w_{n}^{ + } - c \cdot w_{n}^{ - } $$
(11)

The parameters a, b and c of Eq. 11 represent the relative importance of the fluid dynamic quantities which, for the considered flow field, contribute to the convective heat transfer coefficient distribution. The experimental data available on the experimental grids have been used to evaluate the set of parameters (a, b and c) that allow minimizing the sum of the square deviations defined by the following equation:

$$ \Updelta = \sum\limits_{i = 1}^{N} {\left( {\left( {{{Nu} \mathord{\left/ {\vphantom {{Nu} {Nu^{*} }}} \right. \kern-\nulldelimiterspace} {Nu^{*} }}} \right)_{\text{ex}} - \left( {{{Nu} \mathord{\left/ {\vphantom {{Nu} {Nu^{*} }}} \right. \kern-\nulldelimiterspace} {Nu^{*} }}} \right)_{\text{th}} } \right)}^{2} $$
(12)

where N is the total number of grids points. Subscripts ex and th refer, respectively, to Nu/Nu* values either experimentally measured or evaluated with Eq. 11. By performing the above-described minimization procedure, it has been possible to find the following correlation:

$$ \frac{Nu}{{Nu^{*} }} = 2.15 + 0.67 \cdot {\text{TKE}}_{\text{n}} + 1.15 \cdot w_{n}^{ + } - 0.14 \cdot w_{n}^{ - } $$
(13)

The constant K = 2.15 can be considered as a constant value of Nu/Nu* measured on the experimental grids both for the static and for the rotating case, while the high and low heat transfer zones identified in the investigated walls are given by the three matrices (surface distributions) of TKEn, w + n and w − n , affected by different weights represented by the three constants (a = 0.67, b = 1.15 and c = −0.14). Since the parameter b (related to the impinging flows directed toward the wall) has the highest value, it is possible to assert that the w + n is the fluid dynamic quantity, which plays the most important role in the convective heat transfer increase. In particular, the constant of w + n is almost twice that found for TKEn. The reductions in the convective heat transfer coefficient on the investigated surfaces could be ascribed to flow separation that is detected by the normal-to-wall velocity component directed toward the flow core. Indeed, the small negative constant relative to the w − n distribution shows, in terms of absolute value, a much lower influence on Nu/Nu* than that relative to the other two distributions.

In order to check the capability of the proposed empirical correlation to identify the main features of the normalized Nusselt number experimentally measured distributions, in the following, the latter ones are compared with the normalized Nusselt number distributions theoretically predicted by Eq. 13 in the outlet duct (Fig. 22). Before making a comparison with the experimentally measured corresponding distributions (Figs. 5, 11, 20), it ought to be pointed out that the grids (Fig. 4) used to reconstruct the predicted Nusselt number maps do not fill the whole surface measurement domain. For this reason, it has not been possible to calculate the Nusselt number very close to the external and partition walls of the outlet duct.

Fig. 22
figure 22

Normalized Nusselt number distributions evaluated with the Eq. 13 in the outlet duct: a static case (Re = 20,000), b leading wall (rotating case, Re = 20,000 and Ro = 0.3), c trailing wall (rotating case, Re = 20,000 and Ro = 0.3)

Full size image

For the static case, the map reported in Fig. 22a generally shows a good agreement with the corresponding experimental distributions of Fig. 5. However, the Nusselt numbers evaluated in the low heat transfer zones (L-3 and L-4, Fig. 22a) and in the high heat transfer zone that extends along the external wall (H-3, Fig. 22a) are higher than those experimentally measured (L-3, L-4 and H-3, Fig. 5), while the high heat transfer zone H-4 (Fig. 22a), unlike the corresponding zone of Fig. 5, exhibits its local maximum toward the tip of the partition wall. For the rotating case, a good agreement with the corresponding experimental distributions is evident as well. Indeed, on the leading wall (Fig. 22b), the proposed correlation (Eq. 13) seems to be capable to detect the high convective heat transfer zone that extends along the external wall (H-4, Figs. 11, 22b) and the low convective heat transfer zone located in the central part of the outlet duct (L-3, Figs. 11, 22b) but it is able to evidence only a slight increase in the convective heat transfer on the partition wall of the outlet duct (H-5, Figs. 11, 22b). The Nusselt number predicted in the high and low heat transfer zones (H-4 and L-3 Fig. 22b) is respectively lower and higher than those experimentally measured (H-4 and L-3 Fig. 11). At last, the predicted Nusselt number distribution relative to the trailing wall (Fig. 22c) shows the presence of two high heat transfer zones located respectively on the center (H-2, Fig. 22c) and downstream near the partition wall (H-3, Fig. 22c) of the outlet duct. The first zone (H-2, Fig. 22c) is smaller and less intense than the one measured (H-2, Fig. 20), while the second zone (H-3, Fig. 22c) seems to be more intense and larger than the experimental one (H-3, Fig. 20).

From the comparisons made, it comes out that the proposed empirical correlation is sufficiently able to catch zones with a low and high convective heat transfer but some limitations appear evident in quantitative terms. This could be also associated with the fact that, in the present work, it has not been possible to take into account in the parametric analysis the MKE effects on the convective heat transfer, because of the intrinsic limitations already pointed out.

6 Conclusions

Convective heat transfer coefficient distributions and flow fields measurements have been performed and compared by using the IRT and PIV techniques. Their comparison allowed to identify several connections between the Nu/Nu* maps and the two fluid dynamics quantities TKE and w.

For the static case, three high heat transfer zones are identified: the first one on the front wall of the turn, the second one immediately after the second external angle and the third one located one diameter after the second internal angle, nearby the partition wall. The first zone is caused by the presence of counter-rotating vortices in the corners formed by the side and front walls of the turn, while another couple of counter-rotating vortices, positioned along the corners formed by the side and external walls of the turn second half and of the outlet duct, is responsible for the second high heat transfer zone. The third high heat transfer zone is due to both the high values of TKE measured in this region and the characteristics exhibited by the large recirculation bubble, present immediately after the second internal angle, close to the outlet duct partition wall. This bubble, being formed by two vortical flows, avoids the flow entrapment and the consequent reduction in the convective heat transfer coefficient.

In the rotating case, it has been observed that, in the turn region, the flow field is affected by a strong vortex which, promoting an impinging flow in the corner formed by the leading and the front walls, increases at the leading wall the convective heat transfer along the front wall of the turn. Besides, in the turn first half close to the leading wall, this vortex produces a counter-current flow which, striking with the flow coming from the inlet duct, determines an increase in the TKE and consequently an increase in the convective heat transfer on the leading wall at the turn inlet. In the turn second half, the vortex, owing to the strong intensity reduction in the Coriolis force, bends toward the trailing wall generating a strong impinging flow at the turn exit section, which plays a predominant role in the heat transfer increase that is noticed at the trailing wall in the central part of the outlet duct. At the leading wall, a high heat transfer zone that, starting from the second external angle, extends along the external wall of the second part of the turn and of the outlet duct for about 3 hydraulic diameters was found. The part of this zone contained in the turn region seems to be generated both by impinging flows and by high values of the TKE, while the remaining part can be exclusively ascribed to impinging flows. Finally, two high heat transfer zones are noticed at the trailing wall, close to the second-turn external angle and nearby the partition wall of the outlet duct. These are compatible with the presence of impinging flows in such regions.

By performing a parametric analysis, it has been possible to propose an empirical correlation that links the local convective heat transfer coefficient to fluid dynamic quantities as TKE and w. This investigation points out that the impinging flows, for the investigated flow field, are the main cause of the surface heat transfer increase. Indeed, as confirmed by the found correlation, their weight appears almost twice larger than that relative to the TKE.