1 Introduction

Auxetic materials and structures behave contradictory to intuition—while uniaxially stretched, they both elongate and expand laterally and when uniaxially compressed, they both contract longitudinally and shrink laterally, as demonstrated in Fig. 1. In other words, in deformed auxetics, strains in specific directions share the same sign, positive during tension and negative during compression. This behavior is bound to the characteristic negative values of Poisson’s ratio in auxetics and is the cause of their numerous, interesting potential applications.

Fig. 1
figure 1

Deformation during uniaxial loading of conventional materials and auxetics; dashed line—contour prior to loading, solid line—contour after loading

Full size image

While the theoretical range of Poisson’s ratio from − 1 to + 0.5 based on the theory of isotropic linear elasticity was known since the nineteenth century, first observations of materials with negative Poisson’s ratio were reported in the first half of twentieth century by Love (1927) and Voigt (1928). They both noticed the peculiar behavior of pyrite crystals during their experiments. Love described an example of a cubic single-crystal pyrite as a material with negative Poisson’s ratio equal to − 0.14. Almost 60 years later, in 1980s, numerous researchers tried and managed to successfully manufacture a synthetic foam with negative Poisson’s ratio. Bhullar described those stages in more detail in his review (Bhullar 2015). Materials with negative Poisson’s ratio are known as auxetics since 1991, when the term was coined by Evans (1991), derived from the Greek αὐξητικός (transliteration: auxetikos), meaning “that which tends to increase”.

Specific behavior of auxetics is an effect of their internal structures. These structures consist of characteristic geometries, which when subjected to mechanical loading behave similarly to linkage mechanisms. The scale of auxetics’ internal structures differs based on application, from macro- through micro- to nanoscale and molecular-level structures. Regardless of scale, in patterned structures, the auxetic effect depends mostly on the geometry of their unit cells (Lim 2015; Elipe and Lantada 2012). It is possible to obtain an auxetic by shaping a conventional material into a specific auxetic structure. Material obtained in this way is considered auxetic, even though the bulk material is conventional (Evans, Alderson 2000). Due to their unique properties, auxetic materials are considered smart materials. Due to the nature of their periodic structure, multiscale modeling is often applied in research of auxetics to analyze the behavior of elements made from auxetic structures, which are then treated as homogenous materials and have properties based on the results of analysis of a RVE (representative volume element) of the proper structure of the auxetic material. Simulations are mostly performed based on specific unit cells, which are the basic component of auxetic structures (Meena, Singamneni 2019; Wang et al. 2019).

Auxetic structures are based on numerous deformation mechanisms, out of which the most common are the re-entrant mechanism, rotating unit mechanism and chiral mechanism (Cho et al. 2019). Re-entrant auxetic structures consist of thin ribs linked by hinges. Re-entrant unit cells include combinations of acute and reflex internal angles, which cause the structure to unfold outward in both directions during uniaxial stretching and to progressively fold inwards in both directions during uniaxial compression. Deformation pattern of exemplary re-entrant structure is demonstrated in Fig. 2. Rotating unit structures consist of regular rigid unit cells of one or few types of geometries which are connected to neighboring cells only by their corners. Application of force causes the unit cells to rotate, while remaining connected to each other by their corners, which results in a distinct change of pattern formed by the unit cells, and, in an auxetic deformation of the structure. Chiral structures, most commonly, consist of arrangements of unit circles with tangent straight ribs, which connect neighboring circles. Chiral structures are named based on the number of ribs protruding from a single circle in a unit cell, e.g., in trichiral structures, a single circle is connected to its neighbors by three ribs and in tetrachiral structures by four.

Fig. 2
figure 2

Deformation pattern of auxetic hex re-entrant unit cell

Full size image

Unusual behavior of auxetics inspired researchers to think of many interesting potential applications (Evans and Alderson 2000). An intriguing example is a bullet composed of conventional and auxetic components, so that its overall Poisson’s ratio would be equal to zero, which would significantly reduce the loss of bullet’s kinetic energy due to friction during its movement down the barrel. Auxetics’ deformation pattern causes them to also have increased indentation resistance and shock-absorption properties, which might be utilized in personal protective equipment, such as helmets and bullet-proof vests. Another interesting example of utilizing the auxetic effect is the concept of auxetic nail (Ren et al. 2018) which, in comparison to conventional nails, would be easier to push in, due to lateral contraction during compression, and harder to pull out, due to lateral expansion caused by tension. Auxetic materials can also find numerous applications in more concrete load-bearing applications, as indicated by Momoh et al. (2024) in their review of auxetics applications in cementitious composites. Auxetic geometries can be utilized in civil and structural engineering applications as structural load-bearing elements with increased impact energy absorption as well as in functional smart filtration systems.

Since the extent of auxetic effect is dependent mostly on geometry of the structure’s unit cell, properties of the auxetic structure can be adjusted during the design phase to fulfill the desired requirements. Research papers which propose new types of auxetic structures, or new applications of structures that are already well known, often include a portion devoted to optimization of the considered auxetic structure geometry. Novak et al. (2022) proposed a novel 3D graded axisymmetric chiral auxetic structure, which they optimized by parametrizing thicknesses of 9 separate struts and managed to obtain a very significant increase in structure’s stiffness. Other examples of optimization of auxetic structures with functional goals include (Behinfar and Nourani 2024; Bruggi et al. 2016; Gao et al. 2023; Gohar et al. 2021); ; ; .

One of the most notable fields of auxetic materials application is shock absorption, as such strain energy of auxetic structures and maximizing their ability to absorb impact energy is one of the most popular optimization goals. Tan et al. (2021) performed multi-objective optimization of an auxetic hierarchical honeycomb crash box and compared its crushing performance with an aluminum foam-filled crash box and a traditional crash box. The results showed that the auxetic crash boxes presented the strongest energy dissipation capacity, and that the optimization resulted in increase of specific energy absorption and mean crushing force compared to the initial geometry. Wang et al. (2020) performed a similar analysis of crashworthiness for a novel crash box with core of auxetic hex re-entrant structure with collaborative optimization design.

A separate area of research interest that is currently extensively explored is the use of computational intelligence, such as machine learning, for automated optimization of auxetic structures. Wang et al. (2023) proposed the use of machine learning to accelerate the design of auxetic structures. The structures they obtained exhibited very strong auxetic effect (– 1.35 up to – 1.50), which was later confirmed experimentally, but the complex zig-zag geometry of the structure limited the effective strain to which it could be subjected without permanent deformation to 2.526%. Meier et al. (2024) proposed an automated optimization approach in obtaining auxetic and isotropic metamaterials in counterintuitive design spaces. They arranged 8 distinct neither isotropic nor auxetic unit cells together in a 5 × 5 × 5 cubic symmetric lattice structure with controlled automated modeling approach. They managed to obtain a structure which exhibited 0.01 value of Poisson ratio by combining component structures which were not auxetic, to obtain auxetic effect inside the cubic structure which allowed them to obtain almost zero-value lateral strain. Similar work with very different approach was published by Long et al. (2016), where they considered a composite material composed of auxetic phase and conventional phase. They considered homogenous materials with arbitrarily set values of the Poisson’s ratio and Young’s modulus and used computational intelligence method to obtain a cubic structure of composite material with increased Young’s modulus in regard to both component phases.

This paper presents the results of parametric optimization of selected two-dimensional auxetic unit cells with the aim to maximize the auxetic effect while maintaining a safe level of mechanical stress. FEM simulation and optimization were conducted with the use of Ansys® Academic Research Workbench Mechanical 2023 R1 software. Two types of two-dimensional unit cells were analyzed, the 4-vertice star unit cell and the elongated chevron unit cell. 4-vertice star can be considered a part of a larger “family” of unit cells composed of a cross, in which orthogonal arms are connected to each other with a compliant geometry, in this case, the star arm with angle α, other notable examples include the tetra petal unit cell and its variations, like ones considered by Wang et al. (2019). Elongated chevron unit cell is based on the structure often referred to as the “US Patent Pyramid” (Ma 2008, US7910193B2), adjusted to enlarge the contact surfaces between neighboring unit cells and prevent stress concentration. These two unit cells have been selected for optimization as representatives of two different groups of auxetic unit cells. The 4-vertice star is isotropic, while elongated chevron is strongly anisotropic. By investigating the two of them together, it was possible to verify the effectiveness of presented approach on examples of two different specific auxetic unit cells, which represent two different groups of auxetic unit cells.

The novelty of this paper lies in multi-objective optimization and comparison of two very different type of auxetic geometries, with the goal to maximize the auxetic effect of the structures and reduce their equivalent stress. The results can be used in further research of multiphase materials with auxetic phase. The presented method allows to obtain auxetic geometries based on known unit cells with custom-tailored properties, which will allow to design multiphase materials with material properties grounded in separate simulation results, instead of arbitrarily imposed by the authors.

2 Methodology and analyzed unit cells

Poisson’s ratio is the most important measure of auxetic effect. It gives the proportion of transversal strain to axial strain during uniaxial loading:

$$\upsilon = - \frac{{\varepsilon_{\text{T}} }}{{\varepsilon_{\text{A}} }}$$
(2.1)

where \(\upsilon\) is the Poisson’s ratio, \({\varepsilon }_{{\mathrm{T}}}\) is the strain in transversal direction and \({\varepsilon }_{{\mathrm{A}}}\) is the strain in axial direction (direction of loading). In case of auxetic structures analysis, the structure’s effective Poisson’s ratio is more commonly used than the material’s general Poisson’s ratio. In case of effective Poisson’s ratio, only effective strains of the analyzed structure are taken into consideration:

$$\upsilon_{{\text{eff}}} = - \frac{{\varepsilon_{{\text{Teff}}} }}{{\varepsilon_{{\text{Aeff}}} }}$$
(2.2)

Effective strains are calculated based on displacements of the structure’s most external edges, those which would be the contact surfaces with neighboring unit cells in case of periodic structures. For example, in case of 4-vertice star unit cell shown in Figs. 3 and 4, effective strains would be calculated based only on displacements of the four external edges of the star orthogonal arms. For a 4-vertice star unit cell, loaded as shown in Fig. 3 and with dimensions as shown in Fig. 4, the effective strains are calculated as follows:

$$\varepsilon_{{\text{Aeff}}} = \frac{{u_{\text{y}} }}{2b}$$
(2.3)

and:

$$\varepsilon_{{\text{Teff}}} = \frac{{u_{\text{x}} }}{2b}$$
(2.4)

where \({u}_{y}\) is the sum of displacements in the y direction of the cell’s external top and bottom edges, and \({u}_{x}\) is the sum of displacements in the x direction of the cell’s external left and right edges, b is the cell’s arm length, equal to half of its total width or length in undeformed state.

Fig. 3
figure 3

4-vertice star unit cell with marked displacement boundary conditions

Full size image
Fig. 4
figure 4

Analyzed unit cells with geometric parameters: 4-vertice star (left) and elongated chevron (right)

Full size image

Figure 3 demonstrates the displacement boundary conditions assumed during FEM analysis of considered unit cells: rolling support of the bottom edge and vertical displacement of the top edge by the magnitude of – 1 mm. In case of all considered structures, finite elements with quadratic shape function and global element size equal to 0.25 mm were applied, so that there were at least three finite elements at structure’s width. The simulation was conducted with the use of 2-dimensional finite elements with quadratic shape function. QUAD-dominant method was used for meshing, the mesh consisted mostly of uniform quadrilateral elements with some triangular elements in places where algorithm failed to obtain a uniform quadrilateral mesh. Material properties of ABS polymer were assumed: Young’s modulus E equal to 1.628 GPa and Poisson’s ratio \(\upsilon\) equal to 0.4089.

The boundary conditions for 5 × 5 structures were similar to the ones for singular unit cells—a roller support was applied to the bottom edges of unit cells in the bottom row and vertical displacement by the magnitude of 2 mm was applied to the top edges of the unit cells in the top row. Horizontal displacement of all external edges, that would be connected to the next unit cells, of unit cells in the extreme right and left vertical rows were measured and averaged for the determination of the effective Poisson’s ratio. Uniform mesh of finite elements of the same type and size as in singular unit cells’ analyses was applied.

First, analyses and optimization were performed on singular unit cells and later additional analyses were performed on 5 × 5 structures composed of 25 unit cells, to verify the final optimization results in case of each analyzed geometry type. Two types of auxetic unit cells were analyzed and optimized: 4-vertice star and elongated chevron. Analyzed unit cells are shown in Fig. 4. Reference values and optimization range of geometric parameters for each unit cell are given in Tables 1 and 2.

Table 1 Parameters of 4-vertice star unit cell
Full size table
Table 2 Parameters of elongated chevron unit cell
Full size table

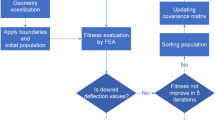
ANSYS software built-in response surface optimization tool was utilized. Multi-objective genetic algorithm (MOGA) method was applied. The utilized built-in optimization tool is based on response surface approximation. First, a series of FEM analyses is conducted for the specified set of input parameters. Then, based on obtained results, the response surface is generated. The response surface is then searched for the best results with the multi-objective genetic algorithm. Finally, the obtained set of candidates (proposed results) is used as input data in FEM analyses to verify whether the approximation was precise, and whether the approximation results are compliant with results of actual FEM simulation. Multi-objective optimization was based on searching the Pareto frontier.

The primary goal of optimization was to maximize the auxetic effect, so to minimize the effective Poisson’s ratio of each unit cell. Secondary goal was to minimize the maximal and averaged equivalent stress (according to Huber–von Mises–Hencky hypothesis). Obtained candidates were verified via static structural simulation. Finally, the best candidates were selected. The best candidates are referred to as “Optimized”, while the reference geometries are referred to as “Reference”, in Figs. 5, 6, 7 and 8. The best candidates of optimized unit cells were then used in composition of 5 × 5 structure. Optimized structures were compared with reference ones. Objective function of optimization was formulated as follows:

$$\begin{gathered} \upsilon_{{\text{eff}}} \left( {\alpha ,\beta , a, b} \right) \Rightarrow \min , \hfill \\ \sigma_{\max } \left( {\alpha ,\beta , a, b} \right) \Rightarrow \min , \hfill \\ \sigma_{{\text{avg}}} \left( {\alpha ,\beta , a, b} \right) \Rightarrow \min \hfill \\ \end{gathered}$$
(2.5)

where \({\sigma }_{{\mathrm{max}}}\) is the maximal equivalent stress (Huber–von Mises–Hencky) observed in the unit cell, \({\sigma }_{{\text{avg}}}\) is the averaged equivalent stress in the unit cell, and \(\alpha ,\beta , a, b\) are the cells’ geometric parameters as specified in Tables 1 and 2 and Fig. 4. Additional constraints of maximal value were applied to the maximal and averaged stress output parameters.

Fig. 5
figure 5

Comparison of directional displacements and equivalent stress of reference and optimized 4-vertice star unit cell

Full size image
Fig. 6
figure 6

Comparison of directional displacements and equivalent stress of reference and optimized elongated chevron unit cell

Full size image
Fig. 7
figure 7

Comparison of directional displacements and equivalent stress of reference and optimized 5 × 5 structures composed of 4-vertice star unit cells

Full size image
Fig. 8
figure 8

Comparison of directional displacements and equivalent stress of reference and optimized 5 × 5 structures composed of elongated chevron unit cells

Full size image

3 Results

Optimization results are given in Tables 3 and 4, respectively for the 4-vertice star and the elongated chevron unit cells. Distributions of displacements and equivalent stress during uniaxial compression obtained by static structural FEM analysis are given in Figs. 5 and 6, and graphs visualizing the changes of input and output parameters during optimization are given in Figs. 9 and 10, respectively, for the 4-vertice star and the elongated chevron unit cells.

Table 3 Optimization results for the 4-vertice star unit cell
Full size table
Table 4 Optimization results for elongated chevron unit cell
Full size table
Fig. 9
figure 9

Changes of 4-vertice star unit cell parameters during optimization

Full size image
Fig. 10
figure 10

Changes of elongated chevron unit cell parameters during optimization

Full size image

3.1 5 × 5 structures

Distributions of displacements and stress for 5 × 5 structures composed of reference and optimized unit cells are shown in Figs. 7 and 8, respectively, for the 4-vertice star and the elongated chevron structures. Comparison of reference and optimized structures’ effective Poisson’s ratio and stress is given in Tables 5 and 6, respectively, for the 4-vertice star and the elongated chevron structures.

Table 5 Optimization results for 5 × 5 structure composed of 4-vertice star unit cells
Full size table
Table 6 Optimization results for 5 × 5 structure composed of elongated chevron unit cells
Full size table

4 Summary and conclusions

The aim of this study was to perform parametric optimization of selected auxetic unit cells with the aim to increase their auxetic effect and reduce equivalent stress. The effectiveness of optimization for the considered unit cells was compared and geometrical parameters with the highest influence on the auxetic effect were identified. The optimization results for singular unit cells were validated by conducting analyses of 5 × 5 structures composed out of the reference unit cells and optimized unit cells.

The conclusions are as follows:

  1. 1.

    Out of the analyzed structures the elongated chevron unit cell exhibited much stronger auxetic effect. It is bound to its distinctively anisotropic behavior, which needs to be taken into consideration while designing applications utilizing this type of structure. In case of 4-vertice star unit cell the effective Poisson’s ratio remains in the range specified by the theory of linear isotropic elasticity and its behavior is isotropic, as was observed during previous studies (Zawistowski and Poteralski 2023).

  2. 2.

    In case of both unit cells, optimization significantly increased the auxetic effect and reduced equivalent stress. It is worth noting that the increase of auxetic effect was even greater in case of 5 × 5 structures composed of optimized unit cells.

  3. 3.

    Observing the plots of parameters change during the course of optimization allows to identify the geometric parameters’ influence on structure’s auxetic effect. In case of 4-vertice star unit cell, it increases with the increase of internal gap a and with the decrease of angle α. Chaotic changes of arm’s length b during optimization suggest that this parameter does not have a strong influence on the magnitude of unit cell’s effective Poisson’s ratio. A similar observation was made in the previous study (Zawistowski and Poteralski 2023). In case of elongated chevron unit cell, the structure’s auxetic effect increases with the increase of chevron’s width b and the decrease of angles α and β, and dimension a.

  4. 4.

    Effective Poisson’s ratio of auxetic unit cells and structures composed out of them is dependent on the values and proportions of their geometric parameters. It is possible to effectively manipulate the magnitude of auxetic effect by changing the values of identified geometric parameters. The results of this work are also applicable to design of micro-scale auxetic structures, by scaling down the unit cells dimensions.

  5. 5.

    As the results show, it is possible to obtain singular auxetic unit cells, and by extension patterned auxetic structures composed out of this unit cells, with custom-tailored values of auxetic effect and reduced stress. This approach can be further utilized, allowing to effectively manipulate the material properties of considered structures, with the use of parametric optimization and known geometries of auxetic unit cells. This can prove useful in design of multiphase composite materials with auxetic phase, as when used together with multiscale modeling, it will allow to obtain component materials with specific material properties grounded in simulation results, instead of arbitrarily selected by the authors.