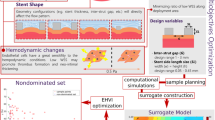
Abstract
The present study examines the mechanical properties of auxetic stents with the tetra-star-chiral structure. The tetra-star-chiral geometry is parametrically modeled. Then, the design of experiments (DOE) is developed by defining the elastic properties of the stents and using the response surface method (RSM). Finite element (FE) analysis is performed in order to find a polynomial relationship between the geometric parameters as inputs and the elastic parameters as the outputs. Then, the optimal stent is found in terms of elasticity parameters by using RSM and NSGA-II methods and the two-dimensional Pareto front is plotted. The optimal parameters of the stent including flexural stiffness, axial elasticity modulus, radial elasticity modulus and Poisson’s ratio are obtained as 10.66 mPa m4, 5.37 MPa, 33.2 MPa and − 0.41, respectively. Moreover, a method is proposed to find an analytical solution for metal elastic stents in order to verify the FE model results, and also the blood vessel compliance of the optimal stent is examined.
Article Highlights
-
Axial tensile and bending tests are performed on a number of auxetic stent at a similar strain and moment respectively.
-
Four main elasticity parameters (i.e., E, Er, EI, \(\nu\)) are calculated as a function of geometry parameters.
-
Using castigliano’s theorem, the results of FEM tests are verified analytically
-
Multi-objective optimization is performed and a set of optimal stents in terms of elasticity parameters is obtained.
-
Using the compliance mathematical criteria, the optimized stent is seen to be suited for vessel wall.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Auxetic metamaterials have been widely used in recent years. They have different elastic characteristics, e.g., a negative Poisson’s ratio [1,2,3,4,5], with respect to regular materials. These irregularities give them some desirable capabilities in mechanical and medical engineering such as energy absorption, fracture resistance and shear resistance [6,7,8]. They have also been employed in medical and biomechanical industries, e.g., as knee straps, in-vessel stents, and orthopedic and sports shoes [9,10,11]. Since auxetic structures can expand simultaneously in the longitudinal and transverse directions, they are widely employed in angiography [12], in which stents and balloons are sent through the blood vessel to widen it.
Khoshgoftar and Abbaszadeh [13] evaluated the effects of the geometric parameters of a honeycomb structure, e.g., thickness, aspect ratio, and the angle between cell components, on Poisson’s ratio; it was shown that a smaller Poisson’s ratio can be obtained by decreasing thickness, cell angle and number of cells. Poncin and Proft [14] evaluated different materials and methods in the fabrication of artery stents. They reported some stainless steel, cobalt, titanium, Nitinol, and magnesium alloys to be optimal materials in terms of body compatibility and ease of fabrication. Eshghi et al. [15] conducted the FE analysis of expanded stents on a balloon within blood vessels in the presence of a plaque. They also reported the diameter variation and bending of stent while the applied inlet pressure increased. Bhullar [16] explored the effects of a negative Poisson’s ratio on the performance of esophagus-placed stents. The properties of a number of stents with different geometries were obtained under tensile loads. Ren et al. [17] employed tensile and compressive tests to analyze the effects of geometrical parameters on the elastic parameters (e.g., Poisson’s ratio) of metal stents, it was found that, in a proper value of pattern scale factor (PSF), Poisson’s ratio and force–displacement curve for both compressive and tensile loading conditions are the same. Wu et al. [18] compared chiral structures with circular and oval nodes. The in-plane elastic properties of the structures were obtained using FEM. Tensile tests were performed, and the geometrical parameters (as the inputs) and Poisson’s ratio (as the output) were related. The two structures were found to show promising performances as a stent in blood vessels due to high expansion and axial stability. Ruan et al. [19] examined anti-chiral stents. Poisson’s ratio was plotted versus geometric parameters. It was found that the maximum stress would be smaller when the number of cells in the axial direction was higher.
A review of the literature on auxetic stents indicates research gaps. For example, studies on the optimization of stent parameters mostly implemented single-objective optimization. Also, the bending performance and analytical solution for mechanical properties of stents have not been studied. In this study, RSM method is used to find a mathematical relationship between geometrical parameters as the inputs and elasticity parameters as the outputs for some typical biomaterials. In order to carry out designed RSM tests, FE modeling is applied. Also, a comprehensive analytical method using Castigliano's theorem to evaluate tetra-star-chiral structure is proposed. Moreover, the multi-objective optimization of stents using NSGA-II and RSM methods is performed. Finally the compliance of the optimized stents is measured as a criterion to evaluate the compatibility of the stent to be used in the blood vessels.
In the next section, we consider to introduce our method of geometric modeling using Catia software, design of FEM experiments using RSM method, analytical solution, multi-objective optimization and compliance analysis of auxetic tetra-star-chiral stents. Section 3 shows the results of analytical solution, multi-objective optimization and compliance analysis and finally in Sect. 4, we discuss the limitations and applications of our paper.
2 Materials and methods
2.1 Geometric modeling
A three-dimensional cylindrical stent with a tetra-star-chiral structure was built in CATIA with the parameters and constraints indicated in Table 1. The constraint ensure that the cell is not self-intersecting, accordingly a custom range that satisfies the constraint is regarded. Also it is notable that the minimum and maximum radius of the modeled stents is 2.54 mm and 8.91 mm respectively (almost analogous to typical blood vessels). In the 2D schematic depicted in Table 1, t is the link thickness, \({L}_{1}\) and \({L}_{2}\) are horizontal and vertical lengths respectively, and \({n}_{1}\) and \({n}_{2}\) are the number of circumferential and axial cells, respectively.
2.2 Design of experiments using RSM method
The parameters under analysis include the axial elasticity modulus (E*), Poisson’s ratio (\({\nu }^{*}\)), radial elasticity modulus (Er), and flexural rigidity (EI). The axial and radial elasticity moduli and Poisson’s ratio are found using tensile tests with FEM linear solver as:
where F is the tensile load at a given strain \({\varepsilon }_{axial}\) (Fig. 1), \({R}_{avg}\) is the average pre-tension stent radius, and \({t}_{3}\) is the stent thickness (assumed to be 0.4 mm) [20] and large deformations were not allowed. Also, the end surfaces are only allowed to have axial tension and other degrees of freedom are closed. It should be noted that \({E}^{*}\) and \({\nu }^{*}\) are calculated for the structure and differ from the elasticity modulus and Poisson’s ratio of the base material. Also, \({\varepsilon }_{radial}\) is the radial strain of the stent which is evaluated at the average radius. Equation (3) is defined for isotropic materials using the Maxwell–Betti’s law for the perpendicular axial and radial directions [11].
In order to measure flexural stiffness, a moment M is applied to the pinned center points of ends of the stent and the end surfaces are coupled to the center points with coupling interaction (Fig. 2a, b), and the deflection in the middle of the stent is measured by:
where \({y}_{max}\) is the deflection in the middle of the span, and \({L}_{stent}\) is the stent length.
To efficiently place the stent into the blood vessel, it is required that \({E}^{*}\) and EI be small enough so that the stent could easily expand in the axial direction and show a suitable flexural stiffness to avoid any damage to the vessel. It is required that the absolute value of the negative Poisson’s ratio be large enough to expand the vessel wall. Also, \({E}_{r}\) should be large enough so that a small reaction force applied by the wall would not transversely compress the vessel [21,22,23].
To obtain an optimal geometry of the stent, it is required to define a design of experiment (DOE). DOE was developed based on RSM to establish a polynomial relation between the input parameters—including both geometrical and material properties—and output parameters (i.e., E*, v*, Er, and EI) amid minimizing the number of experiments. Conventional biocompatible materials were used in the analysis. Table 2 lists the mechanical properties of the select materials.
In the RSM method, continuous quantitative (e.g., the length of a side), discrete quantitative parameters (e.g., the number of cells in the circumferential or axial directions), and qualitative variables (e.g., type of material) can be defined as inputs. The outputs, however, are continuous quantitative variables. In this study, a quadratic regression was suggested by the Design-Expert software between the inputs and outputs. For the tetra-star-chiral structure, the coefficients of the regression curve (i.e., \({c}_{ij}{\text{s}}, {d}_{k}\mathrm{s \,and\, }e)\) can be obtained through 32 tensile tests and 32 bending tests (i.e., the number of runs calculated by the software). The equation below represents the quadratic relation between \(Y\) as the output parameter (i.e., E*, v*, Er, and EI) and \({x}_{1},{x}_{2},\dots ,{x}_{n}\) as the inputs (i.e., geometric parameters):
Tensile and bending tests were implemented using ABAQUS software. Stents were tensioned at a strain of 0.0005 in both ends, leading to a total strain of 0.001. This small tensile strain is applied to ensure that no element fails, besides the axial tensile tests were carried out in various strains (ranging from 0 to 0.4) for a single stent to see how the elastic parameters would change. Since stents have somewhat complex geometries, the present study employed bottom-up meshing in order to apply hexagonal elements and obtain more reliable results. 4482 hexagonal C3D8R elements with a global size of 0.2 mm were used for the bending and tensile tests of the optimized stent. The results remained almost unchanged (within 1% of final value) when a mesh size of less than 0.2 mm was used. Once the tests were completed in FEM using static general solver, the unknown coefficients of Eq. (5) (i.e., \({c}_{ij}{\text{s}}, {d}_{k}\mathrm{s\, and\, }e)\) were derived using response surface method which is a curve fitting technique. Also, the DOE runs listed in “Appendix” are derived from Design-Expert software.
2.3 Analytical solution of the tetra-star-chiral auxetic stent
In order to validate the FEM results, a single planar tetra-star-chiral cell was analytically solved using Castigliano’s theorem and the results were compared with those obtained from FEM of the same cell (see the first paragraph of Sect. 3). The boundary conditions and loading for the single cell is shown in Fig. 3. The energy stored in the cell was assumed to be resulted from only bending and tension, neglecting the shear component. Moreover, a single cell was considered for analytical solution with the internal resulted forces/moments, as shown in Fig. 4 and the force F and Q was applied to the entire cell.
The total energy of bending and tension is given by:
where P(s) and M(s) are the normal force and bending moment along the structure, respectively. The extension of Eq. (6) for two horizontal links of the cell gives the total strain energy as:
in which:
Then \({\Delta }_{1}\) and \({\Delta }_{2}\) which represents the vertical and lateral displacements of the single cell respectively are equal to:
Finally the Poisson’s ratio and the young modulus is calculated as:
The value of Poisson’s ratio for the 2D structure calculated here is consistent with that of Ref. [1] (i.e., equal to − 1 while Q is equal to F) where a planar auxetic configuration was evaluated. As an example, by using the FE (see Sect. 3), it was observed that the ratio of \(\frac{Q}{F}\) is equal to 0.41 for a single cell placed in a 2D auxetic plane, 8*4 array (derived by unrolling the optimized stent in a 2D plane) which was subjected to a vertical displacement of 5 mm. As a result, by considering Eq. 12, the Poisson’s ratio of a single cell is evaluated as − 0.41.
2.4 Multi-objective optimization using NSGA-II and RSM method
To optimize several mechanical properties, the present study implements a multi-objective optimization of the auxetic stent. To identify a set of optimal stents, first RSM multi-objective optimization was performed for four main parameters (i.e., E*, v*, Er, and EI) using Design-Expert software and titanium was found as the most optimal material for the stent. A two-objective optimization using MATLAB software was then carried out for the objective functions of \({\nu }^{*}\) and \({E}^{*}\). The same optimization was also performed for the objective functions of \(EI\) and \({\nu }^{*}\). The RSM results (i.e., the relations derived between inputs and outputs) was used for the MATLAB optimization code. The two-dimensional Pareto front diagrams with Pareto points of the outputs of each generation and the corresponding convergence plots will be presented for the most optimal material (i.e., titanium) in the results section.
2.5 Compliance analysis
Compliance analysis was conducted to evaluate whether the optimized stent geometry complied with the vessel’s characteristics. Then, the typical blood pressure values (i.e., 80 and 120 mmHg) were applied to the inner surface of the stent and the radial expansion of the stent was measured. The compliance parameter was calculated as [24, 25]:
where \({R}_{P1}\) and \({R}_{P2}\) denote the maximum vessel radius (mm) at pressures of \({P}_{1}=80\, {\text{mmHg}}\) and \({P}_{2}=120 \,{\text{mmHg}}\), respectively. A review of earlier works indicated that the compliance parameter had been obtained to be nearly 21%/mmHg for the proximal native artery and 20.4%/mmHg for distal native artery [26]. Thus, the optimized stent should have smaller relative changes in the radius than the vessel wall and, consequently, a lower compliance parameter implies it could be placed within the blood vessel. It should be noted that the compliance parameter is not an objective function for the tests. It just a measure for the optimized stent to check whether the stent can be properly inserted in the blood vessel.
3 Results
The agreement between the results of the analytical solution and FEM of a single cell can be readily examined by building a simple FEM of the auxetic cell; e.g.; using the Eqs. 12 and 13, the Young’s modulus and the Poisson’s ratio of a single cell of the optimized stent were analytically calculated as 4.43 MPa and − 0.41 (while the force Q is equal to 0.41F), respectively, as the same (with a difference of less than 5% due to numerical errors) obtained from the FEM (see Fig. 4).
3.1 RSM modeling results
A quadratic equation was obtained for the elasticity modulus E* (MPa), Poisson’s ratio v*, radial elasticity modulus Er (MPa), and flexural rigidity EI (Pa.m4) as a function of the stent geometry and material as:
where \({n}_{1}\) and \({n}_{2}\) denote the number of cells in the circumferential and axial directions respectively, \({L}_{1}\), \({L}_{2},t\) are the geometrical parameters as introduced in Sect. 2.1 and the term Parameter can be an elastic output. The unknown coefficients (i.e., \({a}_{i}s,{b}_{i}s,{c}_{i}s,{d}_{i}s,{e}_{i}s,{f}_{i}s,\delta ,k\)) would be determined by the Design-Expert software.
Table 3 provides the analysis of variance (ANOVA) results, including the mean, standard deviation, coefficient of variation (CV), correlation coefficient (R2), p-value, and f-value, for the model and the squared residuals.
According to Table 3, the parameter \(k\) and \(\delta\) for every output was determined. Additionally, the coefficient of determination (i.e., R2) was found to be very close to 1, suggesting the adequacy of the fitted model. Linear factors (such as \(t\)) were seen to be more effective than quadratic factors (such as \({L}_{2}{L}_{1},{n}_{1}^{2})\). Besides, the fitted model was found to be significant since the p-value for every output is smaller than 0.05 and the squared residuals are very small.
Table 4 reports the RSM optimization results for a low E*, low EI, high Er, and a more negative Poisson’s ratio as the desired outputs for one sample. Design-Expert software optimization results showed titanium as the most optimal material for the stent (as seen in Table 4) amid three materials of Table 2.
3.2 FEM Results
3.2.1 FEM results of the optimal stent
To validate the fitted mathematical models, the stent with characteristics listed in the Table 4 was subjected to tensile and bending tests in Abaqus software independently. The results (i.e., the four main elastic outputs) were found to be in good agreement with RSM resulted polynomial (Table 5).
By applying some fundamental geometric calculations and knowing the cell parameters of the (Table 4), it was found that the length was 32 mm, and the radius was 2.54 mm. Moreover the Fig. 5a, b show the von Mises stress contours under tension (i.e., with a strain of 0.001) and bending moment (i.e., with a moment value of 1 N mm), respectively and the maximum displacement of 1.63 mm at the middle of the optimized stent was observed. It is worth noting that the bending behavior was considered in this study to check the stent performance in a naturally curved vessel. Otherwise, we would not expect the stent moment in ideal conditions; i.e., the possible effects of unwanted bending were not investigated in the current work.
3.2.2 Optimal stent under various tensile strains
In recent studies, it was observed that the typical cardiovascular stents experienced an average axial plastic strain of 0.05, while they were completely deployed in the vessel [27]. Thus, the purpose of this section is to ensure that our optimal stent (i.e., the first row stent of Table 4) also operate appropriately in larger strains. The optimal stent was subjected to various axial strains, ranging from 0 to 0.4 (i.e., fracture strain of titanium). It was observed in Fig. 6 that the Poisson’s ratio of structure altered between − 0.38 and − 0.55. In order to find the Poisson’s ratio of the stent, the displacements of the middle and end of the stent are measured from the FEM and the corresponding strains (i.e., \({\varepsilon }_{radial}\) and \({\varepsilon }_{axial}\)) are calculated. On the other hand, the Young’s modulus of structure (i.e., \({E}^{*}\)) and maximum Von-Mises stress showed significant changes from when they were evaluated in the elastic strain of 0.001, which is not satisfactory. Consequently, only Poisson’s ratio results are reliable in high axial strains too, while the other two parameters change significantly as the applied strain increases.
3.3 NSGA-II multi-objective optimization
3.3.1 Two-objective optimization of \({{\varvec{\nu}}}^{\boldsymbol{*}}\) and \({{\varvec{E}}}^{\boldsymbol{*}}\)
Figure 7 shows the scatter diagram of titanium stent, where blue spots represent the optimal points in each generation, and the black tangential curve illustrates the optimal data in the last generation. The final Pareto front has the lowest Poisson’s ratio and elasticity modulus and, therefore, it is the most optimal solution. The optimal Poisson’s ratio at a given elasticity modulus could be found through the black curve. As can be seen, the optimum value for \({\nu }^{*}\) varies from − 0.6 to − 0.2 while \({E}^{*}\) optimal values changes from 0 to 25 MPa. Figure 8 depicts the input parameters of each generation (red) and the corresponding Pareto optimal points (black). The parameter \({n}_{1}\) converged to the low values in the range (i.e., 4), while \({L}_{1},{L}_{2}\) and \({n}_{2}\) tended to have the high value in the given range.
3.3.2 Two-objective optimization of v * and EI
Figure 9 plots the distribution of Pareto optimal solutions for different generations and the outputs. It is very similar to Fig. 7 and allows for obtaining the most optimal Poisson’s ratio at a given flexural rigidity. As can be seen, the optimum value for the \({\nu }^{*}\) changes from − 0.44 to − 0.15 while \(EI\) optimal values varies from 0 to10 mPa m4. Figure 10 illustrates the input parameters of each generation (red) and the Pareto optimal data of each generation (black). The parameters \({n}_{1}\), \(t\) converged to the low values in the range (i.e., 4 for \({n}_{1}\) and 0.1 mm for \(t\)). L2 and \({n}_{2}\) however, tended to approach the high values in the range.
3.4 Compliance analysis
The expansion of the optimized stent with a size of first row stent of Table 4 under pressures of 80 and 120 mmHg was measured. The compliance parameter was calculated to be 0.1%/mmHg [using Eq. (14)] which is smaller than the compliance of the natural blood vessel (i.e., [21]). This is because the blood vessel expands more compared to a stent when subjected to a same blood pressure deviation. Thus, the Stent 1 was concluded to be suitable for placement in the vessel. Figure 11a, b depict the von Mises stress contour and boundary conditions of the optimized auxetic stent at an internal pressure of 120 mmHg, respectively. The stent is fixed at both ends and the pressure is applied to the inner wall. It can be also seen that the maximum von Mises stress is 7.8 MPa which is less than the yield stress of Titanium.
4 Discussion
Stenting is applied to treat arteries’ blockages by widening the vessel and making the blood flow back to normal. Auxetic tetra-star-chiral stents have been recently developed due to their capability for expanding in transverse directions when subjected to longitudinal strains. Some attempts have been done to introduce auxetic stents’ influential geometrical parameters and mechanical properties and evaluate them (e.g., [18]), and a number of studies have conducted optimization on one or two parameters [28, 29]. It is for the first time to our knowledge that a multi-objective optimization of aforementioned parameters was conducted. The parameters were used to model tension, bending and expansion behavior of stents mathematically. Also, a polynomial relationship was developed to estimate and link the mechanical properties to geometrical parameters of the stent and after all a set of optimized geometries in terms of elastic parameters as output were found.
The multi-objective optimization conducted in this study was defined to give a tetra-star-chiral stent with a lower negative Poisson’s ratio (\({\nu }^{*}\)), a lower flexural stiffness (EI), a higher radial stiffness (\({E}_{r}\)) and a lower axial Young’s modulus (E*). Accordingly, a more thickness reduction of ligaments led to further link rotation and, consequently, a more negative Poisson’s ratio. The parameter \({L}_{1}\) should be low while \({L}_{2}\) should be high in the assumed ranges to ensure that the average radius of the stent becomes small and, hence, rendering a smaller value of EI. The area moment of inertia, I, had somewhat a direct relationship with the average radius of stent, since I is equal to \(\pi {r}^{3}t\) for a low-thickness torus with radius of \(r\) and thickness of t. Figure 7 implies that a compromise should be implemented between the two parameters of \({\nu }^{*}\, \mathrm{and }\,{E}^{*}\); i.e., when \({E}^{*}\) is low, the structure is more flexible and, therefore, can expand in transverse direction more easily, resulting in an increase in the magnitude of structure’s Poisson’s ratio. The similar explanation can also be used for Fig. 9 that reflects a confliction between two parameters of \({\nu }^{*}\) and EI. Also, from Figs. 5 and 11, it is noticed that the higher stresses were seen near sharp corners in which concentration of stress occurs. This is consistent with the findings of Ref. [30]. Besides, the Poisson’s ratio of the optimized stent was found to be approximately what reported in the [31] for the same number of longitudinal and circumferential cells. Although in [31], the structure was another type of re-entrant (i.e., star—reentrant) and the boundary condition was load controlled (vs. the displacement controlled performed in our work), the relative difference in results is less than 15%. However, in [31] only the tensile tests were performed. For the bending tests using finite element method, boundary conditions are exactly same as which was developed before in [32] for experimental and analytical purposes.
The primary limitations of this work lie within the analytical solution and multi-objective optimization; i.e., in the analytical solution, it is not possible to apply all desired loads to simulate the displacement controlled boundary conditions, since by the mean of Castigliano’s theorem, the strain energy-displacement equations lead to a set of unsolvable integral-form equations. Besides, use of linear elasticity methods like airy solutions for this type of plane-stress problem has its own complexity, since the number of free boundaries is high. Furthermore, analysis of a whole stent using energy methods, is almost impossible, as we face many compatibility equations. A four-objective optimization could not be performed due to solution time and display limitations. For future studies, it is suggested to compare the mechanical parameters like strain energy density, Young’s modulus and Poisson’s ratio of multiple auxetic geometries for stents with similar radius, length and applied boundary conditions. Also, experimental analysis can be performed to verify the FEM results and analytical results. In the end, we think a more sophisticated FE analysis—i.e., to capture the large deformation effects and represent the real loading conditions—would be of importance for further study.
5 Conclusions
In conclusion, the present study conducted a parametric study of an auxetic structure using FEM software and analytical method. The obtained results were verified by analytical methods and from optimization, it was seen that titanium has the most optimal parameters among other materials. The compliance parameter which is an introduced criteria was found to be acceptable, suggesting that the optimized stent could be efficiently placed in blood vessels. Finally the optimal parameters of the stent including flexural stiffness, axial elasticity modulus, radial elasticity modulus and Poisson’s ratio were obtained as 10.66 mPa m4, 5.37 MPa, 33.2 MPa and − 0.41, respectively.
Availability of data and materials
The data that support the findings of this study are available on request from the corresponding author.
Abbreviations
- \({E}^{*}\) :
-
Elasticity modulus of structure (MPa)
- \(EI\) :
-
Flexural rigidity of structure (Pa m4)
- \({E}_{r}\) :
-
Radial elasticity modulus of structure (MPa)
- F:
-
Force (N)
- \({L}_{2}\) :
-
Length of smaller link (mm)
- \({L}_{1}\) :
-
Distance between 2 horizontal link (mm)
- \({L}_{stent}\) :
-
Length of stent (mm)
- M:
-
Moment (N m)
- \({n}_{1}\) :
-
No. of circumferential cells (–)
- \({n}_{2}\) :
-
No. of axial cells (–)
- \({R}_{avg}\) :
-
Average radius of stent (mm)
- \({R}_{Pi}\) :
-
Stent radius at pressure \({p}_{i}\) (mm)
- \(t\) :
-
Thickness of link (mm)
- \({t}_{3}\) :
-
Stent wall thickness (mm)
- \(U\) :
-
Strain energy (J)
- \({\varepsilon }_{axial}\) :
-
Axial strain (–)
- \({\varepsilon }_{radial}\) :
-
Radial strain (–)
- \({\nu }^{*}\) :
-
Poisson’s ratio of structure (–)
- DOE:
-
Design of experiment
- FE:
-
Finite element
- FEM:
-
Finite element method
- GA:
-
Genetic algorithm
- RSM:
-
Response surface method
References
Smith CW, Grima JN, Evans KE. Novel mechanism for generating auxetic behaviour in reticulated foams: missing rib foam model. Acta Mater. 2000;48(17):4349–56. https://doi.org/10.1016/S1359-6454(00)00269-X.
Mizzi L, Attard D, Casha A, Grima JN, Gatt R. On the suitability of hexagonal honeycombs as stent geometries. Phys Status Solidi Basic Res. 2014;251(2):328–37. https://doi.org/10.1002/pssb.201384255.
Gatt R, et al. On the properties of real finite-sized planar and tubular stent-like auxetic structures. Phys Status Solidi Basic Res. 2014;251(2):321–7. https://doi.org/10.1002/pssb.201384257.
Bhullar SK, et al. Design and fabrication of auxetic PCL nanofiber membranes for biomedical applications. Mater Sci Eng C. 2017;81(July):334–40. https://doi.org/10.1016/j.msec.2017.08.022.
Ali MN, Busfield JJC, Rehman IU. Auxetic oesophageal stents: structure and mechanical properties. J Mater Sci Mater Med. 2014;25(2):527–53. https://doi.org/10.1007/s10856-013-5067-2.
Ren X, Das R, Tran P, Ngo TD, Xie YM. Auxetic metamaterials and structures: a review. Smart Mater Struct. 2018;27(2):23001. https://doi.org/10.1088/1361-665x/aaa61c.
Sanami M, Ravirala N, Alderson K, Alderson A. Auxetic materials for sports applications. Proc Eng. 2014;72:453–8. https://doi.org/10.1016/j.proeng.2014.06.079.
Hamzehei R, Rezaei S, Kadkhodapour J, Anaraki AP, Mahmoudi A. 2D triangular anti-trichiral structures and auxetic stents with symmetric shrinkage behavior and high energy absorption. Mech Mater. 2020;142(September 2019):103291. https://doi.org/10.1016/j.mechmat.2019.103291.
Wang Z, Hu H. Auxetic materials and their potential applications in textiles. Text Res J. 2014;84(15):1600–11. https://doi.org/10.1177/0040517512449051.
Duncan O, et al. Review of auxetic materials for sports applications: expanding options in comfort and protection. Appl Sci. 2018. https://doi.org/10.3390/app8060941.
Yang H, Ma L. Design and characterization of axisymmetric auxetic metamaterials. Compos Struct. 2020. https://doi.org/10.1016/j.compstruct.2020.112560.
Behinfar P, Nourani A. Analytical and numerical solution for auxetic stents with re-entrant geometry and it’s multi-objective optimization. J Solid Fluid Mech (Persian). 2023. https://doi.org/10.22044/JSFM.2023.12193.3637.
Khoshgoftar MJ, Abbaszadeh H. Experimental and finite element analysis of the effect of geometrical parameters on the mechanical behavior of auxetic cellular structure under static load. J Strain Anal Eng Des. 2021;56(3):131–8. https://doi.org/10.1177/0309324720957573.
Poncin P, Proft J. Stent tubing: understanding the desired attributes. Med Dev Mater Proc Mater Process Med Dev Conf. 2003;2003(September):253–9.
Eshghi N, Hojjati MH, Imani M, Goudarzi AM. Finite element analysis of mechanical behaviors of coronary stent. Proc Eng. 2011;10:3056–61. https://doi.org/10.1016/j.proeng.2011.04.506.
Bhullar SK. Influence of negative Poisson’s ratio on stent applications. Adv Mater. 2013;2(3):42. https://doi.org/10.11648/j.am.20130203.14.
Ren X, Shen J, Ghaedizadeh A, Tian H, Xie YM. A simple auxetic tubular structure with tuneable mechanical properties. Smart Mater Struct. 2016;25(6):1–9. https://doi.org/10.1088/0964-1726/25/6/065012.
Wu W, Song X, Liang J, Xia R, Qian G, Fang D. Mechanical properties of anti-tetrachiral auxetic stents. Compos Struct. 2018;185(November):381–92. https://doi.org/10.1016/j.compstruct.2017.11.048.
Ruan XL, et al. Mechanical design of antichiral-reentrant hybrid intravascular stent. Int J Appl Mech. 2018;10(10):1–20. https://doi.org/10.1142/S1758825118501053.
Yokomachi K, et al. Neointimal formation after carotid artery stenting: phantom and clinical evaluation of model-based iterative reconstruction (MBIR). Eur Radiol. 2019;29(1):161–7. https://doi.org/10.1007/s00330-018-5598-5.
Dyet JF, Watts WG, Ettles DF, Nicholson AA. Mechanical properties of metallic stents: How do these properties influence the choice of stent for specific lesions? Cardiovasc Intervent Radiol. 2000;23(1):47–54. https://doi.org/10.1007/s002709910007.
Menown IBA, Noad R, Garcia EJ, Meredith I. The platinum chromium element stent platform: from alloy, to design, to clinical practice. Adv Ther. 2010;27(3):129–41. https://doi.org/10.1007/s12325-010-0022-9.
Pauck RG, Reddy BD. Computational analysis of the radial mechanical performance of PLLA coronary artery stents. Med Eng Phys. 2015;37(1):7–12. https://doi.org/10.1016/j.medengphy.2014.09.014.
Soletti L, et al. A bilayered elastomeric scaffold for tissue engineering of small diameter vascular grafts. Acta Biomater. 2010;6(1):110–22. https://doi.org/10.1016/j.actbio.2009.06.026.
Khoffi F, Dieval F, Chakfé N, Durand B. A development of a technique for measuring the compliance of the textile vascular prostheses. Phys Proc. 2011;21:234–9. https://doi.org/10.1016/j.phpro.2011.10.035.
de Valence S, et al. Long term performance of polycaprolactone vascular grafts in a rat abdominal aorta replacement model. Biomaterials. 2012;33(1):38–47. https://doi.org/10.1016/j.biomaterials.2011.09.024.
Ding H, et al. Analysis of vascular mechanical characteristics after coronary degradable stent implantation. Biomed Res Int. 2019. https://doi.org/10.1155/2019/8265374.
Li N, Zhang H, Ouyang H. Shape optimization of coronary artery stent based on a parametric model. Finite Elem Anal Des. 2009;45(6–7):468–75. https://doi.org/10.1016/j.finel.2009.01.001.
Amirjani A, Yousefi M, Cheshmaroo M. Parametrical optimization of stent design: a numerical-based approach. Comput Mater Sci. 2014;90:210–20. https://doi.org/10.1016/j.commatsci.2014.04.002.
Jopek H. Finite element analysis of tunable composite tubes reinforced with auxetic structures. Materials (Basel). 2017. https://doi.org/10.3390/ma10121359.
Carneiro VH, Puga H. Modeling and elastic simulation of auxetic magnesium stents. In: Proceedings of the 2015 IEEE 4th Portuguese meeting on bioengineering ENBENG 2015, vol. February; 2015. p. 26–8. https://doi.org/10.1109/ENBENG.2015.7088856.
Mori K, Saito T. Effects of stent structure on stent flexibility measurements. Ann Biomed Eng. 2005;33(6):733–42. https://doi.org/10.1007/s10439-005-2807-6.
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Contributions
PB did modeling and simulation and wrote the main manuscript text. AN conceptualized and supervised the project and edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
No funding was received to assist with the preparation of this manuscript. The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Behinfar, P., Nourani, A. Analytical and numerical solution and multi-objective optimization of tetra-star-chiral auxetic stents. Discov Appl Sci 6, 39 (2024). https://doi.org/10.1007/s42452-024-05663-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-024-05663-1