Introduction

There are several stochastic models such as stochastic and computational intelligence models for hydrological modelling and prediction purposes used by different researchers (Irvine and Eberhardt 1992; Mohan and Vedula 1995; Ahmad et al. 2001; Yurekli and Kurunc 2005; Yurekli et al. 2005; Abebe and Foerch 2008; Nirmala and Sundaram 2010, Zhang et al. 2011; Ali 2013). Damle and Yalcin (2007) attempted to predict floods in the Mississippi River, USA, by utilizing time series. Their results showed that time series are capable of generating daily discharge data and the resulting predictions are accurate. Mombeni et al. (2013) used SARIMA model for seasonal and non-stationary time series to estimate residential water consumption. Their results allow practitioners and planners to explore realistic decision making scenarios for designing effective water demand management. Valipour (2015) studied the performance of SARIMA and ARIMA models in forecasting long-term runoff in the United States. The results indicated that the SARIMA model outperformed ARIMA with a relative error of less than 5% for all states. Wang et al. (2015) combined the ARIMA model with ensemble empirical mode decomposition (EEMD) to forecast annual runoff time series. It was found that the new model can significantly improve ARIMA time series approach prediction.

On the other hands, Artificial Neural Network (ANN) application in hydrology has also been developed in recent years (Jain et al. 1999; Coulibaly et al. 2000; Xu and Li 2002; Anctil et al. 2004). Kilinç and Cigizoglu (2005) predicted the monthly inflow, storage and evaporation in the Canak Valley area using by the ANN. They used both radial and sigmoid function types in ANN. Their study results signified that the sigmoid function is more accurate than the radial function. Kisi and Cigizoglu (2007) examined different ANN techniques, including Feed-forward Backpropagation (FFBP), Radial Basis Function-based Neural Networks (RBF) and Generalized Regression Neural Networks (GRNN) along with AR modeling in predicting daily discharge flow. The results showed that the RBF technique performs better than the other models.

Stochastic models are usually categorized by linear models and also consider the random component of data whereas ANN models are capable to model the linear and nonlinear parameters in hydrological modelling. Therefore, several researchers have examined stochastic linear models and a variety of methods based on artificial intelligence in predicting hydrological time series (Kisi 2004; Mohammadi et al. 2005; Landeras et al. 2009; Khatibi et al. 2014). Fereydooni et al. (2012) employed the multilayer perceptron using a backpropagation model to predict rainfall, temperature and evaporation data, and compared the results with the ARIMA method. They concluded that ANN performs better than ARIMA. Valipour et al. (2013) used ARMA, ARIMA and ANN models to forecast Dez reservoir monthly inflow. According to the results, the ARIMA model has less error compared with the ARMA model and the ANN model has less error than ARIMA. Golabi et al. (2013) predicted seasonal rainfall using artificial neural network (ANN) and ARIMA models. It was concluded that the ANN model is much more accurate for their datasets. Pektaş and Cigizoglu (2013) modelled the monthly runoff coefficients of 7 southern large basins by using univariate autoregressive integrated moving average (ARIMA), multivariate ARIMA (ARIMAX) and ANN models. The authors indicated that multivariate models are superior to univariate models in predicting monthly runoff coefficients.

According to these studies, the large and comprehensive stochastic and computational intelligence models were used to forecast some hydrological parameters that the models performance was compared by together. The key question is ‘the results would be constant in critical condition?’ In the other words, if the ANN models have the better performance rather than SARIMA models to forecast the river flows, would they be better in forecasting river flows in droughts and floods conditions or not? The second question is ‘how many important to choose the type of algorithm in the computational intelligence models in compare of stochastic models to find the best model performance?’ In the current study, the performance of the Seasonal Autoregressive Integrated Moving Average (SARIMA) models and hybrid Artificial Neural Network-Genetic Algorithm (ANN-GA) method in predicting the input monthly discharge flow to the Jamishan Reservoir located in the west of Iran is compared and evaluated. Therefore, 14 and 80 different input combinations with different time lags are determined and used in the ANN-GA and SARIMA models, respectively.

Materials and Method

Study Area and Data

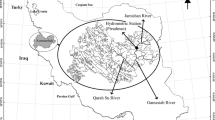
Data from Pirsalman Hydrometric Station (46°40′N, 34°14′E) are used in this research for modeling and forecasting the monthly discharge of the Jamishan River, which is located in the west of Iran. The data include 30 water years worth of data from October 1981 to September 2011. The initial 21 years are used as the calibration period and the 9 remaining years are used as the validation period.

The Jamishan Reservoir dam is currently under construction on the Jamishan River located in southwest Songor Province. This reservoir dam will have a normal volume of 62.8 million cubic meters and is aimed at providing the essential agricultural water for this area, controlling floods and preventing damages caused by flooding.

Data Pre-Processing

In hydrologic time series modelling, time series duration should include droughts and wet periods. Thus, the number of data duration must be adequate for modelling. In this regard, the Hurst coefficient (Hurst et al. 1965) is applied in this study. This coefficient represents the adequacy of time duration. If this ratio is greater than 0.5, the time series will adequate for modelling. This coefficient is as follow:

$$H = \frac{{\text{Log(}\frac{{S_{{\text{max}}} - S_{{\text{min}}} }}{{S_{x} }}\text{)}}}{{\text{Log(}\frac{N}{\text{2}}\text{)}}},$$
(1)

where H is the Hurst coefficient, N is the number of data, Sx is the standard deviation of the data, Smax is the maximum cumulative mean difference and Smin is the minimum cumulative mean difference. In this study, this ratio is obtained by 0.711.

In the ARIMA model, data should follow normal distribution (Salas et al. 1988) The Box-Cox transformation (Box and Cox 1964) is used to stabilize data and for standard deviation normalization. Jarque–Bera testing (Jarque and Bera 1980) serves to investigate discharge flow data normalization. Figure 1 shows the ACF and PACF diagrams for the normalized inflow in the calibration period for delays 1–48. In this figure, LL and UL are the upper and lower limit in the 95% confidence level, respectively. As seen in the figure, the values of both diagrams in the first two lags is high. As a result, maximum two, autoregressive and moving average parameters are needed for the SARIMA model (Cryer and Chen 2008).

Fig. 1
figure 1

ACF and PACF graphs for the normalized data in the calibration period

Full size image

These diagrams also used to determine the seasonal differencing order (D), non-seasonal differencing order (d), and data periodicity (ω) to make the time series stationary. It can be understood that the ACF and PACF diagrams are not damped. The PACF model also changes its sign (while it is high) immediately after the first lag time, which indicates that the time series is non-stationary. The ACF diagram has intervals of 12, signifying that the time series data have seasonal fluctuations (periodical component) with intervals of 12. Thus, one seasonal differencing is required. On the other hand, the ACF diagram is around the symmetrical vertical axis with a mean of nearly 0. This indicates the lack of a “trend component” in the time series. As a result, seasonal differencing is not necessary. Thus, we have ω = 12, d = 0 and D = 1.

Modeling Process with Stochastic Approaches

SARIMA model (p,d,q) (P,D,Q)ω has seasonal and non-seasonal autoregressive and moving average components that are expressed as follows:

$$\begin{aligned} (1 - \varPhi_{1} B^{\omega } - \varPhi_{2} B^{2\omega } - \cdots - \varPhi_{P} B^{P} )(1 - \phi_{1} B^{\omega } - \phi_{2} \times B^{2\omega } - \cdots - \phi_{p} B^{p} )(1 - B^{\omega } )^{D} (1 - B)^{d} x_{t} \hfill \\ = (1 - \varTheta_{1} B^{\omega } - \varTheta_{2} B^{2\omega } - \cdots - \varTheta_{Q} B^{Q} ) \times (1 - \theta_{1} B^{\omega } - \theta_{2} B^{2\omega } - \cdots - \theta_{q} B^{q} )\varepsilon_{t} , \hfill \\ \end{aligned}$$
(2)

where xt is the observed data in time t, εt is the random variable, ω is the periodicity, B is the difference operator B (xt) = xt−1 (1−Bω)D is the Dth seasonal difference measure ω, (1−B)d is the dth non-seasonal difference, p is the non-seasonal autoregressive order, q is the order of the non-seasonal moving average, P is the seasonal autoregressive order, Q is the order of seasonal moving average, φ is the non-seasonal autoregressive parameter, θ is the parameter of non-seasonal moving average, Φ is the seasonal autoregressive parameter and Θ is the seasonal moving average.

After fitting the models, those that have parameters with a significant difference from zero and that also have independent residuals that will be accepted. In this study, the t-student test is used to examine the significance of the model parameters. This test statistic is expressed as:

$$\uptau = \text{Pr/Se}$$
(3)

where τ, Pr and Se are the test statistic, estimated value of each parameter (including Φ, Θ, \(\phi\) and θ) and estimated standard error for each parameter, respectively. By considering 5% as the significance level, the intended parameter is significant when the value of the corresponding probability of τ statistic level is smaller than this value in the t-student distribution (Pτ < 0.05). This means that the parameter effectively participates in modelling.

The Box-Pierce test (Box and Pierce 1970; McLeod 1978) is used to examine the independency of the residuals and this test statistic is as follows:

$$\text{Q}^{\text{*}} = \text{n(n} + \text{2)}\sum\limits_{{\text{l} = \text{1}}}^{\text{L}} {\text{r}_{\text{l}}^{\text{2}} \text{(}\varepsilon \text{)/(n} - \text{1)}}$$
(4)

where Q*, rl(ε), n and L are the test statistic, the residual’s autocorrelation coefficient with lag l, the number of non-missing months after differencing (n = N−d−Dω) and the maximum time lag, respectively. In addition, the number of model parameters is defined as k = p + q + P + Q. In case the level of the corresponding probability of Q* in the Chi-square distribution with a degree of freedom DF = L−K−1 is larger than the intended level of significance, which is 5% (PQ* > 0.05), the residuals series will be independent.

The periodical component is one of the most effective factors that cause dependency in time series. Since monthly discharge data have this component, the model residuals may have the periodical component and they will consequently not be independent. The cumulative periodogram is also used to ensure that the periodical component is completely removed from the residuals. The cumulative periodogram for residuals is expressed as:

$$\text{MSD(h}{}_{\text{j}}\text{)} = 2\left[ {\left( {\sum\limits_{{\text{t} = \text{1}}}^{\text{n}} {\upvarepsilon_{\text{t}} \text{cos(2}\pi \text{h}_{\text{j}} t)} } \right)^{\text{2}} + \left( {\sum\limits_{{\text{t} = \text{1}}}^{\text{n}} {\upvarepsilon_{\text{t}} \text{sin(2}\pi \text{h}_{\text{j}} t\text{)}} } \right)^{\text{2}} } \right]/\text{n}^{\text{2}} \text{, h}_{\text{j}} = \text{j/n}$$
(5)
$$\text{P}_{\text{i}} = \sum\limits_{{\text{j} = \text{1}}}^{\text{i}} {\text{MSD(h}_{\text{j}} {)/\sigma }_{\upvarepsilon}^{\text{2}} } ,\quad i = 1,2, \cdots ,n/2,$$
(6)

where Pi, hj, MSD, εt, and \(\sigma_{\varepsilon }^{2}\) are the cumulative periodogram of residuals, the frequency, the mean squared deviation, the values of residuals in time t and the variance of εt, respectively. If the residual time series is independent, the Pi graph, in terms of hi, will be close to the line that connects the (0, 0) and (0.5, 0) points. The Kolmogorov–Smirnov confidence limits are away from the mentioned lines by ± Kα/√n'. \({n^{\prime}} = \text{(n} - \text{2)/2}\), \({n^{\prime}} = \text{(n} - \text{1)/2}\) for even and odd numbers, respectively. The value of Kα is also equal to 1.36 at the 95% confidence level.

Hybrid Artificial Neural Network-Genetic Algorithm (ANN-GA) Method

The multi-layer perceptron (MLP) neural network is one of the most common artificial intelligence methods. An MLP is formed from three types of layers: an input layer, one or more hidden layers and an output layer, all of which consist of neurons. The neurons in each layer evaluate the weighted summation of the previous layer’s neurons and transfer the result to the next layer. The numbers of input and output layer neurons are equal to the numbers of input and output variables of the problem, respectively. However, there is no specific rule to determine the number of hidden layer neurons and is thus a perplexing problem in MLP simulations. In this study, the novel, hybrid ANN-GA method is employed. The ANN-GA procedure is shown in Fig. 2, which presents the steps in evaluating the optimum ANN-GA model. To begin with, the input variables are presented to the model. Secondly, the random populations of different MLP models with various numbers of hidden layer neurons are constructed. These MLPs perform as chromosomes for the modified GA employed. In the present models, MLPs with two hidden layers are used. Next, each MLP generated in the previous step is run and its cost is evaluated. The calculated costs are then sorted and the ANN-GA termination criteria are checked. If the criteria are fulfilled, the best chromosome is saved as the optimum ANN-GA model. Otherwise, the procedure continues. Next, by using GA operators such as crossover, mutation and the elite process, the next generation is constructed. Lastly, the termination criteria are checked; if fulfilled, the process stops, otherwise the previous step is run again.

Fig. 2
figure 2

ANN-GA flowchart

Full size image

To train the MLP models, the Levenberg–Marquardt (LM) Algorithm (Levenberg 1944) is used. Thus, the MLP models are trained in a random manner. As a result, a high-performance chromosome may be turned off by the GA due to bad luck in the LM training algorithm. In order to solve this defect, a modification is done on the GA. As seen in the flowchart of the modified GA, the elite population runs several times and the best cost of the repeated runs is saved. With this modification, the probability of elite chromosome elimination (due to training defects) is reduced significantly.

According to the ACF graph in Fig. 1, the autocorrelation values take large values in lags 1, 2, 3, 6, 12, and 24, such that they intersect at UL and LL. This indicates that discharges with the above-mentioned lags dramatically affect each other. Therefore, combinations of these discharges are used to select the proper input for the hybrid Artificial Neural Network-Genetic Algorithm (ANN-GA) method. The 14 input combinations considered for the ANN-GA model are presented in Table 1.

Table 1 Different ANN-GA models with different input combinations
Full size table

Evaluation Criteria of the Best Models

The Mean Squared Error (MS) and Corrected Akaike’s Information Criterion (AICc) are used to select the best SARIMA model (the model with the minimum error and minimum number of parameters):

$$\text{AICc} = \text{n}{.Ln(\sigma }_{\upvarepsilon}^{\text{2}} \text{)} + \text{2kn/(n} - \text{k} - \text{1)}$$
(7)
$$\text{MS} = \sum\limits_{{\text{i} = \text{1}}}^{\text{n}} {\text{(Q}_{{\text{ni}}} - {\hat{Q}}_{{\text{ni}}} \text{)}^{\text{2}} /(\text{n} - \text{k} - \text{1)}} ,$$
(8)

where Q ni is the normalized value of the observed discharge, Q ni is the normalized fitted discharge value, k is the number of model parameters and n is the number of non-missing months after differencing in the data sample for the calibration period. Moreover, to ensure the best SARIMA model is selected to subsequently select the best ANN-GA model and compare these two models, Mean Absolute Relative Error (MARE), correlation coefficient (R), Root mean squared errors (RMSE) and Nash-Sucliffie criteria are separately calculated for the calibration and validation periods between the observed and fitted, or forecasted data.

$${\text{MARE}} = \sum\limits_{{\text{i} = \text{1}}}^{\text{n}} {\left| {\frac{{\text{Q}}_{\text{i}} - {\hat{{\text{Q}}}}_{\text{i}} }{{\text{Q}_{\text{i}} }}} \right|} \text{/n}$$
(9)
$$R = \sum\limits_{{i = \text{1}}}^{n} {\text{(}Q_{i} - \bar{Q}_{i} \text{)(}\hat{Q}_{i} - \bar{\hat{Q}}_{i} \text{)/}\sqrt {\sum\limits_{{i = \text{1}}}^{n} {\text{(}Q_{i} - \bar{Q}_{i} \text{)}^{\text{2}} \sum\limits_{{i = \text{1}}}^{n} {\text{(}\hat{Q}_{i} - \bar{\hat{Q}}_{i} \text{)}^{\text{2}} } } } }$$
(10)
$${\text{RMSE}} = \sqrt {\frac{{\sum\nolimits_{{t = {\text{1}}}}^{n} {{\text{(}}Q{\text{(}}t{\text{)}} - \hat{Q}{\text{(}}t{\text{))}}^{{\text{2}}} } }}{n}}$$
(11)
$$\text{Nash-Sucliffe} = 1 - \frac{{\sum\nolimits_{{t = \text{1}}}^{n} {\text{(}Q\text{(}t\text{)} - {\hat{Q}}\text{(}t\text{))}^{\text{2}} } }}{{\sum\nolimits_{{t = \text{1}}}^{n} {\text{(}Q\text{(}t\text{)} - \bar{Q}\text{(}t\text{))}^{\text{2}} } }},$$
(12)

where Qi is the observed discharge in the ith month, \({\hat{Q}}_{\text{i}}\) is the computed discharge in the ith month, \({\bar{Q}}_{\text{i}}\) is the mean of the observed discharges, \({\bar{\hat{Q}}}_{\text{i}}\) is the mean of the computed discharges, n is the number of non-missing months after differencing for calibration or the validation period, and i is the month number. The mean values of the observations obtained are 1.85 and 1.54 m3/s in the calibration and validation periods, respectively. In addition, determining the time error and best time of forecasting, and comparing the performance of the best SARIMA and ANN-GA models, the absolute relative error in month i (Ei), average of cumulative relative errors in month i (Fi), and coefficient of relative error variation (CV) are calculated as follows:

$${\text{E}}_{\text{i}} = \left| {\text{Q}}_{\text{i}} - {\hat{{\text{Q}}}}_{\text{i}} \right|/{\text{Q}}_{\text{i}}$$
(13)
$$\text{F}_{\text{i}} = \sum\limits_{{\text{j} = \text{1}}}^{\text{i}} {\text{E}_{\text{j}} } \text{/i}$$
(14)
$$\text{C}_{\text{v}} = \sqrt {\sum\limits_{{\text{i} = \text{1}}}^{\text{n}} {\frac{{\text{(E}_{\text{i}} - {\bar{E})}}}{\text{n}}\text{/E}} }$$
(15)

where \({\bar{E}}\) is the relative error average.

Results and Discussion

Selecting the Best Models

Different SARIMA and ANN-GA models were applied to the monthly inflow data collected from the Jamishan Reservoir dam. The results obtained by utilizing different statistical indexes for both calibration and validation periods were presented in Table 2. As seen in this table, to select the best model using SARIMA, 5 superior models were fitted from amongst 80 different models that were evaluated with the AICc and MS indexes. These indexes not only consider the difference between the observed and fitted values but also take into account the effects of number of parameters. The SARIMA(1,0,2)(0,1,1)12 model is clearly more accurate than other models. To select the best model presented using ANN-GA, the MARE and R indexes are used for the validation and calibration periods. The maximum value of R calculated is 0.86 in the calibration period for the ANN-GA-14 model. This model has the maximum discharge as input with 1, 2, 6, 12 and 24-month lag times. However, it does not present good results in the validation periods and is amongst the weakest models. The ANN-GA-3 model with the best MARE in calibration and that uses 1 and 12-month lag times in discharge forecasting, is fairly accurate in the validation period. It presents quite similar results in both periods, which is an indication of this model’s flexibility in forecasting monthly discharge. However, since the final objective of modeling is forecasting and the model’s forecasting error is of utmost importance, the ANN-GA-9 model with the best result in the validation period (MARE = 0.715, R = 0.802) as Q = f(Qt−1, Qt−2, Qt−6, Qt−12) is selected as the best model presented using ANN-GA.

Table 2 Evaluation criteria results for determining the best SARIMA and ANN-GA models
Full size table

The t-student test serves as a significance test in examining the significance of parameters. The Box-Pierce test is used as an independence test to examine the independency of the selected SARIMA model’s residuals. The results are presented in Table 3.

Table 3 Independence test results for the residuals and significance test results for the selected SARIMA model parameters
Full size table

The significance test results indicate that the Pτ values are smaller than the intended significance level of 5% for each parameter. The estimated value of each parameter is therefore within this level of significance. In fact, there is a substantial difference between all parameters and 0. Therefore, the parameters effectively participate in modelling and forecasting. Regarding the independence test, since the value of the corresponding probability of Q* in the Chi-square distribution with degree of freedom (DF) per lag L, meaning the PQ* value, is larger than the intended significance level of 5% in different lags, the residuals of the selected SARIMA model are independent based on the results of this independence test and they are not dependent on time. The large difference between the PQ* values and 5 indicates that the residuals are independent with a high degree of confidence.

A cumulative periodogram was employed to make sure that the periodical component was completely removed from the model residuals. Figure 3 shows the cumulative periodogram for the residuals of the best SARIMA model. The vertical axis represents the frequency in this graph and the horizontal axis shows the cumulative periodogram for the residuals. UL and LL are the Kolmogorov–Smirnov confidence limits at the 95% level of confidence. Since the graph of Pi in terms of hi, is close to the line that connects the (0, 0) and (0.5, 0) points and it is within the range between UL and LL, it can be concluded that the periodical component has been perfectly removed from the residuals. This is another reason for the independency of residuals in the SARIMA model selected.

Fig. 3
figure 3

Cumulative periodogram for the best SARIMA model residuals

Full size image

Model’s Ability to Forecast Inflow

Figure 4 represents the monthly discharge time series forecasted by the ANN-GA-9 and SARIMA(1,0,2)(0,1,1)12 models against the observed discharge values. The models identified the monthly discharge changes with regards to time to an acceptable degree. By increasing the observed discharge values, the two model’s furcated values increased and vice versa. This shows that both models identified the monthly mean discharge changes for these datasets very well. These are, however, less accurate as the discharge value increases due to the intense seasonal changes in peak discharge. For instance, the monthly discharge was 0.17 m3/s in September 1994 and 13.34 m3/s in December 1994. These dramatic changes decreased the peak-discharge forecasting accuracy.

Fig. 4
figure 4

SARIMA and ANN-GA model results for the validation period

Full size image

Figure 5 shows the performance of the ANN-GA-9 and SARIMA(1,0,2)(0,1,1)12 models in modeling and forecasting the monthly inflow to the dam in the calibration and validation periods. As shown in this figure, the results for low-flow discharge in both validation and calibration periods are closer to the best fit line than the peak discharge, which indicates that these models perform better for low-value discharge than peak discharge. The SARIMA model outperforms ANN-GA in this respect. The results obtained by SARIMA are underestimated and overestimated for all discharges (low and peak discharges); although, the underestimated, fitted and forecasted discharges have a relative error greater than that of the overestimated ones. The results obtained with ANN-GA are inconsistent with SARIMA as the discharge increases and especially at peak discharges. ANN-GA underestimates most of the discharges as discharge increases. ANN-GA estimates the monthly inflow to the dam with a smaller relative error compared with the validation state where the peak discharge has a smaller value than the calibration state. Regarding the incorrect estimation and large difference from the actual values, ANN-GA will not perform properly for major floods.

Fig. 5
figure 5

Observed and modeled monthly discharge by the SARIMA and ANN-GA models in the calibration and validation periods

Full size image

Evaluation of the Models in Drought and Wet Conditions

Along with MARE criterion based on the relative errors, Nash-Sucliffe and RMSE criteria based on absolute errors, were calculated only for the best models. These criteria calculated for the best ANN-GA model and then it was considered with the same settings for the simple ANN model presented in Table 4. The results show that these criteria are so closely in ANN-GA and ANN models and also using the genetic algorithm in ANN model cause to occur insignificantly changes in prediction accuracy. Therefore, using advanced algorithm in ANN model always not to be useful in increasing of forecasting model accuracy. In addition, Table 4 shows that in comparison of ANN and ANN-GA models, the MARE criterion is significantly improved and the other criteria are also decreased in SARIMA model. Since MARE is obtained based on relative errors, it’s very sensitive in the small values and it changes suddenly in the small values. On the other hand, Nash-Sucliffe and RMSE criteria are obtained based on the absolute errors are more sensitive in large values. As a result, SARIMA model is the best model to forecast the base flows and in drought conditions and also ANN and ANN-GA models are the best models to predict the peak flows and in the flood conditions in this study.

Table 4 Evaluation criteria results for best models
Full size table

Time Changes of the Model’s Forecast Error

Equations 10–12 are used to examine the values forecasted by the models in order to study the forecasting changes with time. Table 5 shows the values of Emin, Cv and \(\bar{E}\) along with Fmin and the month in which this value occurred for the validation period. The CV and \(\bar{E}\) values are smaller for SARIMA, indicating that the error changes are lower and this model is superior to ANN-GA, since the smaller the relative errors, the smaller their mean will be. CV being smaller indicates the fact that the errors are closer to the mean for the SARIMA model, and as a result, the error changes in time and the peak error points are lower in this model. Figure 6 shows the changes in the relative error and average cumulative relative error in time for SARIMA and ANN-GA in the forecast, or validation period. It can be understood from the E index graph that the ANN-GA model has more and much larger peak error points than SARIMA. It is clear from the index F graph in this same figure that this index value is smaller for the SARIMA model than the ANN-GA model. The maximum F value is 0.44 for the SARIMA model and the minimum value of this index is equal to 0.43 for the ANN-GA model (Fmax(SARIMA) ≃ Fmin(ANN-GA)). The F index value for the SARIMA model hardly reached the index value of the ANN-GA model. This also shows the superiority of SARIMA over ANN-GA. Two points can be noted from this graph. First, the minimum error of the SARIMA model occurs in predicting the following month (1 month later). The F value of ANN-GA is 10 times the value of the F index for the SARIMA model in this month, meaning that SARIMA forecasts the discharge of the following month 10 times more precisely than ANN-GA. The second point is that the SARIMA model graph of F index changes become almost horizontal with time and as the forecast horizon increases, such that it reaches a sort of stagnation that does not exist with the ANN-GA model. This graph displays an upward trend for the ANN-GA model, meaning that the ANN-GA model error increases as the forecast horizon increases. These two points indicate that the SARIMA model is capable of making short-term forecasts with much lesser error and long-term forecasts without an increase in error—two abilities lacking in the ANN-GA model. Therefore, the SARIMA model most definitely performs better than ANN-GA in short-term planning such as exploitation and consumption management and in long-term planning such as designing and constructing hydraulic structures.

Table 5 Minimum F and E index values along with the mean and standard deviation of the relative error
Full size table
Fig. 6
figure 6

Graphs of E and F index changes over time for the discharges forecasted by the selected models

Full size image

Conclusion

In this study the abilities of SARIMA and the hybrid Artificial Neural Network-Genetic Algorithm (ANN-GA) method in forecasting the monthly inflow to the Jamishan Dam in the west of Iran were analyzed and their results were compared with simple ANN model. Data from Pirsalman hydrometric station were used, including 30 water years. The initial 21 years served as the calibration period and the 9 final years were used as the validation period. The best SARIMA model had significance parameters and independence residuals. Both models identified the process of monthly discharge changes very well. Forecasting the base flow and low flows was done precisely by the SARIMA model precisely in comparison of ANN and ANN-GA models and also these models are more suitable to forecast the peak flows and flood flows in comparison of SARIMA model. The results show that there were no significant changes between ANN and ANN-GA models while the results of ANN-GA were a little bit better than ANN model. So, SARIMA model is more suitable in the drought years and low flow forecasting and ANN-GA model is more suitable in the wet years and flood flows forecasting. The SARIMA model also had lower error changes over time during the prediction period, such that it had lower error peak points in the E index graph than ANN-GA. Analysing the graph of the F index over time leads to concluding that the SARIMA model had an error less than one tenth of the ANN-GA error in forecasting the following month discharge. On the other hand, the forecast error did not increase much with increasing forecast horizon, meaning the SARIMA model is able to make much more precise short-term forecasts than the ANN-GA model and is also able to make long-term forecasts without a noticeable error increase. Therefore, the SARIMA model definitely outperforms the ANN-GA model in short-term plans such as exploitation and consumption management and in long-term plans such as designing and constructing hydraulic structures.