Statistical Estimation of Exponential Power Distribution on Different Progressive Type-II Censoring Schemes

Abstract

In recent life-testing experiments, Progressive Type-II (PT2) censoring has been used by several researchers in various problems. However, one drawback of PT2 is that the length of the experiment might be fairly long. Progressive Type-II hybrid (PT2H) and later adaptive progressive Type-II (APT2) censorings were used to overcome this disadvantage. This study investigates the advantages and disadvantages of these censoring techniques using the Exponential Power (EP) distribution. The EP distribution is known for its ability to model increasing and bathtub-shaped failure rates, and it has gained acceptance in several domains, especially in the areas of reliability-related decision-making and cost analysis. This makes the EP model a useful alternative to the most widely used Weibull distribution in some instances. To assess the efficiency of both Maximum Likelihood Estimators and Bayesian estimators generated through PT2, PT2H, and APT2, we have conducted a comprehensive simulation study. Additionally, we compare the performance of PT2, PT2H, and APT2 when applied to the EP distribution with popular time models using real data.

Appendix A.

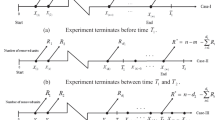
PT2

$$\begin{aligned} \frac{\partial ^{2}\log L_{1}}{\partial \alpha ^{2}}=&-\frac{m}{\alpha ^{2}}+\sum _{i=1}^{m}\left[ 1-(1+(\lambda x_{i})^{\alpha })e^{(\lambda x_{i})^{\alpha }}\right] (\lambda x_{i})^{\alpha }\log ^{2}(\lambda x_{i})-\\&\sum _{i=1}^{m}R_{i}\left[ 1+(\lambda x_{i})^{\alpha }\right] (\lambda x_{i})^{\alpha }\log ^{2}(\lambda x_{i})e^{(\lambda x_{i})^{\alpha }}\\ \frac{\partial ^{2}\log L_{1}}{\partial \alpha \partial \lambda }=&\frac{m}{\lambda }+\sum _{i=1}^{m}\bigl \{\lambda ^{\alpha -1}x_{i}^{\alpha }\left[ 1-(1+R_{i})e^{(\lambda x_{i})^{\alpha }}\right] \left( \alpha \log (\lambda x_{i})+1\right) \\&-\alpha \lambda ^{2\alpha -1}x_{i}^{2\alpha }(1+R_{i})e^{(\lambda x_{i})^{\alpha }}\log (\lambda x_{i})\bigr \}\\ =&\frac{\partial ^{2}\log L_{1}}{\partial \lambda \partial \alpha }\\ \frac{\partial ^{2}\log L_{1}}{\partial \lambda ^{2}}=&-\frac{m\alpha }{\lambda ^{2}}+\sum _{i=1}^{m}\alpha x_{i}^{\alpha }\\&\left[ (\alpha -1)\lambda ^{\alpha -2}\left( 1-(1+R_{i})e^{(\lambda x_{i})^{\alpha }}\right) -\alpha \lambda ^{2\alpha -2}x_{i}^{\alpha }(1+R_{i})e^{(\lambda x_{i})^{\alpha }}\right] \end{aligned}$$

PT2H

$$\begin{aligned} \frac{\partial ^2\log L_{2}}{\partial \alpha ^2}=&-\frac{D}{\alpha ^2}+\sum _{i=1}^{D}(\lambda x_{i})^{\alpha }(\log (\lambda x_{i}))^2\left( (1-e^{(\lambda x_{i})^{\alpha }})-(\lambda x_{i})^\alpha e^{(\lambda x_{i})^{\alpha }}\right) \\&-\sum _{i=1}^{D}R_{i}(\log (\lambda x_{i}))^{2}(\lambda x_{i})^{\alpha }e^{(\lambda x_{i})^{\alpha }}((\lambda x_{i}^\alpha +1))\\&-(n-D-\sum _{i=1}^{D}R_{i})(\lambda T)^\alpha (\log (\lambda T))^2 e^{(\lambda T)^\alpha }((\lambda T)^\alpha +1)\\ \frac{\partial ^2\log L_{2}}{\partial \alpha \partial \lambda }=&\frac{D}{\lambda }-\sum _{i=1}^{D}\lambda ^{\alpha -1}x_{i}^{\alpha }\left( \alpha (\lambda x_{i})^{\alpha }\log (\lambda x_{i})e^{(\lambda x_{i})^{\alpha }}-(1-e^{(\lambda x_{i})^{\alpha }})(\log (\lambda x_{i})^{\alpha }+1)\right) \\&-\sum _{i=1}^{D}R_{i}\lambda ^{\alpha -1}x_{i}^{\alpha }e^{(\lambda x_{i}^{\alpha })}\left( \alpha (\lambda x_{i})^\alpha \log (\lambda x_{i})+\log (\lambda x_{i})^{\alpha }+1\right) \\&-(n-D-\sum _{i=1}^{D}R_{i})\lambda ^{\alpha -1}T^{\alpha }e^{(\lambda T)^{\alpha }}\left( \alpha (\lambda T)^\alpha \log (\lambda T)+\log (\lambda T)^{\alpha }+1\right) \\&=\frac{\partial ^2\log L_{2}}{\partial \lambda \partial \alpha }\\ \frac{\partial ^2\log L_{2}}{\partial \lambda ^2}=&-\frac{D\alpha }{\lambda ^2}+\alpha \sum _{i=1}^{D}\lambda ^{\alpha -2}x_{i}^{\alpha }\left( (\alpha -1)(1-e^{(\lambda x_{i})^{\alpha }})-\alpha (\lambda x_{i})^{\alpha }e^{(\lambda x_{i})^{\alpha }}\right) \\&-\alpha \sum _{i=1}^{D}R_{i}\lambda ^{\alpha -2}x_{i}^{\alpha }e^{(\lambda x_{i})^{\alpha }}(\alpha (\lambda x_{i})^{\alpha }+\alpha -1)\\&-(n-D-\sum _{i=1}^{D}R_{i})\alpha \lambda ^{\alpha -1} T^{\alpha }e^{(\lambda T)^{\alpha }}(\alpha (\lambda T)^{\alpha }+\alpha -1) \end{aligned}$$

APT2

$$\begin{aligned} \frac{\partial ^2\log L_{3}}{\partial \alpha ^2}=&-\frac{m}{\alpha ^2}+\sum _{i=1}^{m}(\lambda x_{i})^\alpha (\log (\lambda x_{i}))^2\left( 1-(1+(\lambda x_{i})^\alpha )e^{(\lambda x_{i})^{\alpha }}\right) \\&-\sum _{i=1}^{j}R_{i}(\lambda x_{i})^{\alpha }(\log (\lambda x_{i}))^2e^{(\lambda x_{i})^\alpha }(1+(\lambda x_{i})^{\alpha })\\&-(n-m-\sum _{i=1}^{j}R_{i})(\lambda x_{m})^{\alpha }(\log (\lambda x_{m}))^2 e^{(\lambda x_{m})^\alpha }(1+(\lambda x_{m})^\alpha )\\ \frac{\partial ^2\log L_{3}}{\partial \alpha \partial \lambda }=&\frac{m}{\lambda }-\sum _{i=1}^{m}x_{i}^{\alpha }\lambda ^{\alpha -1}\left( \alpha (\lambda x_{i})^\alpha \log (\lambda x_{i})e^{(\lambda x_{i})^{\alpha }}-(1-e^{(\lambda x_{i})^{\alpha }})\left( \log (\lambda x_{i})^{\alpha }+1\right) \right) \\&-\sum _{i=1}^{j}R_{i}x_{i}^{\alpha }\lambda ^{\alpha -1}e^{(\lambda x_{i})^{\alpha }}\left( \alpha (\lambda x_{i})^{\alpha }\log (\lambda x_{i})+\log (\lambda x_{i})^{\alpha }+1\right) \\&-\left( n-m-\sum _{i=1}^{j}R_{i}\right) x_{m}^{\alpha }\lambda ^{\alpha -1}e^{(\lambda x_{m})^{\alpha }}\left( \alpha (\lambda x_{m})^{\alpha }\log (\lambda x_{m})+\log (\lambda x_{m})^{\alpha }+1\right) \\&=\frac{\partial ^2\log L_{3}}{\partial \lambda \partial \alpha }\\ \frac{\partial ^2\log L_{3}}{\partial \lambda ^{2}}=&-\frac{m\alpha }{\lambda ^{2}}+\alpha \sum _{i=1}^{m}x_{i}^{\alpha }\lambda ^{\alpha -2}\left( (\alpha -1)(1-e^{(\lambda x_{i})^{\alpha }})-\alpha (\lambda x_{i})^{\alpha }e^{(\lambda x_{i})^{\alpha }}\right) \\&-\alpha \sum _{i=1}^{j}R_{i}x_{i}^{\alpha }\lambda ^{\alpha -2}e^{(\lambda x_{i})^{\alpha }}\left( \alpha (\lambda x_{i})^{\alpha }+\alpha -1\right) \\&-\left( n-m-\sum _{i=1}^{j}R_{i}\right) \alpha x_{m}^{\alpha }\lambda ^{\alpha -2}e^{(\lambda x_{m})^\alpha }\left( \alpha (\lambda x_{m})^\alpha +\alpha -1\right) \end{aligned}$$