Introduction

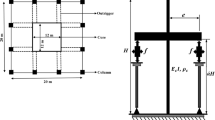
In the construction sector, several structural systems like bridges, buildings, railway systems, and nuclear power plants are the systems that are affected by vibration. The vibration occurs because of lateral load, blast load, impact load, and other dynamic loads. The main design criteria along with the preliminary consideration are vibration control of the structure, so that vibration is reduced to the permissible level. The construction sector in the earlier days in the building design would not consider earthquakes and hurricanes effects as loads for the structure. Earthquakes and hurricanes were considered completely unpredictable in both time occurrence and intensity because there were no suitable techniques to reduce the risk of occurrence. All these reasons lead the construction sector to evolve toward the concept of “Structural Control.” Mainly the tall structure is designed to overcome the hurricanes load and earthquake load that plays a dominant role in structural control. To reduce the wind-induced vibrations in the tall building, a state-of-the-art and state-of-the-practice review has been conducted by Jafari and Alipour in article [1] explaining about passive control system and active control system. Authors state that passive control of tall buildings can be done by structural design by increasing stiffness or mass, aerodynamic design approach can be used by cross-sectional modification, shape modification, and by using smart facades as stated in the article [2]. Authors also state that passive devices can be used by adding energy dissipative material to increase damping ratio or by adding an auxiliary mass system to increase damping level, and active damping devices are used to generate control by aerodynamic control force or by inertial effect. Under the response control method, modification of dynamic interaction between the structure and earthquake ground motion can be done, and minimizing the structural damage and control response can be done. Here the structure is considered as a dynamic system in which some properties typically the stiffness or damping can be adjusted in such a way that the dynamic effect of the load on the building decreases under an acceptable level. The natural frequency of the structure, mode shapes, and corresponding damping values are changed in such a way that dynamic forces coming from natural loads are reduced. These changes in the dynamical response in the structure can be done by varieties of techniques and can be clubbed into four categories like passive control, active control, semi-active control, and hybrid control as stated in the article [3, 4]. The passive control systems [5] are evolving to take maximum advantage of the proposed ideas, and a new column-in-column system is proposed by the inspiration of the tuned mass damper concept where a single column is divided into two parts interior and exterior portion, where the interior column works as a tuned mass damper and the exterior column acts as the primary structure in the system that is designed in ABAQUS shows an effective reduction in the seismic response [6]. In semi-active control, the magneto-rheological (MR) damper has been promising in mitigating response from the literature survey done [7, 8]. All control systems use devices that are installed in the structure that will undergo vibration because of the lateral loads and they will try to overcome the vibrations either by energy dissipation, base isolation, or energy transfer. For better performance of the structure, the bracing system, control device, some algorithms are introduced to regulate these devices during an uncertain event in making it work according to the situations in reducing the total structural response [9]. The different control approaches are used in controlling the structure like classical control, modern control, robust control, optimal control, adaptive control, and nonlinear control. The control systems are a set of hardware and software components that are integrated, to interface within themselves and interact in real time with the real world. In the control system, the sensors are used to tap the response or states of the system, but when noise variances of the state and measurement noise are associated with captured sensor output, the response will be corrupt [10]. In a practical situation, the states of the system cannot be determined directly by observation. Instead, this indirect effect of the internal states of the system needs to be estimated, by knowing the output of the system. A simple example of a tunnel with a vehicle can be explained: when a vehicle enters the tunnel its velocity and the rate can be observed directly and the same when it comes out of the tunnel. However, when the vehicle is inside the tunnel its rate or velocity and cannot be measured directly it only can be estimated by knowing the input and output of the system. Therefore, if a system is observable them the internal states of the system can be estimated by knowing the input and output of the system using an observer [11]. There is a solution to overcome this problem by using an observer that acts as a soft sensor in estimating the states of the system by using the measurement of output of system over the period of time [12, 13]. Figure 1 shows an observer-based control system in the structure.

Fig. 1
figure 1

Observer-based control system in the structure

Full size image

In structural control, the structural type considered in the design also plays important role in reducing the structural response [14]. Many studies have been focusing on the outrigger structural system [15, 16], and article [17] emphasizes on optimum positioning of the outrigger and optimum damping parameter using probabilistic analysis for different outrigger models to get the maximum reduction in the response. Beiraghi and Hedayathi in their article [18] have studied for optimum positioning of outrigger by placing one outrigger fixed at the top using buckling restrained braces by taking into consideration the inter-story drift ratio, to be minimum by placing outrigger in different positions throughout the height of the structure. In article [18], authors suggest the optimum positioning of the outrigger seems to be 0.75 times the height of the structure excited for earthquake, with the study of plastic hinge arrangement over the core wall. Beiraghi et al. in the article [19,20,21] used buckling restrained braces for outriggers and studied the plastic hinge location with a single hinge, three hinges, and extended hinge in the core wall for near-fault and far fault earthquake. In the process of evolution of damped outrigger, article [22] has proposed the design considering first mode damping ratio-oriented design policy, simple equations of optimal damper–connection stiffness ratio to maximize first mode damping ratio, a machine learning model to estimate first mode natural period, and damping ratio. The tuned inertial mass electromagnetic transducer is proposed by authors in the article [23] that is based on the mechanism of a tuned viscous mass damper, but has more energy absorbing capacity by the introduction of the motor instead of the viscous fluid that provides better performance in seismic response reduction. In the process of improving the outrigger system, a novel negative stiffness device is introduced to the outrigger in the article [24] to improve the maximum achievable damping ratio to about 30% with the less use of the coefficient of damping in outrigger that shows a better performance in comparison with the conventional damped outrigger. Islam and Jangid in the article [25] introduced a novel device called negative stiffness inerter damper that is a combination of negative stiffness damper and inerter-based vibration absorbers to mitigate the seismic response. In article [25], authors have found better control in story drift and acceleration in comparison of the result obtained by the proposed device with viscous and viscoelastic damper control. The recent development of the control devices in structural vibration control is a combination of various strategies as found in the literature survey. Therefore, the focus of this study is to reduce seismic vibrations.

In this study, a damped outrigger structure presenting St. Francis Shangri La Place is considered for numerical dynamic analysis excited for the El-Centro earthquake and Kobe earthquake. This damped outrigger structure is primarily parametrically analyzed to get fundamental natural period and fundamental natural frequency. This study aims to mitigate the seismic response of the structure with the use of a semi-active controller. To mitigate the response of the structure, a semi-active MR damper is installed to produce adequate force in the presence of a Kalman observer-based robust proportional–integral–derivative (PID) controller. To regulate the damper, controller gains are designed with the feedback loop to attain robustness; it is achieved by adopting differences in the actual and estimated models considering the effect of the external disturbance, process noise, and measured noise along with the Kalman observer. The observer considered in the study maintains the stability of the integrated system with the robust controller by overcoming uncertainty that might arise due to sensor, external and internal disturbances, and noise associated with the feedback or feedforward loop. The integrated system of observer-based robust PID controller is modeled in MATLAB and Simulink to mitigate the seismic response, but due to saturation in the integrated system, it produced extreme output and a very slow response was obtained. Because the integral windup causes a slowdown in the response of the feedback loop of the system anti-windup technique has been introduced; that refers to augmentation of the controller in the feedback loop. Therefore, this study comprises an observer-based anti-windup robust PID controller for damped outrigger with MR damper in mitigating the vibration of the structure. The adequacy of the proposed strategy is studied in terms of reduction in the following: (a) structural responses like displacement, acceleration, and velocity, (b) optimal control force, and (c) evaluation criteria values. Finally, it has been demonstrated that the proposed control algorithm provides superior performance and stability in comparison with the conventional PID-based techniques.

Methodology

In this study, St. Francis Shangri La Place is modeled according to the finite element approach considering the structural properties as specified by the article [26, 27]. The equation of the motion of the structure is,

$$M\ddot{U}(t)+{C}_{d}\dot{U}(t)+KU(t)=Nf(t)-MR{\ddot{U}}_{g}(t)$$
(1)

\(M, {C}_{d}, K\) represent the mass, damping, and stiffness of the structure, \(\ddot{U},\dot{ U, }U\) represent the acceleration, velocity, and stiffness of the structure, and \(N, f, {R, \ddot{U}}_{g}\) represent the location of the MR damper, the force produced by MR damper, column vector with translation degree with ones and zero, and earthquake acceleration. The mass matrix is of dimension 120 × 120, the stiffness matrix is of dimension 120 × 120 and the damping matrix is of dimension 120 × 120. In this paper, the optimum location of the outrigger is considered as 42nd floor as mentioned in the article [28, 29].

The MR damper dynamic formula of force produced is as follows,

$$f=\alpha z+{c}_{o}\left(\dot{X}-\dot{Y}\right)+{k}_{o}\left(X-Y\right)+{k}_{1}\left(X\right)$$
(2)

In the above formulas, \(f,\) \({k}_{1},{k}_{o}\) represent force produced by MR damper, accumulator stiffness, and stiffness controlled at large velocities, and \({c}_{o}, z, X,Y\) represent the damping at large velocity, evolutionary variable, and external and internal displacement of the damper.

The formulas of the current driver in connection with the MR damper are specified in the article [29, 30]. Table 1 represents the design parameter of the MR damper. The same MR damper is adopted in this study. The details of parameters that are given in Table 2 are obtained from the article.

Table 1 Design parameters of MR damper [26]
Full size table
Table 2 Parameter of MR damper model [26]
Full size table

The MR damper is modeled for 3000 \(kN\) capacity modeled in MATLAB and Simulink. The prototype MR damper which is modeled is tested for 0–5 \(Hz\) sinusoid wave with an amplitude of 25.4 \(mm\) and voltages which was a constant different value of 0–5 \(V\). It is found that this model starts to get saturated at the voltage applied more than 5 \(V\). Therefore, the voltage is restricted between 0 and 5 \(V\).

State-space representation

The state-space is pair of algebraic and linear differential equations as shown in Eqs. 3 and 4.

$$\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+E{\ddot{U}}_{g}(t)+ w$$
(3)
$$y\left(t\right)=Cx\left(t\right)+Du\left(t\right)+{v}_{0}$$
(4)

Here \(x\left( t \right),{ }u\left( t \right), y\left( t \right)\) are the state matrix, input matrix, and output matrix. The constants \(A, B, C, D,{ }E\) are the system matrix, input matrix, output matrix, direct transmission matrix, and disturbance matrix, and \(w\) and \(v_{0}\) are process noise and measured noise.

The equation of motion of the structure is a second-order differential equation, it is converted to a first-order equation to get state-space model parameters, and the procedure is as follows,

$$\left\{ {\ddot{U}\left( t \right)} \right\} + \left[ M \right]^{{ - 1}} \left[ {C_{d} } \right]\left\{ {\dot{U}\left( t \right)} \right\} + \left[ M \right]^{{ - 1}} \left[ K \right]\left\{ {U\left( t \right)} \right\} = \left[ M \right]^{{ - 1}} \left[ N \right]\left\{ {f\left( t \right)} \right\} - \left[ R \right]\left\{ {\ddot{U}_{g} \left( t \right)} \right\}$$
(5)

Defining,

$$x_{1} = U\left( t \right)$$
(6)
$$x_{2} = \dot{x}_{1} = \dot{U}\left( t \right)$$
(7)
$$~\dot{x}_{2} = \ddot{U}\left( t \right) = y$$
(8)
$$\left\{ {\ddot{U}\left( t \right)} \right\} = - \left[ M \right]^{{ - 1}} \left[ {C_{d} } \right]\left\{ {\dot{U}\left( t \right)} \right\} - \left[ M \right]^{{ - 1}} \left[ K \right]\left\{ {U\left( t \right)} \right\} + \left[ M \right]^{{ - 1}} \left[ N \right]\left\{ {f\left( t \right)} \right\} - \left[ R \right]\left\{ {\ddot{U}_{g} \left( t \right)} \right\}$$
(9)
$$\left\{ {~\dot{x}_{2} } \right\} = - \left[ M \right]^{{ - 1}} \left[ {C_{d} } \right]\left\{ {x_{2} } \right\} - \left[ M \right]^{{ - 1}} \left[ K \right]\left\{ {x_{1} } \right\} + \left[ M \right]^{{ - 1}} \left[ N \right]*\left\{ {f\left( t \right)} \right\} - \left[ R \right]\left\{ {\ddot{U}_{g} \left( t \right)} \right\}$$
(10)

The state vector of the state-space system is defined as,

$$x\left( t \right) = \left\{ {\begin{array}{*{20}c} {U\left( t \right)} \\ {\dot{U}\left( t \right)} \\ \end{array} } \right\}$$
(11)

By differentiating,

$$\dot{x}\left( t \right) = ~\left\{ {\begin{array}{*{20}c} {\dot{U}\left( t \right)} \\ {\ddot{U}\left( t \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {~\dot{x}_{1} } \\ {~\dot{x}_{2} } \\ \end{array} } \right\}$$
(12)

From Eqs. (7) and (10)

$$\dot{x}\left( t \right) = \left\{ {\begin{array}{*{20}c} { \dot{x}_{1} } \\ { \dot{x}_{2} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & I \\ { - \left[ M \right]^{ - 1} \left[ K \right]} & { - \left[ M \right]^{ - 1} \left[ {C_{d} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} 0 \\ {\left[ M \right]^{ - 1} \left[ N \right]} \\ \end{array} } \right]\left\{ u \right\} + \left[ {\begin{array}{*{20}c} 0 \\ { - \left[ R \right]} \\ \end{array} } \right]\left\{ u \right\}$$
(13)

The output of the system,

$$y\left( t \right) = \left[ {\begin{array}{*{20}c} { - \left[ M \right]^{{ - 1}} \left[ K \right]} {- \left[ M \right]^{{ - 1}} \left[ {C_{d} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right\} + \left[ {\left[ M \right]^{{ - 1}} \left[ N \right]} \right]\left\{ {u\left( t \right)} \right\}$$
(14)

From the above-derived equations, the system matrix consists of the structural displacement, and velocity constitutes a dimension of 240 × 1. Input matrix has two inputs: One is the force produced by the MR damper proportional to the voltage regulated by the controller and the other one is earthquake acceleration considered as a disturbance to the system. The output matrix is the acceleration of the structure.

$${\text{State vector}},x\left( t \right){ } = \left\{ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \vdots \\ \vdots \\ {x_{239} } \\ {x_{240} } \\ \end{array} } \right\}_{{240{ }X{ }1}} \left\{ {\begin{array}{*{20}c} {U_{1} } \\ \vdots \\ {U_{120} } \\ {\dot{U}_{1} } \\ \vdots \\ {\dot{U}_{120} } \\ \end{array} } \right\}_{{240{ }X{ }1}}$$
(15)
$${\text{Input }}\;{\text{vector}},u\left( t \right) = \left\{ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ \end{array} } \right\}_{{2X{\text{~}}1}} \left\{ {\begin{array}{*{20}c} {\ddot{U}_{g} } \\ f \\ \end{array} } \right\}_{{2{\text{~}}X{\text{~}}1}}$$
(16)
$${\text{Output}}\;{\text{ vector}},y(t) = \left\{ {\begin{array}{*{20}c} {y_{1} } \\ \vdots \\ {y_{{120}} } \\ \end{array} } \right\}_{{120{\text{~}}X{\text{~}}1}} = \left\{ {\begin{array}{*{20}c} {\ddot{U}_{1} } \\ \vdots \\ {\ddot{U}_{{120}} } \\ \end{array} } \right\}_{{120{\text{~}}X{\text{~}}1}}$$
(17)

The constants \(A, B, C, D,{ }E\) are given below as derived from the above equations,

$$A = \left[ {\begin{array}{*{20}c} 0 & I \\ { - \left[ M \right]^{ - 1} \left[ K \right]} & { - \left[ M \right]^{ - 1} \left[ {C_{d} } \right]} \\ \end{array} } \right]_{240 X 240}$$
(18)
$$B = \left[ {\begin{array}{*{20}c} {0_{120 X 1} } \\ {\left[ M \right]^{ - 1} \left[ N \right]_{120 X1} } \\ \end{array} } \right]_{240 X 1}$$
(19)
$$E = \left[ {\begin{array}{*{20}c} {0_{120 X 1} } \\ { - \left[ R \right]_{120 X 1} } \\ \end{array} } \right]_{240 X 1}$$
(20)
$$C = { }\left[ {\begin{array}{*{20}c} { - \left[ M \right]^{ - 1} \left[ K \right]} & { - \left[ M \right]^{ - 1} \left[ {C_{d} } \right]} \\ \end{array} } \right]_{120 X 240}$$
(21)
$$D = \left[ {\begin{array}{*{20}c} {\left[ M \right]^{ - 1} \left[ N \right]_{120 X 1} } & {0_{120 X 1} } \\ \end{array} } \right]_{120 X 2}$$
(22)

The acceleration time histories used for the present simulation are taken from records of past historical earthquakes that occurred in the region of El-Centro. The N–S component of the El-Centro earthquake occurred in the year 1940 (Imperial Valley) which has a peak ground acceleration of 0.3188 g. The Kobe earthquake at Amagasaki in 1995 has a peak ground acceleration of 0.3254 g.

Proportional-integral-derivative (PID) controller

In this study, the PID controller is considered in regulating the voltage required by the damper and it is tuned by the Ziegler–Nichols tuning method. Equations 23 and 24 represent the formula of the PID controller. The variables in the below equation \({\text{\^e }}\left( t \right),~\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} \left( t \right),{\text{~~}}K_{p} ,{\text{~~}}T_{i} ,{\text{~~}}T_{d}\) are the error calculated, the output of the controller, proportional gain, integral time, and derivative time [31].

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} \left( t \right) = K_{p} \times \left\{ {{\text{\^e }}\left( t \right) + \left( {\frac{1}{{T_{i} }} \times \mathop \smallint \limits_{0}^{t} {\text{\^e }}\left( t \right) \times d\left( t \right)} \right) + \left( {T_{d} \times \frac{{d{\text{\^e }}\left( t \right)}}{{dt}}} \right)} \right\}$$
(23)

The following relationship between control point and error,

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} \left( t \right) = K_{p} \left( {1 + \frac{1}{{{\text{s}}.T_{i} }} + T_{d} .s} \right){\text{\^e }}\left( t \right)$$
(24)

Ziegler–Nichols ultimate tuning method

Ziegler–Nichols ultimate tuning method is a heuristic technique to tune PID controller with finding ultimate gain value \(K_{pu}\) and ultimate period of oscillation \(p_{u}\). This is a classical method/simple method for tuning a closed-loop system that can be refined to give a better hold on the controller.

In this method, proportional gain \(K_{pu}\) is found that affect the control loop to oscillate indefinitely at a steady state. The integral gain and derivative gain are set to zero that sets the robustness of the proportional gain influence on the closed-loop in optimizing control of the system. In calculating PID controller gain value the ultimate period \(p_{u}\) (time required to complete one full oscillation while the system is at a steady state) is important to calculate loop tuning constants of the controller [31]. The following procedure is used to find the parameters in closed-loop and to find the tuning constants,

  • Set the system with the PID controller in closed-loop and set a reference as step input.

  • Set the integral and derivative constants to zero, and then, increase or decrease the proportional gain until a sustained oscillation is achieved with constant amplitude and constant period.

  • The constant amplitude is called as ultimate proportional gain \(K_{pu}\) and constant period is called as ultimate period \(p_{u}\); these values need to be recorded.

  • The recorded value is plugged in to find the constants \(K_{p}\),\({ }T_{i}\),\({ }T_{d}\), \(K_{i}\), \(K_{d}\) as shown in Table 3.

  • Plug these values into the Ziegler–Nichols closed-loop equations as shown in Eqs. 23 and 24, and determine the necessary settings for the controller.

Table 3 Calculation of PID parameters
Full size table

According to the design, PID controller parameters are obtained as shown in Tables 4 and 5 by using Ziegler–Nichols ultimate gain rule for different earthquakes considered (Fig. 2).

Table 4 Ziegler–Nichols ultimate gain rules PID parameters
Full size table
Table 5 Parameters of PID controller
Full size table
Fig. 2
figure 2

Block diagram of PID-based MR damper system Sources Created by Author

Full size image

Observer-based anti-windup robust controller design

An earthquake is a severe disaster that damages the whole environment. This tremendous event affects nature along with the structures and its components. The structures are designed with a control system that consists of devices like actuators, sensors, and controllers. During this terrific occurrence, these sensors, actuators, and other devices may stop working or might give a very noisy output or may give partial output. Failure of these devices will lead to failure of the control system, and the structure will be uncontrolled and may collapse. The uncertainty is due to the inadequate placement of the sensors or the inability of the sensor to produce output because it will be corrupt due to some noise involved in it [32]. So there is a need to overcome this limitation, by modifying the control algorithm [33, 34]. Ziegler–Nichols tuning rule is used in the design of the robust PID controller in which the ultimate gain method is used [35]. The formulas of the robust PID control algorithm are given in Eqs. 25–30.

$$\dot{x}\left( t \right) = Ax\left( t \right) + Bu\left( t \right) + w$$
(25)
$$u\left( t \right) = - K_{r} x\left( t \right) + K_{p} \left( {Ref} \right) + K_{p} T_{d} \left( {\mathop {Ref}\limits^{.} } \right)$$
(26)
$$u\left( t \right) = - K_{r} \rlap{--} x\left( t \right) + K_{p} \left( {Ref} \right) + K_{d} \left( {\mathop {Ref}\limits^{.} } \right)$$
(27)
$$y\left( t \right) = Cx\left( t \right) + Du\left( t \right) + v_{0}$$
(28)
$${\text{\^e }}\left( t \right) = \, (Ref) \, - y\left( t \right)$$
(29)
$$K_{p } ,K_{i} ,K_{d}$$
(30)

Here \(K_{r}\) is feedback controller gain of robust PID controller and \(y\left( t \right)\) is the output of the structure. The above robust PID controller logic is combined with the Kalman observer to give robustness against the uncertainties happening due to sensor outputs. In this work, full-order Kalman observer is designed based on the structure state model equations. The equations of the Kalman observer are formulated and shown in Eqs. 31–43. Figure 3 presents an observer-based PID controller with an MR damper.

Fig. 3
figure 3

Observer-based PID controller with MR damper Sources Created by Author

Full size image

To mimic the behavior of the system given by Eq. 25, the estimated system is given as

$$\mathop {\hat{x}}\limits^{.} \left( t \right) = A\hat{x}\left( t \right) + Bu\left( t \right) + w$$
(31)

The error between the true state and estimated state e is given as,

$${\mathbf{e}} = x\left( t \right) - \hat{x}\left( t \right)$$
(32)

From the above, the equation for the observer error is given as,

$$\mathop {\mathbf{e}}\limits^{.} = \dot{x}\left( t \right) - \mathop {\hat{x}}\limits \left( t \right)$$
(33)

To control the observer error in the system observer, Eq. 31 is modified as,

$$\mathop {\hat{x}}\limits^{.} \left( t \right) = A\hat{x}\left( t \right) + Bu\left( t \right) + K_{o} \left( {y\left( t \right) - \hat{y}\left( t \right)} \right) + w$$
(34)

where \(\hat{x}\left( t \right)\) is the estimated state for state \(x\left( t \right),{ }\left( {x\left( t \right) - \hat{x}\left( t \right)} \right)\) is the estimation error, \(\mathop {\mathbf{e}}\limits^{.}\) observer error, \(K_{o}\) is the observer gain, and \(\hat{y}\left( t \right)\) is the output of the observer.

Substituting Eq. 34 for \(\hat{y}\left( t \right)\) as \(C\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\rlap{--} x} \left( t \right)\) neglecting \(Du\left( t \right)\), it is given as below,

$$\mathop {\hat{x}}\limits^{.} \left( t \right) = A\hat{x}\left( t \right) + Bu\left( t \right) + K_{o} y\left( t \right) - K_{o} C\hat{x}\left( t \right) + w$$
(35)
$$\mathop {\hat{x}}\limits^{.} \left( t \right) = \left( {A - K_{o} C} \right)\hat{x}\left( t \right) + Bu\left( t \right) + K_{o} y\left( t \right) + w$$
(36)

Substituting Eqs. 25 and 36 for the observer error Eq. 33 to get the system matrix of the observer,

$$\mathop {\mathbf{e}}\limits^{.} = \left( {Ax\left( t \right) + Bu\left( t \right) + w} \right) - \left( {\left( {A - K_{o} C} \right)\hat{x}\left( t \right) + Bu\left( t \right) + K_{o} y\left( t \right) + w} \right)$$
(37)
$$\mathop {\mathbf{e}}\limits^{.} = Ax\left( t \right) - \left( {A - K_{o} C} \right)\hat{x}\left( t \right) + K_{o} Cx\left( t \right)$$
(38)
$$\mathop {\mathbf{e}}\limits^{.} = \left( {A - K_{o} C} \right)\left( {x\left( t \right) - \hat{x}\left( t \right)} \right)$$
(39)
$$\mathop {\mathbf{e}}\limits^{.} = \left( {A - K_{o} C} \right){*} {\mathbf{e}}$$
(40)

In Eq. 40, \(\left( {A - K_{o} C} \right)\) is system matrix of the observer. The equation of the Kalman observer in calculating the observer gain is as follows,

$$K_{o} = PC^{T} R_{c}^{ - 1}$$
(41)
$$P = P_{0} + \dot{P} \times dt{ }$$
(42)
$$\dot{P} = { } - PC^{T} R_{c}^{ - 1} CP + AP + A^{T} P + Q_{c}$$
(43)

Here \(P_{0}\) is a positive definite matrix that is the initial value for the solution of differential Riccati equation, and \(P\) is the solution for the differential Riccati equation \(\dot{P}\). \(P_{0}\) is chosen to be the square root of the largest eigenvalue of the system matrix \(A\). \(R_{c}\) and \(Q_{c}\) are positive definite matrices, where \(R_{c}\) is the covariance of measurement noise and \(Q_{c} { }\) is the covariance of process noise. \(P_{0} ,\) \(Q_{c}\), and \(R_{c}\) are the positive definite matrices chosen by the designer [34]. Error is continuously recursively calculated according to the Riccati equation as shown in Eq. 43. Figure 4 presents a block diagram of the Kalman observer-based system.

Fig. 4
figure 4

Block diagram of Kalman observer-based system Sources Created by Author

Full size image

The \(\hat{x}\left( t \right)\) and \(\hat{y}\left( t \right)\) estimated from the Kalman observer are used recursively in observer equations to obtain the required output. The vectors \(w\) and \(v_{0}\) are disturbances with unknown statistics with zero mean. The \(Q_{c}\) and \(R_{c}\) values are decided based on the trial-and-error method. Figure 5 shows the block diagram of the Kalman observer-based robust PID controller. It shows the system in state-space form, and the observer is also shown in state-space with observer gain and PID controller with a feedback loop that gives robustness against the uncertainties [34] (Figs. 6 and 7).

Fig. 5
figure 5

Block diagram of robust PID controller with Kalman observer Sources Created by Author

Full size image
Fig. 6
figure 6

Block diagram of anti-windup PID observer-based system Sources Created by Author

Full size image
Fig. 7
figure 7

Simulink block diagram of the observer-based anti-windup robust controller with MR damper system Sources Created by Author

Full size image
Fig. 8
figure 8

Force versus time graph obtained for the model of MR damper

Full size image

Anti-windup approach

Windup term refers to degradation in the performance when saturation occurs at the plant input or in the control feedback loop. The term windup occurs because the saturation in the actuator would slow down the response of the feedback loop with effectively breaking it down and it would cause the integrator state to windup to an excessively large value. The “windup” or “integrator windup” occurs as controllers are in process with input limitation and variation of set points that causes the actuator saturation, leading to deterioration in the performance and closed-loop system instability [36]. To overcome this problem, “anti-windup” is introduced which refers to the augmentation of the controller in the feedback loop that is prone to wind up. The introduction of anti-windup in the feedback loop un-alters the performance of the controller because saturation never occurs and to the possible level an acceptable performance is achieved if even the actuator saturation occurs. The windup can be avoided by giving a proper integrator value when there is saturation in the actuator; thus, the controller should continue performing as there is a change in control error; this method is called tracking or back-calculation [37]. Advantages of anti-windup: Anti-windup will provide stability to the controller when the feedback loop is unaltered by the performance and also try to maintain small errors. Prevent divergence of the integral error when the control cannot keep up with the reference [38].

Evaluation criteria for the damped outrigger structure

The structural response of the damped outrigger is evaluated by observing the acceleration, displacement, and velocity of the structure. These evaluation criteria are the percentage of the controlled response to the uncontrolled response. In this study, the structural response ratio values are calculated: floor displacement ratio (\({\text{G}}_{1}\)), maximum inter-story drift ratio (\({\text{G}}_{2}\)), floor acceleration ratio \(\left( {{\text{G}}_{3} } \right)\) and base shear ratio \(({\text{G}}_{4} )\) to evaluate the efficiency of the proposed observer-based anti-windup robust PID controller. Equations 44 – 49 represent equations adopted for the evaluation of damped outrigger structure [38]. The equations are as follows,

$${\text{G}}_{1} = \begin{array}{*{20}c} {max} \\ {\begin{array}{*{20}c} {El - Centro} \\ {Kobe} \\ \end{array} } \\ \end{array} \left\{ {\frac{{max\left| {U_{i} \left( t \right)} \right|}}{{U^{max} }}} \right\}$$
(44)

\(U_{i} \left( t \right)\) denotes the displacement of the ith floor, i.e., i = 1, 2, 3……60, \(U^{max}\) denotes the maximum uncontrolled displacement, and \(\left| . \right|\) denotes the absolute value

$${\text{G}}_{2} = \begin{array}{*{20}c} {max} \\ {\begin{array}{*{20}c} {El - Centro} \\ {Kobe} \\ \end{array} } \\ \end{array} \left\{ {\frac{{max\left| {\frac{{d_{i} \left( t \right)}}{L}} \right|}}{{d_{n}^{max} }}} \right\}$$
(45)
$$d_{i} \left( t \right) = U_{i} \left( t \right) - U_{i - 1} \left( t \right)$$
(46)
$$d_{n}^{max} = max\left\{ {\frac{{d_{i} \left( t \right)}}{{c_{i} }}} \right\}$$
(47)

\(d_{i} \left( t \right)\) denotes the inter-story drift of the ith floor, i.e., i = 1, 2, 3……60, \(L\) is the height of each floor, and \(d_{n}^{max}\) is the uncontrolled maximum inter-story drift

$${\text{G}}_{3} = \begin{array}{*{20}c} {max} \\ {\begin{array}{*{20}c} {El - Centro} \\ {Kobe} \\ \end{array} ~} \\ \end{array} \left\{ {\frac{{max\left| {\ddot{U}_{i} \left( t \right)} \right|}}{{\ddot{U}^{{max}} }}} \right\}$$
(48)

\(\ddot{U}_{i} \left( t \right)\) is the absolute acceleration of the ith floor, i.e., i = 1, 2, 3……60, and \(\ddot{U}^{{max}}\) is the maximum uncontrolled floor acceleration

$${\text{G}}_{4} = \begin{array}{*{20}c} {max} \\ {\begin{array}{*{20}c} {El - Centro} \\ {Kobe} \\ \end{array} ~} \\ \end{array} \left\{ {\frac{{max\left| {\sum M_{i} \ddot{U}_{i} \left( t \right)} \right|}}{{F_{b}^{{max}} }}} \right\}$$
(49)

\(M_{i}\) is the mass of each floor of the structure of the ith floor, i.e., i = 1, 2, 3……60, and \(F_{b}^{max}\) is the maximum uncontrolled base-shear of the structure.

Results and discussions

The damped outrigger structure is modeled to control its response to the earthquake load in the presence of a semi-active damper. The structural properties are discussed in methodology; accordingly, the structural parameters modeling is done with finite element method considering the core and column as beam and bar element considering Bernoulli–Euler beam theory. The equation of motion of the structure is converted to the state-space model. The damping devices used in this study are MR dampers; these devices are modeled according to the damped outrigger structure model. The dynamic simulation is conducted to obtain the response of the damped outrigger structure excited for an earthquake. The displacement, acceleration, story drift, base shear, and evaluation criteria values of the response of the structure are recorded. The uncontrolled response of the structure is first obtained and the control devices are installed and the results are plotted accordingly. The MR damper is used as a semi-active device with a PID controller to command the required voltage required by the damper in structural response reduction. The restoring force of MR damper can be simulated very well with the phenomenological model used in this study subjected to earthquakes that indicates MR damper can be used effectively in the damped outrigger structure as semi-active controllers. The MR damper is dynamically modeled according to the formulas in Simulink and MATLAB. MR damper is simulated and the results are depicted based on the values presented in the section of MR damper. Results predicted give force versus time, force versus displacement, and force versus velocity graph. Figure 8 gives the force versus time graph of the MR damper. Figure 9 shows the force versus displacement graph, and Fig. 10 shows the force versus velocity graph.

Fig. 9
figure 9

Force versus displacement graph

Full size image
Fig. 10
figure 10

Force versus velocity graph

Full size image
Fig. 11
figure 11

Top story displacement of a structure excited for El-Centro earthquake

Full size image

These force versus time graphs reveal the behavior of the MR damper. As the voltage increases, force required to yield the MR fluid also increases with the increasing time.

As observed in Fig. 9, the loops progress along the clockwise direction. When the voltage is fed at zero, the MR damper acts as a purely viscous damper because the force versus displacement curve is approximately elliptical.

As observed in Fig. 10 the loops progress along the anti-clockwise direction with the increasing time and it is nearly linear. All the graphs observed above exhibits viscous damper characteristics at zero voltage input signal. The phenomenological model of the MR damper presented in the study will very well simulate passive and semi-active cases numerically.

The damped outrigger structure is dynamically simulated to obtain the response of the system excited for an earthquake. The structure is modeled to calculate the fundamental natural period and fundamental frequency in two conditions. The first condition is the structure uncontrolled without any dampers and the second condition with the addition of MR damper. The effect of damping devices on the structural fundamental natural period is tabulated in Table 6.

Table 6 Fundamental natural period of the outrigger structure
Full size table

The fundamental natural period of the building depends on building flexibility and mass, the more the flexibility or the more the mass longer is the natural period. The fundamental natural period is the inherent property of the building, and any modification made to the building will change its fundamental natural period. In this study, the addition of dampers has modified the natural period and frequency of the building. Table 6 presents the modified value in the fundamental natural period with the addition of MR damper mean stiffness for a different condition. In this study, frequency of the structure is modified for every instant of the earthquake frequency by the controller used by modification in the stiffness and damping value of the damper to avoid the resonance condition. This integration of the damper and controller will produce the required force in mitigating the response of the damped outrigger structure by calculating required values in resisting the resonance effect in the presence of an earthquake.

The displacement profile and acceleration profile of the damped outrigger structure of the top story are plotted to emphasize the effectiveness of the controller with the combination of the damper. In this study, a semi-active damper is used to reduce the response of the structure. The uncontrolled response of the outrigger is plotted for the excitement of different earthquake-like the El-Centro earthquake and Kobe earthquake. The MR damper is studied as a semi-active damper to observe its effectiveness in damped outrigger structural control. The robust controller is designed with an anti-windup technique along with the observer to mitigate the structural response. Displacement of the top floor of the damped outrigger structure for El-Centro and Kobe earthquake considering uncontrolled, MR damper with PID controller and observer-based anti-windup robust PID controller is shown in Figs. 11 and 12.

Fig. 12
figure 12

Top story displacement of a structure excited for Kobe earthquake

Full size image
Fig. 13
figure 13

Top story acceleration of the structure excited for El-Centro earthquake

Full size image

In this study, dampers are used in the structure to introduce a physical phenomenon of mitigating the response of the structure through energy dissipation, and it has presented a significant effect in the reduction in the displacement of the structure. The semi-active MR damper has shown promising performance in mitigating the damped outrigger response. MR damper with PID controller has shown a good response in the displacement reduction that exhibits better performance in comparison with the uncontrolled condition as presented in Figs. 11 and 12. MR damper with observer-based anti-windup robust PID controller has shown excellent enhanced performance in comparison with an uncontrolled condition in reducing the displacement. The seismic response of the damped outrigger shows reduced displacement with the peak in the same range as that of the peak input for both the El-Centro and Kobe earthquakes and slowly dies down with the time for control strategy in the presence of semi-active MR damper.

The acceleration of the top floor of the damped outrigger structure for El-Centro and Kobe earthquake considering uncontrolled condition, MR damper with PID controller, and observer-based anti-windup robust PID controller vibrations is shown in Figs. 13 and 14, respectively.

Fig. 14
figure 14

Top story acceleration of the structure excited for Kobe earthquake

Full size image
Fig. 15
figure 15

Force versus time graph representing MR damper output with El-Centro earthquake as input

Full size image

In this study, dampers are used in the structure to introduce a physical phenomenon of mitigating the response of the structure through energy dissipation; it has presented a significant effect in the reduction in the acceleration of the structure. The semi-active MR damper has shown promising performance in mitigating the damped outrigger response. MR damper with PID controller and MR damper with observer-based anti-windup robust PID controller has shown excellent enhanced performance in comparison with all the above-discussed conditions in reducing the acceleration as presented in Figs. 13 and 14.

The force produced by the MR damper according to the voltage regulated by the controller to reduce the structural response for the El-Centro earthquake and Kobe earthquake is plotted in the graph as presented in Figs. 15 and 16.

Fig. 16
figure 16

Force produced by MR damper excited for Kobe earthquake

Full size image

This study mainly focuses on the semi-active MR damper system in producing the required force for every instant so that the minimum response of the system is produced. With the addition of multiple dampers, there is a significant advantage because the damping system could be used to reduce the forces in the structural design. The phenomenological model of the MR damper presented in the study will very well simulate semi-active cases numerically for input earthquakes. The dampers in this study demonstrate stable and reduced response for multi-degree of freedom structural systems.

Absolute maximum values of the damped outrigger structural response are tabulated in Tables 7 and 8 for El-Centro and Kobe earthquake. The evaluation criteria in the control system are based on the maximum response quantities, and the total amount of force produced in controlling the structural response is tabulated in Tables 9 and 10 for El-Centro and Kobe earthquake. The merit of the control system depends on minimum values of the evaluation criteria that are generally desirable. These criteria are the dimensionless measurement of the response that has a relationship between uncontrolled and controlled responses.

Table 7 Absolute maximum values of damped outrigger response for El-Centro earthquake
Full size table
Table 8 Absolute maximum values of damped outrigger response for Kobe earthquake
Full size table
Table 9 Evaluation criteria for the damped outrigger structure for the El-Centro earthquake
Full size table
Table 10 Evaluation criteria for the damped outrigger structure for the Kobe earthquake
Full size table

For further comparison of the proposed strategy, four evaluation criteria that are mentioned in the previous section are used to validate the obtained results. The semi-active control values show better performance with comparing to uncontrolled case. From the tabulated value of evaluation criteria, it has been indicated that the proposed observer-based anti-windup robust PID controller shows minimum values for all the control conditions. The MR damper is used semi-active mode in this study; it works well in reducing the peak response and evaluation criteria value for structure excited for El-Centro and Kobe earthquakes. The MR damper shows a huge reduction in the displacement of the damped outrigger structure subjected to the El-Centro and Kobe earthquakes.

Conclusions

The dynamic simulation of damped outrigger structure in the presence of an integrated controller damper system is presented in this paper. The main aim of the study is to mitigate the seismic response in the presence of a semi-active MR damper, which is achieved by designing an observer-based anti-windup robust PID controller. The observer design will estimate all the states of the damped outrigger system that is tuned to become the same as the true state of the system. The Kalman observer is integrated along with the robust PID controller with enhanced tuning along with MR damper to estimate all the states of the system, to provide reliability. To avoid MR damper saturation, the anti-windup technique has been proposed along with the observer-based robust PID controller that performs well in mitigating the structural response in comparison with MR damper with PID controller for damped outrigger approaches. The numerical simulation with all modes of the structure that are moderately damped in reducing structural response shows the reliability and robustness of the dampers and controllers. The significant reduction in structural response and shift in the fundamental natural period using the proposed method is observed which is highlighted in the result section. Performance evaluation of the optimized damped outrigger structure with proposed observer-based anti-windup robust PID controller emphasizes the huge reduction in the displacement of the structure for earthquakes considered in the study has been elucidated in the result section. In the presence of the proposed controller, the structural acceleration also reduces in comparison with the uncontrolled case. The evaluation criteria in the results section elucidate a minimum ratio in terms of displacement, acceleration, story drift, and shear force. Therefore, the numerical dynamic simulation results demonstrate better mitigation of structural seismic response as presented in graphs and tables. Thus, the proposed semi-active control strategy has potential in the construction section and in other industries that require system control.

The observer-based robust PID controller can be introduced to any other system that needs to be controlled. The base isolation of the structure is widely in the study with passive, semi-active, and hybrid control systems for vibration control of the structure. The proposed control strategy can be hybridized with other dampers in base isolating the structure in mitigating the seismic response. Stochastic control with the proposed strategy can be undertaken for minimizing the system response.