Abstract
Graph-based approaches are revolutionizing the analysis of different real-life systems, and the stock market is no exception. Individual stocks and stock market indices are connected, and interesting patterns appear when the stock market is considered as a graph. Researchers are analyzing the stock market using graph-based approaches in recent years, and there is a need to survey those works from multiple perspectives. We discuss the existing graph-based works from five perspectives: (i) stock market graph formulation, (ii) stock market graph filtering, (iii) stock market graph clustering, (iv) stock movement prediction, and (v) portfolio optimization. This study contains a concise description of major techniques and algorithms relevant to graph-based approaches for the stock market.
Similar content being viewed by others
1 Introduction
A graph is defined as a collection of two sets: a set of nodes and a set of edges between those nodes. Many real-life systems, such as biological structures, social networks, financial systems, and communication networks, can be represented as graphs. Researchers use different tools, techniques, and algorithms to construct graphs and analyze them. Those tools, techniques, and algorithms are regarded as graph-based approaches. The stock market is a financial system that can be considered as a graph. The application of graph-based approaches for analyzing the stock market is increasing rapidly. This study will present a survey of the major researches that apply graph-based approaches for stock market analysis and prediction. The main purpose is to summarize graph-based approaches that are well applied in stock market research, to draw a clear picture of where the research is, how different approaches are categorized and related, and where the new trend is.
There are very few studies so far focusing on surveying the graph-based approaches in stock market analysis and prediction. One study focuses on the application of different graph filtering techniques on correlation-based stock market graphs and assessing the statistical stability of those techniques [52]. Kenet et al. [25] review the applications of network science in finance and economics, a small part of which is contributed to the discussion of the correlation-based stock market graph.
Marti et al. [34] have tried to produce a comprehensive review on the application of correlation networks in the financial market with a major focus on the stock market graph. However, it has only described the results briefly or only mentioned the algorithms in most cases. A sufficient discussion about the stock market graph formation mechanisms, filtering algorithms, clustering methods, and graph-based portfolio design strategies is highly desired while they barely discuss the mathematical perspectives of the methods and algorithms. Most importantly, it has almost no discussion about applying machine learning-based approaches to analyze the stock market graph. Our study will overcome these limitations by discussing the state-of-the-art graph-based methods and algorithms for stock market analysis and prediction critically and in detail. The major contributions of our study are as follows.
-
This is the first study to present a comprehensive discussion about the stock market graph formulation techniques.
-
We have summarized and critically discussed the major filtering and clustering algorithms for the stock market graphs.
-
Ours is the first study to survey the graph-based and machine learning-focused approaches for stock movement prediction and portfolio optimization.
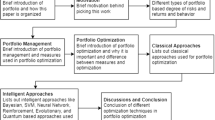
To be consistent with the literature, we will use the words graph and network interchangeably. Likewise, we will do the same for the words stock and node. The rest of the paper is organized as follows. Section 2 discusses the construction of the stock market graph. Different stock market graph filtering mechanisms are discussed in Sect. 3. A detailed discussion of stock market graph clustering techniques is presented in Sect. 4. Different graph-based techniques for stock movement prediction are presented in Sect. 5. Graph-based portfolio optimization techniques are discussed in Sect. 6. The paper is concluded in Sect. 8. A taxonomy of the covered methods is presented in Fig. 1.
2 Stock market graph formulation
2.1 Correlation-based graphs
We will consider a graph \(G=(V, E)\), consisting of nodes V and edges E. In a correlation-based graph, individual stock or market index is considered as a node. It is prevalent to formulate the stock market graph based on Pearson’s correlation coefficient \(\rho _{ij}\) between returns [33, 43, 51] or logarithmic returns [2, 5] of stock pairs. If we consider the close price of stock i as \(C_i\), then the logarithmic return at time t can be defined as follows.
where \(\Delta t\) is the sampling period. It determines the time difference between two consecutive measurements of return, price, or volume. Let us consider \(\varvec{r}_{i,\Delta t}(t)\) as the return series of the stock i and \(\varvec{r}_{j,\Delta t}(t)\) as the return series of the stock j at time t, where \(\varvec{r}_{i,\Delta t}(t)= [r_{i,\Delta t}(t), r_{i,\Delta t}(t-1), r_{i,\Delta t}(t-2) \ldots r_{i,\Delta t}(t-(T-1))]\) and \(\varvec{r}_{j,\Delta t}(t)= [r_{j,\Delta t}(t), r_{j,\Delta t}(t-1), r_{j,\Delta t}(t-2) \ldots r_{j,\Delta t}(t-(T-1))]\).
T is the window size for correlation calculation. T determines the number of previous periods to be considered during the correlation calculation. The correlation can also be calculated between two close prices or traded volumes [8]. It is possible to calculate correlation where \(\varvec{r}_{i,\Delta t}(t)\) and \(\varvec{r}_{j,\Delta t}(t)\) will be considered over the same time period [33], or one will be lagged compared to the other [9]. In the latter case, we can consider the lag period between two return series as \(\tau \). If there is no lag, then \(\tau =0\). Let us first define the mean (\(\overline{r}_{i,\Delta t}(t)\)) and the variance (\(\text {Var}[\varvec{r}_{i,\Delta t}(t)]\)) of the return series for stock i as follows:
Given the notion of the return, window size, sampling period, and lag period, we can define the Pearson’s correlation coefficient \(\rho _{ij}\) as follows:
The correlation can be positive or negative with the minimum value of \(-1\) and the maximum value of \(+1\). It is possible to form both weighted and unweighted stock market graphs based on correlation. For an unweighted graph, a correlation threshold is used [4, 8]. There will be an edge between the node i and j in the correlation threshold method if the corresponding \(\rho _{ij}\) is greater than or equal to a threshold \(\rho _{\text {thres}} \ (\rho _{\text {thres}} \ \epsilon \ [-1,1]\)) [4, 23]. The graphs based on the correlation threshold will be unweighted and undirected graph. It is also possible to formulate a complementary graph based on the correlation threshold. In the complementary graph, there will be an edge between node i and j if \(\rho _{ij} < \rho _{\text {thres}}\) [4].
There are different ways to formulate a weighted graph based on cross-correlation between stock pairs. For example, we can take the absolute value of the correlation as the weight [11]. It is possible to convert the correlation to a distance measure \(d_{ij}\) [33, 43].
The minimum value of \(d_{ij}\) will be 0 (when \(\rho _{ij}=1\)), and the maximum value will be 2 (when \(\rho _{ij}=-1\)). Thus, a higher value of \(d_{ij}\) means less positive correlation or more negative correlation between the stock pairs.
It is possible to construct a stock market graph based on exponentially weighted Pearson’s correlation coefficient [42]. If the correlation between stock i and j on day t is \(\rho _{ij}(t)\), then exponentially weighted Pearson’s correlation coefficient on day t, \(\rho _{ij}^w(t)\), can be defined as follows:
Here, the weight value \(w_s\) is defined as follows:
Here, \(w_0\) is the initial weight value. \(w_s\) is strictly positive (\(w_s > 0\)), and its sum over the calculation period is 1 (\(\sum _{s=t-\xi +1}^{t}w_s=1\)). \(\xi \) is the sliding window size, generally six months or one year when daily data is used [42]. \(\theta \) is the characteristic time horizon. After calculating \(\rho _{ij}^w(t)\), we can use its value to create the stock market graph. It is also possible to define the exponentially weighted Pearson’s correlation coefficient with shrinkage (\(\bar{\rho _{ij}}^w(t)\)) [42].
The shrinkage significantly improves the numerical significance of the correlation matrix [42].
A stock market graph can also be formed based on the Eigen decomposition of the cross-correlation matrix [31]. The Eigenmode of the largest Eigenvalue can be calculated as follows:
where \(\lambda _m\) is the largest Eigenvalue of the cross-correlation matrix, and \(u_i^m\) is the ith component of the largest Eigenvector. \(\rho _{ij}^m\) describes the global interactions between different stocks [31].
It is possible to form a stock market graph based on risk measures such as the value at risk (VaR) [62]. VaR is the worst possible expected loss in a future period given a confidence interval (e.g., 95%, 99%, etc.) and the past data. It is possible to calculate the VaR of a single stock in each trading day and construct a VaR series similar to the return series \(\varvec{r_i}(t)\). Upon construction of the VaR series; the VaR array correlation coefficient can be calculated similarly to equation (4) [62]. A threshold method can be applied to the VaR array correlation to form a risk-based stock market graph [62].
Apart from correlation, it is possible to construct a stock market graph based on partial correlation [26]. Let us consider three stocks: h, i, and j. The partial correlation coefficient \(\rho _{i,j:h}\) between stock i and j based on the stock h is the Pearson’s correlation coefficient between the residuals of stock i and j that are uncorrelated with h [26]. Both stocks i and j are regressed on stock h to obtain these residuals. Thus, we can define the partial correlation coefficient in terms of three Pearson’s correlation coefficients as follows [26]:
For simplicity, we do not include \(\Delta t\), \(\tau \), and T in equation (10). The value of \(\rho _{i,j:h}(t)\) can be small for two reasons. It will be small if the stock h strongly influences the correlation between stock i and j. However, it can also be small if the correlation between stock i and j is small. It is possible to define a new measure called the influence of stock h on the pair of stocks i and j to distinguish these two cases [26].
\(d_{i,j:h}(t)\) will be higher when a significant amount of \(\rho _{i,j}(t)\) can be explained in terms of the stock h. It is possible to generate \(\frac{n(n-1)(n-1)}{2}\) possible \(d_{i,j:h}(t)\). Thus, a filtering technique such as threshold-based filtering can be applied to generate a partial correlation network using \(d_{i,j:h}(t)\) [26].
2.2 Other linear measurement-based graphs
Apart from correlation, it is possible to form a stock market graph based on trading volume only. We can consider individual traders as the nodes of the graph and the trading relationship between them as the edges [30, 50]. The presence of traded volume can be used to create an unweighted graph, and the amount of the traded volume can be used to create a weighted graph [50]. There will be one graph per stock using this traded volume-based strategy. This graph will be directed with directions, e.g., from the seller node towards the buyer node [30, 50].
A stock market graph can be formulated using the conditional Granger causality index (CGCI), a linear measure of the causal relationship [39]. The CGCI is defined using vector autoregressive models. It can be defined as the ratio of the variances of unrestricted and restricted vector autoregressive model residuals [39]. Once CGCI is calculated, its statistical significance can be measured by the F-test. If the CGCI is significant, there will be an edge between the two nodes. As CGCI is a measure of causality, the formulated graph can be directed [39].
It is also possible to use the significance of the linear regression coefficient to formulate a stock market graph [29]. In this method, the return series of one node is regressed against the return series of another node. The F-statistic of regression is used to construct the edge between those nodes [29].
2.3 Nonlinear measurement-based graphs
There are different shortcomings of Pearson’s correlation coefficient between stock returns. It only reveals linear relationships and ignores the heterogeneity of financial data at different times [57]. As a result, it cannot accurately measure the tail correlation [56]. It is possible to use the Copula function, which can construct the joint distribution function without considering the specific form of the marginal distribution to the random variables when measuring the financial market correlation, and it can measure the nonlinear relationships [57].
The first step of forming a stock market graph using the Copula model introduces a marginal distribution function of stock returns such as the GARCH(1,1)-t model [57]. Here, GARCH stands for generalized autoregressive conditional heteroskedasticity. The next step is to choose a suitable Copula model such as the symmetrized Joe-Clayton (SJC) copula [57]. By fitting the marginal distribution function to the selected copula model, one can obtain upper- and lower-tail correlation coefficients between the stock pairs. These correlation coefficients can then be transformed into distance metrics using equation (5) [57].
Another approach to overcome the limitations of Pearson’s correlation is to use consistent dynamic conditional correlation (cDCC), which estimates correlation coefficients using standardized returns [46]. These standardized returns are calculated using an ARMA-FIEGARCH model [46]. Here, ARMA stands for autoregressive moving average, and FIEGARCH stands for fractionally integrated exponential generalized autoregressive conditional heteroskedasticity.
It is possible to use mutual information (MI) as a similarity measure between the stocks [16, 59]. For simplicity, we do not include \(\Delta t\), \(\tau \), and T in the notations of the return series in subsequent discussions. If we consider \(\varvec{r_i}\) and \(\varvec{r_j}\) as discrete random variables, then the MI between them can be defined as follows [16]:
where \(H(\varvec{r}_i)\) and \(H(\varvec{r}_j)\) are the marginal Shannon’s entropies, and \(H(\varvec{r}_i\),\(\varvec{r}_j)\) is the joint Shannon’s entropy of \(\varvec{r}_i\) and \(\varvec{r}_j\). These entropy measures can be defined as follows for discrete random variables such as return series [59]:
where P is the probability. Once the MI is calculated, it can be converted into a distance metric as follows [16]:
\(d_{ij,MI}\) is the mutual information-based distance metric that is symmetric and non-negative [16]. It satisfies triangle inequality and \(d_{ii,MI}=0\) [16].
We can also calculate conditional mutual information (CMI) between two stocks and use that for constructing a stock market graph. CMI measures the conditional dependency between two stocks i and j under the condition of the third stock h and can be defined as follows [59]:
where \(H(\varvec{r}_i,\varvec{r}_j, \varvec{r}_h)\) is the joint entropy of three random variables and can be defined as follows [59]:
When we use MI to construct an edge between two stocks, the strength of that edge may be overestimated, and with CMI, it may be underestimated [59]. We can use partial mutual information (PMI) to tackle these issues. We can start the construction of PMI with the condition of partial independence (\(P^*\)) between stock i and j with respect to the third stock h [59]:
where
Then, we can define the PMI as follows [59]:
We can form a stock market graph using the partial mutual information on mixed embedding (PMIME), a nonlinear measure of the relationship [39]. PMIME measures the fraction of information about the response variable that can be explained only by a predictor variable [39]. It is calculated as the ratio of two mutual information terms. A significance test is applied within the estimation procedure of PMIME. This significance test’s positive value indicates a causal relationship between the predictor and the response variable [39]. The graph formulated based on PMIME is a directed graph.
2.4 Statistically validated network
It is possible to form a stock market graph based on statistical validation of the links [9, 53, 54]. We will describe this method according to [54]. In this method, a bipartite graph is formed first. For a stock market, set A of the bipartite graph is the stocks and set B is the trading days. There will be an edge from stock i of set A to a node of set B based on the excess return of the stock i with respect to all the stocks’ average daily return. There can be three states based on the excess return: up, down, and null. It is possible to statistically validate the co-occurrence of state (either up or down) of stock i and state (either up or down) of stock j. The final network is obtained by linking together the vertices of set A which share at least a common first neighbor element of set B in the bipartite graph.
Let us assume that the degree of stock i is \(\text {deg}_i\) and of stock j is \(\text {deg}_j\). The common neighbors between stock i and j in set B is \(\text {deg}_{i,j}\). The number of nodes in set B is \(n_B\). Under the hypothesis that stock i and j randomly connect to the elements of set B, the probability that stock i and j share X neighbors in set B is given by the hypergeometric distribution as follows [54]:
It is possible to associate a probability or p-value \(P(\text {deg}_{i,j})\) with the actual number \(\text {deg}_{i,j}\) that stock i and j can share, and that can be calculated as follows [54]:
If the p-value is lower than a statistical significance level, there should be an edge between the stock i and j. The statistical significance level takes into account the fact that multiple hypothesis testing is performed. It is possible to use more conservative Bonferroni correction for multiple hypothesis testing or less restrictive false discovery rate (FDR) [54]. The resultant network is called the Bonferroni network or FDR network.
2.5 Graphs from textual data
It is possible to construct a stock market graph by extracting their relationships from textual data, such as whether they are from the same industry or not [14]. This information can be extracted from the documents maintained by the stock exchange. For example, if two stocks belong to the same industry, there will be an edge between them [14, 45, 60]. A graph can also be formed by analyzing the first-order and second-order relations in the statements of Wikidata [14]. If one stock is the subject and the other stock is the object in a statement of Wikidata, there is a first-order relation between those two stocks [14]. There will be a second-order relation if both stocks have a common object in two different statements [14].
Textual data-based stock market graphs can also be constructed using shared trading concepts among stocks such as the company’s business, geographical location, or shareholding structure [18]. Gao et al. [19] propose a stock market graph by combining information from stock description documents and historical return data. First, the topic distribution for each stock description document is extracted as a document feature with a stock attribute by calculating a probability distribution. Each stock’s description document can be considered a sequence of words, and that sequence is mapped to a probability distribution over a certain number of topics [19]. This probability distribution can be regarded as document encoding. The document encoding is then combined with historical sequence encoding (e.g., generated from historical return data using a long short term memory (LSTM) layer) to produce the dynamic interaction function. Finally, the dynamic interaction function is converted to the time-aware relation strength between stock i and j on day t through further processing. This time-aware relation strength is used as the edge weight of the stock market graph on day t.
2.6 Node selection
The most common node for a stock market graph is a single stock. It is also possible to use a market index as the node of a stock market graph [5, 6, 39, 48]. However, the stock markets all over the world are asynchronous. Major complexities of creating a stock market graph with stock indices as the nodes are: i) different stock markets have different opening and closing hours [5, 6], ii) the currencies used for the transaction in different markets fluctuate with respect to each other [5, 6], and iii) difference in national holidays and unexpected events in different countries [39]. It is possible to use a weekly time horizon, where the asynchronous hourly mismatch of data is minimized [6, 57]. After calculating weekly correlation, the statistical average is calculated as a temporal average performed on all the trading days of the investigated time period [6]. Some solutions involve using lower frequency data, removing observations from stock indices that correspond to a non-trading day in other markets, replacing the missing value by the value of the previous day or by the mean of the previous and next observation, and applying linear interpolation [39].
Apart from individual stock or market index, traders can also be considered as the node of a stock market graph [50]. Therefore, there will be a separate graph for each stock in this case.
2.7 The impact of sampling period and window size
The choice of the sampling period or time horizon \(\Delta t\) in the graph formulation method can significantly impact stock market graph’s properties [5]. The most used value of \(\Delta t\) is one period [33, 43, 51], which is one trading day for daily data. However, other values of \(\Delta t\) can also be used, such as \(\frac{1}{2}\), \(\frac{1}{5}\), \(\frac{1}{10}\), or \(\frac{1}{20}\) of a trading day if the correlation is measured using intra-day data [5]. It has been observed that the correlation decreases with the decrement of \(\Delta t\) [5]. This decrement impacts the nature of the hierarchical organization of the stock market graph [5]. Economically meaningful clusters are observed when graph filtering algorithms are applied on the raw stock market graph formulated using the correlation between daily returns [2, 5]. However, those clusters progressively disappear with the decrement of \(\Delta t\) [5]. Thus, the topology of a correlation-based stock market network can be impacted by the sampling time used to monitor the system’s time evolution [5].
The choice of window size T also impacts the structure of the correlation-based stock market graph. When daily data is used, T can vary from several months to several years [48]. The onset of different global financial distress situations can be detected with smaller values of T, whereas those onsets are smeared out with longer values of T [48].
3 Stock market graph filtering
Stock market graphs are formulated based on different measures such as cross-correlation or distance between stock pairs. In general, these graphs are very dense and sometimes can be a complete graph with an edge between every stock pair. A significant portion of the edges can have redundant information or noise. It is required to extract the important edges which can form the backbone network [2]. Different graph filtering techniques can be applied to stock market graphs for this purpose.
3.1 Minimum spanning tree (MST)-based approach
One commonly used technique is the minimum spanning tree (MST) [2, 33]. MST can be considered a sub-graph with n nodes and \((n-1)\) edges with no cycle [5]. Here, \(n=|V|\). An MST is gradually created by linking all the nodes in a graph characterized by a minimal distance between the nodes [33]. MST can provide a sub-graph of stocks with the most relevant connection for each stock [5, 33]. It is possible to extract the hierarchical structure from MST of a stock market graph. That hierarchical structure can be helpful to the theoretical description of the stock market and in search of economic factors affecting specific groups of stocks [33]. MST is also meaningful from the market structure and firm interaction perspectives [2]. One can observe clusters consisting of stocks from homogeneous economic sectors in an MST [5].
It is possible to extend the MST concept to a dynamic spanning tree (DST) by constructing the network using consistent dynamic conditional correlation rather than Pearson’s correlation [46]. The DST shrinks significantly over time while applied to analyze the network of the stock indices from the Asia-Pacific [46]. MST can also be considered the starting point, and further edges can be added to that if the new edges can improve the performance of the subsequent task, such as direction prediction [27].
Although MST is a powerful graph filtering method, it has several limitations. A major limitation is the absence of cycles or cliques. If three stocks are related to each other such as operating in the same industry, MST will keep only two out of three edges here, and some important information will be lost.
3.2 Planar maximally filtered graph (PMFG)-based approach
Planar maximally filtered graph (PMFG) allows maintaining the filtering properties of MST with the presence of extra links, cycles, and cliques in a controlled manner [2]. PMFG is also widely used to filter stock market graphs [2, 42, 43, 51].
PMFG filters the sub-graph by embedding the original graph on an embedded surface with a given genus (g). Some examples of these surfaces are a topological sphere (\(g=0\)), a torus (\(g=1\)), and a double torus (\(g=2\)) [2]. PMFG is produced with \(g=0\). PMFG keeps \((3n-6)\) edges out of \(\frac{n(n-1)}{2}\) possible edges of the original graph [51]. Thus, PMFG has more edges (\(3n-6\)) than MST (\(n-1\)). PMFG is a topological triangulation of the sphere, and cliques of three and four elements are permitted in it [51]. MST is always a sub-graph of PMFG [2]. It has been found that the cliques of the four elements reveal a high degree of homogeneity with respect to the economic sectors [51]. PMFG has a computational complexity of \(O(n^3)\) [35].
3.3 Triangulated maximally filtered graph (TMFG)
TMFG is used to filter the correlation-based stock market graph in [35]. TMFG uses triangulation that maximizes a score function associated with the amount of information retained by the filtered network [35]. A major advantage of TMFG is the improvement in computational complexity compared to PMFG. The computational complexity in TMFG is \(O(n^2)\), whereas it is \(O(n^3)\) for PMFG. TMFG uses several topological moves such as the \(T_1\) move or ‘edge switching’ (replaces the common edge between two triangles with a new edge joining the previously opposite nodes), the \(T_2\) move or ‘node insertion and removal’ (adds a node inside a triangle and connects the previous nodes of the triangle with the new node), the ‘Alexander move’ (deletes the shared edge between two triangles and adds a new node inside the resulting rhombus and joins the added node to the rhombus’vertices) and the ‘vertex swap’ move (swaps two nodes while keeping the neighbors fixed) [1, 35].
TMFG starts from a clique of order 4 and adds nodes gradually by using local moves. At each step, it optimizes a score function such as the sum of the weights of the edges and searches for the node and face pair that leads to the maximum increase in score [35]. It reduces the complexity by incrementally updating a cache with the information about the best possible pairing, updating only the records affected by a move [35]. The cache structure consists of two vectors. The maximum gain vector contains the value of the maximum gain over the remaining vertices for all triangular faces. The best vertex vector contains the list of vertices that attains the maximum gain for the specific triangular face [35]. Overall, TMFG can retain the same amount of information as PMFG but with reduced computational complexity.
3.4 Path-consistency algorithm
The path-consistency algorithm can filter a fully connected graph by removing edges that have an independent correlation [59]. This algorithm works using MI and PMI. In the first step, a threshold is selected, and two stocks (i, j) are said to have independent correlation if the MI between them is less than the threshold and that edge is deleted. The new network after this step is called the zero-order PMI network [59]. In the next step, the first-order PMI is used to remove the edges further. If there is no common neighbor between two stocks, there is no first-order PMI between them, and the edge remains in the network [59]. If there are one or more common neighbors, then first-order PMI is calculated for each edge. If the maximum of these first-order PMI values is less than the threshold value, the edge is removed from the network [59]. This process is repeated for all the edges of the zero-order PMI network, and the first-order PMI network is obtained. It is possible to create a higher-order PMI network by repeating the same process.
4 Stock market graph clustering
Detecting communities or clusters is of great importance for any graph-based study, and the stock market is no different. Clustering a stock market graph can help to retrieve meaningful economic information. It can also help portfolio optimization by identifying less correlated asset classes. Researchers have made significant efforts to identify or propose optimal clustering techniques for stock market graphs. We will discuss five major stock market graph clustering techniques in this section.
4.1 Hierarchical clustering
Hierarchical clustering techniques reveal a multilevel structure of a graph by recursively merging nodes or clusters [17, 43]. Hierarchical clustering techniques can be broadly divided into two categories: i) agglomerative techniques (clusters with high similarities are merged in an iterative manner) and ii) divisive techniques (clusters are split in an iterative manner by removing edges connecting vertices with low similarity) [17]. Hierarchical clustering techniques are widely used to detect clusters in stock market graphs [12, 33, 43, 52]. The similarity is measured by different distance measures such as the one defined in equation (5).
A mechanism is required to calculate the similarity between two clusters as the distance is defined between two nodes, and a cluster has more than one node. In the single linkage technique, the distance between two clusters is the minimum of the distances between any two nodes in the clusters [43, 52]. However, the single linkage method is sensitive to outliers and results in strong heterogeneity in the size of the clusters [38, 43]. In the average linkage technique, the distance is the average of the distances between any two nodes in the clusters [43, 52]. The average linkage method shows a more structured clustering than the single linkage method [38]. The distance between two clusters is defined as the maximum of the distances between any two nodes in the clusters in the complete linkage method [43]. It is also possible to define the distance as the increase of the squared error resulted from the merger of two clusters, and this technique is called Ward’s method [24, 43].
4.2 Role-based clustering
It is possible to cluster the nodes of a stock market graph based on their connectedness [50]. This role-based clustering is applied on a graph where the nodes are individual traders [50]. For each node, we can calculate a z-score as follows:
where \(\text {deg}_i\) is the degree of node i, which is the sum of the in-degree and out-degree, \(\langle \text {deg} \rangle \) is the average degree of all nodes, and \(\langle \text {deg}^2 \rangle \) is the second origin moment [50]. Higher values of \(z_i\) represent a densely connected node, and lower values represent a sparsely connected node. If \(z_i\) is greater than a certain threshold, that node can be considered a hub in the stock market graph. If \(z_i\) is smaller than a certain threshold, we can consider that node as a periphery node. The other nodes can be considered as connector nodes.
4.3 Infomap
Infomap is an information-theoretic approach for detecting clusters or community structures in a weighted graph [44]. This method has been used widely for clustering stock market graphs [48, 53, 54]. Infomap uses the probability flow of random walks on a graph as a proxy for information flow and decomposes the graph into clusters by compressing a description of the probability flow [44]. It considers the clustering problem equivalent to solving a coding problem. The key idea is to create a map that separates the important structures from insignificant details. The graph is first divided into two levels of description [44]. The names of the clusters (top level) are uniquely encoded, and the names of the individual nodes (bottom level) inside the clusters are reused [44]. A coding scheme such as Huffman coding is used for the encoding purpose. Once the coding scheme is selected, a module partition operator is required. The operator clusters n nodes into M modules by minimizing the expected description length of a random walk, which can be defined as follows [44].
where \(P_{\text {swt}}\) is the probability that the random walk switches modules at any given step. \(H_{\text {mod\_names}}\) is the entropy of the module names. \(H_{\text {within}}\) is the entropy of the within-module movements. \(\ P_{\text {within} }^s\) is the fraction of within-module movements that occur in module s, plus the probability of exiting module s.
A key question is how to check the possible partitions that will minimize the expected description length of a random walk. For large networks, it is not feasible to check all of them. According to [44], a computational search can be used, which will first compute the fraction of time each node is visited by a random walker using the power method. Then a deterministic greedy search algorithm will be used, which will explore the space of possible partitions using the previously calculated visited frequencies. Infomap can identify meaningful clusters from stock market graphs, such as investor clusters based on trading actions [53] or stock clusters based on similar economic activity [54].
4.4 Directed bubble hierarchical tree (DBHT)
Directed bubble hierarchical tree (DBHT) is a clustering method that utilizes the hierarchy hidden in the topology of a PMFG filtered graph [38, 43, 49]. Though DBHT is hierarchical in nature, we discuss it separately due to its implementation logic. A significant advantage of DBHT is that it does not require prior information such as the number of clusters [38].
A cycle (such as a 3-clique) will be either separating or non-separating due to inherent planarity in the PMFG filtered graph [49]. Each possible 3-clique in the PMFG filtered graph will result in a set of planar graphs connected to each other by the separating 3-cliques. These planar graphs are called bubbles [49]. A bubble tree can be formed where each node is a bubble, and each edge is a separating 3-clique. A direction between two nodes can be established by comparing the number of connections between the connecting 3-clique and the nodes [49]. The edge will be directed towards the node with more connections with the separating 3-clique. Depending on the direction of the edges, there can be three types of bubbles: i) converging bubble (all edges are incoming), ii) diverging bubble (all edges are outgoing), and iii)passage bubble (contains both inward and outward edges). Converging bubbles are considered the centers of clusters, and any bubble directly connected to a converging bubble is considered a member of the same cluster [48]. Thus, a non-discrete clustering can be obtained. Each node is assigned to the converging bubble to achieve a discrete clustering, which is at the smallest shortest path distance [49]. DBHT can retrieve more information from a stock market graph with fewer clusters than other hierarchical methods [38].
4.5 Spectral clustering
Spectral clustering transforms the graph into a new set of points by using the elements of the Eigenvectors as the coordinates [17]. The main component of spectral clustering is the graph Laplacian (L) which can be defined as follows [11]:
The degree matrix (D) is a diagonal matrix where the diagonal elements are the degree of the corresponding node. The definition of equation (26) represents unnormalized Laplacian. However, it is also possible to use a normalized Laplacian. A graph can be partitioned into two clusters by using the sign of the Eigenvector corresponding to the second smallest Eigenvalue of L [11, 15]. The second smallest Eigenvalue can be used as a measure of separability for clustering [11]. A higher value of the second smallest Eigenvalue indicates that the graph is less suitable for further clustering.
Once we get two clusters, we can get more clusters through repeated bi-partitioning [11]. We can set a threshold, and if the second smallest Eigenvalue is higher than that threshold, the clustering should be stopped [11].
4.6 Comparison between the clustering methods
We will have a comparative analysis of the clustering techniques in this section. The clustering techniques vary in terms of the working principle. The hierarchical clustering techniques are based on distances or similarity measures. The stocks are sorted based on distances, a dendrogram is built by gathering subsets of stocks with the lowest distances, and then the clusters are found from the dendrogram [38]. On the other hand, DBHT identifies all the clusters based on topological considerations on the planar graph, and then the hierarchy is constructed both inter-clusters and intra-clusters [38]. The role-based clustering technique identifies clusters by setting a threshold of connectedness [50]. Infomap uses the probability flow of random walks as a proxy for information flows and clusters the network by compressing a description of the probability flow [44]. Finally, the spectral clustering uses the second Eigenvector of the graph Laplacian to achieve the optimal clustering [11].
We can also compare the clustering techniques based on the requirement of the a priori information. For example, the optimal number of clusters needs to be predefined in the hierarchical clustering techniques [38]. Sometimes a stopping criterion such as optimization of modularity can be used to specify the number of clusters [17]. The optimal number of clusters is implicitly defined in the role-based clustering method through the definition of thresholds. That number can be considered as a hyperparameter and optimized through a deterministic greedy search in the Infomap technique [44]. However, in the DBHT technique, the number of optimal clusters can be identified automatically [38, 49].
If a graph has M clusters, but they are not connected to each other, then the unnormalized Laplacian should have M zero Eigenvalues [17]. If those M clusters are weakly connected, then the lowest \(M-1\) nonzero Eigenvalues should still be close to zero [17]. Thus, it is possible to know the optimal clusters numbers beforehand for spectral clustering. However, the stock market graph is generally fully connected, specially when created based on correlation. As a result, it may not be possible to know the optimal cluster number using the number of nonzero Eigenvalues. A slightly different way is to use the smallest nonzero Eigenvalue \(\lambda _2\), which can be used as a measure of separability of a graph [11]. The larger the value of \(\lambda _2\), the less separable the graph [11]. Thus, the repeated bi-sectioning of the stock market graph using spectral clustering can be stopped once the value of \(\lambda _2\) exceeds a threshold [11].
Another perspective of comparing the graph clustering techniques is the computational complexity. The computational complexity is relatively higher in hierarchical clustering techniques. For example, the computational complexity is \(O(n^2)\) in the single linkage method and \(O(n^2 log(n))\) in the average linkage method [17]. The complexity is O(|E|) in the Infomap technique, where |E| is the total number of edges in the graph [17]. For the DBHT technique, the computational complexity is \(O(n^{2.7})\) as per the empirical results [49]. Generally, the computational complexity of the spectral clustering is \(O(n^3)\) [17]. That makes it computationally infeasible for large graphs. However, there are methods such as ultra-scalable spectral clustering (U-SPEC) or ultra-scalable ensemble clustering (U-SNEC) that can reduce the computational complexity significantly [22].
5 Stock movement prediction using graph-based approach
Traditionally, stock movements are predicted using econometric methods such as the auto-regressive integrated moving average (ARIMA) [10] or the auto-regressive fractionally integrated moving average (ARFIMA) [3]. Application of machine learning (ML) models such as artificial neural network (ANN) or support vector machine (SVM) are on the rise for stock movement prediction [21]. Now-a-days, researchers are combining graph-based approaches with ML techniques for predicting stock movement. In this section, we will discuss different studies which use graph-based approaches for stock movement prediction.
5.1 Output
The typical outputs of stock movement prediction using graph-based techniques are one period ahead return, the direction of return, or actual closing price [7, 28, 32, 50]. Some studies also predict a multi-period trend, such as the n-day trend of the closing price [32]. In most cases, the predicted direction has two values (e.g., up and down), but it is possible to have a three-valued direction (e.g., rise, fall, and flat) [18]. Recently, the researchers are focusing on predicting the ranking of the stocks instead of actual return or direction [14, 45]. Apart from the return, researchers also predict volatility-related measures such as abnormal fluctuation using the graph-based approaches [62].
5.2 Input features
Sun et al. [50] use time series information of the trading network and stock return as input features of a neural network (NN) to predict one day ahead return. However, it is possible to combine the time series information of stock return and the information of stock market graph in a different way, such as using temporal graph convolution (TGC) [14]. In TGC, firstly, a temporal embedding is generated from the stock return time series. The adjacency matrix of the stock market graph and the temporal embedding of the stocks are used to generate a second input set (e.g., relational embedding) [14, 36]. In a slightly different approach, Gao et al. [19] consider the stock’s description document as a sequence of words, and generate document encoding by mapping that sequence to a probability distribution over a certain number of topics. The document encoding is combined with temporal embedding to generate the weighted adjacency matrix of the stock market graph [19]. The temporal embedding is then concatenated with the relational embedding for predicting the stock ranking on the next day [7, 14, 19, 45]. Overall, using one input set from the time series data and another input set from the adjacency matrix is a prevalent graph-based approach among researchers [7, 14, 19, 45].
Another approach of extracting two input feature groups is used by Long et al. in [32]. First, a knowledge graph for the stock market can be constructed between the stocks using different information such as shareholding, relevance, or affiliation [32]. Next, a similarity measure such as cosine similarity is used to identify the relevant stocks of the target stock. Then, a market information vector and a group trading vector are extracted by combining the indicator vectors of the target stock and the relevant stocks. These two input features are then concatenated to generate the final input feature set named as price movement vector [32].
Some researchers also opt for more than two input feature sets. For example, Deng et al. [13] use price series, news corpus, and knowledge graph as their input features sets. The text data of the news corpus are converted to structured event tuples. Each item in event tuples is then linked to knowledge graph and a sub-graph is constructed from the knowledge graph by applying the technique of event linking [13]. A knowledge-driven multi-channel concatenation technique is applied to generate the final event embedding from knowledge graph linking [13]. This event embedding is concatenated with the price data and used as input for the subsequent prediction task.
Researchers use statistical properties of the stock market graph such as Kullback–Leibler (KL) divergence, relative strength, Eigenvector centrality, betweenness centrality, and modularity as the input features [28]. Zhang and Zhuang use the network stability coefficient and Eigenvector centrality of the stock market graph to predict the abnormal fluctuation of the market [62].
5.3 Prediction models
5.3.1 Traditional statistical and machine learning models
Few studies use traditional statistical models for stock movement prediction while using a graph-based approach. For example, an auto regressive integrated moving average (ARIMA) model can be used to predict the actual value of a stock market index using graph-based input features [28]. Some studies use a probit model to predict the abnormal fluctuation of the stock market [62]. ANN and SVM can be considered as traditional machine learning models as they are being used for quite a long time for stock movement prediction. However, their usage in graph-based approaches is limited. Sun et al. [50] use a three-layered feed-forward neural network to predict the one-day ahead return of stocks using graph-based input features.
It is possible to use a combination of supervised and semi-supervised models while predicting stock movement using a graph-based approach [27, 40]. ML models such as ANN or SVM use past time series data for predicting the future direction of different global indices in the supervised part. The semi-supervised part uses the label spreading technique to predict the node type (e.g., rise or fall) for the next period [27]. The main idea is to use the already available label (rise or fall) of the other global markets in a semi-supervised manner to predict the direction of the unlabelled markets [27]. The graph is constructed using the correlation between the stock indices, and the Continuous Kruskal-based Graph (ConKruG) technique is used to filter the most relevant edges. If a market has better supervised prediction performance, that market is used for probability injection in the hybrid prediction [27]. Thus, the supervised and semi-supervised predictions are combined to calculate the final prediction [27].
5.3.2 Application of graph convolution network (GCN) and embedding techniques
The most recent trend for stock movement prediction using a graph-based approach is the application of graph convolution network (GCN) and different node embedding techniques. For example, in TGC, a convolutional neural network (CNN) generates the relational embedding from time series data [14, 45]. Then, a fully connected neural network is used to generate the stock ranking on the next day using the concatenated input features (e.g., temporal embedding and relational embedding). The prediction performance of TGC can be improved by using the list-wise loss instead of the combination of point-wise and pair-wise loss [45]. A node embedding technique such as Node2vec instead of a fully connected CNN can significantly improve the training time while achieving similar prediction performance [45]. Gao et al. [19] use the time-aware relational attention (TRA) layer to generate the time-aware relation strength between two stocks using temporal embedding and document encoding as mentioned in Sect. 5.2. Then, a graph convolution unit is used to aggregate the features of neighboring nodes with time-aware relation strength [19]. The output of the graph convolution unit is concatenated with temporal embedding and fed into a fully connected neural network to predict the stock ranking on the next day [19]. Deng et al. [13] use concatenated price data and event embedding as the input of a temporal convolution network (TCN) layer. The TCN layer uses dilated causal convolutions and residual connections for making the prediction.
Node2vec can be also be used to extract node (e.g., stock) features from a knowledge graph, and the cosine similarity between the stocks can be used to identify relevant stocks for a target stock [32]. Then, the input features of these relevant stocks are combined with the features of the target stock to generate the final input feature vector (e.g., price movement vector), as discussed in Sect. 5.2 [32]. Finally, an attention-based Bi-directional Long Short Term Memory (BiLSTM) network is used to make the prediction from this input feature set [32].
Chen and Wei use two graph-based approaches for stock movement prediction [7]. The first approach, named the pipeline prediction model, is similar to [32]. In the pipeline prediction model, the graph is formulated using the shareholding ratio between two stocks, and three graph embedding techniques (e.g., LINE, Node2vec, and DeepWalk) are used to learn the representation. The features of the target stock and the relevant stocks are combined similarly to [32]. Finally, an LSTM-based encoder layer followed by a classification layer is used to generate the predicted direction. The second approach utilizes a GCN layer. The GCN layer can generate an updated representation of each node by integrating information of all the neighbors rather than the relevant or top neighbors only [7]. The adjacency matrix and the embedding extracted from time series data are used as input to the GCN layer [7]. The GCN layer has learnable weights which are optimized during the training process. An output layer follows the GCN layer to generate the prediction of the next-day direction.
Some studies use less computationally intensive algorithms in their graph-based approach. For example, Fu et al. [18] use a linear layer first to generate a memory from the price data of individual stocks. Then a similarity measurement between two stocks is calculated by taking an inner product of the corresponding entry of the adjacency matrix, followed by a softmax layer. Finally, the relational embedding is calculated by taking the weighted sum of the initial memory of all the neighbors. The similarity measurements are used as weights in this case.
5.4 Evaluation metrics
The evaluation metrics vary depending on the output used for stock movement prediction. If the output is the absolute value of the future return, the common evaluation metrics are mean absolute percentage error (MAPE) [50] or mean squared error (MSE) [14, 19, 28]. A commonly used evaluation metric for directional performance is accuracy [7, 18, 27, 32, 50]. Long et al. use balanced accuracy (BAcc), which takes the cost associated with misclassifying a positive example into account [32] and can be defined as follows
where TP is the true positives, FP is the false positives, TN is the true negatives, FN is the false negatives, and c is the cost associated with the misclassification of a positive example.
If there is an imbalance in the data set, F1-score is also used as an evaluation metric and can be defined as follows [13, 18].
We can define precision and recall as follows.
Some studies use the area under the curve (AUC) as the evaluation metric of the prediction performance [32, 40]. AUC is defined as the area under the receiver operating characteristic curve (ROC).
The evaluation metrics are quite different when it comes to stock ranking prediction. For example, some researchers use the mean reciprocal rank of the top stock (MRRT), which reflects the performance of the topmost stock prediction [14, 19]. On the other hand, Saha et al. use normalized rank biased overlap (NRBO), which measures the ranking performance of top-k stocks [45]. Rank biased overlap (RBO) for the top-k stocks can be defined as follows.
where p is the probability parameter, and \(\text {AG}_s\) is the agreement at depth s. \(\text {AG}_s\) measures the proportion of overlap between the actual rank and the predicted rank. The value of p determines the total weight of top-k stocks. NRBO is a modified version of RBO to ensure that the evaluation metric has a value between 0 and 1. It is defined as follows [45].
Researchers also focus on different investment performances as evaluation metrics. A common evaluation metric is the cumulative investment return ratio (IRR) [14, 19, 45]. Stocks are bought and sold according to the predictions, and IRR is calculated as the cumulative return over the test period. Investment performance is also measured using the Sharpe ratio (SR), which takes both risk and return into account [18, 36]. Some researchers also use the maximum drawdown ratio (MDR) and maximum drawdown period ratio (MDPR) as the evaluation metrics to reflect the investment performance [18]. MDR and MDPR measure the downside risk of the investments.
6 Portfolio optimization using graph-based approach
6.1 Peripherality and centrality measure-based approach
A peripherality measure can be used to identify whether a node is in the center or periphery of a graph. The peripherality of a node is defined by combining five centrality measures: the degree centrality (DC), the betweenness centrality (BC), the eccentricity (EC), the closeness centrality (CC), and the Eigenvector centrality (EVC) [31, 42]. The graph is first filtered using a graph filtering technique, and then the peripherality measure (PM) is calculated [31, 42].
where the superscript w represents the weighted and u represents the unweighted filtered graph.
To calculate \(\text {DC}^w\) and \(\text {EVC}^w\), we can use \(1+\bar{\rho _{ij}}^w\) as the weight [42]. In the case of \(\text {BC}^w\), \(\text {EC}^w\), and \(\text {CC}^w\), the distance measure of equation (5) is used as the weight [42]. The \(\text {PM}\) should be small for central nodes and large for peripheral nodes. The nodes are sorted in ascending order based on the value of \(\text {PM}\). The top-k stocks are selected for the central portfolio, and the bottom-k stocks are selected for the peripheral portfolio [31, 42]. The investment weight for an individual stock can be applied based on different weighting schemes such as uniform weights, Markowitz weights, and with or without short-selling [31, 42].
It is possible to use centrality measures such as Eigenvector centrality and alpha centrality to identify the weakly connected assets and allocate higher investment weights to them [29]. In another centrality measure-based approach, stocks with centrality greater than a certain threshold are selected for portfolio formulation [41]. The cross-sectional correlation between the Eigenvector centrality and the Sharpe ratio is used as the measure of the centrality in this technique [41]. The threshold is selected by using a simulation procedure that uses artificially created sub-samples [41].
6.2 Graph clustering-based approach
In a graph clustering-based approach, nodes are clustered into different segments. Stocks are selected from different clusters to form the portfolio. Hierarchical risk parity (HRP) uses a hierarchical clustering technique to construct the portfolio [12]. HRP assumes that the stock market graph follows a hierarchical structure. HRP has three major steps: tree clustering, quasi-diagonalization, and recursive bisection [12]. A hierarchical clustering algorithm can be applied to combine the stocks into a hierarchical structure of clusters in the tree clustering step. The quasi-diagonalization step reorganizes the rows and columns of the adjacency matrix so that the largest values lie along the diagonal. This step ensures that similar investments are placed together, and dissimilar investments are placed far apart [12]. In the recursive bisection step, the investment weights are allocated in a top-down manner along the hierarchical tree structure [12]. It also ensures that the riskier assets are given fewer investment weights.
In the spectral clustering-based approach, the stock market graph is first clustered into several clusters using the spectral clustering method. One such approach is the portfolio cut method, where repeated bi-partitioning is implemented using successive spectral clustering [11]. This repeated bi-partitioning (K times) results in a hierarchical clustering with \((K+1)\) disjoint clusters or leaves. Different schemes are then used to allocate investment weights to these clusters and constituent stocks. For example, in an equal-weight scheme, each cluster can have an investment weight of \(\frac{1}{2^{K_s}}\) or \(\frac{1}{K+1}\) [11]. Here, \(K_s\) is the number of cuts required to obtain that cluster. These weights can again be distributed equally among the constituent stocks of the clusters.
7 Future direction
The application of the graph-based approaches for stock market analysis and prediction has a long history. However, new potential research areas are emerging with the advent of technological advancement. We will try to summarize several such potential research areas.
Application of the node embedding techniques for stock movement prediction is a potential direction. We have seen several applications so far, such as the usage of Node2vec, LINE, or DeepWalk. However, they are mainly shallow embedding techniques and have several limitations, including lack of parameter sharing, not using node attributes during encoding, and being transductive [20]. Researchers can explore generalized encoder-decoder architectures which can take care of the limitations mentioned above.
Researchers can focus on the application of machine learning techniques to calculate the edge weights. Present studies use mainly variants of correlation or mutual information as the edge weight. Identifying edge weight can be considered as a machine learning task. For example, an LSTM network can be used to capture the relationship between the return series of two different stocks.
Graph attention networks assume different contributions from the neighbors and use attention mechanisms to learn relative weights between two nodes [58]. We have not seen any significant study that applies graph attention networks on the stock market graphs. Researchers can consider the application of different graph attention networks such as graph attention network (GAT) [55], gated attention network [61], or mixture model network as a potential direction [37].
The neural network-based techniques that have been applied on the stock market graph so far are mostly shallow networks. We have not seen any deep network for extracting embeddings or making predictions. It will be interesting to see how the prediction performance changes if the depth of the neural network grows. Moreover, researchers can also focus on applying modern clustering techniques such as ultra-scalable spectral clustering (U-SPEC) [22], ultra-scalable ensemble clustering (U-SNEC) [22], or spectralnet [47].
8 Conclusion
The application of graph-based approaches for stock market analysis and prediction is evolving. Traditionally, the researchers mainly focus on the analysis part, such as filtering, clustering and identifying interesting patterns. However, with the surge of computational power, the focus is increasing on the application for stock movement prediction. This paper discusses the major studies regarding both analysis and prediction.
Two major stock market graph formulation techniques are based on correlation and mutual information and their variants. Researchers apply graph filtering techniques as the stock market graph is densely connected in most cases. Fusion of stock market graph data with traditional time series data can improve the stock movement prediction. Graph-based approaches can also improve portfolio performance. The stock movement prediction and portfolio optimization using graph-based approaches are still in the nascent stage. Future researches should focus on improving the stock movement prediction and portfolio optimization performance using graph-based approaches.
References
Aste, T., Di Matteo, T., Hyde, S.: Complex networks on hyperbolic surfaces. Physica A Stat. Mech. Appl. 346(1), 20–26 (2005)
Aste, T., Shaw, W., Matteo, T.D.: Correlation structure and dynamics in volatile markets. New J. Phys. 12(8), 085009 (2010)
Bhardwaj, G., Swanson, N.R.: An empirical investigation of the usefulness of ARFIMA models for predicting macroeconomic and financial time series. J. Econom. 131(1), 539–578 (2006)
Boginski, V., Butenko, S., Pardalos, P.M.: Statistical analysis of financial networks. Comput. Stat. Data Anal. 48(2), 431–443 (2005)
Bonanno, G., Caldarelli, G., Lillo, F., Vandewalle, S.M.N., Mantegna, R.N.: Networks of equities in financial markets. Eur. Phys. J. B 38(2), 363–371 (2004)
Bonanno, G., Vandewalle, N., Mantegna, R.N.: Taxonomy of stock market indices. Phys. Rev. E 62(6), R7615–R7618 (2000)
Chen, Y., Wei, Z., Huang, X.: Incorporating corporation relationship via graph convolutional neural networks for stock price prediction. In: Proceedings of the 27th ACM International Conference on Information and Knowledge Management, pp. 1655–1658 (2018)
Chi, K.T., Liu, J., Lau, F.C.: A network perspective of the stock market. J. Empir. Finance 17(4), 659–667 (2010)
Curme, C., Tumminello, M., Mantegna, R.N., Stanley, H.E., Kenett, D.Y.: How lead-lag correlations affect the intraday pattern of collective stock dynamics. Available at SSRN 2648490 (2019)
Darrat, A.F., Zhong, M.: On testing the random-walk hypothesis: a model-comparison approach. Financ. Rev. 35(3), 105–124 (2000)
Dees, B.S., Stanković, L., Constantinides, A.G., Mandic, D.P.: Portfolio cuts: a graph-theoretic framework to diversification. In: ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 8454–8458 (2020)
de Prado, M.L.: Building diversified portfolios that outperform out of sample. J. Portf. Manag. 42(4), 59–69 (2016)
Deng, S., Zhang, N., Zhang, W., Chen, J., Pan, J.Z., Chen, H.: Knowledge-driven stock trend prediction and explanation via temporal convolutional network. In: Companion Proceedings of the 2019 World Wide Web Conference, pp. 678–685 (2019)
Feng, F., He, X., Wang, X., Luo, C., Liu, Y., Chua, T.S.: Temporal relational ranking for stock prediction. ACM Trans. Inf. Syst. (TOIS) 37(2), 1–30 (2019)
Fiedler, M.: Algebraic connectivity of graphs. Czechoslov. Math. J. 23(2), 298–305 (1973)
Fiedor, P.: Networks in financial markets based on the mutual information rate. Phys. Rev. E 89, 052801 (2014)
Fortunato, S.: Community detection in graphs. Phys. Rep. 486(3), 75–174 (2010)
Fu, Z., Xu, W., Hu, R., Long, G., Jiang, J.: Mhier-encoder: modelling the high-frequency changes across stocks. Knowl. Based Syst. 224, 107092 (2021)
Gao, J., Ying, X., Xu, C., Wang, J., Zhang, S., Li, Z.: Graph-based stock recommendation by time-aware relational attention network. ACM Trans. Knowl. Discov. Data (TKDD) 16(1), 1–21 (2021)
Hamilton, W.L., Ying, R., Leskovec, J.: Representation learning on graphs: methods and applications. arXiv preprint arXiv:1709.05584 (2017)
Henrique, B.M., Sobreiro, V.A., Kimura, H.: Literature review: machine learning techniques applied to financial market prediction. Expert Syst. Appl. 124, 226–251 (2019)
Huang, D., Wang, C.D., Wu, J.S., Lai, J.H., Kwoh, C.K.: Ultra-scalable spectral clustering and ensemble clustering. IEEE Trans. Knowl. Data Eng. 32(6), 1212–1226 (2019)
Huang, W.Q., Zhuang, X.T., Yao, S.: A network analysis of the Chinese stock market. Physica A Stat. Mech. Appl. 388(14), 2956–2964 (2009)
Ward, J.H., Jr.: Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58(301), 236–244 (1963)
Kenett, D.Y., Havlin, S.: Network science: a useful tool in economics and finance. Mind Soc. 14(2), 155–167 (2015)
Kenett, D.Y., Tumminello, M., Madi, A., Gur-Gershgoren, G., Mantegna, R.N., Ben-Jacob, E.: Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market. PLoS One 5(12), 1–14 (2010)
Kia, A.N., Haratizadeh, S., Shouraki, S.B.: A hybrid supervised semi-supervised graph-based model to predict one-day ahead movement of global stock markets and commodity prices. Expert Syst. Appl. 105, 159–173 (2018)
Kim, M., Sayama, H.: Predicting stock market movements using network science: an information theoretic approach. Appl. Netw. Sci. 2(1), 1–14 (2017)
Konstantinov, G., Chorus, A., Rebmann, J.: A network and machine learning approach to factor, asset, and blended allocation. J. Portf. Manag. 46(6), 54–71 (2020)
Li, M.X., Jiang, Z.Q., Xie, W.J., Xiong, X., Zhang, W., Zhou, W.X.: Unveiling correlations between financial variables and topological metrics of trading networks: evidence from a stock and its warrant. Physica A Stat. Mech. Appl. 419, 575–584 (2015)
Li, Y., Jiang, X.F., Tian, Y., Li, S.P., Zheng, B.: Portfolio optimization based on network topology. Physica A Stat. Mech. Appl. 515, 671–681 (2019)
Long, J., Chen, Z., He, W., Wu, T., Ren, J.: An integrated framework of deep learning and knowledge graph for prediction of stock price trend: an application in Chinese stock exchange market. Appl. Soft Comput. 91, 106205 (2020)
Mantegna, R.N.: Hierarchical structure in financial markets. Eur. Phys. J. B Condens. Matter Complex Syst. 11(1), 193–197 (1999)
Marti, G., Nielsen, F., Bińkowski, M., Donnat, P.: A review of two decades of correlations, hierarchies, networks and clustering in financial markets. arXiv:1703.00485 (2017)
Massara, G.P., Di Matteo, T., Aste, T.: Network filtering for big data: triangulated maximally filtered graph. J. Complex Netw. 5(2), 161–178 (2017)
Matsunaga, D., Suzumura, T., Takahashi, T.: Exploring graph neural networks for stock market predictions with rolling window analysis. arXiv:1909.10660 (2019)
Monti, F., Boscaini, D., Masci, J., Rodola, E., Svoboda, J., Bronstein, M.M.: Geometric deep learning on graphs and manifolds using mixture model CNNs. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5115–5124 (2017)
Musmeci, N., Aste, T., Di Matteo, T.: Relation between financial market structure and the real economy: comparison between clustering methods. PLoS One 10(3), e0116201 (2015)
Papana, A., Kyrtsou, C., Kugiumtzis, D., Diks, C.: Financial networks based on granger causality: a case study. Physica A Stat. Mech. Appl. 482, 65–73 (2017)
Park, K., Shin, H.: Stock price prediction based on a complex interrelation network of economic factors. Eng. Appl. Artif. Intell. 26(5), 1550–1561 (2013)
Peralta, G., Zareei, A.: A network approach to portfolio selection. J. Empir. Finance 38, 157–180 (2016)
Pozzi, F., Matteo, T.D., Aste, T.: Spread of risk across financial markets: better to invest in the peripheries. Sci. Rep. 3(1), 1–7 (2013)
Raffinot, T.: Hierarchical clustering-based asset allocation. J. Portf. Manag. 44(2), 89–99 (2017)
Rosvall, M., Bergstrom, C.T.: Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. 105(4), 1118–1123 (2008)
Saha, S., Gao, J., Gerlach, R.: Stock ranking prediction using list-wise approach and node embedding technique. IEEE Access 9, 88981–88996 (2021)
Sensoy, A., Tabak, B.M.: Dynamic spanning trees in stock market networks: the case of Asia-Pacific. Physica A Stat. Mech. Appl. 414, 387–402 (2014)
Shaham, U., Stanton, K., Li, H., Nadler, B., Basri, R., Kluger, Y.: Spectralnet: Spectral clustering using deep neural networks. arXiv preprint arXiv:1801.01587 (2018)
Song, D.M., Tumminello, M., Zhou, W.X., Mantegna, R.N.: Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Phys. Rev. E 84(2), 026108 (2011)
Song, W.M., Di Matteo, T., Aste, T.: Hierarchical information clustering by means of topologically embedded graphs. PLoS One 7(3), e31929 (2012)
Sun, X.Q., Shen, H.W., Cheng, X.Q.: Trading network predicts stock price. Sci. Rep. 4(1), 1–6 (2014)
Tumminello, M., Aste, T., Di Matteo, T., Mantegna, R.N.: A tool for filtering information in complex systems. Proc. Natl. Acad. Sci. 102(30), 10421–10426 (2005)
Tumminello, M., Lillo, F., Mantegna, R.N.: Correlation, hierarchies, and networks in financial markets. J. Econ. Behav. Organ. 75(1), 40–58 (2010)
Tumminello, M., Lillo, F., Piilo, J., Mantegna, R.N.: Identification of clusters of investors from their real trading activity in a financial market. New J. Phys. 14(1), 013041 (2012)
Tumminello, M., Miccich, S., Lillo, F., Piilo, J., Mantegna, R.N.: Statistically validated networks in bipartite complex systems. PLoS One 6(3), 1–11 (2011)
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., Bengio, Y.: Graph attention networks. arXiv preprint arXiv:1710.10903 (2017)
Wang, G.J., Xie, C.: Tail dependence structure of the foreign exchange market: a network view. Expert Syst. Appl. 46, 164–179 (2016)
Wen, F., Yang, X., Zhou, W.X.: Tail dependence networks of global stock markets. Int. J. Finance Econ. 24(1), 558–567 (2019)
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., Philip, S.Y.: A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 32(1), 4–24 (2020)
Yan, Y., Wu, B., Tian, T., Zhang, H.: Development of stock networks using part mutual information and Australian stock market data. Entropy 22(7), 773 (2020)
Ying, X., Xu, C., Gao, J., Wang, J., Li, Z.: Time-aware graph relational attention network for stock recommendation. In: Proceedings of the 29th ACM International Conference on Information & Knowledge Management, pp. 2281–2284 (2020)
Zhang, J., Shi, X., Xie, J., Ma, H., King, I., Yeung, D.Y.: GAAN: gated attention networks for learning on large and spatiotemporal graphs. arXiv preprint arXiv:1803.07294 (2018)
Zhang, W., Zhuang, X.: The stability of Chinese stock network and its mechanism. Physica A Stat. Mech. Appl. 515, 748–761 (2019)
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by The Business School Research Scholarship of The University of Sydney.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Saha, S., Gao, J. & Gerlach, R. A survey of the application of graph-based approaches in stock market analysis and prediction. Int J Data Sci Anal 14, 1–15 (2022). https://doi.org/10.1007/s41060-021-00306-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-021-00306-9