A greedy algorithm to construct sparse graph by using ranked dictionary

Abstract

$\mathcal {L}_1$ graph is an effective way to represent data samples in many graph-oriented machine learning applications. Its original construction algorithm is nonparametric, and the graphs it generates may have high sparsity. Meanwhile, the construction algorithm also requires many iterative convex optimization calculations and is very time-consuming. Such characteristics would severely limit the application scope of $\mathcal {L}_1$ graph in many real-world tasks. In this paper, we design a greedy algorithm to speed up the construction of $\mathcal {L}_1$ graph. Moreover, we introduce the concept of “Ranked Dictionary” for $\mathcal {L}_1$ minimization. This ranked dictionary not only preserves the locality but also removes the randomness of neighborhood selection during the process of graph construction. To demonstrate the effectiveness of our proposed algorithm, we present our experimental results on several commonly used datasets using two different ranking strategies: One is based on Euclidean distance, and another is based on diffusion distance.

1 Introduction

For graph-oriented learning tasks, a quality graph representation [6] of input data samples is the key to success. In the past few decades, researchers in machine learning area propose many different methods to solve such tasks, for example, k nearest neighbor (kNN) graph and $\epsilon$-ball graphs. These methods are very straightforward and proved to be efficient for general data. The reason of these methods’ success is that their construction algorithm acts as a local smooth “filter” which sets the weight between faraway data points and source point to zero. The built graph is constructed by many such local star-shaped patches (or subgraphs). However, both of them need a user-specified parameter such as k or $\epsilon$ which is chosen empirically. Considering the versatility and uncertainty of the real-world data, a bad selection of parameter k and $\epsilon$ will lead to an inaccurate conclusion for subsequent machine learning tasks. Recently, a nonparametric graph called $\mathcal {L}_1$ graph is proposed by Cheng et al. [4]. Based on existing sparse representation frameworks [21, 25], the construction algorithm of $\mathcal {L}_1$ graph can be described as follows: Given an input data samples $\mathbf {X\,=\,[x_1, x_2,\ldots ,x_n ]}$, where each $\varvec{x_i}, i \in [1,\ldots ,n]$ is a vector that represents one single data sample. The $\mathcal {L}_1$ graph of $\mathbf {X}$ is built by finding a sparse coding [23] of each $\mathbf {x_i}$ with a dictionary constructed from all data samples except $\mathbf {x_i}$ itself. The coefficient of sparse coding is used as the edge weight of resulted $\mathcal {L}_1$-graph. The mathematical definition of sparse coding is:

$$\begin{aligned} \mathbf {(P1)} \quad \min \limits _{\varvec{\alpha _i}}\Vert \varvec{\alpha _i}\Vert _{1}~\mathrm {subject~to}~ \varvec{x_i} \,=\, \varvec{\varPhi }^i\varvec{\alpha _i}, \end{aligned}$$

(1)

where dictionary $\varvec{\varPhi }^i \,=\, \varvec{[x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n]}$, and $\varvec{\alpha }_i \in \mathbb {R}^{n-1}$ is the sparse code of $\varvec{x_i}$. The coefficients of $\varvec{\alpha }_i$ could be negative, depending on the choices of $\mathcal {L}_1$ minimization solvers. To make them have the physical meaning of “Similarity,” the absolute value or nonnegative constraints are employed.

As we could see from the above description, the $\mathcal {L}_1$ graph construction algorithm is nonparametric and the user is not required to input any parameters except for the solver. The construction algorithm is a pure numerical process based on convex optimization. Cheng et al. [4] show that $\mathcal {L}_1$ graph has three advantages comparing traditional graph construction methods. They are: (1) robustness to data noise; (2) sparsity; (3) datum-adaptive neighborhood. Their experimental results also prove that $\mathcal {L}_1$ graph has significant performance improvement in many machine learning applications such as spectral clustering, subspace learning and semi-supervised learning [4]. Nevertheless, just like each sword has double edges, $\mathcal {L}_1$ graph also bears some disadvantages such as: (1) sensitive to duplications. For example, if every data sample has a duplication, the resulted $\mathcal {L}_1$ graph will only have edge connections between the data sample and its duplication; (2) randomness, the edge and edge weight are highly dependent on the solver; (3) high computational cost [4]; (4) lost of the locality [10, 11, 32]. To overcome these disadvantages, many improved algorithms have been proposed in recent years. Now, we would like to classify them into two categories: soft-modification and hard-modification.

• 1. Soft-modification algorithms. Algorithms in this category usually add one or more regularization terms to the original $\mathcal {L}_1$ minimization objective function in Eq. (1). For example, the structure sparsity [33] preserves the local structure information of input data, the auto-grouped sparse regularization [10] adds the group effect to the final graph, and the graph Laplacian regularization [29, 30] lets the closed data samples have similar sparse coding coefficients (or $\varvec{\alpha }_i$).

• 2. Hard-modification algorithms. These algorithms define a new dictionary for each data sample during $\mathcal {L}_1$ minimization. By reducing the solvers’ solution space for each data sample into a local space, the locality of input data is preserved and the computational time of $\mathcal {L}_1$ minimization [Eq. (1)] is reduced. For example, the locality preserved (LOP) $\mathcal {L}_1$ graph is utilizing k nearest neighbors as dictionaries [11].

Fig. 1

Connection of greedy $\mathcal {L}_1$ graph to other graphs. Several of them are: kNN-fused Lasso graph [33], group sparse (GS) $\mathcal {L}_1$ graph, kernelized group sparse (KGS) $\mathcal {L}_1$ graph [10], Laplacian regularized (LR) $\mathcal {L}_1$ graph [30] and locality preserving (LOP) $\mathcal {L}_1$ graph [11]

Fig. 2

$\mathcal {L}_1$ graphs generated by different construction algorithms. From left to right: 2D toy dataset; $\mathcal {L}_1$ graph; Greedy-$\mathcal {L}_1$ graph with Euclidean distance ranking (K $=$ 15); Greedy-$\mathcal {L}_1$ graph with diffusion distance ranking (K $=$ 15)

The soft-modification algorithms preserve the nonparametric feature and improve the quality of $\mathcal {L}_1$ graph by exploiting the intrinsic data information such as geometry structure and group effects. However, those algorithms still have high computational cost. This is unpleasant for the large-scale dataset in this “Big-data” era. To improve, in this paper we propose a greedy algorithm to generate $\mathcal {L}_1$ graph. The generated graphs are called Greedy- $\mathcal {L}_1$ graphs. Our algorithm employs greedy $\mathcal {L}_1$ minimization solvers and is based on nonnegative orthogonal matching pursuit (NNOMP). Furthermore, we use ranked dictionaries with reduced size K which is a user-specified parameter. We provide the freedom to the user to determine the ranking strategy such as nearest neighbors or diffusion ranking [5]. Our algorithm has significant time reduction about generating $\mathcal {L}_1$ graphs. Comparing the original $\mathcal {L}_1$ graph construction method, our algorithm loses the nonparametric characteristics and is only offering a suboptimal solution. However, our experimental results show that the graph generated by our algorithm has equal (or even better) performance as the original $\mathcal {L}_1$ graph by setting K equals to the length of data sample. Our work is a natural extension of existing $\mathcal {L}_1$ graph research. A concise summary of the connection between our proposed Greedy-$\mathcal {L}_1$ graph and other graphs is illustrated in Figs. 1 and 2. This paper is an improved version of accepted conference paper [12]. We summary the main contributions as:

• 1. We propose a greedy algorithm to reduce the computational time of generating $\mathcal {L}_1$ graph.

• 2. We introduce the ranked dictionary for $\mathcal {L}_1$ minimization solver. This new dictionary not only reduces the time of minimization process but also preserves the locality and geometry structure information of input data.

• 3. Our algorithm removes the randomness of edges in final $\mathcal {L}_1$ graph and preserves the uniqueness except for the edge weights. Moreover, our algorithm can generate $\mathcal {L}_1$ graphs with lower sparsity.

• 4. We present experiment and analysis results by applying our algorithm to spectral clustering application with different datasets. Our experimental results show that the graphs generated by our proposed greedy algorithm have equal clustering performance even though it is only providing a suboptimal solution.

• 5. We discuss the connection between $\mathcal {L}_1$ graph and sparse subspace clustering and also explain the different with locally linear embedding [19].

• 6. We review the recent research works related to $\mathcal {L}_1$ graph such as $\mathcal {L}_0$ graph which has better subspace persevering ability in theory [28] and scalable sparse subspace clustering [31] for the computational challenges of large size data.

Fig. 3

Demonstration of dictionary normalization for a toy dataset. The red (bottom left) and blue (up right) points represent two different clusters. Left before normalization; right after normalization. We can see that the neighborhood relationship is changed after normalization (color figure online)

The organization of our paper is as follows. First, an overview of the disadvantages of original $\mathcal {L}_1$ graph construction algorithm will be presented in Sect. 2. Second, we will introduce our proposed greedy algorithm in Sect. 3. After that, we will give a review of existing works on how to improve the quality of $\mathcal {L}_1$ graph. Finally, we will present our experimental results in Sect. 5 and draw conclusion in Sect. 6.

2 Overview

In this section, we make our attempts to address two problems of original $\mathcal {L}_1$ graph construction algorithm. They are: (1) curse of dictionary normalization and (2) nonlocal edges.

2.1 Original $\mathcal {L}_1$ graph construction algorithm

This section reviews the original construction algorithm of $\mathcal {L}_1$ graph (1) in advance for the purpose of comparison with our proposed new algorithm in Sect. 3. The details can be seen as algorithm (1). As we can see from the original construction algorithm, it includes n repeat optimization steps, while n equals to the number of data samples. Moreover, each optimization step involves an over-complete dictionary $\varPhi ^i$ which has size $n-1$. These properties label the original construction algorithm with “time-consuming.” Nevertheless, the original construction algorithm also bears two other disadvantages as we will go details in following two sections.

2.2 Curse of dictionary normalization

While solving $\mathcal {L}_1$ minimization, the atoms of dictionary are normalized to have unit length. The goal of this step is to satisfy the theoretic requirement of compressive sensing. The less-ideal part about this normalization is that it does not preserve neighborhood information of input data. This can be illustrated in Fig. 3. To illustrate this phenomenon, we manually create a toy dataset in 2D and it has two clusters visually. After normalization, we can see that the neighbors of a node are changed. This normalization step projects all data samples onto a unit hypersphere, and the original geometry structure information is lost.

2.3 Nonlocal edges

During the construction of $\mathcal {L}_1$ graph, an over-complete dictionary is created for each data sample. The original method simply selects all other data samples as the dictionary. This strategy affords the nonparametric property of $\mathcal {L}_1$ graph. However, it also introduces nonlocal edges. In other words, it does not preserve the locality of input data [11]. This phenomenon can be illustrated in Fig. 4.

Fig. 4

$\mathcal {L}_1$-graph of path-based dataset. Left the entire graph; right edges of three selected points. We can see the existence of nonlocal edges

Table 1 The effect of unstable solutions caused by using different solvers or with different parameters

2.4 Unstable solutions caused by different $\mathcal {L}_1$ solvers

To solve the optimization problem (1), we need a numerical solver. There are many popular ones with various minimization methods [27] such asgradient projection, homotopy and proximal gradient. Moreover, all these solvers have their own special parameter settings. As a result, if we choose different parameters, the numerical results will be not same, or say, unstable. To illustrate this phenomenon, we exam the UCI Image dataset with “spams-matlab” software [16] and “l1_ls” software [13]. For each solver, we set the parameter $\lambda$ to different values as: [0.01, 0.001, 0.0001]. For the experiment, we select the first sample of image dataset as source sample and others as dictionary. To see the unstable solutions, we list the top five neighbors (Index) and its corresponding weights (Value). The result is shown in Table 1. As we can see, the majority neighbors between “spams-matlab” and “l1_ls” are same except some minor difference. However, the weights are very different and unstable. This unstable situation is not only with different parameter $\lambda$, but also with different solvers. This is a disadvantage for using $\mathcal {L}_1$ graph as similarity graph for graph-oriented machine learning tasks.

3 New algorithm

In this section, we introduce the concept of ranked dictionary and two different ranking strategies: Euclidean distance ranking and diffusion ranking. These different ranking methods are proposed for different types of data. For example, diffusion ranking is suitable for data with manifold structure, and Euclidean distance is the popular choice for general data. Obviously, there are many other distance choices such as cosine distance could be used for ranking, and it is upon user’s judgment for the right choice. Furthermore, we present a greedy algorithm at the end of this section.

3.1 Ranked dictionary

We propose a “ranked dictionary” to substitute the original dictionary $\Phi ^i$ in Eq. (1). Our claim is that the “ranked dictionary” not only preserves the locality of data, which is important for clustering applications, but also solves the “curse of dictionary normalization” dilemma. The idea of “ranked dictionary” is to rank the neighborhood information following a given distance metric such as Euclidean distance in vector space. By selecting the top K nearest neighbors as dictionary, the new dictionary $\Phi ^i_K$ keeps the order of nearest neighbors and captures the local distribution of data samples. Moreover, $\Phi ^i_K$ has smaller size comparing $n-1$, while n equals to the number of data samples.

Fig. 5

Ranked dictionary. Left eight data samples have the same direction but with different lengths. Red cross is the target data sample for calculating sparse coefficients. Right after normalization, those eight data samples have the same location (color figure online)

There is a subtle difference between k value of popular k nearest neighbor (kNN) graph and the K value in our proposed “ranked dictionary” $\Phi ^i_K$. Usually, the users set the value k of kNN graph in the order of $\log (n)$ which is the asymptotic connectivity result [1] that makes the kNN graph to be connected. For K value of $\Phi ^i_K$, it needs to be larger than d which is the dimension of vector $x_i$. This requirement is to let $\Phi ^i_K$ be an over-complete dictionary.

The use of truncated version of dictionary $\Phi$ is proved to be success in building quality $\mathcal {L}_1$ graph for clustering application [11]. However, it cannot solve the dilemma that there might exist data samples with the same direction but different lengths in input data. The dictionary normalization process will project them onto the same location at hypersphere. Since they have the same values, the $\mathcal {L}_1$ minimization solver will choose one of them randomly. To avoid this randomness, we need to rank those atoms (or data samples) of dictionary (Fig. 5).

Euclidean Distance Ranking. Using Euclidean metric to rank atoms of dictionary is quite straightforward. We rank them by distance. The shorter distance will have a higher rank score. The Euclidean distance is defined as:

$$\begin{aligned} \text {dist}\,(\varvec{x}_i,\varvec{x}_j) = \Vert \varvec{x}_i - \varvec{x}_j \Vert _2 = \left( \sum \limits _{k=1}^{n}|x_i(k)-x_j(k)|^2\right) ^{1/2}. \end{aligned}$$

(2)

Diffusion Distance Ranking. As pointed out by Yang et al. [30], many real-world datasets are similar to an intrinsic low-dimensional manifold embedded in high-dimensional ambient space, and the geometry structure of manifold can be used to improve the performance of learning algorithms. We now present a strategy to search dictionaries following the geometry structure of input data. Based on the diffusion theory [5, 7], we rank the atoms of dictionary through diffusion matrix. A diffusion process has three stages [7]: (1) initialization; (2) definition of transition matrix; (3) definition of the diffusion process. In our setting, the first stage is to build an affinity matrix $\varvec{A}$ from the input dataset $\varvec{X}$. We use Gaussian kernel to define the pairwise distance:

$$\begin{aligned} \varvec{A}(i,j) = \exp \left( -\frac{\Vert \varvec{x_i} - \varvec{x_j}\Vert ^2}{2\sigma ^2} \right) , \end{aligned}$$

(3)

where $\varvec{A}(i,j)$ is the distance between data sample $\varvec{x_i}$ and data sample $\varvec{x_j}$, and $\sigma$ is a normalization parameter. In our configuration, we use the median of K nearest neighbors to tune $\sigma$. The second stage is to define the transition matrix $\varvec{P}$:

$$\begin{aligned} \varvec{P} = \varvec{D}^{-1}\varvec{A}, \end{aligned}$$

(4)

where $\varvec{D}$ is a $n \times n$ degree matrix defined as

$$\begin{aligned} \varvec{D}(i,j) = \left\{ \begin{array}{ll} \sum _{j=1}^{n}\varvec{A}(i,j) &{} \quad \text{ if } i=j, \\ 0 &{} \quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

(5)

Now the diffusion process can be defined as:

$$\begin{aligned} \varvec{W}_{t+1} = \varvec{PW}_{t}\varvec{P}^{'}, \end{aligned}$$

(6)

where $\varvec{W}_0= \varvec{A}$ and t is the number of steps for diffusion steps. Each row of $\varvec{W}_{t}$ is the diffusion ranking scores. In this paper, we let t equal to K for the sake of simplicity. Once $\varvec{W}_{t}$ is calculated, the first K data samples with top scores of each row are selected as dictionary. The algorithmic details can be documented as follows:

3.2 Greedy $\mathcal {L}_1$ graph

To solve the $\mathcal {L}_1$ norm minimization problem, we need an efficient solver [27]. For datasets that size are larger than 3, 000 with reasonable dimensions, greedy solver like Basic Pursuit (BP) [3, 8] or Orthogonal Matching Pursuit (OMP) [22] is more suitable [31]. In this section, We propose a greedy algorithm to build $\mathcal {L}_1$ graph. Our proposed algorithm is based on OMP [31] and NNOMP [2, 15]. By using greedy solver, we switch the $\mathcal {L}_1$ minimization problem (P1) back to the original $\mathcal {L}_0$ optimization with (P2)/without (P3) nonnegative constraints as:

$$\begin{aligned} \mathbf {(P2)} \quad \min \limits _{\varvec{\alpha _i}}\Vert \varvec{\alpha _i}\Vert _{0}~\mathrm {subject~to}~ \varvec{x_i}&= \varvec{\varPhi }^i\varvec{\alpha _i}, \varvec{\alpha _i} \ge 0. \end{aligned}$$

(7)

$$\begin{aligned} \mathbf {(P3)} \quad \min \limits _{\varvec{\alpha _i}}\Vert \varvec{\alpha _i}\Vert _{0}~\mathrm {subject~to}~ \varvec{x_i}&= \varvec{\varPhi }^i\varvec{\alpha _i}. \end{aligned}$$

(8)

The main difference between our algorithm and the original OMP and NNOMP is that the atoms of dictionary are ranked. We force the solver to choose and assign weights to atoms that are closer to source data sample before normalization. To clarify our idea, we present the improved version of NNOMP solver in algorithm (3). For OMP solver, the idea and process are same.

3.3 Connection to subspace clustering

$\mathcal {L}_1$ graph is almost the same as the similarity graph of sparse subspace clustering (SSC) algorithm [9]. However, they have different assumptions about the data. The $\mathcal {L}_1$ graph is defined for general data and does not have any specific assumption about data like k nearest neighbor graph, while the similarity graph of SSC assumes the data are lied in a union of low-dimensional subspaces [9].

The success of $\mathcal {L}_1$ graph is first applied to human face images clustering [25, 26]. Those face images data have two sufficient conditions for the success of using $\mathcal {L}_1$ graph for spectral clustering: (1) The dimension of data vector is high. (2) Different human face images stay in different subspaces. However, for general data, these two conditions not always exist. By the experimental results from research work [11], the Ng, Jordan, Weiss et al. (NJW) spectral clustering algorithm [18] with Gaussian similarity graph has better performance than with $\mathcal {L}_1$ graph on several general datasets. So here, we argue that the power of $\mathcal {L}_1$ graph follows the assumption of sparse subspace clustering.

3.4 Connection to locally linear embedding

The idea of “ranked dictionary” has a connection to locally linear embedding (LLE) [19]. LLE solves the following minimization problem:

$$\begin{aligned} \epsilon (w) = \sum _{i}|\mathbf {x}_i - \sum _{j}\mathbf {w}_{ij}\mathbf {x}_j|^2. \end{aligned}$$

(9)

The cost function $\epsilon (w)$ is the add up of the squared distance between all data samples ($x_i$) and their reconstructions $\sum _{j}\mathbf {w}_{ij}\mathbf {x}_j$. There are two constraints during the minimization process: (1) The $\mathbf {x}_j$ are selected to be k nearest neighbor of $\mathbf {x}_i$, where k is a parameter set by user; (2) the row of weight matrix sum to one: $\sum _j\mathbf {w}_{ij} = 1$.

If we compare Eq. 9 of LLE with Eq. 1 of $\mathcal {L}_1$ graph and “ranked dictionary,” we can find that both of them are finding a linear representation relationship between a given data sample and its k nearest neighbors. However, $\mathcal {L}_1$ graph with “ranked dictionary” looks for a sparse reconstruction weights and prefer to assign nonzero weights for nearest neighbors $\mathbf {x}_j$ that stay in the same subspace as the given data sample $\mathbf {x}_i$. The second difference is the unique advantage of $\mathcal {L}_1$ graph.

3.5 Quality as similarity graph for spectral clustering

One major application of $\mathcal {L}_1$ graph is spectral clustering. Researchers use $\mathcal {L}_1$ graph as the similarity graph of spectral clustering algorithm by treating the sparse coefficients as similarity values. The similarity graph models the cluster structure of original data with pre-defined similarity metric and has significant impact on the performance of spectral clustering algorithm. A good similarity graph should have high weights for edges within same cluster and low weights for edges between different clusters. However, there is no explicit measurement of the quality of similarity graph from theoretic research as pointed out by [24]. Instead, the clustering performance, like Mutual Information and Accuracy, is used to tell whether the similarity graph is in high quality or not implicitly. “Locality” is another guidance to judge the quality of similarity graph [10]. “Locality” stresses that the edges of similarity graph should connect data points locally as nonlocal edges will affect the result of graph cut [20] and then the performance of spectral clustering [24]. In this section, we try to explain how $\mathcal {L}_1$ graph with “ranked dictionary” can generate high-quality similarity graphs.

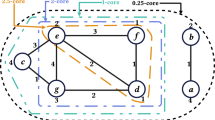
“Ranked dictionary” preserves the locality of data by only selecting k nearest neighbors as dictionary. For a given source data point, “ranked dictionary” constrains the possible candidates that it can connect to. There is a difference between k nearest neighbor of kNN graph and our proposed greedy $\mathcal {L}_1$ graph. We show it in Fig. 6.

Fig. 6

The range difference of “Ranked Dictionary” (RD), “kNN” and original “$\mathcal {L}_1$ graph.” The toy dataset includes two subspace S1 and S2. The selection range of nearest neighbors is shown by dash circles

As we can see, greedy $\mathcal {L}_1$ graph selects a larger range than kNN graph but a much smaller one than original $\mathcal {L}_1$ graph. It preserves the locality of data in a “Hard-modification” way as we introduced in the beginning of this work. And this locality preserving ability has been proved in previous research work [11].

Another important aspect of greedy $\mathcal {L}_1$ graph is that it preserves the local subspaces through OMP solver. As the theory proof in [31], if coherence between the residual vectors (set of $r^i$ in line 13 of algorithm (3)) and subspaces satisfies a data-dependent condition, the OMP solver preserves the subspaces of input data. Based on this, we observe another difference with kNN graph: The greedy $\mathcal {L}_1$ graph prefers to create connections between data samples within same subspace, while the kNN graph selects edges according to the given distance metric.

4 Related works

Original $\mathcal {L}_1$ graph [4] is a pure numerical result and does not exploit the physical and geometric information of input data. To improve the quality of $\mathcal {L}_1$ graph, several research works are proposed to use the intrinsic structure information of data by adding one or several regularization terms to the $\mathcal {L}_1$ minimization P1. For example, consider the elastic net regularization [10], OSCAR regularization [10] and graph Laplacian regularization [30].

Another research direction of $\mathcal {L}_1$ graph is to reduce its high computational cost. Zhou et al. [33] propose a kNN-fused Lasso graph by using the idea of k nearest neighbors in kernel feature space. With a similar goal, Fang et al. [10] propose an algorithm which transfers the data into reproducing kernel Hilbert space and then projects them into a lower-dimensional subspace. By these operations, the dimension of the dataset is reduced and the computational time is reduced.

$\mathcal {L}_1$ graph has strong theory connection with sparse subspace clustering [9]. Recently, Yingzhen et al. [28] propose the $\mathcal {L}_0$ graph which try to solve the same minimization problem P3 as in this paper. They intuition is that $\mathcal {L}_0$ norm has better subspace preserving ability than $\mathcal {L}_1$ norm. Since minimization $\mathcal {L}_0$ norm is NP-hard, there are more nonconvex optimization challenges remained to be solved.

5 Experiments

We present our experimental results in this section. The datasets in our experiments can be divided into small size data and large size data. The reason for this separation is that calculating the global optimization for $\mathcal {L}_1$ minimization is time-consuming for large size data (number of instances are larger than 3000.) For those large size data, we use an efficient OMP solver from “spams-matlab” [16]. As a consequence, the generated $\mathcal {L}_1$ graphs are not from optimal sparse coding solutions.

The effectiveness of our proposed graph construction methods is evaluated through NJW spectral clustering algorithm [18]. To satisfy the input of spectral clustering algorithm, we transform the adjacency matrix of $\mathcal {L}_1$ graph $\varvec{W}$ into a symmetry matrix $\varvec{W}^{'}$ by $\varvec{W}^{'}\,=\,(\varvec{W}+\varvec{W}^T)/2$. All analyses and experiments are carried out by using MATLAB on a server with Intel 12-core 3.4GHz CPU and 64GB RAM.

Table 2 Statistics of small size datasets

Table 3 NMI comparison of graph construction algorithms

Solvers We use three solvers in our experiments. For small size dataset, “l1-ls” is used for creating $\mathcal {L}_1$ graph, and our proposed NNOMP solver is used for greedy $\mathcal {L}_1$ graph. For large dataset, we use “spams-matlab” software [16], which is an efficient implementation of sparse optimization by using multi-thread techniques, to build the $\mathcal {L}_1$ graph and greedy $\mathcal {L}_1$ graph.

Table 4 ACC comparison of different graph construction algorithms

Evaluation metrics We evaluate the spectral clustering performance with Normalized Mutual Information (NMI) and Accuracy (ACC). NMI value ranges from 0 to 1, with higher values meaning better clustering performance. AC is another metric to evaluate the clustering performance by measuring the fraction of its clustering result that is correct. Its value also ranges from 0 to 1, and the higher the better.

5.1 Small size data

5.1.1 Datasets

To demonstrate the performance of our proposed algorithm, we evaluate it on seven UCI benchmark datasets including three biological datasets (BreastTissue, Iris and Soybean), two vision image datasets (Vehicle and Image), one chemistry dataset (Wine) and one physical dataset (Glass), whose statistics are summarized in Table 2. All of these datasets have been popularly used in spectral clustering analysis research. The diverse combinations of datasets are necessary for our comprehensive studies.

5.1.2 Baselines and parameters setting

We compare the spectral clustering performance with Gaussian similarity graph and original $\mathcal {L}_1$ graph. For experiments with small size datasets, we use the l1_ls solver [14] for original $\mathcal {L}_1$ graph construction algorithms. We set the solver’s parameter $\lambda$ to 0.1. The threshold $\theta _{\text {threshold}}$ of greedy solver 3 is set to $1e-5$. For Gaussian graph and greedy-$\mathcal {L}_1$ graph, we select three different K values and document their clustering performance results, respectively. The K is set to be the multiple data attribute sizes. The results are documented in Tables 3 and 4.

Fig. 7

Running time of different $\mathcal {L}_1$ graph construction algorithms. Top original $\mathcal {L}_1$ graph construction algorithm. Bottom the construction of $\mathcal {L}_1$ graph using greedy solver

5.1.3 Greedy-$\mathcal {L}_1$ graph versus Gaussian graph

Overall, the greedy-$\mathcal {L}_1$ graph using Euclidean metric has better average spectral clustering performance than Gaussian graphs. However, we also observe that Gaussian graph has overall better performance on “Iris,” “Soybean” and “Vehicle” datasets.

5.1.4 Greedy-$\mathcal {L}_1$ graph versus $\mathcal {L}_1$ graph

Greedy-$\mathcal {L}_1$ graph has better clustering performance than $\mathcal {L}_1$ graph on average. However, for Iris and Soybean datasets, the $\mathcal {L}_1$ graph shows the best clustering result: Iris (NMI $=$ 0.5943, ACC $=$ 0.74); Soybean (NMI $=$ 0.7373, ACC $=$ 0.6156). The best result of greedy-$\mathcal {L}_1$ graph is: Iris (NMI $=$ 0.5106, ACC $=$ 0.72); Soybean (NMI $=$ 0.6919, ACC $=$ 0.5244).

5.1.5 Euclidean distance ranking versus diffusion ranking

The Euclidean distance ranking appears to have better clustering performance than that of diffusion ranking in general. This is rather a surprising result to us. Only for “Iris” dataset, the result of diffusion ranking is better than that of Euclidean distance ranking.

5.1.6 Running time

We report the running time of generating $\mathcal {L}_1$ graphs using different construction algorithms. As we can see from Fig. 7, the greedy-$\mathcal {L}_1$ graphs have consumed significantly less construction time than that in original $\mathcal {L}_1$ graphs.

5.1.7 Graph sparsity

We check the sparsity of graphs by calculating the edge density:

$$\begin{aligned} \text {Sparsity}(G) = \frac{|E|}{|V|*(|V|-1)}. \end{aligned}$$

(10)

The results are reported in Table 5. We can see that greedy-$\mathcal {L}_1$ graphs with diffusion distance ranking are more sparse than that with Euclidean distance ranking.

Table 5 Graph sparsity comparison of different graph construction algorithms

5.2 Large size data and multiple classes data

In this section, we present the experimental results of three large datasets. To keep the integrity of our experiments, two multiple classes data are also examined.

5.2.1 Datasets

We select following datasets for our experiments. Three large size datasets are: first 2k testing images of MNIST (MNIST4K), COIL 100 objects database (COIL100) and USPS handwritten digit database (USPS). Two multiple classes datasets are: isolet spoken letter recognition dataset (ISOLET), extended Yale face database B (YaleB). The statistics of selected datasets can be described in Table 6.

5.2.2 Spectral clustering performance

The spectral clustering performance is shown in Tables 7 and 8. As we can see, Gaussian graphs have overall better performance than different $\mathcal {L}_1$ graphs. For the performance between original $\mathcal {L}_1$ graph (with OMP greedy solver) and greedy $\mathcal {L}_1$ graphs, the greedy version is better.

Table 6 The statistics of three large datasets and two multiple classes datasets

Table 7 NMI results of spectral clustering with different similarity graphs

5.2.3 Graph sparsity

We also check the sparsity of different similarity graphs. The result in Table 9 shows that greedy $\mathcal {L}_1$ graphs with diffusion ranking are more denser than other $\mathcal {L}_1$ graphs. And the ordinary $\mathcal {L}_1$ graph (OMP) has the lowest sparsity.

It is known that the sparsity of graph will affect the performance of graph cut and then to spectral clustering. And the spectral clustering performance will drop if the sparsity is lower than a threshold [17]. Since $\mathcal {L}_1$ graph is a sparse graph in nature, we want to know the correlation between the sparsity and clustering performance. To evaluate this, we choose the “USPS” dataset and generating graphs with different sparsity by setting the reconstruction approximation error bound to different thresholds. They are: [0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001, 0.00005, 0.00001]. For the size of “ranked dictionary,” we choose size to 2M which is 512. The trend of spectral clustering performance with different sparsity can be shown as the left subplot of Fig. 8. We can see that when the sparsity value is lower than 0.0072 , the spectral clustering performance drops catastrophically. The relationship between the approximation error and the graph sparsity is presented at the right side of Fig. 8. By reading from the curve, we know that the approximation error and sparsity have a negative relationship. To maintain the greedy $\mathcal {L}_1$ as dense as possible, we need to set a lower bound of approximation error.

Table 8 ACC results of spectral clustering with different similarity graphs

Table 9 Graph sparsity results of different similarity graphs

Fig. 8

The impact of graph sparsity to spectral clustering performance. Left graph sparsity versus NMI and ACC. Right $\mathcal {L}_1$ solver approximation error versus graph sparsity

Table 10 Running time of different similarity graphs

5.2.4 Running time

We also record the running time of building different similarity graphs. From Table 10, we see that the running time increases, while the data size becomes larger. However, the “USPS” has lesser running time than “COIL100” even its data size is bigger. The reason is that “USPS” has smaller number of features than “COIL100” and this causes the $\mathcal {L}_1$ solver to need more computation time for finding sparse solutions.

6 Conclusion

In this paper, we have designed a greedy algorithm to construct $\mathcal {L}_1$ graph. Moreover, we introduced the concept of “ranked dictionary,” which not only preserves the locality but also solves the curse of normalization. Moreover, it can construct $\mathcal {L}_1$ graph efficiently for large size data (#instances $\ge$3000.) Except for the Euclidean metric and diffusion metric that have been discussed in this paper, the user can choose other ranking methods such as manifold ranking that could be more appropriate for specific dataset in real applications. Our greedy algorithm can generate sparse $\mathcal {L}_1$ graph faster than the original $\mathcal {L}_1$ graph construction algorithm, and the resulting graphs have better clustering performance on average than original $\mathcal {L}_1$ graph. Nevertheless, our algorithm could be generalized in a straightforward way by introducing regularization terms such as elastic net into the current solver, which would indicate the quality of generated $\mathcal {L}_1$ graphs could be further improved.