Remarks on Parabolicity in a One-Dimensional Interdiffusion Model with the Vegard Rule

Abstract

Until 1948 the interdiffusion theory was based on the Onsager phenomenology, namely thermodynamics of irreversible processes, and a drift was not included. Its main limitation is practical impossibility of the experimental as well as theoretical determination of mobilities (diffusivities) in multicomponent systems ($r > 2$). After experimental discovery of the drift by Smigelskas and Kirkendall (Trans AIME 171:130–142, 1947), Darken (Trans AIME 175:184–201, 1948) formulated his famous model for the binary system. Consequently, the bi-velocity approach dominates interdiffusion studies (e.g. in more than 500 papers in 2020). In this paper, we consider the diffusional transport in a one-dimensional r-component solid solution. The model is expressed by the nonlinear system of strongly coupled evolution differential equations with initial and nonlinear coupled boundary conditions. We present a non-trivial proof of a theorem called the criterion of parabolicity, which implies the generalized parabolicity condition formulated without a proof in our previous works. This condition is a key in the proofs of our previous theorems on existence, uniqueness and properties of global weak solutions of the differential problem studied. The criterion of parabolicity works if diffusion coefficients are not too dispersed, and it is true in many physical systems. The numerical simulations consistent with real experiments for which our criterion works are given.

1 Introduction

We study in the paper the diffusional transport in a one-dimensional r-component solid solution. An inspiring effort dedicated to the rigorous mathematical treatment of the flows occurring in a binary closed mixture with constant concentration has begun with the work of Darken (1948) on the modelling of diffusive flows. The Darken idea of two velocities was extended for multicomponent systems in the cases of closed and open mixture in Holly and Danielewski (1994) and Balluffi et al. (2005). Later, it was proved that it is self-consistent with the Onsager phenomenological description (Bożek et al. 2015). Several attempts to solve the problem in liquid mixtures were not very effective due to arbitrary selection of the reference frame for diffusion. A more fundamental approach is given in Brenner (2010), where a volume transport is considered. The most general model which admits not constant concentration is formulated in Sapa et al. (2018b).

The mathematical model introduced in Sapa et al. (2018b) is expressed by the one-dimensional nonlinear system of strongly coupled evolution differential equations

$$\begin{aligned} \partial _{t}\varrho _{i}=\partial _{x}\left( \varTheta _{i}(\varrho _{1},\ldots ,\varrho _{r})\partial _{x}\varrho _{i}-\varrho _{i}\sum _{j=1}^{r}\frac{\varOmega _{j}\varTheta _{j}(\varrho _{1},\ldots , \varrho _{r})}{M_{j}}\partial _{x}\varrho _{j}-K(t)\varrho _{i}\right) \end{aligned}$$

(1)

for $i=1,\ldots ,r$, with initial and nonlinear coupled boundary conditions (Sect. 2). It is obtained from the local mass conservation law for fluxes which are a sum of the diffusional and Darken drift terms, together with the Vegard rule (Denton and Ashcroft 1991). This rule is a straight application of the Euler homogeneous function theorem. The strong coupling of the equations is caused by a drift velocity $v^{D}$. The drift velocity is concerned with the Kirkendall effect (Smigelskas and Kirkendall 1947; Yu et al. 2012; El Mel et al. 2015; Chee et al. 2019; Morales et al. 2021). It is the motion of the boundary layer between two metals that occurs as a consequence of the difference in diffusion rates of the metal atoms. A detailed analysis of a concept of the drift velocity, a choice of the reference frame, as well as other physical, mathematical and numerical consequences of the proposed formalism can be found in Bożek et al. (2015), Danielewski et al. (1994, 2008), Dayananda (2017), Holly and Danielewski (1994), Sangeeta and Aloke (2015), Wierzba and Skibiński (2015) and Wu et al. (2006) and in references therein.

The theorems on existence, uniqueness, nonnegativity and estimates of global in time weak solutions (in suitable Sobolev spaces) to the nonlinear evolution problem discussed above are given in Sapa et al. (2018b). Moreover, it is shown that if a physical system is closed, then an evolutional solution converges to the stationary one as time goes to infinity. The main tool used in the proof of the existence result is the Galerkin approximation method (Zeidler 1990), the properties of some family of automorphisms and the crucial theorem called criterion of parabolicity. Let us stress that this criterion was proposed for a less general problem in 1994 and then in 2008 without a proof (Danielewski et al. 1994, 2008). The aim of this paper is to prove the delicate criterion of parabolicity (Theorem 5). This criterion follows from Theorem 4. Add that such strongly coupled systems as (1) (i.e. by the second derivatives) are mathematically difficult, and they are still insufficiently explored. They are not studied, for example, in such known monographs as Carl et al. (2007), Coddington and Levinson (1955), Dautray and Lions (1992), Doering and Gibbon (2004), Evans (1998), Ladyzhenskaya et al. (1988), Roubíček (2005) and Zeidler (1990).

The idea of the use of two velocities and the Vegard rule was extended in last years to any dimension $n\in {\mathbb{N}}$ (Bożek et al. 2019; Sapa et al. 2018a, 2020). If $n\ge 2$, then some parabolic–elliptic system is formulated instead of (1).

The paper is organized as follows: In Sect. 2, the initial boundary differential problem in strong and weak forms is formulated, together with the assumptions and known results on existence, uniqueness and asymptotic behaviour of global weak solutions. In Sect. 3, the theorem about properties of some family of automorphisms and the criterion of parabolicity are proved. Section 4 deals with examples of physical problems and numerical simulations.

2 Model of Interdiffusion

2.1 Strong Formulation

Let $\varOmega =(-\varLambda ,\varLambda )\subset {\mathbb{R}}$, $T>0$ and $r\in {\mathbb{N}}{\setminus }\{1\}$ be fixed, and denote ${\mathbb{R}}_{+}=(0,\infty )$. The following data are given:

• (1) $M_{i}={\text{const}}\in {\mathbb{R}}_{+}$, the molecular mass of the ith component of the mixture, $i=1,\ldots ,r$.

• (2) $\varOmega _{i}={\text{const}}\in {\mathbb{R}}_{+}$, the partial molar volume of the ith component of the mixture, $i=1,\ldots ,r$.

• (3) $\varTheta _{i}:{\mathbb{R}}^{r}\rightarrow {\mathbb{R}}$, the diffusion coefficient of the ith component of the mixture, $i=1,\ldots ,r$.

• (4) $\varrho _{0i}:\varOmega \rightarrow {\mathbb{R}}_{+}$, the initial density of the ith component of the mixture, $i=1,\ldots ,r$.

• (5) $j_{i,L},j_{i,R}:[0,T]\rightarrow {\mathbb{R}}$, the evolution of a mass flow of the ith component of the mixture through the left and right boundaries, respectively, $i=1,\ldots ,r$.

The unknowns are the densities of the ith components of the mixture $\varrho _{i}:[0,T]\times \varOmega \rightarrow {\mathbb{R}}_{+}$, $i=1,\ldots ,r$.

Put

$$\begin{aligned} K(t):=\sum _{i=1}^{r}\frac{\varOmega _{i}j_{i,L}(t)}{M_{i}}=\sum _{i=1}^{r}\frac{\varOmega _{i}j_{i,R}(t)}{M_{i}} \quad {\text{for}} \quad t\in [0,T]. \end{aligned}$$

(2)

This is actually an assumption on the boundary evolutions. In Sapa et al. (2018b), the model of multicomponent interdiffusion in a one-dimensional case was expressed by the nonlinear system of strongly coupled (i.e. by the second derivatives) evolution partial differential equations of the form

$$\begin{aligned} \partial _{t}\varrho _{i}&+\partial _{x}\left( -\varTheta _{i}(\varrho _{1},\ldots ,\varrho _{r})\partial _{x}\varrho _{i}+\varrho _{i}\sum _{j=1}^{r}\frac{\varOmega _{j}\varTheta _{j}(\varrho _{1},\ldots , \varrho _{r})}{M_{j}}\partial _{x}\varrho _{j}\right) \nonumber \\&+K(t)\partial _{x}\varrho _{i}=0 \end{aligned}$$

(3)

for $(t,x)\in [0,T]\times \varOmega$, with initial and nonlinear coupled boundary conditions

$$\begin{aligned} \varrho _{i}(0,x)=\varrho _{0i}(x) \quad {\text{for}} \quad x\in \varOmega , \end{aligned}$$

(4)

$$\begin{aligned} \left\{ \begin{array} {l} \left( -\varTheta _{i}(\varrho _{1},\ldots ,\varrho _{r})\partial _{x}\varrho _{i}+\varrho _{i}\left( K(t)+ \sum _{j=1}^{r}\frac{\varOmega _{j}\varTheta _{j}(\varrho _{1},\ldots ,\varrho _{r})}{M_{j}}\partial _{x}\varrho _{j}\right) \right) (t,-\varLambda ) = j_{i,L}(t),\\ \left( -\varTheta _{i}(\varrho _{1},\ldots ,\varrho _{r})\partial _{x}\varrho _{i}+\varrho _{i}\left( K(t) +\sum _{j=1}^{r}\frac{\varOmega _{j}\varTheta _{j}(\varrho _{1},\ldots ,\varrho _{r})}{M_{j}}\partial _{x}\varrho _{j}\right) \right) (t,\varLambda ) = j_{i,R}(t), \end{array} \right. \end{aligned}$$

(5)

for $t\in [0,T]$, $i=1,\ldots ,r$.

The total mass of the ith component of the mixture at the fixed moment $t\in [0,T]$ is given by

$$\begin{aligned} m_{i}(t)=\int _\varOmega \varrho _{i}(t,x){\mathrm{d}}x, \quad i=1,\ldots ,r, \end{aligned}$$

(6)

while by

$$\begin{aligned} {\overline{m}}_{i}(t)=\frac{1}{2\varLambda }\int _{\varOmega }\frac{\varOmega _{i}\varrho _{i}(t,x)}{M_{i}}{\mathrm{d}}x, \quad i=1,\ldots ,r, \end{aligned}$$

(7)

the average value of the local volume fraction $\frac{\varOmega _{i}c_{i}}{\sum _{j=1}^{r}\varOmega _{j}c_{j}}$, where $c_{i}$ means the ith concentration, is denoted. Note that the local volume fraction $\frac{\varOmega _{i}c_{i}}{\sum _{j=1}^{r}\varOmega _{j}c_{j}}=\varOmega _{i}c_{i}=\frac{\varOmega _{i}\varrho _{i}}{M_{i}}$, by the Vegard rule $\sum _{j=1}^{r}\varOmega _{j}c_{j}=1$ used in the construction of (3) (see Sapa et al. 2018b) and the definition of concentrations $c_{i}=\frac{\varrho _{i}}{M_{i}}$. Integrating (3) over the interval $\varOmega$, using (6) and integrating once again over the interval (0, t), we get

$$\begin{aligned} m_{i}(t)=\int _\varOmega \varrho _{0i}(x){\mathrm{d}}x+\int _{0}^{t}\left( j_{i,L}(\tau )-j_{i,R}(\tau )\right) {\mathrm{d}}\tau \end{aligned}$$

(8)

for $t\in [0,T]$, $i=1,\ldots ,r$. Hence ${\overline{m}}_{i}$, $i=1,\ldots ,r$ are known functions also.

2.2 Assumptions and Weak Formulation

Let

$$\begin{aligned} 1^{\perp }=\left\{ \xi =(\xi _{1},\ldots ,\xi _{r})\in {\mathbb{R}}^{r}:\ \xi _{1}+\cdots +\xi _{r}=0\right\} , \end{aligned}$$

(9)

stands for the vector space orthogonal to the vector subspace $\{\alpha 1:\alpha \in {\mathbb{R}}\}$, where $1=(1,\ldots ,1)\in {\mathbb{R}}^{r}$. Define the Sobolev spaces

$$\begin{aligned} H&=\left\{ f=(f_{1},\ldots ,f_{r})\in L^{2}(\varOmega ,1^{\perp }):\ \int _\varOmega f_{i}(x){\mathrm{d}}x=0,\ i=1,\ldots ,r\right\} , \end{aligned}$$

(10)

$$\begin{aligned} V&=\left\{ f\in H^{1}(\varOmega ,1^{\perp }):\ f\in H\right\} . \end{aligned}$$

(11)

The norm in V is generated by the scalar product

$$\begin{aligned} (f,g)_{V}=\int _\varOmega \partial _{x}f\cdot \partial _{x}g {\mathrm{d}}x \end{aligned}$$

(12)

for $f,g\in V$, while in H by the scalar product

$$\begin{aligned} (f,g)_{H}=\int _\varOmega f\cdot g {\mathrm{d}}x \end{aligned}$$

(13)

for $f,g\in H$. The symbol “$\cdot$” means the Euclidean scalar product in ${\mathbb{R}}^{r}$. Then $V\subset H\subset V^{*}$ constitute an evolutional triple with the embeddings being dense, continuous and compact (Adams and Fournier 2008; Zeidler 1990).

Let

$$\begin{aligned} {\mathcal {K}}&=\{\kappa =(\kappa _{1},\ldots ,\kappa _{r})\in {\mathbb{R}}^{r}:\ \kappa _{1}+\cdots +\kappa _{r}=1,\nonumber \\&\quad k_{i}\ge 0,\ i=1,\ldots ,r\}. \end{aligned}$$

(14)

Define the family of linear operators

$$\begin{aligned} A_\kappa :1^{\perp }\mapsto 1^{\perp },\quad A_\kappa \xi =\sum _{i=1}^{r}\varTheta _{i}(\kappa )\xi _{i}e_{i}-(\varTheta (\kappa )\cdot \xi )\kappa \end{aligned}$$

(15)

for $\kappa \in {\mathcal {K}}$, where $\xi \in 1^{\perp }$, $e_{i}=(0,\ldots ,0,1,0,\ldots ,0)$ with 1 in the ith entry, $i=1,\ldots ,n$.

We assume the following conditions.

Assumption H

(H$_{0}$):

$\varrho _{0}(x)=(\varrho _{01}(x),\ldots ,\varrho _{0r}(x))\ge 0$ and

$$\begin{aligned} \sum _{i=1}^{r}\frac{\varOmega _{i}\varrho _{0i}(x)}{M_{i}}=1 \quad {\text{for}}\ x\in \varOmega . \end{aligned}$$

(H$_{1}$):

$\int _\varOmega \varrho _{0i}(x){\mathrm{d}}x+\int _{0}^{t}\left( j_{i,L}(\tau )-j_{i,R}(\tau )\right) {\mathrm{d}}\tau \ge 0$ for $t\in [0,T]$, $i=1,\ldots ,r$.

(H$_{2}$):

$\sum _{i=1}^{r}\frac{\varOmega _{i}j_{i,L}(t)}{M_{i}}=\sum _{i=1}^{r}\frac{\varOmega _{i}j_{i,R}(t)}{M_{i}}$ for $t\in [0,T]$.

(H$_{3}$):

$\varrho _{0}\in L^{2}(\varOmega )$.

(H$_{4}$):

$j_{i,L},j_{i,R}\in L^{\infty }(0,T)$, $i=1,\ldots ,r$.

(H$_{5}$):

$\varTheta _{i}$, $i=1,\ldots ,r$ fulfil the Lipschitz condition and are bounded.

(H$_{6}$):

The following generalized parabolicity condition holds:

$$\begin{aligned} \int _\varOmega (A_{g}\partial _{x}f)\cdot \partial _{x}f{\mathrm{d}}x\ge \mu \Vert f\Vert _{V}^{2}-\nu \Vert f\Vert _{H}^{2} \end{aligned}$$

(16)

for some $\mu >0$, $\nu \ge 0$ and for all $f\in V$, $g=(g_{1},\ldots ,g_{r})\in H^{1}(\varOmega ,{\mathbb{R}}^{r})$, $g_{1}+\cdots +g_{r}=1$, $g_{i}\ge 0$, $i=1,\ldots ,r$.

Note that assumptions (${\text{H}}_{0}$), (${\text{H}}_{2}$) and formulas (6)–(8) imply

$$\begin{aligned} \sum _{i=1}^{r}{\overline{m}}_{i}(t)=1 \end{aligned}$$

(17)

for $t\in [0,T]$. We introduce new variables as follows. The local deviation of volume fraction from its average value is

$$\begin{aligned} w_{i}(t,x)=\frac{\varOmega _{i}\varrho _{i}(t,x)}{M_{i}}-{\overline{m}}_{i}(t),\quad i=1,\ldots ,r, \end{aligned}$$

(18)

for $(t,x)\in [0,T]\times \varOmega$. Put $w=(w_{1},\ldots ,w_{r})$ and ${\overline{m}}=({\overline{m}}_{1},\ldots ,{\overline{m}}_{r})$. For any fixed $w\in L^{2}(0,T;V)$ and $t\in (0,T)$, the symbol $\langle w'(t),\ \rangle _{V^{*}\times V}$ means a linear continuous functional of the form

$$\begin{aligned} \langle w'(t),v\rangle _{V^{*}\times V}=\sum _{i=1}^{r}\langle w_{i}'(t),v_{i}\rangle , \end{aligned}$$

(19)

where $\langle w'_{i}(t),\ \rangle$ is a linear continuous functional acting on $L^{2}(0,T;H^{1}(\varOmega ,{\mathbb{R}}))$, $v\in V$. Denote the functions

$$\begin{aligned} \varGamma _{i,L}(t)&=K(t){\overline{m}}_{i}(t)-\frac{\varOmega _{i}j_{i,L}}{M_{i}}, \quad i=1,\ldots ,r, \nonumber \\ \varGamma _{i,R}(t)&=K(t){\overline{m}}_{i}(t)-\frac{\varOmega _{i}j_{i,R}}{M_{i}}, \quad i=1,\ldots ,r, \end{aligned}$$

(20)

$$\begin{aligned} \varGamma _{L}&=(\varGamma _{1,L},\ldots ,\varGamma _{r,L}),\nonumber \\ \varGamma _{R}&=(\varGamma _{1,R},\ldots ,\varGamma _{r,R}),\nonumber \\ \varGamma&=(\varGamma _{L},\varGamma _{R}), \end{aligned}$$

(21)

for $t\in [0,T]$.

The original initial-boundary value problem (3)–(5) has the following weak version.

Problem P

Find $w\in L^{2}(0,T;V)$ such that $w'\in L^{2}(0,T;V^{*})$, for a.e. $t\in (0,T)$ $w(t)+{\overline{m}}(t)\in {\mathcal {K}}$ and

$$\begin{aligned}&\langle w'(t),v\rangle _{V^{*}\times V} +\int _{\varOmega }\left( A_{w(t)+{\overline{m}}(t)}\partial _{x}w(t)\right) \cdot \partial _{x}v{\mathrm{d}}x\nonumber \\&\qquad -K(t)\int _{\varOmega }w(t)\cdot \partial _{x}v{\mathrm{d}}x\nonumber \\&\quad =\varGamma _{R}(t)\cdot v(\varLambda )-\varGamma _{L}(t)\cdot v(-\varLambda )\quad {\text{for each}}\quad v\in V, \end{aligned}$$

(22)

and the initial condition holds

$$\begin{aligned} w(0)=w_{0}. \end{aligned}$$

(23)

Remark 1

If assumptions (${\text{H}}_{0}$), (${\text{H}}_{2}$) are fulfilled and w is a solution of Problem $\mathbf {P}$, then by (17), (18), the Vegard rule holds

$$\begin{aligned} \sum _{i=1}^{r}\frac{\varOmega _{i}\varrho _{i}(t,x)}{M_{i}}=1 \quad {\text{for}}\ (t,x)\in [0,T]\times \varOmega . \end{aligned}$$

2.3 Known Results

In Sapa et al. (2018b), the following theorems concerning the existence and uniqueness of solutions to Problem $\mathbf {P}$ and their asymptotic behaviour were formulated and proved.

Theorem 1

If Assumption H is satisfied, then Problem P has a solution.

Theorem 2

If Assumption H is satisfied, then Problem P has in $L^{4}(0,T;$ V) at most one solution.

Theorem 3

Let $w:[0,\infty )\rightarrow H$ be a solution of Problem P on each interval [0, T] for $T\in {\mathbb{R}}_{+}$. If Assumption H is satisfied with $j_{i,L}(t)=j_{i,R}(t)\equiv 0$, $t\in [0,\infty )$, $i=1,\ldots ,r$ and $\nu =0$ in (16), then $w\in L^{2}(0,\infty ;V)\cap L^{\infty }(0,\infty ;H)$, $w'\in L^{2}(0,\infty ;V^{*})$, the function $[0,\infty )\ni t\mapsto \Vert w(t)\Vert _{H}^{2}$ is nonincreasing and $\lim _{t\rightarrow \infty }\Vert w(t)\Vert _{H}^{2}=0$.

3 Criterion of Parabolicity

In this main section, we prove Theorem 4 on properties of the family of automorphisms $A_{\kappa }$ and Theorem 5, i.e. the criterion on (16) to be true. They were formulated without proofs for less general problems in Danielewski et al. (1994, 2008), Holly and Danielewski (1994). It follows from the criterion of parabolicity that (16) holds if $\varTheta _{i}$, $i=1,\ldots ,r$ are not too dispersed. It is true in many real physical examples (Sect. 4).

Theorem 4

If $\varTheta _{i}$, $i=1,\ldots ,r$ are constant, then

• (i) $A_\kappa$, $\kappa \in {\mathcal {K}}$ is automorphism of the vector space $1^{\perp }$ and

  $$\begin{aligned} A_\kappa ^{-1}\eta =\sum _{i=1}^{r}\frac{\eta _{i}}{\varTheta _{i}}e_{i}-\frac{ \sum _{k=1}^{r}\frac{\eta _{k}}{\varTheta _{k}} }{ \sum _{k=1}^{r}\frac{\kappa _{k}}{\varTheta _{k}} } \sum _{i=1}^{r}\frac{\kappa _{i}}{\varTheta _{i}}e_{i} \quad \ {\text{for}}\quad \eta \in 1^{\perp }, \end{aligned}$$
• (ii)
  $$\begin{aligned} \min \bigl \{(A_\kappa \xi )\cdot \xi :\ \kappa \in {\mathcal {K}},\ \xi \in 1^{\perp },\ \Vert \xi \Vert =1\bigl \}=\delta +m(\alpha )\sum _{k=1}^{r}(\varTheta _\kappa -\delta ), \end{aligned}$$

  (24)

  where $\delta =\min _{i=1,\ldots ,r}\varTheta _{i}$, $m(\alpha )=0$ if $\varTheta _{1}=\cdots =\varTheta _{r}$ or $r=2$; $m(\alpha )=\min \left\{ x<0: \right.$ $\left. \exists j\in \{1,\ldots ,r\}\ 4r+\sum _{k=1,k\ne j}^{r}\frac{\alpha _{j}+(r-1)\alpha _{k}-1}{\alpha _{k}-x}=0\right\}$ if $\varTheta _{k}\ne \varTheta _{l}$ for some $k\ne l$ and $r>2$, $\alpha =(\alpha _{1},\ldots ,\alpha _{r})$, $\alpha _{i}=\frac{\varTheta _{i}-\delta }{\sum _{k=1}^{r}(\varTheta _{k}-\delta )}$, $i=1,\ldots ,r$,

• (iii)
  $$\begin{aligned} m(\alpha )\ge -\left( \sqrt{\frac{r-1}{2r}}-\frac{1}{2}\right) , \end{aligned}$$

  (25)

• (iv) if $r=3$, then

  $$\begin{aligned} m(\alpha )=-\left( \frac{1}{\sqrt{3}}-\frac{1}{2}\right) \max \{\alpha _{1},\alpha _{2},\alpha _{3}\}. \end{aligned}$$

  (26)

Proof

• (i) Obviously, $A_\kappa$ is linear.

  Let $\xi \in \ker {A_\kappa }$. Hence $\varTheta _{i}\xi _{i}=(\varTheta \cdot \xi )\kappa _{i}$, that is to say $\xi _{i}=(\varTheta \cdot \xi )\frac{\kappa _{i}}{\varTheta _{i}}$, $i=1,\ldots ,r$. Summing the last relations, we get $0=(\varTheta \cdot \xi )\sum _{i=1}^{r}\frac{\kappa _{i}}{\varTheta _{i}}$. In consequence, $\theta \cdot \xi =0$, because $\sum _{i=1}^{r}\frac{\kappa _{i}}{\varTheta _{i}}>0$. Finally, $\xi _{i}=0$, $i=1,\ldots ,r$ and $A_\kappa$ is isomorphism.

  Now let $\eta \in 1^{\perp }$ and $\xi =A_\kappa ^{-1}\eta$. We have $\varTheta _{i}\xi _{i}-(\varTheta \cdot \xi )\kappa _{i}=\eta _{i}$, that is to say $\xi _{i}=\frac{\eta _{i}}{\varTheta _{i}}+(\varTheta \cdot \xi )\frac{\kappa _{i}}{\varTheta _{i}}$, $i=1,\ldots ,r$. Summing the last formulas, we obtain $0=\sum _{i=1}^{r}\frac{\eta _{i}}{\varTheta _{i}}+(\varTheta \cdot \xi )\sum _{i=1}^{r}\frac{\kappa _{i}}{\varTheta _{i}}$ and from here $\varTheta \cdot \xi =-\frac{\sum _{i=1}^{r}\frac{\eta _{i}}{\varTheta _{i}}}{\sum _{i=1}^{r}\frac{\kappa _{i}}{\varTheta _{i}}}$. Hence, $\xi _{i}=\frac{\eta _{i}}{\varTheta _{i}}-\frac{\sum _{k=1}^{r}\frac{\eta _{k}}{\varTheta _{k}}}{\sum _{k=1}^{r}\frac{\kappa _{k}}{\varTheta _{k}}}\frac{w_{i}}{\varTheta _{i}}$, $i=1,\ldots ,r$.

• (ii) Let $\xi \in 1^{\perp }$, $\Vert \xi \Vert =1$. It is clear that

  $$\begin{aligned} (A_\kappa \xi )\cdot \xi =\delta +\sum _{i=1}^{r}(\varTheta _{i}-\delta )\xi _{i}(\xi _{i}-\kappa \cdot \xi ). \end{aligned}$$

  If $\varTheta =(\delta ,\ldots ,\delta )$, then $(A_\kappa \xi )\cdot \xi =\delta$. If $r=2$, then $\min \{(A_\kappa \xi )\cdot \xi :\ \kappa \in {\mathcal {K}},\ \xi \in 1^{\perp },\ \Vert \xi \Vert =1\}=\delta$, because $(A_\kappa \xi )\cdot \xi =\kappa _{2}\varTheta _{1}+\kappa _{1}\varTheta _{2}\in \mathrm{{conv}}\{\varTheta _{1},\varTheta _{2}\}$.

  Assume that $\varTheta \ne (\delta ,\ldots ,\delta )$ and $r>2$. Now $\sum _{k=1}^{r}(\varTheta _{k}-\delta )>0$, $\sum _{i=1}^{r}\alpha _{i}=1$ and we can write

  $$\begin{aligned} (A_\kappa \xi )\cdot \xi =\left( \sum _{k=1}^{r}(\varTheta _{k}-\delta )\right) \left( \frac{\delta }{\sum _{k=1}^{r}(\varTheta _{k}-\delta )}+\sum _{i=1}^{r}\alpha _{i}\xi _{i}(\xi _{i}-\kappa \cdot \xi ) \right) . \end{aligned}$$

  We can study for simplicity the unit sphere $\Vert x\Vert =1$ in ${\mathbb{R}}^{r}$ instead of ${\mathcal {K}}=\mathrm{{conv}}\{e_{i}:\ i=1,\ldots ,r\}$ by setting $\kappa _{k}=x_{k}^{2}$, $k=1,\ldots ,r$. Define two functions

  $$\begin{aligned}&f_\alpha :{\mathbb{R}}^{r}\times {\mathbb{R}}^{r}\ni (\xi ,x)\mapsto \sum _{i=1}^{r}\alpha _{i}\xi _{i}\left( \xi _{i}-\sum _{k=1}^{r}x_{k}^{2}\xi _{k}\right) \in {\mathbb{R}}, \end{aligned}$$

  (27)
  $$\begin{aligned}&g:{\mathbb{R}}^{r}\times {\mathbb{R}}^{r}\ni (\xi ,x)\mapsto \left( \Vert \xi \Vert ^{2}-1,\sum _{i=1}^{r}\xi _{i},\Vert x\Vert ^{2}-1\right) \in {\mathbb{R}}^3. \end{aligned}$$

  (28)

  Observe that the set $\{g=0\}:=\{(\xi ,x)\in {\mathbb{R}}^{r}\times {\mathbb{R}}^{r}:\ g(\xi ,x)=0\}$ is the compact intersection of two unit spheres in $1^{\perp }$ and ${\mathbb{R}}^{r}$, respectively. Our goal is to prove that the conditional minimum

  $$\begin{aligned} m:=\min \{f_\alpha (\xi ,x):\ (\xi ,x)\in \{g=0\}\} \end{aligned}$$

  (29)

  is equal to $m(\alpha )$. It is obvious that

  $$\begin{aligned} \min \{(A_\kappa \xi )\cdot \xi :\ \kappa \in {\mathcal {K}},\ \xi \in 1^{\perp },\ \Vert \xi \Vert =1\}=\delta +m\sum _{k=1}^{r}(\varTheta _\kappa -\delta ). \end{aligned}$$

  (30)

  Firstly we will consider the case when m is attained in a point $(\xi ,x)\in \{g=0\}$ such that ${{\alpha} \cdot {\xi} \ne {0}}$ and $\kappa \cdot \xi \ne 0$, where $\kappa _{k}=x_{k}^{2}$, $k=1,\ldots ,r$. It follows from the Lagrange theorem that there exists $\lambda =(\lambda _{1},\lambda _{2},\lambda _{3})\in {\mathbb{R}}^3{\setminus }\{0\}$ such that $d_{(\xi ,x)}(f_\alpha +\lambda g)=0$. We calculate

  $$\begin{aligned} d_{(\xi ,x)}(f_\alpha&+\lambda g)(h,y)=d_{(\xi ,x)}(f_\alpha +\lambda g)\left( \sum _{k=1}^{r}h_{k}(e_{k},0)+\sum _{k=1}^{r}y_{k}(0,e_{k})\right) \\&=\sum _{k=1}^{r}h_{k}\partial _{\xi _{k}}f_\alpha (\xi ,x)+\sum _{k=1}^{r}h_{k}(\lambda \cdot \partial _{\xi _{k}}g(\xi ,x))\\&\quad +\sum _{k=1}^{r}y_{k}\partial _{x_{k}}f_\alpha (\xi ,x)+\sum _{k=1}^{r}y_{k}(\lambda \cdot \partial _{x_{k}}g(\xi ,x))\\&= \left( 2\sum _{k=1}^{r}\alpha _{k}\xi _{k}e_{k}-(\kappa \cdot \xi )\alpha -(\alpha \cdot \xi )\kappa +2\lambda _{1}\xi +\lambda _{2} 1\right) \cdot h\\&\quad +\left( 2\lambda _{3}x-2(\alpha \cdot \xi )\sum _{k=1}^{r}\xi _{k}x_{k}e_{k}\right) \cdot y=0 \quad {\text{for}}\quad h,y\in {\mathbb{R}}^{r}. \end{aligned}$$

  Hence, we get a system of two equations

  $$\begin{aligned} \left\{ \begin{array}{l} 2\sum _{k=1}^{r}\alpha _{k}\xi _{k}e_{k}-(\kappa \cdot \xi )\alpha -(\alpha \cdot \xi )\kappa +2\lambda _{1}\xi +\lambda _{2} 1=0,\\ \lambda _{3}x=(\alpha \cdot \xi )\sum _{k=1}^{r}\xi _{k}x_{k}e_{k}. \end{array} \right. \end{aligned}$$

  (31)

  Multiplying the second equation in (31) by x implies

  $$\begin{aligned} \lambda _{3}=(\alpha \cdot \xi )(\kappa \cdot \xi ). \end{aligned}$$

  (32)

  In consequence, $(\kappa \cdot \xi )x=\sum _{k=1}^{r}\xi _{k}x_{k}e_{k}$. This leads to the implication

  $$\begin{aligned} \kappa _{k}\ne 0 \Rightarrow \xi _{k}=\kappa \cdot \xi \quad {\text{for}}\quad k=1,\ldots ,r. \end{aligned}$$

  (33)

  Multiplying the first equation in (31) by $\xi$ and 1, respectively, implies

  $$\begin{aligned} \lambda _{1}=(\alpha \cdot \xi )(\kappa \cdot \xi )-\sum _{k=1}^{r}\alpha _{k}\xi _{k}^{2}=-m, \quad \lambda _{2}=\frac{\kappa \cdot \xi -\alpha \cdot \xi }{r}. \end{aligned}$$

  (34)

  Define two sets of indices

  $$\begin{aligned} S=\{k:\ \kappa _{k}\ne 0\}, \quad Z=\{k:\ \kappa _{k}=0\}. \end{aligned}$$

  (35)

  Suppose that $Z=\emptyset$. Hence $\kappa _{k}\ne 0$, $k=1,\ldots ,r$ and by (33), $\xi _{k}=\kappa \cdot \xi$, $k=1,\ldots ,r$. Then $0=\sum _{k=1}^{r}\xi _{k}=r(\kappa \cdot \xi )$ what gives $\kappa \cdot \xi =0$, but it is not true. Thus $Z\ne \emptyset$. The set $S\ne \emptyset$ also, because $\kappa =(\kappa _{1},\ldots ,\kappa _{k})\in {\mathcal {K}}$. Therefore, the numbers

  $$\begin{aligned} |S|:=\sharp {S}, \quad |Z|:=\sharp {Z} \end{aligned}$$

  (36)

  are positive. It is clear that $|S|+|Z|=r$. For $k\in S$, we multiply the first equation in (31) by $e_{k}$ and we get

  $$\begin{aligned} (\kappa \cdot \xi )\alpha _{k}+2(\kappa \cdot \xi )\lambda _{1}+\lambda _{2}=(\alpha \cdot \xi )\kappa _{k}. \end{aligned}$$

  (37)

  After summing (37), we can write

  $$\begin{aligned} (\kappa \cdot \xi )\sum _{k\in S}\alpha _{k}+|S|(2(\kappa \cdot \xi )\lambda _{1}+\lambda _{2})=\alpha \cdot \xi . \end{aligned}$$

  Dividing by $\kappa \cdot \xi$ and denoting $\gamma :=\frac{\alpha \cdot \xi }{\kappa \cdot \xi }$ , we obtain

  $$\begin{aligned} 2r|S|m+(r+|S|)\gamma =|S|+r\sum _{k\in S}\alpha _{k}. \end{aligned}$$

  (38)

  For $k\in Z$ , we multiply the first equation in (31) by $e_{k}$ and we obtain

  $$\begin{aligned} 2\xi _{k}(\alpha _{k}+\lambda _{1})=(\kappa \cdot \xi )\alpha _{k}-\lambda _{2}. \end{aligned}$$

  (39)

  Let $n\in S$. Let $k\in S$. We subtract the equations

  $$\begin{aligned}&(\kappa \cdot \xi )\alpha _{k}+2(\kappa \cdot \xi )\lambda _{1}+\lambda _{2}=(\alpha \cdot \xi )\kappa _{k},\\&(\kappa \cdot \xi )\alpha _{n}+2(\kappa \cdot \xi )\lambda _{1}+\lambda _{2}=(\alpha \cdot \xi )\kappa _{n} \end{aligned}$$

  (see (37)) and we have

  $$\begin{aligned} \kappa _{n}+\frac{1}{\gamma }(\alpha _{k}-\alpha _{n})=\kappa _{k}. \end{aligned}$$

  After summing over $k\in S$ , we obtain the relation

  $$\begin{aligned} \kappa _{n}=\frac{1}{|S|}+\frac{1}{\gamma }\left( \alpha _{n}-\frac{1}{|S|}\sum _{k\in S}\alpha _{k}\right) \quad {\text{for}}\quad n\in S. \end{aligned}$$

  (40)

  Let p be such that $\varTheta _{p}=\delta$. Thus $\alpha _{p}=0$. Define a vector ${\hat{\xi }}\in 1^{\perp }$ as follows

  $$\begin{aligned} {\hat{\xi }}_{p}=\sqrt{\frac{r-1}{r}}, \quad {\hat{\xi }}_{k}=-\frac{1}{r-1}{\hat{\xi }}_{p} \quad {\text{for}}\quad k\ne p. \end{aligned}$$

  (41)

  Let ${\hat{x}}\in {\mathbb{R}}^{r}$ be any vector such that ${\hat{x}}_{p}=0$ and let $\kappa _{k}:={\hat{x}}_{k}^{2}$, $k=1,\ldots ,r$. It easily follows that

  $$\begin{aligned} f_\alpha ({\hat{\xi }},{\hat{x}})=\sum _{k=1}^{r}\alpha _{k}\hat{\xi _{k}^{2}}-\left( \sum _{k=1}^{r}\alpha _{k}\hat{\xi _{k}}\right) \left( \sum _{k=1}^{r}\kappa _{k}\hat{\xi _{k}}\right) =0. \end{aligned}$$

  Hence

  $$\begin{aligned} m\le 0. \end{aligned}$$

  (42)

  Suppose that $m=0$. Let $x'\in {\mathbb{R}}^{r}$ be defined in the following way

  $$\begin{aligned} x_{p}'=0, \quad x_{k}'=\frac{1}{\sqrt{r-1}} \quad {\text{for}}\quad k\ne p \end{aligned}$$

  (43)

  and let $\kappa _{k}'=(x_{k}')^{2}$, $k=1,\ldots ,r$. We choose a family of not the same positive numbers $\kappa _{k}''$, $k\in \{1,\ldots ,r\}{\setminus }\{p\}$ and $\kappa _{p}=0$ such that $\sum _{k=1}^{r}\kappa _{k}=1$, and let $x_{k}'':=\sqrt{\kappa _{k}}$, $k=1,\ldots ,r$. Obviously $({\hat{\xi }},x'),({\hat{\xi }},x'')\in \{g=0\}$ and as was shown above $f_\alpha ({\hat{\xi }},x')=f_\alpha ({\hat{\xi }},x'')=m$. Moreover, $\alpha \cdot {\hat{\xi }}\ne 0$, $\kappa '\cdot {\hat{\xi }}\ne 0$, $\kappa ''\cdot {\hat{\xi }}\ne 0$. Therefore, all earlier found relations from the Lagrange theorem are true for $({\hat{\xi }},x')$, $({\hat{\xi }},x'')$. In particular, denoting $\gamma '=\frac{\alpha \cdot {\hat{\xi }}}{\kappa '\cdot {\hat{\xi }}}$, $\gamma ''=\frac{\alpha \cdot {\hat{\xi }}}{\kappa ''\cdot {\hat{\xi }}}$, the relations like (40) hold

  $$\begin{aligned}&\kappa _{n}'=\frac{1}{|S|}+\frac{1}{\gamma '}\left( \alpha _{n}-\frac{1}{|S|}\sum _{k\in S}\alpha _{k}\right) \quad {\text{for}}\quad n\in S,\\&\quad \kappa _{n}''=\frac{1}{|S|}+\frac{1}{\gamma ''}\left( \alpha _{n}-\frac{1}{|S|}\sum _{k\in S}\alpha _{k}\right) \quad {\text{for}}\quad n\in S, \end{aligned}$$

  where $S=\{k:\ \kappa _{k}'\ne 0\}=\{k:\ \kappa _{k}''\ne 0\}=\{1,\ldots ,r\}{\setminus }\{p\}$. The numbers $\kappa _{n}'$, $n\in S$ are the same, then the numbers $\alpha _{n}$, $n\in S$ are the same. In consequence, the numbers $\kappa _{n}''$, $n\in S$ must be the same. But it is contradiction. Finally,

  $$\begin{aligned} m<0. \end{aligned}$$

  (44)

  Now we will consider the case when m is attained in a point $(\xi ,x)\in \{g=0\}$ such that $\alpha \cdot \xi =0$ or $\kappa \cdot \xi =0$, where $\kappa _{k}=x_{k}^{2}$, $k=1,\ldots ,r$. But in this case $m=f_\alpha (\xi ,x)=\sum _{i=1}^{r}\alpha _{i}\xi _{i}^{2}-(\alpha \cdot \xi )(\kappa \cdot \xi )=\sum _{i=1}^{r}\alpha _{i}\xi _{i}^{2}\ge 0$ what is not possible, by (44).

  Concluding, m is attained only in points $(\xi ,x)\in \{g=0\}$ such that $\alpha \cdot \xi \ne 0$ and $\kappa \cdot \xi \ne 0$, where $\kappa _{k}=x_{k}^{2}$, $k=1,\ldots ,r$.

  The equality (39) is equivalent to

  $$\begin{aligned} \frac{2r}{\kappa \cdot \xi }\xi _{k}(\alpha _{k}+|m|)=r\alpha _{k}+\gamma -1 \quad {\text{for}} \quad k\in Z \end{aligned}$$

  and then

  $$\begin{aligned} \frac{2r}{\kappa \cdot \xi }\xi _{k}=\frac{r\alpha _{k}+\gamma -1}{\alpha _{k}+|m|} \quad {\text{for}} \quad k\in Z. \end{aligned}$$

  Moreover, it follows from implication (33) that

  $$\begin{aligned} \frac{2r}{\kappa \cdot \xi }\xi _{k}=2r \quad {\text{for}}\quad k\in S. \end{aligned}$$

  Adding the last two relations, we get

  $$\begin{aligned} 0=\sum _{k\in Z}\frac{r\alpha _{k}+\gamma -1}{\alpha _{k}+|m|}+2r|S| \end{aligned}$$

  (45)

  and multiplying by $(r+|S|)$ we have

  $$\begin{aligned} 0=\sum _{k\in Z}\frac{r(r+|S|)\alpha _{k}+(r+|S|)\gamma -r-|S|}{\alpha _{k}+|m|}+2r|S|(r+|S|). \end{aligned}$$

  (46)

  The relation (38) is equivalent to

  $$\begin{aligned} (r+|S|)\gamma =|S|+r\sum _{k\in S}\alpha _{k}-2r|S|m. \end{aligned}$$

  Putting this relation to (46), we calculate

  $$\begin{aligned} 0=\sum _{k\in Z}\frac{(r+|S|)\alpha _{k}-\sum _{l\in Z}\alpha _{l}+2|S||m|}{\alpha _{k}+|m|}+2|S|(r+|S|). \end{aligned}$$

  (47)

  Observe that

  $$\begin{aligned} (r+|S|)\alpha _{k}-\sum _{k\in Z}\alpha _{k}+2|S||m|=2|S|(\alpha _{k}+|m|)+|Z|\alpha _{k}-\sum _{k\in Z}\alpha _{k}. \end{aligned}$$

  Hence, (47) takes the form

  $$\begin{aligned} 0=\sum _{k\in Z}\frac{|Z|\alpha _{k}-\sum _{l\in Z}\alpha _{l}}{\alpha _{k}+|m|}+4r(r-|Z|). \end{aligned}$$

  (48)

  Let ${\tilde{Z}}\subset \{1,\ldots ,r\}$ be such that $0<|{\tilde{Z}}|<r$ and let ${\tilde{m}}$ be a negative root of the equation

  $$\begin{aligned} 0=\sum _{k\in {\tilde{Z}}}\frac{|{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}}{\alpha _{k}+|x|}+4r(r-|{\tilde{Z}}|). \end{aligned}$$

  (49)

  We will show that if ${\tilde{m}}$ is negative root of equation (49), then ${\tilde{m}}\ge m$. Denote

  $$\begin{aligned} {\tilde{S}}&=\{1,\ldots ,r\}{\setminus }{\tilde{Z}}, \\ {\tilde{\gamma }}&=\frac{1}{r+|{\tilde{S}}|}\left( |{\tilde{S}}|+r\sum _{k\in {\tilde{S}}}\alpha _{k}+2r|{\tilde{S}}||{\tilde{m}}| \right) , \\ {\tilde{\kappa }}_{k}&=\frac{1}{|{\tilde{S}}|}+\frac{1}{{\tilde{\gamma }}}\left( \alpha _{k}-\frac{1}{|{\tilde{S}}|}\sum _{l\in {\tilde{S}}}\alpha _{l}\right) \quad {\text{for}}\quad k\in {\tilde{S}}, \\ {\tilde{\kappa }}_{k}&=0 \quad {\text{for}}\quad k\in {\tilde{Z}}, \\ \zeta _{k}&=\frac{r\alpha _{k}+{\tilde{\gamma }}-1}{\alpha _{k}+|{\tilde{m}}|} \quad {\text{for}}\quad k\in {\tilde{Z}}, \\ \zeta _{k}&=2r \quad {\text{for}}\quad k\in {\tilde{S}}. \end{aligned}$$

  Note that ${\tilde{S}}\ne \emptyset$, ${\tilde{\gamma }}>0$ and ${\tilde{\kappa }}_{k}>0$ for $k\in {\tilde{S}}$. We calculate

  $$\begin{aligned} 0&=\sum _{k\in {\tilde{Z}}}\frac{|{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}}{\alpha _{k}+|{\tilde{m}}|}+4r(r-|{\tilde{Z}}|)\\&= \sum _{k\in {\tilde{Z}}}\frac{1}{\alpha _{k}+|{\tilde{m}}|}\left( |{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}\right) \\&\quad +2r|{\tilde{S}}|+2(|{\tilde{S}}|+|{\tilde{Z}}|)| {\tilde{S}}|\\&= \sum _{k\in {\tilde{Z}}}\frac{1}{\alpha _{k}+|{\tilde{m}}|}\left( |{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}\right) \\&\quad +2r|{\tilde{S}}|+2|{\tilde{S}}|^{2}+2|{\tilde{S}}| \sum _{k\in {\tilde{Z}}}\frac{\alpha _{k}+|{\tilde{m}}|}{\alpha _{k}+|{\tilde{m}}|}\\&= \sum _{k\in {\tilde{Z}}} \frac{|{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}+2|{\tilde{S}}|(\alpha _{k}+|{\tilde{m}}|)}{\alpha _{k}+|{\tilde{m}}|}+2|{\tilde{S}}|(r+|{\tilde{S}}|)\\&= \sum _{k\in {\tilde{Z}}} \frac{(r+|{\tilde{S}}|)\alpha _{k}-1+\sum _{l\in {\tilde{S}}}\alpha _{l}+2|{\tilde{S}}||{\tilde{m}}|}{\alpha _{k}+|{\tilde{m}}|}+2|{\tilde{S}}|(r+|{\tilde{S}}|)\\&= \sum _{k\in {\tilde{Z}}}\frac{1}{\alpha _{k}+|{\tilde{m}}|}\left( (r+|{\tilde{S}}|)\alpha _{k}-1+\frac{(r+|{\tilde{S}}|){\tilde{\gamma }}-|{\tilde{S}}|}{r}\right) \\&\quad + 2|{\tilde{S}}|(r+|{\tilde{S}}|). \end{aligned}$$

  Multiplying this equality by $\frac{r}{r+|{\tilde{S}}|}$ , we get

  $$\begin{aligned} 0=\sum _{k\in {\tilde{Z}}}\frac{r\alpha _{k}+{\tilde{\gamma }}-1}{\alpha _{k}+|{\tilde{m}}|}+2r|{\tilde{S}}|. \end{aligned}$$

  (50)

  Hence immediately $\sum _{k=1}^{r}\zeta _{k}=0.$ Put

  $$\begin{aligned} {\tilde{x}}_{k}=\sqrt{{\tilde{\kappa }}_{k}}, \quad {\tilde{\xi }}_{k}=\frac{\zeta _{k}}{\Vert \zeta \Vert } \quad {\text{for}}\quad k=1,\ldots ,r. \end{aligned}$$

  It is clear that $({\tilde{\xi }},{\tilde{x}})\in \{g=0\}$. It follows from the definition of ${\tilde{\kappa }}$ and $\zeta$ that

  $$\begin{aligned} {\tilde{\kappa }}\cdot {\tilde{\xi }}=\frac{2r}{\Vert \zeta \Vert }. \end{aligned}$$

  Thus

  $$\begin{aligned} {\tilde{\xi }}_{k}={\tilde{\kappa }}\cdot {\tilde{\xi }} \quad {\text{for}}\quad k\in {\tilde{S}}. \end{aligned}$$

  The definition of $\zeta$ implies the relations

  $$\begin{aligned}&\zeta _{k}(\alpha _{k}+|{\tilde{m}}|)=r\alpha _{k}+{\tilde{\gamma }}-1 \quad {\text{for}}\quad k\in {\tilde{Z}},\nonumber \\&\zeta _{k}(\alpha _{k}+|{\tilde{m}}|)=2r(\alpha _{k}+|{\tilde{m}}|) \quad {\text{for}}\quad k\in {\tilde{S}}. \end{aligned}$$

  (51)

  Adding (51) and using the definition of ${\tilde{\gamma }}$ , we have

  $$\begin{aligned} \alpha \cdot \zeta =|{\tilde{S}}|+r\sum _{k\in {\tilde{S}}}\alpha _{k}+2r|{\tilde{S}}||{\tilde{m}}|+|{\tilde{Z}}||{\tilde{\gamma }}|=2r{\tilde{\gamma }}, \end{aligned}$$

  what after dividing by $\Vert \zeta \Vert$ gives

  $$\begin{aligned} \alpha \cdot {\tilde{\xi }}=({\tilde{\kappa }}\cdot {\tilde{\xi }}){\tilde{\gamma }}. \end{aligned}$$

  But multiplying (51) by $\frac{\zeta _{k}}{\Vert \zeta \Vert ^{2}}$ , we get

  $$\begin{aligned}&\alpha _{k}{\tilde{\xi }}_{k}^{2}+|{\tilde{m}}|{\tilde{\xi }}_{k}^{2}=\frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})\alpha _{k}{\tilde{\xi }}_{k}+ \frac{{\tilde{\kappa }}\cdot {\tilde{\xi }}}{2r}({\tilde{\gamma }}-1){\tilde{\xi }}_{k} \quad {\text{for}}\quad k\in {\tilde{Z}},\nonumber \\&\alpha _{k}{\tilde{\xi }}_{k}^{2}+|{\tilde{m}}|{\tilde{\xi }}_{k}^{2}=({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}\alpha _{k}+({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2} |{\tilde{m}}| \quad {\text{for}}\quad k\in {\tilde{S}}. \end{aligned}$$

  (52)

  We add (52) and then we calculate

  $$\begin{aligned}&\sum _{k=1}^{r}\alpha _{k}{\tilde{\xi }}_{k}^{2}+|{\tilde{m}}|\\&\quad = \frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})\sum _{k\in {\tilde{Z}}}\alpha _{k}{\tilde{\xi }}_{k}+ \frac{{\tilde{\kappa }}\cdot {\tilde{\xi }}}{2r}({\tilde{\gamma }}-1)\sum _{k\in {\tilde{Z}}}{\tilde{\xi }}_{k}\\&\qquad +({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}\sum _{k\in {\tilde{S}}}\alpha _{k}+({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}|{\tilde{m}}||{\tilde{S}}|\\&\quad = \frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})\sum _{k\in {\tilde{Z}}}\alpha _{k}{\tilde{\xi }}_{k}+ \frac{{\tilde{\kappa }}\cdot {\tilde{\xi }}}{2r}(1-{\tilde{\gamma }})\sum _{k\in {\tilde{S}}}{\tilde{\xi }}_{k} +\frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})\sum _{k\in {\tilde{S}}}\alpha _{k}{\tilde{\xi }}_{k}\\&\qquad +\frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}\sum _{k\in {\tilde{S}}}\alpha _{k} +({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}|{\tilde{m}}||{\tilde{S}}|\\&\quad = \frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})\sum _{k=1}^{r}\alpha _{k}{\tilde{\xi }}_{k}+ \frac{1}{2r}\left( {\tilde{\kappa }}\cdot {\tilde{\xi }} - ({\tilde{\kappa }}\cdot {\tilde{\xi }}){\tilde{\gamma }} \right) ({\tilde{\kappa }}\cdot {\tilde{\xi }})|{\tilde{S}}|\\&\qquad +\frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}\sum _{k\in {\tilde{S}}}\alpha _{k} +({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}|{\tilde{m}}||{\tilde{S}}|\\&\quad = \frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }})+\frac{1}{2r}|{\tilde{S}}|({\tilde{\kappa }}\cdot {\tilde{\xi }})\left( {\tilde{\kappa }}\cdot {\tilde{\xi }}-\alpha \cdot {\tilde{\xi }}\right) \\&\qquad +\frac{1}{2}({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}\left( \sum _{k\in {\tilde{S}}}\alpha _{k}+2|{\tilde{m}}||{\tilde{S}}|\right) \\&\quad = \left( \frac{1}{2}-\frac{|{\tilde{S}}|}{2r}\right) ({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }})+\frac{({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}}{2} \left( \frac{|{\tilde{S}}|}{r}+\sum _{k\in {\tilde{S}}}\alpha _{k}+2|{\tilde{S}}||{\tilde{m}}| \right) \\&\quad = \frac{r-|{\tilde{S}}|}{2r}({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }})+\frac{({\tilde{\kappa }}\cdot {\tilde{\xi }})^{2}}{2r}(r+|{\tilde{S}}|) {\tilde{\gamma }}\\&\quad = \frac{r-|{\tilde{S}}|}{2r}({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }}) +\frac{r+|{\tilde{S}}|}{2r}({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }})=({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }}). \end{aligned}$$

  Hence, $\sum _{k=1}^{r}\alpha _{k}{\tilde{\xi }}_{k}^{2}-({\tilde{\kappa }}\cdot {\tilde{\xi }})(\alpha \cdot {\tilde{\xi }})=-|{\tilde{m}}|={\tilde{m}}$, that is to say $f_\alpha ({\tilde{\xi }},{\tilde{x}})={\tilde{m}}$. Thus, ${\tilde{m}}\ge m$.

  Concluding, if ${\tilde{Z}}\subset \{1,\ldots ,r\}$, $0<|{\tilde{Z}}|<r$ and ${\tilde{m}}$ is a negative root of Eq. (49), then ${\tilde{m}}\ge m$.

  We will prove that $|Z|=r-1$. Suppose that

  $$\begin{aligned} |Z|<r-1. \end{aligned}$$

  (53)

  Let $k_{*}\in \{1,\ldots ,r\}{\setminus } Z$ and define

  $$\begin{aligned} {\tilde{Z}}=Z\cup \{k_{*}\}. \end{aligned}$$

  (54)

  Define the rational function

  $$\begin{aligned} R:{\mathbb{R}}_{+}\ni y\mapsto \sum _{k\in {\tilde{Z}}}\frac{|{\tilde{Z}}|\alpha _{k}-\sum _{l\in {\tilde{Z}}}\alpha _{l}}{\alpha _{k}+y}+4r(r-|{\tilde{Z}}|)\in {\mathbb{R}}. \end{aligned}$$

  (55)

  We calculate

  $$\begin{aligned} R(|m|)&=\sum _{k\in Z\cup \{k_{*}\}}\frac{(|Z|+1)\alpha _{k}-(\sum _{l\in Z}\alpha _{l}+\alpha _{k*})}{\alpha _{k}+|m|}+4r(r-|Z|-1)\nonumber \\&= \sum _{k\in Z}\frac{|Z|\alpha _{k}-\sum _{l\in Z}\alpha _{l}}{\alpha _{k}+|m|}+4r(r-|Z|)\nonumber \\&\quad +\sum _{k\in Z}\frac{\alpha _{k}}{\alpha _{k}+|m|}+|Z|\frac{\alpha _{k_{*}}}{\alpha _{k_{*}}+|m|}\nonumber \\&\quad -4r-\alpha _{k_{*}}\sum _{k\in Z}\frac{1}{\alpha _{k}+|m|}-\frac{\sum _{k\in Z}\alpha _{k}}{\alpha _{k_{*}}+|m|}\nonumber \\&\quad< 0+|Z|+|Z|-2r-2r=-(2(r-|Z|)+2r)<0. \end{aligned}$$

  (56)

  Because $\lim _{y\rightarrow \infty }R(y)=4r(r-|{\tilde{Z}}|)>0$, there is $y>|m|$ such that $R(y)>0$. It follows from the Darboux property that there is ${\tilde{y}}>|m|$ such that $R({\tilde{y}})=0$. Put ${\tilde{m}}=-{\tilde{y}}<0$. But $R(|{\tilde{m}}|)=0$ and from here ${\tilde{m}}$ is a negative root of (49). The conclusion before (53) says that ${\tilde{m}}\ge m$. On the other hand, $-{\tilde{m}}={\tilde{y}}>|m|=-m$ what implies ${\tilde{m}}<m$ , and we have contradiction.

  Because $|Z|=r-1$, there is ${\hat{k}}\in \{1,\ldots ,r\}$ such that $Z=\{1,\ldots ,r\}{\setminus }\{{\hat{k}}\}$. In consequence,

  $$\begin{aligned} 0&=\sum _{k\in Z}\frac{|Z|\alpha _{k}-\sum _{l\in Z}\alpha _{l}}{\alpha _{k}+|m|}+4r(r-|Z|)\\&=\sum _{k=1,k\ne {\hat{k}}}^{r} \frac{(r-1)\alpha _{k}+\alpha _{{\hat{k}}}-1}{\alpha _{k}+|m|}+4r. \end{aligned}$$

  Hence $m(\alpha )=\min \left\{ x<0: \exists j\in \{1,\ldots ,r\}\ 4r+\sum _{k=1,k\ne j}^{r}\frac{\alpha _{j}+(r-1)\alpha _{k}-1}{\alpha _{k}+|x|}=0\right\}$ $\le m$, but according to the conclusion before (53) we have $m(\alpha )\ge m$, that is to say $m=m(\alpha )$.

• (iii) Observe that in the proof of point (ii) it is not important an explicit form of $\alpha$ but a fact that $\alpha \in {\mathcal {K}}$ only. So $\alpha$ can be replaced, for example, by $e_{i}$ and $m(\alpha )$ by $m(e_{i})$, $i=1,\ldots ,r$.

  If $r=2$, then

  $$\begin{aligned} -\left( \sqrt{\frac{r-1}{2r}}-\frac{1}{2}\right) =0=m(e_{i}). \end{aligned}$$

  Let $r>2$. Applying (ii) to $e_{i}$ , we see that $m(e_{i})<0$ and there is $j\in \{1,\ldots ,r\}$ such that

  $$\begin{aligned} 4r+\sum _{k=1,k\ne j}^{r}\frac{\kappa _{j}+(r-1)\kappa _{k}-1}{\kappa _{k}+|m(e_{i})|}=0, \end{aligned}$$

  where $\kappa =e_{i}$. Note that $j=i$ is not possible because in this case

  $$\begin{aligned} 0=4r+\sum _{k=1,k\ne i}^{r}\frac{\kappa _{i}+(r-1)\kappa _{k}-1}{\kappa _{k}+|m(e_{i})|}=4r>0. \end{aligned}$$

  Therefore, $j\ne i$ and

  $$\begin{aligned} 0&=4r+\sum _{k=1,k\ne j}^{r}\frac{(r-1)\kappa _{k}-1}{\kappa _{k}+|m(e_{i})|}\nonumber \\&= 4r+\sum _{k=1,k\ne i,j}^{r}\frac{(r-1)\kappa _{k}-1}{\kappa _{k}+|m(e_{i})|}+\frac{(r-1)\kappa _{i}-1}{\kappa _{i}+|m(e_{i})|}\nonumber \\&= \frac{4r}{|m(e_{i})|(1+|m(e_{i})|)}\left( m(e_{i})^{2}-m(e_{i})+\frac{2-r}{4r}\right) . \end{aligned}$$

  (57)

  This implies that $m(e_{i})$ is a negative root of the quadratic trinomial $x^{2}-x+\frac{2-r}{4r}$, and obviously

  $$\begin{aligned} m(e_{i})=-\left( \sqrt{\frac{r-1}{2r}}-\frac{1}{2}\right) . \end{aligned}$$

  Let $(\xi ,x)\in \{g=0\}$ and put $\kappa _{k}=x_{k}^{2}$, $k=1,\ldots ,r$. It is true that

  $$\begin{aligned} f_\kappa (\xi ,x)=\sum _{i=1}^{r}\kappa _{i}\xi _{i}(\xi _{i}-\kappa \cdot \xi )\ge \min _{i=1,\ldots ,r}\xi _{i}(\xi _{i}-\kappa \cdot \xi ) \end{aligned}$$

  (58)

  because $\sum _{i=1}^{r}\kappa _{i}\xi _{i}(\xi _{i}-\kappa \cdot \xi )\in {\text{conv}}\{\xi _{i}(\xi _{i}-\kappa \cdot \xi ):\ i=1,\ldots ,r\}.$ Note that $\kappa \cdot \xi =\sum _{k=1}^{r}\kappa _{k}\xi _{k}\in {\text{conv}}\{\xi _{k}:\ k=1,\ldots ,r\}$ so $\xi _{{\min }}\le \kappa \cdot \xi \le \xi _{{\max }}$, where $\xi _{{\min }}=\min _{k=1,\ldots ,r}\xi _{k}$, $\xi _{{\max }}=\max _{k=1,\ldots ,r}\xi _{k}$. Let $i\in \{i,\ldots ,r\}$ be fixed. If $\xi _{i}\ge 0$, then

  $$\begin{aligned} \xi _{i}(\xi _{i}-\kappa \cdot \xi )\ge \xi _{i}(\xi _{i}-\xi _{{\max }})\ge \min _{j,k=1,\ldots ,r}\xi _{j}(\xi _{j}-\xi _{k}) \end{aligned}$$

  else

  $$\begin{aligned} \xi _{i}(\xi _{i}-\kappa \cdot \xi )\ge \xi _{i}(\xi _{i}-\xi _{{\min }})\ge \min _{j,k=1,\ldots ,r}\xi _{j}(\xi _{j}-\xi _{k}). \end{aligned}$$

  These estimates and (58) give the relations

  $$\begin{aligned} f_\kappa (\xi ,x)\ge \min _{i=1,\ldots ,r}\xi _{i}(\xi _{i}-\kappa \cdot \xi )\ge \min _{j,k=1,\ldots ,r}\xi _{j}(\xi _{j}-\xi _{k})=\min _{j,k=1,\ldots ,r}f_{e_{j}}(\xi ,e_{k}). \end{aligned}$$

  (59)

  Observe that

  $$\begin{aligned} f_{e_{j}}(\xi ,e_{k})\ge m(e_{j})=m(e_{r}). \end{aligned}$$

  (60)

  In consequence, by (59), (60)

  $$\begin{aligned} m(\alpha )\ge m(e_{r}). \end{aligned}$$

  (61)

• (iv) Let $x<0$ fulfils the equation

  $$\begin{aligned} 12+\sum _{k=1,k\ne j}^3\frac{\alpha _{j}+2\alpha _{k}-1}{\alpha _{k}-x}=0 \end{aligned}$$

  (62)

  for some $j\in \{1,2,3\}$. Without loss of generality, we can assume that $\alpha _{k}\ge \alpha _{l}$, $k,l\in \{1,2,3\}{\setminus }\{j\}$. Equation (62) is equivalent to the following one

  $$\begin{aligned} x^{2}-(\alpha _{k}+\alpha _{l})x+\frac{16\alpha _{k}\alpha _{l}-(\alpha _{k}+\alpha _{l})^{2}}{12}=0. \end{aligned}$$

  Hence

  $$\begin{aligned} x=\alpha _{l}\left( \frac{1}{\sqrt{3}}+\frac{1}{2}\right) -\alpha _{k}\left( \frac{1}{\sqrt{3}}-\frac{1}{2}\right) \ge -\alpha _{{\max }}\left( \frac{1}{\sqrt{3}}-\frac{1}{2}\right) , \end{aligned}$$

  where $\alpha _{{\max }}={\max }\{\alpha _{1},\alpha _{2},\alpha _{3}\}$. Note that there is l, k such that $\alpha _{l}=0$, $0<\alpha _{k}=\alpha _{{\max }}$ because the equation

  $$\begin{aligned} x^{2}-\alpha _{k}x-\frac{\alpha _{k}^{2}}{12}=0 \end{aligned}$$

  has a negative root. Thus

  $$\begin{aligned} m(\alpha )=-\alpha _{{\max }}\left( \frac{1}{\sqrt{3}}-\frac{1}{2}\right) . \end{aligned}$$

  The proof is complete. $\square$

Theorem 5

(criterion of parabolicity) If $\varTheta _{i}$, $i=1,\ldots ,r$ are constant and $\delta +m(\alpha )$ $\sum _{k=1}^{r}(\varTheta _{k}-\delta )>0$, then the generalized parabolicity condition (16) is fulfilled with $\mu :=\delta +m(\alpha )\sum _{k=1}^{r}(\varTheta _{k}-\delta )$ and $\nu =0$.

Proof

It follows from Theorem 4 that

$$\begin{aligned} (A_\kappa \xi )\cdot \xi \ge \mu \Vert \xi \Vert ^{2} \quad {\text{for}}\quad \kappa \in {\mathcal {K}} \quad {\text{and}} \quad \xi \in 1^{\perp }, \end{aligned}$$

(63)

because it is equivalent to

$$\begin{aligned} \left( A_\kappa \frac{\xi }{\Vert \xi \Vert }\right) \cdot \frac{\xi }{\Vert \xi \Vert }\ge \mu \quad {\text{for}}\quad \kappa \in {\mathcal {K}} \quad {\text{and}} \quad \xi \in 1^{\perp }. \end{aligned}$$

The inequality (63) implies immediately (16). $\square$

4 Numerical Simulations

To illustrate a class of problems which can be treated with our method, we consider three examples with constant $\varTheta _{i}$, $i=1,2,3$. In these examples, all the assumptions of our theorems are fulfilled, with $\mu$ and $\nu$ found with the use of the criterion of parabolicity (see Theorem 5). The results of numerical simulations are consistent with real experiments (Sapa et al. 2020; Belova et al. 2005; Dąbrowa et al. 2016; Bożek et al. 2021). The numerical solutions are obtained with the use of the Galerkin method described in Sapa et al. (2018b).

Example 1

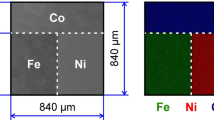
Consider the ternary mixture of nickel (Ni), cobalt (Co) and iron (Fe) with constants $\varTheta _{i}$, $i=1,2,3$ at the temperature 1223 [K]. Let the physical data be given:

$$\begin{aligned}&r=3, \qquad {\text{Ni}}{-}{\text{Co}}{-}{\text{Fe}}, \qquad \varLambda =0.01 \; [{\text{cm}}], \\&(M_{1},M_{2},M_{3}) = (58.69,\ 58.93,\ 55.85),\\&(\varOmega _{1},\varOmega _{2},\varOmega _{3}) = (6.59,\ 6.67,\ 7.09) [{\text{cm}}^{3}/{\text{mol}}],\\&(\varTheta _{1},\varTheta _{2},\varTheta _{3}) = (3.9\cdot 10^{-13},\ 8.7\times 10^{-13},\ 1.1\times 10^{-12}) [{\text{cm}}^{2}/{{\text{s}}}],\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (4.10,\ 3.00,\ 1.58) \quad {\text{for}} \quad x<0,\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (0.00,\ 3.00,\ 5.20) \quad {\text{for}} \quad x>0. \end{aligned}$$

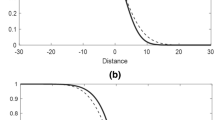
The constant $\mu =3.35081\times 10^{-13}>0$ in Theorem 5. For the times 0, 58, 323, 660 h, we obtained the numerical results displayed in Fig. 1.

Fig. 1

The distributions of densities: $\rho _{1}$ (red), $\rho _{2}$ (blue), $\rho _{3}$ (green). The results are after 0, 58, 323 and 660 h, respectively

Example 2

Consider the ternary mixture of nickel (Ni), chrome (Cr) and aluminium (Al) with constants $\varTheta _{i}$, $i=1,2,3$ at the temperature 1473 [K]. Let the physical data be given:

$$\begin{aligned}&r=3, \qquad {\text{Ni}}{-}{\text{Cr}}{-}{\text{Al}}, \qquad \varLambda =0.02\; [{\text{cm}}], \\&(M_{1},M_{2},M_{3}) = (58.69,\ 51.10,\ 26.98),\\&(\varOmega _{1},\varOmega _{2},\varOmega _{3}) = (7.20,\ 10.00,\ 6.00) \; [{\text{cm}}^{3}/{\text{mol}}],\\&(\varTheta _{1},\varTheta _{2},\varTheta _{3}) = (3.2\times 10^{-10},\ 2.6\times 10^{-9},\ 1.1\times 10^{-9}) \; [{\text{cm}}^{2}/{\text{s}}],\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (4.10,\ 2.00,\ 0.46) \quad {\text{for}} \quad x<0,\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (0.10,\ 2.00,\ 2.47) \quad {\text{for}} \quad x>0. \end{aligned}$$

The constant $\mu =1.43641\times 10^{-10}>0$ in Theorem 5. For the times 0, 6, 12, 24 h, we obtained the numerical results displayed in Fig. 2.

Fig. 2

The distributions of densities: $\rho _{1}$ (red), $\rho _{2}$ (blue), $\rho _{3}$ (green). The results are after 0, 6, 12 and 24 h, respectively

Example 3

Consider the ternary mixture of nickel (Ni), chrome (Cr) and aluminium (Al) with constants $\varTheta _{i}$, $i=1,2,3$ at the temperature 1473 [K]. Let the physical data be given:

$$\begin{aligned}&r=3, \qquad {\text{Ni}}{-}{\text{Cr}}{-}{\text{Al}}, \qquad \varLambda =0.02 \; [{\text{cm}}], \\&(M_{1},M_{2},M_{3}) = (58.69,\ 51.10,\ 26.98),\\&(\varOmega _{1},\varOmega _{2},\varOmega _{3}) = (7.20,\ 10.00,\ 6.00) \; [{\text{cm}}^{3}/{\text{mol}}],\\&(\varTheta _{1},\varTheta _{2},\varTheta _{3}) = (3.2\times 10^{-10},\ 2.6\times 10^{-9},\ 1.1\times 10^{-9})\;[{\text{cm}}^{2}/{\text{s}}],\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (3.10,\ 0.30,\ 2.30) \quad {\text{for}} \quad x<0,\\&(\varrho _{01},\varrho _{02},\varrho _{03}) = (3.10,\ 2.50,\ 0.57) \quad {\text{for}} \quad x>0. \end{aligned}$$

The constant $\mu =1.43641\times 10^{-10}>0$ in Theorem 5. For the times 0, 6, 12, 24 h, we obtained the numerical results displayed in Fig. 3.

Fig. 3

The distributions of densities: $\rho _{1}$ (red), $\rho _{2}$ (blue), $\rho _{3}$ (green). The results are after 0, 6, 12 and 24 h, respectively

In Examples 1, 2, 3, the most interesting is uphill diffusion. Such diffusion was observed in experiments (Belova et al. 2005; Dąbrowa et al. 2016). The initial homogenous concentration of cobalt (Co) in Fig. 1 and chrome in Figs. 2 and 3 (the blue curves) goes out of the equilibrium at the beginning, and as a result of time evolution, this concentration homogenizes.