Skip to main content
SpringerLink
Log in

Numerical Studies for Fractional Pantograph Differential Equations Based on Piecewise Fractional-Order Taylor Function Approximations

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions A: Science Aims and scope Submit manuscript

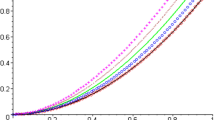
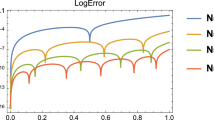
Abstract

Fractional calculus has been used to model physical and engineering processes that are found to be best described by fractional differential equations. Therefore, a reliable and efficient technique as a solution is regarded. In this paper, a new numerical method for solving fractional pantograph differential equations is presented. The fractional derivative is described in the Caputo sense. The method is based upon piecewise fractional-order Taylor function approximations. The piecewise fractional-order Taylor function is presented. An operational matrix of fractional order integration is derived and is utilized to reduce the under study problem to the solution of a system of algebraic equations. Using Newton’s iterative method, this system is solved and the solution of fractional pantograph differential equations is achieved. A bound of the error is given in the sense of Sobolev norms. Five examples are given and the numerical results are shown to demonstrate the efficiency of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Arikoglu A, Ozkol I (2009) Solution of fractional integro-differential equations by using fractional differential transform method. Chaos Solitons Fractals 40:521–529

    Article  MathSciNet  Google Scholar 

  • Bass RF (2011) Real analysis for graduate students. Bass math uconn edu, 2 edn

  • Bhalekar S, Daftardar-Gejji V (2011) A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J Fract Calc Appl 1(5):1–9

    MATH  Google Scholar 

  • Bohannan GW (2008) Analog fractional order controller in temperature and motor control applications. J Vib Control 14:1487–98

    Article  MathSciNet  Google Scholar 

  • El-Sayed AMA, Hashem HHG, Ziada EAA (2014) Picard and Adomian decomposition methods for a quadratic integral equation of fractional order. Comput Appl Math 33(1):95–109

    Article  MathSciNet  Google Scholar 

  • Feliu V, Rivas R, Castillo F (2009) Fractional order controller robust to time delay for water distribution in an irrigation main canal pool. Comput Elect Agri 69(2):185–197

    Article  Google Scholar 

  • Hashim I, Abdulaziz O, Momani S (2009) Homotopy analysis method for fractional IVPs. Commun Nonlinear Sci Numer Simul 14(3):674–684

    Article  MathSciNet  Google Scholar 

  • He JH (1998) Nonlinear oscillation with fractional derivative and its applications. International Conference on Vibrating Engineering, Dalian, pp 288–291

  • He JH (1999) Some applications of nonlinear fractional differential equations and their approximations. Bull Sci Tech 15(2):86–90

    Google Scholar 

  • Iqbal MA, Saeed U, Mohyud-Din ST (2015) Modified Laguerre wavelets method for delay differential equations of fractional-order. Egypt J Basic Appl Sci 2:50–54

    Article  Google Scholar 

  • Irandoust-Pakchin S, Kheiri H, Abdi-Mazraeh S (2013) Chebyshev cardinal functions: An effective tool for solving nonlinear Volterra and Fredholm integro-differential equations of fractional order. Iran J Sci Technol A1:53–62

    MathSciNet  MATH  Google Scholar 

  • Jiang Y, Ma J (2011) High-order finite element methods for time-fractional partial differential equations. J Comput Appl Math 235:3285–3290

    Article  MathSciNet  Google Scholar 

  • Khader MM, Hendy AS (2012) The approximate and exact solutions of the fractional-order delay differential equations using Legendre pseudo-spectral method. Int J Pure Appl Math 74(3):287–297

    MATH  Google Scholar 

  • Kreyszig E (1978) Introductory functional analysis with applications. John Wiley and Sons, New York

    MATH  Google Scholar 

  • Krishnasamy VS, Razzaghi M (2015) The numerical solution of the Bagley–Torvik equation with fractional Taylor method. J Comput Nonlinear Dynam 11(15):1–6

    Google Scholar 

  • Mashayekhi S, Razzaghi M (2016) Numerical solution of distributed order fractional differential equations by hybrid functions. J Comput Phys 315:169–181

    Article  MathSciNet  Google Scholar 

  • Mashayekhi S, Razzaghi M, Wattanataweekul (2016) Analysis of multi-delay and piecewise constant delay systems by hybrid functions approximation. Diff Equ Dyn Syst 24:1–20

    Article  MathSciNet  Google Scholar 

  • Moghaddam BP, Mostaghim ZS (2013) A numerical method based on finite difference for solving fractional delay differential equations. J Taibah Univ Sci 7:120–127

    Article  Google Scholar 

  • Morgado ML, Ford NJ, Lima PM (2012) Analysis and numerical methods for fractional differential equations with delay. J Comput Appl Math 252:159–168

    Article  MathSciNet  Google Scholar 

  • Odibat Z, Momani S (2006) Application of variational iteration method to nonlinear differential equations of fractional order. Int J Nonlinear Sci Numer Simul 7:27–34

    Article  MathSciNet  Google Scholar 

  • Ordokhani Y (2010) An application of Walsh functions for Fredholm–Hammerstein integro-differential equations. Int J Contemp Math Sci 5(22):1055–1063

    MathSciNet  MATH  Google Scholar 

  • Panda R, Dash M (2006) Fractional generalized splines and signal processing. Signal Process 86:2340–50

    Article  Google Scholar 

  • Pimenov VG, Hendy AS (2015) Numerical studies for fractional functional differential equations with delay based on BDF-Type shifted Chebyshev approximations. Abstr Appl Anal 2015:1–12

    Article  MathSciNet  Google Scholar 

  • Rahimkhani P, Ordokhani Y, Babolian E (2016a) An efficient approximate method for solving delay fractional optimal control problems. Nonlinear Dyn 86:1649–1661

    Article  MathSciNet  Google Scholar 

  • Rahimkhani P, Ordokhani Y, Babolian E (2016b) Fractional-order Bernoulli wavelets and their applications. Appl Math Model 40:8087–8107

    Article  MathSciNet  Google Scholar 

  • Rahimkhani P, Ordokhani Y, Babolian E (2017a) A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer Algor 74:223–245

    Article  MathSciNet  Google Scholar 

  • Rahimkhani P, Ordokhani Y, Babolian E (2017b) Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. Comput Appl Math 309:493–510

    Article  MathSciNet  Google Scholar 

  • Raja MAZ (2014) Numerical treatment for boundary value problems of Pantograph functional differential equation using computational intelligence algorithms. Appl Soft Comput 24:806–821

    Article  Google Scholar 

  • Raja MAZ, Ahmad I, Syam MI, Wazwaz AM (2016) Neuro-heuristic computational intelligence for solving nonlinear pantograph systems. Front Inf Technol Electron Eng 10:1631

    Google Scholar 

  • Saadatmandi A, Dehghan M, Azizi MR (2012) The Sinc-Legendre collocation method for a class of fractional convection-diffusion equations with variable coefficients. Commun Nonlinear Sci 17:4125–4136

    Article  MathSciNet  Google Scholar 

  • Saeed U, Rehman M (2014) Hermite wavelet method for fractional delay differential equations. J Diff Equ 2014:1–8

    Article  Google Scholar 

  • Saeed U, Rehman M, Iqbal MA (2015) Modified Chebyshev wavelet methods for fractional delay-type equations. Appl Math Comput 264:431–442

    MathSciNet  MATH  Google Scholar 

  • Saeedi H, Mohseni Moghadam M, Mollahasani N, Chuev GN (2011) A CAS wavelet method for solving nonlinear Fredholm integro-differential equations of fractional order. Commun Nonlinear Sci Numer Simulat 16:1154–1163

    Article  MathSciNet  Google Scholar 

  • Sedaghat S, Ordokhani Y, Dehghan M (2012) Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun Nonl Sci Numer Simulat 17:4815–4830

    Article  MathSciNet  Google Scholar 

  • Si-Ammour A, Djennoune S, Bettayeb M (2009) A sliding mode control for linear fractional systems with input and state delays. Commun Nonlinear Sci Numer Simul 14:2310–2318

    Article  MathSciNet  Google Scholar 

  • Su L, Wang W, Xu Q (2010) Finite difference methods for fractional dispersion equations. Appl Math Comput 216:3329–3334

    MathSciNet  MATH  Google Scholar 

  • Wang Z (2013) A numerical method for delayed fractional-order differential equations. J Appl Math 2013:1–7

    MathSciNet  Google Scholar 

  • Wang Z, Huang X, Zhou J (2013) A numerical method for delayed fractional-order differential equations: based on G-L definition. Appl Math Inf Sci 7(2):525–529

    Article  MathSciNet  Google Scholar 

  • Wang D, Yu J (2008) Chaos in the fractional order logistic delay system. J Electron Sci Tech China 6(3):225–229

    Google Scholar 

  • Wazwaz AM, Raja MAZ, Syam MI (2017) Reliable treatment for solving boundary value problems of pantograph delay differential equations. Rom Rep Phys 69:102

    Google Scholar 

  • Yang Y, Huang Y (2013) Spectral-collocation methods for fractional pantograph delay-integrodifferential equations. Adv Math Phys 2013:1–14

    MathSciNet  MATH  Google Scholar 

  • Yousefi SA, Lotfi A (2013) Legendre multiwavelet collocation method for solving the linear fractional time delay systems. Cent Eur J Phys 11(10):1463–1469

    Google Scholar 

Download references

Acknowledgements

This work is supported by the national elites foundation. Authors are very grateful to one of the reviewers for carefully reading the paper and for his(her) comments and suggestions which have improved the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    Parisa Rahimkhani & Yadollah Ordokhani

Authors
  1. Parisa Rahimkhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yadollah Ordokhani
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yadollah Ordokhani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahimkhani, P., Ordokhani, Y. Numerical Studies for Fractional Pantograph Differential Equations Based on Piecewise Fractional-Order Taylor Function Approximations. Iran J Sci Technol Trans Sci 42, 2131–2144 (2018). https://doi.org/10.1007/s40995-017-0373-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40995-017-0373-z

Keywords

Search

Navigation