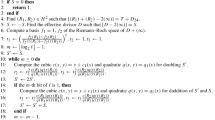Fast norm computation in smooth-degree Abelian number fields

Abstract

This paper presents a fast method to compute algebraic norms of integral elements of smooth-degree cyclotomic fields, and, more generally, smooth-degree Galois number fields with commutative Galois groups. The typical scenario arising in S-unit searches (for, e.g., class-group computation) is computing a $\Theta (n\log n)$-bit norm of an element of weight $n^{1/2+o(1)}$ in a degree-n field; this method then uses $n(\log n)^{3+o(1)}$ bit operations.

An $n(\log n)^{O(1)}$ operation count was already known in two easier special cases: norms from power-of-2 cyclotomic fields via towers of power-of-2 cyclotomic subfields, and norms from multiquadratic fields via towers of multiquadratic subfields. This paper handles more general Abelian fields by identifying tower-compatible integral bases supporting fast multiplication; in particular, there is a synergy between tower-compatible Gauss-period integral bases and a fast-multiplication idea from Rader.

As a baseline, this paper also analyzes various standard norm-computation techniques that apply to arbitrary number fields, concluding that all of these techniques use at least $n^2(\log n)^{2+o(1)}$ bit operations in the same scenario, even with fast subroutines for continued fractions and for complex FFTs. Compared to this baseline, algorithms dedicated to smooth-degree Abelian fields find each norm $n/(\log n)^{1+o(1)}$ times faster, and finish norm computations inside S-unit searches $n^2/(\log n)^{1+o(1)}$ times faster.

1 Introduction

Consider the element $\alpha =3+\zeta _{2048}^{271}+4\zeta _{2048}^{828}$ of the cyclotomic field $K=\mathord {{\mathbb {Q}}}(\zeta _{2048})$; here $\zeta _m$, for any positive integer m, means the complex number $\exp (2\pi i/m)$. Write ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for the determinant of multiplication by $\alpha$ as a $\mathord {{\mathbb {Q}}}$-linear map from K to K, i.e., for the algebraic norm of $\alpha$ from K down to $\mathord {{\mathbb {Q}}}$. (See Sect. 1.4 regarding notation choices.) The following Sage commands print out ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, while measuring how long the computation takes:

Sage 9.5 (the January 2022 version of Sage [83]) takes 61 milliseconds on one core of a 3.5GHz Intel Xeon E3-1275 v3 (Haswell) CPU, around 0.21 $\times$ $10^9$ CPU cycles.

One has ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha = \prod _{c\in \mathord {\left\{ {1,3,5,\dots ,2047}\right\} }}(3+\zeta _{2048}^{271c}+4\zeta _{2048}^{828c})$. The absolute value of the complex number $3+\zeta _{2048}^{271c}+4\zeta _{2048}^{828c}$ is below 8, and one might guess that it is typically somewhere around 4, i.e., that ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ has absolute value around $4^{1024}=2^{2048}$. Sage computes the exact value of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, an integer $272\ldots 618\approx 0.842\cdot 2^{2048}$.

Inside Sage, PARI [76] finds ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ as the resultant of two polynomials in $\mathord {{\mathbb {Z}}}[x]$. The first polynomial is the minimal polynomial of $\zeta _{2048}$ over $\mathord {{\mathbb {Q}}}$, namely $x^{1024}+1$. The second polynomial is $3+x^{271}+4x^{828}$. One can skip Sage’s number-field machinery and directly compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ as a polynomial resultant:

Sage, when asked for a resultant of two polynomials instead of a norm of a number-field element, calls FLINT [55] instead of PARI, and now takes 1.12 $\times$ $10^9$ cycles. The resultant subroutine has a proof=False option allowing randomized algorithms; this option doesn’t save time. What does save time is using NTL [87] polynomials instead of FLINT polynomials:

This takes 0.15 $\times$ $10^9$ cycles.

Why does it take so many cycles to compute a 2048-bit resultant of two input polynomials that have, in dense format, a few thousand small coefficients? The issue is not the number of cycles required per bit for basic arithmetic: for example, Sage takes about 20,000 cycles to multiply two 2048-bit integers. The issue is that standard fast-continued-fraction techniques for computing the resultant of two polynomials in $\mathord {{\mathbb {Z}}}[x]$ have cost growing as essentially the product of the number of input bits and the number of output bits. The resultant of $x^n+1$ and a sparse n-coefficient input, with $n^{1/2+o(1)}$ coefficients $\pm 1$, will typically have $\Theta (n\log n)$ bits; these resultant algorithms then cost $n^2(\log n)^{3+o(1)}$. For some inputs, the output is much smaller and the algorithms are much faster, but this is not the typical case.

It is not a new observation that one can do much better by exploiting transitivity of determinants through a tower of subfields of K. Take F as, e.g., the field $\mathord {{\mathbb {Q}}}(\zeta _{1024})$. Then F is a subfield of K: specifically, $\zeta _{1024}=\zeta _{2048}^2$, so F is the fixed field of the unique automorphism of K that maps $\zeta _{2048}$ to $-\zeta _{2048}$. Hence

$$\begin{aligned} \begin{aligned} {\text {det}}^{K}_{F}\alpha&=\, \left( 3+\zeta _{2048}^{271}+4\zeta _{2048}^{828}\right) \left( 3+(-\zeta _{2048})^{271}+4(-\zeta _{2048})^{828}\right) \\&=9-\zeta _{1024}^{271}+24\zeta _{1024}^{414}+16\zeta _{1024}^{828} =9-\zeta _{1024}^{271}-16\zeta _{1024}^{316}+24\zeta _{1024}^{414}. \end{aligned} \end{aligned}$$

One can then compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ as ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}{\text {det}}^{K}_{F}\alpha$:

Here g*g(-x) gives $g\cdot g(-x)={\text {det}}^{\mathord {{\mathbb {Z}}}[x]}_{\mathord {{\mathbb {Z}}}[x^2]}g$, a polynomial whose value at $\zeta _{2048}$ is ${\text {det}}^{K}_{F}\alpha$; list(g*g(-x)) gives the list of coefficients of $g\cdot g(-x)$; [::2] extracts every second coefficient; ZZx(...) produces the corresponding polynomial, a polynomial whose value at $\zeta _{1024}$ is ${\text {det}}^{K}_{F}\alpha$; and reduces modulo $x^{512}+1$. This is, up to sign, also since $\deg g>0$, but the “Adams” naming is questionable given that this operator on polynomials was already used (for root-finding) by Dandelin in [39, page 49] in 1826; see generally [60].

Sage reports that the evaluation of ${\text {det}}^{K}_{F}$ takes 0.01 $\times$ $10^9$ cycles and that the evaluation of ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}$ takes 0.09 $\times$ $10^9$ cycles. One can save more time by recursively decomposing ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}$ via transitivity, and exploiting the special form of the power-of-2 cyclotomic polynomials to convert each modular reduction into subtraction:

This reduces the total time to just 0.011 $\times$ $10^9$ cycles. Appendix C removes more overhead and takes just 0.0012 $\times$ $10^9$ cycles. The important point to keep in mind is that the typical algorithm cost has dropped from $n^{2+o(1)}$ to $n^{1+o(1)}$.

1.1 Contributions of this paper

As a baseline, Sect. 3 analyzes the costs of various standard ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ techniques that work for arbitrary number fields. The special case of power-of-2 cyclotomics, as in the $\mathord {{\mathbb {Q}}}(\zeta _{2048})$ example above, suffices for seeing that these techniques are not competitive asymptotically, so Sect. 3 focuses on this case. The main conclusion of Sect. 3 is that, in the typical case of $\Theta (n\log n)$-bit outputs for field degree n (see Sect. 2 for why this is typical), all of these techniques use at least $n^2(\log n)^{2+o(1)}$ bit operations.

Section 4 explores the question of which number fields allow lower-cost evaluation of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ via transitivity, in particular reducing $n^2(\log n)^{2+o(1)}$ to $n(\log n)^{3+o(1)}$. It is natural to ask for the field degree to be smooth—a product of small primes—and for the field to have a correspondingly long tower of subfields. The challenge addressed in Sect. 4 is to build algorithms to multiply efficiently on tower-compatible bases for these subfields. Note that this is easy for power-of-2 cyclotomics: standard polynomial bases are compatible with the tower $\mathord {{\mathbb {Q}}}\subset \mathord {{\mathbb {Q}}}(\zeta _4)\subset \mathord {{\mathbb {Q}}}(\zeta _8)\subset \cdots$ and are well known to allow fast multiplication.

Section 5 analyzes applications to one of the standard techniques for computing class groups, unit groups, etc. The technique is to enumerate small elements of the ring of integers, and filter those elements to see which ones are S-units, where S is the set of infinite places and small finite places. This filtering is typically handled by an Eratosthenes-type sieving procedure when degrees are small and discriminants are large, as in the number-field sieve for integer factorization; but if degrees are relatively large, as in the cyclotomic case, then it seems best to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for each element $\alpha$ and then check which ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ factor as desired. The smooth-degree Abelian case uses fewer ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computations (since one can search for S-units modulo automorphisms of the field) and speeds up each ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computation, overall speeding up the sequence of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computations by a factor close to $n^2$. The Abelian case also speeds up the factorizations.

1.2 Previous work on speedups using transitivity

The fact that transitivity of determinants saves effort is standard textbook material. For example, a standard exercise starts with the degree-4 field $K=\mathord {{\mathbb {Q}}}(\zeta _5)$ and the real subfield $F=\mathord {{\mathbb {R}}}\cap K=\mathord {{\mathbb {Q}}}(\sqrt{5})$, and computes ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ as ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}{\text {det}}^{K}_{F}\alpha$. But such small examples give little information regarding how much effort is saved in larger examples.

For any power-of-2 cyclotomic field K, Gentry and Halevi [51, Section 4] used a tower of power-of-2 cyclotomic subfields to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ in essentially linear time, as in the $\mathord {{\mathbb {Q}}}(\zeta _{2048})$ example given above. Bauch, Bernstein, de Valence, Lange, and van Vredendaal [9, Section 3.4], for the case of multiquadratic fields $K=\mathord {{\mathbb {Q}}}(\sqrt{d_1},\sqrt{d_2},\dots ,\sqrt{d_t})$, computed ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ in essentially linear time using a tower of multiquadratic subfields.

Gentry and Halevi also computed ${\text {tr}}^{K}_{\mathord {{\mathbb {Q}}}}(1/\alpha )$ for $\alpha \ne 0$. One can easily obtain the inverse-trace algorithm in [51] by applying the following simple general-purpose conversion, an example of automatic differentiation, to the ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ algorithm in [51]: for any K, take any algebraic algorithm for $\alpha \mapsto {\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, tensor with the jet plane $\mathord {{\mathbb {Q}}}[\epsilon ]/\epsilon ^2$ over $\mathord {{\mathbb {Q}}}$, and apply the resulting algorithm to $\alpha +\epsilon$ to obtain

$$\begin{aligned} {\text {det}}^{K[\epsilon ]/\epsilon ^2}_{\mathord {{\mathbb {Q}}}[\epsilon ]/\epsilon ^2}(\alpha +\epsilon ) =({\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha )(1+\epsilon {\text {tr}}^{K}_{\mathord {{\mathbb {Q}}}}(1/\alpha )). \end{aligned}$$

This conversion loses a small constant factor in performance. This is not how the inverse-trace algorithm in [51] is described, but one can, with some effort, check that this is what the algorithm does.

1.3 Fast-multiplication subroutines

There is a huge literature on FFT-based algorithms to multiply two elements of $R[x]/\varphi$, for any monic $\varphi \in R[x]$ with $\deg \varphi =n$, using $n(\log n)^{1+o(1)}$ operations on coefficients in R. See generally [16].

These algorithms are faster by a constant factor when $\varphi$ is “FFT-friendly”. This constant factor is not visible in the $n(\log n)^{1+o(1)}$ asymptotics, but it becomes visible if one applies the same idea recursively to multiply in a ring presented as a tower such as $(\cdots ((R[x_1]/\varphi _1)[x_2]/\varphi _2)\cdots )[x_t]/\varphi _t$. In a “multidimensional FFT”, each $\varphi _j$ is FFT-friendly (e.g., a size-n Hadamard–Walsh transform has $\varphi _j=x_j^2-1$ and $n=2^t$), and the cost is $\Theta (n\log n)$ for n coefficients; see Sect. 4.12.1. For general $\varphi _j$, a constant-factor loss c at each level of the tower turns into a loss $c^t$ for t levels, increasing costs by a factor $n^{\Theta (1)}$ if $t\in \Theta (\log n)$.

As van der Hoeven and Lecerf pointed out in [59], if one modifies a tower to force $t\in o(\log n)$, by replacing any constant-degree steps with superconstant-degree steps, then the $c^t$ overhead factor mentioned above is $n^{o(1)}$, and one obtains total cost $n^{1+o(1)}$ for multiplication. There is some tension between the idea of reducing t and the idea of exploiting towers to save time in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ computation; but note that if there are t levels, each of relative degree $n^{O(1/t)}$, then there are $n^{O(1/t)}$ multiplications at each level, so reaching total cost $n^{1+o(1)}$ for ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ simply requires t to be superconstant. A closer look shows that one can do better—as an analogy, FFTs are asymptotically better than Toom’s method for univariate multiplication, even though both take essentially linear time—but one should not think that short towers are useless.

For multiquadratic fields $\mathord {{\mathbb {Q}}}(\sqrt{d_1},\sqrt{d_2},\dots ,\sqrt{d_t})$, the multiplication algorithm in [9, Section 3.3] selects enough moduli p for which all of $d_1,d_2,\dots ,d_t$ are squares modulo p, and then uses Hadamard–Walsh transforms twisted by $\sqrt{d_1},\sqrt{d_2},\dots ,\sqrt{d_t}$ modulo p.

One can, with effort, extract from a paper by Arita and Handa [6, Sections 3.3, 3.4, and 4.3] an essentially-linear-time algorithm to multiply on Gauss-period bases of prime-conductor Abelian fields, i.e., subfields of $\mathord {{\mathbb {Q}}}(\zeta _p)$ (beyond $\mathord {{\mathbb {Q}}}$) where p is prime. This algorithm can be viewed as a simple “folding” of an FFT algorithm that Rader introduced in [82], an algorithm having a different flavor from conventional FFTs; see Sect. 4.8. Section 4.12 handles more general Abelian fields, unifying the idea of folding with an extension of Winograd’s generalization [96] of Rader’s idea.

1.4 Notation and terminology

Wessel [95] and independently Argand [3] introduced a geometric description of each complex number $a+bi$ as a line in the plane from (0, 0) to (a, b). Wessel [95, page 469] referred to $(a^2+b^2)^{1/2}$ as the length of the line (“Længde” in Danish). Argand [4, page 208] referred to $(a^2+b^2)^{1/2}$ as the absolute size (“grandeur absolue” in French) and the modulus (“module” in French) of $a+bi$. Gauss [49, page 103] referred to $a^2+b^2$ as the norm (“norma” in Latin) of $a+bi$ for $a,b\in \mathord {{\mathbb {Z}}}$. (One meaning of “norma” in Latin is a carpenter’s square used to measure right angles.)

Subsequent literature reused the “norm” terminology for generalizations (1) to algebraic norms, typically called just “norms”, but also (2) to 2-norms such as the $\ell ^2$ norm and the $L^2$ norm, and beyond that to further generalizations of the concept of length, also typically called just “norms”. Algebraic norms and 2-norms coincide for $a+bi$, aside from quibbles about $a^2+b^2$ vs. $(a^2+b^2)^{1/2}$, but differ in general.

This wouldn’t be problematic if there were a clear dividing line between papers in number theory saying “norm” for algebraic norms and papers in analysis saying “norm” for those other things. The reality, however, is that those other things appear constantly in number theory (and not just in analytic number theory): consider lattices, for example, or Weil height. Perhaps it’s time for number theorists to consider ending the conflict: put the “norm” word down gently and back away.

What, then, should algebraic norms be called? Nobody actually says “algebraic norms” or “field norms” except for disambiguation. Meanwhile there is a well known, standard, unambiguous name for a more general concept: “determinant”. We refer to the trace of multiplication by $\alpha$ as the trace of $\alpha$; shouldn’t we also refer to the determinant of multiplication by $\alpha$ as the determinant of $\alpha$?

There are parameters, of course: in the case of fields, there’s an input field and an output field, with the input field having finite degree over the output field. We all know what the trace map is from the input field to the output field; it’s not a big leap to talk about the determinant map from the input field to the output field.

As for notation, Dirichlet [40, page 295] wrote $N(a+bi)$ for $a^2+b^2$; there were no parameters in the N map. Subsequent literature sometimes uses $N_F$ for a norm to F (as in, e.g., [58, page 204] and [57, page 125]) and sometimes uses $N_F$ for a norm from F (as in, e.g., [30]). The extra effort of writing $N_{L/K}$ resolves the ambiguity (if L and K aren’t objects with a quotient that could be reasonably plugged into the $N_F$ notation), but anyone who has taken a course in differential geometry, the study of superscripts and subscripts, will see that there’s a better place to put the input field. This is not a new idea: see, e.g., [69, page 16] and [41].

As a separate matter, the short name “N” is fine for local notation (notation where brevity is prioritized over broad readability), but it doesn’t work well as global notation given all the other common uses of “N”. Again determinants come to the rescue: the global notations “det” and “tr” are well established. Adding a K subscript for K-linear maps, and an L superscript for taking inputs in L as linear maps from L to L, gives this paper’s notation ${\text {det}}^{L}_{K}\alpha$.

This paper does not attempt to avoid the following common abbreviations: “Rings” are commutative rings. If R is a ring and S is a set then $R^S$ is the ring of S-indexed vectors with entries in R and coordinatewise operations. If R is a ring and H is a finite commutative group then R[H] is the group ring of H over R, the ring of H-indexed vectors with entries in R and convolution as multiplication.

If R is a ring and m is a positive integer then a primitive mth root of 1 in R means an element $\zeta \in R$ such that (1) $\zeta ^m=1$; (2) $\zeta ^{m/p}-1$ is invertible in R for all primes p dividing m; and (3) m is invertible in R (which one can deduce from the other conditions). The notation $\zeta _m$ is specifically the complex number $\exp (2\pi i/m)$.

If B is a basis (of, e.g., a vector space) then the set of entries in B is called a “basis set”; this is not to be confused with B itself, which is a sequence.

2 Sizes

Consider all weight-w elements $\alpha =\alpha _0+\alpha _1\zeta _m+\dots +\alpha _{n-1}\zeta _m^{n-1}$ of the ring of integers $R=\mathord {{\mathbb {Z}}}[\zeta _m]$ of the power-of-2 cyclotomic field $K=\mathord {{\mathbb {Q}}}(\zeta _m)$. Here $n=m/2$, and “weight w” means 2-norm $w^{1/2}$, i.e., $\sum _j \alpha _j^2=w$. This section analyzes the distribution of sizes of the integers $\mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$.

These sizes illustrate the ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ sizes of interest in Sects. 3 and 4; those sections include analyses of the performance of various ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ algorithms, and the analyses depend on the number of bits in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. The distribution considered in this section arises naturally in the standard S-unit search in Sect. 5, which enumerates small-weight elements $\alpha \in R$ and checks whether ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ factors into small primes; presumably ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is more likely to factor appropriately if it is smaller.

One can also ask about the distribution of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for other cyclotomic fields (and other Abelian fields), but the power-of-2 case suffices as an example of what to expect. I haven’t found literature directly on point. There are analyses of the distribution of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ inside the number-field sieve (see, e.g., [11, eprint version, Section 5.1; journal version, Section 2.2]), but NFS considers fields of relatively low degree compared to the discriminant. The analysis below is conceptually similar to [9, Section 8.1], which heuristically analyzes the coefficients of a Dirichlet log vector of a small element of a real multiquadratic field K on a unit basis obtained from fundamental units of quadratic subfields; but the details here are more complex than in [9], since the embeddings $K\rightarrow \mathord {{\mathbb {C}}}$ here are not embeddings $K\rightarrow \mathord {{\mathbb {R}}}$.

2.1 Notation

Throughout this section, $n\in \mathord {\left\{ {2,4,8,16,\dots }\right\} }$; $m=2n$; w is a positive integer; $K=\mathord {{\mathbb {Q}}}(\zeta _m)$; and $R=\mathord {{\mathbb {Z}}}[\zeta _m]$. For each odd integer c, the function $\sigma _c:K\rightarrow \mathord {{\mathbb {C}}}$ is the unique ring morphism taking $\zeta _m$ to $\zeta _m^c$.

2.2 Upper bounds

One has $\mathord {\left| {\zeta _m}\right| }=1$, so $\mathord {\left| {\alpha }\right| }\le \sum _j \mathord {\left| {\alpha _j}\right| }\le \sum _j \alpha _j^2=w$. (For $w>n$, one can do better by replacing the inequality $\sum _j\mathord {\left| {\alpha _j}\right| }\le w$ with Cauchy’s inequality $\sum _j\mathord {\left| {\alpha _j}\right| }\le n^{1/2}w^{1/2}$; but the case of interest in Sect. 5 is that w is asymptotically bounded by $n^{1/2+o(1)}$.) More generally, $\mathord {\left| {\zeta _m^c}\right| }=1$, so $\mathord {\left| {\sigma _c(\alpha )}\right| }\le w$. Hence $\mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| } =\prod _{c\in \mathord {\left\{ {1,3,5,\dots ,m-1}\right\} }}\mathord {\left| {\sigma _c(\alpha )}\right| } \le w^n$.

2.3 The circular approximation to the distribution

If $w=1$ then the above upper bound is achieved, but for larger w one expects $\sigma _c(\alpha )=\sum _j \alpha _j\zeta _m^{cj}$ to have summands $\alpha _j\zeta _m^{cj}$ pointing in different directions in $\mathord {{\mathbb {C}}}$, usually with sum considerably smaller than the upper bound.

Define the circular approximation to the distribution of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ as a normal distribution with mean $n(\log w-\gamma )/2\approx n(\log w)/2-0.28860783245n$, where $\gamma$ is Euler’s constant, and variance $n\pi ^2/24\approx 0.411233516712n$. Notice that this mean is under half of the upper bound $n\log w$ from Sect. 2.2, although the ratio converges up to 1/2 as $w\rightarrow \infty$. The following paragraphs explain how the circular approximation arises from a heuristic analysis of the size of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$.

The first step is to model each $\sigma _c(\alpha )$ as $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$ where each $\rho _{c,j}$ is an independent uniform random element of $\mathord {{\mathbb {R}}}/\mathord {{\mathbb {Z}}}$. The distribution of $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$ is invariant under rotation; the basic strategy here is to recover this distribution from its real part.

To analyze the real part of $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$, note that the variance of $\cos 2\pi \rho$ for uniform random $\rho \in \mathord {{\mathbb {R}}}/\mathord {{\mathbb {Z}}}$ is $\int _0^1(\cos 2\pi \rho )^2\,d\rho =1/2$. The variance of $\sum _j \alpha _j\cos 2\pi \rho _{c,j}$ is $\sum _j \alpha _j^2/2=w/2$ since, by independence, the summands are uncorrelated.

Now apply the heuristic that sums are normally distributed to conclude that $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$ has a complex normal distribution with mean 0 and variance v for some v. By definition of the complex normal distribution, the real and imaginary parts are independent normal random variables with variance v/2, so $v=w$.

If N is a complex normal random variable with mean 0 and variance 1 then $\log \mathord {\left| {N}\right| }$ has mean $-\gamma /2\approx -0.28860783245$ and variance $\pi ^2/24\approx 0.411233516712$. If N is a complex normal random variable with mean 0 and variance w then $\log \mathord {\left| {N}\right| }$ has mean $(\log w-\gamma )/2$ and variance $\pi ^2/24$. If $N_1,\dots ,N_n$ are n uncorrelated complex normal random variables with mean 0 and variance w then $\log \mathord {\left| {N_1\cdots N_n}\right| }$ has mean $n(\log w-\gamma )/2$ and variance $n\pi ^2/24$. Finally, the sums-are-normally-distributed heuristic says that $\log \mathord {\left| {N_1\cdots N_n}\right| }$ is normally distributed.

2.4 Objections to the heuristics

As m increases, the powers $\zeta _m^c$ for uniform random $c\in \mathord {\left\{ {1,3,\dots ,m-1}\right\} }$ approach a uniform distribution on the unit circle in the following sense: for each arc A of the circle, $\lim _{m\rightarrow \infty }\Pr [\zeta _m^c\in A]$ is the fraction of the circle contained in A. The same argument applies to $\zeta _m^{cj}$ for any odd j. One can object, however, that this argument breaks down as more and more powers of 2 appear in j: as an extreme case, $\zeta _m^{cj}$ is always 1 for $j=0$. If w is small then there is a noticeable chance that $\alpha \in F$ for a proper subfield $F\subset K$, and then ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha =({\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}\alpha )^{\deg _F K}$, with distribution determined by the distribution of ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}\alpha$. (For the application to recognizing S-units, one can save time in these cases by simply computing ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}\alpha$ and checking its factorization.)

Even for odd j, one can object to modeling $\zeta _m^{cj}$ as pointing in independent directions as the pair (c, j) varies. For example, if $j'=j+m/4$, then the ratio $\zeta _m^{cj'}/\zeta _m^{cj}=\zeta _m^{c(j'-j)}=i^c$ is limited to the set $\mathord {\left\{ {i,-i}\right\} }$. If $\alpha \in \zeta _m F$ for a proper subfield $F\subset K$ then ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha =({\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}(\alpha /\zeta _m))^{\deg _F K}$, again with distribution determined by the ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}$ output distribution.

Furthermore, even with the uniform random directions in $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$, one can object to the heuristic of treating this sum as having a normal distribution—especially when w is small, since there are at most w nonzero summands. One can similarly object to treating $\log \mathord {\left| {N_1\cdots N_n}\right| }$ as having a normal distribution. The sums-are-normally-distributed heuristic is only a crude approximation to the central-limit theorem.

One could, with more work, remove the sums-are-normally-distributed heuristic in favor of the following computations:

• Compute the distribution of $\sum _j \alpha _j\cos 2\pi \rho _{c,j}$ by convolving scaled cosine distributions. A complication here is that one needs to combinatorially enumerate possibilities for $\#\mathord {\left\{ {j:\mathord {\left| {\alpha _j}\right| }=1}\right\} }$, $\#\mathord {\left\{ {j:\mathord {\left| {\alpha _j}\right| }=2}\right\} }$, etc.; but, for large n and relatively small w, the probabilities are dominated by the first few possibilities, those where $\mathord {\left| {\alpha _j}\right| }$ is rarely above 1.

• Recover the rotationally invariant distribution of $\sum _j \alpha _j\exp 2\pi i\rho _{c,j}$ from the distribution of $\sum _j \alpha _j\cos 2\pi \rho _{c,j}$. The point is that any rotationally invariant random variable can be written in polar coordinates as $r\exp 2\pi i\tau$ where $\tau$ is a uniform random element of $\mathord {{\mathbb {R}}}/\mathord {{\mathbb {Z}}}$ independent of r; so take the distribution of the real part $r\cos 2\pi \tau$, compute the Mellin transform of the density function, divide by the Mellin transform of the density function of $\cos 2\pi \tau$, and compute an inverse Mellin transform to obtain the density function of r. (As noted by Epstein [43], multiplying independent random variables corresponds to multiplying Mellin transforms of density functions.)

• Compute the distribution of $\log \mathord {\left| {N_1\cdots N_n}\right| }$ as a convolution of n copies of the r distribution.

But this still would not handle the actual directions of $\zeta _m^{cj}$.

One can also object that the circular approximation to $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ cannot be exactly correct: for each (n, w), the distribution of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ is discrete, while a normal distribution is continuous; also, $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ is bounded between 0 and $n\log w$, whereas a normal distribution is unbounded.

2.5 Numerical evidence

Table 1 presents, for various choices of (m, w), the mean and variance of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ across two sets of 65536 experiments. The set where “double” is “yes” chooses $\alpha$ uniformly at random from weight-w elements where $\mathord {\left| {\alpha _0}\right| }=2$ and $\mathord {\left| {\alpha _j}\right| }\in \mathord {\left\{ {-1,0,1}\right\} }$ for all other j. The set where “double” is “no” instead takes weight-w elements where $\mathord {\left| {\alpha _j}\right| }\in \mathord {\left\{ {-1,0,1}\right\} }$ for all j.

Table 1 Mean and variance of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ for 65,536 random choices of $\alpha$ in each line. See text for details

Fig. 1

Sage script for experiments used in Table 1

Fig. 2

Rows, top to bottom: m is 64, 128, 256, 512, 1024. Columns, left to right: w is 8, 16, 32, 64. Blue curve in each graph: sorted values of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ for 65536 random choices of $\alpha$. Black curve: circular approximation. Vertical scale: circular $\pm 4\sigma$

These experiments were carried out with the Sage script shown in Fig. 1. The script uses deterministic seeds for reproducibility. The multicore.py used in the script is from [1]. The script also checks the integrals that account for the appearance of $\gamma /2$ and $\pi ^2/24$ in this section.

Table 1 suggests that the actual mean divided by n is always larger than the circular approximation $(\log w-\gamma )/2$, with a gap of roughly $1/4\,m+1/8w$ for the non-double cases, converging down to 0 as m and w jointly increase. The variance divided by n is consistently below the circular approximation $\pi ^2/24$, indicating an anti-correlation not captured by the approximation.

Figure 2 plots the distribution (as a transposed cdf) of $\log \mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ observed in the same non-double experiments (blue curve), and, for comparison, plots the circular approximation (black curve). Both curves are on a vertical scale chosen so that the circular approximation runs from 4 standard deviations below the mean to 4 standard deviations above the mean, so the circular approximation always has the same visual shape; note that this scale covers an interval of length only $8\sqrt{n\pi ^2/24}$ within the interval $[0,n\log w]$.

3 Quadratic techniques

This section reviews various standard algorithms that, for arbitrary number fields K, evaluate $\alpha \mapsto {\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. This section analyzes the cost of these algorithms applied to power-of-2 cyclotomics $K=\mathord {{\mathbb {Q}}}(\zeta _m)$, specifically for the scenario motivated in Sect. 2: namely, $\alpha$ is a nonzero element of $\mathord {{\mathbb {Z}}}[\zeta _m]$ of weight $n^{1/2+o(1)}$ where $n=m/2$, and ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ has $\Theta (n\log n)$ bits.

In short, the modular continued-fraction approach costs $n^2(\log n)^{3+o(1)}$ bit operations, although there are occasional inputs $\alpha$ where a factor $\log n$ disappears because of a short remainder sequence. The complex-embeddings approach costs $n^2(\log n)^{2+o(1)}$ bit operations.

3.1 Why resultant computation is so slow, part 1: big integers

Recall that the Euclid–Stevin algorithm to compute polynomial gcd repeatedly replaces (f, g) with $(g,f\bmod g)$ as long as $g\ne 0$. Tracking degrees and leading coefficients of the remainders $f,g,f\bmod g,\dots$ reveals the resultant. The point here is that

$$\begin{aligned} {\text {resultant}}(f,g)=(-1)^{(\deg f)\deg g} ({\text {leadcoeff}}g)^{\deg f-\deg (f\bmod g)}{\text {resultant}}(g,f\bmod g) \end{aligned}$$

if $g\ne 0$ and $f\bmod g\ne 0$. There are two base cases: one has ${\text {resultant}}(f,g)=g^{\deg f}$ if $\deg g=0$, and one has ${\text {resultant}}(f,g)=0$ if $\deg g>0$ and $f\bmod g=0$.

If $\deg f=n>\deg g$ then the remainder sequence $f,g,f\bmod g,\dots$ inside the Euclid–Stevin algorithm has $O(n^2)$ coefficients and the quotient sequence $\mathord {\left\lfloor {f/g}\right\rfloor },\dots$ has O(n) coefficients. One can compute the quotient sequence in time at most $n(\log n)^{2+o(1)}$; see, e.g., [16, Sections 21–22]. Given n and the quotient sequence, one can compute the sequence of remainder degrees, the sequence of remainder leading coefficients, and the resultant. The total time is at most $n(\log n)^{2+o(1)}$.

However, one must be careful with the concept of “time” used in the previous paragraph. This is actually a count of operations in the base field: operations in $\mathord {{\mathbb {Q}}}$, if the goal is to compute a resultant of polynomials with coefficients in $\mathord {{\mathbb {Q}}}$.

If one takes $f=x^{1024}+1$ and $g=4x^{828}+x^{271}+3$ then there are 211 Euclid–Stevin quotients. The 100th quotient is a polynomial whose coefficients have more than 100,000 bits in each numerator and denominator. The final quotient is a linear polynomial whose coefficients have more than 400,000 bits in each numerator and denominator. The cost of computing these quotients is driven much more by the number of bits than by the number of coefficients.

Collins [36] showed that simply rescaling the Euclid–Stevin remainders produces polynomials with much smaller coefficient bounds. These polynomials are called “subresultants”: their coefficients are determinants of various portions of Sylvester’s resultant matrix. The determinant description shows that the subresultants are in $\mathord {{\mathbb {Z}}}[x]$ when $f,g\in \mathord {{\mathbb {Z}}}[x]$. The bounds in [36] on the coefficients of subresultants come from applying Hadamard’s determinant inequality to bounds on the coefficients of f and g.

One still cannot escape some growth of coefficients. For example, recall that the resultant of $f=x^{1024}+1$ and $g=4x^{828}+x^{271}+3$ has 2048 bits. This growth is not something that suddenly appears at the last moment in the subresultant algorithm: most algorithm steps are, for almost all inputs, working with large integers.

A subsequent paper by Collins [37] suggested a modular approach to computing ${\text {resultant}}(f,g)$ given $f,g\in \mathord {{\mathbb {Z}}}[x]$. If one assumes schoolbook arithmetic then the modular approach gives better cost bounds than the subresultant approach; this comparison appears in, e.g., [86, page 449, top paragraph]. Perhaps fast arithmetic would narrow the gap, but evaluating this would require developing a variant of fast-continued-fraction algorithms that controls coefficient sizes, and the literature does not give any reason to think that this effort would end up with a faster algorithm than the modular approach. So let’s look at the performance of the modular approach.

3.2 Why resultant computation is so slow, part 2: many moduli

The modular approach reconstructs ${\text {resultant}}(f,g)$ from the image of ${\text {resultant}}(f,g)$ in $\mathord {{\mathbb {F}}}_p$ for enough primes p. This image is the same as the resultant of the images of f, g in $\mathord {{\mathbb {F}}}_p[x]$, as long as one avoids “bad” primes p, meaning primes that divide the leading coefficients of f and g.

How does one figure out how many primes are enough? One answer is to use Hadamard’s inequality to quickly bound the resultant. Another answer, suggested by Monagan [71], is to guess that a few primes suffice, then more primes, and so on, stopping when the output is sufficiently stable; this fails with negligible probability if there is enough randomness in the primes. The Sage resultant documentation says that proof=False “may use a randomized strategy that errors with probability no more than $2^{-80}$”.

In the scenario studied in this section, ${\text {resultant}}(f,g)$ has $\Theta (n\log n)$ bits. One can simply choose primes having enough bits for the explicit upper bounds from Sect. 2.2, although the analysis of Sect. 2 suggests that one can usually save a factor above 2 by tuning the number of primes appropriately. Either way, $\prod _p p$ has $\Theta (n\log n)$ bits. The following analysis concludes that the modular approach then costs $n^2(\log n)^{3+o(1)}$, provided that one takes each $\log \log p$ in $(\log n)^{o(1)}$.

Note first that one can take each $\log \log p$ in $(\log n)^{o(1)}$. For example, choose a parameter y, and take all odd primes $p\le y$. By the prime-number theorem, $\prod _{p\le y} p$ reaches the desired $\Theta (n\log n)$ bits for a suitable choice of $y\in \Theta (n\log n)$. One has to skip bad primes, but one can compensate by multiplying $1+\mathord {\left| {{\text {leadcoeff}}fg}\right| }$ into the target for $\prod _{p\le y}p$; the limited coefficient size for f and g implies that the target still has $\Theta (n\log n)$ bits. Now each $p\in O(n\log n)$, implying $\log \log p\in (\log n)^{o(1)}$. There is considerable slack in this argument: one can take much larger p and still have $\log \log p\in (\log n)^{o(1)}$.

Each continued-fraction computation in $\mathord {{\mathbb {F}}}_p[x]$ involves at most $n(\log n)^{2+o(1)}$ operations in $\mathord {{\mathbb {F}}}_p$ (including initial reduction of f and g modulo p; f and g have small coefficients, so one does not need to batch this reduction across p). The cost of each operation in $\mathord {{\mathbb {F}}}_p$ is at most $(\log p)(\log \log p)^{1+o(1)}$, i.e., $(\log p)(\log n)^{o(1)}$, and summing across all p gives $n(\log n)^{1+o(1)}$ since $\sum _p \log p\in \Theta (n\log n)$. The total cost is thus at most $n^2(\log n)^{3+o(1)}$.

Could the cost actually be lower than this? Strassen [92] pointed out that one $\log n$ factor in the cost of continued-fraction computation actually arises as the entropy of the list of quotient degrees in the Euclid–Stevin algorithm. The case of sparse f and sparse g should not be confused with the “normal” case of all quotient degrees 1 (for example, if $f=x^{1024}+1$ and $g=x^{999}+x+1$ then there are just 28 divisions), but experiments suggest that the entropy is usually $\Theta (\log n)$ once g has at least 3 terms.

3.3 Complex embeddings

Another way to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for any degree-n number field K and any $\alpha \in K$ is as $\prod _{\sigma } \sigma (\alpha )$, where $\sigma$ runs through all ring morphisms $K\rightarrow \mathord {{\mathbb {C}}}$. If each complex number $\sigma (\alpha )$ is represented as a floating-point number with $\Theta (n\log n)$ bits of precision then the product $\prod _{\sigma } \sigma (\alpha )$ also has $\Theta (n\log n)$ bits of precision—the $n-1$ multiplications lose, in total, just $\Theta (\log n)$ bits of precision—and if the $\Theta$ constant is adjusted appropriately then this is enough precision to recover the integer ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$.

Belabas [10, Section 5.2] recommended using complex embeddings to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ whenever ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is “relatively small”. The following paragraphs quantify the cost of this approach, including the quantification from [10] but also including speedups beyond [10].

The input $\alpha \in K$ is given in what Cohen [34, Section 4.2] calls the “standard representation” of K: $\alpha$ is represented as a polynomial $g\in \mathord {{\mathbb {Z}}}[x]$ with $g(\theta )=\alpha$ and $\deg g<\deg K$. Here $\theta$ is a fixed integral primitive element of K, a root of a monic irreducible polynomial $f\in \mathord {{\mathbb {Z}}}[x]$; one can think of the complex-embedding approach as another way of computing ${\text {resultant}}(f,g)$. For the power-of-2-cyclotomic case $K=\mathord {{\mathbb {Q}}}(\zeta _m)$, one takes $\theta =\zeta _m$ and $f=x^n+1$.

The first step is to compute $\sigma (\alpha )=g(\sigma (\theta ))$ for each embedding $\sigma$. Belabas views this as multiplying the vector of coefficients of g by a precomputed matrix with complex entries $\sigma (1),\sigma (\theta ),\sigma (\theta ^2),\dots$; this is, e.g., the matrix of powers $\zeta _m^{cj}$ in the case of power-of-2 cyclotomics, where c runs through $\mathord {\left\{ {1,3,\dots ,m-1}\right\} }$. Belabas says that this multiplication costs $O(n^2 M(B))$ where n is the field degree, B is the number of bits of precision required, and M(B) is the cost of B-bit multiplication.

Three speedups noted in [10] are as follows. First, often one already knows a divisor of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, so one can reduce the required precision accordingly. Second, in multiplying complex numbers to obtain ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, one should begin by multiplying the numbers for complex-conjugate $\sigma$, so that subsequent multiplications are in $\mathord {{\mathbb {R}}}$; see Sect. 3.4 below. Third, low-precision complex computations suffice to determine the approximate value of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$, pinpointing how much precision is required for an exact computation—in particular, recognizing cases where ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is unusually small. (One can also use this to avoid the guesswork described above regarding how many primes are required for a modular computation of a resultant.)

Beware that small ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ does not immediately imply that small B suffices: if any particular $\sigma (\alpha )$ is close to 0 then the precision obtained for $\sigma (\alpha )$ is lower than the initial precision of $\sigma (1),\sigma (\theta ),\sigma (\theta ^2),\dots$, so one needs to recompute $\sigma (\alpha )$ in higher precision. The main case of interest in this section is that ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ has $\Theta (n\log n)$ bits, and then one can see that $B\in \Theta (n\log n)$ suffices as follows: each $\mathord {\left| {\sigma (\alpha )}\right| }$ is $n^{O(1)}$ as in Sect. 2.2, but $\mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ is at least 1 (since $\alpha \ne 0$), so each $\mathord {\left| {\sigma (\alpha )}\right| }$ is at least $1/n^{O(n)}$. So assume $B\in \Theta (n\log n)$; the $n^2 M(B)$ from [10] is then $n^3(\log n)^{2+o(1)}$.

An asymptotically better way to compute $g(\sigma (\theta ))$ for all $\sigma$, not noted in [10], is by multipoint evaluation, precomputing a tree of products of $x-\sigma (\theta )$ and then computing a tree of remainders of g modulo those products. Schönhage [84, Section 2] used segmentation to reduce multiplication in $\mathord {{\mathbb {C}}}[x]$ to multiplication in $\mathord {{\mathbb {Z}}}$, obtaining a cost bound $nB(\log nB)^{1+o(1)}$ for n-coefficient polynomials with B bits in each coefficient and all coefficients on the same scale; this cost bound is $n^2(\log n)^{2+o(1)}$ for $B\in \Theta (n\log n)$. Schönhage [84, Section 4] obtained the same cost bound for division in $\mathord {{\mathbb {C}}}[x]$, assuming that one is dividing by polynomials whose roots in $\mathord {{\mathbb {C}}}$ are O(1). A multipoint-evaluation tree has $\Theta (\log n)$ layers, for total cost $n^2(\log n)^{3+o(1)}$.

A particularly efficient form of remainder tree is an FFT tree—exactly what is needed here, since K is assumed to be a power-of-2 cyclotomic. Even simpler than building a tree is using Bluestein’s trick from [24, 25] to reduce DFT to convolution. Schönhage [84, Section 3] used Bluestein’s trick to obtain a cost bound $nB(\log nB)^{1+o(1)}$ for a size-n DFT with B bits of precision; i.e., cost $n^2(\log n)^{2+o(1)}$ for $B\in \Theta (n\log n)$.

The subsequent $n-1$ multiplications of $\sigma (\alpha )$ values, each to B bits of precision, cost $nB(\log B)^{1+o(1)}$. If $B\in \Theta (n\log n)$ then the overall cost is $n^2(\log n)^{2+o(1)}$. This is, for most inputs, asymptotically better than the continued-fraction approach: it avoids an extra $(\log n)^{1+o(1)}$ factor.

3.4 Complex conjugation on complex embeddings

As noted above, inside the complex-embeddings approach, Belabas suggested first multiplying complex-conjugate pairs of complex numbers. In the $3+\zeta _{2048}^{271}+4\zeta _{2048}^{828}$ example, this means computing the real number $(3+\zeta _{2048}^{271c}+4\zeta _{2048}^{828c}) (3+\zeta _{2048}^{-271c}+4\zeta _{2048}^{-828c})$ for each pair $\mathord {\left\{ {c,-c}\right\} }$. Then the subsequent multiplications are multiplications in $\mathord {{\mathbb {R}}}$, which, for any given precision, one expects to be at least twice as fast as multiplications in $\mathord {{\mathbb {C}}}$.

A $2\times$ speedup is not visible at the level of detail of the analyses in this section. However, it is useful to consider what this speedup is accomplishing algebraically, for comparison to the transitivity of determinants exploited in Sect. 4.

The original problem is to evaluate ${\text {det}}^{\mathord {{\mathbb {Q}}}[x]/f}_{\mathord {{\mathbb {Q}}}}$. Complex embeddings tensor with $\mathord {{\mathbb {C}}}$ over $\mathord {{\mathbb {Q}}}$, reducing the original problem to the problem of evaluating ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/f}_{\mathord {{\mathbb {C}}}}$. The ring $\mathord {{\mathbb {C}}}[x]/f$ factors as $\prod _c \mathord {{\mathbb {C}}}[x]/(x-\zeta _m^c)$, and ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/f}_{\mathord {{\mathbb {C}}}}$ factors correspondingly as $\prod _c {\text {det}}^{\mathord {{\mathbb {C}}}[x]/(x-\zeta _m^c)}_{\mathord {{\mathbb {C}}}}$. The image in $\mathord {{\mathbb {C}}}[x]/(x-\zeta _m^c)$ of $g\in \mathord {{\mathbb {C}}}[x]/f$ is simply $g(\zeta _m^c)$, with determinant $g(\zeta _m^c)$. Multiplying these n complex numbers $g(\zeta _m^c)$ produces the desired ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/f}_{\mathord {{\mathbb {C}}}}g={\text {det}}^{\mathord {{\mathbb {Q}}}[x]/f}_{\mathord {{\mathbb {Q}}}}g$.

The complex-conjugation speedup instead tensors with $\mathord {{\mathbb {R}}}$ over $\mathord {{\mathbb {Q}}}$. The ring $\mathord {{\mathbb {R}}}[x]/f$ factors as a product of rings $\mathord {{\mathbb {R}}}[x]/((x-\zeta _m^c)(x-\zeta _m^{-c}))$, and ${\text {det}}^{\mathord {{\mathbb {R}}}[x]/f}_{\mathord {{\mathbb {R}}}}g$ factors correspondingly as a product of ${\text {det}}^{\mathord {{\mathbb {R}}}[x]/((x-\zeta _m^c)(x-\zeta _m^{-c}))}_{\mathord {{\mathbb {R}}}}g$, exactly the real numbers multiplied above.

These real numbers, in turn, are computed as follows: tensor with $\mathord {{\mathbb {C}}}$ over $\mathord {{\mathbb {R}}}$, and then compute the desired ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/((x-\zeta _m^c)(x-\zeta _m^{-c}))}_{\mathord {{\mathbb {C}}}}g$ as the product of ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/(x-\zeta _m^c)}_{\mathord {{\mathbb {C}}}}g$ and ${\text {det}}^{\mathord {{\mathbb {C}}}[x]/(x-\zeta _m^{-c})}_{\mathord {{\mathbb {C}}}}g$, i.e., the product of $g(\zeta _m^c)$ and $g(\zeta _m^{-c})$. One can, alternatively, suppress the role of $\mathord {{\mathbb {C}}}$ here: reduce g modulo $(x-\zeta _m^c)(x-\zeta _m^{-c})\in \mathord {{\mathbb {R}}}[x]$ and directly compute a determinant down to $\mathord {{\mathbb {R}}}$.

3.5 Complex conjugation on the original field

Complex conjugation was used above as an automorphism of $\mathord {{\mathbb {C}}}$ with fixed field $\mathord {{\mathbb {R}}}$. A different way to use complex conjugation is to restrict it to the field $K=\mathord {{\mathbb {Q}}}(\zeta _m)$. This restriction is an easy-to-compute automorphism of K, namely the ring morphism that maps $\zeta _m$ to $\zeta _m^{-1}$. The corresponding automorphism $x\mapsto x^{-1}$ of $\mathord {{\mathbb {Q}}}[x]/f$ maps $1,x,x^2,x^3,\dots ,x^{n-1}$, the usual basis for $\mathord {{\mathbb {Q}}}[x]/f$ as a $\mathord {{\mathbb {Q}}}$-vector space, to $1,-x^{n-1},-x^{n-2},-x^{n-3},\dots ,-x$ respectively. This automorphism is an easy linear map to apply.

The field $\mathord {{\mathbb {R}}}\cap K$ is the fixed field of complex conjugation on K, since $\mathord {{\mathbb {R}}}$ is the fixed field of complex conjugation on $\mathord {{\mathbb {C}}}$. This field $\mathord {{\mathbb {R}}}\cap K$ has degree n/2 if $m\ge 4$, with $\mathord {{\mathbb {Q}}}$-basis $1,\zeta _m+\zeta _m^{-1},\zeta _m^2+\zeta _m^{-2},\dots ,\zeta _m^{n/2-1}+\zeta _m^{-(n/2-1)}$. The corresponding subfield F of $\mathord {{\mathbb {Q}}}[x]/f$ has $\mathord {{\mathbb {Q}}}$-basis $1,x-x^{n-1},x^2-x^{n-2},\dots ,x^{n/2-1}-x^{n/2+1}$. This is the subfield of $\mathord {{\mathbb {Q}}}[x]/f$ fixed by the automorphism $x\mapsto x^{-1}$ of $\mathord {{\mathbb {Q}}}[x]/f$; the latter automorphism is also called complex conjugation.

Given $g\in \mathord {{\mathbb {Q}}}[x]/f$, write h for the product of g and its complex conjugate $g(x^{-1})$. Then $h={\text {det}}^{\mathord {{\mathbb {Q}}}[x]/f}_{F}g\in F$. One can use transitivity of determinants to compute ${\text {det}}^{\mathord {{\mathbb {Q}}}[x]/f}_{\mathord {{\mathbb {Q}}}}g$ as ${\text {det}}^{F}_{\mathord {{\mathbb {Q}}}}h$, which in turn is a product of various values $h(\zeta _m^c)=g(\zeta _m^c)g(\zeta _m^{-c})$.

This is the same as the product of $g(\zeta _m^c)g(\zeta _m^{-c})$ values in Sect. 3.4. The difference is in how the values $g(\zeta _m^c)g(\zeta _m^{-c})$ are computed: as ${\text {det}}^{\mathord {{\mathbb {C}}}}_{\mathord {{\mathbb {R}}}}g(\zeta _m^c)$, or as a real embedding $h(\zeta _m^c)$ of $h={\text {det}}^{\mathord {{\mathbb {Q}}}[x]/f}_{F}g$.

Beware that subfields of general number fields do not capture the full power of multiplying complex conjugates. For example, the field $\mathord {{\mathbb {Q}}}(\root 3 \of {2})$ is isomorphic to $\mathord {{\mathbb {Q}}}[x]/(x^3-2)$ and has no subfields other than $\mathord {{\mathbb {Q}}}$ and itself; but tensoring with $\mathord {{\mathbb {C}}}$ produces $\mathord {{\mathbb {C}}}[x]/(x^3-2)$, which has two complex-conjugate factors. Conversely, multiplying complex conjugates does not capture the full power of subfields; see Sect. 4.

3.6 More morphisms

A common theme in computational number theory is avoiding the hassle of Archimedean precision tracking by switching to the p-adics for a suitable prime p, or a product of p-adics.

Let p be a prime number that is totally split in K, i.e., a prime number for which f has n distinct roots in $\mathord {{\mathbb {F}}}_p$. One can rapidly recognize this case by seeing that $x^p-x$ modulo f is 0. Standard root-finding algorithms—or multipoint evaluation of f on $\mathord {{\mathbb {F}}}_p$ if p is small—then find the roots. One can do even better for special types of f: in particular, for $K=\mathord {{\mathbb {Q}}}(\zeta _m)$, one can take any prime number $p\in 1+m\mathord {{\mathbb {Z}}}$, and there are very fast algorithms to find all primitive mth roots of 1 in $\mathord {{\mathbb {F}}}_p$.

The set of ring morphisms $x\mapsto \rho$ from $\mathord {{\mathbb {Z}}}[x]/f$ to $\mathord {{\mathbb {F}}}_p$, as $\rho$ runs through roots of f in $\mathord {{\mathbb {F}}}_p$, is analogous to the set of complex embeddings $\sigma$ used above. Evaluating all these ring morphisms on a given input $g\in \mathord {{\mathbb {Z}}}[x]/f$ is a simple matter of multipoint evaluation, assuming the roots have been precomputed; the vector of outputs can be viewed as a limited-precision representation of the input. The product of outputs is the image in $\mathord {{\mathbb {F}}}_p$ of ${\text {det}}^{\mathord {{\mathbb {Z}}}[x]/f}_{\mathord {{\mathbb {Z}}}}g={\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}g(\theta )$, where as before $\theta$ is a root of f in K. Repeating for enough primes p (or one large enough p or any intermediate possibility) then determines ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}g(\theta )$.

Overall this approach has similar asymptotics to the continued-fraction approach. Montgomery noted in [72, Section 4.2] that remainder trees seem to be a constant factor more efficient than continued-fraction computations for most inputs.

More generally, to compute ${\text {resultant}}(f,g)$ where f has a known factorization, one can use a remainder tree to reduce g modulo each factor, and then compute ${\text {resultant}}(f,g)$ as a corresponding product. Whether one should take the time to search for factors of f (or for primes p where f factors better) is a different question: this depends on the distribution of f and on how often f will be reused for resultants. In the applications motivating this paper (see Sect. 5), ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ is evaluated on many inputs in K, so many K-dependent precomputations are worthwhile.

3.7 The Galois case: exploiting automorphisms

Another convenient field where f splits completely is K itself—assuming that K is Galois.

Say $f=(x-\rho _1)\cdots (x-\rho _n)$ in K[x]. One can evaluate $g(\rho _1),\dots ,g(\rho _n)$ with a remainder tree, and then use a product tree to compute the product $g(\rho _1)\cdots g(\rho _n)$, which is exactly ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}g(\theta )$.

In the case of a power-of-2 cyclotomic $K=\mathord {{\mathbb {Q}}}(\zeta _m)$, one has $\mathord {\left\{ {\rho _1,\dots ,\rho _n}\right\} }=\mathord {\left\{ {\zeta _m,\zeta _m^3,\dots ,\zeta _m^{m-1}}\right\} }$ with $n=m/2$, since $x^n+1=(x-\zeta _m)(x-\zeta _m^3)\cdots (x-\zeta _m^{m-1})$. Computing $g(\zeta _m^c)$ is simply rearranging and negating coefficients. There are still n choices of c, with n coefficients to handle for each c, and then more work is required for a product.

Consider a 4-factor product $g(\rho _1)g(\rho _2)g(\rho _3)g(\rho _4)$. By assumption g has weight $n^{1/2+o(1)}$, so one expects the maximum coefficient of this product to have $\Theta (\log n)$ bits, so computing this product costs $n(\log n)^{2+o(1)}$. There are $\Theta (n)$ such products, together costing $n^2(\log n)^{2+o(1)}$. There are then $\Theta (\log n)$ layers in the product tree, but one can achieve total cost $n^2(\log n)^{2+o(1)}$ by arranging the tree to have inputs in $\mathord {{\mathbb {Q}}}(\zeta _4)$ for the final multiplication, $\mathord {{\mathbb {Q}}}(\zeta _8)$ for the multiplications on the previous layer, etc.

This approach is using some of the structure that will be exploited in Sect. 4, but still costs $n^{2+o(1)}$ because of the computations—and then multiplications—of n different conjugates of the input.

4 Linear techniques

The fast ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computation in Sect. 1 started with an element $\alpha$ of a power-of-2 cyclotomic field $K=\mathord {{\mathbb {Q}}}(\zeta _{m})$ with m/2 small coefficients, computed a product $\beta =\alpha \sigma (\alpha )$ in $\mathord {{\mathbb {Q}}}(\zeta _{m/2})$ with m/4 double-size coefficients, computed a product $\beta \tau (\beta )$ in $\mathord {{\mathbb {Q}}}(\zeta _{m/4})$ with m/8 quadruple-size coefficients, etc. The amount of data at each layer is essentially linear—unlike the techniques in Sect. 3, which expand each of the m/2 input coefficients to a volume of data comparable to the number of output bits. This section explores the question of how general this speedup is.

4.1 Towers

Consider any tower $\mathord {{\mathbb {Q}}}=K_0\subseteq K_1\subseteq \cdots \subseteq K_t$ of number fields, with absolute degrees $n_0,n_1,\dots ,n_t$ and relative degrees $d_1,\dots ,d_t$. Then $n_0=1$, $n_1=d_1$, $n_2=d_1d_2$, and so on through $n_t=d_1d_2\cdots d_t$. For simplicity assume $d_j\ge 2$ for all j, eliminating trivial steps in the tower.

Consider an algorithm that, given $\alpha \in K_t$, computes successively

$$\begin{aligned} \begin{aligned} \alpha _t&={\text {det}}^{K_t}_{K_t}\alpha&\hbox {as }&\alpha ,\\ \alpha _{t-1}&={\text {det}}^{K_t}_{K_{t-1}}\alpha&\hbox {as }&{{\text {det}}^{K_t}_{K_{t-1}}\alpha _t},\\ \alpha _{t-2}&={\text {det}}^{K_t}_{K_{t-2}}\alpha&\hbox {as }&{{\text {det}}^{K_{t-1}}_{K_{t-2}}\alpha _{t-1}},\\ \vdots \\ \alpha _{1}&={\text {det}}^{K_t}_{K_1}\alpha&\hbox {as }&{{\text {det}}^{K_{2}}_{K_{1}}\alpha _{2}},\\ \alpha _{0}&={\text {det}}^{K_t}_{K_0}\alpha ={\text {det}}^{K_t}_{\mathord {{\mathbb {Q}}}}\alpha&\hbox {as }&{{\text {det}}^{K_{1}}_{K_{0}}\alpha _{1}}. \end{aligned} \end{aligned}$$

I’ll assume from now on that the desired input field K is exactly $K_t$, so the output $\alpha _0$ is ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. Also write $n=n_t$.

(One could, more generally, take K to be any subfield of $K_t$. If $\alpha \in K$ then one can compute $\pm {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }$ as $\alpha _0^{1/e}$ where $e=(\deg K_t)/{\deg K}$. The sign of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is clear if e is odd; one can use low-precision complex embeddings to recover the sign in the general case, if the sign matters for the application. However, so far I haven’t found any cases where allowing $e>1$ saves time compared to reducing to the case $e=1$, i.e., replacing each $K_j$ with $K_j\cap K$, obtaining a tower for K.)

To analyze how costs scale, let’s postulate the following scenario: each $\alpha _j$ has $O(n\log n)$ bits across its $n_j$ coefficients, with $O((n/n_j)\log n)$ bits in each coefficient; $\alpha _j$ has $\Theta (n\log n)$ bits whenever $n_j<n/2$; $\alpha _0$ has $\Theta (n\log n)$ bits. The idea that this is a typical scenario is an extrapolation from Sect. 2.

One might now hypothesize, extrapolating from Sect. 3, that computing $\alpha _{j-1}$ from $\alpha _j$ has cost growing as $d_j^2$ times the number of bits in $\alpha _{j-1}$ times $(\log n)^{e+o(1)}$, where $e=1$ for “FFT-friendly” choices of K and $e=2$ for other choices of K. The total cost in the above scenario is then at most $(d_1^2+\cdots +d_t^2)n(\log n)^{e+1+o(1)}$. (The only reason for saying “at most” under these hypotheses is that not all $\alpha _j$ are assumed to have $\Theta (n\log n)$ bits; in particular, $\alpha _t$ is merely assumed to have $O(n\log n)$ bits.)

The sum $d_1^2+\cdots +d_t^2$ is at least $tn^{2/t}$. It is exactly $tn^{2/t}$ if $d_1=\dots =d_t$. For example, it is $4\log _2 n$ if $d_1=\dots =d_t=2$; $8\log _2 n$ if $d_1=\dots =d_t=4$; and $64\log _2 n$ if $d_1=\dots =d_t=16$. On the other hand, it is $4(t-1)+n^2/4^{t-1}$ if $d_1=d_2=\cdots =d_{t-1}=2$ and $d_t=n/2^{t-1}$.

Define a smooth tower as one where $d_j\in (\log n)^{o(1)}$ for each j. This does not require t to grow as $\Theta (\log n)$: for example, one could have $d_j\in (\log n)^{\Theta (1/{\log \log \log n})}$ for each j, and $t\in \Theta ((\log n)(\log \log \log n)/{\log \log n})$. For a smooth tower, the total cost above—assuming the scenario described above, and assuming the hypothesized cost of each step of the computation—is $n(\log n)^{e+2+o(1)}$.

4.2 Why multiplication is perceived to be fast

Let’s see whether it’s possible to justify the above hypothesis regarding the cost of computing $\alpha _{j-1}$ from $\alpha _j$. Note that, for a smooth tower, $d_j^2$ is a minor cost factor, and larger powers of $d_j$ in the cost would contribute at most $(\log n)^{o(1)}$. The main cost factors to worry about are the $n_{j-1}$ coefficients in $\alpha _{j-1}$ and the number of bits per coefficient, typically giving $\Theta (n\log n)$ bits overall.

Consider the case that $K_j$ has the form $K_{j-1}(\sqrt{\delta })$, with $d_j=2$, where $\delta$ is a non-square in $K_{j-1}$. Write $\sigma$ for the unique automorphism of $K_j$ fixing $K_{j-1}$ and mapping $\sqrt{\delta }$ to $-\sqrt{\delta }$. Then $K_{j-1}$ is the fixed field of $\sigma$, and one can compute $\alpha _{j-1}$ as $\alpha _j\sigma (\alpha _j)$, as in the power-of-2-cyclotomic example in Sect. 1. How quickly can one multiply two elements of $K_j$, namely $\alpha _j$ and $\sigma (\alpha _j)$?

As in Sect. 3.3, let’s use the “standard representation” of a number field as $\mathord {{\mathbb {Q}}}[x]/\varphi$ for some monic irreducible polynomial $\varphi \in \mathord {{\mathbb {Z}}}[x]$, with elements of $\mathord {{\mathbb {Q}}}[x]/\varphi$ in turn expressed as elements of $\mathord {{\mathbb {Q}}}[x]$ of degree below $\deg \varphi$. One of the reasons for the popularity of this representation is that it reduces number-field computations to polynomial computations, which in turn are well known to have fast algorithms.

In particular, multiplying two elements of $\mathord {{\mathbb {Z}}}[x]/\varphi$—let’s not get distracted here by the possibility of integral elements having denominators in this representation—means multiplying two integer polynomials and then reducing the product modulo $\varphi$. There are well-known fast algorithms for each step, and it is easy to prove bounds on the output coefficients.

Specifically, let n and H be positive integers. The product of two n-coefficient polynomials $g,h\in \mathord {{\mathbb {Z}}}[x]$, with each coefficient of g, h in the interval $[-H,H]$, is a $(2n-1)$-coefficient polynomial with each coefficient in $[-nH^2,nH^2]$. One way to compute this product is by segmentation: multiply the integers $g(2^e)$ and $h(2^e)$ where $e=\mathord {\left\lfloor {\log _2(4nH^2)}\right\rfloor }$, and recover gh from $g(2^e)h(2^e)$. The integers $g(2^e)$ and $h(2^e)$ have $O(n\log 2nH)$ bits. Standard integer-multiplication algorithms take time essentially linear in $n\log 2nH$. This approach of combining segmentation with fast multiplication was used by Schönhage [84, Section 2], as noted in Sect. 3.

For reduction, one can multiply gh by a sufficiently precise approximation of the power series $1/\varphi \in \mathord {{\mathbb {Z}}}[[x^{-1}]]$, round down to obtain $\mathord {\left\lfloor {fg/\varphi }\right\rfloor }$, multiply by $\varphi$, and subtract from fg to obtain $fg\bmod \varphi$. All of this is fast when $\varphi$ and the approximation to $1/\varphi$ have small coefficients. For example, if $\varphi$ is the 1009th cyclotomic polynomial $(x^{1009}-1)/(x-1)$, then a sufficiently precise approximation to $1/\varphi$ is $x^{-1008}+x^{-1009}$. As a variant, rather than reducing gh after recovering it from $g(2^e)h(2^e)$, one can first reduce $g(2^e)h(2^e)$ modulo $\varphi (2^e)$ and then recover $gh\bmod \varphi$, provided that e is chosen large enough; see, e.g., [44, Proposition 1].

There are more details to fill in regarding the cost of computing $\sigma$, how to handle $d_j>2$, etc., but the above description might make it seem plausible that one can use any smooth tower for K to quickly compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. A closer look shows, however, that multiplication is not so easy.

4.3 The challenge of multiplying quickly in subfields

The computation at hand isn’t simply multiplying in one field $\mathord {{\mathbb {Q}}}[x]/\varphi$. It’s computing an element of a subfield of, say, half degree, and then continuing recursively with fast operations in that subfield.

Write $K=\mathord {{\mathbb {Q}}}[x]/\varphi$. Assume that $\theta \in K$ generates a subfield F with $\deg F=(\deg K)/2$. Write $\psi$ for the minimal polynomial of $\theta$, and write E for the field $\mathord {{\mathbb {Q}}}[y]/\psi$. The ring morphism $y\mapsto \theta$ from $\mathord {{\mathbb {Q}}}[y]$ to F induces an isomorphism from E to F. Applying the inverse of this isomorphism to ${\text {det}}^{K}_{F}g\in F$ produces an element of E, reducing the problem of evaluating ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ to the half-degree problem of evaluating ${\text {det}}^{E}_{\mathord {{\mathbb {Q}}}}$. But how fast is this inverse isomorphism?

Cohen’s second textbook [35, page 65, top paragraph] considers this problem (mentioning, as an example, taking a “relative trace or norm” from $\mathord {{\mathbb {Q}}}[x]/\varphi$ down to F and representing it as an element of $\mathord {{\mathbb {Q}}}[y]/\psi$) and suggests falling back to linear algebra, treating the isomorphism as a $\mathord {{\mathbb {Q}}}$-module isomorphism and inverting the matrix for this isomorphism.

Simply looking at the matrix inverse already involves a quadratic number of matrix entries. One might hope for a fast inversion method exploiting the structure of this matrix; but, no, the situation is even worse.

Take, for example, $\varphi =(x^{1009}-1)/(x-1)$, and consider the subfield F of $K=\mathord {{\mathbb {Q}}}[x]/\varphi$ generated by $x+1/x$. The minimal polynomial $\psi \in \mathord {{\mathbb {Q}}}[y]$ of $x+1/x$ is

$$\begin{aligned} \begin{aligned}&y^{504} + y^{503} - 503 y^{502} - \dots \\&{} - { \hbox {91728558855094562166903996595485819919819158847006587897135695049090346490842276029300596063250047752380 } }y^{226} \\&{} - \dots + 2667126 y^{3} - 31878 y^{2} - 252 y + 1 \end{aligned} \end{aligned}$$

with coefficients as large as 346 bits.

The effects that force large coefficients in this polynomial $\psi$ also force the inverse matrix mentioned above to have many large entries. The typical outputs of the inverse isomorphism are correspondingly large, no matter what method is used to compute them. Take, e.g., the small element $x^{500}+1/x^{500}=x^{500}+x^{509}$ of K. This has, under the isomorphism, preimage $2T_{500}(y/2)$ where $T_j$ is the jth Chebyshev polynomial of the first kind; 102 coefficients of this polynomial have more than 300 bits each, including 344-bit coefficients of $y^{220},y^{222},y^{224},y^{226}$.

To summarize, the elements of $\mathord {{\mathbb {Q}}}[y]/\psi$ being multiplied won’t normally have small coefficients, and $\psi$ doesn’t have small coefficients. This breaks multiple steps in the argument that arithmetic in this field is fast. If the original input $g\in \mathord {{\mathbb {Q}}}[x]/\varphi$ has very large coefficients, then there isn’t much impact from the extra size of $\psi$ etc., but the applications motivating this paper (see Sect. 5) start with very small coefficients.

4.4 The superfield representation

The inconvenience of working with “the standard representation” of a real-cyclotomic field $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)=\mathord {{\mathbb {Q}}}(\zeta _m+\zeta _m^{-1})$, such as working with $\mathord {{\mathbb {Q}}}[y]/\psi$ for the degree-504 polynomial $\psi$ shown above in the case $m=1009$, is not a new observation. The literature on computations in $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$ typically represents field elements as elements of the larger field $\mathord {{\mathbb {Q}}}(\zeta _{m})$, which in turn is represented as $\mathord {{\mathbb {Q}}}[x]/\Phi _m$ where $\Phi _m$ is the mth cyclotomic polynomial.

However, this representation is redundant, for example with only 504 degrees of freedom in the 1008 coefficients for $m=1009$. Multiplying elements represented in this way is correspondingly redundant. One cannot simply dismiss this effect as a constant-factor slowdown: if elements of a degree-$n_j$ field $K_j$ are represented as elements of a degree-$n_t$ field $K_t$ then there are $n_t/n_j$ times as many coefficients as desired, and $n_t/n_j$ can be on the scale of n.

4.5 Relative representations

Cohen’s second textbook includes a chapter [35, Chapter 2] on “basic relative number field algorithms”, saying [35, Section 2.1.1] that, compared to representing a number field L as an extension of $\mathord {{\mathbb {Q}}}$, representing L as an extension of a nontrivial subfield K is “usually preferable”. Two reasons stated in [35] for this preference are that

• the defining polynomial of L over K is of “lower degree” and

• “the K-structure on L gives considerably more arithmetical information than considering L on its own”.

For example, consider again the case that $K_j=K_{j-1}(\sqrt{\delta })$, where $\delta$ is a non-square in $K_{j-1}$. The $K_{j-1}$-relative representation of $K_j$ (to be more precise, of the pair $(K_j,\sqrt{\delta })$) is as $K_{j-1}[x]/(x^2-\delta )$: the polynomial $\alpha _0+\alpha _1x$ in $K_{j-1}[x]$ represents the element $\alpha _0+\alpha _1\sqrt{\delta }$ of $K_j$. The specified generators of $K_j$ as a $\mathord {{\mathbb {Q}}}$-vector space are simply the generators of $K_{j-1}$ followed by $\sqrt{\delta }$ times the same generators. Extracting $\alpha _0,\alpha _1$ from this representation is simply extracting the first half and the second half of the coefficients.

How quickly can one multiply two elements in the relative representation of $K_j$? A standard Karatsuba-type multiplication of $\alpha _0+\alpha _1x$ by $\beta _0+\beta _1x$ in $K_{j-1}[x]$ involves three multiplications in $K_{j-1}$. One also incurs a multiplication by $\delta$ to reduce modulo $x^2-\delta$, although often one can choose $\delta$ to make this multiplication very fast. At best this algorithm reduces a multiplication problem to three half-size multiplication problems. If this is applied recursively in a 2-power tower then degree-n multiplication involves $n^{\log _2 3}$ multiplications in $\mathord {{\mathbb {Q}}}$, not counting the $\delta$ multiplications.

As noted in Sect. 1, van der Hoeven and Lecerf [59] suggested choosing towers with superconstant relative degrees $d_j$ so as to reduce the number of base-field multiplications to $n^{1+o(1)}$. One can obtain cost $n(\log n)^{O(1)}$ for multiplications in a tower represented in this way by requiring each layer to have multiplication overhead $(\log n)^{O(1/t)}$ for relative degree $n^{\Theta (1/t)}$; this is easy for $t\in \Theta (1)$, but seems hard for $t\in \Theta ((\log n)/{\log \log n})$. See also the discussion of open problems in [59, Conclusion]. I don’t see how this approach can obtain cost $n(\log n)^{O(1)}$ for computing ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ with $\Theta (n\log n)$ bits.

4.6 The Abelian case

From now on, let’s focus on Abelian number fields, i.e., Galois number fields with commutative Galois groups, and see whether this added structure gives faster algorithms.

The Kronecker–Weber theorem states that each Abelian number field is a subfield of some cyclotomic field $\mathord {{\mathbb {Q}}}(\zeta _m)$; see, e.g., [94, Theorem 14.1]. Conversely, subfields of cyclotomic fields are certainly Abelian. The smallest positive integer m such that $K\subseteq \mathord {{\mathbb {Q}}}(\zeta _m)$ is called the conductor of K.

(In this paper, as in [69, page 9], a “number field” is a subfield of $\mathord {{\mathbb {C}}}$ having finite dimension as a $\mathord {{\mathbb {Q}}}$-vector space. Often the literature defines “number field” more broadly as a field containing $\mathord {{\mathbb {Q}}}$ and having finite dimension as a $\mathord {{\mathbb {Q}}}$-vector space; but this broader definition breaks typical statements of the Kronecker–Weber theorem, such as [94, Theorem 14.1]. As a workaround, one could say that each number field in this broader sense is isomorphic to a number field in the strict sense, so each Abelian number field in this broader sense is isomorphic to a subfield of $\mathord {{\mathbb {Q}}}(\zeta _m)$ for some m; or, as in [61, Theorem 5.9], one could say that each Abelian number field in this broader sense has a superfield of the form $\mathord {{\mathbb {Q}}}(\zeta )$ where $\zeta$ is a root of unity.)

In analyses of the costs of algorithms below, I’ll ignore the cost of various per-field precomputations. Formally, this is most easily described as existence of an algorithm $A_K$ for each suitable field K; the cost of evaluating $K\mapsto A_K$ is irrelevant to the cost of evaluating $\alpha \mapsto A_K(\alpha )$. In reality, optimizing the precomputation cost could be of interest, but only in corner cases where m is much larger than n or where there are not many computations for each K. Specifically, all of the precomputations below take time $m^{O(1)}$; I’ll assume that m is $n^{O(1)}$, so the precomputation time is also $n^{O(1)}$, which is, at least asymptotically, outweighed by the number of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluations in Sect. 5.

4.7 The Gauss-period representation for prime conductor

Within the set of Abelian fields, let’s start with the case of odd prime conductor p, specifically by reviewing a standard construction of all of the subfields of $\mathord {{\mathbb {Q}}}(\zeta _p)$; these all have conductor p, except for $\mathord {{\mathbb {Q}}}$, which has conductor 1.

This construction is due to Gauss. The proof that each subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ is one of Gauss’s fields is typically presented today as an application of Galois theory, but my impression is that this application is merely a restatement in different language of facts that Gauss had proven in [48]. Gauss stated facts without proof for more general cyclotomic fields (see [2]); I’ll return later to the difficulties that appear in the general case.

4.7.1 Example: the Gauss periods for $p=17$

Gauss’s ruler-and-compass construction of a 17-gon [48, Section 354] exhibited, in essence, a tower of number fields $\mathord {{\mathbb {Q}}}=K_0\subset K_1\subset K_2\subset K_3\subset K_4=\mathord {{\mathbb {Q}}}(\zeta _{17})$ with $\deg K_j=2^j$. Explicitly, with $\zeta _{17}$ abbreviated as $\zeta$:

• $K_4$ has $\mathord {{\mathbb {Q}}}$-basis $\zeta ^{\pm 1},\zeta ^{\pm 2},\zeta ^{\pm 3},\zeta ^{\pm 4}, \zeta ^{\pm 5},\zeta ^{\pm 6},\zeta ^{\pm 7},\zeta ^{\pm 8}$.

• $K_3$ has $\mathord {{\mathbb {Q}}}$-basis $\zeta +\zeta ^{-1},\zeta ^2+\zeta ^{-2}, \zeta ^3+\zeta ^{-3},\zeta ^4+\zeta ^{-4}, \zeta ^5+\zeta ^{-5},\zeta ^6+\zeta ^{-6}, \zeta ^7+\zeta ^{-7},\zeta ^8+\zeta ^{-8}$. Each basis element displayed here has exponents $c,-c$ modulo 17 for some c; note that $\mathord {\left\{ {1,-1}\right\} }$ is the unique subgroup of $(\mathord {{\mathbb {Z}}}/17)^*$ of order 2.

• $K_2$ has $\mathord {{\mathbb {Q}}}$-basis $\zeta +\zeta ^4+\zeta ^{-4}+\zeta ^{-1}$, $\zeta ^2+\zeta ^8+\zeta ^{-8}+\zeta ^{-2}$, $\zeta ^3+\zeta ^{-5}+\zeta ^{5}+\zeta ^{-3}$, $\zeta ^6+\zeta ^{7}+\zeta ^{-7}+\zeta ^{-6}$. Each basis element displayed here has exponents $c,4c,-4c,-c$ modulo 17 for some c; note that $\mathord {\left\{ {1,4,-4,-1}\right\} }$ is the unique subgroup of $(\mathord {{\mathbb {Z}}}/17)^*$ of order 4.

• $K_1$ has $\mathord {{\mathbb {Q}}}$-basis $\zeta +\zeta ^2+\zeta ^4+\zeta ^8+\zeta ^{-8}+\zeta ^{-4}+\zeta ^{-2}+\zeta ^{-1}$, $\zeta ^3+\zeta ^6+\zeta ^{-5}+\zeta ^7+\zeta ^{-7}+\zeta ^{5}+\zeta ^{-6}+\zeta ^{-3}$. These are $(-1+\sqrt{17})/2$ and $(-1-\sqrt{17})/2$; the field $K_1$ is $\mathord {{\mathbb {Q}}}(\sqrt{17})$.

These basis elements are called “Gauss periods” (or “Gaussian periods”), not to be confused with “Gauss sums”, which are Fourier transforms of Gauss periods. Beware that the literature sometimes uses the terminology “Gauss sums” for Gauss periods; see, e.g., [12].

4.7.2 Constructing Gauss periods for any odd prime p

Let p be an odd prime number. The field $\mathord {{\mathbb {Q}}}(\zeta _p)$ has Galois group isomorphic to $(\mathord {{\mathbb {Z}}}/p)^*$; each element $c\in (\mathord {{\mathbb {Z}}}/p)^*$ corresponds to the unique automorphism $\sigma _c$ of $\mathord {{\mathbb {Q}}}(\zeta _p)$ mapping $\zeta _p$ to $\zeta _p^c$. Note that this automorphism permutes the $\mathord {{\mathbb {Q}}}$-basis $\zeta _p,\zeta _p^2,\dots ,\zeta _p^{p-1}$ of $\mathord {{\mathbb {Q}}}(\zeta _p)$.

The group $(\mathord {{\mathbb {Z}}}/p)^*$ is a cyclic group with $\#(\mathord {{\mathbb {Z}}}/p)^*=p-1$, so, for each divisor d of $p-1$, there is a unique subgroup H of $(\mathord {{\mathbb {Z}}}/p)^*$ with $\#H=d$. The fixed field of the corresponding group of automorphisms is the unique subfield F of $\mathord {{\mathbb {Q}}}(\zeta _p)$ of degree $(p-1)/d$.

Explicitly, the Gauss period $\zeta _p^j+\zeta _p^{cj}+\zeta _p^{c^2j}+\dots +\zeta _p^{c^{d-1}j}$, where $j\in (\mathord {{\mathbb {Z}}}/p)^*$ and d is the order of c in $(\mathord {{\mathbb {Z}}}/p)^*$, is in the fixed field F of $\sigma _c$; it is exactly ${\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _p)}_{F}\zeta _p^j$. The set $\mathord {\left\{ {\smash {{\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _p)}_{F}\zeta _p^j:j\in (\mathord {{\mathbb {Z}}}/p)^*}}\right\} }$ is a $\mathord {{\mathbb {Q}}}$-basis set for F. This follows from the fact that $\mathord {\left\{ {\zeta _p^j:j\in (\mathord {{\mathbb {Z}}}/p)^*}\right\} }$ is a $\mathord {{\mathbb {Q}}}$-basis set for $\mathord {{\mathbb {Q}}}(\zeta _p)$. The point is that $\sigma _c$ maps $\alpha =\sum _{j\in (\mathord {{\mathbb {Z}}}/p)^*} \alpha _j\zeta _p^j$ to $\sum _{j\in (\mathord {{\mathbb {Z}}}/p)^*} \alpha _j\zeta _p^{cj} =\sum _{j\in (\mathord {{\mathbb {Z}}}/p)^*} \alpha _{j/c}\zeta _p^j$, so $\sigma _c$ fixes $\alpha$ exactly when $\alpha _j=\alpha _{j/c}$ for each j, i.e., exactly when $j\mapsto \alpha _j$ is constant on orbits of multiplication by c.

The $\mathord {{\mathbb {Q}}}$-basis $\zeta _p,\zeta _p^2,\dots ,\zeta _p^{p-1}$ of $\mathord {{\mathbb {Q}}}(\zeta _p)$ is an integral basis: its $\mathord {{\mathbb {Z}}}$-span is $\mathord {{\mathbb {Z}}}[\zeta _p]$, the ring of integers of $\mathord {{\mathbb {Q}}}(\zeta _p)$. Consequently the Gauss-period basis for each subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ is an integral basis for that subfield.

Another important feature of the Gauss-period basis is that one can efficiently compute conjugates of field elements represented as $\mathord {{\mathbb {Q}}}$-linear combinations of Gauss periods. For the same reason, the representation is subfield-compatible (and hence compatible with any given tower of subfields): if $K\subseteq L$ are subfields of $\mathord {{\mathbb {Q}}}(\zeta _p)$ then one can efficiently (1) map an element of K from K’s Gauss-period representation to L’s Gauss-period representation, and (2) invert this map on its image.

4.8 Multiplication algorithms for the Gauss-period representation for prime conductor

Bach and Shallit [7, Section 4, “period basis”], crediting Lenstra, used the Gauss-period basis for computations in an Abelian field K of prime conductor p. The multiplication algorithm in [7] for this basis has cost cubic in the degree of K.

Gao, von zur Gathen, and Panario [47, Section 3] instead used the superfield representation of elements of K as elements of $\mathord {{\mathbb {Q}}}(\zeta _p)$, giving multiplication cost essentially linear in p. This cost can be much smaller than cubic in the degree of K, but can also be much larger: consider, as an extreme example, the quadratic field $K=\mathord {{\mathbb {Q}}}(\sqrt{p})$.

The general issue here was noted in [7, page 206, “we would like to avoid using the larger field”]; the issue for $\mathord {{\mathbb {Q}}}(\sqrt{p})$ was noted in [29, Section 7, first paragraph]. This was not a big issue for [47]. The goal of [47] was to multiply in $\mathord {{\mathbb {F}}}_q$ for a given prime power q; the strategy in [47] was to represent $\mathord {{\mathbb {F}}}_q$ as a quotient of a degree-n subring of $\mathord {{\mathbb {Q}}}(\zeta _p)$; in this context, one can safely restrict attention to the case that $p-1$ is not much larger than n. However, if the goal is instead to evaluate ${\text {det}}^{\mathord {{\mathbb {Q}}}(\zeta _p)}_{\mathord {{\mathbb {Q}}}}$ via a smooth tower of subfields of $\mathord {{\mathbb {Q}}}(\zeta _p)$ then one ends up considering subfields of many degrees, with similar data volume in each degree, so one cannot ignore the gap between the degree and $p-1$.

Let’s look more closely at known essentially-linear-time multiplication algorithms for $\mathord {{\mathbb {Q}}}(\zeta _p)$. A conventional FFT modulo $x^m-1$, where m is a power of 2 above 2p, works with the additive structure of the exponent group $\mathord {{\mathbb {Z}}}/m$. A different essentially-linear-time DFT algorithm, introduced by Rader in [82], instead works with the multiplicative structure of $(\mathord {{\mathbb {Z}}}/p)^*$—and we’ll see in a moment that Rader’s algorithm can easily take advantage of the symmetries of the Gauss-period basis for a subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$.

See Appendix A for software to double-check the main algorithms presented here.

4.8.1 Rader’s FFT

The goal is to compute a size-p DFT over a ring R where p is an odd prime: i.e., to compute $g(1),g(\zeta ),\dots ,g(\zeta ^{p-1})$ given $g\in R[x]$ with $\deg g<p$, where $\zeta$ is a primitive pth root of 1 in R.

Write g as $g_0+g_1x+\cdots +g_{p-1}x^{p-1}$. Rader handles $g_0$ separately (simply adding $g_0$ to each output), and handles g(1) separately, easily reducing to the problem of computing $g(\zeta ),\dots ,g(\zeta ^{p-1})$ where $g=g_1x+\cdots +g_{p-1}x^{p-1}$. Let’s now focus on that problem.

View g as an element of the group ring $R[\mathord {{\mathbb {Z}}}/p]$; i.e., view the indices of g as elements of $\mathord {{\mathbb {Z}}}/p$. Let $\omega$ be a generator of $(\mathord {{\mathbb {Z}}}/p)^*$. Then

$$\begin{aligned} g(\zeta ^{\omega ^b}) =\sum _{j\in (\mathord {{\mathbb {Z}}}/p)^*} g_j\zeta ^{\omega ^b j} =\sum _{a\in \mathord {\left\{ {0,1,\dots ,p-2}\right\} }}g_{\omega ^{-a}} \zeta ^{\omega ^{b-a}}. \end{aligned}$$

In other words, $O_b=\sum _a I_a Z_{b-a}$, where $I_a=g_{\omega ^{-a}}$, $Z_b=\zeta ^{\omega ^b}$, and $O_b=g(\zeta ^{\omega ^b})$: the output sequence O is a length-$(p-1)$ cyclic convolution of the input sequence I and the constant sequence Z, i.e., a product in the group ring $R[\mathord {{\mathbb {Z}}}/(p-1)]$. Rader concludes by pointing to essentially-linear-time subroutines for cyclic convolution.

4.8.2 Inverting Rader’s FFT

The standard principle that a DFT with exponents negated is an inverse DFT, aside from scaling by a constant factor, means that one can use a DFT algorithm for an inverse DFT without inspecting the details of the algorithm. However, seeing how to merge this principle into the details of Rader’s algorithm turns out to be useful for the generalized algorithms in Sects. 4.8.4 and 4.12.4.

The details are as follows. Again handle $g_0$ and g(1) separately, easily reducing to the problem of recovering $g=g_1x+\dots +g_{p-1}x^{p-1}$ given $g(\zeta ),\dots ,g(\zeta ^{p-1})$, i.e., recovering the above sequence I from the above sequence O. Define $Z'_b=(Z_{(p-1)/2-b}-1)/p$. The following calculation, where the indices a, b range over $\mathord {{\mathbb {Z}}}/(p-1)$, shows that Z has a convolution inverse, specifically $Z'$:

$$\begin{aligned} \begin{aligned} p \sum _a Z_a Z'_{b-a}&= \sum _a \zeta ^{\omega ^a} \left( \zeta ^{\omega ^{(p-1)/2+a-b}}-1\right) \\&= \sum _a \zeta ^{\omega ^a} \zeta ^{-\omega ^{a-b}} - \sum _a \zeta ^{\omega ^a} = \sum _a \zeta ^{(1-\omega ^{-b})\omega ^a} - \sum _a \zeta ^{\omega ^a}. \end{aligned} \end{aligned}$$

This last quantity is, as desired, p if $b=0$, else 0; the point is that $\sum _a \zeta ^{s\omega ^a}$ is $p-1$ if $s=0$, else $-1$. Hence convolution with $Z'$ is deconvolution with Z; in particular, I is the convolution of O and $Z'$.

4.8.3 Exploiting input symmetries in Rader’s FFT

If g is real, meaning that $g_j=g_{-j}$ for each $j\in (\mathord {{\mathbb {Z}}}/p)^*$, then $g(\zeta ^c)=g(\zeta ^{-c})$. In other words, if the input sequence I is periodic with period $(p-1)/2$, then the output sequence O is also periodic with period $(p-1)/2$. One can exploit this twofold symmetry by folding the Z sequence: one has

$$\begin{aligned} \begin{aligned} O_b&=\sum _a I_a Z_{b-a} =\sum _{0\le a< (p-1)/2} I_a Z_{b-a} +\sum _{(p-1)/2\le a<p-1} I_a Z_{b-a} \\&=\sum _{0\le a< (p-1)/2} I_a (Z_{b-a}+Z_{b-a+(p-1)/2}) =\sum _{0\le a< (p-1)/2} I_a Y_{b-a} \end{aligned} \end{aligned}$$

where $Y_b=Z_b+Z_{b+(p-1)/2}$. This expresses the first half of O as a length-$((p-1)/2)$ cyclic convolution of Y and the first half of I.

More generally, fix a positive integer d dividing $p-1$, and say $g_j=g_{j\omega ^d}$ for all $j\in (\mathord {{\mathbb {Z}}}/p)^*$. (The previous paragraph is the case $d=(p-1)/2$.) Then the input and output sequences are periodic with period d, and are determined by their first d entries, i.e., the entries at positions 0 through $d-1$. The first d entries of the output O are a length-d cyclic convolution of Y and the first d entries of I, where now $Y_b=Z_b+Z_{b+d}+\cdots +Z_{b+p-1-d}$. The number of operations in this convolution, after precomputation of the Y sequence, is essentially linear in d: more precisely, $d(\log d)^{1+o(1)}$.

This folded generalization of Rader’s FFT algorithm is not new. Arita and Handa [6, Sections 3.3-$-$3.4] considered the Gauss-period basis of a subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ (not mentioning that these are Gauss periods), considered DFTs (under another name) of elements of the subfield, and expressed these DFTs as convolutions (not mentioning Rader’s algorithm).

4.8.4 Inverting a folded Rader FFT

Define $Y'_b=Z'_b+Z'_{b+d}+\cdots +Z'_{b+p-1-d} =(Y_{(p-1)/2-b}-(p-1)/d)/p$. Then $Y'$ is the convolution inverse of Y: the folding map from the group ring $R[\mathord {{\mathbb {Z}}}/(p-1)]$ to $R[\mathord {{\mathbb {Z}}}/d]$ maps Z to Y, maps $Z'$ to $Y'$, and maps the equation $ZZ'=1$ to the equation $YY'=1$. Convolution with $Y'$ thus inverts the folded Rader algorithm from Sect. 4.8.3.

In other words: Consider the problem of recovering, from the input described in a moment, a polynomial $g\in R[x]$ with $\deg g<p$, with $g(0)=0$, and with the periodicity $g_j=g_{j\omega ^d}$ for all $j\in (\mathord {{\mathbb {Z}}}/p)^*$, where indices are again interpreted as elements of $\mathord {{\mathbb {Z}}}/p$. The input consists of the first d entries of the d-periodic sequence O defined by $O_b=g(\zeta ^{\omega ^b})$; i.e., the values of g at $\zeta ,\zeta ^\omega ,\zeta ^{\omega ^2},\dots ,\zeta ^{\omega ^{d-1}}$.

To solve this problem, simply apply a length-d cyclic convolution of the input sequence with $Y'$, obtaining the first d entries of the sequence I defined by $I_a=g_{\omega ^{-a}}$. These entries are the coefficients of g on the R-basis

$$\begin{aligned} \begin{aligned}&x^{\omega ^0}+x^{\omega ^d}+x^{\omega ^{2d}}+\dots +x^{\omega ^{p-1-2d}}+x^{\omega ^{p-1-d}}, \\&x^{\omega ^{-1}}+x^{\omega ^{d-1}}+x^{\omega ^{2d-1}}+\dots +x^{\omega ^{p-2-2d}}+x^{\omega ^{p-2-d}}, \\&\vdots \\&x^{\omega ^{1-d}}+x^{\omega ^{1}}+x^{\omega ^{d+1}}+\dots +x^{\omega ^{p-3d}}+x^{\omega ^{p-2d}}. \end{aligned} \end{aligned}$$

Note that replacing x with $\zeta _p$ in these formulas produces the Gauss periods.

Combining the folded Rader FFT with the inverse folded Rader FFT produces a fast multiplication algorithm for this type of periodic polynomial. One is given two periodic polynomials f, g; one uses the folded Rader FFT to evaluate the polynomials at $\zeta ,\zeta ^\omega ,\zeta ^{\omega ^2},\dots ,\zeta ^{\omega ^{d-1}}$; one then multiplies pointwise and uses the inverse folded Rader FFT to interpolate, obtaining a periodic polynomial h with the same values as f, g. The periodicity implies that h has the same values as fg at all powers of $\zeta$, so $h=fg$ in $R[x]/((x^p-1)/(x-1))$. All of this takes just $d(\log d)^{1+o(1)}$ operations in R, after precomputation of the Y sequence.

4.8.5 Integers as a base ring

Again fix a positive integer d dividing $p-1$. Consider d-periodic polynomials $g\in \mathord {{\mathbb {Z}}}[x]$, defined as polynomials $g\in \mathord {{\mathbb {Z}}}[x]$ satisfying $\deg g<p$, $g(0)=0$, and $g_j=g_{j\omega ^d}$ for all $j\in (\mathord {{\mathbb {Z}}}/p)^*$, with indices interpreted as elements of $\mathord {{\mathbb {Z}}}/p$. As above, represent d-periodic polynomials on the period basis: i.e., represent g as the sequence $g_1,g_{\omega ^{-1}},\dots ,g_{\omega ^{1-d}}$. Consider the problem of multiplying d-periodic polynomials: given d-periodic f, g, find d-periodic h with $h=fg$ in $\mathord {{\mathbb {Z}}}[x]/((x^p-1)/(x-1))$.

This problem for $\mathord {{\mathbb {Z}}}$ reduces immediately to the same problem for $\mathord {{\mathbb {Z}}}/M$, if the modulus M is chosen large enough to ensure that the coefficients of h in $\mathord {{\mathbb {Z}}}$ can be recovered from their images in $\mathord {{\mathbb {Z}}}/M$. An easy way to measure “large enough” is to note that the maximum possible coefficient of h in absolute value is $2p-3$ times the maxima for f and g; the factor $2p-3$ fits into $\Theta (\log p)$ bits, and the same factor across all O(p) coefficients fits into $O(p\log p)$ bits, a bound sufficiently small for this paper’s analyses. One can, with more work, compute bounds that are better for most inputs—for example, one can evaluate f and g at 1, and more generally use low-precision complex embeddings to estimate sizes, as mentioned in Sect. 3.3—but a logarithmic factor is to be expected, as explained in Sect. 2.

The reason to reduce to $\mathord {{\mathbb {Z}}}/M$ is that one can also choose M to ensure that $\mathord {{\mathbb {Z}}}/M$ has the primitive roots of 1 needed for the folded Rader FFT. Concretely, take M as a product of distinct primes $q\in 1+pd\mathord {{\mathbb {Z}}}$. Then $\mathord {{\mathbb {Z}}}/M$ contains a primitive pth root of 1 for defining the DFT in the first place, and, less importantly, contains a primitive dth root of 1 so that the length-d cyclic convolutions inside a folded Rader FFT can in turn be handled by traditional FFTs when d is smooth. Given the goal of using folded Rader FFTs, this reduction is the obvious adaptation of a widely used reduction suggested by Pollard [78], independently Nicholson [74, page 532], and independently Schönhage–Strassen [85], namely reducing modulo products of primes $q\in 1+2^k\mathord {{\mathbb {Z}}}$ to support traditional size-$2^k$ FFTs.

There is a logarithmic inefficiency in this reduction when d and M are both large. Specifically, there are $d(\log d)^{1+o(1)}$ multiplications in $\mathord {{\mathbb {Z}}}/M$, and each multiplication in $\mathord {{\mathbb {Z}}}/M$ uses $b(\log b)^{1+o(1)}$ bit operations if M has b bits, so there are two logarithmic factors in the total cost on top of the output size bd. Recall that the usual scenario considered in this paper is $bd\in \Theta (n\log n)$; very often d is between $n^{0.1}$ and $n^{0.9}$, implying $bd(\log b)^{1+o(1)}(\log d)^{1+o(1)}=n(\log n)^{3+o(1)}$. Let’s see how to do better, saving a logarithmic factor and reaching cost $bd(\log bd)^{1+o(1)}=n(\log n)^{2+o(1)}$.

What does not seem to save this logarithmic factor is working separately modulo each prime factor q of M, along with choosing each q small enough to have $\log \log q\in (\log n)^{o(1)}$, as in Sect. 3.2. This would reduce the total cost of the folded Rader FFTs across each $\mathord {{\mathbb {Z}}}/q$ to $n(\log n)^{2+o(1)}$; but how does one reduce $\mathord {{\mathbb {Z}}}/M$ to $\prod _q(\mathord {{\mathbb {Z}}}/q)$ in the first place? Standard algorithms for this reduction, and for the corresponding interpolation at the end of the multiplication, have two logarithmic factors, one for multiplications and one for the height of a product tree. See, e.g., [16, Sections 18 and 23]. This issue did not arise in Sect. 3.2: each reduction there started from small input coefficients, and interpolation used only one large coefficient.

What does save a logarithmic factor, as in Sects. 3.3 and 4.2, is segmentation. It is important here that the folded Rader FFT is simply carrying out a convolution. Segmentation converts length-d convolution over $\mathord {{\mathbb {Z}}}/M$, where M has b bits, into O(bd)-bit multiplication, costing $bd(\log bd)^{1+o(1)}$ bit operations. It suffices here to take M as a product of distinct primes $q\in 1+p\mathord {{\mathbb {Z}}}$.

4.8.6 Application to det evaluation

If K is a degree-n subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$, and if K has a smooth tower (i.e., if n factors into small enough primes), then computing ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ costs $n(\log n)^{3+o(1)}$ in the same $\Theta (n\log n)$-bit scenario. Each step through the tower costs $n(\log n)^{2+o(1)}$ (see Sect. 4.8.5), and there are $(\log n)^{1-o(1)}$ steps.

As a concrete example, the prime $p=1009$ has $p-1=2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 7$, so one can compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for $K=\mathord {{\mathbb {Q}}}(\zeta _{1009})$ by a series of multiplications in subfields of K of degrees 1008, 504, 252, 126, 63, 21, 7, using the Gauss-period representation of each subfield, using cyclic convolutions of lengths 1008, 504, 252, 126, 63, 21, 7 respectively to compute the underlying DFTs.

(In this example, one could also use the prime factors of $p-1$ in the opposite order, or any other order. In general, for each K, all smooth towers for K have the same performance at the level of detail of this paper’s analysis. This is not saying that the towers have exactly the same performance; the analysis absorbs all $(\log n)^{o(1)}$ factors.)

This application of folded Rader FFTs to fast ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computation seems to be new. A helpful speedup in this context is to push conjugation and subfield extraction through the DFTs: to compute ${\text {det}}^{K_j}_{K_{j-1}}\alpha _j$, apply a $K_j$-folded DFT to $\alpha _j$, fold the result $d_j$ times, and apply a $K_{j-1}$-folded inverse DFT.

If one is starting from a very large p and a relatively small subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ then the Y precomputation stated above could be a bottleneck. Each $Y_b$ is a Gauss period, with $\zeta \in R$ substituted for $\zeta _p$; presumably it is possible in time $n^{O(1)}$ to identify the defining equation of the subfield in question and solve for a suitable system of $Y_b$ values (a weak form of reciprocity) without even computing $\zeta$. But such speedups are not necessary for this paper: recall from Sect. 4.6 that m is assumed to be $n^{O(1)}$, and that per-field precomputation cost is not included.

4.9 Arbitrary conductor: difficulties and desiderata

What about arbitrary Abelian number fields, i.e., subfields of arbitrary cyclotomic fields $\mathord {{\mathbb {Q}}}(\zeta _m)$, without the constraint of m being prime?

The general case is not as easy as the prime case. The group $(\mathord {{\mathbb {Z}}}/m)^*$ is not cyclic in general, although if one splits m into prime-power components then non-cyclic components can appear only for the power of 2. More fundamentally, there are many m for which $\mathord {\left\{ {\smash {\zeta _m^j:j\in (\mathord {{\mathbb {Z}}}/m)^*}}\right\} }$ is not a $\mathord {{\mathbb {Q}}}$-basis set for $\mathord {{\mathbb {Q}}}(\zeta _m)$: for example, $\zeta _4=i$ and $\zeta _4^3=-i$ do not form a $\mathord {{\mathbb {Q}}}$-basis for $\mathord {{\mathbb {Q}}}(\zeta _4)$, and $\zeta _8,\zeta _8^3,\zeta _8^5,\zeta _8^7$ do not form a $\mathord {{\mathbb {Q}}}$-basis for $\mathord {{\mathbb {Q}}}(\zeta _8)$. If one starts with a basis $1,\zeta _8,\zeta _8^2,\zeta _8^3$ for $\mathord {{\mathbb {Q}}}(\zeta _8)$ and takes traces down to $\mathord {{\mathbb {Q}}}(\zeta _4)$ then one obtains $2,0,2\zeta _4,0$; the nonzero traces $2,2\zeta _4$ form a $\mathord {{\mathbb {Q}}}$-basis for $\mathord {{\mathbb {Q}}}(\zeta _4)$ but not an integral basis.

Traces from $\mathord {{\mathbb {Q}}}(\zeta _m)$ to K can behave suboptimally even when K has conductor m. Take, for example, $m=8$ and $K=\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _8)$. The integral basis $1,\zeta _8,\zeta _8^2,\zeta _8^3$ of $\mathord {{\mathbb {Q}}}(\zeta _8)$ has trace $2,\zeta _8+\zeta _8^{-1},\zeta _8^2+\zeta _8^{-2},\zeta _8^3+\zeta _8^{-3}$, which is not exactly an integral basis of K. On the other hand, replacing each trace with the sum of distinct conjugates replaces 2 with 1, giving an integral basis. Breuer [29], crediting Hiss and Lenstra, gave an explicit integral basis for every Abelian number field; see [29, Corollary 2] for cases handled by the trace, [29, Lemma 4] for cases handled by sums of distinct conjugates (and not by the trace), and [29, Lemma 3] for the the fact that these cover all cases. See Sect. 4.12 for more on this construction.

Breuer’s stated objective [29, Section 1] was to find an integral basis of each Abelian field that allows efficient arithmetic and efficiently finding “for an arbitrary element of a cyclotomic field the basis representation in the smallest possible field”. This description considers only moving from $\mathord {{\mathbb {Q}}}(\zeta _m)$ to a subfield, but it is natural to consider moving more generally from K to L and from L to K whenever $K\subseteq L$ are subfields of $\mathord {{\mathbb {Q}}}(\zeta _m)$. In ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation via towers, it is important to be able to efficiently move from a subfield $K_j$ to a smaller subfield $K_{j-1}$.

4.10 A sub-cyclotomic-field-compatible integral basis for each cyclotomic field

This subsection reviews one component of the construction from [29]: an integral basis for $\mathord {{\mathbb {Q}}}(\zeta _m)$ introduced by Zumbroich [97] and independently Bosma [26]. As Bosma put it [26, Section 1], this basis allows one to efficiently find “the smallest cyclotomic field in which a given sum of roots of unity lies”. Arithmetic using this basis was implemented in, respectively, CAS, which was later superseded by GAP, and Cayley, which was later superseded by Magma. The GAP implementation is available in Sage as UniversalCyclotomicField.

For each prime p and each positive integer e, choose a set $I_{p,e}$ of $p^{e-1}$ consecutive integers: e.g., the set $\mathord {\left\{ {\smash {1,2,\dots ,p^{e-1}}}\right\} }$. Define $S_{p^e}\subseteq \mathord {{\mathbb {Z}}}/p^e$ as the complement of the image of $I_{p,e}$ in $\mathord {{\mathbb {Z}}}/p^e$. The specified integral basis set for $\mathord {{\mathbb {Q}}}(\zeta _{p^e})$ is $\mathord {\left\{ {\smash {\zeta _{p^e}^j:j\in S_{p^e}}}\right\} }$. In other words, starting from $\zeta _{p^e}^{\mathord {{\mathbb {Z}}}}$, one removes some arc consisting of 1/p of the circle.

More generally, for each positive integer m, define $S_m\subseteq \mathord {{\mathbb {Z}}}/m$ as the set of images in $\mathord {{\mathbb {Z}}}/m$ of all $j\in \mathord {{\mathbb {Z}}}$ such that, for each prime divisor p of m, the set $j-(m/p^e)I_{p,e}=\mathord {\left\{ {j-(m/p^e)s:s\in I_{p,e}}\right\} }$ is disjoint from $p^e\mathord {{\mathbb {Z}}}$, where $e={\text {ord}}_p m$ (i.e., $m\in p^e\mathord {{\mathbb {Z}}}$ and $m\notin p^{e+1}\mathord {{\mathbb {Z}}}$). The specified integral basis set for $\mathord {{\mathbb {Q}}}(\zeta _m)$ is $\mathord {\left\{ {\smash {\zeta _m^j:j\in S_m}}\right\} }$. This no longer has the arc description.

For example, take $m=12$, and choose $I_{p,e}=\mathord {\left\{ {0,1,\dots ,p^{e-1}-1}\right\} }$; in particular, $I_{2,2}=\mathord {\left\{ {0,1}\right\} }$ and $I_{3,1}=\mathord {\left\{ {0}\right\} }$. The allowed exponents j then avoid $4\mathord {{\mathbb {Z}}}+3I_{2,2}=4\mathord {{\mathbb {Z}}}+\mathord {\left\{ {0,3}\right\} }$, and avoid $3\mathord {{\mathbb {Z}}}+4I_{3,1}=3\mathord {{\mathbb {Z}}}$, so $S_{12}=\mathord {\left\{ {1,2,5,10}\right\} }$.

There are two steps in showing that this is an integral basis set. First, this set has the right number of elements. To see this, observe that if p is a prime divisor of m and $e={\text {ord}}_p m$ then the set $(m/p^e)I_{p,e}$ consists of $p^{e-1}$ distinct integers modulo $p^e$. The condition $p^e\mathord {{\mathbb {Z}}}\cap (j-(m/p^e)I_{p,e})=\mathord {\left\{ {}\right\} }$ thus excludes exactly $p^{e-1}$ choices of j modulo $p^e$. These conditions are independent across p, leaving exactly $\prod _p (p^e-p^{e-1})=\#(\mathord {{\mathbb {Z}}}/m)^*$ choices of $j\in S_m$; and the map $j\mapsto \zeta _m^j$ on $S_m$ is injective.

Second, one can express any element of $\mathord {{\mathbb {Z}}}[\zeta _m]$ as a $\mathord {{\mathbb {Z}}}$-linear combination of $\zeta _m^j$ for $j\in S_m$. The proof is constructive. Write the input as $\sum _{a\in \mathord {{\mathbb {Z}}}/m} \alpha _a \zeta _m^a$. For each prime divisor p of m (in, say, increasing order), define $e={\text {ord}}_p m$, and eliminate all $a\in \mathord {{\mathbb {Z}}}/m$ such that $a-(m/p^e)I_{p,e}$ includes a multiple of $p^e$ as follows: use the identity $1=-\zeta _p-\dots -\zeta _p^{p-1}$, together with $\zeta _p=\zeta _m^{m/p}$, to rewrite $\zeta _m^a$ as $-\sum _b \zeta _m^b$ where b ranges over $\mathord {\left\{ {a+m/p,\dots ,a+(p-1)m/p}\right\} }$. Here is why this works:

• The set $b-(m/p^e)I_{p,e}$ cannot include a multiple of $p^e$ for any of the new exponents b. (If it does then the difference $(b-a)-(m/p^e)(I_{p,e}-I_{p,e})$ includes a multiple of $p^e$, say $(b-a)-(m/p^e)\Delta$ where $\Delta \in I_{p,e}-I_{p,e}$. This is also a multiple of $m/p^e$—since by construction $b-a$ is a multiple of m/p—and hence a multiple of m, i.e., 0 in $\mathord {{\mathbb {Z}}}/m$. Hence $(m/p^e)\Delta$ is a multiple of m/p, so $\Delta$ is a multiple of $p^{e-1}$; but the only multiple of $p^{e-1}$ in $I_{p,e}-I_{p,e}=\mathord {\left\{ {-p^{e-1}+1,\dots ,p^{e-1}-1}\right\} }$ is 0, so $\Delta =0$, so $b=a$, but by construction $b\ne a$, contradiction.)

• This property is preserved by any subsequent rewrites, i.e., replacements of $\zeta ^b$ with $\zeta ^c$ where $c-b$ is a multiple of $m/p'$ for a prime $p'\ne p$. (Indeed, $c-b$ is a multiple of $p^e$, so if $c-(m/p^e)I_{p,e}$ includes a multiple of $p^e$ then $b-(m/p^e)I_{p,e}$ also includes a multiple of $p^e$.)

For each p, there are m/p exponents $a\in \mathord {{\mathbb {Z}}}/m$ that require rewrites (if they appear in the input), and each rewrite takes O(p) operations, for a total of $\sum _p O(m)$ operations; this is $O(m(\log m)/{\log \log m})$ by the prime-number theorem. Also, each layer of rewriting converts B-bit coefficients into at most $(B+1)$-bit coefficients, and there are at most $\log _2 m$ layers of rewriting.

The choice $I_{p,e}=\mathord {\left\{ {1,2,\dots ,p^{e-1}}\right\} }$ has the properties $I_{p,e}\cap p^e\mathord {{\mathbb {Z}}}=\mathord {\left\{ {}\right\} }$ and $pI_{p,e}=p\mathord {{\mathbb {Z}}}\cap I_{p,e+1}$. One can then see that the basis for any divisor of m is included in the basis for m, making it trivial to recognize elements of smaller cyclotomic fields. These bases are what Bosma [26] calls “canonical bases for cyclotomic fields”.

GAP instead takes $I_{p,e}$ as $\mathord {\left\{ {-(p^{e-1}-1)/2,\dots ,(p^{e-1}-1)/2}\right\} }$ for odd p, and $\mathord {\left\{ {2^{e-1},\dots ,2^e-1}\right\} }$ for $p=2$. The choice $0\in I_{p,1}$ for odd p gives, e.g., basis $\zeta _p,\zeta _p^2,\dots ,\zeta _p^{p-1}$ for $\mathord {{\mathbb {Q}}}(\zeta _p)$. This does not include a basis element for $\mathord {{\mathbb {Q}}}$: recognizing the subfield $\mathord {{\mathbb {Q}}}$ requires checking for equal coefficients as in [29, Corollary 3]. The advantage of this basis, as in Sect. 4.8, is that conjugation is as easy as possible.

One can freely use one choice of $I_{p,e}$ to simplify conjugation and another choice of $I_{p,e}$ to simplify subfield detection, since it is efficient to rewrite any input using any given choice of $I_{p,e}$. Also, given a rewriting function for one choice of $I_{p,e}$, one can conjugate the input by a power of $\zeta _m$ to obtain a rewriting function for a rotated basis, i.e., a rotated choice of $I_{p,e}$.

4.11 Cyclotomic fields of smooth conductor

Consider computing ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ via a smooth tower of cyclotomic fields $\mathord {{\mathbb {Q}}}=\mathord {{\mathbb {Q}}}(\zeta _{m_0})\subset \mathord {{\mathbb {Q}}}(\zeta _{m_1})\subset \cdots \subset \mathord {{\mathbb {Q}}}(\zeta _{m_t})=K$. This setup requires $m_t$ to be smooth, which is more restrictive than merely requiring $\mathord {{\mathbb {Q}}}(\zeta _{m_t})$ to have smooth degree; on the other hand, this avoids the prime-conductor requirement from Sect. 4.8.

If each $K_j=\mathord {{\mathbb {Q}}}(\zeta _{m_j})$ is represented as in Sect. 4.10 then it is easy to convert elements of $K_{j-1}$ from the $K_j$ representation to the $K_{j-1}$ representation. It is also easy to convert the input, a small element of $\mathord {{\mathbb {Z}}}[\zeta _{m_t}]$, to the $K_t$ representation. One obvious way to compute ${\text {det}}^{K_j}_{K_{j-1}}\alpha _j$, given $\alpha _j\in K_j$, is to multiply $\sigma (\alpha _j)$ across the automorphisms $\sigma$ of $K_j$ that fix $K_{j-1}$, as in Sect. 3.7. The remaining question is how long conjugation and multiplication take in this $K_j$ representation.

Expanding the allowed set of exponents from $S_m$ in Sect. 4.10 to $\mathord {{\mathbb {Z}}}/m$ makes conjugation easy, simply permuting $\mathord {{\mathbb {Z}}}/m$, and reduces multiplication to the problem of multiplying modulo $x^m-1$, using $m(\log m)^{1+o(1)}$ coefficient operations. The rewriting operation from Sect. 4.10, reducing the set of exponents from $\mathord {{\mathbb {Z}}}/m$ to $S_m$, uses at most $m(\log m)^{1+o(1)}$ coefficient operations.

In terms of the degree n of $\mathord {{\mathbb {Q}}}(\zeta _m)$, these costs are $n(\log n)^{1+o(1)}$, since the ratio n/m is $(\log n)^{o(1)}$. (More precisely, $n/m\ge \Theta (1/{\log \log n})$. This is a standard calculation that runs as follows. First, n/m is the product of $1-1/p$ over prime divisors p of m. Choose a positive integer y so that the number of primes $p\le y$ is the number of prime divisors of m; then n/m is at least the product of $1-1/p$ over primes $p\le y$, which is $\Theta (1/{\log y})$ by Mertens’s theorem, while m is at least $\prod _{p\le y}p$, so $\log m$ is at least $\Theta (y)$ by the prime-number theorem. This gives $n/m\ge \Theta (1/{\log \log m})$, also implying $\Theta (\log \log n)=\Theta (\log \log m)$.)

As before, this gives total cost $n(\log n)^{3+o(1)}$ in the $\Theta (n\log n)$-bit scenario. This case does not need Rader’s FFT.

4.12 Using more subgroups

Let’s now unify the ideas of Sects. 4.8 and 4.11: handling $K=\mathord {{\mathbb {Q}}}(\zeta _m)$ for any m using any tower of subgroups of $(\mathord {{\mathbb {Z}}}/m)^*$, without requiring the subgroups to correspond to cyclotomic subfields.

4.12.1 Multicyclic convolution

The following paragraphs review a standard unification of conventional FFTs with fast Hadamard–Walsh transforms.

Let R be a ring. Let t be a nonnegative integer. Let $d_1,d_2,\dots ,d_t$ be integers with $d_j\ge 2$. Write $n=d_1d_2\cdots d_t$. Let $\zeta \in R$ be a primitive nth root of 1. Let $e_1,e_2,\dots ,e_t$ be nonnegative integers. Assume that $e_1\in n\mathord {{\mathbb {Z}}}$ if $t\ge 1$. Let $x_0$ be a unit in R. The goal here is to multiply quickly in the ring

$$\begin{aligned} R_t=R[x_1,x_2,\dots ,x_t]/\left( x_1^{d_1}-x_0^{e_1},x_2^{d_2}-x_1^{e_2},\dots ,x_t^{d_t}-x_{t-1}^{e_t}\right) , \end{aligned}$$

with the conventional representation of ring elements as polynomials of degree below $d_j$ in $x_j$.

If $d_j$ has a prime factor $p<d_j$ then one can replace the modulus $x_j^{d_j}-x_{j-1}^{e_j}$ with the moduli $y^p-x_{j-1}^{e_j},x_j^{d_j/p}-y$ where y is a new variable, obtaining a problem of the same form with $d_j$ replaced by $p,d_j/p$. So it suffices to consider the case that $d_1,d_2,\dots ,d_t$ are primes. Primality does not matter for the algorithm statement, but the cost analysis says that smaller $d_j$ is better.

The multicyclic case, which is the case used in subsequent sections, is the case that $e_j=0$ for all j; in other words, multiplication in the group ring R[G], where G is any finite commutative group. But it is also important to consider non-multicyclic cases to enable the speedup from the previous paragraph.

The algorithm applies an FFT, a fast isomorphism from $R_t$ to $R^n$; multiplies in $R^n$, which is simply n separate multiplications in R; and applies an inverse FFT to recover the product in $R_t$.

For $t=0$, there is nothing to do, so assume $t\ge 1$. The first layer of the FFT algorithm proceeds as follows.

Consider the ring morphism $R[z]/(z^{d_1}-1)\rightarrow R^{d_1}$ where coordinate c of the output, for $0\le c<d_1$, maps z to $\zeta ^{cn/d_1}$. This is a textbook size-$d_1$ DFT, straightforwardly computable using $\Theta (d_1^2)$ operations in R. This is also straightforwardly invertible using $\Theta (d_1^2)$ operations in R, since $d_1$ is invertible in R by definition of primitive roots.

(One can improve these $\Theta (d_1^2)$ operation counts by substituting more complicated DFT algorithms. However, this paper will apply multicyclic convolution to smooth towers, and then $d_1$ is $(\log n)^{o(1)}$, so $d_1^2$ is also $(\log n)^{o(1)}$. At that level of detail, the exponent of $d_1$ in the operation count does not matter.)

By assumption $e_1\in n\mathord {{\mathbb {Z}}}$, so in particular $e_1\in d_1\mathord {{\mathbb {Z}}}$. The ring morphism $R[x_1]\rightarrow R[z]/(z^{d_1}-1)$ mapping $x_1$ to $x_0^{e_1/d_1}z$ is invertible since $x_0$ is a unit, and induces a ring morphism $R[x_1]/(x_1^{d_1}-x_0^{e_1})\rightarrow R[z]/(z^{d_1}-1)$, straightforwardly computable and invertible using $\Theta (d_1)$ operations in R once the necessary powers of $x_0$ have been precomputed. Composing this morphism with the DFT gives a ring morphism $R[x_1]/(x_1^{d_1}-x_0^{e_1})\rightarrow R^{d_1}$ that maps $x_1$ to $x_0^{e_1/d_1}\zeta ^{cn/d_1}$ in the cth coordinate.

Applying this layer to the whole ring

$$\begin{aligned} R_t=R[x_1,x_2,\dots ,x_t]/\left( x_1^{d_1}-x_0^{e_1},x_2^{d_2}-x_1^{e_2},x_3^{d_3}-x_2^{e_3},\dots ,x_t^{d_t}-x_{t-1}^{e_t}\right) , \end{aligned}$$

uses $\Theta (d_1n)$ operations and gives a product of $d_1$ rings of the form

$$\begin{aligned} R[x_2,\dots ,x_t]/\left( x_2^{d_2}-x_0^{e_2e_1/d_1}\zeta ^{e_2cn/d_1},x_3^{d_3}-x_2^{e_3},\dots ,x_t^{d_t}-x_{t-1}^{e_t}\right) . \end{aligned}$$

Each of these rings now has the same structure as $R_t$, except for t being reduced by 1. The point is that $x_0^{e_2e_1/d_1}\zeta ^{e_2cn/d_1}$ can be expressed as a $d_2\cdots d_t$th power, since $e_2e_1/d_1$ and $e_2cn/d_1$ are multiples of $d_2\cdots d_t$; also, $\zeta ^{d_1}$ is a primitive $d_2\cdots d_t$th root of 1. The rest of the DFT proceeds recursively, using a total of $\Theta ((d_1+\cdots +d_t)n)$ operations in R. The inverse also uses $\Theta ((d_1+\cdots +d_t)n)$ operations in R.

The cost is at least $\Theta (n\log n)$. If each $d_j$ is bounded by, say, s then the cost is $O(sn\log n)$. In particular, multiplication in R[G], where G is any finite commutative group whose cardinality $n=\#G$ factors into primes at most s, uses $O(sn\log n)$ operations in R.

Often a primitive nth root of 1 is overkill; it is easy to compute the roots that are actually required given the sequence $d_1,d_2,\dots ,d_t,e_1,e_2,\dots ,e_t$. In the multicyclic case, the algorithm uses only a primitive rth root of 1 for $r={\text {lcm}}\mathopen {}\mathord {\left\{ {d_1,d_2,\dots ,d_t}\right\} }$. In the balanced multicyclic case, where $d_1=d_2=\cdots =d_t$, one has $r=d_1$, usually much smaller than $n=d_1^t$. The Hadamard–Walsh transform is a multicyclic transform with $d_1=d_2=\cdots =d_t=2$, and needs only a primitive 2nd root of 1: i.e., the root $-1$, with 2 invertible in R.

4.12.2 Multicyclic convolution with large coefficients

Consider now the problem of multicyclic convolution over $\mathord {{\mathbb {Z}}}$, i.e., the problem of multiplying in $\mathord {{\mathbb {Z}}}[x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$. Again write $n=d_1\cdots d_t$.

One can reduce multicyclic convolution over $\mathord {{\mathbb {Z}}}/M$ to this problem of multicyclic convolution over $\mathord {{\mathbb {Z}}}$, at the expense of reducing each output coefficient separately modulo M, which costs $O(nb\log b)$ if M has b bits. Conversely, one can reduce multicyclic convolution over $\mathord {{\mathbb {Z}}}$ to multicyclic convolution over a quotient $\mathord {{\mathbb {Z}}}/M$ selected (1) to be sufficiently large to recover the output coefficients in $\mathord {{\mathbb {Z}}}$ and (2) to have appropriate primitive roots of 1 for the standard multicyclic FFTs from Sect. 4.12.1.

However, even in the smooth case, those multicyclic FFTs involve $n(\log n)^{1+o(1)}$ operations in $\mathord {{\mathbb {Z}}}/M$. Many of those operations are multiplications (except in extreme cases such as Hadamard–Walsh transforms), each taking $b(\log b)^{1+o(1)}$ operations if M has b bits. As in Sect. 4.8.5, there is an inefficiency here when both b and n are large. A straightforward use of segmentation replaces the two logarithmic factors with one logarithmic factor times something exponential in t; this was satisfactory in Sect. 4.8.5, with $t=1$, but is not satisfactory in general. One can try to reduce t by replacing $d_1,\dots ,d_t$ with the elementary divisors of the group $\mathord {{\mathbb {Z}}}/d_1\times \dots \times \mathord {{\mathbb {Z}}}/d_t$, but this is not helpful for, e.g., the case $d_1=\cdots =d_t=3$.

To do better, one can inspect standard algorithms for fast integer multiplication (see, e.g., [13]) and observe that many, if not all, of the same ideas naturally support multicyclic convolution. State-of-the-art multicyclic convolution as in [56] is generally more complicated than necessary for this paper, since this paper, unlike [56], freely allows $(\log n)^{o(1)}$ factors; the following paragraphs explain a simpler algorithm. No claims of novelty are made here.

One of the Schönhage–Strassen [85] algorithms to multiply in $\mathord {{\mathbb {Z}}}$ is as follows. There are three parameters: a positive integer $\kappa$, a positive integer $c\in \Theta (\log \kappa )$, and a prime number $p\in 1+\kappa \mathord {{\mathbb {Z}}}$ having $\Theta (\log \kappa )$ bits. Map $\mathord {{\mathbb {Z}}}$ to $\mathord {{\mathbb {Z}}}[y]/(2^c-y)$ and lift to $\mathord {{\mathbb {Z}}}[y]$, splitting each input into coefficients between $-2^{c-1}$ and $2^{c-1}$; map to $\mathord {{\mathbb {Z}}}[y]/(y^\kappa -1)$; map to $(\mathord {{\mathbb {Z}}}/p)[y]/(y^\kappa -1)$; use a length-$\kappa$ FFT to multiply in $(\mathord {{\mathbb {Z}}}/p)[y]/(y^\kappa -1)$. Each product coefficient has absolute value at most $2^{2c-2}\kappa$, so if $p>2^{2c-1}\kappa$ (which is compatible with p having $\Theta (\log \kappa )$ bits) then one easily recovers the product in $\mathord {{\mathbb {Z}}}[y]/(y^\kappa -1)$, and if the output polynomial needed y-degree at most $\kappa -1$ then one easily recovers the original product in $\mathord {{\mathbb {Z}}}$.

Typically $\kappa$ is chosen as a power of 2, so that a traditional power-of-2 FFT uses $\Theta (\kappa \log \kappa )$ operations in $\mathord {{\mathbb {Z}}}/p$. Each operation in $\mathord {{\mathbb {Z}}}/p$ uses $(\log \kappa )^{1+o(1)}$ bit operations, since p has $\Theta (\log \kappa )$ bits. The overall cost is thus $\kappa (\log \kappa )^{2+o(1)}$ for outputs fitting into $\Theta (\kappa \log \kappa )$ bits; i.e., $b(\log b)^{1+o(1)}$ for outputs fitting into b bits.

To handle multicyclic convolution in the same way, take a positive integer $\kappa$, a positive integer $c\in \Theta (\log \kappa n)$, and a prime number $p\in 1+\kappa n\mathord {{\mathbb {Z}}}$ having $\Theta (\log \kappa n)$ bits, with $p>2^{2c-1}\kappa n$. Map the ring $\mathord {{\mathbb {Z}}}[x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$ to the ring $(\mathord {{\mathbb {Z}}}[y]/(2^c-y)) [x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$ and lift to the ring $\mathord {{\mathbb {Z}}}[y,x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$, splitting each of the input coefficients into polynomials in y with coefficients between $-2^{c-1}$ and $2^{c-1}$. Then map to the ring $\mathord {{\mathbb {Z}}}[y,x_1,\dots ,x_t]/(y^\kappa -1,x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$ and further to the ring

$$\begin{aligned} (\mathord {{\mathbb {Z}}}/p)[y,x_1,\dots ,x_t]/\left( y^\kappa -1,x_1^{d_1}-1,\dots ,x_t^{d_t}-1\right) . \end{aligned}$$

Each product coefficient has absolute value at most $2^{2c-2}\kappa n$, so one recovers the product in $\mathord {{\mathbb {Z}}}[y,x_1,\dots ,x_t]/(y^\kappa -1,x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$, and thus the product in $\mathord {{\mathbb {Z}}}[y,x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$ assuming it has y-degree at most $\kappa -1$, and thus the product in $\mathord {{\mathbb {Z}}}[x_1,\dots ,x_t]/(x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$.

The product in $(\mathord {{\mathbb {Z}}}/p)[y,x_1,\dots ,x_t]/(y^\kappa -1,x_1^{d_1}-1,\dots ,x_t^{d_t}-1)$ can be handled as explained in Sect. 4.12.1 if $p\in 1+\kappa n\mathord {{\mathbb {Z}}}$. This uses $O(s\kappa n\log \kappa n)$ operations in $\mathord {{\mathbb {Z}}}/p$ if $\kappa n$ factors into primes at most s. Each operation in $\mathord {{\mathbb {Z}}}/p$ uses $(\log \kappa n)^{1+o(1)}$ bit operations, so the overall cost is at most $s\kappa n(\log \kappa n)^{2+o(1)}$ bit operations for n output coefficients each fitting into $\Theta (\kappa \log \kappa n)$ bits. For this paper, one should think of s as being small: the smooth case emphasized in this paper is that n factors into small primes, and one can easily choose $\kappa$ within any desired range to also factor into small primes.

The applications below focus on reducing various types of FFTs over rings R to multicyclic convolutions, generalizing Sect. 4.8. The application to det computation takes rings R of the form $\mathord {{\mathbb {Z}}}/M$, where M is generally chosen larger and larger as one moves down a tower; one always has $b\ge \Theta (\log n)$, where b is the number of bits in M. One can handle the multicyclic convolutions by the algorithm in the previous two paragraphs, taking $\kappa$ as $b/\Theta (\log bn)$, so $\kappa n$ is $bn/\Theta (\log bn)=bn/\Theta (\log \kappa n)$. The overall cost is then $sbn(\log bn)^{1+o(1)}$ bit operations for n output coefficients each fitting into $\Theta (b)$ bits. This saves a log factor as desired.

4.12.3 A primitive size-m FFT

Let m be a positive integer. Let R be a ring. Let $\zeta$ be a primitive mth root of 1 in R. Write $G=(\mathord {{\mathbb {Z}}}/m)^*$. Consider the ring morphism $R[x]\rightarrow R^G$ that maps g to the vector $b\mapsto g(\zeta ^b)$. The main objective here is to efficiently apply this morphism to $g=g_0+g_1x+\dots +g_{m-1}x^{m-1}$, given $g_0,g_1,\dots ,g_{m-1}\in R$.

This morphism is a “primitive DFT”. This is, for $m>1$, different from a traditional “full DFT”. The difference is that a full DFT evaluates g at $\zeta ^b$ for all $b\in \mathord {{\mathbb {Z}}}/m$, while a primitive DFT evaluates g at $\zeta ^b$ only for $b\in (\mathord {{\mathbb {Z}}}/m)^*$, i.e., only for b coprime to m.

Note that multiplication in $\mathord {{\mathbb {Z}}}/m$ restricts to an action of the group G on $\mathord {{\mathbb {Z}}}/m$, with one orbit $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$ for each positive divisor d of m: for example, this orbit is $(\mathord {{\mathbb {Z}}}/m)^*$ for $d=m$, and $\mathord {\left\{ {0}\right\} }$ for $d=1$. The notation $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$ here uses multiplication by m/d as notation for the map from $\mathord {{\mathbb {Z}}}/d$ to $\mathord {{\mathbb {Z}}}/m$ induced by multiplication by m/d as a map from $\mathord {{\mathbb {Z}}}$ to $\mathord {{\mathbb {Z}}}$.

For each positive divisor d of m, define $I_d$ as the element $\sum _{a\in (\mathord {{\mathbb {Z}}}/d)^*} g_{(m/d)a}a^{-1}$ of the group ring $R[(\mathord {{\mathbb {Z}}}/d)^*]$, and $Z_d$ as the element $\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} \zeta ^{(m/d)b} b$ of the group ring; i.e., these are the vectors $a\mapsto g_{(m/d)a^{-1}}$ and $b\mapsto \zeta ^{(m/d)b}$. Write $O_d$ for the product $I_dZ_d$. Then

$$\begin{aligned} \begin{aligned} O_d&=\sum _{a\in (\mathord {{\mathbb {Z}}}/d)^*} \sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} g_{(m/d)a}a^{-1} \zeta ^{(m/d)b} b =\sum _{a\in (\mathord {{\mathbb {Z}}}/d)^*} \sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} g_{(m/d)a}a^{-1} \zeta ^{(m/d)ba} ba \\&=\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} \sum _{a\in (\mathord {{\mathbb {Z}}}/d)^*} g_{(m/d)a} \zeta ^{(m/d)ba} b =\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} \sum _{j\in (m/d)(\mathord {{\mathbb {Z}}}/d)^*} g_j \zeta ^{bj} b; \end{aligned} \end{aligned}$$

i.e., the entry $(O_d)_b$ in the vector $O_d$ is $\sum _{j\in (m/d)(\mathord {{\mathbb {Z}}}/d)^*} g_{j}\zeta ^{bj}$.

Now $g(\zeta ^b)=\sum _j g_j\zeta ^{bj} =\sum _d \sum _{j\in (m/d)(\mathord {{\mathbb {Z}}}/d)^*} g_j\zeta ^{bj} =\sum _d (O_d)_b$ where d runs through positive divisors of m. The desired vector $b\mapsto g(\zeta ^b)$ is thus the sum of $O_d$ across d. Care is required in the details of this vector addition, for two reasons:

• $O_d$ is represented as a compressed vector, indexed by elements of $(\mathord {{\mathbb {Z}}}/d)^*$. One thus needs to synchronize indices for additions.

• There can be many divisors d of m, and adding each $O_d$ directly into $O_m$ would incur $\#(\mathord {{\mathbb {Z}}}/m)^*$ additions for each d. To more efficiently handle all $O_d$, work upwards through $d<m$, adding each $O_d$ into $O_{dp}$ for the smallest prime p dividing m/d and then forgetting about $O_d$. Each d then incurs $\#(\mathord {{\mathbb {Z}}}/dp)^*\le dp$ additions, and the sum of dp across divisors d of m is bounded by $m(\log m)^{1+o(1)}$.

These additions require computing $O_d$ in the first place for each positive integer d of m, i.e., multiplying $I_d$ by $Z_d$ in $R[(\mathord {{\mathbb {Z}}}/d)^*]$; this is a multicyclic convolution as in Sects. 4.12.1 and 4.12.2. For example, if m is prime then these are multiplications in $R[(\mathord {{\mathbb {Z}}}/m)^*]$ and $R[(\mathord {{\mathbb {Z}}}/1)^*]$, which are cyclic convolutions of lengths $m-1$ and 1 respectively; this special case matches Rader’s original FFT.

If $n=\#(\mathord {{\mathbb {Z}}}/m)^*$ is smooth, meaning all prime factors in $(\log n)^{o(1)}$, then $\#(\mathord {{\mathbb {Z}}}/d)^*$, a divisor of n, also has all prime factors in $(\log n)^{o(1)}$. The convolution algorithm of Sect. 4.12.1 thus uses $O((\log n)^{o(1)}\#(\mathord {{\mathbb {Z}}}/d)^*\log \#(\mathord {{\mathbb {Z}}}/d)^*)$ operations in R, hence $O((\log n)^{1+o(1)}\#(\mathord {{\mathbb {Z}}}/d)^*)$ operations in R. The total cost, the sum of costs over d, is $O(m(\log n)^{1+o(1)})$ since $\sum _d\#(\mathord {{\mathbb {Z}}}/d)^*=m$, hence $O(n(\log n)^{1+o(1)})$ as in Sect. 4.11, hence $n(\log n)^{1+o(1)}$ since the cost for $d=m$ is at least $\Theta (n\log n)$.

When m is a power of an odd prime, this generalization of Rader’s FFT matches the primitive part of a DFT algorithm by Winograd [96, Section 4]. For $m=2^e$, Winograd uses a conventional size-$2^e$ additive FFT to directly solve the original DFT problem, rather than using convolutions to compute primitive DFTs for the multiplicative group $(\mathord {{\mathbb {Z}}}/m)^*$. For general m, Winograd first decomposes a size-m DFT into prime-power DFTs, and then reduces each odd-prime-power DFT to its primitive part. The advantage of working directly with the primitive part of a size-m DFT is that it allows more choices of subgroups, not requiring the subgroups to align with the prime-power decomposition of m.

4.12.4 Inversion

Looking only at the primitive part of a DFT—evaluating $g(\zeta ^b)$ only for $b\in (\mathord {{\mathbb {Z}}}/m)^*$, rather than for all $b\in \mathord {{\mathbb {Z}}}/m$—raises the question of how to recover g from these values. One cannot hope to recover m coefficients of g from only $\#(\mathord {{\mathbb {Z}}}/m)^*$ values for $m>1$, but if one restricts the allowed g indices as in Sect. 4.10 then there is no obvious obstacle to recovering g.

Recall the principle that a full DFT with exponents negated is an inverse full DFT. This implies the same principle for a primitive DFT. Given $v\in R^G$, define $h_j=\sum _{a\in G}v_a\zeta ^{-aj}$ for each $j\in \mathord {{\mathbb {Z}}}/m$; then $\sum _{j\in \mathord {{\mathbb {Z}}}/m} h_j\zeta ^{bj} =\sum _{a\in G}v_a\sum _{j\in \mathord {{\mathbb {Z}}}/m}\zeta ^{(b-a)j}=mv_b$ for $b\in G$. Hence the polynomial $(\sum _j h_j x^j)/m$ has values $v_b$ as desired; note that m is invertible in R since there is a primitive mth root of 1. Among the preimages of v under the map $R[x]/(x^m-1)\rightarrow R^G$, this polynomial is characterized by having value 0 at $\zeta ^b$ if $b\notin G$.

The inverse primitive DFT has a different shape from the forward primitive DFT: it computes m values from $\#(\mathord {{\mathbb {Z}}}/m)^*$ values, rather than the other way around. The inverse can again be reduced to a convolution in the group ring $R[(\mathord {{\mathbb {Z}}}/d)^*]$ for each positive integer d dividing m: the element $H_d=\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} h_{(m/d)b}b$ of the group ring is the product of $Z_d=\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} \zeta ^{(m/d)b}b$ and $V_d=\sum _{a\in G} v_{-1/a} (a\bmod d)$, where $a\bmod d$ means the image of a in $(\mathord {{\mathbb {Z}}}/d)^*$.

To efficiently compute $V_d$ for all d, work downwards through d (reversing how $O_d$ was handled in the forward transform), obtaining $V_d$ for each $d<m$ via $V_{dp}$ for the smallest prime p dividing m/d. The sum of dp is again bounded by $m(\log m)^{1+o(1)}$. This procedure computes all $h_j$ at similar speed to the forward transform.

The following paragraphs explain how to tweak the above procedure to produce an output polynomial where all exponents j are guaranteed to have ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,j}\right\} }$ dividing $m/{{\text {rad}}m}$; here ${\text {rad}}m$ means the radical of m, the product of prime divisors p of m. One can then skip any d not divisible by ${\text {rad}}m$, rather than subsequently eliminating exponents for those d as in Sect. 4.10. For example, when m is prime, the tweaked inversion procedure uses a convolution only for $(\mathord {{\mathbb {Z}}}/m)^*$ (skipping a convolution for $(\mathord {{\mathbb {Z}}}/1)^*$), and produces exponents $1,\dots ,m-1$ (skipping 0), exactly as in Sect. 4.8.4.

Consider any positive integer r dividing ${\text {rad}}m$. Abbreviate ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,r^{\infty }}\right\} }$ as $m_r$, and choose $s_r\in m_r\mathord {{\mathbb {Z}}}\cap (1+(m/m_r)\mathord {{\mathbb {Z}}})$. These quantities $s_r$ have three critical properties:

• If $r=1$ then $s_r\in 1+m\mathord {{\mathbb {Z}}}$.

• If $r>1$ then ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,s_r}\right\} }>1$.

• If a prime divisor p of m does not divide r then the difference $s_r-s_{rp}$ is in $(m/p^{{\text {ord}}_p m})\mathord {{\mathbb {Z}}}$. (Both $s_r$ and $s_{rp}$ are in $m_r\mathord {{\mathbb {Z}}}$ and in $1+(m/m_{rp})\mathord {{\mathbb {Z}}}$, so $s_r-s_{rp}$ is in $m_r\mathord {{\mathbb {Z}}}$ and in $(m/m_{rp})\mathord {{\mathbb {Z}}}$; $m_r$ is coprime to $m/m_{rp}$, so $s_r-s_{rp}$ is in $(mm_r/m_{rp})\mathord {{\mathbb {Z}}}$; and $m_{rp}/m_r=p^{{\text {ord}}_p m}$.)

Define $h'_{j,r}=\sum _{a\in G}v_a\zeta ^{-aj s_r}$. Then $h'_{j,1}=\sum _{a\in G}v_a\zeta ^{-aj}=h_j$ since $s_1\in 1+m\mathord {{\mathbb {Z}}}$, so $\sum _{j\in \mathord {{\mathbb {Z}}}/m} h'_{j,1}\zeta ^{bj}=mv_b$ for $b\in G$. If $r>1$ then $\sum _{j\in \mathord {{\mathbb {Z}}}/m} h'_{j,r}\zeta ^{bj}=0$ for $b\in G$ since ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,s_r}\right\} }>1$.

Define $h'_j=\sum _r \mu (r)h'_{j,r}$ where $\mu$ is the Möbius function. (For example, $h'_j=h'_{j,1}-h'_{j,p}-h'_{j,q}+h'_{j,pq}$ if ${\text {rad}}m$ is the product of primes p, q.) Then $\sum _{j\in \mathord {{\mathbb {Z}}}/m} h'_j\zeta ^{bj}=mv_b$ for $b\in G$.

The polynomial $(\sum _j h'_j x^j)/m$, like the previous polynomial $(\sum _j h_j x^j)/m$, thus has the desired values $v_b$. This polynomial also has the extra feature described above: $h'_j$ can be nonzero only if ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,j}\right\} }$ divides $m/{{\text {rad}}m}$. (Indeed, consider any j for which ${\text {gcd}}\mathopen {}\mathord {\left\{ {m,j}\right\} }$ does not divide $m/{{\text {rad}}m}$, i.e., for which ${\text {ord}}_p j\ge {\text {ord}}_p m$ for some prime p dividing m. If p does not divide r then $s_r-s_{rp}\in (m/p^{{\text {ord}}_p m})\mathord {{\mathbb {Z}}}$, so $js_r-js_{rp}\in m\mathord {{\mathbb {Z}}}$, so $\zeta ^{-ajs_r}=\zeta ^{-ajs_{rp}}$ for each $a\in G$, so $h'_{j,r}=h'_{j,rp}$; hence $h'_j=0$.)

Fast computation of this polynomial works the same way as fast computation of the previous polynomial: the desired $H'_d=\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} h'_{(m/d)b}b$ is the product of $Z'_d$ and $V_d$ in the group ring $R[(\mathord {{\mathbb {Z}}}/d)^*]$, after a precomputation of $Z'_d=\sum _r \mu (r)\sum _{b\in (\mathord {{\mathbb {Z}}}/d)^*} \zeta ^{s_r(m/d)b}b$. If d is not divisible by ${\text {rad}}m$ then $Z'_d=0$; again, the point of this tweak is to skip such values of d.

4.12.5 Folding: the symmetric case

Now let H be a subgroup of G, and write K for the subfield of $\mathord {{\mathbb {Q}}}(\zeta _m)$ fixed by $\mathord {\left\{ {\sigma _c:c\in H}\right\} }$. The objective here is to save a factor essentially $\#H$ for arithmetic on elements of this subfield. The special case of prime m was handled by the folded Rader FFT from Sect. 4.8.

As a starting point, if K has conductor smaller than m, then one can replace m with the conductor, and replace H with the corresponding subgroup for the new conductor. For each change of conductor, one also needs to correspondingly change the input representation; Sect. 4.10 explained how to do this for full cyclotomic fields, and this conversion is compatible with the symmetries described below. So assume from now on that K has conductor m.

Define $H_0=H\cap (1+({\text {rad}}m)(\mathord {{\mathbb {Z}}}/m))$. Section 4.12.7 explains how to handle the possibility that $\#H_0>1$. Assume for now that $\#H_0=1$. For example, if m is squarefree, then ${\text {rad}}m=m$, so $\#H_0=1$.

By [29, Lemma 3(1) and Corollary 2], $\mathord {{\mathbb {Q}}}(\zeta _m)$ has an integral basis set $B\subseteq \zeta _m^{\mathord {{\mathbb {Z}}}}$ such that the usual action of H on $\zeta _m^{\mathord {{\mathbb {Z}}}}$ restricts to a free action of H on B. This implies, as noted in [29, page 281, top paragraph], that $\mathord {\left\{ {\smash {{\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K}\beta :\beta \in B}}\right\} }$ is an integral basis set for K.

These traces ${\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K}\beta$ for $\beta \in B$ generalize the Gauss periods from Sect. 4.7. It seems reasonable to refer to these generalized basis elements as Gauss periods: the periodicity is immediately visible in the coefficients of each trace, thanks to H acting freely on B.

Now represent elements of K as linear combinations of these Gauss periods, generalizing the case of prime m. So far this matches what is proposed in [29, Section 5]. What is not addressed in [29] is how to multiply quickly.

Each input to multiplication is a polynomial $g=g_0+g_1x+\dots +g_{m-1}x^{m-1}$ in $\mathord {{\mathbb {Z}}}[x]/(x^m-1)$ representing $g(\zeta _m)$. This polynomial is not represented on the length-m basis $1,x,\dots ,x^{m-1}$, but rather on a basis of length just $\#(\mathord {{\mathbb {Z}}}/m)^*/\#H$ representing the Gauss periods: the basis set is $\mathord {\left\{ {\sum _{c\in H}x^{bc}:b\in \mathord {{\mathbb {Z}}}/m,\zeta _m^b\in B}\right\} }$. In other words, $g_j=g_{jc}$ for all $j\in \mathord {{\mathbb {Z}}}/m$ and all $c\in H$, and $g_j=0$ when $\zeta _m^j$ is outside B.

Move as usual from $\mathord {{\mathbb {Z}}}$ to a quotient ring R containing the primitive roots of 1 needed for all FFTs that appear. Each input to multiplication is then a polynomial in $R[x]/(x^m-1)$, again represented on the basis set $\mathord {\left\{ {\sum _{c\in H}x^{bc}:b\in \mathord {{\mathbb {Z}}}/m,\zeta _m^b\in B}\right\} }$.

The critical point here is that the H symmetry in the x exponents passes directly through every step in the generalization of Rader’s algorithm from Sect. 4.12.3, producing a generalized folded Rader FFT. For each positive divisor d of m, the input group-ring element $I_d=\sum _{a\in (\mathord {{\mathbb {Z}}}/d)^*} g_{(m/d)a}a^{-1}$ has entries invariant under the action of H on $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$, so one replaces $(\mathord {{\mathbb {Z}}}/d)^*$ with the corresponding quotient group, precomputing a folded version of $Z_d$ in that group. Similar comments apply to the inverse transform from Sect. 4.12.4.

4.12.6 Folding: cost analysis of the symmetric case

Note that sometimes $B\cap \zeta _m^{(m/d)(\mathord {{\mathbb {Z}}}/d)^*}=\mathord {\left\{ {}\right\} }$ so d can simply be skipped in the forward transform. For example, for a prime power $m=p^e$, the basis B in Sect. 4.10 skips some arc of 1/p of the circle; if the arc is chosen to contain 1 then $d=1$ can be skipped.

For the case $m=p$, this leaves just $d=p$, which is why the folded Rader FFT in Sect. 4.8 works exclusively with $(\mathord {{\mathbb {Z}}}/p)^*$. On the other hand, skipping the arc is somewhat deceptive when one tries to generalize; if $e>1$ then one encounters powers of $\zeta _{p^e}$ having different orders. From this perspective, for the case $m=p$ there is expository value in considering the entire circle—as in Rader’s original algorithm, which allows $g_0\ne 0$, doing extra work for a Rader of the lost arc.

For general m, the construction of B in [29, Section 3] avoids any exponent divisible by $p^{{\text {ord}}_p m}$ for any prime divisor p of m; the construction reviewed in Sect. 4.10 also works this way if one chooses the sets $I_{p,e}$ in that section to contain 0. This ensures that the divisors d of m that appear are all divisible by ${\text {rad}}m$. The tweaked inverse transform in Sect. 4.12.4 makes the same guarantee.

If the starting conductor-m field K is a proper subfield of $\mathord {{\mathbb {Q}}}(\zeta _m)$ then requiring the degree n of K to be smooth does not necessarily mean that the degree $\#(\mathord {{\mathbb {Z}}}/m)^*$ of $\mathord {{\mathbb {Q}}}(\zeta _m)$ is smooth. Fortunately, what appears in convolution is not the group $(\mathord {{\mathbb {Z}}}/m)^*$, but the quotient group $(\mathord {{\mathbb {Z}}}/m)^*/H$, which has cardinality n, and, more generally, quotients $((m/d)(\mathord {{\mathbb {Z}}}/d)^*)/H$ having cardinality dividing n, so each cardinality is smooth, giving fast convolution by the algorithm of Sect. 4.12.1.

One also has to check that the total size of the groups $((m/d)(\mathord {{\mathbb {Z}}}/d)^*)/H$ that appear is $n(\log n)^{o(1)}$. The point here is that the action of H on $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$ is free for $d={\text {rad}}m$ (since by assumption $\#H_0=1$ where $H_0=H\cap (1+({\text {rad}}m)(\mathord {{\mathbb {Z}}}/m))$), and thus for each positive divisor d of m divisible by ${\text {rad}}m$. Each element of the quotient $((m/d)(\mathord {{\mathbb {Z}}}/d)^*)/H$ thus corresponds to $\#H$ elements of $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$, and the sets $(m/d)(\mathord {{\mathbb {Z}}}/d)^*$ are disjoint subsets of $\mathord {{\mathbb {Z}}}/m$ as d varies, so the total size of the groups is at most $\mathord {\left\lfloor {m/\#H}\right\rfloor }$. One has $m/\#(\mathord {{\mathbb {Z}}}/m)^*\in (\log n)^{o(1)}$ as in Sect. 4.11, and $\#(\mathord {{\mathbb {Z}}}/m)^*/\#H=n$.

Moving down through a tower of subfields with conductor m corresponds to moving up through a tower of subgroups H of $(\mathord {{\mathbb {Z}}}/m)^*$. If B is chosen so that the largest subgroup H in the tower acts freely on B then the smaller subgroups in the tower will also act freely on B. Moving from the basis for a smaller field to the basis for a larger field is then simply repeating coefficients, and moving the other way (as in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation) is removing redundant coefficients.

4.12.7 Folding: the almost-symmetric case

What happens if instead $\#H_0>1$? One then has $\#H_0=2$ by [29, Lemma 3(2)], with H factoring as a direct product of $H_0$ and another group $H_1$, and [29, Lemma 4] constructs a basis of K that is almost as symmetric as the Gauss periods. Part of the basis consists of traces of the form ${\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K}\zeta ^b$; the other part consists of traces of the form ${\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K_1}\zeta ^b=(1/2){\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K}\zeta ^b$, where $K_1$ is the fixed field of $H_1$ and b is chosen to have ${\text {tr}}^{\mathord {{\mathbb {Q}}}(\zeta _m)}_{K_1}\zeta ^b\in K$. All of this relies on K having conductor m.

The easy approach to fast multiplication here is to represent the elements of K as elements of the superfield $K_1$, using only the $H_1$ symmetry. This reduces to the symmetric case handled above. This loses a factor 2 compared to the desired H symmetry, but this loss is not visible at the level of detail of this section’s cost analyses; $\Theta (\#H_1)$ is the same as $\Theta (\#H)$.

This approach should not be confused with representing the elements of K as elements of $\mathord {{\mathbb {Q}}}(\zeta _m)$, losing the variable factor contemplated in Sect. 4.4. These representations coincide only when $K_1=\mathord {{\mathbb {Q}}}(\zeta _m)$, i.e., when K has half the degree of $\mathord {{\mathbb {Q}}}(\zeta _m)$, i.e., when $\#H_1=1$.

It is instructive to look at the case $\#H_1=1$ more closely. The archetypal examples are the following two half-degree subfields of a power-of-2 cyclotomic field $\mathord {{\mathbb {Q}}}(\zeta _m)$ where $m\ge 8$:

• The subfield fixed by $\sigma _{-1}$, i.e., the real-cyclotomic field $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$.

• The subfield fixed by $\sigma _{m/2-1}$.

Both of these have conductor m, unlike the half-degree cyclotomic subfield $\mathord {{\mathbb {Q}}}(\zeta _{m/2})$, which is the subfield fixed by $\sigma _{m/2+1}$.

In the power-of-2 real-cyclotomic case, the almost-symmetric basis in [29, Lemma 4] consists of the H-traces $\zeta _m+\zeta _m^{-1},\dots ,\zeta _m^{m/4-1}+\zeta _m^{-m/4+1}$ and one $H_1$-trace $\zeta _m^{m/2}=-1$. Because the $H_1$ part of the basis is so short, one can productively use H-folded DFTs to multiply the H-symmetric part of the first input by the H-symmetric part of the second input, and then use schoolbook multiplication to handle the missing products.

4.13 Open questions

Multiquadratic fields $K=\mathord {{\mathbb {Q}}}(\sqrt{d_1},\sqrt{d_2},\dots ,\sqrt{d_t})$ are Abelian. One can apply the machinery from Sect. 4.12 to this case, starting by writing $\sqrt{d_1},\dots ,\sqrt{d_t}$ in terms of Gauss periods. However, the multiplication algorithm in [9, Section 3.3] is considerably simpler, mapping $\mathord {{\mathbb {Z}}}$ to quotient rings $\mathord {{\mathbb {F}}}_p$ for which $\mathord {{\mathbb {F}}}_p[x_1,\dots ,x_t]/(x_1^2-d_1,\dots ,x_t^2-d_t)$ splits into $2^t$ copies of $\mathord {{\mathbb {F}}}_p$. Can one efficiently handle arbitrary towers by the same technique?

(Note that [59] studied tower performance but did not specifically consider the base ring $\mathord {{\mathbb {Z}}}$, and in particular did not consider switching from $\mathord {{\mathbb {Z}}}$ to $\mathord {{\mathbb {F}}}_p$ for a suitably selected p. It would also be interesting to investigate a switch to $\mathord {{\mathbb {R}}}$ or $\mathord {{\mathbb {C}}}$, but using $\mathord {{\mathbb {F}}}_p$ has the virtue of avoiding precision questions.)

One might think that the answer is “Yes, of course”. Start with $R_0=\mathord {{\mathbb {Z}}}$ and $K_0=\mathord {{\mathbb {Q}}}$. For $j\in \mathord {\left\{ {1,2,\dots ,t}\right\} }$, select a monic irreducible polynomial $\varphi _j\in R_{j-1}[x_j]$, define $R_j=R_{j-1}[x_j]/\varphi _j$, and define $K_j=K_{j-1}[x_j]/\varphi _j$. There are infinitely many primes p for which

• $\varphi _1$ splits into linear factors in $\mathord {{\mathbb {F}}}_p[x_1]$;

• $\varphi _2$, with each of the roots of $\varphi _1$ in $\mathord {{\mathbb {F}}}_p$ substituted for $x_1$, splits into linear factors in $\mathord {{\mathbb {F}}}_p[x_2]$;

• etc.;

and then $\mathord {{\mathbb {F}}}_p[x_1,\dots ,x_t]/(\varphi _1,\dots ,\varphi _t)$ is isomorphic to $\mathord {{\mathbb {F}}}_p^n$, where $n=\prod _j\deg \varphi _j$. To compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for a small element $\alpha$ of the ring of integers $\mathcal O$ of $K=K_t$, multiply $\alpha$ by a denominator D known to have $D\mathcal O\subseteq R_t$, and then divide $D^n$ out of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}D\alpha$.

One obvious question is how large the denominator D is. For multiquadratics with coprime squarefree $d_1,\dots ,d_t$, denominator $n=2^t$ suffices; what about other fields? But this question doesn’t seem to matter much for performance, even though D appears to an nth power in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}D\alpha$: in deciding how large $\prod _p p$ needs to be, one can disregard the known divisor $D^n$ of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}D\alpha$ and consider only the size of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. This is the non-Archimedean version of a suggestion from Belabas [10, Section 5.2] mentioned in Sect. 3.3, namely using known divisors to limit the precision of complex embeddings.

A more worrisome question is how large p is. The standard proof that there are infinitely many suitable primes p runs via Chebotarev’s density theorem. This theorem includes the statement that the primes splitting completely in K have density $1/\#G$, where G is the Galois group of K. (An older density theorem due to Frobenius suffices here; see generally [89].) Since the density is nonzero, there are infinitely many such primes. One might have to skip primes that divide D, but there are only finitely many such primes. The density provides enough information to formulate reasonable conjectures regarding the size of p.

The reason this question is worrisome is that Galois groups are generally huge. For example, if n is prime then one expects degree-n fields to have $\#G=n!$, and then one expects p to have $\Theta (n\log n)$ bits—which (1) raises the question of how to find such a p and (2) forces cost $n^{2+o(1)}$ for n-coefficient multiplications. Requiring a smooth tower should bias $\#G$ downwards, but how much?

One might guess that usually $\#G=2^{n-1}$ for a degree-n field having a power-of-2 tower. As a data point, Fig. 3 builds a random-looking tower of fields of degrees 2, 4, 8, 16 and prints out the first 3 primes that split completely in each field. These primes are 11, 13, 23 for degree 2; 61, 157, 181 for degree 4; 181, 647, 1907 for degree 8; and 1331339, 1384861, 1570633 for degree 16. For comparison, 97, 193, 257 split completely in $\mathord {{\mathbb {Q}}}(\zeta _{32})$, a cyclotomic field of degree 16.

Fig. 3

Sage script to build a random-looking tower of fields of degrees 2, 4, 8, 16 and find the first 3 completely split primes in each field

For the case of K being Galois (whether or not Abelian), one has $\#G=n$, so completely split primes p appear with density 1/n. If the goal is to find $n^{1+o(1)}$ such primes, enough primes to have $\Theta (n\log n)$ bits in the product, then one can reasonably conjecture that the maximum prime has only $(2+o(1))\log _2 n$ bits. For weaker bounds assuming GRH, see, e.g., [54, Section 2].

More needs to be done even in the Galois case: fast multiplication in each subfield requires a tower representation that keeps coefficient sizes under control, avoiding the blowups illustrated in Sect. 4.3. For the Abelian case, generalizing Gauss periods as in [29] provides explicit small-coefficient integral bases for each field, and generalizing Rader’s FFT as in this paper provides fast multiplication directly on these bases. Are there explicit subfield-compatible integral bases supporting fast multiplication for Galois number fields beyond Abelian fields?

Another open question is whether one can do better than $n^{2+o(1)}$ for a degree-n Abelian field when n is prime. Perhaps one can achieve $n^{1.5+o(1)}$, analogously to how group structure is used to save an $n^{0.5+o(1)}$ factor in [28, 79, 90], and, in the elliptic case [20].

5 Enumerating small S-units

The primary motivation for this paper comes from the role of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computation inside one of the fundamental tools in computational algebraic number theory: namely, passing all small elements $\alpha \in \mathord {{\mathcal {O}}}$, where $\mathord {{\mathcal {O}}}$ is the ring of integers of K, through a filter that outputs the S-units $\alpha$.

This section reviews parameter choices for this tool, applications of this tool, and the conjectured performance of standard algorithms that work for arbitrary number fields K. This section then analyzes the impact of speedups for the case of smooth-degree cyclotomic fields $K=\mathord {{\mathbb {Q}}}(\zeta _m)$.

5.1 Parameter choices

Beyond the choice of number field K, there is a choice of the set S. Typically an application specifies K, whereas S is something for the algorithm designer to optimize.

The traditional objective in choosing S is to minimize the time required to find filtered S-units that generate the S-unit group, i.e., the time required for a search of all small elements of $\mathord {{\mathcal {O}}}$ to identify small S-units in $\mathord {{\mathcal {O}}}$ that generate the S-unit group. For each S, the group generated by the filtered S-units is the full S-unit group once the search space is large enough, i.e., once the bound on “small” elements of $\mathord {{\mathcal {O}}}$ is large enough; but this raises a quantitative question of how large.

For simplicity, let’s take S specifically as $\infty \cup \mathord {\left\{ {P:\#(\mathord {{\mathcal {O}}}/P)\le y}\right\} }$, where $\infty$ is the set of infinite places, P runs through nonzero prime ideals of $\mathord {{\mathcal {O}}}$, and y is a parameter to be optimized. For algorithms to compute S, see, e.g., [34, Sections 4.8.2 and 6.2].

A nonzero element $\alpha \in \mathord {{\mathcal {O}}}$ is an S-unit if and only if the ideal $\alpha \mathord {{\mathcal {O}}}$ has the form $\prod _{P:\#(\mathord {{\mathcal {O}}}/P)\le y}P^{e(P)}$ for some function $e:\mathord {\left\{ {P:\#(\mathord {{\mathcal {O}}}/P)\le y}\right\} }\rightarrow \mathord {{\mathbb {N}}}$. The S-unit group is the set of nonzero elements $\alpha \in K$ such that the fractional ideal $\alpha \mathord {{\mathcal {O}}}$ has the form $\prod _{P:\#(\mathord {{\mathcal {O}}}/P)\le y}P^{e(P)}$ for some function $e:\mathord {\left\{ {P:\#(\mathord {{\mathcal {O}}}/P)\le y}\right\} }\rightarrow \mathord {{\mathbb {Z}}}$.

For example, in the case $K=\mathord {{\mathbb {Q}}}$, a nonzero rational number is an S-unit if and only if it is y-smooth, i.e., has the form $\pm \prod _{p\le y} p^{e(p)}$. There is an extensive literature on the distribution of y-smooth integers; for surveys see, e.g., [73, 75], and [53]. If integers are chosen independently and uniformly at random from the interval [1, H] then $(\log y)^2$ is conventionally chosen as $(1/2+o(1))(\log H)\log \log H$, giving chance $1/y^{1+o(1)}$ of y-smoothness and giving total time

$$\begin{aligned} y^{2+o(1)}=\exp \left( \left( \sqrt{2}+o(1)\right) \left( \log H\right) ^{1/2}\left( \log \log H\right) ^{1/2}\right) \end{aligned}$$

to find $y^{1+o(1)}$ integers that are y-smooth. See, e.g., [31, Theorem 10.1].

For general number fields, much less has been proven. It is still conventional to choose $(\log y)^2\in (1/2+o(1))(\log H)\log \log H$, where now H is an estimate for the typical size of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. Various applications are then conjectured to find $y^{1+o(1)}$ S-units in total time $y^{2+o(1)}$. See [31, Section 10] for a review of several such conjectures. These conjectures start from the heuristic that, in the words of [31, Section 10], “the auxiliary numbers that ‘would be smooth’ are just as likely to be smooth as random integers of the same approximate magnitude”.

The reason for asking for $y^{1+o(1)}$ S-units is that the rank of the S-unit group is $\#S-1$, which, for reasonably large y, consists mainly of the number of finite places P in S. By Landau’s prime-ideal theorem [65, Section 5], the number of P with $\#(\mathord {{\mathcal {O}}}/P)\le y$ is $(1+o(1))y/{\log y}$.

Some caution is required here. First, Landau’s theorem is a statement as $y\rightarrow \infty$ for a fixed K, not a statement regarding the conventional choice of y as K varies. Furthermore, finding $y^{1+o(1)}$ S-units is not a guarantee of generating the full S-unit group. For the number field $\mathord {{\mathbb {Q}}}(\sqrt{2},\sqrt{3},\sqrt{5},\sqrt{1000003})$, a small search with some notions of smallness will find only elements of $\mathord {{\mathbb {Q}}}(\sqrt{2},\sqrt{3},\sqrt{5})$; Cohen gives a warning in [34, page 354, item (3), last sentence] about small S-units not being “random”.

On the other hand, experiments suggest that, for “balanced” number fields such as $\mathord {{\mathbb {Q}}}(\zeta _m)$, small filtered S-units avoid such conspiracies. See, e.g., Miller’s S-unit computation [70] proving under GRH that $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _{512})$ has class number 1.

The circular approximation in Sect. 2 says that weight-w elements of degree-n power-of-2 cyclotomics have $\log H\approx n(\log w-\gamma )/2$. The conventional choice of y then has $(\log y)^2\in n^{1+o(1)}$ under the mild assumption $w\in n^{O(1)}$. To understand more precisely how large w should be, start from the standard conjectures mentioned above, which say that one needs to search $\exp (n^{1/2+o(1)})$ ring elements to find enough S-units; and then match this to the number of weight-w elements to see that $w\in n^{1/2+o(1)}$. Generating all small ring elements means also using smaller values of w, but almost all of the filtered S-units will be found with $w\in n^{1/2+o(1)}$, and almost all of the computation time is spent with $w\in n^{1/2+o(1)}$. See also [1] for experiments with prime cyclotomics.

5.2 Applications

Filtering small ring elements to find small S-units has a long history. The traditional application is to find fundamental invariants of $\mathord {{\mathcal {O}}}$, such as the class group ${\text {Cl}}\mathord {{\mathcal {O}}}$ and the unit group $\mathord {{\mathcal {O}}}^*$. If the filtered S-units generate the S-unit group then linear algebra on the exponent vectors of the factorizations of S-units (the vectors e above) reveals the unit group (S-units with trivial factorization, i.e., with $e=0$) and, if S is large enough, the class group (all integer vectors modulo the subgroup of “class-group relations”, i.e., the subgroup of S-unit exponent vectors).

For details of this application, see, e.g., Cohen’s description in [34, Section 6.5]. Cohen starts with a more general search that filters small elements of any ideal I to find S-generators of I, and applies this to ideals I obtained as random products of small prime ideals, but also, in [34, page 354, item (3)], mentions taking $I=\mathord {{\mathcal {O}}}$ as an “important speedup”. For simplicity this section focuses on filtering small elements of $\mathord {{\mathcal {O}}}$ to find S-units, but the speedups described below generalize easily to filtering small elements of any I to find S-generators of I.

Starting a few decades ago (see [67]), filtering ring elements to find S-units took on new importance as a critical subroutine inside NFS, the number-field sieve for integer factorization. The number-field sieve is conjectured to factor any positive integer N into primes in time at most $\exp ((\log N)^{1/3+o(1)})$; in this context $\log H\in (\log N)^{2/3+o(1)}$.

A much newer application is “filtered-S-unit attacks” against a problem that has arisen in cryptography, namely finding very short elements of a “worst-case” ideal I, not just the moderately short elements that one finds with, e.g., LLL. See generally [17, 23], and [1]. The simplest S-unit attacks start with an S-generator g of I with $g\in I$, and search for shorter S-generators $gu/v\in I$ where u and v come from a database of S-units. Filtered-S-unit attacks build the database by filtering small elements of $\mathord {{\mathcal {O}}}$, and are conjectured in [17, page 47] to find very short elements (to be precise, “Hermite factor” at most $n^{1/2+o(1)}$; this is overkill for the cryptographic applications) in subexponential time.

Class-group computations, unit-group computations, and NFS carry out linear algebra on the S-unit exponent vectors. The conventional choice of y mentioned above tries to minimize the cost of finding S-units in the first place, without regard to the cost of linear algebra. If linear algebra turns out to be the main bottleneck then algorithm designers can and do improve overall algorithm performance by reducing y; see, e.g., [81, page 115, bottom paragraph]. The cost of finding S-units is then easily visible in the overall algorithm run time.

5.3 The standard filtering procedure

It is straightforward to enumerate all small elements of $\mathord {{\mathcal {O}}}$ for various reasonable notions of “small”. For example, in Sect. 2, one can try all w up to some bound; for each w, enumerate possibilities for a partition of w as a sum of n squares in nonincreasing order; and, for each possibility, enumerate ways to assign the (positive and negative) square roots to $\alpha _0,\alpha _1,\dots ,\alpha _{n-1}$. This rapidly generates small elements $\alpha \in \mathord {{\mathcal {O}}}$. The big problem is to figure out which of these elements $\alpha$ are S-units.

The standard procedure (see, e.g., [34, page 491, step (6)]) computes $N=\mathord {\left| {\smash {{\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha }}\right| }$ and throws $\alpha$ away if N is not y-smooth. The point here is that if $\alpha \mathord {{\mathcal {O}}}=\prod _{P:\#(\mathord {{\mathcal {O}}}/P)\le y}P^{e(P)}$ then $N=\prod _{P:\#(\mathord {{\mathcal {O}}}/P)\le y}\#(\mathord {{\mathcal {O}}}/P)^{e(P)}$; each $\#(O/P)$ is a prime power bounded by y, so N is y-smooth.

As mentioned above, standard conjectures say that $\alpha$ is an S-unit with probability $1/y^{1+o(1)}$ for the conventional choice of y, and that N is y-smooth with probability $1/y^{1+o(1)}$ for the conventional choice of y. This does not mean that these events are identical: if N is y-smooth then the standard procedure still has to check whether $\alpha$ is in fact an S-unit.

Specifically, if N is y-smooth, then, for each prime p dividing N, the standard procedure runs through each P above p (each nonzero prime ideal P of $\mathord {{\mathcal {O}}}$ with $p\in P$) having $\#(\mathord {{\mathcal {O}}}/P)\le y$, computes ${\text {ord}}_P\alpha$ as in [34, Section 4.8.3], and checks whether this accounts for the power of p in N. (The check is simpler if K is Galois: each P above p then has the same $\#(\mathord {{\mathcal {O}}}/P)$, so $\alpha$ is an S-unit if and only if, for each prime p dividing N, some P above p has $\#(\mathord {{\mathcal {O}}}/P)\le y$.) Because N is y-smooth with probability only $1/y^{\Theta (1)}$, this is not a bottleneck asymptotically; as Cohen puts it in [34, page 491], “this will be done quite rarely and does not really increase the running time”.

5.4 Exploiting automorphisms

If $\alpha$ is an S-unit and $\sigma$ is an automorphism of K then $\sigma (\alpha )$ is also an S-unit. Rather than searching all small elements of $\mathord {{\mathcal {O}}}$, one can search orbits of small elements under the automorphism group of K. Typically “small” is defined in a way that is invariant under automorphisms: for example, in Sect. 2, $\sigma (\alpha )$ has weight w if and only if $\alpha$ has weight w.

In particular, if K is Galois, then the automorphism group coincides with the Galois group and has cardinality $n=\deg K$. There are two reasons that this does not imply a speedup factor n; on the other hand, for typical examples, the speedup factor does end up as $\Theta (n)$.

The first reason is that, for $n>1$, some elements of K are in proper subfields and thus have smaller orbits. For example, in Sect. 2, $\alpha =\sum _{0\le j<n}\alpha _j\zeta _m^j$ is in a proper subfield of K if and only if $\alpha _j=0$ for all odd j. However, this is increasingly rare as w grows.

The second reason is that one has to account for the cost of enumerating orbits. The naive approach is to enumerate all small ring elements and then, for each element, try applying automorphisms to see whether the element is an orbit leader (say, first in its orbit in lexicographic order as a vector on a specified basis). One expects to try only $\Theta (\log n)$ automorphisms on average for recognizing that an element isn’t an orbit leader. This might sound fast enough for fields where applying an automorphism costs only $n^{1/2+o(1)}$ in sparse representation—but one wants small costs per orbit, not just small costs per element. Simply writing down an element in sparse form usually costs $n^{1/2+o(1)}$, so writing down all n elements in a size-n orbit usually costs $n^{3/2+o(1)}$. Evaluating ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for the orbit leader $\alpha$ costs more than this in Sect. 3 but less than this in Sect. 4.

In various concrete examples of interest, one can easily modify the generation of small ring elements to more efficiently generate orbit leaders. For example, for power-of-2 cyclotomics, an element $\alpha =\sum _{0\le j<n}\alpha _j\zeta _m^j$ outside all proper subfields can always be conjugated to have $\alpha _1\ne 0$, so one can handle the degree-n/2 subfield recursively and then limit the generation procedure to force $\alpha _1\ne 0$. This reduces the orbit-enumeration cost by a factor $n^{1/2+o(1)}$ for $w\in n^{1/2+o(1)}$: each element has at most w nonzero positions, and position j is moved to position 1 by at most two automorphisms. One can impose further restrictions to further reduce the orbit-enumeration cost; see, e.g., how the cycloshort module in [1] generates orbit leaders in the case of prime m, for orbits not just under automorphisms but also under multiplications by $\zeta _m$.

5.5 Exploiting subfields

Take again a weight-w integral element $\alpha$ in a degree-n power-of-2 cyclotomic field K, and assume $w\in n^{1/2+o(1)}$. The circular approximation in Sect. 2 says that ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ almost always has $\Theta (n\log n)$ bits. Section 1 already explained how to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ in time $n(\log n)^{3+o(1)}$ in this case using a tower of cyclotomic subfields, and Sect. 4 explained how to reach this cost for any Abelian field whose degree is $(\log n)^{o(1)}$-smooth, whereas the best non-subfield methods from Sect. 3 take time $n^2(\log n)^{2+o(1)}$. Combining this $n/(\log n)^{1+o(1)}$ speedup with the $\Theta (n)$ automorphism speedup gives an overall $n^2/(\log n)^{1+o(1)}$ speedup in the sequence of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computations.

Note that this is a speedup from one type of algorithm to another, with both types applied to power-of-2 cyclotomics: namely, a speedup from (1) general-purpose algorithms to (2) algorithms exploiting automorphisms and subfields. The subroutines used for the general-purpose algorithms to reach $n^2(\log n)^{2+o(1)}$ include complex FFTs exploiting the structure of the roots of $x^m-1$; see Sect. 3.3. For a field such as $\mathord {{\mathbb {Q}}}[x]/(x^n-x-1)$ without this structure, the best techniques in Sect. 3 cost $n^2(\log n)^{3+o(1)}$ except when the polynomial-remainder sequence is particularly short, so moving from such a field to a power-of-2 cyclotomic of the same degree gives an $n^2(\log n)^{o(1)}$ speedup. This speedup factor drops to $n^2/(\log n)^{1+o(1)}$ if there is some way to reach cost $n^2(\log n)^{2+o(1)}$ for ${\text {det}}^{\mathord {{\mathbb {Q}}}[x]/(x^n-x-1)}_{\mathord {{\mathbb {Q}}}}$. In any case, given known techniques, it is clear that one should check the field structure, and in particular should take advantage of automorphisms and subfields.

5.6 Better alternatives for limited-dimension search spaces

NFS uses number fields that, compared to cyclotomics with the same size of H and the same size of y, have relatively low degree and relatively high discriminant. Quantitatively, the NFS field degree is only $(\log y)^{1+o(1)}$ rather than $(\log y)^{2+o(1)}$. Furthermore, small ring elements in NFS are tilted towards having a small number of coefficients. Most of the NFS literature considers just two integer coefficients $(\alpha _0,\alpha _1)$ of an element $\alpha =\alpha _0+\alpha _1\theta$ of a selected number field $\mathord {{\mathbb {Q}}}(\theta )$, with a search space of $y^{2+o(1)}$ elements defined by a range of $y^{1+o(1)}$ choices of $\alpha _0$ and a range of $y^{1+o(1)}$ choices of $\alpha _1$; see, e.g., [31, Algorithm 11.1, Step 3].

In this setting, one can fix $\alpha _1$ and view ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ as a polynomial in the integer $\alpha _0$. One can write down successive polynomial values using repeated differences or using asymptotically faster multipoint-evaluation subroutines. NFS algorithm statements usually avoid writing down these values in the first place: instead they observe that the values of $\alpha _0$ for which ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is divisible by p consist of a small number of arithmetic progressions modulo p, and simply mark those positions in an array indexed by $\alpha _0$, assuming free access to RAM. See, e.g., [31, page 57]. This Eratosthenes-like sieving procedure accounts for the “sieve” part of the name of NFS.

To limit RAM usage, more advanced versions of NFS limit the size of p found in this way; they then write down ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ and switch over to “cofactorization” to find larger p. This does not mean that ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation is a bottleneck: these versions of NFS carry out cofactorization only on the occasions that the product of small p found is above a specified cutoff. With this type of “early abort”, NFS is not carrying out a full search for all small S-units; but the requirement of having many small p, like the requirement of having small coefficients, is algebraically compatible with finding the full S-unit group, and analytically is conjectured to have similar smoothness probabilities. Such conjectures are again provable for $\mathord {{\mathbb {Q}}}$; see Pomerance’s early-abort analysis in [81, Section 4].

Sometimes the NFS literature considers two-dimensional lattices of integer pairs $(\alpha _0,\alpha _1)$ for which ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is divisible by p; see, e.g., [80]. One can also consider NFS variants with three or more coefficients in $\alpha$, but normally NFS takes fields where the size of $\theta ^j$ increases rapidly with j, so one would expect the optimal lattice dimension to be small; the question of whether three coefficients are useful in NFS appears in, e.g., [15, fourth slide, bottom two lines].

The literature on class-group computation often considers fields of low degree with large coefficient ranges as in NFS, but it also considers fields of high degree with small coefficient ranges such as cyclotomics. The literature on S-unit attacks focuses on high-degree fields such as cyclotomics. As the lattice dimension increases and the allowed coefficient size decreases, it seems to become more and more difficult to quickly identify small ring elements in a lattice of ring elements divisible by p, except when p is very small. Fast ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation plays an obvious role in these applications when K has high degree.

5.7 Exploiting more cyclotomic structure

A useful step in computing the structure of the cyclotomic field $\mathord {{\mathbb {Q}}}(\zeta _m)$ is to compute the structure of the real-cyclotomic field $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$, which has half the degree if $m\ge 3$.

For the unit group of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$, one can instantly write down generators of a full-rank subgroup, the group of “cyclotomic units”. These generators are also rapidly found by a search of small ring elements.

For example, the set of cyclotomic units is $\zeta _m^{\mathord {{\mathbb {Z}}}}\prod _{c\in \mathord {\left\{ {1,3,\dots ,m-1}\right\} }}(1+\zeta _m^c+\zeta _m^{-c})^{\mathord {{\mathbb {Z}}}}$ in the power-of-2 case. The group of cyclotomic units is conjectured to be the full unit group in this case. See [23, Appendix C] for a review of evidence for this conjecture.

For general m, there is often a gap between the group of cyclotomic units and the full unit group. To test whether the index is divisible by a given prime $\ell$, one can use order-$\ell$ characters to see whether there are products of powers of generators of the known group that are $\ell$th powers of units outside the group; if so, one can adjoin the $\ell$th roots and repeat. (This procedure is often called “$\ell$-saturation” in the context of unit-group computation.) After checking all small primes $\ell$, one can reasonably hope that the full unit group is known.

To confidently obtain the class group of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$, the literature uses filtered S-units, as in [70]. For any number field, confirming the class number also confirms the full unit group by analytic techniques. For $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$ where m is a prime power, these techniques boil down to Kummer’s theorem that the class number of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$ is the index of the cyclotomic units inside the full group of units. See, e.g., [94, Theorem 8.2], and see [88] for a generalization to any m.

Starting from the units of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$, one obtains the units of $\mathord {{\mathbb {Q}}}(\zeta _m)$ by adjoining $\zeta _m$ and, for m not a prime power, $1-\zeta _m$; see [94, page 40]. There is also a standard easy-to-compute formula for the class number of $\mathord {{\mathbb {Q}}}(\zeta _m)$ in terms of the class number of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$; see [94, Theorem 4.17]. For p-units, meaning S-units where the finite places in S are the prime ideals over p, one can efficiently move from the p-units of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$ to the p-units of $\mathord {{\mathbb {Q}}}(\zeta _m)$ by adjoining Jacobi sums and then taking square roots (2-saturation); see [17]. For further S-units of $\mathord {{\mathbb {Q}}}(\zeta _m)$, filtering appears in [17, page 47] and [1].

In short, cyclotomics make many computations easier, but filtering continues to play an important role: filtering gives S-units of $\mathord {{\mathbb {R}}}\cap \mathord {{\mathbb {Q}}}(\zeta _m)$, cyclotomic structure then gives the p-units of $\mathord {{\mathbb {Q}}}(\zeta _m)$, and further filtering gives further S-units of $\mathord {{\mathbb {Q}}}(\zeta _m)$.

5.8 Comparison to the cost of smoothness detection

One might think that checking the y-smoothness of $N={\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ is, at least asymptotically, much more expensive than computing N in the first place. ECM is conjectured to use $\exp ((\sqrt{2}+o(1))(\log y)^{1/2}(\log \log y)^{1/2})$ multiplications mod N; early-abort ECM from [22, Section 3] is conjectured to replace $\sqrt{2}$ with $\sqrt{8/9}$; either way, the cost is exponential in $n^{1/4+o(1)}$ when $\log y\in n^{1/2+o(1)}$.

However, one can merge smoothness tests of many integers N, even without the visible structure from Sect. 5.6. Specifically, if Y is a finite set of primes and S is a finite sequence of positive integers then the batch smoothness-detection algorithm from [14] uses—assuming free RAM access—$O(B(\log B)^{2+o(1)})$ bit operations to find all Y-smooth integers in S (integers that factor into the primes in Y), where B is the total number of bits in Y and S. A closer look shows that if one plugs in the Harvey–van der Hoeven integer-multiplication algorithm [56] then the number of bit operations is $O(B(\log B)^2)$.

In particular, take $Y=\mathord {\left\{ {p:p\le y}\right\} }$; then Y has $\Theta (y)$ bits. Assume that S has $\Theta (y)$ integers, each having $\Theta (n\log n)$ bits. Then $B\in \Theta (yn\log n)$. The conventional choice of y has $\log y\in \Theta (n^{1/2}\log n)$, so the cost $O(B(\log B)^2)$ is $O(yn^2(\log n)^3)$, i.e., $O(n^2(\log n)^3)$ per integer.

This analysis suggests that, with optimized subroutines for general number fields, ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation and batch smoothness detection are balanced—up to a constant factor, which could point in either direction—in the number of bit operations. Saving a constant factor in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation thus makes the entire S-unit search faster by a constant factor. This does not require the work in Sect. 4—the improvement in Sect. 3.3 from $n^2(\log n)^3$ to $n^2(\log n)^2$ for cyclotomics is enough—but further speedups in ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation, as in Sect. 4, make it easier to see speedups in batch smoothness detection.

Understanding the real-world impact of these speedups for concrete sizes requires a much more detailed analysis and optimization of S-unit searches. As an example of the issues that will arise, the real costs of RAM are a bigger problem for batch smoothness detection than for ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation. On the other hand, rather than taking $Y=\mathord {\left\{ {p:p\le y}\right\} }$, one can take Y as the set of primes p where some P over p has $\#(\mathord {{\mathcal {O}}}/P)\le y$. This is particularly effective in the Galois case, reducing $\#Y$ by a factor $n+o(n)$, which also reduces RAM requirements by a factor $n+o(n)$. The same change of Y speeds up conventional trial division. Cyclotomics also provide some speedup for Pollard’s $\rho$ method (use the iteration polynomial $x^m+c$) and Pollard’s $p-1$ method (if $p\in 1+m\mathord {{\mathbb {Z}}}$ then $p-1$ is more likely to factor appropriately), although much less speedup for ECM.

Finally, note that working with orbits under the Galois group as in Sect. 5.4 speeds up a sequence of smoothness tests by the same $\Theta (n)$ factor that it speeds up a sequence of ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluations: there are that many fewer N values to handle. It is clear that known algorithms for S-unit searches are much faster for cyclotomics than for unstructured number fields; the only question is how much.

Appendices

Appendix A: software to check the Gauss-period algorithms

An open-source software package abelianfields is available from [18] for various tests that the main algorithms described in this paper work as specified. This appendix describes the software.

1.1 A.1: software readability

The idea that a test of software S is also a test of algorithm A relies implicitly on the idea that there is a match between S and A. Helping readers check this match was a high priority in the development of the abelianfields software package. This has three important consequences.

First, this software is written in a high-level language, specifically Sage. This has the disadvantage of incurring Sage overhead for each step. This is a large slowdown when one step is an arithmetic operation in a small finite field, as in Sect. 4.12.2. The software does not attempt to show what can be done in reducing overhead per ring operation. See Appendix C for further software illustrating ways to streamline ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}$ evaluation in the case of power-of-2 cyclotomic fields K, using a lower-level language.

Second, abelianfields uses straightforward subroutines for precomputations. Here “precomputations” refers to algorithm steps that depend only on the number field and the number of input bits, independently of the specific input at hand. The paper’s performance evaluation assumes that the results of these precomputations are cached, and that there are enough inputs that the cost of the precomputations does not matter; consequently, various speedups in the precomputations, such as known techniques to accelerate the search for prime fields with appropriate primitive roots of 1, are simply ignored. The software makes a few exceptions for subroutines that seemed likely to cause scaling problems for experiments and that were easy to rewrite in faster ways.

Third, within the main computation, various standard speedups are suppressed because they would compromise readability. For example, FFTs are not cached; software prioritizing speed would include FFT caching, even though this does not affect the $n(\log n)^{3+o(1)}$ asymptotic. As another example, the software includes not just tests of its main functions, but also many assertions inside the functions to highlight assumptions and conclusions; eliminating assertions is a standard speedup.

1.2 A.2: basic subroutines

The following low-level functions inside abelianfields are used in various ways inside the convolution functions described in Appendix A.3, the prime-conductor det functions described in Appendix A.4, and the general-conductor det functions described in Appendix A.5:

• primitive.root_remember, given a ring R, a positive integer n, and a primitive nth root of 1 in R, caches that root for future reference. The caching does not currently move across pairs (R, n), for example to obtain a primitive nth root by squaring a previously cached primitive 2nth root.

• primitive.root returns a primitive nth root of 1 in R, given R and n. This function tries to find and cache a primitive nth root if one has not been previously specified by primitive.root_remember; this search is fast when R is a prime field.

• units.generator, given m, returns a deterministically selected generator of $(\mathord {{\mathbb {Z}}}/m)^*$, if $(\mathord {{\mathbb {Z}}}/m)^*$ is cyclic. Note that applying primitive.root to inputs $R=\mathord {{\mathbb {Z}}}/m$ and $n=\#(\mathord {{\mathbb {Z}}}/m)^*$ often differs from this: for example, $(\mathord {{\mathbb {Z}}}/4)^*$ has a generator 3, but $\mathord {{\mathbb {Z}}}/4$ does not have a primitive 2nd root of 1.

• tree.producttree and tree.remainders are product-tree/remainder-tree subroutines. These are copied from [21], except for minor tweaks to upgrade to Python 3.

• tree.interpolate is an analogous interpolation-tree subroutine. (Sage’s built-in CRT function provides the same results as tree.interpolate aside from details of how inputs are arranged, but uses an algorithm that scales quadratically in most cases. This difference is outside this paper’s algorithm analysis, since interpolation is used only in precomputation.)

• auxmodulus.prime, given B and n, returns the smallest prime number in $\mathord {\left\{ {B,B+1,B+2,\dots }\right\} }\cap (1+n\mathord {{\mathbb {Z}}})$.

• auxmodulus.product, given B and n, returns an integer $M\ge B$ and a sequence P of distinct prime numbers in $1+n\mathord {{\mathbb {Z}}}$ having product M. This function also uses primitive.root_remember to remember a primitive nth root of 1 in $\mathord {{\mathbb {Z}}}/M$, obtained from interpolating (via tree.interpolate) primitive nth roots of 1 in $\mathord {{\mathbb {Z}}}/p$ across p in P. Currently the prime numbers in P are chosen as the smallest prime numbers in $1+n\mathord {{\mathbb {Z}}}$, with the search stopping once the number of bits in the prime numbers minus the number of primes is at least the number of bits in B. More work would usually bring M somewhat closer to B.

The general-conductor det functions also rely on various further manipulations of subgroups and quotient groups of $(\mathord {{\mathbb {Z}}}/m)^*$, which are abstracted by units as follows:

• units.group, given m, returns the group $(\mathord {{\mathbb {Z}}}/m)^*$. This group supports elements (see units.element below), iteration, and the following functions:

  • cardinality returns $\#(\mathord {{\mathbb {Z}}}/m)^*$.

  • modulus returns m.

  • gens returns a vector of independent generators of $(\mathord {{\mathbb {Z}}}/m)^*$. Calling this function repeatedly always returns the same vector.

  • ngens returns the number of generators returned by gens.

  • gens_orders returns a vector showing the order of each generator returned by gens.

  • ring returns $\mathord {{\mathbb {Z}}}/m$, represented as Sage’s Zmod(m).

  • subgroup_1mod, given a positive divisor d of m, returns the kernel (represented as a units.subgroup; see below) of the natural map from $(\mathord {{\mathbb {Z}}}/m)^*$ to $(\mathord {{\mathbb {Z}}}/d)^*$. Internally, this uses a trivial enumeration of $(\mathord {{\mathbb {Z}}}/m)^*$ for simplicity; one can do better for large m.

• units.element, given $(\mathord {{\mathbb {Z}}}/m)^*$ (represented as a units.group) and an element of Sage’s Zmod(m) or ZZ coprime to m (or, alternatively, an exponent vector on units.group(m).gens()), returns an element of $(\mathord {{\mathbb {Z}}}/m)^*$, with support for all of Sage’s AbelianGroupElement features (e.g., multiplication and exponents) and the following extra functions:

  • modulus returns m.

  • inring returns the corresponding element of Zmod(m).

  • reduce, given a positive divisor d of m, returns the element of $(\mathord {{\mathbb {Z}}}/d)^*$ obtained by feeding this element of $(\mathord {{\mathbb {Z}}}/m)^*$ through the natural map from $(\mathord {{\mathbb {Z}}}/m)^*$ to $(\mathord {{\mathbb {Z}}}/d)^*$.

• units.subgroup, given m and $g_1,g_2,\ldots \in (\mathord {{\mathbb {Z}}}/m)^*$, returns the subgroup H of $(\mathord {{\mathbb {Z}}}/m)^*$ generated by $g_1,g_2,\dots$. This subgroup supports elements (as elements of $(\mathord {{\mathbb {Z}}}/m)^*$), iteration, and the following functions:

  • cardinality returns $\#H$.

  • modulus returns m.

  • gens, ngens, and gens_orders are as above, but for independent generators of H rather than independent generators of $(\mathord {{\mathbb {Z}}}/m)^*$.

  • fullgroup returns $(\mathord {{\mathbb {Z}}}/m)^*$.

  • quotient returns the quotient group $(\mathord {{\mathbb {Z}}}/m)^*/H$, represented as a units.quotient (see below).

  • reduce, given a positive divisor d of m, returns the subgroup of $(\mathord {{\mathbb {Z}}}/d)^*$ obtained by feeding H through the natural map from $(\mathord {{\mathbb {Z}}}/m)^*$ to $(\mathord {{\mathbb {Z}}}/d)^*$.

  • extend, given a vector of elements of $(\mathord {{\mathbb {Z}}}/m)^*$, returns the subgroup generated by H and those elements.

  • intersect, given a subgroup $H'$ of $(\mathord {{\mathbb {Z}}}/m)^*$, returns $H\cap H'$.

  • is_subgroup_of, given a subgroup $H'$ of $(\mathord {{\mathbb {Z}}}/m)^*$, returns True if H is a subgroup of $H'$, else False.

  • representatives_mod, given a subgroup $H'$ of H (as a subgroup of $(\mathord {{\mathbb {Z}}}/m)^*$), returns representatives in $(\mathord {{\mathbb {Z}}}/m)^*$ of the quotient $H/H'$.

  • conductor returns the conductor of H.

  • is_radfree returns True if H is rad-free, meaning that H acts freely on $(\mathord {{\mathbb {Z}}}/{{\text {rad}}m})^*$.

  • is_friendly returns True if H is friendly, meaning that (1) m is divisible by 8 and all elements of H are 1 modulo 4 or (2) m is not divisible by 8.

• units.quotient, given m and a subgroup H of $(\mathord {{\mathbb {Z}}}/m)^*$, returns the quotient group $Q=(\mathord {{\mathbb {Z}}}/m)^*/H$. This quotient group supports elements (see units.quotientelement below), iteration, and the following functions:

  • cardinality returns $\#Q$.

  • modulus returns m.

  • gens, ngens, gens_orders are as above, but for independent generators of Q.

  • fullgroup returns $(\mathord {{\mathbb {Z}}}/m)^*$.

  • denominator returns H.

• units.quotientelement, given $Q=(\mathord {{\mathbb {Z}}}/m)^*/H$ as above and an element of $(\mathord {{\mathbb {Z}}}/m)^*$ (or, alternatively, an exponent vector on Q .gens()), returns an element of Q, with support for all of Sage’s AbelianGroupElement features and the following functions:

  • lift returns a preimage of this element under the natural map from $(\mathord {{\mathbb {Z}}}/m)^*$ to Q.

  • reduce, given a positive divisor d of m, returns the element of $(\mathord {{\mathbb {Z}}}/d)^*/H$ obtained by feeding this element of Q through the natural map from $(\mathord {{\mathbb {Z}}}/m)^*/H$ to $(\mathord {{\mathbb {Z}}}/d)^*/H$.

Sage has a built-in Zmod(m).unit_group() that supports some of the above features; abelianfields uses Zmod(m).unit_group() for some tests, and also tests units.subgroup.conductor against PARI’s computation of conductors of fixed fields of subgroups of the Galois group of $\mathord {{\mathbb {Q}}}(\zeta _m)$.

1.3 A.3: convolution functions

The convolution module inside abelianfields handles the standard convolution techniques from Sects. 4.12.1 and 4.12.2:

• convolution.multi_fft evaluates an isomorphism to $R^n$ from the ring $S=R[x_1,x_2,\dots ,x_t]/(x_1^{d_0}-x_0^{e_0}, \dots ,x_t^{d_{t-1}}-x_{t-1}^{e_{t-1}})$, given a ring R, a primitive nth root $\zeta$ of 1 in R, a unit $x_0$ in R, a list d of t positive integers with product n, and a list e of t nonnegative integers where n divides $e_0$ if $t\ge 1$. This function also supports an optional reverse=True argument that inverts the isomorphism.

• convolution.multi multiplies in the above ring S.

• convolution.multi_cyclic multiplies in S in the case $e_0=e_1=\dots =e_{t-1}=0$.

• convolution.cyclic is the case $t=1$, multiplying in $R[x]/(x^d-1)$.

The convolution.multi_fft and convolution.multi functions leave it to the caller to handle replacing $d_i$ with $p,d_i/p$ for speed when $d_i$ is composite and p is a prime divisor of $d_i$. The *cyclic* functions, which are the functions used elsewhere in abelianfields, handle this replacement automatically.

By default, the *cyclic* functions require R to be $\mathord {{\mathbb {Z}}}$ or $\mathord {{\mathbb {Z}}}/M$, and do not require R to contain a primitive nth root of 1. These functions automatically decompose large coefficients into elements of a small prime field $\mathord {{\mathbb {Z}}}/p$, saving a logarithmic factor as described in Sect. 4.12.2. Presumably handling this by segmentation, as in Sect. 4.8.5, would be noticeably faster for small t, and in particular for convolution.cyclic.

The *cyclic* functions also support a guaranteed_primitive=True option that requires R to contain a primitive nth root of 1; in this case R is not required to be $\mathord {{\mathbb {Z}}}$ or $\mathord {{\mathbb {Z}}}/M$. Currently guaranteed_primitive=True also disables decomposing large coefficients into elements of a small prime field.

1.4 A.4: functions for prime-conductor fields

The prime module inside abelianfields handles number fields of odd prime conductor p, along with $\mathord {{\mathbb {Q}}}$. Some of the functions in this module provide size-p FFT algorithms and, more generally, folded Rader FFTs for positive divisors d of $p-1$:

• prime.complete is a size-p DFT. This function is given a ring R, an odd prime number p, a primitive pth root $\zeta$ of 1 in R, and the coefficients $g_0,g_1,\dots ,g_{p-1}$ of a polynomial $g=g_0+g_1x+\dots +g_{p-1}x^{p-1}\in R[x]$; this function returns $g(1),g(\zeta _p),\dots ,g(\zeta _p^{p-1})$. Internally, this function implements Rader’s original FFT algorithm reviewed in Sect. 4.8.1. This function is not used elsewhere; it is provided as a baseline algorithm for comparison.

• prime.folded takes R, p, $\zeta$, a positive integer d dividing $p-1$, and d coefficients $g_0,g_1,\dots ,g_{d-1}$ representing the d-periodic polynomial $g=\sum _j g_j (x^{\omega ^{-j}}+x^{\omega ^{d-j}}+\dots +x^{\omega ^{p-1-d-j}})$ where $\omega$ is units.generator(p). This function returns $g(\zeta ^{\omega ^0}),\dots ,g(\zeta ^{\omega ^{d-1}})$. Internally, this function uses the folded Rader algorithm reviewed in Sect. 4.8.3, so it is simply a length-d cyclic convolution with a precomputed vector. The largest case, $d=p-1$, is close to prime.complete, but prime.complete allows nonzero constant coefficient, also evaluates at 1, and has a different order of inputs and outputs.

• prime.folded_inverse inverts prime.folded for any particular $(R,p,\zeta ,d)$. See Sect. 4.8.4 for the algorithm.

All of these functions currently require R to be $\mathord {{\mathbb {Z}}}$ or some $\mathord {{\mathbb {Z}}}/M$, and internally use convolution.cyclic.

Further prime functions operate on elements of $\mathord {{\mathbb {Z}}}^d$, representing d-periodic polynomials over $\mathord {{\mathbb {Z}}}$, representing (integral) d-periodic elements of $\mathord {{\mathbb {Q}}}(\zeta _p)$, meaning elements of the degree-d subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$. Note that, in particular, the element $(z,z,\dots ,z)\in \mathord {{\mathbb {Z}}}^d$ represents the element $-z$ of $\mathord {{\mathbb {Q}}}(\zeta _p)$. Each function is given p and d along with the further inputs described below:

• prime.multiply takes two elements of $\mathord {{\mathbb {Z}}}^d$ representing d-periodic elements $\alpha ,\beta \in \mathord {{\mathbb {Q}}}(\zeta _p)$, and returns an element of $\mathord {{\mathbb {Z}}}^d$ representing $\alpha \beta$. Internally, prime.multiply computes an easy bound on the absolute coefficients of $\alpha \beta$; uses auxmodulus.product to choose a modulus M above twice this bound with a primitive pth root of 1 in $\mathord {{\mathbb {Z}}}/M$; and finishes with two length-d folded DFTs over $\mathord {{\mathbb {Z}}}/M$, d multiplications in $\mathord {{\mathbb {Z}}}/M$, and one length-d inverse folded DFT over $\mathord {{\mathbb {Z}}}/M$. Each folded DFT boils down to one length-d cyclic convolution with a precomputed sequence.

• prime.subfield takes a positive integer $d_2$ dividing d, and an element of $\mathord {{\mathbb {Z}}}^d$ representing a d-periodic element $\alpha \in \mathord {{\mathbb {Q}}}(\zeta _p)$. It returns an element of $\mathord {{\mathbb {Z}}}^{d_2}$ representing $\alpha$, if $\alpha$ is $d_2$-periodic. In other words, it extracts the first $d_2$ entries of the input sequence, if the input sequence is $d_2$-periodic.

• prime.conjugate takes an integer e, and an element of $\mathord {{\mathbb {Z}}}^d$ representing a d-periodic element $\alpha \in \mathord {{\mathbb {Q}}}(\zeta _p)$. It returns an element of $\mathord {{\mathbb {Z}}}^d$ representing $\sigma (\alpha )$, where $\sigma$ is the unique automorphism of $\mathord {{\mathbb {Q}}}(\zeta _p)$ mapping $\zeta _p$ to $\zeta _p^{\omega ^e}$, where again $\omega$ is units.generator(p). In other words, prime.conjugate rotates the input sequence to the left by e positions.

• prime.det_relative evaluates the determinant map from the degree-d subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ down to the degree-$d_2$ subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$, where $d_2$ is a positive integer dividing d. This function takes $d_2$ and an element of $\mathord {{\mathbb {Z}}}^d$ representing a d-periodic element $\alpha \in \mathord {{\mathbb {Q}}}(\zeta _p)$, and returns an element of $\mathord {{\mathbb {Z}}}^{d_2}$. Internally, this function includes two implementations (tested against each other): the default implementation saves time by pushing conjugation and subfield extraction through the DFTs as explained in Sect. 4.8.6, but there is also a simpler reference implementation, enabled by ref=True, that multiplies conjugates by calling prime.conjugate and prime.multiply as black boxes.

• prime.det_absolute evaluates the determinant map from the degree-d subfield of $\mathord {{\mathbb {Q}}}(\zeta _p)$ down to $\mathord {{\mathbb {Q}}}$. Internally, this function automatically factors d into primes and repeatedly applies prime.det_relative. One could alternatively modify prime.det_relative to internally perform this factorization; either way, the factorization is essential for the speed of this paper’s algorithms.

1.5 A.5: functions for arbitrary-conductor fields

The general module inside abelianfields has a similar structure to the prime module but supports arbitrary conductor. Some of the functions provide the construction from [29, Section 5] of an H-normal basis:

• general.normalbasis, given a rad-free subgroup H of $(\mathord {{\mathbb {Z}}}/m)^*$, returns B/H and a list of rewrite rules. Here B is an H-normal integral basis of $\mathord {{\mathbb {Q}}}(\zeta _m)$ consisting of roots of 1, and the rewrite rules specify how to rewrite arbitrary roots of 1 in terms of B. Internally, the rewriting follows the construction from [97] and [26] reviewed in Sect. 4.10.

• general.canonicalize expresses an H-periodic polynomial as an H-periodic polynomial on the basis B from general.normalbasis, rewriting any other exponents that appear. The input and output use exponents in $(\mathord {{\mathbb {Z}}}/m)/H$ having additive order divisible by ${\text {rad}}m$; the output is guaranteed to be supported on B, which is automatic if m is squarefree but not for general m.

• general.from_conventional also produces an H-periodic polynomial on the basis B, but takes input in its conventional (not H-folded) form as a list of m exponents, with no requirements on the additive order.

Some of the functions provide generalized Rader FFTs and generalized folded Rader FFTs:

• As a warmup without folding, general.primitive is a primitive size-m DFT. This function is given a ring R, a positive integer m, a primitive mth root $\zeta$ of 1 in R, and the coefficients $g_0,g_1,\dots ,g_{m-1}$ of a polynomial $g=g_0+g_1x+\dots +g_{m-1}x^{m-1}\in R[x]$. This function returns $g(\zeta ^c)$ for each $c\in \mathord {\left\{ {0,1,\dots ,m-1}\right\} }$ with ${\text {gcd}}\mathopen {}\mathord {\left\{ {c,m}\right\} }=1$. Internally, this function uses the generalized Rader FFT from Sect. 4.12.3.

• general.primitive_inverse is an inverse primitive size-m DFT. Internally, this uses the inversion algorithm (and tweak) from Sect. 4.12.4.

• general.folded is an H-folded DFT, as in Sect. 4.12.5. This function is given R, m, $\zeta$, a subgroup H of $(\mathord {{\mathbb {Z}}}/m)^*$, and an H-periodic polynomial; it evaluates the polynomial at $\zeta ^c$ for each c in $(\mathord {{\mathbb {Z}}}/m)^*/H$. The subgroup H is required to be rad-free.

• general.folded_inverse is an inverse H-folded DFT.

Finally, as in prime, there are further functions to operate on H-periodic polynomials over $\mathord {{\mathbb {Z}}}$, representing elements of the subfield of $\mathord {{\mathbb {Q}}}(\zeta _m)$ fixed by H. Each function is given m and H along with the further inputs described below:

• general.multiply takes two H-periodic polynomials f, g and returns fg. Internally, this uses H-folded DFTs.

• general.conjugate takes an element $c\in (\mathord {{\mathbb {Z}}}/m)^*$ and an H-periodic polynomial f, and returns $\sigma _c(f)$, where $\sigma _c$ is the unique automorphism of $\mathord {{\mathbb {Q}}}(\zeta _m)$ mapping $\zeta _m$ to $\zeta _m^c$.

• general.subfield changes representation from the subfield K of $\mathord {{\mathbb {Q}}}(\zeta _m)$ fixed by H to the subfield F of $\mathord {{\mathbb {Q}}}(\zeta _{\ell })$ fixed by a subgroup S of $(\mathord {{\mathbb {Z}}}/\ell )^*$, where $F\subseteq K$, assuming the input represents an element of F. This function takes as input a subgroup $H_2$ of $(\mathord {{\mathbb {Z}}}/m)^*$ containing H; the function defines $\ell$ as the conductor of $H_2$, and S as the reduction of $H_2$ to $(\mathord {{\mathbb {Z}}}/\ell )^*$. This function also takes as input an H-periodic polynomial f, and produces as output an S-periodic polynomial. The exact set of pairs (H, S) supported by this function has a complicated description from details of how the function steps through conductors and subgroups; both H and S are required to be rad-free, and none of the default abelianfields tests include any cases where this condition is insufficient.

• general.det_relative has the same input–output format as general.subfield but evaluates ${\text {det}}^{K}_{F}$ rather than evaluating the identity map on F. Internally, this function simply multiplies conjugates using general.conjugate and general.multiply.

• general.det_absolute takes an H-periodic polynomial representing an element $\alpha$ of the subfield K of $\mathord {{\mathbb {Q}}}(\zeta _m)$ fixed by H, and returns ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$. This function requires H to be friendly.

A subroutine general.tower constructs the tower used in general.det_absolute. Internally, general.tower starts with $(\mathord {{\mathbb {Z}}}/m)^*$ and builds a chain of subgroups down towards H. It tries to insert one prime at a time into the field degree so as to obtain a maximum-length tower, but, for $m\in 8\mathord {{\mathbb {Z}}}$, sometimes intersects the current subgroup with $1+4\mathord {{\mathbb {Z}}}$ to preserve the rad-free condition, in effect losing one degree-2 step in the tower. There is no attempt in general.tower to search for alternative chains.

1.6 A.6: output of the tests

Running all internal abelianfields tests on Linux systems with Sage installed is a simple matter of typing make in the package directory. Various notes are printed regarding which test size is in progress, but not regarding all the individual tests. Any failure is printed as a Sage assertion failure.

Along with correctness tests, the tests of the prime module include reporting, for each small prime p, the sizes of convolutions used in computing determinants down to $\mathord {{\mathbb {Z}}}$ of five random small elements of $\mathord {{\mathbb {Z}}}[\zeta _p]$, specifically elements with coefficients $\pm 1$ and all remaining coefficients 0. For example, a typical computation for $p=29$ involved convolutions of lengths 28 (for a forward DFT) and 14 (for an inverse DFT) over $\mathord {{\mathbb {Z}}}/M$ where M has 14 bits, convolutions of lengths 14 and 7 over $\mathord {{\mathbb {Z}}}/M$ where M has 23 bits, and convolutions of lengths 7 and 1 over $\mathord {{\mathbb {Z}}}/M$ where M has 83 bits, as reflected by the following output line:

The product of M bits and n adds up to 1735 in this example. Sizes can vary from one element to another; see generally Sect. 2. To skip most tests and simply see these convolution sizes, one can run make sagelibs and then, inside Sage, run the following, although this still tests the results against Sage’s resultant subroutine:

The totalbits quantity is not monotonic in p: for example, the quantity is typically 9090 or 9480 for $p=59$ and typically just 3099 or 3177 or 3249 for $p=61$, reflecting the fact that $\mathord {{\mathbb {Q}}}(\zeta _{61})$ has a much nicer tower than $\mathord {{\mathbb {Q}}}(\zeta _{59})$ does.

Five experiments with $p=193=1+3\cdot 2^6$ had totalbits being 16739, 17157, 17168, 17228, 16859; five experiments with $p=769=1+3\cdot 2^8$ had totalbits being 83286, 83368, 82804, 82962, 82964. The $5\times$ growth in totalbits from $p=193$ to $p=769$ is, as expected, slightly larger than the $4\times$ growth in p: the number of tower levels is growing logarithmically, and one expects another near-logarithmic factor for reasons explained in Sect. 2.

(Similar comments apply to the general module, with larger sizes since general does not push conjugation and folding through DFTs. For example, five experiments from general.test_sizes(193) had totalbits being 36981, 36711, 38196, 36981, 35703, and five experiments from general.test_sizes(769) had totalbits being 176103, 212355, 176922, 176103, 176067.)

Beyond totalbits, there is a third logarithmic factor in the run time of this paper’s algorithm, reflecting the cost of convolution per bit. However, one cannot expect to see this logarithmic factor in wall-time measurements for this software. Operations in the small prime fields in Sect. 4.12.2 have inherent cost growing with the size of the prime (which is also roughly logarithmic, with some bumps for the distribution of primes), but in Sage the cost is instead dominated by prime-independent overhead. Wall time was monitored experimentally as a sanity check (with repeated runs so that precomputations were cached) and grew approximately $5\times$ from $p=193$ to $p=769$, but this should not be taken as a predictor of the wall-time ratio for optimized software.

Appendix C: faster software for the case of power-of-2 cyclotomics

For the numerical example $\alpha =3+\zeta _{2048}^{271}+4\zeta _{2048}^{828}$ with $K=\mathord {{\mathbb {Q}}}(\zeta _{2048})$, Sect. 1 compared the performance of traditional ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ computation—namely 0.21 $\times$ $10^9$ cycles via PARI, or $0.15\cdot 10^9$ cycles via NTL—to the performance of exploiting a tower of subfields of K—more than $10\times$ faster, namely 0.011 $\times$ $10^9$ cycles.

A closer look shows that this underestimates the speed advantage of exploiting a tower of subfields. The overhead in Python and Sage for computing $g(-x)$, extracting coefficients, etc. turns out to account for most of the 0.011 $\times$ $10^9$ cycles. This issue is essentially nonexistent for the scripts using PARI and NTL: those scripts are bottlenecked by resultant subroutines written in C.

This appendix describes cyclo2power (available from [19] as an accompaniment to this paper), an open-source library to compute ${\text {det}}^{K}_{\mathord {{\mathbb {Q}}}}\alpha$ for integral elements $\alpha$ of power-of-2 cyclotomic fields K. The library is written in C and, like NTL and PARI, uses GMP [52] for integer arithmetic. For the numerical example from Sect. 1, cyclo2power uses just 0.0012 $\times$ $10^9$ cycles on the same machine, more than $100\times$ faster than NTL.

1.1 C.1: representing polynomials as integer values

Segmentation (sometimes called “Kronecker substitution”), also used in Sects. 3.3, 4.2, and 4.8.5, multiplies two polynomials $f,g\in \mathord {{\mathbb {Z}}}[x]$ by multiplying the integers $f(\rho ),g(\rho )$. Here $\rho \in \mathord {{\mathbb {Z}}}$ is chosen to be a power of 10 for traditional hand computation or a power of 2 for software, so it is easy to read off the coefficients of $h=fg$ from the digits or bits of $h(\rho )$. One can think of the integers $f(\rho ),g(\rho ),h(\rho )$ as representations of the polynomials f, g, h respectively.

For example, one way to multiply $3x^2+x+4$ by $2x^2+7x+1$ is to choose $\rho =1000$ and multiply the integers 3001004 and 2007001, obtaining the integer 6023018029004, from which one easily reads off the polynomial product $6x^4+23x^3+18x^2+29x+4$. Of course, for this to work, $\rho$ has to be large enough compared to the polynomial coefficients.

It might seem pointless to reduce polynomial arithmetic to integer arithmetic given that integers, in turn, are normally represented as values of polynomials—for example, the notation “6023018029004” above refers, by definition, to the value at 10 of the polynomial $6y^{12}+2y^{10}+3y^9+y^7+8y^6+2y^4+9y^3+4$. But if one is given GMP for integer arithmetic then segmentation is well known to be an easy way to carry out polynomial arithmetic.

1.2 C.2: tower compatibility of segmentation

Let $n\ge 2$ be a power of 2. Write $m=2n$. As usual, represent each $\alpha \in \mathord {{\mathbb {Z}}}[\zeta _m]$ as the unique $g\in \mathord {{\mathbb {Z}}}[x]/(x^n+1)$ with $g(\zeta _m)=\alpha$. As above, represent g by its value $g(\rho )\in \mathord {{\mathbb {Z}}}/(\rho ^n+1)$ where $\rho$ is a power of 2. One can recover g and thus $\alpha$ from this value if the coefficients of g are small enough compared to $\rho$.

The product $g(\rho )g(-\rho )$ now represents $g\cdot g(-x)$, which in turn represents ${\text {det}}^{\mathord {{\mathbb {Z}}}[x]/(x^n+1)}_{\mathord {{\mathbb {Z}}}[x]/(x^{n/2}+1)}\alpha$. This product $g(\rho )g(-\rho )$ is the same as $G(\rho ^2)$ for the unique $G\in \mathord {{\mathbb {Z}}}[x]/(x^{n/2}+1)$ with $G(x^2)=g\cdot g(-x)$. Now replace $(g,\rho )$ with $(G,\rho ^2)$ and repeat.

This is how cyclo2power works, with $\rho$ chosen as the smallest power of $2^{16}$ such that the maximum absolute value of the coefficients of the input g is below $\rho /2n$. Each coefficient of G is a sum of n products (sometimes negated) of coefficients of g, and is thus below $\rho ^2/4n$ in absolute value. Taking $\rho /2n$ instead of $\rho /n$ simplifies the negative-coefficient rewriting described below, and requiring a power of $2^{16}$ rather than just a power of 2 simplifies the coefficient handling more broadly.

For example, if $n=1024$ and g has small coefficients then cyclo2power chooses $\rho =2^{16}$, so $\rho ^n=2^{16384}$. This is several times more bits than necessary to represent typical outputs; see Sect. 2. Presumably one could obtain some further speed by (1) allowing the initial $\rho$ to be, e.g., $2^4$, despite the cost of handling unaligned data, and (2) reducing $\rho$ partway through the computation, despite the cost of having to switch to a different representation.

Note that multiplying $g(\rho )$ by $g(-\rho )$ is multiplying in $\mathord {{\mathbb {Z}}}/(\rho ^n+1)$. Many integer-multiplication methods benefit from moduli of the special form $\rho ^n+1$ (see generally [16, Section 3]), gaining about a factor 2 in performance compared to multiplying the same inputs in $\mathord {{\mathbb {Z}}}$. However, the documented GMP interface does not provide any of these special multiplication functions.

1.3 C.3: negative coefficients

Consider the polynomial $f=5x^3+6x^2-7x-8$. The value of f at $\rho =1000$ is $f(\rho )=5005992992$. One can recover the coefficients of f from $f(\rho )$ by rewriting the bottom 992 as $1000-8$, producing coefficient $-8$ and quotient 5005993; then rewriting 993 as $1000-7$, producing coefficient $-7$ and quotient 5006; etc.

This rewriting is a considerable part of the cyclo2power code. One cannot reasonably avoid negative coefficients in the context of this paper: this would limit the pool of inputs $\alpha$ in the applications in Sect. 5, and would almost always prohibit converting g into $g(-x)$.

This complication disappears if one instead represents integers using a balanced digit set, such as the redundant digit set $\mathord {\left\{ {-5,-4,\dots ,4,5}\right\} }$ in radix 10: one can then simply negate each coefficient. However, GMP does not represent integers in this way.

1.4 C.4: speedups over NTL

For small n (e.g., $n=4$) and small coefficients (e.g., $\mathord {\left\{ {-1,0,1}\right\} }$), cyclo2power is about twice as fast as NTL’s resultant computation applied to $x^n+1$. The cyclo2power advantage grows rapidly as n increases. For example, for $n=1024$ and coefficients $-1,0,1$ with probability 1/4, 1/2, 1/4 respectively, NTL takes about 0.66 $\times$ $10^9$ cycles while cyclo2power takes about 0.0014 $\times$ $10^9$ cycles, more than 400 times faster. The cyclo2power advantage also grows somewhat as the number of bits per coefficient increases, although this is less striking than the growth with n and less relevant to the applications considered in this paper.

There are also functions in cyclo2power for handling power-of-2 real-cyclotomic fields instead of power-of-2 cyclotomic fields. This boils down to skipping a final squaring. This speedup is most noticeable for small n.