Technical review on coaxial deep borehole heat exchanger

Abstract

This review paper summarizes recent developments regarding geothermal exploitation using coaxial deep borehole heat exchangers (DBHE). Specifically, this study focuses on field tests, analytical and semi-analytical approaches, and numerical simulations. First, field tests and applications of coaxial DBHE are summarized and future work for the field tests is suggested. Then, the ongoing analytical and numerical modeling approaches on coaxial DBHE are evaluated regarding the capability and incapability of describing physical behaviors. Lastly, key factors for the design of coaxial DBHE are summarized and discussed based on collected results. Regarding field tests, future work should focus more on (1) long-term performance; (2) effect of groundwater flow within formation and fractures; (3) technology for larger diameter boreholes; (4) new and cheap materials for insulated inner pipe; (5) treatment of fluid, pipe wall, and different working fluid; (6) economic analysis of coaxial DBHE-based geothermal power plant. As for the analytical methods and numerical simulations, it is important to consider the dependence of fluid and formation properties on pressure and temperature. Besides, verification and calibration of empirical models for working fluids other than water such as CO₂ should be performed based on laboratory and field tests. Different borehole properties and pump parameters should be optimized to obtain the maximum thermal power of a coaxial DBHE, and an insulated inner pipe is recommended by many researchers. An intermittent working pattern of the DBHE could be more realistic when modeling a DBHE. To further improve the performance of coaxial DBHE, continuous research to enhance heat transfer and working fluid performance is still important.

Article highlights

• 1. Summarized ten applications of DBHE from literature to discuss the achievements and future work of geothermal exploitation by DBHE.

• 2. Review of analytical and numerical methods for DBHE simulation focusing on boundary and interface conditions and formation properties.

• 3. Discussed ground thermal properties, borehole properties, ground pump parameters and economic considerations on the design and application of DBHE.

1 Introduction

The utilization of fossil fuels during the last half-century has produced enormous carbon dioxide (CO₂) emissions to the atmosphere, which is the main reason for the continuing increase of global temperature and extreme weather events. To deal with climate change and secure a sustainable future, the most important step is to switch from fossil fuels to clean sources of energy according to the governmental documents of the United Nations, the G7 economies and many countries (UN DESA 2017; Gielen et al. 2019G7 2021).

Geothermal energy has been utilized in hot springs, room heating and agriculture for centuries and is expected to expand to meet 3–5% of global energy demand by 2050 (Craig and Gavin 2018). Based on different ground formation properties, different systems are used to exploit geothermal energy from geothermal reservoirs (White 1966). Hydrothermal systems, according to White et al. (1971), occur in areas with high heat fluxes and high permeability and can yield hot water or hot stream or both fluids that can be used for producing electricity or heating. To extract geothermal energy from formations with low permeability, Enhanced Geothermal Systems (EGS), according to Potter et al. (1974), use hydrofracturing to connect and expand existing fractures or create new fractures in the low permeable hot rock mass, and then inject cold working fluid to flow through the hot fractures and pump out the heated fluid to produce electricity or serve heating systems. Both hydrothermal systems and EGS are open-loop systems, on the other hand, closed-loop systems began to compete with open-loop systems in the late 1970s (Bloomquist 1999). Different from open-loop systems, closed-loop systems circulate fluid without direct contact with hot rock and do not require high permeability of rock and excessive injection pressure, and are free of fluid loss or pumping failure problems. Some researchers reported that abandoned gas and oil single wells could be developed as closed-loop systems for geothermal energy exploitation, U-tube borehole heat exchanger (BHE), or coaxial BHE, have been applied in different applications (Caulk and Tomac 2017; Sui et al. 2018; Gharibiet al. 2018; Śliwa et al. 2018; Kaplanoglu et al. 2019). Besides, doublet BHE using two wells as the closed loop system has also been studied via numerical simulation (Hu et al. 2021; Li et al. 2023).

Based on the availability of geothermal energy at different depths, geothermal energy can be classified as shallow and deep geothermal energy (White 1966). In general, hydrothermal systems can be applied to exploit both shallow and deep geothermal energy as reported by different authors (White et al. 1977, Suemnicht et al. 2007). Besides, EGS is often used for the extraction of deep geothermal energy (Brown et al. 1985; Brown 1995). According to scientific literature, the definition of shallow borehole heat exchanger (SBHE) and deep borehole exchanger (DBHE) varies. For example, in northern Europe, SBHE can reach depths of 400 m below the ground surface (Rybach et al. 1992; Kohl et al. 2002), and China defines SBHE as depths smaller than 200 m (Wang 2015; Pan et al. 2020). Nevertheless, the coaxial DBHE, offering potentially better scope for thermal and hydraulic optimization with smaller land occupancy, is used for deep geothermal exploitation (Rybach and Hopkirk 1995). Other structure types of DBHE such as U-pipe and spiral fin heat exchangers (Syarifudin et al. 2016) might need a large enough well diameter for installation (Muraya 1994), although the spiral fin borehole heat exchanger seems to overperform coaxial DBHE with respect to thermal power based on simulations (Syarifudin et al. 2016). Therefore, spiral fin might be another possible solution for geothermal exploitation using deep boreholes if the installation cost is reasonable based on economic analysis. And this study mainly focuses on research regarding coaxial DBHE for geothermal exploitation and thus other borehole structures will not be reviewed in detail.

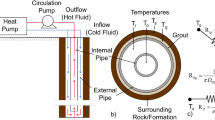
Figure 1 shows the vertical and top view of a typical coaxial DBHE, two coaxial tubes, inner pipe and outer casing, are inserted into the borehole/well and cement/grout is filled between the borehole/well wall and the outer casing. The working fluid, e.g., water, is often injected into the DBHE from the annulus and exchanges heat with the surrounding hot formation and enters the inside pipe at the bottom of the DBHE, and then flows up to the outlet on the top of the borehole driven by pressure from inlet and thermosiphon effect, which is due to the decrease of fluid density with temperature. The hot outlet fluid can be used to produce electricity by using an Organic Ranking Cycle machine (Cheng et al. 2013; Alimonti et al. 2018) or thermal power.

Fig. 1

Schematics of a coaxial DBHE

To install a coaxial DBHE for geothermal energy exploitation, it is necessary to summarize geological background information, conduct a geological survey, configure the installation layout, select proper materials for the construction of DBHE, optimize operation parameters and plan for energy utilization. Nevertheless, the preliminary design of a coaxial DBHE is to determine how much geothermal energy can be extracted and what configurations of the DBHE should be used. Figure 2 shows the major factors affecting the design of a DBHE-based geothermal system following Pouloupatis et al. (2017). In this study, the research regarding coaxial DBHE using different approaches is reviewed and the target of this review is to evaluate the strengths and weaknesses of current coaxial DBHE and different approaches for analyzing the coaxial DBHE, and some new thoughts regarding the coaxial DBHE are also discussed for the future development of coaxial DBHE.

Fig. 2

Parameters affecting coaxial DBHE geothermal system (revised from Pouloupatis et al. 2017)

2 Pioneer applications of coaxial DBHE

According to a National Renewable Energy Laboratory report on the geothermal power production and district heating market of the United States (Robins et al. 2021), most of the current and planned geothermal power projects still use conventional hydrothermal technology. However, pioneer coaxial DBHE projects have been constructed in the United States (Morita et al. 1992), Europe (Schneider et al. 1996), Australia, Japan, and China (Bu et al. 2019) for decades. The thermal production of a DBHE is controlled by depth, thermal gradient, formation thermal conductivity and flow rates. In this regard, several typical coaxial DBHE projects are summarized and evaluated with respect to configurations.

2.1 Hawaii (United States)

A field experiment was conducted on an 876.5 m coaxial DBHE using the Hawaii Geothermal Project–Abbot well on the island of Hawaii from Feb 22 to Mar 1, 1991 (Morita et al. 1992). The DBHE has a steel casing pipe with a diameter of 17.78 cm (7 in) as the outer pipe as shown in Fig. 3a, and a vacuum-insulated tube (VIT) with an outer diameter of 8.89 cm (3.5 in) was used as the insulated inner pipe, which has an equivalent thermal conductivity of approximately 0.06 W/(m K). Water at a temperature of 30 °C was injected into the annulus at a flow rate of 80 l/min (4.8 m³/h). The thermal conductivity of the basaltic formation is 1.6 W/(m K) and the ground water level at the site is about 186 m in depth. The highest outlet temperature of the DBHE during the experiment reached 98 ℃ and the DBHE has a net thermal power of 76 kW after operating for 7 days.

Fig. 3

Casing profile of geothermal well: a Hawaii (Morita et al. 1992); b Weissbad, Switzerland (Kohl et al. 2000); c Qingdao, China (Bu et al. 2019); and d Beppu, Japan (Pokhrel et al. 2022)

2.2 Prenzlau (Germany)

Schneider et al. (1996) and Sapinska-Sliwa et al. (2015) reported a coaxial DBHE near a positive geothermal anomaly in Penzlau. An existing geothermal borehole was extended to 2786 m to install the coaxial DBHE with a measured bottom rock temperature of 108 °C. The outer pipe of the coaxial DBHE has an internal diameter of 24.77 cm (9.75 in) to a depth of 950 m and then 16.83 cm (6.63 in) to the bottom, and the inner pipe used a double steel pipe as the insulated pipe. Water was the working fluid. The heating plant used both the DBHE and a peak part with gas and oil boilers. The DBHE part has a heating capacity of 600 kW for direct heat exchange and a heat pump using NH₃ as the refrigerant/working medium. And the outlet water can reach 60℃ at a volumetric flow rate of 6 m³/h.

2.3 Weggis (Switzerland)

Rybach and Hopkirk (1995) reported a 2300 m deep geothermal borehole with a corrected bottom hole temperature of 78 °C in the center of the community Weggis. Due to the low productivity of the Miocene Lower Freshwater Molasse formation on site, the water yield of the borehole well was negligible, and thus a coaxial DBHE was installed. The coaxial DBHE has a 17.78 cm (7 in) diameter casing to 1902 m and then a 13.7 cm (5.5 in) diameter hanger-liner to the bottom as the outer pipe with a prefabricated bottom seal. As for the inner pipe, a double VIT tube up to 1780 m and then an uninsulated pipe to the bottom was adopted. According to the simulations (Rybach and Hopkirk 1995), maintaining the thermal power at 100 kW can ensure an outlet temperature of around 40 °C after operating for 30 years. Later, Kohl and Rybach (2003) found that the energy production of the Weggis DBHE reached 0.37 GWh and 0.42 GWh in 2000 and 2001, which corresponds to annual average thermal power of 42.2 kW and 49.7 kW.

2.4 Weissbad (Switzerland)

A coaxial DBHE was installed in an abandoned borehole drilled into Tertiary Molasse formations in Weissbad as reported by Kohl et al. (2000). The DBHE has a depth of 1213.3 m with a centralized steel pipe inserted as shown in Fig. 3b. At a water flow rate of 10.5 m³/h, the DBHE was reported to produce energy at a power of 80 kW (Sapinska-Sliwa et al. 2015). However, the DBHE outlet temperature was significantly lower (only 10.6 °C on annual average) than expected. Kohl et al. (2000) performed numerical simulations on the DBHE by considering a heat flow of 75 mW/m² at 1500 m and suggested that the DBHE performance can be improved using a VIT inner pipe, especially for the upper part.

2.5 Aachen (Germany)

A 2500 m deep borehole RWTH-1 was drilled in 2004 near the urban center of Aachen (Dijkshoorn et al. 2013). The rocks on the site are dominated by a series of interlayered sandstones, siltstones, and shales. The installation was intended for space heating and cooling of the buildings at RWTH-Aachen University. Due to the presence of quartzite sandstones, the thermal conductivity of drilled rocks varies between 2.2 and 8.9 W/(m K). And the maximum bottom hole temperature is around 85℃ and the heat flow of the site could be 85–90 mW/m². Dijkshoorn et al. (2013) also mentioned that no natural groundwater flow was detected on the site. At a circulation flow rate of 10 m³/h at maximum, the DBHE could supply the building with water of temperature between 25 °C and 55 °C during winter. However, after 20 years of operation, the outlet temperature might be too low to drive the adsorption unit for cooling during summer. In this regard, Dijkshoorn et al. (2013) stressed the importance of the installation of an insulated inner pipe, but the cost of a VIT inner pipe is too expensive and thus the thermal power for heating was provided by another project using geothermal natural springs.

2.6 Qingdao (China)

A single well was drilled in Qingdao, China to a depth of 2605 m to install a coaxial DBHE for geothermal heating in 2016 (Bu et al. 2019). The DBHE has a Φ 177.8 × 6.91 mm casing as detailed in Fig. 3c and a Φ 110 × 10 mm polypropylene pipe as the inner insulation tube. Other parameters of the DBHE are provided in Table 1. The injection temperature of water was fixed at about 5 °C and the volumetric flow rate was about 30 m³/h. During the experimental test lasting for 138 days, the average extracted thermal power is 448.49 kW and the outlet temperature at the end of the test is about 17.5 °C.

Table 1 Parameters of the geothermal well in Qingdao, China (obtained from Bu et al. 2019)

2.7 Songyuan (China)

A 2044 m coaxial DBHE using an outer pipe with an inner radius of 80.9 mm was installed in a 215.9 mm diameter borehole in Songyuan, China (Huang et al. 2021). And the coaxial DBHE used polyethylene with raised-temperature resistance (PE-RT II) to make the inner insulated pipe at an outer diameter of 55 mm and a thickness of 12.3 mm. The bottom borehole temperature was 107.3 °C, resulting in an average local geothermal gradient of 50.7 °C/km. During the 60 days of experiment, water at a flow rate of 30 m³/h was injected into the annulus and outlet fluid at about 43 °C could be produced.

2.8 Tianjin (China)

Two coaxial DBHEs with a length of 2800 m were installed as an energy station in Tianjin (Jia et al. 2022). The geometry of the DBHE and the soil geo-physical properties at different depths are summarized in Table 2. The ground surface temperature is 22 °C and two scenarios were considered in the experiment: inlet water temperature of 21.5 ℃ at a flow rate of 30 m³/h, and injection temperature of 23.0 °C at a flow rate of 25 m³/h. The thermal power of the DBHE at a flow rate of 30 m³/h is about 800 kW after 5 h, while the thermal power of the DBHE at a flow rate of 25 m³/h is about 600 kW after 60 h. Further numerical simulations based on the experiments indicate that decreasing the BHE operating time per day from 24 to 8 h leads to an increase in the average thermal power from 280 to 567 kW after 3000 h.

Table 2 Geometry of DBHE and geological parameters in Tianjin (obtained from Jia et al. 2022)

2.9 Beppu (Japan)

A field test on a 500 m coaxial DBHE was performed near Beppu, Oita, Japan (Pokhrel et al. 2022). The drilling of the borehole started in 2017 and the test was carried out for 19 days under a constant flow rate of 6 m³/h. The injection temperature of the circulating water in the DBHE is 70 °C. Figure 3d shows the geometry of the DBHE. Before the test, the ground temperature ranged from 20 °C near the surface to 212.7 °C at the bottom of the well, which corresponds to a thermal gradient of 380 °C/km. During the test, a maximum outlet temperature of 169.5 °C was observed after one hour and the outlet water temperature was 98.0 °C at the end of the experiment.

2.10 Beijing (China)

An 1800 m coaxial DBHE was tested at two flow rates of 20.03 and 24.93 m³/h from Nov to Dec 2021 in Beijing, China (Wang et al. 2022a). The average thermal gradient of the site was measured as 24.8 °C/km, indicating no existence of geothermal anomaly. The average thermophysical properties of the ground formation are shown in Table 3. During the test of the first scenario, the DBHE at a flow rate of 20.03 m³/h produced a steady thermal power of 237.24 kW after 40 h. As for the second scenario, after 97 h, the DBHE with a flow rate of 24.93 m³/h produced a thermal power of 256.54 kW.

Table 3 Average thermos-physical properties of formation (obtained from Wang et al. 2022a)

2.11 Knowledge from pioneer DBHE projects

Table 4 summarizes the ten projects on coaxial DBHE. From the summarized pioneer projects, some significant general information can be obtained:

• 1. As can be seen from the thermal gradient, most available pioneer applications of DBHE are in regions with no geothermal anomaly. In this regard, to get a bottom borehole temperature over 100 ℃, the DBHE should be drilled to over 2500 m below the ground surface.

• 2. The thermal power of a coaxial DBHE as shown in Table 4 generally is between 10 and 600 kW, which is one or two orders of magnitude smaller than the power extracted by typical EGS projects (Brown 2009; Genter et al. 2010; Robins et al. 2021) due to lower thermal gradient on the site of coaxial DBHE.

• 3. Generally, the thermal power of a DBHE increases with the depth of DBHE and most boreholes have a diameter less than 50 cm due to the limitation of the drilling tool and the drilling cost (Pan et al. 2020). Higher fluid flow rate results in lower outlet fluid temperature but higher thermal power, which agrees with simulations (Jia et al. 2022; Wang et al. 2022b), a trade-off could be achieved by considering the borehole configuration and geological conditions. The thermal power of DBHE could be improved by using an insulated inner pipe such as VIT (Kohl et al. 2000; Dijkshoorn et al. 2013; Śliwa et al. 2018).

• 4. The operating power of a DBHE is generally less than EGS projects because the closed-loop system is used. As shown in Table 4, the operating power per unit length of DBHE is mostly less than 50 W/m and much less than EGS, whose pumping power per unit length can be 130 W/m to 1750 W/m according to Mines and Nathwani (2013). The injection water pressure of DBHE is between 150 kPa from measurements (Morita et al. 1992) and 3 MPa from simulations (Huang et al. 2021) and is much less than the wellhead pressure of EGS, which can be 10–65 MPa according to Genter et al. (2010), Wyborn (2010).

• 5. The major drawbacks of DBHE compared to EGS include lower thermal power, smaller circulation flow rates, lower outlet temperature, extra maintenance cost for inner pipes such as corrosion/rust removal.

Table 4 Summary of DBHE field test from literature

Although much useful information about DBHE can be obtained from the current pioneer applications, some problems should still be further investigated for field tests on DBHE:

• 1. Many field tests show that the outlet fluid temperature of a coaxial DBHE almost stabilizes after several days of operation, but the long-term performance might not be well monitored because most experiments last less than 2 months. And according to numerical simulations, the thermal power and outlet temperature of a DBHE might keep decreasing for several years (Huang et al. 2021). In this regard, the long-term performance of DBHE over several decades should be further monitored and investigated.

• 2. Most field tests as shown in Table 4 did not record the groundwater flow conditions, but groundwater flow within a wide depth range of the DBHE and in large fractures might affect the performance (Jiao et al. 2021) and should be carefully considered for the layout design of the DBHE wells.

• 3. The diameter of DBHE is constrained by drilling tools and technologies. To increase the contact area of working fluid with the deep hot region and thus thermal power, it is necessary to find new and cheap drilling technologies to drill large-diameter boreholes based on simulations regarding the effect of borehole diameter (Alimonti and Soldo 2016; Holmberg et al. 2016; Thomasson and Abdurafikov 2022).

• 4. Although the insulated inner pipe can improve the thermal power of a DBHE (Morita et al. 2005; Dijkshoorn et al. 2013), the cost of the VIT inner pipe can be the major effect preventing the installation of the VIT pipe (Dijkshoorn et al. 2013). Therefore, it is still necessary to find new and cheap material for the insulated inner pipe of the DBHE.

• 5. Significant pressure loss can be observed during field tests on coaxial DBHEs (Morita et al. 1992; Pokhrel et al. 2022) due to friction, especially at higher flow rates (Huang et al. 2021). Adding nanoparticles to water can decrease the viscosity of water (Zhou et al. 2019). And using different working fluids such as CO₂ might also decrease the pressure loss and increase net thermal power (Zhang et al. 2019). All those approaches should be further investigated by field tests.

• 6. To economically evaluate coaxial DBHE, it is important to estimate the drilling, maintenance, and operation costs of DBHE and related facilities. Field evaluations on the overall feasibility of coaxial DBHE-based geothermal power plants should be further performed.

3 Ongoing analytical and numerical modeling approaches on coaxial DBHE

Apart from field tests, analytical solutions and numerical simulations are widely used to model coaxial DBHE and perform feasibility studies and parametric optimizations of DBHE projects. This section reviews and evaluates the currently available analytical, semi-analytical methods and numerical approaches for DBHE and targets the capability and incapability of those approaches to describe physical behaviors and interactions among pipe, working fluid and ground formation. Note that the analytical and semi-analytical methods are those approaches that derive formulations and develop customized code/scripts specifically for the analysis of coaxial DBHE, which can only be used for analyzing coaxial DBHE. Numerical approaches use commercial or open-source numerical software, which can be used to analyze general hydro-thermo-mechanical problems, to carry out studies on coaxial DBHE.

3.1 Analytical and semi-analytical methods

The heat transfer and flow circulation of a coaxial DBHE is a complex three-dimensional (3D) problem in a conceptional manner, thus simplifications regarding the mechanisms of heat transfer and fluid flow are often made to get rid of complex derivations and calculations. In this regard, this section summarizes several analytical and semi-analytical methods for the coaxial DBHE problem and then evaluates their strengths and weaknesses with respect to capturing physical features.

3.1.1 Analytical methods for heat transfer around borehole

Many researchers have been working on analytically modeling the heat conduction of formation around a borehole and proposed different methods such as the infinite line-source (ILS) method, infinite cylindrical source (ICS) method, and finite line source (FLS) method. Those methods assume a constant heat flux on the borehole surface and the fluid circulation inside the borehole is ignored. In this regard, ILS, ICS and FLS methods can only be used to roughly estimate the overall thermal performance of DBHE and the influence range of the DBHE on the surrounding formation. In order to properly model the heat convection of working fluid, other approaches should be used in conjunction with ILS, ICS and FLS to model the DBHE.

(1) Infinite line-source method

Based on the ILS method by Kelvin (1882), Ingersoll et al. (1950) proposed an analytical solution to the radial heat transfer problem. The BHE is simplified as an infinite line within an infinite homogeneous ground and the heat transfers radially from (towards) the line via conduction to (from) the ground at a constant heat flux. The ILS model can be mathematically described by the governing equation and initial and boundary conditions in cylindrical coordinates:

$$\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}=\frac{1}{{\alpha }_{d, {\text{g}}}}\frac{\partial T}{\partial t}$$

(1a)

$$\left\{ {\begin{array}{*{20}l} { - 2\pi \lambda _{g} \mathop {\lim }\limits_{{r \to 0}} r\frac{{\partial T}}{{\partial t}} = \Phi _{{q,l}} } \hfill \\ {T(r \to \infty ) = T_{0} } \hfill \\ {T(t = 0) = T_{0} } \hfill \\ \end{array} } \right.$$

(1b)

where T = temperature of the ground; $\alpha _{{d,g}}$ = thermal diffusivity of ground, r = radial coordinate; t = time; ${\lambda }_{{\text{g}}}$ = thermal conductivity of the ground; ${\Phi }_{q,l}$ = heat flux through the infinite line; ${T}_{0}$ = initial temperature of the ground. And the exact solution to Eq. (1) is (Ingersoll et al. 1950):

$$T-{T}_{0}=\frac{{\Phi }_{q,l}}{4\pi {\lambda }_{{\text{g}}}}{\int }_{1/\left(4{F}_{o}\right)}^{\infty }\frac{{e}^{-\eta }}{\eta }{{\text{d}}}\eta ,{F}_{o}=\frac{{\alpha }_{d, {\text{g}}}t}{{r}^{2}}$$

(2)

where ${F}_{o}$ = Fourier number defined by radius $r$, and it is suggested to use the ILS method with ${F}_{o}$ larger than 20; $\eta$ = variable of integration.

To consider the influence of groundwater flow on the transient response of BHE, Diao et al. (2004) extended the ILS solution under groundwater convection. Apart from assumptions made in the ILS problem, Diao et al. (2004) also assumed a constant groundwater velocity $u$ in the horizontal direction, and the solution can be expressed as:

$$T-{T}_{0}=\theta \left(r,\varphi ,t\right)=\frac{{\Phi }_{q,l}}{4\pi {\lambda }_{{\text{g}},{\text{a}}}}exp\left(\frac{ur{\rho }_{f}{C}_{s,f}}{2{\lambda }_{{\text{g}},{\text{a}}}}{\text{cos}}\varphi \right){\int }_{0}^{1/\left(4{F}_{o}\right)}\frac{1}{\eta }{\text{exp}}\left(-\frac{1}{\eta }-\frac{{u}^{2}{r}^{2}{\rho }_{f}^{2}{C}_{s,f}^{2}}{16{\lambda }_{{\text{g}},{\text{a}}}^{2}}\eta \right){\text{d}}\eta$$

(3)

where $\varphi$ = circumferential coordinate; $u$ = groundwater velocity; ${\lambda }_{{\text{g}},{\text{a}}}=\varepsilon {\lambda }_{\text{f}}+(1-\varepsilon ) {\lambda }_{{\text{g}}}$, $\varepsilon$ = porosity; ${C}_{s,w}$ = specific heat capacity of water.

(2) Infinite cylindrical source method.

To consider the cylindrical borehole instead of a simplified line in the BHE problem, the constant heat flux through an infinite cylindrical pipe was analyzed by different researchers (Kavanaugh 1985; Hellstrom 1991; Bernier 2001). Similar boundary conditions in the ILS method are assumed for the ICS method. The general form of the solution to the ICS method is:

$$T-{T}_{0}=\frac{{\Phi }_{q}}{{\lambda }_{{\text{g}}}}G({F}_{o})$$

(4a)

$$G\left({F}_{o}\right)=\frac{1}{{\pi }^{2}}{\int }_{0}^{\infty }\frac{{e}^{-{\eta }^{2}{F}_{o}}-1}{{J}_{1}^{2}\left(\eta \right)+{Y}_{1}^{2}\left(\eta \right)}\frac{{J}_{0}\left({r}_{b}^{*}\eta \right){Y}_{1}\left(\eta \right)-{Y}_{0}\left({r}_{b}^{*}\eta \right){J}_{1}\left(\eta \right)}{{\eta }^{2}}{\text{d}}\eta , {r}_{b}^{*}=\frac{r}{{r}_{b}}$$

(4b)

where ${\Phi }_{q}$ = heat flux on the infinite cylindrical borehole; ${J}_{0}$, ${J}_{1}$, ${Y}_{0}$ and ${Y}_{1}$ = Bessel functions of the first and second kind; ${r}_{b}$ = borehole radius. And $G\left({F}_{o}\right)$ is often referred to as the G-function in literature.

(3) Finite line source method.

To consider the finite length of BHE, Eskilson (1987) proposed a two-dimensional (2D) solution to a FLS problem with the BHE represented by a finite line from the ground surface to a specific depth of h. By using the method of mirror images, which is a mathematical method for solving differential equations with a symmetry hyperplane and introduces a mirror borehole to ensure the constant temperature of the ground surface, the solution to the BHE is (Eskilson 1987; Zeng et al. 2002):

$$T-{T}_{0}=\frac{{\Phi }_{q}}{{\lambda }_{{\text{g}}}}G(r,z,t)=\frac{{\Phi }_{q,l}}{4\pi {\lambda }_{{\text{g}}}}{\int }_{0}^{h}\frac{{{\text{erfc}}}\left(\frac{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}-\frac{{{\text{erfc}}}\left(\frac{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{\text{d}}\eta$$

(5)

where ${\text{erfc}}(\eta )$ = complementary error function and ${\text{erfc}}\left(\eta \right)=2{\int }_{0}^{\infty }\frac{1}{\sqrt{\pi }}\text{exp}\left(-{\eta }^{2}\right){\text{d}}\eta$; z = vertical coordinate. Note that Eskilson (1987) also developed the Finite line source-based solution with the consideration of a constant groundwater flow under the steady state, while the transient case with groundwater flow was ignored.

3.1.2 Composite cylindrical source model

To consider the heat transfer inside the borehole, composite media solutions based on the ICS method have been developed for U-tube borehole heat exchangers (Beier and Smith 2003; Bandyopadhyay et al. 2008), and the U-tube inside the borehole is simplified as an equivalent single core. Similarly, the same idea was extended to analyze coaxial DBHE by Gordon et al. (2017), where an annular cylinder source model representing the annulus region and inner pipe region is inserted inside the infinite cylindrical model representing the formation. And the dimensional response functions of the ground, outer annulus region, and inside pipe/shunt are:

$${G}_{ground}\left({t}_{j}\right)=\frac{g\left({F}_{o1},1\right)}{{k}_{s}}$$

(6a)

$${G}_{outer}\left({t}_{j}\right)=\frac{g\left({F}_{o6},1\right)}{{k}_{po}}-\frac{g\left({F}_{o7},1\right)}{{k}_{po}}+\frac{1}{2\pi {h}_{io}{r}_{io}}$$

(6b)

$${G}_{shunt}\left({t}_{j}\right)=\frac{1}{2\pi {h}_{io}{r}_{io}}+\frac{g\left({F}_{o4},1\right)}{{k}_{pi}}-\frac{g\left({F}_{o5},1\right)}{{k}_{pi}}+\frac{1}{2\pi {h}_{ii}{r}_{ii}}$$

(6c)

where ${F}_{o1}=\frac{{\alpha }_{d, g}t}{{r}_{b}^{2}}$; ${F}_{o4}=\frac{{\alpha }_{pi}t}{{r}_{ii}^{2}}$; ${F}_{o5}=\frac{{\alpha }_{pi}t}{{r}_{io}^{2}}$; ${F}_{o6}=\frac{{\alpha }_{po}t}{{r}_{io}^{2}}$; ${F}_{o5}=\frac{{\alpha }_{po}t}{{r}_{oo}^{2}}$; ${k}_{py}$, ${\alpha }_{py}$ refer to the inner or outer pipe (subscript y) thermal conductivity and diffusivities; ${h}_{xy}$, ${r}_{xy}$ are the film coefficient and radius at the inner or outer surface (subscript x) of the inner or outer pipe (subscript y); $g\left({F}_{o},1\right)$ is the G function of the ICS model. Note that the thermal conduction of pipe and convective heat transfer of working fluid can only be indirectly considered, and the heat capacities of pipe and fluid are ignored.

3.1.3 Beier et al. (2014) method

Beier et al. (2014) simplified the heat transfer of the coaxial DBHE problem as three sub-parts: (1) one-dimensional (1D) heat convection through the inner pipe, (2) 1D heat convection through the annulus, and (3) radial heat conduction to grout and ground. And the three sub-problems are coupled together by considering the heat transfer through the inner pipe wall and outer casing. The circulating fluid temperature within the pipe is represented by the velocity-average temperature along the cross-sectional flow and thus the heat convection within the pipe is simplified as a 1D problem. In this regard, the energy function in the dimensionless form of the inner pipe is:

$$\frac{{N}_{s}{H}_{f}{A}_{D1}}{2}\frac{\partial {T}_{D1}}{\partial {t}_{D}}+\frac{\partial {T}_{D1}}{\partial {z}_{D}}+{N}_{12}\left({T}_{D1}-{T}_{D2}\right)=0, 0<{z}_{D}<1.0<{t}_{D}$$

(7)

where ${T}_{D1}=\frac{2\pi {\lambda }_{{\text{g}}}L\left({T}_{1}-{T}_{0}\right)}{Q}$; ${t}_{D}=\frac{{\lambda }_{g}t}{{c}_{g}{r}_{eo}^{2}}$; ${z}_{D}=\frac{z}{L}$; ${N}_{s}=\frac{2\pi {\lambda }_{{\text{g}}}L}{w{c}_{f}}$; ${H}_{f}=\frac{{c}_{f}}{{c}_{g}}$; ${A}_{D1}=\frac{{r}_{pi}^{2}}{{r}_{eo}^{2}}$; ${N}_{12}=\frac{L}{w{c}_{f}{R}_{12}}$; ${T}_{1}$ = temperature of fluid inside the inner pipe; $Q$ = heat input rate; $L$ = depth of the borehole; $w$ = fluid volumetric flow rate; ${c}_{f}$ = volumetric heat capacity of fluid; ${c}_{g}$ = volumetric specific heat capacity of the ground; ${r}_{pi}$ = internal pipe inner wall radius; ${r}_{eo}$ = external pipe outer wall radius; ${R}_{12}$ = thermal resistance per unit length for heat transfer between the fluids in the internal pipe and the annulus.

Similarly, the energy function in the dimensionless form of the annulus is:

$$\frac{{N}_{s}{H}_{f}{A}_{D2}}{2}\frac{\partial {T}_{D2}}{\partial {t}_{D}}-\frac{\partial {T}_{D2}}{\partial {z}_{D}}+{N}_{12}\left({T}_{D2}-{T}_{D1}\right)+\frac{L}{w{c}_{f}{R}_{g}}\left({T}_{D2}-{T}_{Dg,{r}_{D}=1}\right)=0; 0<{z}_{D}<1,0<{t}_{D}$$

(8)

where ${T}_{D2}=\frac{2\pi {\lambda }_{{\text{g}}}L\left({T}_{2}-{T}_{0}\right)}{Q}$; ${T}_{2}$ = temperature of fluid within the annulus; ${T}_{Dg,{r}_{D}=1}$ = normalized temperature of the ground ${T}_{Dg}$ on the outer surface of the external pipe; ${R}_{g}$ = thermal resistance per unit length for heat transfer between the fluid in the annulus and the ground.

The radial heat conduction equation for the ground around the borehole is:

$$\frac{\partial {T}_{Dg}}{\partial {t}_{D}}=\frac{1}{{r}_{D}}\frac{\partial {T}_{Dg}}{\partial {r}_{D}}+\frac{{\partial }^{2}{T}_{Dg}}{\partial {r}_{D}^{2}}$$

(9)

where ${r}_{D}=r/{r}_{eo}$.

And the energy function on the outer wall of the external pipe is:

$$\frac{L}{w{c}_{f}{R}_{g}}\left({T}_{D2}-{T}_{Dg,{r}_{D}=1}\right)={N}_{g}\frac{\partial {T}_{Dg}}{\partial {r}_{D}}$$

(10)

The governing equations Eqs. (7)–(10) are converted into ordinary differential equations in the Laplace domain by using the Laplace transform. Then, an analytical solution to the governing equations in the Laplace domain can be obtained and is further inversely transformed back to the solution in the real-time domain and cylindrical coordinates based on a numerical inverse Laplace transform algorithm.

3.1.4 Holmberg et al. (2016) method

Holmberg et al. (2016) proposed a 2D solution to the coaxial DBHE problem. The thermal resistances of the pipe walls are represented by a network as shown in Fig. 4a. The thermal conduction in the rock surrounding the borehole can be expressed by Fourier’s law using cylindrical coordinates as:

$$\frac{1}{r}\frac{\partial }{\partial r}\left[{\lambda }_{{\text{g}}}r\frac{\partial {T}_{g}}{\partial r}\right]+\frac{\partial }{\partial z}\left[{\lambda }_{{\text{g}}}\frac{\partial {T}_{g}}{\partial z}\right]={\rho }_{g}{C}_{s,g}\frac{\partial {T}_{g}}{\partial t}+{S}_{1}$$

(11)

where ${\rho }_{g}$ and ${C}_{s,g}$ = density and specific heat capacity of formation; ${S}_{1}$ = heat source term.

Fig. 4

a Thermal resistance network (revised from Holmberg et al. 2016); b finite difference mesh of Song et al. (2018)

The energy equation for fluid flowing in the center pipe is:

$$\pi {r}^{2}{\rho }_{f}\frac{\partial {T}_{f1}}{\partial t}+\pi {r}^{2}{\rho }_{f}V\frac{\partial {T}_{f1}}{\partial z}=2\pi rh\Delta T$$

(12)

where ${\rho }_{f}$ = density of fluid; $V$ = fluid velocity; $h$ = heat transfer coefficient; $\Delta T$ = temperature difference between the fluid within the pipe and the pipe wall.

And the heat flux Ф_q on the inner pipe wall and outer wall can be generally expressed as:

$${\Phi }_{q}=-{\lambda }_{{\text{g}}}\frac{\partial T}{\partial r}$$

(13)

Then the governing equations Eqs. (11)–(13) are solved by a finite different-based method.

3.1.5 Song et al. (2018) method

Song et al. (2018) set up a 2D finite difference-based transient heat transfer model for the analysis of coaxial DBHE, the schematic diagram of the model is shown in Fig. 4b. As can be seen, only one element was used for the fluid inside the inner pipe and annulus in the radial direction and thus the variation of velocity on the cross-sectional area cannot be considered. Besides, heat convection is considered for the working fluid and 2D heat conduction is considered for the casing, cement sheath and formation.

The governing equation of the central tube, the outlet in Fig. 4b, can be written as

$${\rho }_{f}q{C}_{s,f}\frac{\partial {T}_{fo}}{\partial z}+\frac{{T}_{fi}-{T}_{fo}}{R}={\rho }_{f}{C}_{s,f}\pi {r}_{1}^{2}\frac{\partial {T}_{fo}}{\partial t}$$

(14)

where $q$ = volumetric flow rate of the working fluid; ${C}_{s,f}$ = specific heat capacity of the working fluid; ${T}_{fo}$ = temperature of the outlet fluid; ${T}_{fi}$ = temperature of the inlet fluid; ${r}_{1}$ is self-evident as shown in Fig. 4b; $R$ = thermal resistance of the inner pipe wall and is a function of convective heat transfer coefficients of the inlet and outlet fluid, which are affected by the size of the pipe and flow type, and thermal conductivity of the inner pipe. Note that the first term on the left side of the equation represents the forced convection, and the second term on the left side refers to heat transfer from the annulus fluid.

Similarly, the governing equation for the working fluid inside the annulus, the inlet in Fig. 4b, is:

$$-{\rho }_{f}q{C}_{s,f}\frac{\partial {T}_{fi}}{\partial z}+\frac{{T}_{fo}-{T}_{fi}}{R}+2\pi {r}_{5}{h}_{3}\left({T}_{w}-{T}_{fi}\right)={\rho }_{f}{C}_{s,f}\pi \left({r}_{5}^{2}-{r}_{4}^{2}\right)\frac{\partial {T}_{fi}}{\partial t}$$

(15)

where ${h}_{3}$ = convective heat transfer coefficient for the casing wall; ${T}_{w}$ = temperature of the casing wall and the third term on the left side of the equation denotes the heat transfer from casing to fluid.

As for the casing, both forced heat transfer from the working fluid inside the annulus and heat conduction of the cement are considered, thus the governing equation is:

$$\begin{aligned} & {\lambda }_{w}\pi \left({r}_{6}^{2}-{r}_{5}^{2}\right)\frac{{\partial }^{2}{T}_{w}}{\partial {z}^{2}}+2 \pi {r}_{5}{h}_{3}\left({T}_{fi}-{T}_{w}\right)+\frac{2 \pi {\lambda }_{wc}}{\text{ln}\left[\left({r}_{6}+{r}_{7}\right)/\left({r}_{5}+{r}_{6}\right)\right]}\left({T}_{c}-{T}_{w}\right)\\ &\quad ={\rho }_{w}{C}_{s,w}\pi \left({r}_{6}^{2}-{r}_{5}^{2}\right)\frac{\partial {T}_{w}}{\partial t} \end{aligned}$$

(16)

where ${T}_{c}$ = temperature of the cement sheath; ${\lambda }_{wc}$ = equivalent thermal conductivity of casing and cement interface; ${\rho }_{w}$ = density of the casing; ${C}_{s,w}$ = specific heat capacity of the casing.

Only heat conduction is considered for the cement sheath and formation and thus the governing equation for the cement sheath and formation can be expressed as

$$\begin{aligned} & {\lambda }_{c}\pi \left({r}_{7}^{2}-{r}_{6}^{2}\right)\frac{{\partial }^{2}{T}_{c}}{\partial {z}^{2}}+\frac{2 \pi {\lambda }_{wc}}{\text{ln}\left[\left({r}_{6}+{r}_{7}\right)/\left({r}_{5}+{r}_{6}\right)\right]}\left({T}_{w}-{T}_{c}\right)+\frac{2 \pi {\lambda }_{cs}}{\text{ln}\left[\left({r}_{7}+{r}_{8}\right)/\left({r}_{6}+{r}_{7}\right)\right]}\left({T}_{g}-{T}_{c}\right)\\ &\quad ={\rho }_{c}{C}_{s,c}\pi \left({r}_{7}^{2}-{r}_{6}^{2}\right)\frac{\partial {T}_{c}}{\partial t} \end{aligned}$$

(17a)

$$\frac{{\partial }^{2}{T}_{g}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}{T}_{g}}{\partial {z}^{2}}=\frac{{\rho }_{g}{C}_{s,g}}{{\lambda }_{g}}\frac{\partial {T}_{g}}{\partial t}$$

(17b)

where ${\lambda }_{cs}$ = equivalent thermal conductivity of cement and formation interface; ${T}_{c}$ = temperature of the cement sheath; ${T}_{g}$= temperature of the ground.

3.1.6 Luo et al. (2019) method

Based on the FLS method, Luo et al. (2019) proposed a segmented finite-line source method for coaxial DBHE under a fixed thermal gradient to consider the change of heat flux on the DBHE wall with time and depth. To model the heat flux on the DBHE with depth, the DBHE is divided into n segments with a unique heat flux ${\Phi }_{q,i}$ being assigned to each segment as shown in Fig. 5a, and therefore the temperature field of the formation motivated by conduction can be expressed as

$${\theta }_{1}(r,z,t)={T}_{1}-{T}_{0}=\sum_{i=1}^{n}\frac{{\Phi }_{q,l}^{\left(i\right)}}{4\pi {\lambda }_{{\text{g}}}}{\int }_{0}^{h}\frac{{\text{erfc}}\left(\frac{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}-\frac{{\text{erfc}}\left(\frac{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{\text{d}}\eta$$

(18)

where ${\theta }_{1}$ is the temperature change due to heat flux caused by coaxial DBHE.

Fig. 5

a Finite line segments of BHE; b heat flux segment with time (revised from Luo et al. 2019)

The heat flux might also change with time and is also modeled by an approach in Fig. 5b, and Eq. (18) can be further modified as

$${\theta }_{1}(r,z,t)=\sum_{j=1}^{N}\sum_{i=1}^{n}\frac{{\Phi }_{q.l}^{\left(i,\frac{t}{\Delta t}-j\right)},{\Phi }_{q.l}^{\left(i,\frac{t}{\Delta t}-j-1\right)}}{4\pi {\lambda }_{{\text{g}}}}{\int }_{0}^{h}\frac{{\text{erfc}}\left(\frac{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z-\eta \right)}^{2}}}-\frac{{\text{erfc}}\left(\frac{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{2r\sqrt{{F}_{o}}}\right)}{\sqrt{{r}^{2}+{\left(z+\eta \right)}^{2}}}{\text{d}}\eta$$

(19)

Besides, the temperature of the formation around the DBHE is also influenced by the initial geothermal gradient. The temperature field of the ground considering vertical conduction under a given thermal gradient can be expressed as

$${\theta }_{2}\left(z,t\right)={\theta }_{s}\left(z\right)+{\theta }_{h}\left(z,t\right)$$

(20a)

$${\theta }_{s}\left(z\right)=\left({g}_{0}-{T}_{\infty }\right)\left(1-\frac{z}{{z}_{\infty }}\right)$$

(20b)

$${\theta }_{h}\left(z,t\right)=\sum_{m=1}^{\infty }\frac{1}{H}\times {{\text{sin}}}{\beta }_{m}z\times {e}^{-{a}_{s}{\beta }_{m}^{2}t}\underset{0}{\overset{2H}{\int }}\left[{T}_{0}\left({z}^{\prime}\right)-{T}_{\infty }-{\theta }_{s}\left({z}^{\prime}\right)\right]{\text{sin}}{\beta }_{m}{z}^{\prime}d{z}^{\prime}$$

(20c)

where ${g}_{0}$ = ground surface temperature; ${T}_{0}\left(z\right)$ = initial ground temperature field; $H$ = height of the DBHE; ${\beta }_{m}$ = eigenvalue of the heat transfer differential equation and ${\beta }_{m}=$ m $\times$ 2π/H.

The temperature field of the formation $\theta$ under the initial thermal gradient and the heat flux by the DBHE should be the superposition of Eqs. (19) and (20)

$$\theta \left(r,z,t\right)=T\left(r,z,t\right)-{T}_{0}\left(z,t\right)={\theta }_{1}\left(r,z,t\right)+{\theta }_{2}\left(z,t\right)$$

(21)

As for the working fluid inside the DBHE, a 1D model is used to calculate the temperature of the fluid with time and the governing equation can be given as

$$\frac{{\text{d}}{T}_{eq1}}{{\text{d}}{z}_{eq}}=\frac{H}{q{c}_{w}{R}_{12}}\left({T}_{eq2}-{T}_{eq1}\right)$$

(22a)

$$\frac{{\text{d}}{T}_{eq2}}{{\text{d}}{z}_{eq}}=\frac{H}{q{c}_{w}{R}_{12}}\left({T}_{eq1}-{T}_{eq2}\right)-\frac{H}{q{c}_{w}{R}_{b}}\left({T}_{eqb}-{T}_{eq2}\right)$$

(22b)

where ${T}_{eq}=\frac{{T}_{w}\left(z\right)-{T}_{rs}}{{T}_{in}-{T}_{rs}}$, ${T}_{w}\left(z\right)$ = temperature of water; ${z}_{eq}=z/H$; ${R}_{b}$ = thermal resistance of the outer wall of the DBHE.

3.1.7 Lamarche (2021) method

As shown in Fig. 4a, it is often practical to simplify the coaxial DBHE as a thermal resistance network and even complex borehole structures such as U-tube can be efficiently modeled using the so-called ‘Thermal resistance and capacity models’ (TRCM) to represent thermal resistances among tubes and grout (De Carli et al. 2010; Bauer et al. 2011a, b). Based on the concept of the thermal resistance network, Lamarche (2021) derived the analytical solution for fluid inside the coaxial DBHE as

$$\begin{aligned} \begin{cases} & \left. {\theta }_{ann}\left(\widetilde{z}\right)={\text{exp}}\left(-\widetilde{z}\gamma \right)\left\{\frac{{\text{cosh}}\left[\eta \left(1-\widetilde{z}\right)\right]+\xi {{\text{sinh}}}\left[\eta \left(1-\widetilde{z}\right)\right]}{{{\text{cosh}}}\left(\eta \right)+\xi {{\text{sinh}}}\left(\eta \right)}\right\} \right.\\ &\left. {\theta }_{cen}\left(\widetilde{z}\right)={\text{exp}}\left(-\widetilde{z}\gamma \right)\left\{\frac{{{\text{cosh}}}\left[\eta \left(1-\widetilde{z}\right)\right]-\xi {{\text{sinh}}}\left[\eta \left(1-\widetilde{z}\right)\right]}{{{\text{cosh}}}\left(\eta \right)+\xi {{\text{sinh}}}\left(\eta \right)}\right\}\right. \end{cases} \left(\text{annulus injection}\right) \end{aligned}$$

(23)

$$\begin{aligned} \begin{cases} & \left. {\theta }_{ann}\left(\widetilde{z}\right)={\text{exp}}\left(\widetilde{z}\gamma \right)\left\{\frac{{{\text{cosh}}}\left[\eta \left(1-\widetilde{z}\right)\right]-\xi {{\text{sinh}}}\left[\eta \left(1-\widetilde{z}\right)\right]}{{{\text{cosh}}}\left(\eta \right)+\xi {\text{sinh}}\left(\eta \right)}\right\} \right.\\ &\left. {\theta }_{cen}\left(\widetilde{z}\right)=\text{exp}\left(\widetilde{z}\gamma \right)\left\{\frac{{\text{cosh}}\left[\eta \left(1-\widetilde{z}\right)\right]+\xi {\text{sinh}}\left[\eta \left(1-\widetilde{z}\right)\right]}{{\text{cosh}}\left(\eta \right)+\xi {\text{sinh}}\left(\eta \right)}\right\}\right. \end{cases} \left(\text{inner pipe injection}\right) \end{aligned}$$

(24)

where $\widetilde{z}=z/H$; $\theta =\frac{{T}_{f}\left(z\right)-{T}_{b}}{{T}_{fi}-{T}_{b}}$; $\gamma =\frac{H}{2\dot{m}{C}_{p}{R}_{1}^{\prime}}$; $\xi =\sqrt{\frac{{R}_{a}^{\prime}}{4{R}_{1}^{\prime}}}$; $\eta =\frac{\gamma }{\xi }$; ${R}_{a}^{\prime}=\frac{4{R}_{1}^{\prime}{R}_{12}^{\prime}}{4{R}_{1}^{\prime}+{R}_{12}^{\prime}}$; ${T}_{b}$ is the temperature of borehole; $\dot{m}$ is mass flow rate; ${R}_{1}^{\prime}$ and ${R}_{12}^{\prime}$ are thermal resistance of inner and outer pipes. Considering different borehole conditions such as uniform temperature, uniform heat flux and linearly varying heat flux, the solutions can be used to analyze the effective thermal resistance of DBHE (Lamarche 2021). Note that the method of Lamarche (2021) takes the borehole temperature as a boundary condition and thus should be analyzed with other approaches for modeling the heat transfer of the formation.

3.1.8 Jia et al. (2022) method

Jia et al. (2022) proposed a finite-volume based-transient approach for analyzing the coaxial DBHE. Specifically, a finite-volume-based transient 1D method is formulated to calculate the fluid temperatures as it travels through the DBHE. A transient model to simulate the heat conduction through the pipe walls and within rock and soil is also formulated. It is assumed that the temperature and velocity of fluid only vary axially, and the governing equations for the fluid are:

$$\frac{\partial }{\partial t}\left(A{\rho }_{f}\right)+\frac{\partial }{\partial x}\left(A{\rho }_{f}u\right)=0 \,\,(\text{continuity equation})$$

(25a)

$$\frac{\partial \left(A{\rho }_{f}u\right)}{\partial t}+\frac{\partial \left(A{\rho }_{f}{u}^{2}\right)}{\partial x}=-\frac{\partial \left(pA\right)}{\partial x}-A{F}_{f}+A{S}_{u}\pm A{\rho }_{f}g\,\, (\text{momentum equation})$$

(25b)

$$\frac{\partial \left(A{\rho }_{f}{C}_{s,f}T\right)}{\partial t}+\frac{\partial \left(A{\rho }_{f}{C}_{s,f}uT\right)}{\partial x}=A{S}_{T} \,\,(\text{energy equation})$$

(25c)

where $A$ = cross-sectional area of the fluid flow; $u$ = average velocity of the fluid; x = axial coordinate; p = average pressure applied on the cross-sectional area; ${F}_{f}$ = frictional force; ${S}_{u}$ = momentum source; $g$ = gravity; ${S}_{T}$ = energy source.

As for the heat conduction within the formation, the energy equation is:

$$\frac{\partial \left({\rho }_{f}{C}_{s,g}T\right)}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left({\lambda }_{g}r\frac{\partial T}{\partial r}\right)$$

(26)

To solve the governing equations Eqs. (23)–(26), the fluid flow passage is divided into N non-overlapping control volumes (CV). All variables are stored at the CV boundaries.

3.1.9 Evaluation of summarized analytical and semi-analytical methods

To better compare different analytical and semi-analytical coaxial DBHE methods, Table 5 compares the summarized methods with respect to the heat transfer models for working fluid and formation. Early studies considered only the radial heat conduction of formation around the coaxial DBHE, later on, radial and longitudinal heat conduction can be analyzed. However, most analytical and semi-analytical solutions consider only 1D axial flow and heat convection. In the following, more detailed comparisons and discussions on the weaknesses and strengths of analytical and semi-analytical methods are carried out.

Table 5 Summary of analytical and semi-analytical methods for DBHE from literature

(1) Boundary and interface conditions.

Due to the complexity of the 3D coaxial DBHE problem, assumptions are made to boundary and interface conditions to simplify the solving process of working fluid and formation domains in analytical and semi-analytical solutions. The ILS, ICS and FLS methods, as shown in Eqs. (2)-(5), assume a constant heat flux on the line or cylindrical surface but the heat flux on the DBHE changes with time and depth due to the variations of the temperature difference between the fluid and the formation with time and locations. According to Li and Lai (2015), differences are observed between the ILS model Eq. (2) and ICS model Eq. (4) when ${F}_{o}=\frac{{\alpha }_{d, {\text{g}}}t}{{r}^{2}}$ is smaller than 10. Besides, due to the ignorance of the ground surface, the ILS and ICS models are significantly different from the FLS model when ${F}_{o}$ is larger than 10,000 according to Li and Lai (2015). In this regard, the ILS-based methods (Ingersoll et al. 1950; Diao et al. 2004) and ICS methods, should be used when $10<{F}_{o}<10000$, which means infinite source methods are not suitable for short-term and long-term predictions of the DBHE behavior.

As for the segmented line source method by Luo et al. (2019), the temperature field is the superposition of two sub-solutions under a FLS and thermal gradient, respectively. And the temperature field caused by the thermal gradient is a 1D solution only considering the vertical thermal gradient and thus the formation temperature changes vertically with time as denoted as ${\theta }_{h}\left(z,t\right)$ in Eq. (20). However, for the formation far away from the DBHE, the temperature of the formation can be seen as undisturbed and thus would not change with time, which means the sub-solution cannot satisfy the far-away boundary condition.

The Laplace transform solution by Beier et al. (2014), finite difference methods (Holmberg et al. 2016; Song et al. 2018); the approach of Lamarche (2021) and finite volume method (Jia et al. 2022), similar to TRCM models, model the interface, i.e., outer casing and inner pipe, as a thermal resistance, which is determined by the size of the casing/pipe, the thermal conductivity of the casing/pipe material and the convective heat transfer coefficient on the casing/pipe surface. Specifically, the thermal resistance contributed by the convective heat transfer on the inner surface of the pipe is (Beier et al. 2014; Holmberg et al. 2016; Song et al. 2018; Jia et al. 2022):

$${R}_{Convection}=\frac{1}{2\pi {r}_{pi}{h}_{pipe}}$$

(27)

where ${r}_{pi}$ = radius of the inner surface of the pipe; ${h}_{pipe}$ = convective heat transfer coefficient and can be expressed by Nusselt number $Nu$ (Gnielinski 1976)

$${h}_{pipe}=\frac{Nu {\lambda }_{f}}{D}$$

(28a)

$$Nu=\frac{\left(\frac{f}{8}\right)\cdot (Re-1000)Pr}{1+12.7\sqrt{\frac{f}{8}} \left({Pr}^\frac{2}{3}-1\right)}$$

(28b)

where $Pr=\frac{{C}_{p,f}\cdot {\mu }_{f}}{{\lambda }_{f}}$ represents the Prandt number; $Re=\frac{{\rho }_{f}\cdot {u}_{f}\cdot D}{{\mu }_{f}}$ represents the Raynolds number; ${\mu }_{f}$ = dynamics viscosity of working fluid; D = 4A/P; P = wetted perimeter; $f$ = Darcy friction factor determined by $Re$ and is different for laminar, transition, and turbulent flow. Note that the empirical equations Eq. (28b) and f are mainly regressed from data on water in smooth pipes and thus should be used with caution when applying to other working fluids (Van Eldik et al. 2014) and pipes with different roughness and special fluid/wall treatments. TRCM models can be utilized to model complex borehole structures such as U-tube (De Carli et al. 2010; Bauer et al. 2011a, b), but details on those TRCM models for complex borehole structures will not be discussed because the focus of this study is coaxial DBHE.

For a fully developed flow in U-tube (Acuña 2010) and coaxial DBHE (Holmberg et al. 2016), the pressure loss due to friction $\Delta {P}_{f}$ can be estimated as:

$$\Delta {P}_{f}=f\frac{L}{D}\frac{{\rho }_{f}{u}_{f}^{2}}{2}$$

(29)

in which L is the length of the pipe. Again, due to the limitation of f, Eq. (29) should be used with caution.

(2) Fluid and formation domain.

For both line source and cylindrical source models, the formation is assumed to be isotropic with constant thermophysical properties within the whole domain, but the real ground is stratified into different layers due to deposition and thus the thermophysical properties change with depth. In this regard, to reduce the computational cost, some researchers use equivalent properties of formation in their models (Lee 2011):

$${K}_{g,e}=\frac{\sum_{i=1}^{N}{K}_{g,i}{b}_{i}}{\sum_{i=1}^{N}{b}_{i}} \,\,(\text{Horizontally layered})$$

(30)

where ${K}_{g,i}$ and ${b}_{i}$ = property and thickness of ith layer. But the utilization of Eq. (30) could bring errors in the result. Except for the FLS model Eq. (5), other ILS/ICS models only consider 1D radial heat transfer, but the difference between the two types of solutions is small only when $10<{F}_{o}<10000$. More recently, the ILS method (Diao et al. 2004) and FLS method (Molina-Giraldo et al. 2011) were extended to consider the heat convection by groundwater flow, and the constant groundwater flow is in the horizontal direction and stretched to the DBHE bottom. Molina-Giraldo et al. (2011) found that the ILS model might overpredict the temperature anomaly size caused by groundwater flow compared with the FLS model. Besides, the constant groundwater flow within the whole depth of the DBHE might not be true because the direction and velocity of groundwater flow depends on the permeability and porosity of the ground, which are not uniform within the whole formation (Wang et al. 2009). In this regard, Hu (2017), Erol and François (2018), and Jiao et al. (2021) further extended the FLS model to consider multiple layers and groundwater flow. And groundwater flow within the 900 m aquifer region rather than the whole domain can also improve the thermal extraction of a 2500 m DBHE (Jiao et al. 2021) by decreasing temperature drop by about 10% within the aquifer.

As for the Laplace transform-based model (Beier et al. 2014) and composite cylindrical source model (Gordon et al. 2017), like the line and cylindrical source models, the formation is assumed to be isotropic within the whole domain and thus has similar problems due to the ignorance of multi-layered formation. The heat convection caused by groundwater flow is not considered by Beier et al. (2014). And 1D model is used to model working fluid as shown in Eqs. (7) and (8), and thus the variation of fluid velocity along the cross-sectional area is ignored. And water as an incompressible fluid with constant physical properties is considered by Beier et al. (2014), thus the thermosiphon effect and the change of thermal properties with temperature such as the thermal conductivity of liquid water, which can be up to 21%, cannot be well reflected.

For the finite difference methods (Holmberg et al. 2016; Song et al. 2018) and the approach by Luo et al. (2019), the heat conduction along radial and vertical directions is considered, while the heat convection within the formation is ignored due to the adoption of symmetric models. Since the finite difference (Holmberg et al. 2016; Song et al. 2018) and finite volume (Jia et al. 2022) models divide the formation domain into meshes, the multi-layered formation can be considered by assigning different thermal properties to different points, but verifications with field tests should be performed for the multi-layered case. Note that the thermal conductivity of both soil and rock can be anisotropic according to laboratory measurements (Dao et al. 2014; Wu et al. 2021), but most analytical and semi-analytical approaches cannot consider the anisotropy of formation in their current format. Again, the variations of fluid velocity along the cross-sectional area cannot be considered due to the 1D models adopted in the finite difference, finite volume, line/cylindrical source models; composite cylindrical source model and the method of Lamarche (2021). To consider different working fluids, Bai et al. (2022) used a customized finite difference-based model to analyze the behavior of DBHE using both water and CO₂ as the working fluid. Bai et al. (2022) suggested considering temperature-dependent properties when using CO₂ as the working fluid and CO₂ seems to be a better option than water when the inlet pressure is 10 MPa.

3.2 Numerical approaches

With the ongoing development of computational techniques, numerical approaches, due to their ability to tackle complex physics and versatile engineering problems, have been widely used for analyzing engineering practices. This section reviews the available numerical approaches using numerical software/code/package for analyzing the DBHE. And the strengths and weaknesses of different software/code/packages for modeling DBHE are focused on. Table 6 summarizes the applications of different numerical software/code/packages for modeling the coaxial DBHE from the literature. As can be seen from Table 6, FRACTure (Kohl and Hopkirk 1995), SHEMAT (Simulator for HEat and MAss Transport) (Clauser 2003), FEFLOW (Diersch 2014), COMSOL Multiphysics (COMSOL 2022), OpenGeoSys (Kolditz et al. 2012), T2Well (Pan and Oldenburg 2014), ANSYS FLUENT (ANSYS 2016) have been applied to analyze coaxial DBHE under different geological conditions and descriptions and evaluations of those simulators are conducted in the followings.

Table 6 Summary of numerical software/code/package for modeling coaxial DBHE

FRACTure is a 3D finite element program developed by Kohl and Hopkirk (1995) to study the coupling of thermal field, hydraulic field and elastic mechanical field in geoscience and in particular to those related to Hot Dry Rock reservoirs. FRACTure can simulate laminar and turbulent flow in porous media or fracture media, diffusive and advective thermal transport and linear elastic mechanical problems (Kohl and Hopkirk 1995). In FRACTure, the formation can be considered as multi-layered, heterogenous, and permeable media, and groundwater flow can be simulated (Kohl et al 2002). Besides, the fluid inside the pipe can either be modeled as 1D elements (Kohl et al 2002) or 3D elements (Signorelli et al. 2007).

SHEMAT (Clauser 2003) is a general-purpose code for a wide variety of thermal and hydrogeological 2D and 3D problems. As shown by the application to a DBHE (Dijkshoorn et al. 2013), SHEMAT can be used to simulate multi-layered, heterogenous, and permeable formation under both heat conduction and convection, but the thermophysical properties of water are assumed constant with respect to temperature and pressure and no applications using other fluids such as CO₂ are available.

FEFLOW (Diersch 2014) is a 3D finite element program developed for simulating groundwater flow, mass transfer and heat transfer in porous media and fractured media with consideration of chemical kinetics for multi-component reaction systems. As for a DBHE, the fluid inside the DBHE can be both modeled by 1D elements (Diersch et al. 2011; Le Lous et al. 2015; Wang et al. 2022a) or 3D elements (Diersch et al. 2011; Dehkordi and Schincariol 2014), and the difference between the results using 1D elements and 3D elements for fluids in the DBHE is small but the calculation using 1D elements for fluids is much faster (Diersch et al. 2011). Note that the available applications of FEFLOW only use water as the working fluid and the properties of water are assumed constant, thus the application of FEFLOW with CO₂ should be further investigated.

COMSOL Multiphysics (COMSOL 2022) is a 3D finite element platform especially for fully coupled multi-physics and single physics modeling problems, providing specialized functionality for electromagnetics, structural mechanics, acoustics, fluid flow, heat transfer, and chemical engineering. As for a coaxial DBHE, COMSOL Multiphysics can model heat conduction and convection due to groundwater flow within the formation and the dependencies of formation properties on temperature and pressure (Zhang et al. 2019). And the fluid within the DBHE can be modeled as 1D elements (Zhang et al. 2019), 2D symmetric elements (Caulk and Tomac 2017) and 3D elements, and different working fluids can be considered (Zhang et al. 2019). However, the verification of COMSOL Multiphysics models for DBHE using CO₂ is not yet made by comparison with field tests to the best of our knowledge.

OpenGeoSys (Kolditz et al. 2012) is an open-source finite element simulator for modeling hermos-hydro-mechanical-chemical (THMC) problems. Similar to other platforms, the groundwater flow can be modeled in OpenGeoSys because the formation around the DBHE is modeled as a permeable media in 3D (Chen et al. 2019). To save computational time, the dual-continuum approach proposed by Al-Khoury et al. (2010) and extended by Diersch et al. (2011), in which the DBHE is represented as 1D line elements, was implemented into OpenGeoSys by Chen et al. (2019). The approach proposed by Chen et al. (2019) was adopted by different authors to analyze DBHE in China and Unite Kingdom (Huang et al. 2021; Kolo et al. 2023). It should be noted that the water properties are assumed to be constant in the approach of Chen et al. (2019) and only water is used as the working fluid.

T2Well (Pan and Oldenburg 2014) is a wellbore-reservoir coupled code from the TOUGH (Transport of Unsaturated Groundwater and Heat) suite by Lawrence Berkeley National Laboratory. Darcy’s law is used to describe the seepage and heat transfer of fluids in the formation and the fluid inside the DBHE is modeled by the drift model and related governing equations as 1D elements (Hu et al. 2020a; Yu et al. 2021). In T2Well, the equations of state for working fluids take temperature and pressure as basic variables and different working fluids such as water and CO₂ can be considered (Hu et al. 2020b).

ANSYS FLUENT (ANSYS 2016) is multi-dimensional fluid simulation software known for its advanced physics modeling capabilities. For the coaxial DBHE problem, the formation can be modeled as porous media and working fluid as incompressible or compressible, but the water is assumed as incompressible fluid by both Pokhrel et al. (2022) and Li et al. (2023) for simplicity. Again, the application of ANSYS FLUENT to simulate other working fluids such as CO₂ inside coaxial DBHE is not yet reported to the best of our knowledge.

4 Key factors for design and application of coaxial DBHE

As shown in Fig. 2, lots of factors affect the behavior of coaxial DBHE and many publications have discussed those factors. In this regard, this section reviews relevant factors in terms of four major categories: ground thermal properties, borehole properties, ground pump parameters and economic considerations.

4.1 Ground thermal properties

Thermal conductivity of formation is one of the most important parameters affecting the thermal power of a coaxial DBHE. Many numerical studies and field tests (Rybach and Hopkirk 1995; Kohl et al. 2000) indicate that the thermal conductivity of a single-layered formation determines the performance of the coaxial DBHE, and higher thermal conductivity leads to higher thermal power. For instance, the thermal power of a 2605 m DBHE in Qingdao (Bu et al. 2019) is about 50% higher than that of a 2800 m DBHE in Tianjin (Jia et al. 2022) when operating 24 h per day after operating for over 100 days mainly because the thermal conductivity at Qingdao site is higher than that at Tianjin site as shown in Table 4. In a multi-layered formation, Wang et al. (2022a) defined a factor to evaluate the contribution of different ground layers as the ratio of the temperature difference in the annular pipe within a specific depth range to the temperature difference within the whole depth and found that the lower half of the formation contributes much higher, above 70%, than the upper half of the formation, below 30%, which also agrees with other numerical simulations (Li et al. 2021; Jiao et al. 2021). In this regard, the thermal power of a coaxial DBHE might be improved with a deeper depth (Caulk and Tomac 2017).

The thermal gradient is an important indicator for geothermal energy exploitation. Higher thermal gradient results in higher outlet fluid temperature and thermal power of the coaxial DBHE according to numerical simulations (Caulk and Tomac 2017; Chen et al. 2019). Field tests from literature also support the great influence of thermal gradient, a 500 m DBHE in Beppu (Pokhrel et al. 2022) produces twice the thermal power of an 876.5 m DBHE in Hawaii (Morita et al. 1992) as shown in Table 4 mainly due to a higher thermal gradient. Besides, the effect of thermal gradient differs for different working fluids according to Zhang et al. (2019), among nine working fluids investigated by Zhang et al. (2019), CO₂, water and R152a are the top three working fluids receiving the highest enhancement of thermal power with the increase of thermal gradient, which indirectly explains why CO₂ is more suitable than water for the hot dry rock geothermal exploitation with high thermal gradient > 60 °C/km (Brown 2000).

Groundwater flow is another factor affecting the behavior of coaxial DBHE. As discussed in Sects. 3.1, different analytical and semi-analytical approaches (Hu 2017; Erol and François 2018; Jiao et al. 2021), as well as numerical simulations (Le Lous et al. 2015; Chen et al. 2019), have been proposed to include the heat convection brought by groundwater flow within the formation. For a 2500 m coaxial DBHE under a thermal gradient of 33 °C/km, groundwater flow of 9.59 × 10^–8 m/s between 850 and 1750 m results in the reduction in heat flux on the DBHE wall by 4–6% within the region with groundwater flow after 30 years of periodic operations (Jiao et al. 2021), which is about 1/3 of the heat flux reduction within the region of no groundwater flow. However, an aquifer with a relatively small thickness of 13 m at a groundwater flow rate of 0.368 m/d (4.26 × 10^–6 m/s) barely affects the thermal power of a 2600 m DBHE according to Chen et al. (2019). In this regard, the effect of groundwater flow highly depends on the thickness of the aquifer and can be negligible if the aquifer is relatively small, e.g., 0.5–2.5% of the DBHE length, compared to the depth of the DBHE (Chen et al. 2019).

Thermal reservoir modification/stimulation techniques such as hydraulic fracturing and acid injection are not suitable for coaxial DBHE due to the high cost of stimulation and low thermal power of DBHE, which explains why reservoir stimulations are often used in doublet systems such as EGS (Westaway 2018). However, the open-type coaxial DBHE could be plausible if a relatively thick aquifer, e.g., 10% of the DBHE length, exists near the end of the borehole according to field tests (Dai et al. 2019). The open-loop coaxial DBHE was referred to as ‘Deep Geothermal Single Well’ (DGSW) by Gel et al. (2016); Collins and Law (2017); Westaway (2018) and ‘downhole coaxial open loop’ (DCOL) by Dai et al. (2019). It was found from field test (Collins and Law 2017) that a 2 km DGSW system can deliver thermal power of 400 kW with a 7-kW electrical pumping input. And DCOL also produced an averaged heat output per unit length of 154 W/m during the field test for two weeks (Dai et al. 2019), which is higher than most field tests of coaxial DBHE in Table 4. In this regard, the open-type DBHE could be a good option if a deep and thick enough aquifer, e.g., 10% of the DBHE length, exists in the formation.

4.2 Borehole properties

Currently, the diameter of the borehole is mainly smaller than 50 cm and the borehole size can be further reduced at deeper depths as shown in Table 2 and Fig. 3. Due to the larger area for heat exchanging with the formation, the DBHE with larger borehole diameter might perform better (Thomasson and Abdurafikov 2022). For example, in the simulations by Pan et al. (2020), increasing the borehole diameter from 0.23 to 0.27 m leads to a 6.7% increase in thermal power for a 2000 m coaxial DBHE. However, drilling a large borehole might be of low economic efficiency, in this regard, local enlargement of the well bore diameter according to Kant et al. (2018) could further increase the size of the borehole locally near the bottom and improve the thermal power of the DBHE, but the effect of local enlargement on borehole stability and integrity should be further investigated.

At a constant thermal gradient, the outlet fluid temperature and thermal power of a coaxial DBHE increase with borehole depth (Holmberg et al. 2016; Caulk and Tomac 2017; Brown et al. 2021). As shown in Table 4, field tests on DBHEs from different locations indicate the increase of thermal power with increasing DBHE length in general. However, both drilling cost and operating expense could also increase with drilling depth, and thus economic efficiency should be combined with thermal power and geological conditions to determine a proper depth for the DBHE.

Grout/cement between the borehole wall and outer casing of the DBHE, although is a thin layer, can significantly affect the performance of a coaxial DBHE (Pan et al. 2020). According to simulations by Pan et al. (2020), the thermal power of a 2000 m coaxial DBHE in sandstone with thermal conductivity of 5.73 W/(m K) increases by 8.2% when the grout thermal conductivity increases from 0.73 to 1.73 W/(m K), and only 2.3% of increment in thermal power can be obtained if the grout thermal conductivity further increases to 2.73 W/(m K), which agrees with simulation by Li et al. (2023). In this regard, it is suggested to use grout with thermal conductivity close to the formation. Furthermore, according to Pan et al. (2020), instead of using a steel outer casing, it could be more economical to apply thermally enhanced grout materials if the borehole stability and impermeability of the grout are satisfactory.

The coaxial DBHE often injects working fluid through the annulus region and pumps the heated fluid out through the inner pipe, and thus the insulated material such as a VIT should be used for the inner pipe (Śliwa et al. 2018), otherwise significant heat loss can occur and the outlet fluid temperature could be too low for heating and cooling after long-term operations (Dijkshoorn et al. 2013). However, according to Zhang et al. (2015), the price for VIT could be 5 times more than bare tubing under normal circumstances for the Cyclic Steam Stimulation process. In this regard, economic analysis should be performed with the consideration of thermal power to determine the use of insulated material.

The outer casing of a coaxial DBHE is limited in size by the borehole size and thus the inner pipe size seems to be a more proper factor when designing a coaxial DBHE. According to Zhang et al. (2019), the thermal power of an 1800 m coaxial DBHE using CO₂ as the working fluid can drop above 50% when the inner pipe diameter increases from 50 mm to about 90 mm, and the thermal power of DBHE with water as working fluid can decrease by about 20% when inner pipe diameter increases from 50 mm to about 90 mm. However, more significant pressure loss can be observed for a DBHE with a smaller inner pipe (Zhang et al. 2019), and thus a trade-off between pressure loss and thermal power should be made to determine the proper inner pipe size.

On the other hand, the material of the pipe and its exposure to chemical attack determine the resistance of coaxial DBHE to corrosion. To improve the corrosion resistance of DBHE, fiberglass pipes (Sliwa et al. 2018), galvanized steel tubes (Sanner and Knoblich 1991), stainless-steel pipes (Mendrinos et al. 2017) and Polyethylene-coated steel pipe (Badenes et al. 2020) rather than plain steel pipes are suggested to be used and higher costs are expected when using the material with higher corrosion resistance. According to the in-situ corrosion tests conducted in a groundwater well at Schwalbach Ground Source Heat Pumps (GSHP) research station, the useful life of plain steel can be expected to be 30–40 years (Sanner and Knoblich 1991). Therefore, the pipe material should be determined based on the designed lifespan, material and maintenance costs of the coaxial DBHE.

Multiple BHE system is used to heat large areas (Kurevijia et al. 2012), and a minimum spacing between boreholes is required to mitigate thermal interference (EST 2007). As for DBHE, the spacing could be larger due to the longer length of DBHE than SBHE. Cai et al. (2021, 2022) reported a pilot project with 5 DBHEs in Xi’an, China and the spacings between boreholes are 15 m and 30 m in the project. By using the same heat extraction rate for each DBHE, the 5 DBHE array produced water 4.7 °C cooler than a single DBHE with the same heat extraction rate after operating for 20 years (Cai et al. 2021). After optimization, Cai et al. (2022) suggested a minimum inter-borehole spacing to be 15 m, and among single-line, polyline and circle layouts of the DBHE, the single-line layout supplies more heat and has higher long-term sustainability than other layouts. On the other hand, for a 922 m deep DBHE group, the minimum inter-borehole spacing is 20 m for line arrays and 30 m for square arrays when operating under an intermittent heat load of 50 kW for 20 years (Brown et al. 2023b).

Water is the most common working fluid for geothermal exploitation, but CO₂ seems a better option for EGS (Brown 2000). It should be noted that CO₂ should maintain the supercritical state during geothermal exploitation (Brown 2000), which requires that the temperature and pressure of CO₂ are higher than 30.98 °C and 7.38 MPa, respectively. Due to the low viscosity and significant density difference between hot outlet CO₂ and cold inlet CO₂ (Brown 2000), the pumping power of a CO₂-based DBHE is less than a water-based system. Zhang et al. (2019) analyzed the performance of nine different working fluids for coaxial DBHE via numerical simulations and found that CO₂ and water are the two best working fluids for an 1800 m DBHE, and CO₂ produces 9% more thermal power than water for the base case at a flow rate of 23 m³/h. Similarly, Bai et al. (2022) also found that the CO₂ seems to be a better option than water when the injection pressure is 10 MPa and the heat extraction rate is between 80 to 120 W/m for a 2500 m DBHE, and He et al. (2021) recommended the use of CO₂ for DBHEs deeper than 2800 m. However, Hu et al. (2020b) suggested that CO₂ is more suitable for geothermal reservoirs with high temperatures and water seems to be a better option for a 3500 m DBHE based on their simulations. Nevertheless, none of the available approaches (Zhang et al. 2019; Hu et al. 2020b; He et al. 2021; Bai et al. 2022) with CO₂ as the working fluid are verified with field tests on CO₂-based DBHE. In this regard, field tests using CO₂ as the working fluid should be performed to further examine the utilization of CO₂ as the working fluid for the coaxial DBHE.

4.3 Pump parameters

Flow rate is the most important parameter for a pump. The volumetric flow rates in Sect. 2 and Table 4 from field tests are between 4.8 and 30 m³/h and 1–45 m³/h from numerical simulations in Sect. 3. In general, the increasing flow rate of a coaxial DBHE leads to a decrease in outlet temperature and an increase in thermal power from numerical simulations (Dijkshoorn et al. 2013; Alimonti and Soldo 2016; Chen et al. 2019) and field tests (Zhang et al. 2019; Wang et al. 2022a; Jia et al. 2022). But the fluid for the heating and cooling system often requires a temperature higher than a specific temperature such as 55 °C for the climate control unit (Dijkshoorn et al. 2013), in this regard, the working flow rate of the DBHE should be determined based on temperature and thermal power requirements.

The injection temperature of working fluid is another parameter that can be controlled in a pumping system. According to Pokhrel et al. (2022), A 20 °C decrease in inlet temperature leads to an approximately 16% increase in total thermal energy from the system and thus a lower inlet temperature is recommended.

Due to the friction of the pipe, working fluid would experience pressure loss when circulating in the coaxial DBHE and thus higher inlet pressure is often needed to compensate for the pressure loss as shown in Morita et al. (1992). In a 2151 m coaxial DBHE (Morita et al. 2005), the pressure loss is proportional to the flow rate, which confirms Song et al. (2018) and Eq. (29). According to Holmberg et al. (2016), the pressure loss increases with DBHE length but increasing the inner pipe diameter can decrease the pressure loss. As for different working fluids, the pressure losses of R600a, pentane and CO₂ are the least among 9 working fluids including water according to Zhang et al. (2019). Note that pressure loss is not the inlet pressure needed for pumping the working fluid because the thermosiphon effect due to density decreases with temperature might compensate for the pressure loss. For example, the pumping power of the 2151 m DBHE (Morita et al. 2005) is zero for 2 years and 8 months because the hot outlet water has a smaller density than the inlet water, leading to a higher gravity head increase than the pressure loss (Alimonti and Soldo 2016), but pumping power is needed later because outlet water temperature gradually decreases. In this regard, the properties of working fluid should be modeled as temperature-dependent to determine the required inlet pressure and thus pumping power at different time.

The flow rate of a coaxial DBHE might fluctuate due to changes in inlet fluid temperature and requirements of power or domestic hot water supplying to the building (Kohl et al. 2002). In summer, the DBHE might only operate 20% of the time a day or even less (Kohl et al. 2002), and thus it is reasonable to consider the recovery of the ground when DBHE is not running. When considering the annual cycle of operation and recovery, Brown et al. (2021) found that the thermal power at the end of the operation of the year reduces by less than 10% from year 1 to year 20. Similarly, according to Wang et al. (2022a), the intermittent pattern can increase the outlet temperature by 8.2–14.9% and the thermal power by 25.4–31.0% under typical flow rate conditions, compared with the continuous operation pattern for an 1800 m DBHE. It should be noted that the intermittent pattern cannot be easily modeled by analytical solutions but can be simulated in numerical simulators such as FEFLOW (Diersch 2014) and OpenGeoSys (Kolditz et al. 2012).

4.4 Economic considerations

Compared with EGS, the coaxial DBHE could reduce drilling costs by reusing/repurposing abandoned wells (Caulk and Tomac 2017). And lower operation costs due to the lower pumping pressure as shown in Table 4 and less maintenance costs due to the adoption of the close-loop system are also expected for coaxial DBHE than for EGS. Among different costs, the well drilling costs are the major portion of a geothermal exploitation plant (Tester et al. 1994). According to Lukawski et al. (2014), the drilling and completion costs of hydrothermal wells and EGS wells drilled between 2008 and 2012 can be empirically estimated from drilling depth as:

$$\text{Geothermal well cost}=1.72\times {10}^{-7}\times {MD}^{2}+2.3\times {10}^{-3}\times MD-0.62$$

(31)

where $MD$ is the measured depth in meters; and the cost is in millions of 2009 U.S. dollars and the expend during operation is not considered.

Because of the simple structure of coaxial DBHE and the high cost of drilling, it is plausible to reuse/convert abandoned oil and gas wells into coaxial DBHE for geothermal exploitation (Śliwa and Kotyza 2003). Table 7 summarizes some applications regarding the reuse of abandoned wells as DBHE from the literature. Note that all the cases summarized in Table 7 are simulations based on specific well configurations and ground conditions and the expected drilling cost savings are estimated from Eq. (31). In general, the reuse of abandoned wells can save millions of USD of drilling cost but the thermal power of DBHE depends on specific ground conditions and should be analyzed case by case. The thermal power of a DBHE is generally less than 1 MW and can be one or two orders of magnitude smaller than the thermal power extracted by typical EGS projects (Brown 2009; Genter et al. 2010; Robins et al. 2021) due to lower thermal gradient on the site.

Table 7 Reuse of abandoned wells as coaxial DBHE from literature

Note that the hot working fluid of DBHE can be used directly for space heating (Dijkshoorn et al. 2013), injected into a heat pump system for a more stable water temperature to use (Nian et al. 2019), or combined with Organic Rankine Cycle (ORC) plant to generate electricity (Alimonti et al. 2019). And the thermal power of the DBHE can only be partially utilized because the efficiency of heat pumps and power turbines can never reach 100%. In this regard, for a real geothermal power plant using DBHE, it is necessary to consider the cost of those facilities, the efficiency of the facilities and the interaction between the coaxial DBHE and facilities. To the best of our knowledge, only few publications are available regarding the geothermal power plant based on DBHE (Alimonti et al. 2019; Nian et al. 2019; Cai et al. 2021, 2022), and thus both field measurements and simulations based on measurements should be further performed to include different economic considerations for the application of coaxial DBHE.

5 Conclusions

This review paper summarizes recent technologies regarding geothermal exploitation using coaxial deep borehole heat exchangers (DBHE). Specifically, the current study focuses on field tests, analytical and semi-analytical approaches and numerical simulations of the DBHE and their advantages and limitations. Although lots of field tests, analytical and numerical investigations are available on the analysis of DBHE performance by considering different borehole sizes, pipe materials and working fluids, the effect of temperature and pressure on fluid properties, heat transfer behavior and long-term behavior should be further stressed and investigated.

Specifically, for field tests: (1) long-term performance should be further monitored because the thermal power and outlet temperature could keep decreasing for years; (2) the effect of groundwater within formation and fractures should be monitored and carefully considered; (3) larger diameter borehole can increase the contact area between fluid and formation, new technology for drilling large borehole should be investigated; (4) to further decrease heat loss, it is important to find new and cheap material for insulated inner pipe; (5) treatment of the working fluid and pipe wall to decrease pressure loss should be investigated, the performance of other working fluid such as CO₂ should be evaluated; (6) economic analysis of DBHE and related facilities should be further investigated.

As for both analytical and numerical models, it is important to consider the dependence of fluid and formation properties and heat transfer mechanism on pressure and temperature when evaluating the coaxial DBHE performance. Due to the adoption of empirical equations and parameters from the literature on water flow, analytical and numerical simulations might not apply to DBHE using other working fluids such as CO₂, which requires further verification of the current equations and models with laboratory and field tests on CO₂ and other working fluids. Pressure loss due to friction in semi-analytical approaches is determined by the Darcy friction coefficient, which is again based on laboratory tests mainly on water, and models for different working fluids and fluid/wall treatments should be further investigated and established. To model DBHEs under complex boundary and operation patterns, 3D numerical simulators are suggested and the use of 1D model for fluid can greatly save computational time.

To optimize the performance of a coaxial DBHE, different factors have been investigated through field tests, analytical analyses and numerical modeling. As for ground thermal properties, thermal conductivity and thermal gradient of the formation are the two major factors affecting the geothermal exploitation of DBHE, the effect of groundwater flow could be negligible if the thickness of the aquifer is much smaller than the length of the DBHE, e.g., 0.5–2.5% of the DBHE length. The open-type DBHE could be a good option if a deep and thick enough aquifer, e.g., 10% of the DBHE length, exists in the formation. Increasing borehole diameter and borehole depth both increase the thermal power of a DBHE, though increased drilling cost should be considered. At a reasonable drilling cost, complex borehole structures such as spiral fin might be a good solution to improve thermal performance. Some researchers found that the lower half of the DBHE contributes more than the upper half due to the higher temperatures at deeper depths. And the use of an insulated inner pipe to reduce heat loss is recommended if economic efficiency can be ensured. Increasing the inner pipe diameter from 50 to 90 mm might lead to a 20% decrease in thermal power. For DBHE arrays, the minimum inter-borehole spacing is around 20 m for line arrays when operating intermittently. Numerical simulations show that CO₂ could be a good alternative to water as the working fluid for DBHE under specific conditions due to the lower viscosity and more significant density change with the temperature of CO₂. Furthermore, for the pump, increasing the flow rate results in a decrease in outlet temperature but an increase in thermal power, and thus the flow rate should be determined based on the requirements of thermal power and outlet temperature. Pressure loss due to friction increases with higher flow rates, deeper DBHE and smaller inner pipe diameter, but the thermosiphon effect due to decreased density of fluid at elevated temperatures could compensate for the pressure loss, especially during the start stage of the operation. The intermittent working pattern of the DBHE can improve the thermal power by up to 30% compared with the DBHE using the continuous pattern. Reuse/repurposing of abandoned wells as coaxial DBHE can greatly save drilling costs and thus is an economic benefit over other geothermal exploitation techniques. To further improve the performance of coaxial DBHE and ensure the readiness of DBHE for the market, continuous research on new technologies to enhance heat transfer and working fluid performance is still important.