1 Introduction

The hydro-mechanical coupling effect is a front and difficult issue of rock mechanics and engineering (Braun et al. 2019; Khadijeh et al. 2022). The excavation of offshore and marine geotechnical engineering, water conservancy and hydropower engineering, underground energy engineering and underground transportation engineering all have potential hydro-mechanical coupling damage and disaster risk (Bernabe 1986; Rutqvist and Stephansson 2003; Guayacán-Carrillo et al. 2017; Fang and Wu 2022). There are abundant initial micropores and microcracks in engineering rock, which provide seepage channels for groundwater. Under the hydro-mechanical coupling conditions, the permeability, strength, pre-peak hardening and post-peak softening characteristics of rock are very complex (Biot 1956; Katz and Thompson 1986; Caine et al. 1996; Rutqvist et al. 2002; Zhou et al. 2019; Li et al. 2021). Especially similar to underground water-sealed oil storage caverns, the stress field and pore pressure field of surrounding rock are coupled during the construction period, and with the oil outlet and inlet process during the operation period, the surrounding rock of the storage cavern undergoes stress cyclic loading and unloading in hydro-mechanical coupling environment (Mitchell and Faulkner 2008; Xiao et al. 2021; Lyakhovsky et al. 2022). The mechanical properties of rock under complex hydro-mechanical coupling states have not been fully revealed, and the suitable hydro-mechanical coupling models are very scarce to provide theoretical guidance for engineering support, excavation design and safe operation. Therefore, it is urgent to carry out in-depth research.

Triaxial compression and cyclic loading and unloading hydro-mechanical coupling tests for rock have achieved some research results (Wang and Park 2002; Tenthorey et al. 2003; Zhang et al. 2013; Zhang et al. 2020). Previous studies have shown that confining pressure, pore pressure and stress path have significant effects on rock mechanical behaviors (including strength, pre-peak hardening, post-peak softening) and permeability (Barton 2002; Mitchell and Faulkner 2008; Zheng et al. 2019, 2022a, 2023a). Some studies have focused on the influence of pore pressure on rock strength and Young’s modulus (Yu et al. 2020; Zhang et al. 2021; Zheng et al. 2022b, 2022c). According to the effective stress principle, the coupling effect of mechanical pressure and pore pressure can be expressed by the effective stress (Zheng et al. 2015; Liu et al. 2018, 2022), and the strength of rock under hydro-mechanical coupling conditions is closely related to effective stress, which increases with increasing effective stress. Some studies have focused on the mechanism of permeability evolution under hydro-mechanical coupling conditions (Zhang 2013; Tian et al. 2019; Zheng et al. 2022d); other studies have focused on the influence of the scale effect on rock permeability (Yang et al. 2017; Putilov et al. 2022); and some scholars have also studied the effects of stress paths such as loading, unloading and loading unloading on the hydro-mechanical coupling characteristics of rock (Shi et al. 2017; Ning et al. 2022). A small number of studies have focused on the progressive failure process, pre-peak hardening and post-peak softening characteristics of rock under hydro-mechanical coupling conditions (Wang et al. 2020; Kou et al. 2021; Zheng et al. 2022e). However, previous studies have mainly focused on high permeability rocks and less on low permeability brittle rocks (such as granite), and the influence of different confining pressures, pore pressures and stress paths needs further study.

The strength of rock is generally considered to be closely related to confining pressure, and many scholars have proposed some strength criteria by analyzing the relationship between strength and confining pressure, such as the Mohr‒Coulomb, Drucker‒Prager and Hoek‒Brown strength criteria (Alejano and Bobet 2012; Si et al. 2019; Hoek and Brown 2019; Xia et al. 2022; Zheng et al. 2023b). Based on these strength criteria, some scholars have proposed hydro-mechanical coupling constitutive models to describe the strength characteristics of rock under hydro-mechanical coupling conditions and have achieved good results (Yang et al. 2018; Wang et al. 2020; Wen et al. 2022). In addition, the deformation and failure processes are the important research issues in the study of rock under hydro-mechanical coupling conditions. To characterize the hydro-mechanical coupling deformation and failure processes of rock, some rock hydro-mechanical coupling models have been proposed, which are mainly divided into five types (Nakshatrala et al. 2018; Wang et al. 2018; Liu et al. 2021b; Rueda et al. 2021; Wu et al. 2022): equivalent continuous model, discrete fracture network model, dual-porosity media model, fracture mechanical model and damage mechanical model. The equivalent continuous model reconstructs the constitutive relation and related parameters of a fractured rock mass through the theory of continuum mechanics, which avoids the difficulty of solving discontinuous problems (Laghaei et al. 2018). The discrete fracture network (DFN) model assumes that the permeability of intact rock mass is much smaller than that of fractures, and the seepage in rock mass only exists in fractures. This model can accurately characterize the small-scale hydro-mechanical coupling characteristics of fractured rock masses (Giuffrida et al. 2019). The dual-porosity media model assumes that the rock mass is composed of pores with water storage properties and fractures with water transmission properties, and the pores and fractures are independent and interconnected. To some extent, the dual-porosity media model can better simulate the seepage problem in complex media (Zhao and Chen 2006; Zhao et al. 2021). The first three models mainly involve the classical elastic‒plastic theory and do not involve the damage and deterioration of the rock mass. The latter two models focus on the more complex coupling effects caused by rock damage and deterioration. Some scholars have proposed hydro-mechanical coupling models from the perspective of micromechanics and macromechanics based on the concepts of fracture mechanics and damage mechanics (Hamiel et al. 2004; Liu et al. 2021a; Xi et al. 2022; Zheng et al. 2023c). Micromechanics explains the inelastic behavior of materials from the perspective of crack propagation and friction sliding, and yet the complexity of the description method of inelastic behavior leads to a complex form of the micromechanics model, which is difficult to numerically implemented and difficult to apply in engineering (Shao and Rudnicki 2000; Zhu and Tang 2004; Jia et al. 2021); macromechanics defines internal variables to describe the plasticity and deterioration behaviors of materials, and the established phenomenological models have a simpler form and can be easily implemented in engineering applications based on finite element methods (Zhou et al. 2001; Zhao et al. 2019; Shen et al. 2022). However, the above models do not consider the post-peak softening behavior due to rock degradation. In addition, there are magnanimous initial micropores and microcracks inside the rock. These micropores and microcracks will be compacted in the initial compaction stage of rock (Baud et al. 2000; Cai et al. 2004; Zhu et al. 2022), and the corresponding stress–strain curve appears as a concave curve with increasing Young’s modulus. There are few studies on the model of initial nonlinear behavior, and most of the previous models do not consider this pre-peak compaction effect (Wang et al. 2021; Hu et al. 2022), resulting in a large strain difference between the numerical simulation results and the test results. A hydro-mechanical coupling damage model considering the pre-peak compaction effect and post-peak softening effects has not been established.

In view of the aforementioned research deficiencies, a series of triaxial compression and cyclic loading and unloading hydro-mechanical coupling tests were carried out to study the mechanical characteristics, deformation and mechanical parameters of rock under different confining pressures and pore pressures. By analyzing the test results, a hydro-mechanical coupling damage model considering the compaction effect, pre-peak hardening and post-peak softening nonlinear behaviors was established within the framework of irreversible thermodynamics based on the effective stress principle. A user-defined material subroutine (UMAT) was compiled in the Fortran language, and the numerical program of the proposed model was implemented in the finite element software ABAQUS. A sensitivity analysis of the key parameters (η and ζ) of the proposed model was carried out, and the proposed model was verified with the test results. The hydro-mechanical coupling characteristics of the rock were predicted.

2 Hydro-mechanical coupling test of granite gneiss

2.1 Specimen and apparatus

The test sample is granite gneiss from a 100 m underground area obtained by core drilling in a China groundwater-sealed oil cavern reservoir project. The porosity of the sample is low, there are no visible cracks, and the surface is dark black with certain white spots. According to the method recommended by the International Society of Rock Mechanics and Engineering (ISRM) (Fairhurst and Hudson 1999; Feng et al. 2019), the sample is processed into a cylinder with a diameter of 50 mm and a height of 100 mm. A typical specimen is shown in Fig. 1a.

Fig. 1
figure 1

a Typical granite gneiss specimen; b hydro-mechanical coupling test apparatus

Full size image

The test system is a fully automatic triaxial microservo hydro-mechanical coupling test apparatus for rock, as shown in Fig. 1b. The test system is composed of a triaxial pressure chamber, pressurization system, computer control system, constant pressure stabilizing device, water pressure control system and automatic information acquisition system. Conventional triaxial tests, triaxial cyclic loading and unloading hydro-mechanical coupling tests of rock can be conducted. The test system can apply the maximum axial pressure, the maximum confining pressure and the maximum pore pressure of 500 MPa, 60 MPa and 30 MPa, respectively, and realize the automatic compensation of axial pressure, confining pressure and pore pressure during the loading process, with an accuracy of ± 0.1 MPa. Axial strain and circumferential strain can be measured by the linear variable differential transformer (LVDT) and circumferential strain measuring ring. In the process of the hydro-mechanical coupling test, the automatic acquisition system can record the test data in real time and realize digital graph.

2.2 Stress path of the conventional triaxial hydro-mechanical coupling test

As the oil storage cavern undergoes the process of oil inlet and outlet, under cyclic loading and unloading conditions, the deformation and stability of the surrounding rock may be affected. To study the strength, deformation and failure characteristics of rock during this loading and unloading process, triaxial cyclic loading and unloading tests are needed. Since the strength of triaxial cyclic loading and unloading tests under different confining pressures cannot be determined, conventional triaxial tests can be conducted in advance to determine the strength of rock under different confining pressures, which provides a basis for the design of triaxial cyclic loading and unloading test processes.

Combined with the geological investigation report and the stress conditions in the sampling area of the test samples (water sealed oil storage project buried depth of approximately 100 m), confining pressures of 2 MPa, 4 MPa and 6 MPa were selected for the conventional triaxial hydro-mechanical coupling test. According to the field water level monitoring data, the pore pressure is about 1 MPa, considering excavation excess pore pressure effect, the pore pressure is set to 1, 2, 3 MPa. To meet engineering practice, all samples should be saturated for at least 4 h at a negative pressure of 0.098 MPa before the test. The test loading process is controlled by stress, and the stress path is shown in Fig. 2a:

  1. 1.

    Apply stress to set confining pressure σ3 and keep confining pressure stable;

  2. 2.

    Apply pore pressure p0 (< σ3) to a set value and keep pore pressure stable;

  3. 3.

    Saturate the specimen until water flows out of the outlet;

  4. 4.

    The deviatoric stress is applied at a rate of 0.75 MPa/min until the specimen is destroyed.

Fig. 2
figure 2

Stress path. a For conventional triaxial hydro-mechanical coupling test; b for triaxial cyclic loading and unloading hydro-mechanical coupling test. (p0 is pore pressure, σp is peak strength)

Full size image

2.3 Stress path of triaxial cyclic loading and unloading hydro-mechanical coupling test

According to the peak strength σp obtained from the conventional triaxial hydro-mechanical coupling test under different confining pressures, confining pressures of 2 MPa, 4 MPa and 6 MPa and a pore pressure of 1 MPa were selected to carry out the triaxial cyclic loading and unloading hydro-mechanical coupling test. Similarly, before the test, all the specimens were saturated for at least 4 h at a negative pressure of 0.098 MPa. The loading and unloading rate during the test process is 0.75 MPa/min, and the stress path is shown in Fig. 2b:

  1. 1.

    Apply stress to set confining pressure σ3, and keep confining pressure stable;

  2. 2.

    Apply pore pressure p0 (< σ3) to set value and keep pore pressure stable;

  3. 3.

    Saturate the specimen until water flows out of the outlet;

  4. 4.

    The deviatoric stress is loaded to 0.4σp and then unloaded to 0.2σp;

  5. 5.

    The deviatoric stress is loaded to 0.6σp and then unloaded to 0.2σp;

  6. 6.

    The deviatoric stress is loaded to 0.8σp and then unloaded to 0.2σp;

  7. 7.

    The deviatoric stress is loaded to 0.9σp and then unloaded to 0.2σp;

  8. 8.

    The deviatoric stress is loaded to σp; if the specimen is still not destroyed, then similarly continue to load to failure.

3 Test results and analysis

3.1 Stress–strain curve characteristics of granite gneiss under hydro-mechanical coupling conditions

3.1.1 Stress–strain curve of granite gneiss under triaxial hydro-mechanical coupling test

The stress–strain curves of granite gneiss under different confining pressures and pore pressures are shown in Fig. 3. (1) In Fig. 3a–c, the constant pore pressure is p0 = 1 MPa, and the confining pressures are σ3 = 2, 4, 6 MPa; (2) in Fig. 3b, d, e, the constant confining pressure is σ3 = 4 MPa, and the pore pressures are p0 = 1, 2, 3 MPa. When pore pressure is 1 MPa and confining pressure are 2, 4, 6 MPa, the strength of rock increases with increasing confining pressure, and the strain corresponding to the peak strength of rock also increases with increasing confining pressure. When confining pressure is 4 MPa and pore pressure are 1, 2, 3 MPa, the strength of rock decreases with increasing pore pressure.

Fig. 3
figure 3

The stress–strain curves of granite gneiss under conventional triaxial hydro-mechanical coupling test. a p0 = 1 MPa, σ3 = 2 MPa; b p0 = 1 MPa, σ3 = 4 MPa, c p0 = 1 MPa, σ3 = 6 MPa; d p0 = 2 MPa, σ3 = 4 MPa; e p0 = 3 MPa, σ3 = 4 MPa

Full size image

According to the shape of the stress–strain curve, it can be divided into three typical stages before the peak strength: compaction stage, linear elastic stage and hardening stage. During the initial loading process of rock, the initial micropores and microcracks are compacted, resulting in an increase in rock stiffness, which shows a concave curve in the compaction stage of the stress–strain curve. After the compaction stage, rock enters the linear elastic stage. At this stage, the micropores and microcracks of rock is almost completely closed, and the stiffness of rock is no longer increased, showing a linear increase of stress–strain curve. Under the action of continuous loading, rock enters the hardening stage. At this stage, new cracks are increasing, and the stress–strain curve begins to show nonlinear characteristics. In addition, the variation trend of the volumetric strain curve of granitic gneiss in the compaction stage and linear elastic stage is consistent with that of the ε1 strain. With the continuous loading of stress, the volume deformation of rock changes from compression to expansion, and the volume strain curve begins to turn.

3.1.2 Stress–strain curve of granite gneiss under triaxial cyclic loading and unloading hydro-mechanical coupling test

The stress–strain curves of granite gneiss under triaxial cyclic loading and unloading hydro-mechanical coupling tests with confining pressures of 2, 4 and 6 MPa and pore pressures of 1 MPa are shown in Fig. 4. With increasing confining pressure, the peak strength and corresponding deformation of rock increase obviously. In the process of stress loading and unloading, the compacted microcracks inside rock are continuously relaxed during stress unloading, and the deformation and Young’s modulus of the rock decreases accordingly. When the stress is reloaded, these relaxed microcracks are recompacted, the deformation and Young’s modulus of the rock increase accordingly.

Fig. 4
figure 4

Stress–strain curves of granite gneiss under triaxial cyclic loading and unloading hydro-mechanical coupling test. a p0 = 1 MPa, σ3 = 2 MPa; b p0 = 1 MPa, σ3 = 4 MPa; c p0 = 1 MPa, σ3 = 6 MPa

Full size image

3.2 Mechanical parameters and strength characteristics of granite gneiss under hydro-mechanical coupling conditions

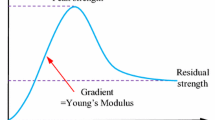
Figure 5 defines the basic mechanical parameters in combination with the typical stress–strain curve of granite gneiss under conventional triaxial hydro-mechanical coupling conditions. Point A represents the crack closure stress σcc, which is the end point of rock compaction stage, and εcc is its corresponding strain. Point B represents the crack initiation stress σci. The stress–strain curve between two points A-B is in the linear elastic stage, and the undamaged Young’s modulus E0 can be derived from the ratio of the axial stress increment ∆σ1 to the strain increment ∆ε1 (E0 = ∆σ1/∆ε1). Poisson’s ratio υ can be derived from the ratio of the lateral strain increment ∆ε3 to the axial strain increment ∆ε1 (υ = ∆ε3/∆ε1). Point C represents the initial yield strength σy of rock, which is the starting point of nonlinear behavior after the linear elastic stage of stress–strain curve, and εy is its corresponding to strain. Point D represents the peak strength σp of rock, and εp is its corresponding strain.

Fig. 5
figure 5

Definition of mechanical parameters based on typical stress–strain curves of granite gneiss. (E0 is Young’s modulus; υ is Poisson’s ratio; σcc and εcc are crack closure stress and corresponding to strain; σci is crack initiation stress; σy and εy are initial yield strength and corresponding to strain; σp and εp are the peak strength and the corresponding to strain)

Full size image

3.2.1 Conventional triaxial hydro-mechanical coupling test

The basic mechanical parameters (E0, υ, σcc, εcc, σy, εy, σp, εp) of granite gneiss in conventional triaxial hydro-mechanical coupling test under different confining pressures and pore pressures are listed in Table 1. The mechanical behaviors of rock are closely related to confining pressure and pore pressure. With increasing confining pressure (σ3 = 2, 4, 6 MPa) and at same pore pressure (p0 = 1 MPa), the peak strength and initial yield strength of rock increased (Fig. 6a). With increasing pore pressure (p0 = 1, 2, 3 MPa) and at same confining pressure (σ3 = 4 MPa), the peak strength and initial yield strength of rock decreased (Fig. 6b). With the change in confining pressure and pore pressure, the undamaged Young’s modulus E0 and Poisson’s ratio υ of granite gneiss do not change obviously, and it can be inferred that these two parameters are not dependent on confining pressure and pore pressure.

Table 1 Strength and deformation parameters of granite gneiss under conventional triaxial hydro-mechanical coupling test
Full size table
Fig. 6
figure 6

Variation of the peak strength σp and initial yield strength σy of granitic gneiss under different σ3 and p0. Conventional triaxial hydro-mechanical coupling test: a p0 = 1 MPa, σ3 = 2, 4, 6 MPa; b σ3 = 4 MPa, p0 = 1, 2, 3 MPa; triaxial cyclic loading and unloading hydro-mechanical coupling test: c p0 = 1 MPa, σ3 = 2, 4, 6 MPa

Full size image

3.2.2 Triaxial cyclic loading and unloading hydro-mechanical coupling test

The basic mechanical parameters (E0, υ, σcc, εcc, σy, εy, σp, εp) of granite gneiss under different confining pressures and pore pressures in triaxial cyclic loading and unloading hydro-mechanical coupling tests are listed in Table 2. Similar to the results of conventional triaxial hydro-mechanical coupling test, the peak strength and initial yield strength of rock vary with the confining pressure (p0 = 1 MPa, σ3 = 2, 4, 6 MPa), as shown in Fig. 6c.

Table 2 Strength and deformation parameters of granite gneiss under cyclic triaxial loading and unloading hydro-mechanical coupling test
Full size table

The peak strength of granite gneiss is different under conventional triaxial compression and cyclic loading and unloading hydro-mechanical coupling tests due to different test loading methods, and the strength parameters of these two tests can be fitted separately, as shown in Fig. 7. According to the effective stress principle, there is a linear relationship between the first invariance of effective stress tensor \(I_{{1}}^{^{\prime}}\) and the second invariance of effective deviatoric stress \(\sqrt {J_{2}^{^{\prime}} }\) in the peak state and the initial yield state under different confining pressures and pore pressures. The Drucker‒Prager criterion can be introduced for linear fitting (Alejano and Bobet 2012):

$$\sqrt {J_{2}^{^{\prime}} } = \alpha I_{{1}}^{^{\prime}} + \kappa$$
(1)
$$J_{2}^{^{\prime}} = \frac{1}{6}\left[ {(\sigma_{1}^{^{\prime}} { - }\sigma_{2}^{^{\prime}} )^{2} + (\sigma_{2}^{^{\prime}} { - }\sigma_{3}^{^{\prime}} )^{2} + (\sigma_{3}^{^{\prime}} { - }\sigma_{1}^{^{\prime}} )^{2} } \right]{; }I_{{1}}^{^{\prime}} = {(}\sigma_{1}^{^{\prime}} + \sigma_{2}^{^{\prime}} + \sigma_{3}^{^{\prime}} {)}$$
(2)
$${\varvec{\sigma}}^{^{\prime}} = {\varvec{\sigma}} - bp_{0} {\varvec{\delta}}$$
(3)

where α and κ are the strength parameters; \(p_{0}\) is the pore pressure; b is the effective stress coefficient, which can be valued as 1 for the rock porous medium material; δ is a second-order unit tensor; σ is the stress tensor; and \({\varvec{\sigma}}^{^{\prime}}\) is the effective stress tensor.

Fig. 7
figure 7

The effective strength test results and Drucker‒Prager linear fitting with the first invariant of effective stress tensor \(I_{{1}}^{^{\prime}}\) and the second invariant of effective deviatoric stress \(\sqrt {J_{2}^{^{\prime}} }\) in peak state and initial yield state. a Conventional triaxial hydro-mechanical coupling test result; b triaxial cyclic loading and unloading hydro-mechanical coupling test result

Full size image

Figure 7a shows the strength parameter fitting results of the conventional triaxial hydro-mechanical coupling test, and Fig. 7b shows the strength parameter fitting results of the triaxial cyclic loading and unloading hydro-mechanical coupling test. Finally, the strength parameters of the peak state and the initial yield state of the conventional triaxial hydro-mechanical coupling test are α = 0.480, κ = 19.62 and α = 0.482, κ = 17.45 (see Fig. 8a); the strength parameters of the peak state and initial yield state of the triaxial cyclic loading and unloading hydro-mechanical coupling test are α = 0.536, κ = 5.29 and α = 0.531, κ = 5.26 (see Fig. 8b).

Fig. 8
figure 8

Strength parameters α and κ under conventional triaxial hydro-mechanical coupling test and triaxial cyclic loading and unloading hydro-mechanical coupling test. a Parameter α; b parameter κ

Full size image

4 A new thermodynamic hydro-mechanical coupling damage constitutive model considering the compaction effect, pre-peak hardening and post-peak softening behaviors

The coupling of plastic deformation and mechanical damage leads to the nonlinear behaviour and failure of rock. Based on the ideal elastic‒plastic yield function, a function of the plastic variable and damage variable can be introduced to describe the nonlinear behaviors of rock. The plastic variable can describe the pre-peak plastic hardening behavior of rock, and the damage variable can model the post-peak damage softening behavior of rock (Shao et al. 2006). According to a large number of existing tests, confining pressure and pore pressure are considered to be closely related to the mechanical behaviors of rock (Tenthorey et al. 2003; Zhang et al. 2020). To study the mechanical and deformation characteristics of granite gneiss under hydro-mechanical coupling conditions, a hydro-mechanical coupling damage constitutive model within the framework of irreversible thermodynamics was established.

4.1 Framework of irreversible thermodynamics

The deformation of rock is considered to be divided into two parts: elastic reversible deformation and plastic irreversible deformation. Generally, rock is assumed to be a material with only small deformation. According to the traditional elastic‒plastic mechanics theory, the deformation of rock can be expressed as:

$${\varvec{\varepsilon}} = {\varvec{\varepsilon}}^{{\text{e}}} + {\varvec{\varepsilon}}^{{\text{p}}} \, {\text{and}} \, d{\varvec{\varepsilon}} = d{\varvec{\varepsilon}}^{{\text{e}}} + d{\varvec{\varepsilon}}^{{\text{p}}}$$
(4)

where \({\varvec{\varepsilon}}^{{\text{e}}}\) = elastic strain tensor; \({\varvec{\varepsilon}}^{{\text{p}}}\) = plastic strain tensor; and \({\varvec{\varepsilon}}\) = total strain tensor.

Rock damage occurs with stress loading, and rock damage feeds back to the evolution of rock mechanical properties. Generally, the damage variable of rock can be expressed by the acoustic emission ring count or deterioration of the Young’s modulus (Lemaitre 1984; Xue et al. 2022). According to the continuum damage mechanics theory, a scalar damage variable is defined by the deterioration of the Young’s modulus during loading:

$$\omega = 1 - \frac{E}{{E_{0} }}$$
(5)

where E0 = the undamaged Young’s modulus of rock; E = E0(1-ω) is the damage Young’s modulus of rock during loading, which can be obtained through triaxial cyclic loading and unloading tests; and ω is a scalar damage variable with a value range of 0–1.

In the process of irreversible plastic and damage, the thermodynamic potential \(\psi\) affected by plastic and damage variables can be divided into two parts:

$$\begin{aligned} \psi ({{\varvec{\upvarepsilon}}}^{{\text{e}}} ,\gamma_{\varvec{p}} ,\omega ) & = \psi_{\varvec{e}} ({{\varvec{\upvarepsilon}}}^{\varvec{e}} ,\omega ) + \psi_{\varvec{p}} (\gamma_{\varvec{p}} ,\omega ) \\ & = \frac{1}{2}{{\varvec{\upvarepsilon}}}^{\varvec{e}} :{\mathbf{C}}(\omega ):{{\varvec{\upvarepsilon}}}^{\varvec{e}} + \psi_{\varvec{p}} (\gamma_{\varvec{p}} ,\omega ) \\ \end{aligned}$$
(6)

where \(\psi_{\varvec{e}} ({{\varvec{\upvarepsilon}}}^{\varvec{e}} ,\omega )\)—the elastic part of the thermodynamic potential; \(\psi_{\varvec{p}} (\gamma_{\varvec{p}} ,\omega )\)—the plastic part of the thermodynamic potential; \(\gamma_{{\text{p}}}\)—the equivalent plastic shear strain; and C(ω) = the rock damage stiffness matrix, which can be written as:

$${\varvec{C}}(\omega ) = 2\mu (\omega )({\varvec{I}} - {\varvec{J}}) + 3k(\omega ){\varvec{J}}$$
(7)

where μ(ω) = the effective shear modulus; k(ω) = the effective bulk modulus; I = the fourth-order unit tensor; and J = the fourth-order tensor, which is:

$${\varvec{J}} = \frac{1}{3}{\varvec{\delta}} \otimes {\varvec{\delta}}$$
(8)

where δ = the second-order unit tensor; and the symbol ‘ ⊗ ’ indicates the Kronecker product.

Since it is difficult to obtain an accurate expression for the thermodynamic potential plastic part, according to the existing research results (Chen et al. 2015; Jia et al. 2021), the expression for the thermodynamic potential plastic part can be introduced as:

$$\psi_{\varvec{p}} (\gamma_{\varvec{p}} ,\omega ) = \zeta (1 - \omega )\left[ {h_{1} \gamma_{\varvec{p}} - \left( {h_{1} - h_{0} } \right)\eta \ln \frac{{\eta + \gamma_{\varvec{p}} }}{\eta }} \right]$$
(9)

where parameters h0, h1, ζ and η control the plastic part characteristics of the thermodynamic potential.

According to the second law of thermodynamics, the Clausius‒Duhem dissipation inequality is:

$${\varvec{\sigma}}:d{\varvec{\varepsilon}}^{{\text{p}}} - d\psi \ge 0$$
(10)

where the sign ‘:’ = the second-order dot production.

The thermodynamic forces Ye, Yp, Yd can be derived by differentiating the thermodynamic potential:

$$Y_{{\text{e}}} = - \frac{{\partial \psi_{\varvec{e}} }}{\partial \omega }$$
(11)
$$Y_{{\text{p}}} = - \frac{{\partial \psi_{\varvec{p}} }}{{\partial \gamma^{\varvec{p}} }}$$
(12)
$$Y_{{\text{d}}} = - \frac{{\partial \psi_{\varvec{p}} }}{\partial \omega }$$
(13)

To satisfy Eq. (10), the following equation can be derived:

$${\varvec{\sigma}} = \frac{\partial \psi }{{\partial {\varvec{\varepsilon}}^{\varvec{e}} }} = {\varvec{C}}(\omega ):({{\varvec{\upvarepsilon}}} - {{\varvec{\upvarepsilon}}}^{\varvec{p}} )$$
(14)

The differential form of Eq. (14) can be written as:

$$d{\varvec{\sigma}} = {\varvec{C}}(\omega ):(d{\varvec{\varepsilon}} - d{\varvec{\varepsilon}}^{\varvec{p}} ) - {\varvec{C}}_{0} :({\varvec{\varepsilon}} - {\varvec{\varepsilon}}^{\varvec{p}} )d\omega$$
(15)

where \({\varvec{C}}_{0}\) = the initial elastic stiffness matrix.

4.2 Elastoplastic hydro-mechanical coupling damage constitutive relationship

According to the strength results of granite gneiss in Sect. 3.2, the Drucker‒Prager yield function can better meet the strength characteristics of granite gneiss. Therefore, according to the effective stress principle, a function that can describe the nonlinear behavior of rock can be introduced on the basis of the Drucker‒Prager yield criterion to better model the deformation characteristics of rock:

$$f_{\varvec{p}} = \alpha I_{{1}}^{^{\prime}} + \sqrt {J_{2}^{^{\prime}} } - \frac{\kappa h}{\zeta } \le 0$$
(16)

where h is a function controlling the hardening and softening characteristics of rock. There are four parameters (\(\zeta , \, h_{1} , \, h_{0} , \, \eta\)) in the function h, which can be derived from the thermodynamic force Yp:

$$h\left( {\gamma_{\varvec{p}} , \, \omega } \right) = \frac{{\partial \psi_{\varvec{p}} }}{{\partial \gamma_{\varvec{p}} }} = - Y_{{\text{p}}} = \zeta (1 - \omega )\left[ {h_{1} + \left( {h_{1} - h_{0} } \right)\frac{{\gamma_{\varvec{p}} }}{{\eta + \gamma_{\varvec{p}} }}} \right]$$
(17)
$$d\gamma_{\varvec{p}} = \sqrt {\frac{2}{3}d{\mathbf{e}}^{\varvec{p}} :d{\mathbf{e}}^{\varvec{p}} } ,d{\mathbf{e}}^{\varvec{p}} = d{{\varvec{\upvarepsilon}}}^{\varvec{p}} - \frac{1}{3}tr\left( {d{{\varvec{\upvarepsilon}}}^{\varvec{p}} } \right){{\varvec{\updelta}}}$$
(18)

where ep = the plastic partial strain tensor; parameter η controls the characteristic rate of plastic hardening of rock; parameter h0 controls the characteristics of the initial yield surface; and parameter h1 controls the characteristics of the plastic failure surface.

Rock shows different pre-peak nonlinear behavior under different effective stress (Wang et al. 2020). An exponential function between the control hardening characteristic parameter η and the effective stress can be proposed:

$$\eta (\sigma_{3}^{^{\prime}} ) = a_{1} e^{{a_{2} \sigma_{3}^{^{\prime}} }} + a_{3}$$
(19)

where parameters a1, a2, and a3 control the characteristics of η.

The non-associated plastic potential function can be expressed as:

$$g = \alpha_{\varvec{g}} I_{{1}}^{^{\prime}} + \sqrt {J_{2}^{^{\prime}} } \le 0$$
(20)

where αg = α.

According to Hooke’s law, the effective stress increment can be expressed as:

$$d{\varvec{\sigma}}^{^{\prime}} = {\varvec{C}}(\omega ):(d{\varvec{\varepsilon}} - d{\varvec{\varepsilon}}^{\varvec{p}} )$$
(21)

where the plastic strain increment dεp can be determined according to the plastic flow law:

$$d{{\varvec{\upvarepsilon}}}^{\varvec{p}} = d\lambda_{\varvec{p}} \frac{\partial g}{{\partial {\varvec{\sigma}}^{^{\prime}} }}$$
(22)

where dλp = the plastic multiplier, which is non-negative, and \(\partial g/\partial {\varvec{\sigma}}^{^{\prime}}\) determines the direction of plastic flow.

According to the traditional plastic mechanics theory, the loading and unloading are given by the Kuhn–Tucker condition:

$$d\lambda_{\varvec{p}} \ge 0; \quad f_{\varvec{p}} ({{\varvec{\upsigma}}}^{^{\prime}} ,\gamma_{\varvec{p}} ,\omega ) \le 0; \, d\lambda_{\varvec{p}} f_{\varvec{p}} ({{\varvec{\upsigma}}}^{^{\prime}} ,\gamma_{\varvec{p}} ,\omega ) = 0$$
(23)

In the plastic deformation and damage process of rock, the stress falls on the yield surface and satisfies the plastic consistency condition dfp = 0:

$$df_{\varvec{p}} ({\varvec{\sigma}}^{^{\prime}} , \, \gamma_{\varvec{p}} ) = \frac{{\partial f_{\varvec{p}} }}{{\partial \sqrt {J_{2}^{^{\prime}} } }}\frac{{\partial \sqrt {J_{2}^{^{\prime}} } }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}d{\varvec{\sigma}}^{^{\prime}} + \frac{{\partial f_{\varvec{p}} }}{{\partial I_{{1}}^{^{\prime}} }}\frac{{\partial I_{{1}}^{^{\prime}} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}d{\varvec{\sigma}}^{^{\prime}} + \frac{{\partial f_{\varvec{p}} }}{{\partial \gamma_{\varvec{p}} }}d\gamma_{\varvec{p}} = 0$$
(24)

The new expression of the effective stress increment tensor is obtained by substituting Eq. (22) into Eq. (21):

$$d{\varvec{\sigma}}^{^{\prime}} = {\varvec{C}}(\omega ):(d{\varvec{\varepsilon}} - d\lambda_{\varvec{p}} \frac{\partial g}{{\partial {\varvec{\sigma}}^{^{\prime}} }})$$
(25)

Then substituting the effective stress increment tensor (Eq. (25)) into the plastic consistency condition (Eq. (24)), the following can be obtained:

$$df_{\varvec{p}} ({\varvec{\sigma}}^{^{\prime}} , \, \gamma_{\varvec{p}} ){ = }\frac{{\partial f_{\varvec{p}} }}{{\partial {{\varvec{\upsigma}}}^{^{\prime}} }}:{\varvec{C}}(\omega ):(d{\varvec{\varepsilon}} - d\lambda_{\varvec{p}} \frac{\partial g}{{\partial {\varvec{\sigma}}^{^{\prime}} }}){ + }\frac{{\partial f_{\varvec{p}} }}{{\partial \gamma_{\varvec{p}} }}\frac{{\partial \gamma_{\varvec{p}} }}{{\partial {{\varvec{\upvarepsilon}}}^{\varvec{p}} }}\frac{\partial g}{{\partial {{\varvec{\upsigma}}}^{^{\prime}} }}d\lambda_{\varvec{p}} { = }0$$
(26)

Finally, the expression of the plastic multiplier can be derived:

$$d\lambda_{\varvec{p}} = \frac{{\frac{{\partial f_{\varvec{p}} }}{{\partial {{\varvec{\upsigma}}}^{^{\prime}} }}:{\varvec{C}}(\omega ):d{{\varvec{\upvarepsilon}}}}}{{H(\gamma_{\varvec{p}} ,\omega )}}$$
(27)
$$H(\gamma_{\varvec{p}} ,\omega ) = \frac{{\partial f_{\varvec{p}} }}{{\partial {{\varvec{\upsigma}}}^{^{\prime}} }}:{\varvec{C}}(\omega ):\frac{\partial g}{{\partial {\varvec{\sigma}}^{^{\prime}} }} - \frac{{\partial f_{\varvec{p}} }}{{\partial \gamma_{\varvec{p}} }}\frac{{\partial \gamma_{\varvec{p}} }}{{\partial {{\varvec{\upvarepsilon}}}^{\varvec{p}} }}\frac{\partial g}{{\partial {{\varvec{\upsigma}}}^{^{\prime}} }}$$
(28)

In addition, the stress–strain relationship of rock (Eq. (21)) can be simplified as:

$$d{\varvec{\sigma}}^{^{\prime}} = {\varvec{C}}^{{\varvec{ep}}} (\gamma_{\varvec{p}} ,\omega ):d{\varvec{\varepsilon}}$$
(29)

where Cep = the elastic‒plastic tangent stiffness matrix of rock, which can be derived by substituting Eq. (27) into Eq. (21):

$${\varvec{C}}^{{\varvec{ep}}} (\gamma_{\varvec{p}} ,\omega ) = {\varvec{C}}(\omega ) - \frac{{{\varvec{C}}(\omega ):\frac{{\partial f_{\varvec{p}} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}:\frac{\partial g}{{\partial {\varvec{\sigma}}^{^{\prime}} }}:{\varvec{C}}(\omega )}}{{H(\gamma_{\varvec{p}} ,\omega )}}$$
(30)

4.3 Irreversible damage evolution for rock nonlinear softening behavior

Irreversible damage of rock leads to nonlinear softening behavior. Generally, irreversible damage is described by the damage variable, which can be updated according to the damage evolution function and driven by the damage force (Shao et al. 2006; Jia et al. 2021). The following exponential damage evolution function was introduced:

$$f_{{\text{d}}} \left( {Y_{{\text{d}}} ,\omega } \right) = \omega_{{\text{c}}} [1 - \exp ( - B_{\upomega } Y_{{\text{d}}} )] - \omega \le {0}$$
(31)
$$Y_{{\text{d}}} (\gamma_{\varvec{p}} ) = - \frac{{\partial \psi_{\varvec{p}} }}{\partial \omega } = \zeta \left[ {h_{1} \gamma_{\varvec{p}} - \left( {h_{1} - h_{0} } \right)\eta \ln \frac{{\eta + \gamma_{\varvec{p}} }}{\eta }} \right]$$
(32)

where ζ controls softening characteristic; Bω controls the damage rate, ωc controls the damage threshold, and the damage force Yd is derived from the plastic part of the thermodynamic potential.

Similar to plasticity, the damage variable needs to meet the consistency condition (\(df_{{\text{d}}} = 0\)). The differential of Eq. (31) can be written as:

$$df_{{\text{d}}} = \frac{{\partial f_{{\text{d}}} }}{{\partial Y_{{\text{d}}} }}dY_{{\text{d}}} + \frac{{\partial f_{{\text{d}}} }}{\partial \omega }d\omega = 0$$
(33)
$$d\omega = \frac{{\partial f_{{\text{d}}} }}{{\partial Y_{{\text{d}}} }}dY_{{\text{d}}}$$
(34)

Rock shows different post-peak nonlinear behaviors under different effective stress (Shi et al. 2017). An exponential function between the control softening characteristic parameter ζ and the effective stresses was provided:

$$\zeta (\sigma_{3}^{^{\prime}} ) = b_{1} e^{{b_{2} \sigma_{3}^{^{\prime}} }} + b_{3}$$
(35)

where parameters b1, b2, and b3 control the characteristics of ζ.

4.4 Characterization of the initial compaction effect of rock

There are inevitably a large number of initial micropores and microcracks inside rock. During the loading process of the compression test, the rock undergoes the compaction stage (Baud et al. 2000; Cai et al. 2004; Zhu et al. 2022), and the micropores and microcracks gradually close under the pressure. In this stage, the rock stiffness increases continuously and finally tends to be stable. This phenomenon is shown as a concave curve with an increasing undamaged Young’s modulus on the pre-peak stress–strain curve, as shown in Fig. 9. If the undamaged Young’s modulus of rock is set to a fixed value, the characteristics of the pre-peak compaction stage of rock cannot be well expressed. Therefore, a compaction function Ck can be introduced to characterize the change in Young’s modulus in the compaction stage:

$$E =C_{{\text{k}}} (1 - \omega )E_{{0}}$$
(36)
$$C_{{\text{k}}} = \left\{ {\begin{array}{*{20}l} {\log_{m} \left[ {\frac{{(m - 1)\varepsilon_{{1}} }}{{\varepsilon_{{{\text{cc}}}} }} + 1} \right]} \hfill & {\varepsilon_{{1}} < \varepsilon_{{{\text{cc}}}} } \hfill \\ 1 \hfill & {\varepsilon_{{1}} \ge \varepsilon_{{{\text{cc}}}} } \hfill \\ \end{array} } \right.$$
(37)

where m is a constant that can be obtained according to the compaction stage of rock.

Fig. 9
figure 9

The evolution Young’s modulus E of rock in the whole failure process. (OA is the compaction stage, AB is the linear elastic stage, BC is the hardening stage, OA represents the undamaged Young’s modulus increases under the influence of compaction effect, AD represents undamaged Young’s modulus E0 tends to be stable, DE represents deterioration of Young’s modulus due to damage)

Full size image

In the initial loading process of rock, the initial micropores and microcracks in rock begin to be compacted, and rock enters the compaction stage. As shown in Fig. 9, in the compaction stage of rock, the increase in the undamaged Young’s modulus of rock can be characterized by the proposed compaction function. As micropores and microcracks continue to compress and tend to close, rock enters the linear elastic stage. In this stage, the undamaged Young’s modulus of rock tends to be stable, and the value of the compaction function tends to 1. As the stress continues to load, new cracks occur inside rock, resulting in the continuous deterioration and damage of rock. At this time, the value of the compaction function is constant at 1, and the damage variable begins to increase, resulting in the continuous deterioration of the Young’s modulus of rock.

4.5 Numerical realization of the proposed model

4.5.1 Secondary development of the proposed model in finite element program

The proposed model cannot be directly used in ABAQUS software, so it is necessary to carry out secondary development of ABAQUS and prepare a user-defined material subroutine (UMAT). The UMAT subroutine is compiled in the FORTRAN language: (1) first, calculate the elastic predicted effective stress \({\varvec{\sigma}}^{{\prime},{\text{trial}}}\), and calculate \(\eta (\sigma_{3}^{^{\prime}} ){\text{ and }}\zeta (\sigma_{3}^{^{\prime}} )\); (2) according to the predicted stress, calculate whether the yield function \(f_{{\text{p}}}^{{\text{trial}}}\) is greater than zero. If the yield function is less than ft (ft = 1 × 10−8), elastic prediction is effective, the stress, strain and other variables are updated, and the program is terminated; (3) if the yield function is greater than ft, it means that the stress state has exceeded the yield surface, and the stress needs to be corrected; (4) update relevant variables and check whether the consistency conditions are met. If not, return to step 2.

4.5.2 Cutting plane return mapping integral method

To verify the correctness of the proposed model, the finite element program of the proposed model can be established in combination with the finite element software ABAQUS. And the return mapping integral method is an effective method to realize the proposed model. In this work, the finite element program of the proposed model can be compiled in the cutting plane return mapping integral method (Simo and Taylor 1986; Xu and Prévost 2016). The cutting plane return mapping integral method mainly includes two parts: elastic prediction and stress correction. The geometric interpretation of the cutting plane return mapping integral method is shown in Fig. 10. The Taylor expansion of the yield function of the k + 1th step can be written as:

$$f_{{\text{p},n}}^{k + 1} = f_{{\text{p},n{ - }1}}^{k + 1} + \frac{{\partial f_{{\text{p},n{ - }{1}}}^{k + 1} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}:\Delta {\varvec{\sigma}}^{^{\prime}} + \frac{{\partial f_{{\text{p},n{ - }{1}}}^{k + 1} }}{{\partial \gamma_{\text{{p}}} }}\Delta \gamma_{\text{{p}}} \approx 0$$
(38)
$$\Delta {\varvec{\sigma}}^{^{\prime}} = - \Delta^{2} \lambda_{{\text{{p}},n{ - }{1}}}^{k + 1} {\varvec{C}}_{{n{ - }{1}}}^{k + 1} :\frac{{\partial g_{{n{ - }{1}}}^{k + 1} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}$$
(39)
$$\Delta \gamma_{{\text{{p}},n{ - }{1}}}^{k + 1} = \Delta^{2} \lambda_{{\text{{p}},n{ - }{1}}}^{k + 1} \frac{{\partial g_{{n{ - }{1}}}^{k + 1} }}{{\partial \sqrt {{3}J_{2}^{^{\prime}} }_{{n{ - }{1}}}^{k + 1} }}$$
(40)

where \(\Delta {\varvec{\sigma}}^{^{\prime}} {\text{ and }}\Delta \gamma_{{\text{p}}}\) are small increments of effective stress tensor and equivalent plastic shear strain between two steps

Fig. 10
figure 10

Geometric interpretation of cutting plane return mapping integral method (Simo and Taylor 1986; Xu and Prévost 2016)

Full size image

Simultaneous Eqs. (38), (39), and (40) can obtain the increment of plastic multiplier ∆2λ:

$$\Delta^{2} \lambda_{{\text{{p}},n{ - }{1}}}^{k + 1} = \frac{{f_{{\text{{p}},n{ - }{1}}}^{k + 1} }}{{\frac{{\partial f_{{{p},n{ - }{1}}}^{k + 1} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }}:{\varvec{C}}_{{n{ - }{1}}}^{k + 1} :\frac{{\partial g_{{n{ - }{1}}}^{k + 1} }}{{\partial {\varvec{\sigma}}^{^{\prime}} }} - \frac{{\partial f_{{\text{{p}},n{ - }{1}}}^{k + 1} }}{{\partial \gamma_{\text{{p}}} }}\frac{{\partial g_{{n{ - }{1}}}^{k + 1} }}{{\partial \sqrt {J_{2}^{^{\prime}} }_{{n{ - }{1}}}^{k + 1} }}}}$$
(41)
$$\Delta \lambda_{\text{{p}}}^{k + 1} = \Delta \lambda_{\text{{p}}}^{k} + \Delta^{2} \lambda_{\text{{p}}}^{k}$$
(42)

And the specific UMAT subroutine algorithm flow is shown in Fig. 11.

Fig. 11
figure 11

user-defined material subroutine (UMAT) algorithm flow with the proposed model

Full size image

5 Determination of model parameters and model verification

5.1 Numerical calculation model and boundary condition

A series of numerical simulations were carried out based on the ABAQUS secondary development user-defined material subroutine (UMAT), and the correctness of the proposed model was verified by comparing the numerical simulation results with the test results. As shown in Fig. 12, according to the actual size (diameter: 50 mm, height: 100 mm) of the cylindrical specimen, a numerical calculation model is established, and the model is divided into 10,395 units. The Z coordinate axis in the software is regarded as the σ1 direction, and the X and Y coordinate axes are regarded as the σ2 and σ3 directions. Apply a displacement boundary condition on the bottom of the model to constrain the vertical displacement of the model and apply a stress boundary condition around the model with a rate of 0.75 MPa/step to simulate the confining pressure σ3. A displacement boundary condition is applied on the top surface of the model to simulate the loading process with a rate of νy (0.01 mm/step). When applying boundary conditions, confining pressure is first applied to the specified value, and then displacement is applied to the top surface of the model.

Fig. 12
figure 12

Element division and boundary conditions of finite element numerical calculation model (Apply vertical restraint at the bottom of the model, apply σ3 around the model, and apply displacement loading rate (νy) on the top of the model)

Full size image

5.2 Determination of mechanical parameters and model parameters

Most of the parameters of the proposed model can be determined by laboratory tests. The values of the undamaged Young’s modulus E0, Poisson’s ratio υ, and strength parameters α and κ were discussed in Sect. 3.2. The change in the undamaged Young’s modulus E0 and Poisson’s ratio υ under different confining pressures is not obvious, and their average value can be taken. Parameter h1 controls the position of the plastic failure surface of rock and can be calibrated by numerical simulation tests. Parameter h0 is the ratio of the initial yield strength to the peak strength. Parameter ωc can be determined at the final failure stage, which controls the maximum value of the damage variable. Parameters η and ζ can be determined through a series of numerical simulation tests and parameter sensitivity analysis in Sect. 5.3 below. Parameter m of the compaction coefficient is determined by the change characteristics of the undamaged Young’s modulus in the compaction stage of the test. Table 3 gives the mechanical and model parameters of granite gneiss under conventional triaxial hydro-mechanical coupling tests; Table 4 gives the mechanical and model parameters of granite gneiss under the triaxial cyclic loading and unloading hydro-mechanical coupling tests.

Table 3 Mechanical and model parameters of granitic gneiss under conventional triaxial hydro-mechanical coupling test
Full size table
Table 4 Mechanical and model parameters of granitic gneiss under triaxial cyclic loading and unloading hydro-mechanical coupling test
Full size table

5.3 Sensitivity analysis of the proposed model parameters η and ζ for rock nonlinear behavior

Parameters η and ζ are difficult to obtain directly from the test data. They can achieve the ideal simulation effect through a series of numerical simulation tests. η controls the pre-peak hardening nonlinear behavior of rock, and ζ controls the post-peak softening nonlinear behavior of rock. To study the influence of these two parameters on the simulation results, sensitivity analysis was carried out under the stress conditions of a confining pressure of 4 MPa and a pore pressure of 1 MPa. Other parameters are unchanged and change η (= 0.0001, 0.0005, 0.001, 0.002, 0.004), and the sensitivity analysis result is shown in Fig. 13a. And other parameters are unchanged and change ζ (= 1, 10, 20, 50, 100, 130), the sensitivity analysis result is shown in Fig. 13b. The more obvious the pre-peak hardening nonlinear behavior of rock with the increase in parameter η; the faster the post-peak softening rate of rock and the more obvious the stress drop with the increase in parameter ζ.

Fig. 13
figure 13

Sensitivity analysis of the proposed model parameters a η and b ζ

Full size image

5.4 Comparison of the proposed model simulation results with and without the initial compaction effect

Based on the conventional triaxial stress level (σ3 = 2 MPa and p0 = 1 MPa), the model numerical simulation result of the stress–strain curve with and without the compaction effect is shown in Fig. 14. The stress–strain curve of the numerical simulation without considering the compaction stage is a straight line in the pre-peak compaction stage. The strain value of the test is slightly larger than the strain value of the numerical simulation under the same stress, and this difference exists in the whole simulation process. The numerical simulation stress–strain curve considering the compaction stage is consistent with the test results in the pre-peak compaction stage, which is a concave curve, and the test and model numerical simulation results are highly consistent. Therefore, it is necessary to introduce the compaction function.

Fig. 14
figure 14

Comparison of numerical simulation results of the proposed model with and without compaction effect

Full size image

5.5 The proposed model numerical validation with test results

The parameters in Tables 1, 2, 3 and 4 were used to simulate the test results of granite gneiss under different confining pressures and pore pressures. Figure 15 compares the stress–strain curves of granite gneiss under different confining pressures and pore pressures in the conventional triaxial hydro-mechanical coupling test; Fig. 16 compares the stress–strain curves of granite gneiss under different confining pressures and pore pressures in the triaxial cyclic loading and unloading hydro-mechanical coupling test. According to the numerical simulation results, the peak strength of rock increase with increasing confining pressure or decreasing pore pressure, and the change trend is the same as the test results. The results of the proposed model numerical simulation and test are in good agreement. The peak strengths of the proposed model numerical simulation and test under different stress levels are given in Tables 5 and 6. Figure 17 compares the peak strengths of the proposed model numerical simulation and test under different stress levels, and these two have good consistency. The proposed model numerical simulation results show that the strength change trend is the same as the test results. The comparison of the numerical simulation and test proves the correctness and effectiveness of the proposed model.

Fig. 15
figure 15

Comparison of granitic gneiss stress–strain curves between the proposed model simulation results and conventional triaxial hydro-mechanical test results under different σ3 and p0. a p0 = 1 MPa, σ3 = 2 MPa; b p0 = 1 MPa, σ3 = 4 MPa; c p0 = 1 MPa, σ3 = 6 MPa; d p0 = 2 MPa, σ3 = 4 MPa; e p0 = 3 MPa, σ3 = 4 MPa

Full size image
Fig. 16
figure 16

Comparison of granitic gneiss stress–strain curves between the proposed model simulation results and triaxial cyclic loading and unloading hydro-mechanical test results under different σ3 and the same p0. a p0 = 1 MPa, σ3 = 2 MPa; b p0 = 1 MPa, σ3 = 4 MPa; c p0 = 1 MPa, σ3 = 6 MPa

Full size image
Table 5 Peak strength comparison of granite gneiss between the proposed model simulation results and conventional triaxial hydro-mechanical coupling test results
Full size table
Table 6 Peak strength comparison of granite gneiss between the proposed model simulation results and triaxial cyclic loading and unloading hydro-mechanical coupling test results
Full size table
Fig. 17
figure 17

Comparison of granite gneiss peak strength between the proposed model simulation results and hydro-mechanical coupling test results. Conventional triaxial test results. a at the same p0 and different σ3: p0 = 1 MPa, σ3 = 2, 4, 6 MPa; b at the same σ3 and different p0: σ3 = 4 MPa, p0 = 1, 2, 3 MPa; triaxial cyclic loading and unloading test results: c at the same p0 and different σ3: p0 = 1 MPa, σ3 = 2, 4, 6 MPa

Full size image

6 The prediction of the untested stress level with the proposed model

According to the above work, the proposed model can better simulate the mechanical behaviors of granite gneiss under different confining pressures and pore pressures. Therefore, the conventional triaxial hydro-mechanical coupling test of granite gneiss under untested stress levels should be preliminarily predicted. The predicted stress levels can be taken as follows: (1) p0 = 1 MPa, σ3 = 1.5, 3, 5, 7, 9 MPa; (2) σ3 = 5 MPa, p0 = 0, 1, 2, 3, 4, 4.5 MPa. Figure 18a shows the stress–strain curve prediction results for stress level (1); Fig. 18b shows the stress–strain curve prediction results for stress level (2). The prediction results show that the rock strength is linearly positively correlated with the effective confining stress (Fig. 19).

Fig. 18
figure 18

The proposed model prediction of granitic gneiss stress–strain curve under untested stress levels. a at the same p0 and different σ3: p0 = 1 MPa, σ3 = 1.5, 3, 5, 7, 9 MPa; b at the same σ3 and different p0: σ3 = 5 MPa, p0 = 0, 1, 2, 3, 4, 4.5 MPa

Full size image
Fig. 19
figure 19

Variation of granitic gneiss peak strength with effective confining pressure under untested stress levels. a at the same p0 and different σ3: p0 = 1 MPa, σ3 = 1.5, 3, 5, 7, 9 MPa; b at the same σ3 and different p0: σ3 = 5 MPa, p0 = 0, 1, 2, 3, 4, 4.5 MPa

Full size image

7 Discussion

7.1 Verification and prediction of post-peak damage characteristics of rock under triaxial hydro-mechanical coupling conditions

The strength of rock after reaching the peak will not immediately drop to zero, but it shows certain post-peak nonlinear deformation characteristics. The nonlinear characteristics of rock under different effective confining pressures is different. With increasing effective confining pressure, the pre-peak hardening nonlinear characteristics of rock is more obvious, the post-peak softening rate is slower. According to the sensitivity analysis in Sect. 5.3, the pre-peak hardening and post-peak softening nonlinear behavior characteristics of rock can be controlled by parameters η and ζ. Therefore, based on the conventional triaxial hydro-mechanical coupling test results of sandstone, which are cited from Yu et al. (2019), the parameters (Table 7) are determined according to the model parameter determination method in Sect. 5.2. The nonlinear characteristics of rock under different effective confining pressures can be better simulated by changing the parameters η and ζ, as shown in Fig. 20. There is a correlation between the key parameters (η and ζ) and the effective confining pressure, as shown in Fig. 21. According Eqs. (19) and (35), the functions of the key parameters (η and ζ) and the effective confining pressure can be fitted:

$$\eta (\sigma_{3}^{^{\prime}} ) = 0.000026e^{{0.424\sigma_{3}^{^{\prime}} }} - 0.000013$$
(43)
$$\zeta (\sigma_{3}^{^{\prime}}) = 112.46e^{{ - 0.48\sigma_{3}^{^{\prime}} }} + 53.88$$
(44)

According to Eqs. (43) and (44), the difference in the pre- and post-peak nonlinear behaviors of rock under different effective confining pressures (\(\sigma_{3}^{^{\prime}} = {9}.{5}\), 14.5, 19.5, 24.5 MPa) can be further predicted, and the prediction result is shown in Fig. 22. With increasing effective confining pressure, the pre-peak nonlinear behavior of rock becomes more obvious, the post-peak softening rate decreases, and the post-peak stress decline rate slows down.

Table 7 Mechanical and model parameters of sandstone (Yu et al. 2019) under conventional triaxial hydro-mechanical coupling test
Full size table
Fig. 20
figure 20

Comparison of sandstone stress–strain curves between the proposed model simulation results and conventional triaxial hydro-mechanical coupling test results (Yu et al. 2019). a σ2 = σ3 = 4 MPa, p0 = 0.5 MPa; b σ2 = σ3 = 6 MPa, p0 = 0.5 MPa; c σ2 = σ3 = 8 MPa, p0 = 0.5 MPa

Full size image
Fig. 21
figure 21

The functions between the proposed model key parameters a η, b ζ and the effective stress

Full size image
Fig. 22
figure 22

The proposed model prediction of pre-peak hardening and post-peak softening behavior characteristics of rock under different effective confining pressures

Full size image

7.2 Verification and prediction of mechanical characteristics of rock under true triaxial hydro-mechanical coupling conditions

Deep rock has undergone complex stress redistribution, and there are not only conventional triaxial stress states (σ1 = σ2 = σ3) but also true triaxial stress states (σ1 > σ2 = σ3) inside rock. In this work, the proposed model can not only consider the influence of confining pressure on rock strength evolution but also consider the influence of intermediate principal stress on rock strength evolution. At present, there are few tests and models considering pore pressure under true triaxial stress. We summarize some true triaxial test results considering pore pressure (Li 2016; Shi et al. 2017) to validate the proposed model, where the mudstone test results are cited from Shi et al. (2017), and the sandstone test results are cited from Li (2016). As shown in Fig. 23, the numerical simulation results with the proposed model are given, where the mechanical parameters and model parameters (Tables 8 and 9) are determined according to the method in Sect. 5.2. According to the comparison of the test and simulation results, the proposed model can well simulate the strength and deformation behaviors of rock under true triaxial stress.

Fig. 23
figure 23

Comparison of stress–strain curves between the proposed model simulation results and true triaxial hydro-mechanical coupling test results. a σ2 = 50, σ3 = 35 MPa, p0 = 15 MPa; b σ2 = 60, σ3 = 35 MPa, p0 = 15 MPa; c σ2 = 20, σ3 = 20 MPa, p0 = 1 MPa; d σ2 = 60, σ3 = 20 MPa, p0 = 1 MPa. Mudstone test results of a and b are cited from Shi et al. (2017); sandstone test results of c and d are cited from Li (2016)

Full size image
Table 8 Mechanical and model parameters of mudstone (Shi et al. 2017) under true triaxial hydro-mechanical coupling test
Full size table
Table 9 Mechanical and model parameters of sandstone (Li 2016) under true triaxial hydro-mechanical coupling test
Full size table

Because there are very few true triaxial hydro-mechanical coupling tests at present and there is no test basis for determining key parameters, the pre- and post-peak nonlinear behaviors transition problem of rock caused by the change in effective stress is not considered temporarily. To study the mechanical behaviors of rocks under more complex stress conditions, based on the test results of Li (2016), the true triaxial compression stress–strain curve characteristics under different confining pressures and pore pressures (σ3 = 20 MPa, p0 = 1 MPa, σ2 = 30, 40, 50, 70 MPa and σ2 = 60 MPa, σ3 = 20 MPa, p0 = 0, 4, 8, 12, 16 MPa) are predicted, as shown in Fig. 24. In Fig. 24a, the rock strength increases with increasing σ2, which is consistent with previous true triaxial test results for dry rock (Mogi 1973; Feng et al. 2019; Zheng et al. 2019, 2020); in Fig. 24b, the rock strength decreases with increasing p0, which should be reasonable because the pore pressure reduces the effective stress resulting in a decrease in strength. In other words, the proposed model can better predict the strength characteristics of rocks under complex true triaxial stress levels.

Fig. 24
figure 24

The proposed model prediction of stress–strain curve characteristics of the proposed model under untested true triaxial stresses. a at the same σ3, p0 and different σ2: σ3 = 20 MPa, p0 = 1 MPa, σ2 = 30, 40, 50, 70 MPa; b at the same σ2, σ3 and different p0: σ2 = 60 MPa, σ3 = 20 MPa, p0 = 0, 4, 8, 12, 16 MPa

Full size image

8 Conclusions

A series of triaxial compression and cyclic loading and unloading hydro-mechanical coupling tests were carried out for granite gneiss to investigate the stress–strain curves, strength and deformation characteristics under different confining pressures and pore pressures. Within the framework of irreversible thermodynamics, an elastic‒plastic hydro-mechanical coupling damage constitutive model considering the compaction effect, pre-peak hardening and post-peak softening behaviors is established. The proposed model can simulate the mechanical characteristics of rock under different confining pressures and pore pressures. The main conclusions are as follows:

  1. 1.

    With decreasing confining pressure or increasing pore pressure, the peak strength and initial yield strength of granitic gneiss decrease. Under hydro-mechanical coupling conditions, the rock failure presents three stages of deformation characteristics: initial compaction, elastic deformation and nonlinear hardening, and confining pressure and pore pressure have a certain influence on it.

  2. 2.

    Within the framework of irreversible thermodynamics, an elastic‒plastic hydro-mechanical coupling damage constitutive model, which can consider the compaction effect and describe the nonlinear behaviors of hardening and softening, is established. This model can better capture the evolution of the strength and deformation of granite gneiss under different confining pressures and pore pressures.

  3. 3.

    A compaction function Ck is introduced to reflect the change in the undamaged Young’s modulus in the compaction stage to characterize the pre-peak compaction effect. The proposed model can better simulate the pre-peak and post-peak nonlinear behaviors of rock by the functional relationship between the key parameters (η and ζ) and the effective stress. The yield function of the proposed model considers the influence of intermediate principal stress and can be applied to the true triaxial stress states.