1 Introduction

Geology and rock mechanics information are dependent on accurate pore structure analyses, and high-temperature conditions create significant challenges in the exploration of rock microstructure characteristics and mechanical behaviors (Zhang et al. 2020). Such conditions are relevant to the development and utilization of geothermal resources, the underground storage of nuclear waste, and the underground gasification of coal. Hence the relevance of the study of the effect of high-temperature treatments on the microstructure characteristics and mechanical behaviors of rocks. The microscopic structure of rock changes under the action of temperature and load (Pathiranagei et al. 2021; Wu et al. 2021a; Zhao et al. 2017), causing the development, growth and extension of micro-defects dispersed in various forms, eventually causing rock instability and failure due to macroscopic cracks (Liu et al. 2018; Ma et al. 2021; Martinez-Ibanez et al. 2021; Sun et al. 2021). With the continuous update of test loading equipment and microscopic detection technology, it has been found that the mechanical response of rock is the macroscopic reflection of changes to the internal microscopic structure (Ding et al. 2020; Li et al. 2021; Liang et al. 2021; Sun et al. 2021). This provides a different perspective for the analysis of the influence of high-temperature on the physical and mechanical properties of rock.

Pores occur naturally in various rock substrates and form the main body of the rock together with its skeleton (Hao et al. 2022; Wang et al. 2022). Pore structure characteristics include the shape, size, distribution, and interconnectivity of the pores and tunnels in the rock (Katika et al. 2018; Xiao et al. 2021; Zhou et al. 2018), and are important in regards to the macro-mechanical characteristics of rock materials (Jiang et al. 2020). In porous rock media, the complex geological environment leads to the complex pore structure, including large-scale ranges, diverse types, and discrete distributions (Li et al. 2018; Zhu et al. 2018). The joint action of primary tectonic action conditions and secondary destructive diagenesis conditions create a large number of micron and nanometer pores. Pore structure evolution characteristics tend to be more complex and variable under high-temperature (up to thousands of degrees Celsius) environments compared to under lower-temperature conditions (Li et al. 2020; Liu and Xu 2015; Kumari et al. 2018). Typical studies include but are not limited to the following: Pathiranagei et al. (2021) conducted a series of laboratory experiments on Beaudesert sandstone, Jimboomba sandstone, basalt and argillite at temperatures ranging from 25 to 800 ℃, and explored the influence of high temperature on rock engineering properties from the perspectives of porosity, mineral composition, threshold temperature, etc. Wu et al. (2021a) investigated the influence of high temperature effect on granite porosity, P-wave velocity, tensile strength and microstructure in order to study the influence of the heat released from the decay of nuclides on the physical and mechanical properties of the surrounding rock of high-level radioactive waste repository. Xu et al. (2021) analyzed the dynamic mechanical properties and hydrothermal damage effect of granite under the condition of 25–150 ℃ water immersion with the help of Hopkinson pressure bar and nuclear magnetic resonance instrument. Kahraman (2022) taking the prediction of high temperature exposure effect of rock mass as the engineering background, emphatically discussed the physical mechanics and microstructure characteristics of Turkish granite after undergoing high temperature and different cooling methods. Li et al. (2022) taking granite and sandstone as objects, explored the microstructure and crack evolution process of rocks under the influence of different temperature gradients and cooling modes.

Advancements in testing methods and techniques have gradually expanded microscopic characteristic analyses from being qualitative to being quantitative. Microscopic characteristics are typically studied using non-image analysis or image analysis testing principles. Non-image analyses have included high-pressure mercury injection tests (Chang et al. 2020; Lyu et al. 2021), gas adsorption tests (Liu et al. 2019; Yuan et al. 2021) and low-field nuclear magnetic resonance tests (Adeyilola et al. 2020; Habina et al. 2017; Hashan et al. 2022; Romero-Sarmiento et al. 2017), etc. The basic principle of non-image analysis is to invert the characteristic parameters of pore structure by obtaining the volume or mass of a fluid or gas injected into pores. However, this method does not directly display spatial information describing the pore structure. Image analysis methods include micron-scale computed tomography (Bandara et al. 2021; Ebadi et al. 2021; Kim et al. 2020; Yu et al. 2021), small-angle X-ray scattering (Zhao et al. 2020b, 2019), and scanning electron microscopy (Das et al. 2021; Wang and Sun 2021). The basic principle of image analysis methods is to directly observe pore structure characteristics such as size, connectivity, and other relevant parameters.

The accuracy of quantitative microscopic structure measurements is directly related to the test methods used to gather them. Different test methods can cause large differences between measurement results, and different methods have unique scopes of application. There are currently many uncertainties and unknowns regarding the evolution of microscopic structure in rocks under the influence of high-temperature, and there is a general lack of research on the subject. In this study, argillaceous sandstone from the Leshan Area, Sichuan Province, China, is taken as the research object. Uniaxial compression tests are performed on samples of this sandstone subjected to a range of temperatures (25 ºC, 300 ºC, 600 ºC, 900 ºC, 1000 ºC, and 1200 ºC) to explore the threshold temperature of key mechanical parameters. SEM is employed to investigate the effect of high temperatures on the microstructure of the argillaceous sandstone from a qualitative perspective. LF-NMR and high-resolution µ-CT system analyses are used to quantitatively characterize the pore structural multi-scale characteristics of the argillaceous sandstone after thermal damage has occurred. The evolution of pore size distribution and porosity with temperature is analyzed, and the difference between the results of the two image-based analyses are discussed. Thermal damage variables are examined using porosity as the reference quantity and the mechanism causing the evolution of thermal damage is investigated. The exploration of the mechanism by which high temperature effects the nonlinear behavior of argillaceous sandstone, using macro-mechanical tests and micro-imaging at different scales, contributes to the further understanding and evaluation of the high-temperature response of rocks.

2 Methodology

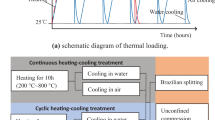
The experimental design consisted of two principal components: uniaxial compression tests to study the effect of temperature on the mechanical parameters of rock, and microscopic tests to study the effect of temperature on rock microstructure. The test process and test equipment are summarized in Fig. 1. Test samples were taken from argillaceous sandstone from the Leshan Area, Sichuan Province, China. Burial depths were between 500 and 800 m below the surface. The appearance of this sandstone is dark red. The sandstone had an average density measured in the rock’s natural state of 2.28 g/cm3, an average p-wave velocity of 3000–3500 m/s and a weighing porosity of 19.6%. The unheated rock had a uniaxial compressive strength (measured using a standard cylinder sample Φ50 × 100 mm) of 35–40 MPa.

Fig. 1
figure 1

Overall technical roadmap for experimental design

Full size image

The rock samples were processed into cylinders. All samples had a surface parallelism value less than 0.05 mm, and a surface flatness less than 0.02 mm. Three different sizes were used: (1) Φ 50 × 100 mm for uniaxial compression tests. This size met the requirements of the International Society of Rock Mechanics (ISRM 2007). Crushed rock fragments with suitable sizes were selected from the results of the uniaxial compression tests for subsequent SEM observation; (2) Φ 25 × 50 mm for the LF-NMR analyses. This size was determined by the size of the nuclear magnetic testing instrument coil; (3) Φ 5 × 10 mm for the µ-CT analyses. This size was based on existing rock core-drilling sampling technology and ensured a minimum size needed for accurate analysis. All processed rock samples were collected from the same batch of blocks from the same place of origin. The samples were screened through ultrasonic longitudinal wave velocity detection to ensure their uniformity. Sample nomenclature followed a code consisting of three parts, X-Y-Z, where X refers to the analysis type used on the sample, Y the temperature treatment applied to the sample, and Z the number of the sample replicate (three in all). Code values are as follows. X: A—uniaxial compression test; B—LF-NMR analysis; C—µ-CT analysis. Y: 1–25 ºC; 2–300 ºC; 3–600 ºC; 4–900 ºC; 5—1000ºC; 6–1200 ºC. Z: 1, 2, or 3. Each sample was heated in a high-temperature furnace to the target treatment temperature, held at this temperature for 1 to 3 h and then naturally cooled. The heating rate used was 10 ºC/min. The time each sample was held at the treatment temperature varied depending on the sample size.

Mechanical tests were then carried out using a rock mechanics testing machine. The displacement control method was used to load a sample until it was damaged. SEM imaging was then used to analyze the microstructure of high-temperature argillaceous sandstone at the 101–102 μm scale. LF-NMR and µ-CT methods were then combined to investigate the pore development characteristics of thermally damaged argillaceous sandstone, thus resolving the shortcomings of either test method. The LF-NMR test equipment used was the MesoMR23-60H-I. A heat-treated rock sample was first placed in a vacuum drying oven until its weight difference between two adjacent time points was less than 0.1%, when it was considered to be completely dry. The completely dried sample was then subjected to vacuum pressurization and water saturation for 24 h until the sample no longer absorbed water and was regarded as completely saturated. Finally, LF-NMR was conducted to test the \(T_{2}\) spectrum transverse relaxation time of the thermally damaged rock sample. The µ-CT test equipment used was a NanoVoxel-4000 series high-resolution X-ray three-dimensional (3D) microscope. Each sample was scanned using 360° rotating µ-CT in all directions. The resulting images were subjected to a series of digital image processes (i.e., image enhancement, image filtering, image segmentation and data reconstruction) in order to obtain high-resolution 3D digital images of the rock core for visual pore structure analysis. Finally, Volume Graphics Studio MAX software was used to quantitatively extract and analyze micro-pore structure data.

3 Results

3.1 Mechanical properties

Typical stress–strain curves of the argillaceous sandstone under uniaxial compression load after being subjected to different high-temperature treatments are presented in Fig. 2, and relevant associated mechanical properties are summarized in Table 1. Figure 3 presents the relationship between uniaxial compression mechanical parameters and treatment temperature. Treatment temperature clearly has a certain influence on the shape of the stress–strain curve. From normal temperature (25 ºC) to 600 ºC, the brittle characteristics of the rock sample are obvious, and this stage can be regarded as a typical brittle failure stage. From 900 to 1000ºC, the brittle characteristics gradually weaken while plastic characteristics gradually appear, and this stage can be regarded as a transition stage from brittle to plastic. At 1200 ºC, the sample presents obvious plastic failure characteristics. At this time, after reaching a peak stress, the sample still has a certain bearing capacity with the increase of strain. The brittle-plastic rock failure transition is a typical high-temperature mechanical response of rock under thermal–mechanical coupling (Ranjith et al. 2012; Sun et al. 2015; Zhao et al. 2020a). The changes seen in strength characteristics (Fig. 3) were as follows. When the treatment temperature was increased from normal temperature to 300 °C, the peak stress did not decrease but increased, indicating that the high-temperature not only did not weaken the bearing capacity of the rock, but improved the effective bearing area by evaporating water (Liu and Xu 2014; Wang et al. 2020), and filling some of the pores. With a further increase of treatment temperature from 300 to 1200 ºC, the peak stress gradually decreased. This suggests that 300ºC treatment provides the extreme value of peak stress. 300 ºC may not be the exact extreme point due to the coarse resolution of the high-temperature heating intervals, but it is certain that the threshold temperature of the uniaxial compressive strength is around 300 ºC. This threshold temperature is consistent with the results of previous studies, although the threshold temperatures for different rock types and heating levels differ (Kang et al. 2021; Ma et al. 2020; Meng et al. 2021; Wu et al. 2021b).

Fig. 2
figure 2

Typical stress–strain curves of argillaceous sandstone specimens subjected to high-temperature treatments

Full size image
Table 1 Statistics of uniaxial compression test results
Full size table
Fig. 3
figure 3

Effect of temperature on the strength and deformation parameters of argillaceous sandstone specimens under uniaxial compression: a Peak stress; b Peak strain; c Elastic modulus

Full size image

The changes seen in the deformation characteristics (Fig. 3) were as follows. With the increase of treatment temperature, the peak strain first decreased and then increased, and the elastic modulus first increased then decreased. Although the evolution directions of the two deformation indicators were opposite, the common point is that both of them exhibited a turning point at 300 °C, which once again confirms the assumption that 300 °C is the threshold temperature of argillaceous sandstone. Not only does the strength have a threshold temperature, but the deformation also has a threshold temperature, and the two threshold temperatures are very close. Hence the uniaxial compression test results demonstrate that argillaceous sandstone has a threshold temperature, but this is only a macroscopic mechanical result, and the effect of high-temperature treatment on rock microstructure needs to be further understood from the perspective of the micro-scale.

3.2 Analysis of SEM results

Figure 4 presents a schematic diagram of part of the microstructure of argillaceous sandstone at normal temperature. Rock samples at normal temperature contain a lot of argillaceous clay minerals (Fig. 4a). The arrangement of mineral particles is relatively random, with no fixed direction, and there are many pores with huge differences in scale between them. The complex microstructure of the rock sample is formed of various kinds of mineral particles by alternately connecting with each other. Many particles are attached with reticular cemented substances on the surface. Region A in Fig. 4a is magnified by 2000 times and shown in Fig. 4b, and Region B is magnified to 10,000 times and shown in Fig. 4c. A large number of micron-nano pores are found densely packed between the reticular cemented materials. The scattered accumulation Region C in Fig. 4a is magnified 2000 times and presented in Fig. 4d. Here, there is a small number of cracks distributed along the boundary of mineral particles.

Fig. 4
figure 4

Representative SEM images of argillaceous sandstone at normal temperature. a × 200; b × 2000; c × 10,000; d × 2000

Full size image

Figure 5 presents part of the microstructure of argillaceous sandstone subjected to high treatment-temperature conditions. From 25 to 300 ºC, dehydration occurs inside the sample, and mineral particles do not expand significantly. At this time, the bearing capacity of the rock sample increases instead of decreasing. At 600 ºC, the mineral particles begin to expand, but there are still a large number of reticular cemented materials, indicating that the temperature has not caused a large amount of mineral decomposition, and the corresponding samples still have a considerable strength. From 900ºC to 1000ºC, the expansion of mineral particles accelerates, the reticular cementation basically disappears, leading to the decrease of friction and cohesion between mineral particles, and the shape of mineral particles begins to change, indicating that at this time the mineral particles in a sample begin to decompose, and the strength of the sample decreases rapidly. At 1200ºC, the mineral particles partially melt, showing the characteristics of coarse and angular particle size, the adhesion between mineral particles further weaken, the pores gradually expand or even connect, and then form a network, and the strength of the sample greatly attenuates.

Fig. 5
figure 5

SEM observations of argillaceous sandstone specimens after thermal treatment (× 200): a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image

3.3 Analysis of LF-NMR results

According to the principles of LF-NMR testing, the transverse relaxation time \(T_{2}\) can directly reflect pore structure. The \(T_{2}\) distribution was first obtained by the inversion of the nuclear magnetic signals, then the pore size distribution was determined using the \(T_{2}\) distributions. The relationship between \(T_{2}\) and signal strength can be determined based on the attenuation of the measured echo (Kenyon 1992):

$$M\left( t \right) = M_{0} e^{{\left( { - \frac{t}{{T_{2} }}} \right)}}$$
(1)

where \(M\left( t \right)\) is the echo signal amplitude corresponding to time \(t\); \(M_{0}\) is the echo signal amplitude corresponding to the initial time; \(T_{2}\) is the transverse relaxation time, ms; \(t\) is the test time, ms. The \(T_{2}\) is closely related to the surface area of the medium, so the expression of \(T_{2}\) can be further obtained (Yao 2015):

$$\frac{1}{T}_{2} = \rho_{2} \left( {\frac{{S_{pore} }}{{V_{pore} }}} \right)$$
(2)

where \(\rho_{2}\) is the transverse surface relaxation strength, µm/s; \(S_{pore}\) is the total pore surface area, µm2; \(V_{pore}\) is the total pore volume, µm3. It is assumed that the rock pore is a tube bundle model with a radius of \(r_{pore}\), and \(\rho_{2}\) = 10 µm/s. The pore size distribution can be obtained by inversion of the distribution:

$$r_{pore} = 0.2T_{2}$$
(3)

Calibration was achieved by fitting a standard sample with known porosity to the nuclear magnetic signal per unit volume (Fig. 6).

Fig. 6
figure 6

Calibration curve of LF-NMR test

Full size image

LF-NMR images of the argillaceous sandstone after being subjected to different high-temperature treatments are presented in Fig. 7 (The procedure of testing and analysis of high-temperature samples is exactly the same as that of normal temperature samples). The bright area in the image is the area where the water molecules are located, and the brighter the color, the more water in the region. Figure 8 presented the LF-NMR \(T_{2}\) spectrum distributions from the argillaceous sandstone samples subjected to different temperature temperatures. They can be divided into two types: bimodal and trimodal, and a right-bias bimodal type is common. For the normal temperature sample, the \(T_{2}\) spectrum distribution range is 0.1–1000 ms and mainly composed of two peaks: the left peak is low, mainly located at 0.065–6.37 ms, and the right peak is steep and high, mainly located at 6.37–333.12 ms. The two peaks are interconnected, and the spectrum shape is narrow, indicating that the sample has low porosity and poor physical properties. When the treatment temperature is 300–900 ºC, the curve shape of the \(T_{2}\) spectrum distribution is similar to that under normal temperature and maintains a right-bias bimodal development. With the increase in heat treatment temperature, the curve shifts rightward and the pore connectivity appears to improve to a certain extent. A turning point emerges at a treatment temperature of 1000 ºC, when the third peak appears in the \(T_{2}\) spectrum distribution and the curve shifts upward. As the temperature increases further to 1200 ºC, the curve recovers from three peaks to two peaks again. Hence, the high-temperature environment damaged the rock sample as reflected in the \(T_{2}\) spectrum distribution curve; it did not lead to a significant right-shift in the curve but rather a large upward shift, indicating that the temperature does not substantially increase pore size but does increase the number of pores.

Fig. 7
figure 7

LF-NMR images for argillaceous sandstone at different treatment temperatures: a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image
Fig. 8
figure 8

LF-NMR \(T_{2}\) spectrum distribution of argillaceous sandstone after thermal damage: a 25 ℃; b 25–1200 °C

Full size image

Figure 9 presents a histogram of the pore size distribution of samples for different treatment temperatures based on LF-NMR \(T_{2}\) spectrum inversion. The division of pore scale directly affects the statistical analysis of pore test results, but there are no uniform requirements provided by classification standards. This paper uses two different detection methods, i.e., µ-CT and LF-NMR test. To facilitate comparative analysis, the pore size scale can be divided into three different ranges: small pores (\(r_{pore} \le 1\;{\mu m}\)), medium pore (\(1 < r_{pore} < 10\;{\mu m}\)), and large pore (\(r_{pore} \ge 10\;{\mu m}\)). The statistics of the pore size distributions for different sample scales are presented in Table 2. Pore size changes after high-temperature treatments are very complicated, but some overall trends are evident. Small pores and medium pores consistently dominate the samples with pore volumes of 98.8–100%. Temperature affects the samples by free water dehydration, thermal expansion, organic matter softening, and thermal decomposition of mineral components, but on the whole, under 1200ºC, small pores decrease as temperature increases while medium and large pores increase. To this effect, temperature causes the small pores to expand and develop into larger-scale pores, which in turn promotes the continuous deterioration of the sample. At 1200 °C, the decomposition of mineral components (mainly clay) in the sample is effectively complete. Ultra-high temperature appears to have caused the melting of some minerals and the blockage of some large pores.

Fig. 9
figure 9

Pore size distribution characteristics of argillaceous sandstone based on LF-NMR technology: a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image
Table 2 Statistics of LF-NMR test results
Full size table

3.4 Analysis of µ-CT results

A µ-CT density image of a sample was obtained by collecting the attenuation information of an X-ray after penetrating the sample. As can be seen in Fig. 10, a typical image gradually transitions from black to bright white, indicating a gradual increase in density from low to high. The black part represents low-density material, which usually characterizes pores of various scales. The bright white part represents high-density material, which usually characterizes the skeleton of the sample as mainly composed of various mineral particles and the cementation of organic or inorganic materials. Quantitative statistics of pores and high-density substances were gathered by threshold segmentation. The percentage of pores in the total volume reflects the porosity. The images qualitatively indicate certain pores in the samples at normal temperature that are dominated by high-density materials.

Fig. 10
figure 10

µ-CT images of argillaceous sandstone specimens at different temperatures: a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image

Digital core technology (Christe et al. 2011; Xia et al. 2020) is an effective means to examine the micro pore structures of rock cores via 3D visualization and quantitative characterization. As shown in Fig. 11, reconstructed 3D digital core pores were simplified and analyzed based on the maximum ball algorithm (Dong et al. 2009) to quantitatively extract pore radius information. The pore size distribution characteristics of rock samples subjected to different treatment temperatures are shown in Fig. 12. After different high-temperature treatments, the pore size distribution satisfies the normal distribution function and the fitting coefficients are generally greater than 0.94. Under normal temperature, the pore size distribution is in the range of 3–66 μm, the main distribution interval is 3 to 40 μm, and the cumulative distribution frequency reaches 98%. When the treatment temperature is 300–600 ºC, the pore size distribution does not significantly change. When the treatment temperature reaches 900 ºC, the pore size distribution ranges from 2 to 88 μm. When the temperature reaches 1000–1200 ºC, the pore size distribution decreases in a range of 3–55 μm. These results are similar to the LF-NMR test results, as pore radius does not increase but decreases under the action of ultra-high temperature. The partitions of µ-CT test results are consistent with those of the LF-NMR results in terms of small pore (\(r_{pore} \le 1\;{\mu m}\)), medium pore (\(1 < r_{pore} < 10\;{\mu m}\)), and large pore (\(r_{pore} \ge 10\;{\mu m}\)) ranges. The statistical pore size distribution information for different scales of sample is presented in Table 3. Considering the resolution of the µ-CT testing machine and the sample size, the final scanning resolution is 8.56 μm, hence there are some small pore sizes missing from the test results compared to the LF-NMR test. The distribution frequency of medium pores is 16.5% to 28.3% and the distribution frequency of large pores is 71.7% to 83.5%; large pores are obviously dominant. It appears that the µ-CT test results with a resolution of 101 μm do not capture the distribution information of some small pores in the argillaceous sandstone when medium and small pores dominate, and that the test does not fully reveal the micro pore structure of the samples.

Fig. 11
figure 11

3D reconstruction of pore structure of argillaceous sandstone specimens at different temperatures: a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image
Fig. 12
figure 12

Pore size distribution characteristics of argillaceous sandstone based on µ-CT technology: a 25 ℃; b 300 ℃; c 600 ℃; d 900 ℃; e 1000 ℃; f 1200 ℃

Full size image
Table 3 Statistics of µ-CT test results
Full size table

4 Discussion

4.1 Changes in porosity

As the ratio of rock pore to rock volume, porosity is a key parameter related to rock pore structures. Porosity measurements largely depend on the test method and parameters utilized to gather them. Figure 13 presents the variations in porosity with treatment temperature based on the LF-NMR and µ-CT test results, and there are certain evident differences between them. The µ-CT porosity ranges from 11.1 to 15.2%, while LF-NMR porosity ranges from 18.9 to 26.3%. For the same treatment conditions, µ-CT porosity is generally smaller than LF-NMR porosity. The essence of the µ-CT test is to directly reflect the pore structure characteristics by the strength of X-ray absorption capacity of different substances in the sample, while that of the LF-NMR test is to indirectly reflect the pore structure characteristics by the water in the pores of the sample. Differences between the two sets of measurement results in this study can be attributed to two main factors. Firstly, because argillaceous sandstone contains a large number of clay matrix mineral particles, the clay easily absorbs water and swells. Moisture absorption in an LF-NMR test increases porosity but does not affect the attenuation of X-ray signals. When µ-CT test samples are dry, so the LF-NMR porosity is generally higher than the µ-CT porosity for the same treatment conditions. Secondly, due to the resolution of the test system and the sample size, theoretically speaking, pores larger than the scanning resolution can be identified by µ-CT while the LF-NMR test results are dominated by small and medium pores, and only some of these pores can discovered by µ-CT test. Hence the two test methods caused differences in the porosity results presented here, but the change trend of porosity with treatment temperature was the same for both methods. Both detection methods also demonstrate the effect of treatment temperature on the micro pore structure. As treatment temperature increases, the micro structure of the pores changes significantly and the overall porosity gradually increases.

Fig. 13
figure 13

Curve of porosity vs temperature

Full size image

LF-NMR and µ-CT testing technology have unique advantages and disadvantages in describing rock pore structures. LF-NMR is independent of the influence of the rock skeleton and reflects the distribution of pores at various scales in a more detailed and comprehensive manner, but for certain types of rock, LF-NMR technology cannot distinguish possible false pores and loses certain relevant details. The advantage of µ-CT scanning is that digital core technology displays the 3D distribution of pores in detail. However, it is limited by the resolution and may not reflect the influence of certain small pores. Micro pore structure analysis should rely on LF-NMR technology to measure the pore size distribution and be combined with µ-CT scanning to reconstruct the 3D structure of rock materials to directly observe the pore space states and pore structure data.

According to our test results, the relation between porosities \(\Phi_{{NMR{ - }T}}\), \(\Phi_{{CT{ - }T}}\) and temperature conforms to the following quadratic polynomial relation:

$$\left\{ \begin{gathered} \Phi_{{NMR{ - }T}} = \;19.578 - 3.440\left( \frac{T}{1000} \right) + 7.825\left( \frac{T}{1000} \right)^{2} \;\left( {R^{2} = 0.979} \right) \hfill \\ \Phi_{{CT{ - }T}} = 12.007 - 1.830\left( \frac{T}{1000} \right) + 4.106\left( \frac{T}{1000} \right)^{2} \;\left( {R^{2} = 0.881} \right) \hfill \\ \end{gathered} \right.$$
(4)

where \(\Phi_{{NMR{ - }T}}\) is the porosity of rock samples after temperature treatment based on the LF-NMR test; and \(\Phi_{{CT{ - }T}}\) is the porosity of rock samples after temperature treatment based on the µ-CT test.

4.2 Changes in damage

A high-temperature environment promotes the initiation, development, and expansion of pores in rock materials in a process of damage evolution. The thermal damage variable of rock defined by porosity can be written as follows:

$$\Delta_{T} = {\raise0.7ex\hbox{${\Phi^{\prime}_{T} }$} \!\mathord{\left/ {\vphantom {{\Phi^{\prime}_{T} } {\left( {1 - \Phi_{N} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {1 - \Phi_{N} } \right)}$}}$$
(5)

where \(\Delta_{T}\) is the thermal damage variable of the rock under the action of temperature \(T\); \(\Phi^{\prime}_{T}\) is the induced porosity of rock at temperature \(T\), %; and \(\Phi_{N}\) is the initial porosity of rock at temperature T, %. The induced porosity can be expressed as:

$$\Phi^{\prime}_{T} = \Phi_{T} - \Phi_{N}$$
(6)

where \(\Phi_{T}\) is the porosity of rock samples after high temperature treatment based on different testing techniques.

The thermal damage variable expressed in terms of porosity can be expressed by combining Eqs. (5) and (6):

$$\Delta_{T} = {\raise0.7ex\hbox{${\left( {\Phi_{T} - \Phi_{N} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {\Phi_{T} - \Phi_{N} } \right)} {\left( {1 - \Phi_{N} } \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {1 - \Phi_{N} } \right)}$}}$$
(7)

According to the LF-NMR and µ-CT test results, the relationship between thermal damage and treatment temperature in argillaceous sandstone after high-temperature treatment can be obtained by fitting the following relation:

$$\left\{ \begin{aligned} \Delta_{{NMR{ - }T}} = - 0.190 - 4.280\left( \frac{T}{1000} \right) + 9.748\left( \frac{T}{1000} \right)^{2} \;\;\left( {R^{2} = 0.979} \right)\; \hfill \\ \Delta_{{CT{ - }T}} = 0.437 - 2.090\left( \frac{T}{1000} \right) + 4.687\left( \frac{T}{1000} \right)^{2} \;\left( {R^{2} = 0.881} \right) \hfill \\ \end{aligned} \right.$$
(8)

where \(\Delta_{{NMR{ - }T}}\) is the thermal damage variable of rock samples after temperature treatment based on the LF-NMR test; and \(\Delta_{{CT{ - }T}}\) is the thermal damage variable of rock samples after temperature treatment based on the µ-CT test.

The correlation coefficients in this case reach 0.979 and 0.881, respectively. This relation can be used to predict the change in argillaceous sandstone thermal damage after different high-temperature treatments. According to the curves of thermal damage and temperature (Fig. 14), the thermal damage calculated by either test technique shows a non-linear relationship with temperature. Although the magnitude of the damage is somewhat different between the two techniques, the evolution trends are basically the same. Under normal temperature, both thermal damage values are 0. When the treatment temperature rises to 300 ºC, both \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) become negative values at -1.0% and − 1.5%, respectively. To this effect, temperature not only degrades the rock but also strengthens it.

Fig. 14
figure 14

Curve of thermal damage variable vs temperature

Full size image

The mechanical test results confirmed that 300 ºC is likely to be the threshold temperature for the change of the high-temperature mechanical nonlinear behavior of argillaceous sandstone. The damage results defined by the porosity obtained by the microscopic testing methods also reflect this result, which suggests the validity of the macroscopic mechanical test and also shows that the thermal damage defined by the porosity can reflect the mechanical results to a certain extent. There is consistency between macroscopic tests and microscopic tests. It is possible that treatment temperatures of 300 °C cause the moisture in the pores to evaporate, improving the physical properties of the pores while decreasing porosity. As treatment temperature is increased, both \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) gradually increase though there is a difference in the magnitude of increase between the two test techniques. At 1200 ºC, \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) are 8.1% and -3.2%, respectively. According to the thermal damage curve, the argillaceous sandstone experienced evolution through strengthening, damage derivation, and damage development as treatment temperature is increased. Therefore, thermal damage variables defined based on porosity can scientifically describe the rock damage evolution mechanism during temperature rise.

5 Conclusions

  1. 1.

    Based on the uniaxial compression test results of argillaceous sandstone after high-temperature treatment, it is found that with increasing treatment temperature, the variation trends of peak stress and elastic modulus are basically the same, which an increase first and then a decrease, while the peak strain decreases first and then increases. The three mechanical parameters all suggest that 300 ºC is probably the threshold temperature for the high-temperature nonlinear mechanical behavior of argillaceous sandstone. According to the SEM results, under 300 ºC treatment, high-temperature causes mineral shrinkage by evaporating part of water, which results in a strengthening effect. Above 300 ºC, the high-temperature will lead to the expansion of mineral particles, resulting in dominant weakening effects.

  2. 2.

    According to LF-NMR test results, the \(T_{2}\) spectrum of high-temperature treated argillaceous sandstone may be bimodal or trimodal. The right-biased bimodal type is typical and common among different samples. Pore size variations are very complex but show some overall trends. Small and medium pores consistently dominate and have pore volumes of 98.8–100%. Under 1200 ºC, small pores decrease with temperature while medium and large pores gradually increase. At 1200 ºC, the super high-temperature melts certain minerals and blocks a portion of the large pores, resulting in a decrease in large pores.

  3. 3.

    According to the µ-CT test results, the pore size distribution satisfies the normal function and the fitting coefficients are generally greater than 0.94. Under normal temperature, the pore size distribution is between 3 and 66 μm, the main interval is 3 to 40 μm, and the cumulative distribution frequency reaches 98%. When treatment temperature is 300–600 ºC, the pore size distribution does not markedly change. When treatment temperature reaches 900ºC, the pore size distribution ranges from 2 to 88 μm. When treatment temperature is 1000–1200 ºC, the pore size distribution does not increase but rather decreases and the range is 3–55 μm. These results are similar to the LF-NMR test results, where large pores do not increase but rather decrease under the action of super high-temperature.

  4. 4.

    The µ-CT porosity ranges from 11.1 to 15.2% and the LF-NMR porosity ranges from 18.9–26.3%. Under the same conditions, the µ-CT porosity is generally smaller than the LF-NMR porosity. Numerous clay matrix mineral particles in the argillaceous sandstone easily absorb water and expand, which causes a porosity increase in an LF-NMR test. In µ-CT tests, water absorption does not affect X-ray signal attenuation. The limited test system resolution also causes the µ-CT test to lose some pores. Although the results of the two methods are different, the porosity variation trends with temperature revealed by the two tests are consistent. Both methods can reflect temperature effects in pore structures.

  5. 5.

    A thermal damage evolution equation was established based on the porosity information gathered in the tests. The thermal damage calculated by both techniques showed a nonlinear relationship with temperature. The damage variables are different but the evolution trends are basically the same. At normal temperature, the two thermal damage values are 0; when temperature rises to 300 ºC, both \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) become negative at − 1.04% and -1.50%, respectively, indicating that temperature not only degrades the rock but also strengthens it. There is consistency between macroscopic tests and microscopic tests. With further increase in temperature, \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) gradually increase but across different ranges for the two test methods. At 1200 ºC, \(\Delta_{{NMR{ - }T}}\) and \(\Delta_{{CT{ - }T}}\) are 8.1% and − 3.2%, respectively. The thermal damage variation curve indicates that argillaceous sandstone evolves through stages of strengthening, damage derivation, and damage development as treatment temperature is increased.