Comparison of six major intact rock failure criteria using a particle flow approach under true-triaxial stress condition

Abstract

Suitability of six major intact rock failure criteria: Mohr–Coulomb, Hoek–Brown, Modified Lade, Modified Wiebols and Cook, Mogi and Drucker–Prager in representing the intact rock strength under the true-triaxial stress condition (σ ₁ ≥ σ ₂ ≥ σ ₃) is examined in this paper. Because the true-triaxial experimental test data available in the literature are limited and do not cover a wide range of confining stresses, the particle flow code (PFC^3D) software was used to simulate synthetic rock material failure of cubic samples of side dimension 160 mm under a broad confining stress range. The synthetic rock was made out of a mixture of gypsum, sand and water. The parallel bond model (PBM) available in PFC^3D with the associated micro parameters was chosen to represent the behavior of the synthetic material. As the first step, uniaxial, triaxial and Brazilian tests were performed in the laboratory to find the macro properties of the synthetic material. As the second step, the effect of some of the micro properties: particle size, coefficient of variation of the normal and shear bond strengths and friction coefficient on the macro properties of the synthetic rock was investigated. Then, the micro parameters of PBM were calibrated based on the aforementioned macro parameter results. Using the calibrated PFC^3D model 29 true-triaxial tests were simulated. All six failure criteria were fitted to these PFC data. Among these criteria, Modified Lade, Mogi and Modified Wiebols and Cook found to be the best failure criteria producing lower root mean square error (RMSE) values of 0.212, 0.219 and 0.304, respectively. Thus those three criteria are recommended for prediction of intact rock strength under true-triaxial stress condition. Another fitting analysis was conducted using only 12 of the 29 data to find the effect of the limited data on the prediction accuracy of the three failure criteria through the RMSE value. The predictions based on these analyses produced RMSE values of 0.40, 0.23 and 0.47 for Modified Lade, Mogi and Modified Wiebols and Cook criteria, respectively. This indicated that the Mogi criterion is the most stable among the three criteria with respect to the prediction accuracy.

1 Introduction

Intact rock strength is one of the basic properties needed to predict rock and rock mass behavior in geomechanics and geoengineering (Ewy 1999). Several researchers have studied on the failure behavior of intact rock and have suggested several failure criteria. Some of the criteria have not incorporated the intermediate principal stress and have considered only the minimum and maximum stresses (Colmenares and Zoback 2002; Fjær and Ruistuen 2002; Benz and Schwab 2008). Some researchers have shown that the effect of the intermediate principal stress on rock strength is considerable (Mogi 1967; Handin et al. 1967; Takahashi and Koide 1989; Chang and Haimson 2000). Therefore, researchers have tried to incorporate the intermediate principal stress as well as the minimum and maximum principal stresses in developing the intact rock strength criteria.

In general, six major failure criteria may be listed to represent strength of intact rock in geomechanics: (a) Mohr–Coulomb; (b) Hoek and Brown (1980); (c) Modified Lade; (d) Modified Wiebols and Cook; (e) Mogi and (f) Drucker–Prager. Figure 1 shows the failure envelopes of these criteria for a sample with cohesion of 2 MPa and internal friction angle of 25°. The Mohr–Coulomb and Hoek–Brown criteria are the most common rock failure criteria, because of the simplicity on one hand and their extensibility to rock masses on the other hand. However, these two criteria unlike all other major failure criteria do not incorporate the intermediate principal stress.

Fig. 1

Failure envelopes for Mohr–Coulomb, Hoek–Brown, Modified Lade, Modified Wiebols and Cook, Mogi and Drucker–Prager for a sample with cohesion of 2 MPa and internal friction angle of 25°

Lade introduced his criterion in 1977 for soils and Ewy in 1999 extended this criterion to rock by adding a parameter to represent the cohesion. He developed this criterion for wellbore stability analysis and it is used in petroleum engineering. Before this criterion, Mohr–Coulomb and Drucker–Prager were the most common failure criteria used in the wellbore stability analysis. However, the Mohr–Coulomb does not incorporate the intermediate principal stress and the Drucker–Prager highly overestimated the strength of rock (Ewy 1999).

Before Ewy, Zhou in 1994 suggested his criterion to model initial shape and extension of borehole breakout around a wellbore. This criterion is the extended form of the Drucker–Prager criterion. It predicts rock strength similar to the Wiebols and Cook criterion and therefore, it is known as the Modified Wiebols and Cook criterion (Colmenares and Zoback 2002).

The last major failure criterion is the Mogi criterion. Mogi introduced his first criterion in 1967 by performing three different kinds of tests (biaxial loading tests, confined compression tests and confined extension tests) on different rock types. He developed his second criterion in 1971 by extending Von Mises’ theory. The Mogi’s criterion incorporates the intermediate principal stress like Modified Lade, Modified Wiebols and Cook and Drucker–Prager, but, unlike these criteria, the Mogi’s criterion is an empirical one.

Choosing the best failure criterion can reduce the risk and cost of a project in rock engineering and it is one of the most important parts of a design in rock engineering. In this paper, an attempt is made to find the best failure criterion for intact rock by considering six major failure criteria available in the literature. Several researchers (Colmenares and Zoback 2002; Benz and Schwab 2008) have tried to find the best criterion based on the available experimental test results. Nevertheless, most of these data like for KTB amphibolite, Dunham dolomite, Solenhofen limestone, Westerly granite and Shirahama sandstone do not have enough data for the high σ ₂ values or low σ ₃ values. Therefore, a possibility exists for this lack of data to influence the strength criteria fitting results. To remove this shortcoming, in this paper numerical modeling is used to model a synthetic rock failure in a wide range of confining stresses.

For numerical modeling particle flow code (PFC^3D) software is chosen. PFC^3D is a distinct element method (DEM) based software, which uses spherical elements to represent particles. DEM method was introduced by Cundall (1971) and developed for granular material by Cundall and Strack (1979). In this method, macro properties of a synthetic material can be numerically estimated by assigning micro mechanical parameter values for particles. This feature helps to observe the effect of confining stresses on strength. However, due to the presence of higher number of micro mechanical parameters compared to the available macro properties and complex behavior of the micro mechanical parameters, calibration of micro mechanical parameters is a complicated procedure (Potyondy and Cundall 2004; Schöpfer et al. 2013; Yang et al. 2015).

In this research, firstly, experimental tests are performed to find macro mechanical properties of a synthetic material. Then, secondly, the micro mechanical parameters of the particle flow model are calibrated based on the obtained macro mechanical properties. In this paper, also some investigations are made to study the effect of some micro parameters on macro properties. As the next step, true-triaxial tests are simulated using the calibrated particle flow model under different confining stresses. The obtained numerical data are then used to fit the aforementioned failure criteria. Finally, these criteria are compared and the accuracy of the criteria is investigated based on the obtained root mean square error (RMSE) values. The RMSE is calculated using the following equation:

$$RMSE = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {\sigma_{i} - \bar{\sigma }_{i} } \right)^{2} }$$

(1)

where, n is the number of data, $\sigma_{i}$ is the ith strength value which is obtained by a failure criterion and $\bar{\sigma }_{i}$ is the ith strength value obtained from numerical modeling.

2 Experimental tests

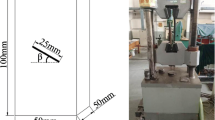
In the experimental part, a synthetic material that is made out of a mixture of gypsum, sand and water is used. This model material exhibits different mechanical properties depending on the mixture ratio. The mixture ratio is designed to obtain a uniaxial compressive strength around 5.5 MPa for the model material. In the experimental part, three uniaxial tests, three triaxial tests and 5 Brazilian tests were performed. Cubic samples of side dimension 160 mm were used for the uniaxial and triaxial tests. For the Brazilian tests, disk samples of diameter 50 mm and thickness 25 mm were used. Tables 1 and 2, and Fig. 2 show the obtained results. Figure 3 illustrates the relation obtained between the minimum and maximum stresses for samples GAA1–GAA6. The summary of macro mechanical properties obtained for the synthetic rock through the results of the aforementioned laboratory tests are given in Table 3. The Young’s modulus and Poisson’s ratio given in this table are calculated based on the uniaxial compression test results.

Table 1 Uniaxial and triaxial test results

Table 2 Brazilian test results

Fig. 2

Uniaxial and triaxial test results: GAA1, GAA2 and GAA3 (σ_x = σ_y = 0); GAA4 (σ_x = σ_y = 0.53 MPa); GAA5 (σ_x = σ_y = 1.11 MPa); GAA6 (σ_x = σ_y = 1.64 MPa)

Fig. 3

Relation between the minimum and maximum principal stresses for samples GAA1–GAA6 and PFC modeling results for the same confining stress combinations

Table 3 Macro mechanical property values estimated for the synthetic rock from laboratory tests and PFC^3D modeling results

3 Numerical modeling

PFC^3D software (Itasca 2008) is chosen to perform numerical modeling. PFC^3D is a DEM based software which uses spherical elements to represent particles. In this method, particles are assumed as rigid and Newton’s second law controls the interactions between the particles. Particles can have contact with adjacent particles and force–displacement law acts at contacts. Compared to other methods, in PFC^3D macro parameter values are not directly used in the model, and micro parameter values applicable between particles should be calibrated using the macro property values and then these micro parameter values are used in PFC^3D modeling (Cundall and Strack 1979; Potyondy and Cundall 2004; Itasca 2008; Potyondy 2015; Yang et al. 2015).

In PFC^3D different contact models can be assigned but each one can have up to three parts, (1) contact stiffness model, (2) slip model and (3) bonding model. The contact stiffness model shows the elastic behavior in normal and shear directions of contacts. In this research, the linear model is used for the contact stiffness. The normal stiffness, $k^{n}$, and shear stiffness, $k^{s}$, are two parameters of the linear model. The normal stiffness and shear stiffness have the following relations with the average radius $\tilde{R}$, of the two particles in a contact, and the Young’s modulus of contact, $E_{c}$.

$$k^{n} = k_{r} k^{s} = 4 E_{c} \tilde{R}$$

(2)

In Eq. 2, $k_{r}$ is the ratio of normal to shear stiffness. In PFC^3D by defining $k_{r}$ and $E_{c}$, normal and shear stiffness are applied to particle contacts.

Slip model lets particles slide on each other when shear force exceeds the maximum allowable shear. Thus the maximum allowable shear force, $F_{s}^{Max}$, can be expressed by Eq. 3.

$$F_{s}^{Max} = \mu F_{n}$$

(3)

In Eq. 3, $F_{n}$ is the normal force and $\mu$ is the friction coefficient of the contact between the two particles.

The two previous models do not stick particles together but bond models provide particles to adhere to each other. The contact bond model (CBM) and parallel bond model (PBM) are two available bond models (Itasca 2008). In CBM, two adjacent particles adhere together at a very negligible area like a point. This bond preserves particles against shear and normal forces by specific strengths. The shear force, $\varphi_{s}$, and normal force, $\varphi_{n}$, have the following relations with the normal bond strength, $\dot{\sigma }_{c} ,$ and shear bond strength, $\dot{\tau }_{c}$:

$$\varphi_{n} = 4\dot{\sigma }_{c} \tilde{R}^{2}$$

(4)

$$\varphi_{s} = 4\dot{\tau }_{c} \tilde{R}^{2}$$

(5)

In PFC^3D shear and normal bond strengths of CBM are defined by the mean and standard deviation values.

The CBM contact cannot resists against moment because the two particles bond at a point. However, the PBM can resists against moment as well as normal and shear forces. The PBM adheres particles in a specific area. This area is a thin cylinder with definable radius, $\bar{R}$, which is expressed by the following equation:

$$\bar{R} = \bar{\lambda }\,\hbox{min} \left( {R_{1} ,R_{2} } \right)$$

(6)

In Eq. 6, $\bar{\lambda }$ is a constant value between 0 and 1, $R_{1}$ and $R_{2}$ are radii of the first and second balls that bond to each other. The relations of shear and normal bond strengths of the PBM with shear force, $F_{s}$, normal force, $F_{n}$, normal moment, $M_{n}$, and shear moment, $M_{s}$, are given by the following equations:

$$\bar{\sigma }_{c} = \frac{{ - F_{n} }}{A} + \frac{{\left| { M_{s} } \right|\bar{R}}}{I}$$

(7)

$$\bar{\tau }_{s} = \frac{{\left| {F_{s} } \right|}}{A} + \frac{{\left| { M_{n} } \right|\bar{R}}}{J}$$

(8)

$$A = \pi \bar{R}^{2}$$

(9)

$$I = \frac{1}{4}\pi \bar{R}^{4}$$

(10)

$$J = \frac{1}{2}\pi \bar{R}^{4}$$

(11)

In the above equations, $I$ is the disk cross section’s moment of inertia, $J$ is the disk cross section’s polar moment of inertia, A is the area of the disc cross section, $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$ are the normal and shear bond strengths of the PBM, respectively. In PFC^3D, normal and shear bond strengths of the PBM are defined by the mean and standard deviation values.

PBM works like a cement material and cement bond particles together. Thus, PBM can model rock material better than CBM. PBM is deformable in shear and normal directions according to the following stiffnesses.

$$\bar{k}^{n} = \bar{k}_{r} \bar{k}^{s} = \frac{{\bar{E}_{c} }}{L}$$

(12)

In Eq. 12, $\bar{k}^{n}$ and $\bar{k}^{s}$ are the normal stiffness and shear stiffness of the PBM, respectively; $\bar{E}_{c}$ is the Young’s modulus; L is the distance between the centers of two spheres that bond to each other and $\bar{k}_{r}$ is the ratio of normal to shear stiffness of the PBM. In PFC^3D $\bar{E}_{c}$ and $\bar{k}_{r}$ are defined instead of $\bar{k}^{n}$ and $\bar{k}^{s}$ (Potyondy and Cundall 2004).

As mentioned above, for the CBM, 7 micro mechanical parameters ($E_{c}$, $k_{r}$, $\mu$, mean and standard deviation of $\dot{\sigma }_{c}$ and $\dot{\tau }_{c}$) and for PBM, 10 micro mechanical parameters ($E_{c}$, $k_{r}$, $\mu$,$\bar{E}_{c}$, $\bar{k}_{r}$, $\bar{\lambda }$, mean and standard deviation of $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$) are necessary. These parameters need to be calibrated using macro properties like the uniaxial and standard triaxial strengths, the Young’s modulus, tensile strength and Poisson’s ratio. Moreover, particle size distribution should be added to micro parameters because the particle size significantly affects macro properties of the modeled sample. Therefore, calibration of micro parameters is a very complicated task and some assumptions should be used to simplify the calibration procedure. Setting of $E_{c} = \bar{E}_{c}$, $k_{r} = \bar{k}_{r}$, $\bar{\sigma }_{c} = \bar{\tau }_{s}$ and $\bar{\lambda } = 1$ in PBM and $\dot{\sigma }_{c} = \dot{\tau }_{c}$ in CBM are some of these assumptions (Potyondy and Cundall 2004; Yang et al. 2015).

Moreover, the effect of each micro parameter on the mechanical behavior of the macro sample should be investigated. The PFC manual and some researchers have explained their experiences of some effects of these micro parameters (Potyondy and Cundall 2004; Cho et al. 2007; Yang et al. 2015). However, the reported findings are not comprehensive and further investigations are required to clarify the remaining doubts. In this paper, mainly the PBM is used for modeling. However, both the CBM and PBM are used in certain sections to investigate the effect of different micro parameters.

The calibration of micro parameters is based on a trial and error procedure in which the micro mechanical parameter values are varied iteratively to match the macro mechanical behaviors of the selected synthetic material. In this study, a special calibration sequence suggested by Yang et al. (2015) was followed to minimize the number of iterations. First, the aforementioned assumptions were chosen to reduce the number of independent parameters. Then, the Young’s modulus was calibrated by setting the material strengths to a large value and varying $E_{c}$ and $\bar{E}_{c}$ to match the Young’s modulus between the numerical and laboratory specimens. Next, by changing $k_{r}$ and $\bar{k}_{r}$, the Poisson’s ratio of the numerically simulated intact synthetic cylindrical specimen was matched to that of the laboratory specimen. After calibrating the aforementioned micro mechanical parameters, the peak strength between the numerical and laboratory specimens was matched by gradually reducing the normal and shear bond strengths of the parallel bonds. The data obtained between the minimum and maximum principal stresses based on PFC modeling for the standard triaxial loading condition are shown in Fig. 3. They match very well with the same relation obtained based on experimental data.

In the sections given below the effects of some of the micro parameters which have not received sufficient attention are explained and investigated based on macro mechanical property values of the synthetic rock that are used in this study.

4 Particle size

The first step in PFC modeling is to select the particle size distribution. In this study the uniform distribution is chosen by defining the minimum radius, $R_{min}$, and the ratio of maximum to minimum radius, $m_{r}$ to represent the particle size distribution. Since the particle size is an inherent part of material properties, it is not an independent parameter that increases the resolution of modeling (Potyondy and Cundall 2004). By reducing the particle size the ratio of contacts to particles can be increased slightly. This ratio increases significantly with reduction of $m_{r}$. In the literature, most of the researchers have chosen a value between 1.5 and 2 for $m_{r}$. In the following section effect of particle size on macro parameters is studied for PBM.

Potyondy and Cundall (2004) showed reduction in the particle size leading to higher Young’s modulus and strength of a macro sample. Figure 4 illustrates this effect on a cubic sample of dimension of 288 mm with micro parameter values of $m_{r} = 1.66$, $E_{c}$ = $\bar{E}_{c}$ = 1.25 GPa, $k_{r}$ = $\bar{k}_{r}$ = 2.5, $\mu$ = 0, $\bar{\lambda }$ = 1, mean $\bar{\sigma }_{c}$ = mean $\bar{\tau }_{s}$ = 4.4 MPa, std. dev. $\bar{\sigma }_{c}$ = std. dev. $\bar{\tau }_{s}$ = 1.1 MPa which were obtained from the calibration of the synthetic material. This figure shows that increase of the ratio of sample dimension to minimum particle diameter through the reduction of the particle size leads to higher strength and Young’s modulus for the modeled sample.

Fig. 4

Uniaxial compression test results for 288 mm cubic sample with minimum particle diameters of 2.7, 5.4, 8.1 and 10.8 mm; the other micro mechanical parameter values are the same as the values given in Table 4

In this modeling, two different methods are used to calculate the stress and strain. The first method is based on creating a measurement region using the “measure” command given in the PFC^3D software. This command makes a spherical region with a definable radius in the sample and calculates stresses and strains based on the forces act between the particles and displacements of the particles that are located in this region. In the second method, the stress is found by dividing the total force acting on each wall by its area and the strain is found by calculating the displacement of each wall. The strength and Young’s modulus of a sample obtained through the two methods are different and the values obtained through the wall method are lower than that obtained through the measurement method for the higher values of the particle size. On the other hand, for lower values of the particle size, the values obtained through the wall method may exceed that obtained through the measurement method. When the ratio of sample dimension to minimum particle size is between 60 and 80, the two methods provide very close values. This behavior is illustrated in Fig. 5.

Fig. 5

Effect of particle size on a Young’s modulus and b UCS of modeled sample

Equations 2 and 12 show that change of the value of radius of particles affects the normal stiffness and shear stiffness of contact and parallel bonds. Therefore, another method was chosen to study the effect of particle size on macro parameters in order to eliminate this effect. In the new method, the minimum particle size was kept constant and the dimension of the sample was increased. 2.7 mm was chosen for the minimum particle diameter and the dimension of the cubic sample was varied from 36 to 288 mm. Figure 6 shows that increase of the ratio of sample dimension to minimum particle diameter by increasing the sample dimension leads to higher strength and Young’s modulus of the sample.

Fig. 6

Uniaxial compression test results for cubic samples with the minimum particle diameter of 2.7 mm, and sample dimensions of 36, 72, 108, 144, 180, 216, 252 and 288 mm; the other micro mechanical parameter values are the same as the values given in Table 4

For this analysis too it was found that the values of strength and Young’s modulus based on the wall method are lower than that based on the measurement method for the lower ratio of sample dimension to minimum particle diameter. However, as the sample dimension increases these values merge and for higher ratio of sample dimension to minimum particle diameter the values based on the wall method exceed that based on the measurement method. When the ratio of sample dimension to minimum particle size is between 70 and 80, the two methods provide very close values. This behavior is illustrated in Fig. 7.

Fig. 7

Effect of ratio of sample dimension to minimum particle diameter on a Young’s modulus and b UCS of modeled sample

Also it should be mentioned that by increasing both the particle size and sample size and keeping the ratio of the sample dimension to minimum particle size constant, increases the uniaxial compressive strength but keeps the Young’s modulus more or less constant. This behavior is shown in Fig. 8 for the cubic sample with the same micro property values as for the cases dealt with previously and having sets of minimum particle size/sample dimension of 1.35/54, 2.7/108, 5.4/216 and 10.8/432 mm, respectively.

Fig. 8

Uniaxial compression test results for cubic samples with the minimum particle size/sample dimension of 1.35/54, 2.7/108, 5.4/216 and 10.8/432 mm, respectively; the other micro mechanical parameter values are the same as the values given in Table 4

As mentioned before, the particle size is not a parameter that increases the resolution of modeling. Therefore, the convergence analysis that is common with the finite element method (FEM) is not applicable in the particle flow approach. Based on all previous illustrations, for further PFC modeling of this study, minimum particle diameter, $D_{min} = 2.7\,{\text{mm}}$ and $m_{r} = 1.66$ were selected to perform modeling with a cubic sample of side dimension of 160 mm. Based on this selection 103,663 particles and 275,824 contacts are produced in the selected sample (Fig. 9).

Fig. 9

Sample used in PFC3D modeling of compression tests

5 Micromechanical strength parameters

Mean values of $\dot{\sigma }_{c}$ and $\dot{\tau }_{c}$ in CBM or mean values of $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$ in PBM are assumed to be equal in most of the PFC modeling research reported in the literature. Yang et al. (2015) showed that changing the ratio of $\bar{\sigma }_{c} /\bar{\tau }_{s}$ in PBM affects the failure mode in the sample and the ratio of 1 is the best value for modeling of synthetic material. Here also this ratio is chosen as 1.

For the standard deviation of $\dot{\sigma }_{c}$ and $\dot{\tau }_{c}$ in the CBM or the standard deviation of $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$ in the PBM researchers generally select values equal to 20–30 % of their mean values (Kulatilake et al. 2006; Potyondy 2012); note that the  % value given here is for the parameter coefficient of variation (cov) of strength. The PFC^3D software manual indicates that the standard deviation influences the yield point and range of the plastic part in compression tests. In this research, an attempt is made to find other effects of this value in modeling. It is clear from the literature that by increasing the cov of the strength and keeping all other parameter values constant, the compressive strength and Young’s modulus of the sample can be reduced significantly. However, by increasing the $E_{c}$, $\dot{\sigma }_{c}$ and $\dot{\tau }_{c}$ in CBM or $E_{c}$, $\bar{E}_{c}$, $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$ in PBM along with increase of the cov of the strength the compressive strength and Young’s modulus of the sample can be kept constant. Under these conditions, increase of the cov of the strength increases the ductile behavior of the sample. Figures 10 and 11 show this effect on CBM and PBM, respectively. Also, note that increase of cov of strength in PBM changes the failure mode as shown in Fig. 12. In Fig. 12, the red discs indicate the tensile failures and blue discs indicate the shear failures. It is important to note that for the same values of cov of strength and $\mu$, the PBM produces more brittle behavior compared to that of the CBM (Fig. 13). Also note that the PBM can produce better failure mode compared to that of CBM (Fig. 14).

Fig. 10

PFC3D simulations of uniaxial compression tests using the PBM with different cov of strength values

Fig. 11

PFC3D simulations of uniaxial compression tests using the CBM with different cov of strength values

Fig. 12

Effect of the cov of strength on failure mode of the PBM a cov of strength = 0.1, b cov of strength = 0.25 and c cov of strength = 1.0; red discs stand for tensile failures and blue discs stand for shear failures

Fig. 13

PFC3D simulations of uniaxial compression tests using the CBM and PBM with the same cov of strength = 0.1 and $\mu$ = 0.5

Fig. 14

Effect of different bond model a PBM and b CBM on failure mode using the same values for cov of strength; red discs stand for tensile failures and blue discs stand for shear failures

6 Coefficient of friction

The other important micro mechanical parameter is $\mu$. The PFC^3D manual indicates that this value affects the post peak behavior; but this effect was found to be insignificant. Generally, the Young’s modulus and compressive strength increase with increasing $\mu$. But by reducing $E_{c}$, $\dot{\sigma }_{c}$ and $\dot{\tau }_{c}$ in CBM or $E_{c}$, $\bar{E}_{c}$, $\bar{\sigma }_{c}$ and $\bar{\tau }_{s}$ in PBM along with increase of $\mu$ the compressive strength and Young’s modulus of the sample can be kept constant (Figs. 15, 16). Accordingly, $\mu$ does not have important influence in the post peak behavior. Numerical modeling shows that by increasing the $\mu$ the internal friction angle of the sample can be increased significantly (Fig. 17).

Fig. 15

PFC3D simulations of uniaxial compression tests using the PBM with different $\mu$

Fig. 16

PFC3D simulations of uniaxial compression tests using the CBM with different $\mu$

Fig. 17

Influence of $\mu$ on the internal friction angle of the modeled sample

Based on all the aforementioned findings, the finally calibrated micro parameter values are given in Table 4. The results of the experimental uniaxial compression tests and the simulated uniaxial compression test through PFC^3D based on the micro parameter values given in Table 4 are illustrated in Fig. 18. Note that in Fig. 18, the laboratory experimental curves show a non-linear portion for low axial stress values. It is not possible to simulate that with PFC^3D modeling. Therefore, for better comparison between the laboratory curves and the PFC^3D simulation, the PFC^3D curve is shifted to the right to skip the non-linear portion of the laboratory curves. Table 3 also shows the obtained macro mechanical parameter values based on PFC^3D simulations. Figure 18 and Table 3 show the accuracy and capability of the particle flow approach for the considered synthetic rock.

Table 4 Calibrated micro mechanical parameter values for the synthetic material

Fig. 18

Comparison between experimental and PFC^3D simulation results of uniaxial compression test

7 True-triaxial tests

True-triaxial tests are performed through PFC modeling on intact rock to find a suitable intact rock failure criterion for the selected model material. In these simulations, cubic samples of side dimension 160 mm were used with micro mechanical property values given in Table 4. Figure 19 shows the true-triaxial test results obtained from PFC modeling. These data show that the intermediate principal stress has a significant effect on intact rock strength and it can increase the intact rock strength up to about 25 %. Moreover, the intermediate principal stress changes the fracturing plane direction in a sample. Figure 20 shows that the distribution of the normal vector direction to the fracturing plane of the bonds is more or less isotropic when the minimum and intermediate principal stresses are equal. However, with increasing difference between the intermediate principal stress and minor principal stress the normal vector direction to the fracturing plane gradually rotates to the minimum principal stress direction.

Fig. 19

True-triaxial test results obtained from PFC3D modeling

Fig. 20

Bond fracturing plane directions on an equal area stereonet at the peak stress for different minor and intermediate principal stress values: a σ₃ = σ₂ = 0; b σ₃ = 0 and σ₂ = 1.128 MPa; c σ₃ = 0 and σ₂ = 2.256 MPa; d σ₃ = σ₂ = 1.128 MPa; e σ₃ = 1.128 MPa and σ₂ = 2.256 MPa; f σ₃ = 1.128 MPa and σ₂ = 3.384 MPa; g σ₃ = σ₂ = 2.256 MPa; h σ₃ = 2.256 MPa and σ₂ = 3.384 MPa; i σ₃ = 2.256 MPa and σ₂ = 4.512 MPa (σ₁ is in the vertical direction, σ₂ is in the north–south direction and σ₃ is in the east–west direction)

In Fig. 21, the tensile and shear fractures are indicated by red and blue color discs, respectively. This figure indicates that the shear fractures (blue discs) increase with increasing confining stresses (compare between Fig. 21a, b). It is important to note that the increasing confining stresses lead to increasing the ratio between the number of shear cracks and tensile cracks that occur on bonds. However, the increasing difference between the intermediate principal stress and minor principal does not affect this ratio.

Fig. 21

Bond fracturing at the peak stress for different minor and intermediate principal stress values: a σ₃ = σ₂ = 1.128 MPa; b σ₃ = σ₂ = 3.384 MPa (σ₁ is in the z direction, σ₂ is in the y and σ₃ is in the x direction; red and blue discs represent tension and shear cracks, respectively)

8 Intact rock failure criteria

In the following sections, the considered six major failure criteria are explained and their fitting results for the data obtained through PFC^3D numerical modeling are discussed in detail.

9 Mohr–Coulomb criterion

This criterion can be considered as the first criterion available in rock mechanics. This criterion assumes that the failure happens when the shear stress on a specific plane reaches the shear strength. This criterion is defined by the following equation:

$$\tau_{max} = c + \tan \varphi \sigma_{n}$$

(13)

where $\tau_{max}$ is the shear strength, $\sigma_{n}$ is normal stress, c is the cohesion and $\varphi$ is the angle of internal friction. The angle of failure plane is $45 + \frac{\varphi }{2}$ to the minimum principal stress direction. The normal vector of this plane is on the plane of maximum principle stress, $\sigma_{1}$, and minimum principle stress, $\sigma_{3}$. Therefore, in this criterion the intermediate principle stress, $\sigma_{2}$, does not have an effect on the strength of rock and this is a shortcoming of this criterion. Equation 13 can be written as Eq. 14 using the principle stresses.

$$\sigma_{1} = \sigma_{c} + q\sigma_{3}$$

(14)

where

$$\sigma_{c} = 2c\tan \left( {45 + \frac{\varphi }{2}} \right)$$

(15)

and

$$q = \tan^{2} \left( {45 + \frac{\varphi }{2}} \right)$$

(16)

$\sigma_{c}$ is the uniaxial compressive strength of intact rock. As given in Eq. 14, the relation between the maximum and minimum principle stresses is linear and this assumption is too simple for intact rock materials. Consequently, Hoek and Brown (1980) introduced a new criterion based on a nonlinear relation between $\sigma_{1}$ and $\sigma_{3}$.

Figure 22 illustrates the regression relation obtained between the major and mor principal stresses of the numerical modeling data for the Mohr–Coulomb failure criterion with R² value of 0.95. Therefore, Eq. 17 can be used to express the Mohr–Coulomb failure criterion for this synthetic rock.

Fig. 22

Relation obtained between the maximum and minimum principal stresses for the Mohr–Coulomb failure criterion (R² value is 0.95)

$$\sigma_{1} = 2.3654\sigma_{3} + 6.8171$$

(17)

Figure 23 shows the comparison obtained between the Mohr–Coulomb failure criterion fitting lines and the true-triaxial data given in Fig. 19. The obtained RMSE value for this criterion is 0.669. It is obvious that this model is not able to capture the effect of intermediate principal stress.

Fig. 23

Obtained Mohr–Coulomb failure criterion fits and the true-triaxial data given in Fig. 18 for the synthetic intact rock

10 Hoek–Brown

Hoek–Brown criterion (Hoek and Brown 1980) is defined by the following equation:

$$\sigma_{1} = \sigma_{3} + \sigma_{c} \left( {m_{i} \frac{{\sigma_{3} }}{{\sigma_{c} }} + s} \right)^{0.5}$$

(18)

In Eq. 18, $m_{i}$ and s are constants that depend on the rock type and s is equal to 1 for the intact rock. Even though this is a non-linear criterion, similar to the Mohr–Coulomb criterion, it does not consider the intermediate principle stress. Figure 24 shows the regression relation obtained between the major and minor principal stresses of the numerical modeling data for the Hoek–Brown failure criterion with R² value of 0.95. The Hoek–Brown failure criterion obtained for the synthetic intact rock material is given by Eq. 19:

Fig. 24

Relation obtained between the maximum and minimum principal stresses for the Hoek–Brown criterion (R² value is 0.96)

$$\sigma_{1} = \sigma_{3} + 6.641 \sqrt {3.748 \times \frac{{\sigma_{3} }}{6.641} + 1}$$

(19)

Figure 25 shows the comparison obtained between the Hoek–Brown failure criterion fitting lines and the true-triaxial data given in Fig. 19. The obtained RMSE value for this criterion is 0.664. It is obvious that the Hoek–Brown failure criterion is not able to capture the effect of intermediate principal stress.

Fig. 25

Obtained Hoek–Brown failure criterion fits and the true-triaxial data given in Fig. 18 for the synthetic intact rock

11 Modified Lade criterion

Lade in 1977 introduced the failure criterion given below in Eqs. 20–22. This criterion considers all three principle stresses and the relation between these three stresses is nonlinear.

$$\left( {\left( {I_{1}^{3} /I_{3} } \right) - 27} \right)\left( {I_{1} /p_{a} } \right)^{{m^{{\prime }} }} = \eta_{1}$$

(20)

$$I_{1} = \sigma_{1} + \sigma_{2} + \sigma_{3}$$

(21)

$$I_{3} = \sigma_{1} \sigma_{2} \sigma_{3}$$

(22)

In Eq. 20, $p_{a}$ is the atmospheric pressure and $m^{{\prime }}$ and $\eta_{1}$ are material constants. This criterion was developed for soils. Ewy in 1999 suggested a modification for this criterion to make it applicable for intact rock by setting $m^{{\prime }}$ zero and introducing two new constants that are related to cohesion and internal friction. This Modified Lade criterion can be expressed by the following equations:

$$\left( {I_{1}^{{{\prime }^{3} }} /I_{3}^{{\prime }} } \right) = 27 + \eta$$

(23)

$$I_{3}^{{\prime }} = \left( {\sigma_{1} + S} \right) + \left( {\sigma_{2} + S} \right) + \left( {\sigma_{3} + S} \right)$$

(24)

$$I_{1}^{{\prime }} = \left( {\sigma_{1} + S} \right)\left( {\sigma_{2} + S} \right)\left( {\sigma_{3} + S} \right)$$

(25)

In the above equations, S and $\eta$ are related to cohesion and internal friction angle through the following equations:

$$S = \frac{{\sigma_{ci} /2\tan \left( {45 + \frac{\varphi }{2}} \right)}}{\tan \varphi }$$

(26)

$$\eta = 4\left( {\tan \varphi } \right)^{2} \left( {9 - 7\sin \varphi } \right)/\left( {1 - \sin \varphi } \right)$$

(27)

Because determination of S and $\eta$ directly by solving Eqs. 23–25 is difficult, an indirect method is chosen to find those. In the indirect method, different values are chosen for S and $\eta$ by selecting values for C and $\varphi$ from a grid in a reasonable range and using Eqs. 26 and 27. Then the failure stresses corresponding to different minimum and intermediate principal stresses are found through Eqs. 23–25. Afterwards, the best combination of C and $\varphi$ is found by minimizing the RMSE. In Fig. 26, the obtained RMSE values are shown for different values of cohesion and internal friction angle. The minimum RMSE found was 0.212 MPa. It resulted in the best values for the internal friction angle and cohesion as 20.38° and 1.97 MPa, respectively.

Fig. 26

Obtained root mean square error values for the modified Lade failure criterion for different combinations of friction angle and cohesion

Figure 27 shows the obtained Modified Lade strength criterion fits along with the true-triaxial data given in Fig. 19. This criterion seems to fit the data well.

Fig. 27

Obtained Modified Lade failure criterion fits and the true-triaxial data given in Fig. 18 for the modeled synthetic intact rock

12 Modified Wiebols and Cook criterion

Wiebols and Cook in 1968 introduced their failure criterion based on the sliding cracks by additional energy storage around cracks. This criterion considers the intermediate principle stress. Zhou (1994) proposed a simpler failure criterion which has high similarity to the Wiebols and Cook criterion and called it the Modified Wiebols and Cook criterion. This modified criterion can be expressed by Eqs. 28–30.

$$J_{2}^{1/2} = A + BJ_{1} + CJ_{1}^{2}$$

(28)

$$J_{1} = \left( {1/3} \right)\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)$$

(29)

$$J_{2}^{1/2} = \sqrt {\frac{1}{6} \left( {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{2} - \sigma_{1} } \right)^{2} } \right)} = \left( {3/2} \right)^{1/2} \tau_{oct}$$

(30)

In the above equations, $J_{1}$ is the mean effective confining stress, $\tau_{oct}$ is the octahedral shear stress and A, B and C are constants that are related to the cohesion and internal friction angle through the following equations:

$$C = \frac{{\sqrt {27} }}{{2\left( {1 + 0.6\tan \varphi } \right)\sigma_{ci} + \left( {q - 1} \right)\sigma_{3} - \sigma_{ci} }} \times \left( {\frac{{\left( {1 + 0.6\tan \varphi } \right)\sigma_{ci} + \left( {q - 1} \right)\sigma_{3} - \sigma_{ci} }}{{2\left( {1 + 0.6\tan \varphi } \right)\sigma_{ci} + \left( {2q + 1} \right)\sigma_{3} - \sigma_{ci} }} - \frac{q - 1}{q + 2}} \right)$$

(31)

$$B = \frac{{\sqrt 3 \left( {q - 1} \right)}}{q + 2} - \frac{C}{3}\left( {2\sigma_{ci} + \left( {q + 2} \right)\sigma_{3} } \right)$$

(32)

$$A = \frac{{\sigma_{ci} }}{\sqrt 3 } - \frac{{\sigma_{ci} }}{3}B - \frac{{\sigma_{ci}^{2} }}{9}C$$

(33)

These equations show that A, B and C are not independent and they are also rated to the minimum principal stress. Therefore, finding these coefficients directly from Eq. 28 is difficult. Thus the best regression should be found by minimizing the RMSE using a procedure similar to that used in working with the Modified Lade criterion.

In Fig. 28, the obtained RMSE values are shown for different values of cohesion and internal friction angle. The minimum RMSE found was 0.304 MPa. It resulted in the best values for the internal friction angle and cohesion as 21.88° and 1.82 MPa, respectively. Figure 29 shows the obtained Modified Wiebols and Cook strength criterion fits along with the true-triaxial data given in Fig. 19. This figure shows that this criterion fits data well but its accuracy is less than that of the Modified Lade criterion fit.

Fig. 28

Obtained root mean square error values for the Modified Wiebols and Cook failure criterion for different combinations of friction angle and cohesion

Fig. 29

Obtained Modified Wiebols and Cook failure criterion fits and the true-triaxial data given in Fig. 18 for the modeled synthetic intact rock

13 Mogi criterion

Mogi suggested his first intact rock strength criterion in 1967 by performing two types of triaxial tests $\left( {\sigma_{1} > \sigma_{2} = \sigma_{3} \,\& \,\sigma_{1} = \sigma_{2} > \sigma_{3} } \right)$ and a biaxial test $\left( {\sigma_{1} > \sigma_{2} > \sigma_{3} = 0} \right)$ on different rock types. From these tests, he realized that the intermediate principal stress has influence on the rock strength but at a level less than that of the other two principle stresses. Thus, he introduced the following empirical equation for his criterion:

$$\left( {\sigma_{1} - \sigma_{3} } \right)/2 = f\left[ {\left( {\sigma_{1} + \beta \sigma_{2} + \sigma_{3} } \right)/2} \right]$$

(34)

In Eq. 34, $\beta$ is a constant, which varies between 0 and 1 and $f$ is an empirical function that depends on the rock type. In 1971, Mogi generalized his criterion using Von Mises’ theory and suggested Eq. 35.

$$\tau_{oct} = g_{1} \left( {\sigma_{1} + \sigma_{3} } \right)$$

(35)

In Eq. 35, $g_{1}$ is a monotonically increasing function. Mogi found that the plane of failure is not exactly parallel to the plane the intermediate principal stress acts. Thus, he modified Eq. 35 to the following equation:

$$\tau_{oct} = g_{2} \left( {\sigma_{1} + \beta \sigma_{2} + \sigma_{3} } \right)$$

(36)

where $\beta$ is a constant, which varies between 0 and 1 and $g_{2}$ like $g_{1}$ is a monotonically increasing function. Mogi also mentioned that results of Eqs. 35 and 36 are almost the same. Mogi’s first criterion (1967) did not fit the PFC^3D data properly. Therefore, in this paper his second criterion given in 1971 is used for the analysis.

Several researchers have shown that linear and power functions are the two best functions for $g_{1}$ and $g_{2}$ (Mogi 1971; Colmenares and Zoback 2002; Al-Ajmi and Zimmerman 2005; Benz and Schwab 2008). Figure 30 shows the linear and power function regressions obtained between $\tau_{oct}$ and $\left( {\sigma_{1} + \sigma_{3} } \right)$ with the same R² value of 0.99. Mogi’s (1971) failure criterion for the modeled synthetic intact rock material c be given by Eqs. 37 and 38:

Fig. 30

Obtained linear and power regression fits between $\tau_{oct}$ and $\left( {\sigma_{1} + \sigma_{3} } \right)$ for the Mogi (1971) failure criterion (R² value for both linear and power regressions is 0.99)

$$\tau_{oct} = 0.1718\left( {\sigma_{1} + \sigma_{3} } \right) + 1.7478$$

(37)

$$\tau_{oct} = 1.0436\left( {\sigma_{1} + \sigma_{3} } \right)^{0.5276}$$

(38)

Figure 31 shows the obtained Mogi’s (1971) criterion fits along with the true-triaxial data given in Fig. 19 for the linear (Eq. 37) and power (Eq. 38) functions. This criterion fits the data very well with the RMSE values of 0.219 and 0.210 for the linear and power functions, respectively. Because the difference between the RMSE values for the linear and power functions is negligible and use of the linear function is simpler, it is recommended to use the linear function.

Fig. 31

Obtained Mogi (1971) criterion fits and the true-triaxial data given in Fig. 18 for the modeled synthetic intact rock based on the linear (Eq. 37) and power (Eq. 38) functions

In the modified Mogi (1971) criterion (based on Eq. 36), the best $\beta$ value should be found properly. Figure 32 shows the effect of $\beta$ on RMSE for the linear and power functions. The best $\beta$ values for the linear and power functions were found to be 0.04 and 0.01, respectively. Since these values are small, the results of this criterion are almost the same as that of Mogi (1971) criterion based on Eq. 35.

Fig. 32

Relation between $\beta$ and RMSE for the modified Mogi (1971) failure criterion (Eq. 36) based on the linear and power functions

The modified Mogi (1971) failure criterion for the modeled synthetic intact rock material can be given by Eqs. 39 and 40:

$$\tau_{oct} = 0.1681\left( {\sigma_{1} + 0.04\sigma_{2} + \sigma_{3} } \right) + 1.7596$$

(39)

$$\tau_{oct} = 1.0437\left( {\sigma_{1} + 0.01\sigma_{2} + \sigma_{3} } \right)^{0.5267}$$

(40)

Figure 33 shows the obtained modified Mogi (1971) criterion fits (based on Eqs. 39 and 40) along with the true-triaxial data given in Fig. 19. This criterion fits the data very well with the obtained RMSE values of 0.200 and 0.208 for the linear and the power functions, respectively.

Fig. 33

Obtained modified Mogi (1971) criterion fits and the true-triaxial data given in Fig. 18 for the modeled synthetic intact rock based on the linear (Eq. 39) and power (Eq. 40) functions

14 Drucker–Prager criterion

Drucker and Prager introduced their criterion in 1952 as an extended Von Mises criterion and both of those were first developed for soils and considered the intermediate stress as well as the minimum and maximum principle stresses. The Drucker–Prager equation is given by:

$$J_{2}^{1/2} = k + \alpha J_{1}$$

(41)

In Eq. 41, k and $\alpha$ express cohesion and internal friction properties of the intact rock respectively. By setting $\alpha = 0$, this criterion reduces to Von Mises criterion. Drucker–Prager criterion has two forms: (a) Inscribed Drucker–Prager criterion and the (b) Circumscribed Drucker–Prager criterion. The relation between cohesion, internal friction, and k and $\alpha$ for the two types of Drucker–Prager criteria can be expressed through the following equations (Colmenares and Zoback 2002):

$$\alpha_{Ins} = \frac{3\sin \varphi }{{\sqrt {9 + 3\sin^{2} \varphi } }} \quad {\rm and} \quad \alpha_{Cir} = \frac{6\sin \varphi }{{\sqrt 3 \left( {3 - \sin \varphi } \right)}}$$

(42)

$$k_{Ins} = \frac{{3\sigma_{c} \cos \varphi }}{{2\tan \left( {45 + \frac{\varphi }{2}} \right)\sqrt {9 + 3\sin^{2} \varphi } }}\quad {\rm and} \quad k_{Cir} = \frac{{\sqrt 3 \sigma_{c} \cos \varphi }}{{\tan \left( {45 + \frac{\varphi }{2}} \right)(3 - \sin \varphi )}}$$

(43)

Figure 34 shows the relation obtained between $J_{1}$ and $J_{2}^{1/2}$ for the Drucker–Prager failure criterion with R² value of 0.88. Therefore, the Drucker–Prager failure criterion for the synthetic intact rock material can be given by Eq. 44:

Fig. 34

Relation obtained between J ₁ and J ^1/2₂ for the Drucker–Prager failure criterion (R² value is 0.88)

$$J_{2}^{1/2} = 0.3652J_{1} + 2.6377$$

(44)

Figure 35 shows the obtained Drucker–Prager lines along with the true-triaxial data given in Fig. 19. This failure criterion lines significantly deviates from the true-triaxial data. The obtained RMSE value of 0.754 for this criterion shows even a higher error than that obtained for Hoek–Brown and Mohr–Coulomb criteria.

Fig. 35

Obtained Drucker–Prager failure criterion fits along with the true-triaxial data given in Fig. 18 for the synthetic intact rock

15 Comparison between failure criteria

The aforementioned analyses show that the three best strength criteria are the Mogi, Modified Lade and Modified Wiebols and Cook. Among these three strength criteria, the Mogi and Modified Lade criteria have lower RMSE values and the RMSE value obtained for the Modified Wiebols and Cook criterion is about 50 % higher than that of the other two criteria. The Modified Wiebols and Cook criterion slightly underestimates the strength for lower values of $\sigma_{2}$ compared to the Mogi and modified Lade criteria. For higher values of $\sigma_{2}$ the Modified Lade and Modified Wiebols and Cook criteria predict higher strength compared to the Mogi criterion. Figure 36 shows clearly the differences between these three strength criteria.

Fig. 36

Comparison between Mogi, Modified Lade and Modified Wiebols and Cook failure criteria for the modeled synthetic intact rock

Several researchers (Colmenares and Zoback 2002; Benz and Schwab 2008; You 2009) tried to find the best criterion based on the available experimental tests results. Most of these data like for KTB amphibolite, Dunham dolomite, Solenhofen limestone, Westerly granite and Shirahama sandstone did not have any data for the high $\sigma_{2}$ values. Therefore, a possibility exists for this lack of data to influence the strength criteria fitting results. To investigate the effects of this issue on these three failure criteria, regression analyses were performed using only a part of the available PFC^3D modeling data. Just the data available for the lowest three $\sigma_{2}$ values for each $\sigma_{3}$ level was chosen for the new analyses termed as “limited data” analyses. Therefore, only 12 data points out of the available 29 data points were used in the limited data analyses.

The RMSE values obtained for the limited data analyses for the Mogi, Modified Lade and Modified Wiebols and Cook criteria based on the aforementioned 12 data points (n = 12 in Eq. 1) turned out to be 0.13, 0.16 and 0.17, respectively. These RMSE values do not show any meaningful difference among the three criteria. The fittings obtained from the limited data analyses were then used to make predictions for all 29 confining stress combinations. The RMSE values resulted from the latter mentioned analyses based on all 29 data (n = 29 in Eq. 1) turned out to be 0.23, 0.40 and 0.47 for the Mogi, Modified Lade and Modified Wiebols and Cook criteria, respectively. This indicated that the Mogi criterion encountered the least effect in extending the prediction from the limited data analysis to full data analysis. In other words it turned out to be the most stable prediction.

Figures 37, 38, 39 show the differences obtained between the failure criteria fits based on the limited data and the total data analyses for all three failure criteria. As you can see the Mogi criterion shows the lowest changes and it is also clearly indicated through the RMSE values given in the previous paragraph.

Fig. 37

Difference between the total data and the limited data fits for the Modified Wiebols and Cook failure criterion

Fig. 38

Difference between the total data and the limited data fits for the Modified Lade failure criterion

Fig. 39

Difference between the total data and the limited data fits for the Mogi failure criterion

16 Conclusions

This paper emphasized the importance of studying the effects of all micro parameter values on macro properties before one goes through calibration of micro parameters in PFC modeling. Even though the particle size has influence on all macro properties of a sample, very little information is available on that aspect in the PFC literature. Therefore, a systematic study was conducted and the results are reported in this paper. This study clearly illustrated that the Young’s modulus and UCS increase due to increase of the ratio of the sample dimension to minimum particle diameter. In addition, the normal stiffness and shear stiffness changes with the particle diameter. Moreover, the study showed that by scaling up the sample size and particle size in equal proportion and keeping the ratio of the sample dimension to minimum particle diameter constant, it is possible to keep the Young’s modulus constant; however, still the UCS increases under those conditions. This means selection of an appropriate particle size is a challenging task.

Another important micro parameter which has received little attention in the PFC literature is the cov of normal and shear strengths. It is clear that the compressive strength and Young’s modulus of a sample reduce significantly due to the increase of the cov of normal and shear strengths while keeping all other micro parameter values constant. However, it was shown that it is possible to keep the compressive strength and Young’s modulus of a sample constant by changing the other micro parameter values along with increasing the cov of normal and shear strengths. Under these conditions, it was shown that the ductile behavior of the sample increases. Moreover, it was shown that the CBM produces more ductile behavior compared to that of the PBM. Also, it should be mentioned that this paper showed that the $\mu$ does not have a significant effect on the post peak behavior of the modeled sample. However, it was found that $\mu$ highly influences the internal friction angle of the modeled sample.

The true-triaxial test simulation results obtained on synthetic rock indicates that the PFC^3D simulations can model the behavior of rock under true-triaxial stress condition and existing failure criteria can be fitted on these data. Moreover, the PFC^3D can help to achieve more data in a broad range of confining stresses in order to find the best failure criteria.

Among the fitted different intact rock failure criteria on the PFC^3D data, Mogi, modified Lade and modified Wiebols and Cook criteria produced lower errors in fitting the synthetic intact rock strength compared to the other failure criteria. Therefore, those three failure criteria are generally recommended for intact rock strength modeling under the true-triaxial stress condition. Among the Mogi, modified Lade and modified Wiebols and Cook intact rock strength criteria, the first two produced the highest accuracy in fitting the synthetic intact rock strength. Also, it should be mentioned that for lower $\sigma_{2}$ the Mogi criterion predicts higher strength compared to that of the Modified Wiebols and Cook criterion. However, for higher values of $\sigma_{2}$ the Modified Lade and Modified Wiebols and Cook criteria predict higher strength compared to that of the Mogi criterion.