Dry Dual Clutch Torque Model with Temperature and Slip Speed Effects

Abstract

Dry dual clutches are widely used in automated manual transmissions. In such systems the clutch engagement maneuvers require a precise knowledge of the characteristics that relate the frictional torque transmitted by the clutches with the corresponding actuators variables. In this paper a temperature and slip speed dependent model of the torque characteristic for dry dual clutches is proposed. Dynamic models of the temperature evolution are determined and linked to the characteristics of the mechanical components influencing the torque. The models, whose parameters are tuned with dedicated experiments and realistic data coming from an industrial automotive environment, show the temperature influence on the torque transmitted by the clutch. Real time simulation results, obtained through a detailed software in the loop driveline model, show that, if not compensated, the temperature variation can determine critical degradations of the clutch engagement performances. It is shown how the use of the clutch temperature estimation in the torque transmissibility model allows to compensate for such negative effects. The torque model is also exploited for the realization of a decoupling clutch engagement controller. The corresponding closed loop results show the effectiveness of the proposed compensations for the dependencies of the clutch torque on temperature and slip speed.

Introduction

Automated manual transmissions with dry dual clutches are wide spreading thanks to their capability to combine high efficiency and comfort. In order to obtain smooth and fast gearshifts it is fundamental to have an accurate knowledge of the torque transmitted by the clutch during the engagements. Unfortunately, it is quite difficult to provide an on-board measurement of this torque and then the use of torque estimators is the typical solution adopted in practice, for both dry and wet clutches [1, 2]. Several phenomena and components influence the torque in a dry dual clutch transmission (DDCT), such as friction, transmission kinematics [3], friction facing wear and diaphragm spring fatigue [4], pressure [5] and, overall, temperature and slip speed between the clutch disk and the flywheel. Some models proposed in the literature are based on the inversion of the driveline dynamic model [6, 7], but the robustness of this solution depends on the availability of the system parameters and on clutch disk acceleration and engine torque measurements. In any case, the engagement controllers are typically equipped with a characteristic that describes the friction phenomena by providing the torque transmitted by the clutch as a function of the throwout bearing force [8] or the throwout bearing position [3, 9].

The influence of the temperature on the clutch torque characteristic has been considered in the literature. In [10] it is shown how the temperature affects the torque through the variations of the so called Incipient Sliding Point (ISP), also called kiss point. In [11] the authors investigated the temperature distributions in automotive dry clutch during single and repeated engagements under two different hypotheses: uniform pressure and uniform wear. In [12], under the assumptions that the friction coefficient is uniform along the whole contact surface, the clutch torque is assumed to be a function of the product between the friction coefficient and the clamping (or contact) force. In these papers, the temperature influence on the two functions is separately considered: the temperature influence on the friction is modeled by using experimental data from [13] while, in order to model the temperature influence on the contact force, a finite element analysis is used. Indeed, finite element analysis is considered by several authors in order to study the temperature distributions in transmissions which include dry clutches. In [8, 14, 15] it is investigated how the flywheel and friction facings temperature distributions change during the engagement. The friction facings temperature distribution is also dependent on the grooves shape [16], and in [17] it is shown that the thermal proprieties are also affected by some manufacturing process parameters. The temperature distributions are usually assumed to be uniform and average temperatures are considered in order to determine the torque characteristic [12, 13].

Since the clutch torque is only controllable through the proper position of the actuator driven throwout bearing, it is fundamental to have an accurate model of the clutch torque characteristic in order to design effective clutch shift and vehicle launch controllers. This point is highlighted in the literature from different perspectives and strategies dedicated to dry clutches: to improve the actuator technology [18, 19], for torque limitations during the engagements [20], for gearshift [4, 7] and sliding mode controllers [21], for the use of multivariable control strategies [22], for real-time estimation [23] and simulation [24]. The clutch torque characteristic, which relates the actuator position to the transmitted torque, is widely used in the clutch engagement controllers because it can be considered as an add-on solution with respect to the classical engagement controllers currently used for automated manual transmissions and also, as a feedforward component, to solutions which adopts clutch torque observers based on the driveline model [23].

In this paper a new dry clutch torque model which includes the temperature and slip speed influences is presented. In Sect.  2 the typical dry clutch system and its configuration will be recalled. The proposed model of the clutch torque as a function of the actuator position is presented in Sect. 3 and its influence on the slip speed and temperature is explicitly analyzed. In Sect. 4 two dynamic thermal models of the DDCT are determined and linked to the torque characteristic. The thermal models are forced by the power dissipated due to friction. The parameters of the torque and thermal models are tuned by using experimental data. In Sect. 5 a decoupling engagement controller which exploits the proposed torque model is presented. The engagement performances are tested by using a software in the loop real time platform. All results are obtained by considering a realistic DDCT powertrain model by Fiat Chrysler Automobiles (FCA); the quantitative values of the variables reported throughout the paper are not indicated because of confidentiality reasons. The results reported in Sect. 6 demonstrate the effectiveness of the proposed dual clutch torque model to compensate the effects of current temperature and slip speed. Finally, Sect. 7 concludes the paper.

Clutch Engagement System

The two most popular implementations of automatic manual transmissions are single clutch transmissions and dual clutch transmissions. From the clutch management point of view, these two implementations are mostly similar. The modeling procedure proposed in this paper for the torque transmitted by the dry clutch is valid for both the implementations. A typical dry clutch system can be represented with the equivalent scheme provided in Fig. 1 which consists of a flywheel (element 2, it can be a central disk in some DDCT configurations), a steel clutch disk (element 10) and a diaphragm spring (element 5). The diaphragm spring transforms the position $x_{to}$ of the throwout bearing (element 3) into a corresponding position $x_{pp}$ of the pressure plate (also called push plate and numbered 6 in Fig. 1) clamped on the diaphragm spring terminal. The clutch disk consists of a flat spring (also called cushion spring and element 9), two friction facings (elements 7 and 8) and a hub (element 11). The hub rotates at the same speed of the mainshaft (element 4), which is also the clutch disk speed, say $\omega _{c}$. The pressure plate presses the clutch disk against the flywheel or keeps it apart. The pressure plate rotates at the same speed of the flywheel, indicated with $\omega _{f}$, and crankshaft (element 1). The friction between the external facings on the two sides of the clutch disk and the flywheel and pressure plate, respectively, generates the torque transmitted, say $T_{fc}$. In the following, the torques generated by the two clutch facings are assumed to be equal. This assumption must be carefully considered if the temperature distribution is not symmetric.

Fig. 1

A scheme of a dry clutch system when the clutch is open: (1) crankshaft, (2) flywheel or central disk, (3) throwout bearing, (4) mainshaft, (5) diaphragm spring, (6) pressure plate, (7) friction facing on the pressure plate side, (8) friction facing on the flywheel side, (9) flat spring, (10) clutch disk, (11) hub

Some nomenclature on the dry clutch shift operating conditions is introduced below. The clutch is said to be open when there is no contact between the clutch disk and the flywheel (or central disk). In this situation the pressure-plate position is such that the flat spring is not at all compressed, like showed in Fig. 1. The clutch is said to be closed when the flat spring is completely compressed. In this operating condition, the flywheel, the pressure plate and the clutch disk rotate at the same speed. The clutch disk can be pushed furthermore in order to avoid undesired clutch unlocking. The further compression forces the diaphragm spring to flex. In this scenario the maximum torque which can be transmitted by the clutch depends on the static friction coefficient $\mu _{s}$ and on the pressure plate force $F_{pp}$ which corresponds to the diaphragm spring elastic force [3]. A typical expression for the maximum frictional torque for the closed clutch is given as in [3, 9]

$$\begin{aligned} T_{fc}^{\max } =n\mu _s R_{eq} F_{pp} \end{aligned}$$

(1)

where $R_{eq}$ is the equivalent radius of the contact surface and n is the number of contact surfaces which generate the friction torques, assumed equals on both sides.

The clutch is said to be locked up when there is no slip between the flywheel and the clutch disk. In this operating condition, also called sticking phase, the transmitted torque is equal to the engine torque. The flat spring and the diaphragm spring are designed so that during a closing maneuver the clutch will be locked up before the flat spring is completely compressed (clutch closed). The smallest value of $x_{to}$ for which the clutch is locked up depends also on the engine torque.

The clutch is at the ISP, also called kiss point, when there is contact between the clutch disk and the flywheel but the flat spring is still uncompressed. We indicate by $u_{{ fs}}$ the flat spring compression and we assume $u_{{ fs}} = 0$ at the ISP and when the clutch is open.

The clutch is said to be in the engagement phase when it is going from open to locked up. By omitting its dependencies, the torque transmitted in this phase can be expressed as

$$\begin{aligned} T_{{ fc}} = nR_\mu F_{{ fc}} \end{aligned}$$

(2)

where $R_{\mu }$ is the equivalent friction radius and $F_{{ fc}}$ is the flat spring elastic force [3]. The torque dependencies on the slip speed $\omega _{{ fc}}=\omega _{f}-\omega _{c}$, on the flat spring compression $u_{{ fs}}$ and on the clutch temperature will be investigated in the next section.

Torque Characteristic

In this section a temperature and slip speed dependent torque model for dry clutch transmissions is proposed. Starting from measures and physical considerations, the model estimates the clutch torque by considering separately the influence of the slip speed and temperature on the friction coefficient and the influence of the temperature on the normal force determined by the flat spring.

Friction Function and Equivalent Friction Radius

It is well known from the literature that the dry friction function depends on sliding velocity, sliding acceleration, pressure [5] and temperature [13]. In this paper two main effects are considered: the sliding velocity and the temperature dependence. Figure 2 illustrates a possible dependence of the friction versus the linear sliding velocity. It is evaluated in quasi-stationary conditions at average pressure of 0.24 MPa [5].

Fig. 2

Friction coefficient versus sliding velocity at 0.24 MPa with a fixed sliding acceleration value of $0.04\,\hbox {m}/\hbox {s}^{2}$ [5]. The circles represent experimental data; the line is the interpolating function

By neglecting the temperature dependence, a friction function interpolating the data can be written as

$$\begin{aligned} \mu (\rho \omega _{{ fc}} )=\mu _s +(\mu _d -\mu _s )\tanh (\gamma \rho \omega _{{ fc}} )^{1/3} \end{aligned}$$

(3)

where $\mu _{s}$ and $\mu _{d}$ represent the friction values for very low and high sliding velocities; ${\upgamma }$ is a geometric parameter used to reproduce the friction behavior at intermediate velocities; $\omega _{{ fc}}$ is the slip speed defined as the difference between the flywheel speed $\omega _{f}$ and the clutch speed $\omega _{c}$; ${\uprho }$ is the radial coordinate of the clutch facings ($\uprho = 0$ at the center of the clutch disk). The model (3) can be generalized by considering also the friction variation in the relevant temperature range, according to typical facings materials datasheet as in [14]. A representation of such dependence is shown in Fig. 3.

Fig. 3

Friction coefficient versus temperature. The circles represent experimental data; the line is the interpolating function

We assume that the temperature dependence is concentrated on the dynamic friction; then, the model (3) is generalized as follows

$$\begin{aligned} \mu (\rho \omega _{{ fc}} ,\theta _{{ fp}} )=\mu _s +(\mu _d (\theta _{{ fp}} )-\mu _s )\tanh (\gamma \rho \omega _{{ fc}} )^{1/3} \end{aligned}$$

(4)

where $\theta _{{ fp}}$ is the friction facing temperature that is assumed uniform over the whole surface and $\mu _{d}(\theta _{{ fp}})$ is the only parameter assumed to be temperature dependent. The friction temperature dependence at high velocities is expressed as

$$\begin{aligned} \mu _d (\theta _{{ fp}} )=c_1 \sin (c_2 \theta _{{ fp}} +c_3 )+c_4 \end{aligned}$$

(5)

where the coefficients $c_{k }$ have been determined with a least square identification procedure on some (confidential) experimental data and the sinusoidal function takes values only in part of a single period. By considering the dependencies described above, the expression of the equivalent friction radius proposed in [3] and used in (2) can be generalized as follows

$$\begin{aligned} R_\mu (\omega _{{ fc}} ,\theta _{{ fp}} )=\frac{1}{R_2 -R_1 }\mathop {\int }\limits _{R_1 }^{R_2 } {\mu (\rho \omega _{{ fc}} ,} \theta _{{ fp}} )\rho d\rho \end{aligned}$$

(6)

where $R_{1}$ and $R_{2}$ are the inner and outer radii of the clutch disk. The corresponding equivalent friction radius map is reported in Fig. 4.

Fig. 4

Equivalent friction radius map as function of the slip speed $\omega _{{ fc}}$ and friction facing temperature $\theta _{{ fp}}$

Fig. 5

a Flat spring compression $u_{{ fs}}$ versus throwout bearing position $x_{to}$, evaluated at different flat spring temperatures. Darker colors are related to higher temperatures; b Flat spring load $F_{{ fc}}$ measure versus flat spring compression $u_{{ fs}}$. c Flat spring load $F_{{ fc}}(u_{{ fs}}(x_{to}\theta _{{ fs}}))$ obtained by combining the results in b with the ones in a

Flat Spring Compression versus Throwout Bearing Position

One of the key hypotheses of this work is that the clutch torque during the engagement is mainly determined by the flat spring elastic force, which corresponds to consider the normal force pushing the clutch disk against the flywheel equal to the flat spring force [3]. Before the engagement, the throwout bearing position $x_{to}$ is increased thus releasing the diaphragm spring and moving the pressure plate against the clutch disk which is moved towards the flywheel, see Fig. 1. When the ISP is reached, the flat spring starts compressing and its reaction force is in equilibrium with the pressure plate pushing force, under quasi-static assumptions.

The flat spring compression $u_{{ fs}}$ can be modeled as a function of the throwout bearing position $x_{to}$ and flat spring temperature $\theta _{{ fs}}$. Figure 5a shows that, for a given temperature, the flat spring is uncompressed until the ISP is reached.

At the ISP the compression starts and $u_{{ fs}}$ linearly increases until the spring is at its maximum compression level at $x_{to,max}$. The flat spring expansion, due to the temperature increase, implies that the ISP is reached earlier in the pressure plate approaching motion toward the clutch disk and the maximum value of the compression, say $u_{\textit{fs},\textit{max}}$, increases for a given actuator stroke. The function in Fig. 5a can then be expressed as

$$\begin{aligned} u_{{ fs}} (x_{to} ,\theta _{{ fs}} )=sat_0^{u_{\textit{fs},\max } (\theta _{\textit{fs}} )} \left\{ {\lambda (x_{to} -x_{to,ISP} (\theta _{{ fs}} ))} \right\} \end{aligned}$$

(7)

where sat{ $\cdot$ } represents the saturation function with the lower limit 0 and the upper limit $u_{fs,max}$, $\lambda$ is the constant positive slope of the characteristic and the upper limit of the saturation can be expressed as

$$\begin{aligned} u_{fs,\max } (\theta _{{ fs}} )=\lambda (x_{to,\max } -x_{to,ISP} (\theta _{{ fs}} )) \end{aligned}$$

(8)

Coherently with some experimental measures, the ISP is modeled as a quadratic function of the gradient temperature:

$$\begin{aligned} x_{to,ISP} (\theta _{{ fs}} )=\lambda _2 (\theta _{{ fs}} -\theta _a )^{2}+\lambda _1 (\theta _{{ fs}} -\theta _a )+\lambda _0 \end{aligned}$$

(9)

where $\theta _{a}$ is the room temperature. The slope $\lambda$ of $u_{{ fs}}$ with respect to $x_{to}$ is unaffected by the temperature because it is determined by the diaphragm spring characteristic that is assumed to be temperature independent. The flat spring stiffness is assumed to be unaffected by the temperature too [12]. Later in this section it will be explained how the parameters $\lambda$, $\lambda _{k}$, $k=0, 1, 2$, and $x_{to,max}$ have been identified. In Fig. 5b the flat spring load versus its compression is reported. The line represents the following interpolating model from experimental data:

$$\begin{aligned} F_{{ fc}} (u_{{ fs}} )=p_3 u_{{ fs}}^3 +p_2 u_{{ fs}}^2 +p_1 u_{{ fs}} \end{aligned}$$

(10)

where the parameters $p_{k}$, k = 1, 2, 3, are obtained by means of a least squares identification procedure. By combining (7)–(10) the map of the flat spring load $F_{{ fc}}(u_{{ fs}}(x_{to},\theta _{{ fs}}))$ shown in Fig. 5c is obtained.

Fig. 6

Three partial clutch engagements. In solid black it is reported the throwout bearing position $x_{to }$ versus time, the measured torque versus time, in light gray, and the modeled torques versus time according to (11), in gray, and (13), in dashed black. Central disk temperature: a 20 $^{\circ }$C, b 144 $^{\circ }$C, c 243 $^{\circ }$C

Torque Characteristic

The torque transmitted by a single clutch is the sum of the friction torques acting on the two sides of the clutch disk. By considering the expression (2), the transmitted torque by a single clutch can be expressed as

$$\begin{aligned}&T_{{ fc}} (x_{to,} \omega _{{ fc}} ,\theta _{fp1} ,\theta _{fp2} ,\theta _{{ fs}} )\nonumber \\&\quad =[R_\mu (\omega _{fc,} \theta _{fp1})\nonumber \\&\qquad +R_\mu (\omega _{fc,} \theta _{fp2} )]F_{{ fc}} (u_{{ fs}} (x_{to} ,\theta _{{ fs}} )) \end{aligned}$$

(11)

where $\theta _{fp1}$ and $\theta _{fp2}$ are the two friction facings temperatures, the equivalent radii are given by (6) with (4)–(5) and the flat spring force is expressed by means of (10) with (7)–(9). In order to simplify the temperatures dependencies in (11) we assume that the average between the friction facings temperatures, which we call clutch temperature

$$\begin{aligned} \theta _c =\frac{\theta _{\textit{fp}1} +\theta _{\textit{fp}2} }{2} \end{aligned}$$

(12)

is the main equivalent temperature variable which influences the torque transmitted by the clutch. This hypothesis has been validated by using dedicated clutch engagement experiments, also for different dissipated powers. Under this hypothesis, the model (11) can be rewritten as

$$\begin{aligned} T_{{ fc}} (x_{to,} \omega _{{ fc}} ,\theta _c )=2R_\mu (\omega _{fc,} \theta _c )F_{{ fc}} (u_{{ fs}} (x_{to} ,\theta _c )) \end{aligned}$$

(13)

where $R_{\mu }(\omega _{{ fc}},\theta _{c})$ and $F_{{ fc}}(u_{{ fs}}(x_{to}\omega _{c}))$ are given by (3)–(6) and (7)–(10) with $\theta _{{ fs}}=\theta _{c}$, respectively. The parameters of the model (13) are the coefficients $\lambda _{k}$, $k=0$, 1, 2, of (9) and the values of $x_{to,ISP}$ and $x_{to,max}$. In order to get an estimation of these parameters, an experimental measurement setup has been applied on a real DDCT transmission adopted in FCA. The throwout bearing position, the pressure plates and central disk temperatures have been directly measured. For the identification and then the validation of the unknown parameters, two sets of data have been collected. Both sets are made of several partial engagements: each engagement is driven by the same $x_{to}$ signal but, due to the increase of the temperature, the ISP changes and higher torque values are obtained. Each set has its own periodic $x_{to}$ signal. The parameter $\lambda _{0}$ in (9) has been chosen in order to match the model with the measured value at the first partial engagement which occurs at room temperature. The parameter $x_{to,max}$ corresponding to the fully compressed flat spring is chosen by using the torque values of the first partial engagement.

The coefficients $\lambda _{1}$ and $\lambda _{2}$ in (9) have been identified by using a genetic algorithm applied to the whole acquisition and by minimizing the error between the measured torque and the estimated one.

Figure 6 shows the validation of the proposed models. This figure reports the measured torque and the torques obtained with the models (11) and (13) in light grey and grey, respectively, along with the corresponding values of the throwout bearing position $x_{to}$ in solid black. The graphs have been extracted from a series of fifty partial engagement maneuvers repeated with the same throwout bearing motion, i.e., $x_{to}$ versus time. The temperature rise due to the sliding of the clutch determines huge differences in the clutch torque.

The following table shows in normalized scales the differences between measured and estimated clutch torque through the models (11) and (13), according to repeated maneuvers as in Fig. 6 (Table 1).

Table 1 Comparison between measured and modeled clutch torques according to (11) and (13).

Fig. 7

Torque map. a Torque (Nm) versus $x_{to}$ (mm) and $\omega _{{ fc}}$ (rad/s) parametrized respect to $\theta _{c}$; darker colors stand for higher temperatures. b Torque versus $x_{to}$ and $\theta _{c}$ ($^{\circ }\hbox {C}$) parametrized respect to $\omega _{{ fc}}$; darker colors stand for higher slip speeds

The table confirms the good capability of the model to reproduce the real thermal phenomenon. In particular the models show high accuracy from the room temperature to about $140\,^{\circ }\hbox {C}$, according to the good match between the measured torque and the modeled ones in Fig. 6a and b. Above that temperature (Fig. 6c), the measured torques and the modeled ones are still comparable, but the accuracy reduces and it seems there is even a qualitative change in the shape of the measured torque. It’s not clear the reason of this effect which might be due to the pressure effect on the friction material or to the change in the slope of the flat spring characteristic, which in the proposed model it is not considered being temperature dependent, but that it is reasonable to assume as temperature influenced too [9, 12].

A further relevant result of the validation process is the agreement between the simplified model (13) and the more general torque model (11). This is an outcome of the compensating average effect between the two friction torques acting on the two sides of the clutch disk. This result justifies the choice to adopt the torque model (13) in the clutch engagement controller since it is simpler and it allows the use of simplified transmission thermal models with only one temperature variable for each clutch.

Figure 7a shows the map of (13) as a function of the throwout bearing position and of the slip speed for some values of the clutch disk temperature. Figure 7b shows the torque as a function of the clutch disk temperature and of the throwout bearing position for some values of the slip speed. These figures show that, for a fixed value of the throwout bearing position and of the slip speed, when the temperature increases the corresponding friction torque can change significantly and it is possible to have torque values that are twice the expected ones if the temperature is not considered. Besides, for high temperatures, the clutch system starts to transmit torque for values of the throwout bearing position for which, at room temperature, the clutch is still open. The considerations above clearly highlight the importance of considering the temperature dependence in the dry clutch torque characteristic. In Sect. 6 it will be shown the importance of considering the temperature and slip speed effects on the torque also from the controller design point of view.

Dual Clutch Thermal Models

As shown in the previous section, the temperature has a strong influence on the torque transmitted by the dry clutch. Therefore, in order to obtain a good torque estimation, it is crucial to know the clutch disk temperature. Due to technical limitations and high costs it is very difficult to develop a measurement system for an online monitoring of the clutch temperatures. To overcome this drawback, in this section two different DDCT thermal models are proposed.

Dynamic Thermal Models

The thermal evolution of a dry dual clutch transmission is a very complex phenomenon and a lot of elements are involved in it, see Fig. 8. The thermal models of DDCT presented below are designed to ensure low computational load without compromising too much the capability of reproducing the system behavior. Both models are introduced through ordinary differential equations and, according to the results in Sect. 3, only one differential equation for the temperature of each clutch is used.

Fig. 8

Schematic representation of a dry dual clutch transmission. (1) Flywheel; (2), (6) pressure plates; (3), (5) clutches formed by two friction facings and a flat spring; (4) central disk; (7) housing

The first model adopts five state variables, one for each element of the scheme reported in Fig. 8: the temperatures of the two pressure plates (the elements 2 and 6 in Fig. 8), say $\theta _{pp1}$ and $\theta _{pp2}$, the temperatures of the two clutch disks (the elements 3 and 5 in Fig. 8), say $\theta _{c1}$ and $\theta _{c2}$, and the temperature of the central disk (the element 4 in Fig. 8), say $\theta _{cd}$. The air temperature in the housing (element 7 in Fig. 8), say $\theta _{h}$, is assumed to be measurable and then considered as an input for the model. For each clutch we consider two different modes which are discriminated by a corresponding logic variable: we set $\beta _{i}=0$ with $i=1,2$, if the i-th clutch is open, i.e., when the clutch disk has no contact with the other elements of the scheme in Fig. 7, and $\beta _{i}=1$ with $i=1,2$, if the i-th clutch is not open in the sense that it is in contact with the adjacent plates either in slipping operating conditions or locked up. When the first clutch is open ($\beta _{1}=0$), the variations of the temperature of the first pressure plate are determined by a convective heat transfer with the air in the housing and the corresponding dynamic equation can be written as

$$\begin{aligned} \dot{\theta }_{pp1} =\alpha _2 (\theta _h -\theta _{pp1} ). \end{aligned}$$

(14)

When the first clutch is not open ($\beta _{1}=1$), the convective exchange with the air in the housing can be neglected because there exist two more relevant contributions for the pressure plate temperature dynamics: the conductive heat exchange with the clutch disk and the heat generation during the clutch engagement due to the friction power losses $T_{fc,1} \omega _{fc,1}$. The corresponding dynamic equation can be written as

$$\begin{aligned} \dot{\theta }_{pp1} =\alpha _1 (\theta _{c1} -\theta _{pp1} )+\alpha _3 T_{\textit{fc}1} \omega _{\textit{fc}1} . \end{aligned}$$

(15)

By combining (14) and (15) one can write

$$\begin{aligned} \dot{\theta }_{pp1} =\alpha _1 \beta _1 (\theta _{c1} -\theta _{pp1} )\,+\,\alpha _2 (1-\beta _1 )(\theta _h -\theta _{pp1} )\,+\,\alpha _3 T_{\textit{fc}1} \omega _{\textit{fc}1} . \end{aligned}$$

(16a)

Note that the friction power losses in the right hand side of (16a) are not required to be multiplied by $\beta _{1}$ because when the clutch is open ($\beta _{1}=0$) the torque transmitted by the clutch is zero. By using analogous arguments and by assuming the symmetry of the structure, the dynamic equation of the temperature of the second pressure plate can be written as

$$\begin{aligned} \dot{\theta }_{pp2} =\alpha _1 \beta _2 (\theta _{c2} -\theta _{pp2} )+\alpha _2 (1-\beta _2 )(\theta _h -\theta _{pp2} )+\alpha _3 T_{\textit{fc}2} \omega _{\textit{fc}2} . \end{aligned}$$

(16b)

The temperature of each clutch disk changes due to the convective flux with the air of the housing (when the clutch is open) and due to the conductive flux with the pressure plate and the central disk together with the heat generation due to the friction. Therefore the dynamic equation of the temperatures of the clutch disks can be written as

$$\begin{aligned} \dot{\theta }_{c1}= & {} \alpha _4 \beta _1 (\theta _{pp1} -\theta _{c1} )+\alpha _5 \beta _1 (\theta _{cd} -\theta _{c1} )\nonumber \\&+\,\alpha _6 (1-\beta _1 )(\theta _h -\theta _{c1})\,+\,\alpha _7T_{\textit{fc}1} \omega _{\textit{fc}1} , \end{aligned}$$

(16c)

$$\begin{aligned} \dot{\theta }_{c2}= & {} \alpha _4 \beta _2 (\theta _{pp2} -\theta _{c2} )+\alpha _5 \beta _2 (\theta _{cd} -\theta _{c2} )\nonumber \\&+\,\alpha _6 (1-\beta _2 )(\theta _h -\theta _{c2})\,+\,\alpha _7T_{\textit{fc}2} \omega _{\textit{fc}2} . \end{aligned}$$

(16d)

The equation of the dynamic model which describes the evolution of the central disk temperature can be obtained by combining the phenomena described above, which leads to the following expression

$$\begin{aligned} \dot{\theta }_{cd}= & {} -\alpha _5 \beta _1 (\theta _{c1} -\theta _{cd} )-\alpha _5 \beta _2 (\theta _{c2} -\theta _{cd} )\nonumber \\&\,+\,\alpha _8 (2-\beta _1 -\beta _2 )(\theta _h -\theta _{cd} )\nonumber \\&\,+\,\alpha _9 (T_{\textit{fc}1} \omega _{\textit{fc}1} +T_{\textit{fc}2} \omega _{\textit{fc}2} ). \end{aligned}$$

(16e)

The first two terms in the right hand side of (16e) are the correspondent to the conductive heat terms in (16c) and (16d), respectively. The third term represents the convective heat transfer with the air in the housing which for the central disk depends on the combinations of the modes of the two clutches, i.e., it is zero if the two clutches are both not open ($\beta _{1}=1$ and $\beta _{2}=1$). The forth term is due to the heat generation of the friction power losses of the two clutches.

A simplified version of the thermal model (16) can be obtained by assuming that the two pressure plates and the central disk are at the same uniform temperature. Consequently the three elements can be considered as a single thermal mass called body [25]. Under this hypothesis a single differential equation can be used to model the body temperature, say $\theta _{b}$. The above assumption is commonly applied to the thermal models of single clutch transmissions and so the proposed model can be also considered an extension of the model in [10].

By using the conditions $\theta _{pp1}=\theta _{pp2}=\theta _{cd}=\theta _{b}$ in (16) the simplified thermal model can be written as

$$\begin{aligned} \dot{\theta }_{c1}= & {} \tilde{\alpha }_1 \beta _1 (\theta _b -\theta _{c1} )+\tilde{\alpha }_2 (1-\beta _1 )(\theta _h -\theta _{c1} )+\tilde{\alpha }_3 T_{\textit{fc}1} \omega _{\textit{fc}1}\nonumber \\ \end{aligned}$$

(17a)

$$\begin{aligned} \dot{\theta }_{c2}= & {} \tilde{\alpha }_1 \beta _2(\theta _b -\theta _{c2} )+\tilde{\alpha }_2 (1-\beta _2 ) (\theta _h -\theta _{c2} )+\tilde{\alpha }_3 T_{\textit{fc}2} \omega _{\textit{fc}2}\nonumber \\ \end{aligned}$$

(17b)

$$\begin{aligned} \dot{\theta }_b= & {} -\tilde{\alpha }_1 \beta _1 (\theta _{c1} -\theta _b )-\tilde{\alpha }_1 \beta _2 (\theta _{c2} -\theta _b )\nonumber \\&\,+\,\tilde{\alpha }_4 (2-\beta _1 -\beta _2 )(\theta _h -\theta _b )+\tilde{\alpha }_3 (T_{\textit{fc}1} \omega _{\textit{fc}1} +T_{\textit{fc}2} \omega _{\textit{fc}2} )\nonumber \\ \end{aligned}$$

(17c)

where (17a) and (17b) are obtained from direct substitution in (16c) and (16d), respectively, and (17c) is obtained by adding (16a), (16b) and (16e) and by introducing a new notation for the model constants with respect to (16) because of the simplifying assumption introduced.

Parameters Tuning

The data used for the identification and the validation of (16) and (17) have been achieved by means of a temperature acquiring system in the framework of the experiments described in Sect. 3.3. For the simplified model (17), the body temperature is considered equal to the average of the two pressure plates and the central disk temperatures.

The parameters corresponding to the convective terms of the two models have been obtained by formulating corresponding least squares problems. These problems use a data-set obtained by bringing the clutch at high operating temperatures and then by leaving the temperature to decrease with a free evolution and by analyzing the transmission thermal behavior with both clutches open. Because of the symmetry of the dry dual clutch system, the data used for the convective heat transfer parameters identifications, which correspond to the even gearbox ratios, are used also for the odd ratios. The other model parameters are obtained by using a genetic algorithm applied to a second data-set, which is the same set used for the parameterization of the torque models. A third data-set is used to validate the parameters. The validation results are shown in Figs. 9 and 10. In particular the body temperature reported in Fig. 10 is obtained by averaging the measured temperatures of the pressure plates and central disk.

Fig. 9

Fifth order model validation. The figure reports: the measured (+) and estimated ($\diamondsuit )$ odd pressure plate temperature; the measured ($\bullet$) and estimated ($\triangledown )$ central disk temperature; the measured air housing temperature ($\square )$; the dotted line is the estimated odd clutch disk temperature

Fig. 10

Third order model validation. The figure reports: the measured ($\bullet$) and estimated ($\triangledown )$ body temperature; the measured air housing temperature ($\square$); the dotted line is the estimated odd clutch disk temperature

These figures show a good capability of the two models to reproduce the real system behavior. The model (16) has a slight different behavior compared to the real system, in the open clutch state (the second part of the acquisition shown in the figures). This can be explained with an unsymmetrical thermal behavior of the real system or it could be due to the larger number of model parameters of (16) compared to those of (17) that it seems unaffected by the problem. A third cause could be the influence of the conductive flux between the clutches and their support. A further result is that for both models the variation of the clutch temperature increases at higher temperatures, which is justified by the corresponding larger torques predicted by the proposed clutch torque model.

Fig. 11

Dual clutch driveline model

Clutch Engagement Controller

In this section a clutch engagement controller is presented. The controller is designed by using a driveline model which includes the clutch torque model described above and implemented in a software in the loop (SIL) DDCT model which is tuned by considering a Fiat 500L 1.4MAir equipped with Fiat DDCT635 transmission. This control scheme allowed the real-time tests as described in the next section. Since the main purpose of this paper is to demonstrate the importance of taking into account the temperature and slip speed effects in the clutch torque modeling, no additional theoretical contribution on the clutch control is given by this paper. Further details on the controller are reported in [22] whereas comments on the future developments of the proposed scheme are provided at the end of this chapter.

Driveline Model

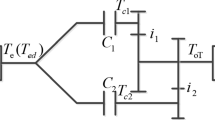
An equivalent scheme for the dynamic driveline model with DDCT is shown in Fig. 11. The scheme includes an engine, a dry dual clutch, a gearbox and a final reducer, as well as equivalent inertias modeling wheels and vehicle.

The engine torque $T_{e}$ is considered as an input for the model and it is obtained by means of a static map depending on the throttle angle and on the engine speed $\omega _{e}$. According to the equivalent scheme reported in Fig. 11, the time evolution of the engine crankshaft speed and the one of the flywheel should be regulated by two different dynamic equations but, by assuming a rigid mainshaft, they will be modeled with a single dynamic equation.

The driveline mechanical equations consist of the following forth order system as extension to dual-clutch transmissions of the models in [6, 9]

$$\begin{aligned} J_{eq} \dot{\omega }_f= & {} T_e -T_{{ fc}1} -T_{fc2} \end{aligned}$$

(18a)

$$\begin{aligned} J_{c1} \dot{\omega }_{c1}= & {} T_{{ fc}1} -T_{godd} \end{aligned}$$

(18b)

$$\begin{aligned} J_{c2} \dot{\omega }_{c2}= & {} T_{{ fc}2} -T_{geven} \end{aligned}$$

(18c)

$$\begin{aligned} J_d \dot{\omega }_{out}= & {} i_{godd} i_f T_{godd} +i_{geven} i_f T_{geven} -T_{Load} \end{aligned}$$

(18d)

where $\omega _{f}$ is the flywheel speed and, by assuming the mainshaft rigidity, it is equal to the engine speed $\omega _{e}$ and mainshaft speed $\omega _{in}$, see Fig. 11; $\omega _{c1}$ and $\omega _{c2}$ are the clutches speeds; $\omega _{out}$ is the output shaft speed and it is equal to the wheels speed (a rigid output shaft is assumed); the inertias are given by $J_{eq}=J_{e}+J_{m}$ and $J_{d}=J_{out}+J_{w}+i_{f}^{2}\, (J_{odd}+J_{even})$ where $J_{w}$ is the equivalent vehicle inertia; $i_{f}, i_{godd}$ and $i_{geven}$ are the output and the transmission gear ratios; $T_{fc1}$ and $T_{fc2}$ are two instances of (13); $T_{Load}$ is the torque resistance acting on the wheels and is a function of the wheel speed, according to the relation

$$\begin{aligned} T_{Load} =f_0 +f_1 v+f_2 v^{2} \end{aligned}$$

(19)

where $v = R_{w}\omega _{out}$, $R_{w}$ is the wheel radius, $f_{0}$, $f_{1}$ and $f_{2}$ are appropriate coefficients.

The slip speeds are obtained according to the algebraic equations linking $\omega _{c1}$ and $\omega _{c2}$ to $\omega _{out}$ (Fig. 11) as follows

$$\begin{aligned} \omega _{{ fc}1}= & {} \omega _f -\omega _{c1} =\omega _f -i_{godd} i_f \omega _{{ out}} \end{aligned}$$

(20a)

$$\begin{aligned} \omega _{{ fc}2}= & {} \omega _f-\omega _{c2} =\omega _f -i_{geven} i_f \omega _{{ out}}. \end{aligned}$$

(20b)

The gear ratios $i_{godd}$ and $i_{geven}$ are the output of the gear shifting mechanism model. The gear actuation model consists of four distinct double action pistons operating the gear engagement forks, and one shifter spool which selects the piston to be actuated. Three flow proportional valves drive these elements as explained in [22].

By substituting $\omega _{c1} =i_{godd} i_f \omega _{out}$ and $\omega _{c2} =i_{geven} i_f \omega _{out}$ in (18b)–(18c) and by multiplying both sides of the two equations by $i_{godd}i_{f}$ and $i_{godd}i_{f,}$ respectively, one obtains

$$\begin{aligned} (i_{godd} i_f )^{2}J_{c1} \dot{\omega }_{out}= & {} i_{godd} i_f T_{fc1} -i_{godd} i_f T_{godd} \end{aligned}$$

(21a)

$$\begin{aligned} (i_{geven} i_f )^{2}J_{c2}\dot{\omega }_{out}= & {} i_{geven} i_f T_{fc2} -i_{geven} i_f T_{geven.} \end{aligned}$$

(21b)

By adding (21a), (21b) and (18d) the entire driveline model can be rewritten as the following second order system

$$\begin{aligned}&J_{eq} \dot{\omega }_f =T_e -T_{fc1} -T_{fc2}\end{aligned}$$

(22a)

$$\begin{aligned}&J_{eq2} \dot{\omega }_{out} =i_{godd} i_f T_{fc1} +i_{geven} i_f T_{fc2} -T_{Load} \end{aligned}$$

(22b)

with $J_{eq2} =(i_{godd} i_f )^{2}J_{c1} +(i_{geven} i_f )^{2}J_{c2} +J_d$ . The simplified driveline model (22) will be used in next section for the controller design. Instead, in the SIL platform adopted for the numerical simulations it is implemented the more general driveline model given by (18) with two instances of (13) and the thermal model (16). The SIL structure is an evolution of the model proposed in [22] which is now capable to reproduce also the temperature influence on the transmitted torque. The SIL model will be also used to perform real time test on the closed loop DDCT controlled by a real traction control unit and it includes the subsystems models required to manage several variable such as: the car key status, the accelerator pedal position, the gear lever position, the clutch actuators and the gearbox driving currents and other control signals monitored by the transmission control unit. Further details on the SIL model are reported in [22]. In Fig. 12 it is shown a comparison between the vehicle velocity obtained with the proposed model and that achieved by a real Fiat 500L with DDCT on a roller test bench. The test considers different accelerator pedal positions with the third gear engaged.

Fig. 12

Vehicle velocity comparison between a real vehicle on a roller bench (gray) and the parametrized model (black) with the third gear engaged and for different accelerator pedal steps from 5 to 20 %

No gearshift is reported because a real transmission control unit model is not available and so a comparison during a gearshift would not be fair because the modeled control unit does not encompass such maneuvers. By the way, this comparison is useful to show the capability of the whole powertrain model to reproduce the real vehicle behavior in the limits of no gearshift occurrence.

Decoupling Controller

The proposed clutch engagement controller is capable to perform different maneuvers by regulating the gears selection through pressure controlled valve models. The main difference between the proposed controller and the ones proposed in [4, 22] is the subsystem in the clutch engagement control loop.

The control scheme for the engagement of the first clutch is shown in Fig. 13 (an analogous scheme can be constructed for the second clutch). The inputs of the controller are the engine and first clutch speeds, which are compared with their corresponding reference values, and the reference torque coming from the controller of the second clutch. Note that it is also considered the scenario when, during the engagement of the first clutch, the second clutch is in the disengagement phase, which is typically controlled in open loop. The outputs of the controller are the throwout bearing position reference signal $x_{to1}^{ref}$ of the first clutch and the reference engine torque which is the input for the engine control unit. The actuators controllers and the engine control unit which connect the scheme in Fig. 13 with the driveline, are not reported.

Fig. 13

Decoupling control scheme for the engagement of the odd clutch in a DDCT

The Proportional Integral (PI) controllers in the scheme in Fig. 13 are designed based on the model (22) specified for the particular engagement under consideration. Let us assume that an engine speed control is implemented. Then, for the design of the corresponding PI$_{\mathrm{e}}$ controller, one can consider (22a) rewritten in the following form

(23)

with

(24)

The engine speed controller can be designed based on the single integrator model (23) by considering as the control input and then by obtaining the reference engine torque by inverting (24) and by using the reference torques coming from the clutches control. In the case that, during the clutch engagement, the reference engine torque is directly generated by the engine control unit based on the driver request, the controller PI$_{\mathrm{e}}$ is not required.

A relevant section of the clutches engagement scheme consists of the control loops on the clutch speeds, which for the first clutch involves the controller PI$_{\mathrm{c}}$ reported in Fig. 13. In order to design the parameters of PI$_{\mathrm{c}}$, the dynamic equation (22b) can be rewritten by substituting $\omega _{out} =\omega _{c1} /i_{godd} i_f$, which leads to

(25)

with

(26)

By solving (26) for the torque transmitted by the first clutch we obtain

(27)

The controller for the first clutch engagement is designed based on the single integrator model (25) by considering as the control input. The parameters of the PI controller can be designed based on the required specifications. Moreover, thanks to the left half plane zero in the controller transfer function, the stability of the closed loop system is ensured for any positive feedback gain, so as it can be easily verified by using the root locus technique. Then, in order to obtain the reference signal for the clutch torque, we can use the decoupling part of the controller which is based on (27). Finally, the throwout bearing reference position for the first clutch is obtained by inverting the torque transmissibility characteristic (13), by using the estimated temperature of the clutch and the slip speed. Note that during the engagement of the first clutch the second one is open or it is controlled in open loop for the opening phase, thus not affecting the stability of the closed loop system. The stability of the closed loop system is then ensured at the design phase by using the driveline model and the robustness of the proposed solution is tested under real experiments, so as it will be shown in next section.

Future Developments of the Controller

As explained with Fig. 13, the inversion of the clutch torque characteristic allows determining the reference value for the actuator position which drives the throwout bearing of the clutch. The torque model inversion, which is used in most clutch engagement control schemes, can be also integrated with a disturbance observer as clutch torque estimator, so as the one proposed in [23]. In this way, the output of the torque inversion could act as feedforward contribution to the reference actuator position, whereas the feedback component comes from a controller on the error between the reference torque and the torque estimated by a disturbance observer.

Anyway, the solution proposed in this paper allows clear advantages even in presence of a disturbance observer. First the nonlinearities of the clutch torque transmission are ideally cancelled by the inversion of the characteristic and compensated for temperature and slip speed dependencies; in the latter sense, this approach can be seen as belonging to the class of global linearization techniques. Second, if a closed loop on the clutch torque is used with a disturbance observer, the inversion of the clutch torque characteristic results in a feedforward contribution and it enables simpler tuning of the torque controller parameters.

Fig. 14

Difference between reference and applied torque during the clutch engagement for different slip speed values and for high (gray) and low (black) accelerator pedal values when the slip speed dependence of the friction material is not considered in the controller

The detailed analysis of the performance attainable by way of such an improved control scheme which considers both the inversion of the clutch torque characteristic and the disturbance observer, is out of the scope for this paper and it is considered as a direction for future research.

Real Time Tests

In the previous sections a powertrain model and the relative controller have been introduced. The model is capable to reproduce several gearshift maneuvers but, for our purposes, only the (most critical) start-up or launch maneuver will be investigated. In this section, it will be shown the crucial role of the thermal and slip speed dependencies on the clutch torque. The two effects will be analyzed separately, i.e., if the slip speed dependence is investigated then ideal temperature compensation is assumed, and vice versa.

The real time tests are obtained by using the SIL model implemented by means of dSpace VeOS for the real time simulation of the driveline model, and dSpace ControlDesk for the data acquisition. In Fig. 14 the difference between the desired torque and the measured one without the compensation of the slip speed effects, is reported. At high slip speeds the error is very small whereas, when the slip speed decreases the discrepancy increases because the feedforward action assumes a constant friction coefficient (whereas it is actually decreasing for lower speeds, see Fig. 2) and the feedback action does not satisfactorily compensate for this decrease. Figure 14 shows also that the errors increase for higher values of the accelerator pedal, which is coherent with the request of higher torques in the clutch engagement operation.

In Fig. 15 it is reported the difference between the reference and the applied torques in the two scenarios corresponding to compensation and not. The plant model includes (18), while the controller is designed based on (22). It is clear that, if the temperature influence is not compensated, large errors in the torque estimation eventually occur. This error is higher when the engagement starts, at high slip speeds, because the feedback action needs some time in order to produce its effects, and it is lower at the end of the engagement, when the feedback partially compensates the overestimation (the figure reports negative values). In the figure it is also reported the compensated scenario. The error is still present due to the different models adopted as plant and in the controller, but it is much less.

By looking at the difference between the reference and applied torques, the temperature and the slip speed have both a strong impact on the transmitted torque and the feedback controllers are not capable to instantaneously and perfectly compensate these effects. Now it will be investigated the influence of these phenomena on the overall system. At this aim, the capability of the system to track the reference signals and the resulting vehicle acceleration are considered.

Fig. 15

Difference between reference and actual clutch torque versus sliding speed in decreasing trend during the clutch engagement. Low (light gray), medium (dark gray) and high temperatures (black) with no compensation of the temperature influence. The dashed line is associated to a compensated scenario

Fig. 16 shows the flywheel and odd clutch speeds during a repeated launch maneuver. The results confirm that the proposed controller is able to compensate for the slip speed influence on the torque characteristic and then the desired speed profiles can be obtained.

Fig. 16

Flywheel (starting from 80 rad/s) and clutch speeds versus time. In gray it is reported the (ideal) maneuver with no slip speed influence on the clutch torque; the dashed line represents the same maneuver with closed loop compensation in the controller in the presence of the slip speed influence

In Figs. 17 and 18 three clutch engagement maneuvers at three different temperatures are reported. The dashed curves show the fully compensated scenario. The first figure reports the flywheel and the odd clutch speeds behavior, while the second figure reports the vehicle acceleration.

Fig. 17 shows that if the torque temperature influence is disregarded in the control, the flywheel and clutch speeds start diverging from the ideal behavior (dashed curves) when the temperature increases. The temperature levels, low, medium and high are referred to the discussion in Sect. 3.3.

Fig. 17

Flywheel (starting from 80 rad/s) and clutch speeds versus time during three launch maneuvers at low (light gray), medium (dark gray) and high (magenta) temperatures without temperature compensation. Dashed line represents the compensated scenario

Fig. 18

Vehicle acceleration versus time during three launch maneuvers at low (light gray), medium (dark gray) and high (black) temperatures without temperature compensation; the dashed lines represent the compensated scenario

Analogously the accelerations reported in Fig. 18 show that, when the temperature increases, a spike appears in the first part of the vehicle acceleration and its amplitude increases with the temperature.

It is interesting to note that after the initial spike, the three accelerations tend to converge in the central part of the figure. This happens because the feedback controller is able to compensate for the uncertainties in the torque estimation until a new fast change occurs. Indeed, in the last engagement the three solutions become more temperature sensitive again. The dashed line in Fig. 17 shows that the spikes disappear when the temperature compensation is adopted, thus confirming that the inclusion of the temperature dependence on the torque estimation allows to improve the closed loop engagement performances.

Conclusions

A transmitted torque model for dry dual clutches has been proposed. The model, whose parameters are tuned with dedicated experiments and realistic data coming from the automotive industry, shows how the temperature and the slip speed influence the torque transmitted by the clutch. Real time simulation results, obtained with a detailed software in the loop model, show that, if not compensated, the temperature increase can determine critical degradations of the clutch engagement performances. The clutch temperature estimation, obtained with a thermal dynamic model of the dry dual clutch transmission, allows to compensate for the temperature effects in the torque characteristic. The inversion of the characteristic provides a global linearization of the nonlinearities due to the clutch torque transmission and the torque model is exploited for the design of a decoupling clutch engagement controller. The corresponding closed loop results show the effectiveness of the proposed compensations for the dependencies of the clutch torque on temperature and slip speed. A direction for future research is the analysis of a closed loop scheme where the inversion of the torque characteristic is combined with a disturbance observer which implements a feedback control on the clutch torque and a load torque estimation.