Introduction

Control of underactuated robots has received significant attention. The design of robotic mechanisms that can be controlled with a smaller number of actuators than their degrees of freedom enables to reduce cost and weight of robots and to succeed robustness in the case of actuators’ failures. The control problem of underactuated robotic manipulators has been studied in several research articles during the last years [1–10]. In [1] the property of differential flatness for a class of planar under-actuated open-chain robots having a specific inertia distribution, but driven by only one or two actuators has been analyzed. In [3] it was shown that closed chain underactuated robots satisfy differential flatness properties and this enables their transformation into a linearized form for which the design of a feedback controller becomes easier. In [4] energy-based control for underactuated robotic manipulators has been proposed. In [5, 6] a Lyapunov-based approach to the design of efficient control for underactuated robots is proposed. In [7] passive velocity field control and decoupling vector field has been applied to the control of underactuated mechanical systems. In [8] the problem of point-to-point control for underactuated robotic manipulators has been presented. In [9] an adaptive neuro-fuzzy inference system is proposed for estimating contact forces in underactuated robotic grippers. In [10] an open loop vibrational control for an underactuated mechanical system has been studied.

Flatness-based control is currently a main direction in the design of nonlinear control systems [11–13]. The paper proposes flatness-based adaptive fuzzy control for nonlinear dynamical systems with unknown parameters. To find out if a dynamical system is differentially flat, the following should be examined: (i) the existence of the so-called flat output, i.e., a new variable which is expressed as a function of the system’s state variables. It should hold that the flat output and its derivatives should not be coupled in the form of an ordinary differential equation (ODE), (ii) the components of the system (i.e., state variables and control input) should be expressed as functions of the flat output and its derivatives [14–22]. Differential flatness is a property characterizing classes of systems. By expressing all system variables as functions of the flat output and its derivatives enables transformation to a linearized form for which the design of the controller becomes easier. By showing that a system is differentially flat one can easily design a reference trajectory as a function of the so-called flat output and find a control law that assures tracking of this desirable trajectory [15, 17]. Results on flatness-based control under linear time-varying models have been provided in [18]. Additionally, approaches on adaptive control based on differential flatness theory have been given in [19, 20].

The paper is particularly concerned with closed-chain underactuated robotic mechanisms which satisfy differential flatness properties and which can be written in the Brunovsky (canonical) form. Transformation into the Brunovsky form can be succeeded for systems that admit static feedback linearization (i.e., a change of coordinates for both the system state variables and the system’s control input). Single-input differentially flat systems admit static feedback linearization and therefore can be finally written in the Brunovsky form [23]. Moreover, flatness-based adaptive fuzzy control can be applied to multi-input dynamical systems. For MIMO dynamical systems which are differentially flat and which admit static feedback linearization, transformation to the canonical (Brunovsky) form can be performed. Moreover, even for MIMO dynamical systems which are differentially flat and do not admit static feedback linearization, however they admit dynamical feedback linearization, it is possible to succeed transformation to the canonical (Brunovsky) form. Therefore, there exists a wide class of nonlinear dynamical systems to which the proposed flatness-based adaptive fuzzy control method can be applied [24].

After transformation to the linear canonical form, the resulting control input for the underactuated robotic mechanism is shown to contain nonlinear elements which depend on the system’s parameters. If the parameters of the system are unknown, then the nonlinear terms which appear in the control signal can be approximated with the use of neuro-fuzzy networks. In the present paper it is shown that a suitable learning law can be defined for the aforementioned neuro-fuzzy approximators so as to preserve the closed-loop system stability. Lyapunov stability analysis proves also that the proposed flatness-based adaptive fuzzy control scheme results in \(H_{\infty }\) tracking performance, in accordance to the results of [25–28].

Fig. 1
figure 1

A two-part underactuated robotic system constituting a closed-chain mechanism

Full size image

Adaptive fuzzy control has been proven to be an efficient nonlinear control method [29–31]. The adaptive fuzzy control system based on differential flatness theory extends the class of systems to which indirect adaptive fuzzy control can be applied. This is particularly important for the design of controllers, capable of efficiently compensating for modeling uncertainties and external disturbances in nonlinear dynamical systems. Unlike other adaptive fuzzy control schemes which are based on several assumptions about the structure of the nonlinear system as well as about the uncertainty characterizing the system’s model, the proposed adaptive fuzzy control scheme based on differential flatness theory offers an exact solution to the design of fuzzy controllers for unknown dynamical systems. The only assumption needed for the design of the controller and for succeeding \(H_{\infty }\) tracking performance for the control loop is that there exists a solution for a Riccati equation associated to the linearized error dynamics of the differentially flat model. This assumption is quite reasonable for several nonlinear systems, thus providing a systematic approach to the design of reliable controllers for such systems [24, 27].

The structure of the paper is as follows: in “Dynamic Model of the Closed-Chain 2-DOF Robotic System” section the dynamic model of the closed-chain underactuated robotic manipulator is analyzed. In “Linearization of the Closed-Chain 2-DOF Robotic System Using Lie Algebra Theory” section linearization of the dynamic model of the robotic mechanism is performed with the use of Lie algebra theory. In “Differential Flatness Theory” section differential flatness theory is analyzed. In “Differential Flatness of the Closed-Chain 2-DOF Robotic System” section it is proven that the dynamic model of the closed-chain underactuated robotic mechanism satisfies differential flatness properties and through the associated diffeomorphism can be transformed to the linear canonical (Brunovsky) form. In “Flatness-Based Adaptive Fuzzy Control” section adaptive fuzzy control based on differential flatness theory is applied to the closed-chain underactuated robotic mechanism. In “Lyapunov Stability Analysis” section Lyapunov stability analysis is provided for the adaptive fuzzy control scheme of the robotic manipulator. In “Simulation Tests” section the performance of the adaptive fuzzy control approach is evaluated through simulation experiments. Finally, in “Conclusions” section concluding remarks are stated.

Dynamic Model of the Closed-Chain 2-DOF Robotic System

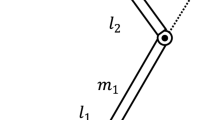
The considered closed-chain 2-DOF robotic system depicted in Fig. 1 consists of four bodies: (i) bodies 1 and 2 are two sliders with masses \(m_1\) and \(m_2,\) respectively [1–3]. Body 3 is connected with a revolute joint to body 1 and has mass \(m_3,\) length \(l_3\) while its moment of inertia is \(I_3.\) Similarly body 4 is connected to body 2 with a revolute joint, has mass \(m_4,\) length \(l_4\) while the associated moment of inertia is \(I_4.\) The motion of the system takes place in the 2D xy plane depicted in Fig. 1 while its dynamics is subjected to gravity.

The state variables for the robotic system are as follows \(q=[q_1,\,q_2,\,q_3,\,q_4]^T{\text {:}}\, q_1\) is the displacement of mass \(m_1\) along the x-axis, \(q_3\) is the turn angle of body 3 round the revolute joint A. \(q_2\) is the displacement of \(m_2\) along the x-axis and \(q_4\) is the turn angle of body 4 round the revolute joint B. The following geometric constraints hold:

$$\begin{aligned}&{l_3}\sin \left( q_3\right) ={l_4}\sin \left( q_4\right) ,\nonumber \\&q_1+{l_3}\cos \left( q_3\right) ={q_2}+{l_4}\cos \left( q_4\right) . \end{aligned}$$
(1)

The control inputs exerted on the robotic model are the horizontal force \(F_1\) that causes the displacement of mass \(m_1\) along the x-axis, the torque \(T_3\) that causes the rotation of the link with length \(l_3\) round the revolute joint A, the horizontal force \(F_2\) that causes the displacement of mass \(m_2\) along the x-axis and the torque \(T_4\) that causes the rotation of the link with length \(l_4\) round the revolute joint B. Thus, in the most generic case the input vector can be \(u=[f_1,\,T_3,\,f_2,\,T_4]^T.\) According the Euler–Lagrange analysis the dynamic model of the robotic manipulator is obtained

$$\begin{aligned} A(q)\ddot{q}+h(q,\,\dot{q})=u, \end{aligned}$$
(2)

where

$$\begin{aligned} A(q)=\begin{pmatrix} a_{11} &{} a_{12} &{} 0 &{} 0 \\ a_{21} &{} a_{22} &{} 0 &{} 0 \\ 0 &{} 0 &{} a_{33} &{} a_{34} \\ 0 &{} 0 &{} a_{43} &{} a_{44} \end{pmatrix}, \end{aligned}$$
(3)

with \(a_{11}=m_1+m_3,\,a_{12}=a_{21}={-}{m_3}l_{c_3}\sin (q_3),\,a_{22}={m_3}{l_{c_3}^2}+I_3,\,a_{33}=m_2+m_4,\,a_{34}=a_{43}={-}{m_4}l_{c_4}\sin (q_4), a_{44}={m_4}{l_{c_4}^2}+I_4,\) and

$$\begin{aligned} h(q,\dot{q})= \begin{pmatrix} -{m_3}l_{c_3}\cos (q_3)\dot{q}_3^2 \\ {m_3}g{l_{c_3}}\cos (q_3) \\ -{m_4}{l_{c_4}}\cos (q_4)\dot{q}_4^2 \\ {m_4}g{l_{c_4}}\cos (q_4) \end{pmatrix}. \end{aligned}$$
(4)

Next, the case in which \(l_3=l_4\) is examined. Moreover, it is considered that the mass \(m_2\) is connected to a spring with elasticity \(k_2.\) Finally, it is assumed that the only inputs applied to the robotic model are \(u_1=f_1\) and \(u_2=T_3.\) Then the dynamic model of the robot becomes

$$\begin{aligned} A\left( q_l\right) \ddot{q}_l+h\left( q_l,\,\dot{q}_l\right) =\left[ u_1,\,u_2\right] ^T, \end{aligned}$$
(5)

where \(q_l=[q_1,\,q_3]^T\) and \(q=[q_1,\,q_2,\,q_3,\,q_4]^T.\) The inertia and Coriolis matrices are defined as

$$\begin{aligned}&A\left( q_l\right) =\left( \begin{array}{l@{\quad }l} M_1+M_2 &{} -2{M_2}{l_3}\sin (q_3) \\ -2{M_2}{l_3}\sin (q_3) &{} I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3) \end{array}\right) , \end{aligned}$$
(6)
$$\begin{aligned}&h\left( q_l,\,\dot{q}_l\right) =\begin{pmatrix} -2{M_2}{l_3}{\dot{q}_3^2}\cos (q_3)+{k_2}{l_d} \\ {k_4}(q_3-\pi )+2{l_3}\sin (q_3)(2{M_2}{l_3}{\dot{q}_3^2}\cos (q_3)-{k_2}{l_d}), \end{pmatrix}\nonumber \\ \end{aligned}$$
(7)

where \(M_1=m_1+m_3,\,M_2=m_2+m_4,\, l_d=q_1+2{l_3}\cos (q_3)-L.\) Denoting \(x=[q_1,\,q_3,\,\dot{q}_1,\,\dot{q}_3]^T\) the robot’s dynamic model can be written in the following state-space form:

$$\begin{aligned} \dot{x}=f(x)+{g_1}(x)u_1+g_2(x)u_2, \end{aligned}$$
(8)

where

$$\begin{aligned} f(x)= & {} \begin{pmatrix} \dot{q}_1 \\ \dot{q}_3 \\ {-{k_2}{l_d}(I_3+I_4)+2{l_3}{M_2}({k_2}(\pi -q_3)sin(q_3)+(I_3+I_4){\dot{q}_3^2}\cos (q_3)} \over {{M_2}(I_3+I_4)+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3)))} \\ \\ {{k_4}(M_1+M_2)(\pi -q_3)+2{I_3}{M_1}\sin (q_3)({k_2}{l_d}-2{l_3}{M_2}{\dot{q}_3^2}\cos (q_3))} \over {{M_2}(I_3+I_4)+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))} \end{pmatrix},\nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned} g_1(x)= & {} \begin{pmatrix} 0 \\ 0 \\ {I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3)} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))} \\ \\ {2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))} \end{pmatrix}, \end{aligned}$$
(10)
$$\begin{aligned} g_2(x)= & {} \begin{pmatrix} 0 \\ 0 \\ {2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))} \\ \\ {M_1+M_2} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))} \end{pmatrix}. \end{aligned}$$
(11)

The robotic system is underactuated when only one of the control inputs is enabled. It can be proven that when the only input is \(u_1=F_1\) then the robotic system is not static feedback linearizable.

Next, the case in which the only control input is \(u_2=T_3\) is examined. When \(k_2\ne 0\) and \(k_4=0\) then the robotic model is static feedback linearizable. Equivalently this means that (i) the distribution \(D_3=\langle g(x),\,ad_{f(x)}g(x),\,ad^2_{f(x)}g(x),ad^3_{f(x)}g(x)\rangle \) has full rank and (ii) the vector fields \(D_0=\langle g(x)\rangle ,\,D_1=\langle g(x),\,ad_{f(x)}g(x)\rangle \) and \(D_2=\langle g(x),\,ad_{f(x)}g(x),\,ad_{f(x)}^2{g(x)}\rangle \) are involutive.

Linearization of the Closed-Chain 2-DOF Robotic System Using Lie Algebra Theory

The following variable is defined first

$$\begin{aligned} z_1=y={h_1}(q)=\left( M_1+M_2\right) q_1+2{M_2}{l_3}\cos \left( q_3\right) . \end{aligned}$$
(12)

Applying Lie-algebra theory, tt holds that [32]

$$\begin{aligned}&{z_2}={L_f}{h_1}= \begin{pmatrix} {{{\partial }{h_1}} \over {{\partial }{q_1}}}&{{{\partial }{h_1}} \over {{\partial }{q_3}}}&{{{\partial }{h_1}} \over {{\partial }{\dot{q}_1}}}&{{{\partial }{h_1}} \over {{\partial }{\dot{q}_3}}} \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_2={L_f}h_1= \begin{pmatrix} (M_1+M_2&-2{M_2}{l_3}\sin (q_3)&0&0) \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_2={L_f}{h_1}=\left( M_1+M_2\right) f_1-2{M_2}{l_3}\sin \left( q_3\right) f_2{\Rightarrow } \nonumber \\&z_2=L_f{h_1}=\left( M_1+M_2\right) \dot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \dot{q}_3. \end{aligned}$$
(13)

Similarly, it holds

$$\begin{aligned}&z_3={L_f^2}{h_1}= \begin{pmatrix} {{{\partial }{z_2}} \over {{\partial }{q_1}}}&{{{\partial }{z_2}} \over {{\partial }{q_3}}}&{{{\partial }{z_2}} \over {{\partial }{\dot{q}_1}}}&{{{\partial }{z_2}} \over {{\partial }{\dot{q}_3}}} \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_3={L_f^2}{h_1}= \begin{pmatrix} 0&-2{M_2}{l_3}\cos (q_3)\dot{q}_3&(M_1+M_2)&-2{M_2}{l_3}\sin (q_3) \end{pmatrix}\nonumber \\&\qquad \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_3={L_f^2}{h_1}=\left( M_1+M_2\right) {f_3}-2{M_2}{l_3}\sin \left( q_3\right) \nonumber \\&\qquad \quad \times {f_4}-2{M_2}{l_3}\cos \left( q_3\right) {\dot{q}_3}f_2. \end{aligned}$$
(14)

It holds that

$$\begin{aligned} \ddot{q}_1= & {} {f_3}+{g_{a_3}}{u_1}+{g_{b_3}}{u_2}{\Rightarrow }\ddot{q}_1={f_3}+{g_{b_3}}{u_2}{\Rightarrow }f_3\nonumber \\= & {} \ddot{q}_1-{g_{b_3}}u_2\nonumber \\ \ddot{q}_3= & {} {f_4}+{g_{a_4}}{u_1}+{g_{b_4}}{u_2}{\Rightarrow }\ddot{q}_4={f_4}+{g_{b_4}}{u_2}{\Rightarrow }f_4\nonumber \\= & {} \ddot{q}_3-{g_{b_4}}u_2. \end{aligned}$$
(15)

Therefore, it holds

$$\begin{aligned}&z_3=\left( M_1+M_2\right) {f_3}-2{M_2}{l_3}\sin \left( q_3\right) f_4-2{M_2}{l_3}\cos \left( \dot{q}_3\right) f_2{\Rightarrow }\nonumber \\&z_3=\left( M_1+M_2\right) \ddot{q}_1-\left( M_1+M_2\right) {g_{b_2}}{u_2}-2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3\nonumber \\&\qquad +2{M_2}{l_3}\sin \left( q_3\right) {g_{b_4}}{u_2}-2{M_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2{\Rightarrow }, \end{aligned}$$
(16)

or equivalently

$$\begin{aligned} z_3= & {} \left( M_1+M_2\right) \ddot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3\nonumber \\&-\,{{(M_1+M_2)2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4)M_2+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}u_2 \nonumber \\&+\,{{(M_1+M_2)2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4)M_2+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}u_2 \nonumber \\&-\,2{M_2}{l_3}\cos (q_3){\dot{q}_3^2}. \end{aligned}$$
(17)

Consequently, it holds that

$$\begin{aligned} z_3=\left( M_1+M_2\right) \ddot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3-2{M_2}{l_3}{\dot{q}_3^2}\cos \left( q_3\right) .\nonumber \\ \end{aligned}$$
(18)

Using Eqs. (5) and (6)–(7) one obtains that

$$\begin{aligned}&\left( M_1+M_2\right) \ddot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3\nonumber \\&\quad =2{M_2}{l_3}{\dot{q}_3^2}\cos \left( q_3\right) -{k_2}{l_d}+u_1, \end{aligned}$$
(19)

with \(u_1=0\) due to underactuation. Therefore, it holds

$$\begin{aligned}&z_3=2{M_2}{l_3}{\dot{q}_3^2}\cos \left( q_3\right) -{k_2}{l_d}-2{M_2}{l_3}{\dot{q}_3^2}\cos \left( q_3\right) {\Rightarrow }\nonumber \\&z_3={-}{k_2}{l_d}{\Rightarrow }z_3={-}{k_2}\left( q_1+2{l_3}\cos \left( q_3\right) -L\right) . \end{aligned}$$
(20)

Similarly, one has

$$\begin{aligned}&z_4={L_f^3}h_1(q)= \begin{pmatrix} {{{\partial }{z_3}} \over {{\partial }{q_1}}}&{{{\partial }{z_3}} \over {{\partial }{q_3}}}&{{{\partial }{z_3}} \over {{\partial }{\dot{q}_1}}}&{{{\partial }{z_3}} \over {{\partial }{\dot{q}_3}}} \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_4=\begin{pmatrix} -{k_2}&2{k_2}{l_3}\sin (q_3)&0&0 \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&z_4={-}{k_2}{f_1}+2{k_2}{l_3}\sin \left( q_3\right) {f_2}{\Rightarrow }\nonumber \\&\quad z_4={-}{k_2}\dot{q}_1+2{k_2}{l_3}\sin \left( q_3\right) \dot{q}_3. \end{aligned}$$
(21)

Moreover, it holds that

$$\begin{aligned} \dot{z}_4={L_f^4}{h_1}+{L_{g_a}}{L_f^3}{h_1}{u_1}+{L_{g_b}}{L_f^3}{h_1}{u_2}. \end{aligned}$$
(22)

It holds that

$$\begin{aligned}&{L_f^4}{h_1}=\begin{pmatrix} {{{\partial }{z_4}} \over {{\partial }{q_1}}}&{{{\partial }{z_4}} \over {{\partial }{q_3}}}&{{{\partial }{z_4}} \over {{\partial }{\dot{q}_1}}}&{{{\partial }{z_4}} \over {{\partial }{\dot{q}_3}}} \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&{L_f^4}{h_1}=\begin{pmatrix} 0&2{k_2}{l_3}\cos (q_3)\dot{q}_3&-k_2&2{k_2}{l_3}\sin (q_3) \end{pmatrix} \begin{pmatrix} f_1 \\ f_2 \\ f_3 \\ f_4 \end{pmatrix}{\Rightarrow }\nonumber \\&{L_f^4}{h_1}=2{k_2}{l_3}\cos \left( q_3\right) {\dot{q}_3}{f_2}-{k_2}{f_3}+2{k_2}{l_3}\sin \left( q_3\right) {f_4}{\Rightarrow }\nonumber \\&{L_f^4}{h_1}=2{k_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2-{k_2}{f_3}+2{k_2}{l_3}\sin \left( q_3\right) {f_4}. \end{aligned}$$
(23)

It holds that \(u_1=0\) and

$$\begin{aligned}&{L_{g_b}}{L_f^3}{h_1}= \begin{pmatrix} {{{\partial }{z_4}} \over {{\partial }{q_1}}}&{{{\partial }{z_4}} \over {{\partial }{q_3}}}&{{{\partial }{z_4}} \over {{\partial }{\dot{q}_1}}}&{{{\partial }{z_4}} \over {{\partial }{\dot{q}_3}}} \end{pmatrix} \begin{pmatrix} g_{b_1} \\ g_{b_2} \\ g_{b_3} \\ g_{b_4} \end{pmatrix}{\Rightarrow }\nonumber \\&{L_{g_b}}{L_f^3}{h_1}= \begin{pmatrix} 0&2{k_3}{l_3}\cos (q_3)\dot{q}_3&-k_2&2{k_2}{l_3}\sin (q_3) \end{pmatrix} \begin{pmatrix} g_{b_1} \\ g_{b_2} \\ g_{b_3} \\ g_{b_4} \end{pmatrix},\nonumber \\ \end{aligned}$$
(24)

which can be also written as

$$\begin{aligned}&{L_{g_b}}{L_f^3}{h_1}={-}{k_2}{{2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}\nonumber \\&\quad +2{k_2}{l_3}\sin \left( q_3\right) {{M_1+M_2} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}{\Rightarrow } \nonumber \\&{L_{g_b}}{L_f^3}{h_1}={{2{k_2}{l_3}\sin (q_3)M_1} \over {(I_3+I_4)M_2+M_1(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}.\nonumber \\ \end{aligned}$$
(25)

Using next the relation

$$\begin{aligned} \dot{z}_4={L_f^{(4)}}{h_1}+{L_{g_a}}{L_f^3}{h_1}{u_1}+{L_{g_b}}{L_f^3}{h_1}{u_2}=v, \end{aligned}$$
(26)

and that \(\dot{z}_1=z_2,\,\dot{z}_2=z_3,\,\dot{z}_3=z_4\) one has that the robotic model can be written in the linear canonical (Brunovsky) form

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \\ \dot{z}_4 \end{pmatrix}= \begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \end{pmatrix}+ \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}v. \end{aligned}$$
(27)

For the linearized system, a suitable feedback control law is

$$\begin{aligned} v= & {} \dot{z}_4^d-{k_1}\left( z_4-z_4^d\right) -{k_2}\left( z_3-z_3^d\right) -{k_3}\left( z_2-z_2^d\right) \nonumber \\&-\,{k_4}\left( z_1-z_1^d\right) . \end{aligned}$$
(28)

Differential Flatness Theory

Overview of Differential Flatness Theory

Differential flatness theory can be applied to the generic class of systems \(\dot{x}=f(x,\,u).\) In this study, the interest is in dynamic models of the form of Eq. (29).

$$\begin{aligned} \dot{x}=f(x,\,t)+g(x,\,t)u. \end{aligned}$$
(29)

The principles of differential flatness theory have been extensively studied in the relevant bibliography [11–23]: a finite dimensional system is considered. This can be written in the form of an ODE, i.e., \(S_i(w,\,\dot{w},\,\ddot{w},\ldots ,w^{(i)}), \, i=1,\,2,\ldots ,q.\) The term w denotes the system variables (these variables are for instance the elements of the system’s state vector and the control input) while \(w^{(i)},\,i=1,\,2,\ldots ,q\) are the associated derivatives. Such a system is said to be differentially flat if there exists a set of m functions \(y=(y_1,\ldots ,y_m)\) of the system variables and of their time-derivatives, i.e., \(y_i=\phi (w,\,\dot{w},\,\ddot{w},\ldots ,w^{(\alpha _i)}), \, i=1,\ldots ,m\) satisfying the following two conditions [15, 23]:

  1. (1)

    There does not exist any differential relation of the form \(R(y,\,\dot{y},\ldots ,y^{(\beta )})=0\) which implies that the derivatives of the flat output are not coupled in the sense of an ODE, or equivalently it can be said that the flat output is differentially independent.

  2. (2)

    All system variables (i.e., the elements of the system’s state vector w and the control input) can be expressed using only the flat output y and its time derivatives \(w_i={\psi _i}(y,\,\dot{y},\ldots ,y^{(\gamma _i)}), \, i=1,\ldots ,s.\) An equivalent definition of differentially flat systems is as follows:

Definition the system \(\dot{x}=f(x,\,u),\, x{\in }{R^n},\,u{\in }{R^m}\) is differentially flat if there exist relations

$$\begin{aligned}&h{\text {:}}\, {R^n}{\times }{{\left( R^m\right) }^{r+1}}{\rightarrow }{R^m},\nonumber \\&\phi {\text {:}}\,{\left( R^m\right) ^r}{\rightarrow }{R^n}\,\text {and}\nonumber \\&\psi {\text {:}}\,\left( R^m\right) ^{r+1}{\rightarrow }{R^m}, \end{aligned}$$
(30)

such that

$$\begin{aligned}&y=h\left( x,\,u,\,\dot{u},\ldots ,u^{(r)}\right) , \nonumber \\&x=\phi \left( y,\,\dot{y},\ldots ,y^{(r-1)}\right) , \, \text {and} \nonumber \\&u=\psi \left( y,\,\dot{y},\ldots ,y^{(r-1)},\,y^{(r)}\right) . \end{aligned}$$
(31)

This means that all system dynamics can be expressed as a function of the flat output and its derivatives, therefore the state vector and the control input can be written as

$$\begin{aligned}&x(t)=\phi \left( y(t),\,\dot{y}(t),\ldots ,y^{(r-1)}(t)\right) ,\,\text {and} \nonumber \\&u(t)=\psi \left( y(t),\,\dot{y}(t),\ldots ,y^{(r)}(t)\right) . \end{aligned}$$
(32)
Fig. 2
figure 2

Flatness-based diffeomorphism and its inverse, enabling the implementation of nonlinear control for the underactuated robotic mechanism

Full size image

Classes of Differentially Flat Systems

For certain classes of dynamical systems it has been proven that they satisfy differential flatness properties. The following classes of nonlinear differentially flat systems are defined [21, 23]:

  1. (1)

    Affine in-the-input systems the dynamics of such systems is given by:

    $$\begin{aligned} \dot{x}=f(x)+{\sum _{i=1}^m}{g_i(x)}{u_i}. \end{aligned}$$
    (33)

    From Eq. (33) it can be concluded that the above state equation can also describe MIMO dynamical systems. Without loss of generality it is assumed that \(G=[g_1,\ldots ,g_m]\) is of rank m. In case that the flat outputs of the aforementioned system are only functions of states x,  then this class of dynamical systems is called 0-flat. It has been proven that a dynamical affine system with n states and \(n-1\) inputs is 0-flat if it is controllable.

  2. (2)

    Driftless systems these are systems of the form

    $$\begin{aligned} \dot{x}={\sum _{i=1}^m}{f_i(x)}u_i. \end{aligned}$$
    (34)

    For driftless systems with two inputs, i.e.,

    $$\begin{aligned} \dot{x}={f_1(x)}{u_1}+{f_2(x)}{u_2}, \end{aligned}$$
    (35)

    the flatness property holds, if and only if the rank of matrix \(E_{k+1}:=\{E_k,\,[E_k,\,E_k]\}, \, k{\ge }0\) with \(E_0:=\{f_1,\,f_2\}\) is equal to \(k+2\) for \(k=0,\ldots ,n-2.\) It has been proven that a driftless system that is differentially flat, is also 0-flat.

Moreover, for flat systems with n states and \(n-2\) control inputs, i.e.,

$$\begin{aligned} \dot{x}={\sum _{i=1}^{n-2}}{u_i}{f_i}(x) \quad x{\in }R^n, \end{aligned}$$
(36)

the flatness property holds, if controllability also holds. Furthermore, the system is 0-flat if n is even.

Differential Flatness of the Closed-Chain 2-DOF Robotic System

Differential Flatness Properties of the Underactuated Robot

The following flat output is chosen:

$$\begin{aligned} y=\left( M_1+M_2\right) {q_1}+2{M_2}{l_3}\cos \left( q_3\right) . \end{aligned}$$
(37)

It holds that

$$\begin{aligned}&\dot{y}=\left( M_1+M_2\right) \dot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \dot{q}_3{\Rightarrow }\nonumber \\&\ddot{y}=\left( M_1+M_2\right) \ddot{q}_1=2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3\nonumber \\&\qquad -\,2{M_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2. \end{aligned}$$
(38)

Using Eqs. (2) and (3)–(4) it holds that

$$\begin{aligned}&\left( M_1+M_2\right) \ddot{q}_1-2{M_2}{l_3}\sin \left( q_3\right) \ddot{q}_3\nonumber \\&\quad =2{M_2}{l_3}{\dot{q}_3^2}\cos \left( q_3\right) -{k_2}{l_d}+u_1, \end{aligned}$$
(39)

where due to underactuation one has \(u_1=F_1=0.\) Therefore, it holds

$$\begin{aligned} \ddot{y}=-{k_2}{l_d}{\Rightarrow }\ddot{y}={-}{k_2}\left( q_1+2{l_3}\cos \left( q_3\right) -L\right) . \end{aligned}$$
(40)

Consequently

$$\begin{aligned} y^{(3)}={-}{k_2}\left[ \dot{q}_1-2{l_3}\sin \left( q_3\right) \dot{q}_3\right] , \end{aligned}$$
(41)

and respectively

$$\begin{aligned} y^{(4)}=-{k_2}{\ddot{q}_1}+2{k_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2+2{k_2}{l_3}\sin \left( q_3\right) \ddot{q}_3. \end{aligned}$$
(42)

From Eq. (37) describing the flat output and from the equations of its higher order derivatives one has a set of equations which can be solved with respect to the state variables \(q_1,\,q_3,\,\dot{q}_1\) and \(\dot{q}_3.\) It holds that

$$\begin{aligned} q_1= & {} {{{k_2}y-{M_2}\ddot{y}+{M_2}{k_2}L} \over {{k_2}M_1}}, \end{aligned}$$
(43)
$$\begin{aligned} q_3= & {} \cos ^{-1}\left( {{\ddot{y}+{k_2}{q_1}-{k_2}L} \over {2{k_2}l_3}}\right) , \end{aligned}$$
(44)
$$\begin{aligned} \dot{q}_1= & {} {{{k_2}\dot{y}+{M_2}y^{(3)}} \over {{k_2}M_1}}, \end{aligned}$$
(45)
$$\begin{aligned} \dot{q}_3= & {} {1 \over {\sin (q_3)}}{{(M_1+M_2)\dot{q}_1-\dot{y}} \over {2{M_2}{l_3}}}. \end{aligned}$$
(46)

Having expressed the elements of the state vector q as functions of the flat output and its derivatives and knowing that \(\ddot{q}_1=f_3+{g_{a_3}}{u_1}+{g_{b_3}}{u_2}\) and \(\ddot{q}_3=f_4+{g_{a_4}}{u_1}+{g_{b_4}}{u_2}\) it holds that the control inputs \(u_1\) and \(u_2\) can be also written as functions of the flat output and its derivatives. Therefore, the robotic system stands for a differentially flat model. The differential flatness theory transformation of the underactuated model and its inverse are depicted in Fig. 2.

Design of a Flatness-Based Controller for the Closed-Chain 2-DOF Robotic System

From the relation \(\dot{q}=f(q)+{g_a}(q){u_1}+{g_b}(q){u_2}\) and the associated relations about \(f(q),\,g_a{q}\) and \(g_b(q)\) it holds

$$\begin{aligned} \ddot{q}_1= & {} {f_3}+{g_{a_3}}u_1+{g_{b_3}}u_2{\Rightarrow }\ddot{q}_1=f_3+{g_{b_3}}{u_2}{\Rightarrow } \nonumber \\ \ddot{q}_1= & {} {{-{k_2}{l_d}(I_3+I_4)+2{l_3}{M_2}[K_4(\pi -q_3)\sin (q_3)+(I_3+I_4){\dot{q}_3^2}\cos (q_3)]} \over {{M_2}(I_3+I_4)+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}\nonumber \\&+\,{{2{M_2}{l_3}\sin (q_3)} \over {(I_3+I_4){M_2}+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}u2. \end{aligned}$$
(47)

Equivalently, one has

$$\begin{aligned} \ddot{q}_3= & {} {f_4}+{g_{a_4}}u_1+{g_{b_4}}u_2{\Rightarrow }\ddot{q}_3=f_3+{g_{b_4}}{u_2}{\Rightarrow } \nonumber \\ \ddot{q}_3= & {} {{{k_4}{(M_1+M_2)}(\pi -q_3)+2{l_3}{M_1}\sin (q_3)[K_2{l_d}-2{l_3}{M_2}{\dot{q}_3^2}\cos (q_3)}] \over {{M_2}(I_3+I_4)+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}\nonumber \\&+\,{{M_1+M_2} \over {(I_3+I_4){M_2}+{M_1}(I_3+I_4+4{M_2}{l_3^2}\sin ^2(q_3))}}u2. \end{aligned}$$
(48)

Consequently, it holds

$$\begin{aligned} y^{(4)}= & {} {-}{k_2}{\ddot{q}_1}+2{k_2}{l_3}\cos \left( q_3\right) {\dot{q}_3^2}+2{k_2}{l_3}\sin \left( q_3\right) \ddot{q}_3{\Rightarrow }\nonumber \\ y^{{(4)}}= & {} {-}{k_2}\left( f_3+{g_{b_3}}\right) u_2+2{k_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2\nonumber \\&+\,2{k_2}{l_3}\sin \left( q_3\right) \left( f_4+{g_{b_4}}u_2\right) {\Rightarrow } \nonumber \\ y^{{(4)}}= & {} 2{k_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2-{k_2}{f_3}+2{k_2}{l_3}\sin \left( q_3\right) {f_4}\nonumber \\&+\,\left[ -{k_2}{g_{b_3}}+2{k_2}{l_3}\sin \left( q_3\right) {g_{b_4}}\right] u_2{\Rightarrow }\nonumber \\ y^{{(4)}}= & {} {f_v}+{g_v}u{\Rightarrow }y^{{(4)}}=v, \end{aligned}$$
(49)

where \(v={f_v}+{g_v}u_2\) with

$$\begin{aligned} f_v= & {} 2{k_2}{l_3}\cos \left( q_3\right) \dot{q}_3^2-{k_2}{f_3}+2{k_2}{l_3}\sin \left( q_3\right) {f_4},\nonumber \\ g_v= & {} {-}{k_2}{g_{b_3}}+2{k_2}{l_3}\sin \left( q_3\right) {g_{b_4}}. \end{aligned}$$
(50)

The following new state variables are defined \(z_1=y,\,z_2=\dot{y},\,z_3=\ddot{y}\) and \(z_4=y^{(3)}.\) For the new state variables a description of the system in the linear canonical (Brunovsky) form is obtained

$$\begin{aligned} \begin{pmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \dot{z}_3 \\ \dot{z}_4 \end{pmatrix}= \begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix} \begin{pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \end{pmatrix}+ \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}v. \end{aligned}$$
(51)

Considering that the linear displacement of the left part of the kinematic chain \(q_1\) is measurable, and that the same holds for the turn angle \(q_3\) of joint A one has that the flat output \(y=(M_1+M_2){q_1}+2{M_2}{l_3}\cos (q_3)\) is also a measurable variable.

Using the description of system in the linear canonical form, the appropriate control law is

$$\begin{aligned} v= & {} \dot{z}_4^d-{k_1}\left( z_4-z_4^d\right) -{k_2}\left( z_3-z_3^d\right) -{k_3}\left( z_2-z_2^d\right) \nonumber \\&-\,{k_4}\left( z_1-z_1^d\right) . \end{aligned}$$
(52)

Flatness-Based Adaptive Fuzzy Control

Nonlinear System Transformation into the Brunovsky form

A single-input differentially flat dynamical system is considered again:

$$\begin{aligned} \dot{x}=f_s(x,\,t)+g_s(x,\,t)(u+\tilde{d}), \quad x{\in }R^n, \quad u{\in }R, \quad \tilde{d}{\in }R,\nonumber \\ \end{aligned}$$
(53)

where \(f_s(x,\,),\,g_s(x,\,t)\) are nonlinear vector fields defining the system’s dynamics, u denotes the control input and \(\tilde{d}\) denotes additive input disturbances. Knowing that the system of Eq. (53) is differentially flat, the next step is to try to write it into a Brunovsky form. It has been shown that, in general, transformation into the Brunovsky (canonical) form can be succeeded for systems that admit static feedback linearization [23]. Single input differentially flat systems, admit static feedback linearization, therefore they can be transformed into the Brunovsky form. For multi-input differentially flat systems there exists a transformation into the Brunovsky form [24].

The selected flat output is again denoted by y. Then, as analyzed in “Differential Flatness Theory” section, for the state variables \(x_i\) of the system of Eq. (53) it holds

$$\begin{aligned} x_i=\phi _i\left( y,\,\dot{y},\ldots ,y^{(r-1)}\right) ,\quad i=1,\ldots ,n, \end{aligned}$$
(54)

while for the control input it holds

$$\begin{aligned} u=\psi \left( y,\,\dot{y},\ldots ,y^{(r-1)},\,y^{(r)}\right) . \end{aligned}$$
(55)
Fig. 3
figure 3

Neuro-fuzzy approximator: \(G_i\) Gaussian basis function, \(N_i\) normalization unit

Full size image

Introducing the new state variables \(y_1=y\) and \(y_i=y^{(i-1)}, \, i=2,\ldots ,n,\) the initial system of Eq. (53) can be written in the Brunovsky form [33, 34]:

$$\begin{aligned} \begin{pmatrix} \dot{y}_1 \\ \dot{y}_2 \\ \cdots \\ \cdots \\ \dot{y}_{n-1}\\ \dot{y}_n \end{pmatrix}= \begin{pmatrix} 0 &{} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 1 &{} \cdots &{} 0 \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 \end{pmatrix} \begin{pmatrix} y_1 \\ y_2 \\ \cdots \\ \cdots \\ y_{n-1} \\ y_n \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ \cdots \\ \cdots \\ 0 \\ 1 \end{pmatrix} v,\nonumber \\ \end{aligned}$$
(56)

where \(v=f(x,\,t)+g(x,\,t)(u+\tilde{d})\) is the control input for the linearized model, and \(\tilde{d}\) denotes additive input disturbances. Thus one can use that

$$\begin{aligned} y^{(n)}=f(x,\,t)+g(x,\,t)(u+\tilde{d}), \end{aligned}$$
(57)

where \(f(x,\,t),\,g(x,\,t)\) are unknown nonlinear functions, while as mentioned above \(\tilde{d}\) is an unknown additive disturbance. It is possible to make the system’s state vector x follow a given bounded reference trajectory \(x_d.\) In the presence of model uncertainties and external disturbances, denoted by \(w_d,\) successful tracking of the reference trajectory is provided by the \(H_{\infty }\) criterion [28, 35]:

$$\begin{aligned} {\int _0^T}{e^T}Qe{dt} \le {\rho ^2} {\int _0^T}{{w_d}^T}{w_d}{dt}, \end{aligned}$$
(58)

where \(\rho \) is the attenuation level and corresponds to the maximum singular value of the transfer function G(s) of the linearized model associated to Eqs. (56) and (57).

Remark 1

From the \(H_{\infty }\) control theory, the \(H_{\infty }\) norm of a linear system with transfer function G(s),  is denoted by \(||G||_{\infty }\) and is defined as \(||G||_{\infty }={sup_{\omega }}{\sigma }_{max}[G(j{\omega })]\) [25, 28]. In this definition sup denotes the supremum or least upper bound of the function \(\sigma _{max}[G(j(\omega )],\) and thus the \(H_{\infty }\) norm of G(s) is the maximum value of \(\sigma _{max}[G(j(\omega )]\) over all frequencies \(\omega .\,H_{\infty }\) norm has a physically meaningful interpretation when considering the system \(y(s)=G(s)u(s).\) When this system is driven with a unit sinusoidal input at a specific frequency, \(\sigma _{max}|G(j{\omega })|\) is the largest possible output for the corresponding sinusoidal input. Thus, the \(H_{\infty }\) norm is the largest possible amplification over all frequencies of a sinusoidal input.

Remark 2

The input additive disturbance term \(\tilde{d}\) in the dynamics of the controlled system does not affect the transformation into the canonical form that is performed according to differential flatness theory. Such a disturbance is efficiently compensated by the proposed adaptive fuzzy control law.

Control Law

For the measurable state vector x of the system of Eqs. (56) and (57), and for uncertain functions \(f(x,\,t)\) and \(g(x,\,t)\) an appropriate control law is

$$\begin{aligned} u={{1 \over {\hat{g}(x,\,t)}}\left[ y_d^{(n)}-\hat{f}(x,\,t)-{K^T}e+{u_c}\right] }, \end{aligned}$$
(59)

with \(e=[e,\,\dot{e},\,\ddot{e},\ldots ,e^{(n-1)}]^T\) and \(e=y-y_d,\,K^T=[k_n,\,k_{n-1},\ldots ,k_1],\) such that the polynomial \(e^{(n)}+{k_1}e^{(n-1)}+{k_2}e^{(n-2)}+\cdots +{k_n}e\) is Hurwitz. The control law of Eq. (59) results into

$$\begin{aligned} e^{(n)}= & {} {-}{K^T}e+{u_c}+[f(x,\,t)-\hat{f}(x,\,t)]\nonumber \\&+\,[g(x,\,t)-\hat{g}(x,\,t)]u+g(x,\,t)\tilde{d}, \end{aligned}$$
(60)

where the supervisory control term \(u_c\) aims at the compensation of the approximation error

$$\begin{aligned} w=[f(x,\,t)-\hat{f}(x,\,t)]+[g(x,\,t)-\hat{g}(x,\,t)]u, \end{aligned}$$
(61)

as well as of the additive disturbance term \(d_1=g(x,\,t)\tilde{d}.\) The above relation can be written in a state-equation form. The state vector is taken to be \(e^T=[e,\,\dot{e},\ldots ,e^{(n-1)}],\) which after some operations yields

$$\begin{aligned} \dot{e}= & {} \left( A-B{K^T}\right) e+B{u_c}+B\left\{ [f(x,\,t)-\hat{f}(x,\,t)]\right. \nonumber \\&\left. \quad +[g(x,\,t)-\hat{g}(x,\,t)]u+d_1\right\} , \end{aligned}$$
(62)

where

$$\begin{aligned} A=\begin{pmatrix} 0 &{} 1 &{} 0 &{} \cdots &{} \cdots &{} 0 \\ 0 &{} 0 &{} 1 &{} \cdots &{} \cdots &{} 0 \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} \cdots &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} \cdots &{} 0 \end{pmatrix}, \quad B=\begin{pmatrix} 0 \\ 0 \\ \cdots \\ \cdots \\ 0 \\ 1 \end{pmatrix}, \end{aligned}$$
(63)

and \(K=[k_n,\,k_{n-1},\ldots ,k_2,\,k_1]^T.\) As explained above, the control signal \(u_c\) is an auxiliary control term, used for the compensation of \(\tilde{d}\) and w,  which can be selected according to \(H_{\infty }\) control theory:

$$\begin{aligned} u_c={-}{1 \over r}{B^T}Pe. \end{aligned}$$
(64)

Approximators of Unknown System Dynamics

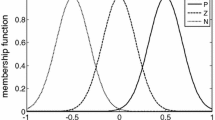
The approximation of functions \(f(x,\,t)\) and \(g(x,\,t)\) of Eq. (57) can be carried out with neuro-fuzzy networks (Fig. 3). The estimation of \(f(x,\,t)\) and \(g(x,\,t)\) can be written as [36, 37]:

$$\begin{aligned} \hat{f}\left( x |\theta _f\right) ={\theta _f^T}{\phi (x)}, \quad \hat{g}\left( x|\theta _g\right) ={\theta _g^T}{\phi (x)}, \end{aligned}$$
(65)

where \(\phi (x)\) are kernel functions with elements

$$\begin{aligned} \phi ^l(x)={ {{\prod _{i=1}^{n}}{\mu _{A_i}^l(x_i)}} \over {\sum _{l=1}^N{\prod _{i=1}^{n}}{\mu _{A_i}^l(x_i)}} } \quad l=1,\,2,\ldots ,N. \end{aligned}$$
(66)

It is assumed that the weights \(\theta _f\) and \(\theta _g\) vary in the bounded areas \(M_{\theta _f}\) and \(M_{\theta _g}\) which are defined as

$$\begin{aligned} M_{\theta _f}= & {} \left\{ \theta _f \in R^h{\text {:}}\, \left\| \theta _f\right\| \le {m_{\theta _f}}\right\} , \nonumber \\ M_{\theta _g}= & {} \left\{ \theta _g \in R^h{\text {:}}\, \left\| \theta _g\right\| \le {m_{\theta _g}}\right\} , \end{aligned}$$
(67)

with \(m_{\theta _f}\) and \(m_{\theta _g}\) positive constants.

The values of \(\theta _f\) and \(\theta _g\) that give optimal approximation are:

$$\begin{aligned} {\theta _f^*}= & {} \text {arg \ min}_{\theta _f \in M_{\theta _f}}\left[ sup_{x \in U_x} \left| f(x)-\hat{f}\left( x|\theta _f\right) \right| \right] ,\nonumber \\ {\theta _g^*}= & {} \text {arg \ min}_{\theta _g \in M_{\theta _g}}\left[ sup_{x \in U_x} \left| g(x)-\hat{g}\left( x |\theta _g\right) \right| \right] . \end{aligned}$$
(68)

The approximation error of \(f(x,\,t)\) and \(g(x,\,t)\) is given by

$$\begin{aligned} w= & {} \left[ \hat{f}\left( x,\,|\theta _f^*\right) -f(x,\,t)\right] +\left[ \hat{g}\left( x|\theta _f^*\right) -g(x,\,t)\right] u \Rightarrow \nonumber \\ w= & {} \left\{ \left[ \hat{f}\left( x|\theta _f^*\right) -\hat{f}\left( x|\theta _f\right) \right] +\left[ \hat{f}\left( x|\theta _f\right) -f(x,\,t)\right] \right\} \nonumber \\&+\,\left\{ \left[ \hat{g}\left( x|\theta _g^*\right) -\hat{g}\left( x|\theta _g\right) \right] +\left[ \hat{g}\left( x|\theta _g\right) -g(x,\,t)\right] u\right\} ,\nonumber \\ \end{aligned}$$
(69)

where: (i) \(\hat{f}(x|\theta _f^*)\) is the approximation of f for the best estimation \(\theta _f^*\) of the weights’ vector \(\theta _f\), (ii) \(\hat{g}(x|\theta _g^*)\) is the approximation of g for the best estimation \(\theta _g^*\) of the weights’ vector \(\theta _g.\)

The approximation error w can be decomposed into \(w_a\) and \(w_b,\) where

$$\begin{aligned} w_a= & {} \left[ \hat{f}\left( x|{\theta _f}\right) -\hat{f}\left( x|{\theta _f^*}\right) \right] +\left[ \hat{g}\left( x|{\theta _g}\right) -\hat{g}\left( x|{\theta _g^*}\right) \right] u,\nonumber \\ w_b= & {} \left[ \hat{f}\left( x|{\theta _f^*}\right) -f(x,\,t)\right] +\left[ \hat{g}\left( x|{\theta _g^*}\right) -g(x,\,t)\right] u.\nonumber \\ \end{aligned}$$
(70)

Finally, the following two parameters are defined:

$$\begin{aligned} \tilde{\theta }_f= & {} \theta _f-\theta _f^*,\nonumber \\ \tilde{\theta }_g= & {} \theta _g-\theta _g^*. \end{aligned}$$
(71)

Lyapunov Stability Analysis

The adaptation law of the weights \(\theta _f\) and \(\theta _g\) as well as of the supervisory control term \(u_c\) is derived by the requirement for negative definite derivative of the quadratic Lyapunov function

$$\begin{aligned} V={1 \over 2}{{e^T}Pe}+{1 \over {2{\gamma _1}}}{\tilde{\theta }_f^T}{\tilde{\theta }_f}+{1 \over {2{\gamma _2}}}{\tilde{\theta }_g^T}{\tilde{\theta }_g}. \end{aligned}$$
(72)

Substituting Eq. (62) into Eq. (72) and differentiating gives

$$\begin{aligned} \dot{V}= & {} {1 \over 2}{\dot{e}^T}Pe+{1 \over 2}{e^T}P{\dot{e}}+ {1 \over {\gamma _1}}{\tilde{\theta }_f^T}{\dot{\tilde{\theta }}_f}+ {1 \over {\gamma _2}}{\tilde{\theta }_g^T}{\dot{\tilde{\theta }}_g} \Rightarrow \nonumber \\ \dot{V}= & {} {1 \over 2}{e^T}\left\{ {\left( A-B{K^T}\right) ^T}P+P\left( A-B{K^T}\right) \right\} e\nonumber \\&+\,{B^T}Pe\left( u_c+w+d_1\right) +{{1 \over {\gamma _1}}{\tilde{\theta }_f^T}{\dot{\tilde{\theta }}}_f}+{{1 \over {\gamma _2}}{\tilde{\theta }_g^T}{\dot{\tilde{\theta }}}_g}. \end{aligned}$$
(73)

Assumption 1

For given positive definite matrix Q and coefficients r and \(\rho \) there exists a positive definite matrix P,  which is the solution of the following matrix equation

$$\begin{aligned}&{{\left( A-B{K^T}\right) }^T}P+P{\left( A-B{K^T}\right) }-{P}B\left( {2 \over r}-{1 \over {\rho ^2}}\right) {B^T}\nonumber \\&\quad {P}+{Q}=0. \end{aligned}$$
(74)

Substituting Eq. (74) into \(\dot{V}\) yields after some operations

$$\begin{aligned} \dot{V}= & {} {-}{1 \over 2}{e^T}Qe+{1 \over 2}{e^T}PB\left( {2 \over r}-{1 \over \rho ^2}\right) {B^T}Pe\nonumber \\&+\,{B^T}Pe\left( {-{1 \over r}{e^T}PB}\right) \nonumber \\&+\,{B^T}Pe{\left( w+d_1\right) }+{1 \over {\gamma _1}}{\tilde{\theta }_f^T}{\dot{\tilde{\theta }}_f}+ {1 \over {\gamma _2}}{\tilde{\theta }_g^T}{\dot{\tilde{\theta }}_g}. \end{aligned}$$
(75)

It holds that

$$\begin{aligned} \dot{\tilde{\theta }}_f= & {} \dot{\theta }_f-\dot{\theta _f^*}=\dot{\theta }_f, \nonumber \\ \dot{\tilde{\theta }}_g= & {} \dot{\theta }_g-\dot{\theta _g^*}=\dot{\theta }_g. \end{aligned}$$
(76)

The following weight adaptation laws are considered [36]

$$\begin{aligned} {\dot{\theta }_f}= & {} {\left\{ \begin{array}{ll} \begin{array}{l} -{\gamma _1}{e^T}{P}B{\phi (x)} \, if \, ||\theta _f||<m_{\theta _f}, \\ 0 \ if \ ||\theta _f|| \ge m_{\theta _f}, \end{array} \end{array}\right. } \end{aligned}$$
(77)
$$\begin{aligned} {\dot{\theta }_g}= & {} {\left\{ \begin{array}{ll} \begin{array}{l} -{\gamma _2}{e^T}{P}B{\phi (x)}{u_c} \, if \, ||\theta _g||<m_{\theta _g}, \\ 0 \ if \ ||\theta _g|| \ge m_{\theta _g}. \end{array} \end{array}\right. } \end{aligned}$$
(78)

\(\dot{\theta }_f\) and \(\dot{\theta }_g\) are set to 0, when

$$\begin{aligned} \left\| \theta _f\right\| \ge m_{\theta _f},\quad \left\| \theta _g\right\| \ge m_{\theta _g}. \end{aligned}$$
(79)

The update of \(\theta _f\) stems from a LMS algorithm on the cost function \({1 \over 2}(f-\hat{f})^2.\) The update of \(\theta _g\) is also of the LMS type, while \(u_c\) implicitly tunes the adaptation gain \(\gamma _2.\) Substituting Eqs.  (77) and (78) in \(\dot{V}\) finally gives

$$\begin{aligned} \dot{V}= & {} {-}{1 \over 2}{e^T}Qe-{1 \over {2\rho ^2}}{e^T}PB{B^T}Pe+{e^T}PB{\left( w+d_1\right) }\nonumber \\&-\,{e^T}PB{\left( \theta _f-\theta _f^{*}\right) ^T}\phi (x)\nonumber \\&-\,{e^T}PB{\left( \theta _g-\theta _g^{*}\right) ^T}\phi (x){u_c} \Rightarrow \nonumber \\ \dot{V}= & {} {-}{1 \over 2}{e^T}Qe-{1 \over {2\rho ^2}}{e^T}PB{B^T}Pe\nonumber \\&+\,{e^T}PB\left( w+d_1\right) +{e^T}PB{w_{\alpha }}. \end{aligned}$$
(80)

Denoting \(w_1=w+d_1+w_{\alpha }\) one gets

$$\begin{aligned} \dot{V}= & {} {-}{1 \over 2}{e^T}Qe-{1 \over {2\rho ^2}}{e^T}PB{B^T}Pe+{e^T}PB{w_1} \nonumber \\&\text {or equivalently},\nonumber \\ \dot{V}= & {} -{1 \over 2}{e^T}Qe-{1 \over {2\rho ^2}}{e^T}PB{B^T}Pe+{1 \over 2}{e^T}PB{w_1}\nonumber \\&+\,{1 \over 2}{w_1^T}{B^T}Pe. \end{aligned}$$
(81)

Lemma

The following inequality holds:

$$\begin{aligned}&{1 \over 2}{e^T}{P}B{w_1}+{1 \over 2}{w_1^T}{B^T}{P}{e}-{1 \over {2{\rho ^2}}}{e^T}{P}B{B^T}{P}{e} \nonumber \\&\quad \le {1 \over 2}{\rho ^2}{w_1^T}{w_1}. \end{aligned}$$
(82)

Proof

The binomial \(\left( {\rho }a-{1 \over \rho }b\right) ^2 \ge 0\) is considered. Expanding the left part of the above inequality one gets

$$\begin{aligned}&{\rho ^2}{a^2}+{1 \over {\rho ^2}}{b^2}-2ab \ge 0 \Rightarrow {1 \over 2}{\rho ^2}{a^2}+{1 \over {2\rho ^2}}{b^2}-ab \ge 0 \Rightarrow \nonumber \\&ab-{1 \over {2\rho ^2}}{b^2} \le {1 \over 2}{\rho ^2}{a^2} \Rightarrow {1 \over 2}ab+{1 \over 2}ab-{1 \over {2\rho ^2}}{b^2} \le {1 \over 2}{\rho ^2}{a^2}.\nonumber \\ \end{aligned}$$
(83)

The following substitutions are carried out: \(a=w_1\) and \(b={e^T}{P}B\) and the previous relation becomes

$$\begin{aligned} {1 \over 2}{w_1^T}{B^T}{P}{e}+{1 \over 2}{e^T}{P}B{w_1}-{{1 \over {2\rho ^2}} {e^T}{P}B{B^T}{P}{e}} \le {1 \over 2} {\rho ^2}{w_1^T}{w_1}.\nonumber \\ \end{aligned}$$
(84)

The previous inequality is used in \(\dot{V},\) and the right part of the associated inequality is enforced

$$\begin{aligned} \dot{V} {\le } -{1 \over 2}{{e^T}Qe}+{1 \over 2}{\rho ^2}{w_1^T}{w_1}. \end{aligned}$$
(85)
Fig. 4
figure 4

Convergence of the robot’s state variables (blue line): a setpoint 1 and b setpoint 2 (red line)

Full size image

Equation (85) can be used to show that the \(H_{\infty }\) performance criterion is satisfied. For \(\rho \) sufficiently small the right part of the previous inequality will remain upper bounded by zero, and in this manner the asymptotic stability of the control loop is demonstrated. Additionally, the integration of \(\dot{V}\) from 0 to T gives

$$\begin{aligned} {\int _0^T}{\dot{V}(t)}dt \le -{1 \over 2} {\int _0^T}{||e||^2}dt+{1 \over 2}{\rho ^2}{\int _0^T}{||w_1||^2}dt \Rightarrow \nonumber \\ 2V(T)+{\int _0^T}{||e||_Q^2}dt \le 2V(0)+ {\rho ^2}{\int _0^T}{||w_1||^2}dt. \end{aligned}$$
(86)

Moreover, if there exists a positive constant \(M_w>0\) such that

$$\begin{aligned} \int _0^{\infty }{\left\| w_1\right\| ^2}dt \le M_w, \end{aligned}$$
(87)

then one gets

$$\begin{aligned} {\int _0^{\infty }}{||e||_Q^2}dt \le 2V(0)+{\rho ^2}{M_w}. \end{aligned}$$
(88)

Thus, the integral \({\int _0^{\infty }}{||e||_Q^2}dt\) is bounded. Moreover, V(T) is bounded and from the definition of the Lyapunov function V in Eq. (72) it becomes clear that e(t) will be also bounded since \(e(t) \in \Omega _e=\{e|{e^T}Pe{\le }2V(0)+{\rho ^2}{M_w}\}.\)

According to the above and with the use of Barbalat’s Lemma one obtains \(lim_{t \rightarrow \infty }{e(t)}=0.\)

Simulation Tests

The efficiency of the proposed adaptive fuzzy control scheme for the underactuated robotic manipulator was evaluated in the tracking of various setpoints for state variable \(q_1,\) i.e., the linear displacement of mass \(M_1\) of the mechanism and state variable \(q_3,\) i.e., the rotation angle of joint A. As it can be observed in Figs. 4, 5 and 6, the proposed control scheme enabled accurate tracking of the reference setpoints by the robot’s state variables. Indicative results about the estimation of unknown functions \(f_v(x,\,t)\) and \(g_v(x,\,t)\) in the robot’s dynamics by the neurofuzzy approximators is shown in Fig.  7. By including an additional term in the control loop that was based on the disturbances estimation it became possible to compensate for the disturbances effects.

Fig. 5
figure 5

Convergence of the robot’s state variables (blue line): a to setpoint 3 and b to setpoint 4 (red line)

Full size image
Fig. 6
figure 6

Convergence of the robot’s state variables (blue line): a to setpoint 5 and b to setpoint 6 (red line)

Full size image
Fig. 7
figure 7

Estimation of functions \(f_v(x,\,t)\) and \(g_v(x,\,t)\) of the robot dynamics by neurofuzzy networks when tracking: a setpoint 1 and b setpoint 2

Full size image

Remark 1 Flatness-based adaptive control approach is a completely model-free control method. Flatness-based adaptive fuzzy control needs no prior knowledge about the system’s dynamics (apart from the order of the system), and also needs no prior knowledge about the values of the parameters of the system’s model. The proposed flatness-based adaptive fuzzy control approach can be applied to both robotic systems that admit static feedback linearization as well as to robotic models that admit dynamic feedback linearization. The necessary and sufficient condition for the application of the proposed adaptive fuzzy control method is the robot system to be differentially flat. This enables the use of adaptive fuzzy control to a wide class of dynamical systems.

Remark 2 Flatness-based control can be applied to a wider class of dynamical systems than Lie algebra-based control. This is because the necessary and sufficient condition for the application of flatness-based adaptive fuzzy control is the system to be differentially flat. This covers the widest class of nonlinear dynamical systems. On the other side, the necessary and sufficient condition for the application of Lie algebra-based control is the system to be input-to-state linearizable. This constrains the application of the method to a more narrow class of dynamical systems. Besides, by using differential flatness theory one can solve simultaneously the control and state estimation problem for the case of nonlinear underactuated robotic manipulators, without the need appearing in the Lie algebra-based approach for computing Jacobian matrices of the system’s transformed state vector.

Remark 3 Comparison of flatness-based adaptive control to other nonlinear control methods. (i) An alternative global linearization-based control method is Lie algebra-based control. However, as mentioned above this is applicable to a more constrained class of robotic systems. Moreover, to solve the associated state estimation and filtering problems the method requires the computation of Jacobian matrices, (ii) another option is local linearization-based control methods. These make use of approximately linearized dynamical models of the robot which are obtained round local operating points (equilibria). This linearization procedure requires Taylor series expansion of the robotic model and the computation of Jacobian matrices, which in the case of multi-DOF robots can be a computationally demanding procedure. Besides, the use of an approximately linearized method introduces to the control loop inherent modelling errors and perturbations which should be continuously suppressed by the robustness of the feedback controller.

Remark 4 The state variables of the underactuated robot are \(x_1=q_1,\,x_2=q_3,\,x_3=\dot{q}_1\) and \(x_4=\dot{q}_3\) where \(q_1\) is displacement of mass \(m_1\) along the horizontal axis x,  and \(q_3\) is rotation angle of the joint mounted on mass \(m_1\) which finally denotes the turn of the first link. State variable \(x_3=\dot{q}_1\) is the first order derivative of \(x_1\) and denotes the linear velocity of mass \(m_1\) along the x axis. State variable \(x_4=\dot{q}_3\) is the first order derivative of \(x_2\) and denotes the angular velocity of the joint mounted on mass \(m_1.\) The flat output of the robot’s state-space model is given in Eq. (37) and is a linear function of state variables \(x_1\) and \(x_3.\) It has been shown that state variables \(x_3\) and \(x_4\) can be directly expressed as differential functions of this flat output. The dynamics of the robot is considered to be described by Eq. (5) which uses as state variables \([q_1,\,q_3]^T\) and their derivatives. According to Eqs. (2)–(4), the right part of the robotic mechanism which is described by state variables \([q_2,\,q_4]^T\) appears to be decoupled from state variables \([q_1,\,q_3]^T,\) therefore its control can be analyzed in a similar manner as in the case of the left part of the mechanism.

Remark 5 A difference between the neurofuzzy approximator depicted in Fig. 3 and a RBF neural network is the normalization layer that appears between the Gaussian basis functions layer and the weights output layer. After normalization, the sum (over the complete set of rules) of the fuzzy membership values of each input pattern becomes equal to 1. The neurofuzzy model provides also linguistic interpretability (in terms of fuzzy rules) about the implemented control law [38].

Conclusions

The paper has examined the problem of flatness-based adaptive fuzzy control for closed-chain underactuated robotic mechanisms. First, the concept of differential flatness was analyzed. It was shown that a system is considered to be differentially flat if (i) the so-called flat-output can be defined (the flat output is a function of the system’s state variables for which it is assured that it is not coupled to its derivatives through an ODE), (ii) the system’s state variables and the control inputs can be all expressed as functions of the differentially flat output and its derivatives.

The paper was concerned with closed underactuated robotic mechanisms which stand for single-input differentially flat systems. However the results can be also generalized for the case of MIMO systems. Such systems can be brought to a Brunovsky (canonical form) through a nonlinear transformation applied to the state variables and to the control input. The resulting control signal was shown to contain nonlinear elements which in turn depend on the system’s parameters. If the parameters of the system are unknown, then the nonlinear elements which appear in the control signal can be calculated by approximating the unknown system dynamics with the use of neuro-fuzzy networks. It was shown that through Lyapunov stability analysis one can compute a learning law for the aforementioned neuro-fuzzy approximators which assures stability of the control loop. Moreover, it was shown that the proposed adaptation law assures \(H_{\infty }\) tracking performance for the closed-loop system. Finally, the efficiency of the considered flatness-based control scheme was tested through simulation experiments on the tracking of various reference setpoints.