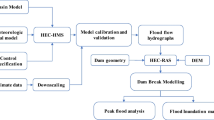
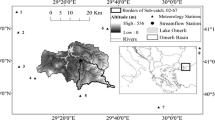
Abstract
The climate change effects on the variation and distribution of precipitation at 15 vital dam sites (large dams) located over the Godavari River Basin (GRB) are investigated in this study. The Time-Varying Downscaling Model (TVDM) technique is employed for this purpose. The data for daily rainfall at 0.25 × 0.25 degrees grid size are obtained from IMD, Pune. The CanESM2 outputs were considered as predictor variables. The calibration and validation of TVDM was carried out using the historical rainfall data (1951–2010). Next, the future variation (2011–2100) of rainfall over the GRB is analyzed using three Representative Concentration Pathway (RCP) climate change scenarios viz. RCP2.6, 4.5 and 8.5. Further, the extreme rainfall events which are generating the floods in the selected locations are analyzed using the extreme percentile values (90th and 95th). The variations of these extreme values in the future (2011–2100) are judge against the baseline (1971–2000) data for analyzing the possible impacts of climate change. The results reveal that the magnitude and the count of extreme events are expected to intensify in the future period. In comparison with the baseline data, all the study locations are expected to experience an increase of 3.61–38.93% in the 95th percentile values according to the RCP8.5 scenario. Furthermore, rainfall frequency analysis is also conducted to evaluate the potential hazards associated with flooding. The results show that the extreme events are more frequent with high magnitude during the future period compared to the baseline data. It implies a vulnerable situation to most of the dams in the GRB during the future period and effect will be worst as per RCP8.5 scenario. The outcomes of this research are expected to aid stakeholders to develop good strategies for safeguarding through the better maintenance, management of the dams and reservoirs in the wake of Climate Change.




Similar content being viewed by others
Data availability
All the data sets used in this study are freely available. However, if readers/users face any difficulty to access the data sets, the authors are happy to provide the same upon gentle request for the same. This study uses the observed rainfall data from IMD, Pune, it can be accessible at https://www.imdpune.gov.in/cmpg/Griddata/Rainfall_25_Bin.html. The large-scale GCM data sets are downloaded from the CMIP-5 web portal which are available upon successful registration to the CMIP web portal at https://esgf-node.llnl.gov/projects/cmip5/.
References
Adib A, Haidari B, Lotfirad M, Sasani H (2023) Evaluating climatic change effects on EC and runoff in the near future (2020–2059) and far future (2060–2099) in arid and semi-arid watersheds. Appl Water Sci. https://doi.org/10.1007/s13201-023-01926-1
Basha G, Kishore P, Ratnam MV, Jayaraman A, Kouchak AA, Ouarda TBMJ, Velicogna I (2017) Historical and projected surface temperature over India during the 20th and 21st century. Sci Rep. https://doi.org/10.1038/s41598-017-02130-3
Bhadoriya UPS, Mishra A, Singh R, Chatterjee C (2020) Implications of climate change on water storage and filling time of a multipurpose reservoir in India. J Hydrol (amst) 590:125542. https://doi.org/10.1016/j.jhydrol.2020.125542
Bombelli GM, Tomiet S, Bianchi A, Bocchiola D (2021) Impact of prospective climate change scenarios upon hydropower potential of Ethiopia in gerd and gibe dams. Water (switzerland) 13(5):716. https://doi.org/10.3390/w13050716
Brekke LD, Maurer EP, Anderson JD, Dettinger MD, Townsley ES, Harrison A, Pruitt T (2009) Assessing reservoir operations risk under climate change. Water Resour Res. https://doi.org/10.1029/2008WR006941
Brown PH, Tullos D, Tilt B, Magee D, Wolf AT (2009) Modeling the costs and benefits of dam construction from a multidisciplinary perspective. J Environ Manag 90(SUPPL. 3):S303–S311. https://doi.org/10.1016/j.jenvman.2008.07.025
Chavan CS, Chipade A, Ghadvir G, Deshpande M (2023) Statistical analysis of rainfall data using non-parametric methods of Solapur District, Maharashtra, India. E3S Web Conf 405:04046. https://doi.org/10.1051/e3sconf/202340504046
Christensen NS, Lettenmaier DP (2007) A multimodel ensemble approach to assessment of climate change impacts on the hydrology and water resources of the Colorado River Basin. Hydrol Earth Syst Sci 11:1417–1434
Cui T, Tian F, Yang T, Wen J, Khan MYA (2020) Development of a comprehensive framework for assessing the impacts of climate change and dam construction on flow regimes. J Hydrol (amst) 590:125358. https://doi.org/10.1016/j.jhydrol.2020.125358
Das J, Umamahesh NV (2016) Downscaling monsoon rainfall over river Godavari basin under different climate-change scenarios. Water Resour Manag 30(15):5575–5587. https://doi.org/10.1007/s11269-016-1549-6
Firoozi F, Roozbahani A, Massah Bavani AR (2020) Developing a framework for assessment of climate change impact on thermal stratification of dam reservoirs. Int J Environ Sci Technol 17(4):2295–2310. https://doi.org/10.1007/s13762-019-02544-8
Fluixá-Sanmartín J, Altarejos-García L, Morales-Torres A, Escuder-Bueno I (2018) Review article: Climate change impacts on dam safety. Nat Hazards and Earth Syst Sci 18(9):2471–2488. https://doi.org/10.5194/nhess-18-2471-2018
Garg S, Mishra V (2019) Role of extreme precipitation and initial hydrologic conditions on floods in Godavari River Basin, India. Water Resour Res 55(11):9191–9210. https://doi.org/10.1029/2019WR025863
Hassan WH, Hashim FS (2020) The effect of climate change on the maximum temperature in Southwest Iraq using HadCM3 and CanESM2 modelling. SN Appl Sci. https://doi.org/10.1007/s42452-020-03302-z
Hossain F, Jeyachandran I, Pielke R (2010) Dam safety effects due to human alteration of extreme precipitation. Water Resour Res. https://doi.org/10.1029/2009WR007704
Jafarpour M, Adib A, Lotfirad M, Kisi Ö (2023) Spatial evaluation of climate change-induced drought characteristics in different climates based on De Martonne Aridity Index in Iran. Appl Water Sci. https://doi.org/10.1007/s13201-023-01939-w
Javaherian M, Ebrahimi H, Aminnejad B (2021) Prediction of changes in climatic parameters using CanESM2 model based on Rcp scenarios (case study): Lar dam basin. Ain Shams Eng J 12(1):445–454. https://doi.org/10.1016/j.asej.2020.04.012
Kingsford RT (2011) Conservation management of rivers and wetlands under climate change: a synthesis. Mar Freshw Res 62(3):217–222. https://doi.org/10.1071/MF11029
Kite G (2001) Modelling the Mekong: hydrological simulation for environmental impact studies. J Hydrol (amst) 253(1–4):1–13. https://doi.org/10.1016/S0022-1694(01)00396-1
Krishnan R, Sanjay J, Chellappan G, Mujumdar M, Kulkarni A, Chakraborty S (2020) Assessment of climate change over the Indian region a report of the Ministry of Earth Sciences (MoES), Government of India
Loza ARA, Fidélis T (2021) Literature review on the analysis of climate change risks in the environmental impact assessment of dams. Impact Assess Project Appraisal 39(4):277–289. https://doi.org/10.1080/14615517.2021.1893928
Maity R, Nagesh Kumar D (2006) Bayesian dynamic modeling for monthly Indian summer monsoon rainfall using El Niño-Southern Oscillation (ENSO) and Equatorial Indian Ocean Oscillation (EQUINOO). J Geophys Res 111(7):1–12. https://doi.org/10.1029/2005JD006539
Malede DA, Agumassie TA, Kosgei JR, Andualem TG, Diallo I (2022) Recent approaches to climate change impacts on hydrological extremes in the Upper Blue Nile Basin, Ethiopia. Earth Syst Environ 6(3):669–679. https://doi.org/10.1007/s41748-021-00287-6
Manapragada NVSK, Shukla AK, Pignatta G, Yenneti K, Shetty D, Nayak BK, Boorla V (2022) Development of the Indian future weather file generator based on representative concentration pathways. Sustainability (switzerland) 14(22):15191. https://doi.org/10.3390/su142215191
Mehrotra R (1999) Sensitivity of runoff, soil moisture and reservoir design to climate change in Central Indian river basins. Clim Chang 42:725–757. https://doi.org/10.1023/A:1005496932343
Momiyama S, Sagehashi M, Akiba M (2020) Assessment of the climate change risks for inflow into Sagami dam reservoir using a hydrological model. J Water Clim Chang 11(2):367–379. https://doi.org/10.2166/wcc.2018.256
Nagesh Kumar D, Maity R (2008) Bayesian dynamic modeling for nonstationary hydroclimatic time series forecasting along with uncertainty quantification. Hydrol Process 22:3488–3499. https://doi.org/10.1002/hyp.6951
Nauman S, Zulkafli Z, Bin Ghazali AH, Yusuf B (2019) Impact assessment of future climate change on streamflows upstream of Khanpur Dam, Pakistan using soil and water assessment tool. Water (switzerland) 11(5):1090. https://doi.org/10.3390/w11051090
Norouzi N (2020) Climate change impacts on the water flow to the reservoir of the Dez Dam basin. Water Cycle 1:113–120. https://doi.org/10.1016/j.watcyc.2020.08.001
Palmer MA et al (2008) Climate change and the world’s river basins: anticipating management options. Ecol Soc America 6(2):81–89. https://doi.org/10.1890/060148
Park JY, Kim SJ (2014) Potential impacts of climate change on the reliability of water and hydropower supply from a multipurpose dam in South Korea. J Am Water Resour Assoc 50(5):1273–1288. https://doi.org/10.1111/jawr.12190
Pham HX, Shamseldin AY, Melville BW (2021) Projection of future extreme precipitation: a robust assessment of downscaled daily precipitation. Nat Hazards 107(1):311–329. https://doi.org/10.1007/s11069-021-04584-1
Pichuka S, Maity R (2018) Development of a time-varying downscaling model considering non-stationarity using a Bayesian approach. Int J Climatol 38(7):3157–3176. https://doi.org/10.1002/joc.5491
Priya P, Krishnan R, Mujumdar M (2020) Uncertainties in river discharge simulations of the upper Indus basin in the Western Himalayas. J Earth Syst Sci. https://doi.org/10.1007/s12040-020-01409-w
Raghav P, Eldho TI (2023) Investigations on the hydrological impacts of climate change on a river basin using macroscale model H08. J Earth Syst Sci. https://doi.org/10.1007/s12040-023-02102-4
Raje D, Mujumdar PP (2010) Reservoir performance under uncertainty in hydrologic impacts of climate change. Adv Water Resour 33(3):312–326. https://doi.org/10.1016/j.advwatres.2009.12.008
Ramabrahmam K, Keesara VR, Srinivasan R, Pratap D, Sridhar V (2023) Climate change impact on water resources of tank cascade systems in the Godavari Sub-Basin, India. Water Resour Manag 37(6–7):2853–2873. https://doi.org/10.1007/s11269-023-03496-y
Sanyal J, Wesley Lauer J, Kanae S (2021) Examining the downstream geomorphic impact of a large dam under climate change. Catena (amst) 196:104850. https://doi.org/10.1016/j.catena.2020.104850
Sarhadi A, Burn DH, Ausin MC, Wiper MP (2016) Time-varying nonstationary multivariate risk analysis using a dynamic Bayesian copula. Water Resour Res 52:2327–2349. https://doi.org/10.1002/2015WR018525
Sharma DK (2020) Impact of climate change on the flow regime and operation of reservoirs: a case study of Bhakra and Pong Dams. INCOLD J 9(1):4–15
Sharma DK, Vyas A, Agarwal T, Singh S (2023) Challenges posed by climate change and sedimentation of reservoirs for flood mitigation and sustained water supply. INCOLD J 10(1):18–30
Shokouhifar Y, Lotfirad M, Esmaeili-Gisavandani H, Adib A (2022) Evaluation of climate change effects on flood frequency in arid and semi-arid basins. Water Supply 22(8):6740–6755. https://doi.org/10.2166/ws.2022.271
Singh AK, Mani M, Vishnoi R (2022) Tehri dam–a savior from climate change led extreme events. INCOLD J 11(2):29–35
Thomas T, Ghosh NC, Sudheer KP (2021) Optimal reservoir operation: a climate change adaptation strategy for Narmada basin in central India. J Hydrol (amst) 598:126238. https://doi.org/10.1016/j.jhydrol.2021.126238
Tyralis H, Koutsoyiannis D (2014) A Bayesian statistical model for deriving the predictive distribution of hydroclimatic variables. Clim Dyn 42(11–12):2867–2883. https://doi.org/10.1007/s00382-013-1804-y
Vrugt JA, Braak CJF, Gupta HV, Robinson BA (2009) Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling? Stoch Env Res Risk Assess 23:1011–1026. https://doi.org/10.1007/s00477-008-0274-y
Watts RJ, Richter BD, Opperman JJ, Bowmer KH (2011) Dam reoperation in an era of climate change. Mar Freshw Res 62(3):321–327. https://doi.org/10.1071/MF10047
West M, Harrison PJ (1997) Bayesian forecasting and dynamic models. Springer, New York
Xu X, Tan Y, Yang G (2013) Environmental impact assessments of the three Gorges Project in China: issues and interventions. Earth Sci Rev 124:115–125. https://doi.org/10.1016/j.earscirev.2013.05.007
Yang J, Reichert P, Abbaspour KC, Yang H (2007) Hydrological modelling of the Chaohe Basin in China: statistical model formulation and Bayesian inference. J Hydrol 340:167–182. https://doi.org/10.1016/j.jhydrol.2007.04.006
Zhang J, Ma S, Song Y (2022) Hydrological and water quality simulation and future runoff prediction under CMIP6 scenario in the upstream basin of Miyun Reservoir. J Water Clim Chang 13(7):2505–2530. https://doi.org/10.2166/wcc.2022.389
Acknowledgements
The Department of Science and Technology (DST), Ministry of Science and Technology, Government of India, provided financial support (SRG/2020/000823) for conducting this research, for which the authors express their gratitude. The authors also extend their thanks to the India Meteorological Department (IMD) for providing the required data for this study.
Funding
DST SERB, SRG/000823/2020, Subbarao Pichuka.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Annexure – I
Table A1 (see Table 6)
Table A2 (see Table 7)
Outline of the time-varying downscaling model (TVDM)
TVDM is developed by considering the time-varying association between large-scale (causal) variables and the target variable. The methodology is developed based on the parameter updating ability of the Bayesian approach (West and Harrison 1997). Many recent studies related to climate change have adopted the Bayesian approach. For instance, the prediction of hydroclimatic variables, the quantification of water quality, uncertain runoff calculations are some of them (Maity and Nagesh Kumar 2006; Nagesh Kumar and Maity 2008; Sarhadi et al. 2016; Tyralis and Koutsoyiannis 2014; Vrugt et al. 2009; Yang et al. 2007).
The monthly meteorological mean of the target time series is hypothesized to have a deterministic component and a stochastic component. The information about causal variables has been used to estimate the stochastic component, which is added to the deterministic part. Then the causal and target variables are standardized. For standardizing a variable, the long-term mean (µ) is subtracted from the variable value at any time step and then it is divided by the long-term standard deviation (σ). Hereafter the causal and target variables are referred as standardized variables. The methodology of TVDM can be found from Pichuka and Maity (2018). For brevity, the key equations of TVDM are presented in this paper as follows
The downscaled target variable at time step t is expressed in the form of
where \(Y_{t}\) is the target variable to be downscaled at time step t,
\(D_{t - 1}\) is the initial information provided by the modeler to initialize the TVDM,
n is degree of freedom.
n for tth time step is given as
The expressions for \(F_{t}\) and \(Q_{t}\) are expressed as –
where \(\overline{{Y_{t} }}\) is the climatological mean value of the target variable at tth time step,
\(x_{t}^{1} ,\,x_{t}^{2} ,\,x_{t}^{3} ,....x_{t}^{z}\) are the standardized causal variables at the tth time step,
\(m_{t - 1}^{1} ,\;m_{t - 1}^{2} ,....m_{t - 1}^{z}\) are the model parameters supplied by the modeler at initial time step.
\(R_{t}\) is expressed as
where \(\delta\) is termed as discount factor and ranges between 0 and 1. The value of \(\delta\) denotes the fact that the system evolution variance increases from time to time (i.e., t to t + 1), i.e., more uncertainty present in the future information. The optimum value of \(\delta\) is obtained based on model performance. The higher the value, the lower the rate of decay of past information and vice versa (West and Harrison 1997).
The optimum value of \(\delta\) is estimated on the basis of model performance. It is also noteworthy that higher values of \(\delta\) indicate slower rate of decay of previous information and vice versa (West and Harrison 1997).
\(S_{t - 1}\) is expressed as
The parameters \(m_{0}\),\(C_{0}\), \(n_{0}\), and \(d_{0}\) are to be supplied to the TVDM as the initial information for all the causal variables. The parameter values (henceforth m values) are updated through a system of equations till the development period. The target variable is obtained at every time step based on Eq. 4. Further, the m values are projected for the future period to obtain the target variable. The projection is carried out by considering the deterministic part (trend and periodicity) and stochastic part of the m values from development period. Once the future m values are projected, the target variable is downscaled from Eq. 4. The required causal variables are obtained from various scenarios (RCPs) of selected GCM. The procedure of updating m values, system of equations to update these m values, and their projection during the future period are presented in the following section.
Updating and projection of the parameter values (m values)
To update the parameters from the time step \(\left( {t - 1} \right)\) to \(t\), where \(t = 2,\,3,\,4,\,...\), N, the value of \(R_{t}\) (given in Eq. 6) is updated for next time step \(t\); to do so, the value of \(C_{t}\) should be known and is given as
Finally, the downscaled target variable at time step t is expressed in the form of Eq. (2) and the downscaled values are obtained using Eqs. (3–5).
The m values are updated through system of equations presented below.
where \(A_{t}\) is given as
For the next step, i.e., \(t + 1\), \(n_{t}\), and \(d_{t}\) are required to calculate \(Q_{t}\) using \(S_{t}\) (Eq. 7). These are expressed as:
The m values, \(m_{t}^{p} \left( {t = 1,\,2, \cdots \,,n\,\;and\,\,p = 1, \cdots ,z} \right)\) develop over time for all the input variables.
Projection of m values for future period
The projection of m values is carried out by considering the deterministic part (trend and periodicity) and stochastic part of the m values from development period. The stochastic part is captured by means of auto-regressive (AR) model. Thus, the time series of historical m values is modeled as:
where \(m_{t}^{{{\text{tr}}}}\), \(m_{t}^{{{\text{pr}}}}\), and \(m_{t}^{{{\text{st}}}}\) represent the linear trend component, periodic component, and the stochastic component, respectively, of the m values at time t. The \(m_{t}^{{{\text{tr}}}}\) is given by
where \(p_{1}\) and \(p_{2}\) are the regression coefficients those are obtained by least square method taking time as the independent variable. The periodic component, i.e., \(m_{t}^{{{\text{pr}}}}\) is modeled after separation of trend from the m values time series.
The equation for \(m_{t}^{{{\text{pr}}}}\) is expressed as
where \(m_{t}^{{{\text{pr}}}} (T)\) is harmonically fitted means at period \(T\) (\(T\) = 1, 2,…. \(P\)) and \(P\) is base period, which is calculated from the periodogram of the detrended time series of m values which is given as
where \(w\) is the index value corresponding to the peak of the periodogram; \(A_{0}\) = mean of historical m values and is given as
where \(X(T)\) is the detrended m values; h is number of harmonics, which is expressed as
\(A_{k}\) and \(B_{k}\) are known as sine and cosine Fourier coefficients, respectively, and written as
where k = 1, 2,…, h.
The residual left (after take out of trend and periodicity) is modeled by an AR model. The AR(1) model is obtained to be sufficient from the autocorrelogram and partial autocorrelogram analyses. Thus, an AR(1) model is given by
where \(m_{t}^{{{\text{st}}}}\) is the modeled stochastic component, \(b\) is the coefficient of the AR(1) model fitted to the residuals, and \(m_{t}^{{\text{e}}}\) is the error at the tth time step. Since the error \(m_{t}^{{\text{e}}}\) is assumed to be normally distributed with a mean 0 and standard deviation \(\sigma_{{{\text{e}}_{t} }}\) the expected value of \(m_{t}^{{{\text{st}}}} \left( { = b \times m_{t - 1}^{{{\text{st}}}} } \right)\) is used in Eq. (14).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Pichuka, S., Roulo, D. Dams and their safety under the extreme climate conditions: study of dams on Godavari River. Sustain. Water Resour. Manag. 10, 32 (2024). https://doi.org/10.1007/s40899-023-01018-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40899-023-01018-7