Abstract
Given an arbitrary set \(\Omega \), we consider the collections \(\textrm{SS}\hspace{0.55542pt}(\Omega )\), \(\textrm{SR}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) of all the set systems, the binary set relations and the set operators on \(\Omega \). We introduce the notion of linking map on \(\Omega \) as any map whose domain and codomain may be chosen between the above collections. After providing a descriptive overview useful for framing the notion of linking map in a broad non-specialized context, we explain how linking maps occur in a very natural way in two specific results. The first of these results concerns the classic identification between the subfamily \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) of all the equivalence relations on \(\Omega \) and the subfamily \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) of all the set partitions on \(\Omega \). Starting from it, we introduce a new subfamily \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) of closure operators on \(\Omega \) and four linking maps whose restrictions to the subfamilies \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\), \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) are bijections. The second result concerns the identification between the subfamily \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\) of all closure set operators on \(\Omega \) and the subfamily \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) of all closure set systems on \(\Omega \). Starting from it, we introduce a new subfamily \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\) of binary set relations and four linking maps whose restrictions to the subfamilies \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\), \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) and \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\) are again bijections. In an attempt to extend in a natural way the above linking maps to categorical isomorphisms, after fixing a nonnegative integer k, we introduce three categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\) and \(\mathbf{SO^k}\), whose detailed study mainly occupies the first part of the present work. Objects and arrows of these three categories are obtained by means of k-iterations of the powerset functor  , and they generalize the notions of set systems, set relations and set operators, respectively. In the second part of the paper, we extend the linking maps previously described at a categorical level in terms of isomorphisms between specific categories of set systems, binary set relations and set operators generalizing the occurring collections introduced before, and also prove numerous other results concerning the main properties of all these categories, such as completeness, cocompleteness and Cartesian closedness.
, and they generalize the notions of set systems, set relations and set operators, respectively. In the second part of the paper, we extend the linking maps previously described at a categorical level in terms of isomorphisms between specific categories of set systems, binary set relations and set operators generalizing the occurring collections introduced before, and also prove numerous other results concerning the main properties of all these categories, such as completeness, cocompleteness and Cartesian closedness.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Motivation and framing of the paper
In many contexts from both mathematics and theoretical computer science three types of families associated with an arbitrary fixed set \(\Omega \) assume a substantial relevance, namely the collection  of all set systems on \(\Omega \) (in the whole paper
of all set systems on \(\Omega \) (in the whole paper  denotes the powerset of \(\Omega \)), the collection
denotes the powerset of \(\Omega \)), the collection  of all set relations on \(\Omega \), and the collection \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) of all the maps
of all set relations on \(\Omega \), and the collection \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) of all the maps  , that are usually called set operators on \(\Omega \).
, that are usually called set operators on \(\Omega \).
More in detail, in the previous contexts, many notions and corresponding results may be reformulated and refined in terms of set systems, set relations, set operators and through appropriate maps between such collections. We will call linking maps on \(\Omega \) these kinds of maps, and set relation geometry on \(\Omega \) any fixed family of linking maps on \(\Omega \).
The main purpose of the present work is twofold:
-
to provide an accurate study of some types of linking maps, which permits to reinterpret classical results for equivalence relations and closure operators in much more general and categorical context (see Theorems 5.4 and 6.6);
-
to frame in a suitable way the notion of linking map in a categorical context, analyzing its functoriality after introducing new concretizable categories and subcategories [25] of set systems, set relations and set operators, by means of iterations of the usual powerset functor of the set category \(\textbf{Set}\).
There are many studies that fit within such a framework, and to this regard we refer the reader to a (not exhaustive) part of these works, some of which on pure mathematics [2, 6, 10, 17, 20, 21], and others on an intermediate scope between mathematics and theoretical computer science [22,23,24, 28, 29, 35]. However, two of the main sources of inspiration for the basic ideas developed in this work can be traced back to the coarse- and weak-shape theories, mainly dealt with in topological contexts (for details on these links, we refer the reader to [31]).
Two very relevant and common cases in large part of both mathematics and theoretical computer science concern the classic notions of equivalence relation and closure operator (recall that a set closure operator is a set operator which is extensive, increasing and idempotent).
Clearly, any element of \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) (i.e. the collection of all equivalence relations on \(\Omega \)) may be also uniquely identified with a corresponding element of \(\textrm{SR}\hspace{0.55542pt}(\Omega )\), simply by identifying any element \(x\in \Omega \) with the singleton  . Therefore we can see \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) as a subfamily of \(\textrm{SR}\hspace{0.55542pt}(\Omega )\). Let moreover \(\textrm{SP}\hspace{0.55542pt}(\Omega ) \subseteq \textrm{SS}\hspace{0.55542pt}(\Omega )\) be the collection of all set partitions on \(\Omega \) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) be the collection of a new type of set operators on \(\Omega \), that we call equivalence set operator. These are extensive set operators \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) for which \(\sigma (X)=\bigcup \hspace{0.55542pt}\{\sigma (\{x\}) \,{|}\, x \in X\}\) for each
. Therefore we can see \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) as a subfamily of \(\textrm{SR}\hspace{0.55542pt}(\Omega )\). Let moreover \(\textrm{SP}\hspace{0.55542pt}(\Omega ) \subseteq \textrm{SS}\hspace{0.55542pt}(\Omega )\) be the collection of all set partitions on \(\Omega \) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) be the collection of a new type of set operators on \(\Omega \), that we call equivalence set operator. These are extensive set operators \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) for which \(\sigma (X)=\bigcup \hspace{0.55542pt}\{\sigma (\{x\}) \,{|}\, x \in X\}\) for each  , and such that the condition \(\sigma (\{x\})=\sigma (\{y\})\) is equivalent to \(\sigma (\{x\})\cap \sigma (\{y\})\ne \varnothing \) for any \(x, y\in \Omega \) (see Definition 5.1).
, and such that the condition \(\sigma (\{x\})=\sigma (\{y\})\) is equivalent to \(\sigma (\{x\})\cap \sigma (\{y\})\ne \varnothing \) for any \(x, y\in \Omega \) (see Definition 5.1).
At a first elementary level, it is well known how to identify to each other the elements of \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SP}\hspace{0.55542pt}(\Omega )\). However, going further the aforementioned level, we can see that two more general maps \(\textrm{Pa}:\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) and \(\textrm{Eq}:\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SR}\hspace{0.55542pt}(\Omega )\), respectively defined by  for any
for any  , where
, where  , and by
, and by  , for each
, for each  , induce such an identification.
, induce such an identification.
It is clear that the two above maps \(\textrm{Pa}\) and \(\textrm{Eq}\) are not inverses of each other. Nevertheless, their corresponding restrictions to the subfamilies \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SP}\hspace{0.55542pt}(\Omega )\), respectively, are inverses of each other, providing the usual identification between equivalence relations and set partitions.
We now analyze the link between set partitions and equivalence set operators by means of maps between \(\textrm{SS}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SO}\hspace{0.55542pt}(\Omega )\). To this regard let \(\textrm{Up }:\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\), defined by  , for each
, for each  and any
and any  , and \(\textrm{Qa}:\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) defined by
, and \(\textrm{Qa}:\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) defined by  , for each \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\). Then, even in this case, the maps \(\textrm{Up}\) and \(\textrm{Qa}\) are not inverses of each other, but they become such after restricting them to the subfamilies \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\), respectively.
, for each \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\). Then, even in this case, the maps \(\textrm{Up}\) and \(\textrm{Qa}\) are not inverses of each other, but they become such after restricting them to the subfamilies \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\), respectively.
Another similar situation occurs when we consider the subfamilies \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\) of all closure set operators on \(\Omega \), \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) of all closure set systems on \(\Omega \) (they are set systems containing \(\Omega \) and closed with respect to arbitrary intersections) and \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\) of all dependence set relations on \(\Omega \) [14] (see Definition 6.1). In this case, let \(\eta :\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\), \(\textrm{Cl}:\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\), \(\Phi :\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SR}\hspace{0.55542pt}(\Omega )\) and \(\textrm{Fix}:\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) be the maps defined respectively by  ,
,  ,
,  and
and  , for any
, for any  ,
,  , \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) and
, \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) and  .
.
Then it results that the restriction of the map \(\textrm{Cl}\) to the subfamily \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) is the inverse of the restriction of the map \(\textrm{Fix}\) to the subfamily \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\). Moreover, the restriction of the map \(\Phi \) to the subfamily \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\) is the inverse of the map \(\eta \) to the subfamily \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\) (see Proposition 5.3).
The previous bijections between equivalence relations, set partitions, equivalence set operators, and between closure set operators, closure set systems, dependence set relations, provide two relevant examples of the possibility to describe classical results in terms of specific maps whose domain and codomain may be chosen between \(\textrm{SS}\hspace{0.55542pt}(\Omega )\), \(\textrm{SR}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SO}\hspace{0.55542pt}(\Omega )\). Because of their importance, we name these maps that we consider as the starting point of the present work.
Definition 1.1
Let \(\mathfrak {B},\mathfrak {C}\in \{\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega )\}\). We call any map \(\beta :\mathfrak {B}\longrightarrow \mathfrak {C}\) a linking map on \(\Omega \). We also call any collection of linking maps on \(\Omega \) a set relation geometry on \(\Omega \).
A particularly interesting situation occurs when one endows the ground set \(\Omega \) with some algebraic, topological, combinatorial or order structure, and investigates a fixed set relation geometry on such a mathematical structure. In fact, such a type of study can help to find new and non-trivial classifications of families of substructures which are naturally induced by the mutual interrelations of the linking maps that constitute the assigned relation geometry on \(\Omega \). Some recent studies in this perspective concern the cases where \(\Omega \) is an abelian variety over a finite field [26], a special type of \(\textrm{DG}\)-module [27], a particular space of polynomial automorphisms [4, 5], an integral domain [15, 19], a left-act of monoid [12], a module on a unitary ring [13], a finite lattice [11]. However, in the present paper we do not take any additional structure on the ground set \(\Omega \).
At this point it is convenient to frame the two specific aforementioned examples in a more formal way, introducing the next notion of sub-bijection, that will be a starting point in order to determine new corresponding categorial isomorphisms.
Definition 1.2
Let \(\mathfrak {B},\mathfrak {C}\in \{\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega )\}\). We say that a formal writing of the type

is a \((\mathfrak {B}, \mathfrak {C})\)-sub-bijection if \(\mathfrak {B}' \!\subseteq \mathfrak {B}\), \(\mathfrak {C}' \!\subseteq \mathfrak {C}\), and \(\beta :\mathfrak {B}\longrightarrow \mathfrak {C}\), \(\gamma :\mathfrak {C}\longrightarrow \mathfrak {B}\) are two linking maps such that:
-
(i)
 for all
for all  and
and  for all
for all  ;
; -
(ii)
 for all
for all  and
and  for all
for all  .
.
Moreover, if \(n\geqslant 2\) and \(\mathfrak {B}_1,\dots , \mathfrak {B}_n \in \{\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega )\}\), we say that the formal writing

is a \((\mathfrak {B}_1,\dots , \mathfrak {B}_n)\)-sub-bijection if

is a \((\mathfrak {B}_k, \mathfrak {B}_{k+1})\)-sub-bijection for each \(k=1,\dots ,n-1\).
By means of the above terminology and notations, we may express the bijection between equivalence relations, set partitions and equivalence set operators in terms of the following \((\textrm{SR}\hspace{0.55542pt}(\Omega ), \textrm{SS}\hspace{0.55542pt}(\Omega ), \textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection (see Proposition 5.3):

and, similarly, we may express the bijection between closure systems, closure operators and dependence relations in terms of the following \((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega ))\)-sub-bijection (see Proposition 6.4):

Clearly, when we have a set relation geometry whose linking maps are sub-bijections it is possible to carry out the results concerning specific subfamilies of set systems, and to express them in terms of set relations or set operators.
Note that in Definition 1.2 the bijections induced by the linking maps \(\beta \) and \(\gamma \) are their respective restrictions on \(\mathfrak {B}'\) and \(\mathfrak {C}'\). Therefore, one could question the real need for the introduction of the maps \(\beta \) and \(\gamma \) on the ambient families \(\mathfrak {B}\) and \(\mathfrak {C}\). The answer to such a legitimate question comes from our explicit desire to highlight that the bijections between \(\mathfrak {B}'\) and \(\mathfrak {C}'\) derive from maps defined on more general domains. To this regard, in fact, it can happen that there are two bijections between two pairs of distinct subfamilies \((\mathfrak {B}'\!,\mathfrak {C}')\) and \((\mathfrak {B}''\!,\mathfrak {C}'')\) of \(\mathfrak {B}\) and \(\mathfrak {C}\) which derive from a same pair \((\beta ,\gamma )\) of linking maps defined between \(\mathfrak {B}\) and \(\mathfrak {C}\). For instance, if \(\mathfrak {B}=\textrm{SS}\hspace{0.55542pt}(\Omega )\), \(\mathfrak {C}=\textrm{SO}\hspace{0.55542pt}(\Omega )\),  and
and  , then we get the further \((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection compared to the first of the sub-bijections explicited in (1)
, then we get the further \((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection compared to the first of the sub-bijections explicited in (1)

Similarly, when \(\Omega \) is a finite arbitrary set, the same maps give rise to the\((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection

where  and
and  \(\text {on }\Omega \}\).Hence, the bijections between different subfamilies of \(\mathfrak {B}\) and \(\mathfrak {C}\) might or might not derive from a same pair \((\beta ,\gamma )\) of linking maps. In other terms, from a conceptual point of view, two distinct situations occur. In our work, we want to highlight the case where the sub-bijections come from a given fixed pair \((\beta ,\gamma )\). The reason for that is related to the observation that various cryptomorphisms [16], beyond those previously described, that occur in matroid theory or topology arise starting from maps defined on domains that are more general than those between which the cryptomorphism is established. Clearly, when proceeding towards a categorical extension, it is not guaranteed that the behavior of the maps \(\beta \) and \(\gamma \) is functorial. Nevertheless, though such an obstruction may occur, in Definition 1.2 we emphasized the fact that the bijections among subfamilies of \(\mathfrak {B}\) and \(\mathfrak {C}\) arise from two fixed maps defined on a more general ambient.
\(\text {on }\Omega \}\).Hence, the bijections between different subfamilies of \(\mathfrak {B}\) and \(\mathfrak {C}\) might or might not derive from a same pair \((\beta ,\gamma )\) of linking maps. In other terms, from a conceptual point of view, two distinct situations occur. In our work, we want to highlight the case where the sub-bijections come from a given fixed pair \((\beta ,\gamma )\). The reason for that is related to the observation that various cryptomorphisms [16], beyond those previously described, that occur in matroid theory or topology arise starting from maps defined on domains that are more general than those between which the cryptomorphism is established. Clearly, when proceeding towards a categorical extension, it is not guaranteed that the behavior of the maps \(\beta \) and \(\gamma \) is functorial. Nevertheless, though such an obstruction may occur, in Definition 1.2 we emphasized the fact that the bijections among subfamilies of \(\mathfrak {B}\) and \(\mathfrak {C}\) arise from two fixed maps defined on a more general ambient.
Set relation geometries with their corresponding linking maps occur, more or less explicitly, in great part of both mathematical and theoretical computer science literature. To this regard, many works have been cited in the first part of the present subsection. Here we can further mention the monographs [32, 33], and again matroid theory, with regard to its classical results [34].
It is worthwhile noticing that all the previous notions rely on the hypothesis that the ground set \(\Omega \) is given. Thus it is natural to ask what happens to both the above collections and corresponding linking maps if the set \(\Omega \) is no longer fixed. In this case, we are clearly led to an analysis of the aforementioned collections and maps from a categorical outlook. In fact, it is natural to think of each element of the collections \(\textrm{SS}\hspace{0.55542pt}(\Omega )\), \(\textrm{SR}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) as a particular object of specific corresponding categories, and, possibly, each linking map as a particular type of functor among these categories or their subcategories. The introduction and the study of these categories, of some of their subcategories and of several functors defined between them is the primary purpose of the present paper, whose detailed content will be described in the next subsection.
1.2 Content of the paper
As mentioned in the previous subsection, our primary goal is to extend some classic linking maps to a categorical level. To this end, we first need to remove the fixed parameter given by the ground set \(\Omega \). Secondly, we need to determine specific families of arrows, allowing us to transform the aforementioned linking maps into suitable functors between these categories or between some of their subcategories. Our constructions rely in natural way on the k-th iterations of the usual powerset functor  , where k is a fixed nonnegative integer. The particular case which includes the study of the aforementioned linking maps corresponds to the value \(k=1\), and the case that includes the equivalence relations to the value \(k=0\).
, where k is a fixed nonnegative integer. The particular case which includes the study of the aforementioned linking maps corresponds to the value \(k=1\), and the case that includes the equivalence relations to the value \(k=0\).
Let us highlight that the categorical extension of linking maps passes from the suitable definition of morphisms. To this regard, as we will work with structures, i.e. sets endowed with set systems, set relations or set operators, a natural choice consists of working with structure-preserving functions.
More in detail, for any fixed integer \(k\geqslant 0\), let  be the composition of k times the powerset functor
be the composition of k times the powerset functor  (the case \(k=0\) corresponds to the identity functor). We first consider the category \(\mathbf{SS^k}\), whose objects are pairs of the form
(the case \(k=0\) corresponds to the identity functor). We first consider the category \(\mathbf{SS^k}\), whose objects are pairs of the form  , where \(\Omega \) is an arbitrary set (no longer fixed) and
, where \(\Omega \) is an arbitrary set (no longer fixed) and  is a set system on
is a set system on  when \(k\geqslant 1\), or simply a subset of \(\Omega \) if \(k=0\). As arrows between two given objects
when \(k\geqslant 1\), or simply a subset of \(\Omega \) if \(k=0\). As arrows between two given objects  and
and  of \(\mathbf{SS^k}\), we take the maps between sets \(f:\Omega \longrightarrow \Omega '\) for which
of \(\mathbf{SS^k}\), we take the maps between sets \(f:\Omega \longrightarrow \Omega '\) for which  , whenever
, whenever  . We call \(\mathbf{SS^k}\) the category of the k-set systems.
. We call \(\mathbf{SS^k}\) the category of the k-set systems.
Next we introduce the category \(\mathbf{SR^k}\) of the k-set relations, whose objects are pairs of the form  , where \(\Omega \) is an arbitrary set and
, where \(\Omega \) is an arbitrary set and  . The arrows of \(\mathbf{SR^k}\) from
. The arrows of \(\mathbf{SR^k}\) from  to
to  are the set maps \(f:\Omega \longrightarrow \Omega '\) such that
are the set maps \(f:\Omega \longrightarrow \Omega '\) such that  , whenever
, whenever  .
.
Finally, for any \(k \geqslant 1\) we introduce three categories of set operators, denoted by \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\), and called the k-set operator, \((k, \sqsubseteq )\)-set operator and \((k, \sqsupseteq )\)-set operator category, respectively. The objects of all these three categories are the pairs \((\Omega , \sigma )\), where \(\Omega \) is an arbitrary set, and \(\sigma \) is a set operator on  . However, they differ with respect to the arrows. More specifically, given two objects \((\Omega , \sigma )\) and \((\Omega , \sigma ')\), the corresponding arrows in the above three categories \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) are ordered pairs \((f,f')\) of set maps \(f, f':\Omega \longrightarrow \Omega '\) such that
. However, they differ with respect to the arrows. More specifically, given two objects \((\Omega , \sigma )\) and \((\Omega , \sigma ')\), the corresponding arrows in the above three categories \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) are ordered pairs \((f,f')\) of set maps \(f, f':\Omega \longrightarrow \Omega '\) such that  ,
,  and
and  , for any
, for any  , respectively.
, respectively.
For set operators, the situation is more complex than for the categories of set systems and set relations. In this case, indeed, it is necessary to introduce the above three specific types of arrows.
In Sect. 3, after introducing all the above categories, we establish the first basic properties of their arrows. To this regard, we characterize monomorphisms, epimorphisms and isomorphisms of the categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) (see Propositions 3.7, 3.8 and 3.9, respectively). With regard to the category \(\mathbf{SO^k}\), we characterize its isomorphisms (see Proposition 3.10), whereas the complete characterization of its monomorphisms and epimorphisms is left as an open question.
Section 4 contains three subsections. More in detail, in Sect. 4.1 we prove that both the categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) are bicomplete (see Theorems 4.1 and 4.2), while in Sect. 4.2 we show that both the categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) are Cartesian closed (see Theorem 4.6).
Finally, in Sect. 4.3 we prove some fundamental properties of the categories \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\). We will see that the two categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) are substantially different, though at a first glance their properties might seem to be in a certain sense dual.
In particular, in Theorem 4.7 we show that the category \(\mathbf{SO^k}\) is neither complete nor cocomplete since it does not admit neither the initial nor the terminal object. With regard to the remaining two categories, using the fact \(\mathbf{SO^{k,\sqsubseteq }}\) has both the initial and terminal object, whereas \(\mathbf{SO^{k,\sqsupseteq }}\) admits no initial object, we prove in Theorem 4.10 that the two categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) cannot be neither equivalent nor dually equivalent. Indeed, the main result of the present section (see Theorem 4.12) ensures the completeness of the category \(\mathbf{SO^{k,\sqsubseteq }}\), whereas in Proposition 4.15 we show that, in general, \(\mathbf{SO^{k,\sqsupseteq }}\) admits no equalizers, so that it turns out to be not complete.
In Sect. 5 we develop the considerations exposed in Sect. 1.1, concerning the extension at categorical level of the sub-bijection obtained in Proposition 5.3. To this regard, we first consider the full subcategory \(\textbf{EQ}\) of \(\mathbf{SR^0}\) whose objects are pairs  , where \(\Omega \) is an arbitrary set and
, where \(\Omega \) is an arbitrary set and  . Next, we introduce the subcategory \(\mathbf{ESO^{1,\sqsubseteq ,=}}\), whose objects are pairs \((\Omega ,\sigma )\), where \(\Omega \) is an arbitrary set and \(\sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\), and whose arrows are those of \(\mathbf{SO^{1,\sqsupseteq }}\) of the form (f, f).
. Next, we introduce the subcategory \(\mathbf{ESO^{1,\sqsubseteq ,=}}\), whose objects are pairs \((\Omega ,\sigma )\), where \(\Omega \) is an arbitrary set and \(\sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\), and whose arrows are those of \(\mathbf{SO^{1,\sqsupseteq }}\) of the form (f, f).
Finally we consider the category \(\textbf{SP}\) whose objects are pairs  , where \(\Omega \) is an arbitrary set,
, where \(\Omega \) is an arbitrary set,  and, for every two of its objects
and, for every two of its objects  and
and  , the corresponding arrows are the set maps \(f:\Omega \longrightarrow \Omega '\) such that
, the corresponding arrows are the set maps \(f:\Omega \longrightarrow \Omega '\) such that  , where \(\preceq \) denotes the usual refining partial order on \(\textrm{SP}\hspace{0.55542pt}(\Omega ')\).
, where \(\preceq \) denotes the usual refining partial order on \(\textrm{SP}\hspace{0.55542pt}(\Omega ')\).
Starting from of the above three categories with their corresponding arrows, we extend the linking maps given in the sub-bijection obtained in Proposition 5.3 to four corresponding functors, through which we prove in Theorem 5.4 the existence of isomorphisms between the categories \(\textbf{EQ}\), \(\mathbf{ESO^{1,\sqsubseteq ,=}}\) and \(\textbf{SP}\).
In Sect. 6 we deal with categories of closure operators, closure systems and dependence relations. Regarding closure set systems, we introduce the category \(\mathbf{CSS^1}\) as the full subcategory of \(\mathbf{SS^1}\) whose objects consists of the pairs  , where \(\Omega \) is an arbitrary set and
, where \(\Omega \) is an arbitrary set and  . Analogously, we consider the full subcategory \(\mathbf{DSR^1}\) of \(\mathbf{SR^1}\) whose objects consists of the pairs
. Analogously, we consider the full subcategory \(\mathbf{DSR^1}\) of \(\mathbf{SR^1}\) whose objects consists of the pairs  , where \(\Omega \) is an arbitrary set and /. Concerning closure operators, we need to introduce two distinct categories, namely \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\). Their objects agree and are the pairs \((\Omega ,\sigma )\), where \(\Omega \) is an arbitrary set and \(\sigma \in \textrm{CSO}\hspace{0.55542pt}(\Omega )\), while the arrows of \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) are those of \(\mathbf{SO^{1,\sqsubseteq }}\) of the form (f, f) (and, similarly, for the arrows of the category \(\mathbf{CSO^{1,\sqsupseteq ,=}}\)).
, where \(\Omega \) is an arbitrary set and /. Concerning closure operators, we need to introduce two distinct categories, namely \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\). Their objects agree and are the pairs \((\Omega ,\sigma )\), where \(\Omega \) is an arbitrary set and \(\sigma \in \textrm{CSO}\hspace{0.55542pt}(\Omega )\), while the arrows of \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) are those of \(\mathbf{SO^{1,\sqsubseteq }}\) of the form (f, f) (and, similarly, for the arrows of the category \(\mathbf{CSO^{1,\sqsupseteq ,=}}\)).
In Theorem 6.5 we show that the category \(\mathbf{DSR^1}\) is complete. Next, we again develop the considerations discussed in Sect. 1.1 about the extension at a categorical level of the sub-bijection obtained in Proposition 6.4. To this regard, such a functorial extension has been provided in Theorem 6.6.
At this point it is appropriate to make a brief consideration regarding a comparison between the statements of Theorems 5.4 and 6.6. In fact, in Theorem 5.4, each of the three factors of the sub-bijection of Proposition 5.3 “extends to a unique category”, while, in Theorem 6.6, closure operators cannot be extended to a unique category in order to obtain the desired categorical isomorphisms. Actually, to achieve such an aim, we need to consider the two distinct categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) which, despite having the same objects, require different types of arrows.
Therefore, although Theorem 6.6 seems to yield a weaker kind of result than that of Theorem 5.4, it might lead to the development of future research perspectives, where one deals with the possible cases occurring when the determination of categorical isomorphisms (or equivalences) needs the introduction of categories, extending specific linking maps, and having the same class of objects but different arrows.
In Proposition 6.7 we prove some further basic results concerning the categories \(\mathbf{CSS^1}\), \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\). Finally, in Theorem 6.11 we prove the commutativity condition \(\Psi \hspace{1.111pt}{\circ }\hspace{1.111pt}\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}=\Psi =\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\Gamma \), where \(\Psi \) and \(\Gamma \) are two linking maps frequently used in theoretical computer science.
2 Notations and brief reviews on categories, set systems and set operators
In this brief preliminary section we introduce the main notations concerning categories and functors that we will use in the whole paper. Next, we also recall some fundamental notions on set systems, set operators and set relations.
If I is an index set and \(f_i:\Omega _i \longrightarrow \Omega '_i\) is a map between sets for any \(i \in I\), we denote by \(\prod \hspace{0.55542pt}\{f_i \,{|} \, i\,{\in }\,I\}\) their Cartesian product and we set  when \(I=\{1,\dots ,k\}\). Moreover, if \(\Omega _i=\Omega \) for any \(i \in I\), we denote by \({\dot{\prod }}\hspace{0.55542pt}\{f_i \,{|} \, i\,{\in }\,I\}\) the map from \(\Omega \) to \(\prod \hspace{0.55542pt}\{\Omega '_i \,{|} \, i\,{\in }\,I\}\) associating the element \((f_i(z))_{i \in I}\) with every \(z \in \Omega \).
when \(I=\{1,\dots ,k\}\). Moreover, if \(\Omega _i=\Omega \) for any \(i \in I\), we denote by \({\dot{\prod }}\hspace{0.55542pt}\{f_i \,{|} \, i\,{\in }\,I\}\) the map from \(\Omega \) to \(\prod \hspace{0.55542pt}\{\Omega '_i \,{|} \, i\,{\in }\,I\}\) associating the element \((f_i(z))_{i \in I}\) with every \(z \in \Omega \).
For all the main notions and results on categories, we refer the reader to [7,8,9], while, for the basics on classes and sets, we refer the reader to [30]. In this paper we only deal with covariant functors, so we use the term functor as equivalent to covariant functor. We denote by Set the usual category whose objects are sets and whose arrows are maps between sets.
Let \(\mathfrak {C}\) be a given category. We denote by \(\textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\) and \(\textrm{Arr}\hspace{0.55542pt}(\mathfrak {C})\) the classes of the objects and arrows (or equivalently morphisms) of \(\mathfrak {C}\), respectively. Moreover, if \(A, B \in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\), we denote by \(\textrm{Arr}_\mathfrak {C}(A, B)\) the arrows \(f\in \textrm{Arr}\hspace{0.55542pt}(\mathfrak {C})\) with A as domain and B as codomain.
If I is an index set and \(\{X_i\,{|}\, i\,{\in }\,I\}\) is a family of sets, we denote by \(\coprod \{X_i\,{|}\, i\,{\in }\,I\}\) the coproduct of \(\{X_i \,{|} \, i\,{\in }\,I\}\) in the category of sets. This is the disjoint union  . However, in this work, we always identify any set \(X_j\) with the subset \(X_j \hspace{0.55542pt}{\times }\hspace{1.111pt}\{j\}\) of \(\coprod \{X_i\,{|}\, i\,{\in }\,I\}\). Notice that if \(\xi _j:X_j \hookrightarrow X\) denotes the inclusion map and
. However, in this work, we always identify any set \(X_j\) with the subset \(X_j \hspace{0.55542pt}{\times }\hspace{1.111pt}\{j\}\) of \(\coprod \{X_i\,{|}\, i\,{\in }\,I\}\). Notice that if \(\xi _j:X_j \hookrightarrow X\) denotes the inclusion map and  , then
, then  .
.
Definition 2.1
A category \(\mathfrak {C}\) is called concretizable if there exists a faithful functor \(F:\mathfrak {C}\longrightarrow \textbf{Set}\).
Let  be the powerset functor on the category \(\textbf{Set}\). For any nonnegative integer k, we denote by \(^k\) the k-th iteration of the functor
be the powerset functor on the category \(\textbf{Set}\). For any nonnegative integer k, we denote by \(^k\) the k-th iteration of the functor  with respect to the composition. In particular,
with respect to the composition. In particular,  agrees with the identity functor of \(\textbf{Set}\) and
agrees with the identity functor of \(\textbf{Set}\) and  . When working in a set-theoretical context, we usually write
. When working in a set-theoretical context, we usually write  instead of
instead of  . For any \(\Omega \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\) and \(h \geqslant 1\), we denote by \(\Omega ^h\) the Cartesian product of h copies of \(\Omega \). In particular, we often write
. For any \(\Omega \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\) and \(h \geqslant 1\), we denote by \(\Omega ^h\) the Cartesian product of h copies of \(\Omega \). In particular, we often write  instead of
instead of  , and so on. If \(f \in \textrm{Arr}\hspace{0.55542pt}(\textbf{Set})\), we usually write \(^{\langle 2 \rangle }\) instead of \(f \hspace{1.111pt}{\times }\hspace{1.111pt}f\). In particular, we write
, and so on. If \(f \in \textrm{Arr}\hspace{0.55542pt}(\textbf{Set})\), we usually write \(^{\langle 2 \rangle }\) instead of \(f \hspace{1.111pt}{\times }\hspace{1.111pt}f\). In particular, we write  instead of
instead of  .
.
Let \(\Omega \) be an arbitrary fixed set. We set  and
and  . We call set system on \(\Omega \) any element
. We call set system on \(\Omega \) any element  and set relation on \(\Omega \) any element
and set relation on \(\Omega \) any element  .
.
We say that a non-empty set system  is:
is:
-
a closure set system on \(\Omega \) if
 and whenever
and whenever 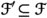 then
then  . We denote by \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) the collection of all closure set systems on \(\Omega \);
. We denote by \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) the collection of all closure set systems on \(\Omega \); -
a set partition on \(\Omega \) if
 and whenever
and whenever  it results that \(X \cap Y =\varnothing \). We denote by \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) the collection of all set partitions on \(\Omega \).
it results that \(X \cap Y =\varnothing \). We denote by \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) the collection of all set partitions on \(\Omega \).
A set operator on \(\Omega \) is any map  , and we denote by \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) the family of all set operators on \(\Omega \). The binary relation \(\sqsubseteq \) on \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) defined by
, and we denote by \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) the family of all set operators on \(\Omega \). The binary relation \(\sqsubseteq \) on \(\textrm{SO}\hspace{0.55542pt}(\Omega )\) defined by

for any \(\sigma ,\sigma '\! \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) is clearly a partial order on \(\textrm{SO}\hspace{0.55542pt}(\Omega )\).
We say that a set operator \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) is:
-
extensive if \(X \subseteq \sigma (X)\), for any
 ;
; -
increasing if whenever
 and \(X \subseteq Y\), then \(\sigma (X) \subseteq \sigma (Y)\);
and \(X \subseteq Y\), then \(\sigma (X) \subseteq \sigma (Y)\); -
idempotent if \(\sigma (\sigma (X))=\sigma (X)\), for any
 ;
; -
a closure set operator on \(\Omega \) if it is extensive, increasing and idempotent, and we denote by \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\) the set of all the closure set operators on \(\Omega \).
If \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\), we set  and
and  , for any integer \(k\geqslant 1\).
, for any integer \(k\geqslant 1\).
3 Categories of set systems, set relations and set operators
Let k be a given nonnegative integer. In this section we introduce and analyze the basic properties of the arrows of three categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\) and \(\mathbf{SO^k}\), and some of their corresponding subcategories, which will be the main topic of the present paper. The objects of such categories are pairs constituted by a ground set and a corresponding set system, set relation or a set operator respectively. The exponent k determines the iteration of the powerset functor  occurring in the definition of the corresponding arrows.
occurring in the definition of the corresponding arrows.
When we fix the ground set \(\Omega \) and an associated set system  , we can consider the pair
, we can consider the pair  as an object of a category. We may take as arrows the maps \(f:\Omega \longrightarrow \Omega '\) for which the k-th iteration
as an object of a category. We may take as arrows the maps \(f:\Omega \longrightarrow \Omega '\) for which the k-th iteration  sends elements of
sends elements of  to elements of
to elements of  . In such a way, we are led to consider the category \(\mathbf{SS^k}\) for which
. In such a way, we are led to consider the category \(\mathbf{SS^k}\) for which

and such that for any pair of its objects  and
and  , the corresponding arrow set is defined by
, the corresponding arrow set is defined by

where the composition law is induced by that of \(\textbf{Set}\). Clearly, the intrinsic nature of the arrows in the category \(\mathbf{SS^k}\) is local, because it is carried on  by means of the application of the k-th iteration of
by means of the application of the k-th iteration of  on any function defined on the ground set \(\Omega \).
on any function defined on the ground set \(\Omega \).
Definition 3.1
We call \(\mathbf{SS^k}\) the category of the k-set systems.
For every k, the category \(\textbf{SS}^k\) has a reflective subcategory isomorphic to \(\textbf{Set}\). Moreover, as one intuitively expects, the category \(\mathbf{SS^k}\) embeds in a quite natural way into the category \(\mathbf{SS^{k+1}}\). In fact, consider the correspondence \(S^k:\mathbf{SS^k} \longrightarrow \mathbf{SS^{k+1}}\), where  for any
for any  , and
, and  for any \(f \in \textrm{Arr}\hspace{0.55542pt}(\mathbf{SS^k})\). Then the following result holds.
for any \(f \in \textrm{Arr}\hspace{0.55542pt}(\mathbf{SS^k})\). Then the following result holds.
Proposition 3.2
\(S^k\) is a full embedding.
Proof
It is immediate to check that \(S^k\) is an embedding by its definition. It remains to prove that \(S^k\) is a full functor. To this end, let  and
and  . Now, since
. Now, since

we deduce that  and, hence,
and, hence,  , so that \(S^k\) is full.\(\square \)
, so that \(S^k\) is full.\(\square \)
As for set systems, when we fix \(\Omega \) and a binary relation  , we can consider the pair
, we can consider the pair  as an object of a category of binary relations. In such a way, we consider the category \(\mathbf{SR^k}\), whose object class is
as an object of a category of binary relations. In such a way, we consider the category \(\mathbf{SR^k}\), whose object class is

and having arrow set given by

for any pair of objects  . Also in this case the composition law is that induced by the corresponding composition law in \(\textbf{Set}\).
. Also in this case the composition law is that induced by the corresponding composition law in \(\textbf{Set}\).
Definition 3.3
We call \(\mathbf{SR^k}\) the category of the k-set relations.
Also for the category \(\mathbf{SR^k}\), we can check in a natural way that \(\mathbf{SR^k}\) embeds into \(\mathbf{SR^{k+1}}\). In fact, consider the correspondence \(R^k:\mathbf{SR^k}\longrightarrow \mathbf{SR^{k+1}}\), where  for any
for any  , and
, and  for any \(f \in \textrm{Arr}\hspace{0.55542pt}(\mathbf{SR^k})\). Then the following result holds.
for any \(f \in \textrm{Arr}\hspace{0.55542pt}(\mathbf{SR^k})\). Then the following result holds.
Proposition 3.4
\(R^k\) is a full embedding.
Proof
It is immediate to verity that \(R^k\) is an embedding. We now show that \(R^k\) is also a full functor.
Let  and
and  . By the definition of \(R^k\), in order to obtain the conclusion of the present part (ii) we must prove that
. By the definition of \(R^k\), in order to obtain the conclusion of the present part (ii) we must prove that  . To this regard, let
. To this regard, let  . Then
. Then  , and therefore
, and therefore

whence  . Hence
. Hence  .\(\square \)
.\(\square \)
Finally we introduce the categories whose objects are set operators induced by maps between sets. In this case, assume \(k \geqslant 1\). We call any map  (that is, equivalently, any arrow
(that is, equivalently, any arrow  a k-set operator on \(\Omega \). In particular, a 0-set operator \(\sigma \) on \(\Omega \) is a map \(\sigma :\Omega \longrightarrow \Omega \) and a 1-set operator \(\sigma \) on \(\Omega \) is a map
a k-set operator on \(\Omega \). In particular, a 0-set operator \(\sigma \) on \(\Omega \) is a map \(\sigma :\Omega \longrightarrow \Omega \) and a 1-set operator \(\sigma \) on \(\Omega \) is a map  (which in literature is usually called a set operator on \(\Omega \)). We introduce now three categories of k-set operators, denoted by \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\), which are induced by means of the functor
(which in literature is usually called a set operator on \(\Omega \)). We introduce now three categories of k-set operators, denoted by \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\), which are induced by means of the functor  . More in detail, we set
. More in detail, we set

and for any \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\),

The composition law in \(\mathbf{SO^k}\) (and analogously in \(\mathbf{SO^{k,\sqsubseteq }}\) and in \(\mathbf{SO^{k,\sqsupseteq }}\)) is naturally defined by
whenever \((f,f') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\) and \((g,g') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega '\!,\sigma '),(\Omega ''\!,\sigma ''))\).
Definition 3.5
We call \(\mathbf{SO^k}\) the category of the k-set operators, \(\mathbf{SO^{k,\sqsubseteq }}\) the category of the \((k, \sqsubseteq )\)-set operators, and \(\mathbf{SO^{k,\sqsupseteq }}\) the category of the \((k, \sqsupseteq )\)-set operators.
Remark 3.6
At a first glance, it might seem that the categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) turn out to be isomorphic. Nevertheless, this does not correspond to reality. In fact, in Theorem 4.10 we will show that they are neither equivalent nor dual.
The forgetful functor \(U:\mathbf{SS^k}\longrightarrow \textbf{Set}\) such that  and \(U(f)=f\) is clearly faithful. A similar functor may be defined on category \(\mathbf{SR^k}\). Furthermore, the categories \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\), \(\mathbf{SO^{k,\sqsupseteq }}\) are also concretizable. In fact, just take the functor \(U:\mathbf{SO^{k,\sqsubseteq }}\longrightarrow \textbf{Set}\), such that \(U((\Omega ,\sigma ))=\Omega \hspace{1.111pt}{\times }\hspace{1.111pt}\Omega \) and \(U((f,f'))=(f,f')\) whenever \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsubseteq }})\) and \((f,f') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\) (the other cases are similar).
and \(U(f)=f\) is clearly faithful. A similar functor may be defined on category \(\mathbf{SR^k}\). Furthermore, the categories \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\), \(\mathbf{SO^{k,\sqsupseteq }}\) are also concretizable. In fact, just take the functor \(U:\mathbf{SO^{k,\sqsubseteq }}\longrightarrow \textbf{Set}\), such that \(U((\Omega ,\sigma ))=\Omega \hspace{1.111pt}{\times }\hspace{1.111pt}\Omega \) and \(U((f,f'))=(f,f')\) whenever \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsubseteq }})\) and \((f,f') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\) (the other cases are similar).
In the next result we determine monomorphisms, epimorphisms and isomorphisms for the category \(\mathbf{SS^k}\).
Proposition 3.7
Let  and
and  . Then:
. Then:
-
(i)
f is a monomorphism of \(\hspace{1.111pt}\mathbf{SS^k}\) \(\iff \) f is an injective map between \(\Omega \) and \(\Omega '\);
-
(ii)
f is an epimorphism of \(\hspace{1.111pt}\mathbf{SS^k}\) \(\iff \) f is a surjective map between \(\Omega \) and \(\Omega '\);
-
(iii)
f is an isomorphism of \(\hspace{1.111pt}\mathbf{SS^k}\) \(\iff \) f is bijective and
 .
.
Proof
(i): Clearly, if f is injective then it is a monomorphism. Conversely, assume that f is a monomorphism and let \(x,y \in \Omega \) be such that \(f(x)=f(y)\). Taking the arrows  sending \(*\) to x and y respectively, we get \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}{\overline{x}}=f \hspace{0.55542pt}{\circ }\hspace{1.111pt}{\overline{y}}\), whence \(x=y\), i.e. f is injective.
sending \(*\) to x and y respectively, we get \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}{\overline{x}}=f \hspace{0.55542pt}{\circ }\hspace{1.111pt}{\overline{y}}\), whence \(x=y\), i.e. f is injective.
(ii): Clearly, if f is surjective then it is an epimorphism. Conversely, let f be an epimorphism and take  and the arrows
and the arrows  defined as follows:
defined as follows:
Hence \(g \hspace{1.111pt}{\circ }\hspace{0.55542pt}f=h \hspace{1.111pt}{\circ }\hspace{0.55542pt}f\), whence \(g=h\), i.e. \(f(\Omega )=\Omega '\).
(iii): Assume first that f is an isomorphism of \(\mathbf{SS^k}\), so that there exists  such that
such that  and
and  . Clearly, f is bijective with g as its inverse. Therefore f is an isomorphism in \(\textbf{Set}\), and consequently
. Clearly, f is bijective with g as its inverse. Therefore f is an isomorphism in \(\textbf{Set}\), and consequently  is also bijective with inverse
is also bijective with inverse  . Fix now
. Fix now  and
and  such that
such that  . Since
. Since  , we easily deduce that
, we easily deduce that  . Thus
. Thus  , and the reverse inclusion is a direct consequence of the choice of f.
, and the reverse inclusion is a direct consequence of the choice of f.
Conversely, assume that f is a bijective map and  . Let
. Let  . Then we get
. Then we get  for each
for each  , whence
, whence  .\(\square \)
.\(\square \)
The case of \(\mathbf{SR^k}\) can be treated in a similar way to \(\mathbf{SS^k}\), and we leave the details to the following result to the reader.
Proposition 3.8
Let  and
and  . Then:
. Then:
-
(i)
f is a monomorphism of \(\hspace{0.55542pt}\mathbf{SR^k}\) \(\iff \) f is an injective map between \(\Omega \) and \(\Omega '\);
-
(ii)
f is an epimorphism of \(\hspace{0.55542pt}\mathbf{SR^k}\) \(\iff \) f is a surjective map between \(\Omega \) and \(\Omega '\);
-
(iii)
f is an isomorphism of \(\hspace{0.55542pt}\mathbf{SR^k}\) \(\iff \) f is bijective and

The situation concerning monomorphisms, epimorphisms and isomorphisms in the previous categories of k-th set operators is more articulated. With regard to the categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) we have the following results.
Proposition 3.9
Let \(\mathfrak {O}\) be one of the categories \(\mathbf{SO^{k,\sqsubseteq }}\) or \(\mathbf{SO^{k,\sqsupseteq }}\). Let \((\Omega , \sigma ), (\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {O})\) and \((f,f') \in \textrm{Arr}_{\mathfrak {O}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Then:
-
(i)
\((f,f')\) is a monomorphism of \(\mathfrak {O}\) \(\iff \) f and \(f'\) are both injective maps between \(\Omega \) and \(\Omega '\);
-
(ii)
\((f,f')\) is an epimorphism of \(\mathfrak {O}\) \(\iff \) f and \(f'\) are both surjective maps between \(\Omega \) and \(\Omega '\);
-
(iii)
\((f,f')\) is an isomorphism of \(\mathfrak {O}\) \(\iff \) f and \(f'\) are both bijective maps between \(\Omega \) and \(\Omega '\) and
 .
.
Proof
We provide the proof in the case in which \(\mathfrak {O}=\mathbf{SO^{k,\sqsubseteq }}\). The other case can be treated in a similar way, therefore we leave the proof to the reader.
(i): Using the characterization of monomorphisms of \(\textbf{Set}\), the implication “\(\Leftarrow \)" is immediate.
Conversely, assume that \((f,f')\) is a monomorphism. We first associate with any pair \((u,v) \in \Omega \hspace{1.111pt}{\times }\hspace{1.111pt}\Omega \) an arrow \(({\overline{u}},{\overline{v}}) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\{u,v\},\tau ),(\Omega ,\sigma ))\) such that \({\overline{u}}(u)={\overline{u}}(v)=u\), \({\overline{v}}(u)={\overline{v}}(v)=v\), and \(\tau (X)=\varnothing \) for each  . Let now \(x,z,y, w\in \Omega \) be such that \((f(x),f'(z))=(f(y),f'(w))\). In order to get the conclusion, we must show that \(x=y\) and \(z=w\). Clearly, the condition \((f(x),f'(z))=(f(y),f'(w))\) can be equivalently written in the form \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}({\overline{x}},{\overline{z}})=(f,f') {\circ }\hspace{1.111pt}({\overline{y}},{\overline{w}})\). Therefore, since \((f,f')\) is a monomorphism of the category \(\mathbf{SO^{k,\sqsubseteq }}\), we deduce that \(({\overline{x}},{\overline{z}})=({\overline{y}},{\overline{w}})\), whence \(x=y\) and \(z=w\).
. Let now \(x,z,y, w\in \Omega \) be such that \((f(x),f'(z))=(f(y),f'(w))\). In order to get the conclusion, we must show that \(x=y\) and \(z=w\). Clearly, the condition \((f(x),f'(z))=(f(y),f'(w))\) can be equivalently written in the form \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}({\overline{x}},{\overline{z}})=(f,f') {\circ }\hspace{1.111pt}({\overline{y}},{\overline{w}})\). Therefore, since \((f,f')\) is a monomorphism of the category \(\mathbf{SO^{k,\sqsubseteq }}\), we deduce that \(({\overline{x}},{\overline{z}})=({\overline{y}},{\overline{w}})\), whence \(x=y\) and \(z=w\).
(ii): Let \((f,f') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Using the characterization of epimorphisms of \(\textbf{Set}\), if f and \(f'\) are surjective we may easily deduce that \((f,f')\) is an epimorphism.
Conversely, assume that \((f,f')\) is an epimorphism and let \((\{0,1\},\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsubseteq }})\), where  for any
for any  . Let now \((g,g'),(h,h') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega '\!,\sigma '),(\{0,1\},\tau )))\) be defined as follows:
. Let now \((g,g'),(h,h') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega '\!,\sigma '),(\{0,1\},\tau )))\) be defined as follows:

Hence \((g,g') \hspace{1.111pt}{\circ }\hspace{1.111pt}(f,f')=(h,h') \hspace{1.111pt}{\circ }\hspace{1.111pt}(f,f')\), so that \((g,g')=(h,h')\) since \((f,f')\) is an epimorphism. This proves that \(f(\Omega )=f'(\Omega )=\Omega '\), i.e. f and \(f'\) are surjective.
(iii): Assume first that \((f,f')\) is an isomorphism. Then there exists \((g,g') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\) such that \((g,g') \hspace{1.111pt}{\circ }\hspace{1.111pt}(f,f')=(\textrm{Id}_\Omega ,\textrm{Id}_\Omega )\) and \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}(g,g')=(\textrm{Id}_{\Omega '},\textrm{Id}_{\Omega '})\), and this implies that f and \(f'\) are both bijective.
Furthermore, as \((g,g') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\), it results that

On the other hand, since \((f,f') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\) and  and
and  are invertible with inverses
are invertible with inverses  and
and  , respectively, we easily get
, respectively, we easily get

Combining together the above conditions we deduce that  , whence, again by the invertibility of both
, whence, again by the invertibility of both  and
and  , we conclude that
, we conclude that  .
.
Conversely, assume that f and \(f'\) are invertible, with inverses denoted by g and \(g'\) respectively, and such that  . Composing the last equality by
. Composing the last equality by  at left and by
at left and by  at right, we clearly get
at right, we clearly get  and, so, we conclude that \((g,g') \in \textrm{Arr}_\mathbf{SO^{k,\sqsubseteq }}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\).\(\square \)
and, so, we conclude that \((g,g') \in \textrm{Arr}_\mathbf{SO^{k,\sqsubseteq }}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\).\(\square \)
In the case of the category \(\mathbf{SO^k}\), the determination of its monomorphisms and epimorphisms is more complex than the previous cases (see Remark 3.11). Now, we provide the following result concerning the characterization of isomorphisms of \(\mathbf{SO^k}\).
Proposition 3.10
Let \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\) and \((f,f') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),((\Omega '\!,\sigma '))\). Then
Proof
Let \((f,f') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Assume first that \((f,f')\) is an isomorphism. Then there exists \((g,g') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\) such that \((g,g') \hspace{1.111pt}{\circ }\hspace{1.111pt}(f,f')=(\textrm{Id}_\Omega ,\textrm{Id}_\Omega )\) and \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}(g,g')=(\textrm{Id}_{\Omega '},\textrm{Id}_{\Omega '})\), and this implies that both f and \(f'\) are bijective.
Conversely, assume that f and \(f'\) are invertible, with inverses denoted by g and \(g'\) respectively. We claim that \((g,g') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega '\!,\sigma '),(\Omega ,\sigma ))\). To this regard, first note that  and
and  are invertible with inverses
are invertible with inverses  and
and  . So, as
. So, as  for any
for any  , composing by
, composing by  we easily conclude that
we easily conclude that  for any
for any  , i.e.
, i.e.  .\(\square \)
.\(\square \)
We leave the characterization of monomorphisms and epimorphisms as an exercise.
Remark 3.11
As we mentioned above, a complete and exhaustive characterization of the monomorphisms and epimorphisms of the category \(\mathbf{SO^k}\) is more complex to be obtained with respect than the two categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) in Proposition 3.9.
More in detail, the condition of equality occurring in the definition of the arrows of \(\mathbf{SO^k}\) is quite strict and this reduces the possibility to construct an arrow between two objects \((\Omega ,\sigma )\) and \((\Lambda ,\tau )\). In fact, when an object \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\) is given, the k-set operator  maps any
maps any  to a
to a  , whose correlation with X is too general without establishing additional conditions on the k-set operator \(\sigma \), such as for instance extensiveness, monotonicity or idempotency (see Sect. 6 where we deal with closure set operators).
, whose correlation with X is too general without establishing additional conditions on the k-set operator \(\sigma \), such as for instance extensiveness, monotonicity or idempotency (see Sect. 6 where we deal with closure set operators).
Thus, since it is difficult to check that the equality  holds for any
holds for any  , some work is needed to characterize an arrow \((f,f') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Lambda ,\tau ))\).
, some work is needed to characterize an arrow \((f,f') \in \textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Lambda ,\tau ))\).
We denote by \(\mathbf{SO^{k,\sqsubseteq ,=}}\), \(\mathbf{SO^{k,\sqsupseteq ,=}}\) and \(\mathbf{SO^{k,=}}\) the wide subcategories of \(\mathbf{SO^{k,\sqsubseteq }}\), \(\mathbf{SO^{k,\sqsupseteq }}\) and \(\mathbf{SO^k}\), respectively, whose arrows have the form (f, f). In the successive sections, we deal with some specific subcategories of the previous categories \(\mathbf{SO^{k,\sqsubseteq ,=}}\), \(\mathbf{SO^{k,\sqsupseteq ,=}}\) and \(\mathbf{SO^{k,=}}\).
Remark 3.12
The analogue of Proposition 3.9 holds for both the categories \(\mathbf{SO^{k,\sqsubseteq ,=}}\) and \(\mathbf{SO^{k,\sqsupseteq ,=}}\). Similarly, the analogue of Proposition 3.10 holds for \(\mathbf{SO^{k,=}}\).
4 Fundamental properties of the categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\) and \(\mathbf{SO^k}\)
Let \(k \in \mathbb {N}\) be fixed. In the present section we provide two fundamental properties of the categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\), i.e. that they are bicomplete (see Theorem 4.1) and Cartesian closed (see Theorem 4.6).
4.1 \(\textbf{SS}^k\) and \(\mathbf{SR^k}\) are bicomplete categories
In this subsection we prove the first fundamental property of the category \(\textbf{SS}^k\), namely that it is a bicomplete category.
Theorem 4.1
\(\mathbf{SS^k}\) is a bicomplete category.
Proof
We first determine the product in \(\mathbf{SS^k}\). To this regard fix  . Set
. Set

where \(\pi _i:X \longrightarrow X_i\) is the usual projection for any \(i \in I\) (notice that  ). We show that
). We show that

By the definition of the arrows of \(\mathbf{SS^k}\) and of the set system  , we get
, we get  , for any \(i\in I\). Let now
, for any \(i\in I\). Let now  and
and  , for any \(i\in I\). Let \({\tilde{h}}:Y \longrightarrow X\) be the usual universal arrow induced by the family of maps \(\{h_i \,{|}\, i\,{\in }\,I\}\) in \(\textbf{Set}\) and
, for any \(i\in I\). Let \({\tilde{h}}:Y \longrightarrow X\) be the usual universal arrow induced by the family of maps \(\{h_i \,{|}\, i\,{\in }\,I\}\) in \(\textbf{Set}\) and  . Since \(\pi _i \hspace{1.111pt}{\circ }\hspace{1.111pt}{\tilde{h}}=h_i\), it follows that
. Since \(\pi _i \hspace{1.111pt}{\circ }\hspace{1.111pt}{\tilde{h}}=h_i\), it follows that

for each \(i \in I\), whence  , and thus
, and thus  . Therefore, in view of the universal property of the map \({\tilde{h}}\) in \(\textbf{Set}\), it follows that \({\tilde{h}}\) is also the unique arrow in
. Therefore, in view of the universal property of the map \({\tilde{h}}\) in \(\textbf{Set}\), it follows that \({\tilde{h}}\) is also the unique arrow in  for which \(h_i=\pi _i \hspace{1.111pt}{\circ }\hspace{1.111pt}{\tilde{h}}\) for any \(i \in I\). This proves (2).
for which \(h_i=\pi _i \hspace{1.111pt}{\circ }\hspace{1.111pt}{\tilde{h}}\) for any \(i \in I\). This proves (2).
We determine now the equalizer of any two arrows of \(\mathbf{SS^k}\). Take  and
and  . Let
. Let  , \(\iota _*:\Omega _* \hookrightarrow \Omega \) be the inclusion map, and
, \(\iota _*:\Omega _* \hookrightarrow \Omega \) be the inclusion map, and  . Now we prove that
. Now we prove that

We clearly have  ,
,  and \(f \hspace{1.111pt}{\circ }\hspace{1.111pt}\iota _*=g \hspace{1.111pt}{\circ }\hspace{1.111pt}\iota _*\). Take
and \(f \hspace{1.111pt}{\circ }\hspace{1.111pt}\iota _*=g \hspace{1.111pt}{\circ }\hspace{1.111pt}\iota _*\). Take  and
and  such that \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}h=g \hspace{1.111pt}{\circ }\hspace{1.111pt}h\). We show that there exists a unique arrow
such that \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}h=g \hspace{1.111pt}{\circ }\hspace{1.111pt}h\). We show that there exists a unique arrow  such that \(\iota _* \hspace{1.111pt}{\circ }\hspace{1.111pt}h_*=h\).
such that \(\iota _* \hspace{1.111pt}{\circ }\hspace{1.111pt}h_*=h\).
To this regard, since \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}h=g \hspace{1.111pt}{\circ }\hspace{1.111pt}h\) it follows that \(h(z) \in \Omega _*\). Define then the map \(h':\Omega '' \! \longrightarrow \Omega _*\) setting  for any \(z \in \Lambda \). We easily deduce that \(h_*\) is the unique map such that \(h=\iota _* \hspace{1.111pt}{\circ }\hspace{1.111pt}h_*\). Fix now
for any \(z \in \Lambda \). We easily deduce that \(h_*\) is the unique map such that \(h=\iota _* \hspace{1.111pt}{\circ }\hspace{1.111pt}h_*\). Fix now  . It is immediate that
. It is immediate that  , whence
, whence  . This proves (3), and consequently the category \(\mathbf{SS^k}\) is complete in view of [7, Theorem 2.8.1].
. This proves (3), and consequently the category \(\mathbf{SS^k}\) is complete in view of [7, Theorem 2.8.1].
We consider now the construction of the coproduct in \(\mathbf{SS^k}\). Let  . We set
. We set  and let \(\xi _i:\Omega _i \longrightarrow {{\widehat{\Omega }}}\) be the inclusion map, for any \(i \in I\). Set moreover
and let \(\xi _i:\Omega _i \longrightarrow {{\widehat{\Omega }}}\) be the inclusion map, for any \(i \in I\). Set moreover  . We prove now that
. We prove now that

Also in this case, by the definition of  and of \(\textrm{Arr}\hspace{0.55542pt}(\mathbf{SS^k})\), we clearly get
and of \(\textrm{Arr}\hspace{0.55542pt}(\mathbf{SS^k})\), we clearly get  , for any \(i\in I\). Let now
, for any \(i\in I\). Let now  and
and  for any \(i\in I\). Let \(t:{{\widehat{\Omega }}} \longrightarrow \Lambda \) be the universal map induced by \(\{s_i\,{|}\, i\,{\in }\,I\}\) in \(\textbf{Set}\), i.e.
for any \(i\in I\). Let \(t:{{\widehat{\Omega }}} \longrightarrow \Lambda \) be the universal map induced by \(\{s_i\,{|}\, i\,{\in }\,I\}\) in \(\textbf{Set}\), i.e.  for any \((x,i) \in {{\widehat{\Omega }}}\). Take now
for any \((x,i) \in {{\widehat{\Omega }}}\). Take now  . Then there exists \(j \in I\) such that
. Then there exists \(j \in I\) such that  and
and  . Thus, since \(s_i=t \hspace{1.111pt}{\circ }\hspace{1.111pt}\xi _i\) for any \(i \in I\), it follows that
. Thus, since \(s_i=t \hspace{1.111pt}{\circ }\hspace{1.111pt}\xi _i\) for any \(i \in I\), it follows that  , whence we get
, whence we get  . Hence
. Hence  . At this point, in view of the universal property of the map t in \(\textbf{Set}\), it follows that t is also the only arrow in
. At this point, in view of the universal property of the map t in \(\textbf{Set}\), it follows that t is also the only arrow in  such that \(t \hspace{1.111pt}{\circ }\hspace{1.111pt}\xi _i=s_i\) for any \(i \in I\). This proves (4).
such that \(t \hspace{1.111pt}{\circ }\hspace{1.111pt}\xi _i=s_i\) for any \(i \in I\). This proves (4).
Finally, we determine the coequalizer of any two arrows of \(\mathbf{SS^k}\). Let again  ,
,  and
and  . We set
. We set  , where \(\sim _\diamond \) is the equivalence relation on \(\Omega '\) generated by the binary relation\(\{(f(x),g(x)) \,{|}\, x\,{ \in }\, \Omega \} \subseteq \Omega '\hspace{0.55542pt}{\times }\hspace{1.111pt}\Omega '\). Let moreover by \(\pi _\diamond :\Omega '\! \longrightarrow \Omega '/{\sim }_\diamond \) be the projection on the quotient and
, where \(\sim _\diamond \) is the equivalence relation on \(\Omega '\) generated by the binary relation\(\{(f(x),g(x)) \,{|}\, x\,{ \in }\, \Omega \} \subseteq \Omega '\hspace{0.55542pt}{\times }\hspace{1.111pt}\Omega '\). Let moreover by \(\pi _\diamond :\Omega '\! \longrightarrow \Omega '/{\sim }_\diamond \) be the projection on the quotient and  . We show then that
. We show then that

We have that  ,
,  and \(\pi _\diamond \hspace{1.111pt}{\circ }\hspace{1.111pt}f=\pi _\diamond \hspace{1.111pt}{\circ }\hspace{1.111pt}g\).
and \(\pi _\diamond \hspace{1.111pt}{\circ }\hspace{1.111pt}f=\pi _\diamond \hspace{1.111pt}{\circ }\hspace{1.111pt}g\).
Take now  and
and  such that \(h \hspace{1.111pt}{\circ }\hspace{0.55542pt}f=h \hspace{1.111pt}{\circ }\hspace{1.111pt}g\). Then there exists a unique map \(h':\Omega _\diamond \longrightarrow \Lambda \) such that \(h' \hspace{1.111pt}{\circ }\hspace{1.111pt}\pi _\diamond =h\).
such that \(h \hspace{1.111pt}{\circ }\hspace{0.55542pt}f=h \hspace{1.111pt}{\circ }\hspace{1.111pt}g\). Then there exists a unique map \(h':\Omega _\diamond \longrightarrow \Lambda \) such that \(h' \hspace{1.111pt}{\circ }\hspace{1.111pt}\pi _\diamond =h\).
We finally claim that  . In fact, let
. In fact, let  . In view of the definition of
. In view of the definition of  , there exists
, there exists  such that
such that  . Thus, since
. Thus, since  , we get
, we get  . Hence
. Hence  , and therefore (5) holds. Consequently, the category \(\mathbf{SS^k}\) is cocomplete in view of [7, Theorem 2.8.1].\(\square \)
, and therefore (5) holds. Consequently, the category \(\mathbf{SS^k}\) is cocomplete in view of [7, Theorem 2.8.1].\(\square \)
In the next result we show that \(\mathbf{SR^k}\) is also a bicomplete category. The proof is similar to that of the category \(\mathbf{SS^k}\) and, hence, we only sketch it, leaving to the reader to fix the details.
Theorem 4.2
\(\mathbf{SR^k}\) is a bicomplete category.
Proof
We first determine the product in \(\mathbf{SR^k}\). To this regard, let  , and we take \(\Omega \) and \(\pi _i\) (where \(i \in I\)) as in (2). We set now
, and we take \(\Omega \) and \(\pi _i\) (where \(i \in I\)) as in (2). We set now  . We leave to the reader the proof of the fact that
. We leave to the reader the proof of the fact that  is the product of
is the product of  in \(\mathbf{SR^k}\).
in \(\mathbf{SR^k}\).
Now determine the equalizer of any two arrows of \(\mathbf{SR^k}\). Let  and
and  . Take
. Take  and \(\iota _*:\Omega _* \hookrightarrow \Omega \) be as in (3) and also set
and \(\iota _*:\Omega _* \hookrightarrow \Omega \) be as in (3) and also set  . Also in this case, we leave to the reader the proof of the fact that
. Also in this case, we leave to the reader the proof of the fact that  is the equalizer of f and g in \(\mathbf{SR^k}\).
is the equalizer of f and g in \(\mathbf{SR^k}\).
We consider now the construction of the coproduct in \(\mathbf{SR^k}\). Take \({{\widehat{\Omega }}}\), \(\xi _i\) (where \(i \in I\)) as in (4) and set  . We leave to the reader the proof of the fact that
. We leave to the reader the proof of the fact that  is the coproduct of
is the coproduct of  in \(\mathbf{SR^k}\).
in \(\mathbf{SR^k}\).
Finally, we determine the coequalizer of any two arrows of \(\mathbf{SR^k}\). Let again  ,
,  and
and  . Take
. Take  and \(\pi _\diamond :\Omega ' \!\longrightarrow \Omega '\!/\sim _\diamond \) as in (5) and set
and \(\pi _\diamond :\Omega ' \!\longrightarrow \Omega '\!/\sim _\diamond \) as in (5) and set  . We leave to the reader the proof of the fact that
. We leave to the reader the proof of the fact that  is the coequalizer of f and g in \(\mathbf{SR^k}\).\(\square \)
is the coequalizer of f and g in \(\mathbf{SR^k}\).\(\square \)
4.2 The categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) are Cartesian closed
The main result of the present subsection is Theorem 4.6, where we determine the exponential objects of both the categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) and deduce that such categories are Cartesian closed.
We now recall two classical basic notions of category theory in the next two definitions.
Definition 4.3
Let \(\mathfrak {C}\) be a category with binary products and \(Z,Y \in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\). We say that a pair \((W, \textrm{eval})\) is a (Z, Y)-exponential object in \(\mathfrak {C}\) if \(W\in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\), \(\textrm{eval} \in \textrm{Arr}_\mathfrak {C}(W\hspace{1.111pt}{\times }\hspace{1.111pt}Y, Z)\) and for any \(X\in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\), \(g\in \textrm{Arr}_\mathfrak {C}( X\hspace{1.111pt}{\times }\hspace{1.111pt}Y, Z)\) there is a unique morphism \(t_g:X\longrightarrow W\) (usually called the transpose of g) such that the diagram

commutes.
Definition 4.4
A category \(\mathfrak {C}\) is said Cartesian closed if it admits finite products and exponential objects exist for any pair of objects.
In the next Theorem 4.6 we exhibit the explicit characterization of the exponential objects for both the categories \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\), proving hence that they are Cartesian closed. To this regard, for any \(X,Y \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\), we consider the map \(\text {ev}_{X, Y}:X^Y {\times }\hspace{1.111pt}Y \longrightarrow X\) defined by
Let now \(\Omega ,\Lambda ,\Theta \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\), \(g \in \textrm{Arr}\hspace{0.55542pt}(\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda ,\Omega )\) and  be arbitrary and fixed. Let moreover \(\pi _1:\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\), \(\pi _2:\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) {\times }\hspace{1.111pt}\Lambda \longrightarrow \Lambda \), \(p_1:\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \Theta \) and \(p_2:\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \Lambda \) denote usual Cartesian projections. Consequently, we define the map \(t_g:\Theta \longrightarrow \textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) such that
be arbitrary and fixed. Let moreover \(\pi _1:\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\), \(\pi _2:\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) {\times }\hspace{1.111pt}\Lambda \longrightarrow \Lambda \), \(p_1:\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \Theta \) and \(p_2:\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda \longrightarrow \Lambda \) denote usual Cartesian projections. Consequently, we define the map \(t_g:\Theta \longrightarrow \textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) such that  for any \(\theta \in \Theta \), where
for any \(\theta \in \Theta \), where  . Clearly, in view of the definition of the exponential object in \(\textbf{Set}\), \( t_g\) is the only map for which
. Clearly, in view of the definition of the exponential object in \(\textbf{Set}\), \( t_g\) is the only map for which
We set now

and, for any  ,
,

At this point we are ready to exhibit a preliminary technical result before providing a complete proof of Theorem 4.6 in the case of \(\mathbf{SR^k}\).
Lemma 4.5
Let \(k \geqslant 1\), \(\Omega ,\Lambda ,\Theta \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\), \(g \in \textrm{Arr}\hspace{0.55542pt}(\Theta \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda ,\Omega )\) and  . Then, with the previous notations, for every
. Then, with the previous notations, for every  we have that:
we have that:
-
(a)
 ;
; -
(b)
 ;
; -
(c)
 .
.
Proof
We proceed inductively on k. Let first \(k=1\). Then we respectively have
and
Let us prove Condition (a). The inclusions  and
and  respectively hold by the definition of \({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \({\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}}\). Conversely, fix
respectively hold by the definition of \({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \({\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}}\). Conversely, fix  . By our choice of \(({\mathscr {Z}},{\mathscr {W}})\), there exist \(\theta \in {\mathscr {X}}\) and \(\delta \in {\mathscr {Y}}\) such that \(t^{\langle 2 \rangle }_g(\theta ,\delta )=(z,w)\). Hence, we clearly have \(((\theta ,\mu ),(\delta ,\nu )) \in ({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}},{\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}})\), proving that
. By our choice of \(({\mathscr {Z}},{\mathscr {W}})\), there exist \(\theta \in {\mathscr {X}}\) and \(\delta \in {\mathscr {Y}}\) such that \(t^{\langle 2 \rangle }_g(\theta ,\delta )=(z,w)\). Hence, we clearly have \(((\theta ,\mu ),(\delta ,\nu )) \in ({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}},{\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}})\), proving that  and
and  .
.
Let us prove Condition (b). By the definitions of \({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \({\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}}\), the inclusions  and
and  hold. Vice versa, let \(\theta '\! \in {\mathscr {X}}\). By our choice of \({\mathscr {Z}}\), we can find an element \((t_g(\theta '),\lambda ') \in {\mathscr {Z}} \cap \pi _1^{-1}(t_g(\theta '))\). Then \((\theta '\!,\lambda ')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \(\theta '\!=p_1(\theta '\!,\lambda ')\), with \((\theta '\!,\lambda ')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\). In such a way, we showed that
hold. Vice versa, let \(\theta '\! \in {\mathscr {X}}\). By our choice of \({\mathscr {Z}}\), we can find an element \((t_g(\theta '),\lambda ') \in {\mathscr {Z}} \cap \pi _1^{-1}(t_g(\theta '))\). Then \((\theta '\!,\lambda ')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \(\theta '\!=p_1(\theta '\!,\lambda ')\), with \((\theta '\!,\lambda ')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\). In such a way, we showed that  . Analogously, we can demonstrate the inclusion
. Analogously, we can demonstrate the inclusion  .
.
Let us prove Condition (c). First observe that from \(p_2=\pi _2 \hspace{1.111pt}{\circ }\hspace{1.111pt}(t_g \hspace{0.55542pt}{\times }\hspace{1.111pt}\textrm{Id}_\Lambda )\) and our definition of \({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and of \({\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}}\), we easily get the inclusions  and
and  . Conversely, let
. Conversely, let  and
and  . By the choice of \(({\mathscr {Z}},{\mathscr {W}})\), it is quite simple to check the existence of \(x''\! \in {\mathscr {X}}\) and \(y'' \!\in {\mathscr {Y}}\) such that \((x''\!,\lambda '')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \((y''\!,\lambda '')\in {\mathscr {U}}_{{\mathscr {Y}},{\mathscr {Z}}}\). This proves that
. By the choice of \(({\mathscr {Z}},{\mathscr {W}})\), it is quite simple to check the existence of \(x''\! \in {\mathscr {X}}\) and \(y'' \!\in {\mathscr {Y}}\) such that \((x''\!,\lambda '')\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and \((y''\!,\lambda '')\in {\mathscr {U}}_{{\mathscr {Y}},{\mathscr {Z}}}\). This proves that  and
and  . This shows Condition (c) for \(k=0\).
. This shows Condition (c) for \(k=0\).
Fix now an integer \(k \geqslant 2\) and suppose that our conclusion holds for every \(j \in \{1,\dots ,k-1\}\). Let then  and
and  . First note that the inclusions
. First note that the inclusions

and

follow from the definition of \({\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\), \({\mathscr {U}}_{{\mathscr {Y}},{\mathscr {W}}}\) and of the equality \(\pi _2 \hspace{1.111pt}{\circ }\hspace{1.111pt}( t_g \hspace{0.55542pt}{\times }\hspace{1.111pt}\textrm{Id}_\Lambda )=p_2\).
We must prove the reverse inclusions to get our conclusions. We only show the three first inclusions, as the others may be obtained in the same way. Take then \(Z_1\in {\mathscr {Z}}\) and set  . As
. As  , we can find some \(X\in {\mathscr {X}}\) such that
, we can find some \(X\in {\mathscr {X}}\) such that  . Set
. Set

Note that \(U_{X,Z_1} \in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) because, by the inductive hypothesis, it clearly results that  and
and  . Thus
. Thus  and (a) holds.
and (a) holds.
Let us now prove the reverse inclusion needed for obtaining Condition (b). Take \(X\in {\mathscr {X}}\) and set  be such that
be such that  and, as before, set
and, as before, set

By the inductive hypothesis, we get  and
and  , so that \(U\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and
, so that \(U\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) and  . So (b) holds.
. So (b) holds.
Finally, by our choice of \(({\mathscr {Z}},{\mathscr {W}})\), if  , then we can easily find \(U\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) such that
, then we can easily find \(U\in {\mathscr {U}}_{{\mathscr {X}},{\mathscr {Z}}}\) such that  , so we get
, so we get  and Condition (c) holds.\(\square \)
and Condition (c) holds.\(\square \)
Let now  and
and  be arbitrary and fixed. We consider the k-set system
be arbitrary and fixed. We consider the k-set system  on \(\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) and the k-set relation
on \(\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) and the k-set relation  on \(\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) defined respectively by:
on \(\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega )\) defined respectively by:


So we get the following characterization that also provides an alternative proof for the Cartesian closedness of \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\). We give the proof only for \(\mathbf{SR^k}\) (part (ii) of Theorem 4.6) leaving as an exercise for readers the case of \(\mathbf{SS^k}\) (part (i) of Theorem 4.6).
Theorem 4.6
Let  and
and  . The following conditions hold:
. The following conditions hold:
-
(i)
 is the exponential object of
is the exponential object of  and \((\Lambda ,\mathscr {G})\);
and \((\Lambda ,\mathscr {G})\); -
(ii)
 is the exponential object of
is the exponential object of  .
.
Therefore \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) are both Cartesian closed categories.
Proof
Clearly,  . Consider now the product
. Consider now the product  in \(\mathbf{SR^k}\) of
in \(\mathbf{SR^k}\) of  and
and  , for a suitable
, for a suitable  . By using (7), we easily get
. By using (7), we easily get

Fix now  and take the product
and take the product  in \(\mathbf{SR^k}\) of
in \(\mathbf{SR^k}\) of  and
and  , for a suitable
, for a suitable  . Take
. Take  . We claim that
. We claim that

that is:

Fix therefore  . We first show our claim when \(k=0\). To this regard, note that
. We first show our claim when \(k=0\). To this regard, note that

Now, if  and \((({\tilde{t}}_{g,{\mathscr {X}}},\lambda ),({\tilde{t}}_{g,{\mathscr {Y}}},\mu )) \in (\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda )^2\), we clearly have
and \((({\tilde{t}}_{g,{\mathscr {X}}},\lambda ),({\tilde{t}}_{g,{\mathscr {Y}}},\mu )) \in (\textrm{Arr}\hspace{0.55542pt}(\Lambda ,\Omega ) \hspace{1.111pt}{\times }\hspace{1.111pt}\Lambda )^2\), we clearly have

as  , whence
, whence  . This shows (8) when \(k=0\).
. This shows (8) when \(k=0\).
Suppose now \(k \geqslant 1\) and take any  such that
such that  . We can then apply Lemma 4.5 to \(({\mathscr {X}},{\mathscr {Y}})\) and \(({\mathscr {Z}},{\mathscr {W}})\), so that
. We can then apply Lemma 4.5 to \(({\mathscr {X}},{\mathscr {Y}})\) and \(({\mathscr {Z}},{\mathscr {W}})\), so that
-
(a)
 ;
; -
(b)
 ;
; -
(c)
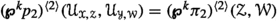 .
.
Note that conditions (b)–(c) imply that  . Thus, as
. Thus, as  , we have that
, we have that  . Next, by condition (a) and by using (6), we get
. Next, by condition (a) and by using (6), we get

so that (8) holds.\(\square \)
4.3 Some basic properties of \(\mathbf{SO^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\)
For the category \(\mathbf{SO^k}\), the properties holding for \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\) are not valid in general. In the next result we show that such a category is neither complete nor cocomplete.
Theorem 4.7
The category \(\mathbf{SO^k}\) is neither complete nor cocomplete.
Proof
In view of [7, Theorem 2.8.1], by proving the non-existence of a terminal object we will check that \(\mathbf{SO^k}\) is not complete. To this regard, assume by contradiction that \((\Omega ,\sigma )\) is the terminal object in the category \(\mathbf{SO^k}\). We clearly have \(\Omega \ne \varnothing \). Moreover, it results that \(|\textrm{Arr}_{\mathbf{SO^k}}((\Lambda ,\tau ),(\Omega ,\sigma ))|=1\) for any \((\Lambda ,\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\). Fix first \((\Lambda ,\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\) such that \(\tau (\varnothing )=\varnothing \), and let (g, h) be the only morphism in \(\textrm{Arr}_{\mathbf{SO^k}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). Thus the equality  holds, and we easily deduce that \(\sigma (\varnothing )=\varnothing \). On the other hand, take \((\Lambda '\!,\tau ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\) such that \(\tau '(\varnothing ) \ne \varnothing \), and denote by \((g'\!,h')\) the only morphism in \(\textrm{Arr}_{\mathbf{SO^k}}((\Lambda '\!,\tau '),(\Omega ,\sigma ))\). Thus the equality
holds, and we easily deduce that \(\sigma (\varnothing )=\varnothing \). On the other hand, take \((\Lambda '\!,\tau ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\) such that \(\tau '(\varnothing ) \ne \varnothing \), and denote by \((g'\!,h')\) the only morphism in \(\textrm{Arr}_{\mathbf{SO^k}}((\Lambda '\!,\tau '),(\Omega ,\sigma ))\). Thus the equality  holds, and we easily deduce that \(\sigma (\varnothing ) \ne \varnothing \), which provides a contradiction.
holds, and we easily deduce that \(\sigma (\varnothing ) \ne \varnothing \), which provides a contradiction.
In view of [7, Theorem 2.8.1], by proving the non-existence of an initial object we will check that \(\mathbf{SO^k}\) is not bicomplete. To this end, assume by contradiction that \((\Omega ,\sigma )\) is the initial object in \(\mathbf{SO^k}\). Hence \(|\textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Lambda ,\tau ))|=1\) for any \((\Lambda ,\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\). Fix now \((\Lambda ,\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\), with \(\tau (\varnothing )=\varnothing \) and denote by (g, h) the only morphism in \(\textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Lambda ,\tau ))\). Thus, as the equality  holds, we easily get \(\sigma (\varnothing )=\varnothing \).
holds, we easily get \(\sigma (\varnothing )=\varnothing \).
On the other hand, \((\Lambda ,\tau ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\), with \(\tau (\varnothing )\ne \varnothing \) and denote again by (g, h) the only morphism in \(\textrm{Arr}_{\mathbf{SO^k}}((\Omega ,\sigma ),(\Lambda ,\tau ))\). Thus, as the equality  holds, we easily get \(\sigma (\varnothing )\ne \varnothing \), which provides a contradiction.\(\square \)
holds, we easily get \(\sigma (\varnothing )\ne \varnothing \), which provides a contradiction.\(\square \)
Remark 4.8
The following conditions hold:
-
(i)
\((\{a\},\sigma )\), where
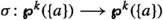 is defined by
is defined by  for each
for each  , is the terminal object in the category \(\mathbf{SO^{k,\sqsubseteq }}\);
, is the terminal object in the category \(\mathbf{SO^{k,\sqsubseteq }}\); -
(ii)
\((\{a\},\sigma )\), where
 is defined by \(\sigma (X)=\varnothing \) for each
is defined by \(\sigma (X)=\varnothing \) for each  , is the terminal object in the category \(\mathbf{SO^{k,\sqsupseteq }}\);
, is the terminal object in the category \(\mathbf{SO^{k,\sqsupseteq }}\); -
(iii)
\((\varnothing ,{\overline{\sigma }})\), where
 is defined by \({\overline{\sigma }}(X)=\varnothing \) for each
is defined by \({\overline{\sigma }}(X)=\varnothing \) for each  , is the initial object in the category \(\mathbf{SO^{k,\sqsubseteq }}\).
, is the initial object in the category \(\mathbf{SO^{k,\sqsubseteq }}\).
Before proving the next Theorem 4.10, we need the following preliminary result that we leave as an exercise to the reader.
Proposition 4.9
Let \(f \in \textrm{Arr}_{\textbf{Set}}(\Omega ,\Omega ')\) and \(k \geqslant 1\) be a given integer. If  is surjective, then
is surjective, then  is also surjective.
is also surjective.
Theorem 4.10
The following conditions hold:
-
(i)
there is no initial object in \(\mathbf{SO^{k,\sqsupseteq }}\);
-
(ii)
the category \(\mathbf{SO^{k,\sqsupseteq }}\) is not cocomplete;
-
(iii)
the categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) are not equivalent;
-
(iv)
the categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) are not dually equivalent.
Proof
(i): Assume by contradiction that \((\Lambda ,\tau )\) is the initial object in \(\mathbf{SO^{k,\sqsupseteq }}\). We cannot have \(\Lambda \ne \varnothing \). In fact, assume that \(\Lambda \ne \varnothing \) and let \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsupseteq }})\), where \(\Omega \) contains at least two elements and  for each
for each  , and let \((f,f')\) be the only arrow in \(\textrm{Arr}_{\mathbf{SO^{k,\sqsupseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). As
, and let \((f,f')\) be the only arrow in \(\textrm{Arr}_{\mathbf{SO^{k,\sqsupseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). As  , we easily deduce that
, we easily deduce that  is surjective and, by Proposition 4.9, we also conclude that \(f'\) is surjective. So \(|\Lambda | \geqslant |\Omega |\). At this point, notice that we can choose f in more than one way, contradicting the uniqueness of \((f,f')\).
is surjective and, by Proposition 4.9, we also conclude that \(f'\) is surjective. So \(|\Lambda | \geqslant |\Omega |\). At this point, notice that we can choose f in more than one way, contradicting the uniqueness of \((f,f')\).
Thus \(\Lambda =\varnothing \) and, moreover, if \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsupseteq }})\) and \((f,f')\) is the only arrow in \(\textrm{Arr}_{\mathbf{SO^{k,\sqsupseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\), we also deduce f and \(f'\) are the empty maps. Nevertheless, the inclusion  cannot hold if we take a non-empty set \(\Omega \) and the k-set operator \(\sigma \) on \(\Omega \) such that
cannot hold if we take a non-empty set \(\Omega \) and the k-set operator \(\sigma \) on \(\Omega \) such that  for each
for each  . In fact, just note that if \(z \in \Omega \), then
. In fact, just note that if \(z \in \Omega \), then  . This shows that \((\Lambda ,\tau )\) cannot exist.
. This shows that \((\Lambda ,\tau )\) cannot exist.
(ii): It is an immediate consequence of the above part (i) and of [7, Theorem 2.8.1].
(iii): Use part (iii) of Remark 4.8, the above part (i) and the fact that equivalence of categories preserve co-limit objects.
(iv): Assume by contradiction that \(\mathbf{SO^{k,\sqsupseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) were dually equivalent categories. Then \(\mathbf{SO^{k,\sqsubseteq }}\) would be equivalent to the dual category of \(\mathbf{SO^{k,\sqsupseteq }}\). Now, by part (i) of Remark 4.8 there exists the terminal object of \(\mathbf{SO^{k,\sqsubseteq }}\) and, hence, even the dual category of \(\mathbf{SO^{k,\sqsupseteq }}\) admits terminal object. This implies that \(\mathbf{SO^{k,\sqsubseteq }}\) has an initial object, in contrast with the above part (i).\(\square \)
Another substantial difference between the categories \(\mathbf{SO^{k,\sqsubseteq }}\) and \(\mathbf{SO^{k,\sqsupseteq }}\) concerns their completeness. In fact, with regard to the category \(\mathbf{SO^{k,\sqsubseteq }}\), we prove in the next Theorem 4.12 that it is complete, while for \(\mathbf{SO^{k,\sqsupseteq }}\) we check that in general it does not admit equalizers (see Proposition 4.15).
In order to prove Theorem 4.12, we need the following construction. Let  be a set-indexed family of sets. For every \(n \in \mathbb {N}\), let
be a set-indexed family of sets. For every \(n \in \mathbb {N}\), let  be the Cartesian product of the family
be the Cartesian product of the family  in \(\textbf{Set}\), and
in \(\textbf{Set}\), and  the i-th projection, for any \(i \in I\). Next, we consider:
the i-th projection, for any \(i \in I\). Next, we consider:
-
for any \(n \geqslant 1\), the map
 defined by setting
defined by setting  ;
; -
for any \(n \in \mathbb {N}\), the map
 defined by inductively setting
defined by inductively setting  and
and  for every \(n \geqslant 1\).
for every \(n \geqslant 1\).
Lemma 4.11
Let  be two families of sets indexed by the same set I, \(f_i \in \textrm{Arr}_\textbf{Set}(X_i,\,Y_i)\) for every \(i \in I\), \(Z \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\) and \(g_i \in \textrm{Arr}_\textbf{Set}(Z,\,Y_i)\) for any \(i \in I\). The following properties hold:
be two families of sets indexed by the same set I, \(f_i \in \textrm{Arr}_\textbf{Set}(X_i,\,Y_i)\) for every \(i \in I\), \(Z \in \textrm{Obj}\hspace{0.55542pt}(\textbf{Set})\) and \(g_i \in \textrm{Arr}_\textbf{Set}(Z,\,Y_i)\) for any \(i \in I\). The following properties hold:
-
(i)
 for any \(i \in I\) and any \(n \geqslant 1\);
for any \(i \in I\) and any \(n \geqslant 1\); -
(ii)
 for any \(n \geqslant 1\);
for any \(n \geqslant 1\); -
(iii)
 for any
for any  and any \(n \geqslant 1\);
and any \(n \geqslant 1\); -
(iv)
 for any \(i \in I\) and \(n \in \mathbb {N}\);
for any \(i \in I\) and \(n \in \mathbb {N}\); -
(v)
 for any \(n \in \mathbb {N}\);
for any \(n \in \mathbb {N}\); -
(vi)
 for any
for any  and any \(n \geqslant 1\).
and any \(n \geqslant 1\).
Proof
(i): Straightforward.
(ii): Let \((\mathcal {K}_i)_{i\in I}\in \Pi _{\mathfrak {G}}^{(n)}\). Then

(iii): Let  . Then
. Then

(iv): We proceed inductively on n. The case \(n=0\) is trivial. Fix now an integer \(n \geqslant 1\) and assume that the claim holds for \(1 \leqslant k \leqslant n-1\). Let \(i \in I\) and consider the following diagram:

In view of the above part (i), we have that  . On the other hand, by the inductive hypothesis we have
. On the other hand, by the inductive hypothesis we have  . Hence, applying
. Hence, applying  to the previous equality, we get the commutativity of the lower triangle of the diagram and we easily deduce the equality
to the previous equality, we get the commutativity of the lower triangle of the diagram and we easily deduce the equality  .
.
(v): We proceed inductively on n. The case \(n=0\) is trivial. Fix now an integer \(n \geqslant 1\) and assume that the claim holds for \(1 \leqslant k \leqslant n-1\). Consider the following diagram:

In view of the above part (ii), we have that the equality  holds. On the other hand, by the inductive hypothesis we get
holds. On the other hand, by the inductive hypothesis we get  . Hence, applying
. Hence, applying  to the previous equality, we get the commutativity of the lower square of the diagram. So, we clearly deduce the equality
to the previous equality, we get the commutativity of the lower square of the diagram. So, we clearly deduce the equality  .
.
(vi): We proceed inductively on n. The case \(n=0\) is trivial. Fix now an integer \(n \geqslant 1\) and assume that our assertion holds for \(1 \leqslant k \leqslant n-1\). Then  for every
for every  . We must prove our claim for n. To this regard, let
. We must prove our claim for n. To this regard, let  . By the above part (iii) it results that
. By the above part (iii) it results that

\(\square \)
At this point we can show the completenesss of the category \(\mathbf{SO^{k,\sqsubseteq }}\).
Theorem 4.12
The category \(\mathbf{SO^{k,\sqsubseteq }}\) is complete.
Proof
In view of [7, Proposition 2.8.1] it suffices to check the existence of the product of any indexed set family of objects and of equalizers. We begin with products. To this regard, let us consider  and \(\{(\Omega _i,\sigma _i) \,{|} \, i\,{\in }\,I\} \subseteq \mathbf{SO^{k,\sqsubseteq }}\). Set moreover
and \(\{(\Omega _i,\sigma _i) \,{|} \, i\,{\in }\,I\} \subseteq \mathbf{SO^{k,\sqsubseteq }}\). Set moreover  and let \(\pi ^{(0)}_{{\mathscr {S}},i}:\Omega \longrightarrow \Omega _i\) be the usual projections for any \(i \in I\) and
and let \(\pi ^{(0)}_{{\mathscr {S}},i}:\Omega \longrightarrow \Omega _i\) be the usual projections for any \(i \in I\) and  . Let us check that \(((\Omega ,\sigma ),\{(\pi ^{(0)}_{{\mathfrak {S}},i},\pi ^{(0)}_{{\mathfrak {S}},i}) \,{|} \, i\,{\in }\,I\})\) is the product of \(\{(\Omega _i,\sigma _i) \,{|} \, i\,{\in }\,I\}\) in \(\mathbf{SO^{k,\sqsubseteq }}\).
. Let us check that \(((\Omega ,\sigma ),\{(\pi ^{(0)}_{{\mathfrak {S}},i},\pi ^{(0)}_{{\mathfrak {S}},i}) \,{|} \, i\,{\in }\,I\})\) is the product of \(\{(\Omega _i,\sigma _i) \,{|} \, i\,{\in }\,I\}\) in \(\mathbf{SO^{k,\sqsubseteq }}\).
We clearly have \((\pi ^{(0)}_{{\mathfrak {S}},i},\pi ^{(0)}_{{\mathfrak {S}},i}) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega _i,\sigma _i))\) for any \(i \in I\) because, by Lemma 4.11 (iv) and of the definition of \(\sigma \), we get

Let now \((\Lambda ,\tau )\in \mathbf{SO^{k,\sqsubseteq }}\) and \((q_i,q'_i) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega _i,\sigma _i))\) for any \(i \in I\). Set first  and
and  .
.
We claim that \((r,r') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\), i.e. that  . By Lemma 4.11 (iv), the definition of r and since \((q_i,q'_i) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega _i,\sigma _i))\) for any \(i \in I\), we have
. By Lemma 4.11 (iv), the definition of r and since \((q_i,q'_i) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega _i,\sigma _i))\) for any \(i \in I\), we have

Furthermore we have \((q_i,q'_i)=(\pi ^{(0)}_{{\mathfrak {S}},i},\pi ^{(0)}_{{\mathfrak {S}},i}) \hspace{1.111pt}{\circ }\hspace{1.111pt}(r,r')\) for each \(i \in I\).
To complete the proof, let us compute the equalizers. To this regard, consider \((\Omega _1,\sigma _1),(\Omega _2,\sigma _2) \in \mathbf{SO^{k,\sqsubseteq }}\) and \((f,f'),(g,g') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega _1,\sigma _1),(\Omega _2,\sigma _2))\). Respectively set

We claim that \(((\Omega ,\sigma ),(\xi ,\xi ))\), where \(\xi :\Omega \longrightarrow \Omega _1\) is the usual set-theoretical inclusion, is the equalizer of \((f,f')\) and \((g,g')\) in \(\mathbf{SO^{k,\sqsubseteq }}\). Clearly, \((\xi ,\xi ) \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Omega ,\sigma ),(\Omega _1,\sigma _1))\) and \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}(\xi ,\xi )=(g,g') \hspace{1.111pt}{\circ }\hspace{1.111pt}(\xi ,\xi )\).
Take now \((\Lambda ,\tau ) \in \mathbf{SO^{k,\sqsubseteq }}\) and \((m,m') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega _1,\sigma _1))\) such that \((f,f') \hspace{1.111pt}{\circ }\hspace{1.111pt}(m,m')=(g,g') \hspace{1.111pt}{\circ }\hspace{1.111pt}(m,m')\). Define the maps \(n:\Lambda \longrightarrow \Omega \) and \(n':\Lambda \longrightarrow \Omega \) respectively setting  and
and  for any \(\lambda \in \Lambda \). We claim that \((n,n') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). To this end, fix
for any \(\lambda \in \Lambda \). We claim that \((n,n') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsubseteq }}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). To this end, fix  . Hence we get the inclusion
. Hence we get the inclusion  , whence our conclusion. Finally, it is obvious that \((n,n')\) is the only morphism such that \((m,m')=(\xi ,\xi ) \hspace{1.111pt}{\circ }\hspace{1.111pt}(n,n')\).\(\square \)
, whence our conclusion. Finally, it is obvious that \((n,n')\) is the only morphism such that \((m,m')=(\xi ,\xi ) \hspace{1.111pt}{\circ }\hspace{1.111pt}(n,n')\).\(\square \)
Exercise 4.13
Using a proof similar as that of Theorem 4.12, it may be easily shown that \(\mathbf{SO^{k,\sqsubseteq ,=}}\) is a complete category.
In order to prove the next Proposition 4.15, we need the following preliminary result.
Lemma 4.14
([7], Proposition 2.4.3) Let \(\mathfrak {C}\) be a category, \(A,B \in \textrm{Obj}\hspace{0.55542pt}(\mathfrak {C})\) and \(f,g \in \textrm{Arr}_\mathfrak {C}(A,B)\). If (H, h) is the equalizer of f and g, the arrow \(h \in \textrm{Arr}_\mathfrak {C}(H,A)\) is a monomorphism.
In the next result we will find two morphisms of \(\mathbf{SO^{k,\sqsupseteq }}\) not admitting equalizers.
Proposition 4.15
In general, the category \(\mathbf{SO^{k,\sqsupseteq }}\) does not admit equalizers.
Proof
Let \((\Omega _1,\sigma _1),(\Omega _2,\sigma _2) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^{k,\sqsupseteq }})\), where \(\Omega _1=\{x\}\), \(\Omega _2=\{a,b\}\),  for each
for each  and \(\sigma _2(Z)=\varnothing \) for each
and \(\sigma _2(Z)=\varnothing \) for each  .
.
Consider moreover the four maps \(f,f'\!,g,g':\Omega _1 \longrightarrow \Omega _2\) defined as follows: \(f(x)=f'(x)=g'(x)=a\) and \(g(x)=b\). Notice that \((f,f'),(g,g') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsupseteq }}}((\Omega _1,\sigma _1),(\Omega _2,\sigma _2))\).
Assume by contradiction that \(((\Lambda ,\tau ),(h,h'))\) is an equalizer of \((f,f')\) and \((g,g')\) in the category \(\mathbf{SO^{k,\sqsupseteq }}\). By Proposition 4.14 it follows that \((h,h')\) is a monomorphism and, thus, by Proposition 3.9 (i) we deduce that both h and \(h'\) are injective maps from \(\Lambda \) to \(\Omega _1\).
On the other hand, as \((h,h') \in \textrm{Arr}_{\mathbf{SO^{k,\sqsupseteq }}}((\Lambda ,\tau ),(\Omega _1,\sigma _1))\), we get the inclusion  and, using our choice of \(\sigma _1\), this implies that
and, using our choice of \(\sigma _1\), this implies that  is surjective. So, by Proposition 4.9 we deduce that \(h'\) is surjective. Thus, \(h'\) is a bijection between \(\Lambda \) and \(\Omega _1\). This shows that \(\Lambda \) contains only one element.
is surjective. So, by Proposition 4.9 we deduce that \(h'\) is surjective. Thus, \(h'\) is a bijection between \(\Lambda \) and \(\Omega _1\). This shows that \(\Lambda \) contains only one element.
Furthermore, we deduce that h is also bijective. Now, since \(((\Lambda ,\tau ),(h,h'))\) is the equalizer of \((f,f')\) and \((g,g')\) in the category \(\mathbf{SO^{k,\sqsupseteq }}\), it result that \(f \hspace{0.55542pt}{\circ }\hspace{1.111pt}h=g \hspace{1.111pt}{\circ }\hspace{1.111pt}h\), whence \(f=g\), in contrast with our choice of f and g. This shows that there is no equalizer of \((f,f')\) and \((g,g')\) in the category \(\mathbf{SO^{k,\sqsupseteq }}\).\(\square \)
As an immediate consequence of Proposition 4.15, we obtain the following result.
Corollary 4.16
The category \(\mathbf{SO^{k,\sqsupseteq }}\) is not complete.
We conclude this section showing that the category \(\mathbf{SO^k}\) does not have neither products nor coproducts.
Proposition 4.17
The following conditions hold:
-
(i)
\(\mathbf{SO^k}\) does not admit products;
-
(ii)
\(\mathbf{SO^k}\) does not admit coproducts.
Proof
In both proofs, we will consider the objects \((\Omega _1,\sigma _1),(\Omega _2,\sigma _2) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{SO^k})\), where \(\Omega _1=\Omega _2=\{x\}\),  for each
for each  and
and  .
.
(i): Assume by contradiction that there exists a product \(((\Omega ,\tau ),(p_1,p'_1),(p_2,p'_2))\) of \((\Omega _1,\sigma _1)\) and \((\Omega _2,\sigma _2)\). Then it follows that

Now, by (9) and the fact that \(\sigma _2(\varnothing )=\varnothing \), we get \(\tau (\varnothing )=\varnothing \) and \(\sigma _1(\varnothing )=\varnothing \), contradicting our choice of \(\sigma _1\). This proves that \((\Omega _1,\sigma _1)\) and \((\Omega _2,\sigma _2)\) do not have a product.
(ii): Assume by contradiction that there exists a coproduct \(((\Omega ,\tau ),(i_1,i'_1),(i_2,i'_2))\) of \((\Omega _1,\sigma _1)\) and \((\Omega _2,\sigma _2)\). Then it follows that

Now, by (10) and the fact that \(\sigma _2(\varnothing )=\varnothing \), we get \(\tau (\varnothing )=\varnothing \) and \(\sigma _1(\varnothing )=\varnothing \), contradicting our choice of \(\sigma _1\). This proves that \((\Omega _1,\sigma _1)\) and \((\Omega _2,\sigma _2)\) do not have a coproduct.\(\square \)
5 A new interpretation of the category of the equivalence relations
In any classical mathematical textbook an equivalence relation  on a given set \(\Omega \) is usually studied in a direct analogy with its corresponding counterpart which is the induced set partition on the same ground set \(\Omega \). In the scope of such an identification, we introduce a new notion, which is a class of Alexandroff closure set operators, and that we call equivalence closure set operators. In this section, we first address the identification of the three notions of equivalence relations, set partitions and equivalence closure set operators within our formalism of sub-bijection (see Proposition 5.3). Next, we extend the above sub-bijection to a categorial level (see Theorem 5.4).
on a given set \(\Omega \) is usually studied in a direct analogy with its corresponding counterpart which is the induced set partition on the same ground set \(\Omega \). In the scope of such an identification, we introduce a new notion, which is a class of Alexandroff closure set operators, and that we call equivalence closure set operators. In this section, we first address the identification of the three notions of equivalence relations, set partitions and equivalence closure set operators within our formalism of sub-bijection (see Proposition 5.3). Next, we extend the above sub-bijection to a categorial level (see Theorem 5.4).
To this regard, for any given set \(\Omega \) we denote by \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) the collection of all the equivalence relations on \(\Omega \), that is all the set relations  which are reflexive, symmetric and transitive. Notice also that we may consider \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) as a subfamily of \(\textrm{SR}\hspace{0.55542pt}(\Omega )\), by means of the identification of any pair \((x,y)\in \Omega \hspace{1.111pt}{\times }\hspace{1.111pt}\Omega \) with the pair
which are reflexive, symmetric and transitive. Notice also that we may consider \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) as a subfamily of \(\textrm{SR}\hspace{0.55542pt}(\Omega )\), by means of the identification of any pair \((x,y)\in \Omega \hspace{1.111pt}{\times }\hspace{1.111pt}\Omega \) with the pair  . Let \(\textbf{EQ}\) be the full subcategory of \(\mathbf{SR^0}\) defined by
. Let \(\textbf{EQ}\) be the full subcategory of \(\mathbf{SR^0}\) defined by

The main purpose of the present section is the proof of the next Theorem 5.4, where we determine two isomorphisms between the above category \(\textbf{EQ}\) and other two categories of set systems and set operators, respectively. We need first to introduce some preliminary linking maps, between binary relations and set systems, and between set systems and set operators. To this regard we define:
-
\(\textrm{Pa}:\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) such that
 for any
for any  , where
, where 
-
\(\textrm{Qa}:\, \textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) defined by
 , for each \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\);
, for each \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\); -
\(\textrm{Up} :\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\) such that
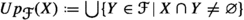 , for each
, for each  and any
and any  ;
; -
\(\textrm{Eq}:\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SR}\hspace{0.55542pt}(\Omega )\) defined by
 , for each
, for each  .
.
We introduce now a new sub-collection of closure set operators, which we call equivalence set operators in view of the categorial isomorphism obtained in Theorem 5.4.
Definition 5.1
We say that a set operator \(\sigma \in \textrm{SO}\hspace{0.55542pt}(\Omega )\) is an equivalence set operator on \(\Omega \) if it satisfies the following properties:
- (E1):
-
\(\sigma \) is extensive;
- (E2):
-
\(\sigma (X)=\bigcup \hspace{0.55542pt}\{\sigma (\{x\}) \,{|}\, x \in X\}\), for any
 ;
; - (E3):
-
for any \(x, y\in \Omega \), the condition \(\sigma (\{x\})=\sigma (\{y\})\) is equivalent to \(\sigma (\{x\})\cap \sigma (\{y\})\ne \varnothing \).
We denote by \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) the family of all equivalence set operators on \(\Omega \).
Remark 5.2
Notice that equivalence set operators are particular types of closure set operators, that is \(\textrm{ESO}\hspace{0.55542pt}(\Omega ) \subseteq \textrm{CSO}\hspace{0.55542pt}(\Omega )\).
A direct consequence of Remark 5.2 and of property (E2) is that any equivalence set operator is also an Alexandroff closure set operator. We refer the interested reader to know further properties of Alexandroff closure set operators to the work [12], where such operators are investigated mainly in relation to their links with monoid actions.
The next result is preliminary to the proof of Theorem 5.4. Here, we frame the collections \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\), \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\) within the formalism of sub-bijections, introduced in Definition 1.2.
Proposition 5.3
We have that

is an \((\textrm{SR}\hspace{0.55542pt}(\Omega ), \textrm{SS}\hspace{0.55542pt}(\Omega ), \textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection.
Proof
The fact that \(\textrm{Pa}\) is a bijection between \(\textrm{EQ}\hspace{0.55542pt}(\Omega )\) and \(\textrm{SP}\hspace{0.55542pt}(\Omega )\), with inverse \(\textrm{Eq}\), is a classical result. So, it suffices to show that \(\textrm{Up}\) is a bijection between \(\textrm{SP}\hspace{0.55542pt}(\Omega )\) and \(\textrm{ESO}\hspace{0.55542pt}(\Omega )\), with inverse \(\textrm{Qa}\).
Let  . We claim that
. We claim that  . To this regard, by the definition of \(\textrm{Up}\) we clearly have that
. To this regard, by the definition of \(\textrm{Up}\) we clearly have that  and, moreover, it is also easy to prove that
and, moreover, it is also easy to prove that  is an extensive and increasing set operator. Furthermore it satisfies property (E3) because, for every \(x \in \Omega \), it results that
is an extensive and increasing set operator. Furthermore it satisfies property (E3) because, for every \(x \in \Omega \), it results that  agrees with the only member of the set partition
agrees with the only member of the set partition  of \(\Omega \) that contains the element x.
of \(\Omega \) that contains the element x.
Let us now prove that  satisfies (E2). To this end, fix
satisfies (E2). To this end, fix  and, for every \(y \in \Omega \), denote by \(B_y\) the only member of
and, for every \(y \in \Omega \), denote by \(B_y\) the only member of  containing y. Then, we clearly have
containing y. Then, we clearly have

This shows (E2) and, so,  .
.
Let \(\sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\). As \(\sigma \) is extensive and by property (E3) we easily deduce that \(\textrm{Qa}\hspace{0.55542pt}(\sigma ) \in \textrm{SP}\hspace{0.55542pt}(\Omega )\).
Now, let us prove that \(\textrm{Up}_{\textrm{Qa}\hspace{0.55542pt}(\sigma )}=\sigma \) for each \(\sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\). To this regard, when \(\sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\), it is sufficient to observe that
On the other hand, we clearly have  for each
for each  .\(\square \)
.\(\square \)
Now, in order to obtain a categorical extension preserving the directions of the arrows of the above sub-bijection, we consider the following \((\textrm{SS}\hspace{0.55542pt}(\Omega ), \textrm{SR}\hspace{0.55542pt}(\Omega ), \textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection induced by that previously obtained in Proposition 5.3:

where  and
and  .
.
We introduce now the following category, whose objects are equivalence set operators.
-
Let \(\mathbf{ESO^{1,\sqsubseteq ,=}}\) be the full subcategory of \(\mathbf{SO^{1,\sqsubseteq ,=}}\) for which \(\textrm{Obj}\hspace{0.55542pt}(\mathbf{ESO^{1,\sqsubseteq ,=}})=\{(\Omega ,\sigma ) \,{|} \, \sigma \in \textrm{ESO}\hspace{0.55542pt}(\Omega )\}\).
Before proving Theorem 5.4, we need to introduce the category \(\textbf{SP}\) whose objects are set partitions, and the candidate correspondences to be the categorial isomorphisms established in Theorem 5.4.
-
Let \(\textbf{SP}\) be the category for which
 , and such that
, and such that  for each
for each  , where the symbol \(\preceq \) denotes the usual partial order on \(\textrm{SP}\hspace{0.55542pt}(\Omega ')\) defined by
, where the symbol \(\preceq \) denotes the usual partial order on \(\textrm{SP}\hspace{0.55542pt}(\Omega ')\) defined by 
We now extended to a functorial level the linking maps \(\textrm{Za}\), \(\textrm{Ta}\), \(\textrm{Pa}\) and \(\textrm{Eq}\), respectively as follows:
-
\(\widehat{\textrm{Za}}:\mathbf{ESO^{1,\sqsubseteq ,=}} \longrightarrow \textbf{EQ}\), where
 and
and  , for \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{ESO^{1,\sqsubseteq ,=}})\) and \((f,f) \in \textrm{Arr}_\mathbf{ESO^{1,\sqsubseteq ,=}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\);
, for \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{ESO^{1,\sqsubseteq ,=}})\) and \((f,f) \in \textrm{Arr}_\mathbf{ESO^{1,\sqsubseteq ,=}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\); -
\(\widehat{\textrm{Ta}}:\textbf{EQ}\longrightarrow \mathbf{ESO^{1,\sqsubseteq ,=}}\), where
 and
and  , whenever
, whenever  and
and  ;
; -
\(\widehat{\textrm{Pa}}:\textbf{EQ}\longrightarrow \textbf{SP}\), where
 and
and  , whenever
, whenever  and
and  ;
; -
\(\widehat{\textrm{Eq}}:\textbf{SP} \longrightarrow \textbf{EQ}\), where
 and
and  , whenever
, whenever  , for any
, for any  .
.
Through the categories \(\mathbf{ESO^{1,\sqsubseteq ,=}}\), \(\textbf{EQ}\) and \(\textbf{SP}\) and the previous correspondences, in the next result we extend to a categorical level the sub-bijection given in (11).
Theorem 5.4
The arrows of the diagram

are isomorphisms of categories, where \(\widehat{\textrm{Pa}}\) is the inverse of \(\widehat{\textrm{Eq}}\) and \(\widehat{\textrm{Za}}\) is the inverse of \(\widehat{\textrm{Ta}}\).
Proof
The claim concerning \(\widehat{\textrm{Pa}}\) and \(\widehat{\textrm{Eq}}\) is easy and straightforward. Let us prove that \(\widehat{\textrm{Za}}\) and \(\widehat{\textrm{Ta}}\) are well defined. To this regard, let us consider \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{ESO^{1,\sqsubseteq ,=}})\) and \((f,f) \in \textrm{Arr}_\mathbf{ESO^{1,\sqsubseteq ,=}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Let moreover \(x_1,x_2 \in \Omega \) be such that \((x_1,x_2) \in \textrm{Za}\hspace{0.55542pt}(\sigma )\). Hence we get  , so that
, so that

and, by (E3), we conclude that \(\sigma '(f(\{x_1\})==\sigma '(f(\{x_2\}))\), i.e. \((f(\{x_1\},f(\{x_2\}) \in \textrm{Za}\hspace{0.55542pt}(\sigma ')\). This proves that \(\widehat{\textrm{Za}}\hspace{0.55542pt}((f,f))=f \in \textrm{Arr}_{\textbf{EQ}}((\Omega ,\textrm{Za}\hspace{0.55542pt}(\sigma )),(\Omega '\!,\textrm{Za}\hspace{0.55542pt}(\sigma ')))\).
Let us analyze the correspondence \(\widehat{\textrm{Ta}}\). Let  and
and  . Take
. Take  . Then we have
. Then we have

At this point, we take an element  . Clearly there exist \(x,y \in X\) such that
. Clearly there exist \(x,y \in X\) such that  and \(y'\!=f(y)\). Therefore, since
and \(y'\!=f(y)\). Therefore, since  , it follows that
, it follows that  , whence
, whence  . Then \(\widehat{\textrm{Ta}}\hspace{0.55542pt}(f)=(f,f) \in \textrm{Arr}_\mathbf{ESO^{1,\sqsubseteq ,=}}((\Omega ,\textrm{Ta}\hspace{0.55542pt}(\sigma )),(\Omega '\!,\textrm{Ta}\hspace{0.55542pt}(\sigma ')))\).\(\square \)
. Then \(\widehat{\textrm{Ta}}\hspace{0.55542pt}(f)=(f,f) \in \textrm{Arr}_\mathbf{ESO^{1,\sqsubseteq ,=}}((\Omega ,\textrm{Ta}\hspace{0.55542pt}(\sigma )),(\Omega '\!,\textrm{Ta}\hspace{0.55542pt}(\sigma ')))\).\(\square \)
In the next result we prove that \(\textbf{EQ}\) is a reflective subcategory of \(\mathbf{SR^0}\).
Proposition 5.5
\(\textbf{EQ}\) is a reflective subcategory of \({\hspace{1.111pt}\textbf{SR}^0}\).
Proof
Let  and consider the transitive closure
and consider the transitive closure  of the binary relation
of the binary relation

Then  and it is immediate to check that
and it is immediate to check that  is the wanted reflection.\(\square \)
is the wanted reflection.\(\square \)
As an immediate corollary we get the following result.
Corollary 5.6
The following conditions hold:
-
(i)
\(\textbf{EQ}\) is bicomplete;
-
(ii)
\(\textbf{SP}\) and \(\mathbf{ESO^{1,\sqsubseteq ,=}}\) are bicomplete.
Proof
(i): It follows by Theorem 4.2 and by Proposition 5.5.
(ii): It is an immediate consequence of Theorem 5.4 and of the above part (i).\(\square \)
6 Closure set operators, closure set systems and dependence set relations
In this section we consider the pairs \((\Omega , \sigma )\), where \(\Omega \) is a fixed ground set and \(\sigma \in \textrm{CSO}\hspace{0.55542pt}(\Omega )\), as the objects of two specific categories, that we denote respectively by \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\).
More in detail, we must introduce two different conditions in order to define the previous two categories. Using the two categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) we prove the main result (Theorem 6.6) of this section. In such a result we obtain a categorical version of the usual bijective correspondence between closure set operators and closure set systems, and, moreover, provide an isomorphism between one among the previous categories of closure set operators and a specific kind of binary relations (called dependence relations) introduced formally in [14].
Let therefore \(\Omega \) be a fixed arbitrary set. We recall the notion of dependence relation on \(\Omega \).
Definition 6.1
([14]) We call any set relation  a dependence set relation on \(\Omega \) if the following conditions hold:
a dependence set relation on \(\Omega \) if the following conditions hold:
- (D1):
-
if
 and \(Y \subseteq X\), then
and \(Y \subseteq X\), then  ;
; - (D2):
-
if
 then
then  ;
; - (D3):
-
 if and only if
if and only if 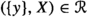 for any \(y \in Y\).
for any \(y \in Y\).
We denote by \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\) the family of all dependence relations on \(\Omega \).
The proof of the next result is easy and we leave it to the reader.
Proposition 6.2
The following conditions hold:
-
(i)
 if and only if it satisfies (D1), (D2) and if
if and only if it satisfies (D1), (D2) and if  then
then  ;
; -
(ii)
if
 and
and  then
then 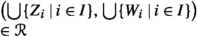 ;
; -
(iii)
if \(\mathfrak {E}\subseteq \textrm{DSR}\hspace{0.55542pt}(\Omega )\) then \(\bigcap \mathfrak {E}\in \textrm{DSR}\hspace{0.55542pt}(\Omega )\).
If  , we set
, we set

Notice that  is the smallest dependence relation on \(\Omega \) containing
is the smallest dependence relation on \(\Omega \) containing  as a subfamily. We say that
as a subfamily. We say that  the dependence closure of
the dependence closure of  .
.
In order to prepare the proof of Theorem 6.6 we first introduce the following new linking maps:
-
\(\eta :\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\) and \(\textrm{Cl}:\textrm{SS}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\), defined respectively by:
 (12)
(12) (13)
(13) -
\(\Phi :\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SR}\hspace{0.55542pt}(\Omega )\) and \(\textrm{Fix}:\textrm{SO}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\), defined respectively by:
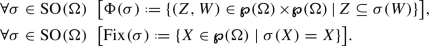
In the next result (whose simple proof is left to the reader) we establish the basic properties of the above linking maps.
Proposition 6.3
Let  and
and  . Then:
. Then:
-
(i)
 ;
; -
(ii)
 ;
; -
(iii)
 .
.
The next result is preliminary to the proof of Theorem 6.6. Here, we frame the collections \(\textrm{DSR}\hspace{0.55542pt}(\Omega )\), \(\textrm{CSS}\hspace{0.55542pt}(\Omega )\) and \(\textrm{CSO}\hspace{0.55542pt}(\Omega )\) within the formalism of sub-bijections, introduced in Definition 1.2.
Proposition 6.4
We have that

is an \((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega ))\)-sub-bijection.
Proof
Using a classical result of Birkhoff concerning closure set systems and closure set operators (see [3]) it results that

is an \((\textrm{SS}\hspace{0.55542pt}(\Omega ),\textrm{SO}\hspace{0.55542pt}(\Omega ))\)-sub-bijection. Therefore it remains to show that also

is an \((\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega ))\)-sub-bijection.
To this regard, since  , in view of Proposition 6.3 (ii) we deduce that
, in view of Proposition 6.3 (ii) we deduce that  . Let now \(\sigma \in \textrm{CSO}\hspace{0.55542pt}(\Omega )\). We first show that \(\Phi (\sigma ) \in \textrm{DSR}\hspace{0.55542pt}(\Omega )\), namely that the set relation \(\Phi (\sigma )\) satisfies the properties (D1), (D2) and (D3). With regard to both the properties (D1) and (D2), they follow respectively by the extensiveness and the monotonicity of the set operator \(\sigma \).
. Let now \(\sigma \in \textrm{CSO}\hspace{0.55542pt}(\Omega )\). We first show that \(\Phi (\sigma ) \in \textrm{DSR}\hspace{0.55542pt}(\Omega )\), namely that the set relation \(\Phi (\sigma )\) satisfies the properties (D1), (D2) and (D3). With regard to both the properties (D1) and (D2), they follow respectively by the extensiveness and the monotonicity of the set operator \(\sigma \).
With regard to the property (D3), let  and \(y\in \Omega \). Then we get \((Y,X) \in \Phi (\sigma )\) if and only if \((\{y\},X) \in \Phi (\sigma )\) for each \(y \in Y\). In fact, notice that \((Y,X) \in \Phi (\sigma )\) if and only if \(Y \subseteq \sigma (X)\), that is equivalent to say that \(y \in \sigma (X)\) for each \(y \in Y\), i.e. \((\{y\},X) \in \Phi (\sigma )\) for any \(y \in Y\). Hence (D3) holds.
and \(y\in \Omega \). Then we get \((Y,X) \in \Phi (\sigma )\) if and only if \((\{y\},X) \in \Phi (\sigma )\) for each \(y \in Y\). In fact, notice that \((Y,X) \in \Phi (\sigma )\) if and only if \(Y \subseteq \sigma (X)\), that is equivalent to say that \(y \in \sigma (X)\) for each \(y \in Y\), i.e. \((\{y\},X) \in \Phi (\sigma )\) for any \(y \in Y\). Hence (D3) holds.
Let now  . We claim that
. We claim that  . To this end, if
. To this end, if  , then
, then  by (12), whence
by (12), whence  . Conversely, if
. Conversely, if  , then
, then  . Therefore, for any element \(y \in Y\) there exists
. Therefore, for any element \(y \in Y\) there exists  for which \(y \in Z_y\) and
for which \(y \in Z_y\) and  . Consequently, since
. Consequently, since  , by (D3) it follows that
, by (D3) it follows that  for each \(y \in Y\). Thus, again by (D3) we deduce that
for each \(y \in Y\). Thus, again by (D3) we deduce that  .
.
At this point, notice that \(\eta _{\Phi (\sigma )}=\sigma \). In fact, if  , we have that
, we have that

Hence (14) is an \((\textrm{SO}\hspace{0.55542pt}(\Omega ),\textrm{SR}\hspace{0.55542pt}(\Omega ))\)-sub-bijection on \(\Omega \).\(\square \)
We now introduce the following new categories of set operators (for brevity we provide explicitly only the definition concerning \(\sqsubseteq \), because the corresponding definition with \(\sqsupseteq \) is similar):
-
the full subcategory \(\mathbf{CSO^{1,\sqsubseteq , =}}\) of \(\mathbf{SO^{1,\sqsubseteq , =}}\), where
 .
.
We will use closure set systems and dependence relations as objects of the following two categories:
-
the full subcategory \(\mathbf{CSS^1}\) of \(\mathbf{SS^1}\), where
 ;
; -
the full subcategory \(\mathbf{DSR^1}\) of \(\mathbf{SR^1}\), where
 .
.
In the next result we prove that the category \(\mathbf{DSR^1}\) is complete.
Theorem 6.5
The category \(\mathbf{DSR^1}\) is complete.
Proof
In view of [7, Theorem 2.8.1], we must prove the existence of products and equalizers in \(\mathbf{DSR^1}\). To this regard, first take  . Consider their product
. Consider their product  in the category \(\mathbf{SR^1}\), computed in the proof of Theorem 4.2. As \(\mathbf{DSR^1}\) is a full subcategory of \(\mathbf{SR^1}\), it suffices to check that
in the category \(\mathbf{SR^1}\), computed in the proof of Theorem 4.2. As \(\mathbf{DSR^1}\) is a full subcategory of \(\mathbf{SR^1}\), it suffices to check that  .
.
To this end, let first  be such that \(Y \subseteq X\). Then, as
be such that \(Y \subseteq X\). Then, as  is increasing and
is increasing and  for any \(i \in I\), we get
for any \(i \in I\), we get  for all \(i\in I\), so that
for all \(i\in I\), so that  .
.
Suppose now that  . We claim that
. We claim that  . To this regard, just observe that our assumptions imply that
. To this regard, just observe that our assumptions imply that  for each \(i \in I\). Hence
for each \(i \in I\). Hence  for each \(i \in I\) because
for each \(i \in I\) because  . This proves that
. This proves that  .
.
Finally let us prove that  if and only if
if and only if  for each \(z \in Z\). To this regard, using the fact that
for each \(z \in Z\). To this regard, using the fact that  , we easily get
, we easily get

This proves that  .
.
Let now  and
and  ,
,  . As \(\mathbf{DSR^1}\) is a full subcategory of \(\mathbf{SR^1}\), we have
. As \(\mathbf{DSR^1}\) is a full subcategory of \(\mathbf{SR^1}\), we have  .
.
Thus we can consider the equalizer  of f and g in \(\mathbf{SR^1}\) computed in the proof of Theorem 4.2. By a straightforward check, we easily deduce that
of f and g in \(\mathbf{SR^1}\) computed in the proof of Theorem 4.2. By a straightforward check, we easily deduce that  .\(\square \)
.\(\square \)
The last tools to be introduced before proving the next Theorem 6.6 are the following correspondences:
-
\(\widehat{\textrm{Fix}}:\mathbf{CSO^{1,\sqsupseteq ,=}}\longrightarrow \mathbf{CSS^1}\), where
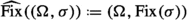 and
and  , whenever \((\Omega ,\sigma ), (\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\);
, whenever \((\Omega ,\sigma ), (\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\); -
\(\widehat{\textrm{Cl}}:\mathbf{CSS^1} \longrightarrow \mathbf{CSO^{1,\sqsupseteq ,=}}\), where
 and
and  , whenever
, whenever 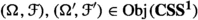 and
and  ;
; -
\({\widehat{\eta }}:\mathbf{DSR^1} \longrightarrow \mathbf{CSO^{1,\sqsubseteq ,=}}\), where
 and
and  , whenever
, whenever  ,
,  and
and  ;
; -
\({\widehat{\Phi }}:\mathbf{CSO^{1,\sqsubseteq ,=}}\!\longrightarrow \mathbf{DSR^1}\), where
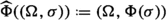 and
and 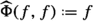 , whenever \((\Omega ,\sigma )\), \((\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\).
, whenever \((\Omega ,\sigma )\), \((\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\).
Now we provide the proof of the main result of the present section.
Theorem 6.6
The arrows of the diagrams

are isomorphisms of categories.
Proof
We must only show the four correspondences are well defined on arrows. Let \((\Omega ,\sigma ), (\Omega '\!, \sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsubseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsubseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Let moreover \((X,Y) \in \Phi (\sigma )\). By the definitions of \(\Phi (\sigma )\) and of the arrows in \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) it follows that  , whence
, whence  and
and  . Thus \({\widehat{\Phi }}\) is well defined.
. Thus \({\widehat{\Phi }}\) is well defined.
We examine now \({\widehat{\eta }}\). To this end, let  and
and  . Let moreover
. Let moreover  . Then, by Proposition 6.3 (i) and since
. Then, by Proposition 6.3 (i) and since  , it follows that
, it follows that  . Hence, in view of the definition of the arrows in the category \(\mathbf{DSR^1}\), it results that
. Hence, in view of the definition of the arrows in the category \(\mathbf{DSR^1}\), it results that  . Again, by Proposition 6.3 (i) and since
. Again, by Proposition 6.3 (i) and since  , we also obtain that
, we also obtain that  , whence
, whence  in view of the arbitrariness of X. This proves that
in view of the arbitrariness of X. This proves that  . Therefore, also the correspondence \({\widehat{\eta }}\) is well defined.
. Therefore, also the correspondence \({\widehat{\eta }}\) is well defined.
We now prove that \(\widehat{\textrm{Fix}}:\mathbf{CSO^{1,\sqsupseteq ,=}}\longrightarrow \mathbf{CSS^1}\) is well defined on arrows. Let therefore \((\Omega ,\sigma ),(\Omega '\!,\sigma ') \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and \((f,f) \in \textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Omega ,\sigma ),(\Omega '\!,\sigma '))\). Let moreover \(X \in \textrm{Fix}\hspace{0.55542pt}(\sigma )\) and set  . By the definition of the arrows of \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) and our choice of X, it follows that
. By the definition of the arrows of \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) and our choice of X, it follows that

On the other hand, since \(\sigma ' \!\in \textrm{CSO}\hspace{0.55542pt}(\Omega ')\), we also have \(Y \subseteq \sigma '(Y)\), so that \(\sigma '(Y)=Y\), i.e. \(Y \in \textrm{Fix}\hspace{0.55542pt}(\sigma ')\). Therefore \(\widehat{\textrm{Fix}}\hspace{0.55542pt}(f,f)=f \in \textrm{Arr}_{\mathbf{CSS^1}}((\Omega ,\widehat{\textrm{Fix}}\hspace{0.55542pt}(\sigma )),(\Omega '\!,\widehat{\textrm{Fix}}\hspace{0.55542pt}(\sigma ')))\), i.e. \(\widehat{\textrm{Fix}}\) is well defined.
Let us examine \(\widehat{\textrm{Cl}}\). Let  and
and  . Since
. Since  is increasing and
is increasing and  , in view of Proposition 6.4 and the definition of the arrows of \(\mathbf{CSS^1}\), it follows that
, in view of Proposition 6.4 and the definition of the arrows of \(\mathbf{CSS^1}\), it follows that

for any  . Thus
. Thus  and the correspondence \(\widehat{\textrm{Cl}}\) is also well defined.\(\square \)
and the correspondence \(\widehat{\textrm{Cl}}\) is also well defined.\(\square \)
In the next result we establish further properties of the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\), \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) and \(\mathbf{CSS^1}\). In particular, we will see that the two categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) are deeply different because they are neither equivalent nor dually equivalent.
Proposition 6.7
The following conditions hold:
-
(i)
there is no initial object in \(\mathbf{CSO^{1,\sqsupseteq ,=}}\);
-
(ii)
\(\mathbf{CSO^{1,\sqsupseteq ,=}}\) is not cocomplete;
-
(iii)
the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) are not equivalent;
-
(iv)
the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) are not dually equivalent;
-
(v)
the category \(\mathbf{CSS^1}\) is not cocomplete;
-
(vi)
the categories \(\mathbf{CSS^1}\) and \(\mathbf{DSR^1}\) are not equivalent;
-
(vii)
the category \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) is complete.
Proof
(i): Assume by contradiction that \((\Lambda ,\tau )\) is the initial object in \(\mathbf{CSO^{1,\sqsupseteq ,=}}\). We cannot have \(\Lambda \ne \varnothing \). In fact, assume that \(\Lambda \ne \varnothing \) and let \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\), where \(\Omega \) contains at least two elements and \(\sigma (X)=\Omega \) for each  , and let (f, f) be the only arrow in \(\textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). As
, and let (f, f) be the only arrow in \(\textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Lambda ,\tau ),(\Omega ,\sigma ))\). As  , taking \(X=\Lambda \), we easily deduce that f is surjective. So \(|\Lambda | \geqslant |\Omega |\) and we can choose the surjective function \(f:\Lambda \longrightarrow \Omega \) in a more than one arbitrary way, contradicting the uniqueness of (f, f).
, taking \(X=\Lambda \), we easily deduce that f is surjective. So \(|\Lambda | \geqslant |\Omega |\) and we can choose the surjective function \(f:\Lambda \longrightarrow \Omega \) in a more than one arbitrary way, contradicting the uniqueness of (f, f).
Thus \(\Lambda =\varnothing \) and  . Moreover, if \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and (f, f) is the only arrow in \(\textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Lambda ,\tau ),(\Omega ,\sigma ))\), we also deduce f is the empty map. Nevertheless, the inclusion
. Moreover, if \((\Omega ,\sigma ) \in \textrm{Obj}\hspace{0.55542pt}(\mathbf{CSO^{1,\sqsupseteq ,=}})\) and (f, f) is the only arrow in \(\textrm{Arr}_{\mathbf{CSO^{1,\sqsupseteq ,=}}}((\Lambda ,\tau ),(\Omega ,\sigma ))\), we also deduce f is the empty map. Nevertheless, the inclusion  cannot hold if we take a non-empty set \(\Omega \) and the set operator \(\sigma \) on \(\Omega \) such that \(\sigma (X)=\Omega \) for each
cannot hold if we take a non-empty set \(\Omega \) and the set operator \(\sigma \) on \(\Omega \) such that \(\sigma (X)=\Omega \) for each  . This shows that \((\Lambda ,\tau )\) cannot exist.
. This shows that \((\Lambda ,\tau )\) cannot exist.
(ii): It follows immediately by the above part (i) and by [7, Theorem 2.8.1].
(iii): In view of Proposition 4.7 (v), the category \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) admits an initial object. Now, if the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) were equivalent, then even \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) would have an initial object, in contrast with the above part (i).
(iv): In view of Proposition 4.7 (iv), the category \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) admits a terminal object. Now, if the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) were dually equivalent, then \(\mathbf{CSO^{1,\sqsupseteq ,=}}\) would admit an initial object, in contrast with the above part (i).
(v): It follows by the above part (ii) and by Theorem 6.6.
(vi): If \(\mathbf{CSS^1}\) and \(\mathbf{DSR^1}\) were equivalent, then by Theorem 6.6 we would get an equivalence between the categories \(\mathbf{CSO^{1,\sqsubseteq ,=}}\) and \(\mathbf{CSO^{1,\sqsupseteq ,=}}\), contradicting the above part (iii).
(vii): It follows immediately by Theorems 6.5 and 6.6.\(\square \)
We conclude the present section proving next Theorem 6.11. With regard to this result, it is convenient first provide a new interpretation of the linking map \(\textrm{Cl}\) when the ground set \(\Omega \) is substituted with  . In fact, with such a choice, it is clear that
. In fact, with such a choice, it is clear that  . Consequently, in view of (13) it follows that \(\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}\) is an element of
. Consequently, in view of (13) it follows that \(\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}\) is an element of  , i.e.
, i.e.

Now, if we interpret \(\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}\) as a linking map between \(\textrm{SR}\hspace{0.55542pt}(\Omega )\) into itself, it is also natural to consider its relationships with a linking map \(\Psi \), from relations to set systems, that is implicitly used (although not explicitly defined) in several scopes of theoretical computer science (see for example [35]).
Formally, we introduce the linking map \(\Psi :\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SS}\hspace{0.55542pt}(\Omega )\) defined by

for any  .
.
The map \(\Psi \) enables us to highlight a fundamental aspect related to the sub-bijections obtained through linking maps. To this end, we consider both the linking maps \(\Psi \) and \(\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\eta \). Then, we have the following result, whose simple proof is left to the reader.
Proposition 6.8
The following conditions hold:
-
(i)
 for any
for any  ;
; -
(ii)
 is a closure set system on \(\Omega \), for any
is a closure set system on \(\Omega \), for any 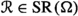 ;
; -
(iii)
there exists
 such that
such that 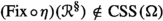 .
.
In view of Proposition 6.8 we observe that the linking maps \(\Psi \) and \(\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\eta \) differ from each other. In fact, by Proposition 6.8 (ii) it follows that \(\Psi \) maps any set relation on \(\Omega \) to a closure set system on the same ground set, while the same does not hold for the linking map \(\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\eta \), as one can see by Proposition 6.8 (iii).
In addition, by Proposition 6.8 (i) we can also notice that the restrictions of \(\Psi \) and \(\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\eta \) to the collection of all dependence relations on \(\Omega \) agree. From this and Proposition 6.4, we then obtain the two following distinct \((\textrm{SR}\hspace{0.55542pt}(\Omega ),\textrm{SS}\hspace{0.55542pt}(\Omega ))\)-sub-bijections:

In the next Theorem 6.11 we will establish the natural commutativities between the linking maps \(\textrm{Fix}\), \(\Psi \) and \(\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}\) when \(\Omega \) is a fixed finite ground set. To this regard it is first necessary to introduce two linking maps \(\Theta ,\Gamma :\textrm{SR}\hspace{0.55542pt}(\Omega ) \longrightarrow \textrm{SO}\hspace{0.55542pt}(\Omega )\) defined by:

With regard to the above linking maps, we get the following results.
Proposition 6.9
Let  , \(k \geqslant 0\),
, \(k \geqslant 0\),  and
and  . Then
. Then  .
.
Proof
Use induction on k and the definition of dependence relation,  and of the set operator \(\Theta \).\(\square \)
and of the set operator \(\Theta \).\(\square \)
Proposition 6.10
For any  , the following conditions hold:
, the following conditions hold:
-
(i)
 ;
; -
(ii)
 .
.
Proof
Straightforward.\(\square \)
At this point we are able to prove the last result of this section.
Theorem 6.11
Let \(\Omega \) be a fixed set. Then the diagram

commutes, i.e. \(\Psi \hspace{1.111pt}{\circ }\hspace{1.111pt}\textrm{Cl}_{\textrm{DSR}\hspace{0.55542pt}(\Omega )}=\Psi =\textrm{Fix} \hspace{1.111pt}{\circ }\hspace{1.111pt}\Gamma \).
Proof
Let  be fixed. The commutativity of the above diagram is equivalent to show that
be fixed. The commutativity of the above diagram is equivalent to show that  . We want first show that
. We want first show that

To this end, we need to show that
Let us check that

To this regard, take  . First note that
. First note that  by (12) and by Proposition 6.10 (i), so that
by (12) and by Proposition 6.10 (i), so that  . By the definition of
. By the definition of  , it is now sufficient to check that
, it is now sufficient to check that  and this is a consequence of Proposition 6.4 because
and this is a consequence of Proposition 6.4 because  by Proposition 6.10 (ii). So (17) holds.
by Proposition 6.10 (ii). So (17) holds.
We now show that  . To this regard, fix
. To this regard, fix  .
.
As  and
and  , by Proposition 6.4 we have that
, by Proposition 6.4 we have that  . Therefore, by (17) and Proposition 6.3 (i), we easily get the inclusion
. Therefore, by (17) and Proposition 6.3 (i), we easily get the inclusion  .
.
Conversely, let  . Then either \(y \in X\) or there exists a minimum integer \(s \geqslant 1\) such that
. Then either \(y \in X\) or there exists a minimum integer \(s \geqslant 1\) such that  . If \(y \in X\), then we get
. If \(y \in X\), then we get  , whence
, whence  .
.
Assume therefore the existence of a minimum integer \(s \geqslant 1\) such that

In view of the minimality of s, there exists  such that
such that  . Thus, by (12), there exists
. Thus, by (12), there exists  such that \(y \in Z_y\) and
such that \(y \in Z_y\) and  . Now, as
. Now, as  , by Proposition 6.9 it follows that
, by Proposition 6.9 it follows that  . So, using (D2) on the pairs \((Z_y,Z)\) and (Z, X), we get
. So, using (D2) on the pairs \((Z_y,Z)\) and (Z, X), we get  , whence
, whence  . Therefore we obtain the inclusion
. Therefore we obtain the inclusion  , so that
, so that  . Then we also get the equality
. Then we also get the equality  by Proposition 6.4. This proves that (16) holds.
by Proposition 6.4. This proves that (16) holds.
At this point, we can conclude the proof of (15). In fact, as  , we get our conclusion using (16) and Proposition 6.8 (i).
, we get our conclusion using (16) and Proposition 6.8 (i).
In order to complete the proof, let us finally show that  . To this end, note first that
. To this end, note first that  since
since  and the map \(\Psi \) is decreasing with respect to set-theoretical inclusion. Take now
and the map \(\Psi \) is decreasing with respect to set-theoretical inclusion. Take now  . We claim that
. We claim that  . To this end, let us check that
. To this end, let us check that  . By the definition of
. By the definition of  , we clearly have
, we clearly have  . Conversely, let
. Conversely, let  . Then there exists
. Then there exists  such that
such that  . At this point, by the definition of
. At this point, by the definition of  , we get \(w \in W\), for some
, we get \(w \in W\), for some  such that
such that  . Since
. Since  and \(Y \subseteq Z\), we deduce that \(W \subseteq Z\), whence \(w \in Z\). Thus
and \(Y \subseteq Z\), we deduce that \(W \subseteq Z\), whence \(w \in Z\). Thus  and, hence,
and, hence,  . Now, using the fact that
. Now, using the fact that  , we deduce that
, we deduce that  , whence
, whence  by virtue of (15). This proves that
by virtue of (15). This proves that  .\(\square \)
.\(\square \)
7 Conclusions
In this paper we introduced new categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\), \(\mathbf{SO^{k,\sqsupseteq }}\) and \(\mathbf{SO^k}\) generalizing at a categorical level the notions of set system, set relation and set operator, respectively. These categories depend on a nonnegative parameter k, on the basis of which the objects and arrows of the above categories were defined by means of k successive compositions of the classic powerset functor.
In the first part of the paper we studied the basic properties of these categories. A particular attention has been addressed towards the analysis of the main properties of the previous categories; among the most important, we proved for instance the bi-completeness and Cartesian closedness of \(\mathbf{SS^k}\) and \(\mathbf{SR^k}\).
In the second part of the work we extended both the bijection between equivalence relations, set partitions and equivalence set operators, and also that between closure set operators, closure set systems and dependence set relations, determining more general categorical isomorphisms. In order to establish the aforementioned isomorphisms, we have also introduced and studied in detail suitable relevant subcategories of the main categories \(\mathbf{SS^k}\), \(\mathbf{SR^k}\), \(\mathbf{SO^{k,\sqsubseteq }}\), \(\mathbf{SO^{k,\sqsupseteq }}\) and \(\mathbf{SO^k}\).
The study of these sub-categories may be seen as the starting point of the development of an articulated framework, which we believe is worthy of being investigated even in successive works.
The future research perspectives appear to be quite promising, because of the novelty of these categories and since we can study them relatively with topics typical of various sectors of both pure mathematics (e.g. commutative algebra, topology and matroid theory, to name few specific examples), and of theoretical computer science (e.g. granular and soft computing, rough set theory, or functional programming).
Furthermore, the complete investigation of such categories is far to be reached, because most of the usual properties of the aforementioned categories have not been yet analyzed. So, many possible open problems (which we believe to be not appropriate to list in this short final section) occur and this situation may constitute an interesting future research perspective.
References
Awodey, S.: Category Theory. Oxford Logic Guides, vol. 52, 2nd edn. Oxford University Press, Oxford (2010)
Baker, S., Bowler, N.: Matroids over partial hyperstructures. Adv. Math. 343, 821–863 (2019)
Birkhoff, G.: Lattice Theory, vol. 25, 3rd edn. American Mathematical Society Colloquium Publications. American Mathematical Society, Providence (1967)
Bisi, C.: On commuting polynomial automorphisms of \(\mathbb{C} ^{k}\), \(k \geqslant 3\). Math. Z. 258(4), 875–891 (2008)
Bisi, C.: A Landau’s theorem in several complex variables. Ann. Mat. Pura Appl. 196(2), 737–742 (2017)
Böcker, S., Dress, A.W.M.: Patchworks. Adv. Math. 157(1), 1–21 (2001)
Borceux, F.: Handbook of Categorical Algebra: Basic Category Theory. Encyclopedia of Mathematics and its Applications, vol. 50, vol. 1. Cambridge University Press, Cambridge (1994)
Borceux, F.: Handbook of Categorical Algebra: Basic Category Theory. Encyclopedia of Mathematics and its Applications, vol. 51, vol. 2. Cambridge University Press, Cambridge (1994)
Borceux, F.: Handbook of Categorical Algebra: Categories of Sheaves. Vol. 3. Encyclopedia of Mathematics and its Applications, vol. 52. Cambridge University Press, Cambridge (1994)
Bühler, T.: Exact categories. Expo. Math. 28(1), 1–69 (2010)
Chiaselotti, G., Gentile, T., Infusino, F.: Lattice representations with set partitions induced by pairings. Electron. J. Combin. 27(1), P1.19 (2020)
Chiaselotti, G., Infusino, F.G.: Alexandroff topologies and monoid actions. Forum Math. 32(3), 795–826 (2020)
Chiaselotti, G., Infusino, F.: Some classes of abstract simplicial complexes motivated by module theory. J. Pure Appl. Algebra 225(1), 106471 (2021)
Chiaselotti, G., Infusino, F., Oliverio, P.A.: Dependency relations. Boll. Unione Mat. Ital. 12(4), 525–548 (2019)
Chiaselotti, G., Infusino, F., Oliverio, P.A.: Set relations and set systems induced by some families of integral domains. Adv. Math. 363, Art. No. 106999 (2020)
Crapo, H.H., Rota, G.-C.: On the Foundations of Combinatorial Theory, 10699. M.I.T. Press, Cambridge (1970)
Dress, A.W.M., Wenzel, W.: Perfect matroids. Adv. Math. 91(2), 158–208 (1992)
Dress, A.W.M.: Basic noncommutative Galois theory. Adv. Math. 110(1), 141–173 (1995)
Epstein, N.: A guide to closure operations in commutative algebra. In: Francisco, C., et al. (eds.) Progress in Commutative Algebra, vol. 2, pp. 1–37. De Gruyter, Berlin (2012)
Ge, L., Kadison, R.: On tensor products for von Neumann algebras. Invent. Math. 123(3), 453–466 (1996)
Ge, L., Popa, S.: On some decomposition properties for factors of type \({\rm II}_1\). Duke Math. J. 94(1), 79–101 (1998)
Goranko, V.: Transformations of multi-player normal form games by preplay offers between players. Axioms 11(2), 73 (2022)
Goranko, V., Kuusisto, A., Rönnholm, R.: Alternating-time temporal logic ATL with finitely bounded semantics. Theoret. Comput. Sci. 797, 129–155 (2019)
Gurov, D., Goranko, V., Lundberg, E.: Knowledge-based strategies for multi-agent teams playing against Nature. Artif. Intell. 309, Art. No. 103728 (2022)
Mac Lane, S.: Categories for the Working Mathematician. Graduate Texts in Mathematics, vol. 5, 2nd edn. Springer, New York (1998)
Rybakov, S.: The groups of points on abelian varieties over finite fields. Cent. Eur. J. Math. 8(2), 282–288 (2010)
Rybakov, S.: DG-modules over de Rham DG-algebra. Eur. J. Math. 1(1), 25–53 (2015)
Shen, L., Zhang, D.: Categories enriched over a quantaloid: Isbell adjunctions and Kan adjunctions. Theory Appl. Categ. 28(20), 577–615 (2013)
Shen, L., Tao, Y., Zhang, D.: Chu connections and back diagonals between \(\cal{Q} \)-distributors. J. Pure Appl. Algebra 220(5), 1858–1901 (2016)
Smullyan, R.M., Fitting, M.: Set Theory and the Continuum Problem. Oxford Logic Guides, vol. 34. Oxford Science Publications. Clarendon Press, New York (1996)
Uglešić, N.: On the quotient shapes of topological spaces. Topology Appl. 239, 142–151 (2018)
Vasconcelos, W.V.: Arithmetic of Blowup Algebras. London Mathematical Society Lecture Note Series, vol. 195. Cambridge University Press, Cambridge (1994)
Vasconcelos, W.: Integral Closure. Springer Monographs in Mathematics, Springer, Berlin (2005)
Welsh, D.J.A.: Matroid Theory. London Mathematical Society Monographs, vol. 8. Academic Press, London (1976)
Zhang, G.-Q., Shen, G.: Approximable concepts, Chu spaces, and information systems. Theory Appl. Categ. 17(5), 80–102 (2006)
Acknowledgements
We are extremely grateful to the anonymous reviewer who helped us to improve the quality of our manuscript by checking it carefully and giving us thorough remarks and valuable suggestions.
Funding
Open access funding provided by Università della Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Contributions
All the authors of this work have contributed in equal parts to its final version.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chiaselotti, G., Gentile, T. & Infusino, F.G. On some categories of structured sets. European Journal of Mathematics 10, 23 (2024). https://doi.org/10.1007/s40879-024-00733-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-024-00733-5
Keywords
- Set systems
- Set operators
- Dependence relations
- Closure operators
- Categories
- Functors
- Complete and Cartesian closed categories
- Linking maps




 for all
for all  and
and  for all
for all  ;
; for all
for all  and
and  for all
for all  .
. and whenever
and whenever  then
then  . We denote by
. We denote by  and whenever
and whenever  it results that
it results that  ;
; and
and  ;
; .
.
 .
. ;
; ;
; .
. is the exponential object of
is the exponential object of  and
and  is the exponential object of
is the exponential object of  .
. ;
; ;
;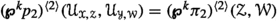 .
.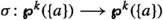 is defined by
is defined by  for each
for each  , is the terminal object in the category
, is the terminal object in the category  is defined by
is defined by  , is the terminal object in the category
, is the terminal object in the category  is defined by
is defined by  , is the initial object in the category
, is the initial object in the category  defined by setting
defined by setting  ;
; defined by inductively setting
defined by inductively setting  and
and  for every
for every  for any
for any  for any
for any  for any
for any  and any
and any  for any
for any  for any
for any  for any
for any  and any
and any  for any
for any  , where
, where 
 , for each
, for each 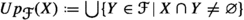 , for each
, for each  and any
and any  ;
; , for each
, for each  .
. ;
; , and such that
, and such that  for each
for each  , where the symbol
, where the symbol 
 and
and  , for
, for  and
and  , whenever
, whenever  and
and  ;
; and
and  , whenever
, whenever  and
and  ;
; and
and  , whenever
, whenever  , for any
, for any  .
. and
and  ;
; then
then  ;
; if and only if
if and only if 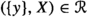 for any
for any  if and only if it satisfies (D1), (D2) and if
if and only if it satisfies (D1), (D2) and if  then
then  ;
; and
and  then
then 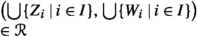 ;
;

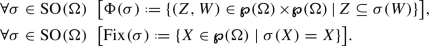
 ;
; ;
; .
. .
. ;
; .
.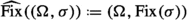 and
and  , whenever
, whenever  and
and  , whenever
, whenever  and
and  ;
; and
and  , whenever
, whenever  ,
,  and
and  ;
;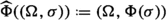 and
and 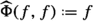 , whenever
, whenever  for any
for any  ;
; is a closure set system on
is a closure set system on  ;
; such that
such that 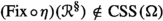 .
. ;
; .
.