Abstract
We prove that Chevalley groups over polynomial rings \(\mathbb {F}_q[t]\) and over Laurent polynomial \(\mathbb {F}_q[t,t^{-1}]\) rings, where \(\mathbb {F}_q\) is a finite field, are boundedly elementarily generated. Using this we produce explicit bounds of the commutator width of these groups. Under some additional assumptions, we prove similar results for other classes of Chevalley groups over Dedekind rings of arithmetic rings in positive characteristic. As a corollary, we produce explicit estimates for the commutator width of affine Kac–Moody groups defined over finite fields. The paper contains also a broader discussion of the bounded generation problem for groups of Lie type, some applications and a list of unsolved problems in the field.
Similar content being viewed by others
Notes
The difference between the number and function cases is subtle enough and may be overlooked when approaching from outside. We quote from page 2 of the memoir [28]: ‘...G is known to be boundedly generated by X only in a few cases, namely, when R is a finite extension of \({\mathbb {Z}}\) or F[t], with F a finite field.’ In a sense, the present paper, along with [51], can be viewed as a first step along the long and painful road to justification of this brave claim.
After the preliminary version of the present paper has been finished, there appeared a preprint of Alexander Trost [81] where the statement of our Theorem A was established for the ring of integers R of an arbitrary global function field K, with a bound of the form
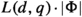 , where the factor L depends on q and of the degree d of K. His method is similar to Morris’ approach in [49]. The subsequent preprint [82] contains further improvements for the group
, where the factor L depends on q and of the degree d of K. His method is similar to Morris’ approach in [49]. The subsequent preprint [82] contains further improvements for the group 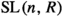 , \(n\geqslant 3\), over an arbitrary global function ring R.
, \(n\geqslant 3\), over an arbitrary global function ring R.On the other hand, since \(B\cap U^-=e\), it is never a product of three such unipotents, unless \(\varepsilon =1\).
In the literature, expressions bounded generation and finite width are used in several related but significantly different contexts. Oftentimes one calls a group G boundedly generated if it has bounded generation with respect to the powers of some finite generating set. This amounts to the group being a finite product of several cyclic subgroups. In many situations it is equally meaningful to consider groups which are finite products of abelian subgroups. Finally, one calls families \(G_i\) of finitely presented groups boundedly generated if they can be presented in such a way that the sums of the number of generators and relations of \(G_i\) are uniformly bounded.
In the literature, three of four completely different commodities are merchandised under the common name of Gauß decomposition: (1) the big cell decomposition LU, as in the affine group schemes textbooks, (2) the Birkhoff LPU-decomposition as in Ellers–Gordeev [25], (3) the LUP-decomposition, as in the computational linear algebra textbooks. Here we speak of (4) the DULU-decomposition, consult [68] for the historical background.
Well, explicit use of infinitesimals does make life easier, sometimes. Say, in R itself there are no non-obvious ideals such that \(I^2=I\), whereas in \({}^*R\) there is such an ideal
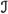 consisting of all infinitesimal elements, which can be very handy. But these simplifications are mostly relevant in the [difficult] case \(n=2\), see the next subsection.
consisting of all infinitesimal elements, which can be very handy. But these simplifications are mostly relevant in the [difficult] case \(n=2\), see the next subsection.See [89], where it is [essentially] proven for \(R=\mathbb {Z}[1/p]\), again modulo GRH.
Recall that our standing assumption \(|S|\geqslant 2\) excludes the problematic case \(R=\mathbb {Z}\).
As we know from Sect. 4, this does not influence boundedness or lack thereof, but may affect the actual bounds.
There is an exception: in [9] the term ‘local units’ is used for calling nonzero elements of the local field \(K_v\), where v is a place of K. We avoid using such a terminology because ‘local unit’ commonly refers to an invertible element of the valuation ring \(O_v\).
References
Abért, M., Lubotzky, A., Pyber, L.: Bounded generation and linear groups. Internat. J. Algebra Comput. 13(4), 401–413 (2003)
Adian, S.I., Mennicke, J.: Bounded generation of \({{\rm SL}}(n,{ Z})\). Internat. J. Algebra Comput. 2(4), 357–365 (1992)
Arlinghaus, F.A., Vaserstein, L.N., You, H.: Commutators in pseudo-orthogonal groups. J. Austral. Math. Soc. Ser. A 59(3), 353–365 (1995)
Aschenbrenner, M., Khélif, A., Naziazeno, E., Scanlon, T.: The logical complexity of finitely generated commutative rings. Int. Math. Res. Not. IMRN 2020(1), 112–166 (2020)
Avni, N., Lubotzky, A., Meiri, C.: First order rigidity of non-uniform higher rank arithmetic groups. Invent. Math. 217(1), 219–240 (2019)
Avni, N., Meiri, C.: Words have bounded width in \({\rm SL}(n,{\mathbb{Z} })\). Compositio Math. 155(7), 1245–1258 (2019)
Bass, H., Milnor, J., Serre, J.-P.: Solution of the congruence subgroup problem for \({\rm SL}_n (n\geqslant 3)\) and \({\rm Sp}_{2n} (n\geqslant 2)\). Inst. Hautes Études Sci. Publ. Math. 33, 59–137 (1967)
Behr, H.: Arithmetic groups over function fields. I: A complete characterization of finitely presented arithmetic subgroups of reductive algebraic groups. J. Reine Angew. Math. 495, 79–118 (1998)
Carter, D., Keller, G.: Bounded elementary generation of \({{\rm SL}}_n({{\mathscr {O}}})\). Amer. J. Math. 105(3), 673–687 (1983)
Carter, D., Keller, G.: Elementary expressions for unimodular matrices. Commun. Algebra 12(3–4), 379–389 (1984)
Carter, D., Keller, G.E.: Bounded elementary expressions in \({{\rm SL}}(2,{{\mathscr {O}}})\). Preprint, University of Virginia, 1–11 (1985)
Carter, D., Keller, G.E., Paige, E.: Bounded expressions in \({{\rm SL}}(2,{{\mathscr {O}}})\). Preprint, University of Virginia, 1–21 (1985)
Carter, R.W.: Simple Groups of Lie Type. Pure and Applied Mathematics, vol. 28. Wiley, London (1972)
Carter, R.W., Chen, Y.: Automorphisms of affine Kac–Moody groups and related Chevalley groups over rings. J. Algebra 155(1), 44–94 (1993)
Chang, C.C., Keisler, H.J.: Model Theory. 2nd edn. Studies in Logic and the Foundations of Mathematics, vol. 73. North Holland, Amsterdam (1977)
Cohn, P.M.: On the structure of the \({{\rm GL}}_2\) of a ring. Inst. Hautes Études Sci. Publ. Math. 30, 5–53 (1966)
Cooke, G.E.: A weakening of the Euclidean property for integral domains and applications to algebraic number theory. I. J. Reine Angew. Math. 282, 133–156 (1976)
Cooke, G.E.: A weakening of the Euclidean property for integral domains and applications to algebraic number theory. II. J. Reine Angew. Math. 283(284), 71–85 (1976)
Cooke, G., Weinberger, P.J.: On the construction of division chains in algebraic number rings, with applications to \({{\rm SL}}_2\). Commun. Algebra 3, 481–524 (1975)
Corvaja, P., Demeio, J., Rapinchuk, A., Ren, J., Zannier, U.: Bounded generation by semi-simple elements: quantitative results (2022). arXiv:2203.00755
Corvaja, P., Rapinchuk, A.S., Ren, J., Zannier, U.M.: Non-virtually abelian anisotropic linear groups are not boundedly generated. Invent. Math. 227(1), 1–26 (2022)
Demeyer, J.: Recursively enumerable sets of polynomials over a finite field are Diophantine. Invent. Math. 170(3), 655–670 (2007)
Dennis, R.K., Vaserstein, L.N.: On a question of M. Newman on the number of commutators. J. Algebra 118(1), 150–161 (1988)
Dennis, R.K., Vaserstein, L.N.: Commutators in linear groups. \(K\)-Theory 2(6), 761–767 (1989)
Ellers, E.W., Gordeev, N.: On the conjectures of J. Thompson and O. Ore. Trans. Amer. Math. Soc. 350(9), 3657–3671 (1998)
Erovenko, I.V.: \({{\rm SL}}_n(F[x])\) is not boundedly generated by elementary matrices: explicit proof. Electron. J. Linear Algebra 11, 162–167 (2004)
Erovenko, I.V., Rapinchuk, A.S.: Bounded generation of \(S\)-arithmetic subgroups of isotropic orthogonal groups over number fields. J. Number Theory 119(1), 28–48 (2008)
Ershov, M., Jaikin-Zapirain, A., Kassabov, M.: Property \((T)\) for Groups Graded by Root Systems. Memoirs of the American Mathematical Society, vol. 249(1186). American Mathematical Society, Providence (2017)
Estes, D., Ohm, J.: Stable range in commutative rings. J. Algebra 7, 343–362 (1967)
Garland, H.: The arithmetic theory of loop groups. Inst. Hautes Études Sci. Publ. Math. 52, 5–136 (1980)
Gvozdevsky, P.: Improved \({K}_1\)-stability for the embedding \(D_5\) into \(E_6\). Commun. Algebra 48(11), 4922–4931 (2020)
Gvozdevsky, P.: Bounded reduction of orthogonal matrices over polynomial rings. J. Algebra 602, 300–321 (2022)
Hazrat, R., Stepanov, A., Vavilov, N., Zhang, Z.: Commutator width in Chevalley groups. Note Mat. 33(1), 139–170 (2013)
Hodges, W.: Model Theory. Encyclopedia of Mathematics and its Applications, vol. 42. Cambridge University Press, Cambridge (1993)
Jordan, B.W., Zaytman, Y.: On the bounded generation of arithmetic \({{\rm SL}}_2\). Proc. Natl. Acad. Sci. USA 116(38), 18880–18882 (2019)
Kac, V.G.: Infinite-Dimensional Lie Algebras, 3rd edn. Cambridge University Press, Cambridge (1990)
Kharlampovich, O., Myasnikov, A.: What does a group algebra know about a free group. Ann. Pure Appl. Logic 169(6), 523–547 (2018)
Kharlampovich, O., Myasnikov, A., Sohrabi, M.: Rich groups, weak second-order logic, and applications. In: Kharlampovich, O., Sklinos, R. (eds.) Groups and Model Theory, pp. 127–193. de Gruyter, Berlin (2021)
Lenstra, H.W., Jr.: On Artin’s conjecture and Euclid’s algorithm in global fields. Invent. Math. 42, 201–224 (1977)
Liebeck, M.W., O’Brien, E.A., Shalev, A., Tiep, P.H.: The Ore conjecture. J. Eur. Math. Soc. (JEMS) 12(4), 939–1008 (2010)
Liebeck, M.W., O’Brien, E.A., Shalev, A., Tiep, P.H.: Commutators in finite quasisimple groups. Bull. London Math. Soc. 43(6), 1079–1092 (2011)
Liehl, B.: On the group \({{\rm SL}}_2\) over orders of arithmetic type. J. Reine Angew. Math. 323, 153–171 (1981)
Loukanidis, D., Murty, V.K.: Bounded generation for \({{\rm SL}}_n\) (\(n\geqslant 2\)) and \({\rm Sp}_{n}\) (\(n\geqslant 1\)) (1994). Preprint
Luzgarev, A.Yu., Stavrova, A.A.: The elementary subgroup of an isotropic reductive group is perfect. St. Petersburg Math. J. 23(5), 881–890 (2012)
Magurn, B.A.: Algebraic Introduction to \(K\)-Theory. Encyclopedia of Mathematics and its Applications, vol. 87. Cambridge University Press, Cambridege (2002)
Matsumoto, H.: Sur les sous-groupes arithmétiques des groupes semi-simples déployés. Ann. Sci. Éc. Norm. Sup. 2, 1–62 (1969)
Milnor, J.: Introduction to Algebraic \(K\)-Theory. Annals of Mathematics Studies, vol. 72. Princeton University Press, Princeton (1971)
Morgan, A.V., Rapinchuk, A.S., Sury, B.: Bounded generation of \({{\rm SL}}_2\) over rings of \(S\)-integers with infinitely many units. Algebra Number Theory 12(8), 1949–1974 (2018)
Morris, D.W.: Bounded generation of \({{\rm SL}}(n,A)\) (after D. Carter, G. Keller, and E. Paige). New York J. Math. 13, 383–421 (2007)
Murty, V.K.: Bounded and finite generation of arithmetic groups. In: Dilcher, K. (ed.) Number Theory (Halifax, NS, 1994). CMS Conference Proceedings, vol. 15, pp. 249–261. American Mathematical Society, Providence (1995)
Nica, B.: On bounded elementary generation for \({{\rm SL}}_n\) over polynomial rings. Israel J. Math. 225(1), 403–410 (2018)
Nies, A.: Separating classes of groups by first-order sentences. Internat. J. Algebra Comput. 13(3), 287–302 (2003)
Oger, F., Sabbagh, G.: Quasi-finitely axiomatizable nilpotent groups. J. Group Theory 9(1), 95–106 (2006)
O’Meara, O.T.: On the finite generation of linear groups over Hasse domains. J. Reine Angew. Math. 217, 79–108 (1965)
Peterson, D.H., Kac, V.G.: Infinite flag varieties and conjugacy theorems. Proc. Nat. Acad. Sci. USA 80(6), 1778–1782 (1983)
Platonov, V.P., Rapinchuk, A.S.: Abstract properties of \(S\)-arithmetic groups and the congruence problem. Russ. Acad. Sci. Izv. Math. 40(3), 455–476 (1993)
Plotkin, E.B.: Surjective stabilization for \(K_1\)-functor for some exceptional Chevalley groups. J. Soviet Math. 64(1), 751–766 (1993)
Plotkin, E.: On the stability of the \({\mathscr {K}}_1\)-functor for Chevalley groups of type \({ E}_7\). J. Algebra 210(1), 67–85 (1998)
Queen, C.: Some arithmetic properties of subrings of function fields over finite fields. Arch. Math. (Basel) 26, 51–56 (1975)
Rapinchuk, A.S.: The congruence subgroup problem for arithmetic groups of finite width. Soviet Math. Dokl. 42(2), 664–668 (1991)
Rapinchuk, A.S.: Representations of groups of finite width. Soviet Math. Dokl. 42(3), 816–820 (1991)
Roquette, P.: Class field theory in characteristic \(p\), its origin and development. In: Miyake, K. (ed.) Class Field Theory-its Centenary and Prospect (Tokyo, 1998). Advanced Studies in Pure Mathematics, vol. 30, pp. 549–631. Mathematical Society of Japan, Tokyo (2001)
Rosen, M.: Number Theory in Function Fields. Graduate Texts in Mathematics, vol. 210. Springer, New York (2002)
Segal, D., Tent, K.: Defining \(R\) and \(G(R)\), J. Europ. Math. Soc. https://doi.org/10.4171/JEMS/1255. arXiv:2004.13407
Sinchuk, S., Smolensky, A.: Decompositions of congruence subgroups of Chevalley groups. Internat. J. Algebra Comput. 28(6), 935–958 (2018)
Sivatski, A., Stepanov, A.: On the word length of commutators in \({\rm GL}_n(R)\). \({\mathscr {K}}\)-Theory 17(4), 295–302 (1999)
Smolensky, A.: Commutator width of Chevalley groups over rings of stable rank \(1\). J. Group Theory 22(1), 83–101 (2019)
Smolensky, A., Sury, B., Vavilov, N.: Gauss decomposition for Chevalley groups, revisited. Internat. J. Group Theory 1(1), 3–16 (2011)
Sohrabi, M., Myasnikov, A.G.: Bi-interpretability with \({ Z}\) and models of the complete elementary theories of \(SL_n({\mathscr {O}})\), \(T_n({\mathscr {O}})\) and \({\rm GL}_n({\mathscr {O}})\), \(n\geqslant 3\) (2020). arXiv:2004.03585
StackExchange discussion. https://math.stackexchange.com/questions/2690954/laurent-series-of-root-of-polynomials
Stein, M.R.: Generators, relations, and coverings of Chevalley groups over commutative rings. Amer. J. Math. 93, 965–1004 (1971)
Stein, M.R.: Surjective stability in dimension 0 for \(K_2\) and related functors. Trans. Amer. Math. Soc. 178, 165–191 (1973)
Stein, M.R.: Stability theorems for \({\mathscr {K}}_1\), \({\mathscr {K}}_2\) and related functors modeled on Chevalley groups. Japan J. Math. (N.S.) 4(1), 77–108 (1978)
Steinberg, R.: Générateurs, relations et revêtements de groupes algébriques. In: Colloq. Théorie des Groupes Algébriques (Bruxelles, 1962), pp. 113–127. Librairie Universitaire, Louvain (1962)
Steinberg, R.: Lectures on Chevalley Groups. University Lecture Series, vol. 66. American Mathematical Society, Providence (2016)
Stepanov, A.: Structure of Chevalley groups over rings via universal localization. J. Algebra 450, 522–548 (2016)
Stepanov, A., Vavilov, N.: On the length of commutators in Chevalley groups. Israel J. Math. 185, 253–276 (2011)
Tavgen, O.I.: Bounded generation of Chevalley groups over rings of algebraic \(S\)-integers. Math. USSR-Izv. 36(1), 101–128 (1991)
Thompson, R.C.: Commutators in special and general linear groups. Trans. Amer. Math. Soc. 101, 16–33 (1961)
Tits, J.: Uniqueness and presentation of Kac–Moody groups over fields. J. Algebra 105(2), 542–573 (1987)
Trost, A.A.: Bounded generation by root elements for Chevalley groups defined over rings of integers of function fields with an application in strong boundedness (2021). arXiv:2108.12254
Trost, A.A.: Elementary bounded generation for \({{\rm SL}}_n\) for global function fields and \(n\geqslant 3\) (2022). arXiv:2206.13958
van der Kallen, W.: \({{\rm SL}}_3({\mathbb{C} }[X])\) does not have bounded word length. In: Dennis, R.K. (ed.) Algebraic K-theory, Part I (Oberwolfach 1980). Lecture Notes Mathematics, vol. 966, pp. 357–361. Springer, Berlin (1982)
Vaserstein, L.N.: Bounded reduction of invertible matrices over polynomial rings by addition operations. Preprint, Pennsylvania State University (2006). http://www.personal.psu.edu/lxv1/pm2.pdf
Vaserstein, L.N.: Polynomial parametrization for the solution of Diophantine equations and arithmetic groups. Ann. Math. 171(2), 979–1009 (2010)
Vaserstein, L.N., Wheland, E.: Commutators and companion matrices over rings of stable rank \(1\). Linear Algebra Appl. 142, 263–277 (1990)
Vavilov, N.: Structure of Chevalley groups over commutative rings. In: Yamaguti, K., Kawamoto, N. (eds.) Nonassociative Algebras and Related Topics (Hiroshima, 1990), pp. 219–335. World Scientific Publishing, River Edge (1991)
Vavilov, N., Plotkin, E.: Chevalley groups over commutative rings. I: Elementary calculations. Acta Appl. Math. 45(1), 73–113 (1996)
Vavilov, N.A., Smolensky, A.V., Sury, B.: Unitriangular factorizations of Chevalley groups. J. Math. Sci. (N.Y.) 183(5), 584–599 (2012)
Vsemirnov, M.: Short unitriangular factorizations of \({{\rm SL}}_2({\mathbb{Z} }[1/p])\). Q. J. Math. 65(1), 279–290 (2014)
Acknowledgements
Very special thanks go to Inna Capdeboscq. This paper started jointly with her as a discussion of the bounded commutator width of various classes of Kac–Moody groups over finite fields, and for a long time it was supposed to be a work of four authors. Our sincere thanks go to Nikolai Gordeev, Olga Kharlampovich, Jun Morita, Alexei Myasnikov, Denis Osipov, Alexei Stepanov, and Igor Zhukov for useful discussions regarding various aspects of this work. We thank the referees for careful reading and meticulous remarks.
Author information
Authors and Affiliations
Corresponding author
Additional information
In memory of Irina Suprunenko, our dear friend and colleague.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Research of Boris Kunyavskiĭ and Eugene Plotkin was supported by the ISF Grants 1623/16 and 1994/20. Nikolai Vavilov thanks the “Basis” Foundation Grant N. 20-7-1-27-1 “Higher Symbols in Algebraic K-Theory”
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kunyavskiĭ, B., Plotkin, E. & Vavilov, N. Bounded generation and commutator width of Chevalley groups: function case. European Journal of Mathematics 9, 53 (2023). https://doi.org/10.1007/s40879-023-00627-y
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00627-y


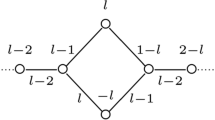

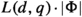 , where the factor L depends on q and of the degree d of K. His method is similar to Morris’ approach in [
, where the factor L depends on q and of the degree d of K. His method is similar to Morris’ approach in [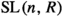 ,
, 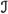 consisting of all infinitesimal elements, which can be very handy. But these simplifications are mostly relevant in the [difficult] case
consisting of all infinitesimal elements, which can be very handy. But these simplifications are mostly relevant in the [difficult] case