Abstract
We prove that a variety of generalized cardinal characteristics, including meeting numbers, the reaping number, and the dominating number, satisfy an analogue of the Galvin–Hajnal theorem, and hence also of Silver’s theorem, at singular cardinals of uncountable cofinality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the seminal results in cardinal arithmetic, and one of the first indications that there are nontrivial \(\textsf{ZFC}\) constraints on the behavior of the continuum function at singular cardinals, is Silver’s theorem.
Theorem 1.1
(Silver [21]) Suppose that \(\kappa \) is a singular cardinal of uncountable cofinality,  is an ordinal, and the set of cardinals
is an ordinal, and the set of cardinals

is stationary in \(\kappa \). Then  .
.
Silver’s original proof of this theorem involves a generic ultrapower argument; a purely combinatorial argument for the theorem was soon provided by Baumgartner and Prikry [1]. Around the same time, a generalization of Silver’s theorem was proven by Galvin and Hajnal. The following statement of (a corollary of) their theorem involves the notion of the Galvin–Hajnal rank \(\Vert \varphi \Vert _S\) of a function \(\varphi \); see Definition 2.1 below for its formal definition.
Theorem 1.2
(Galvin–Hajnal [4]) Suppose that \(\kappa \) is a singular cardinal of uncountable cofinality,  is an increasing, continuous sequence of cardinals converging to \(\kappa \),
is an increasing, continuous sequence of cardinals converging to \(\kappa \),  is stationary, and \(\varphi :S \rightarrow \textrm{On}\) is a function such that, for all \(i \in S\), we have
is stationary, and \(\varphi :S \rightarrow \textrm{On}\) is a function such that, for all \(i \in S\), we have  . Then
. Then  .
.
This theorem does indeed generalize Silver’s theorem, since, as we shall see, given any stationary subset S of a regular uncountable cardinal \(\theta \), and given any ordinal \(\eta < \theta \), if \(\varphi \) is the constant function on S taking value \(\eta \), then \(\Vert \varphi \Vert _S = \eta \).
One of the central aspects of research into cardinal arithmetic is the study of certain methods of measuring the “size” of the power set of a cardinal \(\kappa \) that are in a sense finer than simply looking at the value of \(2^\kappa \). At singular cardinals, these methods come from two primary sources, with some overlap between the two:
-
Shelah’s PCF theory;
-
generalizations of cardinal characteristics of the continuum to singular cardinals.
Certain of these methods are known to satisfy versions of Silver’s theorem or the Galvin–Hajnal theorem. For example, in [19, Chapter 2, Claim 2.4], Shelah proves a variation of Theorem 1.2 involving PCF-theoretic pseudopowers \(\textrm{pp}_J(\kappa )\) and \(\textrm{pp}_J(\kappa _i)\) in place of the cardinals \(2^\kappa \) and \(2^{\kappa _i}\); in [18, Lemma 3.8], Rinot proves a version of Silver’s theorem for covering numbers; and in [12], Kojman proves that certain density numbers satisfy an analogue of Silver’s theorem (see Sect. 3 for details).
In this paper, we prove versions of the Galvin–Hajnal theorem for a variety of cardinal characteristics of the continuum generalized to singular cardinals of uncountable cofinality, focusing in particular on meeting numbers, the reaping number, and the dominating number. Before proceeding to a summary of our results, let us say a few words about our approach to cardinal characteristics at singular cardinals in general. There are often multiple natural ways to generalize familiar cardinal characteristics of the continuum to singular cardinals. For example, when defining the dominating number \({\mathfrak {d}}_\kappa \) at a singular cardinal \(\kappa \), any of the following possible definitions of \({\mathfrak {d}}_\kappa \) seems potentially reasonable (see the end of this introduction for any undefined notation):
-
 , where, given \(f,g \in {^\kappa }\kappa \), we let \(f \,{<}_0\, g\) if and only if \(|\{i< \kappa \,{|}\, g(i) \leqslant f(i)\}|< \kappa \);
, where, given \(f,g \in {^\kappa }\kappa \), we let \(f \,{<}_0\, g\) if and only if \(|\{i< \kappa \,{|}\, g(i) \leqslant f(i)\}|< \kappa \); -
 , where, given \(f,g \in {^\kappa }\kappa \), we let \(f \,{<}_1\, g\) if and only if \(\{i < \kappa \,{|}\, g(i) \leqslant f(i)\}\) is bounded below \(\kappa \);
, where, given \(f,g \in {^\kappa }\kappa \), we let \(f \,{<}_1\, g\) if and only if \(\{i < \kappa \,{|}\, g(i) \leqslant f(i)\}\) is bounded below \(\kappa \); -
 , where, given
, where, given  , we let \(f \,{<}_2\, g\) if and only if
, we let \(f \,{<}_2\, g\) if and only if  .
.
In all such choices that we face here, we opt for the definition that emphasizes the cardinality of \(\kappa \) over its cofinality, as, at least in this context, this seems to be what gives rise to the most genuinely new behavior at the singular cardinal \(\kappa \). So, for instance, we will define \({\mathfrak {d}}_\kappa \) to be what is called  above. (It is not difficult to show that what is called
above. (It is not difficult to show that what is called  above is in fact nothing other than
above is in fact nothing other than  .)
.)
We also note here that in this paper we are only considering cardinal characteristics at a singular cardinal \(\kappa \) that are provably strictly greater than \(\kappa \). In particular, we are not considering the bounding number \({\mathfrak {b}}_\kappa \), the splitting number \({\mathfrak {s}}_\kappa \), or the almost disjointness number \({\mathfrak {a}}_\kappa \), since, at least when generalized in accordance with the principles laid out in the previous paragraph, these cardinal characteristics are provably at most  ,
,  , and
, and  , respectively (though we will have more to say about the almost disjointness number in Sect. 6).
, respectively (though we will have more to say about the almost disjointness number in Sect. 6).
A slightly suboptimal but succinct summary of our main results can be stated as follows (we refer the reader to Sect. 2 for the definition of canonical function and to Sect. 5 for the precise definition of the cardinal characteristics under consideration):
MainCorollary
Suppose that
-
\(\kappa \) is a singular cardinal with
 ;
; -
\(\langle \kappa _i \,{|}\, i < \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \);
-
\(\beta \) is an ordinal for which the canonical function on \(\theta \) of rank \(\beta \), \(\varphi ^\theta _\beta \), exists;
-
 for all \(\mu < \kappa \);
for all \(\mu < \kappa \); -
\(S \subseteq \theta \) is stationary;
-
\(\mathfrak {cc}\) is one of the cardinal characteristics \(m(\theta , \kappa ),d(\theta , \kappa ),\mathfrak r_\kappa \), or \(\mathfrak d_\kappa \), and, for all \(i < \theta \), \(\mathfrak {cc}_i\) is the corresponding cardinal characteristic
 , \(\mathfrak r_{\kappa _i}\), or \(\mathfrak d_{\kappa _i}\);
, \(\mathfrak r_{\kappa _i}\), or \(\mathfrak d_{\kappa _i}\); -
for all \(i \in S\), we have \(\mathfrak {cc}_i \leqslant \kappa _i^{+\varphi ^\theta _\beta (i)}\).
Then \(\mathfrak {cc} \leqslant \kappa ^{+\beta }\).
The slight suboptimality in this statement comes from the assumption that \(\mu ^\theta \leqslant \kappa ^{+\beta }\) for all \(\mu < \kappa \). As we will see, a weaker hypothesis, in which \(\mu ^\theta \) is replaced by some cardinal characteristic that is provably at most \(\mu ^\theta \), is sufficient for our results; the precise weakening depends on the specific cardinal characteristic under consideration and will require some further notation to state, so we leave the exact details for the statement of Main Theorem at the end of Sect. 5.
The structure of the remainder of the paper is as follows. In Sect. 2, we review the definitions and facts regarding canonical functions and the Galvin–Hajnal rank that we will need for our results. In Sect. 3, we recall certain notions of density. This is important for two reasons: first, because the analogue of Silver’s theorem for density numbers proven in [12] was direct inspiration for this paper, and secondly and more immediately, these density numbers will appear in the precise formulations of our results. After this, we begin with the proof of our Main Theorem. The proofs of our various analogues of the Galvin–Hajnal theorem all have the same general shape, so in Sect. 4 we develop an abstract framework that will apply to all of our specific instances. In Sect. 5, we apply this abstract framework to our cardinal characteristics under consideration to obtain our Main Theorem, which is precisely stated at the end of the section. Finally, in Sect. 6, we record some questions that remain open and sketch a consistent negative answer to the question about whether a version of Silver’s theorem holds for the existence of Aronszajn trees at double successors of singular cardinals.
1.1 Notation and conventions
Unless otherwise noted, we believe our notation and terminology to be standard. We refer the reader to [11] for any undefined notions or notations from set theory, and we refer the reader to [2] for an introduction to cardinal characteristics of the continuum, generalizations of which form the subject of this paper.
If X is a set and \(\rightsquigarrow \) is a binary relation on X, then  denotes the minimal cardinality of a subset \(Y \subseteq X\) such that, for all \(x \in X\), there is \(y \in Y\) for which \(x \rightsquigarrow y\). If \(\theta \) is a regular uncountable cardinal, then \(\textrm{NS}_\theta \) denotes the nonstationary ideal on \(\theta \). If \(S \subseteq \theta \) is a stationary set, then, formally, \(\textrm{NS}_\theta \,{\restriction }\, S\) is the ideal on \(\theta \) generated by
denotes the minimal cardinality of a subset \(Y \subseteq X\) such that, for all \(x \in X\), there is \(y \in Y\) for which \(x \rightsquigarrow y\). If \(\theta \) is a regular uncountable cardinal, then \(\textrm{NS}_\theta \) denotes the nonstationary ideal on \(\theta \). If \(S \subseteq \theta \) is a stationary set, then, formally, \(\textrm{NS}_\theta \,{\restriction }\, S\) is the ideal on \(\theta \) generated by  ; in practice, we will typically think of \(\textrm{NS}_\theta \,{\restriction }\, S\) as the ideal of nonstationary subsets of S, considered as an ideal on S. If X is a set and \(\kappa \) is a cardinal, then
; in practice, we will typically think of \(\textrm{NS}_\theta \,{\restriction }\, S\) as the ideal of nonstationary subsets of S, considered as an ideal on S. If X is a set and \(\kappa \) is a cardinal, then  . If X and Y are two sets, then \({^Y}X\) denotes the set of all functions with domain Y and codomain X.
. If X and Y are two sets, then \({^Y}X\) denotes the set of all functions with domain Y and codomain X.
To facilitate clean statements of hypotheses, we adopt the convention that 0 is not a limit ordinal.
2 Canonical functions and the Galvin–Hajnal rank
Suppose that S is an infinite set and I is a proper ideal on S. As usual, we let \(I^+\) denote the set of I-positive subsets of S, i.e.,  . Given two functions \(\varphi , \psi \in {^S}\textrm{On}\), we write \(\varphi \,{<}_I\, \psi \) to denote the assertion that the set \(\{i \in S \,{|}\, \psi (i) \leqslant \varphi (i)\}\) is in I. Define \(=_I\), \(\leqslant _i\), etc. in the obvious way. We will be particularly interested in the case in which S is a stationary subset of a regular uncountable cardinal \(\theta \) and \(I = \textrm{NS}_\theta {\restriction }\, S\), i.e., I is the collection of nonstationary subsets of S. In this context, given two functions \(\varphi ,\psi \in {^S}\textrm{On}\), we will write \(\varphi \,{<}_S\, \psi \) instead of \(\varphi <_{\textrm{NS}_\theta {\restriction } S} \psi \) (and similarly with \(\leqslant _S\), \(=_S\), etc.). In particular, for functions \(\varphi , \psi \in {^\theta }\textrm{On}\), \(\varphi \,{<}_\theta \, \psi \) will denote \(\varphi \,{<}_{\textrm{NS}_\theta }\, \psi \). Note that \(\varphi \,{<}_S\, \psi \) if and only if there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S\), we have \( \varphi (i) < \psi (i)\).
. Given two functions \(\varphi , \psi \in {^S}\textrm{On}\), we write \(\varphi \,{<}_I\, \psi \) to denote the assertion that the set \(\{i \in S \,{|}\, \psi (i) \leqslant \varphi (i)\}\) is in I. Define \(=_I\), \(\leqslant _i\), etc. in the obvious way. We will be particularly interested in the case in which S is a stationary subset of a regular uncountable cardinal \(\theta \) and \(I = \textrm{NS}_\theta {\restriction }\, S\), i.e., I is the collection of nonstationary subsets of S. In this context, given two functions \(\varphi ,\psi \in {^S}\textrm{On}\), we will write \(\varphi \,{<}_S\, \psi \) instead of \(\varphi <_{\textrm{NS}_\theta {\restriction } S} \psi \) (and similarly with \(\leqslant _S\), \(=_S\), etc.). In particular, for functions \(\varphi , \psi \in {^\theta }\textrm{On}\), \(\varphi \,{<}_\theta \, \psi \) will denote \(\varphi \,{<}_{\textrm{NS}_\theta }\, \psi \). Note that \(\varphi \,{<}_S\, \psi \) if and only if there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S\), we have \( \varphi (i) < \psi (i)\).
Fix for the remainder of this section a regular uncountable cardinal \(\theta \). Given a stationary set \(S \subseteq \theta \), the corresponding relation \(<_S\) is well-founded and therefore has a rank function, which yields what is known as the Galvin–Hajnal rank.
Definition 2.1
([4]) Suppose that \(\theta \) is an uncountable regular cardinal and \(S \subseteq \theta \) is stationary. The Galvin–Hajnal rank of a function \(\varphi \in {^S}\textrm{On}\), denoted \(\Vert \varphi \Vert _S\), is defined by recursion on \(<_S\) by letting

for all \(\varphi \in {^S}\textrm{On}\).
It is readily verified by recursion on \(\Vert \varphi \Vert _S\) that, for all stationary \(T \subseteq S \subseteq \theta \) and all \(\varphi \in {^S}\textrm{On}\), we have \(\Vert \varphi \Vert _S \leqslant \Vert \varphi \,{\restriction }\, T\Vert _T\). In general, it is quite possible to have strict inequality here. However, if \(\varphi \) is what is known as a canonical function, this inequality is in fact always an equality. With this in mind, let us now recall the definition of and some basic facts about canonical functions.
By recursion on ordinals \(\alpha \), attempt to define the canonical function on \(\theta \) of rank \(\alpha \), \(\varphi ^\theta _\alpha \in {^\theta }\textrm{On}\), as follows. If \(\beta \) is an ordinal and \(\varphi ^\theta _\alpha \) has been defined for all \(\alpha < \beta \), then let \(\varphi ^\theta _\beta \) be the least upper bound for \(\langle \varphi ^\theta _\alpha \,{|}\, \alpha \,{<}\, \beta \rangle \) with respect to \(<_\theta \), if such a least upper bound exists. In other words, \(\varphi ^\theta _\beta \in {^\theta }\textrm{On}\) is a function such that
-
\(\varphi ^\theta _\beta \) is a \(<_\theta \)-upper bound for \(\langle \varphi ^\theta _\alpha \,{|}\, \alpha < \beta \rangle \);
-
if \(\psi \) is another \(<_\theta \)-upper bound for \(\langle \varphi ^\theta _\alpha \,{|}\, \alpha < \beta \rangle \), then \(\varphi ^\theta _\beta \leqslant _\theta \psi \).
If such a least upper bound does not exist, then \(\varphi ^\theta _\beta \) is undefined (and therefore \(\varphi ^\theta _\gamma \) is undefined for all \(\gamma > \beta \) as well).
Note that \(\varphi ^\theta _\beta \) is not uniquely determined, but is unique up to \(=_\theta \)-equivalence. We will let \(\Phi ^\theta _\beta \) denote the set of all canonical functions on \(\theta \) of rank \(\beta \). We will slightly abuse notation and use \(\varphi ^\theta _\beta \) to denote an arbitrary element of \(\Phi ^\theta _\beta \). We will always be working in contexts that are invariant under \(=_\theta \)-equivalence, so this will not result in any loss of generality. The following well-known fact (see [14, Section 1] for an introduction to canonical functions of rank less than \(\theta ^+\)) shows that, for all \(\beta < \theta ^+\), there are canonical functions on \(\theta \) of rank \(\beta \).
Fact 2.2
Let \(\beta < \theta ^+\), and let \(e:\theta \rightarrow \beta \) be a surjection. Then the function \(\varphi \in {^\theta }\theta \) defined by letting  for all \(i < \theta \) is in \(\Phi ^\theta _\beta \).
for all \(i < \theta \) is in \(\Phi ^\theta _\beta \).
The following proposition follows almost immediately from the definition of canonical function.
Proposition 2.3
Suppose that \(\beta \) is an ordinal for which \(\varphi ^\theta _\beta \) is defined, \(\psi \,{\in }\, {^\theta }\textrm{On}\), and the set  is stationary in \(\theta \). Then there is a stationary \(S' \subseteq S\) and an \(\alpha < \beta \) such that \(\psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\).
is stationary in \(\theta \). Then there is a stationary \(S' \subseteq S\) and an \(\alpha < \beta \) such that \(\psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\).
Proof
Suppose not. Then, for all \(\alpha < \beta \), there is a club \(C_\alpha \subseteq \theta \) such that \(\varphi ^\theta _\alpha (i) < \psi (i)\) for all \(i \in S \cap C_\alpha \). Define a function \(\tau \in {^\theta }\textrm{On}\) by letting

Then, by our assumptions, \(\tau \) is a \(<_\theta \)-upper bound for \(\langle \varphi ^\theta _\alpha \,{|}\, \alpha \,{<}\, \beta \rangle \), so, by the definition of canonical function we must have \(\varphi ^\theta _\beta \,{\leqslant }_\theta \, \tau \), contradicting the fact that \(S \subseteq \theta \) is stationary and, for all \(i \in S\), we have \(\tau (i) = \psi (i) < \varphi ^\theta _\beta (i)\).\(\square \)
The following basic facts will be relevant to our arguments. Throughout the remainder of the paper, given a function \(\varphi \) taking ordinal values, we let \(\varphi + 1\) denote the function \(\psi \) defined by setting  and \(\psi (i) = \varphi (i)+1\) for all
and \(\psi (i) = \varphi (i)+1\) for all  .
.
Proposition 2.4
Suppose that \(\beta > 0\) is an ordinal such that \(\varphi ^\theta _\beta \) is defined.
-
(1)
\(\varphi ^\theta _{\beta +1}\) is defined and \(\varphi ^\theta _{\beta + 1} =_\theta \varphi ^\theta _\beta +1\).
-
(2)
If \(\beta \) is a limit ordinal, then there is a club \(C \subseteq \theta \) such that \(\varphi ^\theta _\beta (i)\) is a limit ordinal for all \(i \in C\).
Proof
(1) Clearly, \(\varphi ^\theta _\beta + 1\) is a \(<_\theta \)-upper bound for \(\langle \varphi ^\theta _\alpha \,{|}\, \alpha \,{\leqslant }\, \beta \rangle \). Moreover, if \(\psi \) is any other \(<_\theta \)-upper bound, then there must be a club \(C \subseteq \theta \) such that \(\varphi ^\theta _\beta (i) + 1 \leqslant \psi (i)\) for all \(i \in C\), and therefore \(\varphi ^\theta _\beta + 1 \,{\leqslant }_\theta \, \psi \). It follows that \(\varphi ^\theta _{\beta +1} =_\theta \varphi ^\theta _\beta + 1\).
(2) Suppose for sake of contradiction that \(\beta \) is a limit ordinal and yet there is a stationary set \(S \subseteq \theta \) such that \(\varphi ^\theta _\beta (i) = \gamma _i + 1\) is a successor ordinal for all \(i \in S\). Define a function \(\psi \in {^\theta }\textrm{On}\) by letting
for all \(i < \theta \). By Proposition 2.3, we can find a stationary  and an ordinal \(\alpha < \beta \) such that \(\psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\), and hence, by removing a nonstationary subset from \(S'\) if necessary, we can assume that \(\psi (i) + 1 \leqslant \varphi ^\theta _{\alpha +1}(i)\) for all \(i \in S'\). But, by our definition of \(\psi \), we have \(\psi (i) + 1 = \varphi ^\theta _\beta (i)\) for all \(i \in S'\), and hence \(\varphi ^\theta _{\alpha +1} \,{\not <}_\theta \, \varphi ^\theta _\beta \), contradicting the fact that \(\alpha + 1 < \beta \).\(\square \)
and an ordinal \(\alpha < \beta \) such that \(\psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\), and hence, by removing a nonstationary subset from \(S'\) if necessary, we can assume that \(\psi (i) + 1 \leqslant \varphi ^\theta _{\alpha +1}(i)\) for all \(i \in S'\). But, by our definition of \(\psi \), we have \(\psi (i) + 1 = \varphi ^\theta _\beta (i)\) for all \(i \in S'\), and hence \(\varphi ^\theta _{\alpha +1} \,{\not <}_\theta \, \varphi ^\theta _\beta \), contradicting the fact that \(\alpha + 1 < \beta \).\(\square \)
Proposition 2.5
Suppose that \(\theta \) is a regular uncountable cardinal, \(\beta \) is an ordinal such that \(\varphi ^\theta _\beta \) is defined, and \(S \subseteq \theta \) is stationary. Then \(\Vert \varphi ^\theta _\beta \,{\restriction }\, S\Vert _S = \beta \).
Proof
The proof is by induction on \(\beta \), so we assume that, for all \(\alpha < \beta \) and all stationary \(T \subseteq \theta \), we have \(\Vert \varphi ^\theta _\alpha \,{\restriction }\, T \Vert _T = \alpha \). Since \(\varphi ^\theta _\alpha \,{<}_\theta \, \varphi ^\theta _\beta \) for all \(\alpha < \beta \), it follows that \(\Vert \varphi ^\theta _\beta \,{\restriction }\, S\Vert _S \geqslant \beta \).
For the opposite inequality, fix a function \(\psi \in {^S}\textrm{On}\) with \(\psi \,{<}_S\, \varphi ^\theta _\beta \,{\restriction }\, S\); it suffices to show that \(\Vert \psi \Vert _S < \beta \). An application of Proposition 2.3 yields a stationary \(T \subseteq S\) and an \(\alpha < \beta \) such that \(\psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in T\). By the induction hypothesis, we have \(\Vert \varphi ^\theta _\alpha \,{\restriction }\, T\Vert _T = \alpha \), so it follows that \(\Vert \psi \,{\restriction }\, T\Vert _T \leqslant \alpha \). But then, since \(T \subseteq S\), this implies that \(\Vert \psi \Vert _S \leqslant \alpha < \beta \), as desired.\(\square \)
We now recall two results from [10], the first of which is already implicit in [19].
Theorem 2.6
([10, Corollary 2.3]) Suppose that A is an infinite set, I is an ideal on A, and \(\langle \mu _a \,{|}\, a \in A \rangle \) is a sequence of regular cardinals such that \(\mu _a > |A |^+\) for all \(a \in A\). Then there exist a set \(B \in I^+\), a regular cardinal \(\lambda > |A |^+\), and a sequence \(\vec {f} = \langle f_\alpha \,{|}\, \alpha < \lambda \rangle \) such that \(\vec {f}\) is \(<_{I {\restriction } B}\)-increasing and \(<_{I {\restriction } B}\)-cofinal in \(\prod _{a \in B} \mu _a\).
Our statement of the next theorem is less general than its statement in [10]; we focus on ideals of the form \(\textrm{NS}_\theta {\restriction }\, S\) rather than the arbitrary normal ideals of [10].
Theorem 2.7
([10, Main Theorem]) Suppose that
-
(1)
\(\kappa \) is a singular cardinal and
 ;
; -
(2)
\(\langle \kappa _i \,{|}\, i \,{<}\, \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \);
-
(3)
\(\langle \mu _i \,{|}\, i \,{<}\, \theta \rangle \) is an increasing sequence of regular cardinals such that, for some function \(\varphi \in {^\theta }\textrm{On}\), we have \(\mu _i = \kappa _i^{+\varphi (i)}\) for all \(i < \theta \);
-
(4)
\(S \subseteq \theta \) is stationary;
-
(5)
\(\lambda \) is a regular cardinal and \(\vec {f} = \langle f_\alpha \,{|}\, \alpha \,{<}\, \lambda \rangle \) is a \(<_S\)-increasing and \(<_S\)-cofinal sequence from \(\prod _{\,i \in S} \mu _i\).
Then \(\lambda \leqslant \kappa ^{+\Vert \varphi {\restriction } S\Vert _S}\).
Putting these two results together yields the following corollary.
Corollary 2.8
Suppose that \(\theta \) is a regular uncountable cardinal, \(S \subseteq \theta \) is stationary, and \(\beta \) is an ordinal such that \(\varphi ^\theta _\beta \) is defined. Suppose also that \(\kappa \) is a singular cardinal,  , and \(\langle \kappa _i \,{|}\, i \,{<}\, \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \) with \(\kappa _0 > \theta \). Then there is a stationary
, and \(\langle \kappa _i \,{|}\, i \,{<}\, \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \) with \(\kappa _0 > \theta \). Then there is a stationary  and a sequence \(\vec {f} = \langle f_\alpha \,{|}\, \alpha \,{<}\, \lambda \rangle \) from \(\prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)+1}\) such that
and a sequence \(\vec {f} = \langle f_\alpha \,{|}\, \alpha \,{<}\, \lambda \rangle \) from \(\prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)+1}\) such that
-
(1)
\(\vec {f}\) is \(<_{S'}\)-increasing and \(<_{S'}\)-cofinal in \(\prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)+1}\);
-
(2)
\(\lambda \leqslant \kappa ^{+\beta + 1}\).
In particular, there exists a \(<_{S'}\)-cofinal subset  such that
such that  .
.
Proof
By Proposition 2.4, we have \(\varphi ^\theta _{\beta + 1} = \varphi ^\theta _\beta + 1\). For each \(i \in S\), let  . Then, applying Theorem 2.6 to the set S, the ideal \(\textrm{NS}_\theta {\restriction }\, S\), and the sequence \(\langle \mu _i \,{|}\, i \,{\in }\, S \rangle \) of regular cardinals, we obtain a stationary
. Then, applying Theorem 2.6 to the set S, the ideal \(\textrm{NS}_\theta {\restriction }\, S\), and the sequence \(\langle \mu _i \,{|}\, i \,{\in }\, S \rangle \) of regular cardinals, we obtain a stationary  , a regular cardinal \(\lambda > |A |^+\), and a sequence \(\vec {f} = \langle f_\alpha \,{|}\, \alpha \,{<}\, \lambda \rangle \) such that \(\vec {f}\) is \(<_{S'}\)-increasing and \(<_{S'}\)-cofinal in \(\prod _{\,i \in S'} \mu _i\). Then Theorem 2.7 implies that \(\lambda \leqslant \kappa ^{+\Vert \varphi ^\theta _{\beta + 1} {\restriction } S'\Vert _{S'}}\), so, by Proposition 2.5, we have \(\lambda \leqslant \kappa ^{+\beta +1}\).\(\square \)
, a regular cardinal \(\lambda > |A |^+\), and a sequence \(\vec {f} = \langle f_\alpha \,{|}\, \alpha \,{<}\, \lambda \rangle \) such that \(\vec {f}\) is \(<_{S'}\)-increasing and \(<_{S'}\)-cofinal in \(\prod _{\,i \in S'} \mu _i\). Then Theorem 2.7 implies that \(\lambda \leqslant \kappa ^{+\Vert \varphi ^\theta _{\beta + 1} {\restriction } S'\Vert _{S'}}\), so, by Proposition 2.5, we have \(\lambda \leqslant \kappa ^{+\beta +1}\).\(\square \)
3 Density
In this section, we recall some notions of density that will play a role throughout the paper. The first of these notions was the subject of Kojman’s [12].
Definition 3.1
([12]) Suppose that \(\theta \leqslant \mu \) are infinite cardinals. The \(\theta \)-density of \(\mu \), denoted \(d(\theta , \mu )\), is the minimal cardinality of a set  that is dense in
that is dense in  , i.e., for all \(x \in [\mu ]^\theta \), there is
, i.e., for all \(x \in [\mu ]^\theta \), there is  such that \(y \subseteq x\).
such that \(y \subseteq x\).
If \(\theta < \mu \), then \(\underline{[\mu ]^\theta }\) denotes the set of \(x \in [\mu ]^\theta \) such that  , and the lower \(\theta \)- density of \(\mu \), denoted \(\underline{d(\theta , \mu )}\), is the minimal cardinality of a set
, and the lower \(\theta \)- density of \(\mu \), denoted \(\underline{d(\theta , \mu )}\), is the minimal cardinality of a set  that is dense in
that is dense in  .
.
Remark 3.2
In [12], the \(\theta \)-density of \(\mu \) is denoted by  . We have chosen the notation \(d(\theta , \mu )\) to match the established notation \(m(\theta , \mu )\) for meeting numbers, which are among the cardinal characteristics considered here. Our notation for both density numbers and meeting numbers follows [17].
. We have chosen the notation \(d(\theta , \mu )\) to match the established notation \(m(\theta , \mu )\) for meeting numbers, which are among the cardinal characteristics considered here. Our notation for both density numbers and meeting numbers follows [17].
Note that, if \(\theta < \mu \), then \(\underline{d(\theta , \mu )} = \mu \cdot \sum _{\nu < \mu } d(\theta , \nu )\). Therefore, if  for all \(\nu < \mu \), then \(\underline{d(\theta , \mu )} = \mu \).
for all \(\nu < \mu \), then \(\underline{d(\theta , \mu )} = \mu \).
As remarked in [12], if  , then
, then

In particular, if  and
and  for all \(\nu < \mu \), then \(d(\theta , \mu ) = \mu \).
for all \(\nu < \mu \), then \(d(\theta , \mu ) = \mu \).
If  , then a routine diagonalization argument shows that \(d(\theta , \mu ) \geqslant \mu ^+\).
, then a routine diagonalization argument shows that \(d(\theta , \mu ) \geqslant \mu ^+\).
The main result of [12] is a version of Silver’s theorem for the density number  ; this result served as direct motivation for the initial work that led to the results of this paper. Our main result here, when applied to the density number, will generalize and slightly improve upon the results of [12].
; this result served as direct motivation for the initial work that led to the results of this paper. Our main result here, when applied to the density number, will generalize and slightly improve upon the results of [12].
If I is an ideal over a set X, then the density of I, which we will denote d(I), is the minimal cardinality of a set  such that, for all \(S \in I^+\), there is
such that, for all \(S \in I^+\), there is  such that
such that  . We will particularly be interested in densities of the form \(d(\textrm{NS}_\theta {\restriction }\, S)\), where S is a stationary set of a regular uncountable cardinal \(\theta \). Concretely, \(d(\textrm{NS}_\theta {\restriction }\, S)\) is the minimal cardinality of a collection
. We will particularly be interested in densities of the form \(d(\textrm{NS}_\theta {\restriction }\, S)\), where S is a stationary set of a regular uncountable cardinal \(\theta \). Concretely, \(d(\textrm{NS}_\theta {\restriction }\, S)\) is the minimal cardinality of a collection  of stationary subsets of S such that, for every stationary
of stationary subsets of S such that, for every stationary  , there is
, there is  such that
such that  is nonstationary in \(\theta \).
is nonstationary in \(\theta \).
Finally, we introduce a notion of density that, in a sense, combines the two notions introduced in this section thus far.
Definition 3.3
Suppose that \(\theta \) and \(\kappa \) are infinite cardinals, with \(\theta \) regular, and suppose that \(S \subseteq \theta \) is stationary. Then the stationarity density of \({^S}\kappa \), which we denote by \(d_{\textrm{stat}}({^S}\kappa )\), is the minimal cardinality of a family  of functions such that
of functions such that
-
(1)
every
 is a function from a stationary subset of S to \(\kappa \);
is a function from a stationary subset of S to \(\kappa \); -
(2)
for every function g from a stationary subset of S to \(\kappa \), there is
 such that the set
such that the set 
is nonstationary. (Less precisely but more evocatively, f is contained in g modulo a nonstationary set.)
In analogy with lower density, we define the lower stationary density of \({^S}\kappa \), denoted \(\underline{d_{\textrm{stat}}({^S}\kappa )}\), in the same way as \(d_{\textrm{stat}}({^S}\kappa )\), except that, in item (2), we only consider functions whose ranges are bounded below \(\kappa \) (and hence we can require that all of our functions in  also have ranges bounded below \(\kappa \)).
also have ranges bounded below \(\kappa \)).
Remark 3.4
Note that \(d(\textrm{NS}_\theta {\restriction }\, S) \leqslant \underline{d_{\textrm{stat}}({^S}\kappa )}\). Also, whenever \(T \subseteq S\) are stationary subsets of \(\theta \), we have
-
\(d(\textrm{NS}_\theta {\restriction }\, T) \leqslant d(\textrm{NS}_\theta {\restriction }\, S)\);
-
\(d_{\textrm{stat}}({^{T}}\kappa ) \leqslant d_{\textrm{stat}}({^S}\kappa )\);
-
\(\underline{d_{\textrm{stat}}({^{T}}\kappa )} \leqslant \underline{d_{\textrm{stat}}({^S}\kappa )}\).
4 The general framework
The cardinal characteristics we consider in this paper all have the following form: a set  and a binary relation \(\rightsquigarrow \) on
and a binary relation \(\rightsquigarrow \) on  are fixed, and the relevant cardinal characteristic is then
are fixed, and the relevant cardinal characteristic is then  , i.e., the minimal cardinality of a subset
, i.e., the minimal cardinality of a subset  such that, for all
such that, for all  , there is
, there is  such that \(x \rightsquigarrow y\).
such that \(x \rightsquigarrow y\).
Because of the structural similarity of these cardinal characteristics, the inductive steps in the proofs of our main results end up being essentially the same, so in this section we prove a general lemma that we can directly apply to all of the specific situations under consideration here, and that we expect will find application beyond the scope of this paper, as well.
In order to state and prove our general lemma, let us fix some objects and notation for the remainder of this section:
-
\(\kappa \) is a singular cardinal and
 ;
; -
\(\langle \kappa _i \,{|}\, i \,{<}\, \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \), with \(\kappa _0 > \theta \);
-
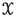 is a set and \(\rightsquigarrow \) is a binary relation on
is a set and \(\rightsquigarrow \) is a binary relation on  ;
; -
for each \(i < \theta \),
 is a set and \(\rightsquigarrow _i\) is a binary relation on
is a set and \(\rightsquigarrow _i\) is a binary relation on  ;
; -
for each \(i < \theta \),
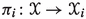 is a function;
is a function; -
\(e:\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\) is a function such that, for all stationary \(T \subseteq S \subseteq \theta \), we have \(e(T) \leqslant e(S)\).
Remark 4.1
To help orient the reader, let us preview here some of the eventual interpretations of these objects. In a typical application, we might have  ,
,  , and \(\pi _i(x) = x \cap \kappa _i\), or
, and \(\pi _i(x) = x \cap \kappa _i\), or  ,
,  , and \(\pi _i(x)\) is a modification of \(x \,{\restriction }\, \kappa _i\) to ensure that it takes values in \(\kappa _i\). The function e will typically (though not always) output one of the density numbers introduced in Sect. 3.
, and \(\pi _i(x)\) is a modification of \(x \,{\restriction }\, \kappa _i\) to ensure that it takes values in \(\kappa _i\). The function e will typically (though not always) output one of the density numbers introduced in Sect. 3.
In this context, if \(S \subseteq \theta \) is stationary and \(\beta \) is an ordinal for which the canonical function \(\varphi ^\theta _\beta \) is defined (recall the discussion of canonical functions following Definition 2.1), then let \(\Psi (S, \beta )\) denote the following assertion:
If
and
are such that
- (1)
and
for all \(i \in S\);
- (2)
for all \(i \in S\);
- (3)
for all
, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S\), there is
for which \(\pi _i(z) \rightsquigarrow _i y\);
then there is
such that
and, for all
, there is
for which \(z \rightsquigarrow y\).
Let \(\Psi ^*(S, \beta )\) be defined in the same way, except, in the conclusion, we only require  .
.
Lemma 4.2
Suppose that \(S \subseteq \theta \) is stationary and \(\Psi (T, 0)\) holds for all stationary \(T \subseteq S\). Then, for all ordinals \(\beta \) for which the canonical function \(\varphi ^\theta _\beta \) is defined, \(\Psi (S, \beta )\) holds.
Proof
The proof is by induction on \(\beta \), simultaneously for all stationary \(S \subseteq \theta \). Thus, fix an ordinal \(\beta \) for which \(\varphi ^\theta _\beta \) is defined and a stationary set \(S \subseteq \theta \). By the hypothesis of the lemma, we can assume that \(\beta > 0\), and by the inductive hypothesis, we can assume that \(\Psi (T, \alpha )\) holds for all \(\alpha < \beta \) and all stationary \(T \subseteq S\). Fix  and
and  as in the hypothesis of \(\Psi (S, \beta )\); we will find
as in the hypothesis of \(\Psi (S, \beta )\); we will find  as in its conclusion. For each \(i \in S\), enumerate
as in its conclusion. For each \(i \in S\), enumerate  as \(\bigl \langle y_{i, \xi } \,{|}\, \xi < \kappa _i^{+\varphi ^\theta _\beta (i)} \bigr \rangle \) (with repetitions if
as \(\bigl \langle y_{i, \xi } \,{|}\, \xi < \kappa _i^{+\varphi ^\theta _\beta (i)} \bigr \rangle \) (with repetitions if  ).
).
Suppose first that \(\beta = \beta ' + 1\) is a successor ordinal. By Proposition 2.4, we can assume that  . Then, by Corollary 2.8, we can fix a stationary
. Then, by Corollary 2.8, we can fix a stationary  and a \(<_{S'}\)-cofinal family
and a \(<_{S'}\)-cofinal family  such that
such that  . For each
. For each  , let
, let  , and note that
, and note that  . Let
. Let  be the set of
be the set of  for which there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S'\), there is
for which there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S'\), there is  such that \(\pi _i(z) \rightsquigarrow _i y\). Recalling that \(d(\textrm{NS}_\theta {\restriction }\, S') \leqslant d(\textrm{NS}_\theta {\restriction }\, S)\) and \(e(S') \leqslant e(S)\), apply
such that \(\pi _i(z) \rightsquigarrow _i y\). Recalling that \(d(\textrm{NS}_\theta {\restriction }\, S') \leqslant d(\textrm{NS}_\theta {\restriction }\, S)\) and \(e(S') \leqslant e(S)\), apply  to
to  and
and  to find
to find  such that
such that  and, for all
and, for all  , there is
, there is  such that \(z \rightsquigarrow y\).
such that \(z \rightsquigarrow y\).
Let  ; we claim that
; we claim that  is as desired. It is evident that
is as desired. It is evident that  and
and  , so it remains to verify that, for all
, so it remains to verify that, for all  , there is
, there is  such that \(z \rightsquigarrow y\). For this, it suffices to show that
such that \(z \rightsquigarrow y\). For this, it suffices to show that  . To this end, fix
. To this end, fix  . By assumption, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S'\), there is \(\xi _i < \kappa _i^{+\varphi ^\theta _\beta (i)}\) for which \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\). Define a function \(g \in \prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)}\) by letting
. By assumption, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S'\), there is \(\xi _i < \kappa _i^{+\varphi ^\theta _\beta (i)}\) for which \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\). Define a function \(g \in \prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)}\) by letting
for all \(i \in S'\). Since  is \(<_{S'}\)-cofinal in \(\prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)}\), we can find
is \(<_{S'}\)-cofinal in \(\prod _{\,i \in S'} \kappa _i^{+\varphi ^\theta _\beta (i)}\), we can find  such that \(g \,{<}_{S'} f\), i.e., there is a club \(D \subseteq \theta \) such that, for all \(i \in D \cap S'\), we have \(g(i) < f(i)\). But then, for all \(i \in D \cap C \cap S'\), we have \(\xi _i < f(i)\) and \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\), so \(D \cap C\) witnesses that z is in
such that \(g \,{<}_{S'} f\), i.e., there is a club \(D \subseteq \theta \) such that, for all \(i \in D \cap S'\), we have \(g(i) < f(i)\). But then, for all \(i \in D \cap C \cap S'\), we have \(\xi _i < f(i)\) and \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\), so \(D \cap C\) witnesses that z is in  , and we are done.
, and we are done.
Finally, suppose that \(\beta \) is a limit ordinal. By Proposition 2.4, we can assume that \(\varphi ^\theta _\beta (i)\) is a limit ordinal for all \(i \in S\). Let  be a collection of stationary subsets of S such that
be a collection of stationary subsets of S such that  and, for every stationary
and, for every stationary  , there is
, there is  such that
such that  . For each \(\alpha < \beta \) and each \(i \in S\), let
. For each \(\alpha < \beta \) and each \(i \in S\), let  . For each \(\alpha < \beta \) and each
. For each \(\alpha < \beta \) and each  , let
, let  be the set of all
be the set of all  for which there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is
for which there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is  such that \(\pi _i(z) \rightsquigarrow _i y\). Apply \(\Psi (T, \alpha )\) to
such that \(\pi _i(z) \rightsquigarrow _i y\). Apply \(\Psi (T, \alpha )\) to  and
and  to find
to find  such that
such that  and, for all
and, for all  , there is
, there is  such that \(z \rightsquigarrow y\).
such that \(z \rightsquigarrow y\).
Let  ; we claim that
; we claim that  is as desired. As in the successor case, it suffices to verify that
is as desired. As in the successor case, it suffices to verify that  . To this end, fix
. To this end, fix  . By hypothesis, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S\), there is \(\xi _i < \kappa _i^{+\varphi ^\theta _\beta (i)}\) for which \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\). For each such i, use the fact that \(\varphi ^\theta _\beta (i)\) is a limit ordinal to find \(\gamma _i < \varphi ^\theta _\beta (i)\) such that \(\xi _i < \kappa _i^{+\gamma _i}\). Define a function \(\psi \in {^\theta }\textrm{On}\) by letting
. By hypothesis, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap S\), there is \(\xi _i < \kappa _i^{+\varphi ^\theta _\beta (i)}\) for which \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\). For each such i, use the fact that \(\varphi ^\theta _\beta (i)\) is a limit ordinal to find \(\gamma _i < \varphi ^\theta _\beta (i)\) such that \(\xi _i < \kappa _i^{+\gamma _i}\). Define a function \(\psi \in {^\theta }\textrm{On}\) by letting
for all \(i < \theta \). By Proposition 2.3, we can find a stationary  and an \(\alpha < \beta \) such that \(\gamma _i = \psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\). We can subsequently find a
and an \(\alpha < \beta \) such that \(\gamma _i = \psi (i) \leqslant \varphi ^\theta _\alpha (i)\) for all \(i \in S'\). We can subsequently find a  and a club \(D \subseteq \theta \) such that \(D \cap T \subseteq S'\). Then, for all \(i \in D \cap T\), we have
and a club \(D \subseteq \theta \) such that \(D \cap T \subseteq S'\). Then, for all \(i \in D \cap T\), we have  and \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\), so D witnesses that z is in
and \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\), so D witnesses that z is in  , and we are done.\(\square \)
, and we are done.\(\square \)
Notice that the only place in which the value of \(d(\textrm{NS}_\theta {\restriction }\, S)\) plays a role in the proof of Lemma 4.2 is in the case in which \(\beta \) is a limit ordinal (in the successor case it only makes an appearance via the inductive hypothesis). Therefore, if \(\beta < \omega \) and \(\Psi ^*(T, 0)\) holds for all stationary \(T \subseteq \theta \), then we can do away with \(d(\textrm{NS}_\theta {\restriction }\, S)\) in the conclusion of the lemma. More precisely, the proof of the successor case of Lemma 4.2 yields the following corollary.
Corollary 4.3
Suppose that \(S \subseteq \theta \) is stationary and \(\Psi ^*(T, 0)\) holds for all stationary \(T \subseteq S\). Then \(\Psi ^*(S, n)\) holds for all \(n < \omega \).
The translation from Lemma 4.2 and Corollary 4.3 to our main results will happen via the following corollary.
Corollary 4.4
Suppose that
-
(1)
\(\beta \) is an ordinal for which \(\varphi ^\theta _\beta \) is defined;
-
(2)
 is stationary in \(\theta \);
is stationary in \(\theta \); -
(3)
\(\Psi (T, 0)\) holds for all stationary \(T \subseteq S\).
Then  . If, moreover, \(\beta < \omega \) and \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq S\), then
. If, moreover, \(\beta < \omega \) and \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq S\), then  .
.
Proof
By Lemma 4.2, we know that \(\Psi (S, \beta )\) holds. Let  and, for each \(i \in S\), let
and, for each \(i \in S\), let  be such that
be such that  and
and  is \(\rightsquigarrow _i\)-cofinal in
is \(\rightsquigarrow _i\)-cofinal in  . In particular, for all
. In particular, for all  and all \(i \in S\), there is
and all \(i \in S\), there is  such that \(\pi _i(z) \rightsquigarrow _i y\). Therefore, applying \(\Psi (S, \beta )\) to
such that \(\pi _i(z) \rightsquigarrow _i y\). Therefore, applying \(\Psi (S, \beta )\) to  and
and  yields a set
yields a set  such that
such that  and, for all \(z \in Z\), there is
and, for all \(z \in Z\), there is  such that \(z \rightsquigarrow y\), i.e.,
such that \(z \rightsquigarrow y\), i.e.,  is \(\rightsquigarrow \)-cofinal in
is \(\rightsquigarrow \)-cofinal in  .
.
For the “moreover” clause, if \(\beta < \omega \) and \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq S\), then Corollary 4.3 implies that \(\Psi ^*(S, \beta )\) holds. Applying \(\Psi ^*(S, \beta )\) to the  and
and  of the previous paragraph then yields
of the previous paragraph then yields  such that
such that  and
and  is \(\rightsquigarrow \)-cofinal in
is \(\rightsquigarrow \)-cofinal in  .\(\square \)
.\(\square \)
5 Specific instances
We now turn to applications of the general framework introduced in the previous section to particular cardinal characteristics at singular cardinals. Let us fix for this entire section cardinals \(\kappa \) and \(\theta \) such that  , as well as an increasing, continuous sequence of cardinals \(\langle \kappa _i \,{|}\, i < \theta \rangle \) converging to \(\kappa \), with \(\kappa _0 > \theta \).
, as well as an increasing, continuous sequence of cardinals \(\langle \kappa _i \,{|}\, i < \theta \rangle \) converging to \(\kappa \), with \(\kappa _0 > \theta \).
Each cardinal characteristic \(\mathfrak {cc}_\kappa \) we consider will entail a choice of a set  and a binary relation \(\rightsquigarrow \) on
and a binary relation \(\rightsquigarrow \) on  such that
such that  . The sets
. The sets  and relations \(\langle \rightsquigarrow _i {|}\, i < \theta \rangle \) will be defined analogously, so that
and relations \(\langle \rightsquigarrow _i {|}\, i < \theta \rangle \) will be defined analogously, so that  for each \(i < \theta \). We will also have natural restriction operations
for each \(i < \theta \). We will also have natural restriction operations  for each \(i < \theta \). Together with an appropriate choice of function \(e:\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\), these assignments give rise to instances of the formulas \(\Psi (S, \beta )\) and \(\Psi ^*(S, \beta )\) from the previous section. The primary work of this section will consist of proving that all of these instances of \(\Psi ^*(T, 0)\) hold; Corollary 4.4 will then directly yield our main results.
for each \(i < \theta \). Together with an appropriate choice of function \(e:\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\), these assignments give rise to instances of the formulas \(\Psi (S, \beta )\) and \(\Psi ^*(S, \beta )\) from the previous section. The primary work of this section will consist of proving that all of these instances of \(\Psi ^*(T, 0)\) hold; Corollary 4.4 will then directly yield our main results.
We will begin by introducing each of the cardinal characteristics we will be considering and specifying the appropriate assignments for  , \(\rightsquigarrow \),
, \(\rightsquigarrow \),  , and e for each characteristic. We will then prove a lemma indicating that, for all of these assignments, the corresponding instance of \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq \theta \).
, and e for each characteristic. We will then prove a lemma indicating that, for all of these assignments, the corresponding instance of \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq \theta \).
We note that for some of the cardinal characteristics, we will only define  , \(\rightsquigarrow _i\), and \(\pi _i\) for limit ordinals \(i < \theta \). Since the clubs C in the statement of \(\Psi (S, \beta )\) can always be assumed to consist entirely of limit ordinals, this is sufficient for our purposes.
, \(\rightsquigarrow _i\), and \(\pi _i\) for limit ordinals \(i < \theta \). Since the clubs C in the statement of \(\Psi (S, \beta )\) can always be assumed to consist entirely of limit ordinals, this is sufficient for our purposes.
5.1 Meeting numbers
The first cardinal characteristics we consider are the meeting numbers.
Definition 5.1
([17]) Suppose that \(\sigma \leqslant \lambda \) are infinite cardinals. Then the meeting number \(m(\sigma , \lambda )\) is the minimal cardinality of a collection  such that, for all \(x \in [\lambda ]^\sigma \), there is \(y\) such that \(|x \cap y |= \sigma \).
such that, for all \(x \in [\lambda ]^\sigma \), there is \(y\) such that \(|x \cap y |= \sigma \).
The meeting number \(m(\sigma , \lambda )\) is of special interest when  , in which case a routine diagonalization argument implies that \(m(\sigma , \lambda ) > \lambda \). A result of Matet indicates that Shelah’s Strong Hypothesis, a statement in PCF theory, is equivalent to the statement that all such meeting numbers take their minimal possible value:
, in which case a routine diagonalization argument implies that \(m(\sigma , \lambda ) > \lambda \). A result of Matet indicates that Shelah’s Strong Hypothesis, a statement in PCF theory, is equivalent to the statement that all such meeting numbers take their minimal possible value:
Theorem 5.2
(Matet, [16, Theorem 1.1]) The following are equivalent:
-
(1)
Shelah’s Strong Hypothesis;
-
(2)
for every singular cardinal \(\lambda \) of countable cofinality, \(m(\aleph _0, \lambda ) = \lambda ^+\);
-
(3)
for all infinite cardinals \(\sigma < \lambda \), we have \(m(\sigma , \lambda ) = \lambda ^+\) if
 and \(m(\sigma , \lambda ) = \lambda \) if
and \(m(\sigma , \lambda ) = \lambda \) if 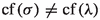 .
.
We now specify assignments to define a version of the formula \(\Psi ^*(T, 0)\) appropriate for the meeting number. Let  and, for each limit ordinal \(i < \theta \), let
and, for each limit ordinal \(i < \theta \), let  . Define relations \(\rightsquigarrow \) on
. Define relations \(\rightsquigarrow \) on  and \(\rightsquigarrow _i\) on
and \(\rightsquigarrow _i\) on  by letting \(x \rightsquigarrow y\) iff \(|x \cap y |= \theta \) and \(x \rightsquigarrow _i y\) iff
by letting \(x \rightsquigarrow y\) iff \(|x \cap y |= \theta \) and \(x \rightsquigarrow _i y\) iff  for all limit ordinals \(i < \theta \). It is then evident that
for all limit ordinals \(i < \theta \). It is then evident that  and
and  for all limit \(i < \theta \).
for all limit \(i < \theta \).
For each limit ordinal \(i < \theta \), define a map  as follows. For any \(i < \theta \) and
as follows. For any \(i < \theta \) and  , if
, if  , then let \(\pi _i(x)\) be an arbitrary unbounded subset of \(x \cap \kappa _i\) of order type
, then let \(\pi _i(x)\) be an arbitrary unbounded subset of \(x \cap \kappa _i\) of order type  . If
. If  , then simply let \(\pi _i(x)\) be an arbitrary element of
, then simply let \(\pi _i(x)\) be an arbitrary element of  . Note that, for every
. Note that, for every  that is unbounded in \(\kappa \), the set
that is unbounded in \(\kappa \), the set  is a club in \(\theta \).
is a club in \(\theta \).
Let \(e:\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\) be the constant function taking value \(\sum _{j < \theta } m(\theta , \kappa _j)\).
5.2 Density
As mentioned above, a version of Silver’s theorem for density is proven in [12]. We include density here for completeness, since our results are slightly more general than those of [12].
We are interested in particular in the number \(d(\theta , \kappa )\). The setup for density will be similar to that for the meeting number. Again let  and, for each limit ordinal \(i < \theta \), let
and, for each limit ordinal \(i < \theta \), let  . Define relations \(\rightsquigarrow \) on
. Define relations \(\rightsquigarrow \) on  and \(\rightsquigarrow _i\) on
and \(\rightsquigarrow _i\) on  by letting \(x \rightsquigarrow y\) or \(x \rightsquigarrow _i y\) iff \(x \supseteq y\). Then
by letting \(x \rightsquigarrow y\) or \(x \rightsquigarrow _i y\) iff \(x \supseteq y\). Then  and
and  for all limit \(i < \theta \).
for all limit \(i < \theta \).
Define maps  for limit ordinals \(i < \theta \) exactly as in the case of the meeting number in the previous subsection. Let \(e :\textrm{NS}^+_\theta \rightarrow \textrm{Card}\) be the constant function taking value \(\underline{d(\theta , \kappa )} = \sum _{j < \theta } d(\theta , \kappa _j)\) (recall Definition 3.1).
for limit ordinals \(i < \theta \) exactly as in the case of the meeting number in the previous subsection. Let \(e :\textrm{NS}^+_\theta \rightarrow \textrm{Card}\) be the constant function taking value \(\underline{d(\theta , \kappa )} = \sum _{j < \theta } d(\theta , \kappa _j)\) (recall Definition 3.1).
5.3 The reaping number
Definition 5.3
Let \(\lambda \) be an infinite cardinal.
-
(1)
If \(x,y \in [\lambda ]^\lambda \), then we say that x splits y if
 .
. -
(2)
A family
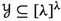 is unreaped if there is no single \(x \in [\lambda ]^\lambda \) that splits every element of
is unreaped if there is no single \(x \in [\lambda ]^\lambda \) that splits every element of  .
. -
(3)
The reaping number \({\mathfrak {r}}_\lambda \) is the minimum cardinality of an unreaped family in \([\lambda ]^\lambda \).
A standard diagonalization argument shows that \({\mathfrak {r}}_\lambda > \lambda \) for every infinite cardinal \(\lambda \).
Let  and, for each \(i < \theta \), let
and, for each \(i < \theta \), let  . Define a relation \(\rightsquigarrow \) on
. Define a relation \(\rightsquigarrow \) on  by letting \(x \rightsquigarrow y\) iff x does not split y, i.e., either \(|y \cap x |< \kappa \) or \(|y {\setminus } x |< \kappa \). Similarly, for each \(i < \theta \), define \(\rightsquigarrow _i\) on
by letting \(x \rightsquigarrow y\) iff x does not split y, i.e., either \(|y \cap x |< \kappa \) or \(|y {\setminus } x |< \kappa \). Similarly, for each \(i < \theta \), define \(\rightsquigarrow _i\) on  by letting \(x \rightsquigarrow _i y\) iff x does not split y. Then it is evident that
by letting \(x \rightsquigarrow _i y\) iff x does not split y. Then it is evident that  and
and  for all \(i < \theta \).
for all \(i < \theta \).
For each \(i < \theta \), define a map  as follows. For all
as follows. For all  , if \(|x \cap \kappa _i |= \kappa _i\), then let \(\pi _i(x) = x \cap \kappa _i\). Otherwise, let \(\pi _i(x) = \kappa _i\). Note that, for all \(x \in [\kappa ]^\kappa \), the set of \(i < \theta \) for which \(|x \cap \kappa _i |= \kappa _i\), and hence for which \(\pi _i(x) = x \cap \kappa _i\), is a club in \(\theta \). Finally, as in the case of density, let \(e :\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\) be the constant function taking value \(\underline{d(\theta , \kappa )}\).
, if \(|x \cap \kappa _i |= \kappa _i\), then let \(\pi _i(x) = x \cap \kappa _i\). Otherwise, let \(\pi _i(x) = \kappa _i\). Note that, for all \(x \in [\kappa ]^\kappa \), the set of \(i < \theta \) for which \(|x \cap \kappa _i |= \kappa _i\), and hence for which \(\pi _i(x) = x \cap \kappa _i\), is a club in \(\theta \). Finally, as in the case of density, let \(e :\textrm{NS}_\theta ^+ \rightarrow \textrm{Card}\) be the constant function taking value \(\underline{d(\theta , \kappa )}\).
5.4 The dominating number
Definition 5.4
Suppose that \(\lambda \) is an infinite cardinal.
-
(1)
If \(f, g \in {^\lambda }\textrm{On}\), then \(f \,{<}^* g\) if and only if \(|\{\eta< \lambda \,{|}\, g(\eta ) \leqslant f(\eta )\} |< \lambda \).
-
(2)
The dominating number \({\mathfrak {d}}_\lambda \) is the minimal cardinality of a family
 such that for every \(g \in {^\lambda }\lambda \), there is
such that for every \(g \in {^\lambda }\lambda \), there is  such that \(g \,{<}^* f\).
such that \(g \,{<}^* f\). -
(3)
More generally, for any limit ordinal \(\sigma \), \({\mathfrak {d}}_{\lambda , \sigma }\) is the minimal cardinality of a family
 such that, for every \(g \in {^\lambda }\sigma \), there is
such that, for every \(g \in {^\lambda }\sigma \), there is  such that \(g \,{<}^* f\).
such that \(g \,{<}^* f\).
Proofs of the following basic facts can be found in [7].
Proposition 5.5
([7, Claim 3.2 and Lemma 3.1]) Suppose that \(\lambda \) is an infinite cardinal.
-
(1)
\({\mathfrak {d}}_\lambda > \lambda \) and
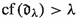 .
. -
(2)
 .
.
The proofs of [7, Claim 3.2 and Lemma 3.1] can be routinely adapted to yield the following generalization of the preceding proposition.
Fact 5.6
Suppose that \(\lambda \) is an infinite cardinal and \(\sigma \) is a limit ordinal.
-
(1)
\({\mathfrak {d}}_{\lambda , \sigma } > \lambda \) and
 .
. -
(2)
 .
.
Recently, Shelah proved that, if \(\kappa \) is a singular strong limit cardinal, then \({\mathfrak {d}}_\kappa \) always attains its maximal possible value. More precisely, he proved the following theorem:
Theorem 5.7
( [20, Claim 1.5 (2)]) Suppose that \(\kappa \) is a singular cardinal and \(\mu ^{\textrm{cf}(\kappa )} < \kappa \) for all \(\mu < \kappa \). Then \({\mathfrak {d}}_\kappa = 2^\kappa \).
We now specify assignments to define a version of the formula \(\Psi ^*(T, 0)\) appropriate for the dominating number. Let  and, for each limit ordinal \(i < \theta \), let
and, for each limit ordinal \(i < \theta \), let  . Let \(\rightsquigarrow \) and \(\rightsquigarrow _i\) be the relations \(<^*\) on
. Let \(\rightsquigarrow \) and \(\rightsquigarrow _i\) be the relations \(<^*\) on  and
and  , respectively. By Proposition 5.5 and Fact 5.6, we have
, respectively. By Proposition 5.5 and Fact 5.6, we have  and, for all limit \(i < \theta \), we have
and, for all limit \(i < \theta \), we have  .
.
For each limit ordinal \(i < \theta \), define a map  as follows. For all
as follows. For all  and all \(\eta < \kappa _i\), let
and all \(\eta < \kappa _i\), let
Note that we do indeed have  , as desired. Finally, let \(e:\textrm{NS}^+_\theta \rightarrow \textrm{Card}\) be defined by letting \(e(S) = \underline{d_{\textrm{stat}}({^S}\kappa )}\) for all stationary \(S \subseteq \theta \) (recall this notation from Definition 3.3).
, as desired. Finally, let \(e:\textrm{NS}^+_\theta \rightarrow \textrm{Card}\) be defined by letting \(e(S) = \underline{d_{\textrm{stat}}({^S}\kappa )}\) for all stationary \(S \subseteq \theta \) (recall this notation from Definition 3.3).
5.5 The general lemma
We now show that, in all of the cases introduced in this section, the corresponding version of \(\Psi ^*(T, 0)\) holds for all stationary \(T \subseteq \theta \). Note that we may assume that \(\varphi ^\theta _0(i) = 0\) for all \(i < \theta \), so clause (2) in the definition of \(\psi (T, 0)\) asserts that  for all \(i \in T\).
for all \(i \in T\).
Lemma 5.8
For any cardinal characteristic  , the corresponding formula \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq \theta \).
, the corresponding formula \(\Psi ^*(T, 0)\) holds for every stationary \(T \subseteq \theta \).
Proof
We begin with some general preliminaries and then split into cases depending on the cardinal characteristic under consideration.
Fix a stationary set \(T \subseteq \theta \); we may assume that every element of T is a limit ordinal. Fix assignments for  , \(\rightsquigarrow \),
, \(\rightsquigarrow \),  , and e corresponding to one of the cardinal characteristics introduced in this section. To verify \(\Psi ^*(T, 0)\), fix a set
, and e corresponding to one of the cardinal characteristics introduced in this section. To verify \(\Psi ^*(T, 0)\), fix a set  and, for each \(i \in T\), a set
and, for each \(i \in T\), a set  such that
such that
-
for all \(i \in T\),
 ;
; -
for all
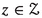 , there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is
, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is 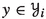 for which \(\pi _i(z) \rightsquigarrow _i y\).
for which \(\pi _i(z) \rightsquigarrow _i y\).
For each \(i \in T\), enumerate  as \(\langle y_{i, \xi } \,{|}\, \xi \,{<}\, \kappa _i \rangle \) (with repetitions if
as \(\langle y_{i, \xi } \,{|}\, \xi \,{<}\, \kappa _i \rangle \) (with repetitions if  ). We will find
). We will find  such that
such that  and, for all
and, for all  , there is
, there is  for which \(z \rightsquigarrow y\). Our method for doing this will depend on the precise cardinal characteristic.
for which \(z \rightsquigarrow y\). Our method for doing this will depend on the precise cardinal characteristic.
Case 1: \(m(\theta , \kappa )\). Recall that in this case \(e(T) = \sum _{j < \theta } m(\theta , \kappa _j)\). Therefore, for each \(j < \theta \), we can fix a family  such that
such that
-
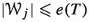 ;
; -
for all
 , there is
, there is  such that \(|w \cap u |= \theta \).
such that \(|w \cap u |= \theta \).
Let  . For each
. For each  , let \(y^*_w = \bigcup \, \{y_{i, \xi } \,{|}\, (i, \xi ) \in w\}\), and note that \(y^*_w \in [\kappa ]^{\leqslant \theta }\).
, let \(y^*_w = \bigcup \, \{y_{i, \xi } \,{|}\, (i, \xi ) \in w\}\), and note that \(y^*_w \in [\kappa ]^{\leqslant \theta }\).
Also, for each \(j < \theta \), let  be such that
be such that  and, for all \(x \in [\kappa _j]^\theta \), there is
and, for all \(x \in [\kappa _j]^\theta \), there is  such that \(|y \cap x |= \theta \). Finally, let
such that \(|y \cap x |= \theta \). Finally, let

We claim that  is as desired. It is evident that
is as desired. It is evident that  and
and  . It remains to show that, for all
. It remains to show that, for all  , there is
, there is  such that \(z \rightsquigarrow y\), i.e., \(|y \cap z |= \theta \). To this end, fix
such that \(z \rightsquigarrow y\), i.e., \(|y \cap z |= \theta \). To this end, fix  . If there is \(j < \theta \) such that \(z \subseteq \kappa _j\), then there is
. If there is \(j < \theta \) such that \(z \subseteq \kappa _j\), then there is  such that \(|y \cap z |= \theta \), and we are done. Therefore, we may assume that z is unbounded in \(\kappa \). By assumption, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we have
such that \(|y \cap z |= \theta \), and we are done. Therefore, we may assume that z is unbounded in \(\kappa \). By assumption, there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we have
-
 , and hence \(\pi _i(z)\) is an unbounded subset of \(z \cap \kappa _i\) of order type
, and hence \(\pi _i(z)\) is an unbounded subset of \(z \cap \kappa _i\) of order type  ;
; -
there is \(\xi _i < \kappa _i\) for which \(\pi _i(z) \rightsquigarrow _i y_{i, \xi _i}\), i.e.,
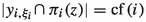 .
.
Since each \(i \in T\) is a limit ordinal, we can apply Fodor’s lemma to find a fixed \(j < \theta \) and a stationary  such that \(\xi _i < \kappa _j\) for all \(i \in T'\). Let \(u = \{(i, \xi _i) \,{|}\, i \in T'\}\). Then
such that \(\xi _i < \kappa _j\) for all \(i \in T'\). Let \(u = \{(i, \xi _i) \,{|}\, i \in T'\}\). Then  , so, by our choice of
, so, by our choice of  , we can find
, we can find  such that \(|w \cap u |= \theta \). It follows that the set
such that \(|w \cap u |= \theta \). It follows that the set  is unbounded in \(\theta \).
is unbounded in \(\theta \).
Consider the set  . Note that, for all \(i \in T''\), we know that \(\pi _i(z)\) is an unbounded subset of \(z \cap \kappa _i\) of order type
. Note that, for all \(i \in T''\), we know that \(\pi _i(z)\) is an unbounded subset of \(z \cap \kappa _i\) of order type  , and we know that
, and we know that  . It follows that
. It follows that  is an unbounded subset of \(z \cap \kappa _i\), and therefore \(y^*_w \cap z\) is an unbounded subset of z. In particular,
is an unbounded subset of \(z \cap \kappa _i\), and therefore \(y^*_w \cap z\) is an unbounded subset of z. In particular,  and \(z \rightsquigarrow y^*_w\), as desired.
and \(z \rightsquigarrow y^*_w\), as desired.
Case 2: \(d(\theta , \kappa )\). The argument in this case is very similar to that in the previous case, so we suppress some details. Since \(e(T) = \underline{d(\theta , \kappa )} = \sum _{j < \theta } d(\theta , \kappa _j)\), we can fix, for each \(j < \theta \), a family  that is dense in
that is dense in  and has cardinality at most e(T). Let
and has cardinality at most e(T). Let  and, for each
and, for each  , let
, let  .
.
Also, for each \(j < \theta \), fix  that is dense in
that is dense in  and has cardinality at most e(T). Let
and has cardinality at most e(T). Let  .
.
It is evident that  and
and  . To verify that
. To verify that  is as desired, fix
is as desired, fix  . We must find
. We must find  such that \(y \subseteq z\). If there is \(j < \theta \) such that \(z \subseteq \kappa _j\), then there is
such that \(y \subseteq z\). If there is \(j < \theta \) such that \(z \subseteq \kappa _j\), then there is  such that \(y \subseteq z\), and we are done. Thus, suppose that z is unbounded in \(\kappa \). Then there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we have
such that \(y \subseteq z\), and we are done. Thus, suppose that z is unbounded in \(\kappa \). Then there is a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we have
-
 ;
; -
there is \(\xi _i < \kappa _i\) for which
 .
.
We can again find a stationary  and a fixed \(j < \theta \) such that \(\xi _i < \kappa _j\) for all \(i \in T'\). Let \(u = \{(i, \xi _i) \,{|}\, i \in T'\}\), and find
and a fixed \(j < \theta \) such that \(\xi _i < \kappa _j\) for all \(i \in T'\). Let \(u = \{(i, \xi _i) \,{|}\, i \in T'\}\), and find  such that \(w \subseteq u\). As before, the set
such that \(w \subseteq u\). As before, the set  is unbounded in \(\theta \); moreover, w is precisely \(\{(i, \xi _i) \,{|}\, i \in T''\}\). Therefore, \(y^*_w = \bigcup \,\{y_{i,{\xi _i}} \,{|}\, i \in T''\} \subseteq z\). It also follows exactly as in the previous case that \(y^*_w\) is unbounded in \(\kappa \) and is therefore an element of
is unbounded in \(\theta \); moreover, w is precisely \(\{(i, \xi _i) \,{|}\, i \in T''\}\). Therefore, \(y^*_w = \bigcup \,\{y_{i,{\xi _i}} \,{|}\, i \in T''\} \subseteq z\). It also follows exactly as in the previous case that \(y^*_w\) is unbounded in \(\kappa \) and is therefore an element of  .
.
Case 3: \(\mathfrak r_\kappa \). In this case, \(e(T) = \underline{d(\theta , \kappa )}\). Therefore, for each \(j < \theta \), we can fix as in the previous case a set  such that
such that  is dense in
is dense in  and
and  . Let
. Let  and, for each
and, for each  , let \(y^*_w = \bigcup \, \{y_{i, \xi } \,{|}\, (i,\xi ) \in w\}\). Finally, let
, let \(y^*_w = \bigcup \, \{y_{i, \xi } \,{|}\, (i,\xi ) \in w\}\). Finally, let  .
.
We claim that  is as desired. It is evident that
is as desired. It is evident that  and
and  . It remains to verify that no element of
. It remains to verify that no element of  splits every element of
splits every element of  . To this end, fix
. To this end, fix  . By assumption, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we can find \(\xi _i < \kappa _i\) such that either
. By assumption, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), we can find \(\xi _i < \kappa _i\) such that either  or
or  . We can also assume that, for all \(i \in C\), we have \(|z \cap \kappa _i |= \kappa _i\), and hence \(\pi _i(z) = z \cap \kappa _i\).
. We can also assume that, for all \(i \in C\), we have \(|z \cap \kappa _i |= \kappa _i\), and hence \(\pi _i(z) = z \cap \kappa _i\).
Find a stationary \(S_0 \subseteq C \cap T\) such that either
-
(1)
for all \(i \in S_0\),
 ; or
; or -
(2)
for all \(i \in S_0\),
 .
.
Without loss of generality, assume that (1) holds (the proof is symmetric if (2) holds). For each limit ordinal \(i \in S_0\), we can find \(j(i) < i\) such that  . Since \(S_0\) is a stationary subset of \(\theta \), we can therefore find a stationary \(S_1 \subseteq S_0\) and a fixed \(j < \theta \) such that \(j(i) = j\) for all \(i \in S_1\).
. Since \(S_0\) is a stationary subset of \(\theta \), we can therefore find a stationary \(S_1 \subseteq S_0\) and a fixed \(j < \theta \) such that \(j(i) = j\) for all \(i \in S_1\).
Let \(u = \{(i, \xi _i) \,{|}\, i \in S_1\}\). Then  , so we can find
, so we can find  such that \(w \subseteq u\). Note that \(\{i \in S_1 \,{|}\, (i, \xi _i) \in w\}\) must be unbounded in \(\theta \), so we have \(|y^*_w |= \kappa \), and hence
such that \(w \subseteq u\). Note that \(\{i \in S_1 \,{|}\, (i, \xi _i) \in w\}\) must be unbounded in \(\theta \), so we have \(|y^*_w |= \kappa \), and hence  . Moreover,
. Moreover,

Since  for all \(i \in S_1\) and \(\kappa _j > \theta = |S_1 |\), it follows that \(|y^*_w \cap z |\leqslant \kappa _j < \kappa \), so z does not split \(y^*_w\), i.e., we have \(z \rightsquigarrow y^*_w\), as desired.
for all \(i \in S_1\) and \(\kappa _j > \theta = |S_1 |\), it follows that \(|y^*_w \cap z |\leqslant \kappa _j < \kappa \), so z does not split \(y^*_w\), i.e., we have \(z \rightsquigarrow y^*_w\), as desired.
Case 4: \(\mathfrak d_\kappa \). In this case, \(e(T) = \underline{d_{\textrm{stat}} } (^{T} \kappa )\). Therefore, we can fix a family  such that
such that
-
 ;
; -
every element of
 is a function from a stationary subset of T to \(\kappa \) whose range is bounded below \(\kappa \);
is a function from a stationary subset of T to \(\kappa \) whose range is bounded below \(\kappa \); -
for every function g from a stationary subset of T to \(\kappa \) such that the range of g is bounded below \(\kappa \), there is a function
 such that
such that  is nonstationary in \(\theta \).
is nonstationary in \(\theta \).
Recall also that, for each \(i \in T\) and each \(\xi < \kappa _i\), we have \(y_{i, \xi } \in {^{\kappa _i}}i\).
For each  , define a function \(y^*_h \in {^\kappa }\theta \) as follows. Let
, define a function \(y^*_h \in {^\kappa }\theta \) as follows. Let  . Since the range of h is bounded below \(\kappa \), we know that, for all sufficiently large \(i \in T'\), we have \(h(i) < \kappa _i\), and hence \(y_{i, h(i)}\) is defined. Therefore, for all sufficiently large \(i \in T'\) and all \(\eta < \kappa _i\), we have \(y_{i, h(i)}(\eta ) < i\). Therefore, by Fodor’s lemma, for each \(\eta < \kappa \), we can find a \(j < \theta \) such that
. Since the range of h is bounded below \(\kappa \), we know that, for all sufficiently large \(i \in T'\), we have \(h(i) < \kappa _i\), and hence \(y_{i, h(i)}\) is defined. Therefore, for all sufficiently large \(i \in T'\) and all \(\eta < \kappa _i\), we have \(y_{i, h(i)}(\eta ) < i\). Therefore, by Fodor’s lemma, for each \(\eta < \kappa \), we can find a \(j < \theta \) such that

is stationary in \(\theta \). Let \(y^*_h(\eta )\) be the least such j.
Let  . We claim that
. We claim that  is as desired. It is evident that
is as desired. It is evident that  and
and  . It remains to verify that, for every
. It remains to verify that, for every  , there is
, there is  such that \(z \,{<}^* y\). To this end, fix
such that \(z \,{<}^* y\). To this end, fix  . By assumption, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is \(\xi _i < \kappa _i\) for which \(\pi _i(z) \,{<}^* y_{i, \xi _i}\). For each \(i \in C \cap T\), let
. By assumption, we can find a club \(C \subseteq \theta \) such that, for all \(i \in C \cap T\), there is \(\xi _i < \kappa _i\) for which \(\pi _i(z) \,{<}^* y_{i, \xi _i}\). For each \(i \in C \cap T\), let
and note that \(|E_i |< \kappa _i\). By two applications of Fodor’s lemma, we can find a \(j < \theta \) and a stationary \(T' \subseteq C \cap T\) such that  for all \(i \in T'\). Then the map from \(T'\) to \(\kappa \) defined by sending each \(i \in T'\) to \(\xi _i\) has range bounded below \(\kappa \), so we can find
for all \(i \in T'\). Then the map from \(T'\) to \(\kappa \) defined by sending each \(i \in T'\) to \(\xi _i\) has range bounded below \(\kappa \), so we can find  and a club \(D \subseteq \theta \) such that, letting
and a club \(D \subseteq \theta \) such that, letting  , the following statement holds: for all \(i \in D \cap T''\), we have \(i \in T'\) and \(h(i) = \xi _i\).
, the following statement holds: for all \(i \in D \cap T''\), we have \(i \in T'\) and \(h(i) = \xi _i\).
We claim that  . To see this, first let
. To see this, first let  , and note that
, and note that  . It therefore suffices to show that \(z(\eta ) < y^*_h(\eta )\) for all
. It therefore suffices to show that \(z(\eta ) < y^*_h(\eta )\) for all  . To this end, fix
. To this end, fix  . Fix \(\ell < \theta \) such that \(\eta < \kappa _\ell \) and \(z(\eta ) < \ell \). Then, for all
. Fix \(\ell < \theta \) such that \(\eta < \kappa _\ell \) and \(z(\eta ) < \ell \). Then, for all  , we have \(\pi _i(z)(\eta ) = z(\eta )\). Moreover, for all such i, we have \(\eta \notin E_i\), and hence \(z(\eta ) < y_{i, \xi _i}(\eta ) = y_{i, h(i)}(\eta )\). Recall that \(y^*_h(\eta )\) was defined in such a way that there is a stationary set
, we have \(\pi _i(z)(\eta ) = z(\eta )\). Moreover, for all such i, we have \(\eta \notin E_i\), and hence \(z(\eta ) < y_{i, \xi _i}(\eta ) = y_{i, h(i)}(\eta )\). Recall that \(y^*_h(\eta )\) was defined in such a way that there is a stationary set  such that \(y^*_h(\eta ) = y_{i, h(i)}(\eta )\) for all \(i \in T^*\). Since D is a club in \(\theta \), we can fix
such that \(y^*_h(\eta ) = y_{i, h(i)}(\eta )\) for all \(i \in T^*\). Since D is a club in \(\theta \), we can fix  . But then we have \(z(\eta ) < y_{i^*, h(i^*)}(\eta ) = y^*_h(\eta )\), as desired.\(\square \)
. But then we have \(z(\eta ) < y_{i^*, h(i^*)}(\eta ) = y^*_h(\eta )\), as desired.\(\square \)
Combining the results of this and the previous section, we obtain the precise statement of our main result.
MainTheorem
Suppose that
-
\(\kappa \) is a singular cardinal and
 ;
; -
\(\langle \kappa _i \,{|}\, i < \theta \rangle \) is an increasing, continuous sequence of cardinals converging to \(\kappa \);
-
\(\beta \) is an ordinal for which \(\varphi ^\theta _\beta \) exists;
-
\(S \subseteq \theta \) is stationary;
-
\(\mathfrak {cc}\) is one of the cardinal characteristics \(m(\theta , \kappa )\), \(d(\theta , \kappa )\), \(\mathfrak r_\kappa \), or \(\mathfrak d_\kappa \), and, for each \(i < \theta \), \(\mathfrak {cc}_i\) is the corresponding cardinal characteristic
 ,
, 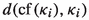 , \(\mathfrak r_{\kappa _i}\), or \(\mathfrak d_{\kappa _i}\);
, \(\mathfrak r_{\kappa _i}\), or \(\mathfrak d_{\kappa _i}\); -
for all \(i \in S\), we have \(\mathfrak {cc}_i \leqslant \kappa _i^{+\varphi ^\theta _\beta (i)}\).
Then:
-
(1)
If \(\mathfrak {cc} = m(\theta , \kappa )\), then \(\mathfrak {cc} \leqslant \kappa ^{+\beta } + \sum _{j < \theta } m(\theta , \kappa _j) + d(\textrm{NS}_\theta {\restriction }\, S)\). Moreover, if \(\beta < \omega \), then \(\mathfrak {cc} \leqslant \kappa ^{+\beta } + \sum _{j < \theta } m(\theta , \kappa _j)\).
-
(2)
If \(\mathfrak {cc} = d(\theta , \kappa )\) or \(\mathfrak {cc} = \mathfrak r_\kappa \), then \(\mathfrak {cc} \leqslant \kappa ^{+\beta } + \underline{d(\theta , \kappa )} + d(\textrm{NS}_\theta {\restriction }\, S)\). Moreover, if \(\beta < \omega \), then \(\mathfrak {cc} \leqslant \kappa ^{+\beta } + \underline{d(\theta , \kappa )}\).
-
(3)
If \(\mathfrak {cc} = \mathfrak d_\kappa \), then \(\mathfrak {cc} \leqslant \kappa ^{+\beta } + \underline{d_{\textrm{stat}}({^S}\kappa )}\).
Proof
This follows directly from Lemma 5.8 and Corollary 4.4.\(\square \)
6 Open questions
Throughout this section, \(\kappa \) will denote an arbitrary infinite cardinal. We feel that the most prominent cardinal characteristic at singular cardinals that is not covered by our results here is the ultrafilter number, a close relative of the reaping number.
Definition 6.1
The ultrafilter number \({\mathfrak {u}}_\kappa \) is the minimal size of a base for a uniform ultrafilter over \(\kappa \). In other words, it is the minimal cardinal \(\lambda \) for which there exists a uniform ultrafilter U over \(\kappa \) and a family  such that
such that  and, for all \(Y \in U\), there is
and, for all \(Y \in U\), there is  such that
such that  .
.
It is provable that \({\mathfrak {u}}_\kappa > \kappa \), and the ultrafilter number at singular cardinals has been extensively studied (cf. [6, 7, 9], among others).
Question 6.2
Does a version of our Main Theorem hold for the ultrafilter number?
We briefly mentioned the almost disjointness number in the introduction; we feel that some interesting questions can be formulated around it. We first recall the relevant definitions.
Definition 6.3
An almost disjoint family over \(\kappa \) is a family  such that, for all distinct
such that, for all distinct  , we have \(|A \cap B |< \kappa \). Such a family is a maximal almost disjoint family (MAD family) over \(\kappa \) if, moreover, there is no almost disjoint family
, we have \(|A \cap B |< \kappa \). Such a family is a maximal almost disjoint family (MAD family) over \(\kappa \) if, moreover, there is no almost disjoint family  over \(\kappa \) with
over \(\kappa \) with  .
.
There are trivial ways to form MAD families over \(\kappa \) (as an extreme case, \(\{\kappa \}\) is a MAD family over \(\kappa \)). The almost disjointness number \({\mathfrak {a}}_\kappa \) is defined to be the minimal cardinality of a nontrivial MAD family over \(\kappa \). It remains to specify what nontriviality means. The most natural solution seems to be to say that a MAD family is nontrivial if and only if its cardinality is greater than  (this is the approach taken, for instance, in [13]). Under this definition, it is not difficult to prove that
(this is the approach taken, for instance, in [13]). Under this definition, it is not difficult to prove that  . However, there always exist MAD families over \(\kappa \) of cardinality strictly greater than \(\kappa \), so one could also declare that a MAD family over \(\kappa \) is nontrivial if and only if its cardinality is greater than \(\kappa \). Let us denote the version of the almost disjointness number arising from this more stringent definition of nontriviality by \({\mathfrak {a}}^*_\kappa \).
. However, there always exist MAD families over \(\kappa \) of cardinality strictly greater than \(\kappa \), so one could also declare that a MAD family over \(\kappa \) is nontrivial if and only if its cardinality is greater than \(\kappa \). Let us denote the version of the almost disjointness number arising from this more stringent definition of nontriviality by \({\mathfrak {a}}^*_\kappa \).
Question 6.4
Does a version of our Main Theorem hold for \({\mathfrak {a}}^*_\kappa \)?
The most immediate specific incarnation of this question would be the following:
Question 6.5
Suppose that \(\kappa \) is a singular strong limit cardinal of uncountable cofinality and there is a stationary subset \(S \subseteq \kappa \) consisting of singular cardinals such that, for all \(\mu \in S\), there is a MAD family over \(\mu \) of cardinality \(\mu ^+\). Must there be a MAD family over \(\kappa \) of cardinality \(\kappa ^+\)?
Definition 6.6
A graph G is universal for graphs of size \(\kappa \) if, for every graph H with at most \(\kappa \)-many vertices, there is an induced subgraph of G that is isomorphic to H. Let \(\mathfrak {ug}_\kappa \) denote the minimal number of vertices in a graph G that is universal for graphs of size \(\kappa \).
Question 6.7
Does a version of our Main Theorem hold for \(\mathfrak {ug}_\kappa \)?
We are also interested in whether analogues of Silver’s theorem hold for statements that are not naturally formulated as statements about cardinal characteristics but which are consequences of \(2^\kappa = \kappa ^+\). We record here some particularly prominent examples.
Definition 6.8
The polarized partition relation \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\) is the assertion that, for every function  , there are sets \(A \in [\kappa ^+]^{\kappa ^+}\) and \(B \in [\kappa ]^{\kappa }\) such that \(c \,{\restriction }\, A \times B\) is constant. The negation of this relation is denoted by \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \not \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\).
, there are sets \(A \in [\kappa ^+]^{\kappa ^+}\) and \(B \in [\kappa ]^{\kappa }\) such that \(c \,{\restriction }\, A \times B\) is constant. The negation of this relation is denoted by \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \not \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\).
Erdős, Hajnal, and Rado prove in [3] that, if \(2^\kappa = \kappa ^+\), then \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \not \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\). On the other hand, Garti and Shelah prove in [5] that, assuming the consistency of a supercompact cardinal, the positive relation \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\) consistently holds for a singular strong limit cardinal \(\kappa \) (in their result, \(\kappa \) can have either countable or uncountable cofinality).
Question 6.9
Suppose that \(\kappa \) is a singular cardinal of uncountable cofinality and there is a stationary set \(S \subseteq \kappa \) consisting of singular cardinals such that, for all \(\mu \in S\), we have \(\left( {\begin{matrix} \mu ^{+} \\ \mu \end{matrix}}\right) \not \rightarrow \left( {\begin{matrix} \mu ^+ \\ \mu \end{matrix}}\right) ^{1,1}_2\). Must it be the case that \(\left( {\begin{matrix} \kappa ^{+} \\ \kappa \end{matrix}}\right) \not \rightarrow \left( {\begin{matrix} \kappa ^+ \\ \kappa \end{matrix}}\right) ^{1,1}_2\)?
In an early draft of this paper, we included here a question about Aronszajn trees at double successors of singular cardinals. We then realized that existing work of Golshani and Mohammadpour [8] provides an answer to this question, so we give a very brief account of this here.
Recall that, for a regular uncountable cardinal \(\lambda \), a \(\lambda \)-Aronszajn tree is a tree of height \(\lambda \) with no levels or branches of cardinality \(\lambda \). If \(\lambda = \mu ^+\), then a \(\lambda \)-Aronszajn tree T is special if there is a function \(f:T \rightarrow \lambda \) that is injective on chains. Note that a special \(\mu ^+\)-Aronszajn tree remains special in any outer model in which \(\mu ^+\) is preserved. By a result of Specker [22], if \(\mu \) is regular and  , then there is a special \(\mu ^+\)-Aronszajn tree. In particular, if \(2^\kappa = \kappa ^+\), then there is a \(\kappa ^{++}\)-Aronszajn tree. Therefore, the nonexistence of Aronszajn trees at the double successor of a singular strong limit cardinal requires a failure of the Singular Cardinals Hypothesis. In an earlier draft of this paper, we asked whether the existence of \(\kappa ^{++}\)-Aronszajn trees satisfies a version of Silver’s theorem. Here, we give a consistent negative answer to this question that follows almost immediately from the work in [8].
, then there is a special \(\mu ^+\)-Aronszajn tree. In particular, if \(2^\kappa = \kappa ^+\), then there is a \(\kappa ^{++}\)-Aronszajn tree. Therefore, the nonexistence of Aronszajn trees at the double successor of a singular strong limit cardinal requires a failure of the Singular Cardinals Hypothesis. In an earlier draft of this paper, we asked whether the existence of \(\kappa ^{++}\)-Aronszajn trees satisfies a version of Silver’s theorem. Here, we give a consistent negative answer to this question that follows almost immediately from the work in [8].
Theorem 6.10
Suppose that \(\kappa \) is supercompact and \(\lambda > \kappa \) is measurable. Then there is a forcing extension in which \(\kappa \) is a singular cardinal of uncountable cofinality, there are \(\mu ^{++}\)-Aronszajn trees for all \(\mu < \kappa \), but there are no \(\kappa ^{++}\)-Aronszajn trees.
Proof sketch
We can assume that \(\textsf{GCH}\) holds in V. Therefore, by the aforementioned result of Specker, there is a special \(\mu ^{++}\)-Aronszajn tree for all \(\mu \). By the techniques of [15], we can arrange so that the supercompactness of \(\kappa \) is preserved after adding any number of Cohen subsets to \(\kappa \) by forcing with an Easton-support iteration of length \(\kappa \) with the property that, for all \(\alpha < \kappa \), either the \(\alpha ^{\textrm{th}}\) iterand is forced to be trivial or \(\alpha \) is inaccessible and the \(\alpha ^{\textrm{th}}\) iterand is forced to be of the form  for some \(\beta < \kappa \). Moreover, this iteration can be defined so that it preserves all cardinals. (More precisely, we can let \(f:\kappa \rightarrow V_\kappa \) be a Laver function and, for all \(\alpha < \kappa \), let the \(\alpha ^{\textrm{th}}\) iterand be forced to be trivial unless \(\alpha \) is inaccessible, \(f(\alpha )\) is a cardinal, and \(f[\alpha ] \subseteq V_\alpha \), in which case the \(\alpha ^{\textrm{th}}\) iterand is forced to be
for some \(\beta < \kappa \). Moreover, this iteration can be defined so that it preserves all cardinals. (More precisely, we can let \(f:\kappa \rightarrow V_\kappa \) be a Laver function and, for all \(\alpha < \kappa \), let the \(\alpha ^{\textrm{th}}\) iterand be forced to be trivial unless \(\alpha \) is inaccessible, \(f(\alpha )\) is a cardinal, and \(f[\alpha ] \subseteq V_\alpha \), in which case the \(\alpha ^{\textrm{th}}\) iterand is forced to be  .)
.)
Let \(V_1\) be the extension of V by this forcing iteration. Since V and \(V_1\) have the same cardinals, it remains true in \(V_1\) that there is a special \(\mu ^{++}\)-Aronszajn tree for all \(\mu \). Moreover, in \(V_1\) it is the case that the supercompactness of \(\kappa \) is preserved after adding any number of Cohen subsets to \(\kappa \).
Let \(\delta < \kappa \) be a regular uncountable cardinal. By the results of [8] (in particular the results of Sects. 4 and 5 of that paper), there is in \(V_1\) a forcing notion \(\mathbb {R}\) with the following properties:
-
\(\mathbb {R}\) preserves all cardinals below \(\kappa ^+\);
-
 ;
; -
\(V_1^{\mathbb {R}} \models 2^\kappa = \lambda = \kappa ^{++}\);
-
\(V_1^{\mathbb {R}} \models \text {there are no } \kappa ^{++}\text {-Aronszajn trees}\).
Since \(\mathbb {R}\) preserves all cardinals below \(\kappa ^+\), it remains true in \(V_1^{\mathbb {R}}\) that there is a special \(\mu ^{++}\)-Aronszajn tree for all \(\mu < \kappa \). Therefore, \(V_1^{\mathbb {R}}\) is the desired forcing extension.\(\square \)
References
Baumgartner, J.E., Prikry, K.: On a theorem of Silver. Discrete Math. 14(1), 17–21 (1976)
Blass, A.: Combinatorial cardinal characteristics of the continuum. In: Foreman, M., Kanamori, A. (eds.) Handbook of Set Theory, vols. 1, 2, 3, pp. 395–489. Springer, Dordrecht (2010)
Erdős, P., Hajnal, A., Rado, R.: Partition relations for cardinal numbers. Acta Math. Acad. Sci. Hungar. 16, 93–196 (1965)
Galvin, F., Hajnal, A.: Inequalities for cardinal powers. Ann. Math. 101(3), 491–498 (1975)
Garti, S., Shelah, S.: A strong polarized relation. J. Symbolic Logic 77(3), 766–776 (2012)
Garti, S., Shelah, S.: The ultrafilter number for singular cardinals. Acta Math. Hungar. 137(4), 296–301 (2012)
Garti, S., Shelah, S.: Remarks on generalized ultrafilter, dominating and reaping numbers. Fund. Math. 250(2), 101–115 (2020)
Golshani, M., Mohammadpour, R.: The tree property at double successors of singular cardinals of uncountable cofinality. Ann. Pure Appl. Logic 169(2), 164–175 (2018)
Honzik, R., Stejskalová, Š: Small \({\mathfrak{u} }(\kappa )\) at singular \(\kappa \) with compactness at \(\kappa ^{++}\). Arch. Math. Logic 61(1–2), 33–54 (2022)
Jech, T.: A variation on a theorem of Galvin and Hajnal. Bull. London Math. Soc. 25(2), 97–103 (1993)
Jech, T.: Set Theory, 3rd edn. Springer Monographs in Mathematics. Springer, Berlin (2003)
Kojman, M.: On the arithmetic of density. Topol. Appl. 213, 145–153 (2016)
Kojman, M., Kubiś, W., Shelah, S.: On two problems of Erdős and Hechler: new methods in singular madness. Proc. Amer. Math. Soc. 132(11), 3357–3365 (2004)
Krueger, J., Schimmerling, E.: An equiconsistency result on partial squares. J. Math. Log. 11(1), 29–59 (2011)
Laver, R.: Making the supercompactness of \(\kappa \) indestructible under \(\kappa \)-directed closed forcing. Israel J. Math. 29(4), 385–388 (1978)
Matet, P.: Meeting numbers and pseudopowers. MLQ Math. Log. Q. 67(1), 59–76 (2021)
Matet, P.: Towers and clubs. Arch. Math. Logic 60(6), 683–719 (2021)
Rinot, A.: On the consistency strength of the Milner–Sauer conjecture. Ann. Pure Appl. Logic 140(1–3), 110–119 (2006)
Shelah, S.: Cardinal Arithmetic. Oxford Logic Guides, vol. 29. The Clarendon Press, New York (1994)
Shelah, S.: On \({\mathfrak{d} }_\mu \) for \(\mu \) singular. Acta Math. Hungar. 161(1), 245–256 (2020)
Silver, J.: On the singular cardinals problem. In: Proceedings of the International Congress of Mathematicians (Vancouver, B. C., 1974), Vol. 1, pp. 265–268. Canadian Mathematical Congress, Montreal (1975)
Specker, E.: Sur un problème de Sikorski. Colloq. Math. 2, 9–12 (1949)
Acknowledgements
The results of this paper were presented at the Bar-Ilan University Set Theory Seminar in June 2022. We thank the organizers for the invitation and the seminar’s participants for a number of insightful questions and comments. We thank Moti Gitik for valuable conversations regarding Theorem 6.10. Finally, we thank the anonymous referee for their suggestions and corrections.
Funding
Open access publishing supported by the National Technical Library in Prague.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author was supported by the Czech Academy of Sciences (RVO 67985840).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lambie-Hanson, C. A Galvin–Hajnal theorem for generalized cardinal characteristics. European Journal of Mathematics 9, 12 (2023). https://doi.org/10.1007/s40879-023-00610-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40879-023-00610-7




 , where, given
, where, given  , where, given
, where, given  , where, given
, where, given  , we let
, we let  .
. ;
; for all
for all  ,
,  ;
; is a function from a stationary subset of S to
is a function from a stationary subset of S to  such that the set
such that the set 
 ;
;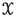 is a set and
is a set and  ;
; is a set and
is a set and  ;
;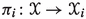 is a function;
is a function; and
and  are such that
are such that  and
and  for all
for all  for all
for all  , there is a club
, there is a club  for which
for which  such that
such that  and, for all
and, for all  , there is
, there is  for which
for which  is stationary in
is stationary in  and
and 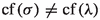 .
. .
.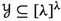 is unreaped if there is no single
is unreaped if there is no single  .
. such that for every
such that for every  such that
such that  such that, for every
such that, for every  such that
such that 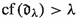 .
. .
. .
. .
. ;
;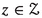 , there is a club
, there is a club 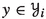 for which
for which 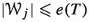 ;
; , there is
, there is  such that
such that  , and hence
, and hence  ;
;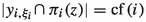 .
. ;
; .
. ; or
; or .
. ;
; is a function from a stationary subset of T to
is a function from a stationary subset of T to  such that
such that  is nonstationary in
is nonstationary in  ;
; ,
, 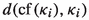 ,
,  ;
;